Removing Time Dispersion from Elastic Wave Modeling with the pix2pix Algorithm Based on cGAN
Abstract
1. Introduction
2. Theory and Method
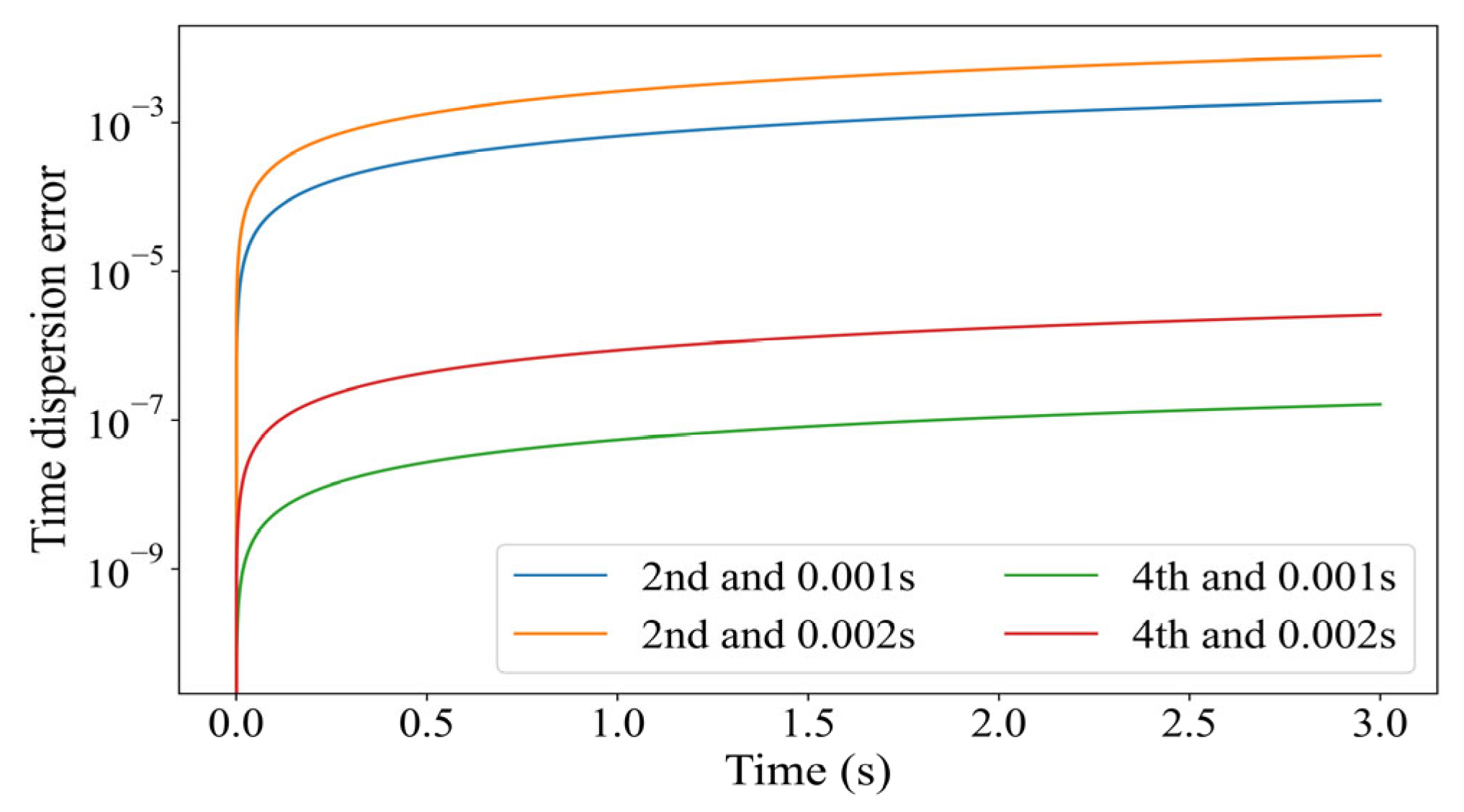
2.1. Time Dispersion Analysis
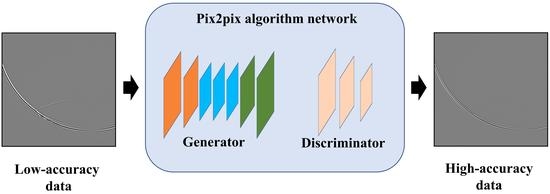
2.2. The Improvement of pix2pix Algorithm Based on cGAN
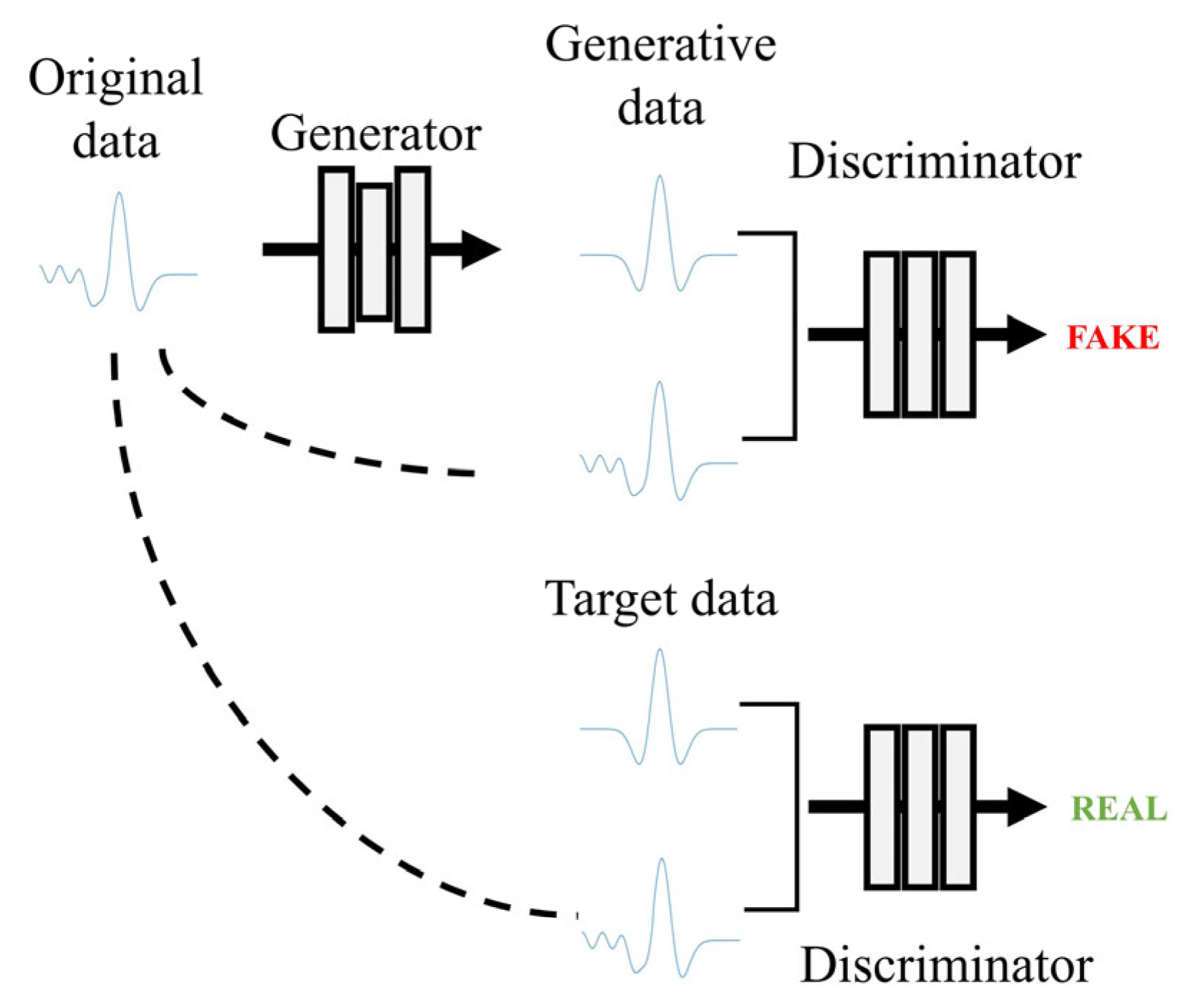
2.2.1. Loss Function
2.2.2. Generator
2.2.3. Discriminator
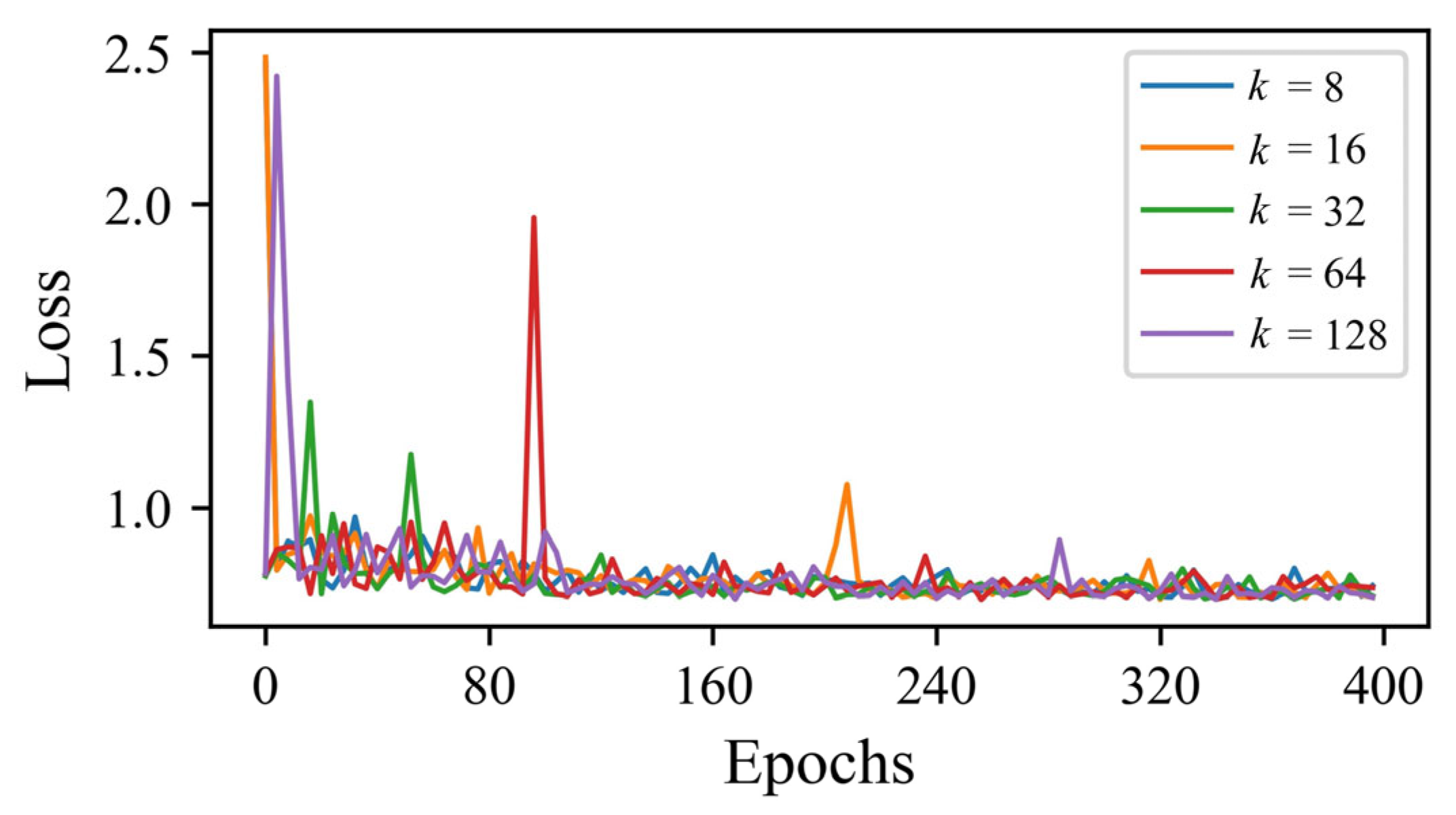
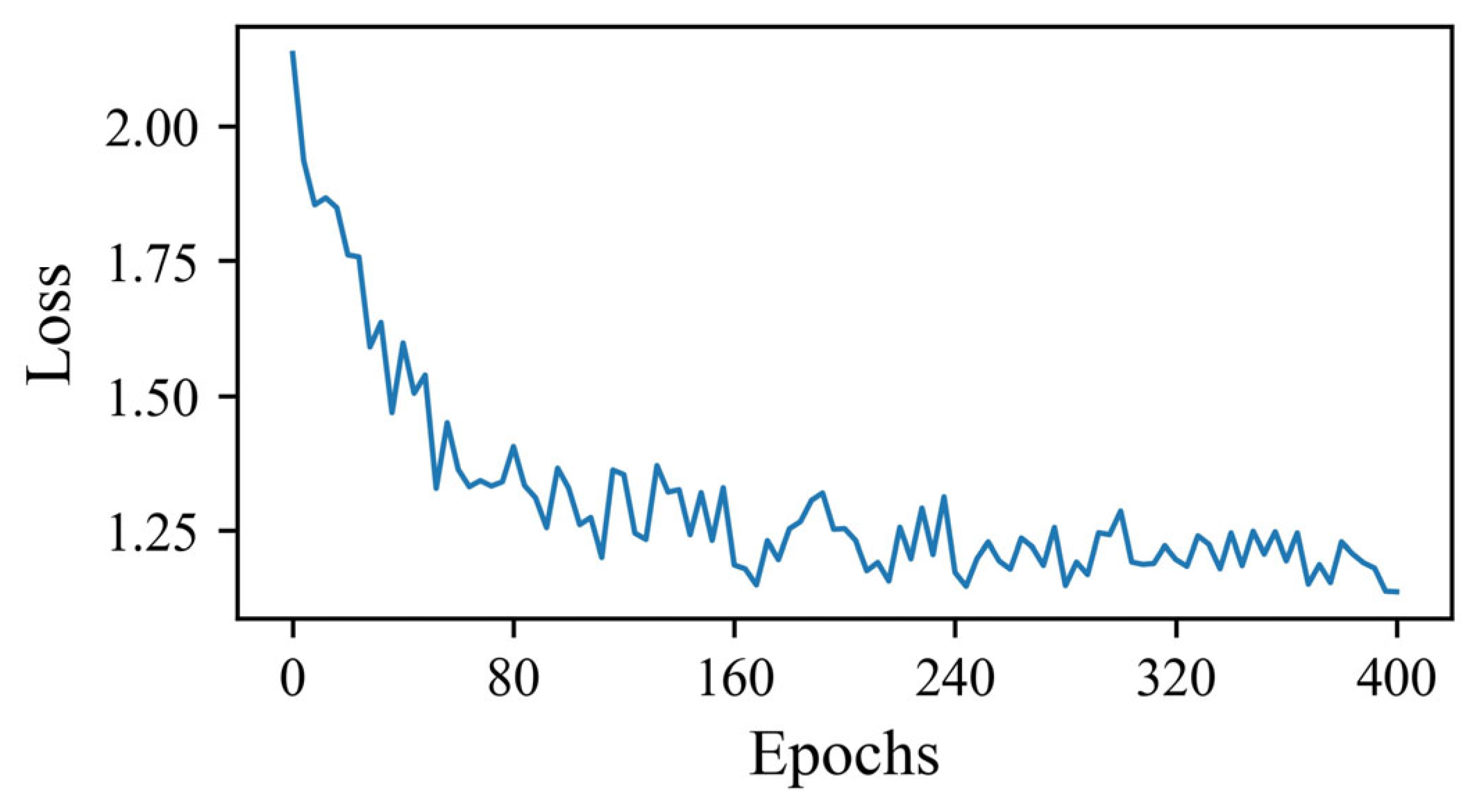
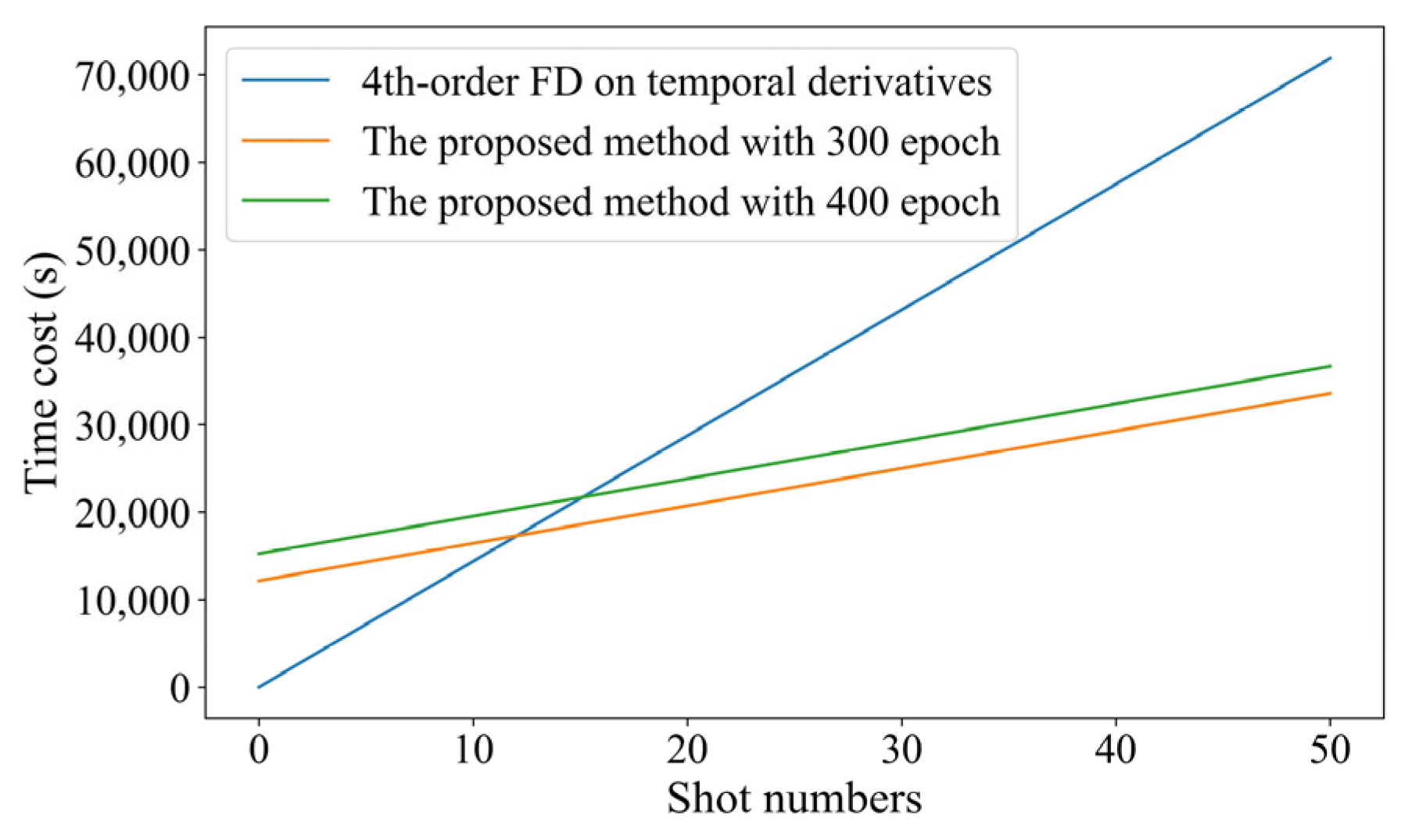
2.3. Training Set Size
3. Numerical Experiments
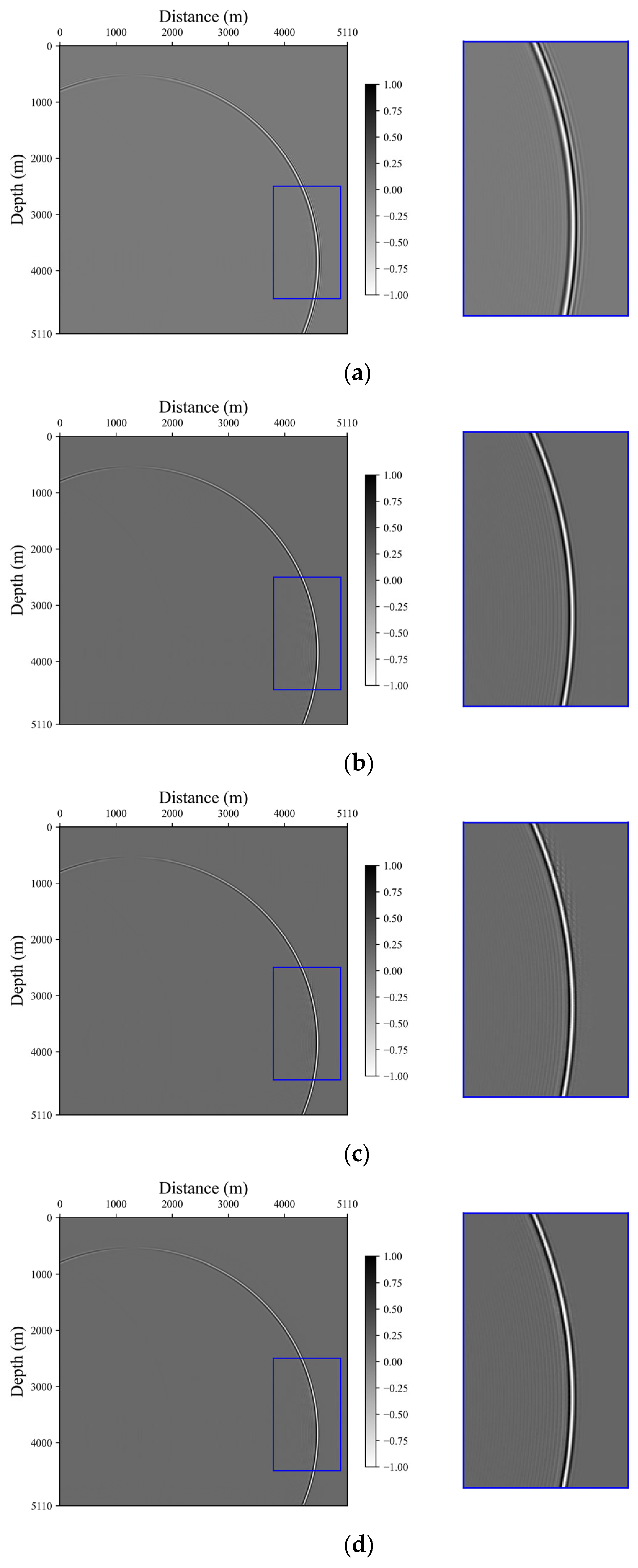
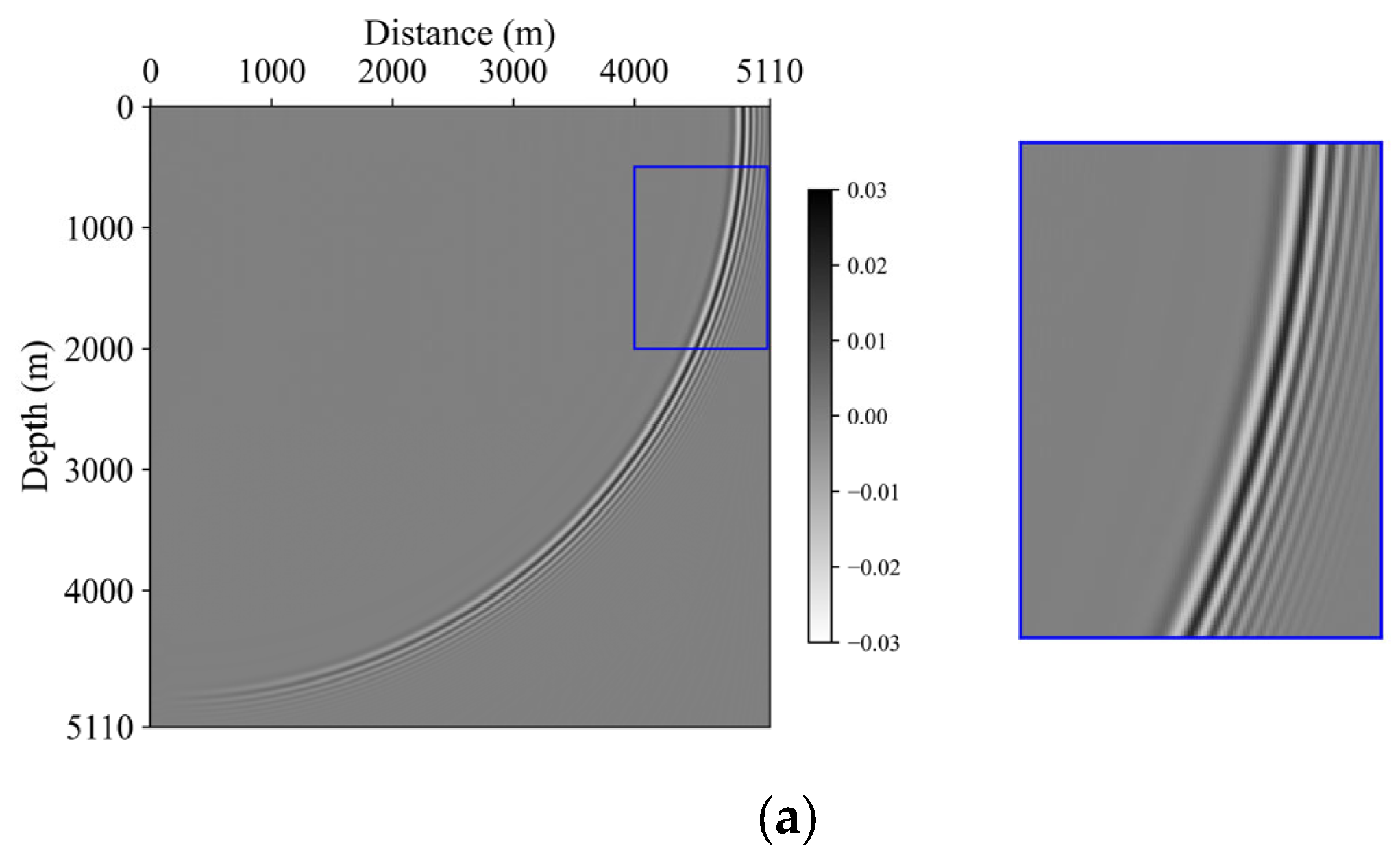
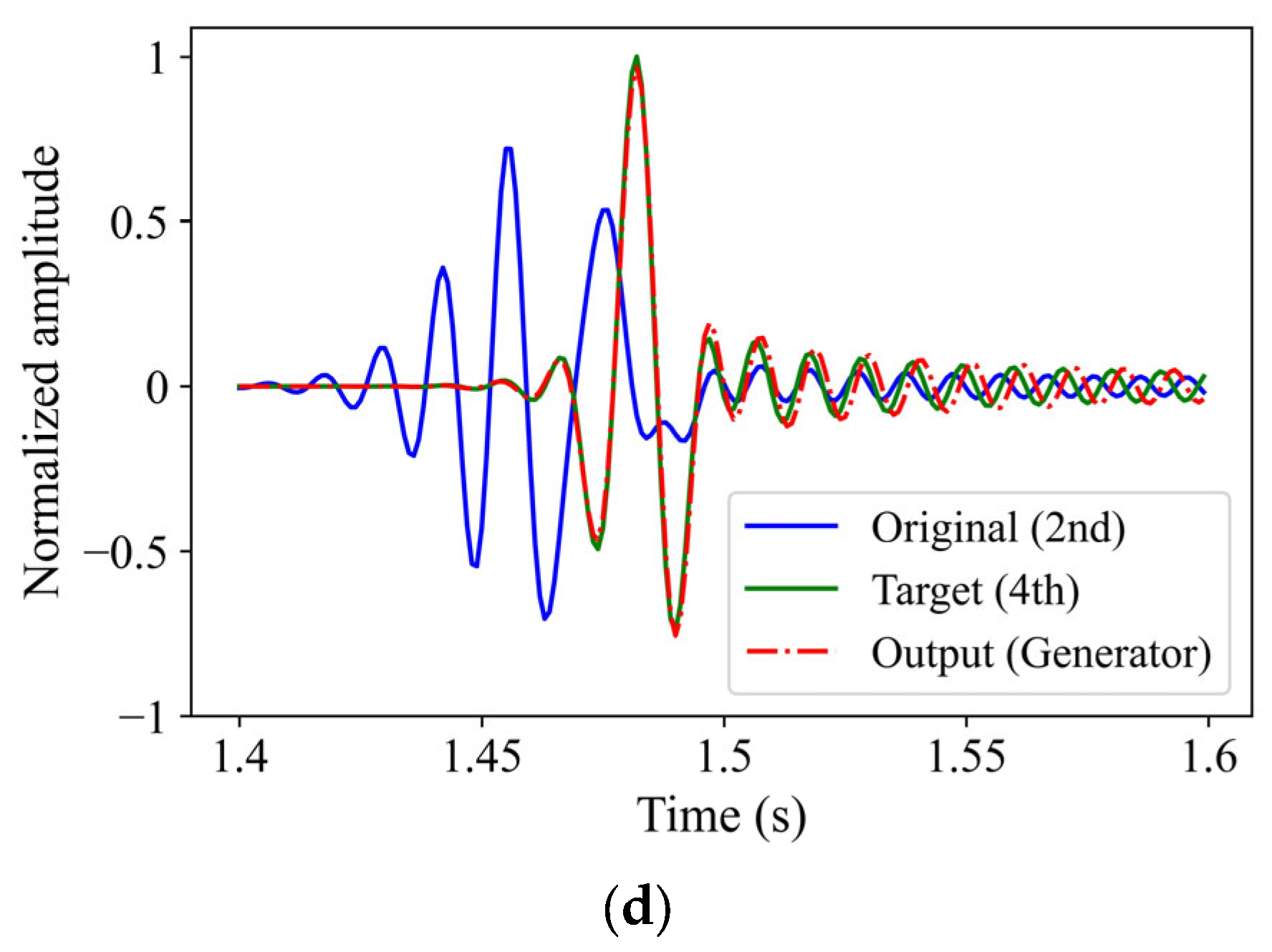
3.1. Homogeneous Model
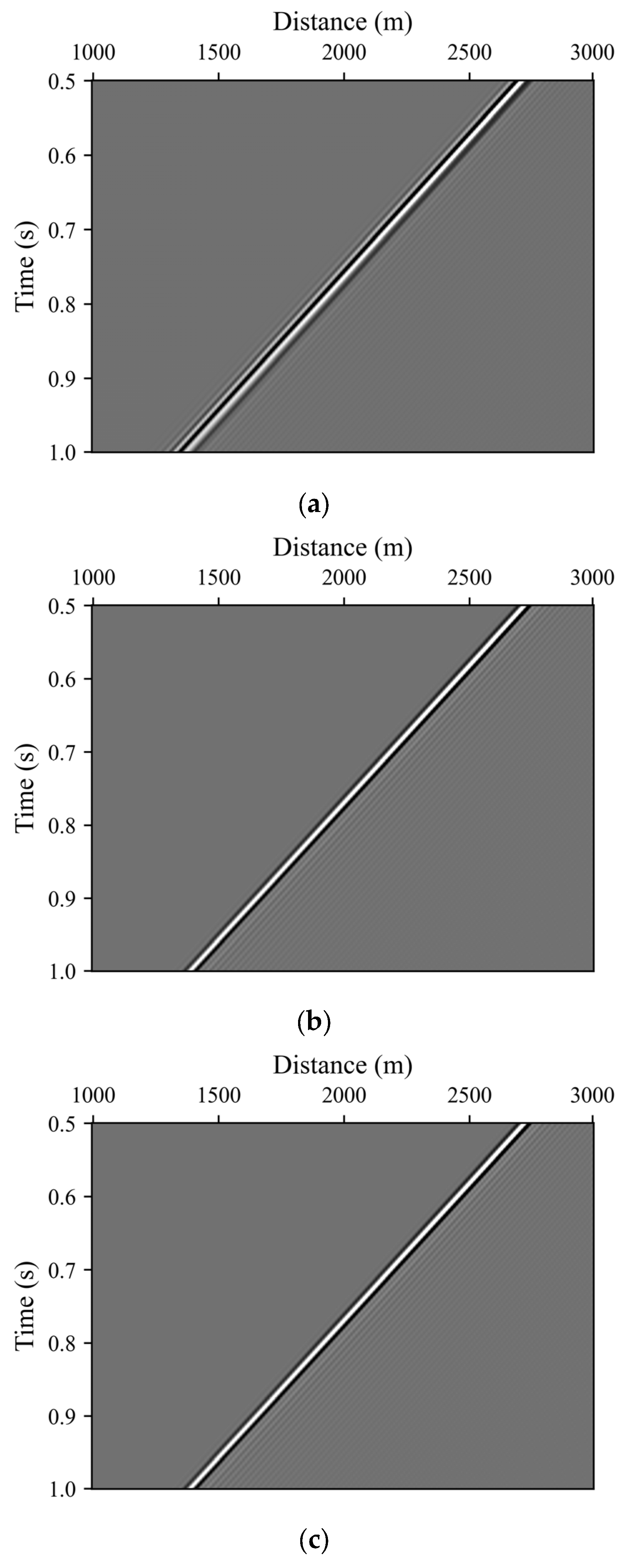
3.2. Two-Layer Model
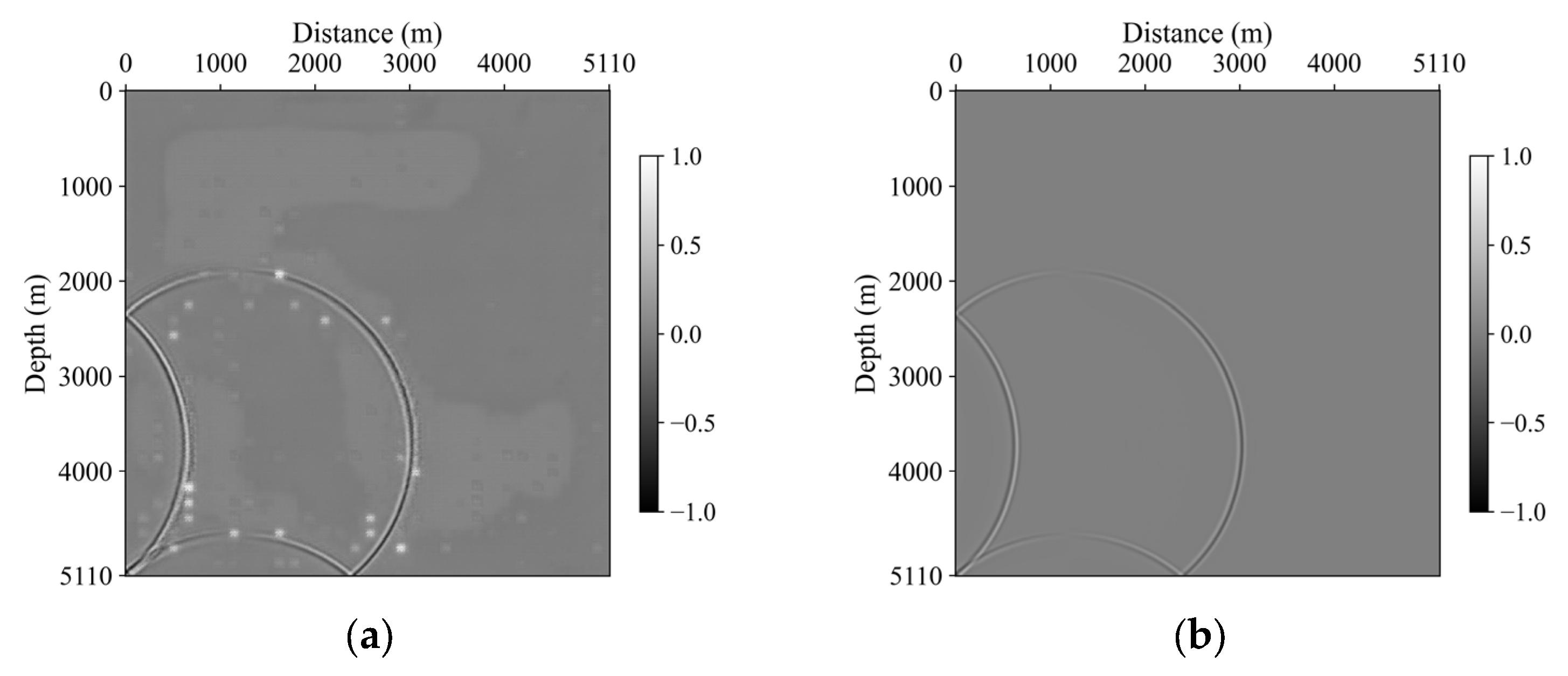
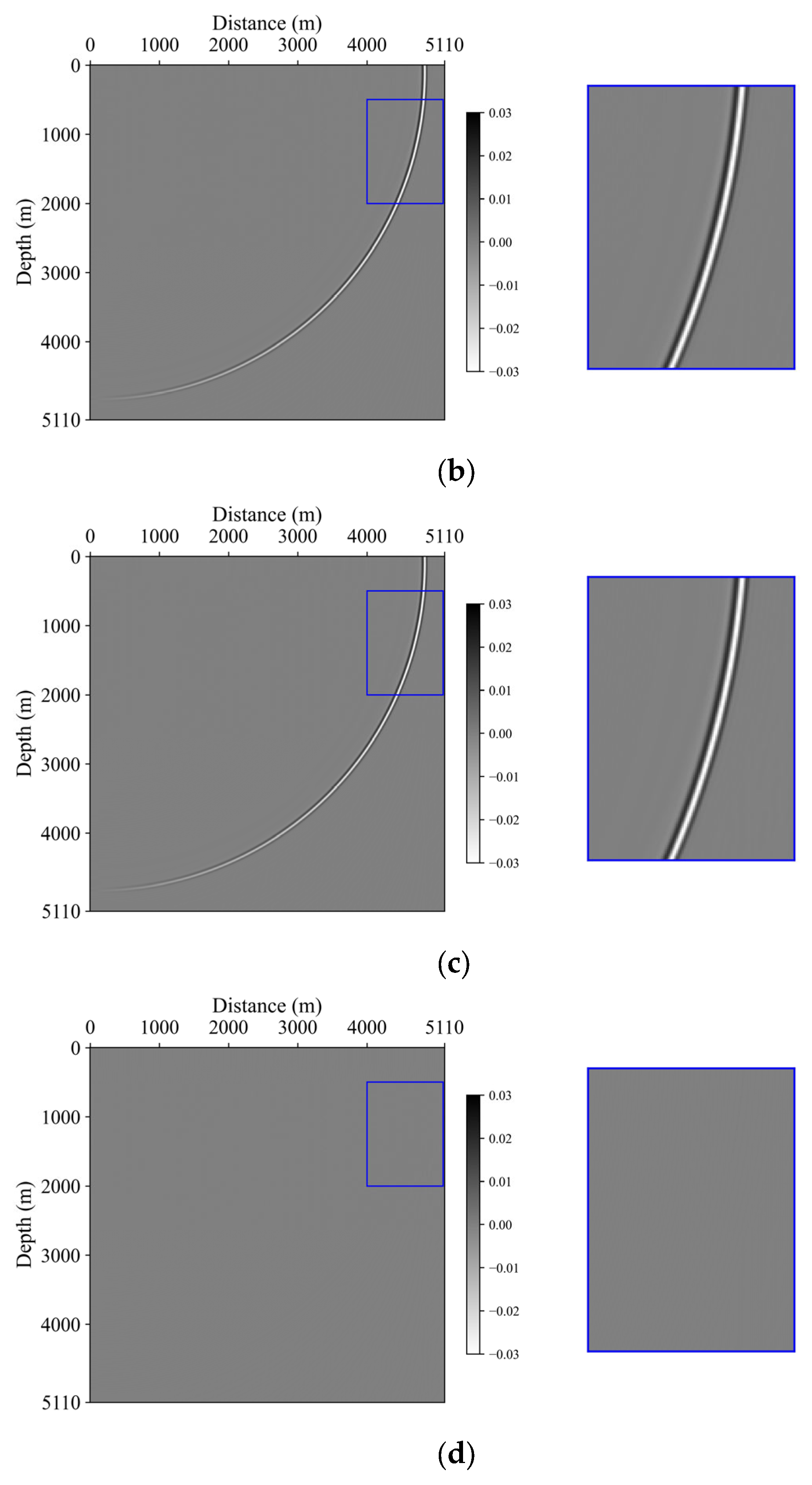
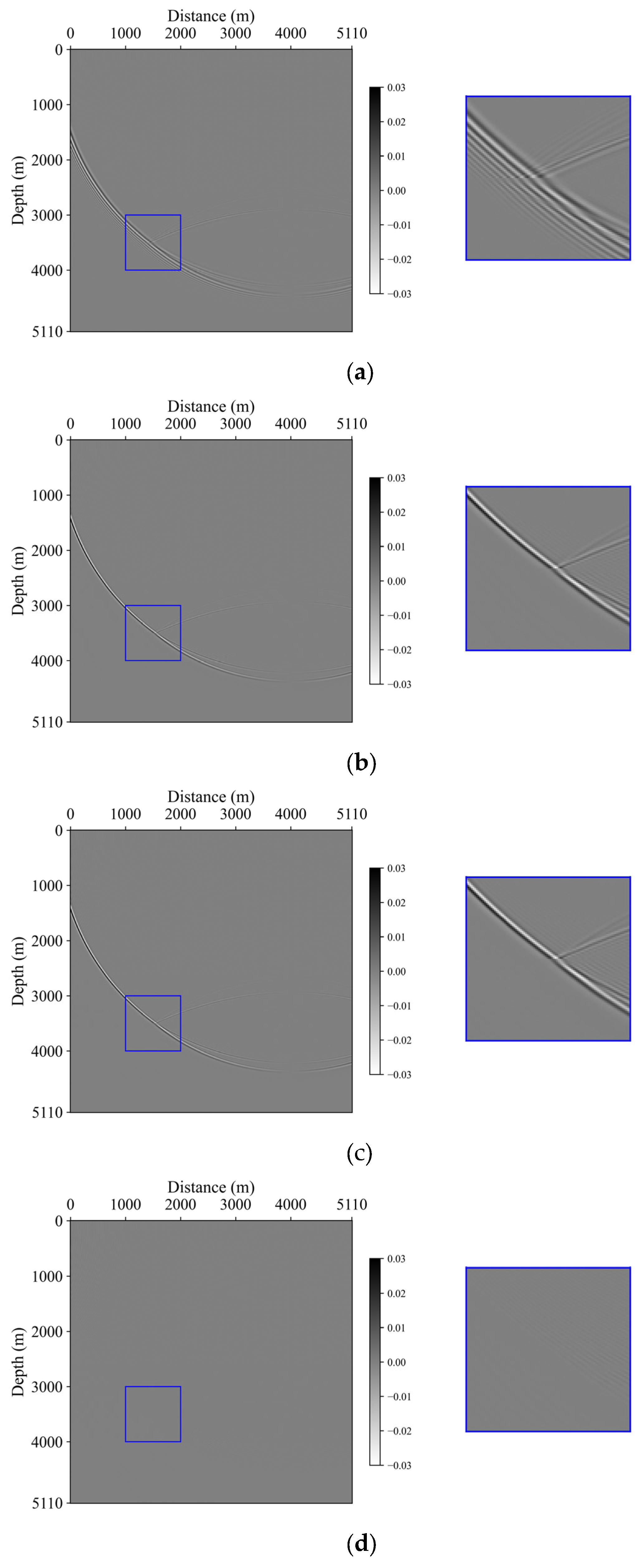
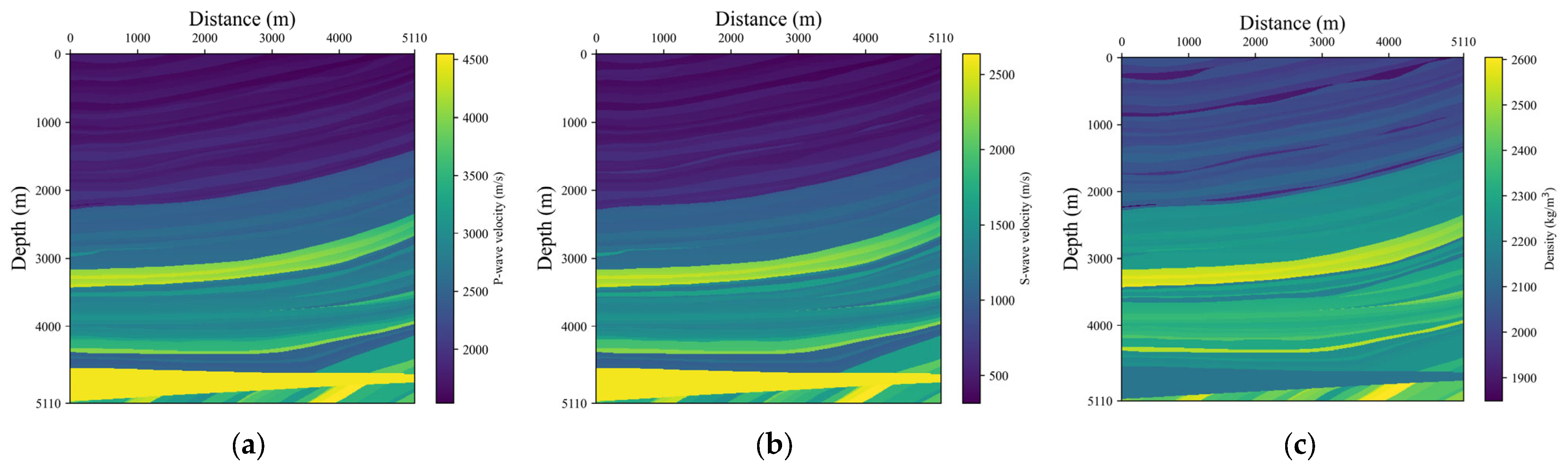
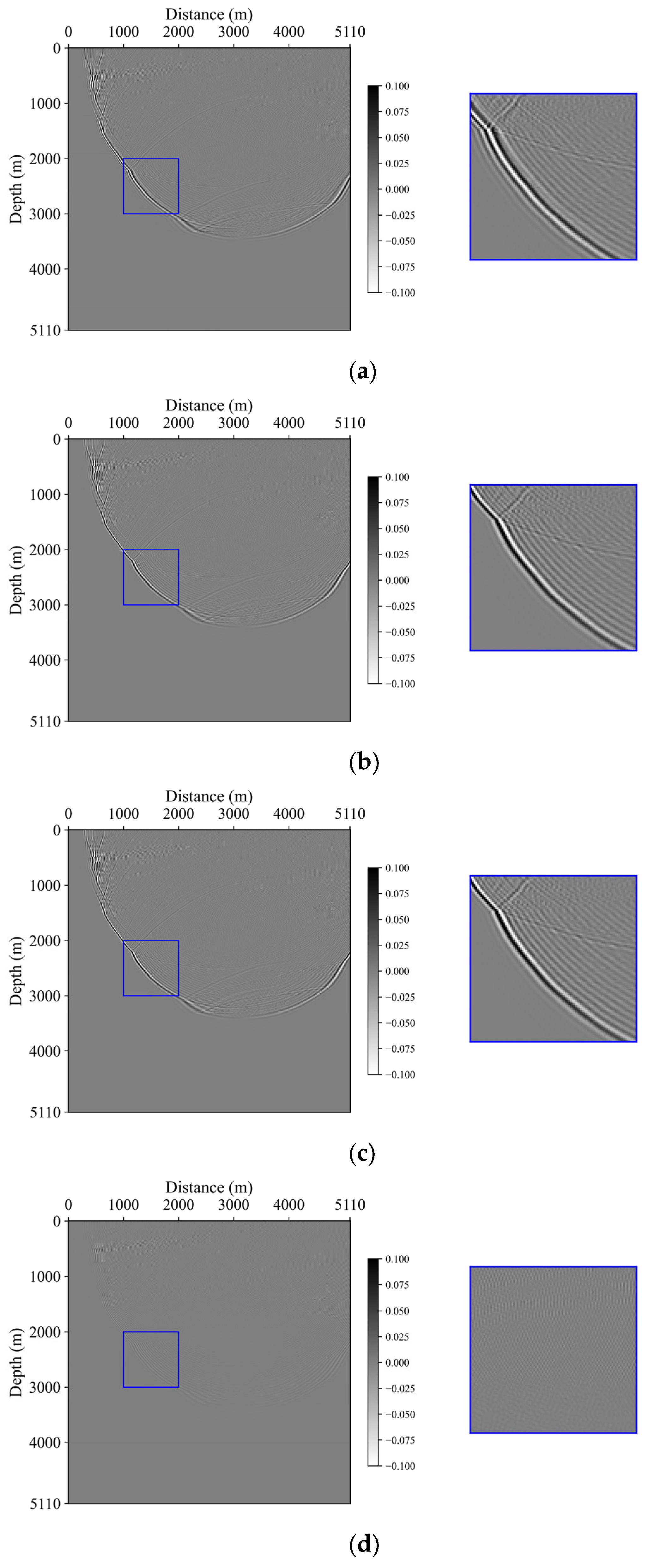
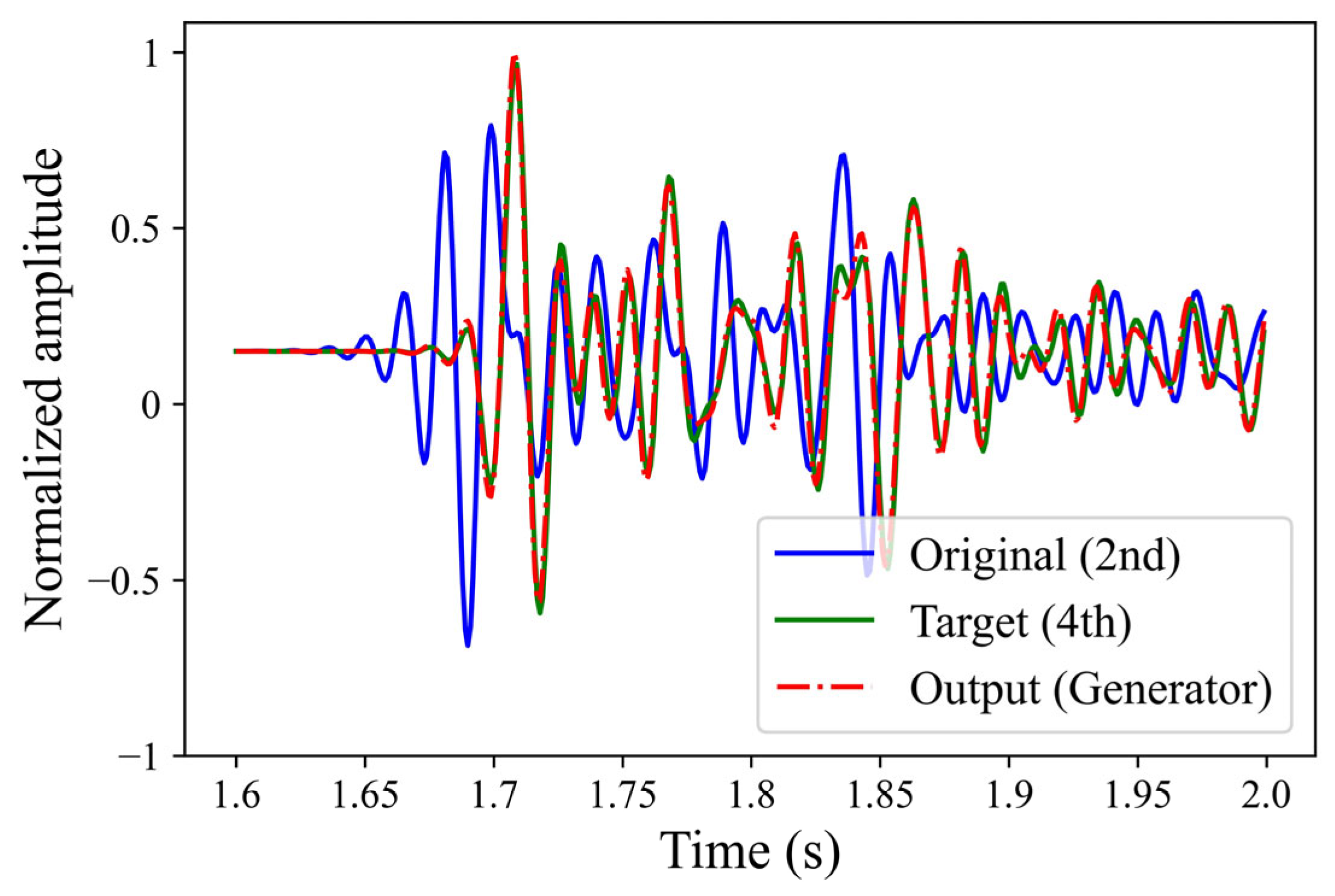
3.3. Marmousi Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Takougang, E.M.T.; Ali, M.Y.; Bouzidi, Y.; Bouchaala, F.; Sultan, A.A.; Mohamed, A.I. Characterization of a carbonate reservoir using elastic full-waveform inversion of vertical seismic profile data. Geophys. Prospect. 2020, 68, 1944–1957. [Google Scholar] [CrossRef]
- Pei, Z.; Mu, Y. Numerical simulation of seismic wave propagation. Prog. Geophys. 2004, 19, 933–941. [Google Scholar]
- Alterman, Z.; Karal, F., Jr. Propagation of elastic waves in layered media by finite difference methods. Bull. Seismol. Soc. Am. 1968, 58, 367–398. [Google Scholar]
- Lysmer, J.; Drake, L.A. A finite element method for seismology. Methods Comput. Phys. 1972, 11, 181–216. [Google Scholar]
- Kosloff, D.D.; Baysal, E. Forward modeling by a Fourier method. Geophysics 1982, 47, 1402–1412. [Google Scholar] [CrossRef]
- Kristek, J.; Moczo, P.; Chaljub, E.; Kristekova, M. A discrete representation of a heterogeneous viscoelastic medium for the finite-difference modelling of seismic wave propagation. Geophys. J. Int. 2019, 217, 2021–2034. [Google Scholar] [CrossRef]
- Matsushima, J.; Ali, M.Y.; Bouchaala, F. Propagation of waves with a wide range of frequencies in digital core samples and dynamic strain anomaly detection: Carbonate rock as a case study. Geophys. J. Int. 2021, 224, 340–354. [Google Scholar] [CrossRef]
- Dong, G. Dispersive problem in seismic wave propagation numerical modeling. Nat. Gas Ind. 2004, 24, 53–56. [Google Scholar]
- Tal-Ezer, H. Spectral methods in time for hyperbolic equations. SIAM J. Numer. Anal. 1986, 23, 11–26. [Google Scholar] [CrossRef]
- Ren, Z.; Bao, Q.; Gu, B. Time-dispersion correction for arbitrary even-order Lax-Wendroff methods and the application on full-waveform inversionTime-dispersion correction. Geophysics 2021, 86, T361–T375. [Google Scholar] [CrossRef]
- Stork, C. Eliminating nearly all dispersion error from FD modeling and RTM with minimal cost increase. In Proceedings of the 75th EAGE Conference & Exhibition incorporating SPE EUROPEC 2013, London, UK, 10–13 June 2013. [Google Scholar]
- Dai, N.; Wu, W.; Liu, H. Solutions to numerical dispersion error of time FD in RTM. In SEG Technical Program Expanded Abstracts 2014; Society of Exploration Geophysicists: Houston, TX, USA, 2014; pp. 4027–4031. [Google Scholar]
- Wang, M.; Xu, S. Finite-difference time dispersion transforms for wave propagation. Geophysics 2015, 80, WD19–WD25. [Google Scholar] [CrossRef]
- Li, Y.E.; Wong, M.; Clapp, R. Equivalent accuracy at a fraction of the cost: Overcoming temporal dispersion. Geophysical 2016, 81, T189–T196. [Google Scholar] [CrossRef]
- Koene, E.F.M.; Robertsson, J.O.A.; Broggini, F.; Andersson, F. Eliminating time dispersion from seismic wave modeling. Geophys. J. Int. 2018, 213, 169–180. [Google Scholar] [CrossRef]
- Xu, Z.; Jiao, K.; Cheng, X.; Sun, D.; King, R.; Nichols, D.; Vigh, D. Time-dispersion filter for finite-difference modeling and reverse time migration. In Proceedings of the 2017 SEG International Exposition and Annual Meeting, Houston, TX, USA, 24–27 September 2017. [Google Scholar]
- Amundsen, L.; Pedersen, Ø. Elimination of temporal dispersion from the finite-difference solutions of wave equations in elastic and anelastic models. Geophysics 2019, 84, T47–T58. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J. Deep learning for geophysics: Current and future trends. Rev. Geophys. 2021, 59, e2021RG000742. [Google Scholar] [CrossRef]
- Moseley, B.; Nissen-Meyer, T.; Markham, A. Deep learning for fast simulation of seismic waves in complex media. Solid Earth 2020, 11, 1527–1549. [Google Scholar] [CrossRef]
- Wei, W.; Fu, L.-Y. Small-data-driven fast seismic simulations for complex media using physics-informed Fourier neural operators. Geophysics 2022, 87, T435–T446. [Google Scholar] [CrossRef]
- Rasht-Behesht, M.; Huber, C.; Shukla, K.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for wave propagation and full waveform inversions. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023120. [Google Scholar] [CrossRef]
- Kaur, H.; Fomel, S.; Pham, N. Overcoming numerical dispersion of finite-difference wave extrapolation using deep learning. In Proceedings of the SEG Technical Program Expanded Abstracts 2019, San Antonio, TX, USA, 15–20 September 2019; pp. 2318–2322. [Google Scholar]
- Han, Y.; Wu, B.; Yao, G.; Ma, X.; Wu, D. Eliminate time dispersion of seismic wavefield simulation with semi-supervised deep learning. Energies 2022, 15, 7701. [Google Scholar] [CrossRef]
- Siahkoohi, A.; Louboutin, M.; Herrmann, F.J. The importance of transfer learning in seismic modeling and imaging. Geophysics 2019, 84, A47–A52. [Google Scholar] [CrossRef]
- Gadylshin, K.; Vishnevsky, D.; Gadylshina, K.; Lisitsa, V. Numerical dispersion mitigation neural network for seismic modeling. Geophysics 2022, 87, T237–T249. [Google Scholar] [CrossRef]
- Virieux, J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics 1986, 51, 889–901. [Google Scholar] [CrossRef]
- Baysal, E.; Kosloff, D.D.; Sherwood, J.W.C. Reverse time migration. Geophysics 1983, 48, 1514–1524. [Google Scholar] [CrossRef]
- Stepanishen, P.; Ebenezer, D. A joint wavenumber-time domain technique to determine the transient acoustic radiation loading on planar vibrators. J. Sound Vib. 1992, 157, 451–465. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Neural Information Processing Systems 2014, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Arjovsky, M.; Bottou, L. Towards principled methods for training generative adversarial networks. arXiv 2017, arXiv:1701.04862. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Pan, W.; Torres-Verdín, C.; Pyrcz, M.J. Stochastic pix2pix: A new machine learning method for geophysical and well conditioning of rule-based channel reservoir models. Nat. Resour. Res. 2021, 30, 1319–1345. [Google Scholar] [CrossRef]
- Guo, L.; Song, G.; Wu, H. Complex-valued Pix2pix—Deep neural network for nonlinear electromagnetic inverse scattering. Electronics 2021, 10, 752. [Google Scholar] [CrossRef]
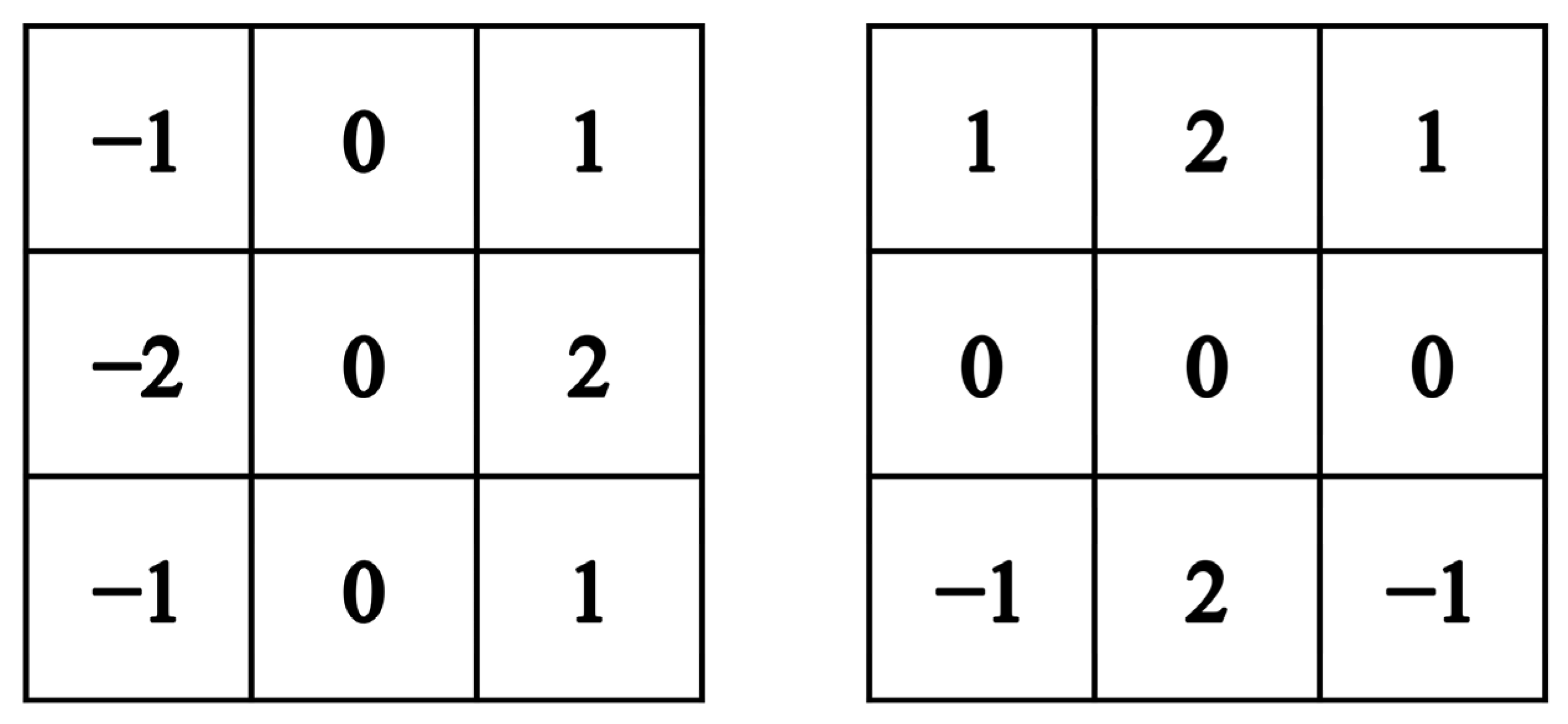
- Sobel, I.; Feldman, G. A 3×3 Isotropic Gradient Operator for Image Processing. 1973. Available online: https://www.researchgate.net/publication/285159837_A_33_isotropic_gradient_operator_for_image_processing (accessed on 2 May 2023).
- Qin, Z.; Lu, M.; Zheng, X.; Yao, Y.; Zhang, C.; Song, J. The implementation of an improved NPML absorbing boundary condition in elastic wave modeling. Appl. Geophys. 2009, 6, 113–121. [Google Scholar] [CrossRef]



| Number of Samples | 100 | 200 | 300 | 400 | 500 |
|---|---|---|---|---|---|
| APS (100 epochs) | 2.53 | 2.62 | 2.31 | 2.55 | 2.64 |
| APS (200 epochs) | 1.82 | 2.37 | 2.06 | 2.01 | 2.75 |
| APS (300 epochs) | 2.42 | 2.04 | 2.07 | 1.62 | 2.41 |
| APS (400 epochs) | 2.06 | 2.29 | 1.98 | 1.59 | 2.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Yan, H.; Yu, H.; Zhang, Z. Removing Time Dispersion from Elastic Wave Modeling with the pix2pix Algorithm Based on cGAN. Remote Sens. 2023, 15, 3120. https://doi.org/10.3390/rs15123120
Xu T, Yan H, Yu H, Zhang Z. Removing Time Dispersion from Elastic Wave Modeling with the pix2pix Algorithm Based on cGAN. Remote Sensing. 2023; 15(12):3120. https://doi.org/10.3390/rs15123120
Chicago/Turabian StyleXu, Teng, Hongyong Yan, Hui Yu, and Zhiyong Zhang. 2023. "Removing Time Dispersion from Elastic Wave Modeling with the pix2pix Algorithm Based on cGAN" Remote Sensing 15, no. 12: 3120. https://doi.org/10.3390/rs15123120
APA StyleXu, T., Yan, H., Yu, H., & Zhang, Z. (2023). Removing Time Dispersion from Elastic Wave Modeling with the pix2pix Algorithm Based on cGAN. Remote Sensing, 15(12), 3120. https://doi.org/10.3390/rs15123120