Modified Auto-Focusing Algorithm for High Squint Diving SAR Imaging Based on the Back-Projection Algorithm with Spectrum Alignment and Truncation
Abstract
1. Introduction
- The imaging grids for the BP algorithm are modified to utilize the full energy for azimuth domain processing and ensure the PGA can extract the whole energy of the targets.
- To accurately estimate the phase gradient, wavenumber spectrum shifting to align the spectrum center of targets and spectrum truncation to avoid the extra phase noise from outside the target’s bandwidth are both proposed.
- The length of spectrum truncation after wavenumber center alignment is first given in this paper for general SAR auto-focusing algorithms.
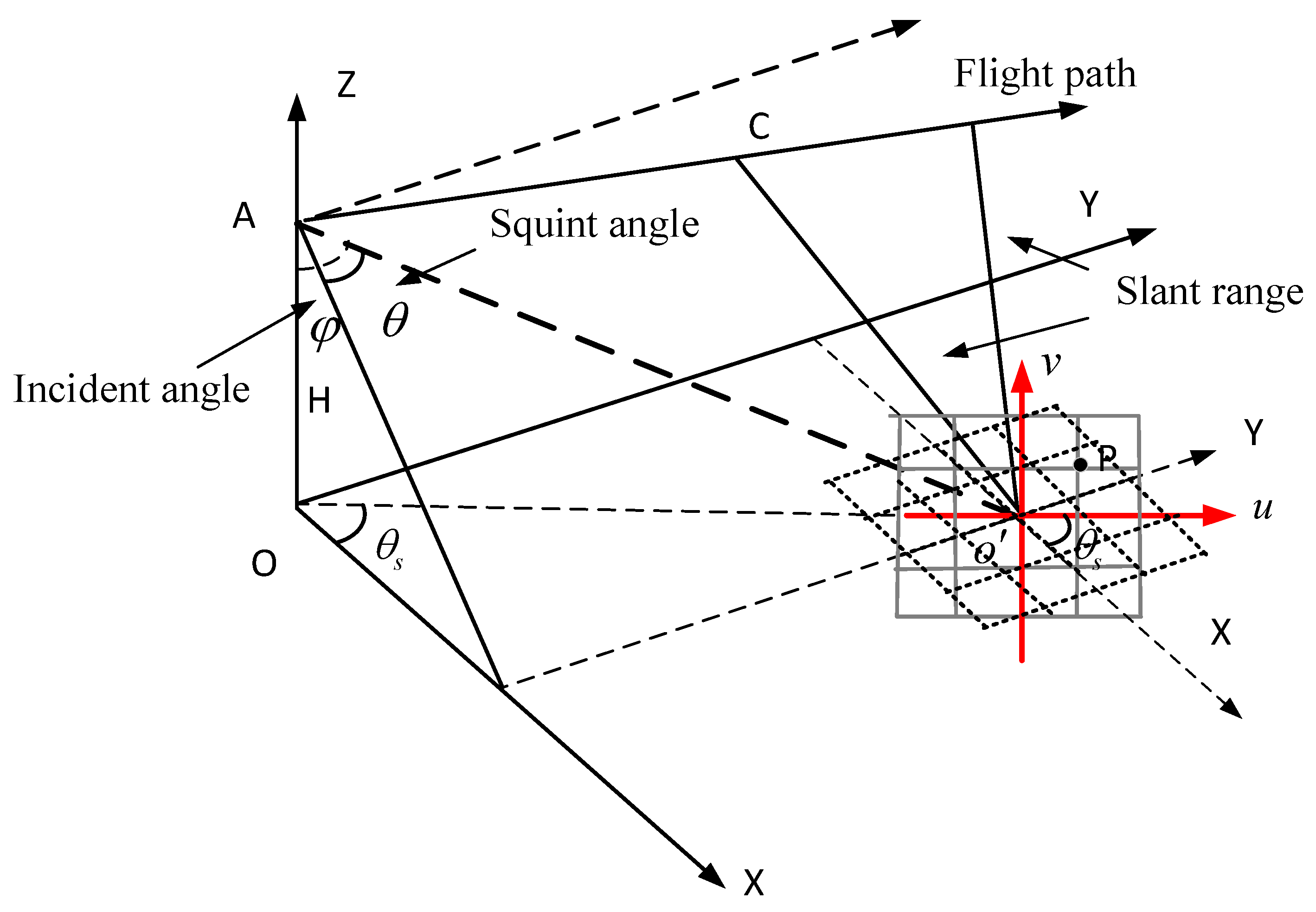
2. Problem Formulation
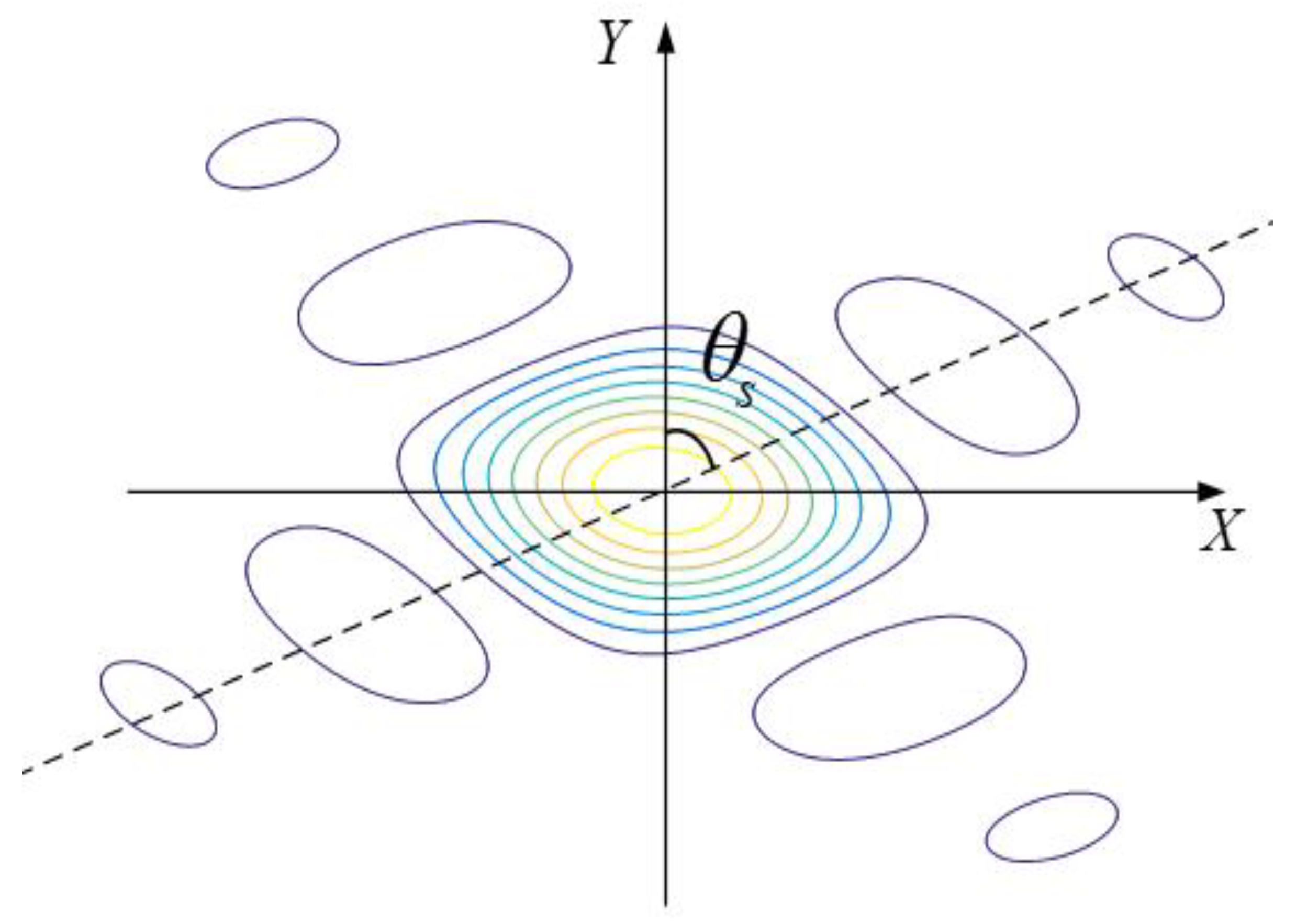
3. Derivation of the Proposed Method
3.1. Spectrum Center Shifting
3.2. Wavenumber Spectrum Truncation
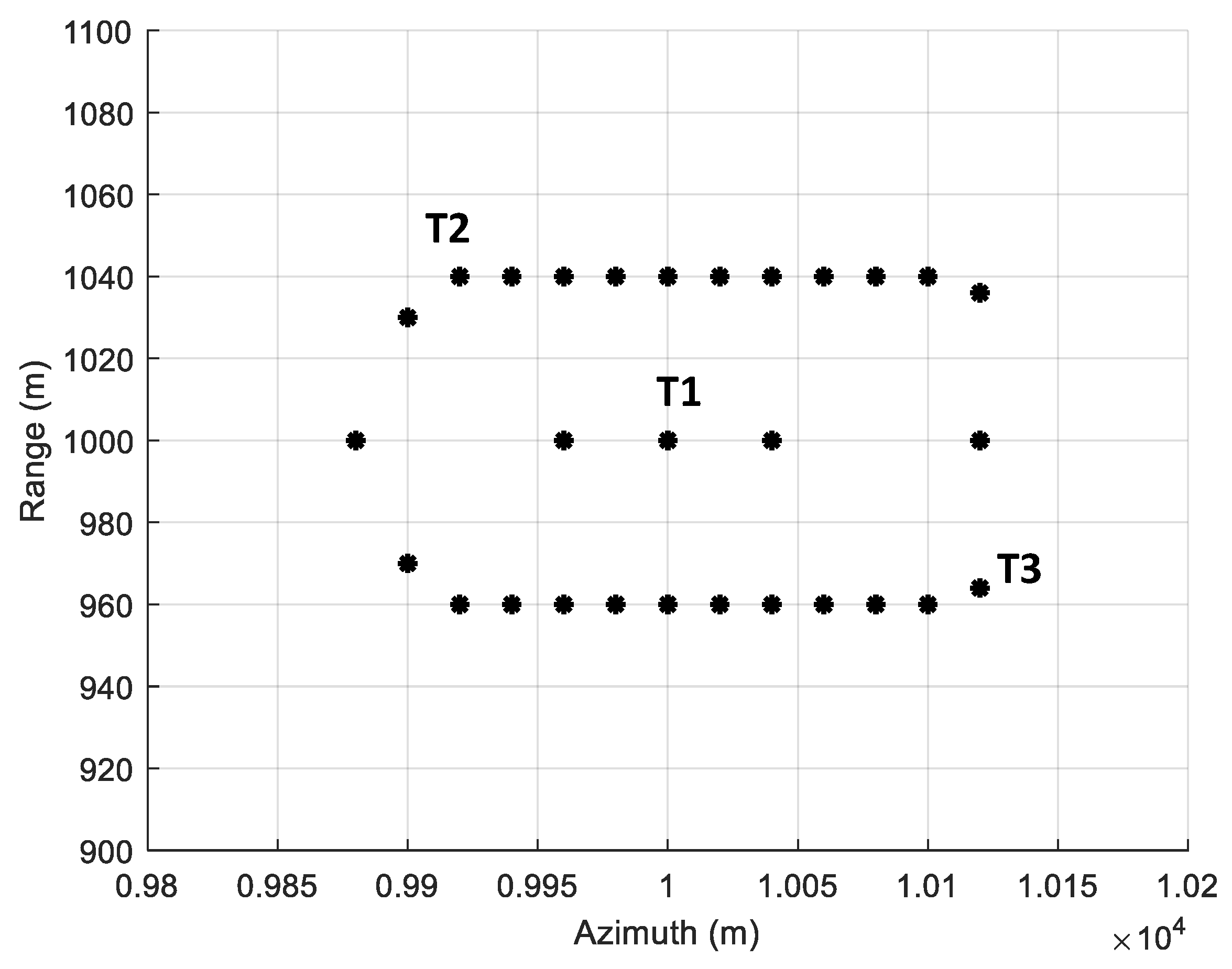
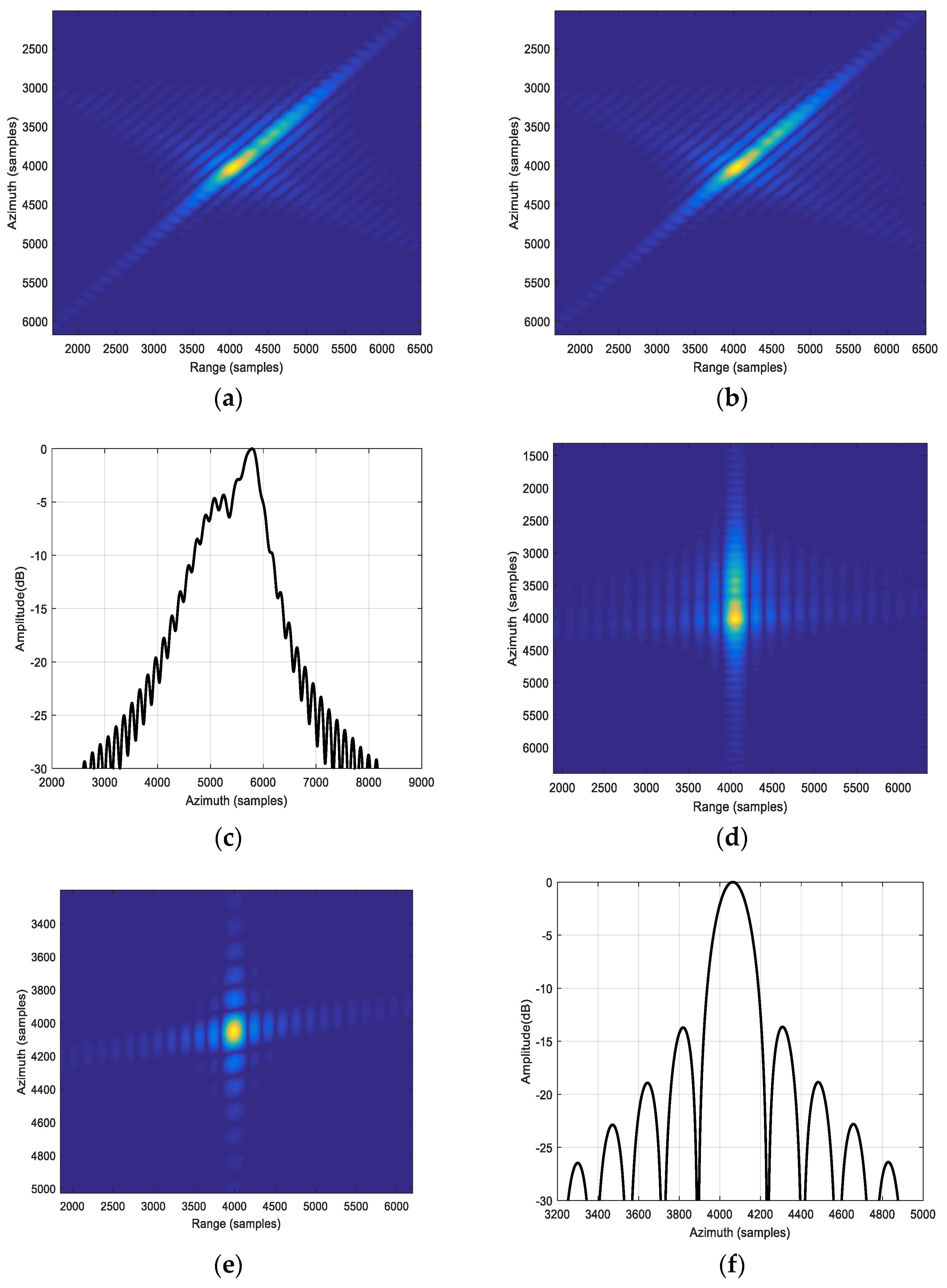
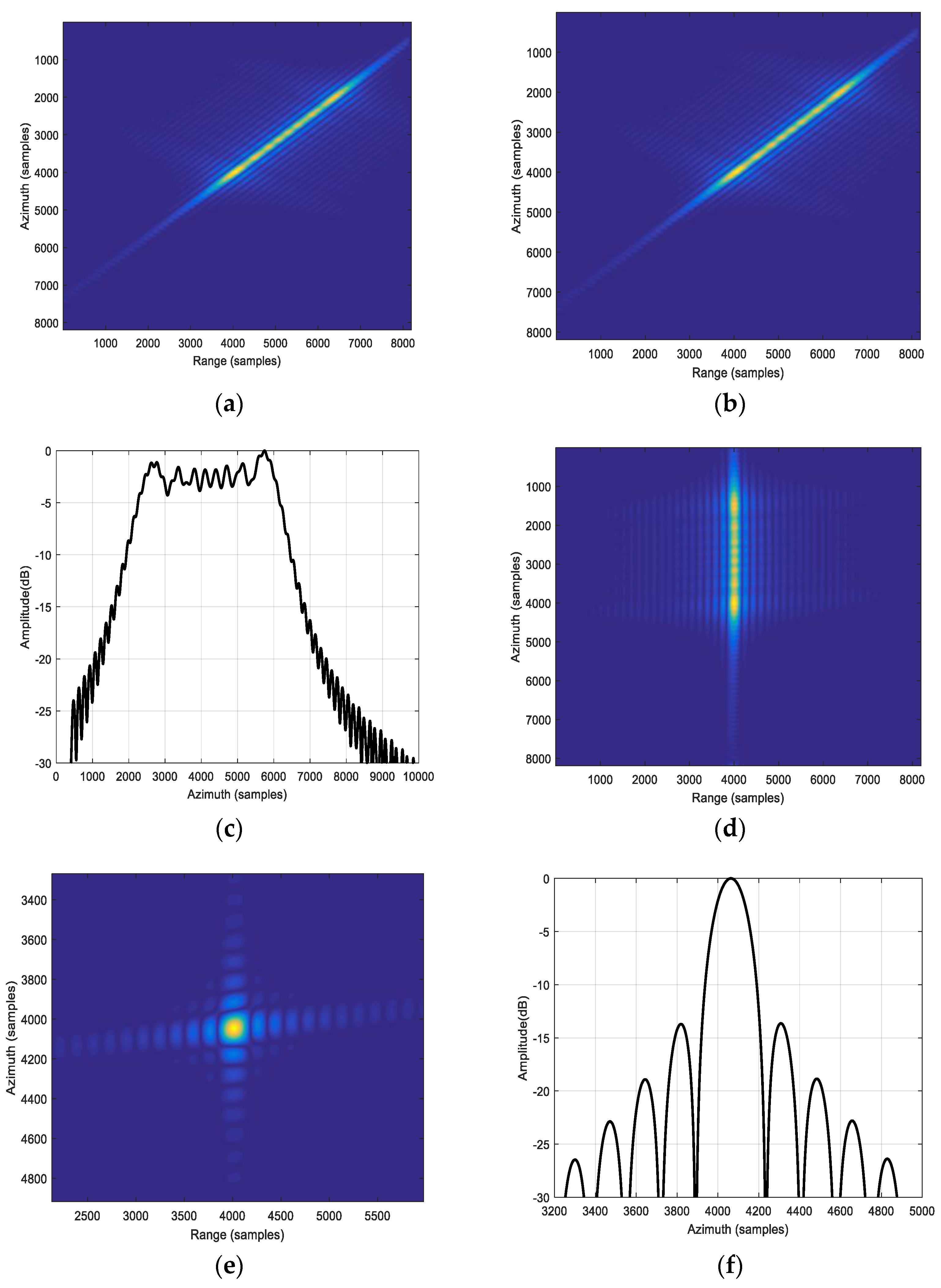
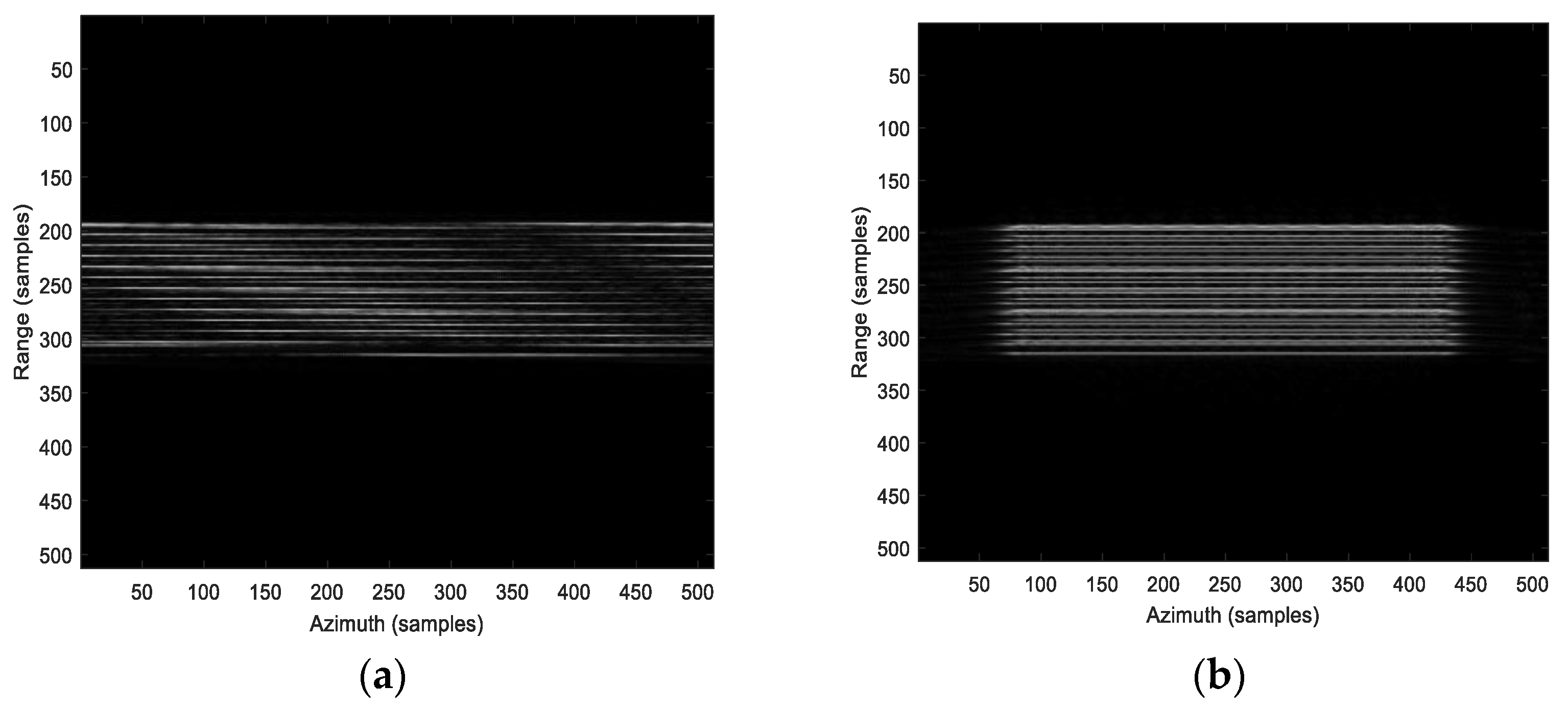
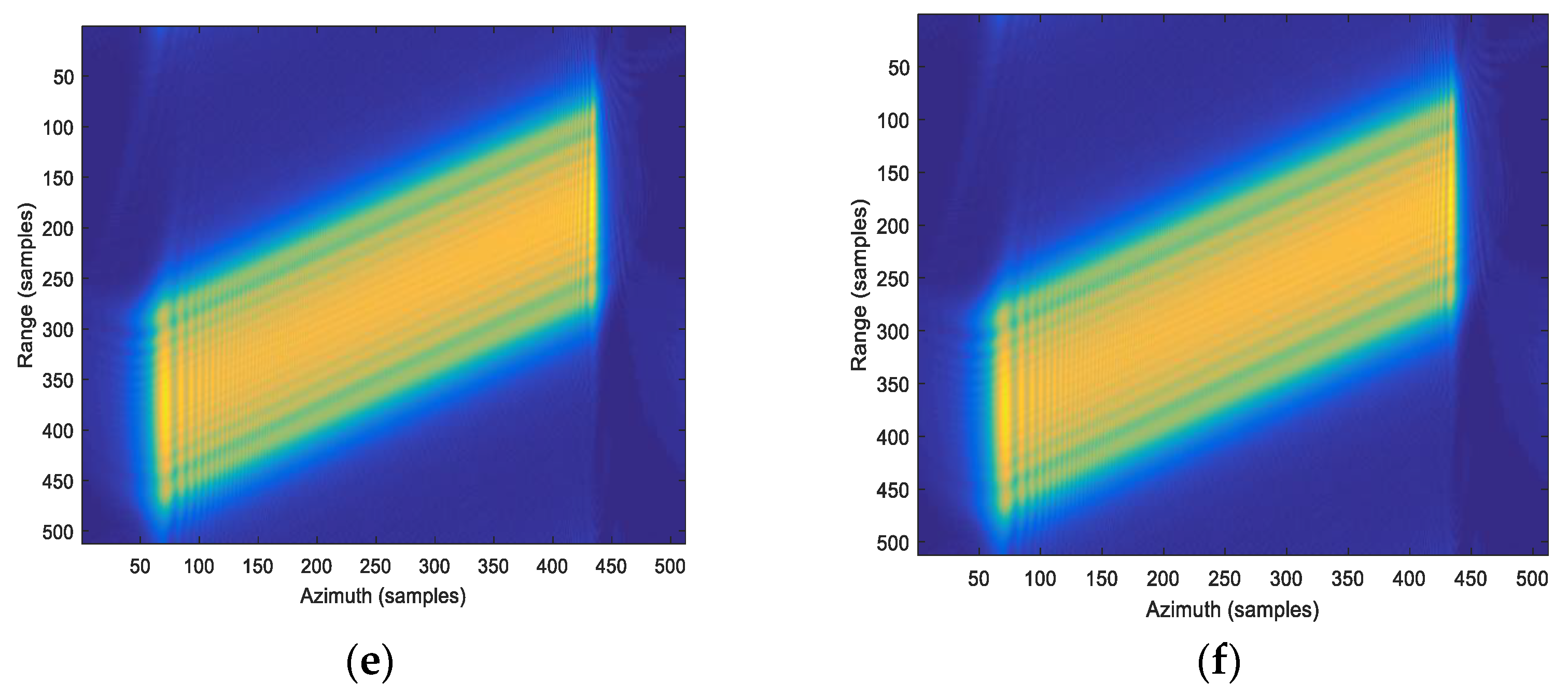
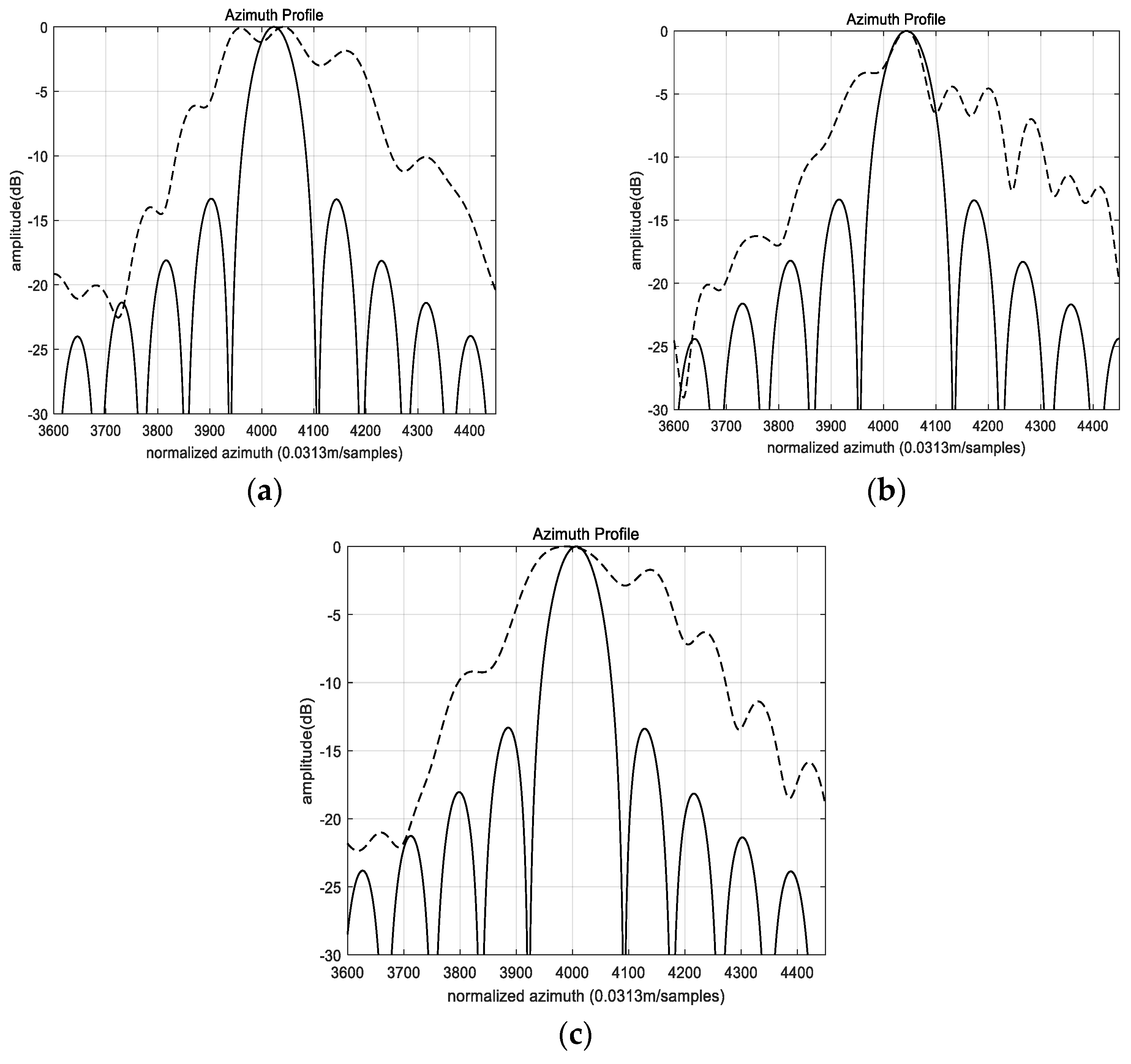
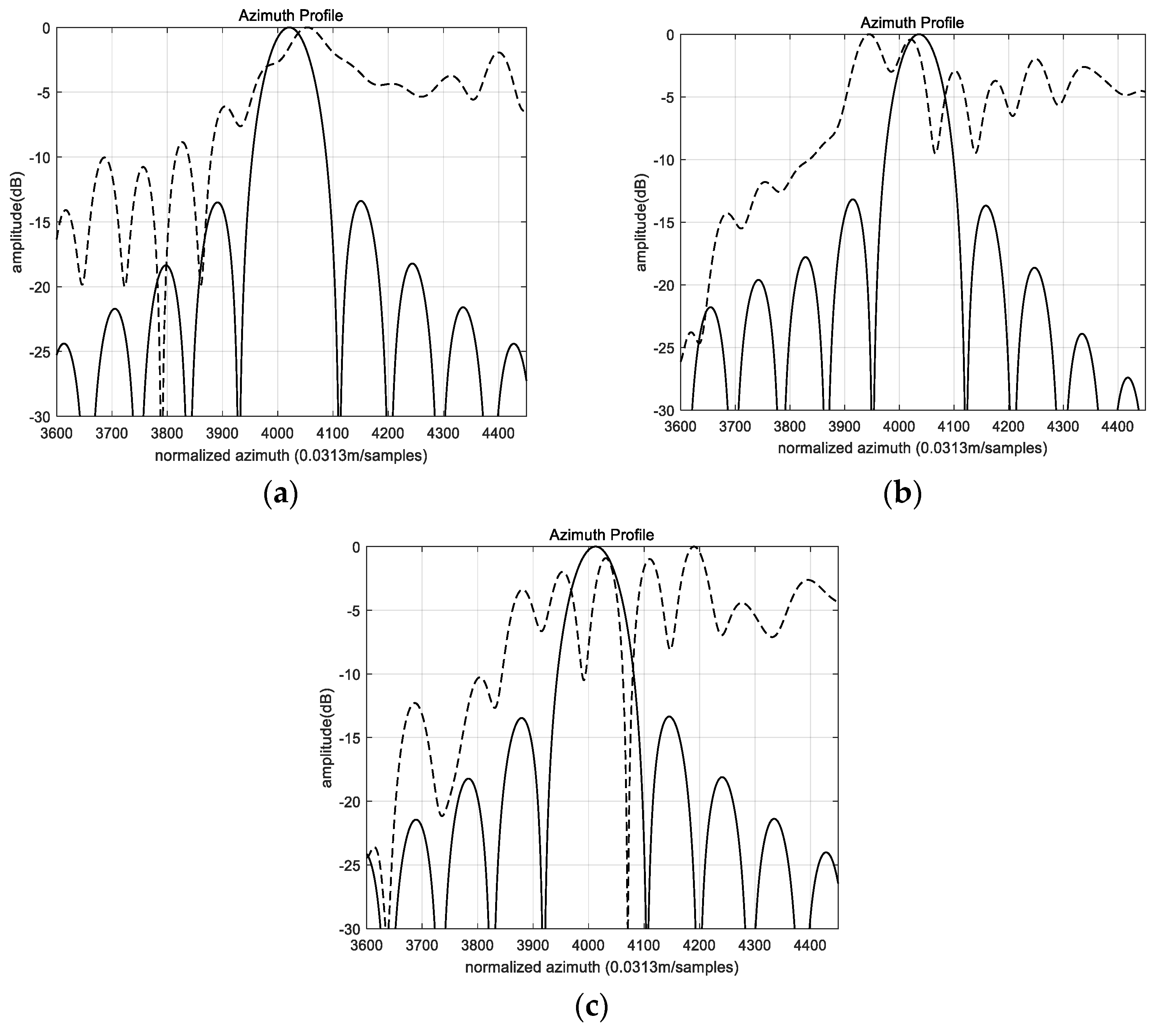
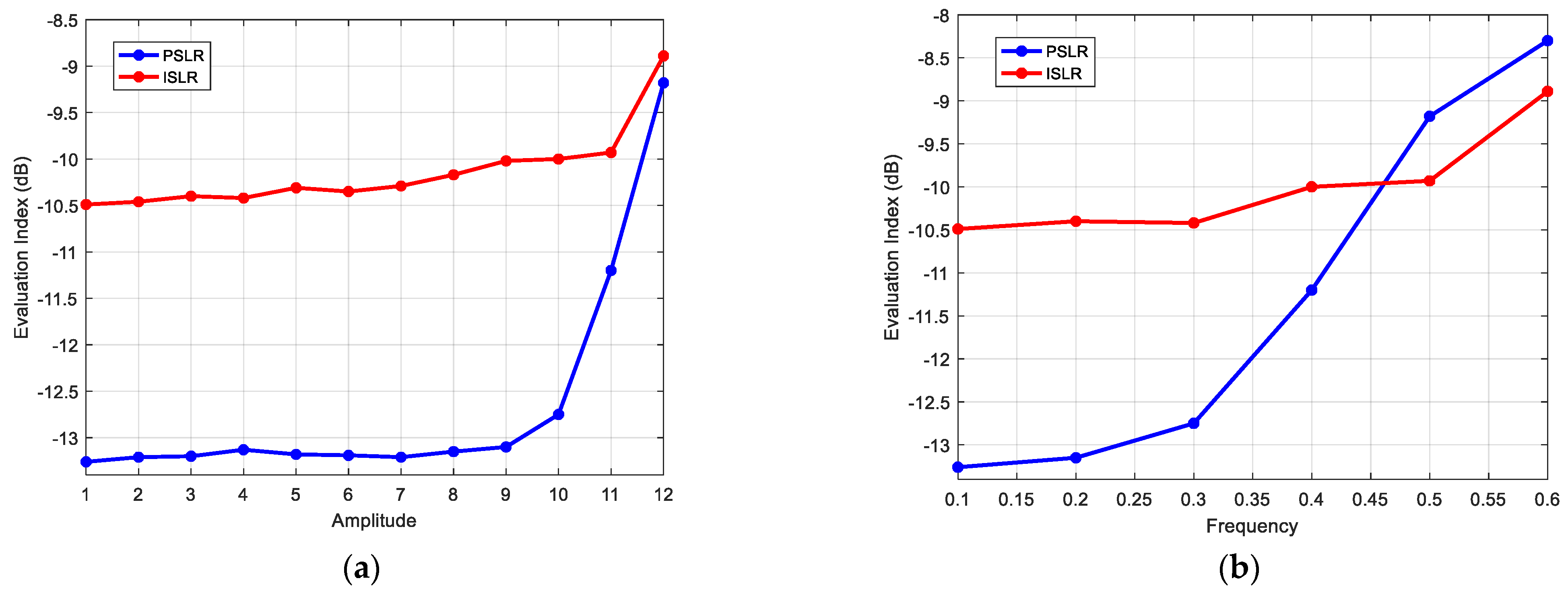
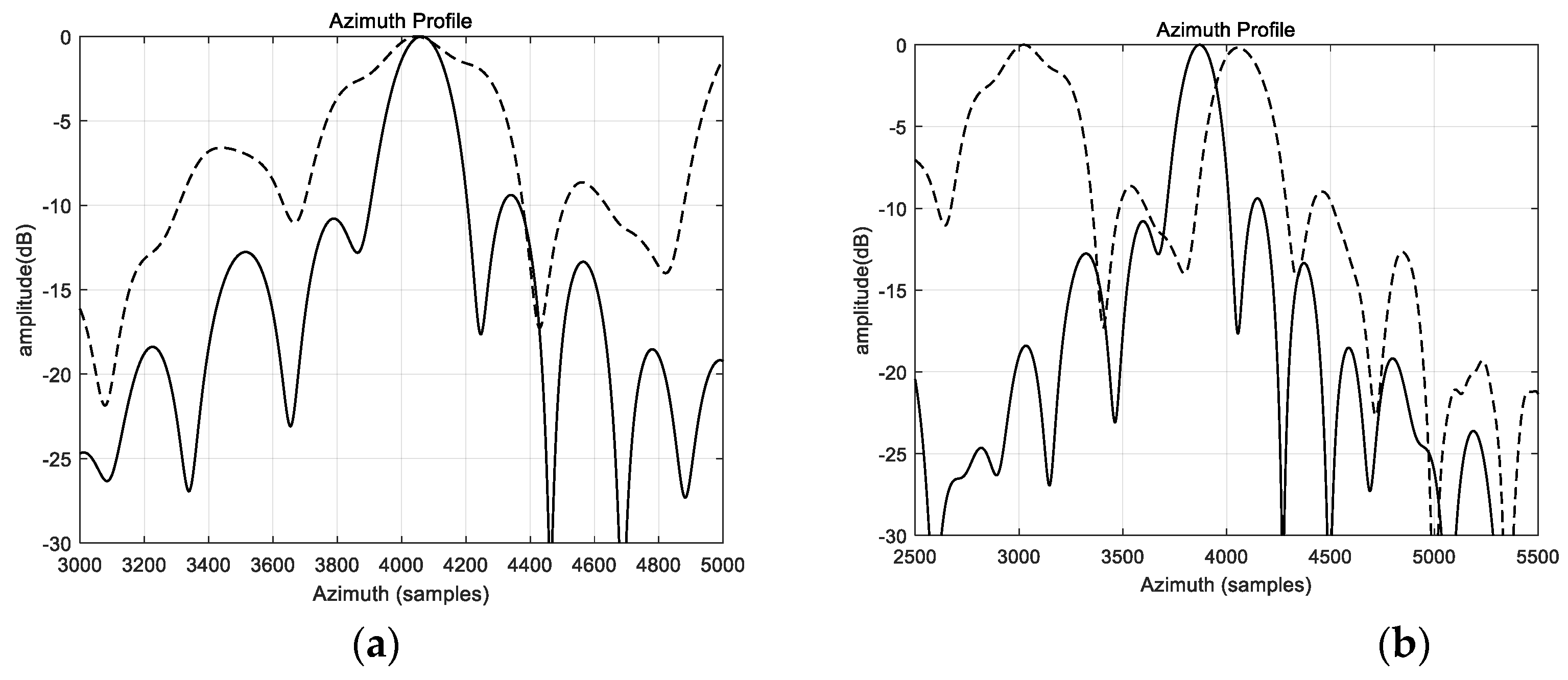
4. Simulation and Real Data Processing
4.1. The Influence of the PSF
4.2. The Influence of the Wavenumber Spectrum Shifting and Truncation
4.3. Real Data Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeng, T.; Li, Y.; Ding, Z.; Long, T.; Yao, D.; Sun, Y. Subaperture Approach Based on Azimuth-Dependent Range Cell Migration Correction and Azimuth Focusing Parameter Equalization for Maneuvering High-Squint-Mode SAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6718–6734. [Google Scholar] [CrossRef]
- Li, Z.; Xing, M.; Liang, Y.; Gao, Y.; Chen, J.; Huai, Y.; Zeng, L.; Sun, G.-C.; Bao, Z. A Frequency-Domain Imaging Algorithm for Highly Squinted SAR Mounted on Maneuvering Platforms with Nonlinear Trajectory. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4023–4038. [Google Scholar] [CrossRef]
- Li, Z.; Liang, Y.; Xing, M.; Huai, Y.; Gao, Y.; Zeng, L.; Bao, Z. An Improved Range Model and Omega-K-Based Imaging Algorithm for High-Squint SAR with Curved Trajectory and Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2016, 13, 656–660. [Google Scholar] [CrossRef]
- Wang, P.; Liu, W.; Chen, J.; Niu, M.; Yang, W. A High-Order Imaging Algorithm for High-Resolution Spaceborne SAR Based on a Modified Equivalent Squint Range Model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1225–1235. [Google Scholar] [CrossRef]
- Li, Z.; Liang, Y.; Xing, M.; Huai, Y.; Zeng, L.; Bao, Z. Focusing of Highly Squinted SAR Data with Frequency Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2016, 13, 23–27. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Sun, G.-C. Acceleration Model Analyses and Imaging Algorithm for Highly Squinted Airborne Spotlight-Mode SAR with Maneuvers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1120–1131. [Google Scholar] [CrossRef]
- Li, Z.; Xing, M.; Xing, W.; Liang, Y.; Gao, Y.; Dai, B.; Hu, L.; Bao, Z. A Modified Equivalent Range Model and Wavenumber-Domain Imaging Approach for High-Resolution-High-Squint SAR with Curved Trajectory. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3721–3734. [Google Scholar] [CrossRef]
- Liang, Y.; Huai, Y.; Ding, J.; Wang, H.; Xing, M. A Modified Algorithm for HS-SAR Small-Aperture Data Imaging. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3710–3721. [Google Scholar] [CrossRef]
- Zeng, L.; Liang, Y.; Xing, M.; Huai, Y.; Li, Z. A Novel Motion Compensation Approach for Airborne Spotlight SAR of High-Resolution and High-Squint Mode. IEEE Geosci. Remote Sens. Lett. 2016, 13, 429–433. [Google Scholar] [CrossRef]
- Xi, Z.; Duan, C.; Zuo, W.; Li, C.; Huo, T.; Li, D.; Wen, H. Focus Improvement of Spaceborne-Missile Bistatic SAR Data Using the Modified NLCS Algorithm Based on the Method of Series Reversion. Remote Sens. 2022, 14, 5770. [Google Scholar] [CrossRef]
- Yeo, T.S.; Tan, N.L.; Zhang, C.B.; Lu, Y.H. A new subaperture approach to high squint SAR processing. IEEE Trans. Geosci. Remote Sens. 2001, 39, 954–968. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, G.-C.; Xia, X.-G.; Xing, M.; Yang, J.; Bao, Z. An Azimuth Frequency Non-Linear Chirp Scaling (FNCS) Algorithm for TOPS SAR Imaging with High Squint Angle. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 213–221. [Google Scholar] [CrossRef]
- Bie, B.; Quan, Y.; Xu, K.; Sun, G.; Xing, M. High Speed Maneuvering Platform Squint TOPS SAR Imaging Based on Local Polar Coordinate and Angular Division. Remote Sens. 2021, 13, 3329. [Google Scholar] [CrossRef]
- Guo, Z.; Fu, Z.; Chang, J.; Wu, L.; Li, N. A Novel High-Squint Spotlight SAR Raw Data Simulation Scheme in 2-D Frequency Domain. Remote Sens. 2022, 14, 651. [Google Scholar] [CrossRef]
- Feng, D.; An, D.; Huang, X. An Extended Fast Factorized Back Projection Algorithm for Missile-Borne Bistatic Forward-Looking SAR Imaging. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2724–2734. [Google Scholar] [CrossRef]
- Xie, H.; Shi, S.; Mao, J.; An, D.; Li, F.; Zhou, Z.; Wang, G. Fast Time-domain Imaging Method for Bistatic Circular SAR. J. Phys. Conf. Ser. 2018, 960, 012021. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, L.; Zhao, L.; Wang, Y.; Zhang, C. An Improved Fast Time-Domain Algorithm for Bistatic Forward-Looking Sar Imaging. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2587–2590. [Google Scholar]
- Hu, X.; Xie, H.; Zhang, L.; Hu, J.; He, J.; Yi, S.; Jiang, H.; Xie, K. Fast Factorized Back projection Algorithm in Orthogonal Elliptical Coordinate System for Ocean Scenes Imaging Using Geosynchronous Spaceborne–Airborne VHF UWB Bistatic SAR. Remote Sens. 2023, 15, 2215. [Google Scholar] [CrossRef]
- Brown, W.D.; Ghiglia, D.C. Some methods for reducing propagation-induced phase errors in coherent imaging systems I Formalism. J. Opt. Soc. Am. A 1988, 5, 924–941. [Google Scholar] [CrossRef]
- Marechal, N. High frequency phase errors in sar imagery and implications for autofocus. In Proceedings of the International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31–31 May 1996. [Google Scholar]
- Yang, L.; Zhang, F.; Sun, Y.; Chen, L.; Li, Z.; Wang, D. Motion Error Estimation and Compensation of Airborne Array Flexible SAR Based on Multi-Channel Interferometric Phase. Remote Sens. 2023, 15, 680. [Google Scholar] [CrossRef]
- Samczynski, P.; Kulpa, K.S. Coherent MapDrift Technique. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1505–1517. [Google Scholar] [CrossRef]
- Ye, W.; Yeo, T.S.; Bao, Z. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2487–2494. [Google Scholar] [CrossRef]
- Li, G.; Xu, J.; Peng, Y.; Xia, X.-G. Improved RDM for SAR autofocus processing. In Proceedings of the 2007 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 5–9 November 2007; pp. 401–403. [Google Scholar]
- Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Speckle processing method for synthetic-aperture-radar phase correction. Opt. Lett. 1989, 14, 1–3. [Google Scholar] [CrossRef]
- Wahl, D.; Eichel, P.; Ghiglia, D.; Jakowatz, C. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef]
- Warner, D.W.; Ghiglia, D.C.; Fitzgerrell, A.; Beaver, J. Two-dimensional phase gradient autofocus. In Image Reconstruction from Incomplete Data; SPIE: Bellingham, WA, USA, 2000; Volume 4123, pp. 162–173. [Google Scholar] [CrossRef]
- Chen, X.; Sun, G.-C.; Xing, M.; Li, B.; Yang, J.; Bao, Z. Ground Cartesian Back-Projection Algorithm for High Squint Diving TOPS SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5812–5827. [Google Scholar] [CrossRef]
- Dong, Q.; Sun, G.-C.; Yang, Z.; Guo, L.; Xing, M. Cartesian Factorized Backprojection Algorithm for High-Resolution Spotlight SAR Imaging. IEEE Sens. J. 2018, 18, 1160–1168. [Google Scholar] [CrossRef]
- Guo, Y.; Yu, Z.; Li, J.; Li, C. Focusing Multistatic GEO SAR with Two Stationary Receivers Using Spectrum Alignment and Extrapolation. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4018805. [Google Scholar] [CrossRef]
- Yuan, S.; Yu, Z.; Li, C.; Wang, S. A Novel SAR Sidelobe Suppression Method Based on CNN. IEEE Geosci. Remote Sens. Lett. 2020, 18, 132–136. [Google Scholar] [CrossRef]
- Davidson, G.W.; Cumming, I. Signal properties of spaceborne squint-mode SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 611–617. [Google Scholar] [CrossRef]
- Beard, G.S. Performance Factors for Airborne Short-Dwell Squinted Radar Sensors. Ph.D. Thesis, University College London, London, UK, 2011. [Google Scholar]
- Zhang, Q.; Yin, W.; Ding, Z.; Zeng, T.; Long, T. An Optimal Resolution Steering Method for Geosynchronous Orbit SAR. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1732–1736. [Google Scholar] [CrossRef]
- Ding, Z.; Yin, W.; Zeng, T.; Long, T. Radar Parameter Design for Geosynchronous SAR in Squint Mode and Elliptical Orbit. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2720–2732. [Google Scholar] [CrossRef]
- Zeng, T.; Cherniakov, M.; Long, T. Generalized approach to resolution analysis in BSAR. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 461–474. [Google Scholar] [CrossRef]







| Parameters | Value |
|---|---|
| Wavelength | 0.02 m |
| Bandwidth | 90 MHz |
| Pulse duration | 3 μs |
| Sampling frequency | 108 MHz |
| Pulse repetition frequency | 300 Hz |
| Altitude | 4000 m |
| Squint angle | 68° |
| Velocity | (0, 100, −20) m/s |
| Target | The Classical PGA | The Proposed Method | |||
|---|---|---|---|---|---|
| PSLR (dB) | ISLR (dB) | PSLR (dB) | ISLR (dB) | Azi Res (m) | |
| T1 | −2.73 | −5.43 | −13.16 | −9.71 | 2.32 |
| T2 | −3.21 | −5.19 | −13.26 | −9.98 | 2.38 |
| T3 | −2.68 | −6.21 | −13.13 | −9.75 | 2.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, A.; Sun, B.; Yan, M.; Xue, C.; Li, J. Modified Auto-Focusing Algorithm for High Squint Diving SAR Imaging Based on the Back-Projection Algorithm with Spectrum Alignment and Truncation. Remote Sens. 2023, 15, 2976. https://doi.org/10.3390/rs15122976
Gao A, Sun B, Yan M, Xue C, Li J. Modified Auto-Focusing Algorithm for High Squint Diving SAR Imaging Based on the Back-Projection Algorithm with Spectrum Alignment and Truncation. Remote Sensing. 2023; 15(12):2976. https://doi.org/10.3390/rs15122976
Chicago/Turabian StyleGao, Anqi, Bing Sun, Mengyuan Yan, Chen Xue, and Jingwen Li. 2023. "Modified Auto-Focusing Algorithm for High Squint Diving SAR Imaging Based on the Back-Projection Algorithm with Spectrum Alignment and Truncation" Remote Sensing 15, no. 12: 2976. https://doi.org/10.3390/rs15122976
APA StyleGao, A., Sun, B., Yan, M., Xue, C., & Li, J. (2023). Modified Auto-Focusing Algorithm for High Squint Diving SAR Imaging Based on the Back-Projection Algorithm with Spectrum Alignment and Truncation. Remote Sensing, 15(12), 2976. https://doi.org/10.3390/rs15122976






