Figure 1.
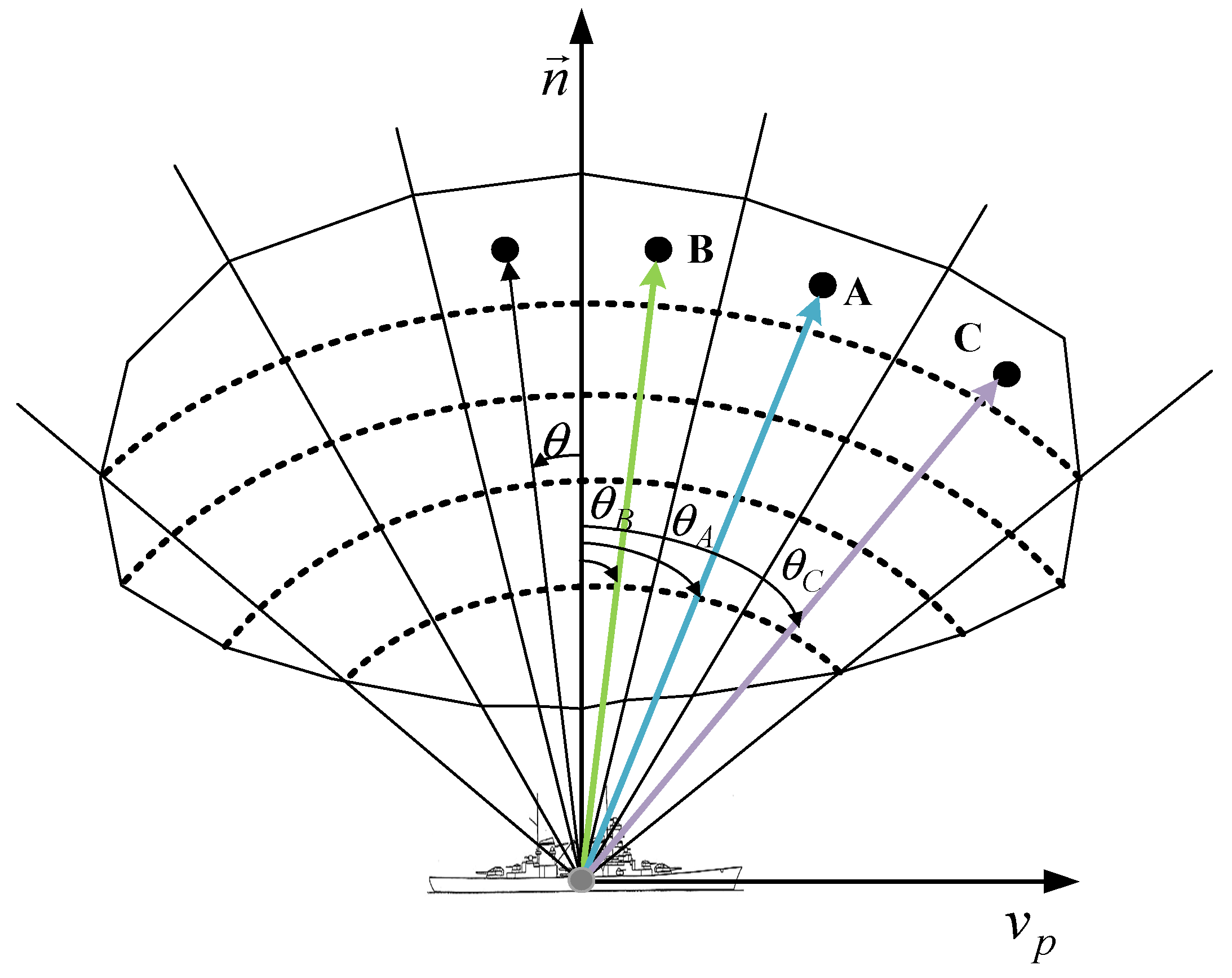
Incident directions of different sea echoes with adjacent sea cells.
Figure 1.
Incident directions of different sea echoes with adjacent sea cells.
Figure 2.
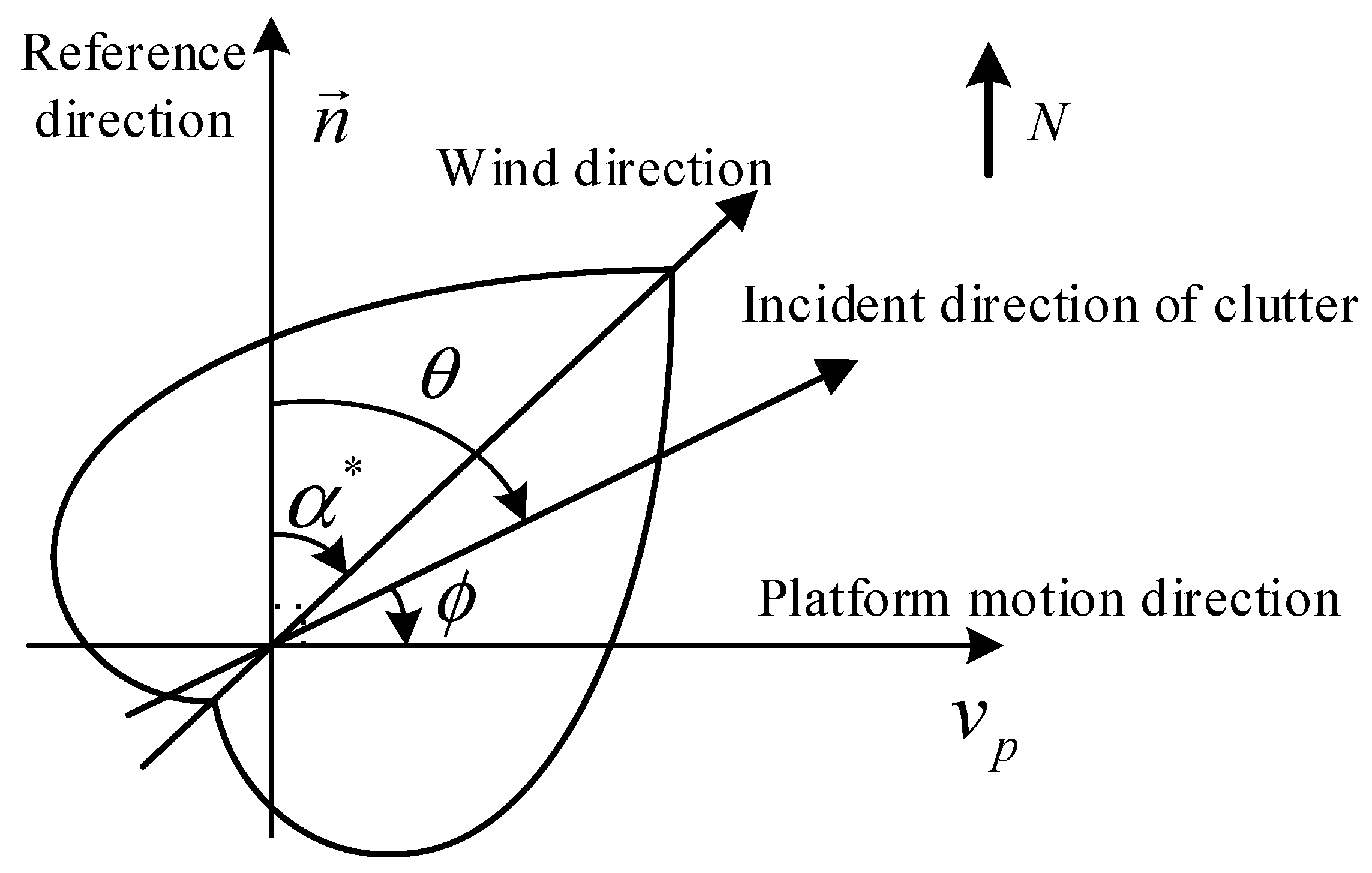
Diagram of a modified cosine model based on the relationship between the sailing platform, the sea echo, and the wind direction.
Figure 2.
Diagram of a modified cosine model based on the relationship between the sailing platform, the sea echo, and the wind direction.
Figure 3.
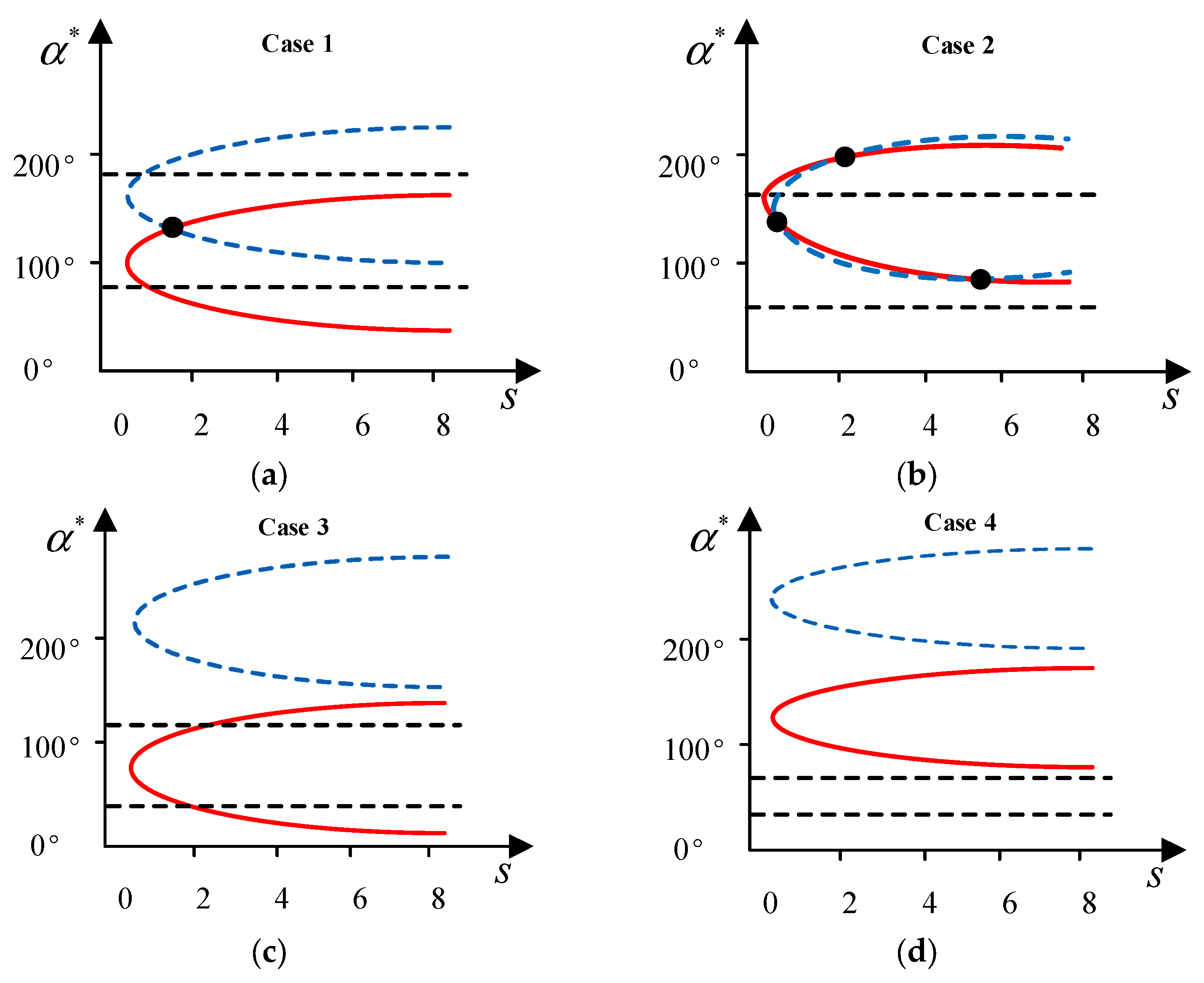
Relationship between wind direction interval and two curves of the relationship between the spreading parameter and the wind direction: (a) Unique intersection in wind direction interval. (b) Multiple intersections in wind direction interval. (c) No intersection in wind direction interval. (d) Disjoint between the wind direction interval and the curve of cell A.
Figure 3.
Relationship between wind direction interval and two curves of the relationship between the spreading parameter and the wind direction: (a) Unique intersection in wind direction interval. (b) Multiple intersections in wind direction interval. (c) No intersection in wind direction interval. (d) Disjoint between the wind direction interval and the curve of cell A.
Figure 4.
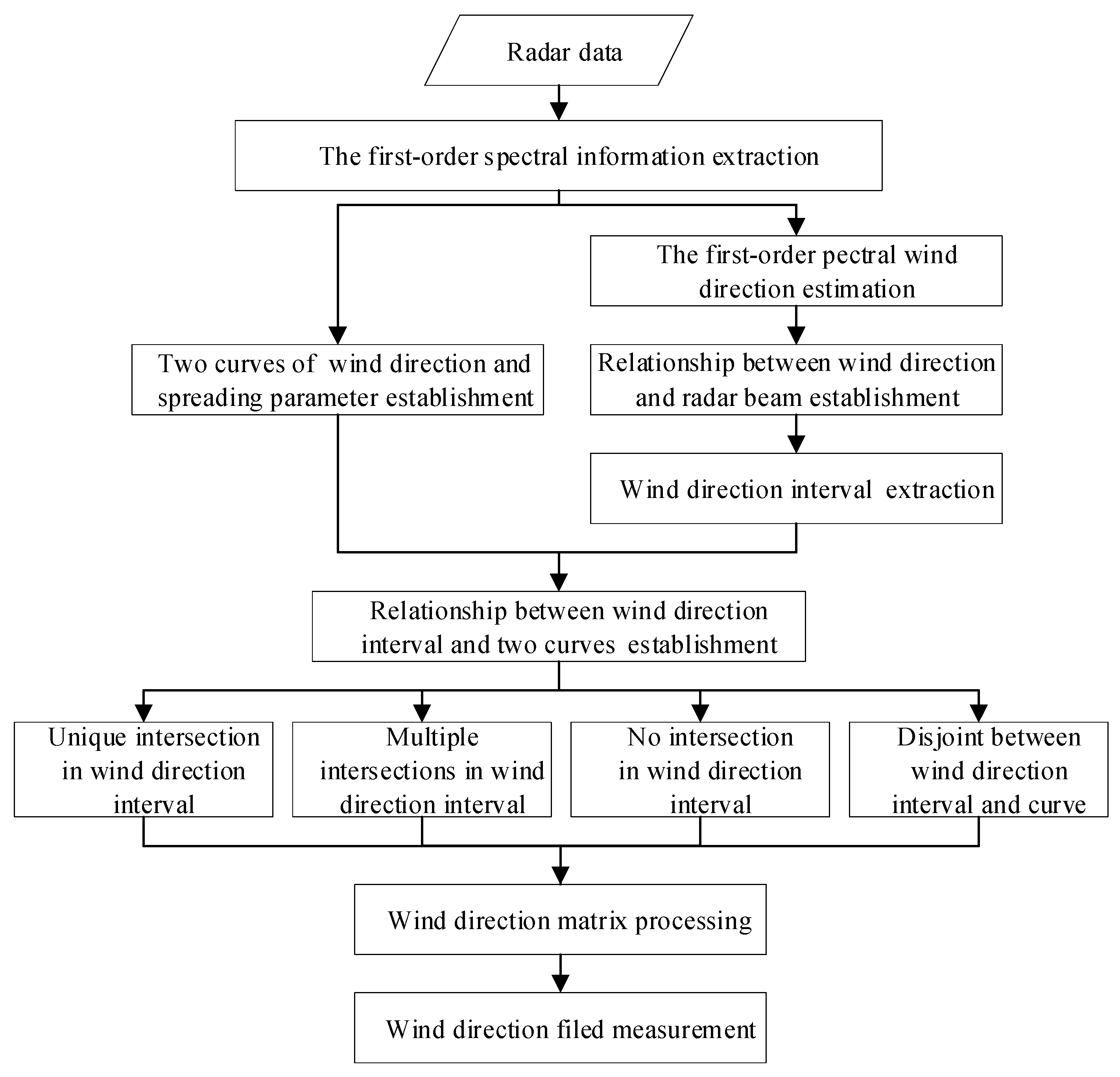
Processing of the unambiguous wind direction measurement method.
Figure 4.
Processing of the unambiguous wind direction measurement method.
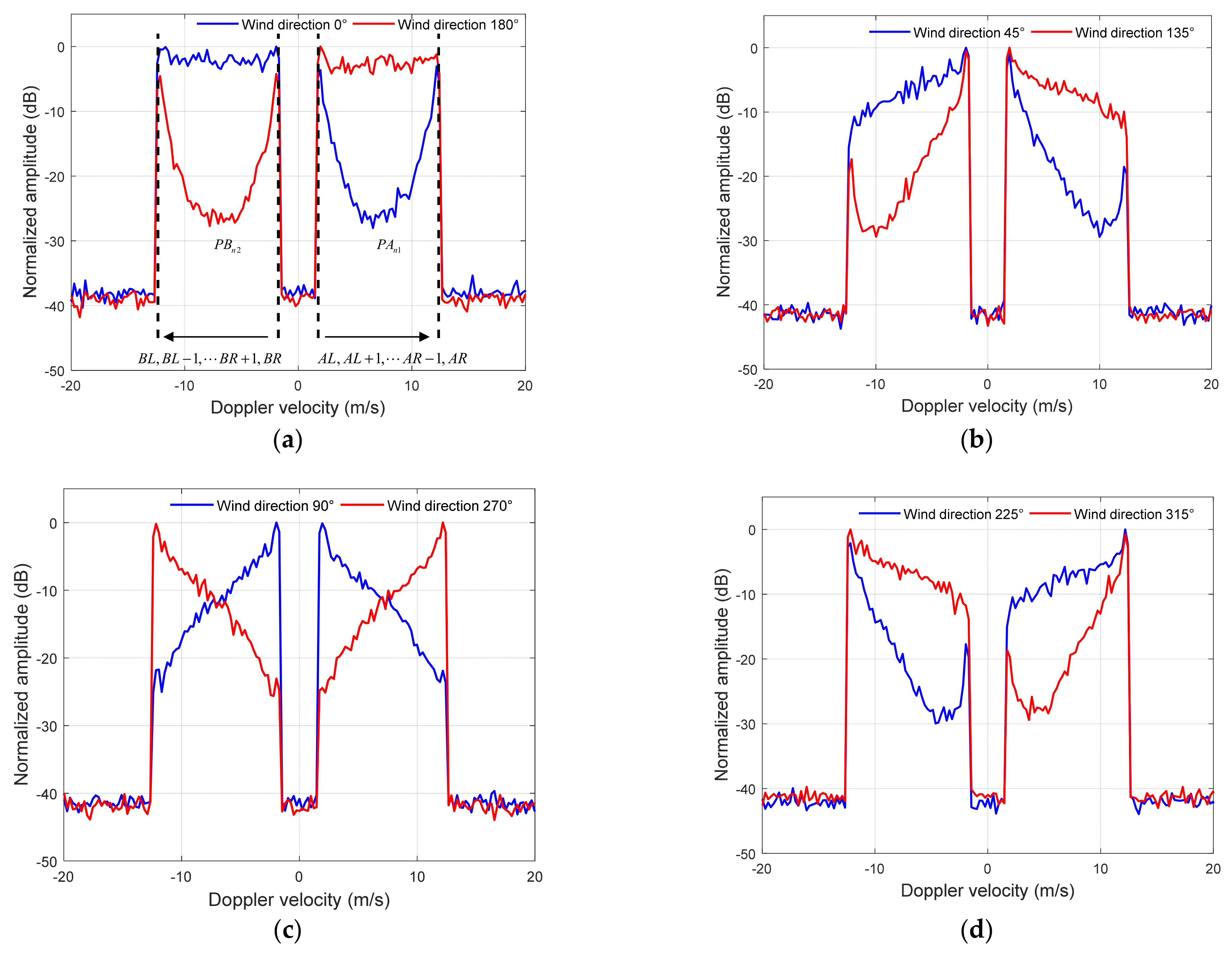
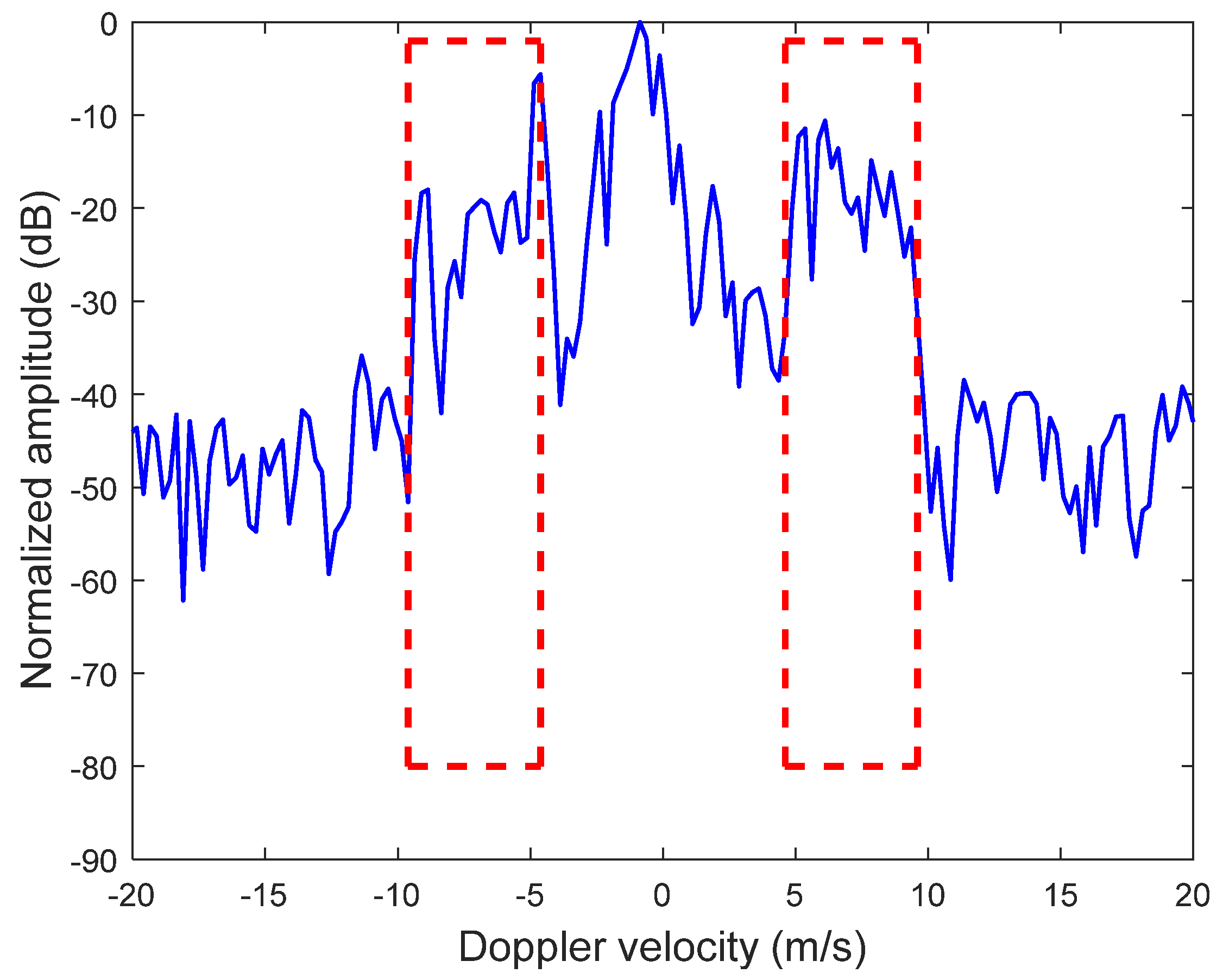
Figure 5.
The broadened Doppler spectra for different wind directions: (a) The wind directions are 0° and 180°. (b) The wind directions are 45° and 135°. (c) The wind directions are 90° and 270°. (d) The wind directions are 225° and 315°.
Figure 5.
The broadened Doppler spectra for different wind directions: (a) The wind directions are 0° and 180°. (b) The wind directions are 45° and 135°. (c) The wind directions are 90° and 270°. (d) The wind directions are 225° and 315°.
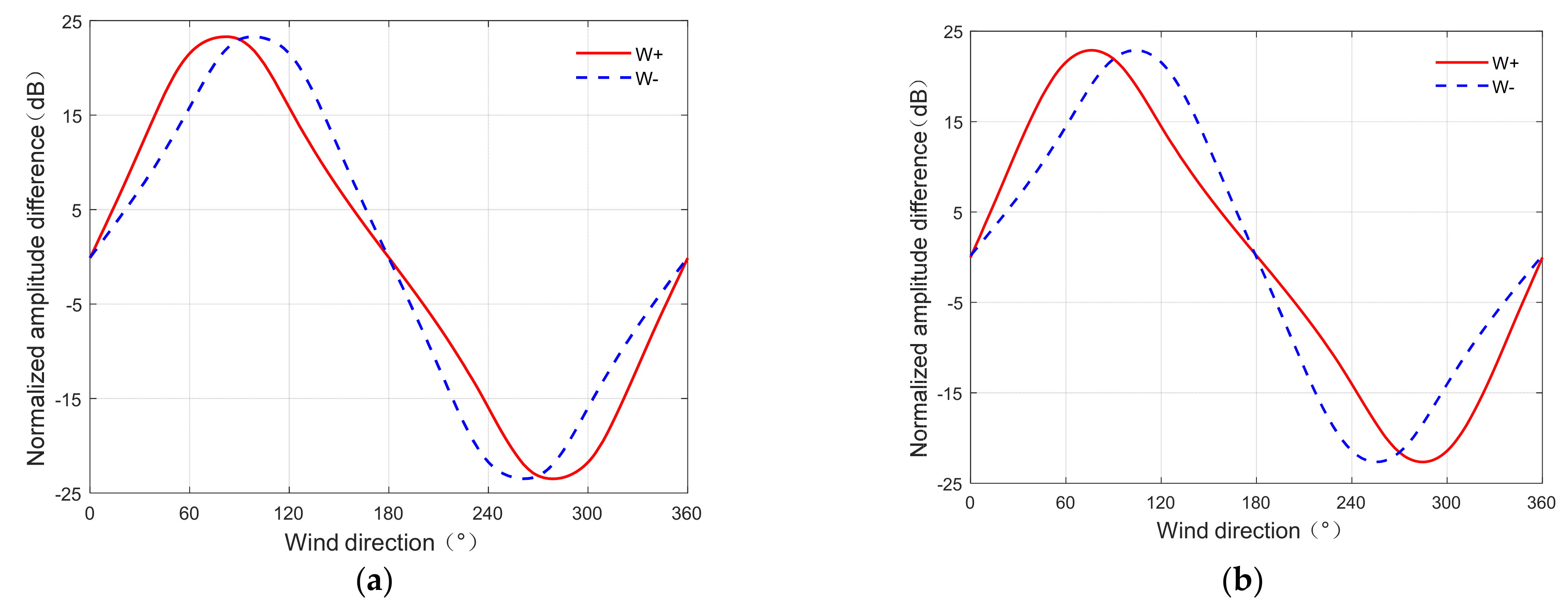
Figure 6.
Relationship between the normalized amplitude differences and the wind directions: (a) The ship speed is 5 m/s. (b) The ship speed is 2.3 m/s.
Figure 6.
Relationship between the normalized amplitude differences and the wind directions: (a) The ship speed is 5 m/s. (b) The ship speed is 2.3 m/s.
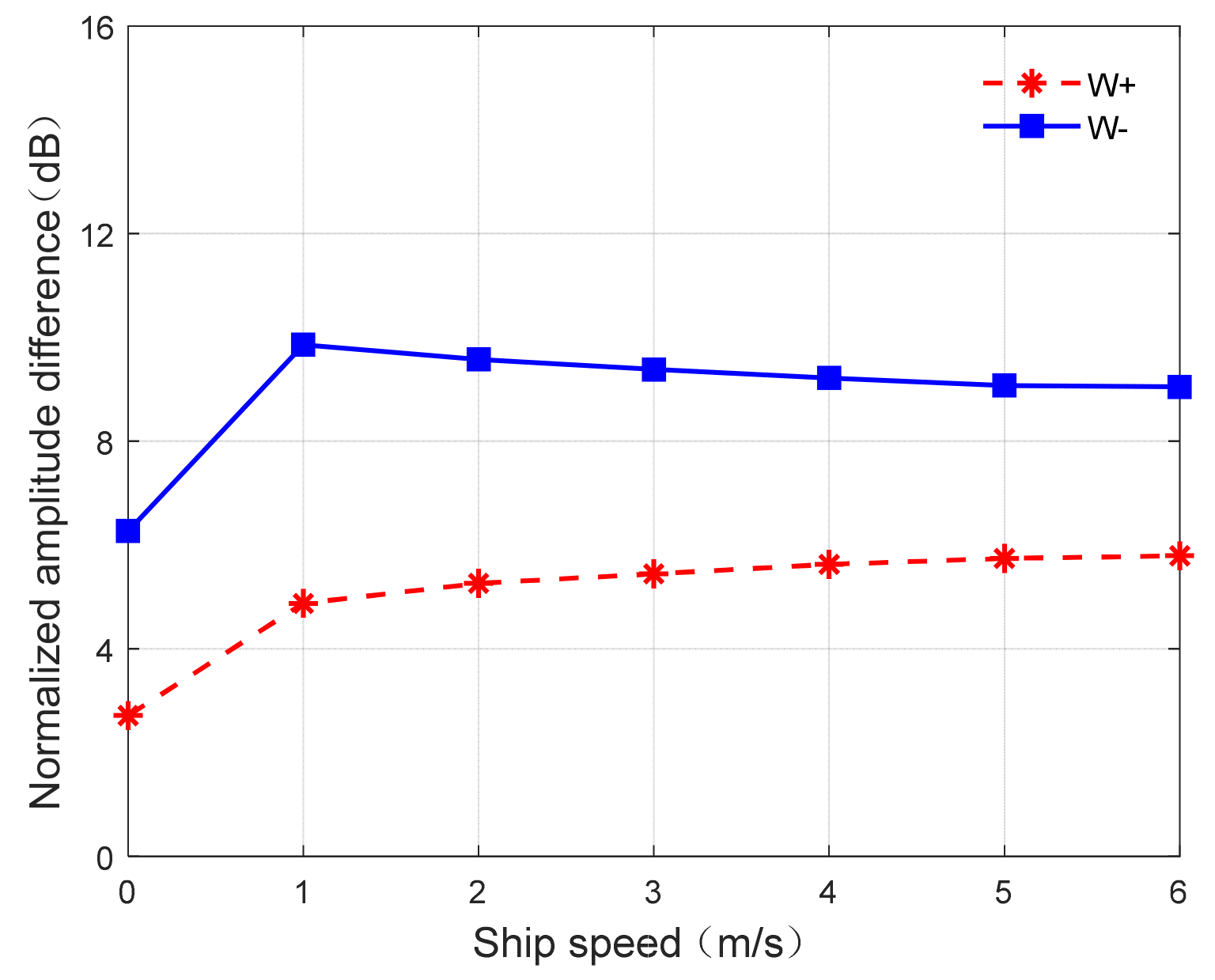
Figure 7.
Relationship between ship speed and normalized amplitude differences of boundary regions.
Figure 7.
Relationship between ship speed and normalized amplitude differences of boundary regions.
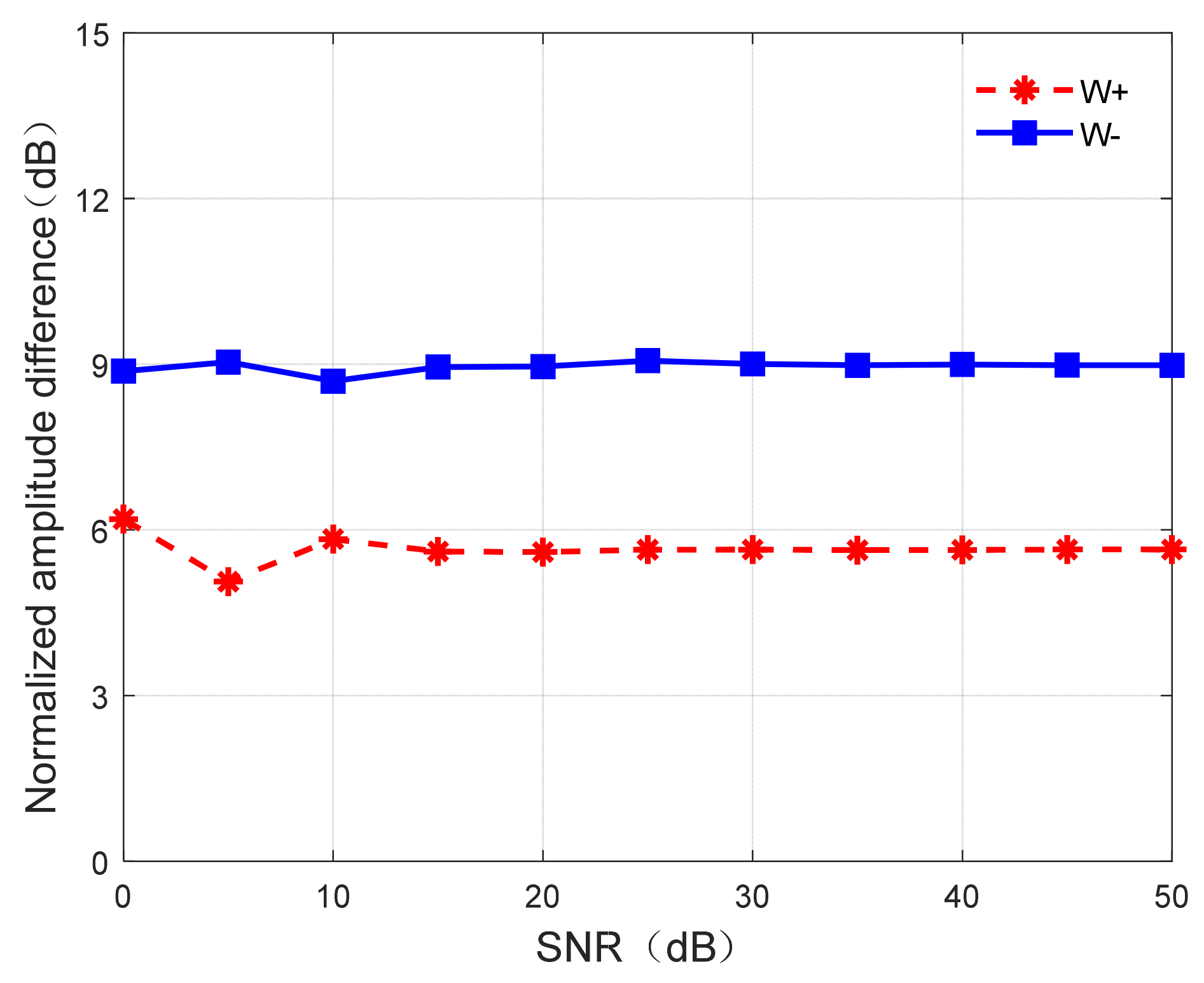
Figure 8.
Relationship between noise and normalized amplitude differences of boundary regions.
Figure 8.
Relationship between noise and normalized amplitude differences of boundary regions.
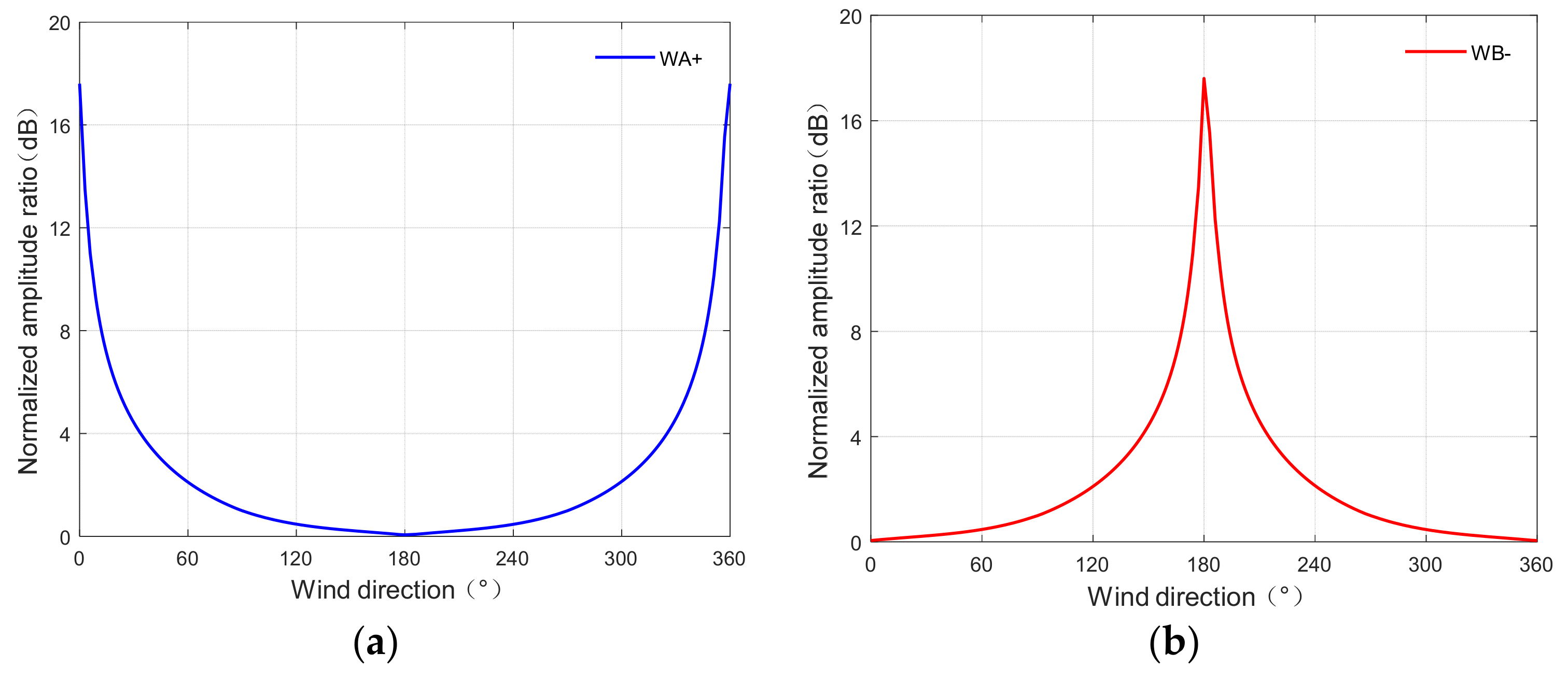
Figure 9.
Relationship between the normalized amplitude ratios of broadened regions and the wind direction: (a) Normalized amplitude ratios of the positive-to-negative broadened region. (b) Normalized amplitude ratios of the negative-to-positive broadened region.
Figure 9.
Relationship between the normalized amplitude ratios of broadened regions and the wind direction: (a) Normalized amplitude ratios of the positive-to-negative broadened region. (b) Normalized amplitude ratios of the negative-to-positive broadened region.
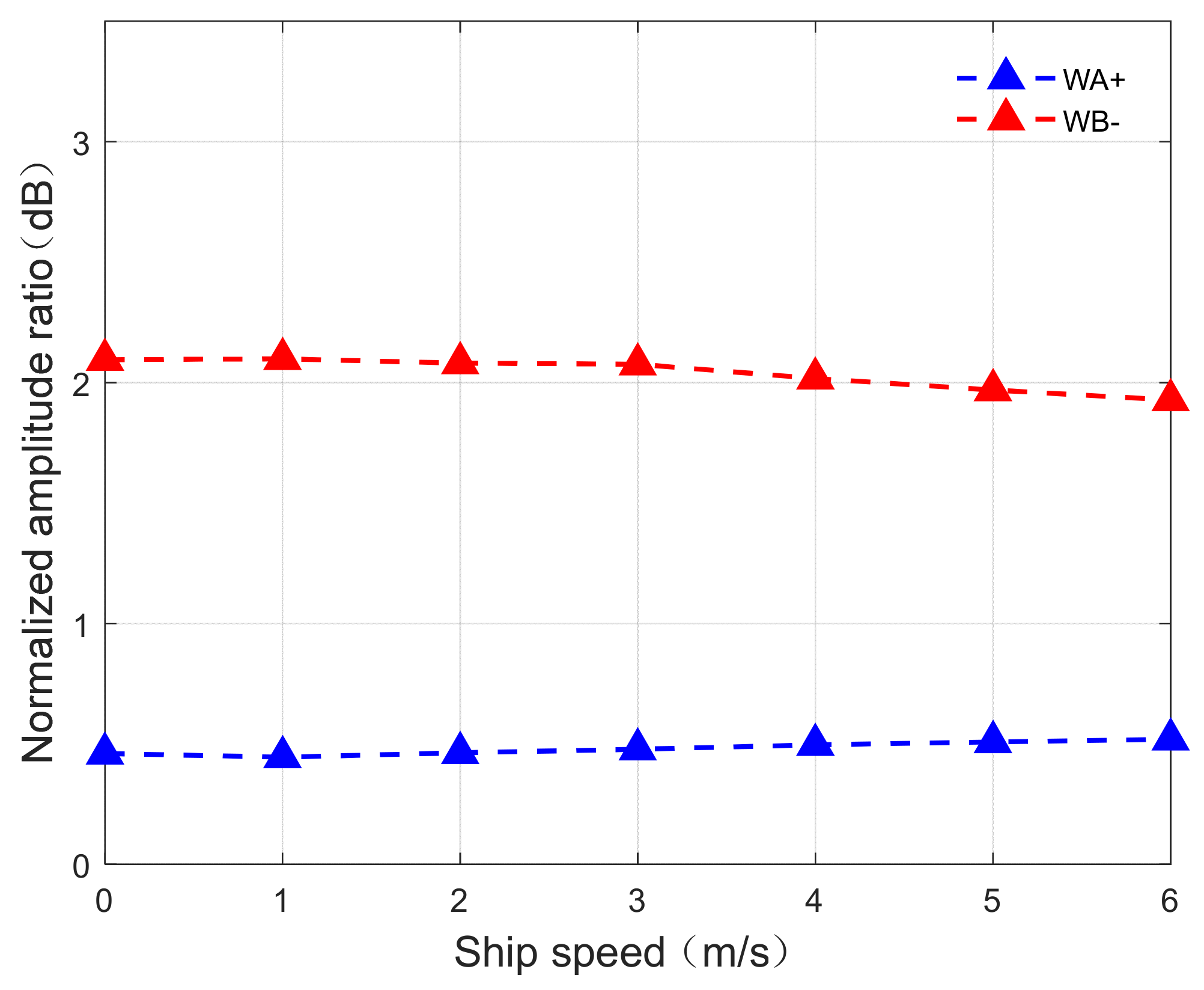
Figure 10.
Relationship between the ship speed and the normalized amplitude ratios of the broadened regions.
Figure 10.
Relationship between the ship speed and the normalized amplitude ratios of the broadened regions.
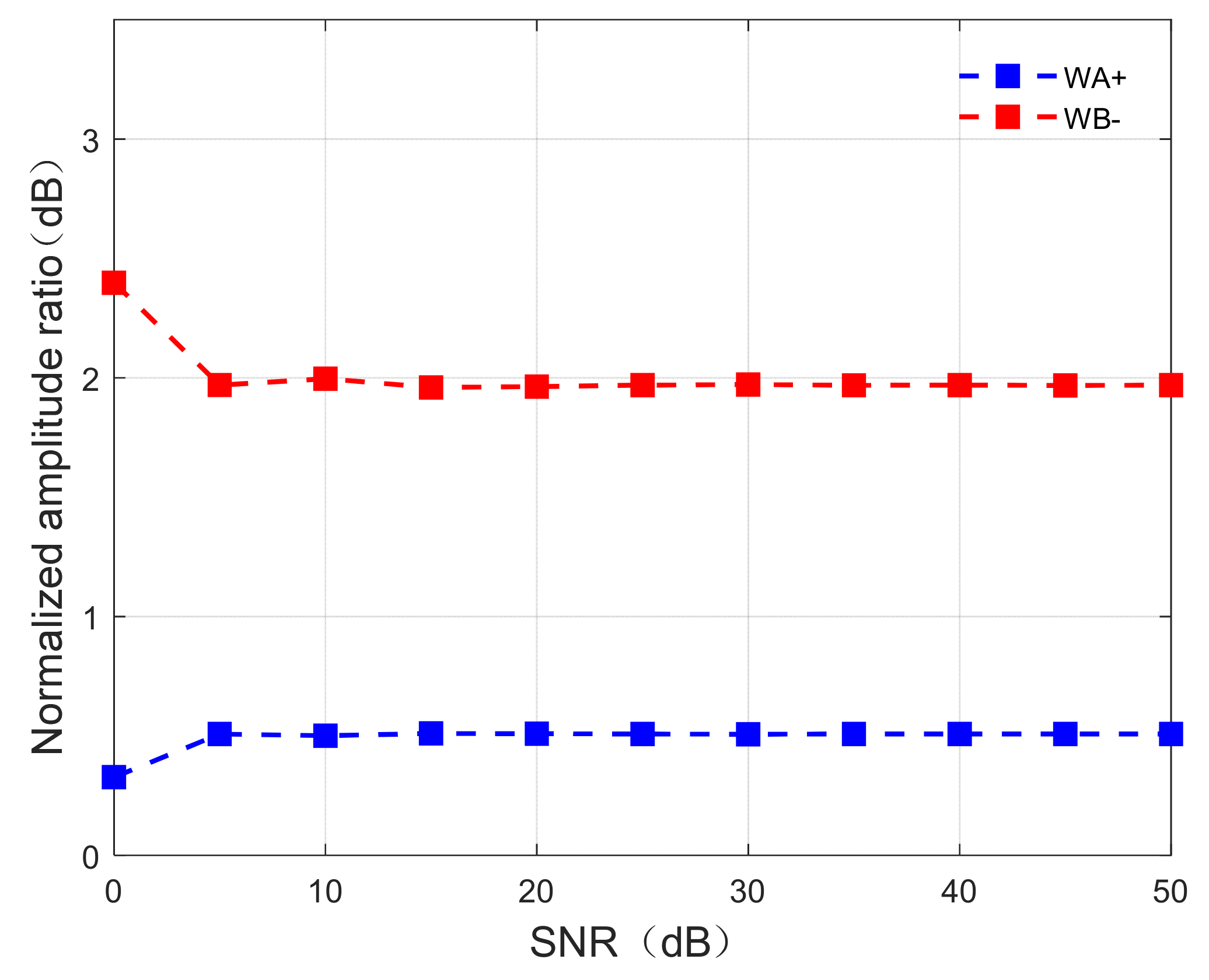
Figure 11.
Relationship between noise and the normalized amplitude ratios of the broadened regions.
Figure 11.
Relationship between noise and the normalized amplitude ratios of the broadened regions.
Figure 12.
Diagram between the wind direction and the radar beam: (a) The wind direction of 156° estimation solution. (b) The wind direction of 240° estimation solution.
Figure 12.
Diagram between the wind direction and the radar beam: (a) The wind direction of 156° estimation solution. (b) The wind direction of 240° estimation solution.
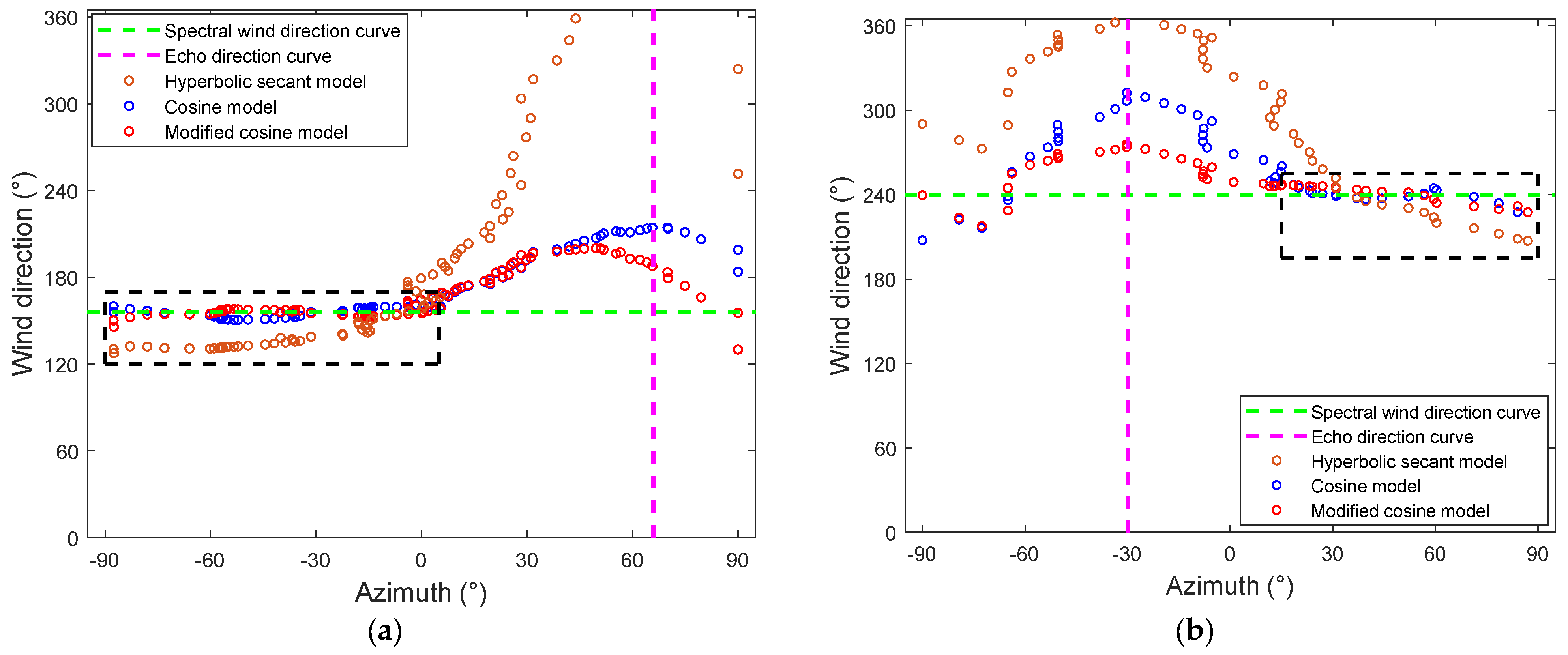
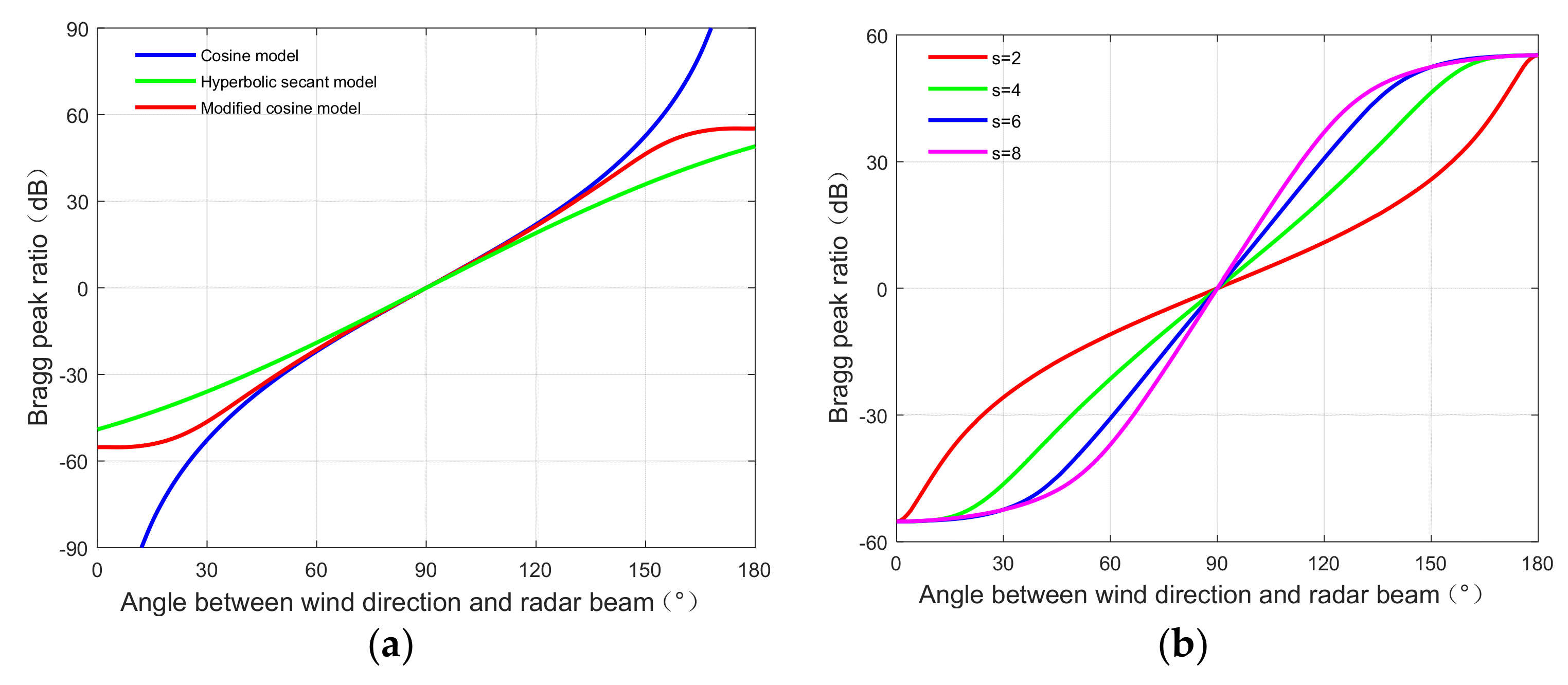
Figure 13.
Relationship between the Bragg peak ratio and the included angle of wind direction and radar beam: (a) Solutions corresponding to three wave directional spreading models. (b) Solutions corresponding to different spreading parameters.
Figure 13.
Relationship between the Bragg peak ratio and the included angle of wind direction and radar beam: (a) Solutions corresponding to three wave directional spreading models. (b) Solutions corresponding to different spreading parameters.
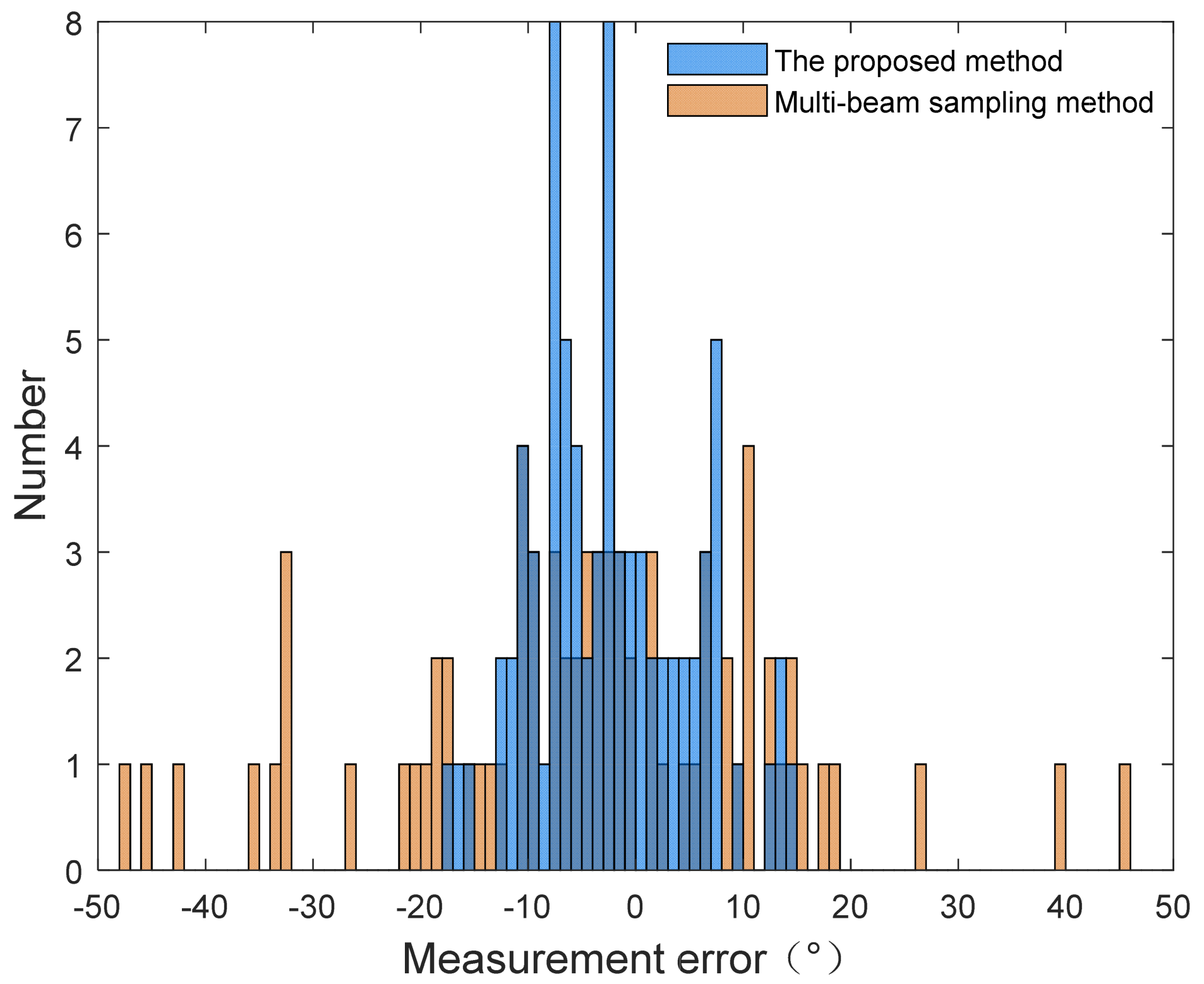
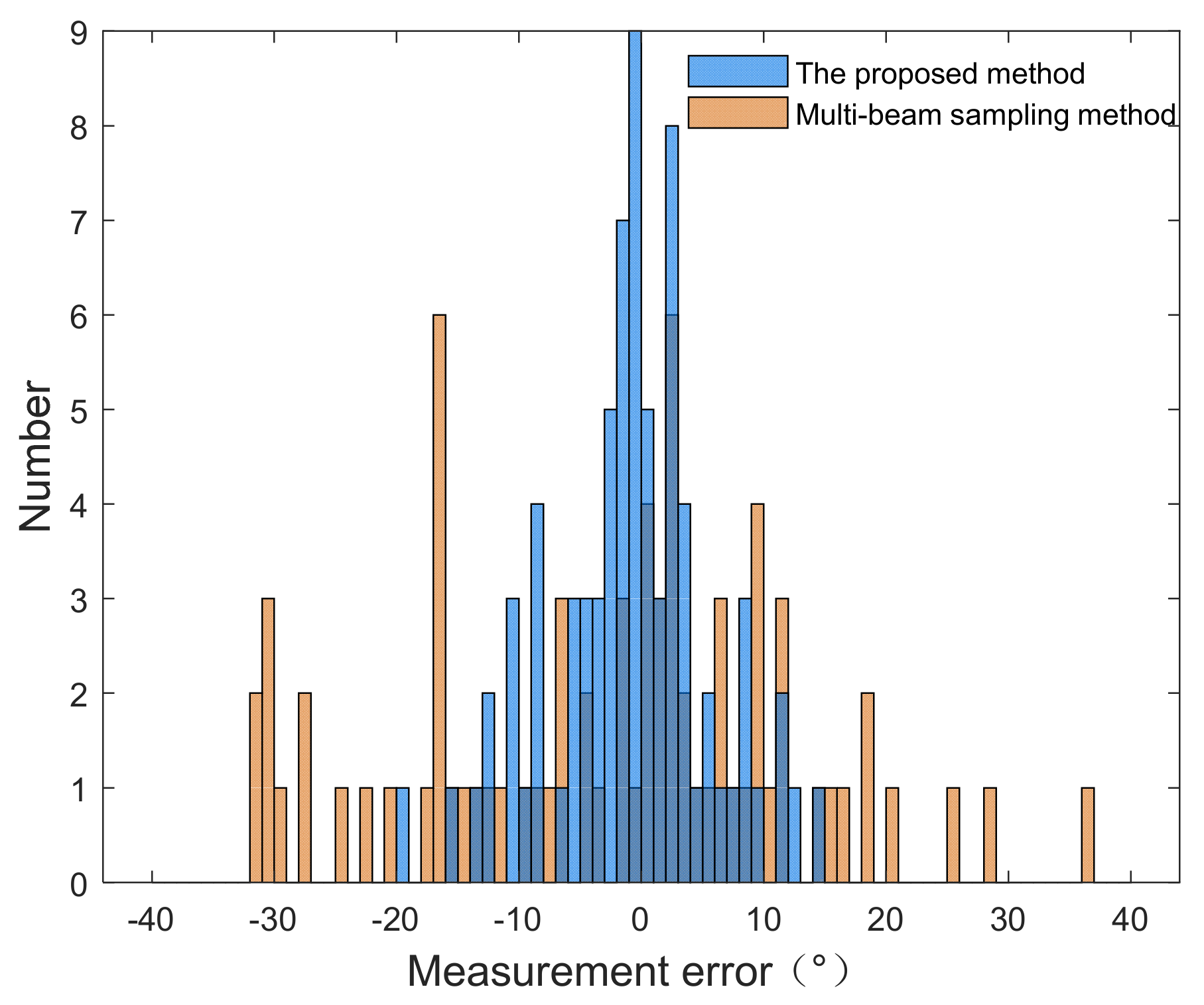
Figure 14.
Histograms of wind direction measurement error: (a) The proposed method. (b) The multi-beam sampling method.
Figure 14.
Histograms of wind direction measurement error: (a) The proposed method. (b) The multi-beam sampling method.
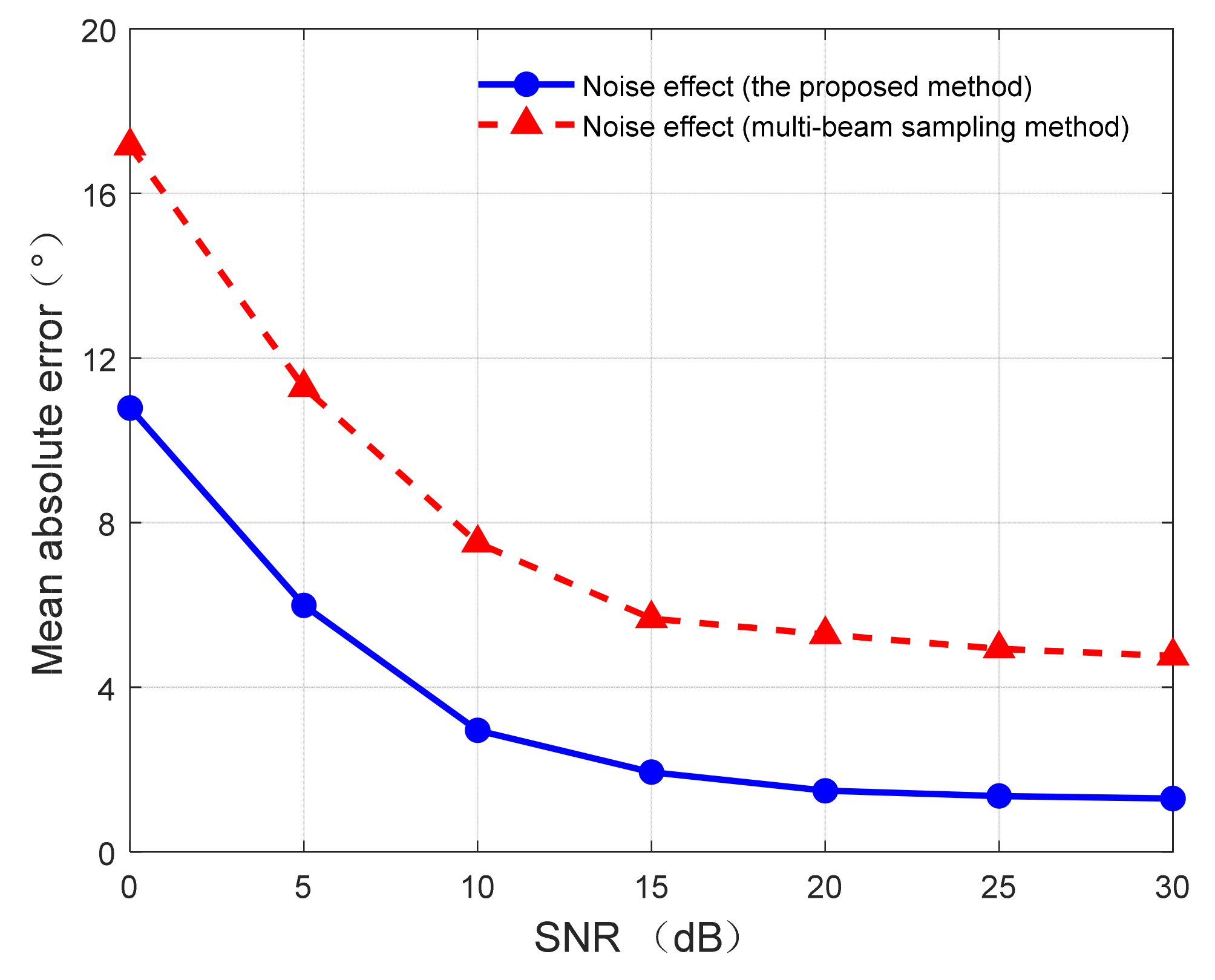
Figure 15.
Diagram between the wind direction error and SNR.
Figure 15.
Diagram between the wind direction error and SNR.
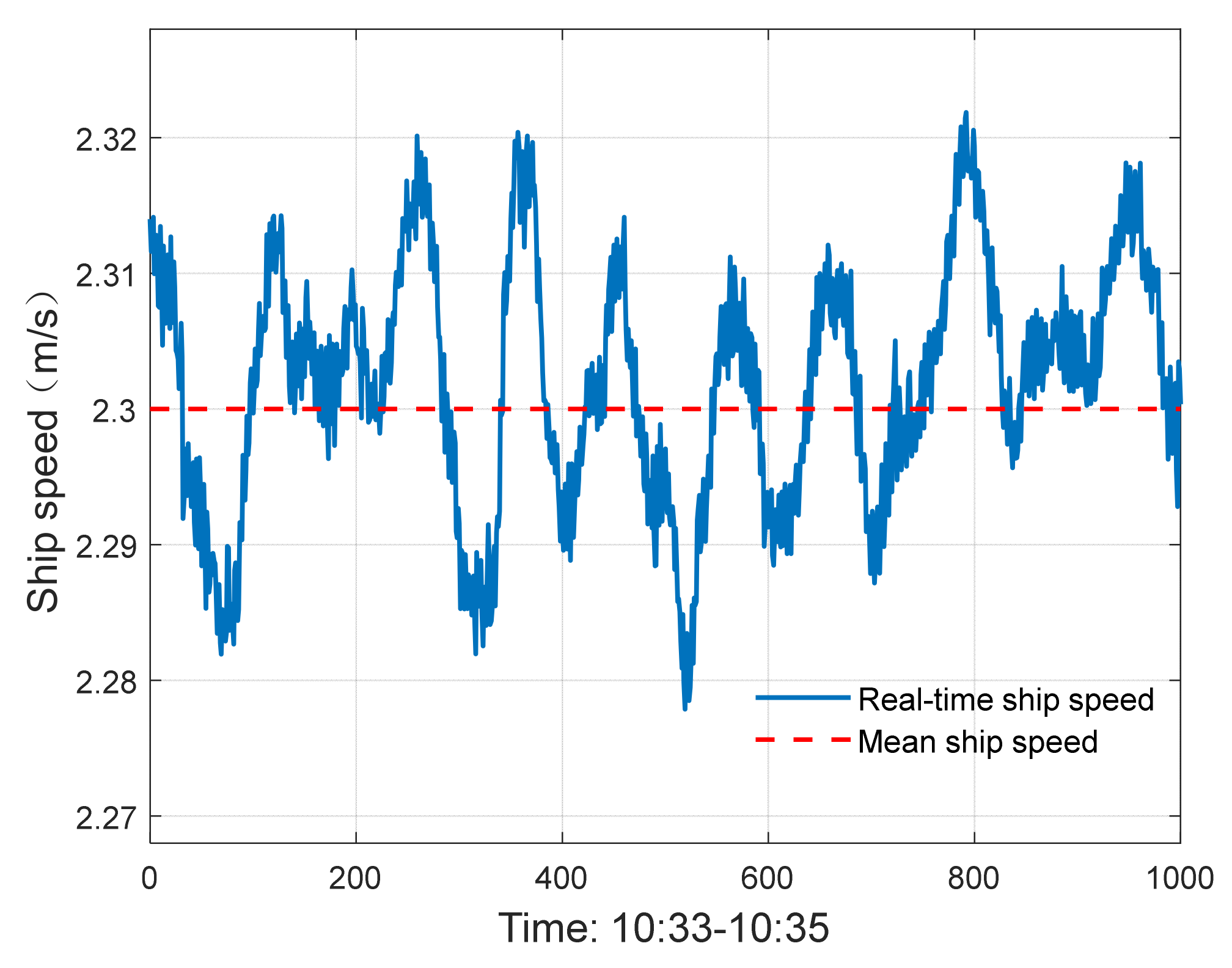
Figure 16.
Real-time ship speed.
Figure 16.
Real-time ship speed.
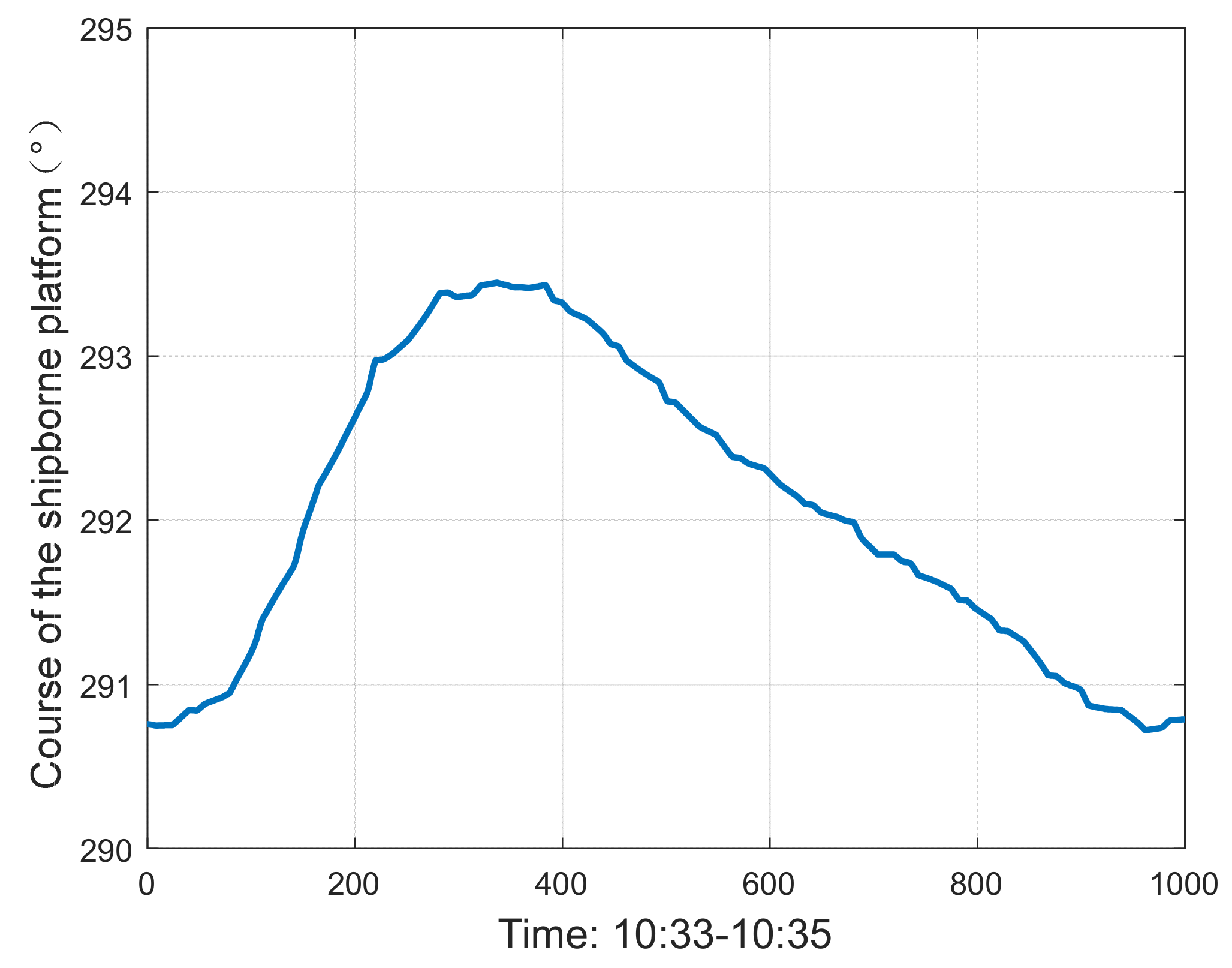
Figure 17.
Real-time course of the shipborne platform.
Figure 17.
Real-time course of the shipborne platform.
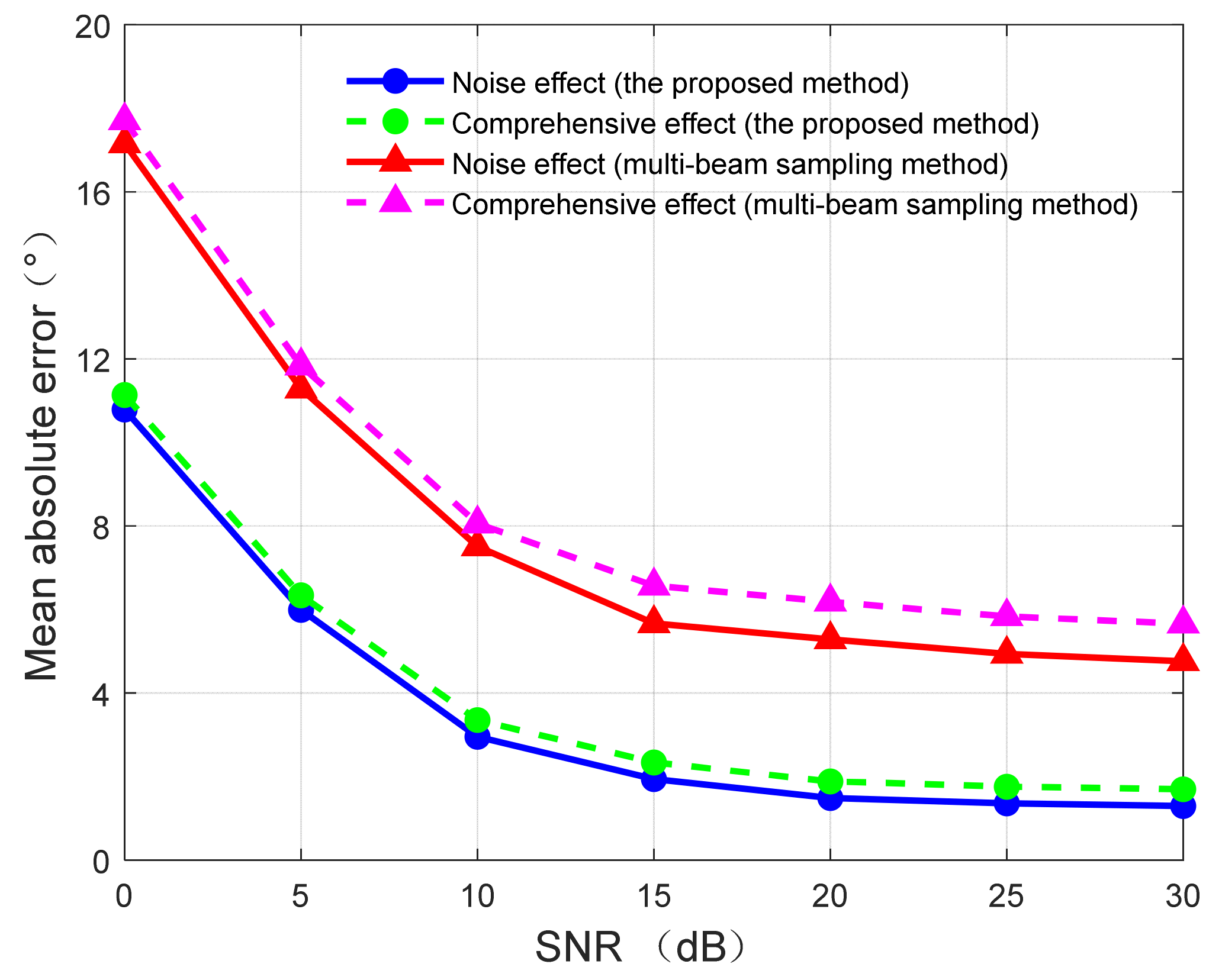
Figure 18.
Diagram between wind direction estimation error and comprehensive factors.
Figure 18.
Diagram between wind direction estimation error and comprehensive factors.
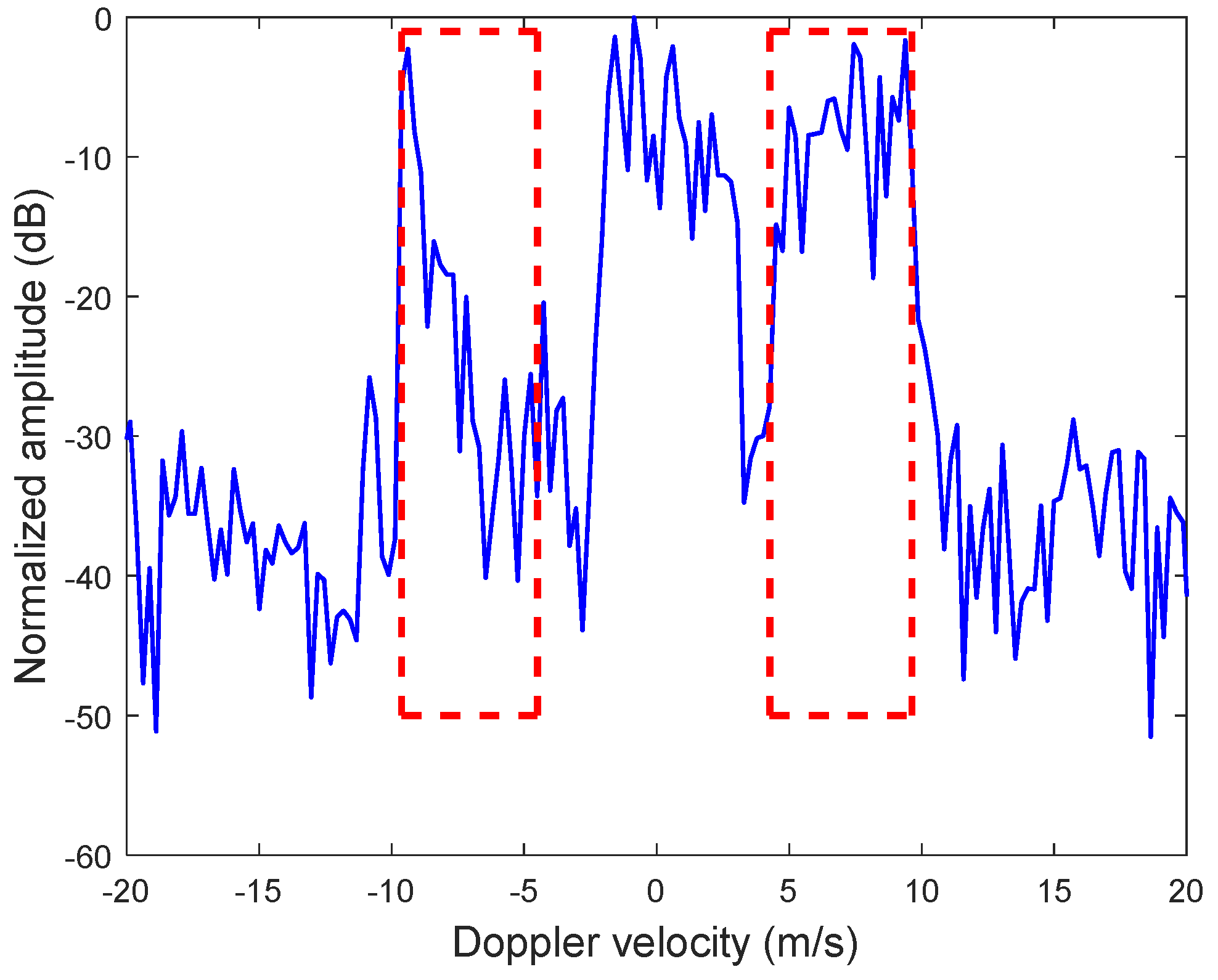
Figure 19.
Radar-measured Doppler spectrum for experiment I.
Figure 19.
Radar-measured Doppler spectrum for experiment I.
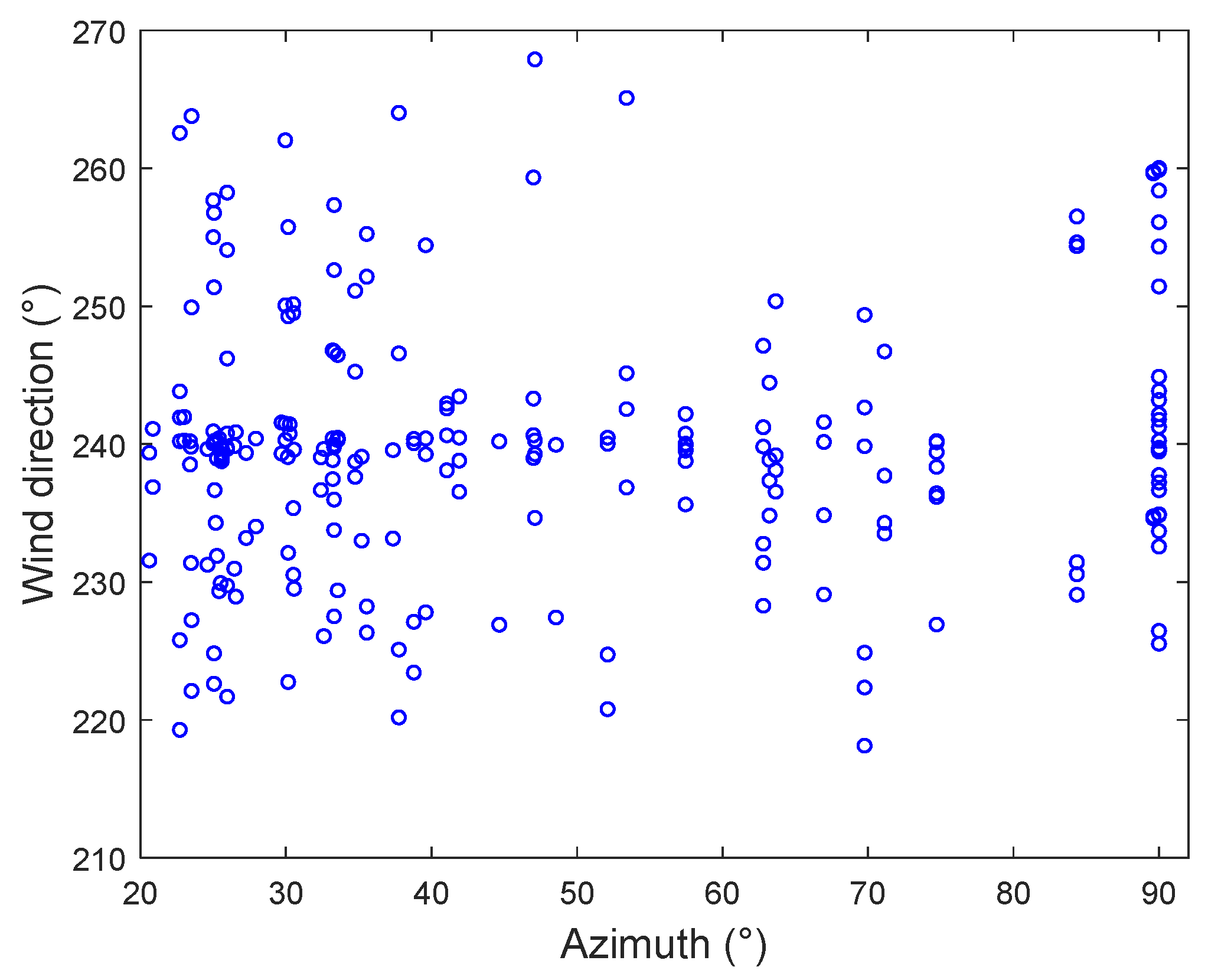
Figure 20.
Statistical results of wind direction measurement from experiment I.
Figure 20.
Statistical results of wind direction measurement from experiment I.
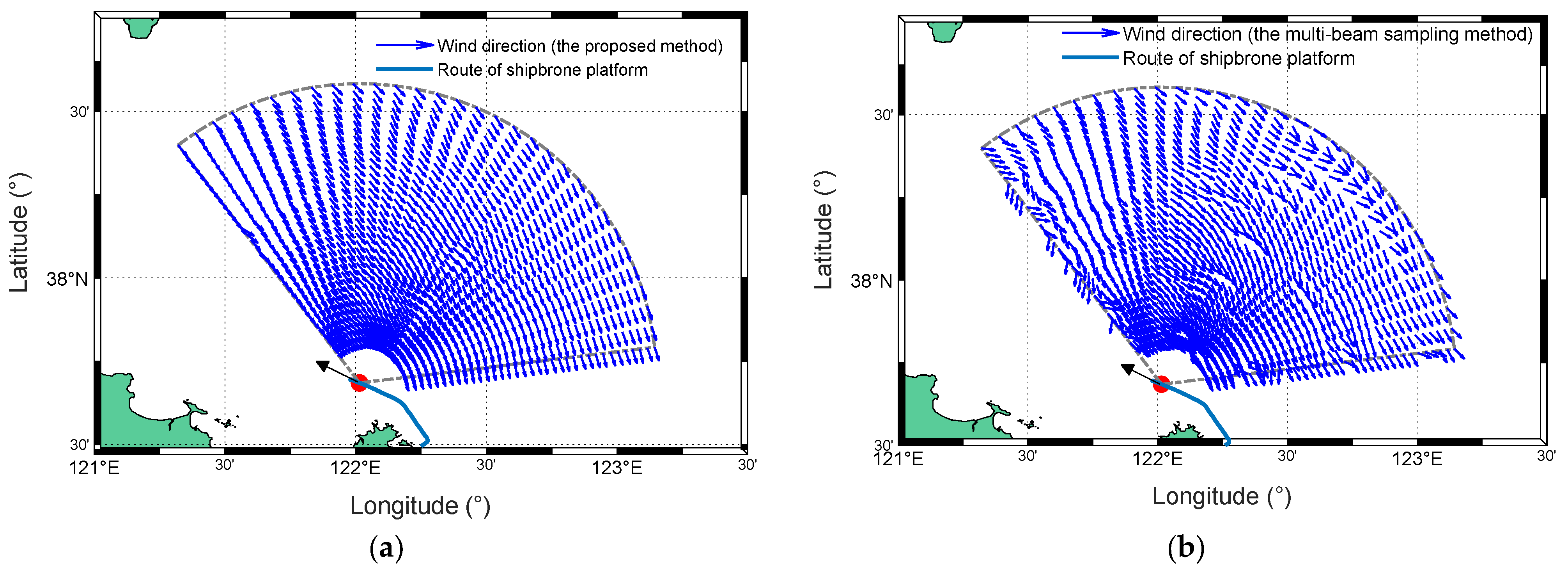
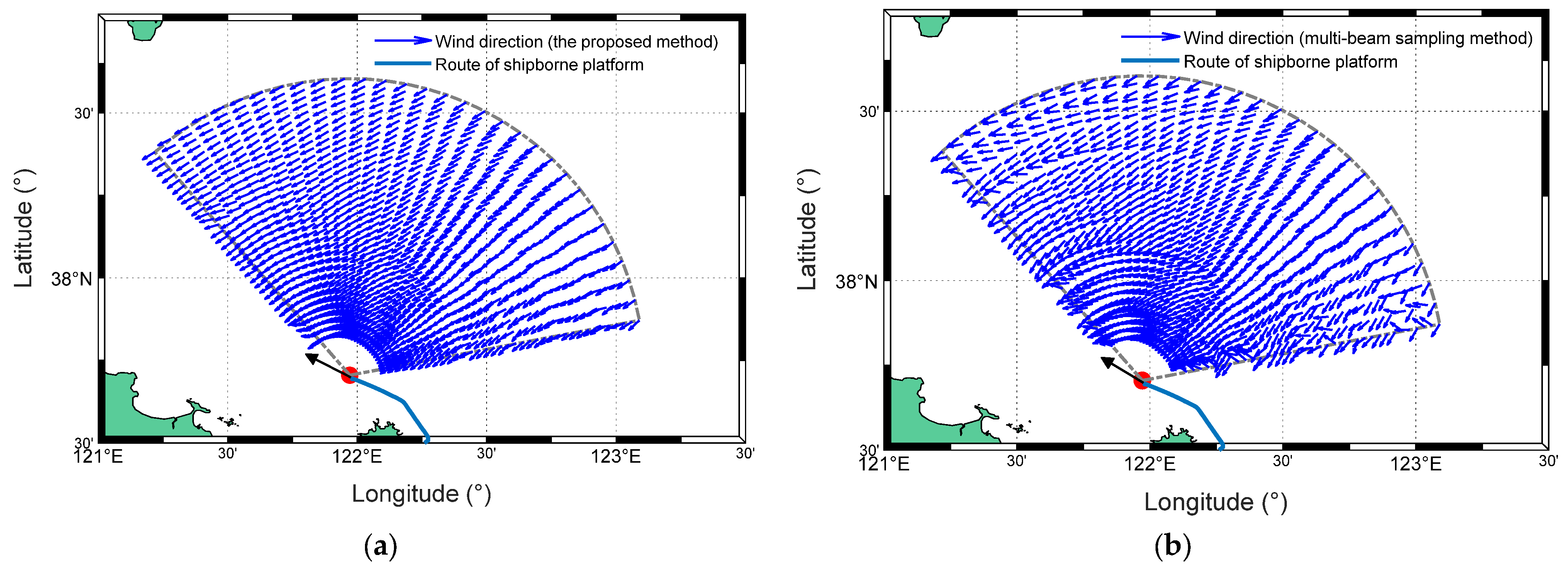
Figure 21.
Radar-measured wind direction maps with modified cosine model from experiment I: (a) The proposed method. (b) The multi-beam sampling method.
Figure 21.
Radar-measured wind direction maps with modified cosine model from experiment I: (a) The proposed method. (b) The multi-beam sampling method.
Figure 22.
Histograms of radar-measured wind field with modified cosine model from experiment I: (a) The proposed method. (b) The multi-beam sampling method.
Figure 22.
Histograms of radar-measured wind field with modified cosine model from experiment I: (a) The proposed method. (b) The multi-beam sampling method.
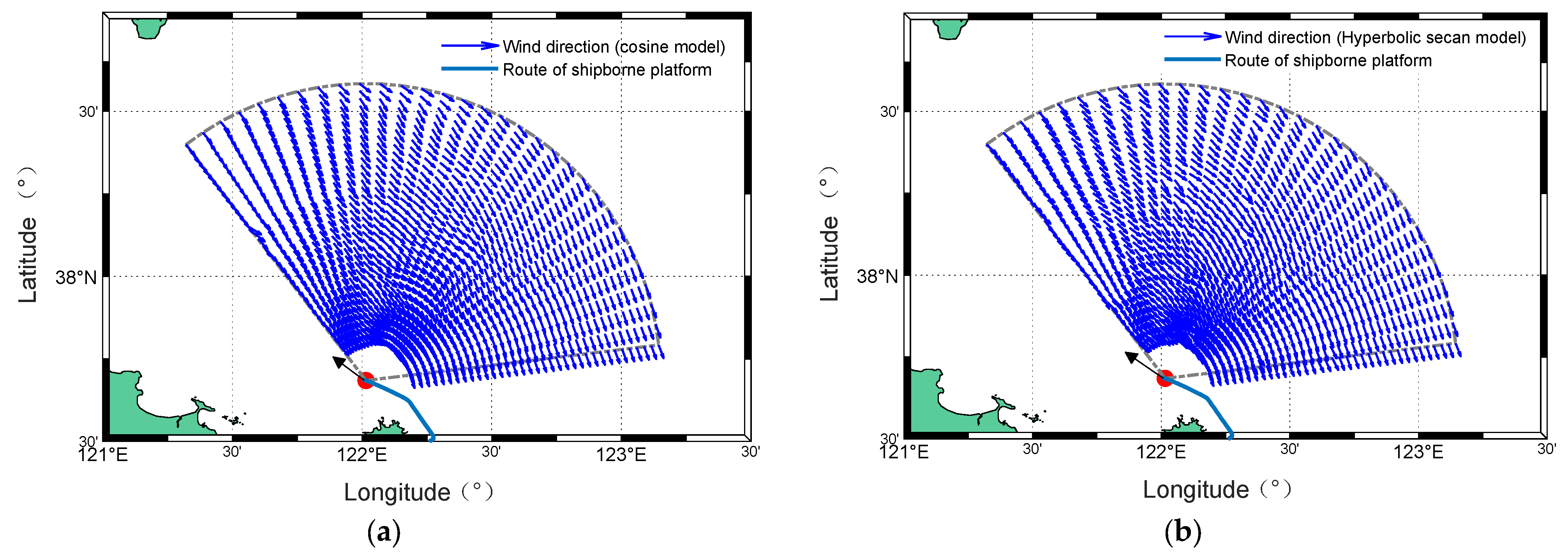
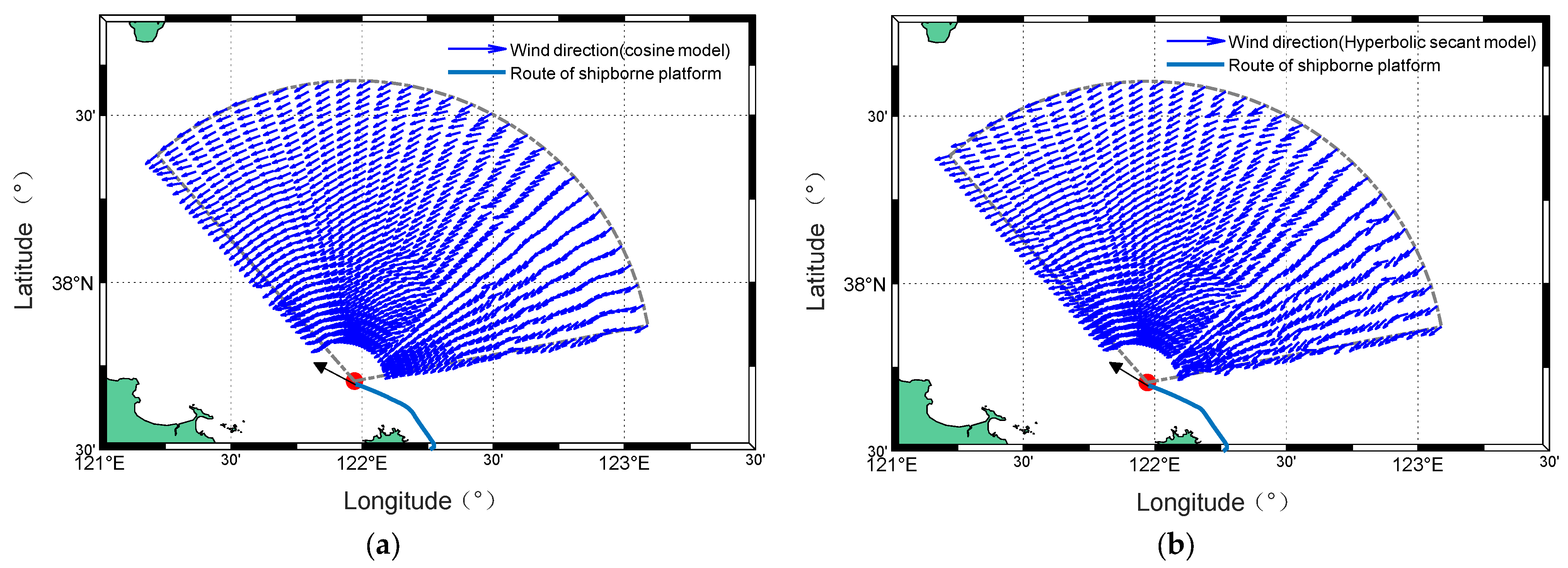
Figure 23.
Radar-measured wind direction maps under two models from experiment I: (a) Cosine model. (b) Hyperbolic secant model.
Figure 23.
Radar-measured wind direction maps under two models from experiment I: (a) Cosine model. (b) Hyperbolic secant model.
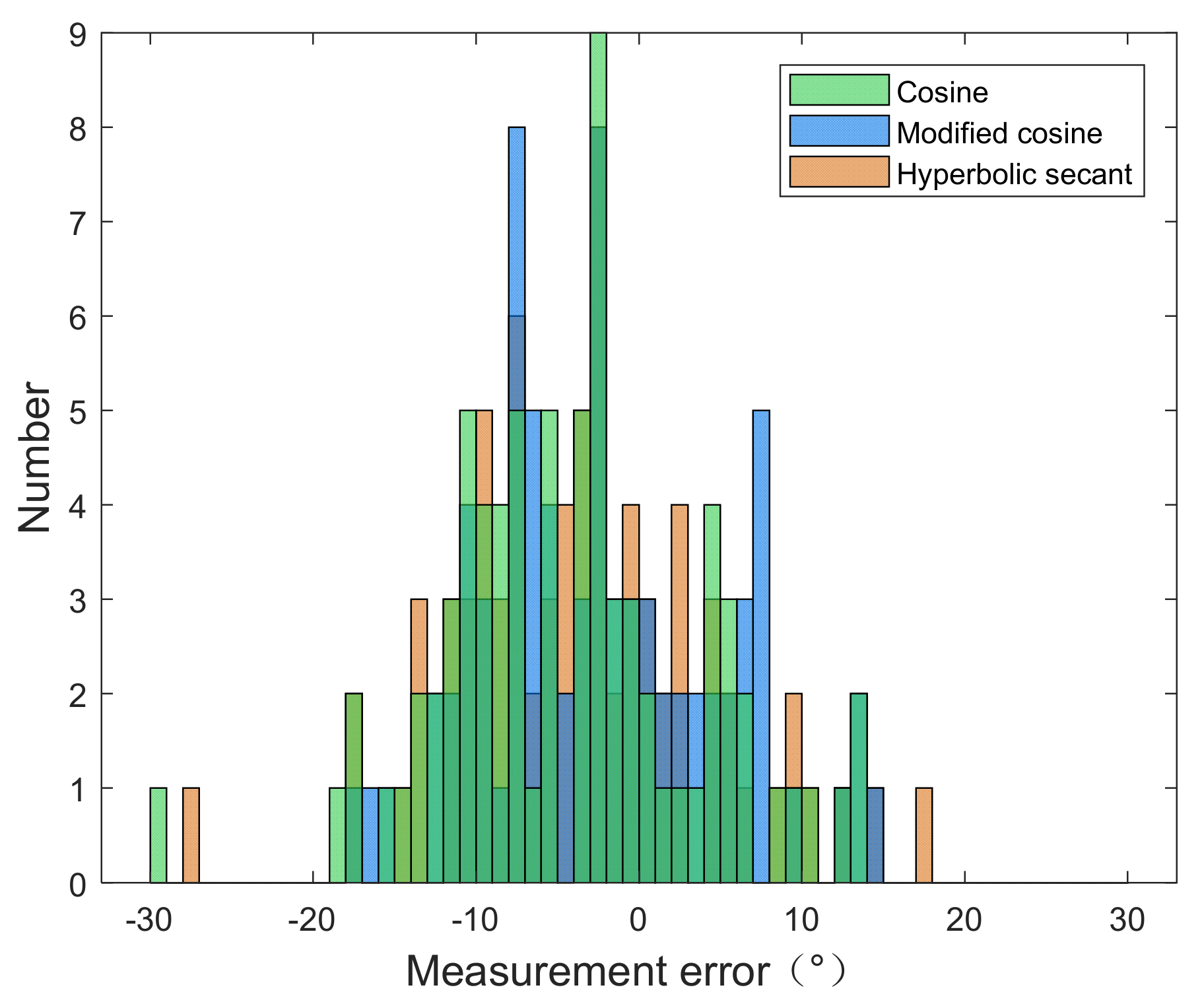
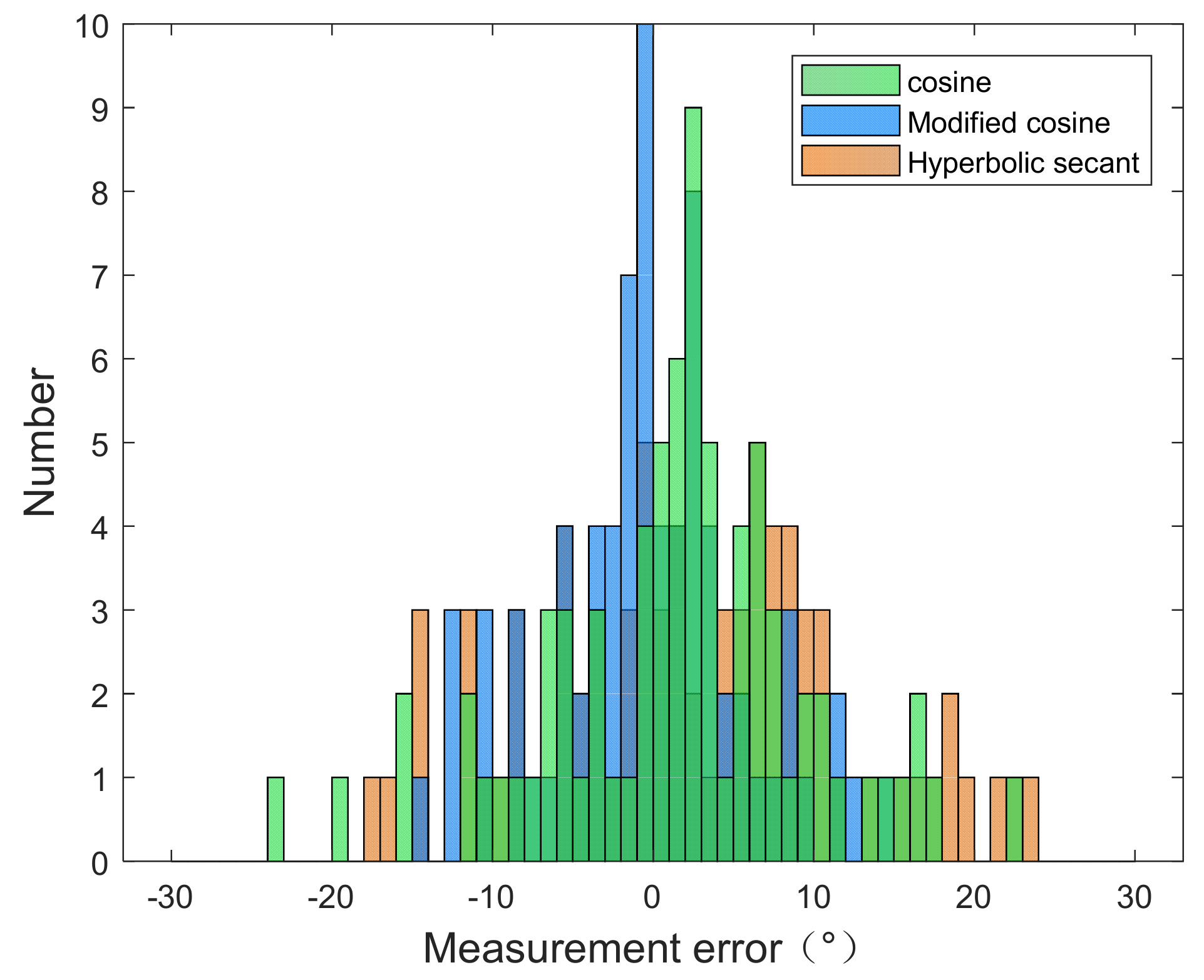
Figure 24.
Histograms of radar-measured wind field with two models from experiment I: (a) Cosine model. (b) Hyperbolic secant model.
Figure 24.
Histograms of radar-measured wind field with two models from experiment I: (a) Cosine model. (b) Hyperbolic secant model.
Figure 25.
Radar-measured Doppler spectrum for experiment II.
Figure 25.
Radar-measured Doppler spectrum for experiment II.
Figure 26.
Statistical results of wind direction measurement from experiment II.
Figure 26.
Statistical results of wind direction measurement from experiment II.
Figure 27.
Radar-measured wind direction maps with modified cosine model from experiment II: (a) The proposed method. (b) The multi-beam sampling method.
Figure 27.
Radar-measured wind direction maps with modified cosine model from experiment II: (a) The proposed method. (b) The multi-beam sampling method.
Figure 28.
Histograms of radar-measured wind field with modified cosine model from experiment II: (a) The proposed method. (b) The multi-beam sampling method.
Figure 28.
Histograms of radar-measured wind field with modified cosine model from experiment II: (a) The proposed method. (b) The multi-beam sampling method.
Figure 29.
Radar-measured wind direction maps with the two models from experiment II: (a) Cosine model. (b) Hyperbolic secant model.
Figure 29.
Radar-measured wind direction maps with the two models from experiment II: (a) Cosine model. (b) Hyperbolic secant model.
Figure 30.
Histograms of radar-measured wind field under the two models from experiment II: (a) Cosine model. (b) Hyperbolic secant model.
Figure 30.
Histograms of radar-measured wind field under the two models from experiment II: (a) Cosine model. (b) Hyperbolic secant model.
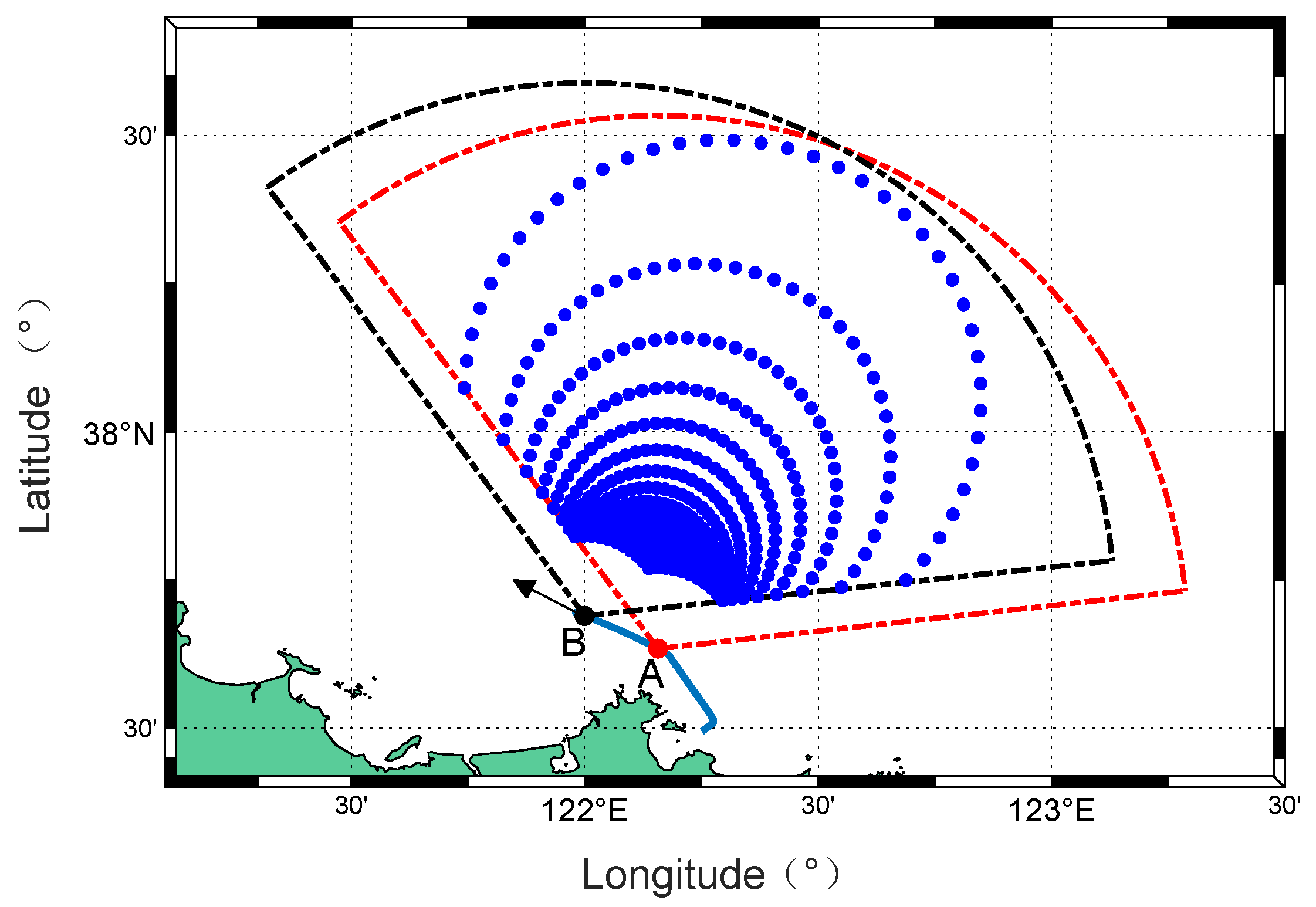
Figure 31.
Sailing diagram of the shipborne platform.
Figure 31.
Sailing diagram of the shipborne platform.
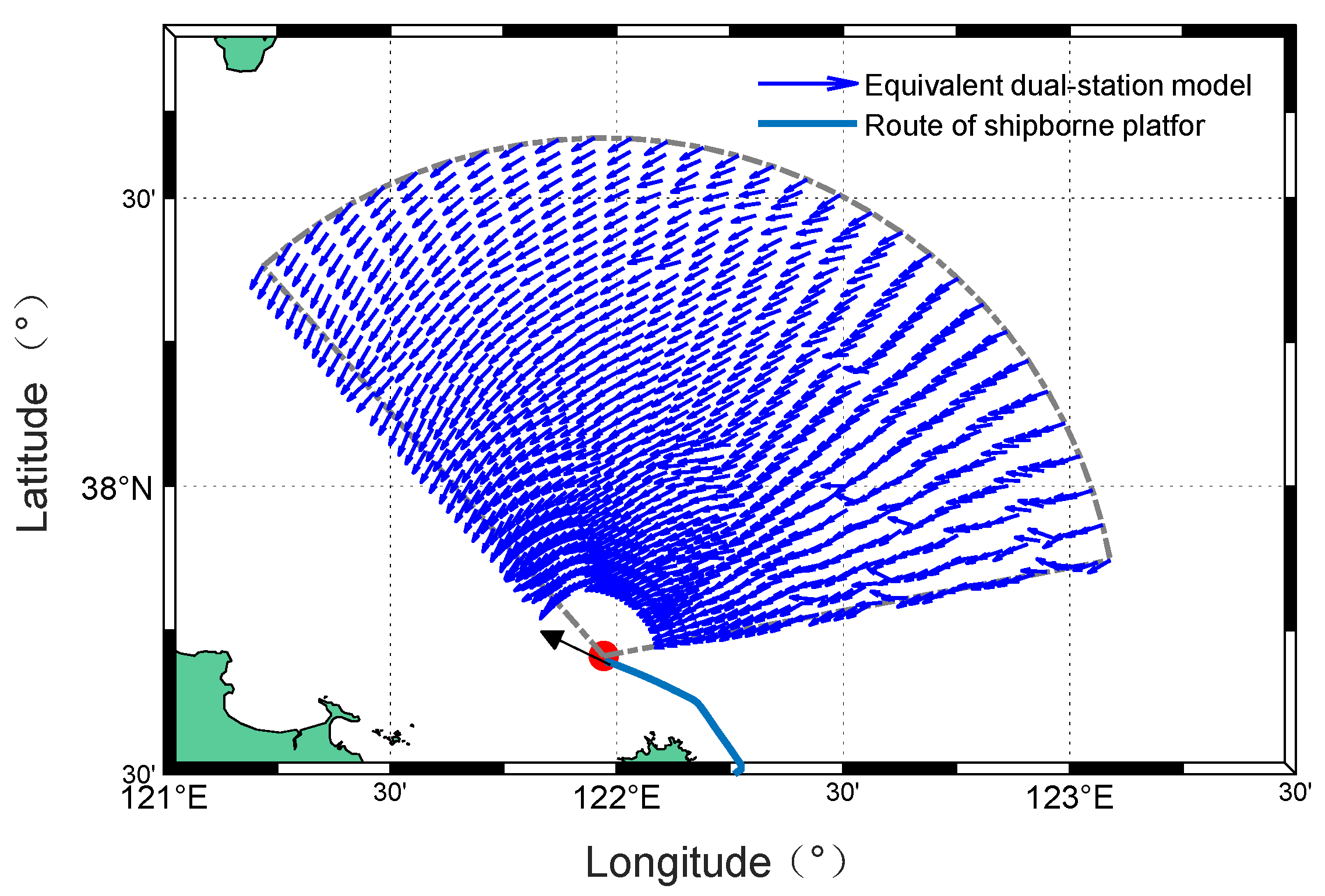
Figure 32.
Radar-B-measured wind direction map under a equivalent dual-station model from experiment III.
Figure 32.
Radar-B-measured wind direction map under a equivalent dual-station model from experiment III.
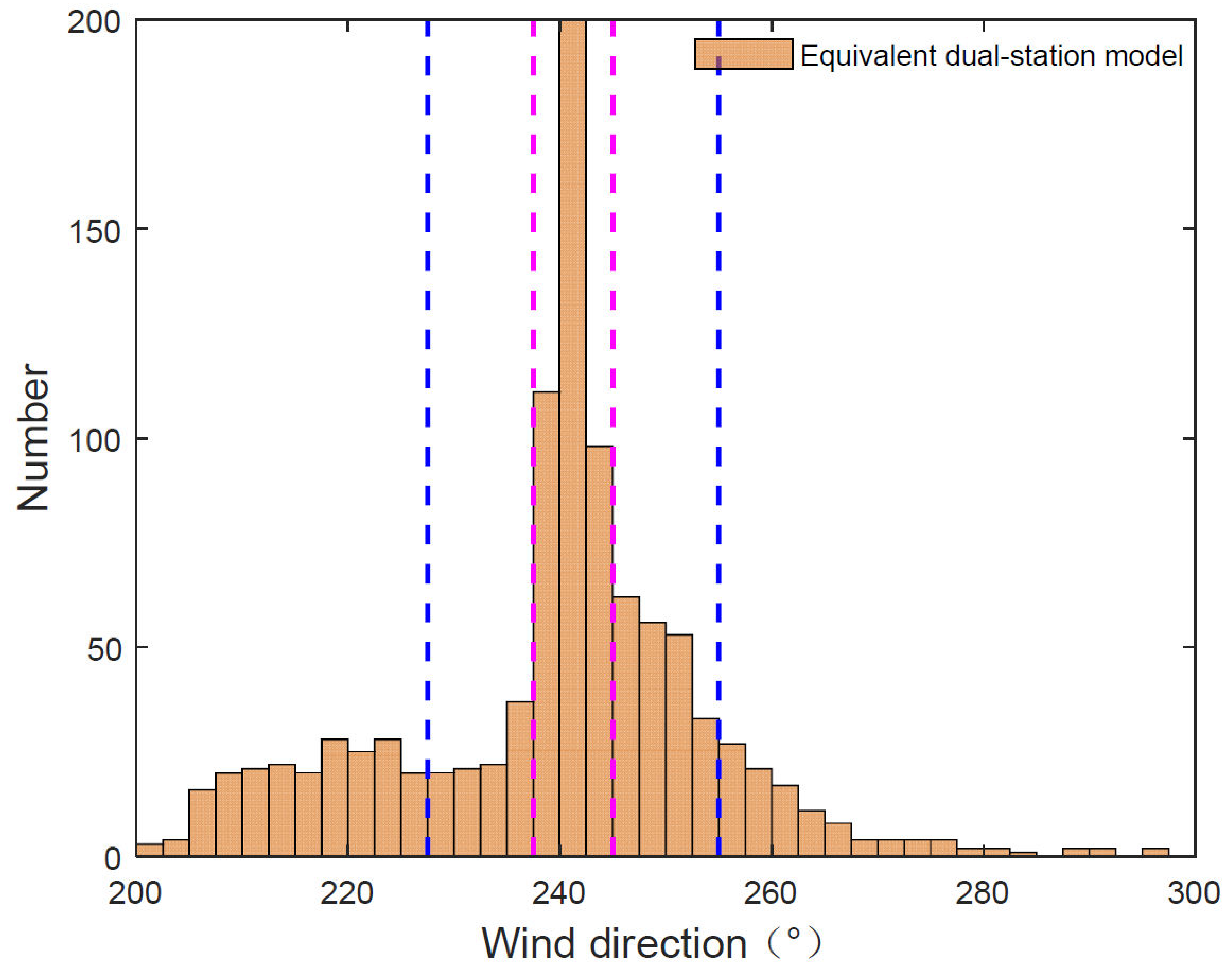
Figure 33.
Histograms of radar-measured wind field under a equivalent dual-station model from experiment III.
Figure 33.
Histograms of radar-measured wind field under a equivalent dual-station model from experiment III.
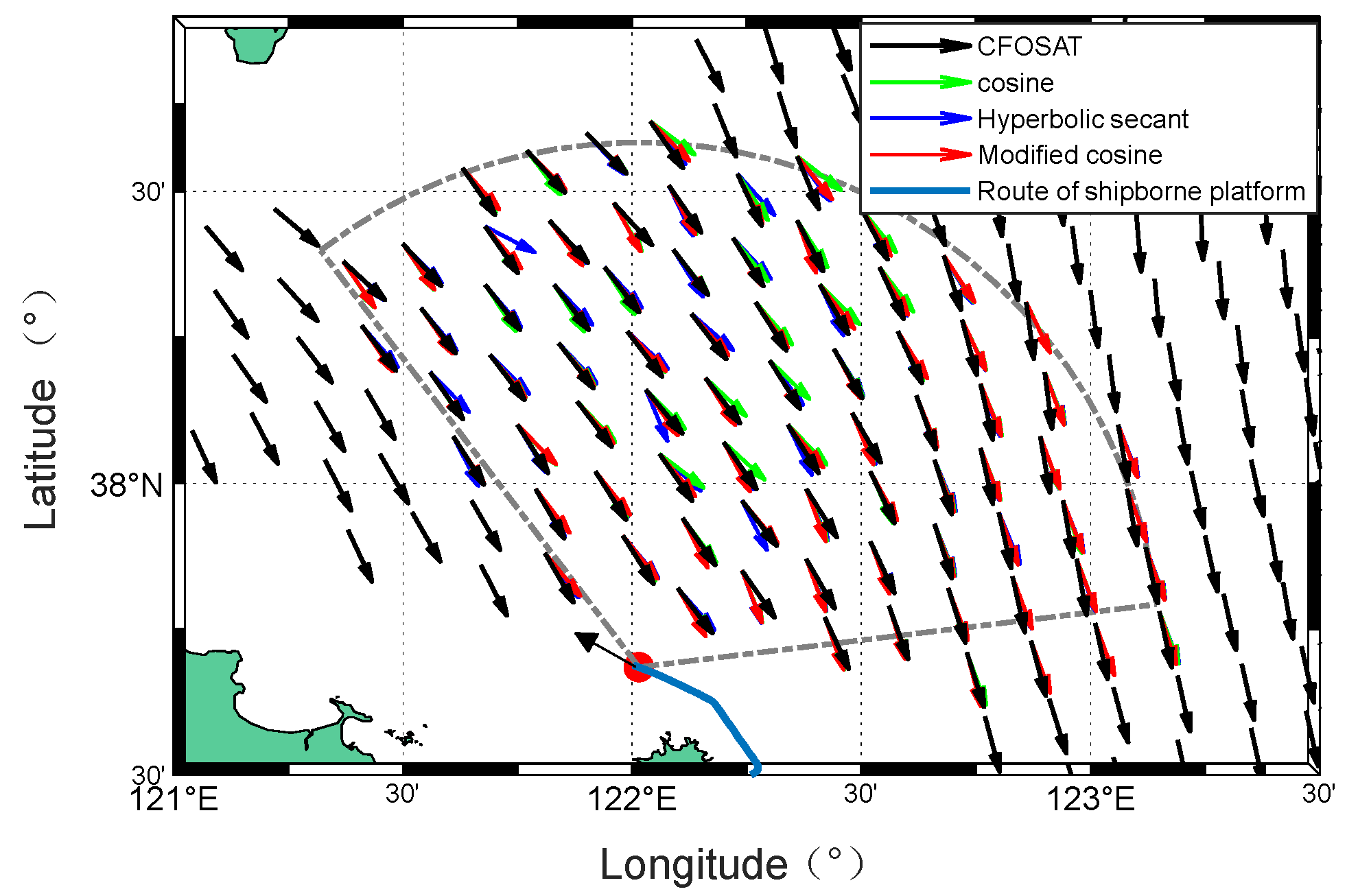
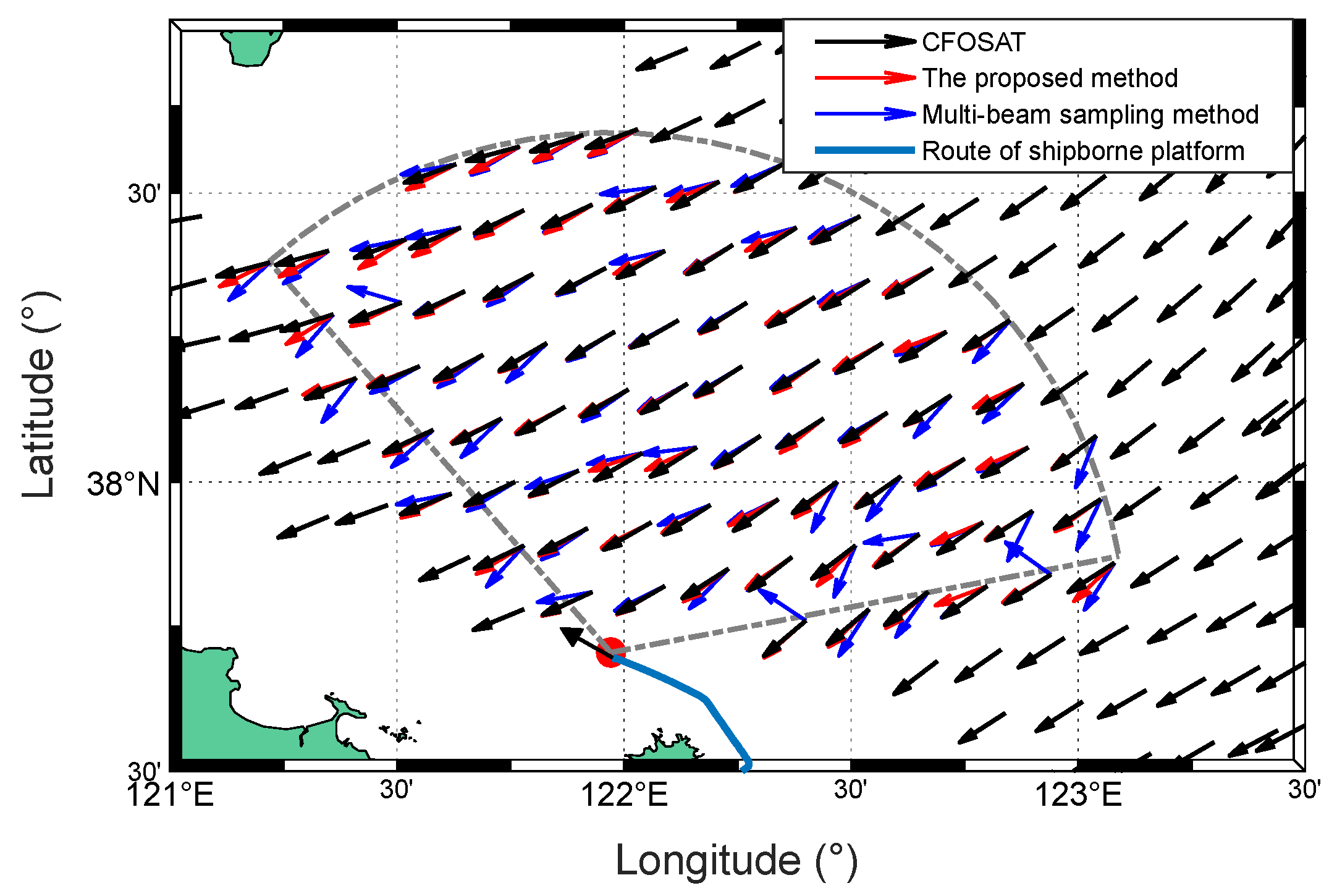
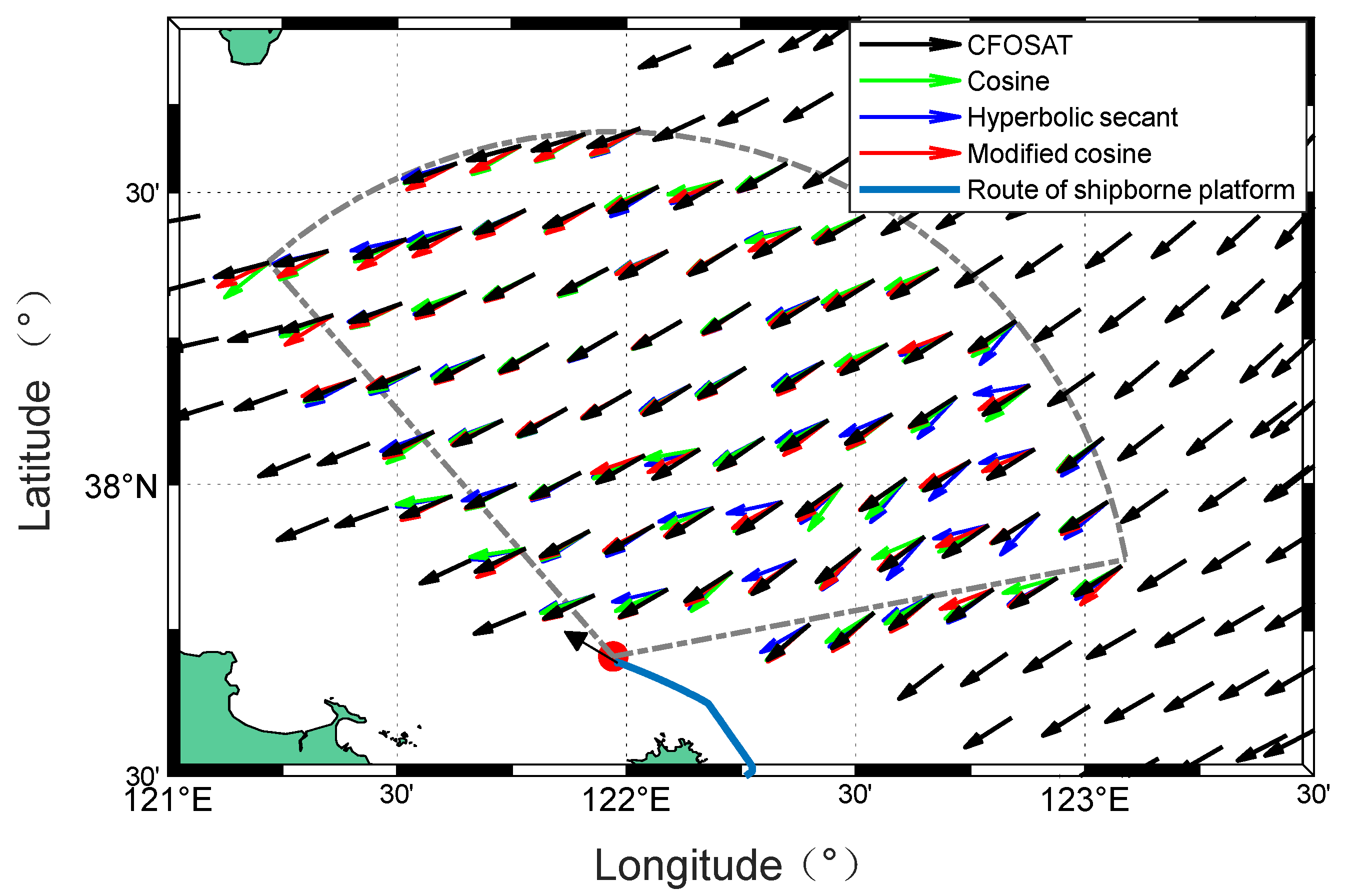
Figure 34.
Comparison of wind direction maps obtained by CFOSAT (black) and the radar (red and blue) from experiment I.
Figure 34.
Comparison of wind direction maps obtained by CFOSAT (black) and the radar (red and blue) from experiment I.
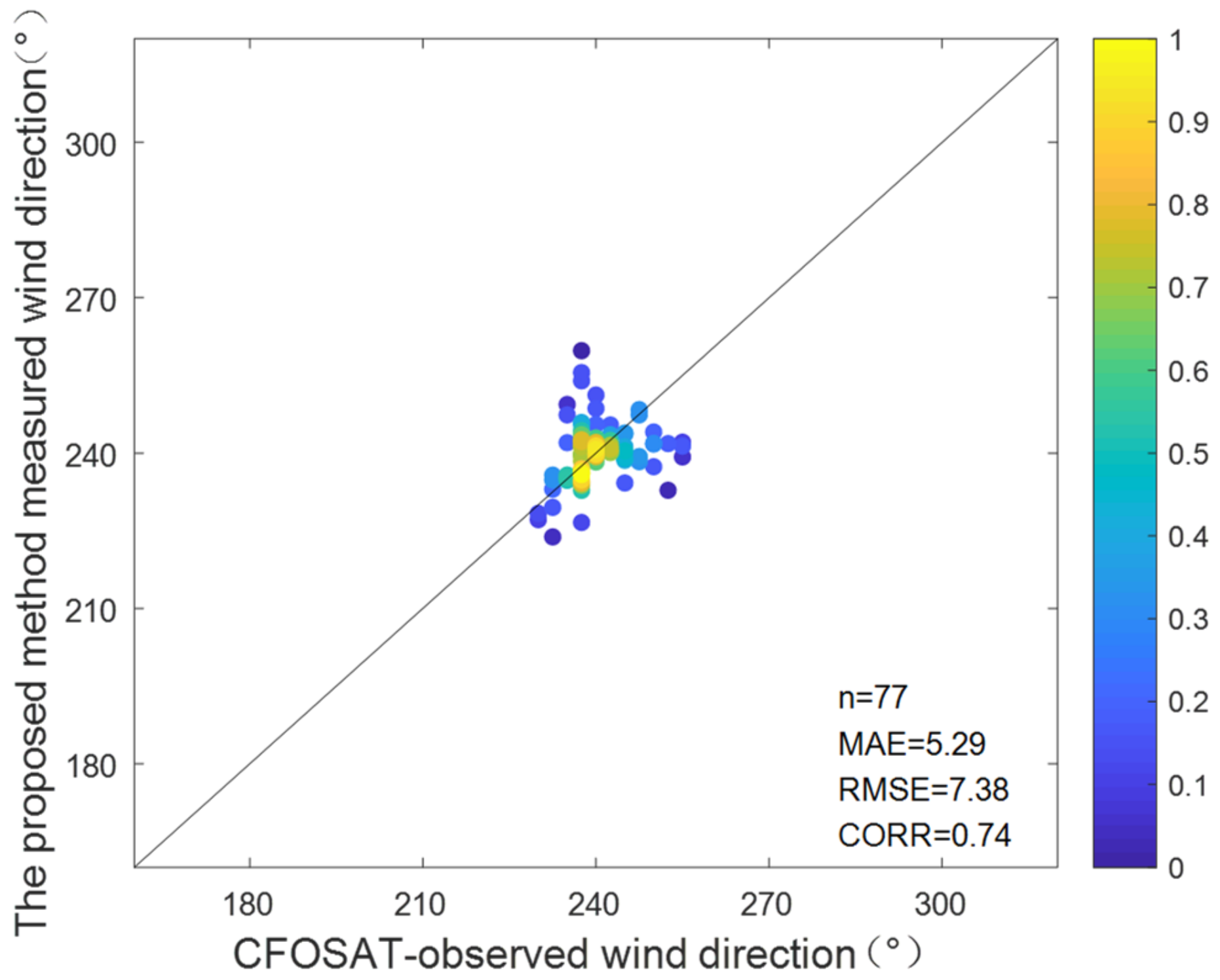
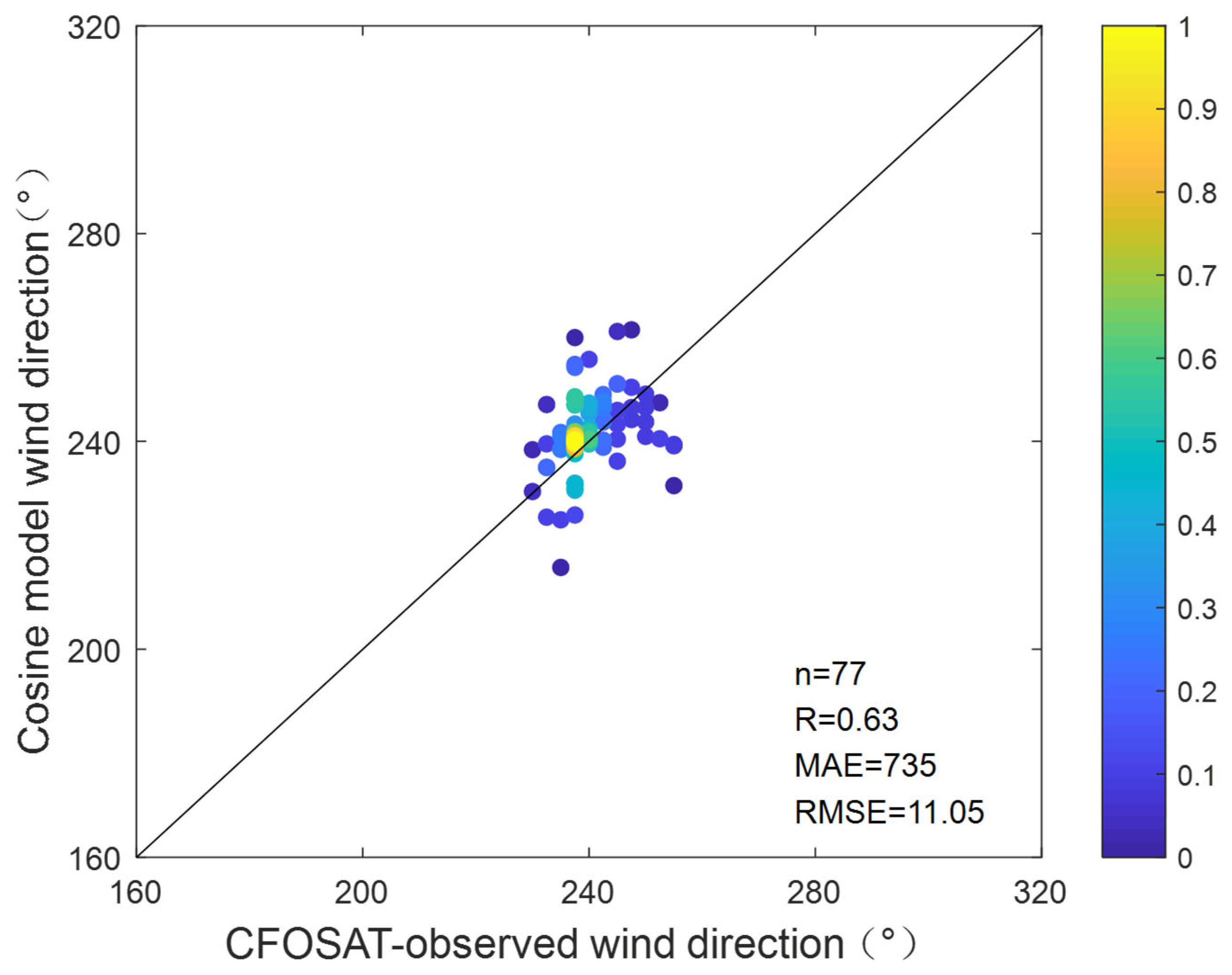
Figure 35.
Scatterplots for the comparisons of wind direction between the radar (the proposed method using modified cosine model) and CFOSAT from experiment I.
Figure 35.
Scatterplots for the comparisons of wind direction between the radar (the proposed method using modified cosine model) and CFOSAT from experiment I.
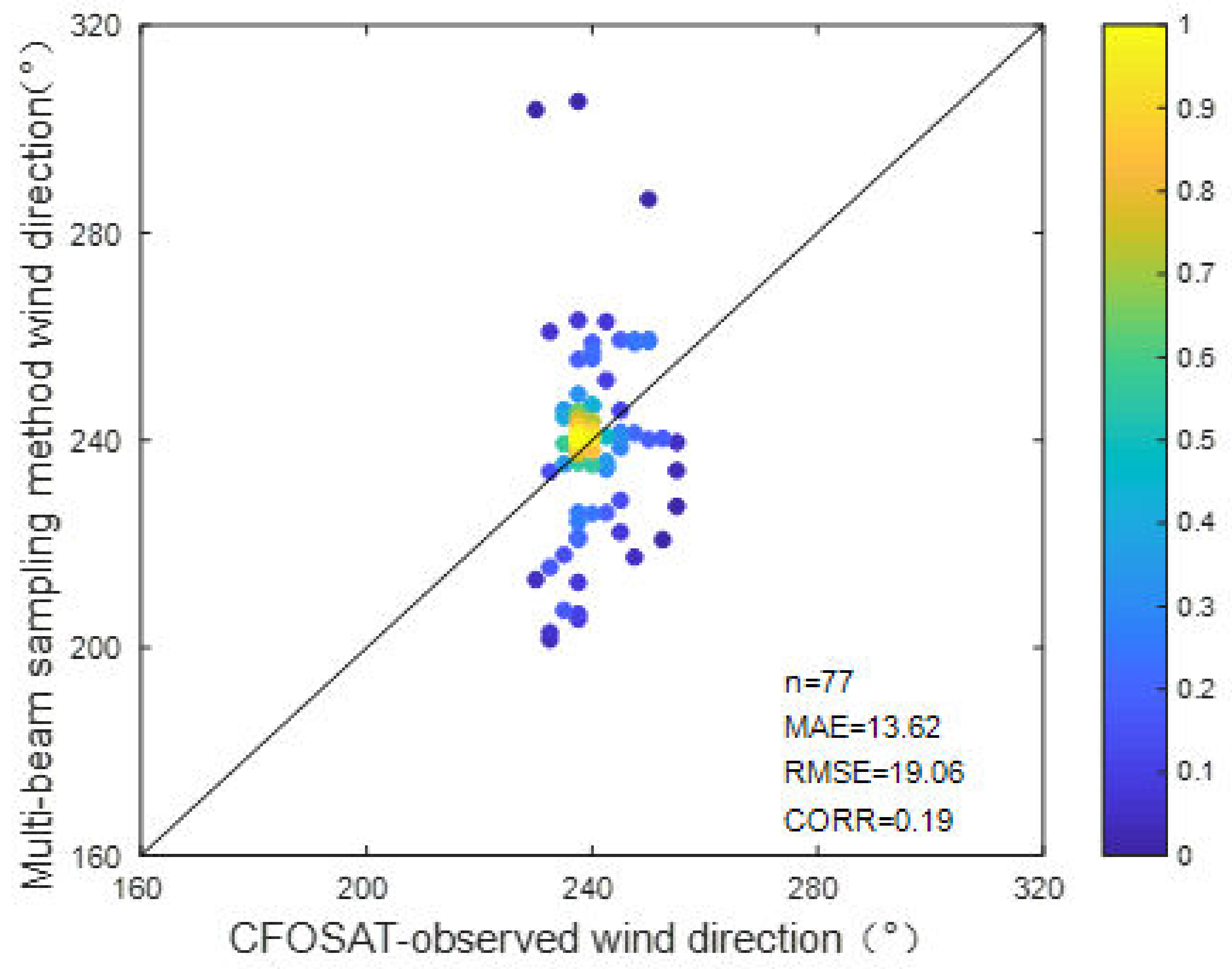
Figure 36.
Scatterplots for the comparisons of wind direction between the radar (the multi-beam sampling method using modified cosine model) and CFOSAT from experiment I.
Figure 36.
Scatterplots for the comparisons of wind direction between the radar (the multi-beam sampling method using modified cosine model) and CFOSAT from experiment I.
Figure 37.
Histograms of wind direction field measurement error between the radar and CFOSAT from experiment I.
Figure 37.
Histograms of wind direction field measurement error between the radar and CFOSAT from experiment I.
Figure 38.
Comparison of wind direction maps obtained by CFOSAT (black) and the radar using the three models from experiment I.
Figure 38.
Comparison of wind direction maps obtained by CFOSAT (black) and the radar using the three models from experiment I.
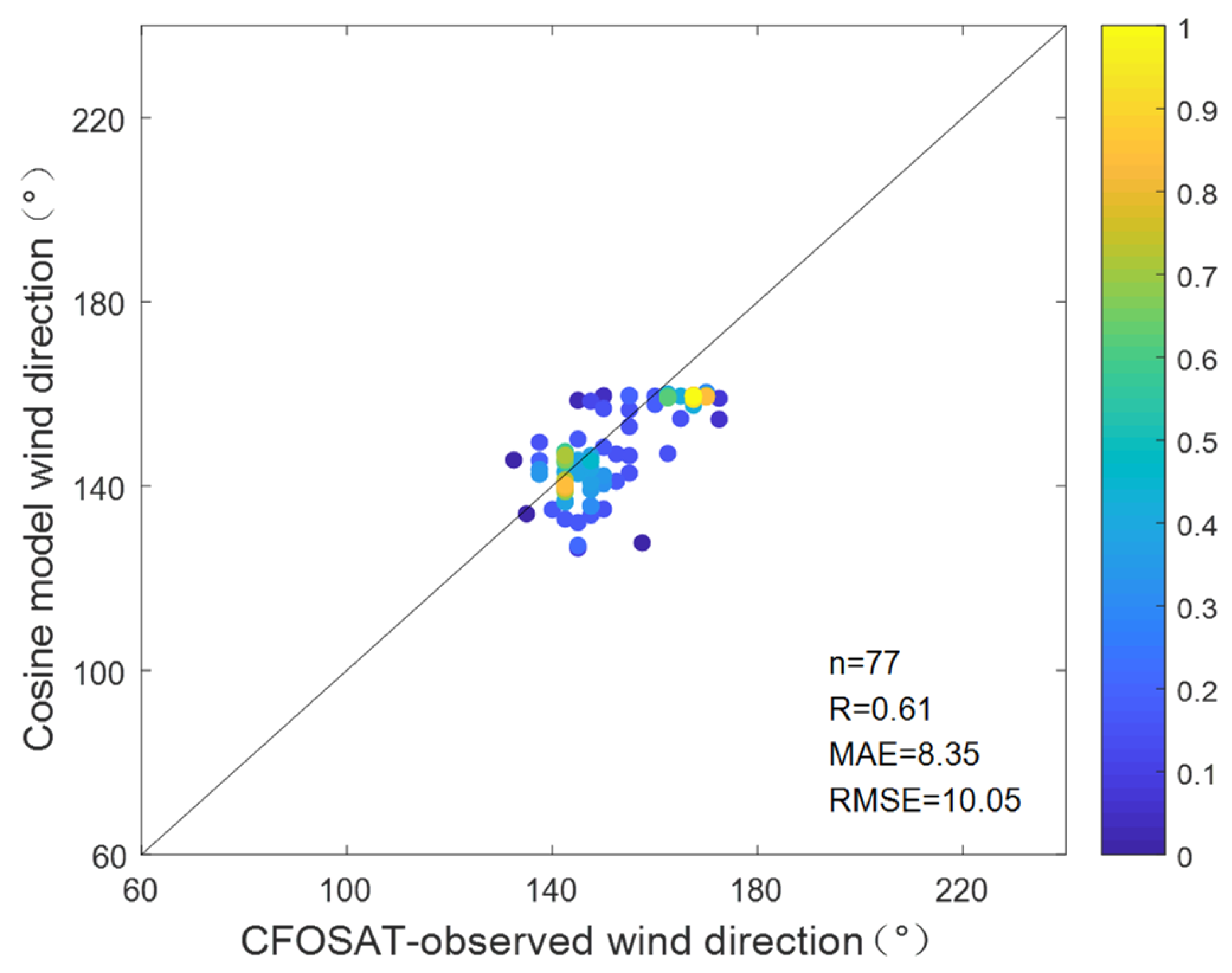
Figure 39.
Scatterplots for the comparisons of wind direction between CFOSAT and the radar using the cosine model from experiment I.
Figure 39.
Scatterplots for the comparisons of wind direction between CFOSAT and the radar using the cosine model from experiment I.
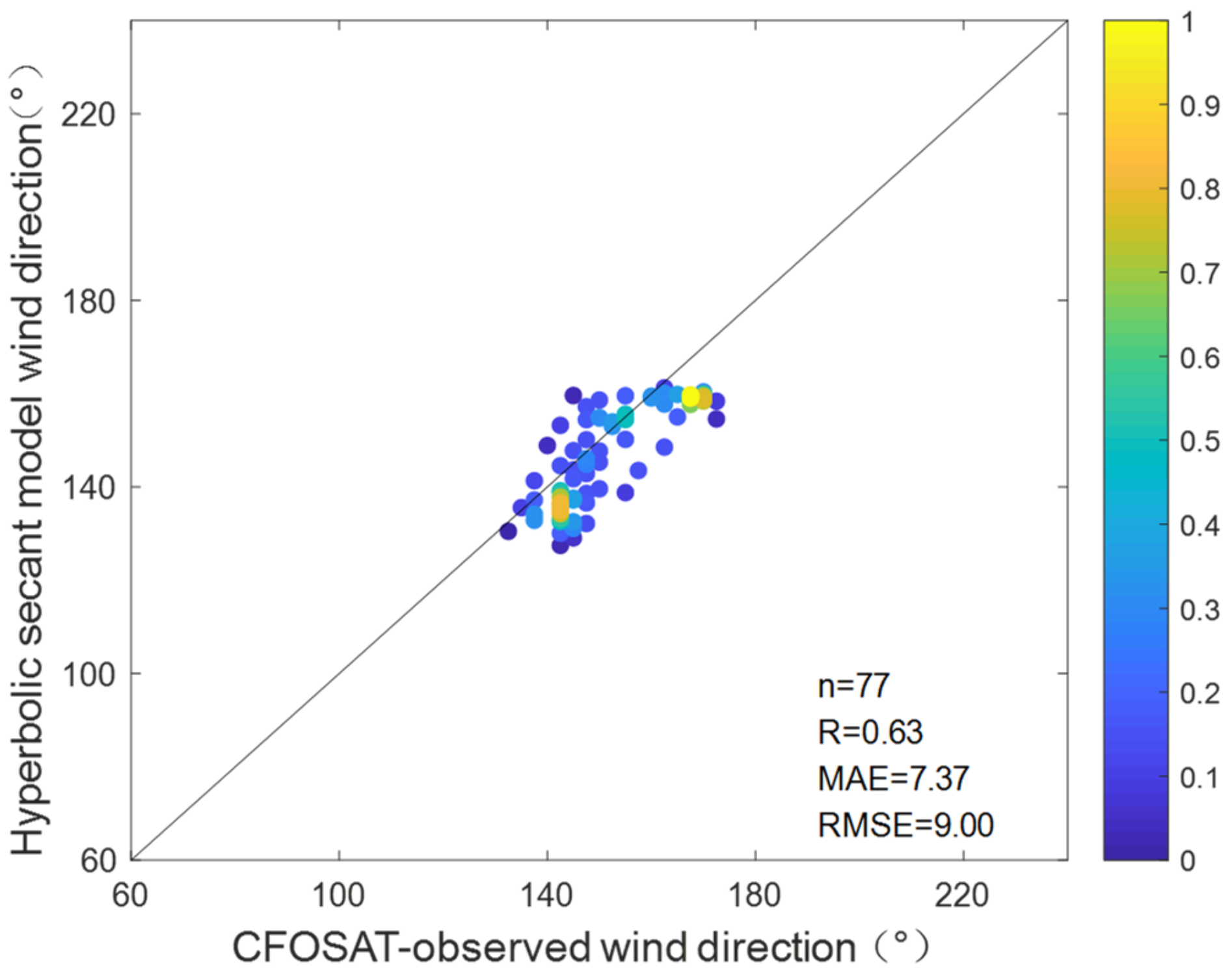
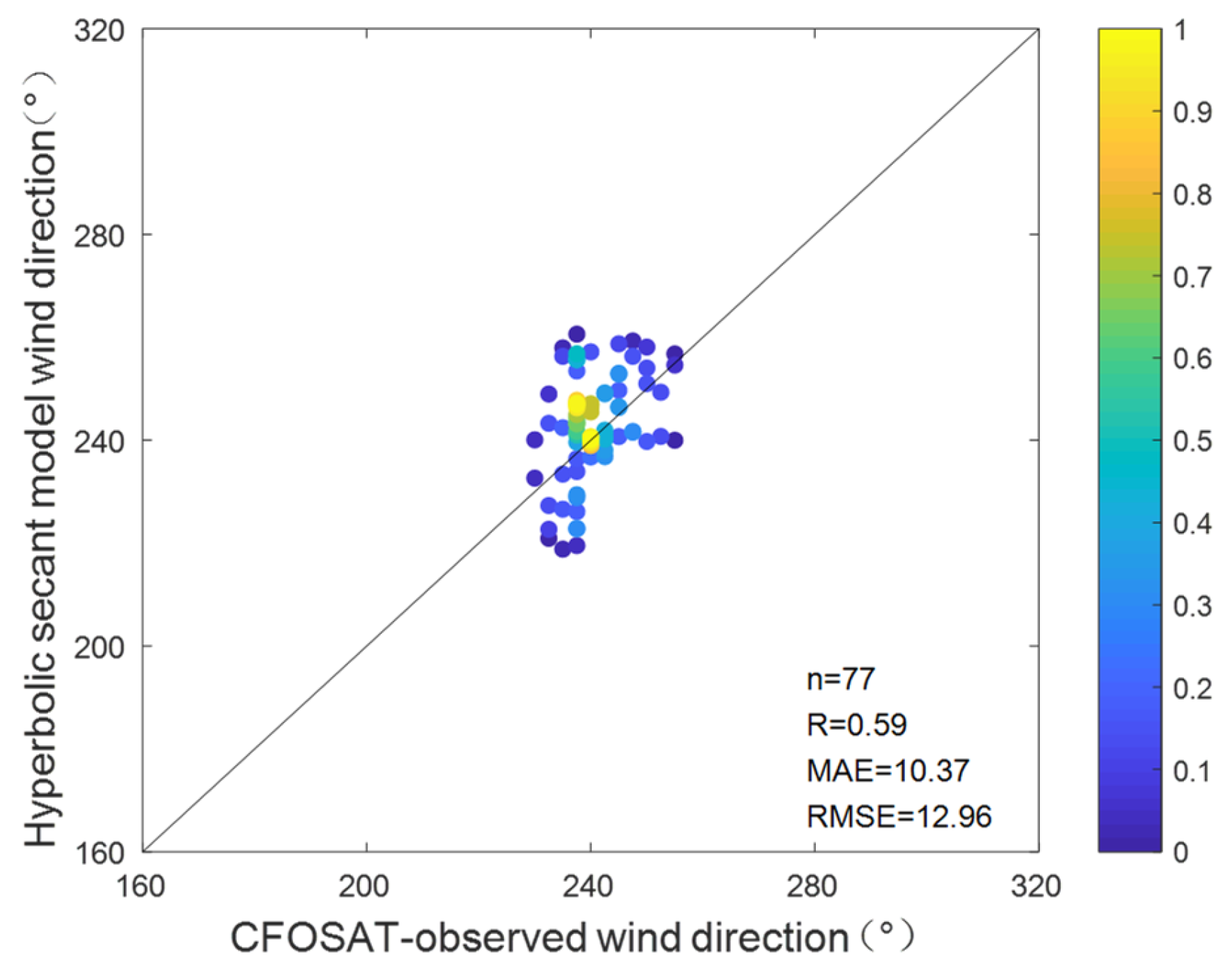
Figure 40.
Scatterplots for the comparisons of wind direction between CFOSAT and the radar using the hyperbolic secant model from experiment I.
Figure 40.
Scatterplots for the comparisons of wind direction between CFOSAT and the radar using the hyperbolic secant model from experiment I.
Figure 41.
Histograms of wind direction field measurement error between CFOSAT and the radar using the three models from experiment I.
Figure 41.
Histograms of wind direction field measurement error between CFOSAT and the radar using the three models from experiment I.
Figure 42.
Comparison of wind direction maps obtained by CFOSAT (black) and the radar (red and blue) from experiment II.
Figure 42.
Comparison of wind direction maps obtained by CFOSAT (black) and the radar (red and blue) from experiment II.
Figure 43.
Scatterplots for the comparisons of wind direction between the radar (the proposed method using the modified cosine model) and CFOSAT from experiment II.
Figure 43.
Scatterplots for the comparisons of wind direction between the radar (the proposed method using the modified cosine model) and CFOSAT from experiment II.
Figure 44.
Scatterplots for the comparisons of wind direction between the radar (the multi-beam sampling method using the modified cosine model) and CFOSAT from experiment II.
Figure 44.
Scatterplots for the comparisons of wind direction between the radar (the multi-beam sampling method using the modified cosine model) and CFOSAT from experiment II.
Figure 45.
Histograms of wind direction field measurement error between the radar and CFOSAT from experiment II.
Figure 45.
Histograms of wind direction field measurement error between the radar and CFOSAT from experiment II.
Figure 46.
Comparison of wind direction maps obtained by CFOSAT (black) and the radar using the three models from experiment II.
Figure 46.
Comparison of wind direction maps obtained by CFOSAT (black) and the radar using the three models from experiment II.
Figure 47.
Scatterplots for the comparisons of wind direction between CFOSAT and the radar using the cosine model from experiment II.
Figure 47.
Scatterplots for the comparisons of wind direction between CFOSAT and the radar using the cosine model from experiment II.
Figure 48.
Scatterplots for the comparisons of wind direction between CFOSAT and the radar using the hyperbolic secant model from experiment II.
Figure 48.
Scatterplots for the comparisons of wind direction between CFOSAT and the radar using the hyperbolic secant model from experiment II.
Figure 49.
Histograms of wind direction field measurement error between CFOSAT and the radar using the three models from experiment II.
Figure 49.
Histograms of wind direction field measurement error between CFOSAT and the radar using the three models from experiment II.
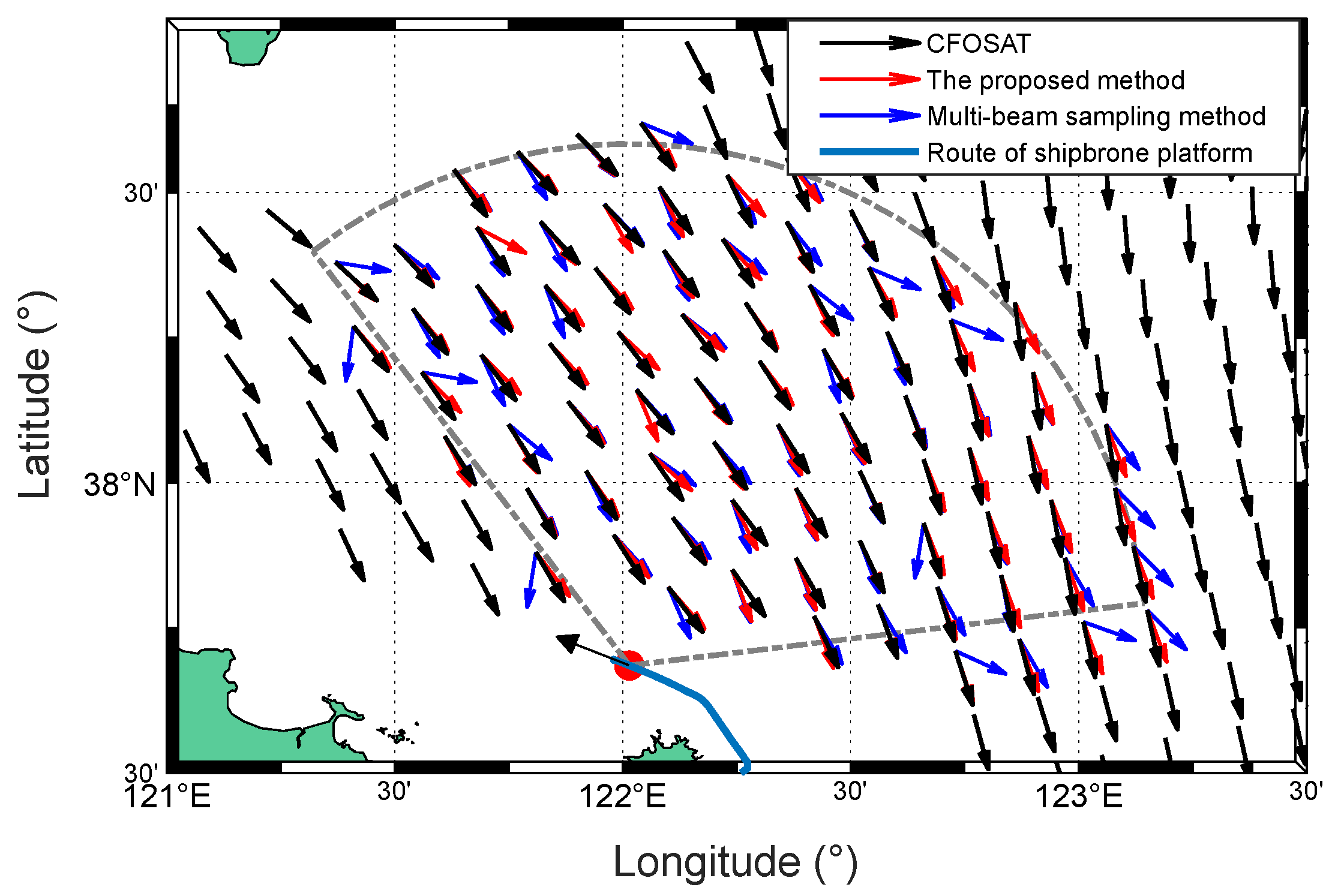
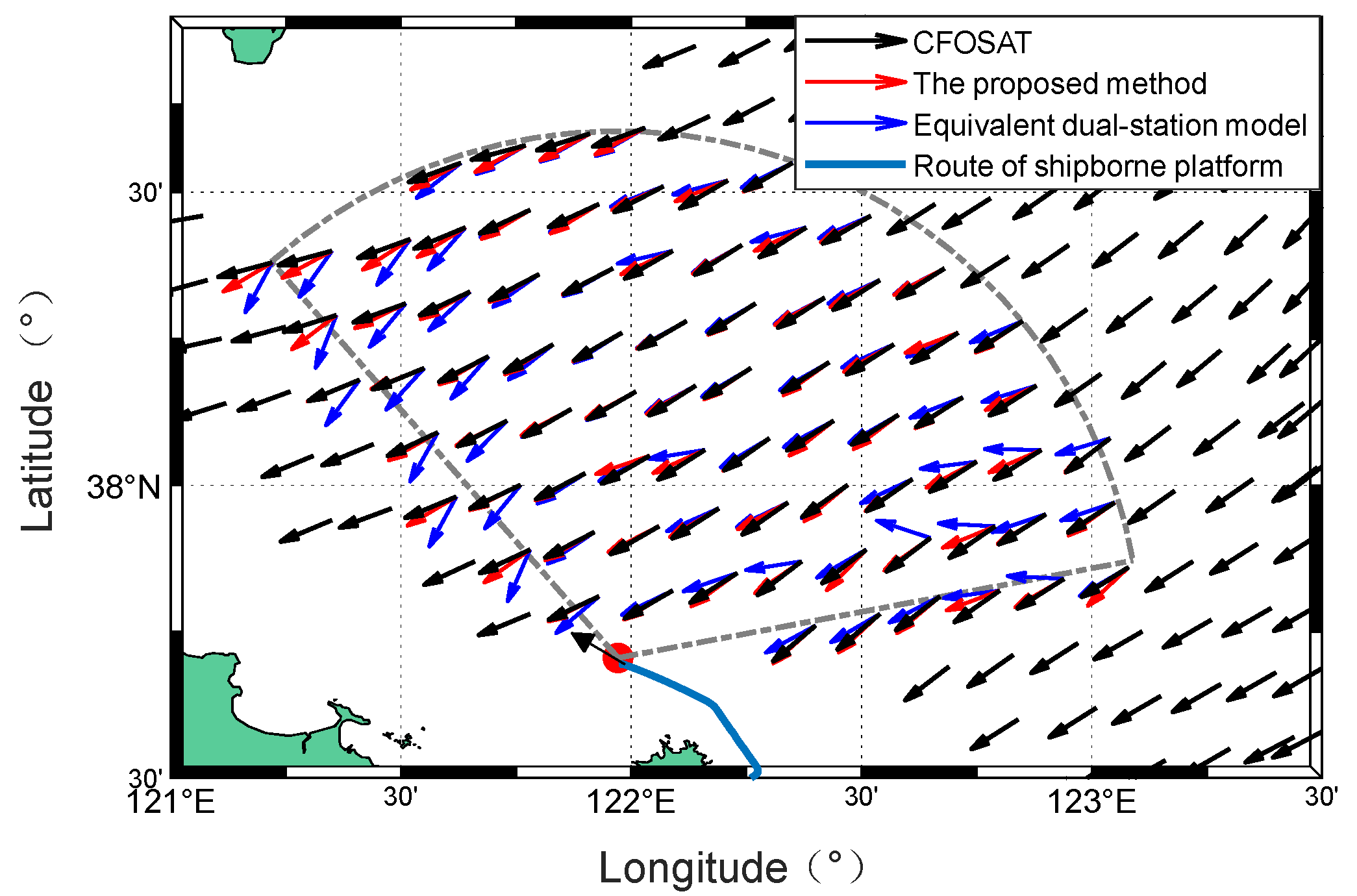
Figure 50.
Comparison of wind direction maps obtained by CFOSAT (black) and the radar (red and blue) from experiment III.
Figure 50.
Comparison of wind direction maps obtained by CFOSAT (black) and the radar (red and blue) from experiment III.
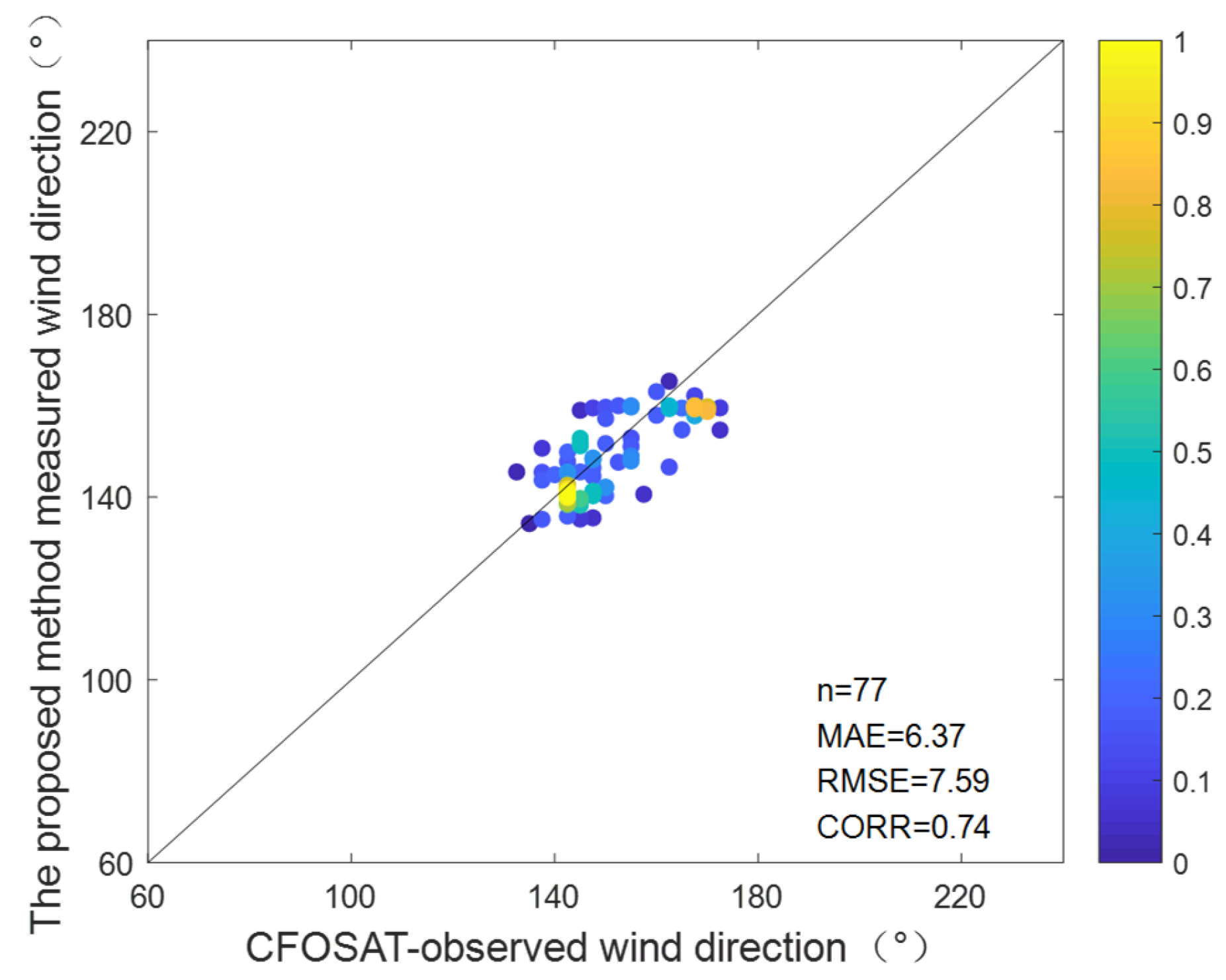
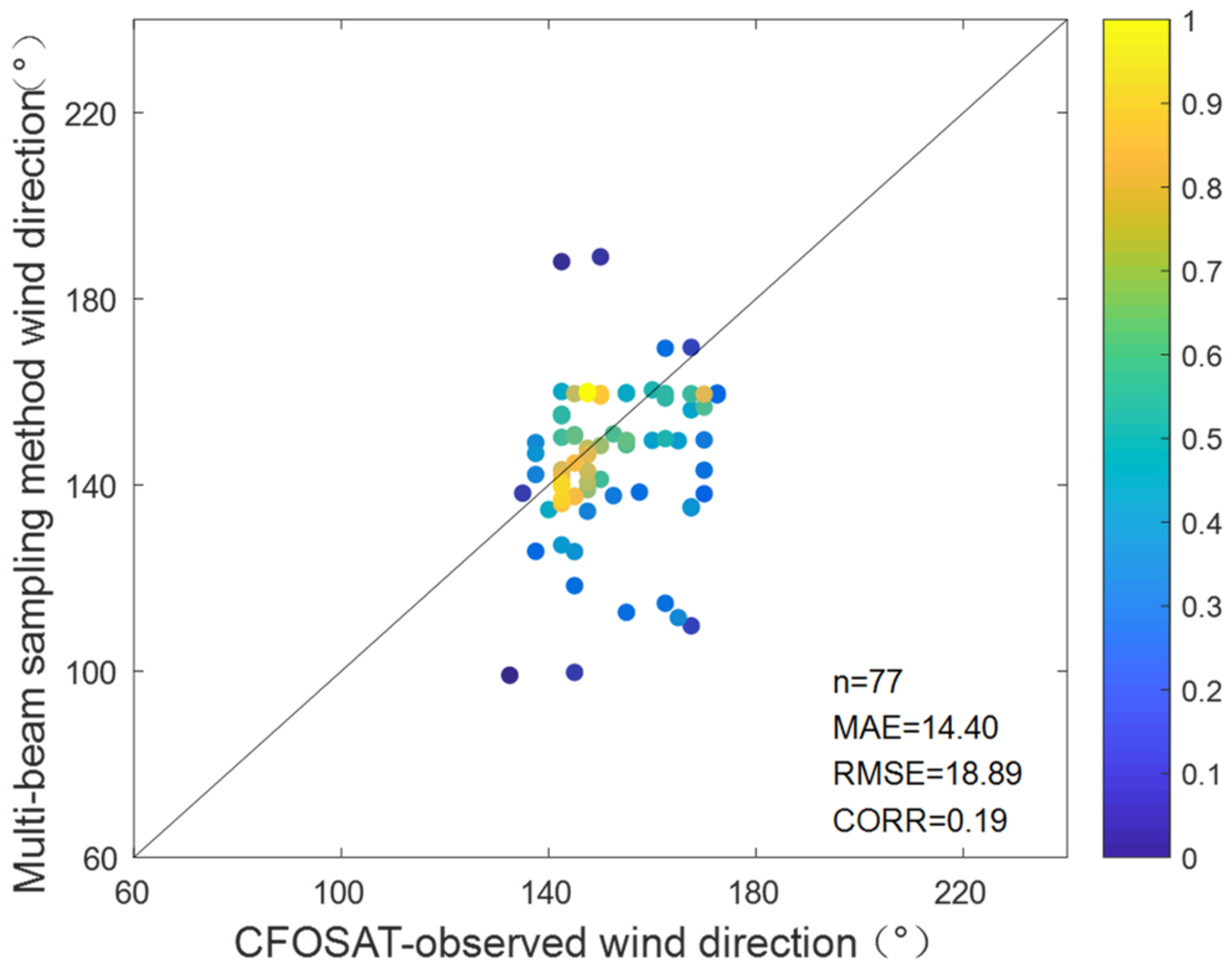
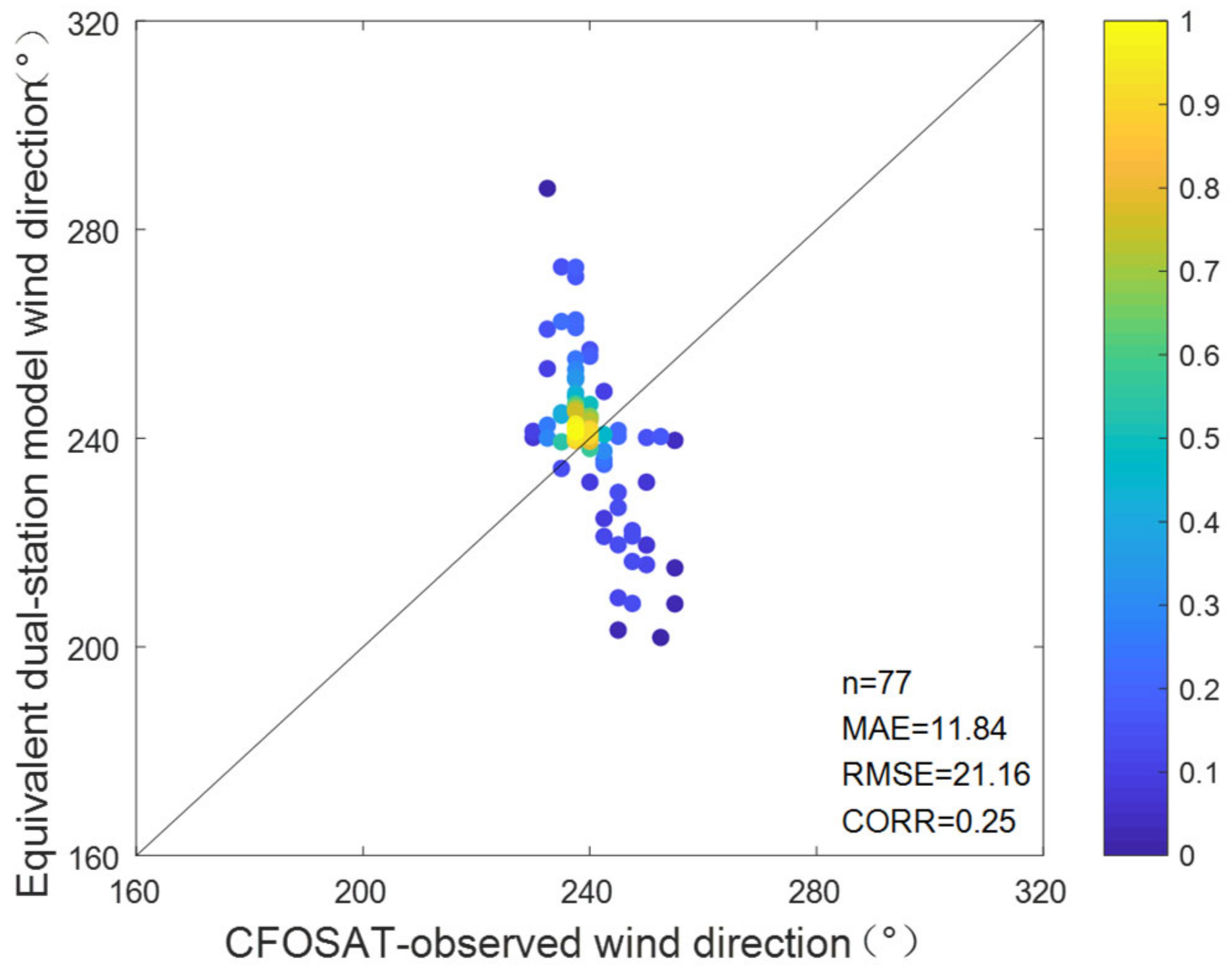
Figure 51.
Scatterplots for the comparisons of wind direction between the radar using a equivalent dual-station model and CFOSAT from experiment III.
Figure 51.
Scatterplots for the comparisons of wind direction between the radar using a equivalent dual-station model and CFOSAT from experiment III.
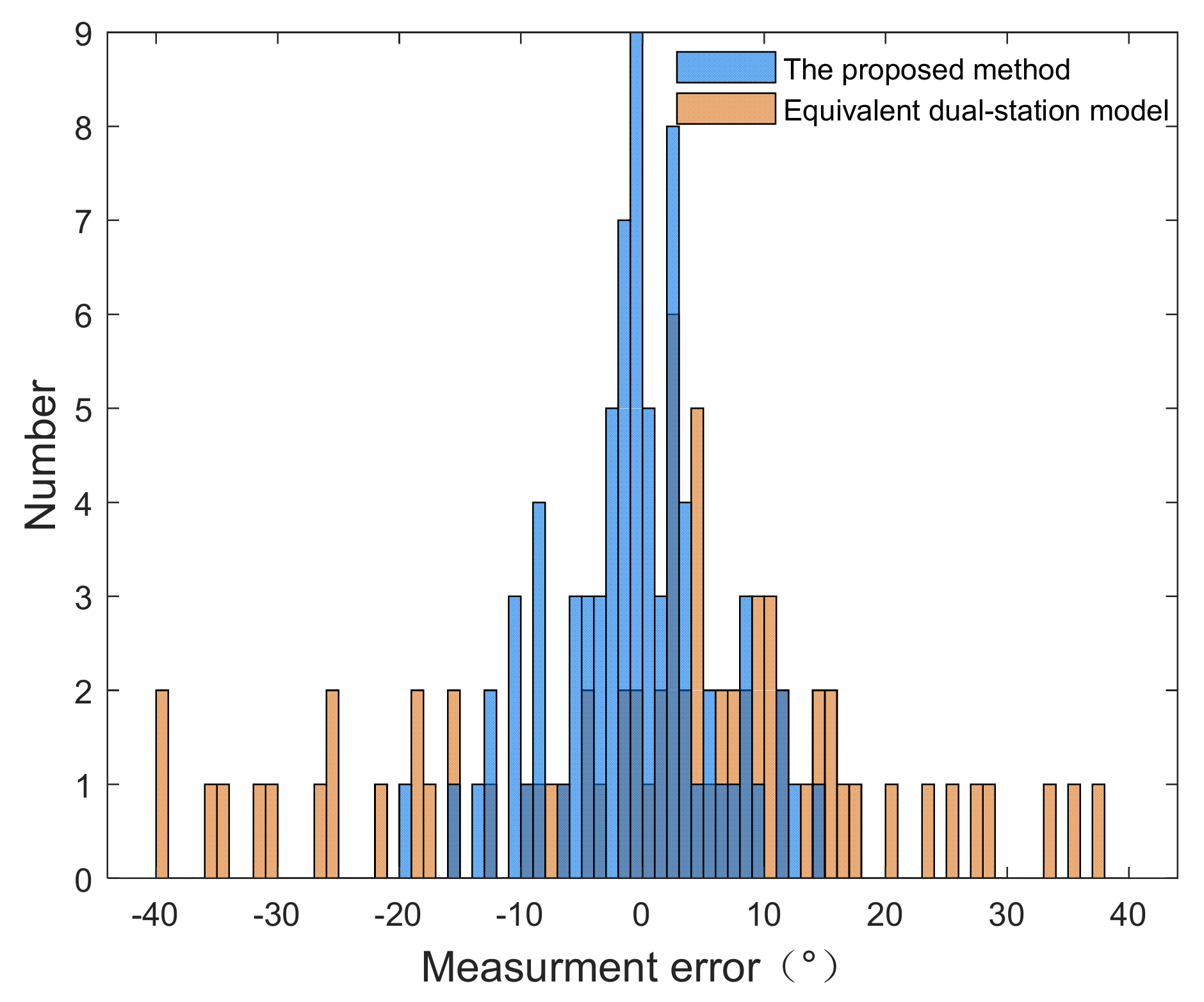
Figure 52.
Histograms of wind direction field measurement error between the radar using the two methods and CFOSAT from experiment III.
Figure 52.
Histograms of wind direction field measurement error between the radar using the two methods and CFOSAT from experiment III.
Table 1.
Statistical results of wind direction measurement.
Table 1.
Statistical results of wind direction measurement.
| Item | The Proposed Method | The Multi-Beam Sampling Method |
|---|
| Percentage of wind direction error within −2°~2° | 56.76% | 22.23% |
| Mean absolute error | 1.97° | 9.26° |
| Standard deviation | 2.06° | 12.72° |
Table 2.
Radar operating parameters.
Table 2.
Radar operating parameters.
| Parameter | Parameter Value |
|---|
| Operating frequency (MHz) | 4.7 |
| Range resolution (km) | 2.5 |
| Bandwidth (kHz) | 60 |
| Coherent integration time (CIT) (s) | 128 |
| Number of transmitting antenna | 2 |
| Number of receiving antenna | 5 |
Table 3.
Normalized Doppler amplitude differences and ratios of boundary and broadened regions from experiment I.
Table 3.
Normalized Doppler amplitude differences and ratios of boundary and broadened regions from experiment I.
| Item | Batch 1 | Batch 2 | Batch 3 | Batch 4 | Batch 5 |
|---|
| (dB) | 5.31 | 5.28 | 5.35 | 5.41 | 5.31 |
| (dB) | 9.78 | 9.71 | 9.72 | 9.61 | 9.73 |
| (dB) | 0.19 | 0.18 | 0.19 | 0.20 | 0.18 |
| (dB) | 5.27 | 5.24 | 5.25 | 5.10 | 5.36 |
Table 4.
Statistical results of radar-measured wind direction using two methods in experiment I.
Table 4.
Statistical results of radar-measured wind direction using two methods in experiment I.
| Item | The Proposed Method
(Modified Cosine Model) | The Multi-Beam Sampling Method |
|---|
| Percentage of wind directions within 155°~162.5° | 54.84% | 48.11% |
| Percentage of wind directions within 145°~172.5° | 78.44% | 67.92% |
| Mean wind direction | 155.53° | 158.22° |
| Standard deviation | 13.84° | 22.67° |
Table 5.
Statistical results of radar-measured wind direction using the two models from experiment I.
Table 5.
Statistical results of radar-measured wind direction using the two models from experiment I.
| Item | Cosine Model | Hyperbolic Secant Model |
|---|
| Percentage of wind directions within 155°~162.5° | 50.23% | 46.27% |
| Percentage of wind directions within 145°~172.5° | 73.82% | 77.79% |
| Mean wind direction | 156.07° | 153.55° |
| Standard deviation | 17.37° | 15.12° |
Table 6.
Normalized Doppler amplitude differences and ratios of boundary and broadened regions from experiment II.
Table 6.
Normalized Doppler amplitude differences and ratios of boundary and broadened regions from experiment II.
| Item | Batch 1 | Batch 2 | Batch 3 | Batch 4 | Batch 5 |
|---|
| (dB) | −14.10 | −14.02 | −14.04 | −14.12 | −14.07 |
| (dB) | −21.42 | −21.43 | −21.43 | −21.42 | −21.43 |
| (dB) | 0.47 | 0.46 | 0.47 | 0.49 | 0.44 |
| (dB) | 2.14 | 2.14 | 2.14 | 2.20 | 2.13 |
Table 7.
Statistical results of radar-measured wind direction using the two methods ffrom experiment II.
Table 7.
Statistical results of radar-measured wind direction using the two methods ffrom experiment II.
| Item | The Proposed Method
(Modified Cosine Model) | The Multi-Beam Sampling Method |
|---|
| Percentage of wind directions within 237.50°~245° | 43.13% | 40.10% |
| Percentage of wind directions within 227.50°~255° | 74.47% | 67.74% |
| Mean wind direction | 239.65° | 243.38° |
| Standard deviation | 13.45° | 19.71° |
Table 8.
Statistical results of radar-measured wind direction using the two models from experiment II.
Table 8.
Statistical results of radar-measured wind direction using the two models from experiment II.
| Item | Cosine Model | Hyperbolic Secant Model |
|---|
| Percentage of wind directions within 237.50°~245° | 37.51% | 40.28% |
| Percentage of wind directions within 227.50°~255° | 70.51% | 74.97% |
| Mean wind direction | 242.13° | 247.60° |
| Standard deviation | 15.74° | 17.38° |
Table 9.
Statistical results of radar-measured wind direction using the two methods from experiment III.
Table 9.
Statistical results of radar-measured wind direction using the two methods from experiment III.
| Item | The Proposed Method | The Equivalent Dual-Station Model |
|---|
| Percentage of wind directions within 237.50°~245° | 43.13% | 39.33% |
| Percentage of wind directions within 227.50°~255° | 74.47% | 62.67% |
| Mean wind direction | 239.65° | 237.51° |
| Standard deviation | 13.45° | 19.71° |