Abstract
Both the vastness of pasturelands and the value they contain—e.g., food security, ecosystem services—have resulted in increased scientific and industry efforts to remotely monitor them via satellite imagery and machine learning (ML). However, the transferability of these models is uncertain, as modelers commonly train and test on site-specific or homogenized—i.e., randomly partitioned—datasets and choose complex ML algorithms with increased potential to overfit a limited dataset. In this study, we evaluated the accuracy and transferability of remote sensing pasture models, using multiple ML algorithms and evaluation structures. Specifically, we predicted pasture above-ground biomass and nitrogen concentration from Sentinel-2 imagery. The implemented ML algorithms include principal components regression (PCR), partial least squares regression (PLSR), least absolute shrinkage and selection operator (LASSO), random forest (RF), support vector machine regression (SVR), and a gradient boosting model (GBM). The evaluation structures were determined using levels of spatial and temporal dissimilarity to partition the train and test datasets. Our results demonstrated a general decline in accuracy as evaluation structures increase in spatiotemporal dissimilarity. In addition, the more simplistic algorithms—PCR, PLSR, and LASSO—out-performed the more complex models RF, SVR, and GBM for the prediction of dissimilar evaluation structures. We conclude that multi-spectral satellite and pasture physiological variable datasets, such as the one presented in this study, contain spatiotemporal internal dependence, which makes the generalization of predictive models to new localities challenging, especially for complex ML algorithms. Further studies on this topic should include the assessment of model transferability by using dissimilar evaluation structures, and we expect generalization to improve for larger and denser datasets.
Keywords:
pasture; transferability; machine learning; Sentinel-2; satellite data; biomass; yield; nitrogen; cross-validation; complexity 1. Introduction
Grazing lands comprise about 25% of the earth’s land area and are essential for global food security and the delivery of ecosystem services [1]. Satellite remote sensing (SRS) technology offers a highly valuable tool for monitoring the expansive and heterogenous nature of these systems [2,3]. Researchers have demonstrated the potential for SRS models to estimate key pasture variables—forage quantity and nutritive value—which are critical for pastoral decision-making and improved management [4,5]. Multi-spectral satellite products—e.g., Sentinel-2 (S2), Landsat, MODIS—are often used for this purpose, and machine learning (ML) algorithms are increasingly used to model the spectral data to physiological variables of interest. However, the transferability of these models is uncertain, as modelers commonly train and evaluate on site-specific data or choose evaluation structures that homogenize multi-site data—e.g., random K-fold cross-validation (CV). Moreover, the impact of ML algorithm selection on generalization has been well-documented, and complex algorithms have been shown to overfit limited datasets [6]. Therefore, the primary objective of this study is to assess the accuracy and transferability of SRS pasture models using multiple ML algorithms and evaluation structures.
Previous studies of empirical SRS pasture models vary in approach and accuracy, with, for example, R2 values from 0.4 to 0.97 [3]. Vegetation indices (VI)—e.g., NDVI—offer a simple method of dimensionality reduction, which have been effectively fit to estimate pasture biomass with linear and exponential regression models [7,8]. However, simple VI models are confounded by various biophysical states—e.g., soil and moisture conditions—and therefore lack generalizability to other sampling locations [9,10,11]. To leverage the full range of spectral data provided by optical SRS platforms, ML algorithms offer a more robust alternative. Linear regression algorithms with added regularization or dimension reduction—e.g., LASSO, PCR, and PLSR—have been previously used to model pasture AGB with effective accuracy [12]. Researchers have also implemented more complex algorithms such as random forest (RF), support vector machine (SVM), and gradient boosting models (GBM) to predict pasture AGB with high accuracy [3]. In addition to AGB, nitrogen concentration (%N) of the forage is an important variable for pasture management decision-making, as it informs on both the nutritive value and productivity of the pasture. Although less studied than AGB, the potential to empirically model %N of pasture from SRS multispectral data has been demonstrated using both VI and ML approaches [13,14,15]. To our knowledge, our study is the first to develop AGB and %N SRS models for bahiagrass (Paspalum notatum), a valuable forage species in the Southeastern United States.
SRS predictions of pasture biomass and quality can inform decision-making, which would be enhanced by the quantification of how well predictions generalize to other—e.g., data-poor—conditions. However, the majority of SRS pasture-modeling publications focus on model accuracy, while transferability is infrequently discussed. This may be due to small experimental datasets from which extrapolation is not possible. Where studies do involve multi-site and multi-temporal data, models are often evaluated as a single locality without evaluation of how well the model predicts spatially and temporally autocorrelated subgroups within the dataset. This is a critical issue since ecological data are well-known to contain internal dependence structures that are unaccounted for by random resampling methods, resulting in overly optimistic estimates of model performance [16]. This phenomenon has been observed in SRS data as well, and the challenge of model transferability has been documented for several SRS modeling applications—e.g., land cover classification [17,18] and forest biomass prediction [19,20]. To account for this spatiotemporal autocorrelation, it has been demonstrated that blocking CV methods provide more realistic estimates of model error than randomized CV [16,21,22]. Moreover, choosing CV folds to deliberately induce extrapolation provides an estimate of model transferability [22,23]. Therefore, our study investigated the transferability of SRS pasture models by implementing a variety of different spatiotemporal CV blocking schemes.
In addition to training/evaluation structure, choice of ML algorithm has a large impact on model transferability [22,23]. The challenge of transferability is closely related to the bias-variance tradeoff, in that the model must not overfit the training data in order to extrapolate [24]. In theory, complex ML algorithms are more prone to overfitting as the increased number parameters allow for model greater flexibility, resulting in enhanced learning of training data and decreased potential for effective transfer [25]. Moreover, if the training data contains noise or “difficult” learning cases, the more complex algorithms are increasingly vulnerable to overfitting those unique instances [26]. Nonetheless, complex algorithms are increasingly used to model pasture variables from SRS data [3], as the research objectives of these studies are frequently limited to interpolative evaluations. Studies investigating the impact of algorithms on transferability indicate mixed results, and a “silver bullet” algorithm is unlikely for all circumstances [23]. Thus, to address our objective of assessing the accuracy and transferability of SRS pasture models, we tested six ML algorithms—LASSO, PCR, PLSR, RF, SVR, and GBM.
Based on the effectiveness of previous studies for modeling pasture AGB and %N from multi-spectral data, we hypothesize that our models will return similarly effective accuracies, especially when employing less extrapolative evaluation structures. We expect these accuracies to decline as the spatiotemporal groupings increase in dissimilarity. In addition, given our relatively small experimental dataset, we expect the enhanced learning of complex ML algorithms to result in higher accuracies for the interpolative evaluations and lower accuracies for the extrapolative evaluations, in comparison to the relatively simple linear algorithms. From these results, we will draw conclusions on the transferability of SRS pasture models and the necessity of diverse evaluation methods in this research area.
2. Materials and Methods
2.1. Experimental Sites and In Situ Measurements
The data for our SRS pasture models were acquired from two experiments—one specifically designed for S2 ground truthing at the Beef Research Unit (BRU) in Gainesville, Florida and the other a grazing trial at the North Florida Research and Education Center (NFREC) in Marianna, FL, for which S2 imagery was acquired retroactively. Both experimental areas consist of multiple paddocks containing Pensacola bahiagrass managed by the University of Florida Agronomy Department. The soil order at BRU is Spodosol with 0 to 2% slopes and moderately poor drainage, while NFREC contains well-drained Ultisol soils with 2 to 5% slopes.
The BRU experiment included 20 large scale (30 m × 30 m) plots located by Garmin GPS to surround the Sentinel-2 20 m pixel grids with a 5 m buffer (Figure 1). The plots were maintained and monitored for the duration of the 2021 growing season (April–September). The study included two replications of a gradient-design manipulation of the pasture height by chopping, i.e., mowing and removing residue. Ten pasture height treatments were implemented through the use of various mower height settings and a rotational chopping schedule. To initialize the first five treatments, the spring bahiagrass growth was chopped to heights of approximately 4, 14, 23, and 33 cm, as well as an uncut treatment. The same mower heights were used on the second half of the plots 10 days later. Due to the 10-day regrowth period, each of the 10 treatments had a different pasture height (except the uncut treatments), and the gradient was initialized and ready for monitoring and continued maintenance. The plot maintenance included chopping the tallest treatment to a height of 4 cm each week for the remainder of the growing season. Thus, each individual plot was cut 2 or 3 times over the duration of the experiment, and at any given time, the 10 treatments were manipulated to contain different gradations of pasture height. The gradient of pasture height treatments resulted in a range of physiological variables (e.g., AGB, %N) available for the ground-truthing of ongoing Sentinel-2 observations.

Figure 1.
Aerial view of (a) BRU experimental plots 1–10, (b) BRU experimental plots 11–20, (c) NFREC paddocks. The yellow squares represent the 20 m S2 pixels contained within the experimental boundaries, indicated in red.
The NFREC grazing trial site included six 0.85 ha bahiagrass paddocks (Figure 1), and data were taken during the 2019, 2020, and 2021 growing season (May–October). These experimental units are larger than the BRU plots, therefore the representative samples of both experimental and spectral data were averaged for each paddock. Three of these paddocks received 224 kg N ha−1 yr−1, and three were unfertilized. An approximately equivalent grazing pressure was maintained over each growing season using a put and take system. Methods for this experiment are detailed in Jaramillo et al. (2021) [27].
The AGB of both the BRU plots and NFREC paddocks were estimated using double sampling instruments common to pasture research. A digital rising plate meter (RPM) was used at BRU, and an analog falling plate meter (FPM) was used at NFREC. The RPM and FPM readings were taken in an approximately equidistant grid in order to obtain a representative sample from each experimental unit. At BRU, the plots were experimentally measured within 5 days of each cloud-free Sentinel-2 observation of the growing season, while the NFREC paddocks were sampled on a regular biweekly schedule. Calibrating samples for both instruments were taken monthly to determine the linear regression models between readings and AGB. In addition, biweekly forage samples were taken from the NFREC plots for %N analysis. These samples were selected from leaves in the upper canopy to simulate the typical grazing behavior of cattle.
2.2. Sentinel-2 Imagery Processing
S2 Level-2A surface reflectance imagery was retrieved from Google Earth Engine. To simplify various S2 pixel sizes, the ten-meter bands were aggregated to 20 m. Experimental pixels were verified to be cloud-free by visual inspection of RGB images, and band 10 (Cirrus—1375 nm) of the level-1C images was used to detect cirrus clouds. Any experimental pixels containing clouds were discarded. The aerosols and water vapor bands were discarded, returning the ten S2 bands used commonly for landscape observation—2, 3, 4, 5, 6, 7, 8, 8A, 11, and 12. Ten commonly used vegetation indices were calculated from the S2 bands to be included as additional features for ML modeling (Table 1). This list of indices was determined from a review of the index-based SRS pasture-modeling literature, especially studies of the Sentinel-2 platform [8,28].

Table 1.
Vegetation indices applied to Sentinel-2 datasets. represents reflectance, and represents the central wavelength (nm) of the band.
At BRU, six good S2 images were identified over the course of the 2021 growing season and successively sampled within a 5-day window. The S2 pixel contained in each BRU experimental plot was extracted and paired to the mean RPM-estimate of AGB, resulting in 120 rows of data. At NFREC, 25 good S2 images were retroactively identified to be within 5 days of the experimental dates throughout the 2019, 2020, and 2021 growing seasons. The mean reflectance was taken for each paddock—each containing between 7 and 14 S2 pixels without overlap of the boundaries—and paired to the mean FPM-estimates of AGB and %N values. Thus, the NFREC AGB dataset contained 140 rows of data and 145 rows of data for %N. The BRU and NFREC AGB datasets were merged for ML modeling and evaluation.
2.3. Evaluation Structures
Eight evaluation structures were used for the training and testing of the ML algorithms, including seven nested CV evaluations and one train/test holdout (Table 2). The nested CV structures included an outer loop to partition the training/test sets for prediction and accuracy evaluation, and the inner loop was used to tune model hyperparameters. Thus, the nested CVs allowed the development and evaluation of multiple models and the use of the full dataset. Predictions were pooled across all iterations, followed by calculation of overall error metrics R2 and RMSE. The train/test holdout evaluation involved training on the BRU data and testing on NFREC and only one CV for hyperparameter tuning.

Table 2.
Summary of data partitioning structures. Hyperparameter tuning was performed on the training partition for each evaluation.
Since our objective was to investigate transferability, different spatial and temporal CV fold structures were used with increasing dissimilarity. The least dissimilar evaluation structures involved conventional random K-fold CV evaluations for both AGB and %N datasets. The next evaluations used the spatial plots (and paddocks) as the partitioning unit for a Leave One Group Out CV (LOGOCV) for both pasture variables. To test temporal extrapolation, a LOGOCV was used with the individual S2 images as the partitioning unit. The final AGB model evaluation structure was the train/test holdout trained on BRU data and tested on NFREC data. The final %N model evaluation structure used LOGOCV with the year as the partitioning unit. Each evaluation structure also included a parameter tuning method, detailed in Table 2.
2.4. ML Algorithms and Hyperparameters
The ML algorithms were selected based on prevalence in the literature and theoretical efficacy for regressing a relatively small dataset and moderately sized feature space. The relative simplicity of the linear models—LASSO, PCR, and PLSR—are theoretically less prone to overfitting, while offering feature selection or dimensionality reduction. RF, SVR, and GBM—herein referred to as complex algorithms—were selected as algorithms capable of regressing more complex response patterns. The models were implemented in Python, using the Xgboost (XGB) library for the GBM [36] and scikit-learn for all other algorithms [37]. The simplistic algorithms contained only one hyperparameter for tuning, while the complex algorithms contained multiple.
Hyperparameter tuning was conducted using cross validation and an exhaustive grid search function [38]. For each algorithm, the most frequently manipulated hyperparameters were identified and a wide-ranging grid of acceptable values were identified for tuning. Hyperparameter ranges and final values are reported in Supplementary Tables S1 and S2.
The six ML regression algorithms were implemented for each of the eight evaluation structures. Additionally, each model fit was performed on two feature sets—S2 bands only and S2 bands + VI—resulting in 96 model fits. Only the more accurate of the feature sets was included for each model fit, leading to 48 model evaluations for publication.
3. Results
All AGB and %N models, including all ML algorithms, performed effectively (test R2 = 0.50–0.73) when evaluated with the two most interpolative evaluation structures—random CV and CV grouped by plot (Table 3 and Table 4). The difference between the error metrics of these two evaluation structures was negligible. For the date-level evaluation (i.e., extrapolation to new S2 images), the model performances (R2 = 0.20–0.60) exhibited an overall decline in accuracy, with some models yielding ineffective predictions. All models were less effective (R2 < 0.4) for the most rigorous evaluation strictures—extrapolation to different location for AGB and extrapolation to different years for %N.

Table 3.
Performance metrics of AGB (kg ha−1) prediction models for the four evaluation structures.

Table 4.
Performance metrics of %N prediction models for the four evaluation structures.
For the two most interpolative evaluation structures, SVR returned the best error metrics of these evaluations, especially within AGB models as SVR algorithm yielded an RMSE of 656 kg ha−1 (approximately 100 kg ha−1 lower than any of the simplistic models). Moreover, all the complex algorithms outperformed the simple models for AGB prediction with the interpolative evaluation structures. For the %N models, the performance of SVR was equivalent to the simple models for the random evaluation, but SVR exceeded the accuracy of the simple models for the plot-level CV evaluation. The decision tree-based algorithms exhibited lower %N predictive accuracy than the simple algorithms for both of these evaluation structures, despite having a very high test accuracy (R2 = 0.98–1.0).
The next evaluation structure was more extrapolative, evaluating the models by S2 image acquisition date. Here, there is a wider divide in performance between the complex and linear algorithms. For AGB, the PCR algorithm returned the best error metrics (R2 = 0.60, RMSE = 800 kg ha−1). The other simple models performed slightly worse but still effectively (R2 = 0.58–0.59, RMSE = 811–825 kg ha−1). In contrast, the complex models performed markedly less effectively (R2 = 0.45–0.49). Again, the decision tree-based algorithms (RF and XGB) exhibited very low training error.
For the %N models of the date-level evaluations, the simple models outperformed the complex models except for SVR which performed equivalently. LASSO returned the best performance metrics (R2 = 0.6, RMSE = 0.36), and PCR, PLSR, and SVR had similar metrics. In contrast, the decision tree-based algorithms were ineffective for predicting %N in this evaluation structure. They exhibited overfitting, with low training and high test error.
The final evaluation structure was the most extrapolative, using the NFREC data as the test set for the AGB models and the different years of the NFREC data as groupings for %N models. For these evaluations, the decision tree-based models were entirely ineffective, with an R2 near or below zero. PLSR provided the best metrics for AGB (R2 = 0.31), with a slightly worse performance from LASSO, PCR, and SVR. For the %N models, LASSO performed best (R2 = 0.36), followed by PCR, PLSR, and SVR. None of the models demonstrate an effective prediction for the most extrapolative evaluation structures.
Figure 2 and Figure 3 compare the predictive accuracy of the best-performing complex algorithm (SVR) to the best-performing simple algorithm for both the AGB and %N datasets. Figure 2 demonstrates that the complex SVR performed best for the interpolative AGB evaluations, while the simplistic PLSR was better for extrapolation. Figure 3 demonstrates that the simplistic LASSO was superior or equivalent to SVR for all model evaluations.
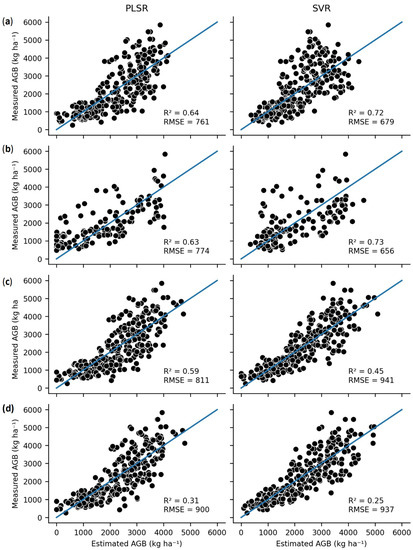
Figure 2.
Comparison of the PLSR and SVR model predictions of AGB across the four evaluation structures: (a) random, (b) plot, (c) date, and (d) location.
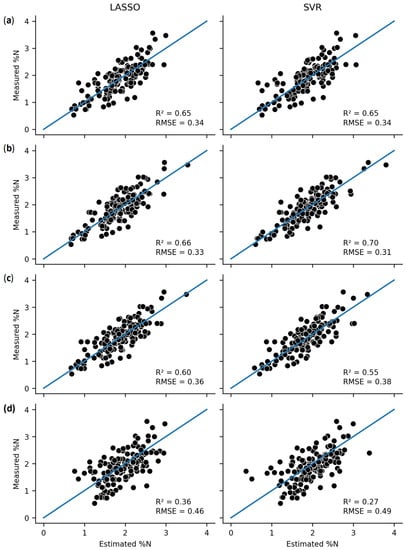
Figure 3.
Comparison of the LASSO and SVR model predictions of %N across the four evaluation structures: (a) random, (b) plot, (c) date, and (d) year.
To summarize our results, Figure 4 displays the means and standard deviations of the models grouped by variable, algorithm complexity, and evaluation structure. Overall, the figure illustrates how the mean model accuracies decreased as the dissimilarity of evaluation structure increased, especially when the transferability of the models was evaluated at different locations and years. Moreover, Figure 4 highlights the extent of the inaccuracy of the complex ML algorithms at increased levels of extrapolation, indicating increased over-fitting in comparison to the simpler algorithms. Additionally, the increased standard deviation of the complex algorithm accuracy is attributable to the divergence of performance between SVR and the decision tree-based algorithms, which exhibited more instances of overfitting than the other algorithms.
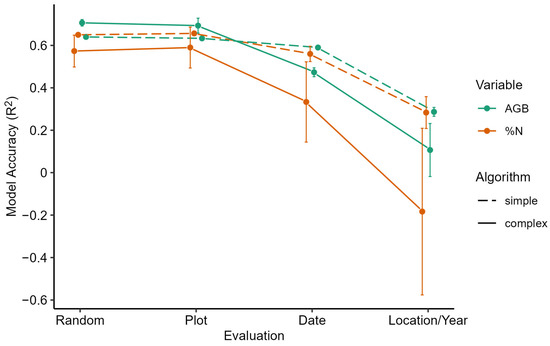
Figure 4.
Means and standard deviations (error bars) of model accuracies (R2) grouped by variable (color) and ML algorithm complexity (line type) and reported in order of increasing degree of extrapolation.
4. Discussion
The most important finding of this study is the demonstrated inverse relationship between model performance and level of extrapolative evaluation (Figure 4), which demonstrates a lack of transferability for SRS pasture models. Numerous examples of accurate site-specific SRS pasture modeling exist in the literature, and the error metrics of the interpolative evaluation of our AGB and %N models are within the range of accuracy exhibited by those studies [3,39]. However, since our models declined in model accuracy when extrapolated to unseen experimental dates or locations, we expect other ML pasture models from similar datasets to follow this trend. Moreover, our results of ML algorithm comparison across evaluation structures reveal that complex algorithms may not be the best choice for the objective of transferability in SRS pasture models, although we expect generalization to improve for larger and denser datasets. Our findings are especially important if the goal is to develop a serviceable tool that can work across multiple sites and temporalities. In this case, model overfitting and extrapolation accuracy must be evaluated to decrease the probability of ill-informed management decisions.
The potential for SRS modeling of pasture physiological variables to improve management has been noted for many years [2] and is gaining attention as data-driven tools are becoming more available to the livestock industry [40]. Advances in data capture technology, such as hyperspectral sensors, generate larger and denser datasets that necessitate the use of ML algorithms for the prediction of complex variables. Pasture physiological variables AGB and %N have been previously modeled from SRS data. However, to our knowledge, we are the first to publish these models for bahiagrass, a prevalent forage in the southeastern US, especially in the large cow-calf industry of Florida. Our results indicate that with in situ data, a reliable model can be developed for both of these important variables, but a global model, transferable to the larger bahiagrass pasture agroecosystem, remains a challenge.
To our knowledge, this study is the first assessment of the transferability of SRS pasture models. Roberts et al. [16] published an important description of the phenomenon of autocorrelation within ecological datasets, which provides a theoretical rationale for the challenge of extrapolation. This concept has been demonstrated for several SRS modeling applications [17,18,19,20], and researchers have reported a shift of both magnitude and direction of regression model parameters when training on different sites [19,20]. However, it is common for SRS pasture studies to ignore the spatial dependence within multi-site data and to evaluate models through randomly selected test sets. Our results indicate that many of these literature models are dataset-specific, and reassessment with extrapolative evaluation methods will result in diminished performance. If the transferability of the SRS models is an objective, we recommend choosing an evaluation structure that reflects the expected degree of extrapolation.
In addition to the choice of evaluation structure, our results indicate that the selection of the ML algorithm has an impact on SRS pasture model transferability. Decision tree algorithms, although highly accurate for interpolative evaluations, exhibited significant overfitting and inaccurate predictions of unseen experimental locations and dates. The other complex model tested, SVR, was less vulnerable to overfitting but was still outperformed in extrapolative evaluations by PLSR for AGB and LASSO for %N models. More hyperparameters were tuned for the decision tree-based algorithms, potentially contributing to increased overfitting. Studies have demonstrated that the overfitting of complex algorithms can be avoided by limiting the number of parameters used in the modeling [22,41]. However, this approach may not improve transferability for all algorithms, as Wenger and Olden (2012) reported minimal improvement in RF transferability after setting hyperparameters to constrain complexity—e.g., reducing the maximum number of nodes per tree [22]. As a pioneering study of this specific topic—transferability of SRS pasture models—we hypothesize that our findings would be reaffirmed in investigations of comparable datasets. However, other studies of transferability have demonstrated conflicting results for the performance of complex and decision tree-based algorithms [22,42]. Thus, we recommend the testing of multiple algorithms in addition to the implementation of multiple evaluation structures for the development of transferable models.
Although our results demonstrate transferability to be a challenge, we remain optimistic that larger and richer data can enable effective agroecosystem-wide SRS-pasture models. Enhancement of on-board spectral resolution, such as the hyperspectral EnMAP satellite [43], will provide deeper datasets, theoretically enabling the prediction of more complex response variables. For such datasets, complex algorithms may be more capable of controlling for confounding variables and noise while effectively capturing the data patterns of the variable of interest.
For the train/test holdout evaluation of our AGB model, we speculate that the different soil types of the two experimental locations are the main cause of divergent reflectance distributions. For the evaluations extrapolating by date and year, we suggest senesced vegetation to be the largest source of confounding variation. Both senescence and soil brightness are well known to impact the reflectance of vegetative canopies [44]. Other potential sources of bias include shifts in soil or vegetation moisture, as well as sampling error. Moreover, the more extrapolative evaluations involved larger test partitions and, therefore, smaller training partitions, which may have exacerbated the degree of extrapolation/overfitting. Thus, future studies should make use of larger datasets and integrate additional data types with the potential to inform on these sources of bias, which contaminate SRS modeling across spatial and temporal groupings. In addition to hyperspectral technology, the fusion of other RS data has the potential to improve transferability. The incorporation of soil data, such as texture, moisture, and organic matter, could be instrumental to the elimination of confounding variables in SRS pasture models. In addition, synthetic aperture radar and light detection and ranging (LiDAR) have been studied for their potential to measure crop canopy height and volume, especially in conjunction with optical data [45]. Another potential solution is the inclusion of SRS data into process models—e.g., radiative transfer models or crop simulation models—which offer enhanced transferability in theory, provided that the parameter distributions include the range of potential test conditions.
5. Conclusions
Overall, our results demonstrated an inverse relationship between ML model performance and the degree of extrapolative evaluation, providing evidence for the challenge of transferability in SRS pasture models. Moreover, we found that the relatively simple ML algorithms (LASSO, PCR, PLSR) predicted dissimilar spatiotemporal groupings more accurately than the complex algorithms (SVR, RF, XGB), suggesting that the less complex algorithms offer greater potential for transferable SRS pasture modeling. Regardless of model choice, our study has demonstrated the impact of test set partitioning on model performance, and we recommend future studies implement multiple spatiotemporal evaluation structures to assess the transferability of their SRS pasture models.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15112940/s1, Table S1: Complete AGB model evaluations including tuned hyperparameters; Table S2: Complete %N model evaluations including tuned hyperparameters. Table S3. Parameter ranges for all algorithms.
Author Contributions
Conceptualization, H.D.S. and C.H.W.; methodology, H.D.S., C.H.W. and A.Z.; software, H.D.S.; validation, H.D.S. and C.H.W.; formal analysis, H.D.S.; investigation, H.D.S.; resources, H.D.S., C.H.W. and J.C.B.D.; data curation, H.D.S. and J.C.B.D.; writing—original draft preparation, H.D.S.; writing—review and editing, all co-authors.; visualization, H.D.S.; supervision, C.H.W.; project administration, C.H.W.; funding acquisition, all co-authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deseret Cattle and Citrus.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We wish to thank the UF personnel that assisted in the field data collection, especially Amber Riner, Karine Moura, Hannah Rusch, and Stacy Smith.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Conant, R.T. Challenges and Opportunities for Carbon Sequestration in Grassland Systems; Integrated Crop Management; FAO: Rome, Italy, 2010; Volume 9. [Google Scholar]
- Schellberg, J.; Hill, M.J.; Gerhards, R.; Rothmund, M.; Braun, M. Precision agriculture on grassland: Applications, perspectives and constraints. Eur. J. Agron. 2008, 29, 59–71. [Google Scholar] [CrossRef]
- Reinermann, S.; Asam, S.; Kuenzer, C. Remote sensing of grassland production and management—A review. Remote Sens. 2020, 12, 1949. [Google Scholar] [CrossRef]
- Ali, I.; Cawkwell, F.; Dwyer, E.; Barrett, B.; Green, S. Satellite remote sensing of grasslands: From observation to management. J. Plant Ecol. 2016, 9, 649–671. [Google Scholar] [CrossRef]
- Sollenberger, L.E.; Aiken, G.E.; Wallau, M.O. Managing Grazing in Forage–Livestock Systems. In Management Strategies for Sustainable Cattle Production in Southern Pastures; Academic Press: Cambridge, MA, USA, 2020; pp. 77–100. [Google Scholar]
- Hawkins, D.M. The problem of overfitting. J. Chem. Inf. Comput. Sci. 2004, 44, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Anderson, G.L.; Hanson, J.D.; Haas, R.H. Evaluating Landsat Thematic Mapper derived vegetation indices for estimating above-ground biomass on semiarid rangelands. Remote Sens. Environ. 1993, 45, 165–175. [Google Scholar] [CrossRef]
- Cisneros, A.; Fiorio, P.; Menezes, P.; Pasqualotto, N.; Van Wittenberghe, S.; Bayma, G.; Furlan Nogueira, S. Mapping productivity and essential biophysical parameters of cultivated tropical grasslands from sentinel-2 imagery. Agronomy 2020, 10, 711. [Google Scholar] [CrossRef]
- Liu, H.Q.; Huete, A. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Garroutte, E.L.; Hansen, A.J.; Lawrence, R.L. Using NDVI and EVI to map spatiotemporal variation in the biomass and quality of forage for migratory elk in the Greater Yellowstone Ecosystem. Remote Sens. 2016, 8, 404. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M. Examining the potential of Sentinel-2 MSI spectral resolution in quantifying above ground biomass across different fertilizer treatments. ISPRS J. Photogramm. Remote Sens. 2015, 110, 55–65. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Integrating imaging spectroscopy and neural networks to map grass quality in the Kruger National Park, South Africa. Remote Sens. Environ. 2004, 90, 104–115. [Google Scholar] [CrossRef]
- Ramoelo, A.; Cho, M.A.; Mathieu, R.; Madonsela, S.; Van De Kerchove, R.; Kaszta, Z.; Wolff, E. Monitoring grass nutrients and biomass as indicators of rangeland quality and quantity using random forest modelling and WorldView-2 data. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 43–54. [Google Scholar] [CrossRef]
- Ramoelo, A.; Cho, M.A. Explaining leaf nitrogen distribution in a semi-arid environment predicted on Sentinel-2 imagery using a field spectroscopy derived model. Remote Sens. 2018, 10, 269. [Google Scholar] [CrossRef]
- Roberts, D.R.; Bahn, V.; Ciuti, S.; Boyce, M.S.; Elith, J.; Guillera-Arroita, G.; Hauenstein, S.; Lahoz-Monfort, J.J.; Schröder, B.; Thuiller, W.; et al. Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. Ecography 2017, 40, 913–929. [Google Scholar] [CrossRef]
- Tong, X.Y.; Xia, G.S.; Lu, Q.; Shen, H.; Li, S.; You, S.; Zhang, L. Land-cover classification with high-resolution remote sensing images using transferable deep models. Remote Sens. Environ. 2020, 237, 111322. [Google Scholar] [CrossRef]
- Qin, R.; Liu, T. A review of landcover classification with very-high resolution remotely sensed optical images—Analysis unit, model scalability and transferability. Remote Sens. 2022, 14, 646. [Google Scholar] [CrossRef]
- Foody, G.M.; Boyd, D.S.; Cutler, M.E. Predictive relations of tropical forest biomass from Landsat TM data and their transferability between regions. Remote Sens. Environ. 2003, 85, 463–474. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Gao, S.; Hu, T.; Liu, J.; Guo, Q. The transferability of Random Forest in canopy height estimation from multi-source remote sensing data. Remote Sens. 2018, 10, 1183. [Google Scholar] [CrossRef]
- Lyons, M.B.; Keith, D.A.; Phinn, S.R.; Mason, T.J.; Elith, J. A comparison of resampling methods for remote sensing classification and accuracy assessment. Remote Sens. Environ. 2018, 208, 145–153. [Google Scholar] [CrossRef]
- Wenger, S.J.; Olden, J.D. Assessing transferability of ecological models: An underappreciated aspect of statistical validation. Methods Ecol. Evol. 2012, 3, 260–267. [Google Scholar] [CrossRef]
- Yates, K.L.; Bouchet, P.J.; Caley, M.J.; Mengersen, K.; Randin, C.F.; Parnell, S.; Fielding, A.H.; Bamford, A.J.; Ban, S.; Barbosa, A.M.; et al. Outstanding challenges in the transferability of ecological models. Trends Ecol. Evol. 2018, 33, 790–802. [Google Scholar] [CrossRef] [PubMed]
- Heikkinen, R.K.; Marmion, M.; Luoto, M. Does the interpolation accuracy of species distribution models come at the expense of transferability? Ecography 2012, 35, 276–288. [Google Scholar] [CrossRef]
- Ying, X. An Overview of Overfitting and Its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Paris, G.; Robilliard, D.; Fonlupt, C. Exploring overfitting in genetic programming. In International Conference on Artificial Evolution (Evolution Artificielle); Springer: Berlin/Heidelberg, Germany, 2003; pp. 267–277. [Google Scholar]
- Jaramillo, D.M.; Dubeux, J.C.; Sollenberger, L.E.; Vendramini, J.M.; Mackowiak, C.; DiLorenzo, N.; Garcia, L.; Queiroz, L.M.D.; Santos, E.R.; Homem, B.G.; et al. Water footprint, herbage, and livestock responses for nitrogen-fertilized grass and grass–legume grazing systems. Crop Sci. 2021, 61, 3844–3858. [Google Scholar] [CrossRef]
- Qin, Q.; Xu, D.; Hou, L.; Shen, B.; Xin, X. Comparing vegetation indices from Sentinel-2 and Landsat 8 under different vegetation gradients based on a controlled grazing experiment. Ecol. Indic. 2021, 133, 108363. [Google Scholar] [CrossRef]
- Gower, J.F.R. Observations of in situ fluorescence of chlorophyll-a in Saanich Inlet. Bound. -Layer Meteorol. 1980, 18, 235–245. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A.; Rundquist, D.C. Towards a unified approach for remote estimation of chlorophyll-a in both terrestrial vegetation and turbid productive waters. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Huete, A.R.; Liu, H.; van Leeuwen, W.J. The use of vegetation indices in forested regions: Issues of Linearity and Saturation. In Proceedings of the IGARSS’97—1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings. Remote Sensing—A Scientific Vision for Sustainable Development; New York, NY, USA, 3–8 August 1997, Volume 4, pp. 1966–1968.
- Delegido, J.; Alonso, L.; Gonzalez, G.; Moreno, J. Estimating chlorophyll content of crops from hyperspectral data using a normalized area over reflectance curve (NAOC). Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 165–174. [Google Scholar] [CrossRef]
- Van Deventer, A.P.; Ward, A.D.; Gowda, P.H.; Lyon, J.G. Using thematic mapper data to identify contrasting soil plains and tillage practices. Photogramm. Eng. Remote Sens. 1997, 63, 87–93. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. Ser. B Methodol. 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Morais, T.G.; Teixeira, R.F.; Figueiredo, M.; Domingos, T. The use of machine learning methods to estimate aboveground biomass of grasslands: A review. Ecol. Indic. 2021, 130, 108081. [Google Scholar] [CrossRef]
- Eastwood, C.; Ayre, M.; Nettle, R.; Rue, B.D. Making sense in the cloud: Farm advisory services in a smart farming future. NJAS-Wagening J. Life Sci. 2019, 90, 100298. [Google Scholar] [CrossRef]
- Sarle, W.S. Stopped training and other remedies for overfitting. In Proceedings of the 27th Symposium on the Interface of Computing Science and Statistics, Fairfax, VA, USA, 21–24 June 1995; pp. 352–360. [Google Scholar]
- Cracknell, M.J.; Reading, A.M. Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Colwell, J.E. Vegetation canopy reflectance. Remote Sens. Environ. 1974, 3, 175–183. [Google Scholar] [CrossRef]
- Wachendorf, M.; Fricke, T.; Möckel, T. Remote sensing as a tool to assess botanical composition, structure, quantity and quality of temperate grasslands. Grass Forage Sci. 2018, 73, 1–14. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).