Combining Radiative Transfer Model and Regression Algorithms for Estimating Aboveground Biomass of Grassland in West Ujimqin, China
Abstract
1. Introduction
2. Materials and Methods
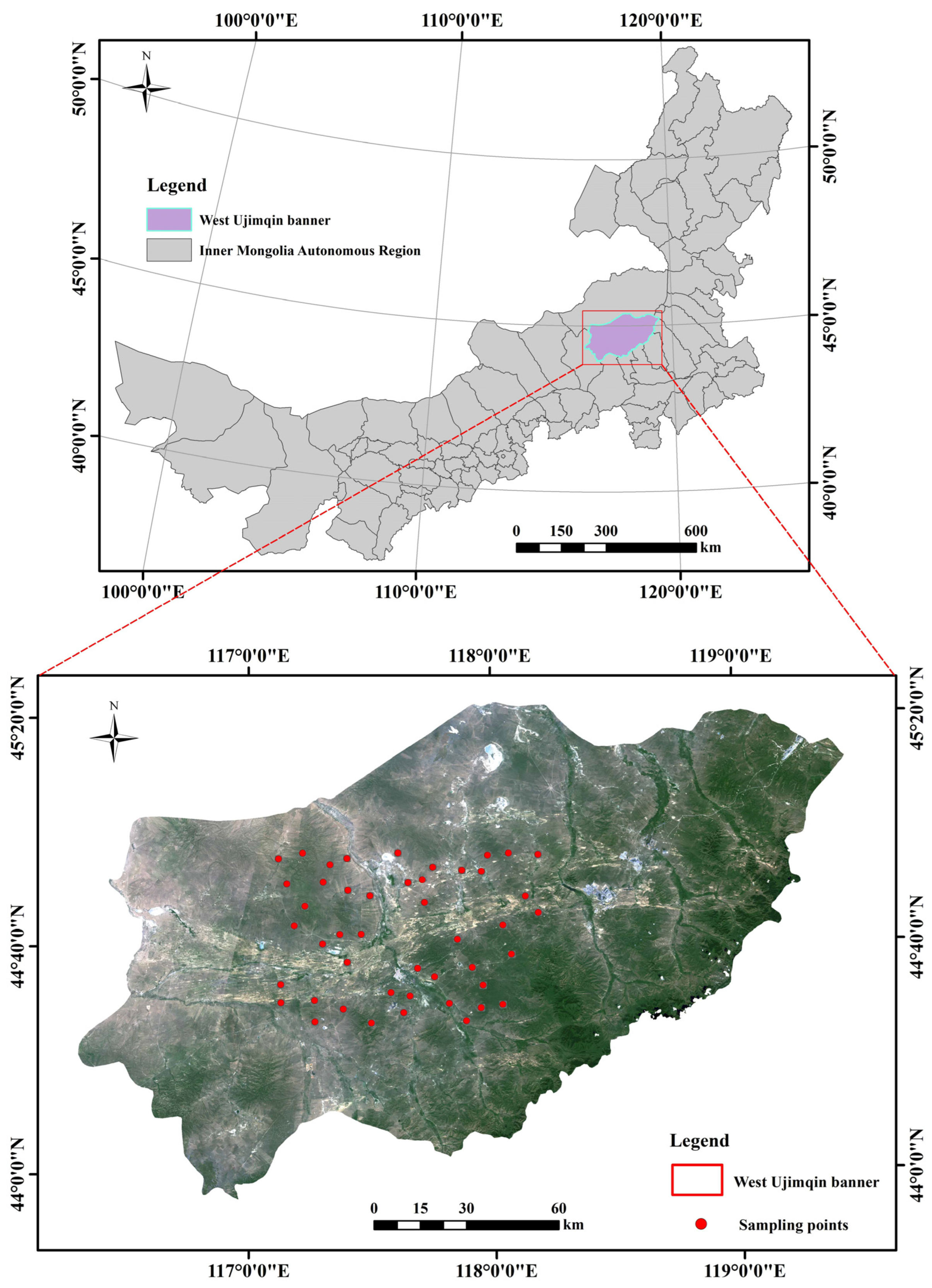
2.1. Study Area
2.2. Datasets
2.2.1. Field Data Collection
2.2.2. Satellite Images Acquisition and Preprocessing
2.3. Methods
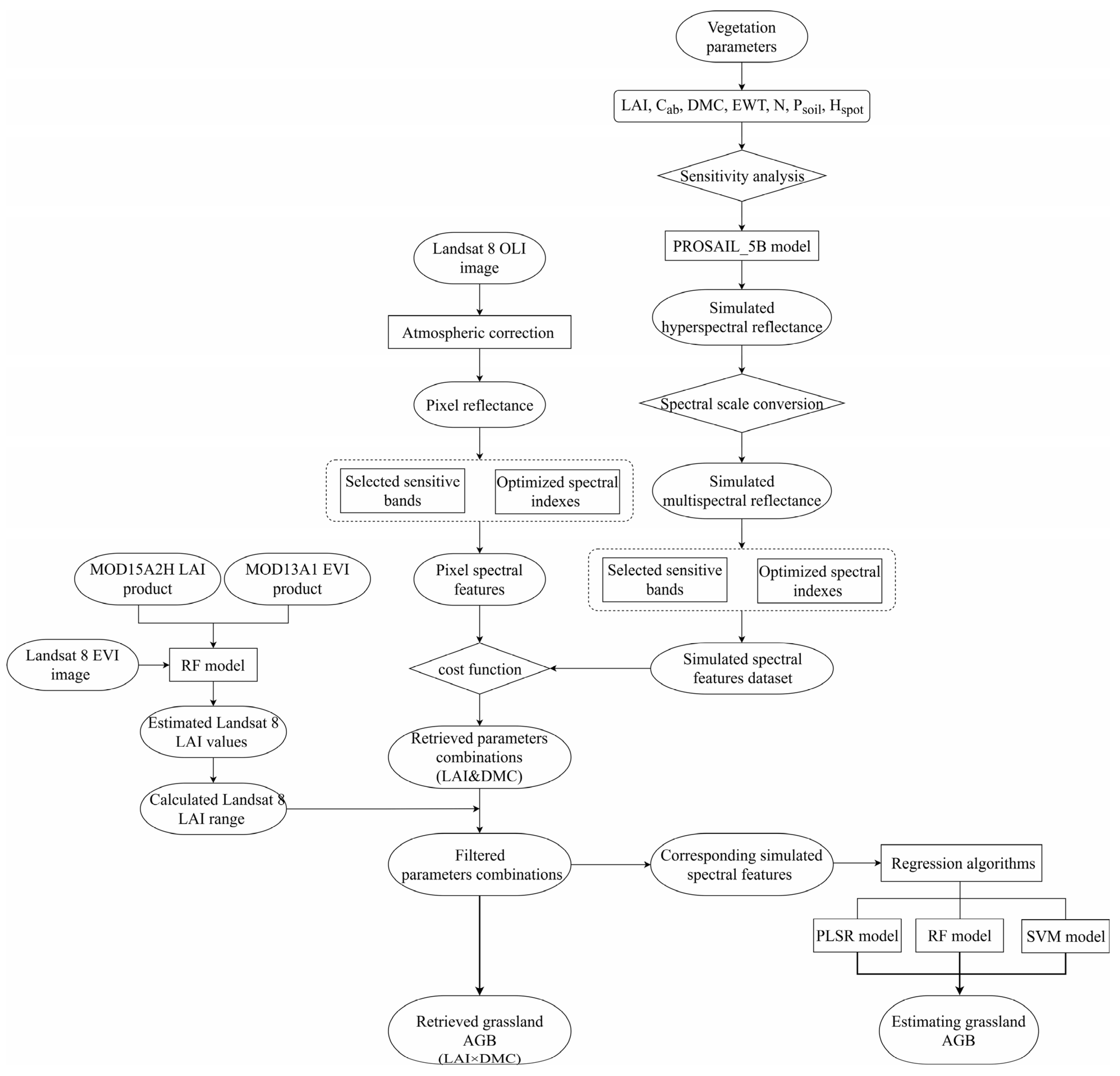
2.3.1. Construction of the Simulated Canopy Spectral Dataset
- PROSAIL model
- Sensitivity analysis
- Spectral scale conversion
- Spectral indices
2.3.2. LUT-Based Method
2.3.3. Regression Algorithms
- PLSR
- RF
- SVM
2.3.4. Model Validation
3. Results
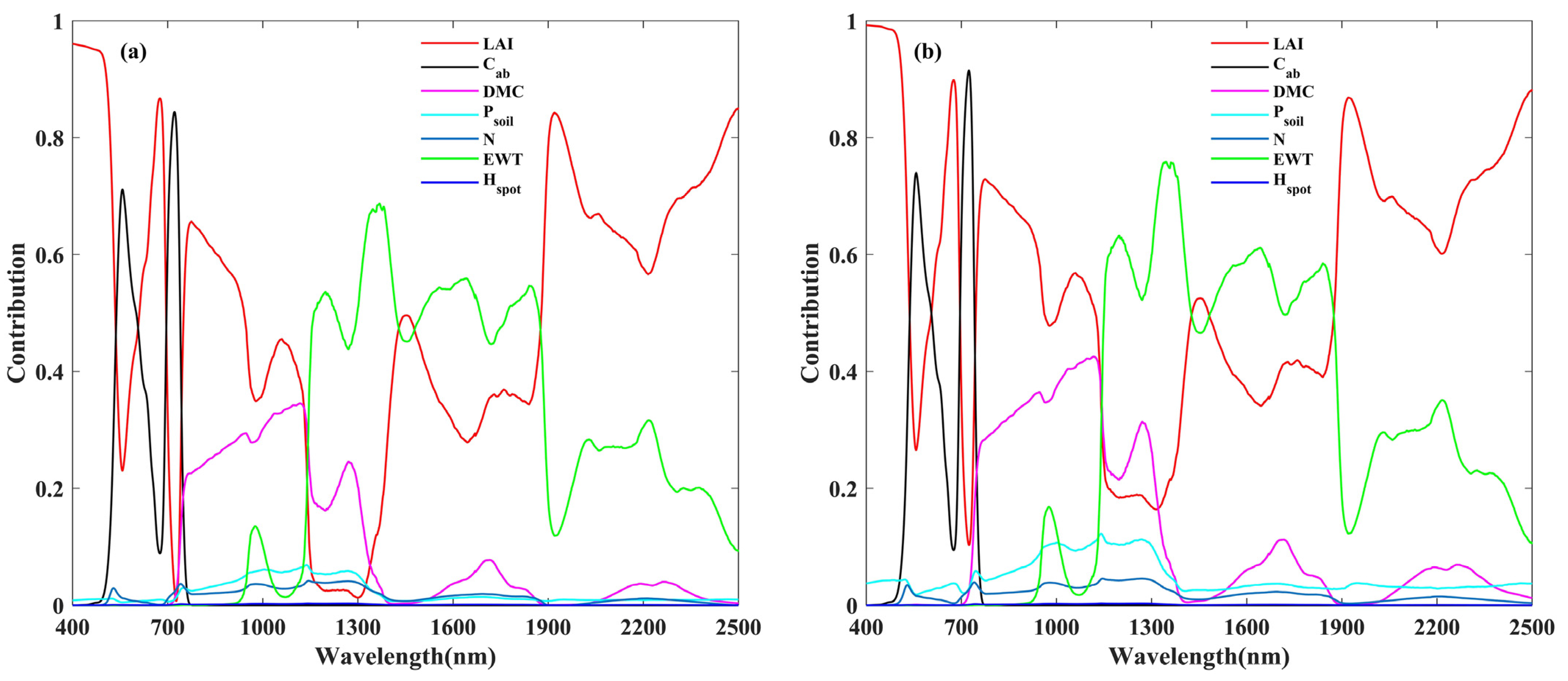
3.1. Sensitivity Analysis
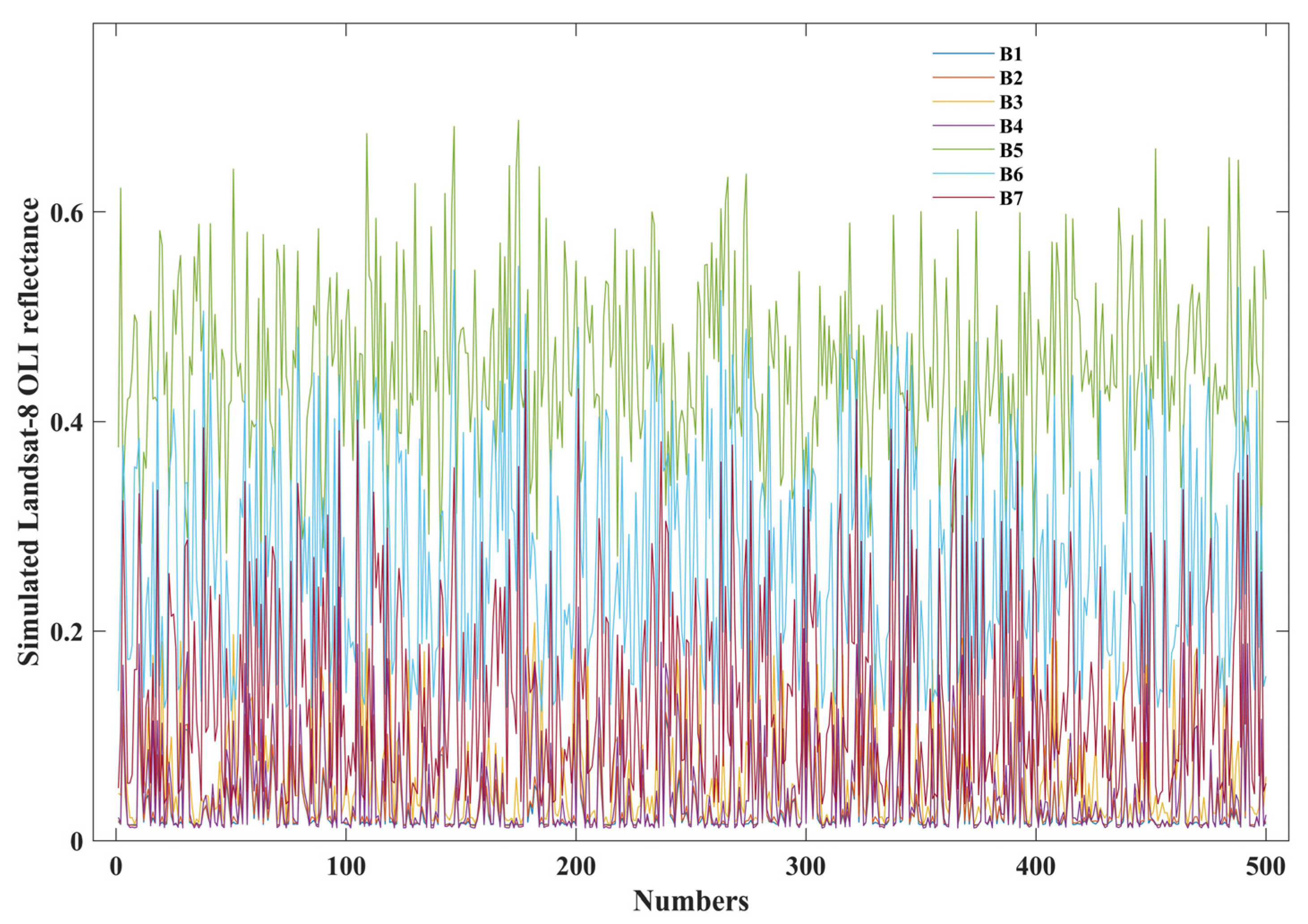
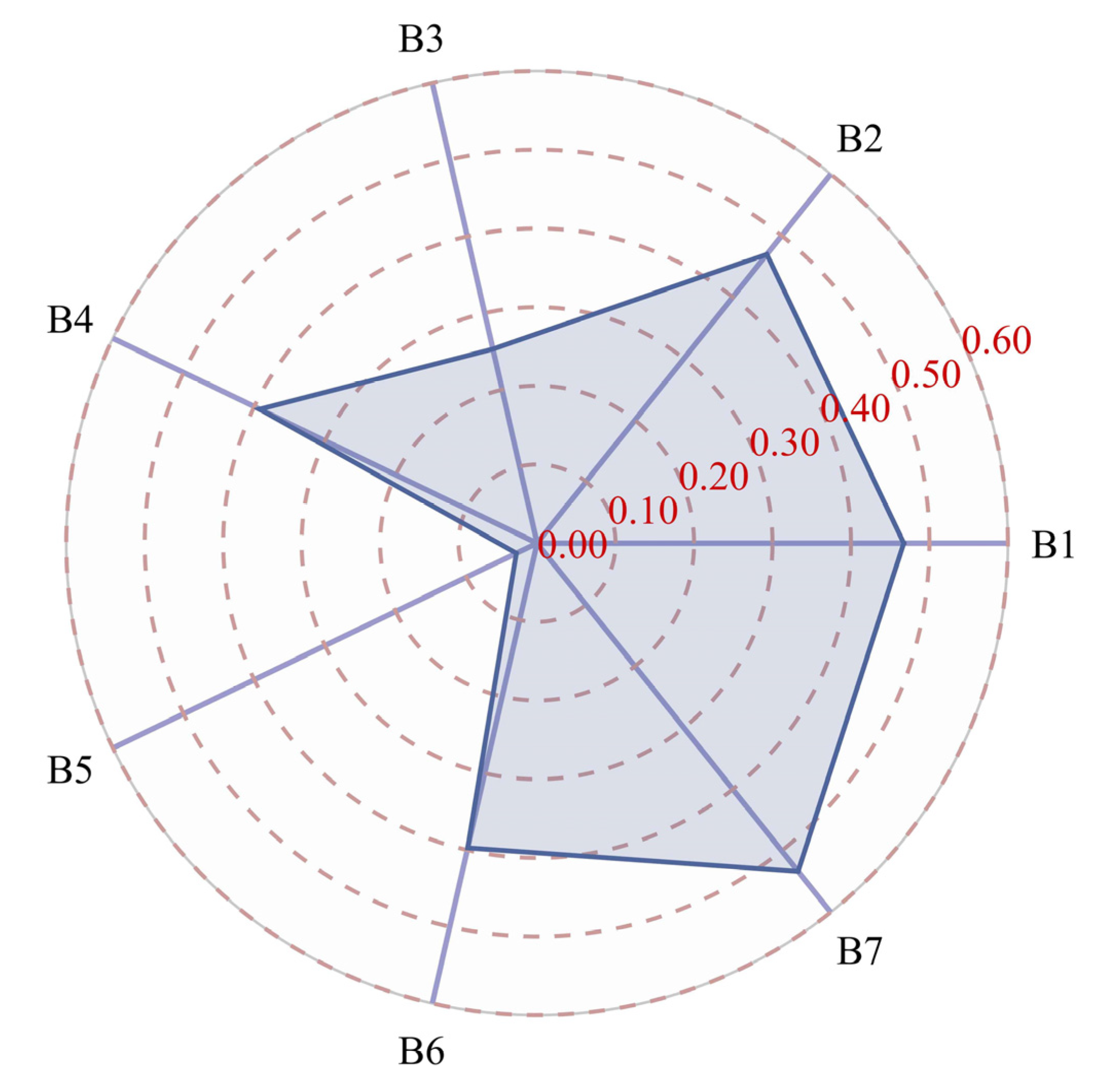
3.2. Spectral Scale Conversion and Correlation Analysis
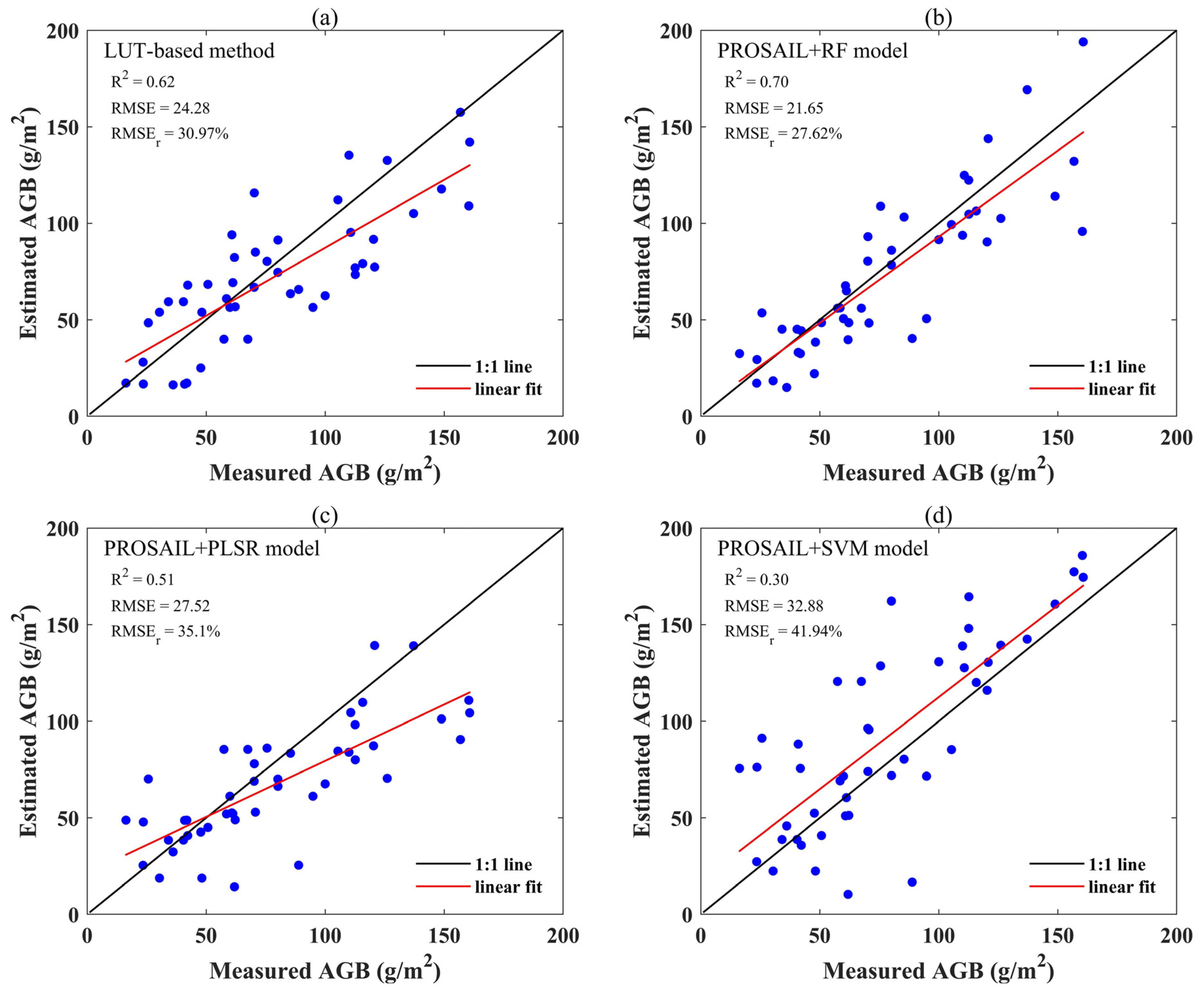
3.3. AGB Model Performance
3.3.1. Estimation Accuracy Based on LUT-Based Method
3.3.2. Estimation Accuracy Based on PROSAIL and Regression Algorithms
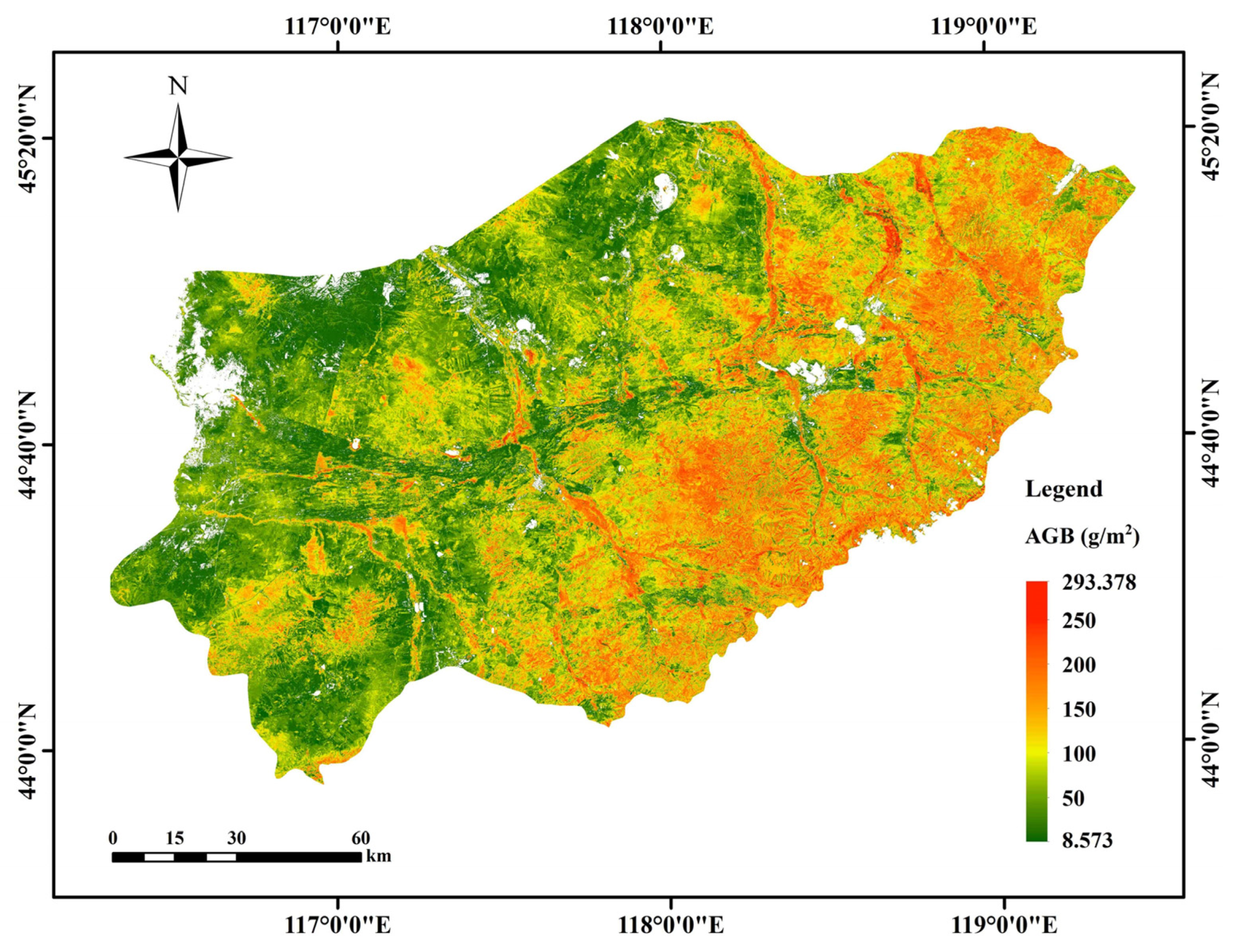
3.3.3. Spatial Distribution of Grassland AGB
4. Discussion
4.1. The Simulated Dataset Based on PROSAIL Model
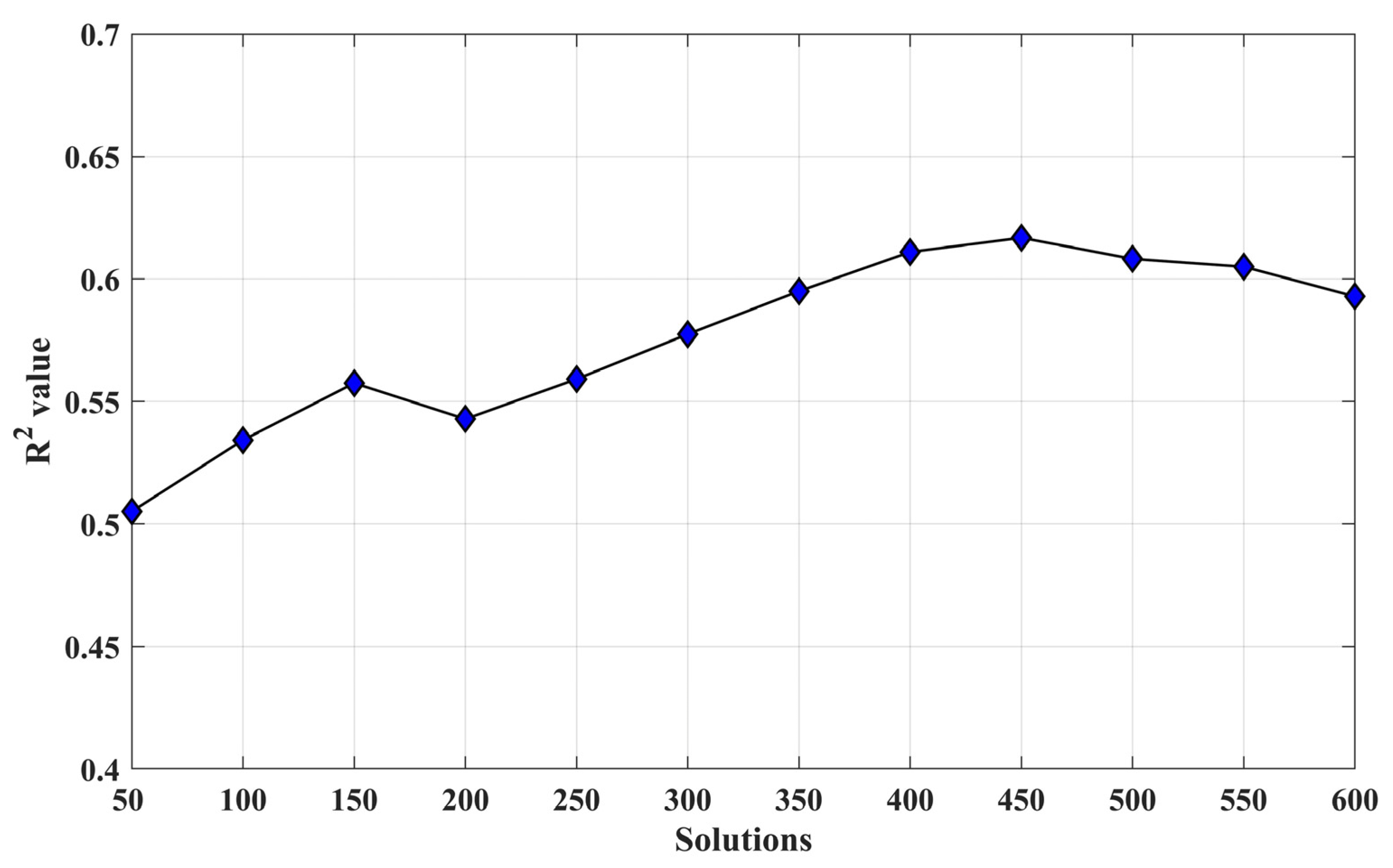
4.2. Dataset Optimization Based on LUT Method
4.3. Estimation Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dusseux, P.; Hubert-Moy, L.; Corpetti, T.; Vertès, F. Evaluation of SPOT imagery for the estimation of grassland biomass. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 72–77. [Google Scholar] [CrossRef]
- Fu, X.; Tang, C.; Zhang, X.; Fu, J.; Jiang, D. An improved indicator of simulated grassland production based on MODIS NDVI and GPP data: A case study in the Sichuan province, China. Ecol. Indic. 2014, 40, 102–108. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping forest aboveground biomass in the Northeastern United States with ALOS PALSAR dual-polarization L-band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
- Jia, W.X.; Liu, M.; Yang, Y.H.; He, H.L.; Zhu, X.D.; Yang, F.; Yin, C.; Xiang, W.N. Estimation and uncertainty analyses of grassland biomass in Northern China: Comparison of multiple remote sensing data sources and modeling approaches. Ecol. Indic. 2016, 60, 1031–1040. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; Zhou, L.; Tan, K.; Tao, S. Changes in biomass carbon stocks in China’s grasslands between 1982 and 1999. Global Biogeochem. Cycles 2007, 21. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yu, M.; Bai, Y.; Zhang, L. A comparison of two models with Landsat data for estimating above ground grassland biomass in Inner Mongolia, China. Ecol. Model. 2009, 220, 1810–1818. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Wu, C.; Wang, J.; Xie, Q.; Zhang, Z.; Nan, X.; Jin, H.; Bian, J.; Lei, G. Seamless Upscaling of the Field-Measured Grassland Aboveground Biomass Based on Gaussian Process Regression and Gap-Filled Landsat 8 OLI Reflectance. ISPRS Int. J. Geo-Inf. 2018, 7, 242. [Google Scholar] [CrossRef]
- Barrachina, M.; Cristobal, J.; Tulla, A.F. Estimating above-ground biomass on mountain meadows and pastures through remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 184–192. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Chen, Q. Modeling aboveground tree woody biomass using national-scale allometric methods and airborne lidar. ISPRS J. Photogramm. Remote Sens. 2015, 106, 95–106. [Google Scholar] [CrossRef]
- Wang, D.L.; Xin, X.P.; Shao, Q.Q.; Brolly, M.; Zhu, Z.L.; Chen, J. Modeling Aboveground Biomass in Hulunber Grassland Ecosystem by Using Unmanned Aerial Vehicle Discrete Lidar. Sensors 2017, 17, 180. [Google Scholar] [CrossRef] [PubMed]
- Schlund, M.; Davidson, M.W.J. Aboveground Forest Biomass Estimation Combining L- and P-Band SAR Acquisitions. Remote Sens. 2018, 10, 1151. [Google Scholar] [CrossRef]
- Jin, Y.X.; Yang, X.C.; Qiu, J.J.; Li, J.Y.; Gao, T.; Wu, Q.; Zhao, F.; Ma, H.L.; Yu, H.D.; Xu, B. Remote Sensing-Based Biomass Estimation and Its Spatio-Temporal Variations in Temperate Grassland, Northern China. Remote Sens. 2014, 6, 1496–1513. [Google Scholar] [CrossRef]
- Lu, D.S.; Chen, Q.; Wang, G.X.; Liu, L.J.; Li, G.Y.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhao, K.G.; Neuenschwander, A.; Lin, C.S. Satellite lidar vs. small footprint airborne lidar: Comparing the accuracy of aboveground biomass estimates and forest structure metrics at footprint level. Remote Sens. Environ. 2011, 115, 2786–2797. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Liu, Y.Y.; van Dijk, A.; de Jeu, R.A.M.; Canadell, J.G.; McCabe, M.F.; Evans, J.P.; Wang, G.J. Recent reversal in loss of global terrestrial biomass. Nat. Clim. Chang. 2015, 5, 470–474. [Google Scholar] [CrossRef]
- Quan, X.W.; He, B.B.; Yebra, M.; Yin, C.M.; Liao, Z.M.; Zhang, X.T.; Li, X. A radiative transfer model-based method for the estimation of grassland aboveground biomass. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 159–168. [Google Scholar] [CrossRef]
- Balzter, H.; Rowland, C.S.; Saich, P. Forest canopy height and carbon estimation at Monks Wood National Nature Reserve, UK, using dual-wavelength SAR interferometry. Remote Sens. Environ. 2007, 108, 224–239. [Google Scholar] [CrossRef]
- Svoray, T.; Shoshany, M. SAR-based estimation of areal aboveground biomass (AAB) of herbaceous vegetation in the semi-arid zone: A modification of the water-cloud model. Int. J. Remote Sens. 2010, 23, 4089–4100. [Google Scholar] [CrossRef]
- Eisfelder, C.; Kuenzer, C.; Dech, S. Derivation of biomass information for semi-arid areas using remote-sensing data. Int. J. Remote Sens. 2012, 33, 2937–2984. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Belaud, G.; Zribi, M.; Cheviron, B.; Courault, D.; Hagolle, O.; Charron, F. Irrigated Grassland Monitoring Using a Time Series of TerraSAR-X and COSMO-SkyMed X-Band SAR Data. Remote Sens. 2014, 6, 10002–10032. [Google Scholar] [CrossRef]
- Fu, L.Y.; Liu, Q.W.; Sun, H.; Wang, Q.Y.; Li, Z.Y.; Chen, E.X.; Pang, Y.; Song, X.Y.; Wang, G.X. Development of a System of Compatible Individual Tree Diameter and Aboveground Biomass Prediction Models Using Error-In-Variable Regression and Airborne LiDAR Data. Remote Sens. 2018, 10, 325. [Google Scholar] [CrossRef]
- Kayad, A.; Rodrigues, F.A., Jr.; Naranjo, S.; Sozzi, M.; Pirotti, F.; Marinello, F.; Schulthess, U.; Defourny, P.; Gerard, B.; Weiss, M. Radiative transfer model inversion using high-resolution hyperspectral airborne imagery - Retrieving maize LAI to access biomass and grain yield. Field Crops Res. 2022, 282, 108449. [Google Scholar] [CrossRef]
- Jung, J.; Kim, S.; Hong, S.; Kim, K.; Kim, E.; Im, J.; Heo, J. Effects of national forest inventory plot location error on forest carbon stock estimation using k-nearest neighbor algorithm. ISPRS J. Photogramm. Remote Sens. 2013, 81, 82–92. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Chen, Z.L.; Jia, K.; Xiao, C.C.; Wei, D.D.; Zhao, X.; Lan, J.H.; Wei, X.Q.; Yao, Y.J.; Wang, B.; Sun, Y.; et al. Leaf Area Index Estimation Algorithm for GF-5 Hyperspectral Data Based on Different Feature Selection and Machine Learning Methods. Remote Sens. 2020, 12, 2110. [Google Scholar] [CrossRef]
- Meng, B.P.; Liang, T.G.; Yi, S.H.; Yin, J.P.; Cui, X.; Ge, J.; Hou, M.J.; Lv, Y.Y.; Sun, Y. Modeling Alpine Grassland Above Ground Biomass Based on Remote Sensing Data and Machine Learning Algorithm: A Case Study in East of the Tibetan Plateau, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2986–2995. [Google Scholar] [CrossRef]
- Vamvakoulas, C.; Alexandris, S.; Argyrokastritis, I. Dry Above Ground Biomass for a Soybean Crop Using an Empirical Model in Greece. Energies 2020, 13, 201. [Google Scholar] [CrossRef]
- Yebra, M.; Chuvieco, E.; Riaño, D. Estimation of live fuel moisture content from MODIS images for fire risk assessment. Agric. For. Meteorol. 2008, 148, 523–536. [Google Scholar] [CrossRef]
- He, L.; Li, A.; Yin, G.; Nan, X.; Bian, J. Retrieval of Grassland Aboveground Biomass through Inversion of the PROSAIL Model with MODIS Imagery. Remote Sens. 2019, 11, 1597. [Google Scholar] [CrossRef]
- Chaabouni, S.; Kallel, A.; Houborg, R. Improving retrieval of crop biophysical properties in dryland areas using a multi-scale variational RTM inversion approach. Int. J. Appl. Earth Obs. Geoinf. 2021, 94, 102220. [Google Scholar] [CrossRef]
- Zhu, X.; Skidmore, A.K.; Darvishzadeh, R.; Wang, T.J. Estimation of forest leaf water content through inversion of a radiative transfer model from LiDAR and hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 120–129. [Google Scholar] [CrossRef]
- Quan, X.W.; He, B.B.; Li, X.; Tang, Z. Estimation of Grassland Live Fuel Moisture Content from Ratio of Canopy Water Content and Foliage Dry Biomass. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1903–1907. [Google Scholar] [CrossRef]
- Atzberger, C.; Darvishzadeh, R.; Immitzer, M.; Schlerf, M.; Skidmore, A.; le Maire, G. Comparative analysis of different retrieval methods for mapping grassland leaf area index using airborne imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 19–31. [Google Scholar] [CrossRef]
- Wang, Z.H.; Skidmore, A.K.; Wang, T.J.; Darvishzadeh, R.; Hearne, J. Applicability of the PROSPECT model for estimating protein and cellulose plus lignin in fresh leaves. Remote Sens. Environ. 2015, 168, 205–218. [Google Scholar] [CrossRef]
- Zimmerman, N.; Presto, A.A.; Kumar, S.P.N.; Gu, J.; Hauryliuk, A.; Robinson, E.S.; Robinson, A.L.; Subramanian, R. A machine learning calibration model using random forests to improve sensor performance for lower-cost air quality monitoring. Atmos. Meas. Tech. 2018, 11, 291–313. [Google Scholar] [CrossRef]
- Ali, A.M.; Darvishzadeh, R.; Skidmore, A.; Gara, T.W.; Heurich, M. Machine learning methods’ performance in radiative transfer model inversion to retrieve plant traits from Sentinel-2 data of a mixed mountain forest. Int. J. Digit. Earth 2021, 14, 106–120. [Google Scholar] [CrossRef]
- Sawut, R.; Li, Y.; Liu, Y.; Kasim, N.; Hasan, U.; Tao, W. Retrieval of betalain contents based on the coupling of radiative transfer model and SVM model. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102340. [Google Scholar] [CrossRef]
- Hishe, S.; Bewket, W.; Nyssen, J.; Lyimo, J. Analysing past land use land cover change and CA-Markov-based future modelling in the Middle Suluh Valley, Northern Ethiopia. Geocarto Int. 2019, 35, 225–255. [Google Scholar] [CrossRef]
- Baret, F.; Jacquemoud, S.; Guyot, G.; Leprieur, C. Modeled analysis of the biophysical nature of spectral shifts and comparison with information content of broad bands. Remote Sens. Environ. 1992, 41, 133–142. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Li, X.J.; Du, H.Q.; Cui, L.; Mao, F.J.; Liu, Y.L.; Li, Y.G.; Zhu, D.E. Simulating canopy reflectance time series for typical subtropical forest by coupling PROSPECT5 and 4SAIL models. Chin. J. Appl. Ecol. 2017, 28, 2461–2469. [Google Scholar]
- Feilhauer, H.; Schmid, T.; Faude, U.; Sanchez-Carrillo, S.; Cirujano, S. Are remotely sensed traits suitable for ecological analysis? A case study of long-term drought effects on leaf mass per area of wetland vegetation. Ecol. Indic. 2018, 88, 232–240. [Google Scholar] [CrossRef]
- Xu, M.; Liu, R.; Chen, J.M.; Liu, Y.; Shang, R.; Ju, W.; Wu, C.; Huang, W. Retrieving leaf chlorophyll content using a matrix-based vegetation index combination approach. Remote Sens. Environ. 2019, 224, 60–73. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Si, Y.; Schlerf, M.; Zurita-Milla, R.; Skidmore, A.; Wang, T. Mapping spatio-temporal variation of grassland quantity and quality using MERIS data and the PROSAIL model. Remote Sens. Environ. 2012, 121, 415–425. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, T.; Yi, G.; He, D.; Zhou, X.; Li, J.; Bie, X.; Miao, J. Dynamic Changes of NDVI in the Growing Season of the Tibetan Plateau During the Past 17 Years and Its Response to Climate Change. Int. J. Environ. Res. Public Health 2019, 16, 3452. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity estimates for nonlinear mathematical models. Math.model.comput.exp. 1993, 1, 112–118. [Google Scholar]
- Zhao, J.; Li, J.; Liu, Q.H.; Wang, H.Y.; Chen, C.; Xu, B.D.; Wu, S.L. Comparative Analysis of Chinese HJ-1 CCD, GF-1 WFV and ZY-3 MUX Sensor Data for Leaf Area Index Estimations for Maize. Remote Sens. 2018, 10, 68. [Google Scholar] [CrossRef]
- Soudani, K.; François, C.; le Maire, G.; Le Dantec, V.; Dufrêne, E. Comparative analysis of IKONOS, SPOT, and ETM+ data for leaf area index estimation in temperate coniferous and deciduous forest stands. Remote Sens. Environ. 2006, 102, 161–175. [Google Scholar] [CrossRef]
- Gonenc, A.; Ozerdem, M.S.; Acar, E.; IEEE. Comparison of NDVI and RVI Vegetation Indices Using Satellite Images. In Proceedings of the 8th International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Istanbul, Turkey, 16–19 July 2019. [Google Scholar]
- Gu, Y.X.; Wylie, B.K.; Howard, D.M.; Phuyal, K.P.; Ji, L. NDVI saturation adjustment: A new approach for improving cropland performance estimates in the Greater Platte River Basin, USA. Ecol. Indic. 2013, 30, 1–6. [Google Scholar] [CrossRef]
- Rodrigues, F.A.; Blasch, G.; Defourny, P.; Ortiz-Monasterio, J.I.; Schulthess, U.; Zarco-Tejada, P.J.; Taylor, J.A.; Gerard, B. Multi-Temporal and Spectral Analysis of High-Resolution Hyperspectral Airborne Imagery for Precision Agriculture: Assessment of Wheat Grain Yield and Grain Protein Content. Remote Sens. 2018, 10, 930. [Google Scholar] [CrossRef] [PubMed]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Camacho, F. Optimal modalities for radiative transfer-neural network estimation of canopy biophysical characteristics: Evaluation over an agricultural area with CHRIS/PROBA observations. Remote Sens. Environ. 2011, 115, 415–426. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Yan, G.; Chen, C.; Yang, B.; Liu, Z.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements. Remote Sens. 2016, 8, 359. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Yan, G.J.; Liu, Z.; Yang, B.; Chen, C.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 2: Validation and Intercomparison. Remote Sens. 2016, 8, 460. [Google Scholar] [CrossRef]
- Fu, G.; Zhang, J.; Shen, Z.X.; Shi, P.L.; He, Y.T.; Zhang, X.Z. Validation of collection of 6 MODIS/Terra and MODIS/Aqua gross primary production in an alpine meadow of the Northern Tibetan Plateau. Int. J. Remote Sens. 2017, 38, 4517–4534. [Google Scholar] [CrossRef]
- Brown, L.A.; Meier, C.; Morris, H.; Pastor-Guzman, J.; Bai, G.; Lerebourg, C.; Gobron, N.; Lanconelli, C.; Clerici, M.; Dash, J. Evaluation of global leaf area index and fraction of absorbed photosynthetically active radiation products over North America using Copernicus Ground Based Observations for Validation data. Remote Sens. Environ. 2020, 247, 111935. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.; Corsi, F.; van Wieren, S.E.; Sobhan, I. Estimation of green grass/herb biomass from airborne hyperspectral imagery using spectral indices and partial least squares regression. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 414–424. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Atzberger, C.; Skidmore, A.; Schlerf, M. Mapping grassland leaf area index with airborne hyperspectral imagery: A comparison study of statistical approaches and inversion of radiative transfer models. ISPRS J. Photogramm. Remote Sens. 2011, 66, 894–906. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Vapnik, V. Statistical Learning Theory; Wiley-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Jing, Z.; Jing, L.; Liu, Q. Based on PROSAIL and four scale model to estimation LAI from HJ-1B CCD2 data in Zhangye. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Rivera, J.P.; Verrelst, J.; Delegido, J.; Veroustraete, F.; Moreno, J. On the Semi-Automatic Retrieval of Biophysical Parameters Based on Spectral Index Optimization. Remote Sens. 2014, 6, 4927–4951. [Google Scholar] [CrossRef]
- Wang, Z.H.; Sun, Y.H.; Zhang, T.Y.; Ren, H.Z.; Qin, Q.M.; IEEE. Optimization of spectral indices for the estimation of leaf area index based on sentinel-2 multispectral imagery. In Proceedings of the 38th IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 5441–5444. [Google Scholar]
- Yang, L.C.; Deng, S.; Zhang, Z. New spectral model for estimating leaf area index based on gene expression programming. Comput. Electr. Eng. 2020, 83, 15. [Google Scholar] [CrossRef]
- Jay, S.; Gorretta, N.; Morel, J.; Maupas, F.; Bendoula, R.; Rabatel, G.; Dutartre, D.; Comar, A.; Baret, F. Estimating leaf chlorophyll content in sugar beet canopies using millimeter- to centimeter-scale reflectance imagery. Remote Sens. Environ. 2017, 198, 173–186. [Google Scholar] [CrossRef]
- Yin, C.M.; He, B.B.; Quan, X.W.; Liao, Z.M. Chlorophyll content estimation in arid grasslands from Landsat-8 OLI data. Int. J. Remote Sens. 2016, 37, 615–632. [Google Scholar] [CrossRef]
- Boren, E.J.; Boschetti, L. Landsat-8 and Sentinel-2 Canopy Water Content Estimation in Croplands through Radiative Transfer Model Inversion. Remote Sens. 2020, 12, 2803. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Liang, X.; Li, Z.; Huang, N.; Gao, S.; Wang, C.; Muhammad, S. Geostatistical modeling using LiDAR-derived prior knowledge with SPOT-6 data to estimate temperate forest canopy cover and above-ground biomass via stratified random sampling. Int. J. Appl. Earth Obs. Geoinf. 2015, 41, 88–98. [Google Scholar] [CrossRef]
- Liang, T.; Yang, S.; Feng, Q.; Liu, B.; Zhang, R.; Huang, X.; Xie, H. Multi-factor modeling of above-ground biomass in alpine grassland: A case study in the Three-River Headwaters Region, China. Remote Sens. Environ. 2016, 186, 164–172. [Google Scholar] [CrossRef]
- Lü, J. Hyperspectral Remote Sensing Inversion Models of Crop Chlorophyll Content Based on Machine Learning and Radiative Transfer Models. Ph.D. Thesis, China University of Geosciences (Beijing), Beijing, China, 2012. [Google Scholar]


| Model | Parameter | Symbol | Range | Unit | Source |
|---|---|---|---|---|---|
| PROSPECT_5B | Leaf structure parameter | N | 1–2 | - | Feilhauer et al. [46] |
| Chlorophyll content | Cab | 5–100 | μg/cm2 | Xu et al. [47] | |
| Equivalent water thickness | EWT | 0.003–0.03 | g/cm2 | Liang et al. [48] | |
| Dry matter content | DMC | 0.001–0.01 | g/cm2 | Si et al. [49] | |
| Carotenoid content | Car | 8 | μg/cm2 | Model default | |
| Leaf brown pigment | Cbrown | 0 | - | Field survey | |
| 4SAIL | Leaf area index | LAI | 0.3–8 | m2∙m−2 | Si et al. [49] & MOD15A2H |
| Hot spot factor | Hspot | 0.05–0.1 | - | He et al. [31] | |
| Soil moisture ratio | Psoil | 0–1 | - | Huang et al. [50] | |
| Leaf inclination distribution | LIDFa | −0.35 | - | Field survey | |
| LIDFb | −0.15 | - | Field survey | ||
| Sun zenith angle | θs | 27.26 | Degree (°) | Landsat-8 metadata | |
| View zenith angle | θv | 0 | Degree (°) | Landsat-8 metadata | |
| Relative azimuth angle | θz | 0 | Degree (°) | Landsat-8 metadata |
| Parameter Symbol | Range | Step | Unit |
|---|---|---|---|
| Cab | 5–100 | 10 | μg/cm2 |
| LAI | 0.3–8 | 0.1 | m2·m−2 |
| DMC | 0.001–0.01 | 0.001 | g/cm2 |
| EWT | 0.003–0.03 | 0.01 | g/cm2 |
| Psoil | 0.5 | fixed | - |
| N | 1.25 | fixed | - |
| Hspot | 0.075 | fixed | - |
| Characteristics | R | |
|---|---|---|
| Spectral bands | B1 | −0.47 |
| B2 | −0.47 | |
| B7 | −0.53 | |
| Spectral indices | NDSIb3, b4 | −0.46 |
| NDSIb5, b6 | −0.44 | |
| NDSIb5, b7 | −0.54 | |
| NDSIb6, b7 | −0.66 | |
| RSIb3, b4 | −0.45 | |
| RSIb5, b6 | −0.41 | |
| RSIb5, b7 | −0.54 | |
| RSIb6, b7 | −0.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Gao, H.; Zhang, X. Combining Radiative Transfer Model and Regression Algorithms for Estimating Aboveground Biomass of Grassland in West Ujimqin, China. Remote Sens. 2023, 15, 2918. https://doi.org/10.3390/rs15112918
Zhang L, Gao H, Zhang X. Combining Radiative Transfer Model and Regression Algorithms for Estimating Aboveground Biomass of Grassland in West Ujimqin, China. Remote Sensing. 2023; 15(11):2918. https://doi.org/10.3390/rs15112918
Chicago/Turabian StyleZhang, Linjing, Huimin Gao, and Xiaoxue Zhang. 2023. "Combining Radiative Transfer Model and Regression Algorithms for Estimating Aboveground Biomass of Grassland in West Ujimqin, China" Remote Sensing 15, no. 11: 2918. https://doi.org/10.3390/rs15112918
APA StyleZhang, L., Gao, H., & Zhang, X. (2023). Combining Radiative Transfer Model and Regression Algorithms for Estimating Aboveground Biomass of Grassland in West Ujimqin, China. Remote Sensing, 15(11), 2918. https://doi.org/10.3390/rs15112918






