Abstract
A representative general polarimetric model-based decomposition framework was proposed by Chen et al., which implements a simultaneous full-parameter inversion by using complete polarimetric information and solves several limitations in previous decomposition methods. However, there are still shortcomings in Chen’s work. Firstly, only the real part of the parameter in the generalized surface scattering model is considered. Secondly, inappropriate initial input values may lead to local optima in the nonlinear least squares optimization algorithm. Thirdly, the volume scattering component is underestimated in the volume scattering-dominated scene, but overestimated in buildings with large orientation (LOB) areas. Finally, nonlinear optimization is time-consuming computationally. To overcome those issues, an improved generalized polarimetric model-based decomposition method is proposed in this paper. The imaginary part of the parameter is incorporated into the decomposition framework of the proposed method. Ingeniously utilizing the internal relationship in the generic equations composed of coherent matrix elements, the model parameters can be inversed by simplifying the nonlinear equations to linear equations. Therefore, compared with Chen’s method, the proposed method does not rely on the initial input values, and improves the computational efficiency. In addition, a hierarchical decomposition scheme is presented to solve the problem of underestimation or overestimation of volume scattering component mentioned above. The performance and advantages of this method are evaluated with L-band and C-band polarimetric synthetic aperture radar (PolSAR) data sets. Comparison studies are carried out with other model-based decomposition methods, demonstrating that the proposed method can further improve decomposition performance, especially in LOB areas.
1. Introduction
Synthetic aperture radar (SAR) can provide wide-area, all-day and nearly all-weather operations, playing an important role in earth observation [1,2]. Compared with the normal SAR, polarimetric synthetic aperture radar (PolSAR) takes the additional complete measurement of the target polarization information. Hence, PolSAR can reveal the scattering mechanisms of the target by the polarimetric decomposition principle [3,4,5]. Based on the basic principle, decomposition methods [6,7,8,9,10,11] are derived and applied to several scenarios, such as target detection and monitoring [12,13,14,15], land cover classification [16,17,18,19,20,21,22,23], and geophysical parameter inversion [24,25,26]. For the derived decomposition methods, eigenvalue–eigenvector-based decomposition and model-based decomposition (MBD) are the two most widely used types of noncoherent PolSAR decomposition [6].
For the MBD method, polarization decomposition and interpretation lie in finding reasonable scattering models to match received PolSAR data [27]. The pioneering work of MBD is Freeman–Durden decomposition [28], which has been successfully applied to the natural distributed target areas under the well-known reflection symmetry condition. Due to the advanced methodology of MBD, a lot of improvements have been derived based on this method, such as Yamaguchi-based decomposition methods [29,30,31,32], seven-component model-based decomposition method [33], feature-driven superpixel segmentation method [34], and L1-regularization approach [35], etc.
A representative MBD-derived study is the general polarimetric model-based decomposition method proposed by Chen et al. [36]. In Chen’s work, generalized double-bounce and surface scattering models were developed for the first time by separating their independent orientation angles. Many limitations are improved compared with traditional MBD methods, such as model inversion priority, branch conditions, orientation effect, and negative powers. Xie et al. [37,38,39] refined some boundary conditions and feasibility, and reduced the optimization calculation of model selection.
However, there is still room for improvement in Chen’s and Xie’s work.
- (1)
- Limited by the number of equations, only the real part of the unknown parameter in the generalized surface scattering model is considered. However, for manmade targets (e.g., urban buildings), their imaginary parts cannot be ignored [40].
- (2)
- In their work, the initial values of the matched model parameters are necessary and dominate the decomposition results. However, inappropriate initial values would lead to local minima model parameter results in solving nonlinear least squares optimization.
- (3)
- Unsolved under- and overestimated problems in volume scattering-dominated natural areas (e.g., forest/vegetation areas) and LOB areas still exist [39,41].
- (4)
- Model inversion processes are all based on solving nonlinear least squares optimization. The computation and optimum value finding are famous difficulties in nonlinear optimization problem-solving.
To this end, a generalized polarimetric model-based decomposition method is proposed, and several targeted promotions are designed to solve the above problems.
- (1)
- The imaginary part of in the generalized surface scattering model is included into the model inversion parameter set by using the constraint condition of minimizing residual.
- (2)
- Ingeniously utilizing the internal relationship in the generic equations composed of coherent matrix elements, the model parameter inversion will be transformed into a linear problem rather than a nonlinear problem. By doing so, the requirement of initial input values can be avoided, and the computational efficiency of model parameter inversion is improved. Moreover, a suitable volume scattering model selected to reduce the number of optimization iterations in Xie’s work [39] was absorbed into the proposed approach, which further improves the computational efficiency.
- (3)
- To solve the under- and overestimated problems in typical areas, a hierarchical decomposition scheme is presented. The key to this scheme is the introduction of a criterion area descriptor [41] to discriminate between urban and nonurban areas. With this discrimination, different areas can apply to different processes. For urban areas, the cross-scattering model [42] is incorporated into the generalized decomposition framework to avoid overestimating problems. For volume scattering-dominated nonurban areas, to avoid underestimation of the volume scattering component, we apply the classic Yamaguchi four-component decomposition method (i.e., Yamaguchi-2005 algorithm) [29] to improve the proportion of its volume scattering component.
The rest of this paper is organized as follows. In Section 2, the generalized scattering models and Chen’s decomposition algorithm [36] are briefly reviewed. In Section 3, an improved generalized polarimetric model-based decomposition method is proposed, and the flowchart of a hierarchical decomposition scheme is presented in detail. Comparison studies and further analyses are carried out in Section 4, using L-band AIRSAR and C-band space borne Radarsat-2 satellite data sets. Computational efficiency analysis and residual examination for further discussion and conclusions are given in Section 5 and Section 6, respectively.
2. Review of General Polarimetric Model-Based Decomposition
2.1. Generalized Scattering Models
This includes four scattering models in Chen’s method [36], i.e., volume scattering model, generalized surface scattering model, generalized double-bounce scattering model, and helix scattering model.
- (1)
- Volume scattering model
Volume scattering is often modeled as randomly oriented dipoles. Chen’s work incorporates multiple volume scattering models and gives a general model consisting of four classic volume scattering models. The first volume scattering model (named ) was proposed in the classic Freeman–Durden three-component decomposition [28]. Another two usual volume scattering models whose PDFs obey sine and cosine distribution were first proposed in the Yamaguchi 2005 algorithm [29], denoted as and . The fourth volume scattering model referring to the highest entropy was proposed by An et al. [43], denoted as . The coherency matrix of the volume scattering model can be expressed in a unified form [36]:
where corresponds to the contribution of the volume scattering to polarization echo power, the superscript is a conjugate operator, and elements on the diagonal of are real-valued. Then, the four types of volume scattering models can be written as:
In Chen’s work [36], by using the nonlinear least squares algorithm that minimized the sum of squares of the residual, the type of volume scattering models can be selected to best fit the observed data.
- (2)
- Generalized surface scattering model
The basic surface scattering model is represented by surface scattering phenomena from slightly rough surfaces, neglecting the cross-polarization component [28]. The corresponding coherency matrix is:
where corresponds to the contribution of the surface scattering to polarization echo power and is theoretically a complex value. However, Chen et al. [36] considered that is approximately real-valued, as its imaginary part can usually be negligible in most natural scenes for microwave regimes.
As the orientation effect of terrain slopes can rotate the polarization basis and induce significant cross-polarization power, Chen et al. [36] proposed a generalized surface scattering model by modeling with the rotation angle , i.e.,
where the superscript H denotes the conjugate transposition operator and is the rotation matrix, i.e.,
- (3)
- Generalized double-bounce scattering model.
The double-bounce scattering model describes the scattering from a dihedral corner reflector, and its coherency matrix can be described as [29]:
where corresponds to the contribution of the double-bounce scattering to polarization echo power, is complex-valued, and .
Oriented buildings can also induce significant cross-polarization power by rotating the polarization basis. Similarly, a generalized double-bounce scattering model proposed in Chen’s method [36] can be written as:
where denotes the induced rotation angle.
- (4)
- Helix scattering model.
The roll-invariant helix scattering model proposed by Yamaguchi et al. [29] is aimed at describing the reflection asymmetry condition, whose coherency matrix is:
where corresponds to the contribution of the helix scattering to polarization echo power and is the imaginary unit.
2.2. Chen’s Method
Compared with the conventional four-component decomposition method, Chen’s method has the following advantages. Firstly, the occurrence of negative power is theoretically avoided using the boundary conditions during the optimization. Secondly, the generalized surface and double-bounce scattering models account for the off-diagonal terms of coherency matrix T, and also fit well with the observations where the surface slopes and oriented dihedral reflectors can induce significant cross-polarization power by rotating the polarization basis. Thirdly, the representative volume scattering models can be adaptively selected by using the nonlinear least squares optimization method, so that the scattering mechanism of a target can fit the observations well. Finally, most model-based decomposition methods [29,30,31,32,33,34,35] usually subtract the helix scattering contribution at first, and then obtain the volume scattering contribution, or reassign the decomposed power by manual intervention. This strategy may lead to overestimation or underestimation of the power weights of the scattering components, or even negative power. Chen’s work overcame these limitations. By solving the nonlinear least squares algorithm, the unknown model parameters are determined under the minimum residual.
The general decomposition framework is given by [36]:
where T is the observed coherency matrix and is the residual error matrix introduced by model mismatch and observation noise.
As T is a Hermitian matrix, it only has nine real independent observations. In the general decomposition framework, the number of unknown parameters is also nine (i.e., , , , , , , , and ). Hence, Chen et al. [36] adopted a nonlinear least squares optimization method to solve these unknown parameters, and the optimization criterion is to minimize the residual:
where is the L2-norm of .
Solving the problem in (11), initial values and boundary conditions are necessary. In Chen’s and Xie’s work, the initial values adopt the outputs from the conventional Yamaguchi model-based decomposition in [29,30,31,32] or the modified initial values in [38], and the boundary conditions for the model parameter set are:
where is the total power.
3. Improved Generalized Polarimetric Model-Based Decomposition Method
In this section, the cross-scattering model (CSM) proposed by Xiang et al. [42] and the generalized volume scattering model (GVSM) proposed by Antropov et al. [44] are first reviewed. Then, based on that, a generalized decomposition framework in conjunction with model inversion algorithm is proposed. Finally, a hierarchical decomposition scheme is presented in detail.
3.1. Cross-Scattering and Generalized Volume Scattering Models
The CSM is derived from a rotated dihedral structure with varied polarimetric orientation angle (POA). It enables the separation of the cross-scattering caused by oriented buildings, especially largely oriented buildings, from the overall cross-polarization components [42]. The cross-scattering matrix can be written as:
where corresponds to the contribution of CSM to polarization echo power and , , is the POA. The expression of the POA can be found in [30].
The GVSM has been proved to be more general than other traditional models for characterizing canopy scattering [44]. Xie et al. adopted the GVSM to replace the four-volume scattering models in Chen’s method [36]. In addition to being more general, the optimization processing times were reduced from four to one, which improved the model inversion efficiency. Therefore, the GVSM is incorporated into the proposed general decomposition framework by absorbing Xie’s improvement work [39]. The coherency matrix of the GVSM can be written as [44]:
where corresponds to the contribution of GVSM to polarization echo power, , , , and represents the co-polarization power ratio of HH and VV components, i.e., , which can be estimated directly from the PolSAR data.
According to (13) and (14), the volume scattering model in (1) can be rewritten in a unified form to facilitate the model inversion problem description:
where a, b, c and d are real-valued [42,44]. The selection of or will be discussed in Section 3.3.
3.2. General Decomposition Framework and Model Inversion Algorithm
Differently from the work proposed by Chen et al. [36], the coherent matrix T is rotated with angle as in [30] before implementing decomposition. This procedure has two advantages. One is reducing the cross-polarization component, which can avoid the overestimation of the volume scattering in LOB areas; the other is improving the computational efficiency of model inversion. Denote T multiplying the rotation matrix with angle as , (10) can be rewritten as:
Substitute (5), (8), (9) and (15) into (16), and the upper triangular elements of the coherency matrix are used. Let , then, the generic nine equations are:
where is the entry of the coherency matrix , and and are real and imaginary part of , respectively. In the generic nine equations, it should contain ten unknowns, while Chen et al. [36] only considered nine unknowns (ignoring the imaginary part of ). However, in our proposed method, all unknowns can be inverted numerically by minimizing the residual.
We first assume that . According to (25), can be obtained directly, but the expression of is modified to (26) in view of the residual:
where is used to measure how well the helix scattering model fits the observations, with .
Using the internal relationship in (18)–(24), , , , , , , , , , and as a function of and can be obtained by solving three sets of linear equations. The detailed derivation is given as follows.
Under the assumption that ~ equals zero, the generic nine equations in (17)–(25) can be rewritten as:
Firstly, according to (35), we can directly obtain the expansion coefficient of the helix scattering component , and it is a function of .
Secondly, according to (28), (29) and (34), the following equations can be formed.
By solving the above equations, , and as a function of and can be obtained, i.e., , and .
Thirdly, according to (30) and (32), the following equations can be formed.
By solving the above equations, .and can be obtained. Similarly, according to (31) and (33), the following equations can be formed.
Finally, according to (38), and can be obtained in the same way. Then, and as a function of and can be given by:
According to and , as a function of and can be obtained:
Moreover, according to and , as a function of and can be determined:
Hitherto, as a function of , and , , , , , , , , , and as a function of and have been obtained here.
Based on that, we substitute , , , , , , , , and into (17)–(24). According to the boundary conditions in (12), , and are traversed numerically at equal intervals, and the model parameter set is determined by minimizing . Finally, the scattering powers , , and can be computed as:
In addition, according to (34), since [32], and , , the value ranges of and have two cases. One is , , and the other is , . We traverse numerically for , and , respectively, in the two cases, and then find the case of the minimum , which corresponds to the optimal model inversion parameter set. The detailed flowchart of the model inversion is shown in Figure 1.
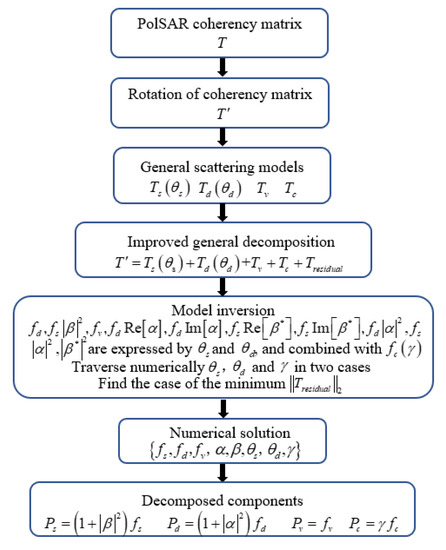
Figure 1.
Flowchart of model inversion algorithm.
3.3. Hierarchical Decomposition Scheme
The MBD approach aims to provide an interpretation based on a sensible physical model [6]. It reveals physical scattering mechanisms that lead to the observed backscatter in the PolSAR data. Chen’s method [36], including the improved method, has good performance in the areas with mixed scattering mechanism. However, on the one hand, in the volume scattering-dominated areas, due to the constraint of minimum , part of the energy of the volume scattering component is transferred to the surface and double-bounce scattering component, resulting in a low estimation of the volume scattering component in Chen’s and Xie’s methods. On the other hand, in built-up areas, especially in LOB areas, the volume scattering component is overestimated due to the large cross-polarization component [39]. Therefore, to avoid underestimating the volume scattering component in the volume scattering-dominated areas and overestimating one in the built-up areas, different volume scattering models need to be considered between urban and nonurban areas.
Based on the above consideration, a hierarchical decomposition scheme is proposed here. In this scheme, a criterion area descriptor in [41] is introduced, and the expression is:
where
and stands for average operation. This area descriptor for discriminating between urban and nonurban areas is given by:
where is the discriminating threshold.
In the hierarchical decomposition scheme, according to the threshold , the CSM is used to consider the cross-scattering of oriented buildings, thus making it more flexible and adaptive for urban areas, while the GVSM is applicable to nonurban areas. In addition, we use a branch condition to solve the underestimation of the volume scattering in the volume scattering-dominated areas, where is volume scattering power in the Yamaguchi 2005 algorithm [29]. To be specific, the Yamaguchi 2005 algorithm is first applied to nonurban areas. When [45], we use the decomposition results of the Yamaguchi 2005 algorithm; otherwise we use the decomposition results of the algorithm proposed in this paper. By doing so, the decomposition results of the proposed method are close to the actual scene. The detailed flowchart of the hierarchical decomposition scheme is shown in Figure 2.
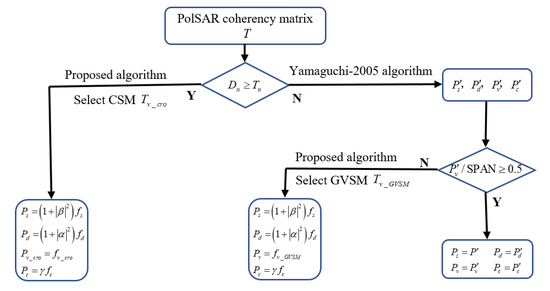
Figure 2.
Flowchart of the hierarchical decomposition scheme.
4. Experimental Results and Analysis
AIRSAR L-band and Radarsat-2 satellite C-band data sets are used to demonstrate the proposed general decomposition. A detailed analysis and different methods (i.e., general four-component decomposition with unitary transformation method (G4U) [30], general model-based decomposition method incorporating generalized volume scattering model (GMD-GVSM) [39], Chen’s method [36], and proposed method) comparison are presented next.
4.1. Decomposition Comparison with AIRSAR Data
The first study area is located in Long Beach, USA. It has good coverage of buildings with different orientations. The data were acquired on 24 October 1998, and the resolution of the original image corresponds to 4.62 m × 3.33 m (azimuth × ground range) in the ground area. Figure 3 displays the fully polarimetric AIRSAR L-band data with Pauli color coding. The red channel describes double-bounce scattering, the green channel describes volume scattering, and the blue channel describes single-bounce scattering. A large scale of green tone (consists of areas of LOB and natural targets) appears in the Pauli RGB image, leading to confusion in distinguishing these land covers.

Figure 3.
Pauli RGB image.
In order to evaluate the performance of the proposed method, the National Land Cover Database 2011 (NLCD 2011) is used for the ground reference data, as also shown in Figure 4 [41,46]. The decomposition results from the four methods are shown in Figure 5, where the red channel describes double-bounce and cross-scattering (urban scattering mechanism), the green channel describes volume scattering (shrub areas), and the blue channel describes surface scattering (ocean areas).
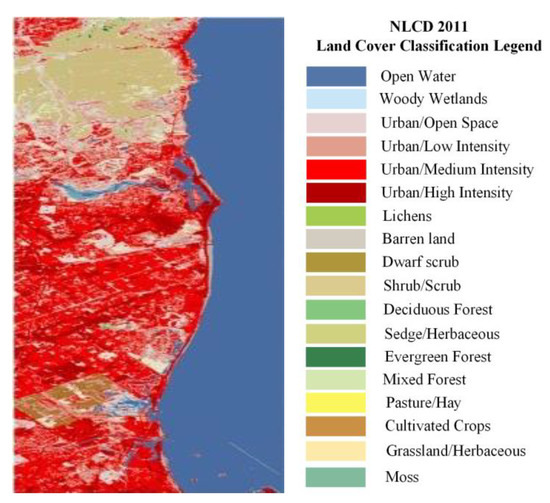
Figure 4.
NLCD 2011 shown for the PolSAR image.

Figure 5.
Decomposition results from AIRSAR data, and A~D in (a) correspond to patches A~D, respectively. (a) G4U method. (b) GMD-GVSM method. (c) Chen’s method. (d) Proposed method. The images are colored by (red), (green), and (blue).
It’s noted that, based on Chen’s, GMD-GVSM, and G4U methods, built-up areas with larger orientations (i.e., LOB areas) all display the characteristic of volume scattering, leading to indistinct classification between urban and nonurban areas. However, the results of the proposed method seem redder and LOB areas are identified more clearly due to the power of volume scattering decreased obviously. Moreover, the areas dominated by volume scattering are greener than other decomposition methods in Figure 5. Thus, compared with the other three methods, the decomposition result of the proposed method seems clearer and closer to the actual situation.
To quantitatively evaluate the performance of different decomposition methods and ascertain the discriminating threshold, four types of land cover classes are considered in the image (the red box area in Figure 5a): shrub/scrub areas (patch A), building with small orientation (SOB) areas (patch B), LOB areas (patch C) and ocean areas (patch D). The corresponding feature histograms are given in Figure 6. It can be observed that there is a significant distinction in the criteria area descriptors between urban areas (patch B and patch C) and natural areas (patch A and patch D). This makes it easy to separate the building areas from other land cover areas. According to the literature [41] and Figure 6, the discriminating threshold can be set as 1.1 for the case of the AIRSAR data. After determining the threshold value, the corresponding normalized scattering power statistics are shown in Table 1.
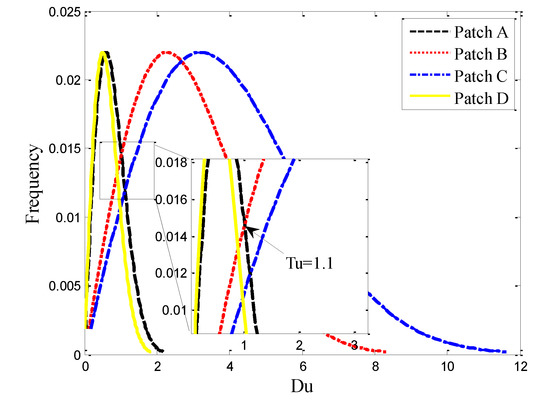
Figure 6.
Histograms of the criterion area descriptor for four selected patches.

Table 1.
Normalized scattering power statistics of AIRSAR image in selected areas with different land cover classes.
For shrub/scrub areas (patch A), the dominant scattering components for all methods are consistently volume scattering. Compared with the other three methods, the results from the proposed method somehow reduce the surface scattering and double-bounce scattering components and increase the volume scattering component. In fact, for the volume scattering-dominated areas, we do not need to suppress the volume scattering power by the rotation of the coherency matrix (e.g., G4U). In GMD-GVSM and Chen’s method [36], under the constraint of minimizing the residual, some power must be assigned to surface scattering and double-bounce scattering, so the contribution of volume scattering is further reduced compared with G4U. However, in the proposed decomposition scheme, by setting the two branch conditions of threshold and , the natural areas dominated by volume scattering can be selected, and the Yamaguchi 2005 algorithm is used to maintain a high-volume scattering contribution in the shrub/scrub areas. For SOB areas (patch B), all methods consistently show a high double-bounce scattering, and the proposed method retrieves a lower volume scattering component in comparison to the other three methods.
For LOB areas (patch C), the color is mostly green in Figure 5a–c, which means G4U, GMD-GVSM and Chen’s method [36] all face the problems of volume scattering overestimation. The respective percentages are 45.21%, 36.14%, and 42.38%. However, the proposed method solves this problem: the volume scattering power decreases to 19.78%. In addition, compared with the other three patches, the cross-scattering power is significantly increased. This phenomenon proves the effectivity, reducing the overestimation of volume scattering for LOB areas, and also explains the cross-scattering matrix being able to effectively model the cross-polarization component from these highly oriented dense urban areas. For ocean areas (patch D), all methods show very high surface scattering. In addition, since the imaginary part of the parameter in the generalized surface scattering model is considered, the surface scattering in urban areas increase observably. This is reasonable, because these areas mainly contain surface, double-bounce, and cross-scattering [47].
4.2. Decomposition Comparison with Radarsat-2 Data
In the test, a portion of the whole image in C-band is selected, in which ocean, built-up and forest areas are included, as shown in Figure 7. Figure 8 shows the decomposition result in comparison. Forest areas are green, where volume scattering is dominant. Ocean areas are blue, where surface scattering is dominant. Built-up areas is red in general, as double-bounce scattering is dominant.
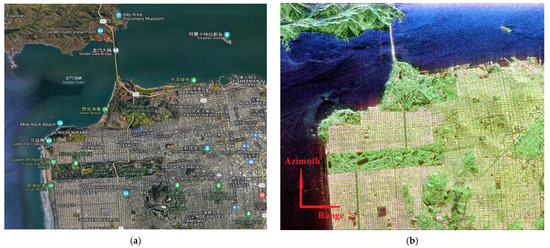
Figure 7.
Radarsat-2 satellite data with C band. (a) Optical image. (b) Pauli RGB image.


Figure 8.
Decomposition results from Radarsat-2 satellite data, and A~D in (a) correspond to patches A~D, respectively. (a) G4U method. (b) GMD-GVSM method. (c) Chen’s method. (d) Proposed method. The images are colored by (red), (green), and (blue).
LOB areas such as the triangle areas located in the right-middle of Figure 8a (denoted as patch C) are mostly green. The volume scattering component at LOB areas is still overestimated in C-band. For more detailed comparison, four types of land cover are considered: forest areas (patch A), SOB areas (patch B), LOB areas (patch C), and ocean areas (patch D). Boundaries of these areas are marked in red in Figure 8a. In the same manner as threshold selection, the discriminating threshold is set as 0.22 for the Radarsat-2 satellite data. The corresponding normalized scattering power statistics are listed in Table 2.

Table 2.
Normalized scattering power statistics of Radarsat-2 image in selected areas with different land cover classes.
In forest areas (patch A), although all four methods are dominated by volume scattering, as the selected forest areas (patch A) exhibit a large trunk but a low-density crown [39], which eases the radar wave to penetrate through the crown and reach the ground, all methods present a decrease in volume scattering component and an increase in double-bounce scattering component. Moreover, the proposed method and G4U estimate lower surface scattering components than GMD-GVSM and Chen’s methods. The reason for this is that the Yamaguchi 2005 algorithm was chosen for approximately 42.3% of the pixels in our proposed method. In SOB areas (patch B), similarly to the conclusion in Figure 8, all methods are dominated by double-bounce scattering and surface scattering, and the proportion of volume scattering in the proposed method is the smallest (only 9.54%). For LOB areas (patch C) in Radarsat-2 satellite data, it is proved again that more urban information can be mined from the PolSAR image by incorporating the cross-scattering model into the decomposition framework, and it is more suitable for urban area identification. In the ocean areas (patch D), as expected, all methods consistently show a very high surface scattering, as in the C-band case.
5. Computational Efficiency Analysis and Residual Examination
It is intuitive from the analysis in Section 3 that the computational efficiency of the proposed method is the best compared to the GMD-GVSM and Chen’s methods. To quantitatively analyze the computational efficiency of GMD-GVSM, Chen’s, and the proposed methods, we compared their time consumption for decomposing L-band AIRSAR and C-band space borne Radarsat-2 satellite data sets on the same computer. MATLAB R2016b was the software environment used to process the same PolSAR data sets, and all the output results are realized with the same image preprocessing procedure for each method. The central processing unit (CPU) used was an Intel(R) Core(TM) I5-10400 at 2.90 GHz, with a memory of 16 GB. Windows 10 64-bit was the operating system used. In the nonlinear least squares optimization, the tolerance used for both GMD-GVSM and Chen’s methods and residual is and the maximum iteration is . For the proposed method, the value intervals of , and are rad, rad and 0.05, respectively. The average processing time of each pixel is recorded in Table 3. It can be seen from Table 3 that the GMD-GVSM method relies on only one optimization stage instead of four as in Chen’s method [36], and its computational efficiency is significantly improved compared with Chen’s method [36]. The average time consumption of each pixel of the proposed method is the least among these methods. The reason is that the proposed method not only absorbs an optimization process of the GMD-GVSM method but also uses a linear algorithm involving matrix operation, which has high CPU utilization, thus further improving the computational efficiency.

Table 3.
Normalized scattering power statistics of Radarsat-2 image in selected areas with different land cover classes.
Furthermore, the minimized residuals are normalized by the corresponding measured coherency matrices for further examination. The mean values of are also listed in Table 3, and all the values are very small. The average of Chen’s method [36] is the least, followed by the proposed method, and the highest is the GMD-GVSM method. The reason is that the GMD-GVSM and proposed methods have fewer degrees of freedom to select the volume scattering model compared with Chen’s method [36], and the GMD-GVSM method redefines boundary conditions. However, according to the decomposition results for different patches in Section 4, the GVSM is closer to the physical scattering mechanism in the real scene than the four general volume models in Chen’s method [36]. Overall, experimental results demonstrate that compared with the other two methods, the best performance is achieved by the proposed decomposition under the premise of ensuring small residual and high computational efficiency.
6. Conclusions
An improved generalized polarimetric model-based decomposition method is proposed in this paper based on Chen’s and Xie’s works. In the proposed method, the imaginary part of the generalized surface scattering component is incorporated into the general decomposition framework to fit scenes including the manmade target. By simplifying the nonlinear equations to linear equations and solving them numerically instead of using the nonlinear least squares optimization technique, the initial value selection problems are avoided, and the optimal solution can be obtained within the range of variables and grid division accuracy. On this basis, a hierarchical decomposition scheme is presented to solve the underestimation or overestimation problem of volume scattering components in some typical terrain scenes.
Under the same PolSAR data sets, compared with GMD-GVSM and Chen’s methods, the proposed method not only improves the computational efficiency of model inversion but also has more reasonable decomposition results in the volume scattering-dominated and built-up areas, especially in LOB areas. Further investigations will mainly focus on selecting different volume scattering models without using the hierarchical decomposition scheme or developing a representative and generalized volume scattering model, and incorporating it into the general decomposition framework.
Author Contributions
Y.L. (Yongzhen Li) conceived the study. Y.L. (Yemin Liu) designed the experiment and analyzed PolSAR datasets in consultation with X.L., H.L., G.W., S.X. and Y.L. (Yemin Liu) wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, fund number 61971429.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors are grateful to all the reviewers for giving many valuable comments and suggestions that have greatly improved this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| coherency matrix | |
| coherent matrix of rotation | |
| polarization orientation angle | |
| rotation angle with respect to generalized surface scattering model | |
| rotation angle with respect to generalized double-bounce scattering model | |
| surface scattering model | |
| generalized surface scattering model | |
| double-bounce scattering model | |
| generalized double-bounce scattering model | |
| helix scattering model | |
| volume scattering model | |
| cross-scattering model | |
| generalized volume scattering model | |
| residual error matrix introduced by model mismatch | |
| contribution of the surface scattering to polarization echo power | |
| contribution of the double-bounce scattering to polarization echo power | |
| contribution of the helix scattering to polarization echo power | |
| contribution of the volume scattering to polarization echo power | |
| contribution of cross-scattering model to polarization echo power | |
| contribution of generalized volume scattering model to polarization echo power | |
| total power | |
| descriptor to discriminate between urban and nonurban areas | |
| threshold for discriminating between urban and nonurban areas | |
| volume scattering power in the Yamaguchi-2005 algorithm |
References
- Jansen, R.W.; Sletten, M.A.; Ainsworth, T.L.; Raj, R.G. Multi-channel Synthetic Aperture Radar Based Classification of Maritime Scenes. IEEE Access 2020, 8, 127440–127449. [Google Scholar] [CrossRef]
- Wang, Q.; Doulgeris, A.P.; Eltoft, T. Physics-Aware Training Data to Improve Machine Learning for Sea Ice Classification from Sentinel-1 SAR Scenes. In Proceedings of the IGARSS 2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 4992–4995. [Google Scholar]
- Fan, H.; Quan, S.; Dai, D.; Wang, X.; Xiao, S. Refined Model-Based and Feature-Driven Extraction of Buildings from PolSAR Images. Remote Sens. 2019, 11, 1379. [Google Scholar] [CrossRef]
- Li, H.; Li, Q.; Wu, G.; Chen, J.; Liang, S. The impacts of buildings orientation on polarimetric orientation angle estimation and model-based decomposition for multi-look polarimetric SAR data in urban areas. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5520–5532. [Google Scholar] [CrossRef]
- Atwood, D.K.; Thirion-Lefevre, L. Polarimetric phase and implications for urban classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1278–1289. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy-based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- van Zyl, J.J. Application of Cloude’s target decomposition theorem to polarimetric imaging radar data. In Radar Polarimetry; SPIE: Bellingham, WA, USA, 1993; Volume 1748, pp. 184–212. [Google Scholar]
- Touzi, R. Target scattering decomposition in terms of roll-invariant target parameters. IEEE Trans. Geosci. Remote Sens. 2007, 45, 73–84. [Google Scholar] [CrossRef]
- Paladini, R.; Famil, L.F.; Pottier, E.; Martorella, M.; Berizzi, F.; Mese, E.D. Lossless and sufficient Ψ-invariant decomposition of random reciprocal target. IEEE Trans. Geosci. Remote Sens. 2012, 55, 3487–3501. [Google Scholar] [CrossRef]
- Freeman, A. Fitting a two-component scattering model to polarimetric SAR data from forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Wang, W.; Ji, Y.; Lin, X. A novel fusion-based ship detection method from Pol-SAR images. Sensors 2015, 15, 25072–25089. [Google Scholar] [CrossRef]
- Xiang, D.; Tang, T.; Hu, C.; Fan, Q.; Su, Y. Built-up area extraction from PolSAR imagery with model-based decomposition and polarimetric coherence. Remote Sens. 2016, 8, 685. [Google Scholar] [CrossRef]
- Quan, S.; Zhang, T.; Wang, W.; Kuang, G.; Wang, X.; Zeng, B. Exploring Fine Polarimetric Decomposition Technique for Built-up Area Monitoring. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5204719. [Google Scholar] [CrossRef]
- Shibayama, T.; Yamaguchi, Y.; Yamada, H. Polarimetric scattering properties of landslides in forested areas and the dependence on the local incidence angle. Remote Sens. 2015, 7, 15424–15442. [Google Scholar] [CrossRef]
- Lee, J.-S.; Grunes, M.; Ainsworth, T.; Du, L.-J.; Schuler, D.; Cloude, S. Unsupervised classification using polarimetric decomposition and the complex Wishart classifier. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2249–2258. [Google Scholar]
- Pallotta, L.; Tesauro, M. Screening Polarimetric SAR Data via Geometric Barycenters for Covariance Symmetry Classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 4002905. [Google Scholar] [CrossRef]
- Famil, L.F.; Pottier, E.; Lee, J.S. Unsupervised classification of multifrequency and fully polarimetric SAR images based on the H/A/Alpha-Wishart classifier. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2332–2342. [Google Scholar] [CrossRef]
- Shimoni, M.; Borghys, D.; Heremans, R. Fusion of PolSAR and PolInSAR data for land cover classification. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 169–180. [Google Scholar] [CrossRef]
- Qi, Z.; Yeh, A.G.-O.; Li, X.; Lin, Z. A novel algorithm for land use and land cover classification using RADARSAT-2 polarimetric SAR data. Remote Sens. Environ. 2012, 118, 21–39. [Google Scholar] [CrossRef]
- Antropov, O.; Rauste, Y.; Astola, H. Land cover and soil type mapping from spaceborne POLSAR data at L-band with probabilistic neural network. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5256–5270. [Google Scholar] [CrossRef]
- Hong, S.-H.; Kim, H.-O.; Wdowinski, S.; Feliciano, E. Evaluation of polarimetric SAR decomposition for classifying wetland vegetation types. Remote Sens. 2015, 7, 8563–8585. [Google Scholar] [CrossRef]
- Zhang, X.; Dierking, W.; Zhang, J.; Meng, J. Polarimetric decomposition method for ice in the bohai sea using C-band PolSAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 47–66. [Google Scholar] [CrossRef]
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of surface parameters from polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 727–744. [Google Scholar] [CrossRef]
- Hajnsek, I.; Jagdhuber, T.; Schon, H.; Papathanassiou, K.P. Potential of estimating soil moisture under vgetation cover by means of PolSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 442–454. [Google Scholar] [CrossRef]
- Jagdhuber, T.; Hajnsek, I.; Papathanassiou, K.P. An iterative generalized hybrid decomposition for soil moisture retrieval under vegetation cover using fully polarimetric SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3911–3922. [Google Scholar] [CrossRef]
- Chen, S.-W.; Li, Y.-Z.; Wang, X.-S.; Xiao, S.-P.; Sato, M. Modeling and interpretation of scattering mechanisms in polarimetric synthetic aperture radar: Advances and perspectives. IEEE Trans. Signal Process. 2014, 31, 79–89. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Sato, A.; Boerner, W.M.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2251–2258. [Google Scholar] [CrossRef]
- Sato, A.; Yamaguchi, Y.; Singh, G.; Park, S.-E. Four-component scattering power decomposition with extended volume scattering model. IEEE Geosci. Remote Sens. Lett. 2012, 9, 166–170. [Google Scholar] [CrossRef]
- Singh, G.; Yamaguchi, Y.; Park, S.E. General four-component scattering power decomposition with unitary transformation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3014–3022. [Google Scholar] [CrossRef]
- Fan, H.; Quan, S.; Dai, D.; Wang, X.; Xiao, S. Seven-Component Model-Based Decomposition for PolSAR Data with Sophisticated Scattering Models. Remote Sens. 2019, 11, 2802–2813. [Google Scholar] [CrossRef]
- Quan, S.; Xiang, D.; Wang, W.; Xiong, B.; Kuang, G. Scattering Feature-Driven Super pixel Segmentation for Polarimetric SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 99, 2173–2183. [Google Scholar] [CrossRef]
- Ainsworth, T.L.; Wang, Y.; Lee, J.S. Model-Based Polarimetric SAR Decomposition: An L1 Regularization Approach. IEEE Trans. Geosci. Remote Sens. 2021, 99, 5208013. [Google Scholar] [CrossRef]
- Chen, S.-W.; Wang, X.-S.; Xiao, S.-P.; Sato, M. General polarimetric model-based decomposition for coherency matrix. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1843–1855. [Google Scholar] [CrossRef]
- Xie, Q.H.; Ballester-Berman, J.D.; Lopez-Sanchez, J.M.; Zhu, J.; Wang, C. Monte Carlo simulation tests for general polarimetric model-based decomposition method from the perspective of quantitative application. In Proceedings of the 11th European Conference on Synthetic Aperture Radar (EUSAR2016), Hamburg, Germany, 6–9 June 2016; p. 977. [Google Scholar]
- Xie, Q.; Ballester-Berman, J.D.; Lopez-Sanchez, J.M.; Zhu, J.; Wang, C. Quantitative Analysis of Polarimetric Model-Based Decomposition Methods. Remote Sens. 2016, 8, 977–991. [Google Scholar] [CrossRef]
- Xie, Q.; Ballester-Berman, J.D.; Lopez-Sanchez, J.M.; Zhu, J.; Wang, C. On the use of generalized volume scattering models for the improvement of general polarimetric model-based decomposition. Remote Sens. 2017, 9, 117–128. [Google Scholar] [CrossRef]
- Xi, Y.; Lang, H.; Tao, Y.; Huang, L.; Pei, Z. Four-Component Model-Based Decomposition for Ship Targets Using PolSAR Data. Remote Sens. 2017, 9, 825–836. [Google Scholar] [CrossRef]
- Quan, S.; Xiong, B.; Xiang, D.; Kuang, G. Derivation of the Orientation Parameters in Built-Up Areas: With Application to Model-Based Decomposition. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4714–4730. [Google Scholar] [CrossRef]
- Xiang, D.L.; Ban, Y.F.; Yi, S. Model-based decomposition with cross scattering for polarimetric SAR urban areas. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2496–2500. [Google Scholar] [CrossRef]
- An, W.; Cui, Y.; Yang, J. Three-Component Model-Based Decomposition for Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2732–2739. [Google Scholar]
- Antropov, O.; Rauste, Y.; Hame, T. Volume scattering modeling in POLSAR decompositions: Study of ALOS PALSAR data over boreal forest. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3838–3848. [Google Scholar] [CrossRef]
- Duan, D.F.; Wang, Y. An Improved Algorithm to Delineate Urban Targets with Model-Based Decomposition of PolSAR Data. Remote Sens. 2017, 9, 1037. [Google Scholar] [CrossRef]
- Jin, S.; Yang, L.; Danielson, P.; Homer, C.; Fry, J.; Xian, G. A comprehensive change detection method for updating the national land cover database to circa 2011. Remote Sens. Environ. 2013, 132, 159–175. [Google Scholar] [CrossRef]
- Xiang, D.; Tang, T.; Ban, Y.; Su, Y.; Kuang, G. Unsupervised polarimetric SAR urban area classification based on model-based decomposition with cross scattering. ISPRS J. Photogramm. Remote Sens. 2016, 116, 86–100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).