Prediction of Mean Sea Level with GNSS-VLM Correction Using a Hybrid Deep Learning Model in Australia
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Dataset
2.2. Data Preprocessing
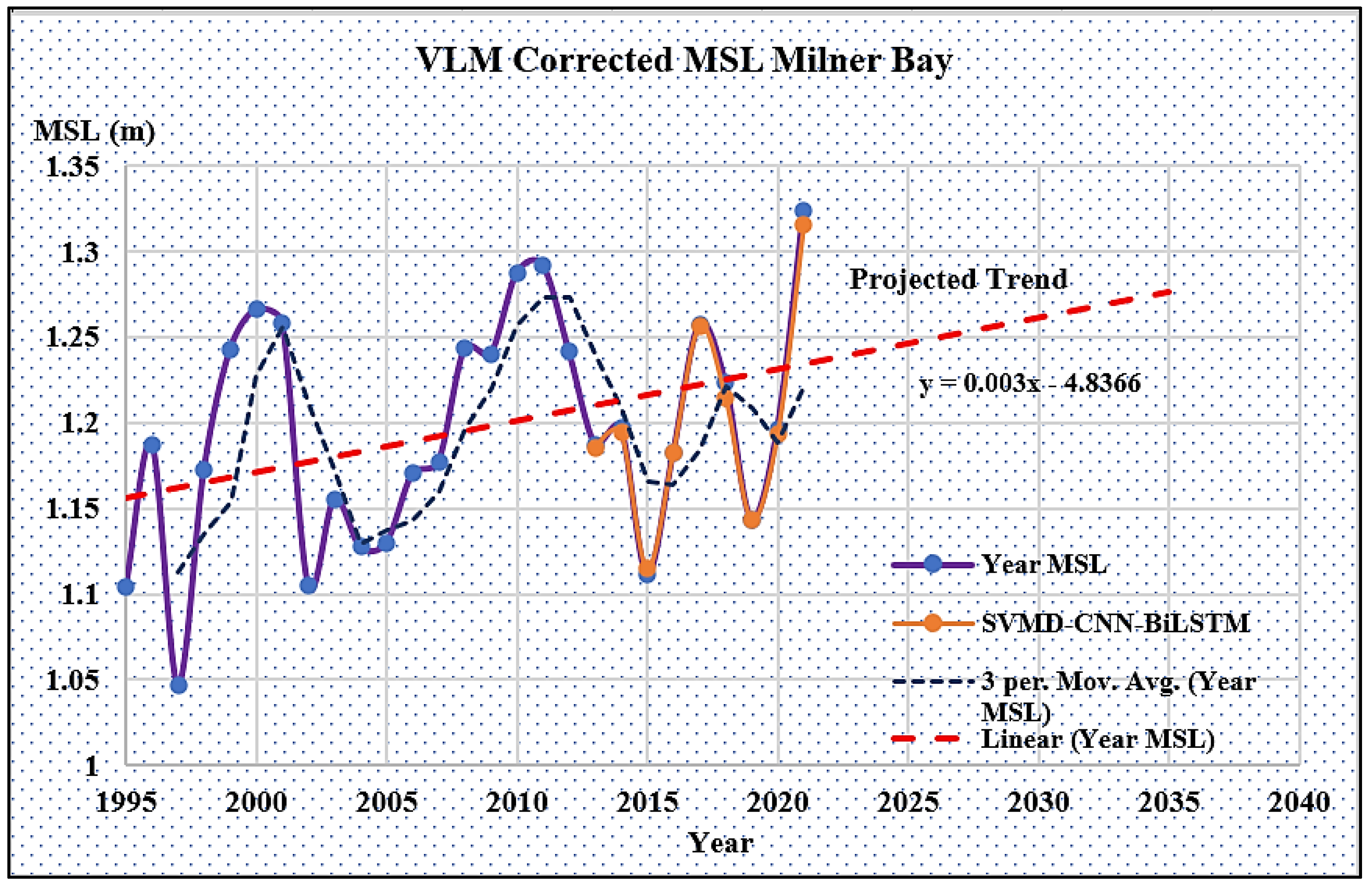
2.3. GNSS-VLM Correction of Port Kembla and Milner Bay
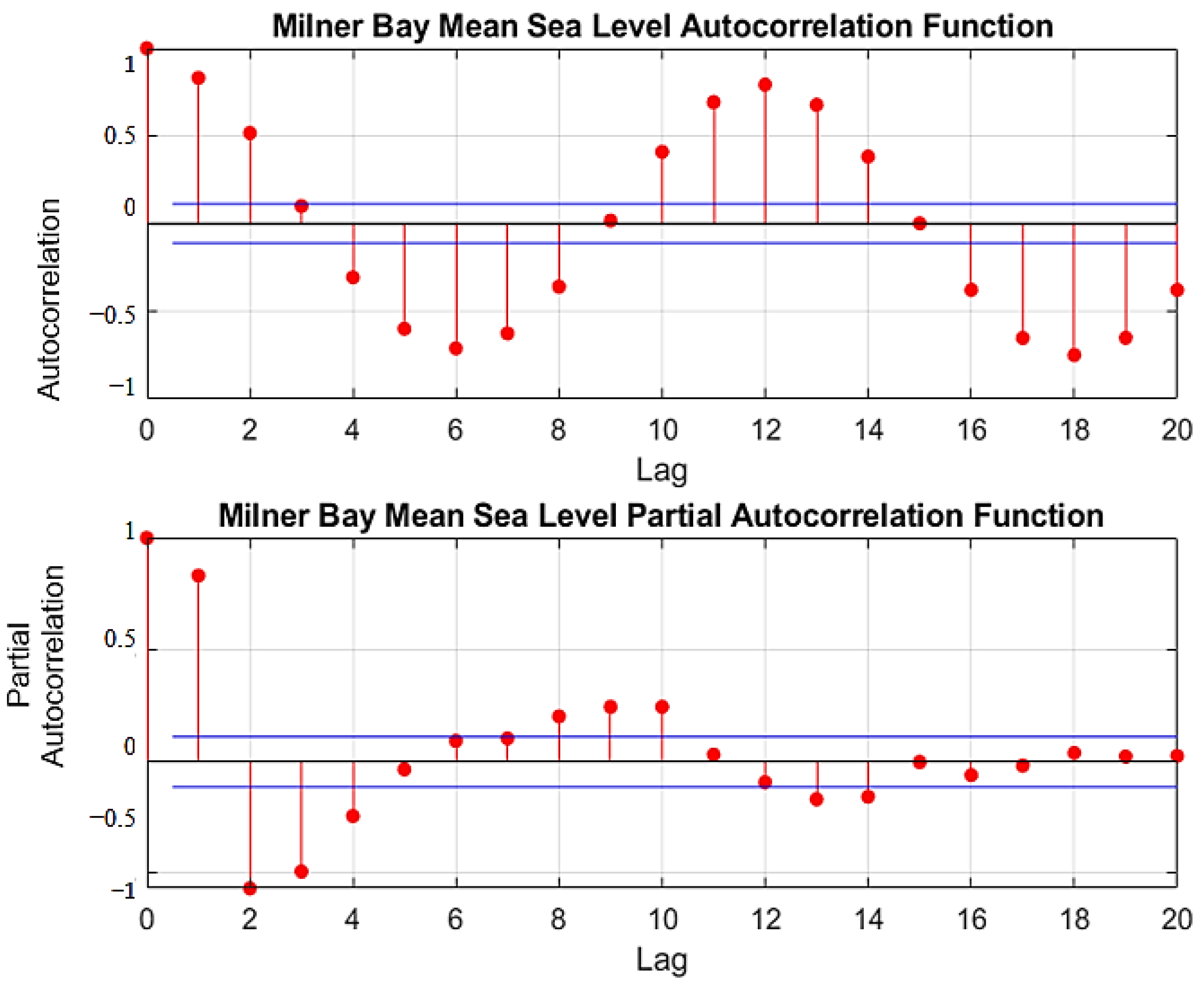
2.4. Signal Decomposition by Successive Variational Mode Decomposition (SVMD)
2.5. Data Partition
2.6. Objective Model and Modeling Process
2.7. Benchmark Models
2.7.1. Multi-Layer Perceptron
2.7.2. Gradient Boosting
2.7.3. Support Vector Regression
2.8. Performance Evaluation Metrics
- Correlation Coefficient (r)
- Willmott’s Index of Agreement (d)
- Nash–Sutcliffe Coefficient (NS)
- Legates and McCabe Index (LM)
- Root Mean Square Error (RMSE)
- Mean Absolute Error (MAE)
- Relative Root Mean Square Error (RRMSE)
- Mean Absolute Percentage Error (MAPE)where is the simulated data and is the observed data.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hinrichsen, D. Coastal Waters of the World: Trends, Threats, and Strategies; Island Press: Washington, DC, USA, 1998. [Google Scholar]
- Janif, S.Z.; Nunn, P.D.; Geraghty, P.; Aalbersberg, W.; Thomas, F.R.; Camailakeba, M. Value of traditional oral narratives in building climate-change resilience: Insights from rural communities in Fiji. Ecol. Soc. 2016, 21, 2. [Google Scholar] [CrossRef]
- Bijlsma, L.; Ehler, C.N.; Klein, R.J.T.; Kulshrestha, S.M.; McLean, R.F.; Mimura, N.; Nicholls, R.J.; Nurse, L.A.; Nieto, H.P.; Stakhiv, E.Z.; et al. Coastal Zones and Small Islands; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1996; pp. 289–324. [Google Scholar]
- Santamaría-Gómez, A.; Gravelle, M.; Dangendorf, S.; Marcos, M.; Spada, G.; Wöppelmann, G. Uncertainty of the 20th century sea-level rise due to vertical land motion errors. Earth Planet. Sci. Lett. 2017, 473, 24–32. [Google Scholar] [CrossRef]
- Nazari, M.; Sakhaei, S.M. Successive variational mode decomposition. Signal Process. 2020, 174, 107610. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Raj, N.; Brown, J. An EEMD-BiLSTM Algorithm Integrated with Boruta Random Forest Optimiser for Significant Wave Height Forecasting along Coastal Areas of Queensland, Australia. Remote Sens. 2021, 13, 1456. [Google Scholar] [CrossRef]
- Oelsmann, J.; Passaro, M.; Dettmering, D.; Schwatke, C.; Sánchez, L.; Seitz, F. The zone of influence: Matching sea level variability from coastal altimetry and tide gauges for vertical land motion estimation. Ocean. Sci. 2021, 17, 35–57. [Google Scholar] [CrossRef]
- Hu, Y.; Huber, A.; Anumula, J.; Liu, S.-C. Overcoming the vanishing gradient problem in plain recurrent networks. arXiv 2018, arXiv:1801.06105 2018. [Google Scholar]
- Nelson, B.K. Time series analysis using autoregressive integrated moving average (ARIMA) models. Acad. Emerg. Med. 1998, 5, 739–744. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Tilburg, C.E.; Garvine, R.W. A simple model for coastal sea level prediction. Weather Forecast. 2004, 19, 511–519. [Google Scholar] [CrossRef]
- Khatibi, R.; Ghorbani, M.A.; Naghipour, L.; Jothiprakash, V.; Fathima, T.A.; Fazelifard, M.H. Inter-comparison of time series models of lake levels predicted by several modeling strategies. J. Hydrol. 2014, 511, 530–545. [Google Scholar] [CrossRef]
- El-Shafie, A.; Alsulami, H.M.; Jahanbani, H.; Najah, A. Multi-lead ahead prediction model of reference evapotranspiration utilizing ANN with ensemble procedure. Stoch. Environ. Res. Risk Assess. 2013, 27, 1423–1440. [Google Scholar] [CrossRef]
- Balogun, A.-L.; Adebisi, N. Sea level prediction using ARIMA, SVR and LSTM neural network: Assessing the impact of ensemble Ocean-Atmospheric processes on models’ accuracy. Geomat. Nat. Hazards Risk 2021, 12, 653–674. [Google Scholar] [CrossRef]
- Bistacchi, A.; Mittempergher, S.; Martinelli, M.; Storti, F. On a new robust workflow for the statistical and spatial analysis of fracture data collected with scanlines (or the importance of stationarity). Solid Earth 2020, 11, 2535–2547. [Google Scholar] [CrossRef]
- Cheung, Y.-W.; Lai, K.S. Lag order and critical values of the augmented Dickey–Fuller test. J. Bus. Econ. Stat. 1995, 13, 277–280. [Google Scholar]
- Paparoditis, E.; Politis, D.N. The asymptotic size and power of the augmented Dickey–Fuller test for a unit root. Econom. Rev. 2018, 37, 955–973. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System; Schweizerische Geodätische Kommission Zürich: Zürich, Switzerland, 1999; Volume 59. [Google Scholar]
- Dawoud, S. GNSS Principles and Comparison; Potsdam University: Brandenburg, Germany, 2012. [Google Scholar]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS–Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Blewitt, G.; Hammond, W.C.; Kreemer, C. Harnessing the GPS data explosion for interdisciplinary science. Eos 2018, 99, 485. [Google Scholar] [CrossRef]
- Achlerkar, P.D.; Samantaray, S.R.; Manikandan, M.S. Variational mode decomposition and decision tree based detection and classification of power quality disturbances in grid-connected distributed generation system. IEEE Trans. Smart Grid 2016, 9, 3122–3132. [Google Scholar] [CrossRef]
- Huang, J.; Li, C.; Xiao, X.; Yu, T.; Yuan, X.; Zhang, Y. Adaptive multivariate chirp mode decomposition. Mech. Syst. Signal Process. 2023, 186, 109897. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, H.; Singh, V.P. Forward prediction of runoff data in data-scarce basins with an improved ensemble empirical mode decomposition (EEMD) model. Water 2018, 10, 388. [Google Scholar] [CrossRef]
- Xu, Y.; Goodacre, R. On splitting training and validation set: A comparative study of cross-validation, bootstrap and systematic sampling for estimating the generalization performance of supervised learning. J. Anal. Test. 2018, 2, 249–262. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Li, J.; Wang, J.; Qin, L. A CNN-BiLSTM-AM method for stock price prediction. Neural Comput. Appl. 2021, 33, 4741–4753. [Google Scholar] [CrossRef]
- Ta, V.-D.; Liu, C.-M.; Tadesse, D.A. Portfolio optimization-based stock prediction using long-short term memory network in quantitative trading. Appl. Sci. 2020, 10, 437. [Google Scholar] [CrossRef]
- Cook, R.; Lapeyre, J.; Ma, H.; Kumar, A. Prediction of compressive strength of concrete: Critical comparison of performance of a hybrid machine learning model with standalone models. J. Mater. Civ. Eng. 2019, 31, 04019255. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-term water quality variable prediction using a hybrid CNN–LSTM deep learning model. Stochastic Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Sharma, E.; Deo, R.C.; Soar, J.; Prasad, R.; Parisi, A.V.; Raj, N. Novel hybrid deep learning model for satellite based PM10 forecasting in the most polluted Australian hotspots. Atmos. Environ. 2022, 279, 119111. [Google Scholar] [CrossRef]
- Rosenblatt, F. Principles of Neurodynamics. Perceptrons and the Theory of Brain Mechanisms; Cornell Aeronautical Lab Inc.: Buffalo, NY, USA, 1961. [Google Scholar]
- Al Bataineh, A.; Kaur, D.; Jalali, S.M.J. Multi-layer perceptron training optimization using nature inspired computing. IEEE Access 2022, 10, 36963–36977. [Google Scholar] [CrossRef]
- Zhang, Y.; Haghani, A. A gradient boosting method to improve travel time prediction. Transp. Res. Part C Emerg. Technol. 2015, 58, 308–324. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar]
- Raj, N. Prediction of Sea Level with Vertical Land Movement Correction Using Deep Learning. Mathematics 2022, 10, 4533. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe efficiency index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Gleckler, P.J.; Taylor, K.E.; Doutriaux, C. Performance metrics for climate models. J. Geophys. Res. Atmos. 2008, 113, D06104. [Google Scholar] [CrossRef]
- Samuel, K.; Katherine, S.; Mal, R.; Richard, F. Vulnerability of Indigenous heritage sites to changing sea levels: Piloting a GIS-based approach in the Illawarra, New South Wales, Australia. Archaeol. Rev. Camb. 2017, 32. [Google Scholar]
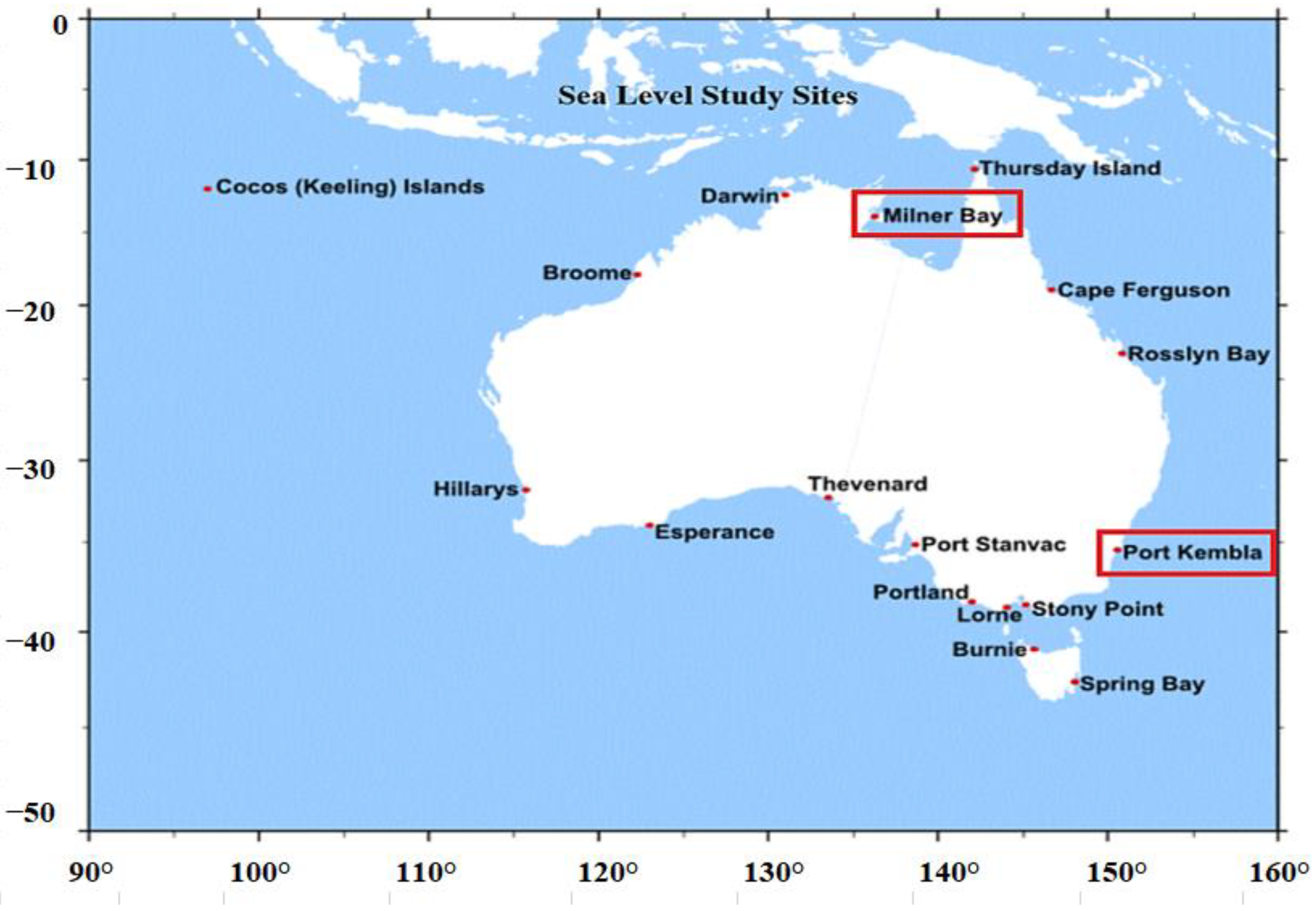









| State | Tide Gauge Location | Geographical Location |
|---|---|---|
| New South Wales | Port Kembla | 34°28′48.27″S and 150°54′1.78″E |
| Northern Territory | Milner Bay | 13°51′20.88″S and 136°24′52.56″E |
| Test Statistic | −4.020307 |
| p-value | 0.001308 |
| Lags Used | 13 |
| Number of Observations Used | 306 |
| Critical Value (1%) | −3.451902 |
| Critical Value (5%) | −2.871032 |
| Critical Value (10%) | −2.571827 |
| Longitude | Latitude | Imaged Vertical Rate (mm/year) | Imaged Aleatory Uncertainty | Spatial Structure Function (SSF) | Nearest Neighbor Spatial Variability (mm/year) | Non-Seasonal Temporal Variability (mm/year) |
|---|---|---|---|---|---|---|
| Tide Gauge: Port Kembla | ||||||
| 136.416 | −13.860 | 0.195 | 0.367 | 0.558 | 1.145 | 1.775 |
| Tide Gauge: Milner Bay | ||||||
| 150.912 | −34.474 | −1.220 | 0.426 | 0.930 | 0.721 | 1.506 |
| Partition | Training | Validation | Testing |
|---|---|---|---|
| Oceanic Dataset | January 1995–December 2010 | January 2011–December 2011 | January 2012–August 2021 |
| Optimizer | Activation Function | Loss Function | Weight Regularization | Dropout |
|---|---|---|---|---|
| Adam | Rectified Linear Unit (ReLU) | Mean Square Error | L1 = 0, L2 = 0.01 | 0.1 |
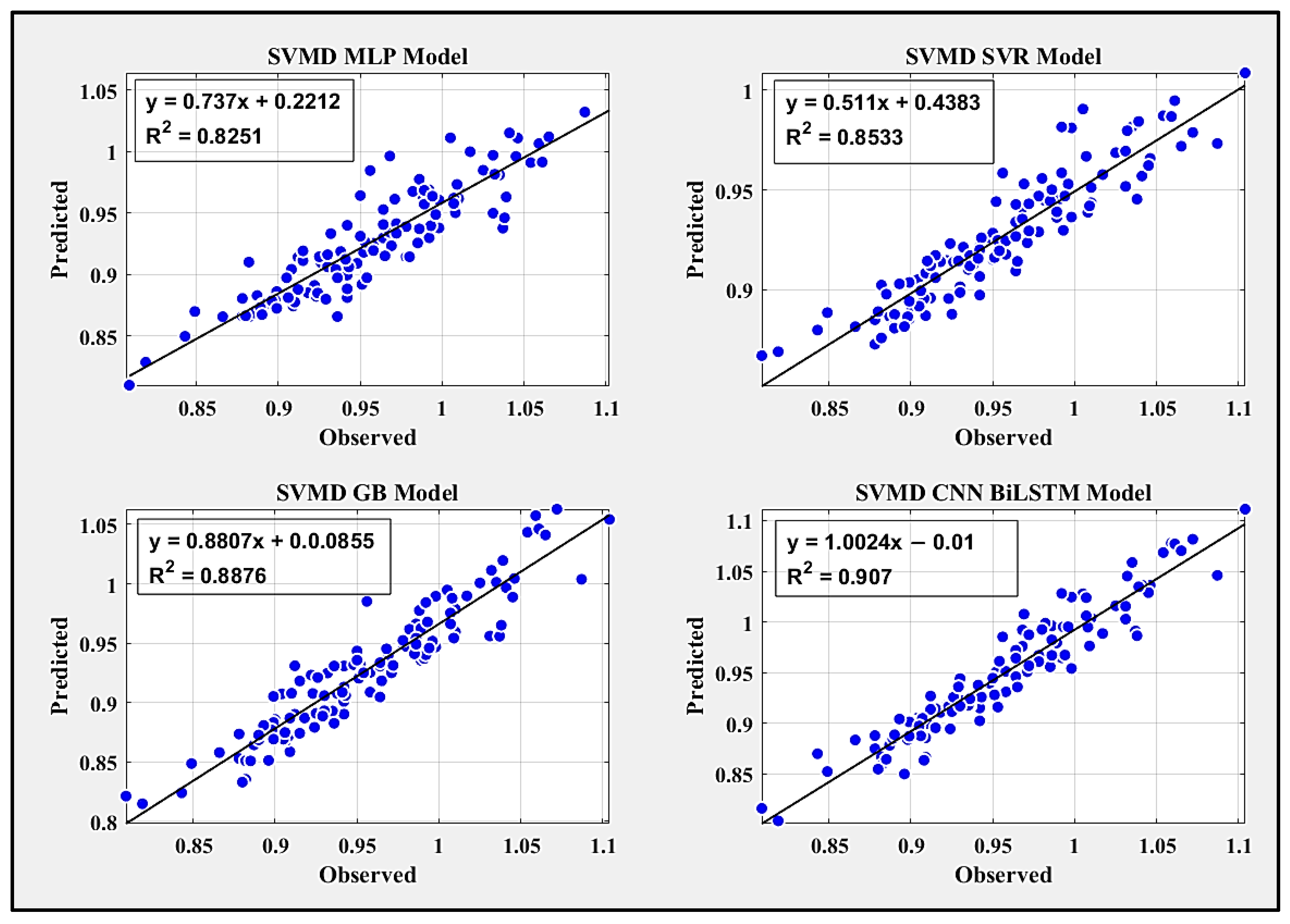
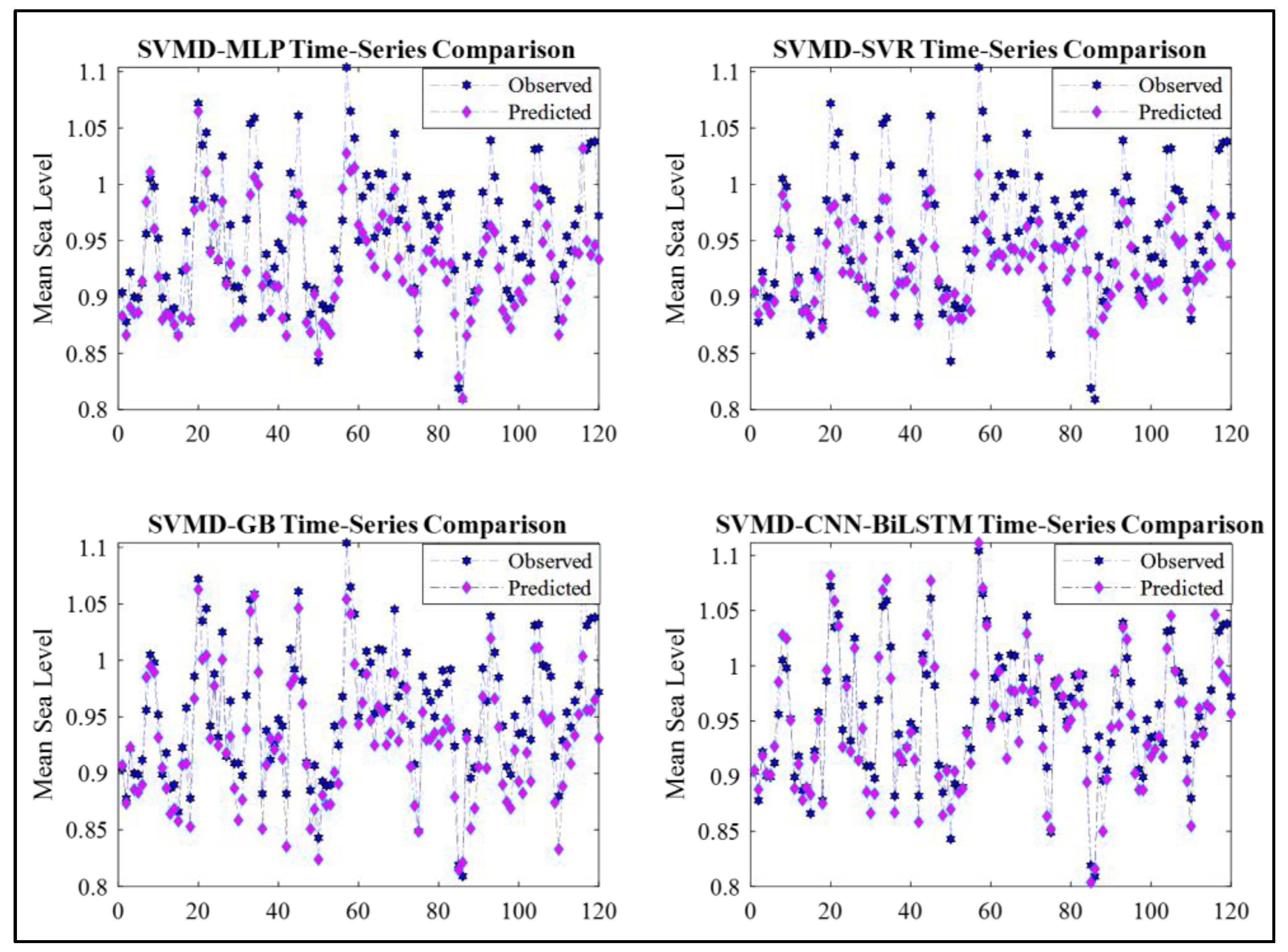
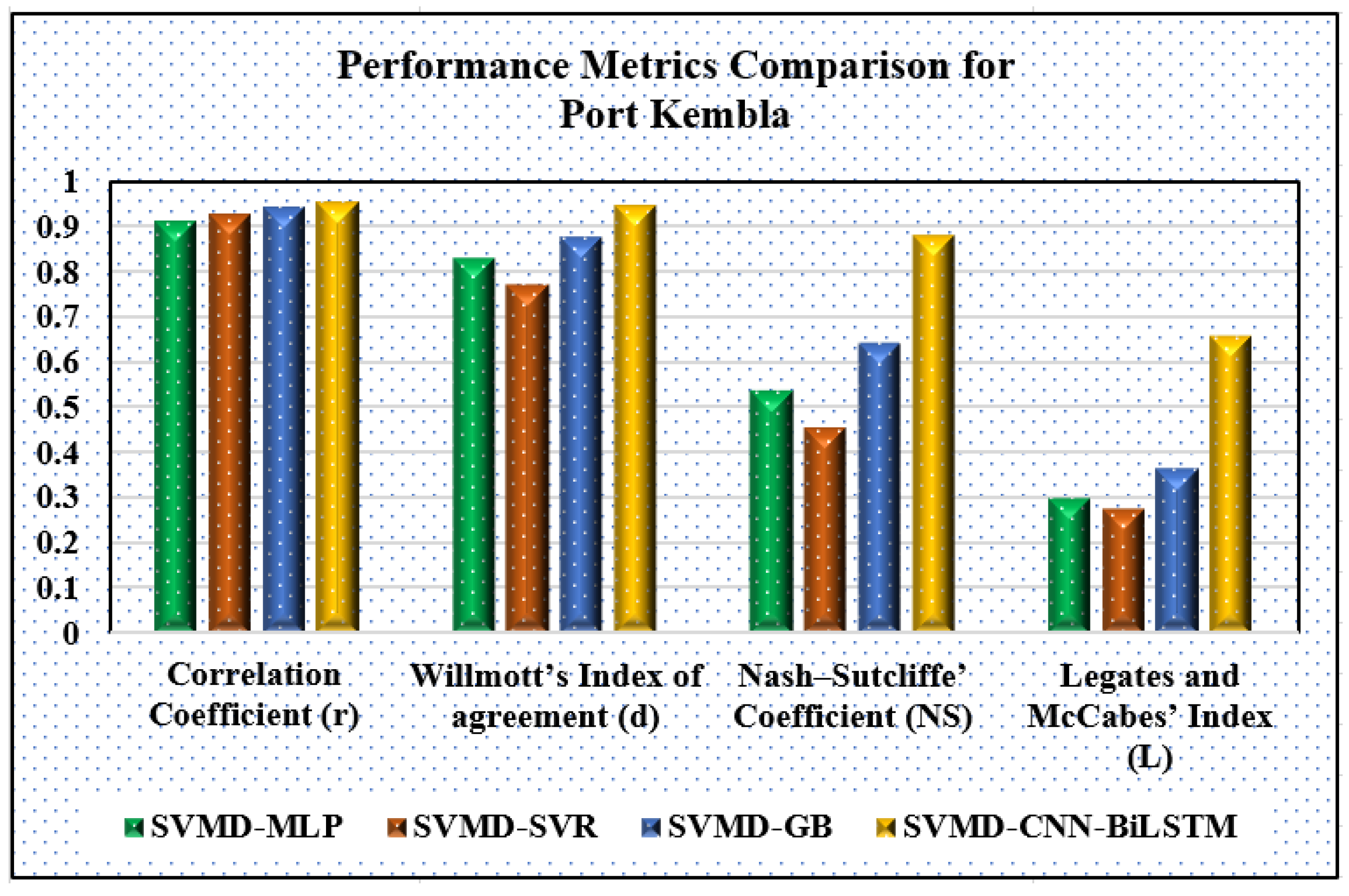
| Model | Correlation Coefficient (r) | Willmott’s Index of Agreement (d) | Nash–Sutcliffe Coefficient (NS) | Legates and McCabe Index (L) |
|---|---|---|---|---|
| SVMD-MLP | 0.9084 | 0.8296 | 0.5377 | 0.2999 |
| SVMD-SVR | 0.9238 | 0.7682 | 0.4543 | 0.2760 |
| SVMD-GB | 0.9421 | 0.8729 | 0.6409 | 0.3654 |
| SVMD-CNN-BiLSTM | 0.9524 | 0.9457 | 0.8790 | 0.6581 |
| Model | RMSE | MAE | RRMSE | MAPE |
|---|---|---|---|---|
| SVMD-MLP | 0.0392 | 0.0329 | 4.0971 | 3.3719 |
| SVMD-SVR | 0.0426 | 0.0341 | 4.4513 | 3.4571 |
| SVMD-GB | 0.0345 | 0.0299 | 3.6111 | 3.0948 |
| SVMD-CNN-BiLSTM | 0.0200 | 0.0161 | 2.0957 | 1.6740 |
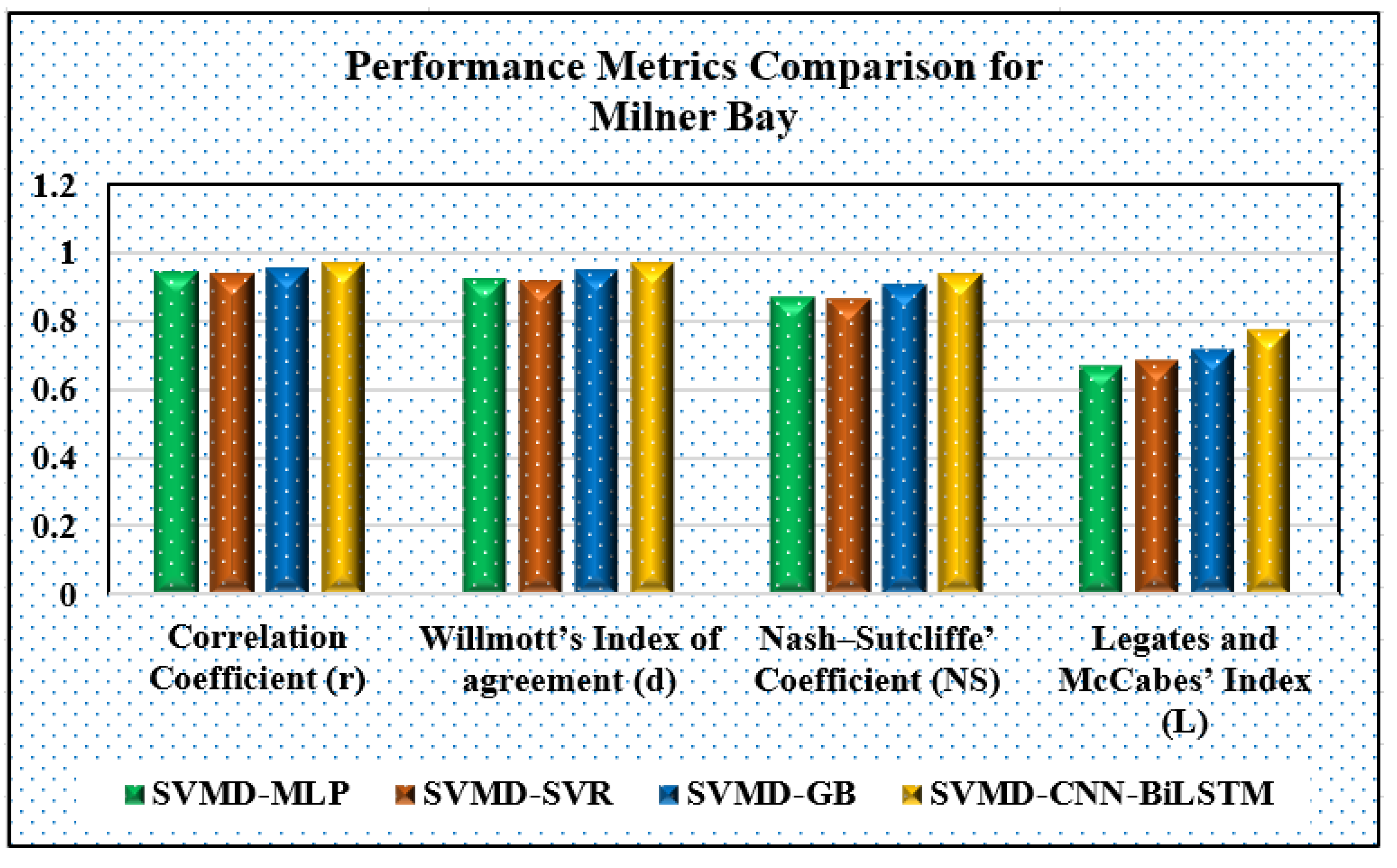
| Model | Correlation Coefficient (r) | Willmott’s Index of Agreement (d) | Nash–Sutcliffe Coefficient (NS) | Legates and McCabe Index (L) |
|---|---|---|---|---|
| SVMD-MLP | 0.9487 | 0.9270 | 0.8746 | 0.6727 |
| SVMD-SVR | 0.9401 | 0.9201 | 0.8685 | 0.6858 |
| SVMD-GB | 0.9584 | 0.9543 | 0.9099 | 0.7209 |
| SVMD-CNN-BiLSTM | 0.9736 | 0.9717 | 0.9439 | 0.7781 |
| Model | RMSE | MAE | RRMSE | MAPE |
|---|---|---|---|---|
| SVMD-MLP | 0.0760 | 0.0602 | 6.2579 | 5.0577 |
| SVMD-SVR | 0.0778 | 0.0578 | 6.4084 | 4.7697 |
| SVMD-GB | 0.0644 | 0.0513 | 5.3038 | 4.1757 |
| SVMD-CNN-BiLSTM | 0.0508 | 0.0408 | 4.1839 | 3.4031 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raj, N.; Brown, J. Prediction of Mean Sea Level with GNSS-VLM Correction Using a Hybrid Deep Learning Model in Australia. Remote Sens. 2023, 15, 2881. https://doi.org/10.3390/rs15112881
Raj N, Brown J. Prediction of Mean Sea Level with GNSS-VLM Correction Using a Hybrid Deep Learning Model in Australia. Remote Sensing. 2023; 15(11):2881. https://doi.org/10.3390/rs15112881
Chicago/Turabian StyleRaj, Nawin, and Jason Brown. 2023. "Prediction of Mean Sea Level with GNSS-VLM Correction Using a Hybrid Deep Learning Model in Australia" Remote Sensing 15, no. 11: 2881. https://doi.org/10.3390/rs15112881
APA StyleRaj, N., & Brown, J. (2023). Prediction of Mean Sea Level with GNSS-VLM Correction Using a Hybrid Deep Learning Model in Australia. Remote Sensing, 15(11), 2881. https://doi.org/10.3390/rs15112881







