Global Analysis of the Cover-Management Factor for Soil Erosion Modeling

Abstract

Land use and management practices (LUMPs) play a critical role in regulating soil loss. The cover-management factor (C-factor) in Universal Soil Loss Equation (USLE)-type models is an important parameter for quantifying the effects of LUMPs on soil erosion. However, accurately determining the C-factor, particularly for large-scale assessments using USLE-type models, remains challenging. This study aims to address this gap by analyzing and comparing the methods used for C-factor quantification in 946 published articles, providing insights into their strengths and weaknesses. Through our analysis, we identified six main categories of methods for C-factor quantification in USLE-type modeling. Many studies have relied on empirical C-factor values for different land-use types or calculated C-factor values based on vegetation indices (VIs) in large study areas (>100 km²). However, we found that no single method could robustly estimate C-factor values for large-scale studies. For small-scale investigations, conducting experiments or consulting the existing literature proved to be more feasible. In the context of large-scale studies, employing methods based on VIs for C-factor quantification can enhance our understanding of the relationship between vegetation changes and soil erosion potential, particularly when considering spatial and spatiotemporal variations. For the global scale, we recommend the combined use of different equations. We suggest further efforts to develop C-factor datasets at large scales by synthesizing field-level experiment data and combining high-resolution satellite imagery. These efforts will facilitate the development of effective soil conservation practices, ensuring sustainable land use and environmental protection.

1. Introduction

Soil erosion is a pervasive problem that poses a significant threat to regional and national food security, due to its negative effects on soil quality, agricultural productivity [1,2], and food production [3]. Consequently, soil erosion modeling and prediction have garnered increasing attention due to their crucial role in informing policy decisions related to land use [3,4]. Over the past few decades, numerous soil erosion assessments have been conducted [5] to identify areas at high risk of erosion and to understand the underlying drivers of soil erosion [6].

Land use and management practices (LUMPs), including vegetation cover, crop type, and tillage practice, play a crucial role in regulating soil erosion [7]. Therefore, it is essential to quantify the effects of LUMPs for accurate soil erosion assessment [8]. Various soil erosion models, including the USLE/RUSLE [9,10], SEMMED [11], WEEP [12], SWAT [13], InVEST [14], and PESERA [15], widely consider LUMPs. Among these models, the USLE-type models have been the most widely used tools [6,16,17,18]. The effects of LUMPs on soil erosion are often parameterized in the cover-management factor (C-factor) in USLE-type models [7,19].

The C-factor measures the combined effect of all land cover, crops, and crop management practices, and the C-factor value is defined as the ratio of soil loss [10,20]. However, calculating the C-factor value requires detailed information from field experiments, which is not readily available in large geographic areas [7]. Consequently, several alternative approaches have been proposed to quantify the C-factor for large scales [6,16]. Although USLE-type models have been used at various spatial scales (e.g., slope, watershed, region), one C-factor quantification method is usually not applicable for all scales [21]. Moreover, there is a lack of information and guidance on the applicability of various C-factor estimation methods adopted in the literature, and a global benchmarking dataset is not available yet. Therefore, there is a need for a comprehensive comparison of the different C-factor estimation methods used in the literature to facilitate the selection of the most suitable approach for different spatial scales.

In this paper, we reviewed the methods for calculating the C-factor in USLE-type models. We selected 946 published studies that used USLE-type models, collected and analyzed the reported C-factor values, C-factor quantification methods, and the data requirements. This study aims to fill this gap in knowledge by providing a detailed evaluation of the various C-factor estimation methods and their applicability.

2. Data and Methods

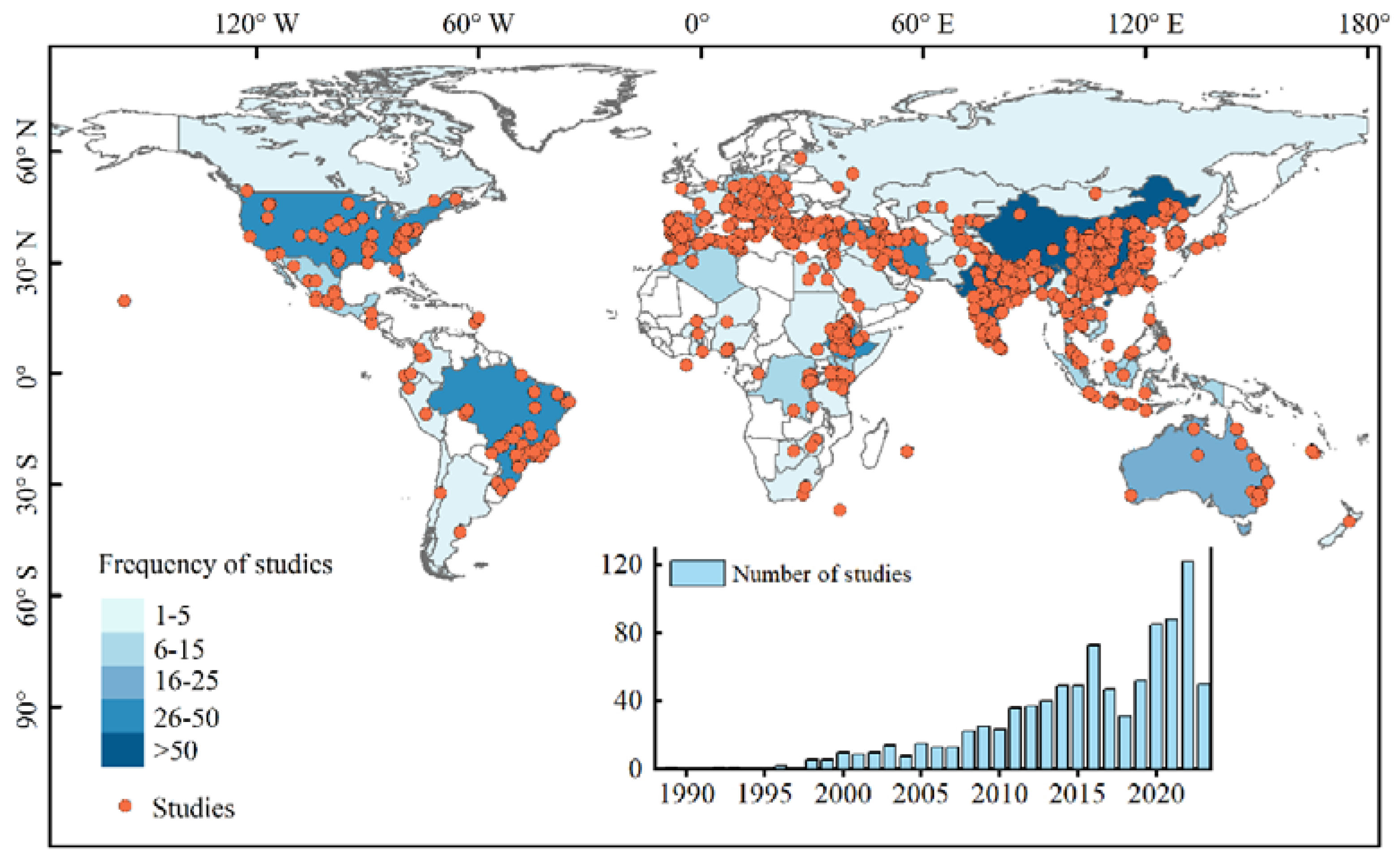
2.1. Search Strategy and Selection Criteria

We performed a systematic search of the published literature and developed a database by collecting and compiling C-factor information from published articles. We obtained publications from the Web of Science, Science Direct, and the China National Knowledge Infrastructure using two keywords (i.e., USLE and RUSLE). Studies were included for analysis according to the following criteria: study sites were clearly described, and the C-factor values were reported. In total, we retained 946 studies in the database, including 10 global-scale studies.

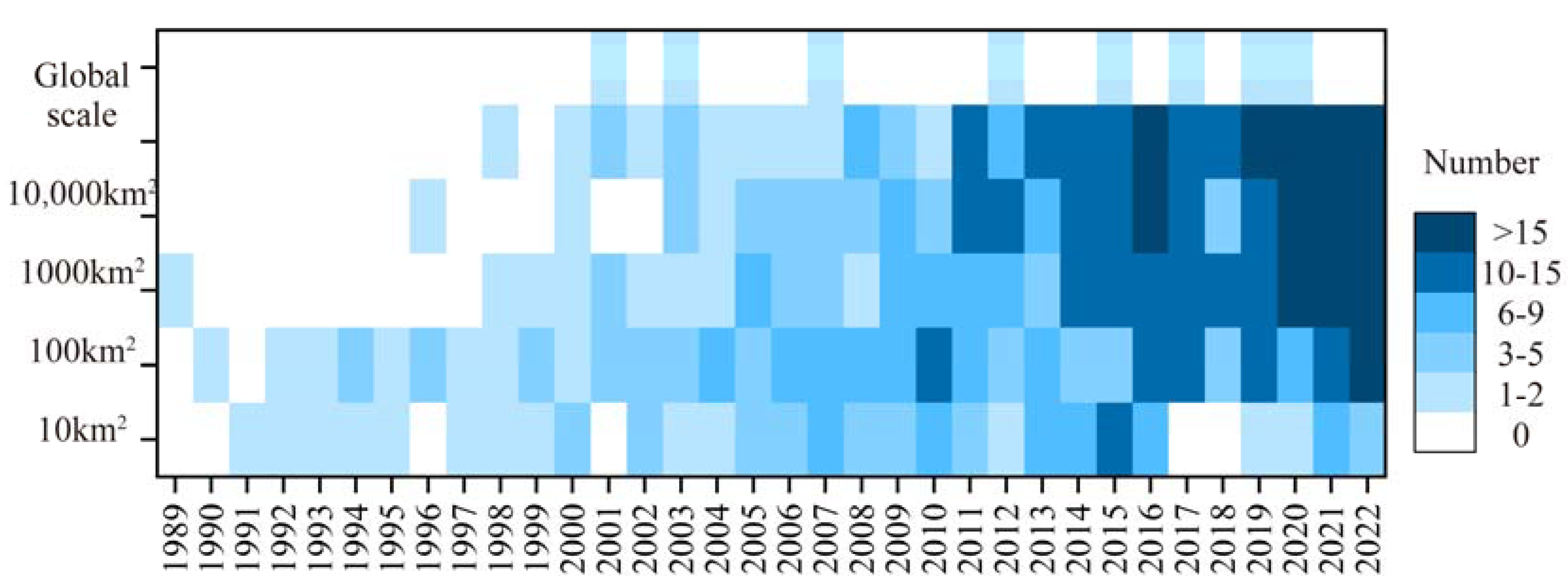
2.2. Data Extraction and Analysis

The following information was collected from the 946 studies to develop the C-factor database: (1) study location (coordinates); (2) publication year; (3) size of the study area (km²); (4) land-use types; (5) C-factor values; and (6) C-factor estimation methods. Figure 1 shows the location of the study sites, except for 10 European-scale studies, 22 national-scale studies, and 10 global-scale studies. Most of the studies were located in China (198 studies), India (95 studies), the USA, and some European countries.

There was heterogeneity in the environmental conditions of these studies. Specifically, the size of the study areas varied by thousands of orders of magnitude, and the methods used for calculating the C-factor values were very diverse. In addition, there were different land-use types among studies, including cropland, grassland, shrubland, etc. Below, we analyzed the methods for C-factor estimation.

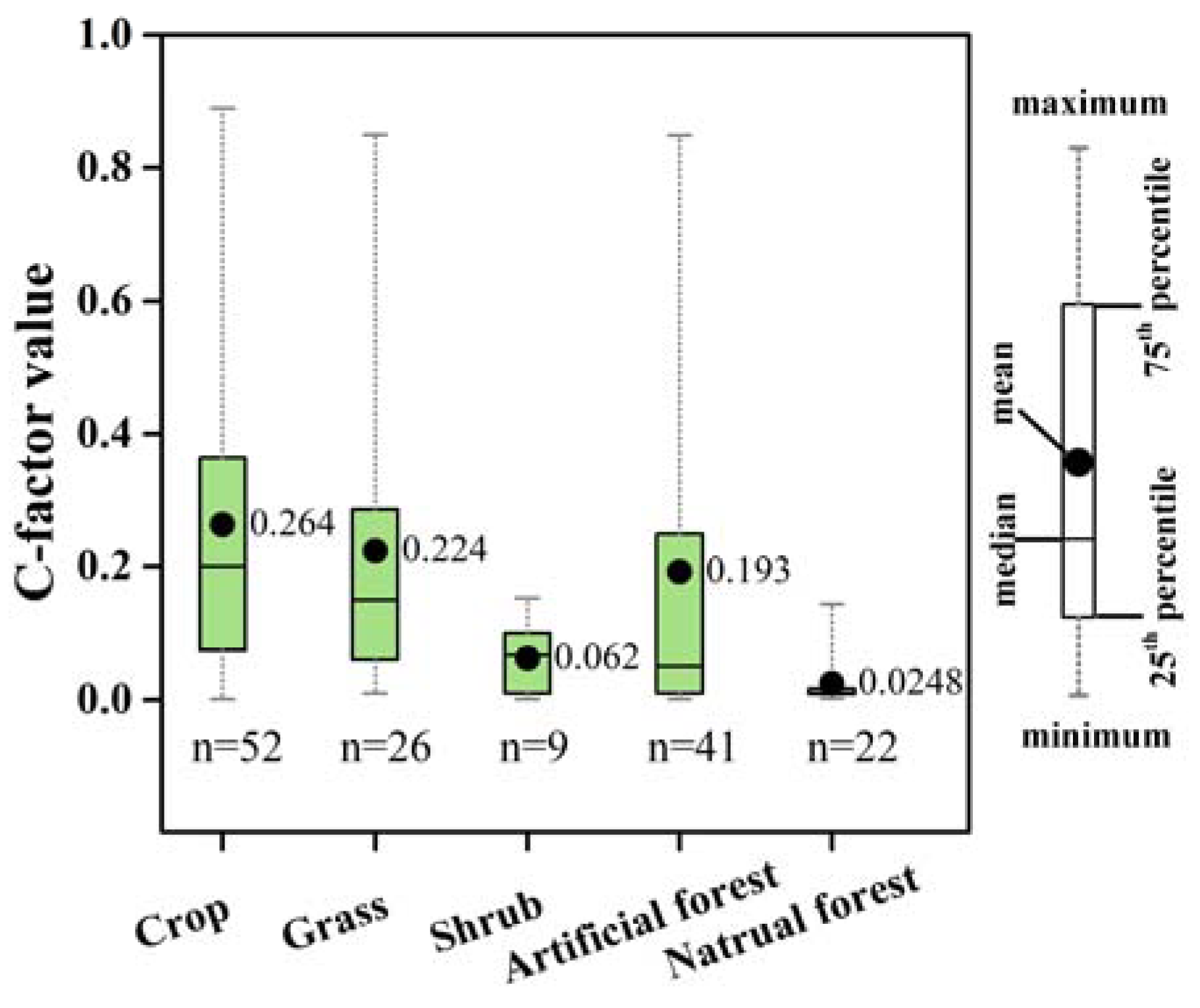
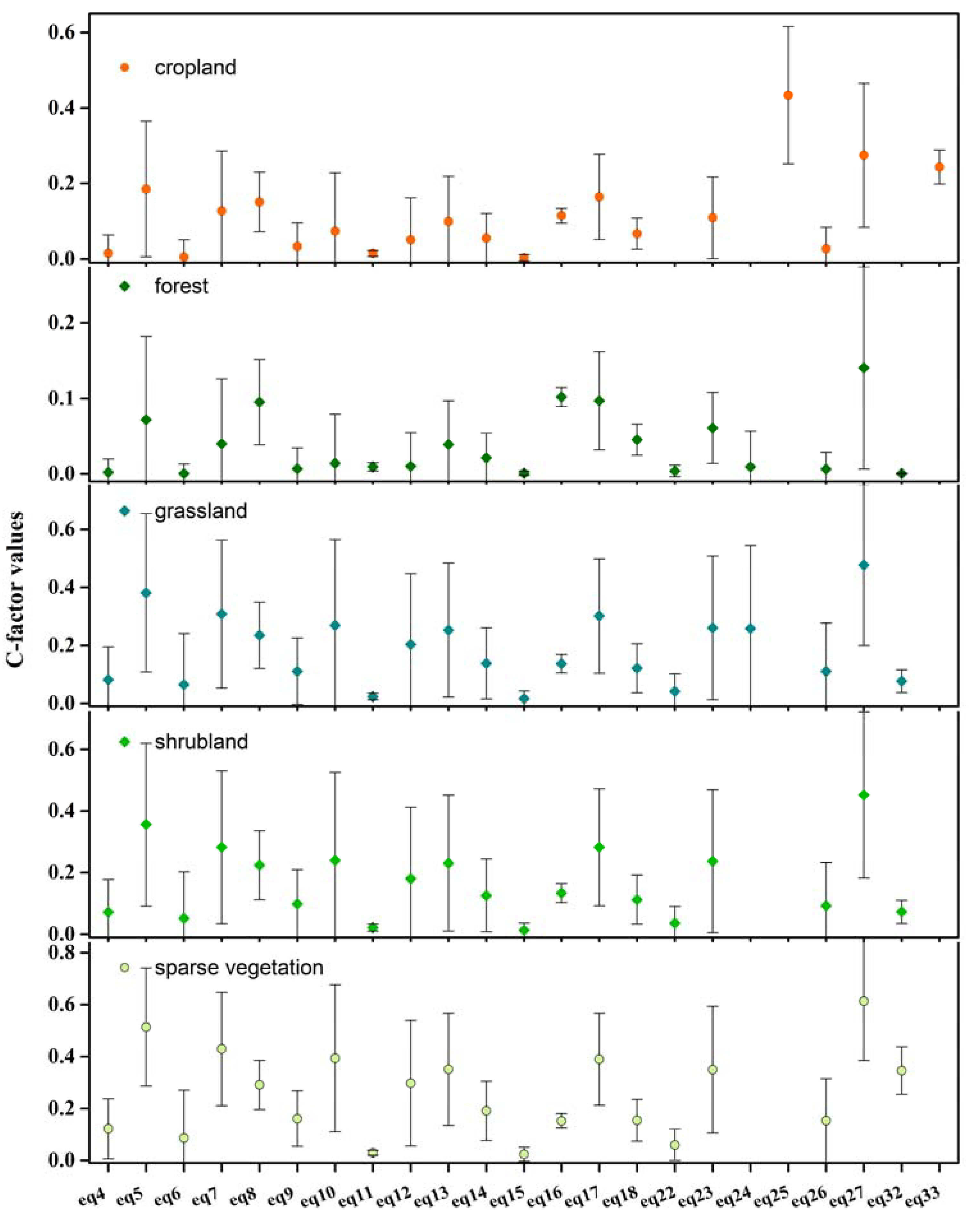
3. C-Factor Values Based on Field Experiments

The C-factor value could be determined by soil loss ratios (SLRs) in field experiments [10]. The overall C-factor value can be calculated by SLRs, the fraction of the rainfall erosivity (EI) for each time period (i), as Equation (1):

$$\mathrm{C}={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{SLR}}_{\mathrm{i}}\times {\mathrm{EI}}_{\mathrm{i}}\right)/{\mathrm{EI}}_{\mathrm{t}}$$

(1)

where SLR_i is the average value for time period i, EI_i is the percentage of EI during the time period i, n is number of periods occurring over the total time t being examined, and EI_t is sum of the EI percentages for the entire time period.

Here, we analyzed the C-factor values measured in field experiments. These field experiments were located in China, the USA, Japan, Portugal, Brazil, Belgium, Tanzania, Greece, and France. The majority of the plots in the field experiments followed the standard of USLE unit plots created by Wischmeier and Smith (1978) [10]. The C-factor values were estimated according to Equation (1). Figure 2 shows the C values derived from existing datasets for crops, grass, shrubs, and forests.

Figure 2 shows that there was a high degree of variability in the measured C-factor values. Specifically, the C-factor values of crops had the widest range, compared to other land-use types. The smallest C-factor value was observed for natural forest (0.0248 ± 0.0367), followed by shrubs (0.0622 ± 0.0525), artificial forest (0.193 ± 0.263), grass (0.224 ± 0.223), and crops (0.264 ± 0.228). The results indicate that natural vegetation was most effective in controlling soil erosion. The C-factor values based on field experiments can provide a valuable reference and benchmarking dataset for C.

4. Quantification of C-Factor for USLE-Type Modeling

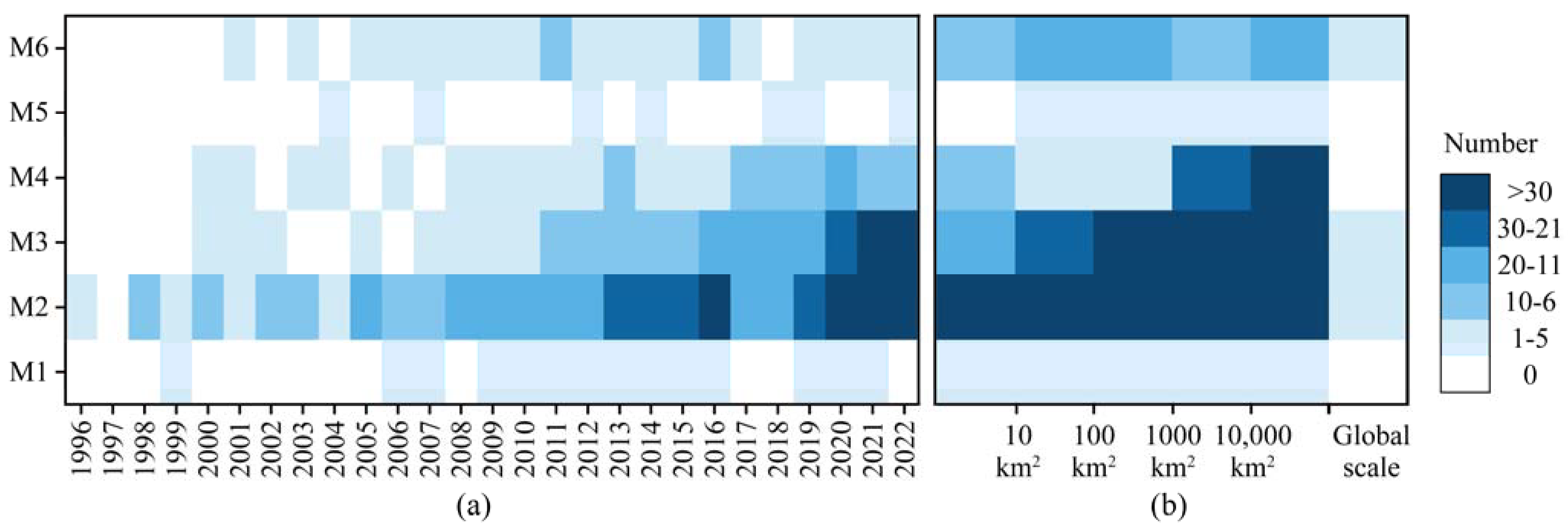
4.1. Methods for Quantifying the C-Factor Values

Normally, the C-factor is estimated from long-term field experiments. However, because of the absence of experiments, various methods have been developed to quantify the C-factor for USLE-type modeling in the literature. A simple and widely used method is referencing studies that have reported C-factor values for similar land cover. In addition, many studies have reported various formulas for deriving C-factor values [6,16,19,21,22,23]. In general, the methods for calculating C-factor values can be classified into six categories: (1) C-factor estimated based on subfactors (M1); (2) C-factor estimated according to land cover classifications (M2); (3) C-factor estimated by vegetation indices (VIs) (M3); (4) C-factor estimated by vegetation coverage (VC) (M4); (5) C-factor estimated by spectral mixture analysis (SMA) (M5); and (6) C-factor estimated based on other methods (M6). The six types of methods are described and discussed in detail below.

4.1.1. C-Factor Estimation Based on Subfactors (M1)

Following the RUSLE handbook, the C-factor is computed of five subfactors [9] as following Equation (2):

$$\mathrm{C}=\mathrm{PLU}\times \mathrm{CC}\times \mathrm{SC}\times \mathrm{SR}\times \mathrm{SM}$$

(2)

where PLU is the land-use subfactor, CC is the canopy cover subfactor, SC is the surface cover subfactor, SR is the surface roughness subfactor, and SM is the soil moisture subfactor [9]. Individual subfactors are expressed as functions of more variables, so this method requires details of the cover characteristics including canopy cover, canopy height, and prior cropping [7], which are mainly used in field level investigations [24,25,26]. It is evident that Equation (2) is not feasible for large-scale investigations, because of the data availability [6]. Hence, the C-factor value has been calculated from VC through the CC subfactor for large-scale soil erosion modeling in some studies [27,28,29] as Equation (3):

$$\mathrm{C}=\mathrm{CC}=1-f_c\times \exp \left(-0.0305\times H\right)$$

(3)

where f_c is the fraction of the land surface covered by canopy, and H (m) is the distance that raindrops fall after striking the canopy [9].

4.1.2. C-Factor Estimated According to Land Cover Classification (M2)

In most of the previous studies, the C-factor values were determined for each corresponding type of land use, and the values were obtained from available experimental data as tabulated in previous research works [30,31,32,33]. This simplified method assumes that the same land covers have the same values [7], and has been widely applied for large-scale soil erosion modeling, including the country-scale soil erosion assessment in Australia [34,35], South Korea [36], North Korea [37], Hungary [38,39] and even for global-scale modeling [40,41]. In addition, the C-factor values were also assigned to corresponding crop types in certain cases [30,42,43]. For example, Borrelli et al. (2017) determined C-factor values for fourteen crop groups (including 170 crops) according to the literature thresholds [17].

Here, we found 479 out of 946 studies had adopted empirical C-factor values for different land-use types according to previous research works (M2 method). There was a high degree of variability in the reported C-factor values among each type of land use (Figure 3). Specifically, the C-factor values for bare land and urban/village had the widest range (0–1), compared to other land-use types. The smallest C-factor value was observed for natural forest (0.013 ± 0.013), followed by wetlands (0.059 ± 0.105), shrub (0.092 ± 0.140), grass (0.105 ± 0.112), artificial forest (0.113 ± 0.142), sparse vegetation (0.207 ± 0.167), urban or village (0.22 ± 0.335), and crop (0.301 ± 0.114). The mean value reported for bare land was 0.58 (SD = 0.389). The C-factor values generally agree with those from field experiments (Figure 3). The observed smallest and largest C-factor values were associated with different land use types. The smallest C-factor value was found for natural forest. This can be attributed to the dense vegetation cover and complex root systems present in natural forests, which effectively reduce soil erosion. On the other hand, the largest C-factor values were observed for bare land and urban/village. These land use types often have minimal or no vegetation cover, resulting in high vulnerability to erosion processes. Factors such as land management, topography, climate, and conservation measures influence C-factor variations [7]. Moreover, the reported values represent the observed range and may differ based on geography and research methods. Further investigation is needed to understand the specific reasons for C-factor variations within each land use type and their impact on soil erosion processes.

The results indicate that the reported C-factor values generally align with those obtained from field experiments, as depicted in Figure 3. Furthermore, these results highlight the considerable variability in C-factor values across different land-use types and emphasize the need for accurate and context-specific estimations. The agreement between the reported C-factor values and those from field experiments strengthens the reliability of the empirical values used in our study.

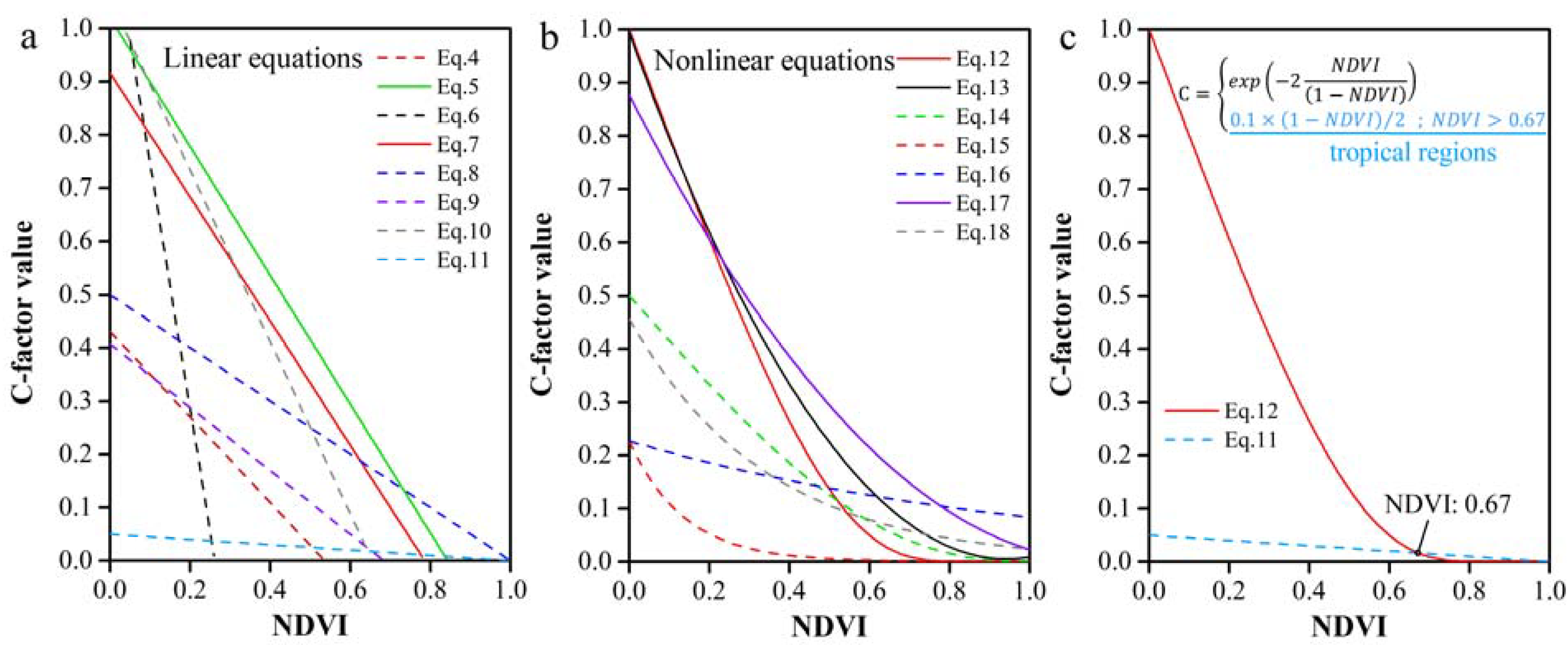
4.1.3. C-Factor Estimated by Vegetation Indices (M3)

Previous studies have proposed several empirical equations that relate VIs to C-factor values. The most commonly used VIs was the Normalized Difference Vegetation Index (NDVI) [21,44,45], and linear relations between C-factor value and NDVI were fitted, which had been used in different regions as following equations [46,47,48,49,50,51,52,53]:

$$\mathrm{C}=0.431-0.805\times NDVI$$

(4)

$$\mathrm{C}=1.02-1.21NDVI$$

(5)

$$\mathrm{C}=1.2079-4.6133NDVI$$

(6)

$$\mathrm{C}=0.9167-1.1667NDVI$$

(7)

$$\mathrm{C}=\left(1-NDVI\right)/2$$

(8)

$$\mathrm{C}=0.407-0.5953NDVI$$

(9)

$$\mathrm{C}=1.056-1.612NDVI$$

(10)

$$\mathrm{C}=0.1\times \left(1-NDVI\right)/2$$

(11)

The Equations (4), (8) and (9) only hold valid for photosynthetic and not senescent vegetations [46] and are unable to predict C-factor values over 0.5 (Figure 4a), while Equations (6) and (10) are unable to predict the differences of C-factor values when the NDVI is over 0.26 and 0.68, respectively. The C-factor values calculated by Equations (5) and (7) tend to be larger under natural vegetation conditions with a high NDVI. In 2018,Colman performed a comparison between the C-factor values estimated by NDVI and those computed with experimental plots in Brazil [53,54], and found a 10-fold systematic bias from Equation (8) [50]. Hence, Colman recommended that Equation (11) was suitable in tropical regions [55]. Due to these limitations, the linear equations were used in very limited studies [56,57,58].

There are various nonlinear relationships between the NDVI and the C-factor value have been proposed as following (Figure 4b) [59,60,61,62,63,64,65]:

$$\mathrm{C}=exp\left(-2\frac{NDVI}{\left(1-NDVI\right)}\right)$$

(12)

$$\mathrm{C}=1.1119NDV{I}^2-2.0976NDVI+0.9944$$

(13)

$$\mathrm{C}={\left[\left(1-NDVI\right)/2\right]}^{\left(1+NDVI\right)}$$

(14)

$$\mathrm{C}=0.227exp\left(-7.337NDVI\right)$$

(15)

$$\mathrm{C}=0.227exp\left(-0.997NDVI\right)$$

(16)

$$\mathrm{C}=0.625NDV{I}^2-1.4793NDVI+0.8771$$

(17)

$$\mathrm{C}=exp\left(-2.9298NDVI-0.7842\right)$$

(18)

Van der Knijff et al. developed Equation (12), which has been widely used to compute C-factor values [59,66,67,68,69,70]. However, the C-factor values calculated by Equation (12) tend to be smaller in tropical climate zones with more intense rainfall [50]. Almagro et al. compared Equations (11) and (12), and found that Equation (12) was not suitable to estimate the C-factor for most land uses, presenting larger values than those from experiments [55]. The C-factor values of polynomial equations (Equations (13) and (17)) indicate an overestimation related to land uses with a relatively high NDVI (Figure 4b). The power equation (Equation (14)) and exponential equations (Equations (15), (16) and (18)) are unable to predict C-factor values over 0.5 (Figure 4b), which means that these equations are limited in land uses with relatively high C-factor values, such as croplands.

The NDVI has a high correlation with the Leaf Area Index (LAI) [71], making it possible to estimate C-factor values through LAI as the flowing equation [72]:

$$\mathrm{C}=1.005\times exp\left[-0.426\left(PVI+0.012\right)\right]$$

(19)

However, there are some issues associated with the NDVI and the LAI, due to the effects of soil reflectance, the sensitivity to vegetation conditions, etc. [21]. Hence, several alternative VIs have been used to quantify the C-factor [72,73]. For example, Yoshino and Ishioka developed a regression model to estimate C-factor values using the perpendicular vegetation index (PVI) [71]:

$$\mathrm{C}=exp\left[-7.291\left(EVI\right)\right]$$

(20)

The enhanced vegetation index (EVI) was also employed to estimate the C-factor value [73], while the transformed soil adjusted vegetation index (TSAVI) has been recommended for use in arid and semi-arid areas [74,75].

$$\mathrm{C}=-0.177\times \ln \left(LAI\right)+0.184$$

(21)

Feng et al. found that the C-factor is sensitive to yellow VIs, such as the normalized difference tillage index (NDTI) and the normalized difference senescent vegetation index (NDSVI) [21]. The normalized bare soil index (NBIL) and the modified soil-adjusted vegetation index (MSAVI) have also been used to calculate the C-factor [76,77].

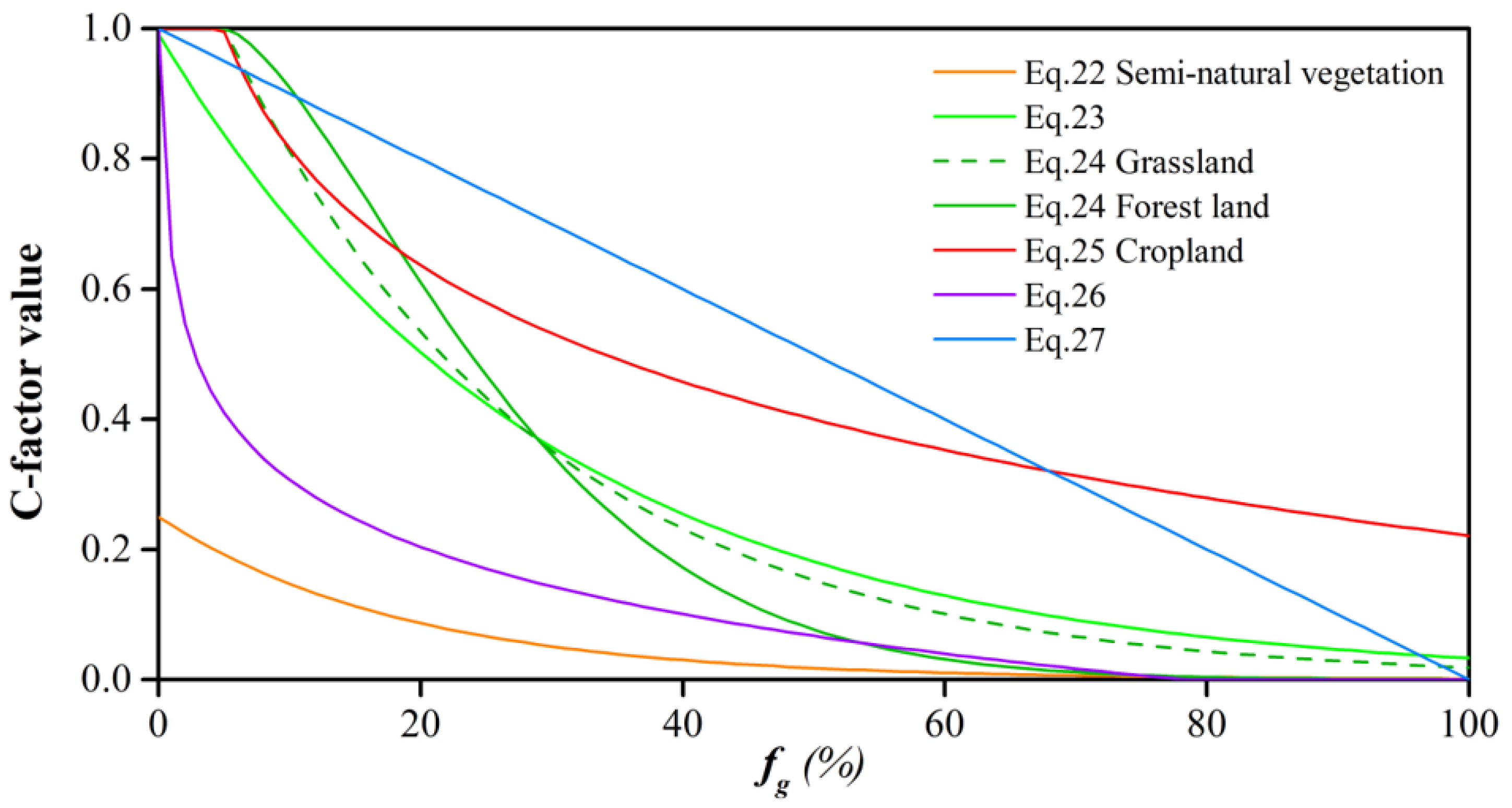
4.1.4. C-Factor Estimated by Vegetation Coverage (M4)

Vegetation coverage (VC) is also a dependable index for estimating the C-factor [78]. Thus, several alternative approaches based on VC have been established to quantify the C-factor as the following equations (Figure 5) [79,80,81,82,83,84]:

$$\mathrm{C}=0.25\times exp\left(-0.0529f_g\right)$$

(22)

$$\mathrm{C}=0.992\times exp\left(-0.034f_g\right)$$

(23)

$$\mathrm{C}=\left\{\begin{array}{cc} exp\left[-0.0418\left(f_g-5\right)\right]& f_g>5,\mathrm{Grassland}\hfill \\ exp\left[-0.0085{\left(f_g-5\right)}^{1.5}\right]& f_g>5,\mathrm{Forest\; land}\hfill \\ 1& f_g\le 5\hfill \end{array}\right.$$

(24)

$$\mathrm{C}=0.221-0.595\log (f_g/100)$$

(25)

$$\mathrm{C}=\left\{\begin{array}{cc}1& f_g=0\hfill \\ 0.6508-0.3436\lg f_g& 0<f_g\le 78.3\hfill \\ 0& f_g>78.3\hfill \end{array}\right.$$

(26)

$$\mathrm{C}=1-0.01\ast f_g$$

(27)

where f_g is the VC (%). Among these, Equation (26) developed by Cai et al. has been used to estimate the C-factor values for all land-use types in many studies in China [79,85,86,87,88,89,90]. However, Equation (26) was developed based on runoff plots of croplands and orchards [79], the Equation (22) was developed based on semi natural vegetation [80], the Equation (24) was developed based on grassland and forest land [82], which means the accuracy of the estimated C-factor values for other land-use types cannot be ensured. For large-scale studies, the VC was often calculated using the NDVI derived from the MODIS images:

$$f_g=100\times \frac{NDVI-NDV{I}_{min}}{NDV{I}_{max}-NDV{I}_{min}}$$

(28)

where f_g is the VC (%), NDVI_max refers to the regional maximum NDVI, NDVI_min is the NDVI of bare soil [91]. In some cases, the cumulative percentages of 5% and 95% were used to determine the corresponding values of NDVI_min and NDVI_max [21]. In addition, a linear relationship exists between f_g and NDVI (Equation (29)) [92], which has also been used for C-factor estimation [88].

$$f_g=108.49\times \mathrm{NDVI}+0.717$$

(29)

4.1.5. C-Factor Estimated by Spectral Mixture Analysis (M5)

As an alternative to NDVI-based approaches, spectral mixture analysis (SMA) of Landsat ETM data can estimate the fractional abundance of vegetation, and have been used to quantify the C-factor [93,94,95]. Lu et al. developed Equation (30) to estimate the C-factor [96].

$$\mathrm{C}=\frac{f_{soil}}{1+f_{gv}+f_{shade}+f_{gv}\times f_{shade}}$$

(30)

where f_soil is the fraction of soil, f_gv is the fraction of green vegetation, and f_shade is the fraction of shade.

De Asis and Omasa presented a linear SMA (LSMA) to map the C-factor, which used the fractional abundance of bare soil and ground cover to estimate the C-factor on a pixel-by-pixel basis [8]:

$$\mathrm{C}=\frac{f_{soil}}{1+f_{gv}+f_{NPM}}$$

(31)

where f_NPM is the fraction of non-photosynthetic materials. De Asis and Omasa compared the C-factor among the LSMA-derived method (Equation (31)), the NDVI-derived method (Equation (4)), and field experiments in the Philippines [8]. The results showed that the LSMA-derived values correlated more strongly with the field-measured values, and the LSMA-derived C-factor showed a more detailed spatial variability, which indicated that this method can generate a more reliable estimate of soil erosion. However, there are some limitations of the SMA-derived C-factor; for example, this method assumes that its value is 0 under densely vegetated areas, which could lead to underestimated soil erosion in those areas [8].

4.1.6. C-Factor Estimation Based on other Methods (M6)

Traditionally, C-factor values are simply determined based on the literature or field data. Such methods assume that the same land-cover class has the same C-factor value [7,96]. However, the C-factor is largely related to vegetation conditions. Panagos et al. proposed a method for C-factor estimation (Equations (32) and (33)), which considers the combined effects of land-use type and VC [7].

$$C=Min\left(C_{landuse}\right)+\left[Max\left(C_{landuse}\right)-Min\left(C_{landuse}\right)\right]\times \left(1-F_{cover}\right)$$

(32)

where F_cover is the percentage of land covered by vegetation; C_landuse is the value of each land-use type according to the literature data. The C-factor reaches its maximum value with F_cover = 0 (i.e., no vegetation), while it reaches its minimum with F_cover = 1 (i.e., land is fully covered by vegetation). However, the F_cover is not appropriate for croplands, as the VC changes during the year. Hence, this method has been used to estimate the C-factor for non-arable lands [7,17,97].

For arable lands, the C values of cropland in each country were calculated using following formula:

$${\mathrm{C}}_{\mathrm{crop}}={\displaystyle \sum }_{\mathrm{n}=1}^{14}{\mathrm{C}}_{\mathrm{cropn}}{\times \%\mathrm{Region}}_{\mathrm{Cropn}}$$

(33)

where C_cropn represents the C-factor of the n-crop and %Region_Cropn represents the share of this crop in the agricultural land of the given region [7].

In some cases, the C-factor and P-factor (support practice factor) have been treated together as the CP factor [4,98,99,100,101,102,103,104,105,106,107]. For a managed artificial forest, the C-factor is closely related to the forest’s age [108].

4.2. Application of the Methods for C-Factor Quantification

Figure 6 shows the size of the study area and the publication year of the 946 studies. The study areas ranged from plot scale (1–100 m²) to global scale, and there was an increasing trend in the number of studies, with more studies focusing on large-scale assessments in recent years.

Figure 7a shows the number of studies using different methods for each year. Most studies adopted empirical uniform values for different land uses according to previous studies (M2 method, 478 studies) or calculated the C-factor based on the VIs (M3 method, 254 studies) (Figure 7a). Most of the previous studies using the M2 and M3 methods were conducted in large study areas (>100 km²) (Figure 7b). The M2, M3, and M4 methods are often applied using remote sensing data, such that the seasonal cycle of the C-factor can be determined in large areas, which can help to identify the periods within the year with severe soil erosion (Ferreira and Panagopoulos 2014).

4.3. Comparison of the Methods of C-Factor for Large Study Areas

The M2 and M3 methods have been commonly used in large study areas (Figure 7b); we use the NDVI of the year 2015 from the Global Inventory Modeling and Mapping Studies (GIMMS) NDVI3g data to estimate the global C-factor values according to the equations (Equations (4)–(27)). The half-month NDVI was combined for yearly data (Supplementary Figure S1a) using the maximum value composite method. Additionally, the landcover of the year 2015 from ESA CCI-LC at a 300 m spatial resolution (Supplementary Figure S1b), and crop harvested area data of each country from the FAO database, were used to estimate the C-factor values according to the method of Panagos et al. [7].

Figure 8 shows the mean and standard deviation for C-factor values of cropland, forest, grassland, shrubland, and sparse vegetation for the year 2015. The data demonstrate a high degree of variation in C-factor values among different land uses (Figure 8 and Figure S2 and Table S1). The mean C-factor value for cropland based on field experiments was found to be 0.264 (SD = 0.228) (Figure 3), which was greater than those obtained from theoretical equations, including Equations (4)–(18), (23), and (26). Additionally, the mean C-factor value for cropland, as estimated by Equation (25), was 0.434 (Figure 8 and Supplementary Table S1), indicating that the aforementioned equations were not effective for estimating the C-factor values of croplands on a large scale. The results of the study indicate that Equations (33) and (27) are suitable for estimating the C-factor values of cropland, as the mean values obtained by these equations were 0.244 (SD = 0.045) and 0.275 (SD = 0.190), respectively, consistent with those derived from field experiments. However, when applied to natural vegetation (such as forest, grassland, and shrubland), the C-factor values calculated using Equation (27) were significantly higher than those reported in the historical literature. Therefore, Equation (27) is considered to be unsuitable for natural vegetation. The other equations employed in the study also exhibited limitations in accurately estimating C-factor values for all land uses. Specifically, the mean C-factor values for grass, shrub, and forest, calculated using Equations (8), (32), and (14), were 0.235 (SD = 0.115), 0.073 (SD = 0.037), and 0.0215 (SD = 0.032), respectively, and were consistent with the results obtained from field experiments. The results suggest that the combined use of Equations (33) or (27) for cropland, Equation (8) for grass, Equation (32) for shrub, and Equation (14) for forest can be applied at a global scale. These results provide valuable insights for researchers and practitioners seeking to estimate C-factor values for large-scale soil erosion assessments.

5. Discussions

Our systematic review summarizes the methods for calculating C-factor values adopted by 946 studies. The C-factor has experienced a process of simplification to assess the potential impact on soil erosion over larger areas [55]. The most widely used methods were the M2 (478 studies), M3 (254 studies), and M4 (101studies) methods.

5.1. Comparison of the Main Methods of C-Factor for USLE-Type Modeling

The M2 method assumes that the same types of land use have an equal C-factor value [7]. Due to its simplicity, it was the most widely used method, given the difficulties in collecting and processing all of the necessary parameters. However, the accuracy of the C-factor values estimated by the M2 method largely depend on the accuracy of land cover classification. In addition, the same type of land use would have different C-factor values, due to the spatial heterogeneity in vegetation density [6,19] or management practices [7] in large geographic areas.

The M3 method uses VIs to assess C-factor values. Despite the fact that this method is generally accepted and has been widely used, some studies found that there were low correlations between VIs and the C-factor [19]. For example, in the regions covered by non-photosynthetic vegetation (NPV), the correlations between VIs and the C-factor value are low [8,19], because dry and dead vegetation could still exert influences on the C-factor [109]. Yang et al. found that incorporating NPV information can significantly improve the accuracy of C-factor estimation for China’s Loess Plateau [110]. Moreover, C-factor estimation only through VIs tends to result in overestimation, because this method ignores the differences in types of land use with the same VIs [44]. Recently, combining different VIs has been proposed as an alternative strategy to address this issue [21,109]. For example, Puente et al. used thirty VIs to identify the reliable relation between VIs and measured C-factor values from long-term experiments in Mexico, and found that the correlation coefficients with conventional VIs (such as NDVI and EVI) were low in general, showing that current VIs could not provide all of the information of the vegetation required by erosion models [109]. Feng et al. compared the estimates of C-factor values based on various VIs in the Loess Plateau of China, and found that a combination of green VIs (NDVI, PVI, TSAVI, and EVI) and yellow VIs (NDTI and NDSVI) could greatly improve the accuracy of C-factor values than those based on a single VI [21].

The M4 method estimates C-factor values based on VC, and the equations have been mainly developed in China. Since the VC has often been represented by the NDVI, the M4 method shares similar weaknesses with the M3 method. Each equation of M3 and M4 (Equations (12)–(27)) may be suitable to estimate the C-factor for some land-use types, but not all land uses. The M5 method has shown promising application, due to its capability for detecting both the healthy (green) and non-photosynthetic (dry and dead) vegetation [111]. However, this method cannot be used in areas completely covered by vegetation [19,111]. Thus, the M5 method has only been adopted by a few studies (seven studies), and was further constrained by its complex calculation procedures [22].

Each method has its own strengths and weaknesses, and no single method can meet all of the requirements. The C-factor values measured on plots under natural rainfall conditions (Figure 2) showed that the same type of land use even with the same VIs or VC could lead to different C-factor values [7,112]. Hence, the use of the M3, M4, and M5 methods, without on-site knowledge, may produce uncertainties that can reduce the accuracy of soil erosion predictions and assessments. Overall, for small-scale studies, it is more feasible to quantify the C-factor through experiments, estimates based on subfactors (M1 method), or obtain values from the literature (M2 method). At large scales, the M3, M4, and M5 methods can contribute to identify the impacts of vegetation change on soil erosion potential, especially when considering sub-monthly, monthly, or yearly vegetation change [6]. Notably, the resolution of satellite images is a common issue that would impair the robustness of the three methods. For example, Meusburger et al. showed that the resolution of a satellite image could affect the derivation of VIs, with subsequent impacts on the estimation of C-factor values and soil erosion [113]. The choice of methods should depend on the scale of the area, the objective of the studies, and the availability of data. For a given large-scale region, it may be better to use different equations for various types of land use than use the same equation for all types.

5.2. C-Factor Estimation for USLE-Type Modeling at Large Scale

In previous studies, the C-factor has been mainly quantified using the M2 method at national or regional scales. However, these studies did not fully consider the C-factor for soil erosion assessment (

Table 1. Summary of national and global scale soil erosion assessments using the USLE-type models.

Study Area	C-Factor Value	References
Europe	M3: Equation (12)	[115,116]
Italy	M3: Equation (12)	[59,117]
Australia	M2	[34]
Australia	M4	[118]
South Africa	M2	[119]
Spain	M2	[120]
Slovakia	M2	[121]
Europe	M2	[122]
South Korea	M2	[36]
Spain	M6	[123]
China	M4: Equation (26)	[124,125]
Europe	M2	[126,127,128]
Europe	M6	[1,7,18]
Mediterranean Europe	M3: Equation (12)	[68]
Australia	M2	[35]
Hungary	M2	[38,39]
Italy	M6	[114]
Greece	M6	[129]
Uganda	M3: Equation (12)	[130]
Kenya	M2	[131]
Italy	M6	[132]
North Korea	M2	[37]
Global	M2	[40,41,133]
Central Asia	M4: Equation (26)	[134]
Central Asia	M3: Equation (12)	[135]
South America	M2	[136]
Global	No C-factor	[137]
Global	M2	[138,139]
Global	M3: Equation (4)	[140]
Global	M6	[17,97]
Global	M3: Equation (12)	[141]

), except for the study by Panagos et al. Specifically, Panagos et al. proposed a methodology for estimating the C-factor values using pan-European datasets, biophysical attributes, and census data for arable lands [7]. The C-factor value of arable lands was estimated using crop statistics (% of land per crop) and information on management practices such as conservation tillage and mulching. In non-arable lands, the C-factor was quantified by weighting the literature values according to the fraction of vegetation cover [7]. Borrelli et al. also used this method to calculate the C-factor values at the national scale (Table 1) [114].

In recent years, USLE-type models have been applied for soil erosion assessment on a global scale (Table 1). Pham et al. conducted the first study on global soil erosion estimates using the USLE model, in which uniform C-factor values were applied for different types of land use [40]; this method was also used in the studies by Yang et al. and Ito [41,133]. Scherer and Pfister and Doetterl et al. used a global crop-type abundance map to estimate C-factor values [138,139]. Recently, Naipal et al. calculated the C-factor according to Equation (4) [140], but produced a positive bias in winter. Following previous pan-European studies [7], Borrelli et al. incorporated the types and spatial distribution of global croplands into a global USLE-type model [17,97]. Liu et al. quantified the C-factor according to Equation (12) [141].

Previous studies have shown that there are various crop management practices (CMPs, e.g., mulching, strip-cropping) on arable lands [142] and found that biological techniques can reduce the soil loss rate by around 88% based on a global analysis of runoff plots. Prosdocimi et al. reported the beneficial effects of mulching in reducing soil erosion by up to 90% [143]. Conservation agriculture occupies approximately 15% of global cropland [17], with CMPs widely applied in erosion-sensitive regions. However, the effects of CMPs on soil erosion were not fully considered in existing C-factor estimation methods.

5.3. Limitations and Future Improvements

Determination of the C-factor value is difficult, due to its dependence on many parameters such as the land cover, vegetative canopy cover, soil biomass, and surface roughness [16,19,128]. Our systematic literature review and analysis revealed several limitations in current estimations of C-factor values.

First, no single method is applicable in all regions and meets all of the requirements, especially for global-scale investigations. Second, the effects of CMPs have not been fully considered for croplands in existing C-factor estimation methods. Third, the estimated C-factor values based on VIs (Equations (12)–(21)) and VC (Equations (22)–(27)) were not well validated in field experiments, and each equation based on VIs and VC may be suitable to estimate the C-factor for some land-use types, but not all land uses. Indeed, different types of land use with even the same VIs or VC could have different C-factor values. Fourth, the accuracy of the C-factor value largely depends on the quality of the satellite images, as the land cover classification and VIs were directly derived from satellite images. High-resolution images can offer the advantage of capturing fine-scale details and accurately differentiating between various land cover types and vegetation densities. This allows for a more precise estimation of the C-factor by taking into account variations in vegetation cover. However, coarse spatial resolution satellite images, such as Landsat, are commonly used, as fine-resolution satellite images that can detect conservation practices are not freely available.

Here, we identify four key areas that require further efforts for improving the estimation of C-factor values: (1) Building regional and global scale C-factor databases through the collection and integration of field experiment data; (2) leveraging high-resolution satellite imagery and advanced image processing techniques for C-factor quantification; (3) combining multiple methods to enhance the robustness of soil erosion assessment; (4) strengthening the quantification of the uncertainty of C-factor values.

6. Conclusions

This study contributes a comprehensive database encompassing C-factor values, quantification methods, and study sites derived from an extensive analysis of 946 published articles. The increasing trend in studies focused on soil erosion assessment in recent years and the development of numerous methods to determine C-factor values indicate the importance of this research area. Our findings demonstrate that LUMPs play a significant role in mitigating soil erosion, with natural vegetation emerging as the most effective land use type. Through meticulous examination, we identified six prominent approaches for quantifying C-factor values, each carrying distinct advantages and limitations, indicating that a combination of methods is required for the robust estimation of C-factor values for different land-use types. We recommend the combined use of specific equations for cropland, grass, shrub, and forest to estimate C-factor values at the global scale. Further efforts are necessary to develop C-factor datasets at large scales by synthesizing field-level experiment data and combining high-resolution satellite imagery. The results of this study provide useful implications for C-factor quantification at various spatial scales and significantly improve our understanding of the uncertainties involved in soil erosion assessment using USLE-type models. These findings can inform decision-making processes and provide valuable guidance for soil conservation strategies, contributing to sustainable land use and environmental protection.