A Review of Hyperspectral Image Super-Resolution Based on Deep Learning
Abstract
1. Introduction
- (1)
- This paper presents a comprehensive summary of HSI SR techniques based on DL, including upsampling frameworks, upsampling methods, network design, loss functions, representative works with different strategies, and future directions. We also analyze the advantages or limitations of each component.
- (2)
- In this paper, we carry out a scientific and precise classification of traditional HSI SR algorithms, based on the difference of underlying ideas.
- (3)
- To explore the influence of multi-channel two-dimensional (2D) convolution and three-dimensional (3D) convolution on the performance of the HSI SR model, two sets of comparative experiments are designed, based on the CAVE dataset and Pavia Centre dataset, and the advantages and shortcomings of each are compared.
- (4)
- This paper summarizes the challenges faced in this field and proposes future research directions, providing valuable guidance for subsequent research.
2. Preparations
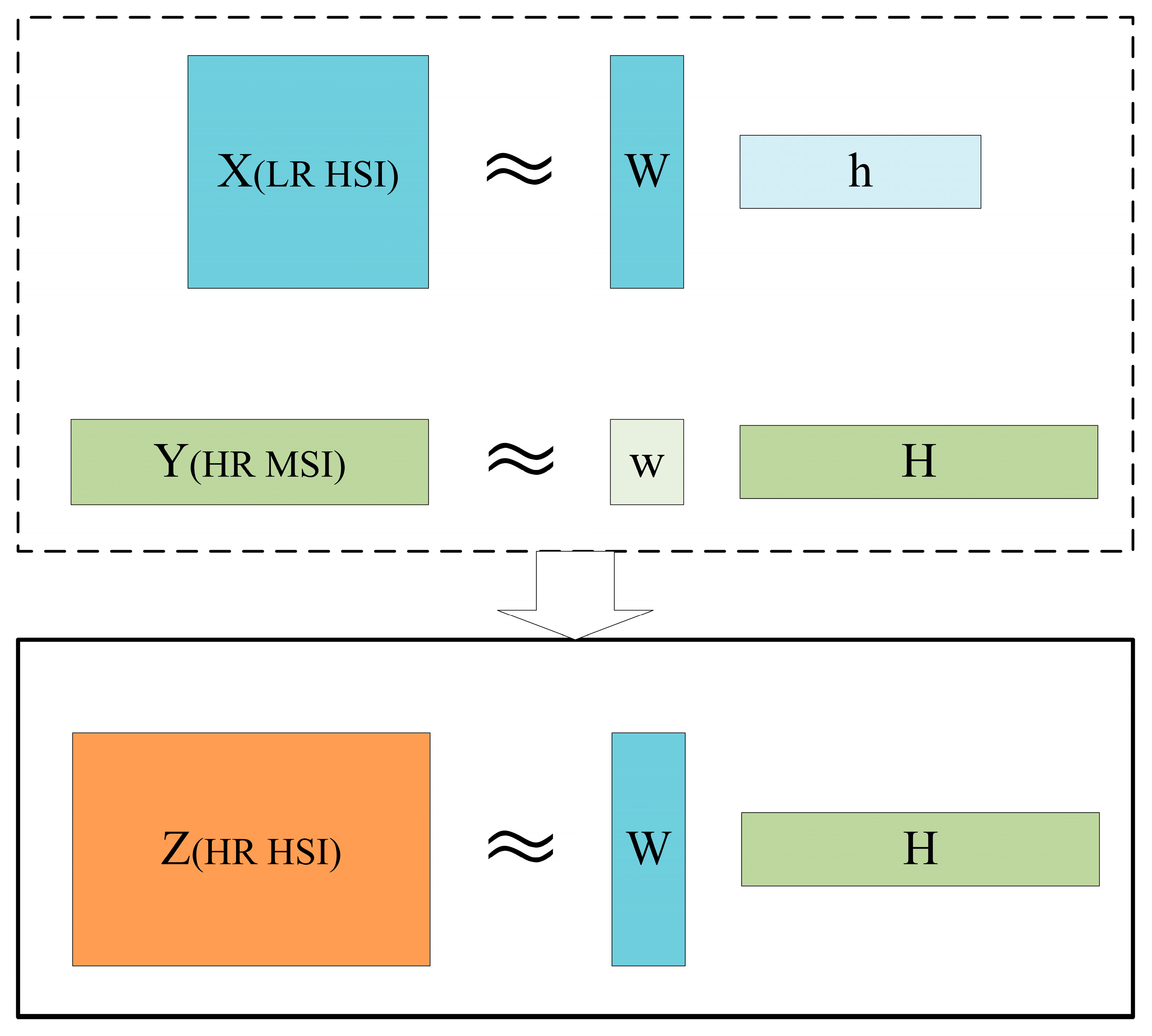
2.1. Problem Formulation
2.2. Datasets
2.3. Image Quality Assessment
3. Traditional Methods
3.1. Wavelet Transform-Based Methods
3.2. MAP-Based Methods
3.3. Spectral Mixing Analysis-Based Methods
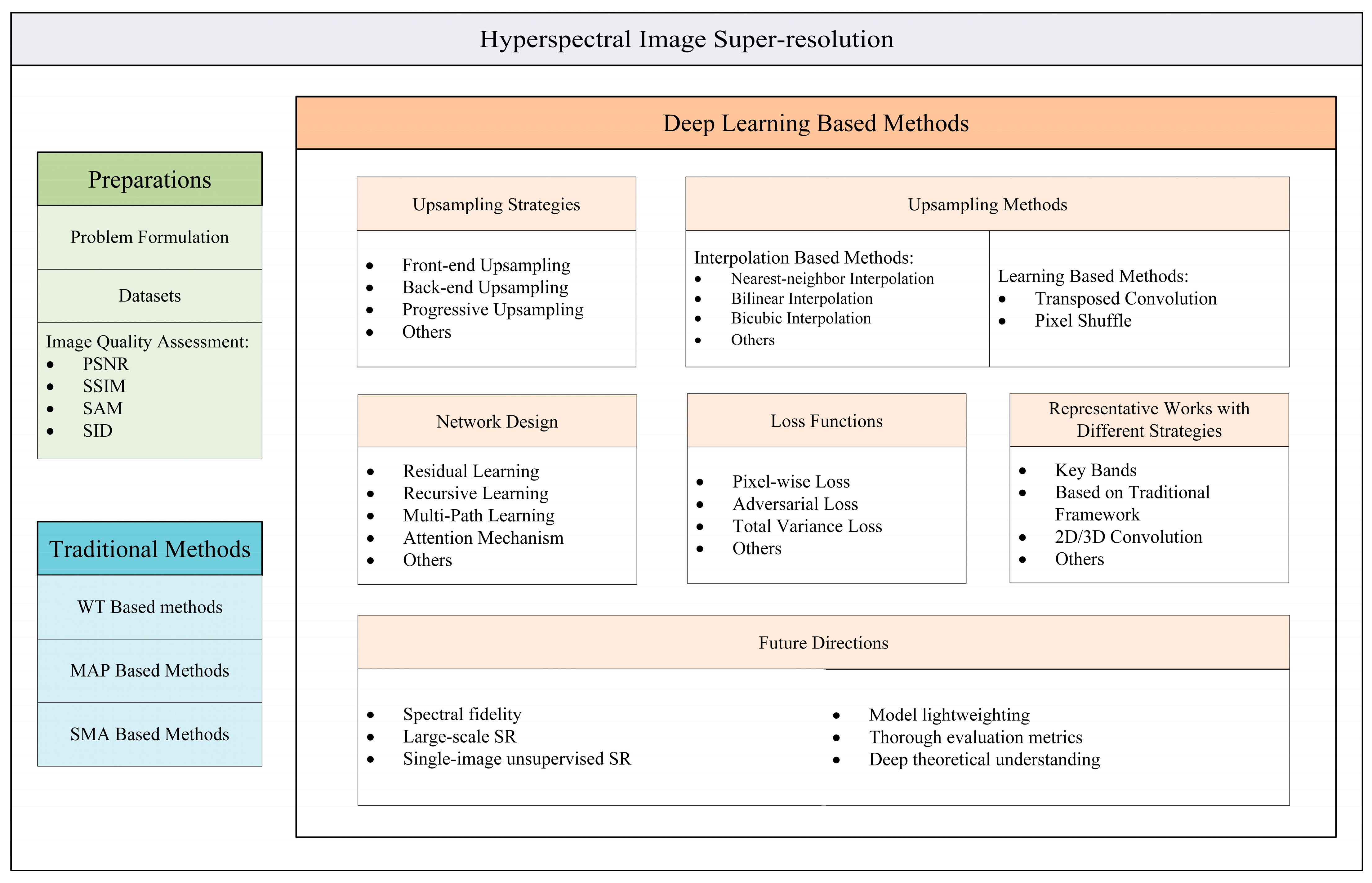
4. Deep-Learning-Based Methods
4.1. Upsampling Frameworks
4.2. Upsampling Methods
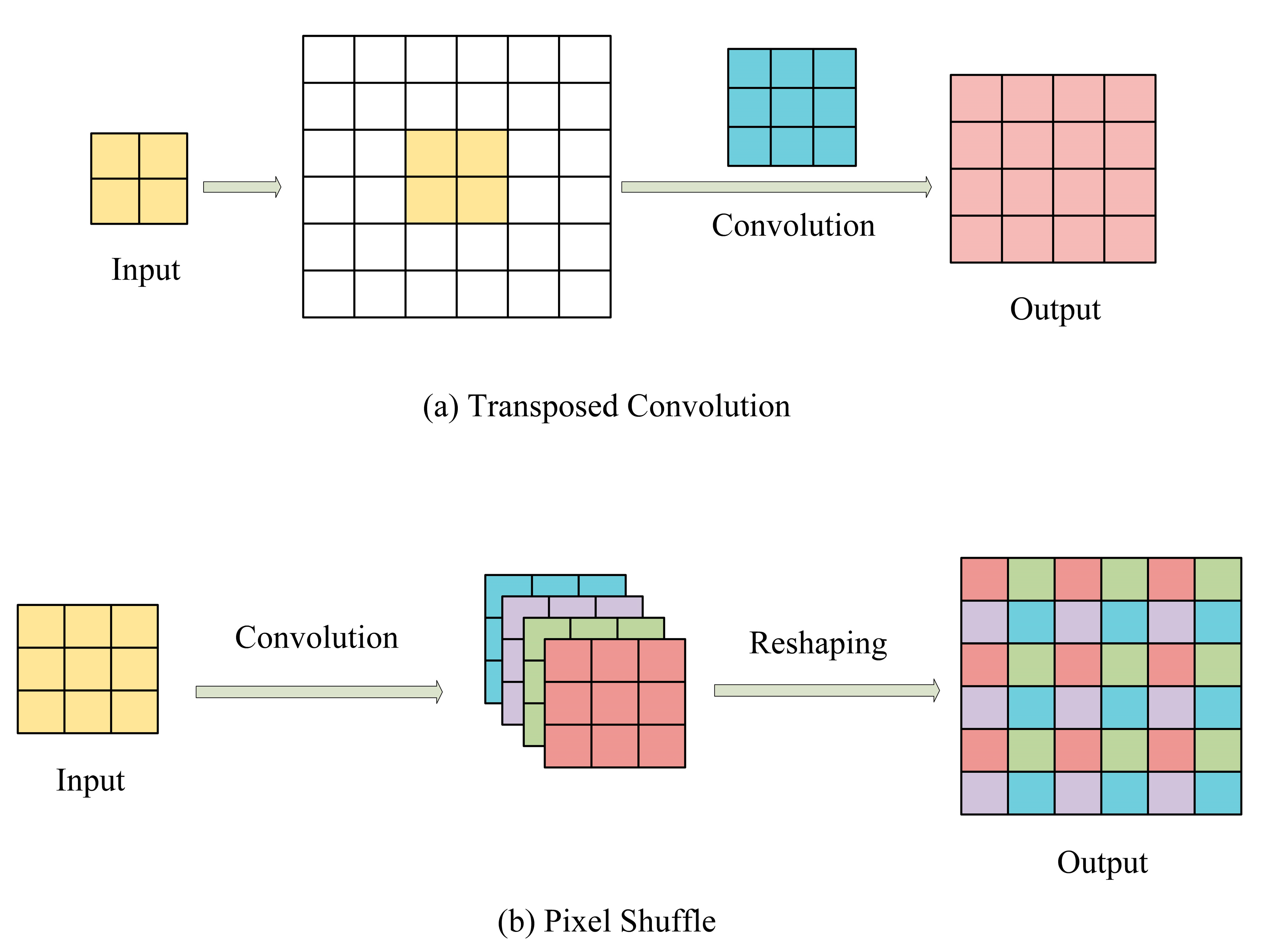
4.2.1. Interpolation-Based Upsampling
4.2.2. Learning-Based Upsampling
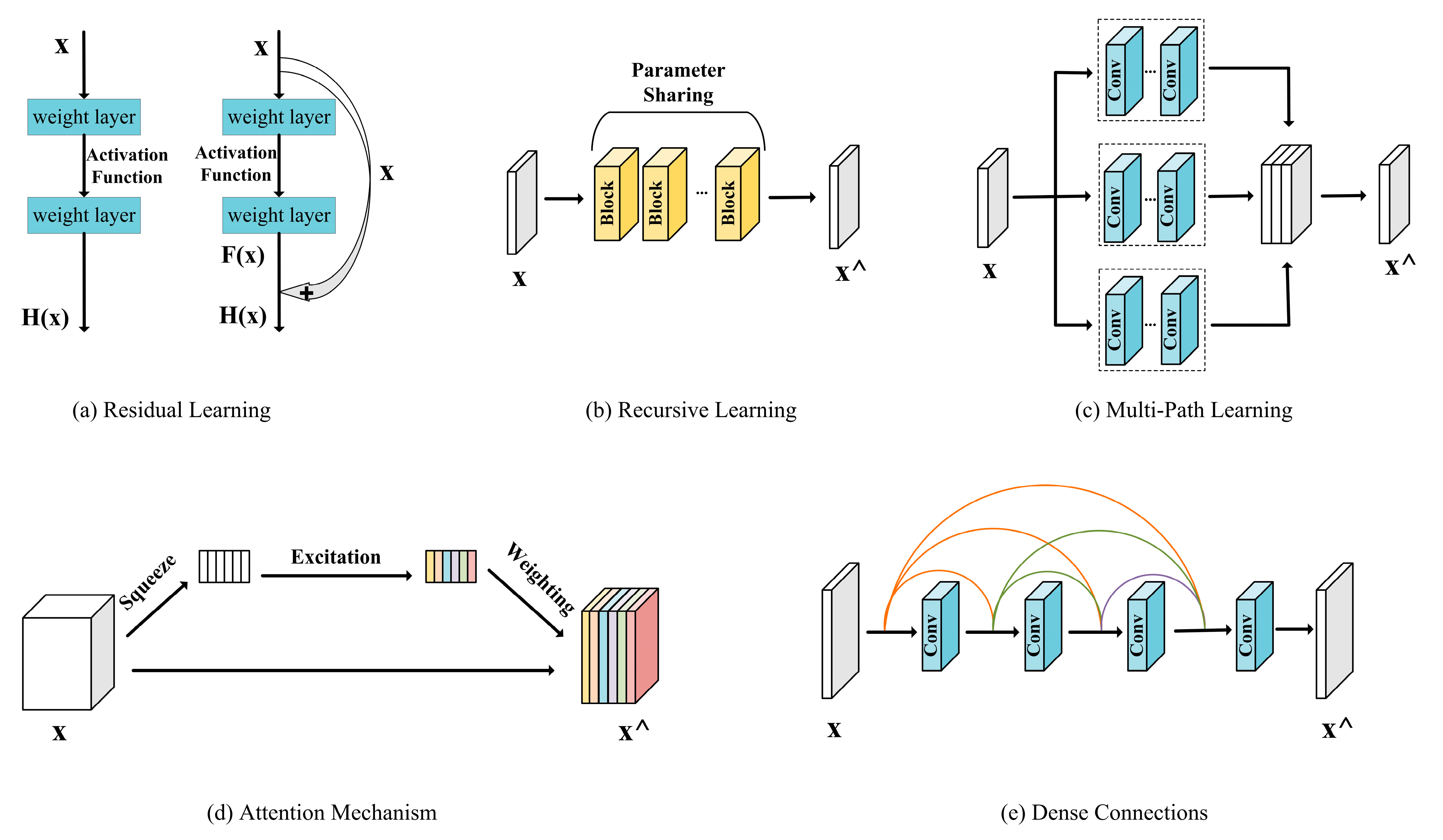
4.3. Network Design
4.4. Loss Functions
4.5. Representative Works with Different Strategies
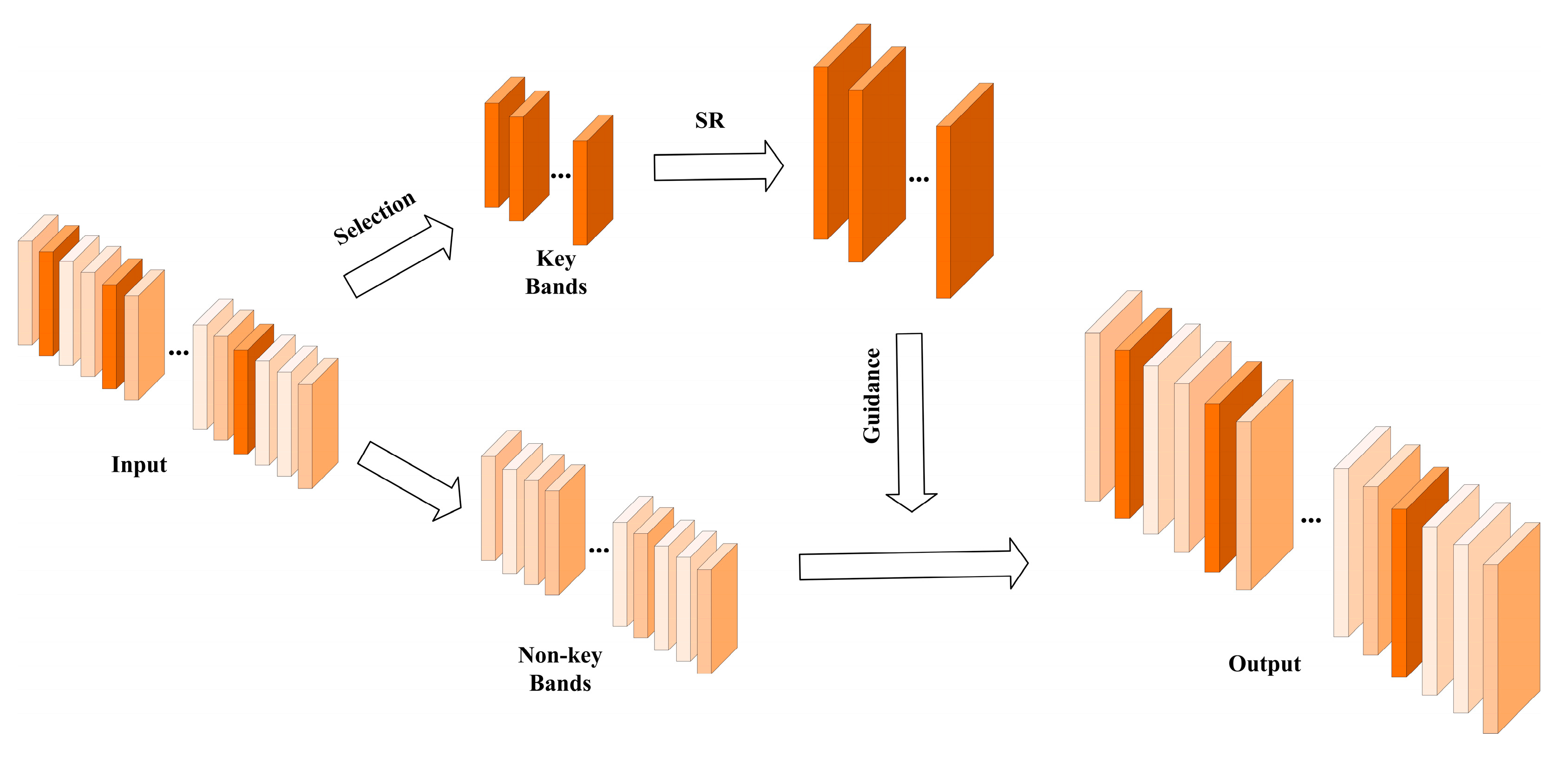
4.5.1. Key Bands
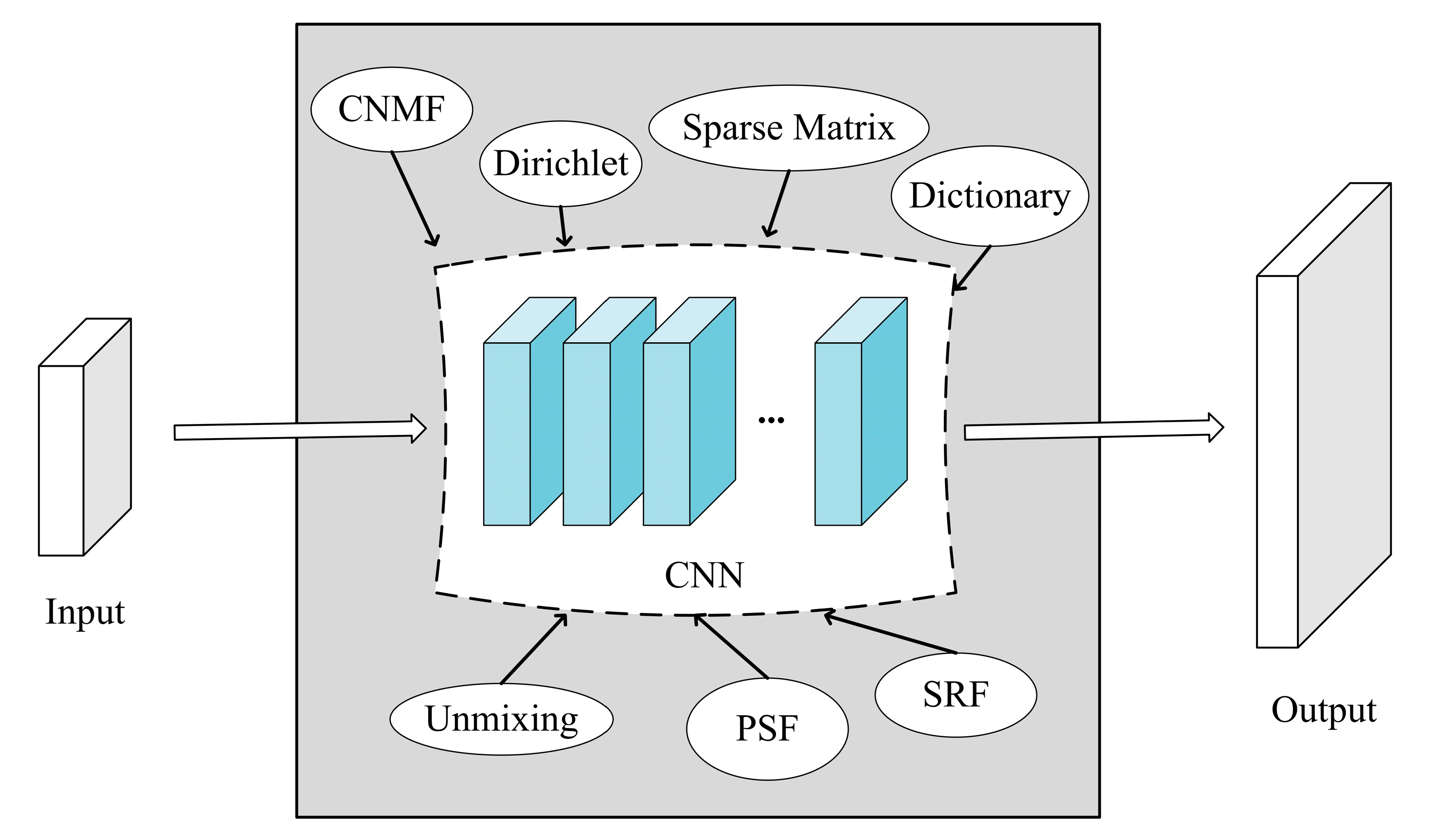
4.5.2. Based on Traditional Framework
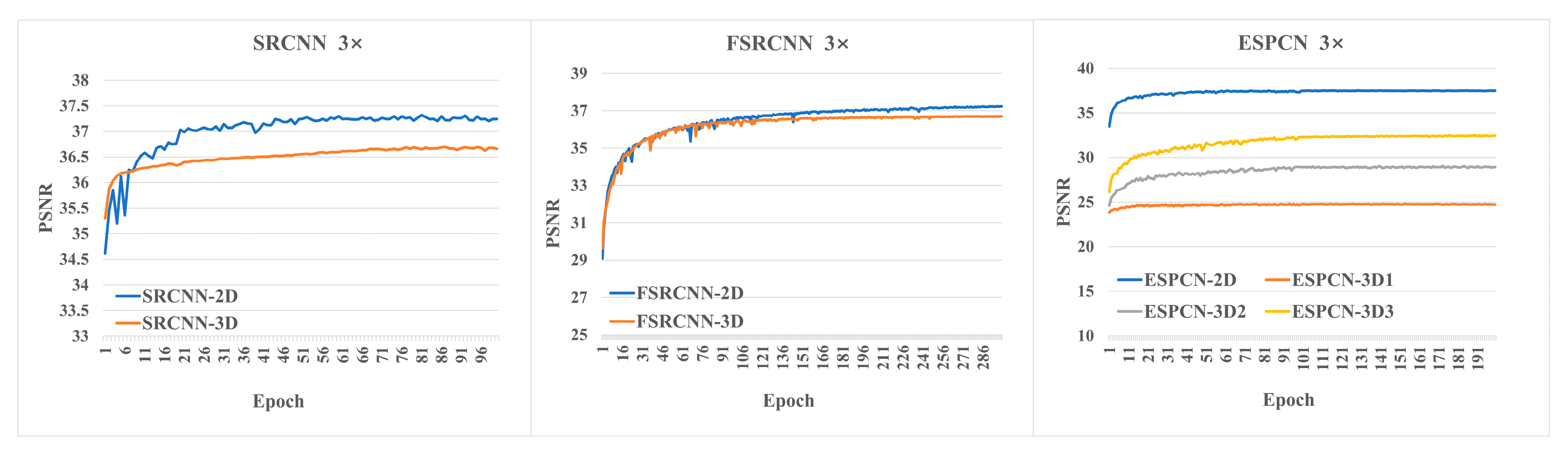
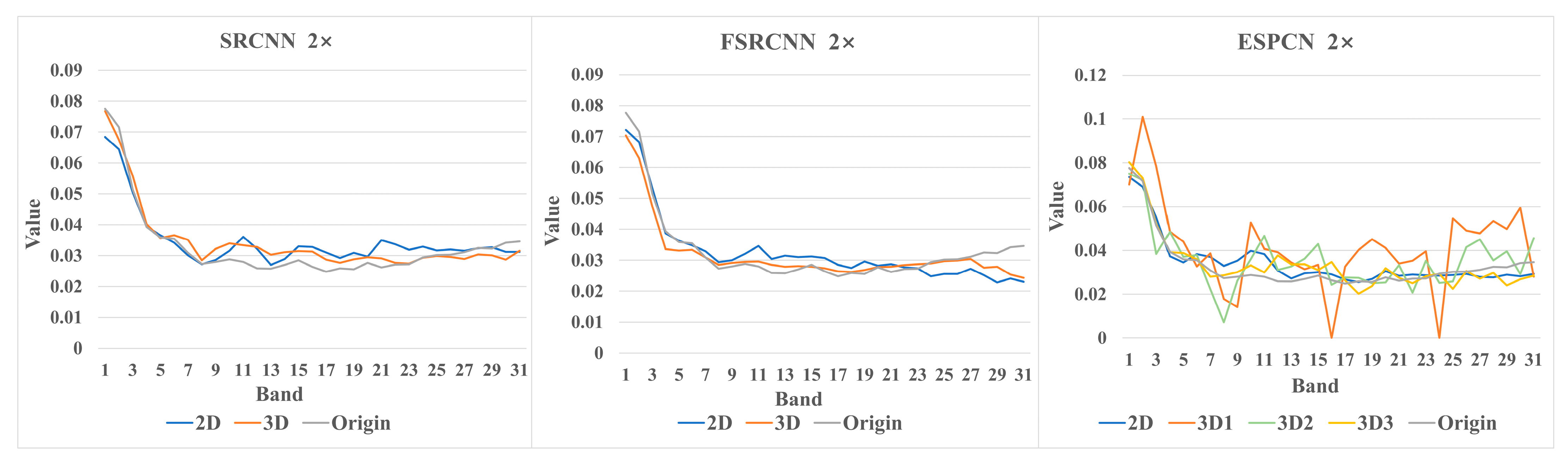
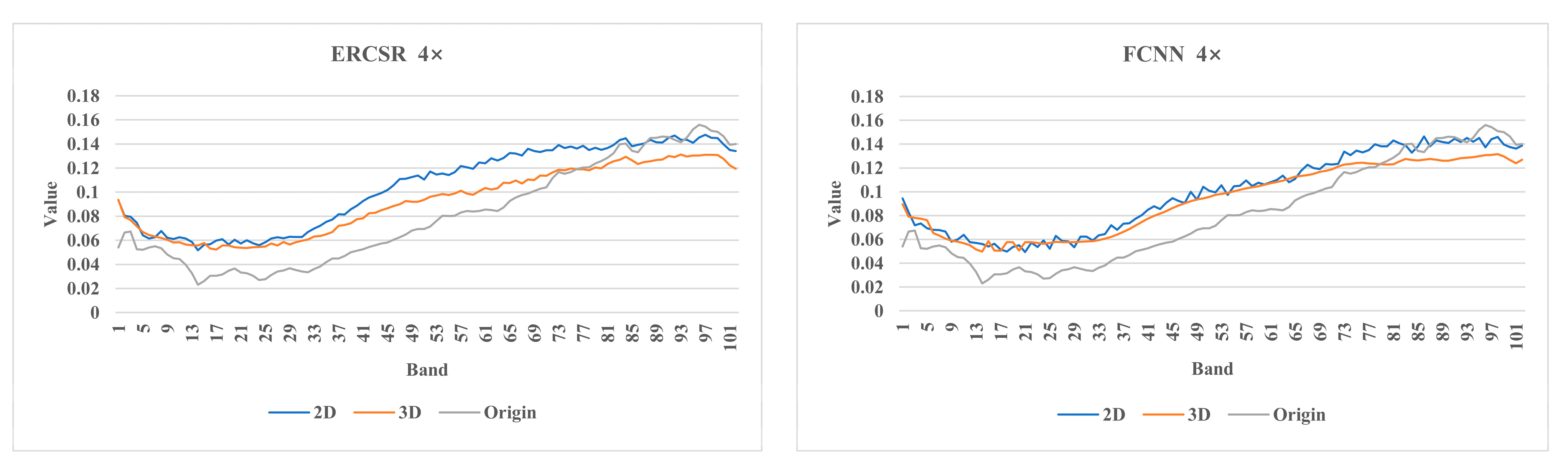
4.5.3. 2D/3D Convolution
Mechanisms
Experiments and Results
4.5.4. Brief Summary
4.6. Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.H.; Chen, J.; Hoi, S.C.H. Deep learning for image super-resolution: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3365–3387. [Google Scholar] [CrossRef]
- Chen, H.G.; He, X.H.; Qing, L.B.; Wu, Y.Y.; Ren, C.; Sheriff, R.E.; Zhu, C. Real-world single image super-resolution: A brief review. Inf. Fusion 2022, 79, 124–145. [Google Scholar] [CrossRef]
- Yang, W.M.; Zhang, X.C.; Tian, Y.P.; Wang, W.; Xue, J.H.; Liao, Q.M. Deep learning for single image super-resolution: A brief review. IEEE Trans. Multimed. 2019, 21, 3106–3121. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Y.C.; Zhang, X.; Xu, D.D.; Wang, X.D.; Ben, G.L.; Zhao, Z.K.; Li, Z. A multi-degradation aided method for unsupervised remote sensing image super resolution with convolution neural networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5600814. [Google Scholar] [CrossRef]
- Xiang, P.; Ali, S.; Jung, S.K.; Zhou, H.X. Hyperspectral anomaly detection with guided autoencoder. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5538818. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Qu, Y.; Zhao, C.H.; Tao, R.; Du, Q. Prior-based tensor approximation for anomaly detection in hyperspectral imagery. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1037–1050. [Google Scholar] [CrossRef]
- Zhuang, L.; Gao, L.R.; Zhang, B.; Fu, X.Y.; Bioucas-Dias, J.M. Hyperspectral image denoising and anomaly detection based on low-rank and sparse representations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5500117. [Google Scholar]
- Hong, D.F.; Han, Z.; Yao, J.; Gao, L.R.; Zhang, B.; Plaza, A.; Chanussot, J. Spectralformer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Luo, F.L.; Zou, Z.H.; Liu, J.M.; Lin, Z.P. Dimensionality reduction and classification of hyperspectral image via multistructure unified discriminative embedding. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5517916. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.R.; Zheng, Y.H.; Wu, Z.B. Spectralspatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522214. [Google Scholar]
- Berger, K.; Verrelst, J.; Feret, J.B.; Wang, Z.H.; Wocher, M.; Strathmann, M.; Danner, M.; Mauser, W.; Hank, T. Crop nitrogen monitoring: Recent progress and principal developments in the context of imaging spectroscopy missions. Remote Sens. Environ. 2020, 242, 111758. [Google Scholar] [CrossRef]
- Zhong, Y.F.; Hu, X.; Luo, C.; Wang, X.Y.; Zhao, J.; Zhang, L.P. Whu-hi: Uav-borne hyperspectral with high spatial resolution (h-2) benchmark datasets and classifier for precise crop identification based on deep convolutional neural network with crf. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, L.; Zhang, X.L. Three-dimensional convolutional neural network model for tree species classification using airborne hyperspectral images. Remote Sens. Environ. 2020, 247, 111938. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.G.; He, K.M.; Tang, X.O. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the 13th European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; Springer International Publishing Ag: Zurich, Switzerland, 2014; pp. 184–199. [Google Scholar]
- Anwar, S.; Barnes, N. Densely residual laplacian super-resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1192–1204. [Google Scholar] [CrossRef]
- Yi, P.; Wang, Z.Y.; Jiang, K.; Jiang, J.J.; Lu, T.; Ma, J.Y. A progressive fusion generative adversarial network for realistic and consistent video super-resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 2264–2280. [Google Scholar] [CrossRef]
- Dong, R.M.; Zhang, L.X.; Fu, H.H. Rrsgan: Reference-based super-resolution for remote sensing image. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5601117. [Google Scholar] [CrossRef]
- Mei, S.H.; Yuan, X.; Ji, J.Y.; Zhang, Y.F.; Wan, S.; Du, Q. Hyperspectral image spatial super-resolution via 3d full convolutional neural network. Remote Sens. 2017, 9, 1139. [Google Scholar] [CrossRef]
- Wang, X.H.; Chen, J.; Wei, Q.; Richard, C. Hyperspectral image super-resolution via deep prior regularization with parameter estimation. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 1708–1723. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.M.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Loncan, L.; Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.Z.; Licciardi, G.A.; Simoes, M.; et al. Hyperspectral pansharpening: A review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Yasuma, F.; Mitsunaga, T.; Iso, D.; Nayar, S.K. Generalized assorted pixel camera: Postcapture control of resolution, dynamic range, and spectrum. IEEE Trans. Image Process. 2010, 19, 2241–2253. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Zickler, T. Statistics of real-world hyperspectral images. In In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; IEEE: Colorado Springs, CO, USA, 2011; pp. 193–200. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image-processing system (sips)—Interactive visualization and analysis of imaging spectrometer data. In Proceedings of the International Space Year Conference on Earth and Space Science Information Systems, Pasadena, CA, USA, 10–13 February 1992; Aip Press: Pasadena, CA, USA, 1993; pp. 192–201. [Google Scholar]
- Chang, C.-I. Spectral information divergence for hyperspectral image analysis. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium. IGARSS’99 (Cat. No. 99CH36293), Hamburg, Germany, 28 June–2 July 1999; IEEE: Piscataway Township, NJ, USA, 1999; pp. 509–511. [Google Scholar]
- Wald, L. Quality of high resolution synthesised images: Is there a simple criterion? In Proceedings of the Third conference Fusion of Earth data: Merging point measurements, raster maps and remotely sensed images, Sophia Antipolis, France, 26–28 January 2000; SEE/URISCA; pp. 99–103. [Google Scholar]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Gomez, R.B.; Jazaeri, A.; Kafatos, M. Wavelet-based hyperspectral and multispectral image fusion. In Proceedings of the Conference on Geo-Spatial Image and Data Exploitation II, Orlando, FL, USA, 16 April 2001; Spie-Int Soc Optical Engineering: Orlando, FL, USA, 2001; pp. 36–42. [Google Scholar]
- Zhang, Y.; He, M. Multi-spectral and hyperspectral image fusion using 3-d wavelet transform. J. Electron. 2007, 24, 218–224. [Google Scholar] [CrossRef]
- Zhang, Y.F.; De Backer, S.; Scheunders, P. Noise-resistant wavelet-based bayesian fusion of multispectral and hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3834–3843. [Google Scholar] [CrossRef]
- Patel, R.C.; Joshi, M.V. Super-resolution of hyperspectral images: Use of optimum wavelet filter coefficients and sparsity regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1728–1736. [Google Scholar] [CrossRef]
- Hardie, R.C.; Eismann, M.T.; Wilson, G.L. Map estimation for hyperspectral image resolution enhancement using an auxiliary sensor. IEEE Trans. Image Process. 2004, 13, 1174–1184. [Google Scholar] [CrossRef]
- Eismann, M.T.; Hardie, R.C. Application of the stochastic mixing model to hyperspectral resolution, enhancement. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1924–1933. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Zhang, L.P.; Shen, H.F. A super-resolution reconstruction algorithm for hyperspectral images. Signal Process. 2012, 92, 2082–2096. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral super-resolution by coupled spectral unmixing. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; IEEE: Santiago, Chile, 2015; pp. 3586–3594. [Google Scholar]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Bendoumi, M.A.; He, M.Y.; Mei, S.H. Hyperspectral image resolution enhancement using high-resolution multispectral image based on spectral unmixing. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6574–6583. [Google Scholar] [CrossRef]
- Yang, J.C.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Huang, B.; Song, H.H.; Cui, H.B.; Peng, J.G.; Xu, Z.B. Spatial and spectral image fusion using sparse matrix factorization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1693–1704. [Google Scholar] [CrossRef]
- Wycoff, E.; Chan, T.H.; Jia, K.; Ma, W.K.; Ma, Y. A non-negative sparse promoting algorithm for high resolution hyperspectral imaging. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; IEEE: Vancouver, BC, Canada, 2013; pp. 1409–1413. [Google Scholar]
- Akhtar, N.; Shafait, F.; Mian, A. Sparse spatio-spectral representation for hyperspectral image super-resolution. In Proceedings of the 13th European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; Springer International Publishing Ag: Zurich, Switzerland, 2014; pp. 63–78. [Google Scholar]
- Li, J.; Yuan, Q.Q.; Shen, H.F.; Meng, X.C.; Zhang, L.P. Hyperspectral image super-resolution by spectral mixture analysis and spatial-spectral group sparsity. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1250–1254. [Google Scholar] [CrossRef]
- Dong, W.S.; Fu, F.Z.; Shi, G.M.; Cao, X.; Wu, J.J.; Li, G.Y.; Li, X. Hyperspectral image super-resolution via non-negative structured sparse representation. IEEE Trans. Image Process. 2016, 25, 2337–2352. [Google Scholar] [CrossRef]
- Li, S.T.; Dian, R.W.; Fang, L.Y.; Bioucas-Dias, J.M. Fusing hyperspectral and multispectral images via coupled sparse tensor factorization. IEEE Trans. Image Process. 2018, 27, 4118–4130. [Google Scholar] [CrossRef]
- Veganzones, M.A.; Simoes, M.; Licciardi, G.; Yokoya, N.; Bioucas-Dias, J.M.; Chanussot, J. Hyperspectral super-resolution of locally low rank images from complementary multisource data. IEEE Trans. Image Process. 2016, 25, 274–288. [Google Scholar] [CrossRef]
- Kawakami, R.; Wright, J.; Tai, Y.W.; Matsushita, Y.; Ben-Ezra, M.; Ikeuchi, K. High-resolution hyperspectral imaging via matrix factorization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; IEEE: Colorado Springs, CO, USA, 2011; pp. 2329–2336. [Google Scholar]
- Dian, R.W.; Fang, L.Y.; Li, S.T. Hyperspectral image super-resolution via non-local sparse tensor factorization. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Honolulu, HI, USA, 2017; pp. 3862–3871. [Google Scholar]
- Zhang, L.; Wei, W.; Bai, C.C.; Gao, Y.F.; Zhang, Y.N. Exploiting clustering manifold structure for hyperspectral imagery super-resolution. IEEE Trans. Image Process. 2018, 27, 5969–5982. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Bayesian sparse representation for hyperspectral image super resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; IEEE: Boston, MA, USA, 2015; pp. 3631–3640. [Google Scholar]
- Akgun, T.; Altunbasak, Y.; Mersereau, R.M. Super-resolution reconstruction of hyperspectral images. IEEE Trans. Image Process. 2005, 14, 1860–1875. [Google Scholar] [CrossRef] [PubMed]
- He, S.Y.; Zhou, H.W.; Wang, Y.; Cao, W.F.; Han, Z. Super-resolution reconstruction of hyperspectral images via low rank tensor modeling and total variation regularization. In Proceedings of the 36th IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; IEEE: Beijing, China, 2016; pp. 6962–6965. [Google Scholar]
- Li, Y.; Zhang, L.; Ding, C.; Wei, W.; Zhang, Y.N. Single hyperspectral image super-resolution with grouped deep recursive residual network. In Proceedings of the 4th IEEE International Conference on Multimedia Big Data (BigMM), Xi’an, China, 13–16 September 2018; IEEE: Xi’an, China, 2018; pp. 1–4. [Google Scholar]
- Zhang, L.; Nie, J.T.; Wei, W.; Zhang, Y.N.; Liao, S.C.; Shao, L. Unsupervised adaptation learning for hyperspectral imagery super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Electr Network, Seattle, WA, USA, 2020, 14–19 June 2020; IEEE: Seattle, WA, USA, 2020; pp. 3070–3079. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X.O. Accelerating the super-resolution convolutional neural network. In Proceedings of the 14th European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; Springer International Publishing Ag: Amsterdam, The Netherlands, 2016; pp. 391–407. [Google Scholar]
- Shi, W.Z.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z.H. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 27–30 June 2016; IEEE: Seattle, WA, USA, 2016; pp. 1874–1883. [Google Scholar]
- Li, Q.; Wang, Q.; Li, X.L. Exploring the relationship between 2d/3d convolution for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8693–8703. [Google Scholar] [CrossRef]
- Jiang, R.T.; Li, X.; Gao, A.; Li, L.X.; Meng, H.Y.; Yue, S.G.; Zhang, L. Learning spectral and spatial features based on generative adversarial network for hyperspectral image super-resolution. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; IEEE: Yokohama, Japan, 2019; pp. 3161–3164. [Google Scholar]
- Li, Q.; Wang, Q.; Li, X.L. Mixed 2d/3d convolutional network for hyperspectral image super-resolution. Remote Sens. 2020, 12, 1660. [Google Scholar] [CrossRef]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5835–5843. [Google Scholar]
- Jiang, J.J.; Sun, H.; Liu, X.M.; Ma, J.Y. Learning spatial-spectral prior for super-resolution of hyperspectral imagery. IEEE Trans. Comput. Imaging 2020, 6, 1082–1096. [Google Scholar] [CrossRef]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Deep back-projection networks for super-resolution. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Salt Lake City, UT, USA, 2018; pp. 1664–1673. [Google Scholar]
- Hu, J.F.; Huang, T.Z.; Deng, L.J.; Jiang, T.X.; Vivone, G.; Chanussot, J. Hyperspectral image super-resolution via deep spatiospectral attention convolutional neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7251–7265. [Google Scholar] [CrossRef]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar]
- Ahn, N.; Kang, B.; Sohn, K.A. Fast, accurate, and lightweight super-resolution with cascading residual network. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer International Publishing Ag: Munich, Germany, 2018; pp. 256–272. [Google Scholar]
- Li, Z.; Yang, J.L.; Liu, Z.; Yang, X.M.; Jeon, G.; Wu, W.; Soc, I.C. Feedback network for image super-resolution. In Proceedings of the 32nd IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; Ieee Computer Soc: Long Beach, CA, USA, 2019; pp. 3862–3871. [Google Scholar]
- Wang, X.Y.; Hu, Q.; Jiang, J.J.; Ma, J.Y. A group-based embedding learning and integration network for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5541416. [Google Scholar] [CrossRef]
- Hu, J.; Li, Y.S.; Xie, W.Y. Hyperspectral image super-resolution by spectral difference learning and spatial error correction. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1825–1829. [Google Scholar] [CrossRef]
- Hu, J.; Jia, X.P.; Li, Y.S.; He, G.; Zhao, M.H. Hyperspectral image super-resolution via intrafusion network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7459–7471. [Google Scholar] [CrossRef]
- Liu, Y.T.; Hu, J.W.; Kang, X.D.; Luo, J.; Fan, S.S. Interactformer: Interactive transformer and cnn for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5531715. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Salt Lake City, UT, USA, 2018; pp. 7132–7141. [Google Scholar]
- Zhang, Y.L.; Li, K.P.; Li, K.; Wang, L.C.; Zhong, B.N.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer International Publishing Ag: Munich, Germany, 2018; pp. 294–310. [Google Scholar]
- Li, J.J.; Cui, R.X.; Li, B.; Song, R.; Li, Y.S.; Dai, Y.C.; Du, Q. Hyperspectral image super-resolution by band attention through adversarial learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4304–4318. [Google Scholar] [CrossRef]
- Zheng, Y.X.; Li, J.J.; Li, Y.S.; Guo, J.; Wu, X.Y.; Chanussot, J. Hyperspectral pansharpening using deep prior and dual attention residual network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8059–8076. [Google Scholar] [CrossRef]
- Liu, D.H.; Li, J.; Yuan, Q.Q. A spectral grouping and attention-driven residual dense network for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7711–7725. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Honolulu, HI, USA, 2017; pp. 2261–2269. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.J.; Gao, Q.Q. Image super-resolution using dense skip connections. In Proceedings of the 16th IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; IEEE: Venice, Italy, 2017; pp. 4809–4817. [Google Scholar]
- Zhang, Y.L.; Tian, Y.P.; Kong, Y.; Zhong, B.N.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Salt Lake City, UT, USA, 2018; pp. 2472–2481. [Google Scholar]
- Dong, W.Q.; Qu, J.H.; Zhang, T.Z.; Li, Y.S.; Du, Q. Context-aware guided attention based cross-feedback dense network for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5530814. [Google Scholar] [CrossRef]
- Hui, Z.; Wang, X.M.; Gao, X.B. Fast and accurate single image super-resolution via information distillation network. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Salt Lake City, UT, USA, 2018; pp. 723–731. [Google Scholar]
- Bruhn, A.; Weickert, J.; Schnorr, C. Lucas/kanade meets horn/schunck: Combining local and global optic flow methods. Int. J. Comput. Vis. 2005, 61, 211–231. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2014, 63, 139–144. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.H.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar]
- Sajjadi, M.S.M.; Scholkopf, B.; Hirsch, M. Enhancenet: Single image super-resolution through automated texture synthesis. In Proceedings of the 16th IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; IEEE: Venice, Italy, 2017; pp. 4501–4510. [Google Scholar]
- Aly, H.A.; Dubois, E. Image up-sampling using total-variation regularization with a new observation model. IEEE Trans. Image Process. 2005, 14, 1647–1659. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.; Alahi, A.; Li, F.F. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the14th European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; pp. 694–711. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. Arxiv 2014, arXiv:1409.1556. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the 16th IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar]
- Yuan, Y.; Liu, S.Y.; Zhang, J.W.; Zhang, Y.B.; Dong, C.; Lin, L. Unsupervised image super-resolution using cycle-in-cycle generative adversarial networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 814–823. [Google Scholar]
- Irani, M.; Peleg, S. Improving resolution by image registration. Cvgip-Graph. Model. Image Process. 1991, 53, 231–239. [Google Scholar] [CrossRef]
- Kim, K.I.; Kwon, Y. Single-image super-resolution using sparse regression and natural image prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1127–1133. [Google Scholar]
- Shan, Q.; Li, Z.R.; Jia, J.Y.; Tang, C.K. Fast image/video upsampling. ACM Trans. Graph. 2008, 27, 1–7. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.M. Image super-resolution via deep recursive residual network. In Proceedings of the30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2790–2798. [Google Scholar]
- Park, S.J.; Son, H.; Cho, S.; Hong, K.S.; Lee, S. Srfeat: Single image super-resolution with feature discrimination. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 455–471. [Google Scholar]
- Wang, X.T.; Yu, K.; Wu, S.X.; Gu, J.J.; Liu, Y.H.; Dong, C.; Qiao, Y.; Loy, C.C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 63–79. [Google Scholar]
- Bell-Kligler, S.; Shocher, A.; Irani, M. Blind super-resolution kernel estimation using an internal-gan. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Shocher, A.; Cohen, N.; Irani, M. "Zero-shot" super-resolution using deep internal learning. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 3118–3126. [Google Scholar]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. Multispectral and hyperspectral image fusion using a 3-d-convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 639–643. [Google Scholar] [CrossRef]
- Yang, J.X.; Zhao, Y.Q.; Chan, J.C.W. Hyperspectral and multispectral image fusion via deep two-branches convolutional neural network. Remote Sens. 2018, 10, 800. [Google Scholar] [CrossRef]
- Xu, S.; Amira, O.; Liu, J.M.; Zhang, C.X.; Zhang, J.S.; Li, G.H. Ham-mfn: Hyperspectral and multispectral image multiscale fusion network with rap loss. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4618–4628. [Google Scholar] [CrossRef]
- Dian, R.W.; Li, S.T.; Kang, X.D. Regularizing hyperspectral and multispectral image fusion by cnn denoiser. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1124–1135. [Google Scholar] [CrossRef]
- Zhang, L.; Nie, J.T.; Wei, W.; Li, Y.; Zhang, Y.N. Deep blind hyperspectral image super-resolution. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2388–2400. [Google Scholar] [CrossRef]
- Xie, Q.; Zhou, M.H.; Zhao, Q.; Xu, Z.B.; Meng, D.Y. Mhf-net: An interpretable deep network for multispectral and hyperspectral image fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1457–1473. [Google Scholar] [CrossRef]
- Qu, J.H.; Shi, Y.Z.; Xie, W.Y.; Li, Y.S.; Wu, X.Y.; Du, Q. Mssl: Hyperspectral and panchromatic images fusion via multiresolution spatialspectral feature learning networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5504113. [Google Scholar] [CrossRef]
- Guan, P.Y.; Lam, E.Y. Multistage dual-attention guided fusion network for hyperspectral pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5515214. [Google Scholar] [CrossRef]
- Guan, P.Y.; Lam, E.Y. Three-branch multilevel attentive fusion network for hyperspectral pansharpening. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 1087–1090. [Google Scholar]
- Zhuo, Y.W.; Zhang, T.J.; Hu, J.F.; Dou, H.X.; Huang, T.Z.; Deng, L.J. A deep-shallow fusion network with multidetail extractor and spectral attention for hyperspectral pansharpening. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 7539–7555. [Google Scholar] [CrossRef]
- Dong, W.Q.; Yang, Y.F.; Qu, J.H.; Xie, W.Y.; Li, Y.S. Fusion of hyperspectral and panchromatic images using generative adversarial network and image segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5508413. [Google Scholar] [CrossRef]
- Xie, W.Y.; Jia, X.P.; Li, Y.S.; Lei, J. Hyperspectral image super-resolution using deep feature matrix factorization. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6055–6067. [Google Scholar] [CrossRef]
- Sun, W.W.; Ren, K.; Meng, X.C.; Xiao, C.C.; Yang, G.; Peng, J.T. A band divide-and-conquer multispectral and hyperspectral image fusion method. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5502113. [Google Scholar] [CrossRef]
- Yuan, Y.; Zheng, X.T.; Lu, X.Q. Hyperspectral image superresolution by transfer learning. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 1963–1974. [Google Scholar] [CrossRef]
- Qu, Y.; Qi, H.R.; Kwan, C. Unsupervised sparse dirichlet-net for hyperspectral image super-resolution. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Salt Lake City, UT, USA, 2018; pp. 2511–2520. [Google Scholar]
- Zheng, K.; Gao, L.R.; Liao, W.Z.; Hong, D.F.; Zhang, B.; Cui, X.M.; Chanussot, J. Coupled convolutional neural network with adaptive response function learning for unsupervised hyperspectral super resolution. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2487–2502. [Google Scholar] [CrossRef]
- Xie, Q.; Zhou, M.H.; Zhao, Q.; Meng, D.Y.; Zuo, W.M.; Xu, Z.B.; Soc, I.C. Multispectral and hyperspectral image fusion by ms/hs fusion net. In Proceedings of the 32nd IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; Ieee Computer Soc: Long Beach, CA, USA, 2019; pp. 1585–1594. [Google Scholar]
- Wei, W.; Nie, J.T.; Zhang, L.; Zhang, Y.N. Unsupervised recurrent hyperspectral imagery super-resolution using pixel-aware refinement. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5500315. [Google Scholar] [CrossRef]
- Liu, J.J.; Wu, Z.B.; Xiao, L.; Wu, X.J. Model inspired autoencoder for unsupervised hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522412. [Google Scholar] [CrossRef]
- Liu, C.; Fan, Z.H.; Zhang, G.X. Gjtd-lr: A trainable grouped joint tensor dictionary with low-rank prior for single hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5537617. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Q.; Li, X.L. Hyperspectral image superresolution using spectrum and feature context. IEEE Trans. Ind. Electron. 2021, 68, 11276–11285. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Hou, J.H.; Chen, J.; Zeng, H.Q.; Zhou, J.T. Hyperspectral image super-resolution via deep progressive zero-centric residual learning. IEEE Trans. Image Process. 2021, 30, 1423–1438. [Google Scholar] [CrossRef]
- Arun, P.V.; Buddhiraju, K.M.; Porwal, A.; Chanussot, J. Cnn-based super-resolution of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6106–6121. [Google Scholar] [CrossRef]
- Chen, W.J.; Zheng, X.T.; Lu, X.Q. Hyperspectral image super-resolution with self-supervised spectral-spatial residual network. Remote Sens. 2021, 13, 1260. [Google Scholar] [CrossRef]
- Hu, J.F.; Huang, T.Z.; Deng, L.J.; Dou, H.X.; Hong, D.F.; Vivone, G. Fusformer: A transformer-based fusion network for hyperspectral image super-resolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6012305. [Google Scholar] [CrossRef]
- Li, J.J.; Cui, R.X.; Li, B.; Li, Y.S.; Mei, S.H.; Du, Q. Dual 1d-2d spatial-spectral cnn for hyperspectral image super-resolution. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; IEEE: Yokohama, Japan, 2019; pp. 3113–3116. [Google Scholar]
- Li, Q.; Gong, M.G.; Yuan, Y.; Wang, Q. Symmetrical feature propagation network for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536912. [Google Scholar] [CrossRef]
- Zhao, M.H.; Ning, J.W.; Hu, J.; Li, T.T. Hyperspectral image super-resolution under the guidance of deep gradient information. Remote Sens. 2021, 13, 2382. [Google Scholar] [CrossRef]
- Zhang, J.; Shao, M.H.; Wan, Z.K.; Li, Y.S. Multi-scale feature mapping network for hyperspectral image super-resolution. Remote Sens. 2021, 13, 4108. [Google Scholar] [CrossRef]
- Gong, Z.R.; Wang, N.N.; Cheng, D.; Jiang, X.R.; Xin, J.W.; Yang, X.; Gao, X.B. Learning deep resonant prior for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5532414. [Google Scholar] [CrossRef]




| Dataset | Amount | Size | Wavelength (nm) | Number of Bands | Sensor | Contents |
|---|---|---|---|---|---|---|
| CAVE | 32 | 512 × 512 | 400–700 | 31 | Apogee Alta U260 | Stuff, Skin and Hair, Paints, Food and Drinks, etc. |
| Harvard | 77 | 1392 × 1040 | 420–720 | 31 | Nuance FX | 50 daylight images and 27 additional images. |
| Pavia Centre | 1 | 1096 × 715 | 430–860 | 102 | ROSIS | Water, Trees, Asphalt, Self-Blocking Bricks, etc. |
| Pavia University | 1 | 610 × 340 | 430–860 | 103 | ROSIS | Gravel, Trees, Asphalt, Self-Blocking Bricks, etc. |
| Washington DC | 1 | 1208 × 307 | 400–2400 | 191 | HYDICE | Roofs, Streets, Gravel Roads, Grass, Trees, Shadows. |
| Houston | 1 | 1905 × 349 | 380–1050 | 144 | ITRES CASI-1500 | Healthy Grass, Stressed Grass, Trees, Soil, Water, etc. |
| Chikusei | 1 | 2517 × 2335 | 363–1018 | 128 | Headwall Hyperspec-VNIR-C | Water, Bare Soil, Grass, Forest, Row Crops, etc. |
| Scale Factor | Model | PSNR ↑ | SSIM ↑ | SAM ↓ | Running Time/Epoch |
|---|---|---|---|---|---|
| 2× | SRCNN-2D | 41.558 | 0.9874 | 3.247 | 13.21 |
| SRCNN-3D | 41.43 | 0.9884 | 2.811 | 98.33 | |
| 3× | SRCNN-2D | 37.243 | 0.9711 | 3.749 | 20.41 |
| SRCNN-3D | 36.692 | 0.9701 | 3.512 | 208.86 | |
| 4× | SRCNN-2D | 34.765 | 0.9523 | 4.199 | 33.96 |
| SRCNN-3D | 34.265 | 0.9507 | 3.982 | 363.42 | |
| 2× | FSRCNN-2D | 40.849 | 0.9862 | 3.627 | 14 |
| FSRCNN-3D | 40.327 | 0.9865 | 3.152 | 21.26 | |
| 3× | FSRCNN-2D | 37.244 | 0.9704 | 4.188 | 16.18 |
| FSRCNN-3D | 36.716 | 0.9696 | 3.802 | 24.19 | |
| 4× | FSRCNN-2D | 34.928 | 0.9532 | 4.677 | 19.19 |
| FSRCNN-3D | 34.291 | 0.9492 | 4.614 | 28.08 | |
| 2× | ESPCN-2D | 42.083 | 0.9889 | 3.05 | 10.975 |
| ESPCN-3D1 | 25.989 | 0.8397 | 20.482 | 28.51 | |
| ESPCN-3D2 | 30.804 | 0.923 | 10.12 | 78.87 | |
| ESPCN-3D3 | 34.68 | 0.9617 | 6.778 | 142.52 | |
| 3× | ESPCN-2D | 37.491 | 0.9726 | 3.66 | 14.145 |
| ESPCN-3D1 | 24.728 | 0.7698 | 23.887 | 30.65 | |
| ESPCN-3D2 | 28.928 | 0.8653 | 13.11 | 81.435 | |
| ESPCN-3D3 | 32.455 | 0.9254 | 8.549 | 139.155 | |
| 4× | ESPCN-2D | 35.024 | 0.9556 | 4.121 | 19.76 |
| ESPCN-3D1 | 24.545 | 0.7322 | 23.641 | 35.865 | |
| ESPCN-3D2 | 28.307 | 0.8312 | 14.354 | 85.545 | |
| ESPCN-3D3 | 31.303 | 0.9009 | 10.087 | 143.045 |
| Scale Factor | Model | PSNR ↑ | SSIM ↑ | SAM ↓ | Running Time/Epoch |
|---|---|---|---|---|---|
| 2× | FCNN-2D | 36.026 | 0.9614 | 4.841 | 30 |
| FCNN-3D | 34.296 | 0.9481 | 4.823 | 206.74 | |
| 3× | FCNN-2D | 31.184 | 0.8909 | 6.076 | 43.72 |
| FCNN-3D | 30.258 | 0.8695 | 6.039 | 413.2 | |
| 4× | FCNN-2D | 28.015 | 0.7896 | 7.578 | 115.56 |
| FCNN-3D | 27.865 | 0.7793 | 7.378 | 800.12 | |
| 2× | ERCSR-2D | 34.602 | 0.9524 | 5.081 | 13.95 |
| ERCSR-3D | 33.856 | 0.9452 | 5.166 | 104.99 | |
| 3× | ERCSR-2D | 30.58 | 0.8788 | 6.507 | 16.13 |
| ERCSR-3D | 30.405 | 0.8803 | 6.246 | 121.8 | |
| 4× | ERCSR-2D | 28.419 | 0.8049 | 7.763 | 21.96 |
| ERCSR-3D | 28.275 | 0.7979 | 7.326 | 150.32 |
| Method | Uf. | Um. | Res. | Rec. | Mul. | Att. | Den. | 2D | 3D | Keywords |
|---|---|---|---|---|---|---|---|---|---|---|
| 3D-FCNN [18] | Front. | Bic. | √ | 3D Convolution | ||||||
| GDRRN [56] | Front. | Bic. | √ | √ | √ | Recursive Blocks | ||||
| HSRGAN [61] | Back. | Sub. | √ | √ | √ | Generative Adversarial Network | ||||
| SSPSR [64] | Pro. | Sub. | √ | √ | √ | √ | Spatial–Spectral Prior | |||
| MCNet [62] | Back. | Dec. | √ | √ | √ | √ | Mixed 2D/3D Convolution | |||
| BASR [77] | Back. | Dec. | √ | √ | √ | Band Attention | ||||
| ERCSR [60] | Back. | Dec. | √ | √ | √ | Split Adjacent Spatial and Spectral Convolution | ||||
| SGARDN [79] | Back. | Dec. | √ | √ | √ | √ | √ | Group Convolution | ||
| Interactformer [74] | Back. | Dec. | √ | √ | √ | √ | Transformer | |||
| GELIN [71] | Back. | Dec. | √ | √ | √ | Neighboring-Group Integration | ||||
| DRPSR [132] | Pro. | Bil. | √ | √ | √ | Deep Resonant Prior |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Wang, Y.; Zhang, N.; Zhang, Y.; Zhao, Z. A Review of Hyperspectral Image Super-Resolution Based on Deep Learning. Remote Sens. 2023, 15, 2853. https://doi.org/10.3390/rs15112853
Chen C, Wang Y, Zhang N, Zhang Y, Zhao Z. A Review of Hyperspectral Image Super-Resolution Based on Deep Learning. Remote Sensing. 2023; 15(11):2853. https://doi.org/10.3390/rs15112853
Chicago/Turabian StyleChen, Chi, Yongcheng Wang, Ning Zhang, Yuxi Zhang, and Zhikang Zhao. 2023. "A Review of Hyperspectral Image Super-Resolution Based on Deep Learning" Remote Sensing 15, no. 11: 2853. https://doi.org/10.3390/rs15112853
APA StyleChen, C., Wang, Y., Zhang, N., Zhang, Y., & Zhao, Z. (2023). A Review of Hyperspectral Image Super-Resolution Based on Deep Learning. Remote Sensing, 15(11), 2853. https://doi.org/10.3390/rs15112853







