A Novel Fast Sparse Bayesian Learning STAP Algorithm for Conformal Array Radar
Abstract
1. Introduction
- (1)
- The concept of conjugate function will be introduced to make up a surrogate function for the SBL cost function. The STAP performance is similar to the conventional SBL method, and converges faster. Meanwhile, the proposed method has lower computational burden than the SBL and FCSBL methods.
- (2)
- The proposed method obtains the hyper-parameter by iteratively minimizing the surrogate function. For each minimizing step, a close-form solution can be achieved, which will guarantee the convergence.
- (3)
- The extension of the novel SBL method to the multiple measurement vector (MMV) condition is rather straightforward.
- (4)
- Detailed comparison of clutter suppression performance and Capon spectrum between the proposed method and other STAP algorithms are expressed.
2. Signal Model and SR-STAP Model and Principle
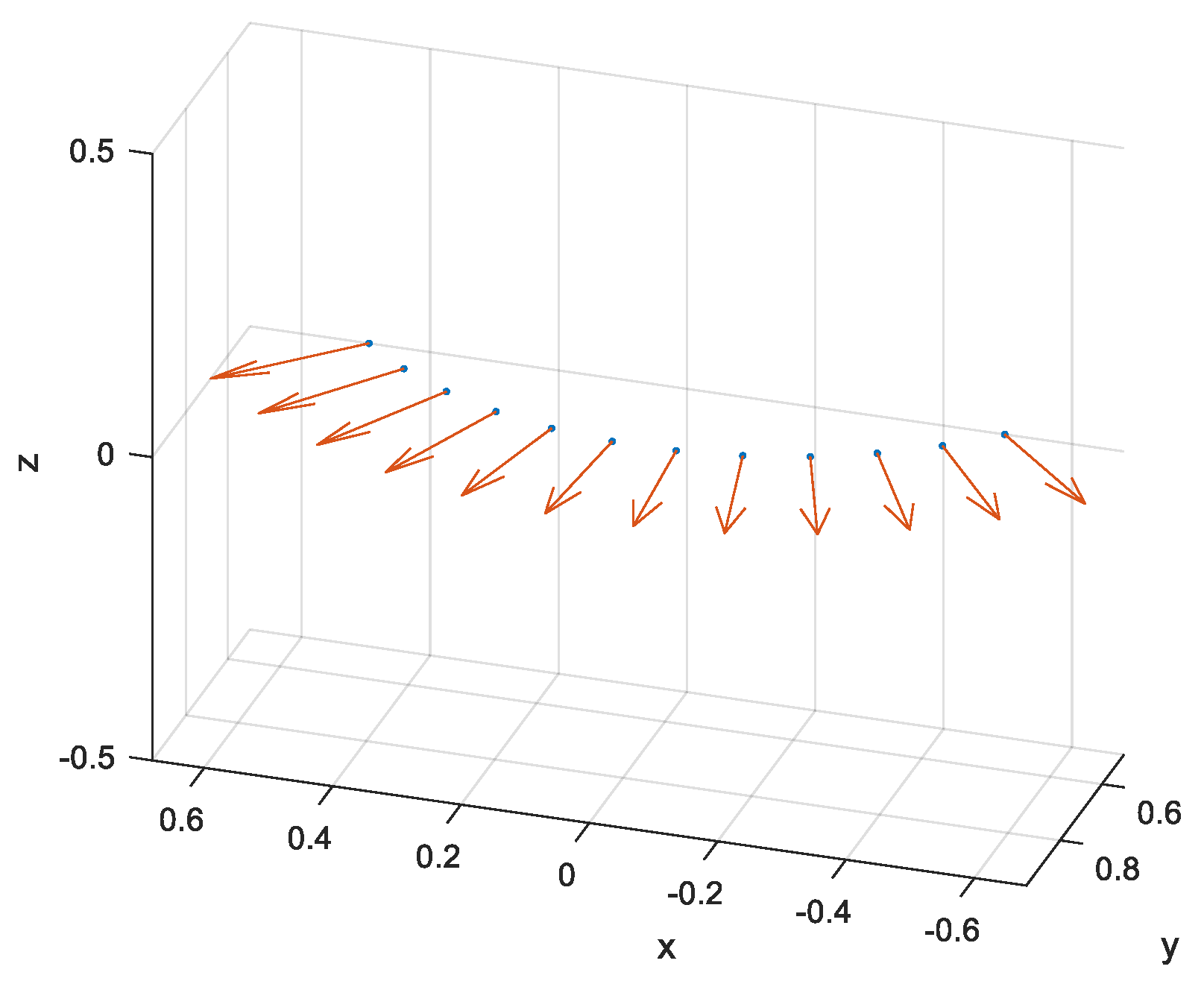
2.1. Signal Model
2.2. SR-STAP Formulation
3. The Proposed Method
3.1. Derivation of the Proposed Method
3.2. The Estimation of
- The number of iterations reaches the upper limit.
- The estimate of hyper-parameter meet , where is a small positive number.
| Algorithm 1: NFSBL Method | |
| Step 1 | Input data and dictionary matrix |
| Step 2 | Initialize and |
| Step 3 | Update the mean vector using (32) |
| Step 4 | Update and using (54) and (55), respectively |
| Step 5 | Repeat step 3–4 until the convergence criterion is met |
| Step 6 | Calculate CNCM |
| Step 7 | Compute STAP weight |
3.3. Extension to the MMV Case
| Algorithm 2: M-NFSBL Method | |
| Step 1 | Input data and dictionary matrix |
| Step 2 | Initialize and |
| Step 3 | Update the mean matrix using (58) |
| Step 4 | Update and using (59) and (60), respectively |
| Step 5 | Repeat steps 3–4 until the convergence criterion is met |
| Step 6 | Calculate CNCM |
| Step 7 | Compute STAP weight |
4. Discussion
4.1. Complexity Analysis
4.2. Convergence Analysis
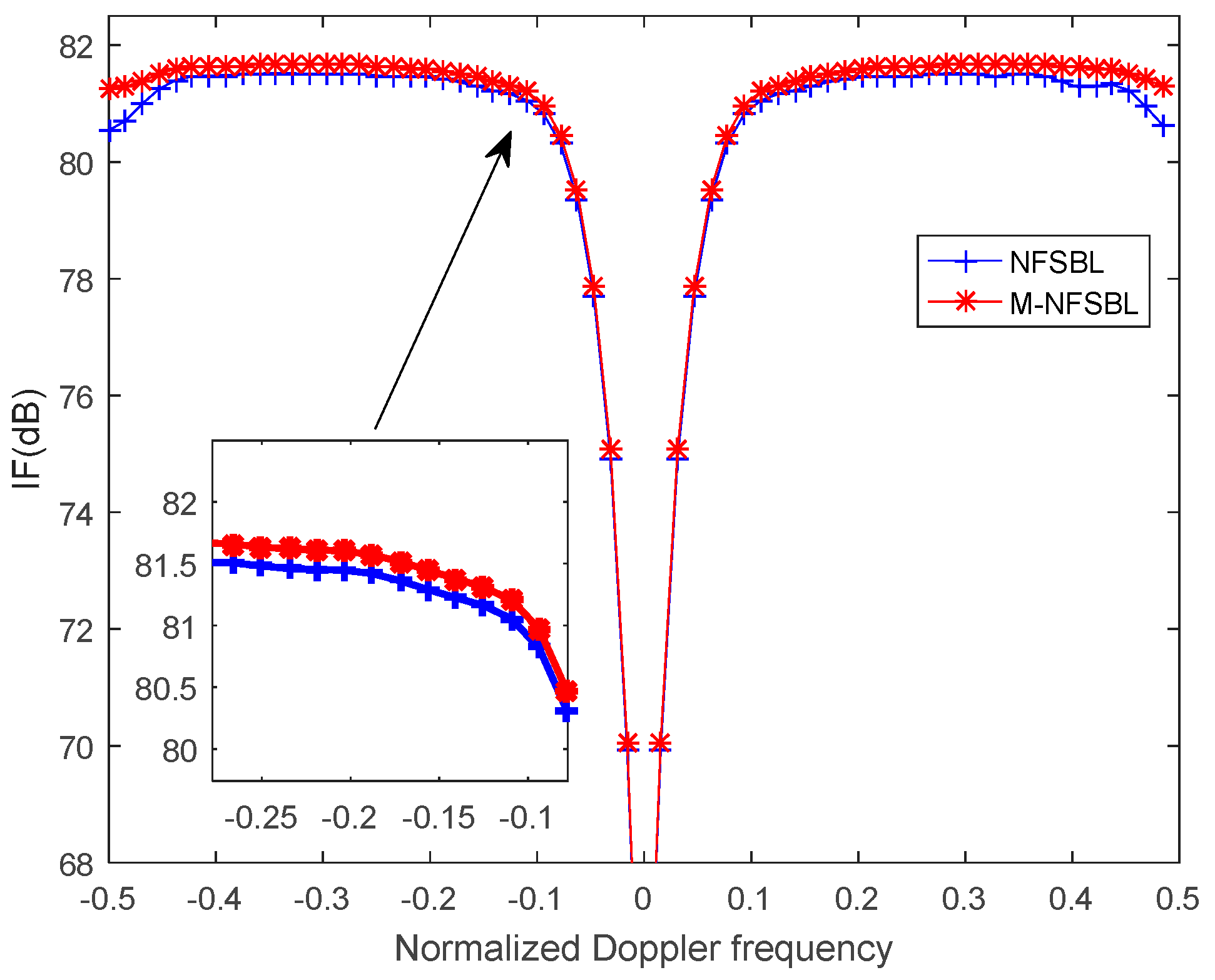
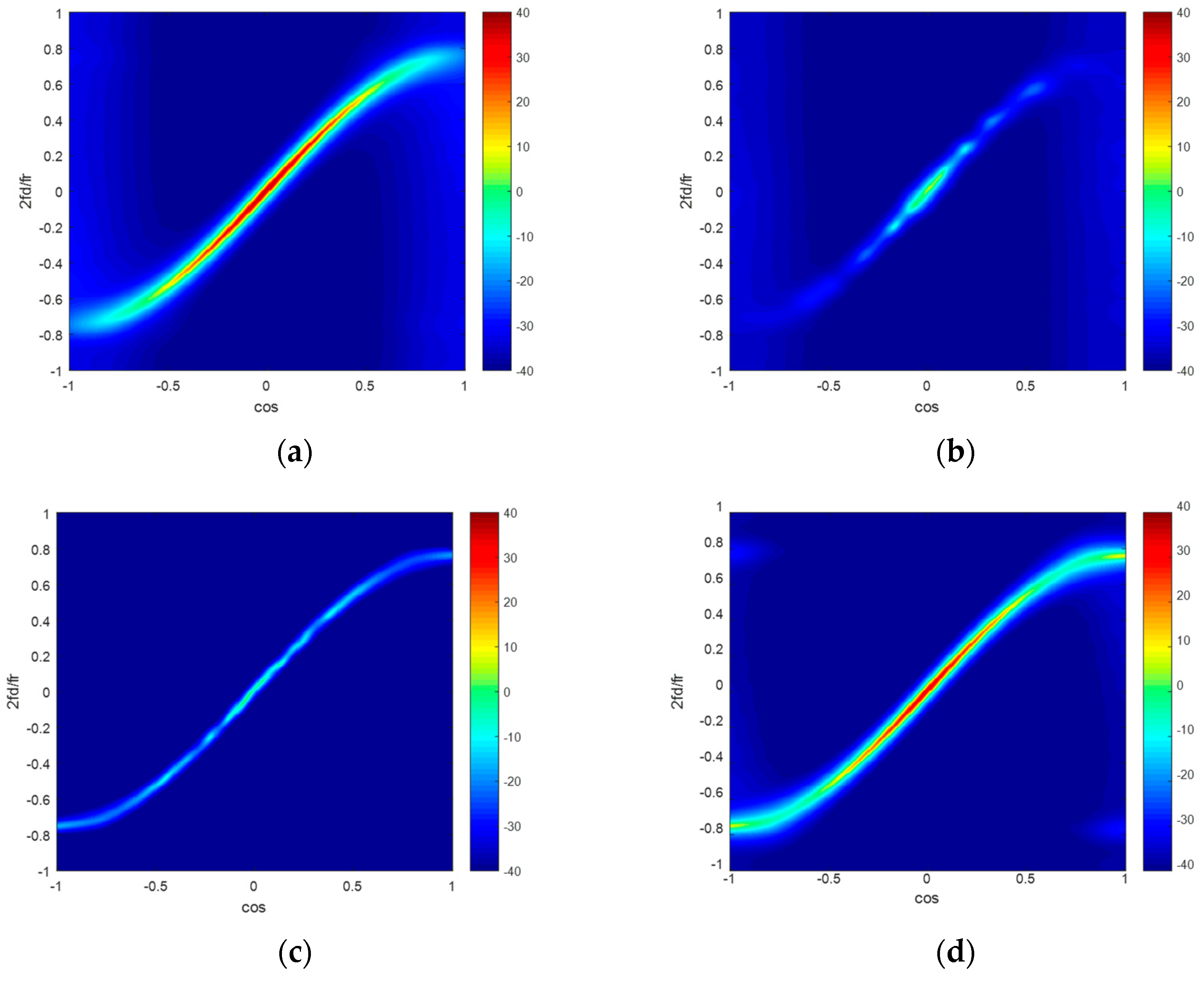
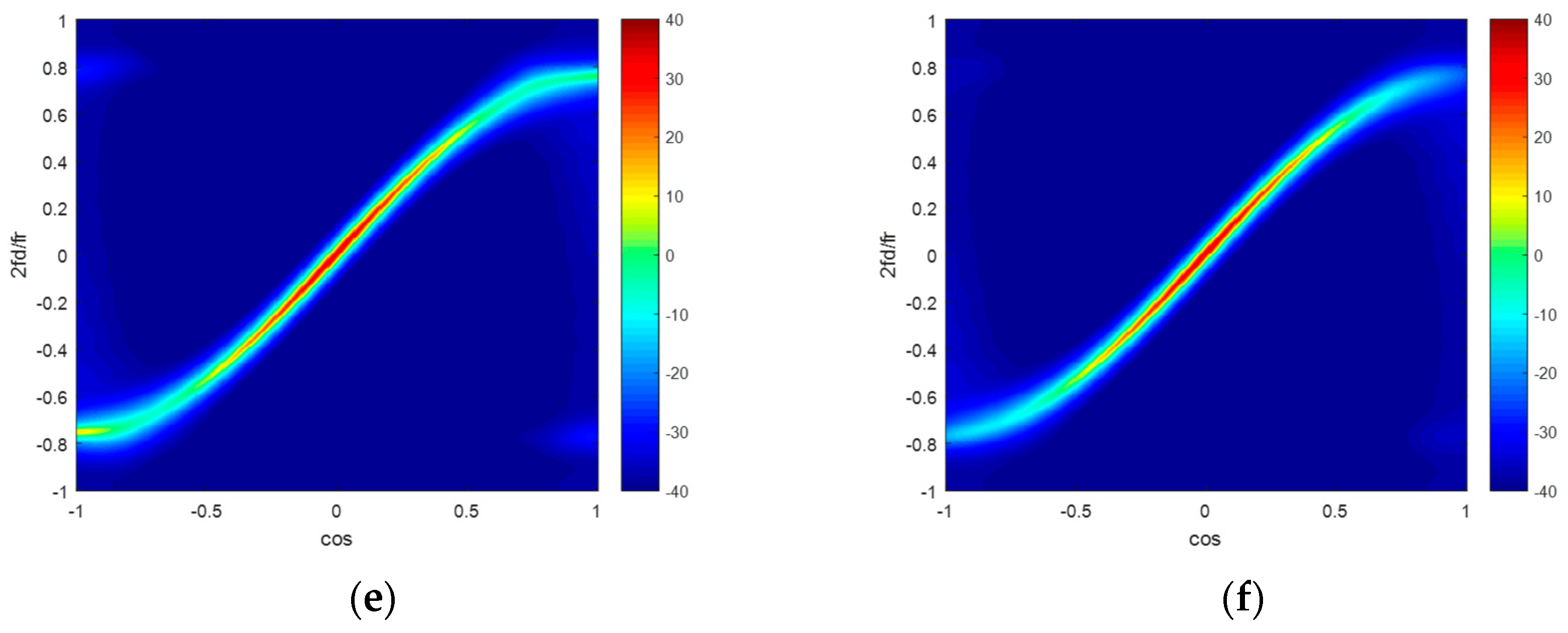
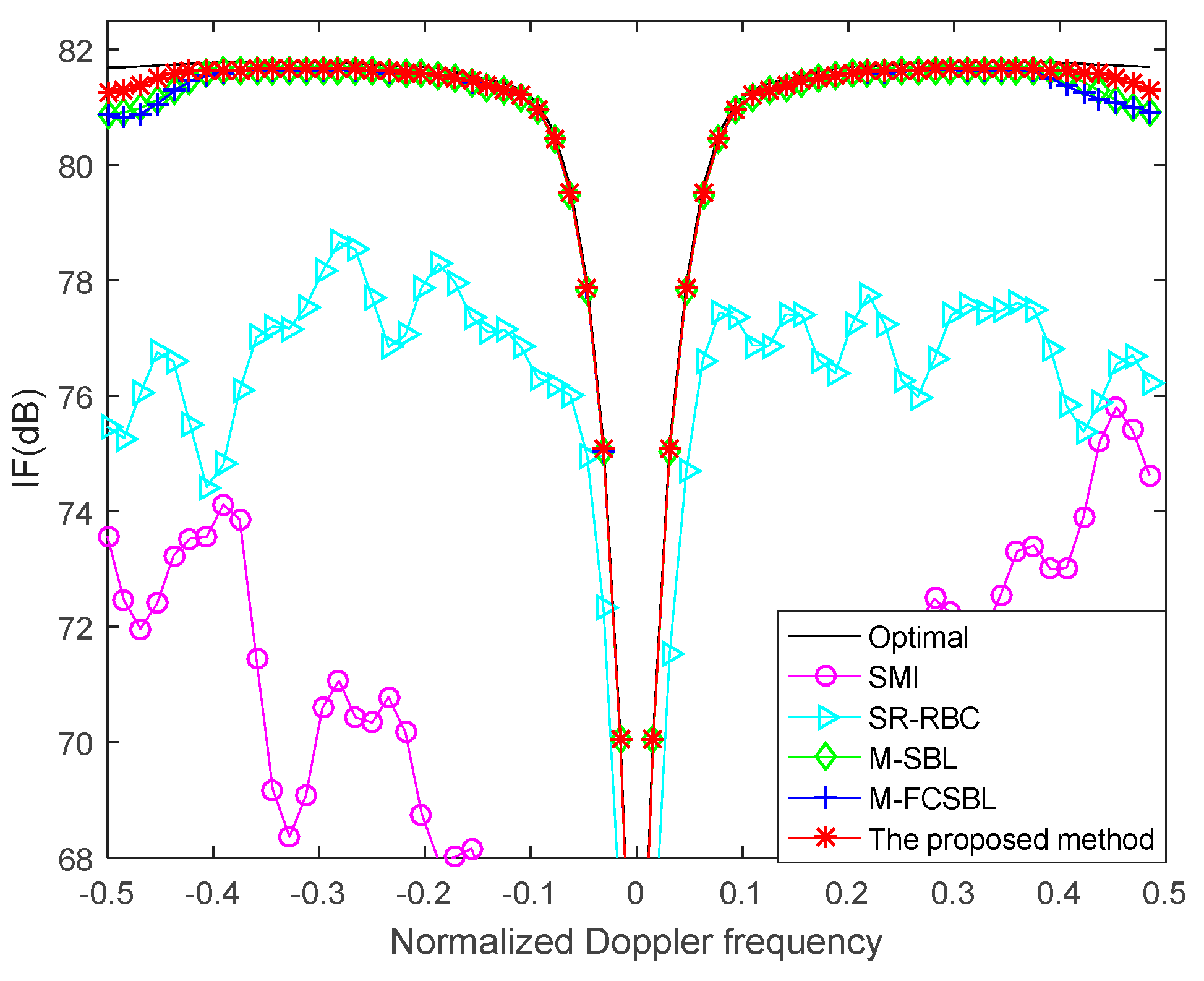
5. Simulation Results
5.1. Ideal Condition
5.2. Non-Ideal Condition
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hersey, R.K.; Melvin, W.L.; McClellan, J.H.; Culpepper, E. Adaptive ground clutter suppression for conformal array radar systems. IET Radar Sonar Navig. 2009, 3, 357–372. [Google Scholar] [CrossRef]
- Ward, J. Space-Time Adaptive Processing for Airborne Radar; Technical Report, 1015; MIT Lincoln Laboratory: Lexington, MA, USA, 1994. [Google Scholar]
- Klemm, R. Principles of Space-Time Adaptive Processing, 3rd ed.; IET: London, UK, 2006. [Google Scholar]
- Wu, Y.F.; Wang, T.; Wu, J.X. Robust training samples selection algorithm based on spectral similarity for space-time adaptive processing in heterogeneous interference environments. IET Radar Sonar Navig. 2015, 9, 778–782. [Google Scholar]
- Reed, I.S.; Mallett, J.D.; Brennan, L.E. Rapid convergence rate in adaptive arrays. IEEE Trans. Aerosp. Electron. Syst. 1974, 10, 853–863. [Google Scholar] [CrossRef]
- Klemm, R. The Applications of Space-Time Adaptive Processing, 2nd ed.; IEE Press: Stevenage, UK, 2004. [Google Scholar]
- Himed, B.; Zhang, Y.; Hajjari, A. STAP with angle-Doppler compensation for bistatic airborne radars. In Proceedings of the IEEE National Radar Conference, Long Beach, CA, USA, 25 April 2002. [Google Scholar]
- Melvin, W.; Himed, B.; Davis, M. Doubly adaptive bistatic clutter filtering. In Proceedings of the IEEE National Radar Conference, Hunstville, AL, USA, 8 May 2003. [Google Scholar]
- Melvin, W.; Davis, M. Adaptive cancellation method for geometry-induced nonstationary bistatic clutter environment. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 651–672. [Google Scholar] [CrossRef]
- Han, X.; Luo, T.; Yu, W.; Wu, M. Space-time adaptive processing for airborne radar with conformal array. In Proceedings of the IET International Radar Conference, Hangzhou, China, 14–16 October 2015; pp. 5–10. [Google Scholar]
- Varadarajan, V.; Krolik, J.L. Joint space-time interpolation for distorted linear and bistatic array geometries. IEEE Trans. Signal Process. 2006, 56, 848–860. [Google Scholar] [CrossRef]
- Ries, P.; Lapierre, F.D.; Verly, J.G. Geometry-induced range-dependence compensation for bistatic STAP with conformal arrays. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 275–294. [Google Scholar] [CrossRef]
- Klemm, R. Adaptive airborne MTI: An auxiliary channel approach. IEEE Proc. F Commun. Radar Signal Process. 1987, 134, 269–276. [Google Scholar] [CrossRef]
- Wang, Y.X.; Li, X.M.; Gao, W. Dimension-reduced bi-iterative space-time adaptive processing method for airborne radar. J. Eng. 2019, 2019, 8138–8141. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.; Yang, J.X. Reduced-dimension space-time adaptive processing for airborne radar with co-prime array. J. Eng. 2019, 2019, 5971–5974. [Google Scholar] [CrossRef]
- Hua, Y.; Nikpour, M.; Stoica, P. Optimal reduced rank estimation and filtering. IEEE Trans. Signal Process. 2001, 49, 457–469. [Google Scholar]
- Sarkar, T.K. A deterministic least-squares approach to space-time adaptive processing (STAP). IEEE Trans. Antennas Propag. 2001, 49, 91–103. [Google Scholar] [CrossRef]
- Melvin, W.L.; Showman, G.A. An approach to knowledge-aided covariance estimation. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1021–1042. [Google Scholar] [CrossRef]
- Wicks, M.C.; Rangaswamy, M.; Adve, R.; Hale, T.B. Space-time adaptive processing: A knowledge-based perspective for airborne radar. IEEE Signal Process. Mag. 2006, 23, 51–65. [Google Scholar] [CrossRef]
- Yang, Z.C.; Li, X.; Wang, H.Q.; Jiang, W.D. On clutter sparsity analysis in space-time adaptive processing airborne radar. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1215–1218. [Google Scholar]
- Sen, S. Low-rank matrix decomposition and spatio-temporal sparse recovery for STAP radar. IEEE J. Sel. Top. Signal Process. 2015, 9, 1510–1523. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Candés, E. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Sun, K.; Meng, H.D.; Fabian, D.L. Registration-based compensation using sparse representation in conformal-array STAP. Signal Process. 2011, 91, 2268–2276. [Google Scholar] [CrossRef]
- Tao, F.Y.; Wang, T.; Wu, J.X.; Su, Y.Y. A knowledge aided SPICE space time adaptive processing method for airborne radar with conformal array. Signal Process. 2018, 152, 54–62. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. 2001, 1, 211–244. [Google Scholar]
- Wipf, D.P.; Rao, B.D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem. IEEE Trans. Signal Process. 2007, 55, 3704–3716. [Google Scholar] [CrossRef]
- Wang, Z.T.; Xie, W.C.; Duan, K.Q.; Wang, Y.L. Clutter suppression algorithm based on fast converging sparse Bayesian learning for airborne radar. Signal Process. 2017, 130, 159–168. [Google Scholar] [CrossRef]
- Ren, B.; Wang, T. Space-time adaptive processing based on modified sparse learning via iterative minimization for conformal array radar. Sensors 2022, 22, 6917. [Google Scholar] [CrossRef] [PubMed]
- Burger, H.A. Use of Euler-Rotation angles for generating antenna patterns. IEEE Antennas Propag. Mag. 1995, 37, 56–63. [Google Scholar] [CrossRef]
- Milligan, T. More applications of Euler rotation angles. IEEE Antennas Propag. Mag. 1999, 41, 78–83. [Google Scholar] [CrossRef]
- Zhuang, Z.W. Radar Polarization Information Processing and Application, 1st ed.; National Defense Industrial Press: Beijing, China, 1999. [Google Scholar]
- Wipf, D.; Nagarajan, S. A new view of automatic relevance determination. In Advances in Neural Information Processing Systems 20; MIT Press: New York, NY, USA, 2008. [Google Scholar]





| Algorithm | Computational Load for an Iteration |
|---|---|
| M-CVX | |
| M-SBL | |
| M-FCSBL | |
| M-NFSBL |
| Parameter | Value | Unit |
|---|---|---|
| Pulse number | 16 | - |
| Element number | 12 | - |
| Platform velocity | 200 | m/s |
| Wavelength | 0.2 | m |
| Bandwidth | 5 | MHz |
| CNR | 60 | dB |
| Distance between elements | 0.1 | m |
| Pulse repetition frequency | 5000 | Hz |
| Platform height | 3000 | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, B.; Wang, T. A Novel Fast Sparse Bayesian Learning STAP Algorithm for Conformal Array Radar. Remote Sens. 2023, 15, 2824. https://doi.org/10.3390/rs15112824
Ren B, Wang T. A Novel Fast Sparse Bayesian Learning STAP Algorithm for Conformal Array Radar. Remote Sensing. 2023; 15(11):2824. https://doi.org/10.3390/rs15112824
Chicago/Turabian StyleRen, Bing, and Tong Wang. 2023. "A Novel Fast Sparse Bayesian Learning STAP Algorithm for Conformal Array Radar" Remote Sensing 15, no. 11: 2824. https://doi.org/10.3390/rs15112824
APA StyleRen, B., & Wang, T. (2023). A Novel Fast Sparse Bayesian Learning STAP Algorithm for Conformal Array Radar. Remote Sensing, 15(11), 2824. https://doi.org/10.3390/rs15112824





