A High Spatiotemporal Enhancement Method of Forest Vegetation Leaf Area Index Based on Landsat8 OLI and GF-1 WFV Data
Abstract
1. Introduction
2. Materials and Methods
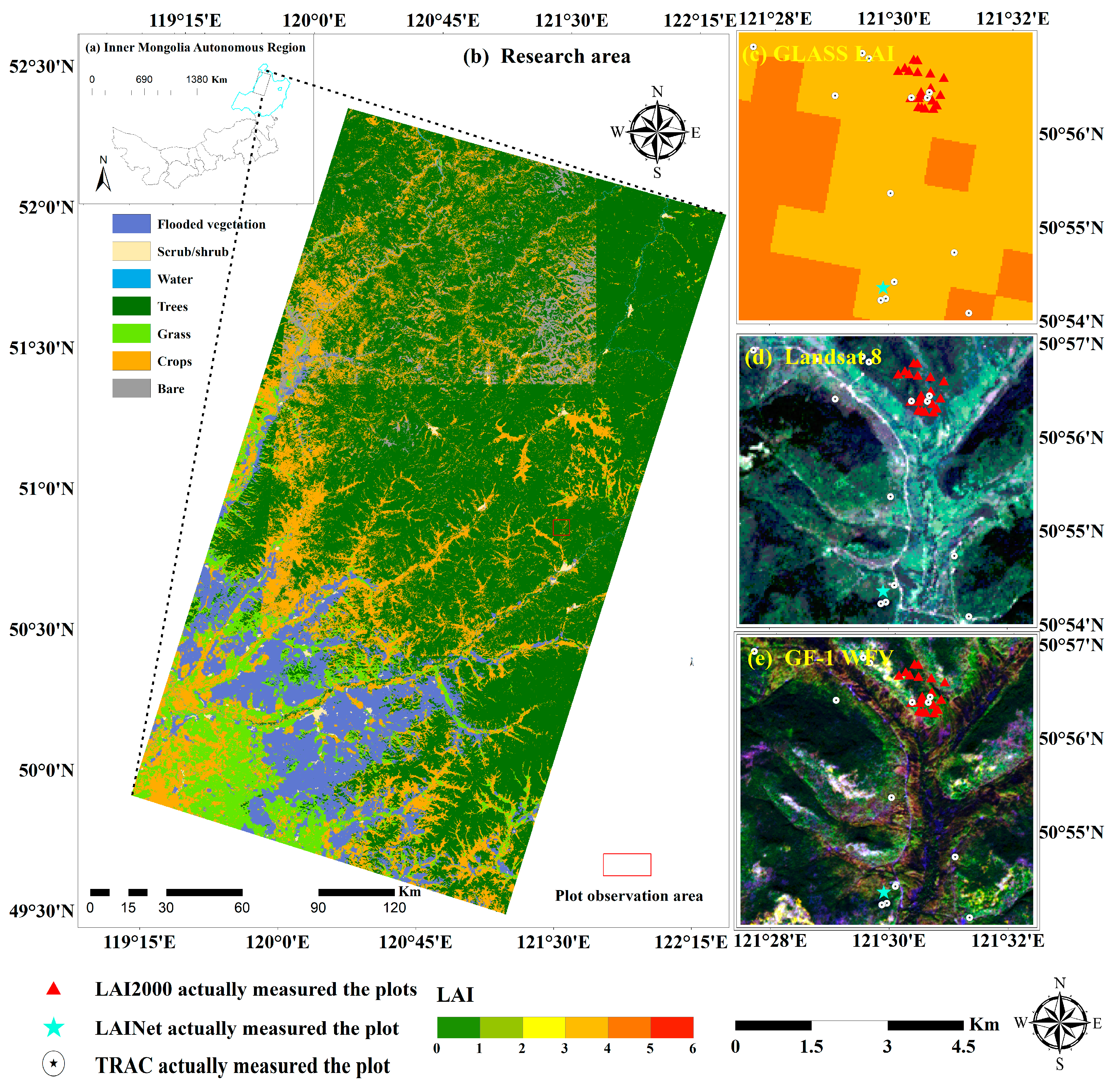
2.1. Study Area
2.2. Datasets and Processing
2.2.1. Satellite Data
2.2.2. Field Measurements Using LAI Datasets
2.2.3. Remote Sensing Image Dataset Preprocessing
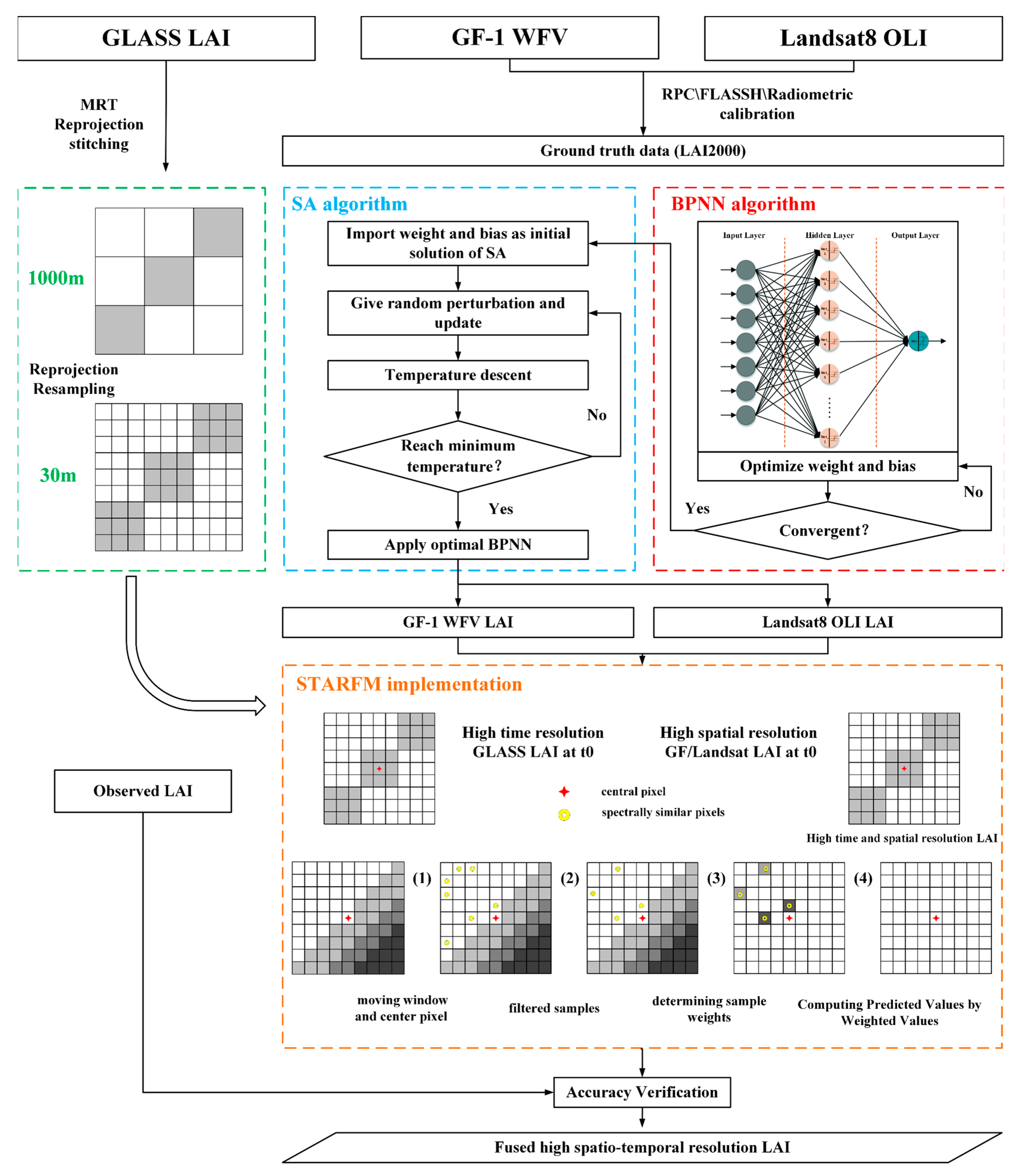
2.3. LAI Data Fusion Based on the STARFM Model
- (1)
- The acquisition and preprocessing: acquisition and preprocessing of remote sensing image data and verification data;
- (2)
- GF-1 WFV and Landsat8 OLI images, along with ground-measured LAI-2000 data, were preprocessed and used to train the SA-BPNN model. The model was then utilized to estimate LAI for GF-1 WFV (2013, 2016, and 2017) and Landsat8 OLI (2014 and 2015) images;
- (3)
- The estimated GF-1 WFV LAI and Landsat8 OLI LAI were fused with GLASS LAI (2013~2017) using the STARFM model to obtain an LAI with high temporal and spatial resolution in the study area;
- (4)
- The fused high-temporal and high-spatial-resolution LAI was verified using LAINet, TRAC LAI, and LAI-2200 data from the plot survey. The technology roadmap is shown in Figure 2.
2.3.1. LAI Estimation Model
- (1)
- Initialization: Initialize the weights and thresholds of the BPNN and set the initial temperature, cooling rate, and termination temperature;
- (2)
- Input samples: Input the samples into the BPNN and calculate the output;
- (3)
- Calculate the error: Calculate the error between the output and the expected output;
- (4)
- Update weights and thresholds: Update the weights and thresholds of the BPNN based on the error to reduce it;
- (5)
- Determine whether to accept: According to the principle of simulated annealing, calculate the difference between the new error and the old error, as well as the current temperature, to determine whether to accept the new solution;
- (6)
- Cooling: Reduce the temperature according to the set cooling rate;
- (7)
- Determine whether to stop: When the temperature reaches the set termination temperature or other stopping conditions are met, the algorithm stops and outputs the final BPNN model.
2.3.2. Spatiotemporal Adaptive Reflectance Fusion Model (STARFM)
- At time t0, the smaller the 0-spectrum difference between the data, the greater the weight of the corresponding position, and the formula is:
- The smaller the time difference between the input GLASS LAI at time and the predicted LAI at time , the greater the weight of its corresponding position. The formula is:
- The closer the distance between the central pixel (, ) in the moving window and the central pixel in the period, the greater the weight. The formula is:
2.4. Accuracy Assessment
3. Results and Analysis
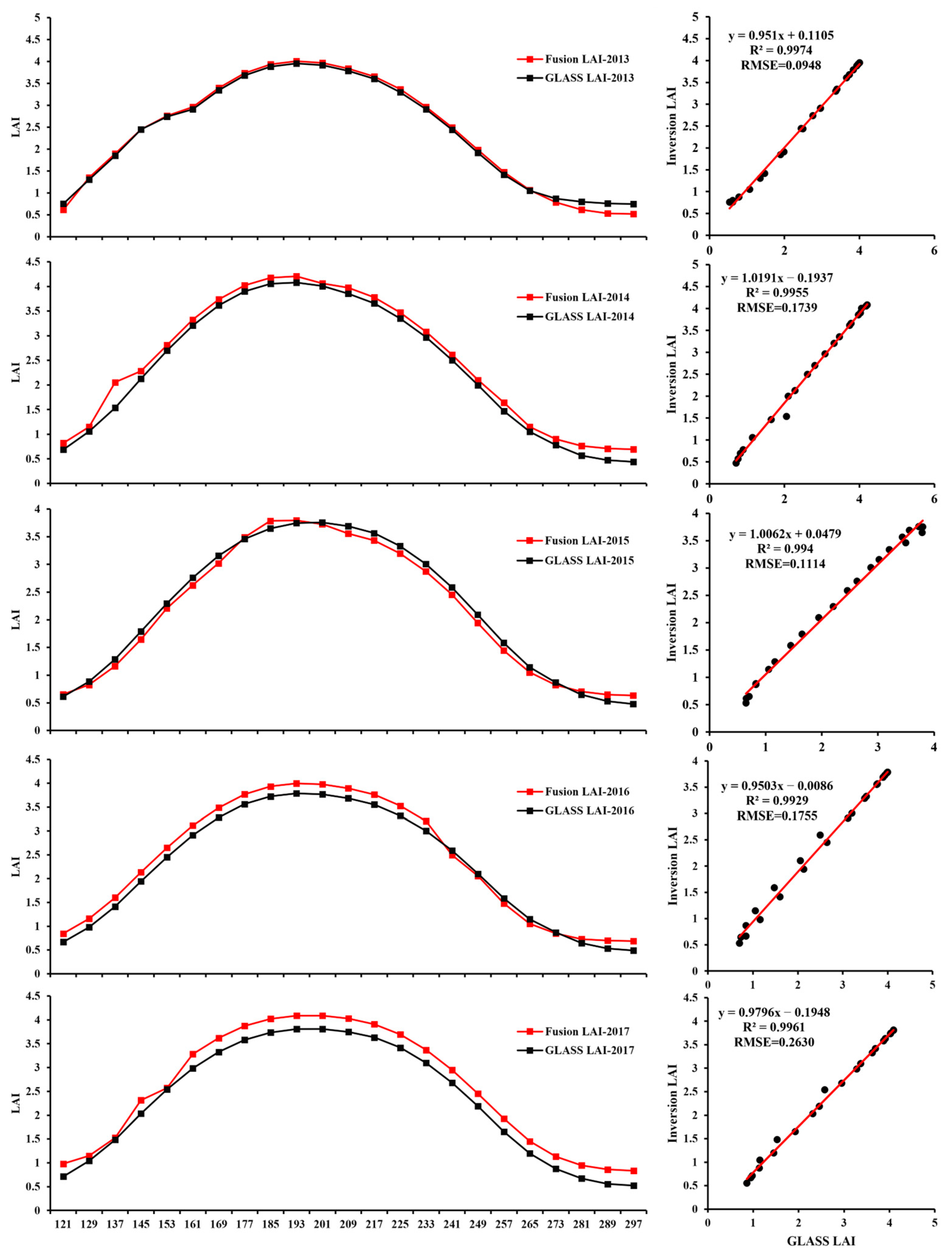
3.1. Inversion LAI Based on SA-BPNN Model
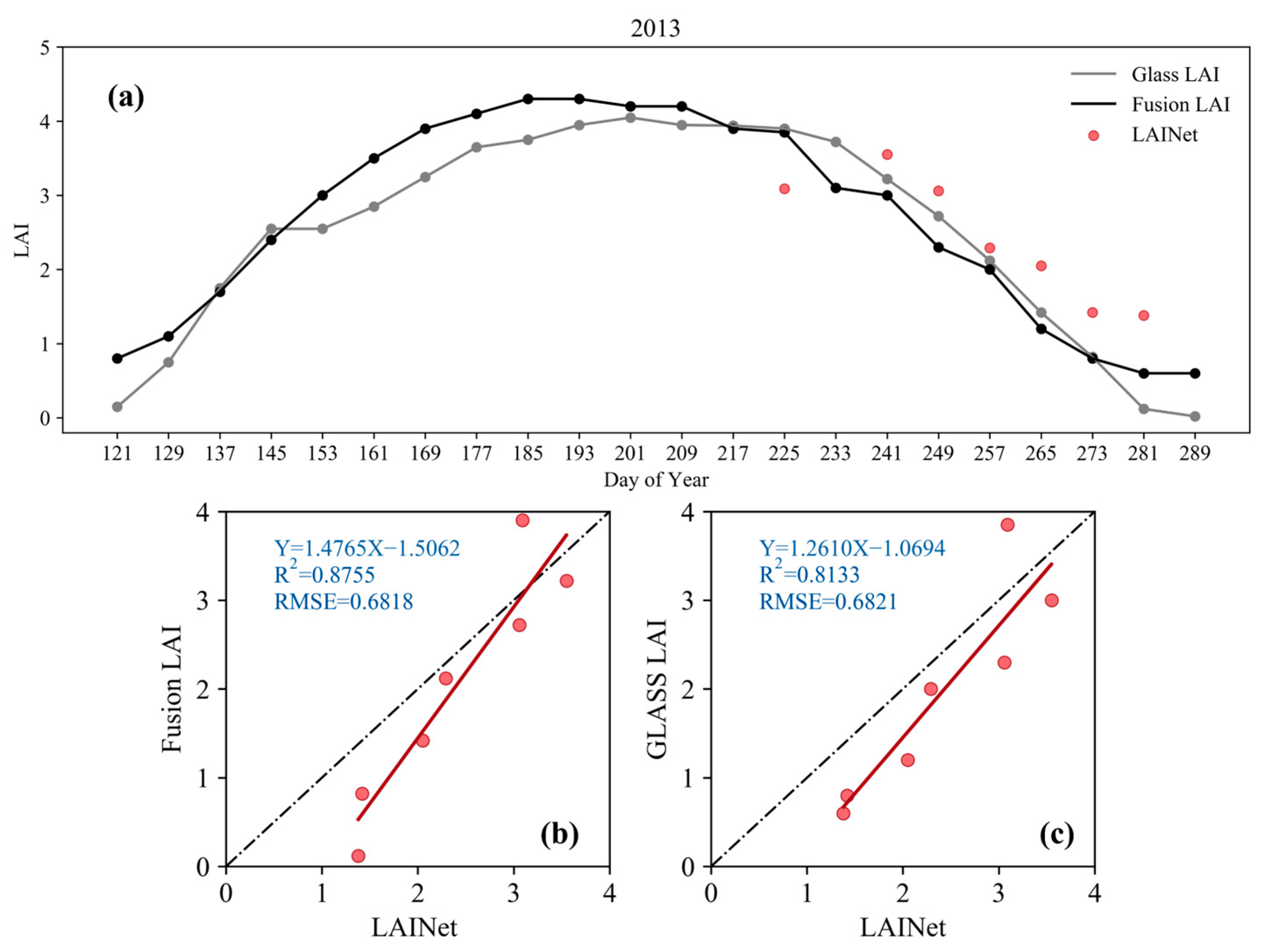
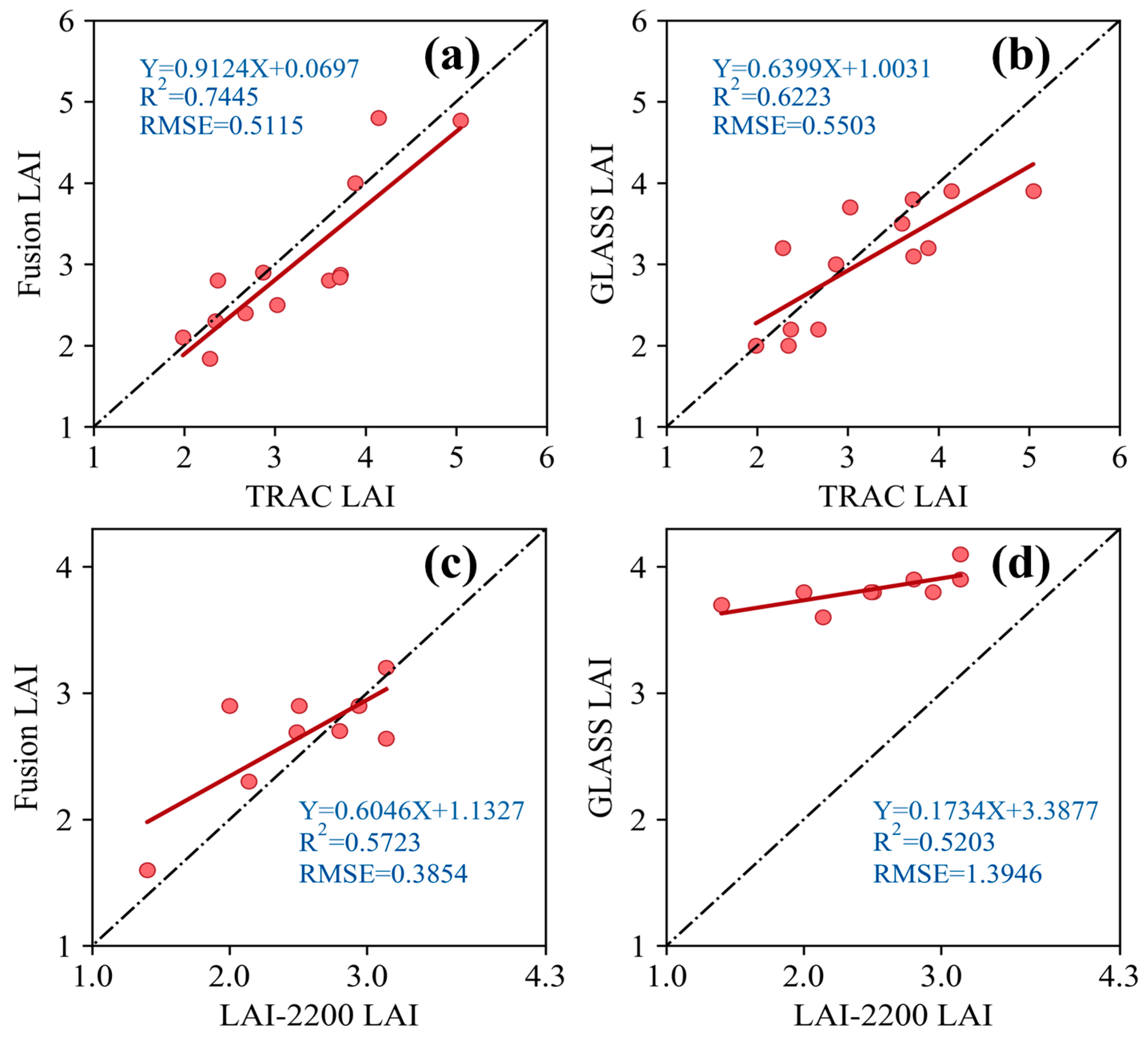
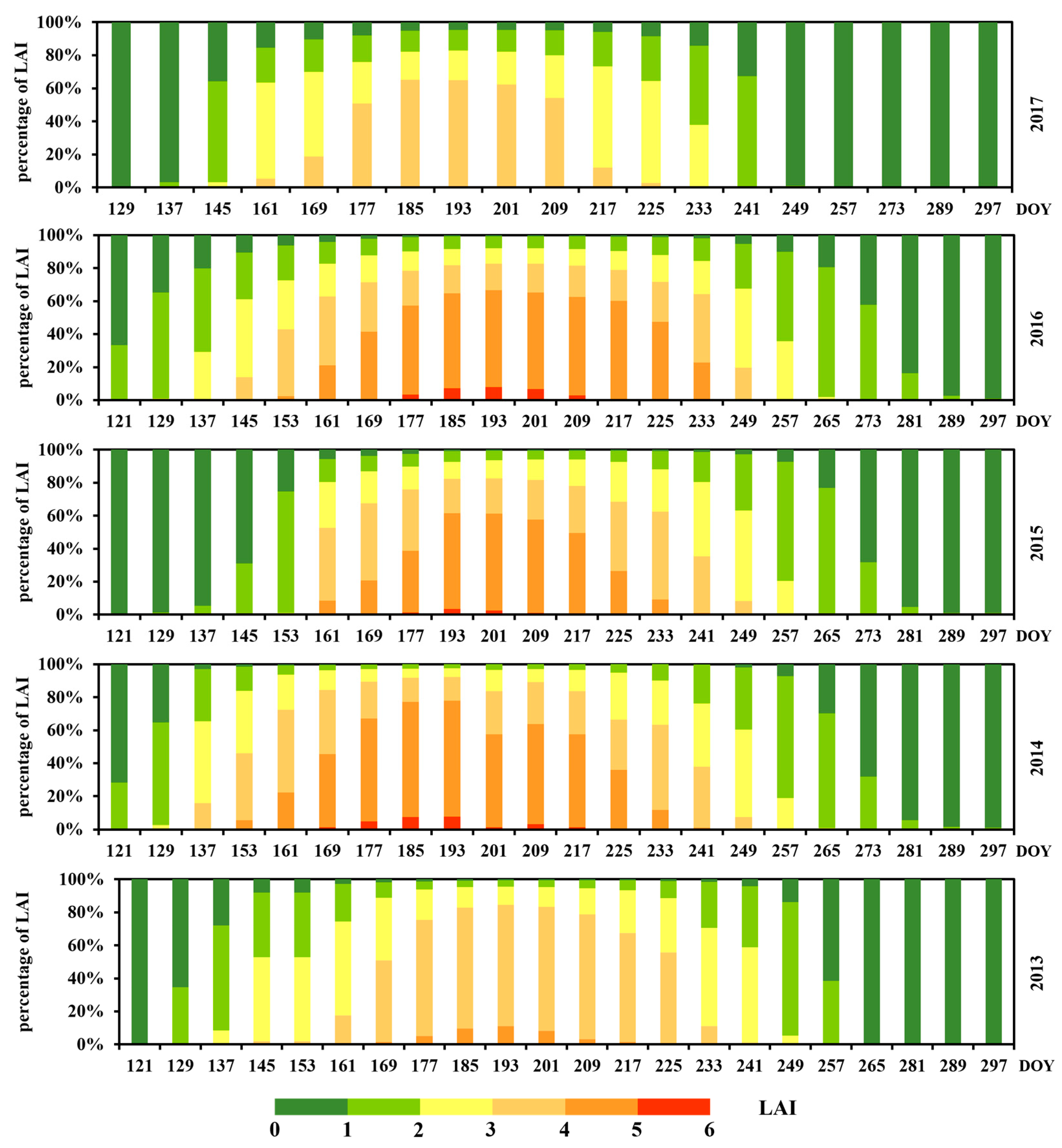
3.2. Time Series of LAI Assimilation
3.3. Spatiotemporal Distribution of LAI Enhancement Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.M.; Black, T.A. Defining Leaf Area Index for Non-Flat Leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Bonan, G.B. Importance of Leaf Area Index and Forest Type When Estimating Photosynthesis in Boreal Forests. Remote Sens. Environ. 1993, 43, 303–314. [Google Scholar] [CrossRef]
- Asner, G.P.; Scurlock, J.M.O.; Hicke, J.A. Global Synthesis of Leaf Area Index Observations: Implications for Ecological and Remote Sensing Studies. Glob. Ecol. Biogeogr. 2003, 12, 191–205. [Google Scholar] [CrossRef]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the Exchanges of Energy, Water, and Carbon Between Continents and the Atmosphere. Science 1997, 275, 502–509. Available online: https://www.science.org/doi/abs/10.1126/science.275.5299.502 (accessed on 30 November 2022). [CrossRef]
- Colombo, R.; Bellingeri, D.; Fasolini, D.; Marino, C.M. Retrieval of Leaf Area Index in Different Vegetation Types Using High Resolution Satellite Data. Remote Sens. Environ. 2003, 86, 120–131. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F.; Gao, F. A Spatio-Temporal Enhancement Method for Medium Resolution LAI (STEM-LAI). Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 15–29. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; García-Haro, F.J.; Camps-Valls, G.; Grau-Muedra, G.; Nutini, F.; Crema, A.; Boschetti, M. Multitemporal and Multiresolution Leaf Area Index Retrieval for Operational Local Rice Crop Monitoring. Remote Sens. Environ. 2016, 187, 102–118. [Google Scholar] [CrossRef]
- Xu, J.; Quackenbush, L.J.; Volk, T.A.; Im, J. Forest and Crop Leaf Area Index Estimation Using Remote Sensing: Research Trends and Future Directions. Remote Sens. 2020, 12, 2934. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep Learning Classifiers for Hyperspectral Imaging: A Review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, J.; Chen, C.; Tian, X. NDVI-Net: A Fusion Network for Generating High-Resolution Normalized Difference Vegetation Index in Remote Sensing. ISPRS J. Photogramm. Remote Sens. 2020, 168, 182–196. [Google Scholar] [CrossRef]
- Wang, W.; Ma, Y.; Meng, X.; Sun, L.; Jia, C.; Jin, S.; Li, H. Retrieval of the Leaf Area Index from MODIS Top-of-Atmosphere Reflectance Data Using a Neural Network Supported by Simulation Data. Remote Sens. 2022, 14, 2456. [Google Scholar] [CrossRef]
- Nandan, R.; Bandaru, V.; He, J.; Daughtry, C.; Gowda, P.; Suyker, A.E. Evaluating Optical Remote Sensing Methods for Estimating Leaf Area Index for Corn and Soybean. Remote Sens. 2022, 14, 5301. [Google Scholar] [CrossRef]
- Zhang, G.; Ma, H.; Liang, S.; Jia, A.; He, T.; Wang, D. A Machine Learning Method Trained by Radiative Transfer Model Inversion for Generating Seven Global Land and Atmospheric Estimates from VIIRS Top-of-Atmosphere Observations. Remote Sens. Environ. 2022, 279, 113132. [Google Scholar] [CrossRef]
- Li, J.; Xiao, Z.; Sun, R.; Song, J. Retrieval of the Leaf Area Index from Visible Infrared Imaging Radiometer Suite (VIIRS) Surface Reflectance Based on Unsupervised Domain Adaptation. Remote Sens. 2022, 14, 1826. [Google Scholar] [CrossRef]
- Min, Y.; Jie, L.; Gu, Z.; Tong, G.; Yongbing, W.; Zhang, J.; Lu, X. Leaf Area Index Retrieval Based on Landsat 8 OLI Multi-Spectral Image Data and BP Neural Network. Sswcc 2015, 8, 86–93. [Google Scholar]
- Zhu, D.E.; Xu, X.J.; Du, H.Q.; Zhou, G.M.; Mao, F.J.; Li, X.J.; Li, Y.G. Retrieval of leaf area index of Phyllostachys praecox forest based on MODIS reflectance time series data. J. Appl. Ecol. 2018, 29, 2391–2400. [Google Scholar] [CrossRef]
- Liu, B.; Wang, R.; Zhao, G.; Guo, X.; Wang, Y.; Li, J.; Wang, S. Prediction of Rock Mass Parameters in the TBM Tunnel Based on BP Neural Network Integrated Simulated Annealing Algorithm. Tunn. Undergr. Space Technol. 2020, 95, 103103. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, C.; Zhang, G.; Xue, H.; Wang, J.; Wan, H. Generating a Spatio-Temporal Complete 30 m Leaf Area Index from Field and Remote Sensing Data. Remote Sens. 2020, 12, 2394. [Google Scholar] [CrossRef]
- Li, K.; Zhang, W.; Yu, D.; Tian, X. HyperNet: A Deep Network for Hyperspectral, Multispectral, and Panchromatic Image Fusion. ISPRS J. Photogramm. Remote Sens. 2022, 188, 30–44. [Google Scholar] [CrossRef]
- Liu, P.; Li, J.; Wang, L.; He, G. Remote Sensing Data Fusion With Generative Adversarial Networks: State-of-the-Art Methods and Future Research Directions. IEEE Geosci. Remote Sens. Mag. 2022, 10, 295–328. [Google Scholar] [CrossRef]
- Xu, F.; Liu, J.; Song, Y.; Sun, H.; Wang, X. Multi-Exposure Image Fusion Techniques: A Comprehensive Review. Remote Sens. 2022, 14, 771. [Google Scholar] [CrossRef]
- Azarang, A.; Kehtarnavaz, N. A Generative Model Method for Unsupervised Multispectral Image Fusion in Remote Sensing. SIViP 2022, 16, 63–71. [Google Scholar] [CrossRef]
- Wen, J.; Wu, X.; You, D.; Ma, X.; Ma, D.; Wang, J.; Xiao, Q. The Main Inherent Uncertainty Sources in Trend Estimation Based on Satellite Remote Sensing Data. Appl. Clim. 2022, 151, 915–934. [Google Scholar] [CrossRef]
- Wen, J.; Wu, X.; Wang, J.; Tang, R.; Ma, D.; Zeng, Q.; Gong, B.; Xiao, Q. Characterizing the Effect of Spatial Heterogeneity and the Deployment of Sampled Plots on the Uncertainty of Ground “Truth” on a Coarse Grid Scale: Case Study for Near-Infrared (NIR) Surface Reflectance. J. Geophys. Res. Atmos. 2022, 127, e2022JD036779. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the Blending of the Landsat and MODIS Surface Reflectance: Predicting Daily Landsat Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Gevaert, C.M.; García-Haro, F.J. A Comparison of STARFM and an Unmixing-Based Algorithm for Landsat and MODIS Data Fusion. Remote Sens. Environ. 2015, 156, 34–44. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, J. Fusion of Spatiotemporal Remote sensing Data for Changing Surface Characteristics. J. Beijing Norm. Univ. (Nat. Sci.) 2017, 53, 727–734. [Google Scholar]
- Tao, G.; Jia, K.; Zhao, X.; Wei, X.; Xie, X.; Zhang, X.; Wang, B.; Yao, Y.; Zhang, X. Generating High Spatio-Temporal Resolution Fractional Vegetation Cover by Fusing GF-1 WFV and MODIS Data. Remote Sens. 2019, 11, 2324. [Google Scholar] [CrossRef]
- Wang, S.; Yang, X.; Li, G.; Jin, Y.; Tian, C. Research on Spatio-Temporal Fusion Algorithm of Remote Sensing Image Based on GF-1 WFV and Sentinel-2 Satellite Data. In Proceedings of the 2022 3rd International Conference on Geology, Mapping and Remote Sensing (ICGMRS), Zhousan, China, 22–24 April 2022; pp. 667–678. [Google Scholar]
- Wen, J.; Lin, X.; Wu, X.; Bao, Y.; You, D.; Gong, B.; Tang, Y.; Wu, S.; Xiao, Q.; Liu, Q. Validation of the MCD43A3 Collection 6 and GLASS V04 Snow-Free Albedo Products Over Rugged Terrain. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Chen, B.; Xu, B.; Zhu, Z.; Yuan, C.; Suen, H.P.; Guo, J.; Xu, N.; Li, W.; Zhao, Y.; Yang, J. Stable Classification with Limited Sample: Transferring a 30-m Resolution Sample Set Collected in 2015 to Mapping 10-m Resolution Global Land Cover in 2017. Sci. Bull. 2019, 64, 370–373. [Google Scholar] [CrossRef]
- Xiang, Y.; Xiao, Z.Q.; Liang, S.; Wang, J.D.; Song, J.L. Validation of Global LAnd Surface Satellite (GLASS) Leaf Area Index Product. J. Remote Sens. 2014, 18, 573–596. [Google Scholar] [CrossRef]
- Singla, J.G.; Trivedi, S. Generation of State of the Art Very High Resolution DSM over Hilly Terrain Using Cartosat-2 Multi-View Data, Its Comparison and Evaluation–A Case Study near Alwar Region. J. Geomat. 2022, 16, 23–32. [Google Scholar]
- Li, X.; Wang, T.; Cui, H.; Zhang, G.; Cheng, Q.; Dong, T.; Jiang, B. SARPointNet: An Automated Feature Learning Framework for Spaceborne SAR Image Registration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6371–6381. [Google Scholar] [CrossRef]
- Bin, W.; Ming, L.; Dan, J.; Suju, L.; Qiang, C.; Chao, W.; Yang, Z.; Huan, Y.; Jun, Z. A Method of Automatically Extracting Forest Fire Burned Areas Using Gf-1 Remote Sensing Images. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July 2019; pp. 9953–9955. [Google Scholar]
- Kong, Z.; Yang, H.; Zheng, F.; Yang, Z.; Li, Y.; Qi, J. Atmospheric Correction Assessment for GF-1 WFV. In Proceedings of the International Conference on Environmental Remote Sensing and Big Data (ERSBD 2021), Wuhan, China, 9 December 2021; SPIE: Bellingham, WA, USA, 2021; Volume 12129, pp. 270–275. [Google Scholar]
- Han, W.; Chen, D.; Li, H.; Chang, Z.; Chen, J.; Ye, L.; Liu, S.; Wang, Z. Spatiotemporal Variation of NDVI in Anhui Province from 2001 to 2019 and Its Response to Climatic Factors. Forests 2022, 13, 1643. [Google Scholar] [CrossRef]
- Li, S.; Zhang, R.; Xie, L.; Zhan, J.; Song, Y.; Zhan, R.; Shama, A.; Wang, T. A Factor Analysis Backpropagation Neural Network Model for Vegetation Net Primary Productivity Time Series Estimation in Western Sichuan. Remote Sens. 2022, 14, 3961. [Google Scholar] [CrossRef]
- Hecht-nielsen, R. III.3–Theory of the Backpropagation Neural Network. In Neural Networks for Perception; Wechsler, H., Ed.; Academic Press: Cambridge, MA, USA, 1992; pp. 65–93. ISBN 978-0-12-741252-8. [Google Scholar]
- Zhang, Y.; Hu, Q.; Li, H.; Li, J.; Liu, T.; Chen, Y.; Ai, M.; Dong, J. A Back Propagation Neural Network-Based Radiometric Correction Method (BPNNRCM) for UAV Multispectral Image. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 112–125. [Google Scholar] [CrossRef]
- Fan, Y.; Li, G.; Wu, J. Research on Monitoring Overground Carbon Stock of Forest Vegetation Communities Based on Remote Sensing Technology. Proc. Indian Natl. Sci. Acad. 2022, 88, 705–713. [Google Scholar] [CrossRef]
- Smith, J.A. LAI Inversion Using a Back-Propagation Neural Network Trained with a Multiple Scattering Model. IEEE Trans. Geosci. Remote Sens. 1993, 31, 1102–1106. [Google Scholar] [CrossRef]
- Li, L.; Chen, Y.; Xu, T.; Liu, R.; Shi, K.; Huang, C. Super-Resolution Mapping of Wetland Inundation from Remote Sensing Imagery Based on Integration of Back-Propagation Neural Network and Genetic Algorithm. Remote Sens. Environ. 2015, 164, 142–154. [Google Scholar] [CrossRef]
- Xu, S.; Li, S.; Tao, Z.; Song, K.; Wen, Z.; Li, Y.; Chen, F. Remote Sensing of Chlorophyll-a in Xinkai Lake Using Machine Learning and GF-6 WFV Images. Remote Sens. 2022, 14, 5136. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, R.; Guo, J.; Yi, S.; Meng, B.; Liu, J. Vegetation Coverage in the Desert Area of the Junggar Basin of Xinjiang, China, Based on Unmanned Aerial Vehicle Technology and Multisource Data. Remote Sens. 2022, 14, 5146. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Li, J.; Tian, L.; Wang, Y.; Jin, S.; Li, T.; Hou, X. Optimal Sampling Strategy of Water Quality Monitoring at High Dynamic Lakes: A Remote Sensing and Spatial Simulated Annealing Integrated Approach. Sci. Total Environ. 2021, 777, 146113. [Google Scholar] [CrossRef]
- Yang, P.; Hu, J.; Hu, B.; Luo, D.; Peng, J. Estimating Soil Organic Matter Content in Desert Areas Using In Situ Hyperspectral Data and Feature Variable Selection Algorithms in Southern Xinjiang, China. Remote Sens. 2022, 14, 5221. [Google Scholar] [CrossRef]
- Xue, H.; Wang, C.; Zhou, H.; Wang, J.; Wan, H. BP Neural Network Based on Simulated Annealing Algorithm for High Resolution LAI Retrieval. Remote Sens. Technol. Appl. 2020, 35, 1057–1069. [Google Scholar]
- Cao, Y.; Du, P.; Zhang, M.; Bai, X.; Lei, R.; Yang, X. Quantitative Evaluation of Grassland SOS Estimation Accuracy Based on Different MODIS-Landsat Spatio-Temporal Fusion Datasets. Remote Sens. 2022, 14, 2542. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Q.; Shao, F.; Li, S. Spatio–Temporal–Spectral Collaborative Learning for Spatio–Temporal Fusion with Land Cover Changes. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Yang, Y.; Anderson, M.C.; Gao, F.; Hain, C.R.; Semmens, K.A.; Kustas, W.P.; Noormets, A.; Wynne, R.H.; Thomas, V.A.; Sun, G. Daily Landsat-Scale Evapotranspiration Estimation over a Forested Landscape in North Carolina, USA, Using Multi-Satellite Data Fusion. Hydrol. Earth Syst. Sci. 2017, 21, 1017–1037. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Jin, H.; Zhao, W.; Bian, J.; Qu, Y.; Zeng, Y.; Xu, B. Derivation of Temporally Continuous LAI Reference Maps through Combining the LAINet Observation System with CACAO. Agric. For. Meteorol. 2017, 233, 209–221. [Google Scholar] [CrossRef]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Macé, D.; Pragnère, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of Canopy Biophysical Variables from Bidirectional Reflectance: Using Prior Information to Solve the Ill-Posed Inverse Problem. Remote Sens. Environ. 2003, 84, 1–15. [Google Scholar] [CrossRef]
- Si, Y.; Schlerf, M.; Zurita-Milla, R.; Skidmore, A.; Wang, T. Mapping Spatio-Temporal Variation of Grassland Quantity and Quality Using MERIS Data and the PROSAIL Model. Remote Sens. Environ. 2012, 121, 415–425. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; García-Haro, F.J.; Camps-Valls, G.; Grau-Muedra, G.; Nutini, F.; Busetto, L.; Katsantonis, D.; Stavrakoudis, D.; Minakou, C.; Gatti, L.; et al. Exploitation of SAR and Optical Sentinel Data to Detect Rice Crop and Estimate Seasonal Dynamics of Leaf Area Index. Remote Sens. 2017, 9, 248. [Google Scholar] [CrossRef]
- Gao, F.; Hilker, T.; Zhu, X.; Anderson, M.; Masek, J.; Wang, P.; Yang, Y. Fusing Landsat and MODIS Data for Vegetation Monitoring. IEEE Geosci. Remote Sens. Mag. 2015, 3, 47–60. [Google Scholar] [CrossRef]

| Sensor | Band | Spectral Range (nm) | Acquisition Time (DOY) | Spatial Resolution | Revisit Period |
|---|---|---|---|---|---|
| Landsat8 OLI | 1–AEROSOL | 435–451 | 2014 (151) 2015 (186) | 30 m | 16-days |
| 2–Blue | 452–512 | ||||
| 3–Green | 533–590 | ||||
| 4–Red | 636–673 | ||||
| 5–NIR | 851–879 | ||||
| 6–SWIR1 | 1560–1651 | ||||
| 7–SWIR2 | 2107–2294 | ||||
| GF-1 WFV | 1–Blue | 450–520 | 2013 (270) 2016 (235) 2017 (263) | 16 m | 4-days |
| 2–Green | 520–590 | ||||
| 3–Red | 630–690 | ||||
| 4–NIR | 770–890 | ||||
| GLASS LAI | / | / | 2013–2017 (121–128, 129–136, 137–144, 145–152, 153–160, 161–168, 169–176, 177–184, 185–192, 193–200, 201–208, 209–216, 217–224, 225–232, 233–240, 241–248, 249–256, 257–264, 265–272, 273–280, 281–288, 289–296, 297–305) | 1 km | 8-days |
| LAI | Collection Time (DOY) | Number of Samples |
|---|---|---|
| LAI 2000 | 2013 (221, 223, 226, 227, 247) | 53 |
| 2016 (147, 157, 169, 185, 199, 215, 230, 248, 260, 266) | 140 | |
| LAINet | 2013 (221, 223, 226, 227, 247) | 50 |
| TRAC | 2013 (224, 232, 248) | 13 |
| LAI 2200 | 2013 (222, 225, 228) | 9 |
| Models | Parameter Name | Parameter Value |
|---|---|---|
| BPNN | input layer node number | 7 (Landsat8), 4 (GF-1 WFV) |
| number of neural network layers | 3 | |
| number of hidden layer nodes | 1 | |
| output layer node number | 1 | |
| epoch times | 3000 | |
| learning rate µ | 0.001 | |
| SA | initial temperature | 100 |
| cooling decay parameter | 0.95 | |
| termination temperature | 0.01 | |
| Weight interval | [−3, 3] | |
| number of iterations per temperature | 150 |
| Highs Spatial Resolution | High Time Resolution | High Time Resolution | High Temporal and Spatial |
|---|---|---|---|
| GF-1 WFV LAI 2013(270) | GLASS LAI 273-280 | The Other GLASS LAI datasets (22 scenes) | GF-1 WFV LAI 2013 (22 scenes) |
| Landsat8 OLI LAI 2014(151) | GLASS LAI 145-152 | Landsat8 OLI LAI 2014 (22 scenes) | |
| Landsat8 OLI LAI 2015(186) | GLASS LAI 184-192 | Landsat8 OLI LAI 2015 (22 scenes) | |
| GF-1 WFV LAI 2016(235) | GLASS LAI 241-248 | GF-1 WFV LAI 2016 (22 scenes) | |
| GF-1 WFV LAI 2017(263) | GLASS LAI 265-272 | GF-1 WFV LAI 2017 (22 scenes) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Jin, L.; Tian, X.; Chen, S.; Wang, H. A High Spatiotemporal Enhancement Method of Forest Vegetation Leaf Area Index Based on Landsat8 OLI and GF-1 WFV Data. Remote Sens. 2023, 15, 2812. https://doi.org/10.3390/rs15112812
Luo X, Jin L, Tian X, Chen S, Wang H. A High Spatiotemporal Enhancement Method of Forest Vegetation Leaf Area Index Based on Landsat8 OLI and GF-1 WFV Data. Remote Sensing. 2023; 15(11):2812. https://doi.org/10.3390/rs15112812
Chicago/Turabian StyleLuo, Xin, Lili Jin, Xin Tian, Shuxin Chen, and Haiyi Wang. 2023. "A High Spatiotemporal Enhancement Method of Forest Vegetation Leaf Area Index Based on Landsat8 OLI and GF-1 WFV Data" Remote Sensing 15, no. 11: 2812. https://doi.org/10.3390/rs15112812
APA StyleLuo, X., Jin, L., Tian, X., Chen, S., & Wang, H. (2023). A High Spatiotemporal Enhancement Method of Forest Vegetation Leaf Area Index Based on Landsat8 OLI and GF-1 WFV Data. Remote Sensing, 15(11), 2812. https://doi.org/10.3390/rs15112812






