Impacts of Quasi-Biennial Oscillation and El Niño–Southern Oscillation on Stratospheric Isentropic Mixing Process
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
2.2.1. Calculation of the Equivalent Length
2.2.2. Multiple Linear Regression Model
2.2.3. Eliassen–Palm Flux
2.2.4. Selection of MEI Index and QBO Index
2.2.5. Composite Analysis
3. Results and Analysis
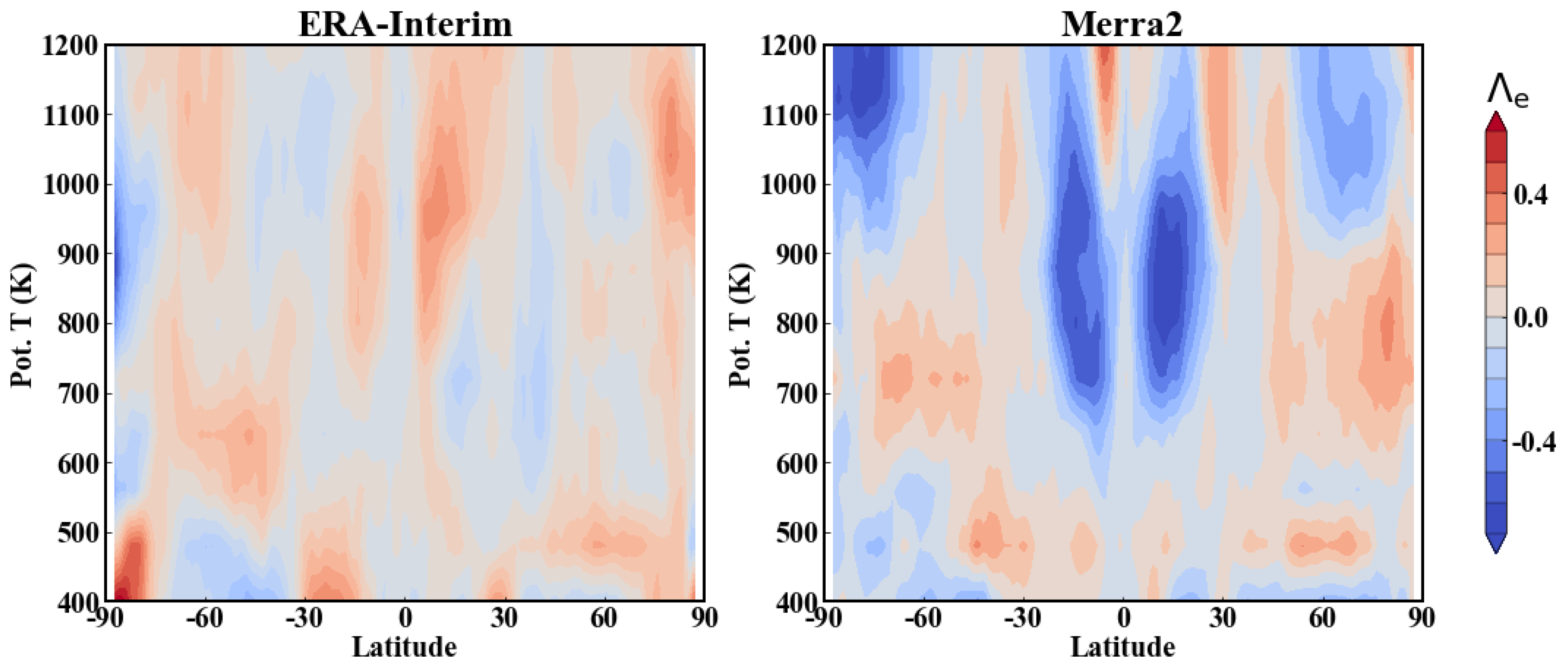
3.1. Interannual Variability of Isentropic Mixing Intensity
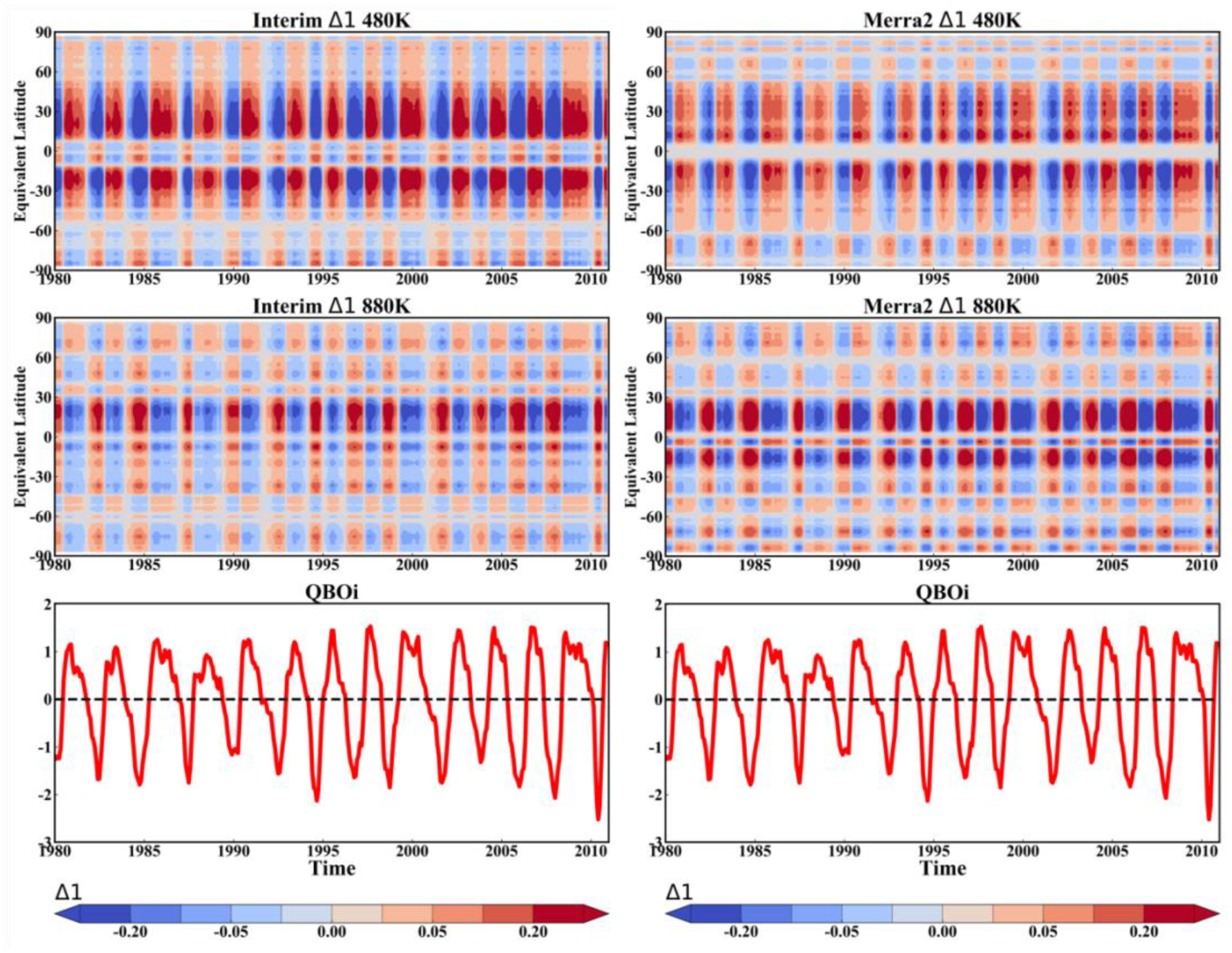
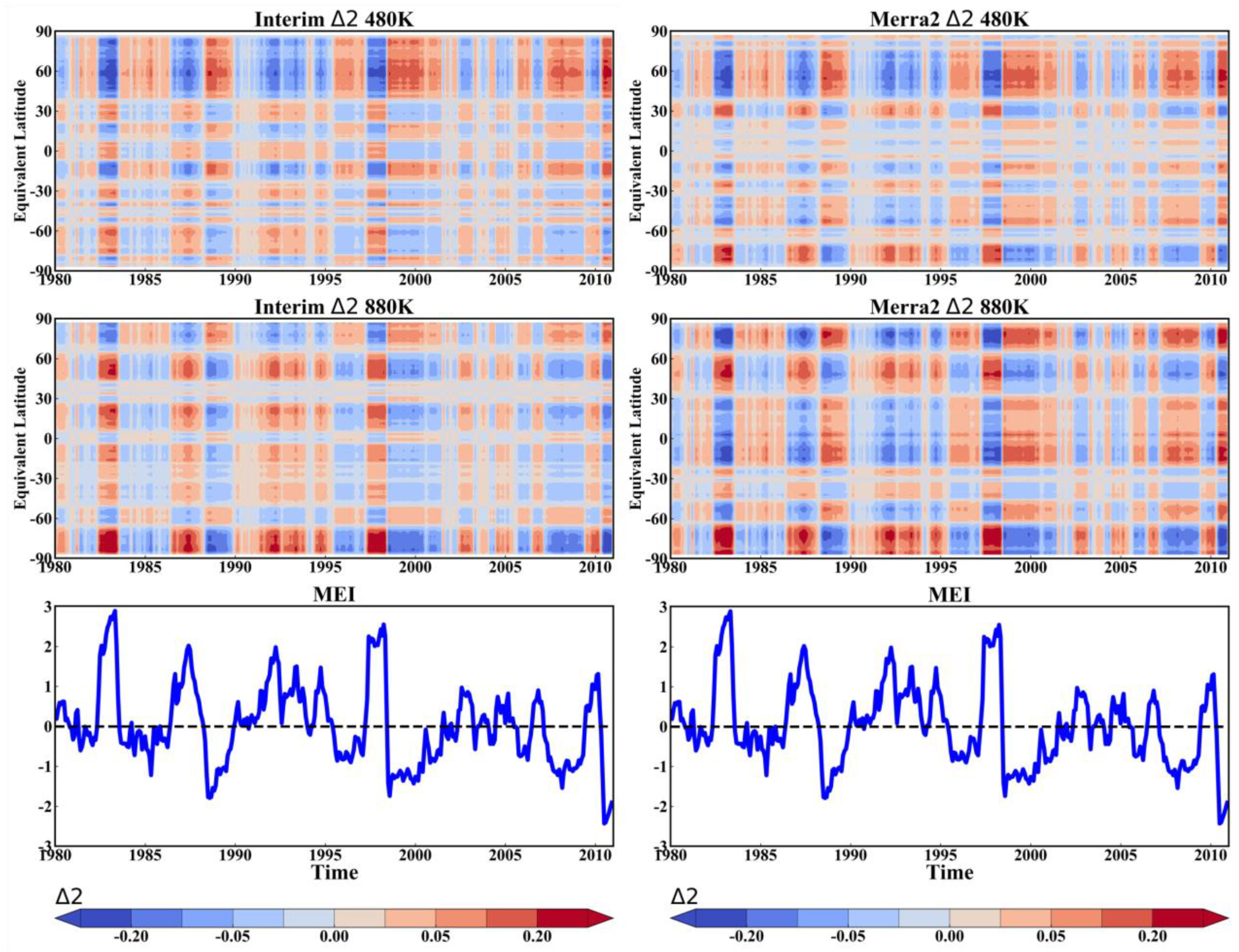
3.2. Multiple Regression Model
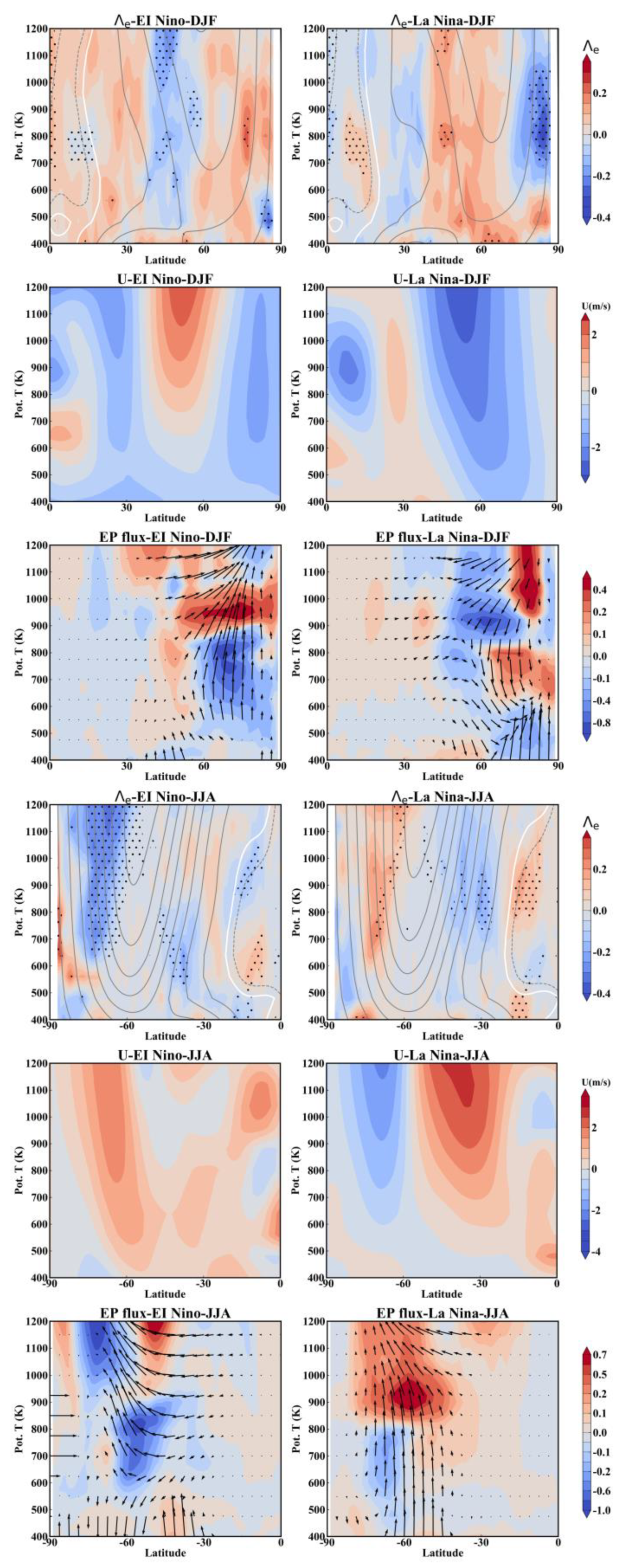
3.3. Composite Analysis of Modulation of Stratospheric Mixing by QBO and ENSO
4. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alan, P.R. Stratospheric Transport. J. Meteorol. Soc. Jpn. Ser. II 2002, 80, 793–809. [Google Scholar]
- Shepherd, T.G. Transport in the Middle Atmosphere. J. Meteorol. Soc. Jpn. Ser. II 2007, 85, 165–191. [Google Scholar] [CrossRef]
- Mcintyre, M.E.; Palmer, T.N. The ‘surf zone’ in the stratosphere. J. Atmos. Terr. Phys. 1984, 46, 825–849. [Google Scholar] [CrossRef]
- Nakamura, N. Two-dimensional mixing, edge formation, and permeability diagnosed in an area coordinate. J. Atmos. 1996, 53, 1524–1537. [Google Scholar] [CrossRef]
- Nakamura, N.; Ma, J. Modified Lagrangian-mean diagnostics of the stratospheric polar vortices: 2. Nitrous oxide and seasonal barrier migration in the cryogenic limb array etalon spectrometer and SKYHI general circulation model. J. Geophys. Res. Atmos. 1997, 102, 25721–25735. [Google Scholar] [CrossRef]
- Haynes, P.; Shuckburgh, E. Effective Diffusivity as a diagnostic of atmospheric transport. Part 1: Stratosphere. J. Geophys. Res. Atmos. 2000, 105, 22777–22794. [Google Scholar] [CrossRef]
- Haynes, P.; Shuckburgh, E. Effective diffusivity as a diagnostic of atmospheric transport: 2. Troposphere and lower stratosphere. J. Geophys. Res. 2000, 105, 22795. [Google Scholar] [CrossRef]
- Mcintyre, M.E.; Palmer, T. Breaking waves in the stratosphere. Nature 1983, 305, 593–600. [Google Scholar] [CrossRef]
- Chen, P. The Influences of Zonal Flow on Wave Breaking and Tropical-Extratropical Interaction in the Lower Stratosphere. J. Atmos. Sci. 1996, 53, 2379–2392. [Google Scholar] [CrossRef]
- O’Sullivan, D.; Ping, C. Modeling the quasi biennial oscillation’s influence on isentropic tracer transport in the subtropics. J. Geophys. Res. Atmos. 1996, 101, 6811–6821. [Google Scholar] [CrossRef]
- Manzini, E.; Giorgetta, M.A.; Esch, M.; Kornblueh, L.; Roeckner, E. The Influence of Sea Surface Temperatures on the Northern Winter Stratosphere: Ensemble Simulations with the MAECHAM5 Model. J. Clim. 2006, 19, 3863–3881. [Google Scholar] [CrossRef]
- Camp, C.D.; Tung, K.K. Stratospheric polar warming by ENSO in winter: A statistical study. Geophys. Res. Lett. 2007, 34, 545–559. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, W.; Wang, Z.; Xie, F.; Wang, F. The Influence of ENSO on Northern Midlatitude ozone during the Winter to Spring Transition. J. Clim. 2015, 28, 4774–4793. [Google Scholar] [CrossRef]
- Xie, F.; Li, J.; Tian, W.; Fu, Q.; Jin, F.F.; Hu, Y.; Zhang, J.; Wang, W.; Sun, C.; Feng, J.; et al. A connection from Arctic stratospheric ozone to El Nio-Southern oscillation. Environ. Res. Lett. 2016, 11, 124026. [Google Scholar] [CrossRef]
- Ruzmaikin, A.; Feynman, J.; Jiang, X.; Fu, Q.; Jin, F.-F.; Hu, Y.; Zhang, J.; Wang, W.; Sun, C.; Feng, J.; et al. Extratropical signature of the quasi-biennial oscillation. J. Geophys. Res. Atmos. 2005, 110, 124026. [Google Scholar] [CrossRef]
- Garfinkel, C.I.; Shaw, T.A.; Hartmann, D.L.; Waugh, D.W. Does the Holton–Tan Mechanism Explain How the Quasi-Biennial Oscillation Modulates the Arctic Polar Vortex? J. Atmos. Sci. 2012, 69, 1713–1733. [Google Scholar] [CrossRef]
- Wen, C.; Takahashi, M.; Graf, H.F. Interannual variations of stationary planetary wave activity in the northern winter troposphere and stratosphere and their relations to NAM and SST. J. Geophys. Res. Atmos. 2003, 108, 4797. [Google Scholar] [CrossRef]
- And, C.; Hartmann, D.L. Effects of the El Niño–Southern Oscillation and the Quasi-Biennial Oscillation on polar temperatures in the stratosphere. J. Geophys. Res. Atmos. 2007, D19112. [Google Scholar] [CrossRef]
- Ineson, S.; Scaife, A.A. The role of the stratosphere in the European climate response to El Niño. Nat. Geosci. 2009, 2, 32–36. [Google Scholar] [CrossRef]
- Holton, J.R.; Tan, H.C. The Influence of the Equatorial Quasi-Biennial Oscillation on the Global Circulation at 50 mb. J. Atmos. 1980, 37, 2200–2208. [Google Scholar] [CrossRef]
- Plumb, R.A.; Bell, R.C. A model of the quasi-biennial oscillation on an equatorial beta-plane. Q. J. R. Meteorol. Soc. 1982, 108, 335–352. [Google Scholar] [CrossRef]
- White, I.P.; Lu, H.; Mitchell, N.J. Seasonal evolution of the QBO-induced wave forcing and circulation anomalies in the northern winter stratosphere. J. Geophys. Res. Atmos. 2018, 121, 410–411. [Google Scholar] [CrossRef]
- Silverman, V.; Lubis, S.W.; Harnik, N.; Matthes, K. A Synoptic View of the Onset of the Midlatitude QBO Signal. J. Atmos. Sci. 2021, 78, 3759–3780. [Google Scholar]
- Sassi, F. Effect of El Nino–Southern Oscillation on the dynamical, thermal, and chemical structure of the middle atmosphere. J. Geophys. Res. 2004, 109, D17108. [Google Scholar] [CrossRef]
- García-Herrera, R.; Calvo, N.; Garcia, R.R.; Giorgetta, M.A. Propagation of ENSO temperature signals into the middle atmosphere: A comparison of two general circulation models and ERA-40 reanalysis data. J. Geophys. Res. Atmos. 2006, D06101. [Google Scholar] [CrossRef]
- Thompson, E.P.L.H. Seasonal Evolution of Stratosphere-Troposphere Coupling in the Southern Hemisphere and Implications for the Predictability of Surface Climate. J. Geophys. Res. D Atmos. JGR 2018, 123, 12002–12016. [Google Scholar]
- Loon, H.V.; Zerefos, C.S.; Repapis, C.C. The Southern Oscillation in the Stratosphere. Mon. Weather Rev. 1982, 110, 225–229. [Google Scholar] [CrossRef]
- Loon, H.V.; Labitzke, K. The Southern Oscillation. Part V: The Anomalies in the Lower Stratosphere of the Northern Hemisphere in Winter and a Comparison with the Quasi-Biennial Oscillation. Mon. Weather Rev. 1987, 115, 559–565. [Google Scholar]
- Hamilton, K. An examination of observed Southern Oscillation effects in the Northern Hemisphere stratosphere. J. Atmos. 1993, 50, 3468–3474. [Google Scholar] [CrossRef]
- Shuckburgh, E.; Norton, W.; Iwi, A.; Haynes, P. Influence of the quasi-biennial oscillation on isentropic transport and mixing in the tropics and subtropics. J. Geophys. Res. Atmos. 2001, 106, 14327–14337. [Google Scholar] [CrossRef]
- Garny, H.; Bodeker, G.; Dameris, M. Trends and variability in stratospheric mixing: 1979–2005. Atmos. Chem. Phys. 2007, 7, 5611–5624. [Google Scholar] [CrossRef]
- Chen, G.; Lu, J.; Frierson, D.M.W. Phase Speed Spectra and the Latitude of Surface Westerlies: Interannual Variability and Global Warming Trend. J. Clim. 2008, 21, 5942–5959. [Google Scholar] [CrossRef]
- Shuckburgh, E.; D Ovidio, F.; Legras, B. Local Mixing Events in the Upper Troposphere and Lower Stratosphere. Part II: Seasonal and Interannual Variability. J. Atmos. Sci. 2009, 66, 3695–3706. [Google Scholar] [CrossRef]
- Yang, H.; Chen, G.; Domeisen, D.I.V. Sensitivities of the Lower-Stratospheric Transport and Mixing to Tropical SST Heating. J. Atmos. Sci. 2014, 71, 2674–2694. [Google Scholar] [CrossRef]
- Abalos, M.; Legras, B.; Shuckburgh, E. Interannual variability in effective diffusivity in the upper troposphere/lower stratosphere from reanalysis data. Q. J. R. Meteorol. Soc. 2016, 142, 1847–1861. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Mcintyre, M.E.; Robertson, A.W. On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 1985, 111, 877–946. [Google Scholar] [CrossRef]
- Bodeker, G.E.; Scott, J.C.; Kreher, K.; McKenzie, R.L. Global ozone trends in potential vorticity coordinates using TOMS and GOME intercompared against the Dobson network: 1978–1998. J. Geophys. Res. 2001, 106, 23029. [Google Scholar] [CrossRef]
- Waugh, D.W.; Rong, P.P. Interannual Variability in the Decay of Lower Stratospheric Arctic Vortices. J. Meteorol. Soc. Jpn. 2002, 80, 997–1012. [Google Scholar] [CrossRef]
- Abalos, M.; Randel, W.J.; Birner, T. Phase-speed Spectra of Eddy Tracer Fluxes Linked to Isentropic Stirring and Mixing in the Upper Troposphere and Lower Stratosphere. J. Atmos. Sci. 2016, 73, 4711–4730. [Google Scholar] [CrossRef]
- Diallo, M.; Legras, B.; Chédin, A. Age of stratospheric air in the ERA-Interim. Atmos. Chem. Phys. 2012, 12, 17087–17134. [Google Scholar] [CrossRef]
- Diallo, M.; Ploeger, F.; Konopka, P.; Birner, T.; Müller, R.; Riese, M.; Riese, M.; Garny, H.; Legras, B.; Ray, E.; et al. Significant Contributions of Volcanic Aerosols to Decadal Changes in the Stratospheric Circulation. Geophys. Res. Lett. 2017, 44, 710–780. [Google Scholar] [CrossRef]
- Diallo, M.; Riese, M.; Birner, T.; Konopka, P.; Müller, R.; Hegglin, M.I.; Santee, M.L.; Baldwin, M.; Legras, B.; Ploeger, F. Response of stratospheric water vapor and ozone to the unusual timing of El Niño and the QBO disruption in 2015–2016. Atmos. Chem. Phys. 2018, 18, 13055–13073. [Google Scholar] [CrossRef]
- Wolter, K.; Timlin, M.S. El Niño/Southern Oscillation behaviour since 1871 as diagnosed in an extended multivariate ENSO index (MEI.ext). Int. J. Clim. 2011, 31, 1074–1087. [Google Scholar] [CrossRef]
- Andrews, D.G.; Holton, J.R.; Leovy, C.B. Middle Atmosphere Dynamics; Academic Press: San Diego, CA, USA, 1987. [Google Scholar]
- Edmon, H.J., Jr.; Hoskins, B.J.; McIntyre, M.E. Eliassen-palm cross sections for the troposphere. J. Atmos. Sci. 1980, 37, 2600–2616. [Google Scholar] [CrossRef]
- Kiem, A.S.; Franks, S.W. On the identification of ENSO-induced rainfall and runoff variability: A comparison of methods and indices. Int. Assoc. Sci. Hydrol. Bull. 2001, 46, 715–727. [Google Scholar] [CrossRef]
- Lu, A.; Zhu, W.; Jia, S. Assessment of the sensitivity of vegetation to El-Nino/Southern Oscillation events over China. Adv. Space Res. 2012, 50, 1362–1373. [Google Scholar] [CrossRef]
- Bastos, A.; Running, S.W.; Gouveia, C.; Trigo, R.M. The global NPP dependence on ENSO: La Nina and the extraordinary year of 2011. J. Geophys. Res. Biogeosci. 2013, 118, 1247–1255. [Google Scholar] [CrossRef]
- Wen, C.; Lei, Y.; Ronghui, H.; Qihong, Q. Diagnostic Analysis of the Impact of Tropical QBO on the General Circulation in the Northern Hemisphere Winter. Chin. J. Atmos. Sci. 2004, 28, 161–173. [Google Scholar]
- Domeisen, D.; Garfinkel, C.I.; Butler, A.H. The Teleconnection of El Niño Southern Oscillation to the Stratosphere. Rev. Geophys. 2019, 57, 5–47. [Google Scholar] [CrossRef]
- Calvo, N.; Garcia, R.R.; Randel, W.J.; Marsh, D. Dynamical Mechanism for the Increase in Tropical Upwelling in the Lowermost Tropical Stratosphere during Warm ENSO Events. J. Atmos. Sci. 2009, 67, 2331–2340. [Google Scholar] [CrossRef]
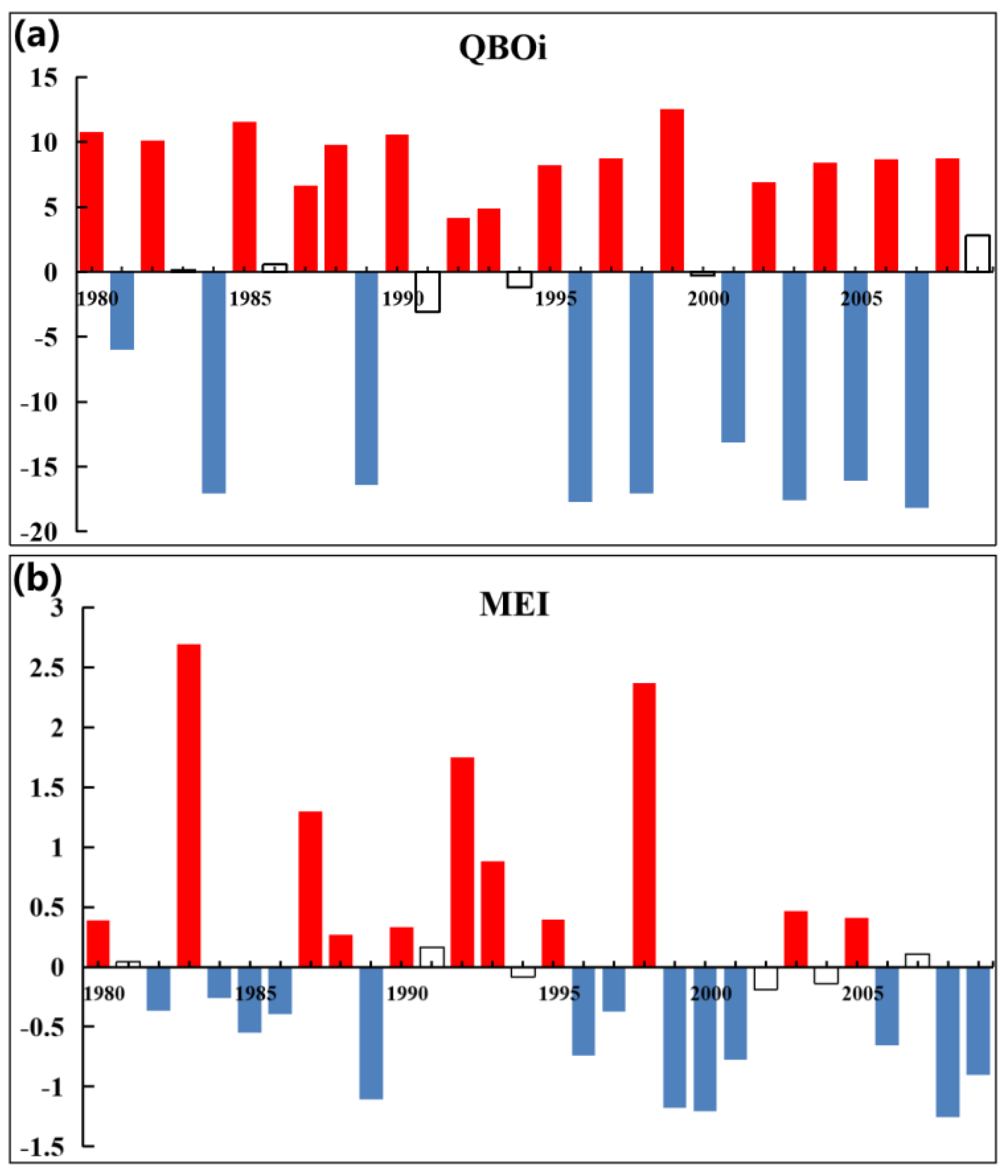

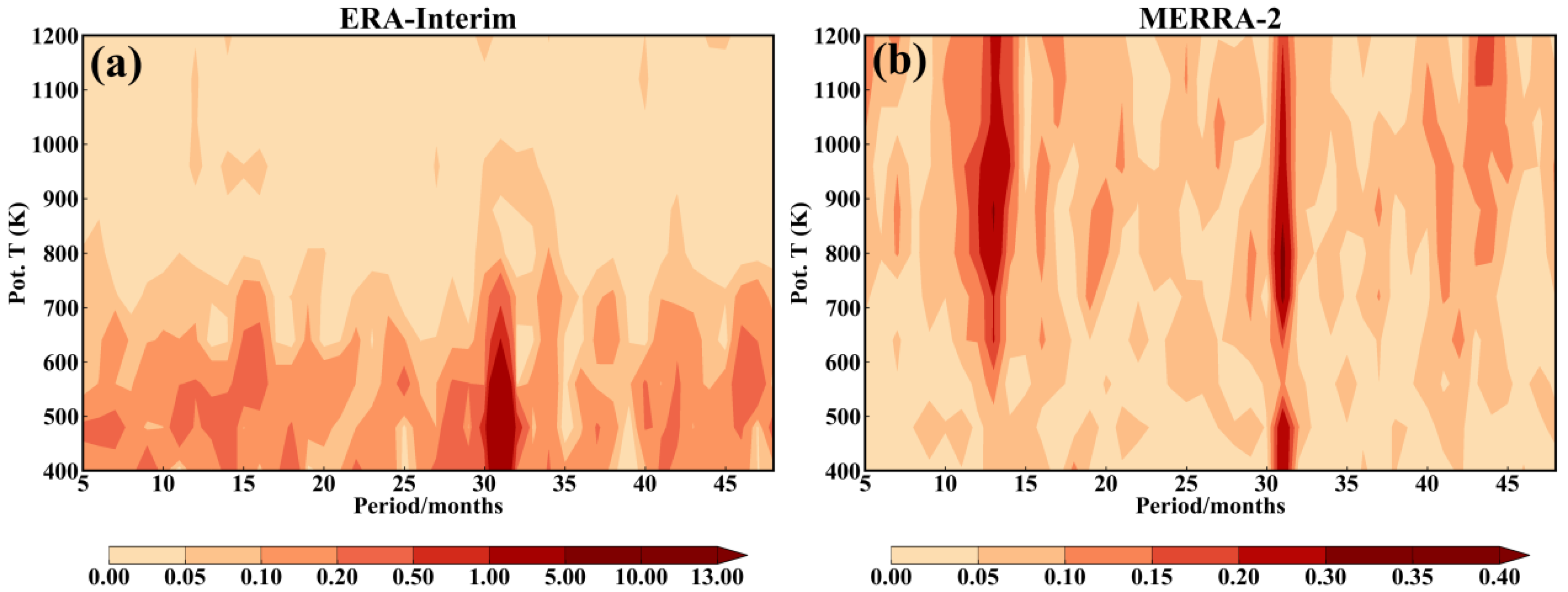
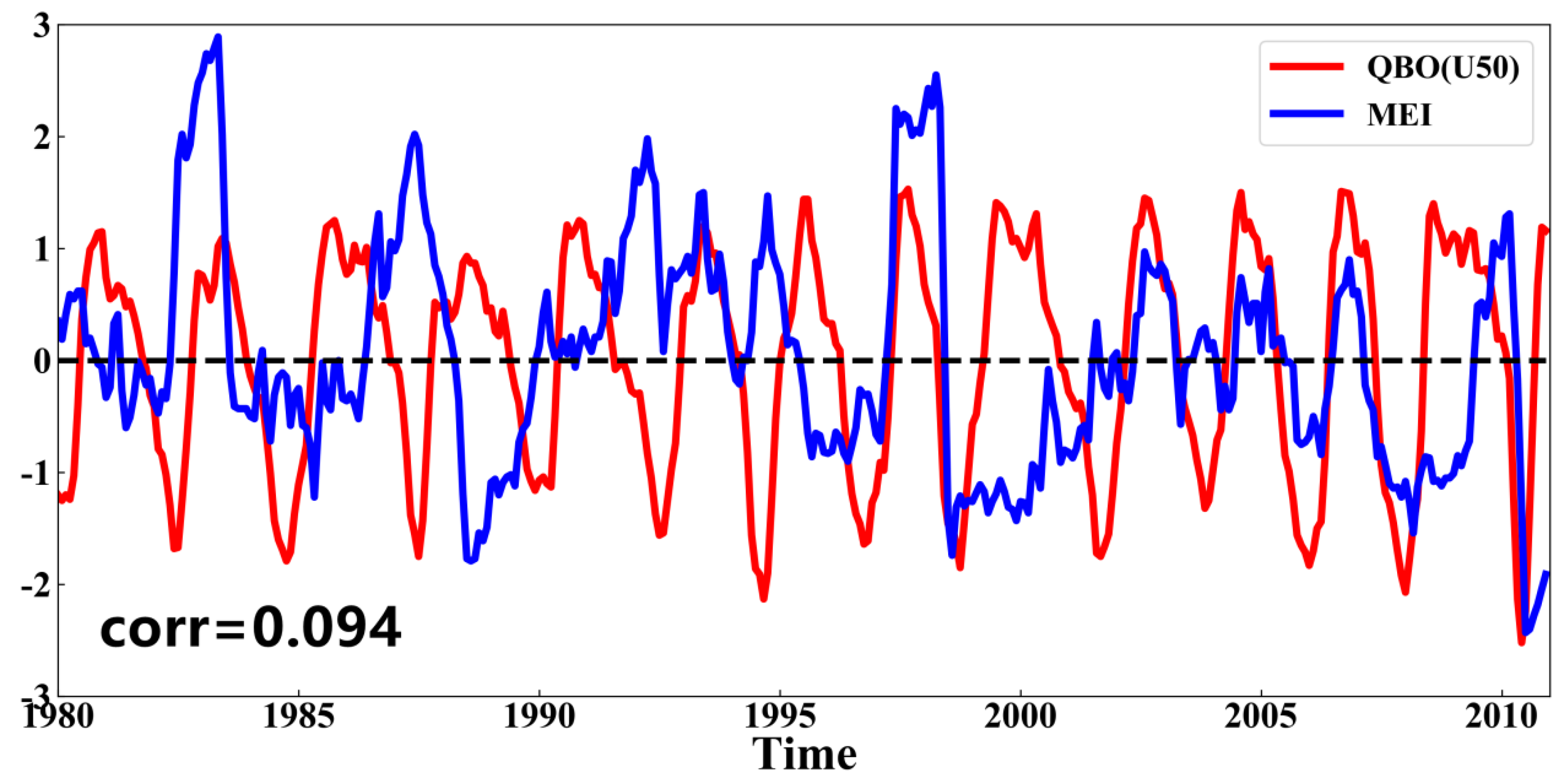
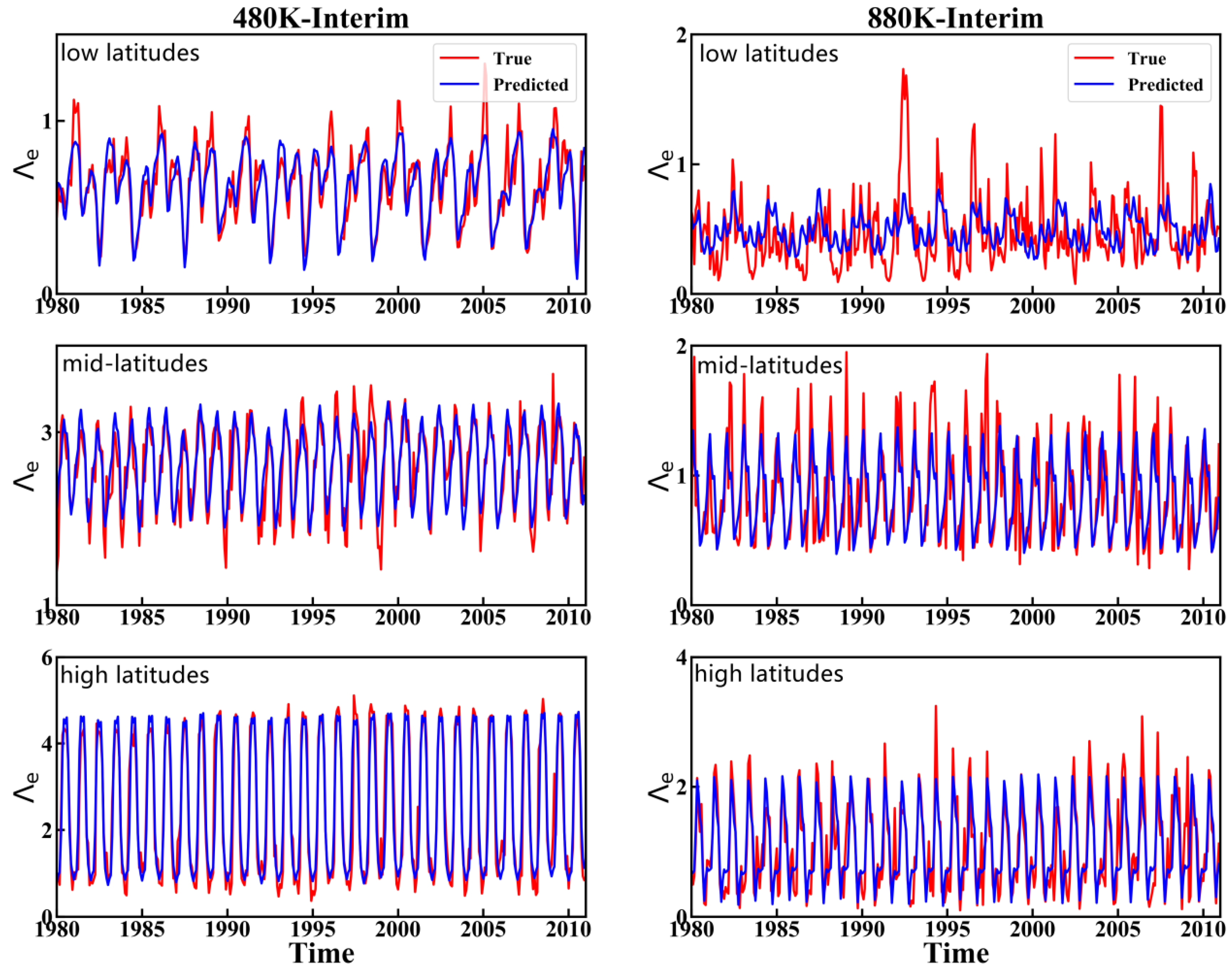

| Event | Year |
|---|---|
| EQBO | 1981, 1984, 1989, 1996, 1998, 2001, 2003, 2005, 2007 |
| WQBO | 1980, 1982, 1985, 1987, 1988, 1990, 1992, 1993, 1995, 1997, 1999, 2002, 2004, 2006, 2008 |
| Event | Year |
|---|---|
| El Niño | 1980, 1983, 1987, 1988, 1990, 1992, 1993, 1995, 1998, 2003, 2005 |
| La Niña | 1982, 1984, 1985, 1986, 1989, 1996, 1997, 1999, 2000, 2001, 2006, 2008, 2009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Wang, Z.; Zhang, Z.; Luo, J. Impacts of Quasi-Biennial Oscillation and El Niño–Southern Oscillation on Stratospheric Isentropic Mixing Process. Remote Sens. 2023, 15, 2715. https://doi.org/10.3390/rs15112715
Liang J, Wang Z, Zhang Z, Luo J. Impacts of Quasi-Biennial Oscillation and El Niño–Southern Oscillation on Stratospheric Isentropic Mixing Process. Remote Sensing. 2023; 15(11):2715. https://doi.org/10.3390/rs15112715
Chicago/Turabian StyleLiang, Jing, Zhiting Wang, Zhiyi Zhang, and Jiali Luo. 2023. "Impacts of Quasi-Biennial Oscillation and El Niño–Southern Oscillation on Stratospheric Isentropic Mixing Process" Remote Sensing 15, no. 11: 2715. https://doi.org/10.3390/rs15112715
APA StyleLiang, J., Wang, Z., Zhang, Z., & Luo, J. (2023). Impacts of Quasi-Biennial Oscillation and El Niño–Southern Oscillation on Stratospheric Isentropic Mixing Process. Remote Sensing, 15(11), 2715. https://doi.org/10.3390/rs15112715






