An HMM-DNN-Based System for the Detection and Classification of Low-Frequency Acoustic Signals from Baleen Whales, Earthquakes, and Air Guns off Chile
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Methodological Approach
2.3. Acoustic Data Annotation
| Event Class | Reference | Class Label | N Events Train Set | N Frames Train Set | N Events Test Set | N Frames Test Set | N Events Dev Set | N Frames Dev Set |
|---|---|---|---|---|---|---|---|---|
| Possible fin whale 13 Hz call | - | 13H | 82 | 1605 | 10 | 198 | 25 | 497 |
| Antarctic blue whale | [13,66] | AA | 1403 | 47,762 | 386 | 13,589 | 437 | 15,199 |
| Antarctic blue whale overlapped with Fin Whale Song | - | AAFWS | 112 | 575 | 21 | 106 | 37 | 191 |
| Southeast Pacific blue whale song 2 (SEP2) unit A | [15,67] | S21 | 120 | 5802 | 28 | 1488 | 25 | 1218 |
| Southeast Pacific blue whale song 2 (SEP2) unit B | [15,67] | S22 | 51 | 2496 | 17 | 862 | 15 | 697 |
| Southeast Pacific blue whale song 2 (SEP2) units C and D | [15,67] | S23 | 812 | 26,688 | 270 | 8852 | 257 | 8309 |
| Southeast Pacific blue whale song 1 (SEP1) unit C | [67,68,69,70] | S13 | 39 | 1465 | 22 | 790 | 10 | 347 |
| Southeast Pacific blue whale song, Undefined Unit | - | SEP | 66 | 2583 | 25 | 878 | 24 | 943 |
| Fin Whale, 20 Hz Song | [71,72] | FWS | 13,381 | 72,106 | 4671 | 25,199 | 4413 | 24,017 |
| Fin whale Downsweep Type 1 | [71,72] | FWD | 691 | 2983 | 254 | 1079 | 242 | 1068 |
| Fin whale Downsweep Type 2 | [71,72] | FWD2 | 399 | 1872 | 104 | 499 | 121 | 496 |
| Fin whale Downsweep Type 3 | [73,74] | FWD3 | 267 | 1480 | 62 | 333 | 104 | 565 |
| Sei whale Upsweep | [66] | SWU | 227 | 1371 | 44 | 260 | 64 | 369 |
| Sei whale Downsweep | [73,74] | SWD | 118 | 694 | 31 | 186 | 40 | 233 |
| Minke whale Pulse Trains | [75,76,77] | MI | 103 | 1240 | 30 | 385 | 19 | 244 |
| Undefined biological sound | - | UND | 69 | 715 | 27 | 262 | 19 | 158 |
| Earthquake | [2,5,50,78,79,80] | ERQ | 161 | 22,002 | 55 | 7269 | 57 | 7687 |
| Unidentified Ambient Noise | - | AN | 115 | 6363 | 36 | 1924 | 62 | 3845 |
| Seismic air gun | [20] | AG | 325 | 6192 | 103 | 2078 | 124 | 2462 |
2.4. Signal-to-Noise Ratio Computation
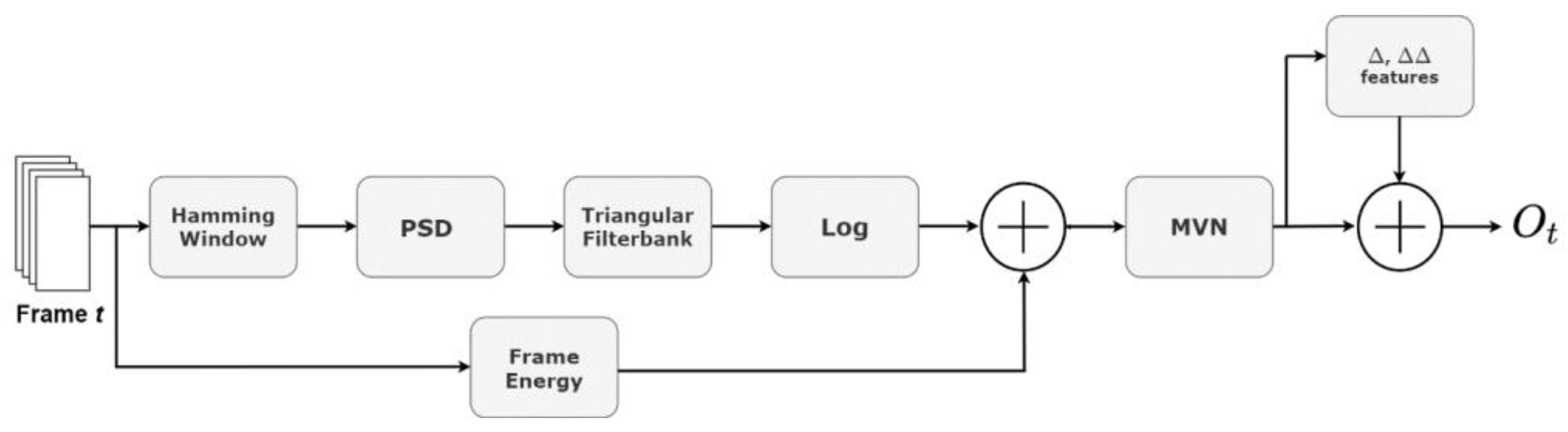
2.5. Feature Extraction
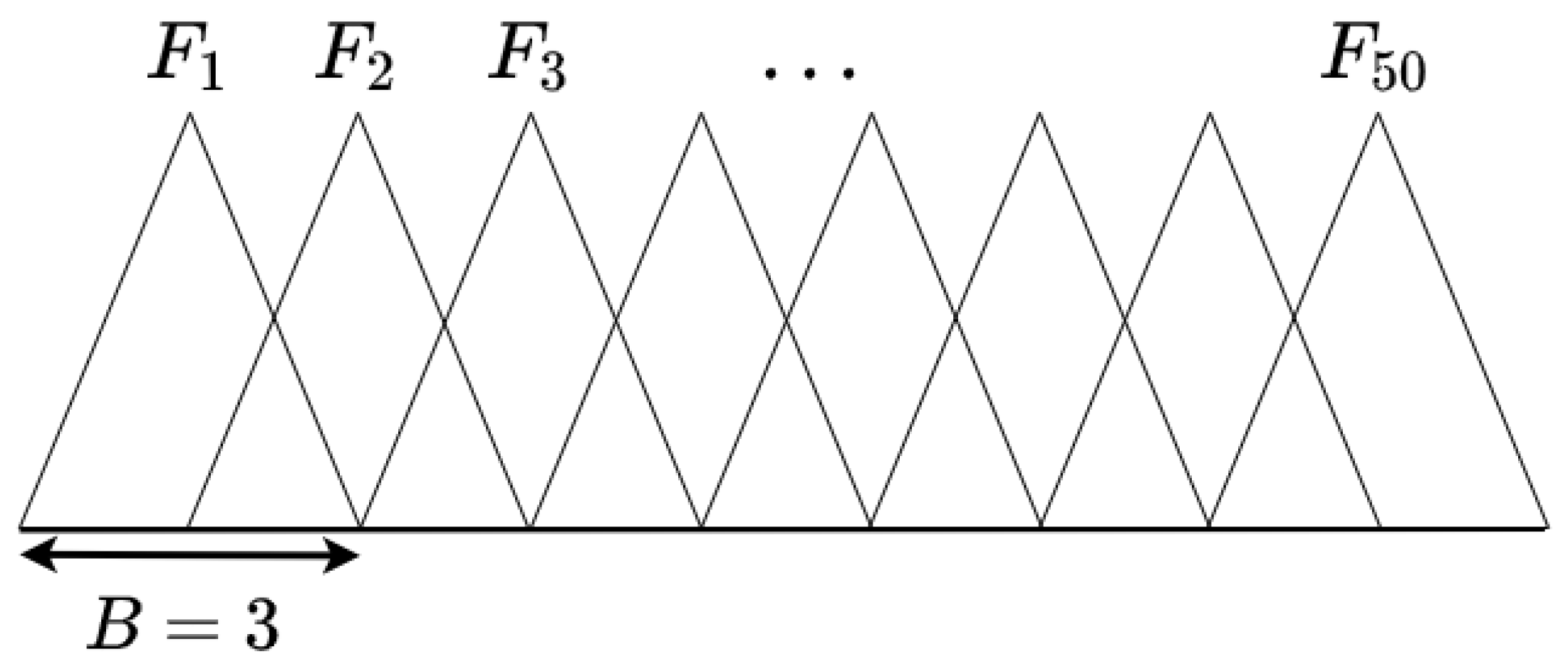
2.5.1. Filterbank Feature Extraction
2.5.2. Linear Discriminant Analysis and Maximum Linear Likelihood Transformation
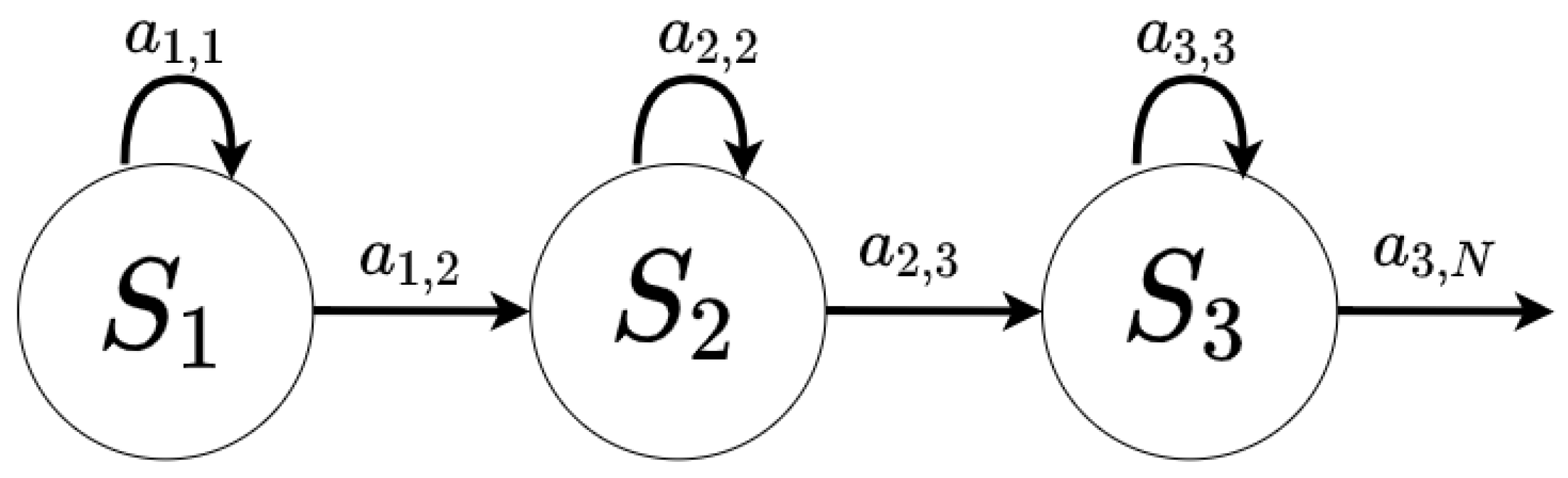
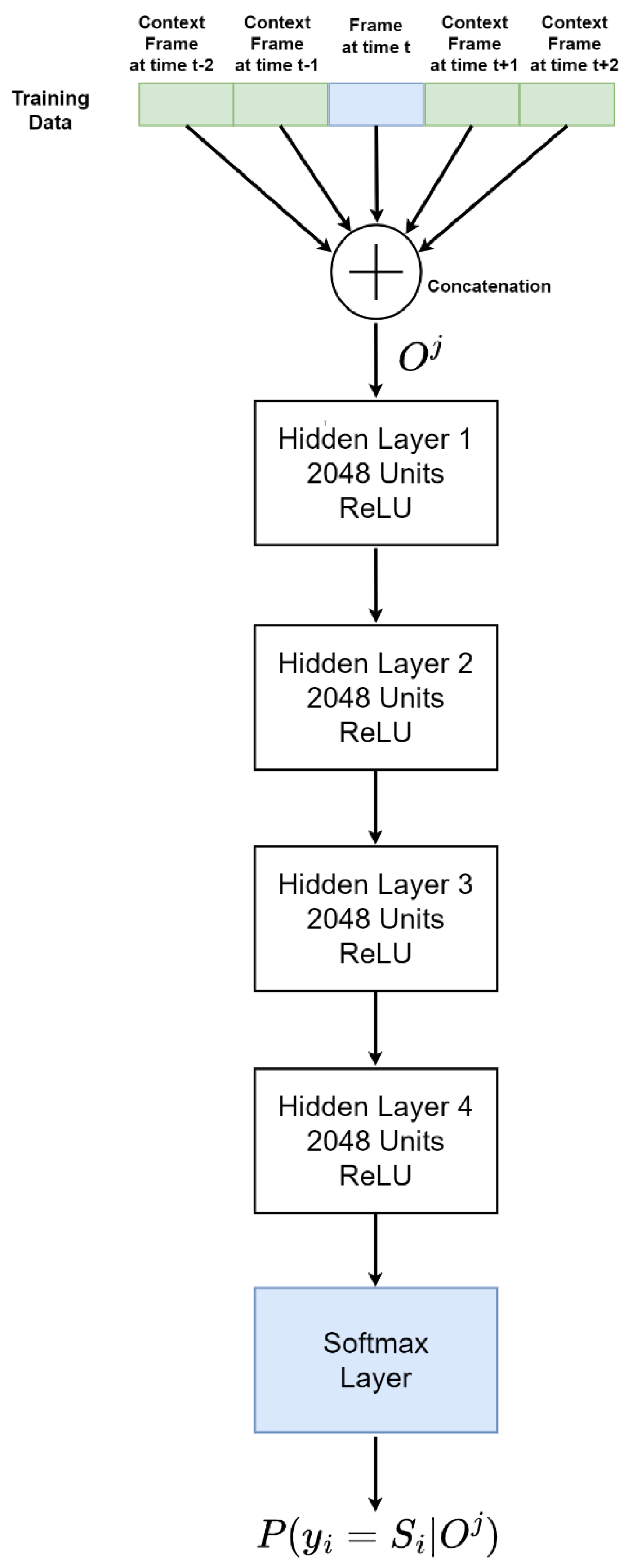
2.6. Hidden Markov Model and Deep Neural Network Architecture
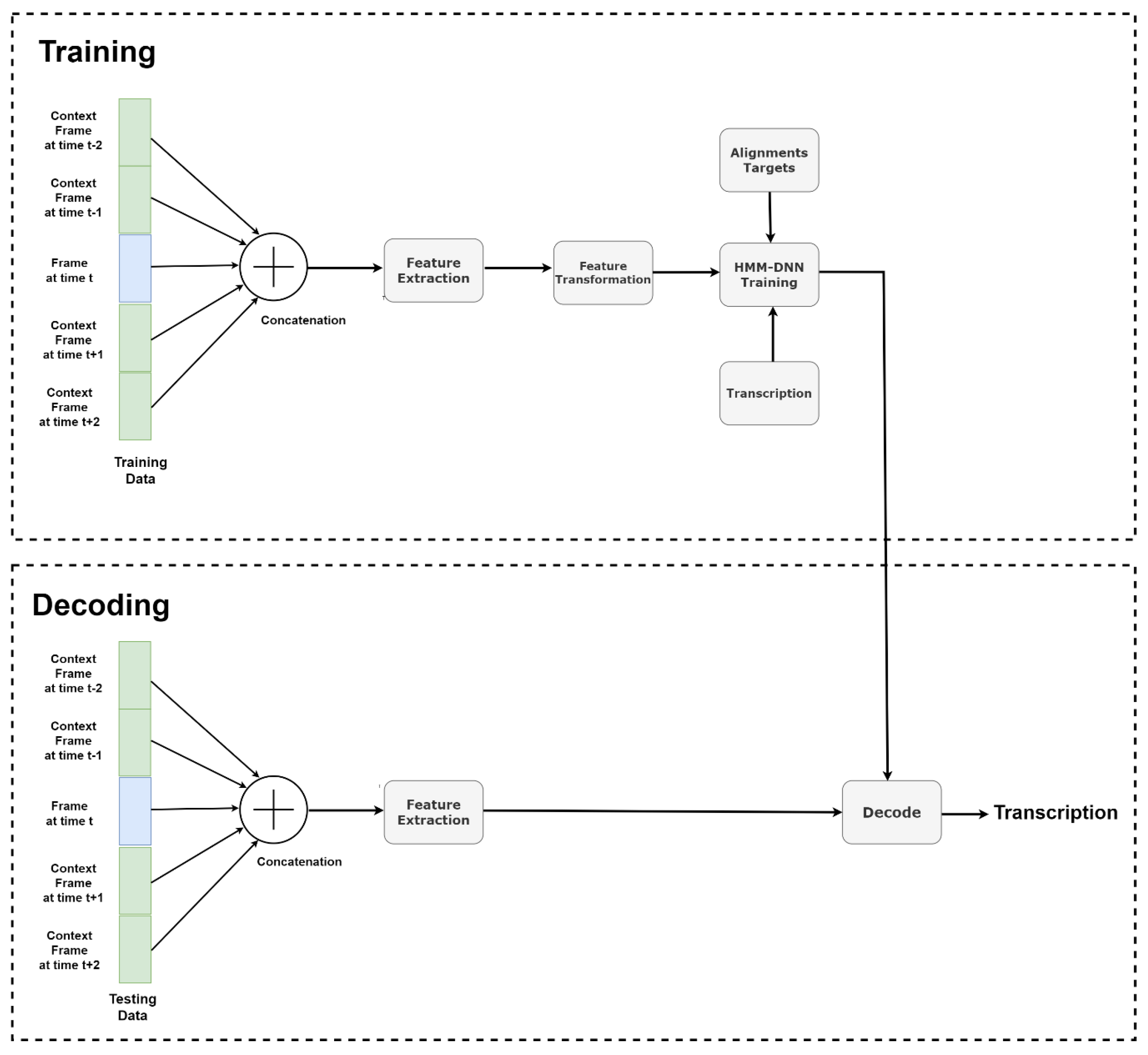
2.6.1. Deep Neural Network for Acoustic Modelling
2.6.2. Hyperparameter Tuning and Feature Selection
2.7. Comparison with the HMM-GMM System
2.8. A SNR Filter for the HMM-DNN System
2.9. Train, Test, and Dev Sets
2.10. Performance Metrics
3. Results
3.1. Performance of Each Class
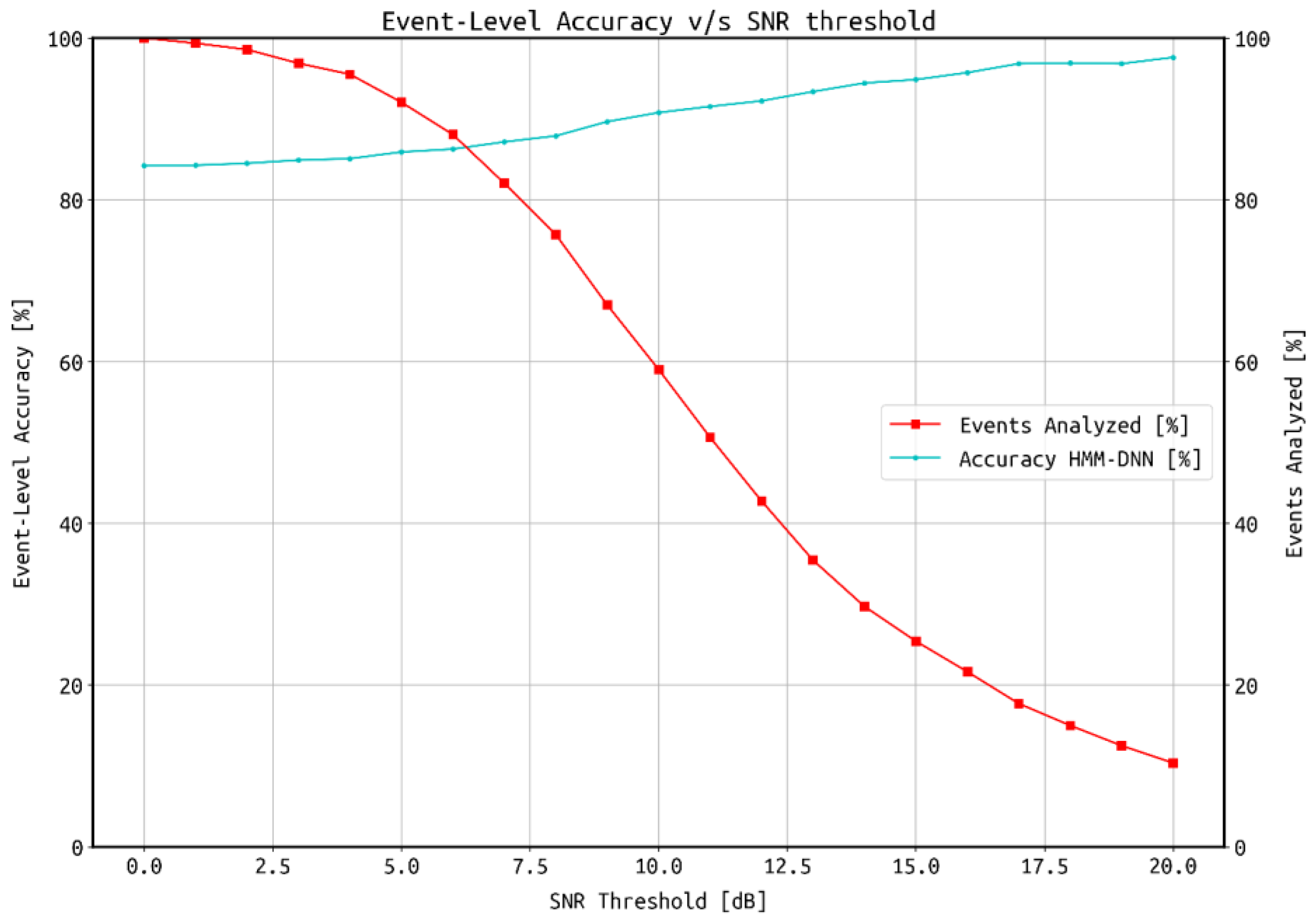
3.2. HMM-DNN Performance with SNR Filter
3.3. A Comparison with the Ordinary HMM-GMM System
4. Discussion
4.1. HMM-DNN System Performance and Event-Level Performance
4.1.1. Baleen Whale Acoustic Signals
4.1.2. Air Guns
4.1.3. Earthquakes
4.2. HMM-DNN System Performance as a Function of SNR Thresholds
4.3. Comparison of HMM-DNN and HMM-GMM Systems
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Parijs, S.M.; Clark, C.W.; Sousa-Lima, R.S.; Parks, S.E.; Rankin, S.; Risch, D.; Van Opzeeland, I.C. Management and research applications of real-time and archival passive acoustic sensors over varying temporal and spatial scales. Mar. Ecol. Prog. Ser. 2009, 395, 21–36. [Google Scholar] [CrossRef]
- Fox, C.G.; Matsumoto, H.; Lau, T.-K.A. Monitoring Pacific Ocean seismicity from an autonomous hydrophone array. J. Geophys. Res. Solid Earth 2001, 106, 4183–4206. [Google Scholar] [CrossRef]
- Sukhovich, A.; Irisson, J.; Perrot, J.; Nolet, G. Automatic recognition of T and teleseismic P waves by statistical analysis of their spectra: An application to continuous records of moored hydrophones. J. Geophys. Res. Solid Earth 2014, 119, 6469–6485. [Google Scholar] [CrossRef]
- Matsumoto, H.; Haralabus, G.; Zampolli, M.; Özel, N.M. T-phase and tsunami pressure waveforms recorded by near-source IMS water-column hydrophone triplets during the 2015 Chile earthquake. Geophys. Res. Lett. 2016, 43, 12511–12519. [Google Scholar] [CrossRef]
- Caplan-Auerbach, J.; Dziak, R.P.; Bohnenstiehl, D.R.; Chadwick, W.W.; Lau, T.-K. Hydroacoustic investigation of submarine landslides at West Mata volcano, Lau Basin. Geophys. Res. Lett. 2014, 41, 5927–5934. [Google Scholar] [CrossRef]
- Bohnenstiehl, D.R.; Dziak, R.P.; Matsumoto, H.; Conder, J.A. Acoustic response of submarine volcanoes in the Tofua Arc and northern Lau Basin to two great earthquakes. Geophys. J. Int. 2013, 196, 1657–1675. [Google Scholar] [CrossRef]
- Hay, A.E.; Hatcher, M.G.; Clarke, J.E.H. Underwater noise from submarine turbidity currents. JASA Express Lett. 2021, 1, 070801. [Google Scholar] [CrossRef]
- Pettit, E.C.; Lee, K.M.; Brann, J.P.; Nystuen, J.A.; Wilson, P.S.; O’Neel, S. Unusually loud ambient noise in tidewater glacier fjords: A signal of ice melt. Geophys. Res. Lett. 2015, 42, 2309–2316. [Google Scholar] [CrossRef]
- Glowacki, O.; Deane, G.B. Quantifying iceberg calving fluxes with underwater noise. Cryosphere 2020, 14, 1025–1042. [Google Scholar] [CrossRef]
- Glowacki, O.; Moskalik, M.; Deane, G.B. The impact of glacier meltwater on the underwater noise field in a glacial bay. J. Geophys. Res. Oceans 2016, 121, 8455–8470. [Google Scholar] [CrossRef]
- Merchant, N.D.; Blondel, P.; Dakin, D.T.; Dorocicz, J. Averaging underwater noise levels for environmental assessment of shipping. J. Acoust. Soc. Am. 2012, 132, EL343–EL349. [Google Scholar] [CrossRef]
- Hatch, L.; Clark, C.; Merrick, R.; Van Parijs, S.; Ponirakis, D.; Schwehr, K.; Thompson, M.; Wiley, D. Characterizing the relative contributions of large vessels to total ocean noise fields: A case study using the Gerry E. Studds stellwagen bank national marine sanctuary. Environ. Manag. 2008, 42, 735–752. [Google Scholar] [CrossRef]
- Stafford, K.M.; Fox, C.G.; Clark, D.S. Long-range acoustic detection and localization of blue whale calls in the northeast Pacific Ocean. J. Acoust. Soc. Am. 1998, 104, 3616–3625. [Google Scholar] [CrossRef]
- Mellinger, D.; Stafford, K.; Moore, S.; Dziak, R.; Matsumoto, H. An overview of fixed passive acoustic observation methods for cetaceans. Oceanography 2007, 20, 36–45. [Google Scholar] [CrossRef]
- Buchan, S.J.; Stafford, K.M.; Hucke-Gaete, R. Seasonal occurrence of southeast Pacific blue whale songs in southern Chile and the eastern tropical Pacific. Mar. Mammal Sci. 2014, 31, 440–458. [Google Scholar] [CrossRef]
- Wall, C.C.; Simard, P.; Lembke, C.; Mann, D.A. Large-scale passive acoustic monitoring of fish sound production on the West Florida Shelf. Mar. Ecol. Prog. Ser. 2013, 484, 173–188. [Google Scholar] [CrossRef]
- Prior, M.K.; Meless, O.; Bittner, P.; Sugioka, H. Long-range detection and location of shallow underwater explosions using deep-sound-channel hydrophoness. IEEE J. Ocean. Eng. 2011, 36, 703–715. [Google Scholar] [CrossRef]
- Woodman, G.H.; Wilson, S.C.; Li, V.Y.; Renneberg, R. Acoustic characteristics of fish bombing: Potential to develop an automated blast detector. Mar. Pollut. Bull. 2002, 46, 99–106. [Google Scholar] [CrossRef] [PubMed]
- Braulik, G.; Wittich, A.; Macaulay, J.; Kasuga, M.; Gordon, J.; Davenport, T.R.; Gillespie, D. Acoustic monitoring to document the spatial distribution and hotspots of blast fishing in Tanzania. Mar. Pollut. Bull. 2017, 125, 360–366. [Google Scholar] [CrossRef]
- Nieukirk, S.L.; Mellinger, D.K.; Moore, S.E.; Klinck, K.; Dziak, R.P.; Goslin, J. Sounds from airguns and fin whales recorded in the mid-Atlantic Ocean, 1999–2009. J. Acoust. Soc. Am. 2012, 131, 1102–1112. [Google Scholar] [CrossRef]
- Sutin, A.; Bunin, B.; Sedunov, A.; Sedunov, N.; Fillinger, L.; Tsionskiy, M.; Bruno, M. Stevens Passive Acoustic System for underwater surveillance. In Proceedings of the 2010 International WaterSide Security Conference, Carrara, Italy, 3–5 November 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Usman, A.M.; Ogundile, O.O.; Versfeld, D.J.J. Review of Automatic Detection and Classification Techniques for Cetacean Vocalization. IEEE Access 2020, 8, 105181–105206. [Google Scholar] [CrossRef]
- Yang, W.; Luo, W.; Zhang, Y. Classification of odontocete echolocation clicks using convolutional neural network. J. Acoust. Soc. Am. 2020, 147, 49–55. [Google Scholar] [CrossRef] [PubMed]
- Ogundile, O.O.; Babalola, O.P.; Odeyemi, S.G.; Rufai, K.I. Hidden Markov models for detection of Mysticetes vocalisations based on principal component analysis. Bioacoustics 2022, 31, 710–738. [Google Scholar] [CrossRef]
- Vickers, W.; Milner, B.; Risch, D.; Lee, R. Robust North Atlantic right whale detection using deep learning models for denoising. J. Acoust. Soc. Am. 2021, 149, 3797–3812. [Google Scholar] [CrossRef]
- Zhong, M.; Torterotot, M.; Branch, T.A.; Stafford, K.M.; Royer, J.-Y.; Dodhia, R.; Ferres, J.L. Detecting, classifying, and counting blue whale calls with Siamese neural networks. J. Acoust. Soc. Am. 2021, 149, 3086–3094. [Google Scholar] [CrossRef]
- Waddell, E.E.; Rasmussen, J.H.; Širović, A. Applying Artificial Intelligence Methods to Detect and Classify Fish Calls from the Northern Gulf of Mexico. J. Mar. Sci. Eng. 2021, 9, 1128. [Google Scholar] [CrossRef]
- Buchan, S.J.; Mahú, R.; Wuth, J.; Balcazar-Cabrera, N.; Gutierrez, L.; Neira, S.; Yoma, N.B. An unsupervised Hidden Markov Model-based system for the detection and classification of blue whale vocalizations off Chile. Bioacoustics 2019, 29, 140–167. [Google Scholar] [CrossRef]
- Baumgartner, M.F.; Ball, K.; Partan, J.; Pelletier, L.-P.; Bonnell, J.; Hotchkin, C.; Corkeron, P.J.; Van Parijs, S.M. Near real-time detection of low-frequency baleen whale calls from an autonomous surface vehicle: Implementation, evaluation, and remaining challenges. J. Acoust. Soc. Am. 2021, 149, 2950–2962. [Google Scholar] [CrossRef] [PubMed]
- Vieira, M.; Pereira, B.P.; Pousão-Ferreira, P.; Fonseca, P.J.; Amorim, M.C.P. Seasonal variation of captive meagre acoustic signalling: A manual and automatic recognition approach. Fishes 2019, 4, 28. [Google Scholar] [CrossRef]
- Bianco, M.J.; Gerstoft, P.; Traer, J.; Ozanich, E.; Roch, M.A.; Gannot, S.; Deledalle, C.-A. Machine learning in acoustics: Theory and applications. J. Acoust. Soc. Am. 2019, 146, 3590–3628. [Google Scholar] [CrossRef]
- Bahoura, M.; Simard, Y. Serial combination of multiple classifiers for automatic blue whale calls recognition. Expert Syst. Appl. 2012, 39, 9986–9993. [Google Scholar] [CrossRef]
- Caruso, F.; Dong, L.; Lin, M.; Liu, M.; Gong, Z.; Xu, W.; Alonge, G.; Li, S. Monitoring of a Nearshore Small Dolphin Species Using Passive Acoustic Platforms and Supervised Machine Learning Techniques. Front. Mar. Sci. 2020, 7, 267. [Google Scholar] [CrossRef]
- Ruff, Z.J.; Lesmeister, D.B.; Duchac, L.S.; Padmaraju, B.K.; Sullivan, C.M. Automated identification of avian vocalizations with deep convolutional neural networks. Remote Sens. Ecol. Conserv. 2019, 6, 79–92. [Google Scholar] [CrossRef]
- Rasmussen, J.H.; Širović, A. Automatic detection and classification of baleen whale social calls using convolutional neural networks. J. Acoust. Soc. Am. 2021, 149, 3635–3644. [Google Scholar] [CrossRef] [PubMed]
- Shiu, Y.; Palmer, K.J.; Roch, M.A.; Fleishman, E.; Liu, X.; Nosal, E.-M.; Helble, T.; Cholewiak, D.; Gillespie, D.; Klinck, H. Deep neural networks for automated detection of marine mammal species. Sci. Rep. 2020, 10, 607. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, J.; Borchers, D.L. Automated call detection for acoustic surveys with structured calls of varying length. Methods Ecol. Evol. 2022, 13, 1552–1567. [Google Scholar] [CrossRef]
- Saffari, A.; Khishe, M.; Zahiri, S.-H. Fuzzy-ChOA: An improved chimp optimization algorithm for marine mammal classification using artificial neural network. Analog. Integr. Circuits Signal Process. 2022, 111, 403–417. [Google Scholar] [CrossRef]
- Madhusudhana, S.; Shiu, Y.; Klinck, H.; Fleishman, E.; Liu, X.; Nosal, E.-M.; Helble, T.; Cholewiak, D.; Gillespie, D.; Širović, A.; et al. Improve automatic detection of animal call sequences with temporal context. J. R. Soc. Interface 2021, 18, 20210297. [Google Scholar] [CrossRef]
- Rabiner, L. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Gales, M.; Young, S. The Application of Hidden Markov Models in Speech Recognition. Found. Trends Signal Process. 2007, 1, 195–304. [Google Scholar] [CrossRef]
- Ogundile, O.; Usman, A.; Babalola, O.; Versfeld, D. A hidden Markov model with selective time domain feature extraction to detect inshore Bryde’s whale short pulse calls. Ecol. Inform. 2020, 57, 101087. [Google Scholar] [CrossRef]
- Putland, R.; Ranjard, L.; Constantine, R.; Radford, C. A hidden Markov model approach to indicate Bryde’s whale acoustics. Ecol. Indic. 2018, 84, 479–487. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.; Liu, W.; Gao, Y.; Lei, M.; Tan, H.; Yang, D. DNN-HMM based acoustic model for continuous pig cough sound recognition. Int. J. Agric. Biol. Eng. 2020, 13, 186–193. [Google Scholar] [CrossRef]
- Trawicki, M.B. Multispecies discrimination of whales (cetaceans) using Hidden Markov Models (HMMS). Ecol. Inform. 2021, 61, 101223. [Google Scholar] [CrossRef]
- Vieira, M.; Amorim, M.C.P.; Sundelöf, A.; Prista, N.; Fonseca, P. Underwater noise recognition of marine vessels passages: Two case studies using hidden Markov models. ICES J. Mar. Sci. 2019, 77, 2157–2170. [Google Scholar] [CrossRef]
- Kyhn, L.; Wisniewska, D.; Beedholm, K.; Tougaard, J.; Simon, M.; Mosbech, A.; Madsen, P. Basin-wide contributions to the underwater soundscape by multiple seismic surveys with implications for marine mammals in Baffin Bay, Greenland. Mar. Pollut. Bull. 2018, 138, 474–490. [Google Scholar] [CrossRef]
- Hanson, J.A. Indian Ocean ridge seismicity observed with a permanent hydroacoustic network. Geophys. Res. Lett. 2005, 32, 102931. [Google Scholar] [CrossRef]
- Metz, D.; Watts, A.B.; Grevemeyer, I.; Rodgers, M. Tracking Submarine Volcanic Activity at Monowai: Constraints from Long-Range Hydroacoustic Measurements. J. Geophys. Res. Solid Earth 2018, 123, 7877–7895. [Google Scholar] [CrossRef]
- Yun, S.; Ni, S.; Park, M.; Lee, W.S. Southeast Indian Ocean-Ridge earthquake sequences from cross-correlation analysis of hydroacoustic data. Geophys. J. Int. 2009, 179, 401–407. [Google Scholar] [CrossRef]
- Ingale, V.; Bazin, S.; Royer, J.-Y. Hydroacoustic observations of two contrasted seismic swarms along the Southwest Indian ridge in 2018. Geosciences 2021, 11, 225. [Google Scholar] [CrossRef]
- Tsang-Hin-Sun, E.; Royer, J.-Y.; Perrot, J. Seismicity and active accretion processes at the ultraslow-spreading Southwest and intermediate-spreading Southeast Indian ridges from hydroacoustic data. Geophys. J. Int. 2016, 206, 1232–1245. [Google Scholar] [CrossRef]
- Gomez, B.; Kadri, U. Earthquake source characterization by machine learning algorithms applied to acoustic signals. Sci. Rep. 2021, 11, 23062. [Google Scholar] [CrossRef] [PubMed]
- Benitez, M.C.; Ramirez, J.; Segura, J.C.; Ibanez, J.M.; Almendros, J.; Garcia-Yeguas, A.; Cortes, G. Continuous HMM-based seismic-event classification at deception Island, Antarctica. IEEE Trans. Geosci. Remote Sens. 2006, 45, 138–146. [Google Scholar] [CrossRef]
- Gutierrez, L.; Ibanez, J.; Cortes, G.; Ramirez, J.; Benitez, C.; Tenorio, V.; Isaac, A. Volcano-seismic signal detection and classification processing using hidden Markov models. Application to San Cristóbal volcano, Nicaragua. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 4, pp. IV-522–IV-525. [Google Scholar] [CrossRef]
- Trujillo-Castrillón, N.; Valdés-González, C.M.; Arámbula-Mendoza, R.; Santacoloma-Salguero, C.C. Initial processing of volcanic seismic signals using Hidden Markov Models: Nevado del Huila, Colombia. J. Volcanol. Geotherm. Res. 2018, 364, 107–120. [Google Scholar] [CrossRef]
- Beyreuther, M.; Wassermann, J. Continuous earthquake detection and classification using discrete Hidden Markov Models. Geophys. J. Int. 2008, 175, 1055–1066. [Google Scholar] [CrossRef]
- Ebel, J.E.; Chambers, D.W.; Kafka, A.L.; Baglivo, J.A. Non-Poissonian Earthquake Clustering and the Hidden Markov Model as Bases for Earthquake Forecasting in California. Seism. Res. Lett. 2007, 78, 57–65. [Google Scholar] [CrossRef]
- Pertsinidou, C.E.; Tsaklidis, G.; Papadimitriou, E.; Limnios, N. Application of hidden semi-Markov models for the seismic hazard assessment of the North and South Aegean Sea, Greece. J. Appl. Stat. 2016, 44, 1064–1085. [Google Scholar] [CrossRef]
- Haver, S.M.; Klinck, H.; Nieukirk, S.L.; Matsumoto, H.; Dziak, R.P.; Miksis-Olds, J.L. The not-so-silent world: Measuring Arctic, Equatorial, and Antarctic soundscapes in the Atlantic Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 2017, 122, 95–104. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, Y.; Tian, J.; Sun, C.; Zhao, W.; Li, Z.; Ma, Y. Long-term ambient noise statistics in the northeast South China Sea. J. Acoust. Soc. Am. 2019, 145, EL501–EL507. [Google Scholar] [CrossRef]
- Wilcock, W.S.; Stafford, K.M.; Andrew, R.K.; Odom, R.I. Sounds in the Ocean at 1–100 Hz. Annu. Rev. Mar. Sci. 2014, 6, 117–140. [Google Scholar] [CrossRef]
- Buchan, S.; Gutierrez, L.; Balcazar-Cabrera, N.; Stafford, K. Seasonal occurrence of fin whale song off Juan Fernandez, Chile. Endanger. Species Res. 2019, 39, 135–145. [Google Scholar] [CrossRef]
- Peddinti, V.; Povey, D.; Khudanpur, S. A time delay neural network architecture for efficient modeling of long temporal contexts. In Proceedings of the Sixteenth Annual Conference of the International Speech Communication Association, INTERSPEECH, Dresden, Germany, 6–10 September 2015; Volume 2015, pp. 3214–3218. [Google Scholar] [CrossRef]
- Viterbi, A. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inf. Theory 1967, 13, 260–269. [Google Scholar] [CrossRef]
- Calderan, S.; Miller, B.; Collins, K.; Ensor, P.; Double, M.; Leaper, R.; Barlow, J. Low-frequency vocalizations of sei whales (Balaenoptera borealis) in the Southern Ocean. J. Acoust. Soc. Am. 2014, 136, EL418–EL423. [Google Scholar] [CrossRef]
- Buchan, S.; Hucke-Gaete, R.; Rendell, L.; Stafford, K. A new song recorded from blue whales in the Corcovado Gulf, Southern Chile, and an acoustic link to the Eastern Tropical Pacific. Endanger. Species Res. 2014, 23, 241–252. [Google Scholar] [CrossRef]
- Cummings, W.C.; Thompson, P.O. Underwater Sounds from the Blue Whale, Balaenoptera musculus. J. Acoust. Soc. Am. 1971, 50, 1193–1198. [Google Scholar] [CrossRef]
- Charif, R.A.; Mellinger, D.K.; Dunsmore, K.J.; Fristrup, K.M.; Clark, C.W. Estimated source levels of fin whale (Balaenoptera physalus) vocalizations: Adjustments for surface interference. Mar. Mammal Sci. 2002, 18, 81–98. [Google Scholar] [CrossRef]
- Watkins, W.A.; Tyack, P.; Moore, K.E.; Bird, J.E. The 20-Hz signals of finback whales (Balaenoptera physalus). J. Acoust. Soc. Am. 1987, 82, 1901–1912. [Google Scholar] [CrossRef]
- Watkins, W.A. Activities and underwater sounds of fin whales. Sci. Rep. Whales Res. Inst. 1981, 33, 83–117. [Google Scholar]
- Delarue, J.; Martin, B.; Hannay, D.; Berchok, C.L. Acoustic Occurrence and Affiliation of Fin Whales Detected in the Northeastern Chukchi Sea, July to October 2007—10. Arctic 2013, 66, 159–172. Available online: http://www.jstor.org/stable/23594680 (accessed on 15 July 2021). [CrossRef]
- Baumgartner, M.F.; Fratantoni, D.M. Diel periodicity in both sei whale vocalization rates and the vertical migration of their copepod prey observed from ocean gliders. Limnol. Oceanogr. 2008, 53, 2197–2209. [Google Scholar] [CrossRef]
- Español-Jiménez, S.; Bahamonde, P.A.; Chiang, G.; Häussermann, V. Discovering sounds in Patagonia: Characterizing sei whale (Balaenoptera borealis) downsweeps in the south-eastern Pacific Ocean. Ocean Sci. 2019, 15, 75–82. [Google Scholar] [CrossRef]
- Mellinger, D.K.; Carson, C.D.; Clark, C.W. Characteristics of minke whale (Balaenoptera acutorostrata) pulse trains recorded near puerto rico. Mar. Mammal Sci. 2000, 16, 739–756. [Google Scholar] [CrossRef]
- Schevill, W.E.; Watkins, W.A. Intense Low-Frequency Sounds from An Antarctic Minke Whale: Balaenoptera acutorostrata; Woods Hole Oceanographic Institution: Falmouth, MA, USA, 1972. [Google Scholar]
- Shabangu, F.W.; Findlay, K.; Stafford, K.M. Seasonal acoustic occurrence, diel-vocalizing patterns and bioduck call-type composition of Antarctic minke whales off the west coast of South Africa and the Maud Rise, Antarctica. Mar. Mammal Sci. 2020, 36, 658–675. [Google Scholar] [CrossRef]
- De Angelis, S.; McNutt, S.R. Observations of volcanic tremor during the January–February 2005 eruption of Mt. Veniaminof, Alaska. Bull. Volcanol. 2007, 69, 927–940. [Google Scholar] [CrossRef]
- Dziak, R.P.; Fox, C.G.; Matsumoto, H.; Schreiner, A.E. The April 1992 Cape Mendocino Earthquake Sequence: Seismo-Acoustic Analysis Utilizing Fixed Hydrophone Arrays. Mar. Geophys. Res. 1997, 19, 137–162. [Google Scholar] [CrossRef]
- Nishimura, C.E. Monitoring Whales and Earthquakes by Using SOSUS; Naval Research Laboratory: Washington, DC, USA, 1994. [Google Scholar]
- Charif, R.; Strickman, L.M.; Waack, A.M. Raven Pro 1.4 User’s Manual; The Cornell Lab of Ornithology: Ithaca, NY, USA, 2010. [Google Scholar]
- Davis, S.; Mermelstein, P. Comparison of parametric representations for monosyllabic word recognition in continuously spoken sentences. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 357–366. [Google Scholar] [CrossRef]
- Pedersen, P. The Mel Scale. J. Music. Theory 1965, 9, 295–308. Available online: https://about.jstor.org/terms (accessed on 15 July 2022). [CrossRef]
- Gales, M. Semi-tied covariance matrices for hidden Markov models. IEEE Trans. Speech Audio Process. 1999, 7, 272–281. [Google Scholar] [CrossRef]
- Povey, D.; Mittal, S. The Kaldi Speech Recognition Toolkit. 2011. Available online: http://kaldi.sf.net/ (accessed on 15 July 2022).
- Leonard, B.E.; Ted, P.; George, S.; Norman, W. A maximization technique occurring in the statistical analysis of probabilistic functions of markov chains. Ann. Math. Stat. 1970, 41, 164–171. [Google Scholar]
- Maas, A.L.; Qi, P.; Xie, Z.; Hannun, A.Y.; Lengerich, C.T.; Jurafsky, D.; Ng, A.Y. Building DNN acoustic models for large vocabulary speech recognition. Comput. Speech Lang. 2017, 41, 195–213. [Google Scholar] [CrossRef]
- Rath, S.P.; Povey, D.; Veselý, K.; Cernocký, J. Improved feature processing for Deep Neural Networks. In Proceedings of the 14th Annual Conference of the International Speech Communication Association, Lyon, France, 25–29 August 2013. [Google Scholar]
- Paul, D.B.; Baker, J.M. The Design for the Wall Street Journal-based CSR Corpus *. In Proceedings of the Speech and Natural Language: Proceedings of a Workshop, Harriman, NY, USA, 23–26 February 1992. [Google Scholar]
- Peddinti, V.; Wang, Y.; Povey, D.; Khudanpur, S. Low latency acoustic modeling using temporal convolution and LSTMs. IEEE Signal Process. Lett. 2017, 25, 373–377. [Google Scholar] [CrossRef]
- Zhang, Z.; Sabuncu, M.R. Generalized Cross Entropy Loss for Training Deep Neural Networks with Noisy Labels. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Fred Agarap, A.M. Deep Learning Using Rectified Linear Units (ReLU). 2018. Available online: https://github.com/AFAgarap/relu-classifier (accessed on 15 July 2022).
- Bengio, Y.O.; de Mori, R.; Cardin, R. Speaker Independent Speech Recognition with Neural Networks and Speech Knowledge. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 27–30 November 1989. [Google Scholar]
- Wang, D.; Wang, X.; Lv, S. An Overview of End-to-End Automatic Speech Recognition. Symmetry 2019, 11, 1018. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.-R.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Hollmann, H. A relation between Levenshtein-type distances and insertion-and-deletion correcting capabilities of codes. IEEE Trans. Inf. Theory 1993, 39, 1424–1427. [Google Scholar] [CrossRef]
- Širović, A.; Hildebrand, J.A.; Wiggins, S.M.; McDonald, M.A.; Moore, S.E.; Thiele, D. Seasonality of blue and fin whale calls and the influence of sea ice in the Western Antarctic Peninsula. Deep Sea Res. Part II Top. Stud. Oceanogr. 2004, 51, 2327–2344. [Google Scholar] [CrossRef]
- Nieukirk, S.L.; Stafford, K.M.; Mellinger, D.K.; Dziak, R.P.; Fox, C.G. Low-frequency whale and seismic airgun sounds recorded in the mid-Atlantic Ocean. J. Acoust. Soc. Am. 2004, 115, 1832–1843. [Google Scholar] [CrossRef]
- De Caro, M.; Montuori, C.; Frugoni, F.; Monna, S.; Cammarano, F.; Beranzoli, L. T-Phases Observed at the Ionian Seafloor: Seismic Source and Bathymetric Effects. Seism. Res. Lett. 2020, 92, 481–493. [Google Scholar] [CrossRef]


| Class Label | Precision HMM-DNN | Sensitivity HMM-DNN | F1-Score HMM-DNN | N |
|---|---|---|---|---|
| FWS | 94.05% | 88.50% | 91.19% | 4671 |
| AA | 83.01% | 91.51% | 87.05% | 386 |
| AG | 97.02% | 75.84% | 85.13% | 103 |
| SWD | 96.40% | 69.76% | 80.95% | 36 |
| AN | 81.03% | 79.01% | 80.01% | 31 |
| FWD | 83.33% | 67.23% | 74.42% | 254 |
| S23 | 75.55% | 67.07% | 71.06% | 104 |
| FWD2 | 71.66% | 67.34% | 69.43% | 22 |
| ERQ | 55.01% | 88.33% | 67.80% | 270 |
| FWD3 | 83.11% | 57.14% | 67.72% | 55 |
| SWU | 63.61% | 70.45% | 66.86% | 62 |
| S13 | 60.00% | 74.35% | 66.41% | 44 |
| AAFWS | 50.13% | 73.43% | 59.58% | 21 |
| S21 | 46.02% | 68.00% | 54.89% | 28 |
| 13H | 32.35% | 95.21% | 48.29% | 27 |
| MI | 63.91% | 28.57% | 39.49% | 10 |
| UND | 45.56% | 33.33% | 38.50% | 49 |
| SEP | 20.26% | 46.21% | 28.17% | 25 |
| S22 | 23.39% | 12.96% | 16.68% | 17 |
| System | Minimum Number of Exemplars | Event-Level Accuracy | I | D | S | WER | |
|---|---|---|---|---|---|---|---|
| HMM-DNN | 70 | 84.46% | 589 | 757 | 209 | 25.02 | 6215 |
| HMM-GMM | 70 | 82.35% | 548 | 889 | 208 | 26.47 | 6215 |
| HMM-DNN | 500 | 89.01% | 460 | 583 | 100 | 23.75 | 4812 |
| HMM-GMM | 500 | 84.63% | 351 | 861 | 94 | 27.14 | 4812 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buchan, S.J.; Duran, M.; Rojas, C.; Wuth, J.; Mahu, R.; Stafford, K.M.; Becerra Yoma, N. An HMM-DNN-Based System for the Detection and Classification of Low-Frequency Acoustic Signals from Baleen Whales, Earthquakes, and Air Guns off Chile. Remote Sens. 2023, 15, 2554. https://doi.org/10.3390/rs15102554
Buchan SJ, Duran M, Rojas C, Wuth J, Mahu R, Stafford KM, Becerra Yoma N. An HMM-DNN-Based System for the Detection and Classification of Low-Frequency Acoustic Signals from Baleen Whales, Earthquakes, and Air Guns off Chile. Remote Sensing. 2023; 15(10):2554. https://doi.org/10.3390/rs15102554
Chicago/Turabian StyleBuchan, Susannah J., Miguel Duran, Constanza Rojas, Jorge Wuth, Rodrigo Mahu, Kathleen M. Stafford, and Nestor Becerra Yoma. 2023. "An HMM-DNN-Based System for the Detection and Classification of Low-Frequency Acoustic Signals from Baleen Whales, Earthquakes, and Air Guns off Chile" Remote Sensing 15, no. 10: 2554. https://doi.org/10.3390/rs15102554
APA StyleBuchan, S. J., Duran, M., Rojas, C., Wuth, J., Mahu, R., Stafford, K. M., & Becerra Yoma, N. (2023). An HMM-DNN-Based System for the Detection and Classification of Low-Frequency Acoustic Signals from Baleen Whales, Earthquakes, and Air Guns off Chile. Remote Sensing, 15(10), 2554. https://doi.org/10.3390/rs15102554






