An Image Planar Positioning Method Base on Fusion of Dual-View Airborne SAR Data
Abstract
1. Introduction
2. Fusion Positioning Algorithm of Dual-View Airborne SAR Images
2.1. Transformation of Geospatial Position and Pixel Position Based on Affine
2.2. Systematic Positioning Error Estimation of the Initial Ground-Range Airborne SAR Imagery
2.3. The Flow of Fusion Positioning Algorithm
- (1)
- For two initial ground-range airborne SAR images that have good intersection effect and relatively consistent systematic positioning errors in both range and azimuth directions, according to the positioning auxiliary parameters of each SAR image, the transformation matrices (C1, D1) and (C2, D2) between the target pixel positions and the target initial geographic positions in each SAR image are, respectively, solved.
- (2)
- Select the same road intersection, building corner, or prominent natural landmark that could be readily identified, which is contained in two initial ground-range airborne SAR images as a Hp, and then use Equation (3) to set up the equivalent equation of Hp’s actual geographic position.
- (3)
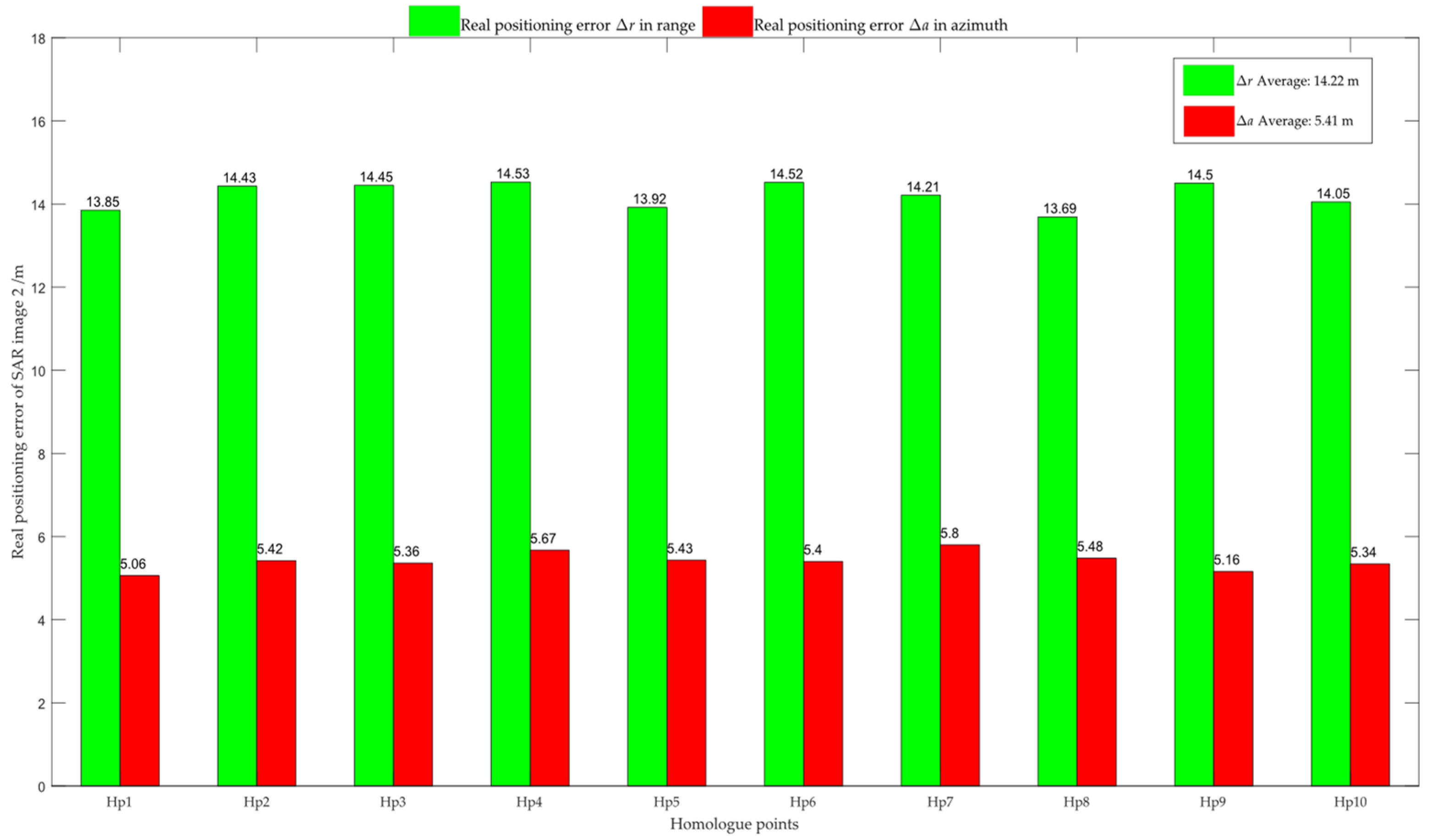
- Assess the systematic positioning errors (Δr, Δa) of the initial ground-range airborne SAR imagery according to Equation (4) and accomplish the high-precision plan positioning of each image pixel. To enhance the stability of the proposed positioning method, we can select multiple homologue points in the initial SAR images and use each homologue point to assess the systematic positioning errors of the initial SAR imagery individually, and, finally, take the average value of the assessed systematic positioning errors as the actual systematic positioning errors of the initial SAR imagery.
3. Experiment Results and Analysis
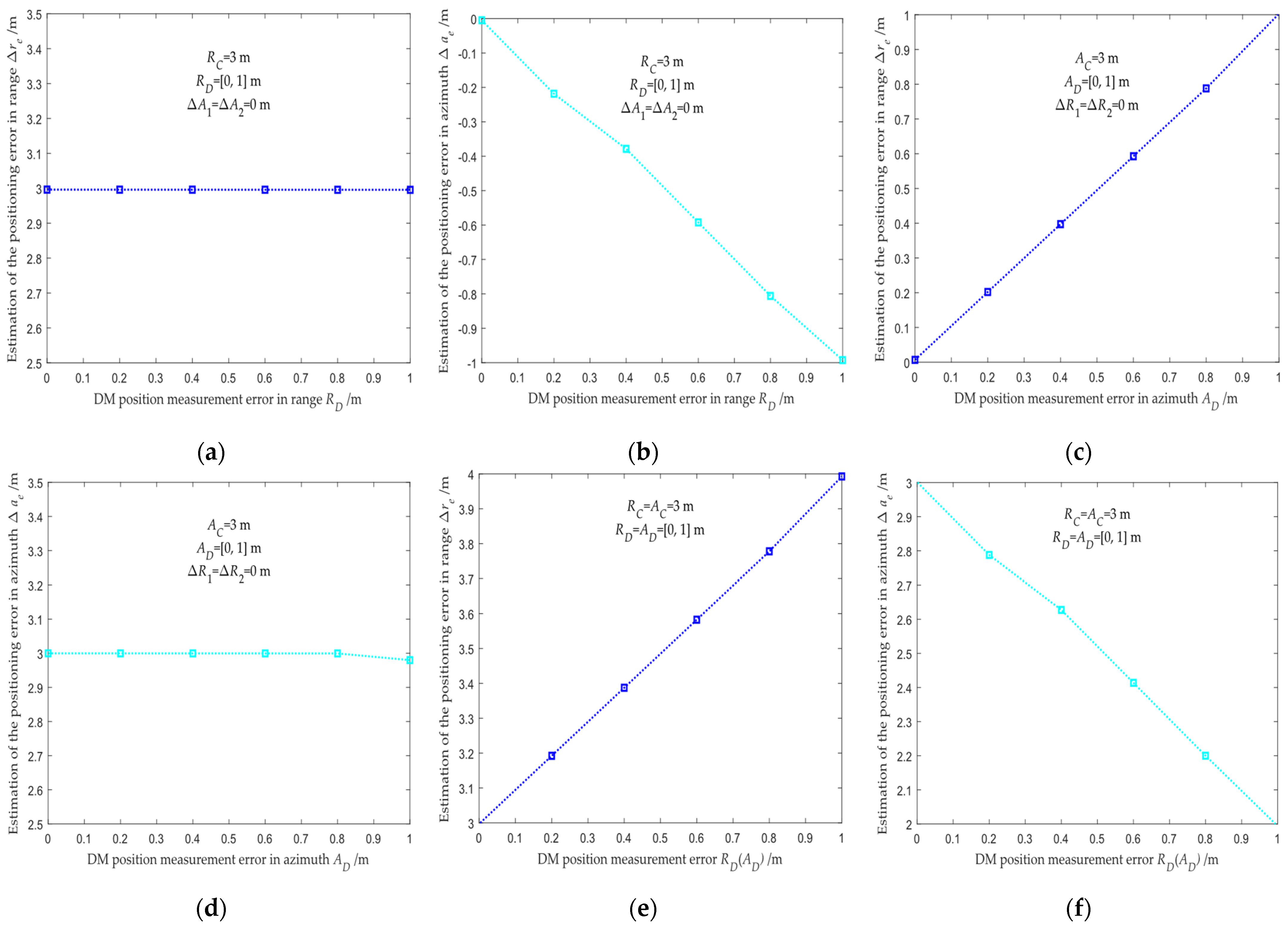
3.1. Algorithm Validation Based on Simulation Data
3.2. Experiment on the Real Recorded Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Tanaka, T.; Parwata, I.N.S.; Yastika, P.E. Synthetic aperture radar interferometry: Utilizing radar principles. IEEE Geosci. Remote Sens. Mag. 2020, 8, 111–116. [Google Scholar] [CrossRef]
- Deng, M.; Zhang, G.; Cai, C.; Xu, K.; Zhao, R.; Guo, F.; Suo, J. Improvement and Assessment of the Absolute Positioning Accuracy of Chinese High-Resolution SAR Satellites. Remote Sens. 2019, 11, 1465. [Google Scholar] [CrossRef]
- Daout, S.; Parsons, B.; Walker, R. Post–earthquake fold growth imaged in the Qaidam basin, China, with interferometric synthetic aperture radar. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021241. [Google Scholar] [CrossRef]
- Jiao, N.; Wang, F.; You, H.; Qiu, X. Geolocation Accuracy Improvement of Multiobserved GF-3 Spaceborne SAR imagery. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1747–1751. [Google Scholar] [CrossRef]
- Song, Y.; Li, J.; Gao, P.; Li, L.; Tian, T.; Tian, J. Two–Stage Cross–Modality Transfer Learning Method for Military–Civilian SAR Ship Recognition. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4506405. [Google Scholar] [CrossRef]
- Chen, X.; Ling, J.; Wang, S.; Yang, Y.; Luo, L.; Yan, Y. Ship detection from coastal surveillance videos via an ensemble Canny–Gaussian–morphology framework. J. Navig. 2021, 74, 1252–1266. [Google Scholar] [CrossRef]
- Liu, C.-A.; Chen, Z.; Wang, D.; Li, D. Assessment of the X– and C–Band Polarimentric SAR Data for Plastic–Mulched Farmland Classification. Remote Sens. 2019, 11, 660. [Google Scholar] [CrossRef]
- He, Z.; Li, Z.; Chen, X.; Yu, A.; Yi, T.; Dong, Z. Detecting Moving Target on Ground Based on Its Shadow by Using VideoSAR. Remote Sens. 2021, 13, 3291. [Google Scholar] [CrossRef]
- Cao, R.; Wang, S.; Sun, S.; Zhang, Y. Three Dimension Airborne SAR Imaging of Rotational Target With Single Antenna and Performance Analysis. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5225417. [Google Scholar] [CrossRef]
- Liu, X.; Teng, X.; Li, Z.; Yu, Q.; Bian, Y. A Fast Algorithm for High Accuracy Airborne SAR Geolocation Based on Local Linear Approximation. IEEE Trans. Instrum. Meas. 2022, 71, 550161. [Google Scholar] [CrossRef]
- Li, M. Research of Airborne High Resolution SAR Imaging and Location Techniques. Master’s Thesis, Xidian University, Xi’an, China, 2018. [Google Scholar]
- Jiang, W.; Yu, A.; Dong, Z. Refined polynomial geometric correction methods for spaceborne SAR image. In Proceedings of the 2016 CIE International Conference on Radar, Guangzhou, China, 10–13 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Kim, N.; Choi, Y.; Bae, J.; Sohn, H.G. Estimation and Improvement in the Geolocation Accuracy of Rational Polynomial Coefficients with Minimum Gcps Using KOMPSAT-3A. GISci. Remote Sens. 2020, 57, 719–734. [Google Scholar] [CrossRef]
- Han, J.; Guo, J.; Chou, J. A Direct Determination of the Orientation Parameters in the Collinearity Equations. IEEE Geosci. Remote Sens. Lett. 2011, 8, 313–316. [Google Scholar] [CrossRef]
- Wu, C.; Qin, Q.; Ma, G.; Fu, Z.; Wu, B. Improved Altitude Spatial Resection Algorithm for Oblique Photogrammetry. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1441–1445. [Google Scholar] [CrossRef]
- Liu, J.; Liu, D.; Zhang, Y.; Wang, Q. Research on Geometry Rectification and Accuracy Evaluation for the ZY-3 Remote Sensing Imagery Based on the Sparse Control Points. In Proceedings of the 8th International Conference on Digital Image Processing (ICDIP), Chengdu, China, 20–23 May 2016. [Google Scholar] [CrossRef]
- Leberl, F.W.; Kobrick, M.; Domik, G. Mapping with aircraft and satellite radar images. Photogramm. Rec. 1985, 11, 647–665. [Google Scholar] [CrossRef]
- Curlander, J.C. Location of Spaceborne Sar Imagery. IEEE Trans. Geosci. Remote Sens. 1982, 20, 359–364. [Google Scholar] [CrossRef]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Sun, W.; An, C.; Zhang, C. Range–Doppler Approach for Calibration and Location of Air–borne SAR Image. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar] [CrossRef]
- Yu, M.; Li, F.; Deng, Y.; Zhang, H.; Yu, W.; Wang, R. Preliminary Analgsis of Geometric Positioning Accuracy Based on Gaofen-3 Data. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2937–2940. [Google Scholar] [CrossRef]
- Wang, D.; Liu, A.; Xia, X. New method for airborne SAR image positioning. J. Eng. 2019, 19, 6021–6023. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, C.; Cao, G. Stereo localization method for air-borne SAR image based on range equation. Zhongguo Kexueyuan Daxue Xuebao 2020, 37, 798–804. [Google Scholar] [CrossRef]
- Liang, Y.; Sun, K.; Dang, Y.F.; Li, Q.Q.; Wu, J.X.; Xing, M.D. SAR platform positioning method based on improved Gauss–Newton–genetic hybrid algorithm. IET Radar Sonar Navig. 2019, 13, 1154–1161. [Google Scholar] [CrossRef]
- Wilamowski, B.M.; Yu, H. Improved computation for Levenberg–Marquardt training. IEEE Trans. Neural Netw. 2010, 21, 930–937. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Qiu, X.; Dong, Q.; Fu, K. A robust stereo positioning solution for multiview spaceborne SAR images based on Range–Doppler model. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4008705. [Google Scholar] [CrossRef]
- Jing, G.; Wang, H.; Xing, M.; Lin, X. A Novel Two-Step Registration Method for Multi-Aspect SAR Images. In Proceedings of the 2018 China International SAR Symposium (CISS), Shanghai, China, 10–12 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Walterscheid, I.; Brenner, A.R. Multistatic and multi-aspect SAR data acquisition to improve image interpretation. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium, Melbourne, VIC, Australia, 21–26 July 2013; pp. 4194–4197. [Google Scholar] [CrossRef]
- Miao, H.; Wang, Y.; Zhang, B.; Huang, Q. Influence of the motion error to airborne SAR geolocation accuracy. Electron. Meas. Technol. 2007, 1, 63–67. [Google Scholar] [CrossRef]
- Song, W.; Zhu, D.; Li, Y. Airborne Spotlight SAR Geolocation Accuracy. J. Data Acquis. Process. 2014, 29, 555–561. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, A.; Chen, X.; Wang, Z.; Dong, Z. Comparative Analysis of Single-View and Multi-View Airborne SAR Positioning Error and Course Planning for Multi-View Airborne SAR Optimal Positioning. Remote Sens. 2022, 14, 3055. [Google Scholar] [CrossRef]
- Song, J.; Liao, J. A 3-dimensional polynomial model for geometric corrections of airborne SAR images. In Proceedings of the 17th China Conference on Remote Sensing, Hangzhou, China, 15 August 2011. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, G.; Xu, Q.; Li, X. Accurate Positioning with stereo SAR Images and One Ground Control Point. J. Radars. 2014, 3, 85–91. Available online: http://radars.ac.cn/article/doi/10.3724/SP.J.1300.2014.13138 (accessed on 3 May 2023).


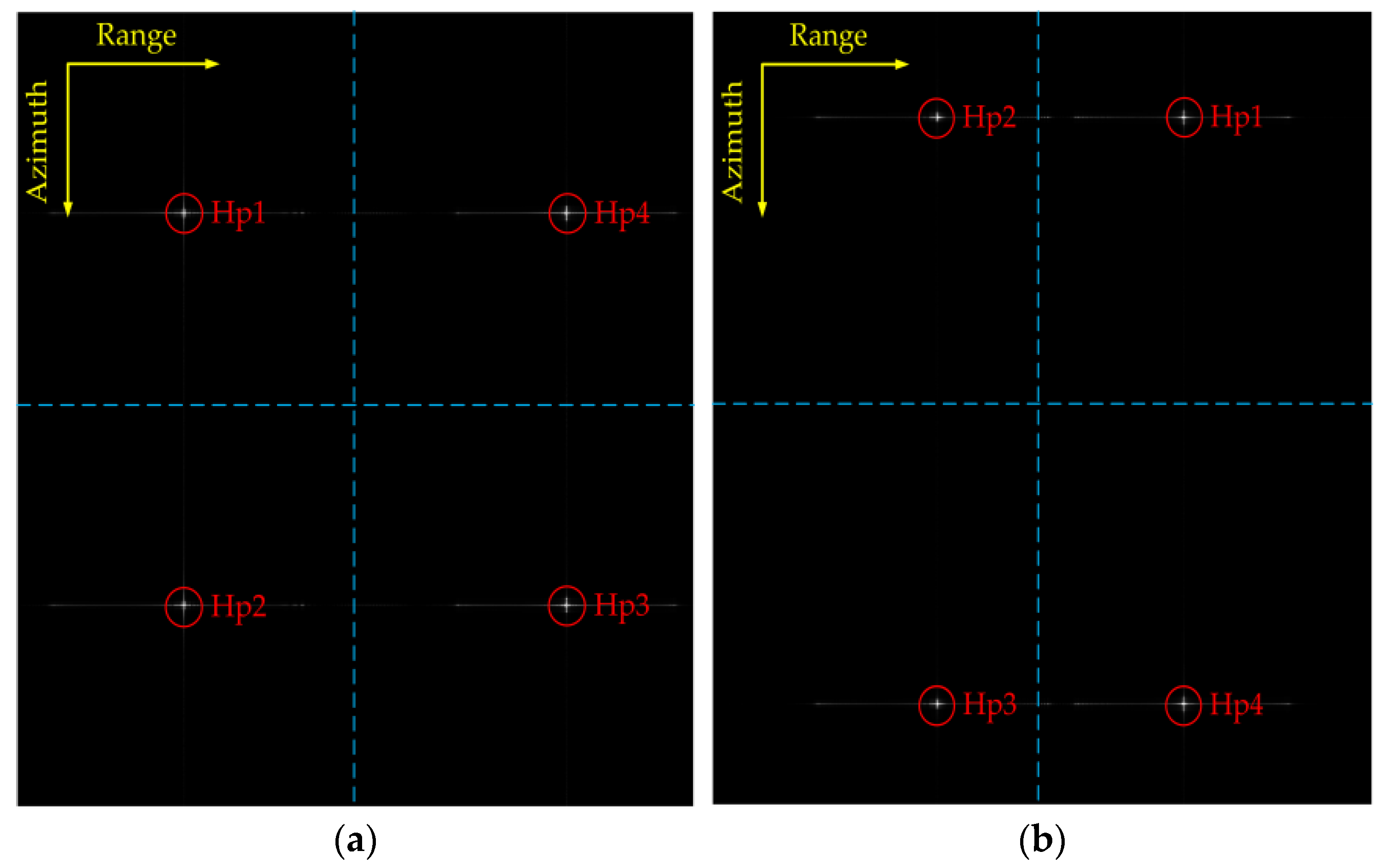
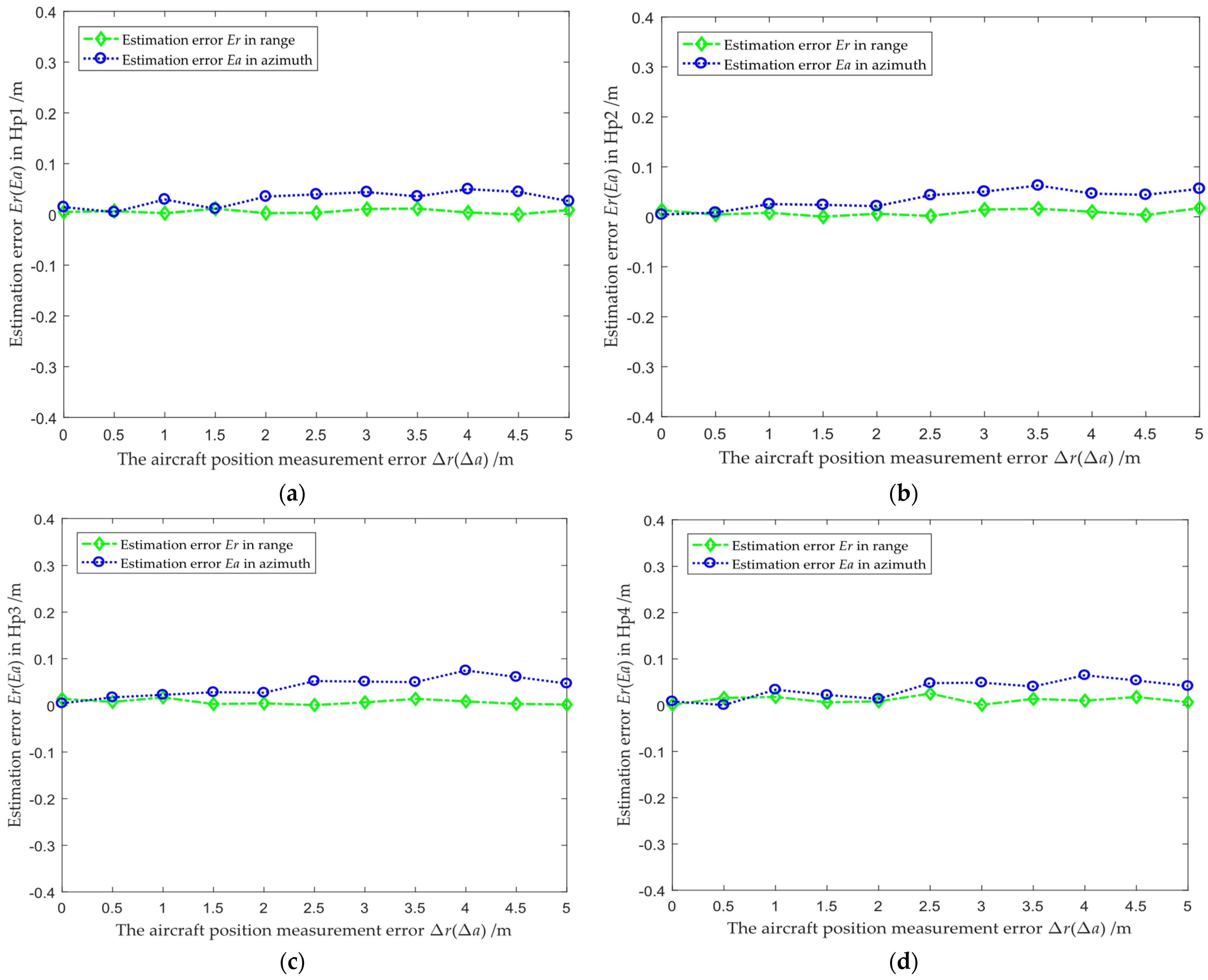
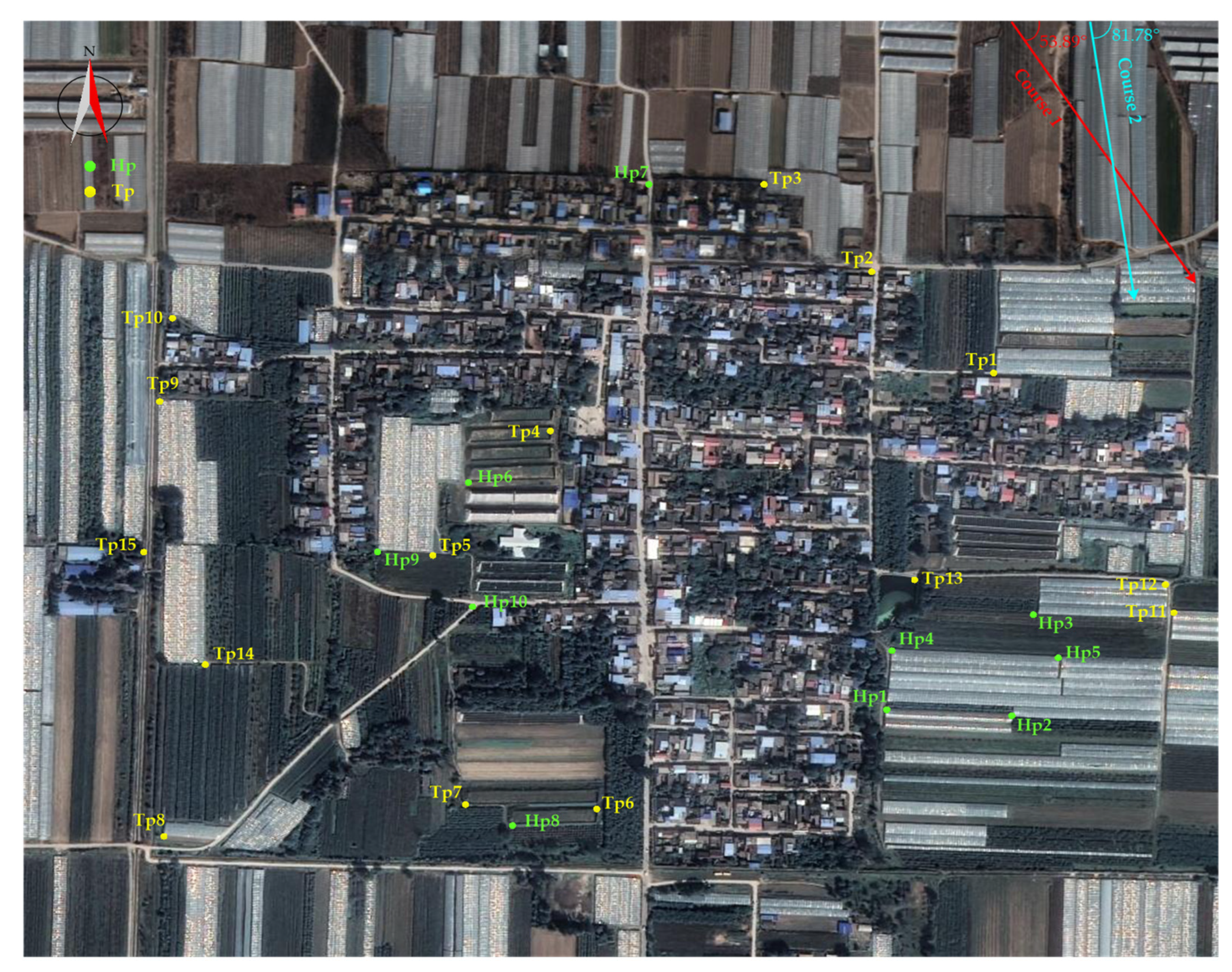

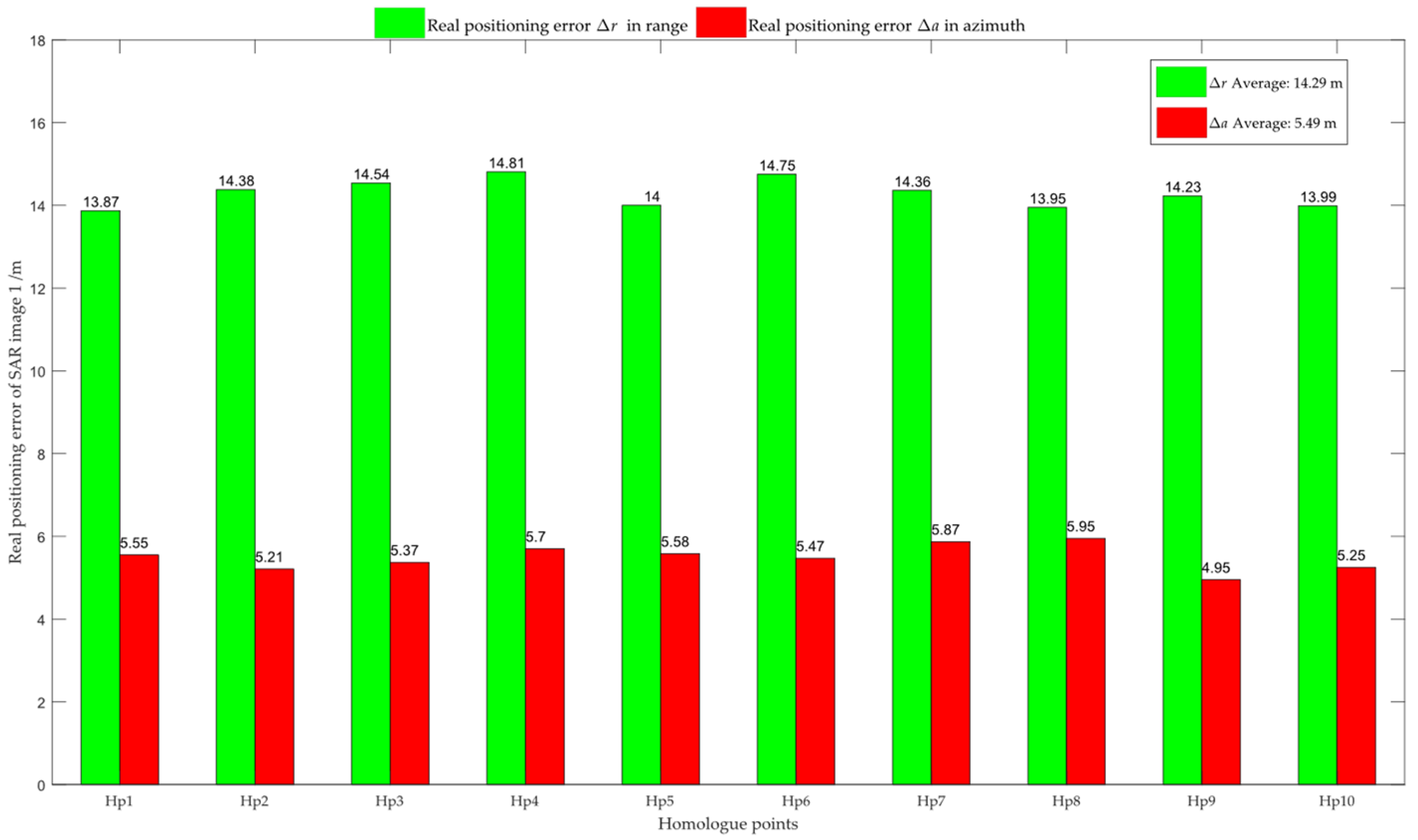




| Parameters | Value |
|---|---|
| Carrier frequency | 17 GHz |
| Bandwidth | 80 MHz |
| Platform height | 4 km |
| Platform velocity | 150 m/s |
| Slant-range of scene center | 10 km |
| Squint angle | 0° |
| Range sampling interval | 1.773 m |
| Azimuth sampling interval | 1.250 m |
| Type | Longitude/(°) | Latitude/(°) | Altitude/m |
|---|---|---|---|
| Starting position 1 | −90 | 0 | 4000.00 |
| Starting position 2 | −89.9543176 | 0.1189882 | 4000.00 |
| Hp1 | −89.9446175 | 0.0185621 | 3.31 |
| Hp2 | −89.9446175 | 0.0547369 | 5.87 |
| Hp3 | −89.8907187 | 0.0547368 | 14.49 |
| Hp4 | −89.8907187 | 0.0185621 | 11.93 |
| Parameters | First Imaging | Second Imaging |
|---|---|---|
| Frequency band | Ku | Ku |
| Imaging resolution (m × m) | 0.2 × 0.2 | 0.2 × 0.2 |
| Platform height (m) | 4266 | 4260 |
| Platform velocity (m/s) | 149.0450 | 173.2956 |
| Heading angle (°) | 143.89 | 171.78 |
| Longitude of imaging center (°) | 110.0676 | 110.0611 |
| Latitude of imaging center (°) | 34.7892 | 34.7937 |
| Range sampling interval (m) | 0.1259 | 0.1259 |
| Azimuth sampling interval (m) | 0.1380 | 0.0899 |
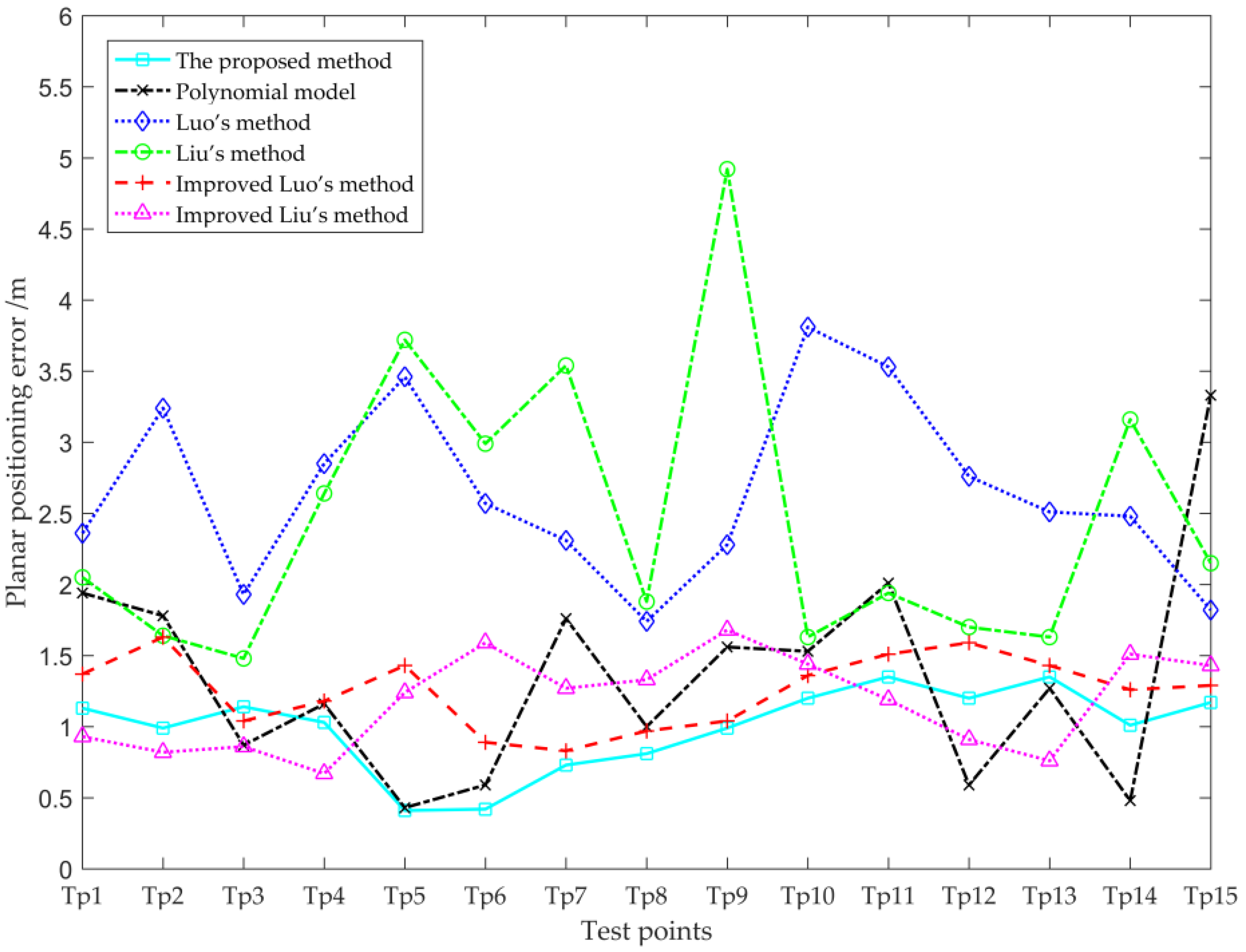
| Point Number | Polynomial Model | Luo’s Method | Liu’s Method | Improved Luo’s Method | Improved Liu’s Method | The Proposed Method |
|---|---|---|---|---|---|---|
| Tp1 | 1.94 | 2.36 | 2.05 | 1.37 | 0.93 | 1.13 |
| Tp2 | 1.78 | 3.24 | 1.64 | 1.63 | 0.82 | 0.99 |
| Tp3 | 0.87 | 1.93 | 1.48 | 1.04 | 0.86 | 1.14 |
| Tp4 | 1.16 | 2.85 | 2.64 | 1.18 | 0.67 | 1.03 |
| Tp5 | 0.43 | 3.46 | 3.72 | 1.43 | 1.24 | 0.41 |
| Tp6 | 0.59 | 2.57 | 2.99 | 0.89 | 1.59 | 0.42 |
| Tp7 | 1.76 | 2.31 | 3.54 | 0.83 | 1.27 | 0.73 |
| Tp8 | 0.99 | 1.74 | 1.88 | 0.97 | 1.33 | 0.81 |
| Tp9 | 1.56 | 2.28 | 4.92 | 1.04 | 1.68 | 0.99 |
| Tp10 | 1.53 | 3.81 | 1.63 | 1.36 | 1.44 | 1.20 |
| Tp11 | 2.01 | 3.53 | 1.94 | 1.51 | 1.19 | 1.35 |
| Tp12 | 0.59 | 2.76 | 1.70 | 1.59 | 0.91 | 1.20 |
| Tp13 | 1.27 | 2.51 | 1.63 | 1.43 | 0.76 | 1.35 |
| Tp14 | 0.48 | 2.48 | 3.16 | 1.26 | 1.51 | 1.01 |
| Tp15 | 3.33 | 1.82 | 2.15 | 1.29 | 1.43 | 1.17 |
| Category | Polynomial Model | Luo’s Method | Liu’s Method | Improved Luo’s Method | Improved Liu’s Method | The Proposed Method |
|---|---|---|---|---|---|---|
| MAE | 1.35 | 2.64 | 2.47 | 1.25 | 1.17 | 0.99 |
| RMSE | 1.54 | 2.71 | 2.65 | 1.27 | 1.21 | 1.03 |
| Absolute Difference | Δi1 | Δj1 | Δi2 | Δj2 |
|---|---|---|---|---|
| |Δre2−Δre1| | 0.2252Δi1 | 0.3471Δj1 | 0.3511Δi2 | 0.2260Δj2 |
| |Δae2−Δae1| | 0.2478Δi1 | 0.0477Δj1 | 0.2478Δi2 | 0.0588Δj2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Yu, A.; Chen, X.; Tang, F.; Zhang, Y. An Image Planar Positioning Method Base on Fusion of Dual-View Airborne SAR Data. Remote Sens. 2023, 15, 2499. https://doi.org/10.3390/rs15102499
Zhang B, Yu A, Chen X, Tang F, Zhang Y. An Image Planar Positioning Method Base on Fusion of Dual-View Airborne SAR Data. Remote Sensing. 2023; 15(10):2499. https://doi.org/10.3390/rs15102499
Chicago/Turabian StyleZhang, Ben, Anxi Yu, Xing Chen, Feixiang Tang, and Yongsheng Zhang. 2023. "An Image Planar Positioning Method Base on Fusion of Dual-View Airborne SAR Data" Remote Sensing 15, no. 10: 2499. https://doi.org/10.3390/rs15102499
APA StyleZhang, B., Yu, A., Chen, X., Tang, F., & Zhang, Y. (2023). An Image Planar Positioning Method Base on Fusion of Dual-View Airborne SAR Data. Remote Sensing, 15(10), 2499. https://doi.org/10.3390/rs15102499






