Spatial Prediction of Soil Organic Carbon Stock in the Moroccan High Atlas Using Machine Learning
Abstract
1. Introduction
2. Materials and Methods
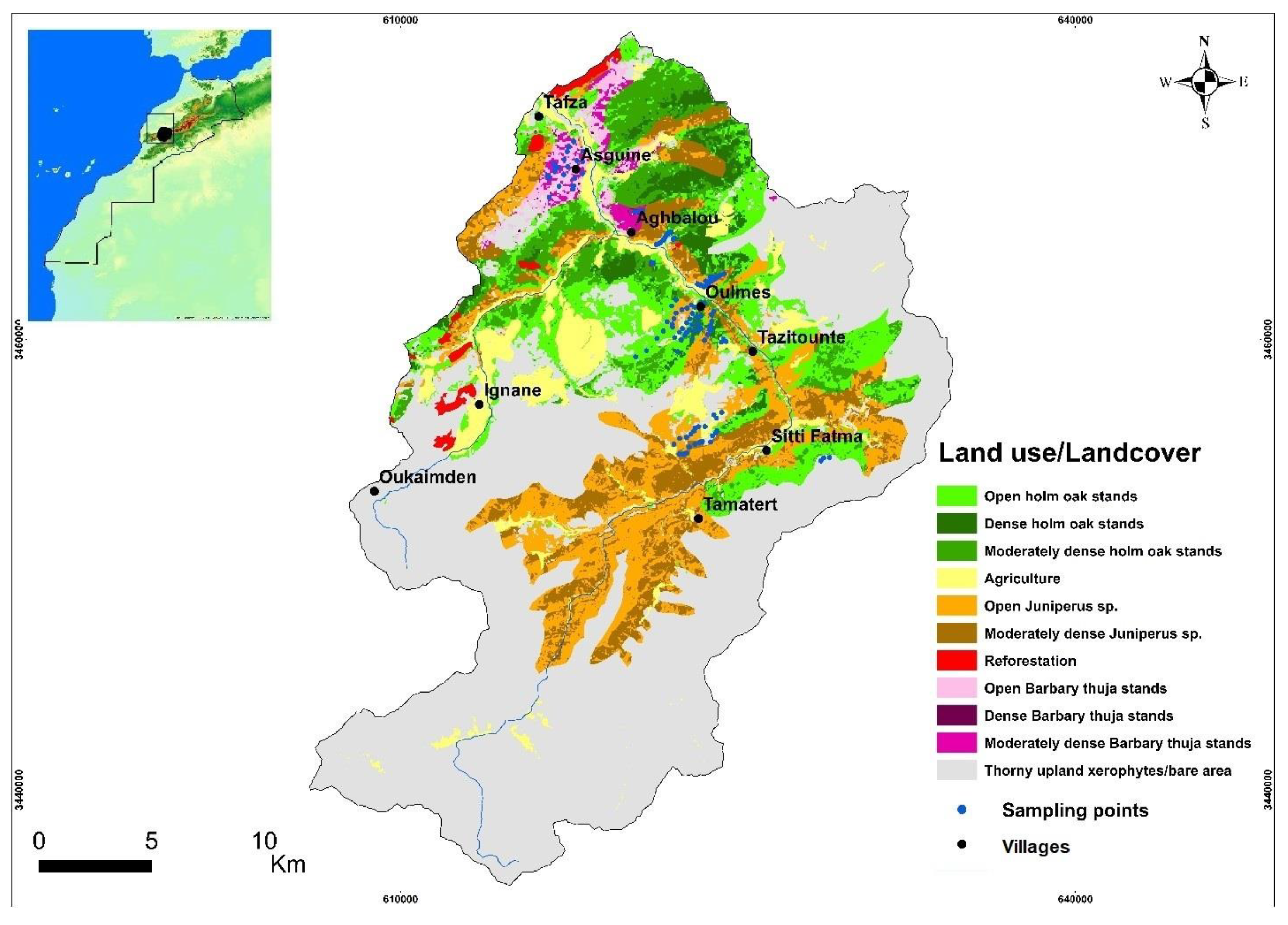
2.1. Study Area
2.2. Sample Collection and Analysis
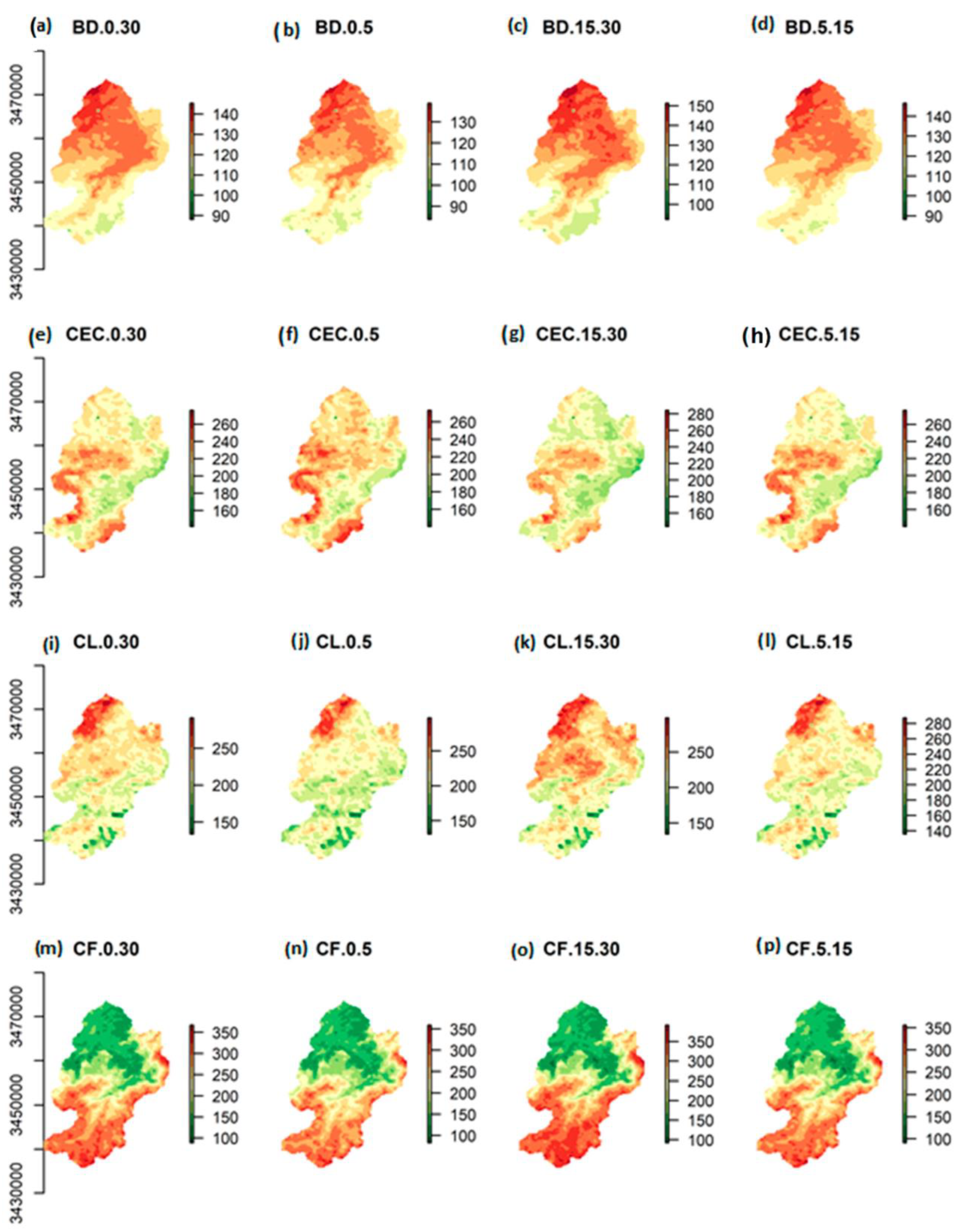
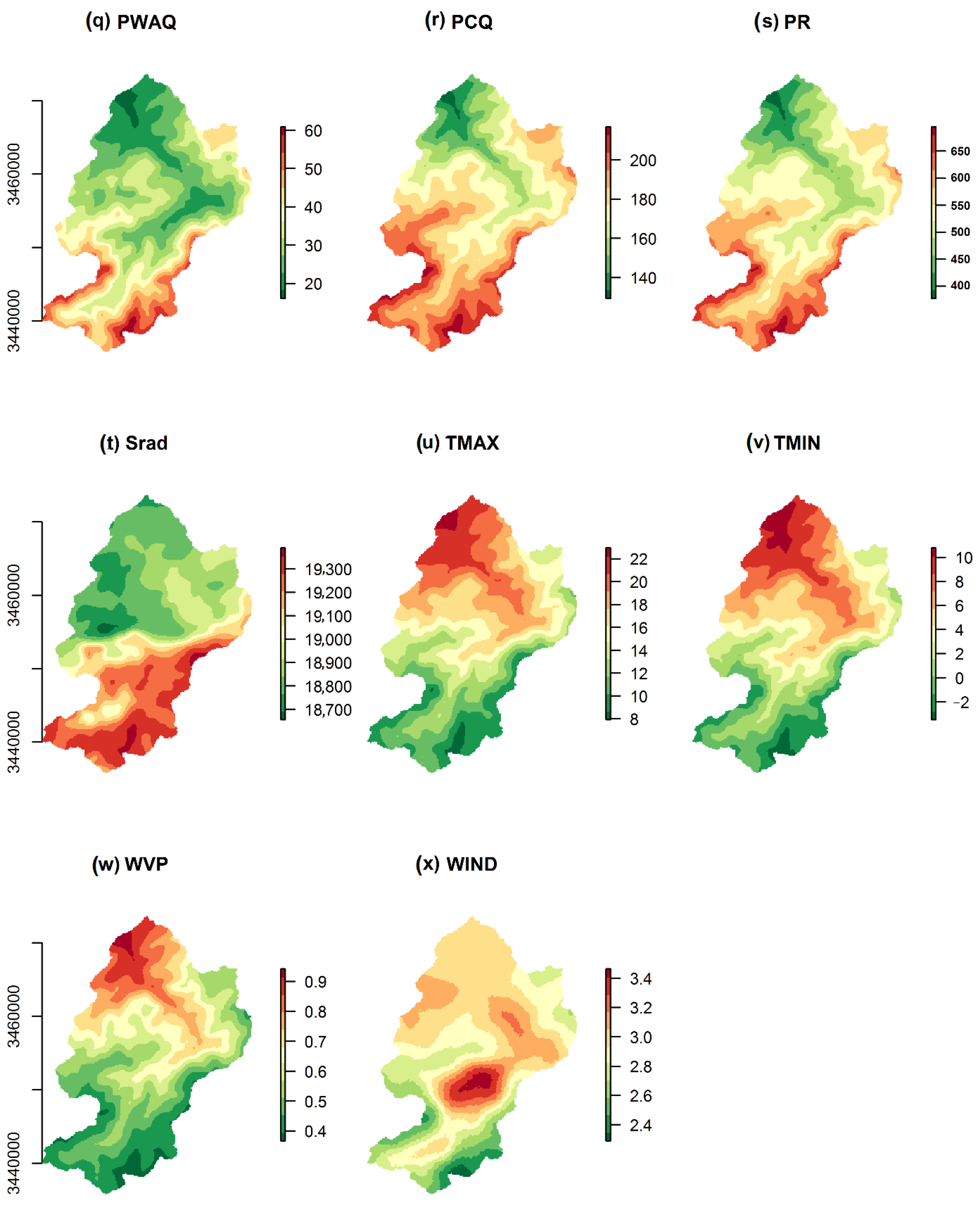
2.3. Predictor Variables for Modeling
2.4. Regression Algorithms
2.4.1. Random Forest (RF)
2.4.2. Cubist
2.4.3. Support Vector Machine (SVM)
2.4.4. Gradient Boosting Machine (GBM)
2.5. Variable Selection and Cross Validation
2.6. Modeling, Models Comparison and Validation
3. Results
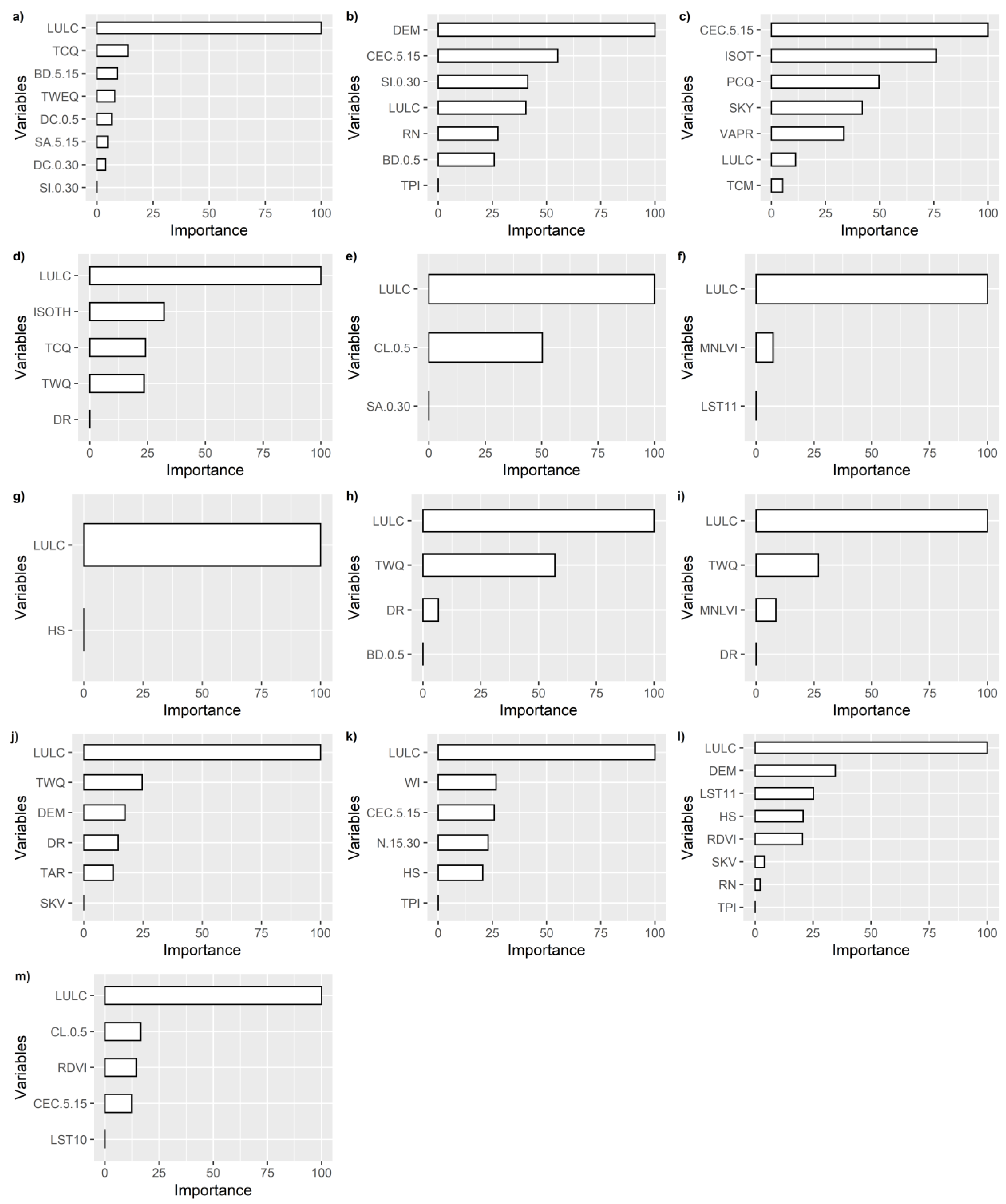
3.1. Variable Selection and Variable Importance
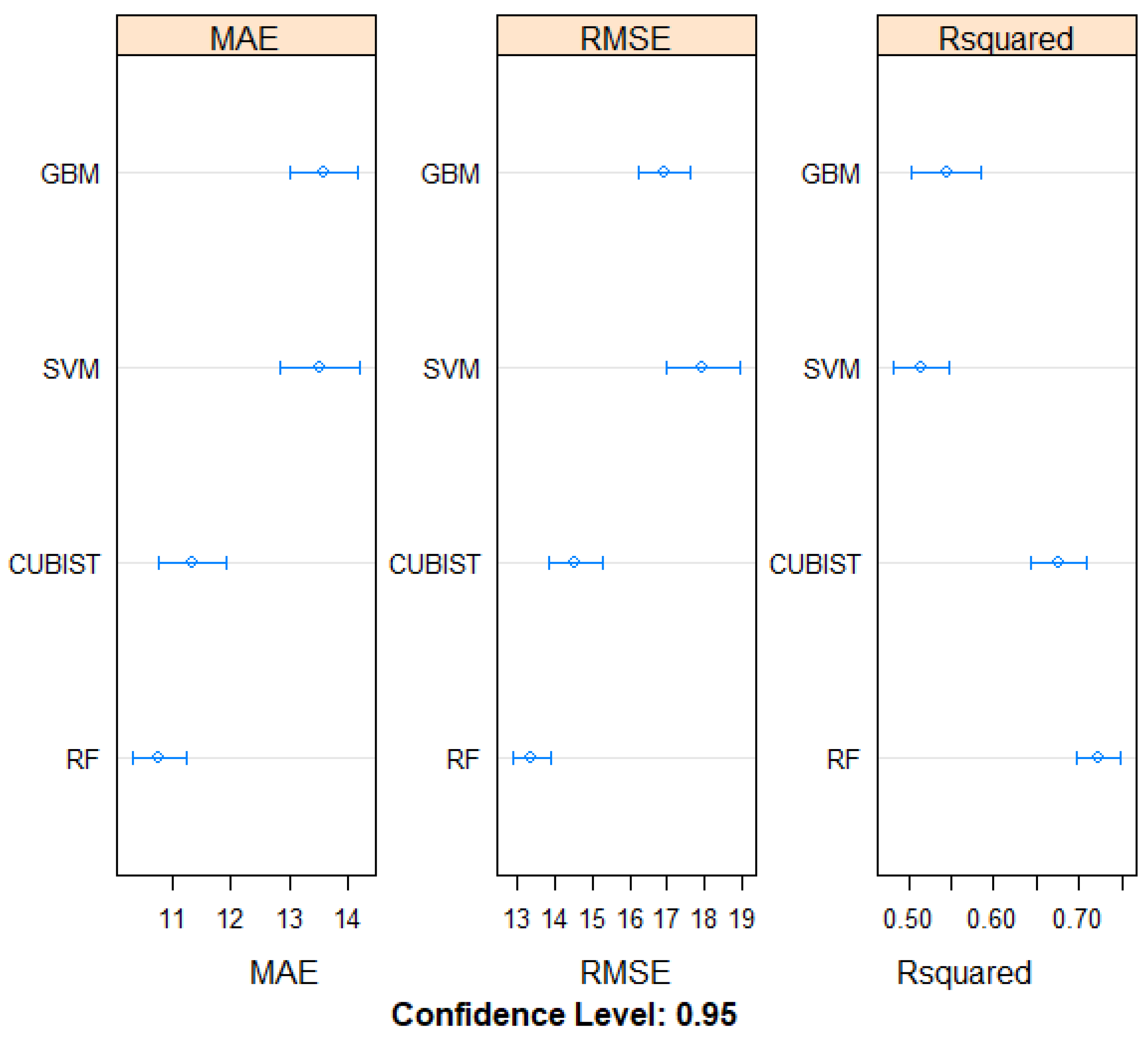
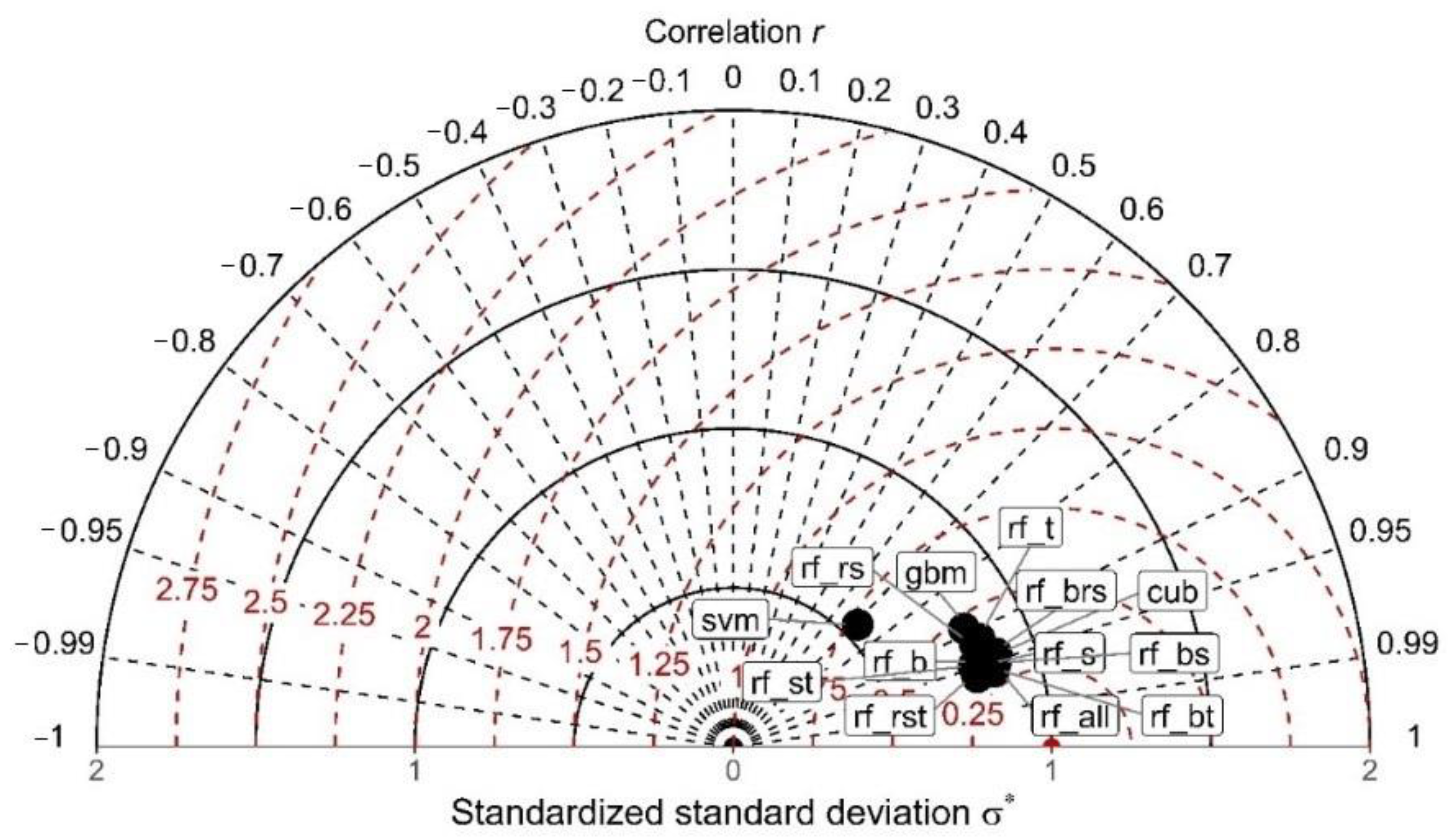
3.2. Model Evaluation Using Cross Validation
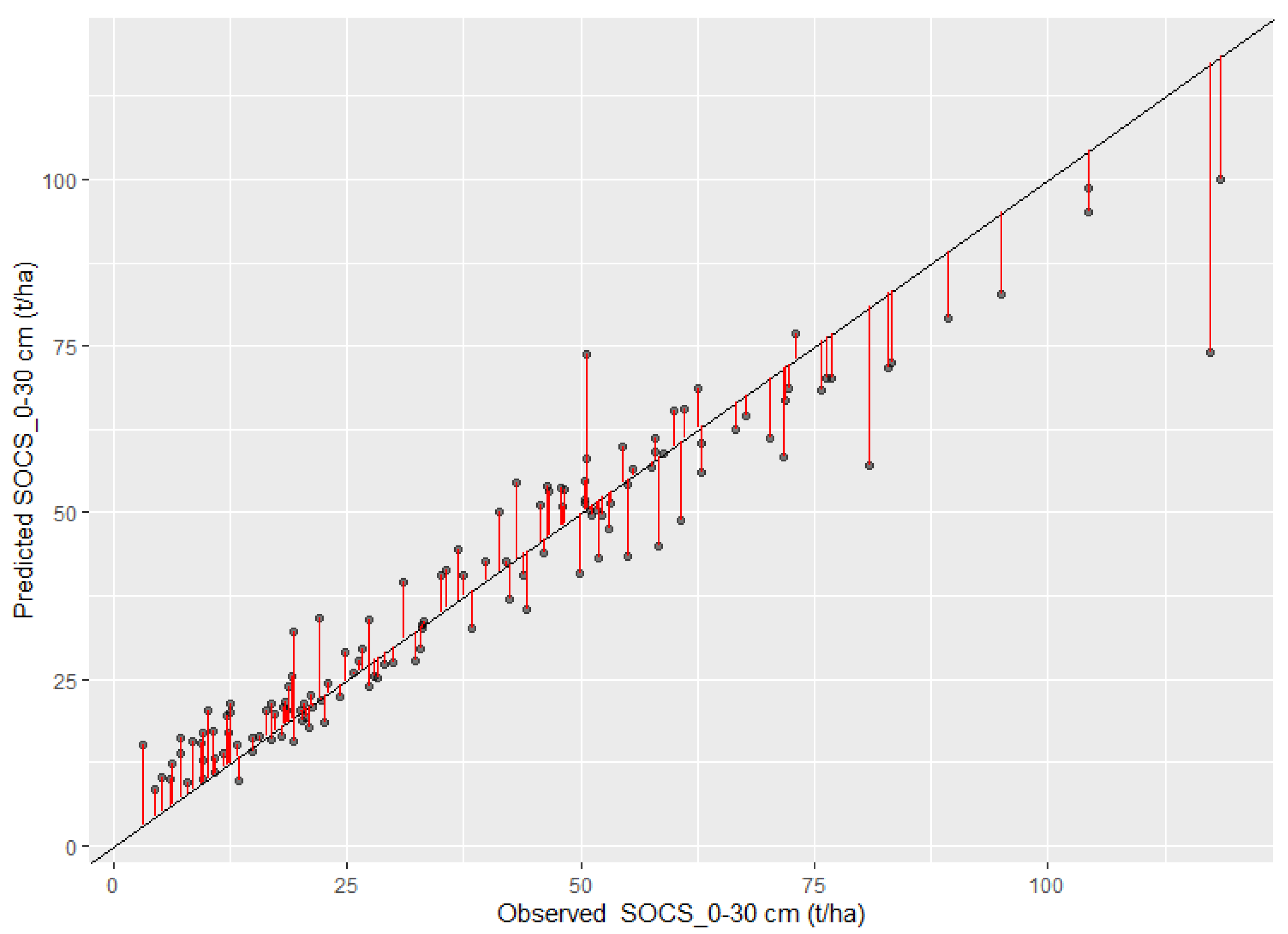
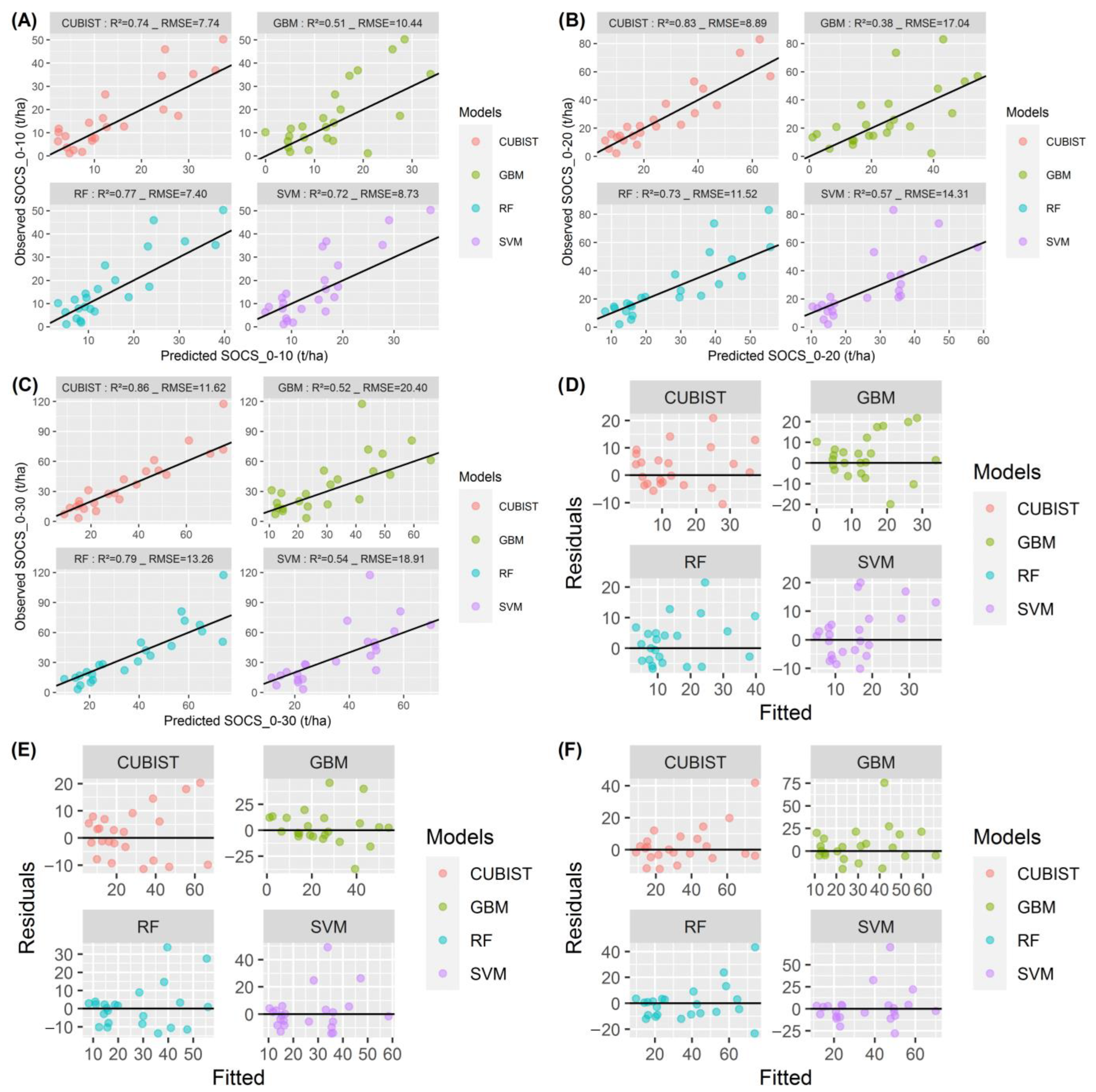
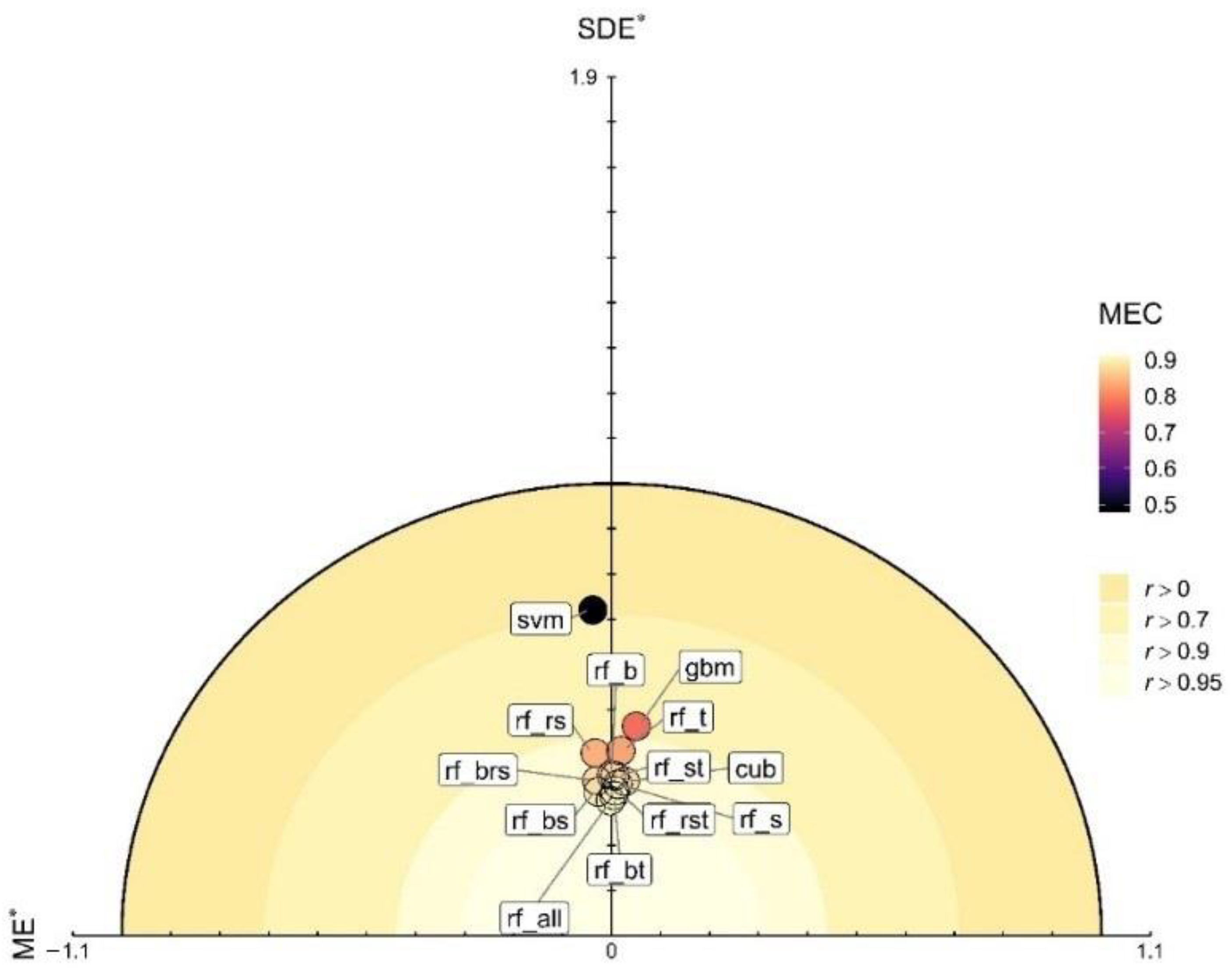
3.3. Model Evaluation and Comparison Based on the Testing Data
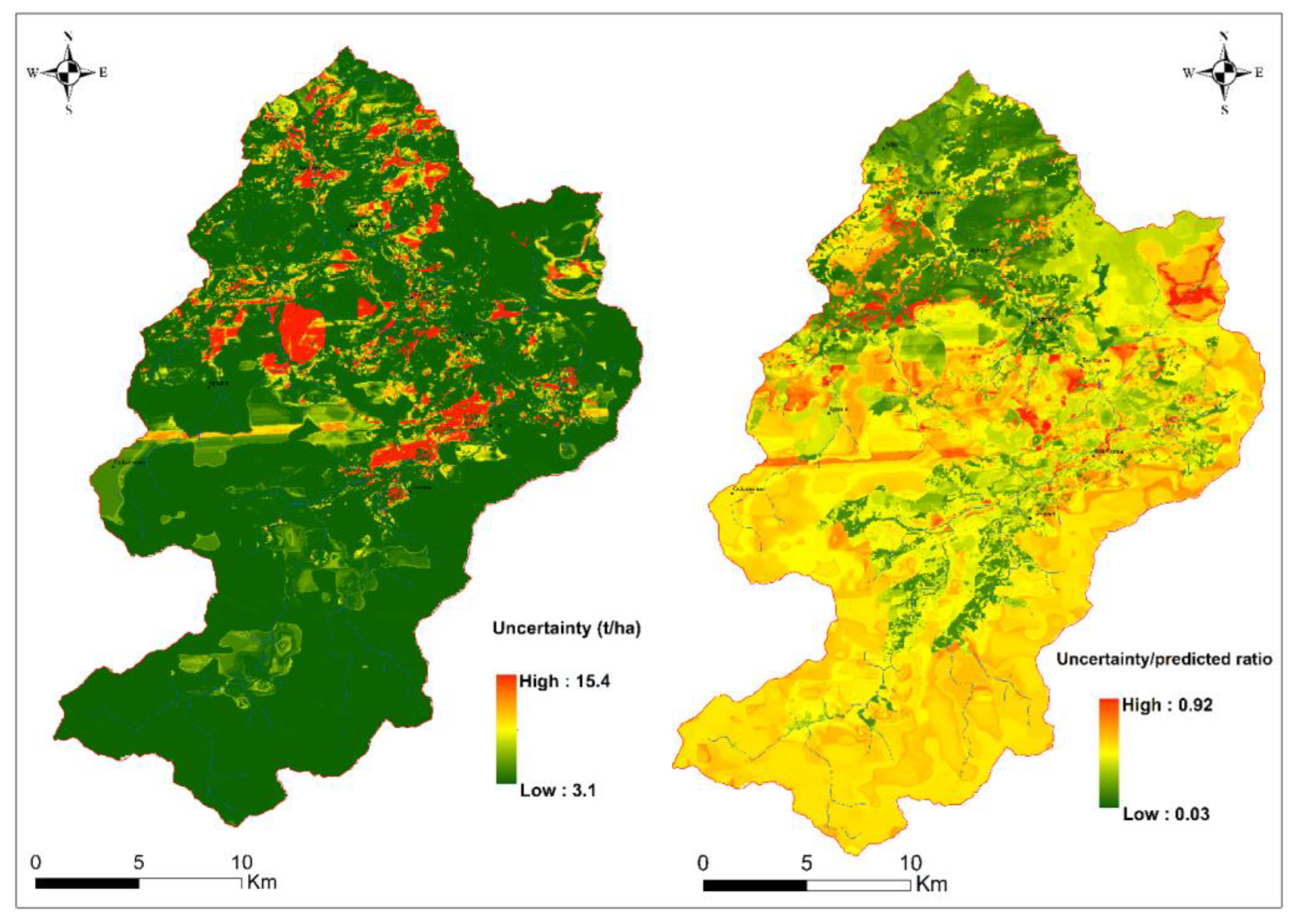
3.4. Contribution of Explanatory Factors and Integrated Evaluation of the Predictions
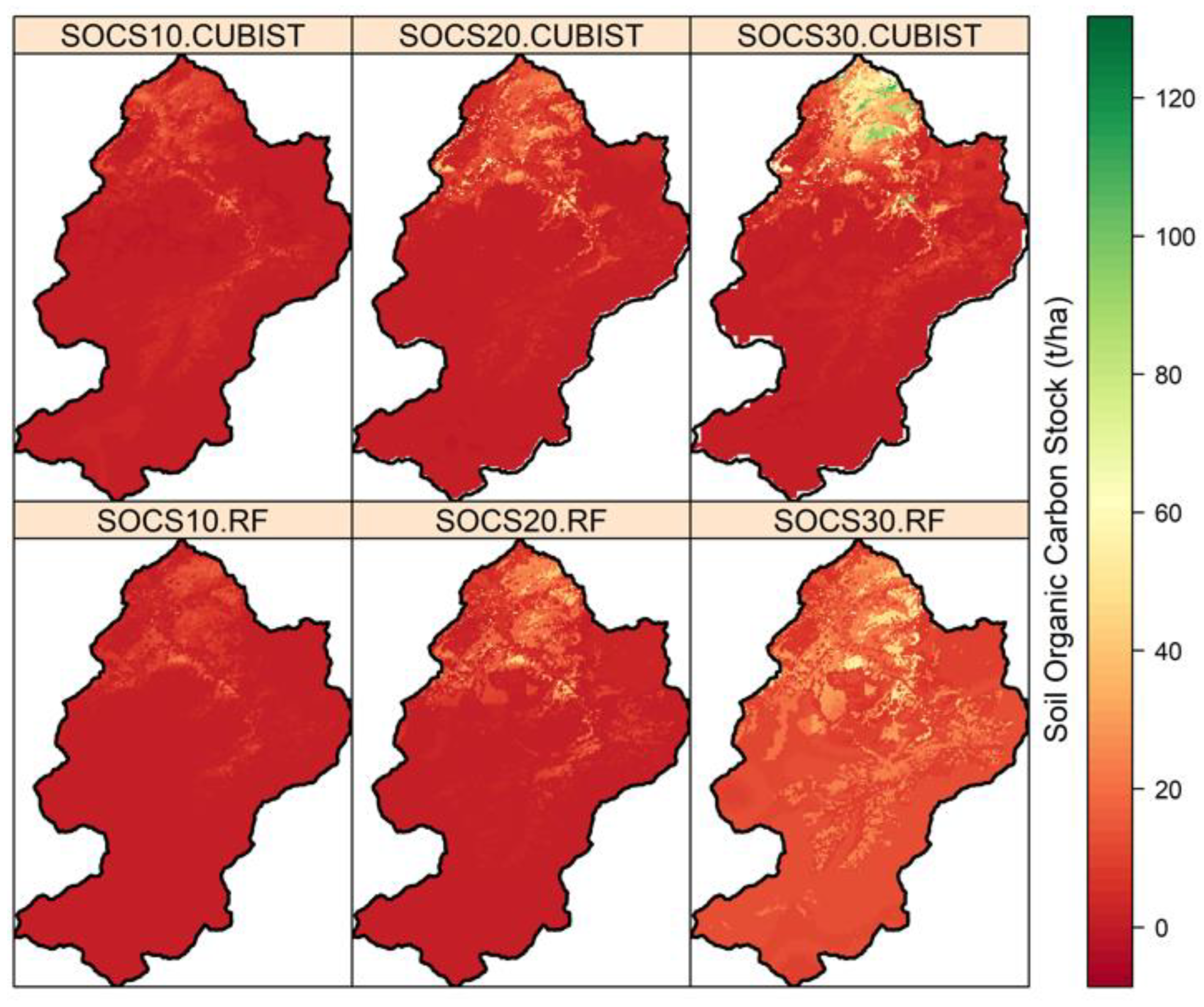
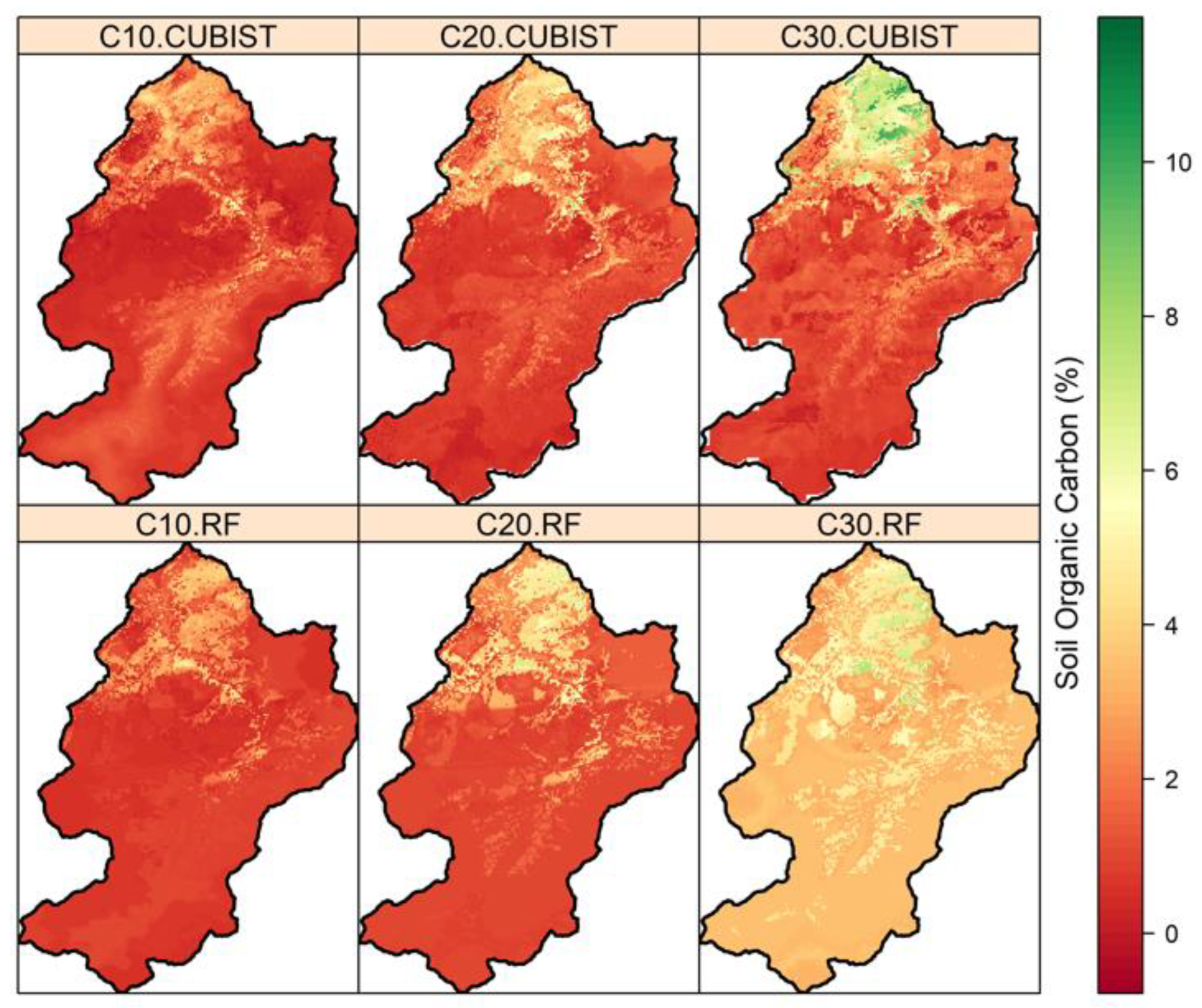
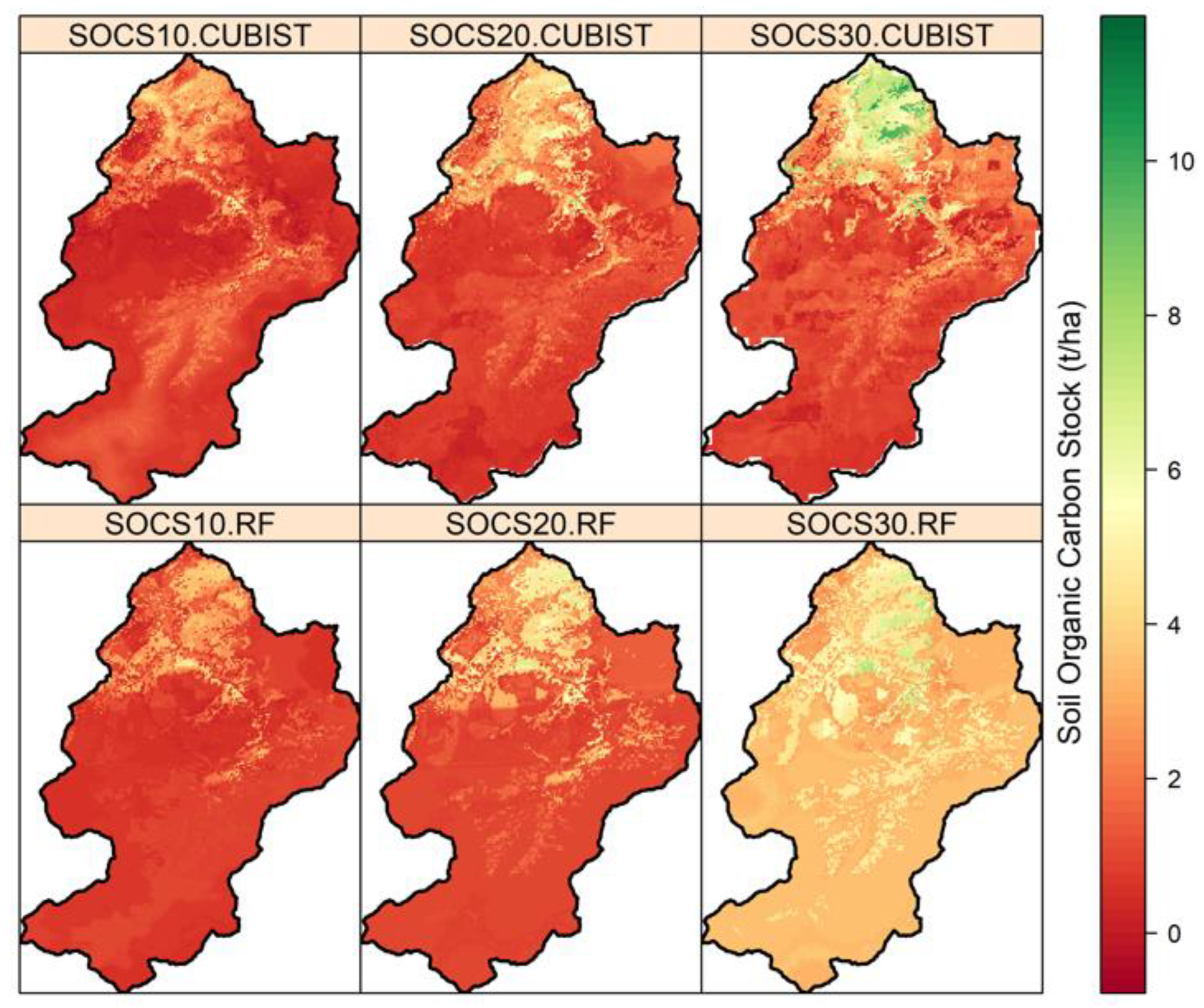
3.5. Spatial Prediction of SOC and SOCS
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A





References
- Lal, R. Soil Carbon Sequestration to Mitigate Climate Change. Geoderma 2004, 123, 1–22. [Google Scholar] [CrossRef]
- Aticho, A. Evaluating organic carbon storage capacity of forest soil. Case study in Kafa Zone BitaDistrict, Southwestern Ethiopia. Am. Eurasian J. Agric. Environ. Sci. 2013, 13, 95–100. [Google Scholar]
- Stockmann, U.; Adams, M.A.; Crawford, J.W.; Field, D.J.; Henakaarchchi, N.; Jenkins, M.; Minasny, B.; McBratney, A.B.; de Courcelles, V.d.R.; Singh, K.; et al. The knowns, known unknownsand unknowns of sequestration of soil organic carbon. Agric. Ecos. Environ. 2013, 164, 80–99. [Google Scholar] [CrossRef]
- Jandl, R.; Rodeghiero, M.; Martinez, C.; Cotrufo, M.F.; Bampa, F.; Wesemael, B.V.; Harrison, R.B.; Guerrini, I.A.; Richter, D.D.; Rustad, L.; et al. Currentstatus, uncertainty and future needs in soil organiccarbon monitoring. Sci. Total Environ. 2014, 468, 376–383. [Google Scholar] [CrossRef]
- Shelukindo, H.B.; Semu, E.; Msanya, B.; Singh, B.R.; Munishi, P. Soil organic carbon stocks in the dominant soils of the Miombo woodland ecosystem of Kitonga Forest Reserve, Iringa, Tanzania. Int. J. Agric. Policy Res. 2014, 2, 167–177. [Google Scholar]
- Greve, M.H.; Greve, M.B.; Bou Kheir, R.; Bøcher, P.K.; Larsen, R.; McCloy, K. Comparing Decision Tree Modeling and Indicator Kriging for Mapping the Extent of Organic Soils in Denmark; Digital Soil Mapping Bridging Research, Environmental Application, and Operation; Boettinger, J.L., Howell, D.W., Moore, A.C., Hartemink, A.E., Kienast-Brown, S., Eds.; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; London, UK; New York, NY, USA, 2009. [Google Scholar]
- Luo, Z.; Wang, E.; Sun, O.J. Soil carbon change and its responses to agricultural practices in Australian agro-ecosystems: A review and synthesis. Geoderma 2010, 155, 211–223. [Google Scholar] [CrossRef]
- Elbasiouny, H.; Abowaly, M.; Abu Alkheir, A.; Gad, A. Spatial variation of soil carbon and nitrogen pools by using ordinary Kriging method in an area of north Nile Delta, Egypt. Catena 2014, 113, 70–78. [Google Scholar] [CrossRef]
- Lal, R. Forest Soils and Carbon Sequestration. For. Ecol. Manag. 2005, 220, 242–258. [Google Scholar] [CrossRef]
- Batjes, N. Total Carbon and Nitrogen in the Soils of the World. Eur. J. Soil. Sci. 1996, 47, 151–163. [Google Scholar] [CrossRef]
- Guo, P.T.; Li, M.F.; Luo, W.; Tang, Q.F.; Liu, Z.W.; Lin, Z.M. Digital mapping of soil organic matter for rubber plantation at regional scale: An application of random forest plus residuals kriging approach. Geoderma 2015, 237, 49–59. [Google Scholar] [CrossRef]
- Bian, Z.; Guo, X.; Wang, S.; Zhuang, Q.; Jin, X.; Wang, Q.; Jia, S. Applying statistical methods to map soil organic carbon of agricultural lands in northeastern coastal areas of China. Arch. Agron. Soil. Sci. 2019, 66, 532–544. [Google Scholar] [CrossRef]
- Lefèvre, C.; Fatma, R.; Viridiana, A.; Liesl, W. What is SOC? In Soil Organic Carbon the Hidden Potential; Liesl, W., Ed.; FAO: Rome, Italy, 2017; pp. 1–9. [Google Scholar]
- Shi, M.J.; Yang, Z.L.; Lawrence, D.M.; Dickinson, R.E.; Subin, Z.M. Spin-up processes in the Community Land Model version 4 with explicit carbon and nitrogen components. Ecol. Modell. 2013, 263, 308–325. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Koster, R.D.; Reichle, R.H.; Mahanama, S.P.P.; Liu, Q. An updated treatment of soil texture and associated hydraulic properties in a global land modeling system. J. Adv. Model. Earth Syst. 2014, 6, 957–979. [Google Scholar] [CrossRef]
- Li, X.; McCarty, G.W.; Du, L.; Lee, S. Use of Topographic Models for Mapping Soil Properties and Processes. Soil. Syst. 2020, 4, 32. [Google Scholar] [CrossRef]
- Adhikari, K.; Hartemink, A.E.; Minasny, B.; Kheir, R.B.; Greve, M.B.; Greve, M.H. Digital mapping of soil organic carbon contents and stocks in Denmark. PLoS ONE 2014, 9, e105519. [Google Scholar] [CrossRef]
- Fang, H.; Cheng, S.; Yu, G.; Zheng, J.; Zhang, P.; Xu, M.; Li, Y.; Yang, X. Responses of CO2 efflux from an alpine meadow soil on the Qinghai Tibetan Plateau to multi-form and low-level N addition. Plant Soil 2012, 351, 177–190. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Miltz, J.; Don, A. Optimising Sample Preparation and near Infrared Spectra Measurements of Soil Samples to Calibrate Organic Carbon and Total Nitrogen Content. J. Near Infrared Spectrosc. 2012, 20, 695–706. [Google Scholar] [CrossRef]
- Walkley, A.J.; Black, I.A. Estimation of soil organic carbon by the chromic acid titration method. Soil. Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Mebius, L.J. A Rapid Method for the Determination of Organic Carbon in Soil. Anal. Chim. Acta 1960, 22, 120–124. [Google Scholar] [CrossRef]
- Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon, and organic matter. In Methods of Soil Analysis. Part 3; Sparks, D.L., Page, A.L., Helmke, P.A., Loeppert, R.H., Eds.; SSSA Book Series: Madison, WI, USA, 1996; pp. 961–1010. [Google Scholar]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Kerry, R. Digital mapping of soil organic carbon at multiple depths using different data mining techniques in Baneh region, Iran. Geoderma 2016, 266, 98–110. [Google Scholar] [CrossRef]
- Tajik, S.; Ayoubi, S.; Shirani, H.; Zeraatpisheh, M. Digital mapping of soil invertebrates using environmental attributes in a deciduous forest ecosystem. Geoderma 2019, 353, 252–263. [Google Scholar] [CrossRef]
- Goydaragh, M.G.; Taghizadeh-Mehrjardi, R.; Jafarzadeh, A.A.; Triantafilis, J.; Lado, M. Using environmental variables and Fourier Transform Infrared Spectroscopy to predict soil organic carbon. Catena 2021, 202, 105280. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Spatial prediction of soil properties using EBLUP with Matern covariance function. Geoderma 2007, 140, 324–336. [Google Scholar] [CrossRef]
- Maynard, J.J.; Dahlgren, R.A.; O’Geen, A.T. Soil carbon cycling and sequestration in a seasonally saturated wetland receiving agricultural runoff. Biogeosciences 2011, 8, 3391–3406. [Google Scholar] [CrossRef]
- Mondal, A.; Khare, D.; Kundu, S.; Mondal, S.; Mukherjee, S.; Mukhopadhyay, A. Spatial soil organic carbon (SOC) prediction by regression kriging using remote sensing data. Egypt. J. Remote Sens. Space Sci. 2017, 20, 61–70. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, Y.; Shen, C.; Ye, H.; Du, Y. Spatial prediction of soil organic matter using terrain indices and categorical variables as auxiliary information. Geoderma 2012, 171, 35–43. [Google Scholar] [CrossRef]
- Veronesi, F.; Schillaci, C. Comparison between geostatistical and machine learning models as predictors of topsoil organic carbon with a focus on local uncertainty estimation. Ecol. Indic. 2019, 101, 1032–1044. [Google Scholar] [CrossRef]
- Siewert, M.B. High-resolution digital mapping of soil organic carbon in permafrost terrain using machine learning: A case study in a sub-Arctic peatland environment. Biogeosciences 2018, 15, 1663–1682. [Google Scholar] [CrossRef]
- Pouladi, N.; Møller, A.B.; Tabatabai, S.; Greve, M.H. Mapping soil organic matter contents at field level with Cubist, random forest and kriging. Geoderma 2019, 342, 85–92. [Google Scholar] [CrossRef]
- Lamichhane, S.; Kumar, L.; Wilson, B. Digital soil mapping algorithms and covariates for soil organic carbon mapping and their implications: A review. Geoderma 2019, 352, 395–413. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Jafari, A.; Bodaghabadi, M.B.; Ayoubi, S.; Taghizadeh-Mehrjardi, R.; Toomanian, N.; Kerry, R.; Xu, M. Conventional and digital soil mapping in Iran: Past, present, and future. Catena 2020, 188, 104424. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Garosi, Y.; Owliaie, H.R.; Ayoubi, S.; Taghizadeh-Mehrjardi, R.; Scholten, T.; Xu, M. Improving the spatial prediction of soil organic carbon using environmental covariates selection: A comparison of a group of environmental covariates. Catena 2022, 208, 105723. [Google Scholar] [CrossRef]
- Jenny, H. Factors of Soil Formation; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Ließ, M.; Schmidt, J.; Glaser, B. Improving the Spatial Prediction of Soil Organic Carbon Stocks in a Complex Tropical Mountain Landscape by Methodological Specifications in Machine Learning Approaches. PLoS ONE 2016, 11, e0153673. [Google Scholar] [CrossRef]
- Wang, B.; Waters, C.; Orgill, S.; Cowie, A.; Clark, A.; Li Liu, D.; Simpson, M.; McGowen, I.; Sides, T. Estimating soil organic carbon stocks using different modelling techniques in the semi-arid rangelands of eastern Australia. Ecol. Indic. 2018, 88, 425–438. [Google Scholar] [CrossRef]
- Lal, R. Soil erosion and the global carbon budget. Environ. Int. 2003, 29, 437–450. [Google Scholar] [CrossRef]
- Offiong, R.; Iwara, A. Quantifying the Stock of Soil Organic Carbon using Multiple Regression Model in a Fallow Vegetation, Southern Nigeria. Ethiop. J. Environ. Stud. Manag. 2012, 5, 166–172. [Google Scholar] [CrossRef]
- Berthier, L.; Pitres, J.C.; Vaudour, E. Prédiction spatiale des teneurs en carbone organique des sols par spectroscopie de terrain visible proche infrarouge et imagerie satellitale SPOT. Exemple au niveau d’un périmètre d’alimentation en eau potable en Beauce. Etude Gest. Des. Sols 2008, 15, 161–172. [Google Scholar]
- Cai, J.; Cai, H.; Chen, J.; Yang, X. Identifying “many-to-many” relationships between gene-expression data and drug-response data via sparse binary matching. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 17, 165–176. [Google Scholar]
- Chen, S.; Richer-de-Forges, A.C.; Leatitia Mulder, V.; Martelet, G.; Loiseau, T.; Lehmann, S.; Arrouays, D. Digital mapping of the soil thickness of loess deposits over a calcareous bedrock in central France. Catena 2021, 198, 105062. [Google Scholar] [CrossRef]
- Elmalki, M.; Mounir, F.; Ichen, A.; Khai, T.; Aarab, M. A diachronic study of Ourika watershed land in the High Atlas of Morocco. E3S Web Conf. 2021, 234, 00080. [Google Scholar] [CrossRef]
- Evans, R.D.; Lange, O.L. Biological Soil Crusts and Ecosystem Nitrogen and Carbon Dynamics. In Biological Soil Crusts: Structure, Function, and Management; Ecological Studies (Analysis and Synthesis); Belnap, J., Lange, O.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 150. [Google Scholar]
- Cerri, C.E.P.; Easter, M.; Paustian, K.; Killian, K.; Coleman, K.; Bernoux, M.; Cerri, C.C. Simulating SOC changes in 11 land use change chronosequences from the Brazilian Amazon with RothC and Century models. Agric. Ecosyst. Environ. 2007, 122, 46–57. [Google Scholar] [CrossRef]
- Zhou, C.; Zhou, G.; Zhang, D.; Wang, Y.; Liu, S. CO2 efflux from different forest soils and impact factors in Dinghu Mountain. Sci. China Earth Sci. 2005, 48, 198–206. [Google Scholar]
- Blanco-Canqui, H.; Shapiro, C.; Wortmann, C.; Drijber, R.; Mamo, M.; Shaver, T.; Ferguson, R. Soil organic carbon: The value to soil properties. J. Soil. Water Conserv. 2013, 68, 129A–134A. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Urbanski, L.; Hobley, E.; Lang, B.; von Lützow, M.; Marin-Spiotta, E.; van Wesemael, B.; Rabot, E.; Ließ, M.; Garcia-Franco, N.; et al. Soil organic carbon storage as a key function of soils—A review of drivers and indicators at various scales. Geoderma 2019, 333, 149–162. [Google Scholar] [CrossRef]
- Adhikari, K.; Mishra, U.; Owens, P.R.; Libohova, Z.; Wills, S.A.; Riley, W.J.; Smith, D.R. Importance and strength of environmental controllers of soil organic carbon changes with scale. Geoderma 2020, 375, 114472. [Google Scholar] [CrossRef]
- Gray, J.M.; Bishop, T.F.A.; Wilson, B.R. Factors controlling soil organic carbon stocks with depth in eastern Australia. Soil Sci. Soc. Am. J. 2016, 79, 1741–1751. [Google Scholar] [CrossRef]
- Jobbagy, E.G.; Jackson, R.B. The vertical distribution of soil organic carbon and its relation to climate and vegetation. Ecol. Appl. 2000, 10, 423–436. [Google Scholar] [CrossRef]
- Von Lützow, M.; Kogel-Knabner, I.; Ekschmitt, K.; Matzner, E.; Guggenberger, G.; Marschner, B.; Flessa, H. Stabilization of organic matter in temperate soils: Mechanisms and their relevance under different soil conditions—A review. Eur. J. Soil Sci. 2006, 57, 426–445. [Google Scholar] [CrossRef]
- Zinn, Y.L.; Lal, R.; Bigham, J.M.; Resck, D.V.S. Edaphic controls on soil organic carbon retention in the Brazilian cerrado: Texture and mineralogy. Soil Sci. Soc. Am. J. 2007, 71, 1204–1214. [Google Scholar] [CrossRef]
- Matus, F.; Garrido, E.; Hidalgo, C.; Paz Pellat, F.; Etchevers, J.; Merino, C.; Báez-Pérez, A. Carbon saturation in the silt and clay particles in soils with contrasting mineralogy. Terra Latinoam. 2016, 34, 311–319. [Google Scholar]
- Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.M.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed]
- Fick, S.E.; Hijmans, R.J. Worldclim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, Australia, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Vapnik, V. The Support Vector Method of Function Estimation. In Nonlinear Modeling; Springer: Boston, MA, USA, 1998; pp. 55–85. [Google Scholar]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving performance of spatio-temporal machine learning models using forward feature selection and target-oriented validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Wadoux, A.M.J.-C.; Heuvelink, G.B.M.; de Bruin, S.; Brus, D.J. Spatial cross-validation is not the right way to evaluate map accuracy. Ecol. Model. 2021, 457, 109692. [Google Scholar] [CrossRef]
- Wadoux, A.M.J.-C.; Walvoort, D.J.J.; Brus, D.J. An integrated approach for the evaluation of quantitative soil maps through Taylor and solar diagrams. Geoderma 2022, 405, 115332. [Google Scholar] [CrossRef]
- Brus, D.J.; Kempen, B.; Heuvelink, G.B.M. Sampling for validation of digital soil maps. Eur. J. Soil. Sci. 2011, 62, 394–407. [Google Scholar] [CrossRef]
- Piikki, K.; Wetterlind, J.; Söderström, M.; Stenberg, B. Perspectives on validation in digital soil mapping of continuous attributes-A review. Soil Use Manag. 2021, 37, 7–21. [Google Scholar] [CrossRef]
- Efron, B. Jackknife-after-bootstrap standard errors and influence functions. J. R. Stat. Soc. Ser. B 1992, 54, 83–111. [Google Scholar] [CrossRef]
- Efron, B. Estimation and Accuracy after Model Selection. J. Am. Stat. Assoc. 2014, 109, 991–1007. [Google Scholar] [CrossRef] [PubMed]
- Wager, S.; Hastie, T.; Efron, B. Confidence intervals for random forests: The jackknife and the infinitesimal jackknife. J. Mach. Learn. Res. 2014, 15, 1625–1651. [Google Scholar]
- Wiesmeier, M.; Barthold, F.; Blank, B.; Kögel-Knabner, I. Digital mapping of soil organic matter stocks using Random Forest modeling in a semi-arid steppe ecosystem. Plant Soil 2011, 340, 7–24. [Google Scholar] [CrossRef]
- Ostle, N.J.; Levy, P.E.; Evans, C.D.; Smith, P. UK land use and soil carbon sequestration. Land. Use Policy 2009, 26S, S274–S283. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Spörlein, P.; Geuß, U.; Hangen, E.; Haug, S.; Reischl, A.; Schilling, B.; von Lützow, M.; Kögel-Knabner, I. Soil organic carbon stocks in southeast Germany (Bavaria) as affected by land use, soil type and sampling depth. Glob. Chang. Biol. 2012, 18, 2233–2245. [Google Scholar] [CrossRef]
- Were, K.; Bui, D.T.; Dick, Ø.B.; Singh, B.R. A comparative assessment of support vector regression, artificial neural networks, and random forests for predicting andmapping soil organic carbon stocks across an Afromontane landscape. Ecol. Indic. 2015, 52, 394–403. [Google Scholar] [CrossRef]
- John, K.; Isong, I.A.; Kebonye, N.M.; Ayito, E.O.; Agyeman, P.C.; Afu, S.M. Using Machine Learning Algorithms to Estimate Soil Organic Carbon Variability with Environmental Variables and Soil Nutrient Indicators in an Alluvial Soil. Land 2020, 9, 487. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Chen, J.; Pan, J.; Haase, D.; Lausch, A. High-resolution digital mapping of soil organic carbon and soil total nitrogen using DEM derivatives, Sentinel-1 and Sentinel-2 data based on machine learning algorithms. Sci. Total. Environ. 2020, 729, 138244. [Google Scholar] [CrossRef]
- Mishra, U.; Gautam, S.; Riley, W.J.; Hoffman, F.M. Ensemble Machine Learning Approach Improves Predicted Spatial Variation of Surface Soil Organic Carbon Stocks in Data-Limited Northern Circumpolar Region. Front. Big Data 2020, 3, 528441. [Google Scholar] [CrossRef]
- Akpa, S.I.C.; Odeh, I.O.A.; Bishop, T.F.A.; Hartemink, A.E.; Amapu, I.Y. Total soil organic carbon and carbon sequestration potential in Nigeria. Geoderma 2016, 271, 202–215. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. Comparison between Random Forests, Artificial Neural Networks and Gradient Boosted Machines Methods of On-Line Vis-NIR Spectroscopy Measurements of Soil Total Nitrogen and Total Carbon. Sensors 2017, 17, 2428. [Google Scholar] [CrossRef] [PubMed]
- Nussbaum, M.; Spiess, K.; Baltensweiler, A.; Grob, U.; Keller, A.; Greiner, L.; Schaepman, M.E.; Papritz, A. Evaluation of digital soil mapping approaches with large sets of environmental covariates. Soil 2018, 4, 1–22. [Google Scholar] [CrossRef]
- Sharma, G.; Sharma, L.K.; Sharma, K.C. Assessment of land use change and its effect on soil carbon stock using multitemporal satellite data in semiarid region of Rajasthan, India. Ecol. Process. 2019, 8, 42. [Google Scholar] [CrossRef]
- Silatsa, F.B.T.; Yemefack, M.; Tabi, F.O.; Heuvelink, G.B.M.; Leenaars, J.G.B. Assessing countrywide soil organic carbon stock using hybrid machine learning modelling and legacy soil data in Cameroon. Geoderma 2020, 367, 114260. [Google Scholar] [CrossRef]
- Beesley, L. Carbon storage and fluxes in existing and newly created urban soils. J. Environ. Manag. 2012, 104, 158–165. [Google Scholar] [CrossRef]
- Bae, J.; Ryu, Y. High soil organic carbon stocks under impervious surfaces contributed by urban deep cultural layers. Landsc. Urban. Plan. 2020, 204, 103953. [Google Scholar] [CrossRef]
- Sheikh, M.A.; Kumar, M.; Bussmann, R.W. Altitudinal variation in soil organic carbon stock in coniferous subtropical and broadleaf temperate forests in Garhwal Himalaya. Carbon. Balance Manag. 2009, 4, 6. [Google Scholar] [CrossRef]
- Bangroo, S.; Najar, G.; Rasool, A. Effect of altitude and aspect on soil organic carbon and nitrogen stocks in the Himalayan Mawer Forest Range. Catena 2017, 158, 63–68. [Google Scholar] [CrossRef]
- Sabir, M.; Sagno, R.; Tchintchin, Q.; Zaher, H.; Benjelloun, H. Chapitre 3. Évaluation des stocks de carbone organique dans les sols au Maroc. In Carbone des Sols En Afrique: Impacts des Usages Des Sols et Des Pratiques Agricoles; Chevallier, T., Razafimbelo, T.M., Chapuis-Lardy, L., Brossard, M., Eds.; IRD Éditions: Rome, Italy; Marseille, France, 2020. [Google Scholar] [CrossRef]
- Ougougdal, H.A.; Khebiza, M.H.; Messouli, M.; Bounoua, L.; Karmaoui, A. Delineation of vulnerable areas to water erosion in a mountain region using SDR-InVEST model: A case study of the Ourika watershed, Morocco. Sci. Afr. 2020, 10, e00646. [Google Scholar] [CrossRef]
- Song, Y.Q.; Yang, L.A.; Li, B.; Hu, Y.M.; Wang, A.L.; Zhou, W.; Cui, X.S.; Liu, Y.L.; Song, Y.Q.; Yang, L.A. Spatial prediction of soil organic matter using a hybrid geostatistical model of an extreme learning machine and ordinary kriging. Sustainability 2017, 9, 754. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, H.; Jiang, X.; Luo, Y.; Wang, C.; Yue, T.; Li, B.; Gao, X. Spatially distributed modeling of soil organic carbon across China with improved accuracy. J. Adv. Model. Earth Syst. 2017, 9, 1167–1185. [Google Scholar] [CrossRef]

| LU/LC | Area (%) | Number of Samples |
|---|---|---|
| Irrigated cereals | 6.64 | 7 × 3 |
| Rainfed cereals | 7 × 3 | |
| Mixed arboriculture-cereals | 7 × 3 | |
| Arboriculture | 7 × 3 | |
| Reforestation | 0.75 | 7 × 3 |
| Dense holm oak stands | 2.74 | 7 × 3 |
| Moderately dense holm oak stands | 6.09 | 7 × 3 |
| Open holm oak stands | 10.03 | 7 × 3 |
| Dense Barbary thuja stands | 0.06 | 7 × 3 |
| Moderately dense Barbary thuja stands | 0.86 | 7 × 3 |
| Open Barbary thuja stands | 1.31 | 7 × 3 |
| Moderately dense Juniperus phoenicea stands | 7.27 | 7 × 3 |
| Moderately dense Juniperus oxycedrus stands | 7 × 3 | |
| Moderately dense Juniperus thufifera stands | 7 × 3 | |
| Open Juniperus phoenicea stands | 11.28 | 7 × 3 |
| Open Juniperus oxycedrus stands | 7 × 3 | |
| Open Juniperus thufifera stands | 7 × 3 | |
| Forest clearing | 7 × 3 | |
| Thorny upland xerophytes | 45.07 | 7 × 3 |
| Cemetery area | 0.00 | 7 × 3 |
| Bare area | 7.69 | - |
| Built-up area | 0.21 | - |
| Total | 100.00 | 420 |
| Model | Used Predictors with FFS | Abbreviation |
|---|---|---|
| Cubist | All predictors | Cub |
| GBM | All predictors | GBM |
| SVM | All predictors | SVM |
| RF | All predictors | rf_all |
| RF | Bioclimatic variables | rf_b |
| RF | SoilGrids soil variables | rf_s |
| RF | Remote sensing variables | rf_rs |
| RF | Topographical variables | rf_t |
| RF | Bioclimatic and SoilGrids soil variables | rf_bs |
| RF | Bioclimatic and Remote sensing variables | rf_brs |
| RF | Bioclimatic and topographic variables | rf_bt |
| RF | SoilGrids soil variables and topographic variables | rf_st |
| RF | Remote sensing and topographic variables | rf_rst |
| RF | SoilGrids soil variables and remote sensing variables | rf_srs |
| Models | ME | MAE | RMSE | R2 |
|---|---|---|---|---|
| rf_all | −0.07 | 5.33 | 7.58 | 0.92 |
| cub | 0.7 | 6.43 | 8.68 | 0.89 |
| svm | −0.98 | 13.39 | 18.29 | 0.51 |
| gbm | 1.29 | 7.92 | 11.82 | 0.79 |
| rf_b | −0.01 | 6.39 | 9.01 | 0.89 |
| rf_s | 0.33 | 6.16 | 8.49 | 0.9 |
| rf_rs | −0.86 | 7.04 | 10.29 | 0.85 |
| rf_t | 0.49 | 7.64 | 10.38 | 0.84 |
| rf_bs | −0.7 | 6.03 | 8.09 | 0.91 |
| rf_brs | −0.77 | 5.78 | 8.74 | 0.89 |
| rf_bt | 0.13 | 5.59 | 7.87 | 0.92 |
| rf_st | 0.17 | 6.02 | 8.97 | 0.9 |
| rf_rst | 0.18 | 5.65 | 8.12 | 0.92 |
| rf_srs | −0.57 | 5.78 | 8.05 | 0.91 |
| LU/LC | Mean Predicted SOCS (t/ha) | MSE (t/ha) | MSE/Mean Predicted SOCS Ratio |
|---|---|---|---|
| Thorny upland xerophytes | 16.62 | 3.22 | 0.19 |
| Open holm oak stands | 18.05 | 3.31 | 0.18 |
| Dense holm oak stands | 57.27 | 3.93 | 0.07 |
| Moderately dense holm oak stands | 50.23 | 3.52 | 0.07 |
| Agriculture | 41.19 | 4.37 | 0.11 |
| Open juniper stands | 20.26 | 3.31 | 0.16 |
| Moderately dense juniper stands | 47.05 | 4.22 | 0.09 |
| Reforestation | 25.80 | 3.38 | 0.13 |
| Open Barbary thuja stands | 25.04 | 3.52 | 0.14 |
| Dense Barbary thuja stands | 67.17 | 3.82 | 0.06 |
| Moderately dense Barbary thuja stands | 54.42 | 3.91 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meliho, M.; Boulmane, M.; Khattabi, A.; Dansou, C.E.; Orlando, C.A.; Mhammdi, N.; Noumonvi, K.D. Spatial Prediction of Soil Organic Carbon Stock in the Moroccan High Atlas Using Machine Learning. Remote Sens. 2023, 15, 2494. https://doi.org/10.3390/rs15102494
Meliho M, Boulmane M, Khattabi A, Dansou CE, Orlando CA, Mhammdi N, Noumonvi KD. Spatial Prediction of Soil Organic Carbon Stock in the Moroccan High Atlas Using Machine Learning. Remote Sensing. 2023; 15(10):2494. https://doi.org/10.3390/rs15102494
Chicago/Turabian StyleMeliho, Modeste, Mohamed Boulmane, Abdellatif Khattabi, Caleb Efelic Dansou, Collins Ashianga Orlando, Nadia Mhammdi, and Koffi Dodji Noumonvi. 2023. "Spatial Prediction of Soil Organic Carbon Stock in the Moroccan High Atlas Using Machine Learning" Remote Sensing 15, no. 10: 2494. https://doi.org/10.3390/rs15102494
APA StyleMeliho, M., Boulmane, M., Khattabi, A., Dansou, C. E., Orlando, C. A., Mhammdi, N., & Noumonvi, K. D. (2023). Spatial Prediction of Soil Organic Carbon Stock in the Moroccan High Atlas Using Machine Learning. Remote Sensing, 15(10), 2494. https://doi.org/10.3390/rs15102494






