Timeliness of Correcting Baseline Error in Wide-Swath Altimeter Based on Reference Topography Data

Abstract

The baseline error is a primary error source of the wide-swath altimeter, directly related to the cross-track distance, and can lead to serious height errors at the swath’s outer edge. Cross-calibration using discrepancies with reference data can effectively estimate and correct the baseline error. However, building a reference surface that accurately describes the sea surface at the observation time is necessary to use this cross-correction method. The dynamic ocean environments where the sea surface structure changes over time are challenging. This paper proposes a method for constructing reference topography data (RTD) based on multi-source data products to correct the baseline error of the wide-swath altimeter. The effectiveness of the proposed method is evaluated using HYCOM ocean model data to assess the timeliness of the baseline error correction. The results demonstrate that using RTD at the observation time of the wide-swath altimeter can significantly correct the baseline error. The RMSE of the corrected sea surface height (SSH) in different regions is typically between 1~2 cm, except in some regions with strong currents where the RMSE is approximately 3~4 cm. However, the time interval between the RTD and the observation time of the wide-swath altimeter can affect the accuracy of the baseline error correction. The timeliness of this correction is influenced by the variability of SSH in different regions. In regions with relatively slow SSH changes near the equator, the effective time based on HYRTD and MORTD can basically reach more than 7 days. In regions where the SSH changes more rapidly, the correction result may no longer be reliable in only 1~3 days.

1. Introduction

In the past few decades, spaceborne radar altimeters have continuously observed the global sea surface height (SSH). The large amount of data has greatly improved research in ocean dynamic process observation, sea surface topography mapping, Earth’s gravity field measurement, seabed topography inversion, global sea level rise, and climate change [1,2,3,4,5,6]. However, due to their orbit spacing ranging from tens to hundreds of kilometers and revisit period ranging from a few days to dozens of days, the observational capabilities of global ocean dynamics processes of traditional altimeters, such as Jason-3, and synthetic aperture radar (SAR) altimeters, such as Sentinel-3, have been limited from large to mesoscale [7]. The wide-swath altimeter, such as the Surface Water and Ocean Topography (SWOT) mission launched in December 2022, combines traditional radar altimetry, aperture synthesis, and interferometric measurement technologies [8,9]. It can conduct high spatial resolution and high-precision wide-swath measurements of the sea surface, allowing it to observe ocean sub-mesoscale phenomena and processes directly. Some research results based on high-resolution ocean model data and ocean observation system simulation experiments have shown that the wide-swath altimeter can capture finer sea surface structures [10,11]. The resolution of gridded data based on the wide-swath measurement exceeded those of multiple nadir altimeters [12,13,14].

The along-track measurement accuracy of traditional nadir altimeters is generally about 5 cm [15,16]. Although the main advantage of the wide-swath altimeter lies in its three-dimensional SSH capability and its improved spatial resolution, it still requires centimeter-level accuracy of SSH to ensure observation of submesoscale ocean dynamic processes, such as submesoscale eddies, fronts, internal solitary waves, etc. [17,18]. Wide-swath altimetry is subject to various sources of errors during the measurement process, which restricts measurement accuracy [19]. The atmospheric delay, ionospheric delay, and sea state bias that nadir altimeters encounter also exist in wide-swath altimeters. Due to the deviation from the nadir measurement, correction methods for the nadir direction need to be developed or modified with targeted error correction models [20,21,22]. On the other hand, errors such as phase errors and baseline errors are introduced during interferometric processing and need to be adequately corrected [23,24]. Among them, baseline error is a source with typical spatial propagation characteristics that seriously impact the measurement results. Due to the fact that the wide-swath altimeter uses the phase difference between two antennas to invert the SSH, it is very sensitive to the relative position of the two antennas. According to the principle of interferometric measurement, changes in roll angle (the angle between the two antennas and the flight plane) and baseline length (the projection of the distance between the two antennas onto the vertical plane perpendicular to the flight direction) will significantly alter the interferometric geometry. When the baseline parameters used for height inversion are not completely consistent with the actual baseline parameters during the actual measurement process, baseline error will occur [25]. Based on the sensitivity of the measured height accuracy to baseline parameters, it can be concluded that the SSH error caused by baseline error increases rapidly with increasing cross-track distance. The baseline parameters need to be extremely accurate to ensure SSH accuracy within the entire swath. Taking SWOT parameters as an example, a roll error of 1 arcsec and a baseline length error of 1 mm would cause approximately 30 cm and 40 cm of SSH error, respectively, at the far edge of swath [26]. Spaceborne wide-swath altimeters usually need to be equipped with high-precision gyroscopes and other auxiliary instruments to measure the satellite’s flight attitude in real time. However, considering the measurement noise and instrument drift of auxiliary payloads and the vibration and thermal deformation of the platform’s mechanical structure, it is still difficult to meet the requirements with only auxiliary payloads.

Due to the cross-track distance dependence, the cross-calibration method can estimate and correct the baseline error. After ideal correcting for other errors, the wide-swath SSH is matched with reference data to extract the spatial structural characteristics of the height differences in the cross-track direction and estimate the baseline parameter error. The core idea of the cross-calibration method is to accurately separate the cross-track trend structures caused by the baseline error from other factors in the height measurement results. Rodriguez and Pollard proposed a scheme to calibrate the baseline roll error by using the wide swath self-intersection discrepancy value in the concept and performance analysis of the WSOA mission [27]. Borner et al. assumed that the baseline error between the ascending and descending rails was uncorrelated and the sea surface change and other measurement noises were zero-mean stationary Gaussian processes. Then they proposed a method for estimating the baseline error based on the slope of the cross-track topography within the rhombus of the ascending and descending tracks [28]. Dibarboure et al. studied the impact of roll error and baseline length error on the SWOT mission and the empirical cross-calibration method. They constructed reference data for baseline error estimation using the reference digital elevation model (DEM), the nadir altimeter cross-calibration, and the wide-swath altimeter self-calibration. Simulation results show that when the reference data are relatively reliable, this cross-calibration method can achieve ideal correction results for the low-frequency part of the baseline error. However, more error statistical feature information input is needed for the high-frequency part [29]. Dibarboure and Ubelmann evaluated the performance of four empirical cross-calibration methods, including reference DEM, crossover, subcycle, and collinear, to correct the SWOT roll error. The results showed that the “direct method” based on reference DEM had relatively high coverage and small residual errors after correction, but the correction results may be affected by miscorrection due to ocean variability [30]. However, they neither provided the reference DEM construction methods that can be used for operational satellites nor fully explored the timeliness of the cross-calibration results in different oceanic regions. Metref et al. studied a method based on data assimilation to reduce spatial errors (including roll error, baseline length error, systematic phase error, and timing drift error) in SWOT measurements. The data assimilation of the SSH field is performed, and the simulation results show that this method can effectively reduce the influence of spatial structure errors in the SWOT measurement results [31]. Miao et al. conducted a simulation study to estimate and correct the baseline error using the cross-matching method of different numbers of nadir altimeter constellations and wide-swath altimeters. The results showed that the correction ability using a single nadir altimeter as reference data is limited, but using a constellation consisting of 3~5 nadir altimeters can provide an ideal estimation of wide-swath altimeter baseline error [26]. Miao et al. investigated the baseline error correction method by constructing reference topography data (RTD) using mean sea surface products and daily SSH anomaly products. The results showed that the correction ability is related to the spatiotemporal variability of the target area’s SSH structure, and the correction may be affected when there are differences between the RTD and “true” SSH [32]. However, this preliminary study only conducted experiments in several typical areas using low-resolution input data of 1/4°.

It is obvious that the results of the cross-calibration method for processing wide-swath baseline error mainly depend on the accuracy of the reference data. This reference data can be provided by nadir and/or wide-swath altimeters or constructed using multi-source data products. Their spatial resolution may not be very high, but they should express the relative slope of the sea surface as accurately as possible at the observation time of the wide-swath altimeter, especially in the cross-track direction. Unlike the estimation of baseline parameters for land-based InSAR, the ocean is dynamic and lacks a single data source that can provide a stable and reliable reference digital elevation model (DEM) or ground control point (GCP) to represent the instantaneous sea surface topography accurately. Furthermore, the SSH structure itself changes over time [33]. Based on the sea surface geometry, constructing RTD using multiple data products that can accurately depict the sea surface topography structure at the time of wide-swath altimeter observations is key to obtaining reliable cross-calibration results. Because oceanic energy is unevenly distributed globally, and the severity of SSH changes varies in different regions, the timeliness of correcting wide-swath altimeter baseline error based on RTD will vary by region.

2. Methods

2.1. Baseline Error of Wide-Swath Altimeter

The baseline error of the wide-swath altimeter is caused by the difference between the baseline parameters used in the data processing and the true values in the interferometric measurement. There are several concepts for baseline parameters:

• True value, which corresponds to the instantaneous baseline parameters at the time of the wide-swath altimeter observation;
• Nominal value, which is the baseline constant in the design of the wide-swath altimeter system;
• Measured value, which refers to the baseline parameters measured by the satellite-borne auxiliary instrument in real time;
• Estimated value, which refers to the value obtained by estimating the baseline parameters through specific methods or auxiliary data;
• Used value, which is the baseline parameter used in the SSH inversion.

When using the measured value directly for SSH inversion, the baseline parameter error equals the measurement error of the auxiliary instrument. If the more accurate estimated value of the baseline parameters is used for interferometric processing, the baseline error can be well controlled. However, suppose the satellite lacks corresponding auxiliary instruments to measure baseline parameters in real-time or has unreliable estimated results, and only uses nominal values for SSH inversion. In that case, the baseline error may seriously impact the results. In this study, the difference between the measured value and the true value is taken as the baseline parameter error. This definition more accurately reflects the actual conditions of the satellite and the characteristics of the data. Under these situations, the baseline parameters are preliminarily estimated to be close to the true value but still require further correction.

Taking into account the curvature of the Earth, the principle of the wide-swath altimeter is shown in Figure 1. A₁ and A₂ are the master and slave antennas, respectively. The master antenna transmits signals, and both antennas receive echoes. B is the baseline length, which is the line connecting the phase centers of the two antennas, and α is the angle between the baseline and the horizontal direction, i.e., the roll angle. O is the center of the Earth, R_e is the local radius of the Earth, h is the height of the ground target point P relative to the reference ellipsoid, and H is the height of the master antenna relative to the reference ellipsoid. R₁ is the slant range from the master antenna to the target point, θ is the looking angle, and R₂ is the slant range from the slave antenna to the target point.

Based on the geometry in Figure 1, the following equations can establish the relationship between the interferometric phase and the SSH.

$${\left(h+R_e\right)}^2={\left(H+R_e\right)}^2+R_1^2-2R_1\left(H+R_e\right)\cos \theta ,$$

(1)

$$\cos \left(\frac{\pi }{2}-\theta +\alpha \right)=\frac{R_1^2+B^2-R_2^2}{2B{R}_1},$$

(2)

$${\varphi }_{abs}=-\frac{2\pi }{\lambda }\left(2R_1-\left(R_1+R_2\right)\right)=\frac{2\pi }{\lambda }\left(R_2-R_1\right),$$

(3)

According to the measurement principle of the wide-swath altimeter and the interferometric geometry relationship in Figure 1, in the case of neglecting the coupling relationship between the baseline parameters, taking the partial derivative of Equation (1) with respect to α and B, the impact of roll error and baseline length error on the height measurement results can be obtained, as shown in Equations (4) and (5).

$$\mathsf{\Delta }{h}_{\alpha }=R_1\sin \theta \cdot \delta \alpha \approx \left(1+H/R_e\right)x\cdot \delta \alpha ,$$

(4)

$$\mathsf{\Delta }{h}_B=-\frac{R_1\sin \theta }{B}\tan \left(\theta -\alpha \right)\cdot \delta B\approx -\frac{\left(1+H/R_e\right)}{HB}{x}^2\cdot \delta B,$$

(5)

where δα and δB are the roll parameter error and the baseline length parameter error, respectively, ∆h_α and ∆h_B are the corresponding SSH errors, and the cross-track distance, x, can be obtained from $\left(1+H/R_e\right)x\approx R_1\sin \theta$ according to the geometric relationship and the influence of the curvature of the earth. Equations (4) and (5) demonstrated that the SSH error caused by the roll error is linearly related to the cross-track distance, while the SSH error caused by the baseline length error is quadratically related to the cross-track distance.

2.2. Cross-Calibration Method

Due to the cross-track propagation characteristics of the baseline error, cross-calibration based on reliable reference data is an effective method for estimating and correcting the baseline error. After other errors have been ideally corrected, the observed data from the wide-swath altimeter and reference data are temporally and spatially matched. The sea surface height anomaly (SSHA) is calculated as shown in Equation (6).

$$\begin{array}{cc}\hfill \mathsf{\Delta }H\left(lat,lon,t\right)& =H_{swath}\left(lat,lon,t\right)-H_{ref}\left(lat,lon,t’\right)\hfill \\ & =\left[H_{swath}\left(lat,lon,t\right)-H_{real}\left(lat,lon,t\right)\right]\hfill \\ & -\left[H_{ref}\left(lat,lon,t’\right)-H_{real}\left(lat,lon,t’\right)\right]+\delta H_{real}\left(t-t’\right)\hfill \\ & =\Delta h_{\alpha }+\Delta h_B+{\epsilon }_{swath}\left(lat,lon,t\right)-{\epsilon }_{ref}\left(lat,lon,t’\right)+\delta H_{real}\left(t-t’\right),\hfill \end{array}$$

(6)

where ∆H(lat,lon,t) represents the SSHA, H_real is the true SSH, H_swath is the observed value from the wide-swath altimeter, H_ref is the reference data at the target location. There may be a time interval δt = (t−t’) between the observation and reference times, and the variation of the SSH structure within the time interval, δH_real(t−t’), is related to ocean dynamic processes. Moreover, after accounting for the correction of other error sources, the height error induced by baseline parameter error denoted as ∆h_α + ∆h_B and the residual error denoted as ε_swath represent the discrepancy between the observed value and the true value. The difference between the real SSH and the reference data, ε_ref, is mainly caused by the errors in the reference data and interpolation errors due to insufficient spatiotemporal resolution.

At a specific observation time, the wide-swath altimeter can obtain a measurement line in the cross-track direction. The observation points corresponding to different cross-track distances have the same baseline parameters. Assuming that the other terms in Equation (6) are not significantly correlated with the cross-track distance, baseline parameter error estimation can be performed using the least squares method:

$$P_{est}\left(\alpha ,B\right)={\left(M^{T}M\right)}^{-1}{M}^T\Delta H,$$

(7)

where P_est is the estimated result of the baseline parameter errors, and M is the mapping model that includes the cross-track propagation characteristics of the baseline error. The size of the M matrix is n × 2, where the first column consists of coefficients linearly related to the cross-track distance x, and the second column consists of coefficients linearly related to x². n is the number of points at different cross-track distances at the same observation time. M^T represents the matrix transposition, and (M^TM)⁻¹ represents the inverse of the matrix. Finally, the baseline parameter error of the wide-swath altimeter can be calculated and corrected for height error caused by the baseline error using Equations (4) and (5) based on the fitted roll error and baseline length error.

During the application process, the results of baseline error cross-calibration based on reference data may be affected by the last three terms in Equation (6):

• Other residual errors, such as cross-track correlated systematic phase errors, cannot be fully eliminated by current methods. However, merging them with the baseline error can improve the correction.
• The cross-track trend caused by errors in reference data and insufficient spatiotemporal resolution can be mistakenly identified as the baseline error, resulting in SSHA.
• Reference data are created by actual observed data, which have release time delays. When using data with a time interval (such as several days ago) to create the reference data and estimate the baseline error, the changes in SSH structure during this time interval may lead to misidentification.

It is difficult to accurately separate the cross-track trend structure caused by the baseline error from other factors under the last two cases. Misidentification can reduce the effectiveness of correcting the baseline error of the wide-swath altimeter and even lead to more serious height measurement errors. Therefore, efforts should be made to minimize the presence of these two influencing factors in the reference data.

2.3. Reference Topography Data

When estimating and correcting the baseline error of wide-swath altimeters through the cross-calibration method, the accuracy of reference data plays an important role in the correction capability. Among the common cross-matching schemes, the gridded prior topography data have uniform spatial and temporal distribution and high coverage over the wide-swath altimeter observations to be corrected, which is an ideal cross-calibration scheme [30]. However, the ocean is dynamic, and no single data source can provide a stable and reliable reference DEM to describe the instantaneous sea surface topography. This paper proposes a method of using multiple data products to construct the RTD based on the sea surface geometric.

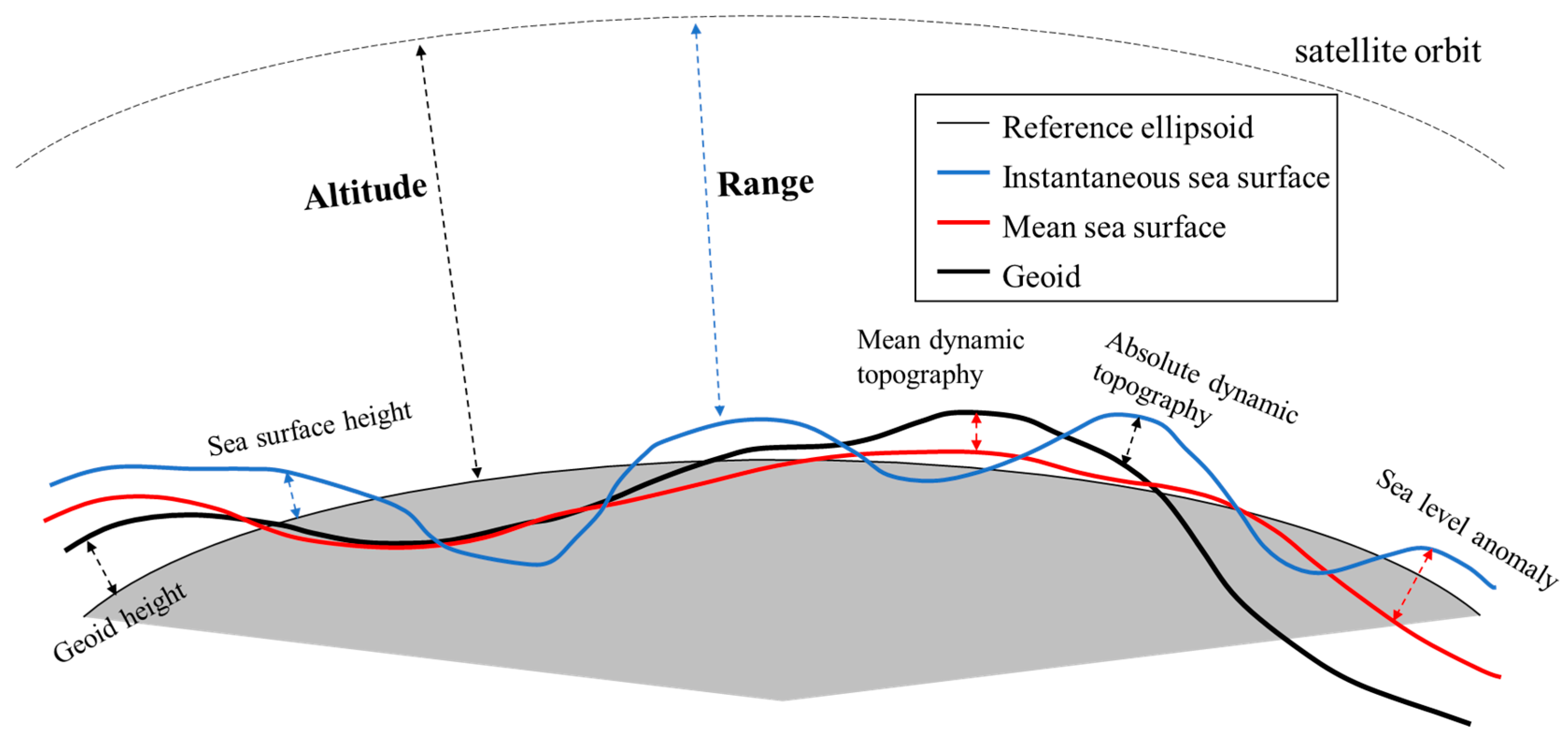
In the process of measuring SSH with altimeters, there are many concepts related to reference surfaces and relative heights. The main parts of them are illustrated in Figure 2.

In order to describe the shape of the Earth mathematically, a reference ellipsoid surface is defined as the biaxial spheroid closest to the Earth’s surface. The distance between the sea surface and the reference ellipsoid is the SSH corresponding to satellite altimetry. Due to the uneven distribution of the Earth’s gravity field, the equipotential surface closest to the mean sea surface (MSS) is the Geoid. The distance between the Geoid and the reference ellipsoid is called the geoid height, which varies globally from about −106 m to 83 m. The difference between the MSS and the Geoid is the mean dynamic topography (MDT). The MSS and the MDT represent the relatively stable height structure of the ocean surface caused by continuous dynamic processes. The distance between the instantaneous sea surface and the Geoid is called dynamic ocean topography, or absolute dynamic topography (ADT).

According to the principle of traditional altimetry, when the microwave signal transmitted by a satellite reaches the sea surface, the footprint of the signal will illuminate an area called the instantaneous sea surface. Based on altimetry geometry, the instantaneous SSH is calculated from the satellite altitude Alt relative to the reference ellipsoid and the one-way signal transmission distance Range after corrected transmission errors, as shown in Equation (8), where ∆R_i represents transmission errors.

$$\mathrm{SSH}=Alt-\left(Range+{\displaystyle \sum _i\Delta R_i}\right),$$

(8)

Over the past few decades, multiple satellite altimetry missions have been conducted to observe the global SSH continuously for a long time, accumulating a large amount of observational data. The MSS data product has been produced based on the multi-year average of SSH.

$$\mathrm{MSS}={\langle \mathrm{SSH}\rangle }_N,$$

(9)

The difference between the SSH measured in a single measurement and the MSS is called sea level anomaly (SLA), which characterizes the temporal and spatial variations of the sea surface. Since tides and atmospheric forcing play a significant role in undulating the sea surface, various tidal effects and dynamic atmospheric correction (DAC) are usually calculated and removed after error correction of the SSH in satellite altimetry products. Then, the MSS is subtracted to obtain the along-track SLA. The along-track SLA data obtained from multiple satellite altimetry missions can be merged and gridded to produce a gridded SLA data product.

$$\mathrm{SLA}=\mathrm{SSH}-\mathrm{Tides}-\mathrm{DAC}-\mathrm{MSS},$$

(10)

As shown in Equations (8) to (10), the SSH observed by satellite altimetry includes not only the stable MSS and calculable tides and DAC but also the SLA related to ocean dynamic processes. Therefore, according to Equation (10), combined with data products and models of MSS, SLA, tides, and DAC, the reference topography data (RTD) that depict the characteristics of the sea surface topography structure at the time of the wide-swath altimetry observation can be constructed to some extent.

$$\mathrm{RTD}=\mathrm{MSS}+\mathrm{Tides}+\mathrm{DAC}+\mathrm{SLA},$$

(11)

Based on the relationship between the above reference surface and relative distance, the construction of RTD using multiple data products can provide reference data for the cross-calibration of wide-swath altimetry baseline error. In a study aimed at correcting baseline errors in China’s Tiangong-2 space lab’s Interferometric Imaging Radar Altimeter (InIRA), we utilized multi-source data products to generate the RTD that is time-coincident with the observation time of the wide-swath altimeter [34]. The RTD was then used to correct the baseline errors in the InIRA data. The data products used include the MSS data from CNES2015, daily SLA data provided by Copernicus Climate Change Service, geocentric ocean tides computed using the FES2014 model, solid tides calculated using the tidal response analysis method, polar tides calculated using the tidal proportion constant, and DAC data released by AVISO.

The accuracy of RTD is directly related to the results of baseline error correction. However, some auxiliary data products may have a time delay in their release since they are made from actual measurement data. For wide-swath altimetry in operational processes, real-time RTD may not be available, and only reference data with a specific time interval can be used. As shown in Equation (6), this will affect the results of baseline error correction. As MSS can be treated as a fixed dataset, tides exhibit periodicity that can be computed based on time and spatial location [35,36,37], and DAC can be derived using sea surface pressure and wind data products independent from the altimeter [38]. Hence, SLA is more sensitive to time intervals during the construction of the RTD. To assess the timeliness of correcting baseline errors in the RTD, we will conduct a simulation experiment.

3. Materials

To investigate the results and main influencing factors of the cross-calibration method based on reference topographic data for correcting the baseline error of wide-swath altimeters, this paper used SSH data provided by the Hybrid Coordinate Ocean Model (HYCOM). Error-containing simulated observations were executed using the wide-swath altimeter simulation software SWOT Simulator developed by the SWOT team, corresponding RTDs were constructed and the baseline error was corrected. The influence of RTD error and time differences between RTD and wide-swath altimeter observation data on the correction results were analyzed.

3.1. HYCOM Data

HYCOM is a key component of the US Global Ocean Data Assimilation Experiment (GODAE), which employs a high-resolution three-dimensional model to assess the real-time ocean state and provide various data types. These products provide height, temperature, salinity, ocean current, and other parameters at the sea surface and different depths. The Global Ocean Forecasting System (GOFS) of HYCOM generates SSH data products. It employs 3D variational data assimilation, which uses model forecast values as the initial guess field. Various actual measurement data are used as observations, including satellite altimeters, in situ observation instruments, expendable bathythermographs, Argo floats, and moored buoys.

The SSH data analysis product (GLBu0.08) with a global daily 1/12° spatial resolution was used in this paper, excluding tides. This SSH data product is the dynamic height relative to a long-term mean reference surface, essentially equivalent to the ADT in the altimeter data products after excluding the reference surface difference. Some studies have shown that the temporal and spatial variability of SSH provided by HYCOM is highly consistent with actual satellite altimeter measurements [39,40]. The data used in the simulation experiment range from 1 April 2015 to 31 May 2015 and are divided into 288 simulation experiment regions with a size of 10° × 10° in the range of 60°S~60°N, which are mainly marine areas, as shown in Figure 3. The color map of the base map is the global distribution of SSH on 1 April 2015.

3.2. Simulated Wide-Swath Data

A 42 day (corresponding to 2 cycles) simulation observation is performed for each simulation experiment region using the SWOT Simulator [41]. First, the SWOT Simulator calculates the observation swath coordinates using parameters such as satellite orbit, swath width, and spatial resolution. Then, it performs temporal and spatial interpolation on the input original SSH data to obtain an error-free model value within the swath, which is called SSH_model. Then, the total height error SSH_error is calculated based on the error spectrum of each major error source in the error budget requirement. The total error is then superimposed onto the error-free model value to obtain the wide-swath simulation observation result SSH_obs. Since the SWOT mission is configured with a traditional altimeter to perform nadir observations, the SWOT Simulator generates corresponding nadir observation values by adding random errors that meet the mission requirements to the error-free model value.

The SWOT Simulator incorporates six primary error sources, including roll error, baseline length error, systematic phase error, timing drift, random noise, and residual wet tropospheric delay, which are corrected by the microwave radiometer. Among them, random noise and residual wet tropospheric delay are directly generated based on the error budget. The other four error sources generate corresponding one-dimensional parameter errors based on the error power spectrum budget and then calculate the related height errors using the error propagation relationship.

The default configuration of the SWOT Simulator represents simulated observation results that have been fully corrected for all error sources. In the simulation experiment, the roll parameter error and baseline length parameter error were magnified by a factor of 5 to correspond to the “not yet fully corrected” baseline error. The main parameters used in the wide-swath altimeter simulation observation experiment are shown in

Table 1. Main parameters of wide-swath altimeter simulation observation experiment.

Parameter	Value
Altitude	890 km
Repetition period	21 day
Baseline length	10 m
Roll angle	0°
Swath width	±10~60 km
Cross-track resolution	2 km
Along-track resolution	2 km
Nadir observation resolution	1 s
Start date	16 April 2015
Execution duration	42 days
Time resolution of data to be observed	1 day
Spatial resolution of data to be observed	0.08° × 0.08°

.

As an example, Figure 4 shows a set of simulated observation results and error distributions.

Figure 4 shows that under the influence of various error sources, the observed SSH has significant differences from the true SSH. Among them, the baseline error will bring about obvious trend structures in the measurement results of the wide-swath altimeter, and a roll parameter error of about 1 arcsec will cause a height error of more than 30 cm. A baseline length parameter error of sub-millimeter level will also cause height errors ranging from centimeters to decimeters. The baseline error exhibits obvious spatial structural features concerning cross-track distance, while other height errors, except for the baseline error, have relatively weak relationships with cross-track distance.

3.3. RTD Construction

Two types of RTD were constructed based on the original HYCOM SSH data in the simulation experiment to explore the influence of the RTD error and time differences between the RTD and the wide-swath altimeter observations on the correction results. The first type was created by directly using the HYCOM data with the original resolution within the simulation region to form a complete time sequence of reference sea surface topography for the entire experimental period in a time-series manner. Then, the data were sliced starting from the time when the wide-swath altimeter observations needed to be corrected and interpolated spatially to the wide-swath observation coordinates with a time interval of 0 to 10 days, resulting in an RTD with time differences of 0 to 10 days relative to the wide-swath observations. This type of RTD is referred to as HYRTD and was used as the reference benchmark to investigate the influence of RTD error and time interval on the correction results. Taking the simulation observation data in Figure 4 as an example, the complete HYRTD sequence within the simulation region and the HYRTD with partial time intervals are shown in Figure 5.

In actual data processing, constructing the original resolution and error-free RTD is difficult. Therefore, a downsampling method was used to create the second type of RTD. The HYCOM original resolution data were downscaled within the simulation region to a spatial resolution of 1/4 degree. Model error was added to represent the reference data that can be used to correct the baseline error in actual wide-swath observations. This type of RTD is referred to as MORTD. The downscaled data were combined like HYRTD to form a complete time sequence within the simulation region. The time sequence data were then sliced and interpolated spatially to obtain MORTD with a time interval of 0 to 10 days relative to the wide-swath observations, as shown in Figure 6.

It can be seen from Figure 5 and Figure 6 that both HYRTD and MORTD can basically represent the overall structure of the SSH, but there are some local changes as the time interval increases. In addition, MORTD has a lower spatial resolution, more obvious “gridding”, and minor model error. These changes over time and model error can cause error recognition during the baseline error correction of the wide-swath altimeter data, reducing the correction ability.

4. Results

4.1. Case Study

For each set of wide-swath altimetry observations, baseline parameter errors are estimated and corrected based on HYRTD and MORTD at different time intervals using Equations (6) and (7), respectively. Then, the baseline errors are calculated and corrected using Equations (4) and (5) to obtain the residual error after correction by comparing the corrected SSH with the error-free SSH. Taking the simulated observation data in Figure 4 as an example, the corrected SSH and residual errors after baseline error correction based on HYRTD and MORTD are shown in Figure 7 and Figure 8, respectively.

It can be seen from Figure 7 and Figure 8 that using RTD at the time of observation can provide a better correction result of the baseline error, resulting in a small residual error after correction, mainly represented as a random error. Taking the observation data corresponding to Figure 4 as an example, the root-mean-square error (RMSE) between the pre-correction observation results and the measured SSH is 14.58 cm, while after correcting the baseline error based on HYRTD and MORTD with a 0 day time interval, the RMSE is 2.14 cm and 3.61 cm, respectively, indicating that the baseline error is well corrected. It can also be seen that interpolation errors and model errors can influence the correction results, with the baseline error correction result based on MORTD being slightly worse than that based on HYRTD. Moreover, Figure 7 and Figure 8 demonstrate that the increasing time interval between RTD and wide-swath observations can cause a gradual increase in the variation of SSH structure, leading to the cross-track trend in this variation being mistakenly identified as a baseline error. This could result in the misidentification of errors and compromise the accuracy of the correction process. When the time interval is large (such as the 4 day or 6 day time intervals in Figure 7 and Figure 8), the corrected SSH structure is significantly distorted, indicating that these baseline error correction results are no longer reliable.

To quantify the timeliness between correction results and time interval, we set the expected correction value to less than 6 cm for the residual error after baseline error correction. On the one hand, this is the average statistical result obtained in all experimental areas worldwide based on the default configuration of the SWOT Simulator, which corresponds to the power spectrum budget of the main error sources in the SWOT mission error budget [41]. On the other hand, this value is comparable to the measurement accuracy of nadir altimeters. Then the relationship between the residual error after baseline error correction based on RTD at different time intervals and the time interval is established. When the curve reaches the expected correction value, the corresponding number of days is taken as the effective time. In particular, if the residual error after correction is less than 6 cm throughout the entire 10 day period, the effective time will be set as 10 days. The longer the effective time, the smaller the influence of the time interval on the correction results. Taking the data in Figure 4 as an example, the RMSE after baseline error correction based on HYRTD and MORTD varies with time intervals are shown in Figure 9.

It can be seen from Figure 9 that the effective times for baseline error correction based on HYRTD and MORTD for these observation data are 2.16 days and 1.13 days, respectively. RTD beyond the effective time cannot effectively correct the baseline error and may even cause more severe mistakes in the results.

4.2. Global Study

Baseline error correction based on HYRTD and MORTD with different time intervals was performed separately on all observation data segments with an effective length of more than 400 km in each simulation experiment region. The RMSE after RTD correction with a 0 day time interval and the effective time were statistically analyzed in the simulation experiment region, as shown in Figure 10 and Figure 11.

It can be seen from Figure 10 that the baseline error of the wide-swath altimeter can be well estimated and corrected by HYRTD with a 0 day time interval. The corrected SSH’s RMSE in different regions is typically between 1~2 cm, which agrees with the random error in the error source. In most global experiment regions, the MORTD with a 0 day time interval can also estimate and correct the baseline error of the wide-swath altimeter well. However, the results are somewhat inferior in specific regions with strong currents, such as the Kuroshio region, Gulf Stream region, and Antarctic Circumpolar Current region, with an RMSE of approximately 3~4 cm. This may primarily be due to the RTD model error because the sea surface structure changes more drastically in time and space in these regions, causing larger model errors in constructing RTD than in other regions. It may lead to a trend difference between the RTD and the actual SSH, resulting in the RTD model error being mistaken for the baseline error and reducing the correction result.

Figure 11 shows that the distribution characteristics of effective time in different regions are similar to the distribution of RMSE after 0 day time interval correction. In regions with relatively slow SSH changes near the equator, the effective time based on HYRTD and MORTD can basically reach more than 7 days, and some experiment regions even exceed 10 days. In regions where the SSH changes more rapidly, the correction ability of baseline error is seriously affected by the time interval, and the correction result may no longer be reliable in only 1~3 days. In addition, the difference in the effective time of baseline error between HYRTD and MORTD is small. This suggests that as the time interval between RTD and wide-swath observations increases, the main factor that influences baseline error correction, namely the time difference, will cause the SSH to change on its own.

The above results show that if an RTD consistent with the time of the wide-swath observation data can be constructed or the time interval is small enough, meanwhile the RTD itself has a small error, the baseline error of the wide-swath altimeter can be effectively corrected. When the two are consistent or close in time, the correction result of the baseline error will mainly be influenced by RTD error, including the data error and interpolation error caused by the insufficient resolution of the RTD itself. As the time interval increases, the real SSH will change, and the baseline error correction result will gradually deteriorate. For regions where the SSH changes more slowly, these influences are relatively low, and good correction of baseline error can be achieved even with a time interval of several days. However, the results are more limited by the time interval for regions where the SSH changes more dramatically.

5. Conclusions

Baseline error is a major error source for wide-swath altimeters. Even minor errors in the baseline parameters can lead to significant errors in SSH measurements. The baseline error must be accurately corrected to ensure the quality of wide-swath altimetry data. Due to the cross-track spatial distribution of the baseline error, cross-calibration can be performed after other error sources have been adequately corrected, using the height difference between wide-swath altimetry results and reference data. However, the accuracy of the reference data constrains the results of baseline error cross-calibration. Since the ocean is dynamic, the surface topography structure changes over time, and no single data source can provide a stable and reliable reference DEM.

This paper proposes a scheme for constructing RTD using multi-source data products including MSS, SLA, tides, and DAC, which can provide a reference for the baseline error correction of future operational wide-swath altimeters. The simulation experience was carried out based on HYCOM SSH data to investigate the ability of RTD-based methods to correct the baseline error and the main influencing factors in different regions. The simulation results demonstrate that an RTD that is consistent with the wide-swath observation time can effectively correct the baseline error. However, the RTD error has some influence on the correction results, and in regions with strong ocean dynamics, the correction results are relatively worse. Furthermore, as the time interval between the RTD and wide-swath observation data increases, some of the cross-track trends in the changes of the real SSH may be mistakenly identified as the baseline error, leading to a deterioration of the baseline error correction results.