1. Introduction
The use of positioning methods has become a common practice among the different means of transport to monitor and enhance different aspects of vehicles, such as the efficiency of the driving, the route, safety, or location of freight [
1,
2]. Of all the available options, GNSS-based positioning has become the most employed technology as it is based on an already deployed infrastructure that allows the user to locate any object with just a receiver, this being an easy and scalable low-cost option. This technology offers global positioning to every receiver that has a minimum of four satellites in its range of visibility. When navigating through urban environments, the surrounding objects such as buildings may block the Line-of-Sight (LOS) signal coming from a low-elevation satellite, leading to a reception based on just Non-Line-of-Sight signal components, which can result in a poor position estimation [
3,
4,
5,
6]. Consequently, and due to the fact that the signals received from low-elevation satellites have lower Signal-to-Noise-Ratio (SNR) and are more vulnerable to atmospheric effects, the elevation masks are usually increased to filter all satellites with an a priori poor-quality signal. This fact leads to a higher chance of encountering the unavailability of GNSS navigation due to low accuracies or the lack of continuity caused by the absence of the required minimum number of satellites in indoor environments.
The multisensor navigation approach is a common option to face this problem. In the last decades, sensors such as inertial measurement units (IMU), barometers, odometers, magnetometers and digital compasses have been used. However, according to the author in [
7], recent trends have focused on the use of image-based, terrain-based collaborative navigation. They also stated that the choice of sensors should be aligned with the characteristics of the use case and the target application. Similarly, the author in [
8] affirmed that this choice should take into account the environment, dynamics, budget, accuracy requirements, and the degree of robustness or integrity required. As an example, it discusses the use of odometers, magnetic compasses, barometers, and map-matching algorithms as a typical augmentation in road vehicles, while trains may also use Doppler radar. Furthermore, it mentions that cell phone, UWB, and WLAN positioning may supplement GNSS indoors and in urban areas.
In fact, the use of Ultra-Wideband (UWB) radio technology in urban environments is a reliable option when trying to solve the main drawback of GNSS in low-visibility scenarios, indoor environments and even outdoor-indoor transitions, as the sub-meter accuracy and the tailored transmitting anchor geometry provide reliable information source at the time of positioning vehicles, tracking assets in warehouses, improving productivity in assembly lines, etc. [
9,
10,
11]. Previous research shows that, as the UWB technology is analogous to GNSS as the positioning is based on the trilateration of the signals received from transmitting anchors, the two technologies can be fused using different algorithms and strategies [
12,
13,
14,
15]. This fact could allow deploying UWB transmitting anchors in low-visibility areas, such as urban canyons, underground garages, or tunnels (see
Figure 1), in order to not lose the continuity of the positioning and even improve GNSS’ accuracy in required areas.
In spite of the improvement in performance that UWB can imply to GNSS, it is still a radio frequency-based technology and, consequently, it is also vulnerable to interferences or error sources such as multipath, electromagnetic noise, and jamming [
17,
18,
19]. These error sources are the same ones that degrade the signal reception in the GNSS receivers and cause a bad estimation of the ranges between receivers and transmitting nodes such as anchors or satellites, which leads to a bad position solution. Moreover, due to the vulnerability of UWB signals to multipath, inappropriate UWB anchor geometries or anchor locations may induce the degradation of certain signals as a result of the multipath effect.
Fault Detection and Exclusion methods were created as an extension to the Receiver Autonomous Integrity Monitoring (RAIM) methods that were developed for navigating in the aviation domain. These methods were developed to perform an autonomous self-check of the integrity of each and every GNSS observable and exclude the ones that are assumed to be faulty. In this document, the continuation of the research work discussed in [
16] is presented in
Section 2. As shown in [
16], the Fault Detection and Exclusion (FDE) methods originally developed for GNSS-based navigation can be utilized for the improvement of UWB-based navigation. In the current piece of work, the performance-improving effect of said methods is shown when applied to the innovation vector of a Kalman Filter when this is used to employ UWB signals as an augmentation for GNSS navigation. The main purpose, accordingly, is to prove that FDE methods can be used to exclude faulty augmentation observations since the misbehavior of said augmentation systems could lead to unexpected and critical faults instead of improving the performance of the standalone GNSS.
For said purpose, a theoretical approach to the performed research is presented in
Section 2. To do so, the Kalman Filter-based fusion is first presented, in order to, then, discuss the employed FDE method. Afterwards, the description of the measurement site is introduced in
Section 3, only to then show and analyze the results of applying this FDE method to the UWB-augmented fusion algorithm in
Section 4. Finally, the obtained conclusions are presented in
Section 5.
2. Theoretical Approach
The following section presents a theoretical approach to the employed navigation algorithm, known as the Kalman Filter. Moreover, the fusion between GNSS and UWB will be discussed. Afterwards, the Kalman Filter-based reliability testing is explained, in order to then explain the employed FDE scheme.
2.1. Kalman Filtering-Based GNSS and UWB Fusion
The Kalman Filter is the basis of most of the estimation algorithms used in navigation, as it is employed for different purposes such as smoothing navigation solutions and even fusing GNSS data with other navigation sensors. Its main characteristic is that it is able to maintain real-time estimates of continuously changing system parameters like position and velocity. This is carried out using both deterministic and statistical properties of the mentioned parameters and making assumptions about the input measurements and their characteristics and uncertainties. Moreover, due to the recursive nature of this algorithm, it employs past measurements together with a dynamic model of the navigation system for the aim of achieving a more accurate PVT estimation.
In this research work, the nonlinear version of the Kalman Filter was employed, also known as an Extended Kalman Filter (EKF), which linearizes an estimate of the current mean and covariance [
20]. This algorithm is usually initialized with a time-invariant parameter x that has been computed employing a snapshot algorithm such as the LSE method, for example. It is then assumed that this parameter is not only time-variant but that it can be described by a dynamic model that relates two adjacent epochs as
where
is the estimated parameter;
describes the dynamic model-dependent transition matrix, which defines the change of the state vector with time as a function of the system’s dynamics;
describes the last known value of the parameter to estimate;
models the system process noise, and
is the covariance matrix of the process noise.
For this research work, the transition matrix,
, has been modelled following a constant velocity dynamical assumption (see [
20] for more information about the dynamical modeling of a system). Consequently, the employed state vector if formed as
where
describe the computed position,
describe the computed velocity of the rover and
describe the receiver’s clock offset and clock drift, accordingly.
This estimation of parameter
, nevertheless, comes from an uncertain method as the LSE is and, consequently, the uncertainty about this estimation is inherited by the future values. It is, thus, necessary to propagate said uncertainty, so that its unbounded propagation degrades the results. Of the numerous forms of covariance propagation in use, one of the most common is the following one:
where
is the propagated covariance matrix;
describes the dynamic model-dependent transition matrix;
describes the a priori covariance matrix, and
represents the covariance matrix of the system noise, which defines the increase with time of the uncertainties of the state estimates (i.e., unmeasured dynamics and instrument noise).
The KF does not only trust the quality of the input state or the propagated estate. Instead of this, it determines a weight of measure of trust for the measured information and for the estimated state in order to combine both of them, avoiding poor estimations and observation outliers. This is carried out by means of the Kalman Gain matrix, which is computed as
where
is the computed Kalman Gain matrix;
represents the measurement matrix, which defines how the measurement vector varies with the state vector;
describes the measurement noise covariance matrix and
models the de innovation vector’s covariance matrix. Note that the employed measurement matrix was formed as shown in [
16], but it was expanded in order to fit UWB observables. This matrix is formed as follows:
where
and
(both for GNSS and UWB) represent the unitary vectors (in ECEF x-y-z coordinates) that link the receiver’s position and each of the transmitting satellite/anchor’s position. This weighting matrix is applied, as mentioned, as a measure of trust that is given to the measurements and the estimations. Having computed the mentioned parameters, this yields
where
represents the computed state;
corresponds to the read measurement vector; and
represents the innovation vector, which describes the difference between the read measurement and the expected measurement.
Due to the similarity of the measurements between GNSS and UWB, the fusion between these two can be intuitively performed by adding the UWB ranges to the observable vector,
, this being
where
is the pseudorange measurement for the
satellite;
represents the range measurement for the
anchor;
contains the Doppler measurement for the
satellite;
denotes the number of visible GNSS satellites and the number of observable pairs; and
is the number of visible UWB anchor measurements. Another design parameter of the Kalman Filter that depends on the number of measurements and their characteristics is the measurement covariance matrix described by
. In this research, the elements of this diagonal matrix were weighted according to the power spectral density (PSD) and reweighted, then, according to the signal SNR and satellite elevation in the case of the satellite signals and according to the elevation in the case of the UWB signals. The diagonal elements of the matrix that correspond to satellite signals are characterized as
while the diagonal elements that correspond to UWB signals are characterized as
The fusion of these two types of measurements is based on the assumption that UWB range estimations have significantly higher accuracy than the ones provided by a low-cost GNSS receiver. Accordingly, even if the estimation of the range of UWB observables would get slightly degraded, these should still be valid as an augmentation source, since the range estimation error would still be better than the one corresponding to GNSS. Consequently, slight errors in the location of the anchors or slight errors in the synchronization of said ranges with the ones incoming from the GNSS receiver should still improve the performance of the standalone GNSS.
2.2. Reliability Testing
As can be deduced from (6), the existence of an outlier in the measurement vector,
, may induce an error in the computed result,
. Thus, testing the internal consistency of the observations, which is to say, detecting the presence of any bias or outlier, turns out to be necessary if ensuring the reliability of the solution is pursued. Accordingly, a wide variety of research lines have studied fault diagnosis and prognosis functions using system theory and statistical decision theory [
21,
22,
23]. In this research work, similarly to what was presented in [
16,
23], a test statistic was introduced in order to estimate or quantify the consistency of the measurements. This parameter was obtained from the normalized square sum of the innovation vector,
, of the Kalman Filter, which can be computed as
This test statistic, , follows a central chi-square distribution (i.e., ) with degrees of freedom when the observation errors are distributed according to a zero-mean normal distribution (i.e., ). On the other hand, when there are bias errors along with the measurements (i.e., ), the test statistic follows a non-central chi-square distribution with a centrality parameter (i.e., ). This parameter is used to compare its value against a certain threshold so that the following hypotheses can be verified
Hypothesis H0.
No fault is present in the observations (Nominal condition).
Hypothesis Ha.
A fault is present in the observations (Fault condition).
According to these hypotheses, two decisions can be taken: rejecting the measurement or accepting it (see
Table 1). Therefore, four different scenarios can take place
Therefore, the false alarm concept is defined as an indication of positioning failure when this has not occurred. In a similar way, a missed detection event is defined as an indication of positioning failure that has not been detected, which must be minimized as it can lead to fatal events. These hypotheses are tested by comparing the test statistic computed as (10) and a threshold that depends on the probability of false alarm and the degrees of freedom of the distribution, which can be denoted as
, being
the false alarm rate and
p the degrees of freedom. This comparison is known as Global Test (GT) and is used to detect anomalies in the measurements. According to this, as seen in
Figure 2, there is a user-defined frontier value of
that intersects both curves, which acts as a delimiter to choose between the curves. This threshold value, then, delimits the faulty and non-faulty measurements. In other words, if the test statistic falls below this threshold value, it will be considered a non-faulty observation, while if it falls above the threshold, it will be considered a faulty observation. Note that as the curves in
Figure 2 intersect, there are values of the non-faulty distribution that will be considered as faulty and values of the faulty distribution that will be thought of as non-faulty ones. The former case’s probability will be denoted by the probability of a false alarm (
), while the latter one will be called the probability of missed detection (
). These values can be computed from the graphs integrating the corresponding probability density function (pdf) from zero to the threshold in the case of
and from the threshold to infinity in the case of
. The threshold,
, can be computed as the inverse of a chi-square distribution with
degrees of freedom and probability of false alarm
:
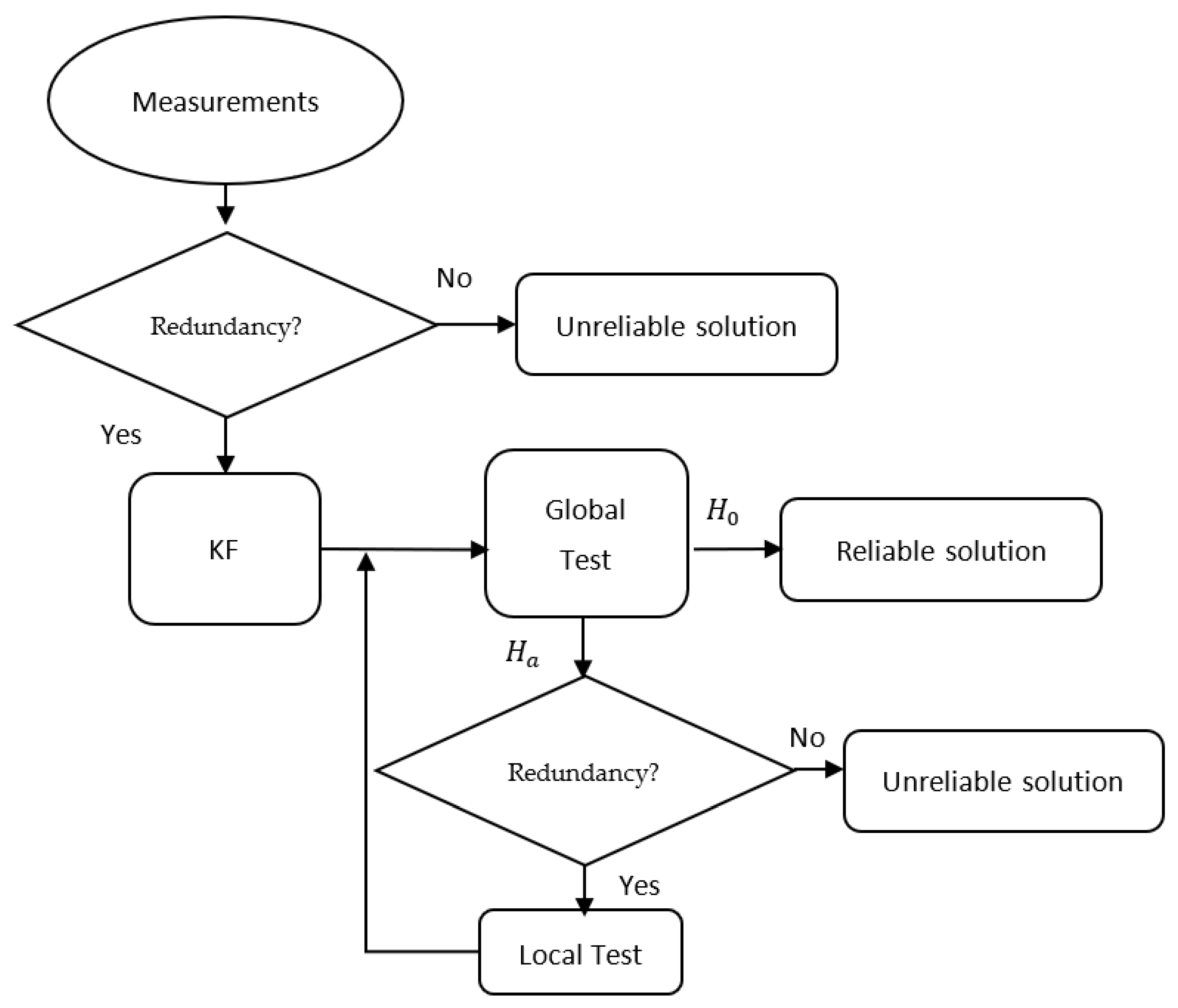
This statistical behavior is the base of the Global Test that measures the reliability of the observations. This test is used to estimate the scenario hypothesis and, if necessary, to proceed to a Local Test with more specific alternative hypotheses for failure isolation.
The outlier detection and isolation are based on assumptions according to estimated observational residuals. These residuals, nevertheless, are just indicatives of both the behavior of a mathematical model and the observations. As a consequence, the differentiation of both is not easy, as a bad geometrical model and model assumptions or bad observations affect the residuals in the same way [
24]. However, the author in [
24] states that the most likely reason for the rejection of the null hypothesis is the existence of outliers and their corresponding detection during the global test. In these processes, an assumption of Gaussian zero-mean noise is made for the unbiased error-free case of the linearized model.
Therefore, failure isolation may not be as straightforward as expected, since matrix
involves the cross-correlations of the state components. Consequently, the effect of the faulty measurement could leak into the rest of the observables, leading to mistaken error exclusions. In order to solve such an issue, the author in [
25] proposed normalizing the innovation vector by the Cholesky decomposition of matrix
, which results in a positive semi-definite matrix with no more correlations between its elements, as these are removed. This can be denoted as
where
represents the uncorrelated normalized innovation vector and
denotes the positive semidefinite uncorrelated covariance matrix, which is the outcome of the Cholesky decomposition.
Having normalized the innovation vector, it is assumed that the element with the highest value is the one to be isolated. Note that this approach is compatible with an iterative scheme, which will be introduced in the following
Section 2.3.
2.3. Fault Detection and Exclusion Scheme
As discussed in previous research [
16], the classical FDE method was originally developed as an extension of the classical Receiver Autonomous Integrity Monitoring (RAIM) for GNSS and was designed under a single failure assumption, due to the friendly radiofrequency-related conditions available in the sky. This single failure assumption could have been enough for the aviation domain, where the probability of observable failure was much lower than the systemic failure of GNSS, which implied a single execution of the Global test—Local test pair. Nevertheless, this may not be enough for an urban scenario, where the probability of finding a faulty observable is significantly higher than in open scenarios (i.e, the sky). Moreover, the likelihood of finding faulty observables increases when
observables are used due to the combination of GNSS and UWB technologies.
Consequently, the classical FDE scheme can be conveniently adapted to an iterative scheme (see
Figure 3) in which the global and local test combination is executed until no more observable failures are detected or there is no longer enough observable redundancy. Intuitively, and due to the high confidence that is given to the UWB observables as they act as an augmentation system, UWB range measurements turn out to be the most probable values to be excluded first under the existence of a faulty UWB measurement.
Note that other FDE schemes such as the ones discussed in [
24,
26,
27,
28,
29] could also be used, just by adapting the local test to the condition discussed in the previous subsection. Depending on the number of augmentation UWB anchors, nevertheless, the computation time could drastically increase, as commented in [
16].
4. Result and Discussion
This section shows and analyzes the results obtained when applying the employed FDE methods to the fusion between GNSS and UWB by means of a Kalman Filter. These results were obtained after processing the data collected in the measurements explained in the previous
Section 3. The computation of the error was performed by comparing the calculated solution’s position against the ground truth’s coordinates with the closest temporal value. Since the output data rate of this ground truth was ten times higher than the one of the developed navigation algorithm, a maximum time error of 0.1 s could be suffered and, thus, added to the computed error. Due to the fact that UWB anchors were deployed just in the surrounding area of the garage (see
Figure 8), the results analysis is divided into two main parts, being intuitively classified depending on the use of UWB as an augmentation system.
Accordingly, the two main regions of interest to be distinguished are the one in which UWB signals are received and the one in which they are not. Due to the fact that the 40º satellite elevation mask reduces the probability of finding a faulty GNSS observable (a fact that will be shown in later figures), the main region of interest for this research work is the one that comprises UWB signal coverage. As a consequence, the following result discussion will refer to the effects of the employed FDE method inside this coverage region.
The following
Table 3 summarizes the results of the multiple measurement rounds performed in the test site described in the previous
Section 3. This table evaluates each of the performed seven rounds in terms of the number of computed solutions and horizontal error, divided into the minimum, mean and maximum values, together with its variance. Note that, due to the high observable redundancy created by the number of visible satellites and the eight deployed anchors, the likelihood of reducing system solution continuity due to excessive exclusions or lack of redundancy was significantly reduced. Accordingly, only two epochs were declared unreliable, as seen in rounds 1 and 5.
In the said table, it can be seen that, overall, applying the described FDE technique improves the performance of the GNSS + UWB positioning algorithm. Due to the fact that applying FDE especially focuses on the detection of outliers, it is only normal to observe that the results showed an improvement in the maximum values of the error, which is then reflected in the means and the variances. Accordingly, the minimum error values did not significantly vary, as the minimum values usually corresponded to the best observable situations, observables which should not be excluded by the FDE methods; if they are, this may be due to a non-sufficient probability of the false alarm, .
Table 4 shows the effect of applying FDE methods to the UWB-augmented GNSS navigation, as it shows the percentage variation of the two halves of
Table 3. This way, the reductions in the positioning error are colored in green, while the increases are colored in red. Accordingly, the improvement in the maximum positioning error becomes obvious, since it reached reductions up to 64%, which led to a decrease in the mean positioning error by up to 12%. Note that the reductions in the number of solutions are colored in yellow since these cannot be evaluated at the same time in terms of accuracy, integrity and continuity. Having said this, the reduction in the number of solutions induced a slight decrease in the continuity of the system as compensation for the improvement in the mean error, and a reduction of the maximum error.
Furthermore, it is meaningful to mention that in the part of the track in which UWB was not used or, what is to say, the part outside the entrance of the garage, the results of the GNSS and UWB fusions with and without applying the FDE method performed almost identically. Note that, after losing the coverage of the UWB anchors, the GNSS + UWB and GNSS + UWB + FDE solutions need some time to converge to the same standalone GNSS solution.
Moreover, as shown in
Figure 9, the result at the beginning of the track of the GNSS + UWB and GNSS + UWB + FDE methods are almost identical, being both of them much closer to the ground truth than the GNSS-only one, which showed an initial offset of about 4 m from the reference (see
Figure 10). The cause of this is that the convergence time at the beginning of the measurement allows the algorithm to make use of UWB’s accuracy to obtain an accurate initial position. Moreover, the similarity between the GNSS + UWB and GNSS + UWB + FDE methods can be confirmed by the number of excluded observables at the beginning of the measurement; which can be seen in
Figure 11. It can be seen that the only observables that are excluded are the UWB ones due to two main reasons. The first one, as commented in the introduction of this document, is related to the elevation mask applied to the satellites in view which, as it is set to be higher than 40º, reduces the probability of employing multipath or NLOS-containing satellite pseudoranges. The second one is caused by the high confidence value that is assigned to UWB ranges by the measurement covariance matrix,
, due to their lower noise Power Spectral Density (PSD). This high confidence also implies higher visibility at the time of fault detection, making them easier to be detected, as expected.
After losing sight of the last anchor and navigating through the outdoor part of the track, it is at the time of recoupling with the UWB anchors where the biggest differences in results can be found. As seen in
Figure 9, the three methods (GNSS, GNSS + UWB and GNSS + UWB + FDE) did not show the same solution position at the beginning of the entrance of the garage, being the GNSS-only method further from the reference than the UWB-employing ones. Moreover, it is only meaningful to comment that, as happened at the start of the mission, the only UWB anchors in view were the ones from A0 to A5, which is intuitively expectable due to the proximity and the geometry of the garage. However, the weak reception of the signal coming from anchor A5, which may be caused by the lack of line-of-sight reception, is what makes the difference between using and not using FDE methods to obtain higher accuracy and integrity.
This single fault isolation seen in
Figure 11 of the range incoming from anchor A5 causes the qualitative improvement that can be seen in
Figure 9 (removal of the green divergence at the middle of the garage entrance and the removal of the green noisy cloud at the end of the measurement). Moreover, this improvement is quantitatively observed in
Figure 10 and round 5 in
Table 3, as the cumulative distribution function of the FDE-using method limits its maximum value to 5.1 m, which is considerably lower than the 10.64m error shown by the non-FDE GNSS + UWB fusing method.
Moreover, not only does
Figure 10 show the overall improvement of the UWB-augmented GNSS system against the standalone GNSS navigation, but it also shows that the degradation in performance of said sensor fusion is caused by incorrect UWB signal couplings or uncouplings, which are modelled as biased observables, thus, excluded by the FDE methods. Accordingly, the maximum positioning error is decreased, improving the behavior of the CDF that corresponds to GNSS + UWB + FDE with respect to the one corresponding to GNSS + UWB.
When analyzing
Figure 12, which shows the visibility of each anchor during round 5 of the measurement campaign, a coherent behavior can be observed. To begin with, since an initial convergence time was awaited at the initial point of the track (right in front of the garage), a stationary phase can be observed in the UWB range estimations. Note that in this very point, Line-Of-Sight signals could be read at the UWB tag, which is represented by the eight observables scatter lines.
It is only when the vehicle starts its mission that the UWB range estimations began to change their values and disappear due to the lack of LOS of NLOS signals that the first excluded observable can be seen in
Figure 11. This excluded range from anchor 5 is caused by the lack of LOS component in the received signal before it disappeared at the same time that the vehicle abandoned the UWB coverage area.
Analogously, no more UWB range exclusion could be found until the moment in which the car proceeded into the UWB coverage region, a moment in which no LOS component can be received from the signal incoming from anchor 5. Once again, this anchor seems to be close enough to receive its NLOS signal components, but it is not located in an appropriate location in order to receive its LOS signal component.