Multivehicle 3D Cooperative Positioning Algorithm Based on Information Geometric Probability Fusion of GNSS/Wireless Station Navigation

Abstract

With the rapid development of large urban agglomerations and the increasing complexity of urban roads, the high-precision positioning of vehicles has become the cornerstone for the application of vehicle core technologies such as automatic driving. The real-time positioning accuracy of satellite navigation is easily affected by urban canyons, and its stability is poor; thus, how to use the information of the internet of vehicles to achieve satellite navigation fusion has become a difficult problem of multivehicle cooperative positioning. Aiming at this problem, this paper proposes a multivehicle 3D cooperative positioning algorithm based on information geometric probability fusion of GNSS/wireless station navigation (MVCP-GW), which creatively converts various navigation source information into an information geometric probability model, unifies navigation information time–frequency parameters, and reduces the impact of sudden error. Combined with the Kullback–Leibler algorithm (KLA) fusion method, it breaks off the shackles of the probabilistic two-dimensional model and achieves multivehicle three-dimensional cooperative positioning. Compared with the existing cooperative positioning algorithms in the performance of accuracy stability, applicability, obstruction scenarios, and physical verification, the simulation results and physical verification show that the MVCP-GW algorithm can effectively improve real-time vehicle positioning and the stability of vehicle positioning, as well as resist the impact of obstructed environments.

1. Introduction

With the rapid development of smart city core businesses, such as autonomous driving and intelligent transportation, the demand for real-time and high-precision positioning of vehicles is increasing [1,2]. In related technologies, vehicle navigation systems generally use the motion information of vehicles in two-dimensional plane to locate and navigate [3]. They focus on the motion information of vehicles in the horizontal direction, ignoring the motion information in the vertical (height) direction, which leads to low positioning accuracy of vehicles in some scenes. For example, when a vehicle is driving in an overpass or viaduct area, the vehicle navigation system cannot tell whether it is above or below the bridge; when the vehicle is in a multistory three-dimensional parking garage, the vehicle navigation system cannot distinguish the parking lot where the vehicle is located.

To improve vehicle positioning accuracy, global navigation satellite systems (GNSSs), inertial navigation systems (INSs), wireless station positioning systems, radio detection and ranging (RADAR), light detection and ranging (LiDAR), and 5G mmWave are widely used in vehicle positioning [4]. Although they can measure and solve the vehicle position through relevant algorithms to obtain accurate positioning information, they also have the problems of sensor working characteristic deficiencies and environmental limitations. GNSS can provide full coverage and all-weather positioning, but it leads to poor positioning accuracy and stability due to the urban canyon effect [5]. INS can provide continuous attitude information, which is independent of environmental conditions and not easily disturbed, but the inertial unit produces cumulative errors during use and cannot work independently for a long time [6]. The positioning methods based on wireless networks calculate the position through information such as the time of arrival or received signal strength, and the result is susceptible to communication delay and multipath effects [7]. RADAR and LiDAR achieve relative positioning by measuring the position of surrounding objects, but the former method has low accuracy, while the latter method is greatly affected by the weather, and its performance drops significantly in cloud, rain, and fog environments [8,9]. Simultaneous localization and mapping (SLAM) technology based on visual navigation and LiDAR is suitable for unknown environments. The map constructed by SLAM contains rich driving assistance information, but it is difficult to save and update, and the natural cumulative errors cannot be eliminated [10]. In recent years, with the rapid development of 5G millimeter waves, vehicle positioning based on millimeter waves has also become a hot issue in the field of navigation [11]. However, the high demand for millimeter wave technology for antenna arrays and transmission power makes it difficult to achieve popularization in the field of household cars [12]. Because of the inherent problems of a single navigation source, vehicle real-time and high-precision positioning is impossible. The fusion of different types of navigation sources has become the core problem in the field of vehicle positioning [13].

In the current vehicle ranging and positioning information fusion, the perception of the surrounding environment of the vehicle is mainly accomplished through various ranging, direction-finding, and perception sensors. The existing fusion technology mainly fuses navigation sources through a Kalman filter (KF) [14]. However, the scalability of KF is not strong. When more than three sources are fused, the computational complexity increases exponentially, and the real-time performance is affected [15]. In addition, KF cannot adequately solve the problems of vehicle plug-and-play under the internet of vehicles. Because of the rapid development of the internet of vehicles, the interactive information between vehicles has increased, and the vehicle cooperative positioning technologies represented by neural networks and factor graphs have also been applied to the field of vehicle positioning [16,17]. The positioning accuracy of these methods is obviously improved, but the computational complexity is too high, especially in the three-dimensional positioning of vehicles, which cannot meet the real-time positioning requirements under the condition of large-scale vehicle networking and high-speed vehicle movement. Therefore, how to combine the relative distance between vehicles, satellite navigation, and wireless station navigation to achieve three-dimensional cooperative positioning of multiple vehicles is a difficult problem in the current development of intelligent vehicles.

To solve the problems of vehicle plug-and-play under the internet of vehicles, obstruction and interference of navigation systems, and the poor real-time positioning performance caused by the high complexity of existing navigation source fusion technologies, this paper proposes a fusion architecture based on information geometric probability and achieves a large-scale vehicle three-dimensional cooperative positioning algorithm by combining the distance measurement information of vehicles under the internet of vehicles. The main innovations are as follows:

• The first innovation is to introduce the idea of information geometry into multisource fusion. Aiming at the inconsistency of the time and frequency of the output navigation information, we convert the two types of navigation source information into an information geometric probability model to unify the time and frequency of the navigation information for large-scale vehicles under the internet of vehicles. The unification of positioning information parameters can effectively reduce the complexity of the algorithm, enhance the scalability of the fusion algorithm, and successfully solve the problem of vehicle plug-and-play under the internet of vehicles.
• The second innovation is to introduce the idea of multisource fusion into cooperative positioning, and transform cooperative positioning into multisource fusion in different spatial distributions by taking nodes as sources. Aiming at the problem that the information geometric probability model is two-dimensional and cannot be directly fused and positioned in three-dimensional space, we propose a three-dimensional KLA navigation information fusion method based on the ranging information of the vehicle network. The method uses relative entropy theory to measure the difference in the probability of navigation distribution information among multiple vehicles in the vehicle network and rapidly fuses navigation information under the minimum difference criterion. This method can ensure the real-time performance of multivehicle positioning and effectively suppress the sudden error.
• We construct a physical verification platform for multivehicle cooperative positioning and verify the performance comparison between the MVCP-GW algorithm and the current main algorithms through simulations of accuracy stability, applicability, and obstruction scenarios. The results show that the MVCP-GW algorithm has high accuracy, strong robustness, and a wide application range. When satellite navigation or wireless navigation signals are lost or abruptly changed, the MVCP-GW algorithm can adequately suppress the impact of errors. In addition, compared with other distributed cooperative positioning algorithms, the MVCP-GW algorithm has the fastest convergence speed of more than 40%.

The remaining paper is organized as follows: Section 2 reviews the related technologies of cooperative positioning; Section 3 introduces the positioning scenario and system model; Section 4 focuses on the multivehicle 3D cooperative positioning algorithm based on information geometric probability; Section 5 shows the simulation results.

2. Related Work

With the rise in technologies such as the internet of things and intelligent transportation, continuous, accurate, and highly reliable positioning information is the basis for autonomous path planning and motion control of intelligent vehicles, which have been highly valued by many scholars.

Because of various limitations and defects, a single sensor cannot meet the high-precision and strong robust positioning requirements of intelligent vehicles. Therefore, multi-sensor information fusion technology has become a new research object. Among them, the Kalman filter (KF) and its extension methods are the most widely used, such as the extended Kalman filter (EKF), unscented Kalman filter, and cubature Kalman filter (CKF). The study in [18] used the EKF to fuse GPS and IMU, which solves the problem of positioning distortion caused by GPS signal loss and improves the positioning accuracy and reliability of the navigation system. The study in [19] investigated the positioning of low-speed unmanned vehicles in the area of GNSS signal suppression and proposed a low-speed unmanned vehicle positioning algorithm based on the multistate constrained Kalman filter (MSCKF) algorithm integrating low-cost binocular cameras and IMU, which effectively solved the problem of vehicle positioning in the GNSS rejection domain. The study in [20] comprehensively considered the advantages and disadvantages of GPS, the strapdown inertial navigation system, and the odometer (OD) and proposed a GPS/INS/OD navigation algorithm based on EKF. The experimental results show that OD can correct the IMU error and improve the navigation performance, while the algorithm can provide accurate positioning information in the absence of a GPS signal. The method of multi-sensor fusion can effectively improve the problem of large error or low robustness of a single sensor. However, the fusion method based on KF has weak scalability and high algorithm complexity. In addition, in the case of long-term loss of GNSS signals and difficulty in building high-precision maps due to similar features in long tunnels, there are still many defects in single-vehicle positioning.

Therefore, how to make full use of the rich ranging and direction-finding information between vehicles to further improve the positioning accuracy and increase the robustness of the system has gradually become a new research hotspot. The early centralized cooperative positioning of vehicles was mainly used in wireless sensor networks, which mainly achieved whole-network data fusion through one or more central nodes and transmitted the positioning results to the node users of the whole network [21,22]. However, the above methods are not suitable for the needs of multivehicle cooperative positioning under the internet of vehicles; hence, the distributed cooperative positioning method has become the main research direction of multivehicle positioning under the internet of vehicles. According to the rapid change in vehicle number and position in multivehicle cooperative positioning, the authors of [23] proposed an algorithm for multivehicle cooperative positioning based on semi-defined programming, which can achieve target vehicle positioning by collecting ranging information, and positioning information between surrounding vehicles and target vehicles. The study in [24] proposed a second-order cone programming (SOCP) model on the basis of [23], which achieved a rapid increase in positioning speed by optimizing the structure. However, when any vehicle involved in cooperative positioning has a sudden error, the accuracy of cooperative positioning of other surrounding vehicles is greatly affected. To improve the accuracy of multivehicle cooperative positioning, the authors of [25] proposed a vehicle cooperative positioning algorithm based on a factor graph. This algorithm used the surrounding vehicles to evaluate the positioning accuracy of target vehicles, established a confidence degree model, and achieved the positioning solution under the whole-vehicle network through a factor graph network. The study in [26] proposed a positioning technology for the Internet of Vehicles based on a neural network, which used a neural network to construct the positioning information learning model. These two algorithms could effectively improve the positioning accuracy, but they had the problems of high algorithm complexity and long positioning time in the large-scale internet of vehicles.

The existing distributed multivehicle positioning fusion technology cannot meet the needs of real-time and fast positioning due to the rapidly changing characteristics of vehicles, and the different time–space–frequency parameters, such as the navigation information format and output frequency among vehicles, will affect the fusion efficiency. In addition, when the local vehicle positioning information has a sudden error, the positioning performance of the entire internet of vehicles will be reduced. To solve the above problems, this paper creatively converts navigation information into an information probability model and uses the information geometry principle to rapidly fuse distributed vehicle positioning. The concept of information geometry was first proposed for radar target detection in 2013. The advantage of this method is to use multiple distributed detection signals to fuse the detection probability of the target, which greatly improves the target detection accuracy [27,28]. The study in [27] proposed a total Bregman divergence-based matrix information geometry (TBD-MIG) detector and applied it to detect targets emerged into nonhomogeneous clutter, which can achieve great performances due to their power of discrimination and robustness to interferences. The study in [28] proposed a novel type of learning discriminative matrix information geometry (MIG) detectors in the unsupervised scenario through principal component analysis (PCA) theory, whose performance improvements could be achieved compared with the conventional detectors and their state-of-the-art counterparts within nonhomogeneous environments. Aiming at the problem that information probability cannot be directly fused in multivehicle cooperative positioning, this paper designs a KLA fusion architecture based on the ranging information between multiple vehicles, which breaks off the shackles of information probability fusion, which is difficult to calculate.

3. System Model

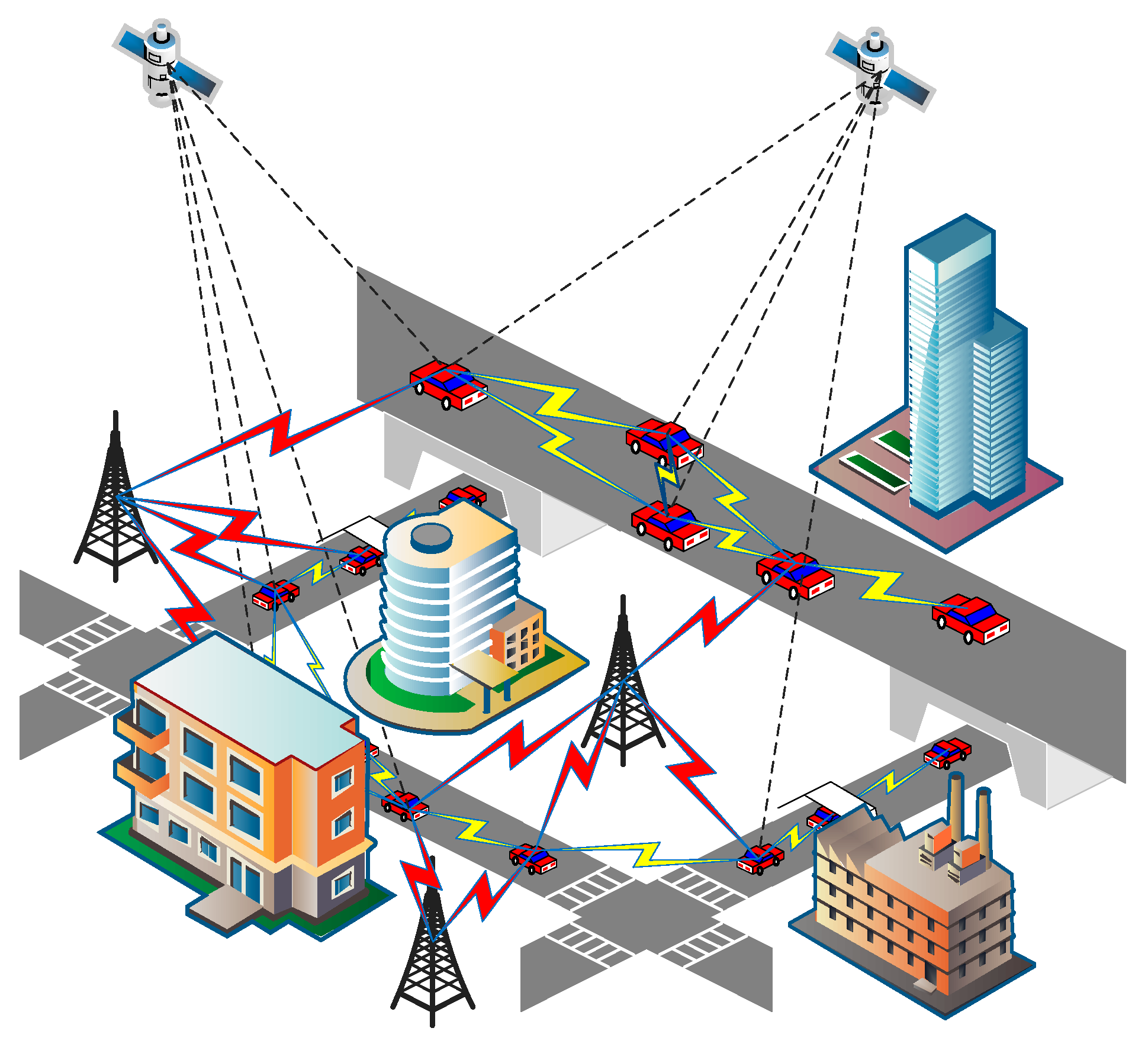
3.1. Diagram of Multivehicle 3D Cooperative Positioning Scene

Because of the ubiquity of the urban canyon effect, electromagnetic multipath interference and vehicle movement, a single vehicle achieves continuous positioning with difficulty. Therefore, multivehicle cooperative positioning has become an important research direction. The multivehicle 3D cooperative positioning scene studied in this paper is shown in Figure 1.

In Figure 1, the red link indicates the communication link between the vehicle and the base station, the yellow link indicates the distance measurement communication link between the vehicles, and the dashed line between the satellite and the vehicle indicates that the vehicle can be positioned through the navigation satellite. Some vehicles can be positioned through the navigation satellite, some vehicles can be positioned through the wireless station, and some vehicles can only be positioned through surrounding vehicles.

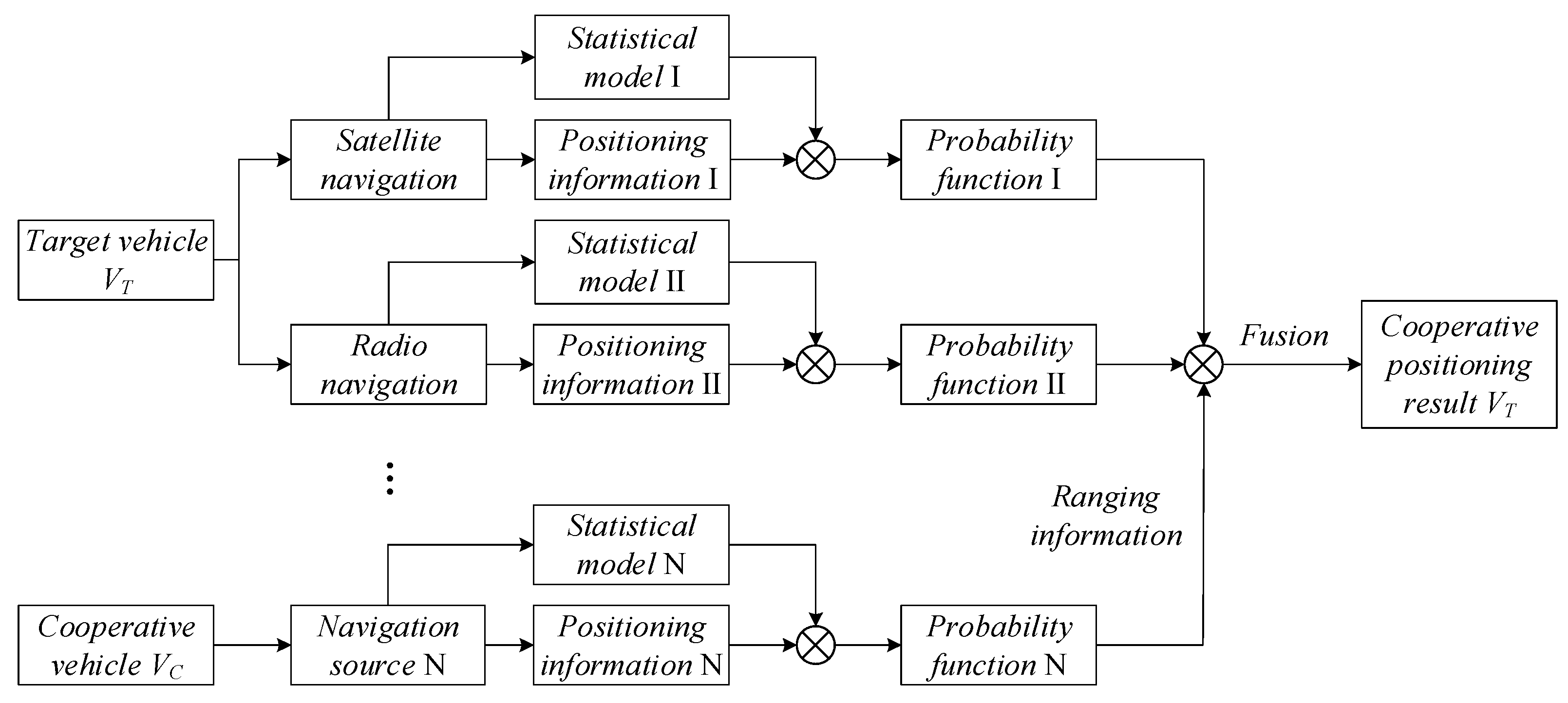
3.2. Fusion Architecture Based on Information Geometric Probability

The topology of the internet of vehicles will change over time, which can lead to a single vehicle being unable to achieve long-term single navigation source positioning. Therefore, the core difficulty is in achieving multitype ranging, positioning information interaction, and fusion between multiple vehicles with the help of the information interaction characteristics of the internet of vehicles.

In multivehicle cooperative positioning, the time–frequency information of the positioning information received by the distributed vehicles in the internet of vehicles is completely different, and the plug-and-play characteristics of vehicles will make the time and frequency very difficult to synchronize, which will reduce the precision of multivehicle cooperative positioning; the spatial ranging error between vehicles will further increase the positioning error. To achieve the rapid fusion of real-time multitype positioning information among multiple vehicles, this paper proposes using the correlation between vehicle positioning information probability and positioning accuracy to establish the geometric probability model of satellite positioning and wireless station positioning, and to achieve rapid positioning fusion between multiple vehicles combined with ranging information between vehicles. The fusion architecture based on information geometric probability is shown in Figure 2.

First of all, we construct the statistical model functions of various navigation sources, and then obtain the positioning results and positioning ambiguity of navigation sources according to the actual measurement parameters. In this way, we can convert satellite positioning information and wireless station positioning information into information geometric probability model, which realizes the unification of heterogeneous navigation sources. Assuming that the probability distribution of navigation information is Gaussian, its positioning result can be represented by mean value $\mu$, and its positioning ambiguity can be represented by variance ${\sigma }^2$, such that the navigation information will be transformed into information geometric probability density function $N\left(\mu ,{\sigma }^2\right)$.

Then, the different navigation sources of the target vehicle are fused to improve the positioning accuracy of single vehicle. Finally, according to the positioning results of the cooperative vehicles and the abundant ranging and direction information in the internet of vehicles, multivehicle cooperative positioning is carried out to improve the positioning accuracy and stability of the whole-vehicle networking.

4. KLA Information Geometry Fusion Method

4.1. Three-Dimensional Geometric Probability Model of Positioning Information

In the internet of vehicles, because of the plug-and-play characteristics of vehicles, the time and frequency parameters of the base station positioning signal of each vehicle are difficult to synchronize, resulting in a significant decline in the positioning accuracy after vehicle cooperative positioning. Therefore, this paper uses vehicle positioning information and ranging information to construct the geometric probability model of positioning information to unify the time and frequency parameters.

The position of the positioned vehicle is set as $\mathit{v}=\left(x,y,z\right)$, the number of cooperative vehicles is set as $n \left(n\ge 4\right)$, whose positions are ${\mathit{V}}_i=\left\{\left(X_i,Y_i,Z_i\right)|i=1,2,3,\cdots ,n\right\}$, and the ranging information between $\mathit{v}$ and ${\mathit{V}}_i$ is set as $\mathit{d}=\left(d_1,d_2,\cdots ,d_n\right)$. Then, we get the following system of equations:

$$\{\begin{array}{c}{\left(X_1-x\right)}^2+{\left(Y_1-y\right)}^2+{\left(Z_1-z\right)}^2=d_1{}^2\\ {\left(X_2-x\right)}^2+{\left(Y_2-y\right)}^2+{\left(Z_2-z\right)}^2=d_2{}^2\\ ⋮\\ {\left(X_n-x\right)}^2+{\left(Y_n-y\right)}^2+{\left(Z_n-z\right)}^2=d_n{}^2\end{array}.$$

(1)

To reduce the influence of the inherent ranging error of the vehicle, the two adjacent equations can be subtracted to obtain Equation (2).

$$\{\begin{array}{c}2\left(X_2-X_1\right)x+2\left(Y_2-Y_1\right)y+2\left(Z_2-Z_1\right)z=\\ d_1{}^2-d_2{}^2-\left(X_1{}^2-X_2{}^2\right)-\left(Y_1{}^2-Y_2{}^2\right)-\left(Z_1{}^2-Z_2{}^2\right)\\ 2\left(X_3-X_2\right)x+2\left(Y_3-Y_2\right)y+2\left(Z_3-Z_2\right)z=\\ d_2{}^2-d_3{}^2-\left(X_2{}^2-X_3{}^2\right)-\left(Y_2{}^2-Y_3{}^2\right)-\left(Z_2{}^2-Z_3{}^2\right)\\ ⋮\\ 2\left(X_n-X_{n-1}\right)x+2\left(Y_n-Y_{n-1}\right)y+2\left(Z_n-Z_{n-1}\right)z=\\ d_{n-1}{}^2-d_n{}^2-\left(X_{n-1}{}^2-X_n{}^2\right)-\left(Y_{n-1}{}^2-Y_n{}^2\right)-\left(Z_{n-1}{}^2-Z_n{}^2\right)\end{array}.$$

(2)

The following can be defined:

$$\mathit{A}=\left[\begin{array}{ccc}2\left(X_2-X_1\right)& 2\left(Y_2-Y_1\right)& 2\left(Z_2-Z_1\right)\\ 2\left(X_3-X_2\right)& 2\left(Y_3-Y_2\right)& 2\left(Z_3-Z_2\right)\\ ⋮& ⋮& ⋮\\ 2\left(X_n-X_{n-1}\right)& 2\left(Y_n-Y_{n-1}\right)& 2\left(Z_n-Z_{n-1}\right)\end{array}\right],$$

(3)

$$\mathit{B}={\mathit{d}}^2-{\tilde{\mathit{d}}}^2=\left[\begin{array}{c}{d}_1{}^2\\ d_2{}^2\\ ⋮\\ d_n{}^2\end{array}\right]-\left[\begin{array}{c}{X}_1{}^2+Y_1{}^2+Z_1{}^2\\ X_2{}^2+Y_2{}^2+Z_2{}^2\\ ⋮\\ X_n{}^2+Y_n{}^2+Z_n{}^2\end{array}\right],$$

(4)

$$\mathit{Q}=\left[\begin{array}{cccccc}1& -1& 0& 0& \cdots & 0\\ 0& 1& -1& \ddots & \ddots & ⋮\\ 0& 0& \ddots & \ddots & 0& 0\\ ⋮& \ddots & \ddots & 1& -1& 0\\ 0& \cdots & 0& 0& 1& -1\end{array}\right].$$

(5)

Then,

$$\begin{array}{c}\mathit{A}\mathit{v}=\mathit{Q}\mathit{B}\end{array}.$$

(6)

The following can also be defined:

$$\mathit{P}={\left({\mathit{A}}^T\mathit{A}\right)}^{-\mathbf{1}}{\mathit{A}}^T={\left[\begin{array}{ccc}{a}_1^1& a_1^2& a_1^3\\ a_2^1& a_2^2& a_2^3\\ ⋮& ⋮& ⋮\\ a_{n-1}^1& a_{n-1}^2& a_{n-1}^3\end{array}\right]}^T,$$

(7)

where the superscript indicates the column number.

The solution according to the least-squares method is

$$\widehat{\mathit{v}}={\left({\mathit{A}}^{\mathit{T}}\mathit{A}\right)}^{-\mathbf{1}}{\mathit{A}}^{\mathit{T}}\mathit{b}=\mathit{P}\mathit{Q}\mathit{B}.$$

(8)

Because of the movement of the vehicle and the working range of the base station, the ranging information between different base stations is set to be completely independent. The covariance of the vehicle’s position result $\widehat{\mathit{v}}$ is

$${\mathit{D}}_{\widehat{\mathit{v}}}={\mathit{P}\mathit{Q}\mathit{D}}_{\mathit{B}}{\left(\mathit{P}\mathit{Q}\right)}^T=\mathit{P}\mathit{Q}\left({\mathit{D}}_{{\mathit{d}}^2}+{\mathit{D}}_{{\tilde{\mathit{d}}}^2}\right){\left(\mathit{P}\mathit{Q}\right)}^T,$$

(9)

where

$$\mathit{P}\mathit{Q}=\left[\begin{array}{ccccc}{a}_1^1& a_2^1-a_1^1& a_3^1-a_2^1& \cdots & -a_{n-1}^1\\ a_1^2& a_2^2-a_1^2& a_3^2-a_2^2& \cdots & -a_{n-1}^2\\ a_1^3& a_2^3-a_1^3& a_3^3-a_2^3& \cdots & -a_{n-1}^3\end{array}\right],$$

(10)

$${\mathit{D}}_{\mathit{B}}=\mathrm{diag}\left(D_1,D_2,\cdots ,D_n\right),$$

(11)

$$D_i=D{d}_i{}^2+D{\tilde{X}}_i{}^2+D{\tilde{Y}}_i{}^2+D{\tilde{Z}}_i{}^2+2\mathrm{cov}\left({\tilde{X}}_i{}^2,{\tilde{Y}}_i{}^2\right)+2\mathrm{cov}\left({\tilde{X}}_i{}^2,{\tilde{Z}}_i{}^2\right)+2\mathrm{cov}\left({\tilde{Y}}_i{}^2,{\tilde{Z}}_i{}^2\right),$$

(12)

$$\left[\begin{array}{c}{\tilde{X}}_i\\ {\tilde{Y}}_i\\ {\tilde{Z}}_i\end{array}\right]=\left[\begin{array}{c}{X}_i-x\\ Y_i-y\\ Z_i-z\end{array}\right]={\mathit{V}}_i-\mathit{v}.$$

(13)

Therefore, Equation (9) can be described as

$${\mathit{D}}_{\widehat{\mathit{v}}}=\left[\begin{array}{ccc}\mathrm{cov}\left(H_1,H_1\right)& \mathrm{cov}\left(H_1,H_2\right)& \mathrm{cov}\left(H_1,H_3\right)\\ \mathrm{cov}\left(H_2,H_1\right)& \mathrm{cov}\left(H_2,H_2\right)& \mathrm{cov}\left(H_2,H_3\right)\\ \mathrm{cov}\left(H_3,H_1\right)& \mathrm{cov}\left(H_3,H_2\right)& \mathrm{cov}\left(H_3,H_3\right)\end{array}\right],$$

(14)

where

$$\begin{array}{c}cov\left(H_i,H_j\right)=\left(a_1^i-0\right)\left(a_1^j-0\right)D_1+\left(a_2^i-a_1^i\right)\left(a_2^j-a_1^j\right)D_2+\cdots \\ +\left(a_{n-1}^i-a_{n-2}^i\right)\left(a_{n-1}^j-a_{n-2}^j\right)D_{n-1}+\left(0-a_{n-1}^i\right)\left(0-a_{n-1}^j\right)D_n\end{array}.$$

(15)

Supposing that the normally random variable $X$ satisfies $X~N\left(\mu ,{\sigma }^2\right)$,

$$D{X}^2=2{\sigma }^4+4{\mu }^2{\sigma }^2.$$

(16)

Supposing that the normally random variables $X$ and $Y$ satisfy $\left(X,Y\right)~N\left({\mu }_1,{\mu }_2,{\sigma }_1{}^2,{\sigma }_2{}^2,\rho \right)$,

$$\mathrm{cov}\left(X^2,Y^2\right)=2{\rho }^2{\sigma }_1{}^2{\sigma }_2{}^2+4\rho {\mu }_1{\mu }_2{\sigma }_1{\sigma }_2.$$

(17)

The initial value of the vehicle position can be obtained through the least-squares method, as shown in Equation (8), and the covariance matrix of the vehicle position information after error transfer can be obtained through Equations (9)–(17).

4.2. KLA Information Fusion Algorithm

For any vehicle in the vehicle network, the number of geometric density functions of other vehicles and its own positioning information are set as $N$, and the geometric density function of each positioning information is set as $p^i(·)$, with the corresponding weight ${\pi }^i$. Thus, the fusion position result $\overline{p}$ is

$$\overline{p}=\arg \inf {\displaystyle \sum }_{i=1}^N{\pi }^{i}D\left(p||p^i\right),$$

(18)

where $D\left(P_i\Vert P_j\right)$ denotes the Kullback–Leibler distance on the information geometry, and

$$D\left(P_i\Vert P_j\right)={{\displaystyle \int }}^{ }{P}_i\mathit{ln}\left(P_i/P_j\right).$$

(19)

To reduce the effect of vehicles with large errors on other vehicles in the internet of vehicles, this paper uses the inverse of the variance of the geometric density function of the positioning information to identify the weights in the fusion. The result of the fusion probability density under the KLA algorithm can be expressed as

$$\overline{p}\left(x\right)=\frac{{{\displaystyle \prod }}_{i=1}^N{\left[p^i\left(x\right)\right]}^{{\pi }^i}}{{{\displaystyle \int }}^{ }{{\displaystyle \prod }}_{i=1}^N{\left[p^i\left(x\right)\right]}^{{\pi }^i}\mathrm{dx}}.$$

(20)

The probability density function of the $n$-dimensional normal distribution is

$$N\left(x|\mu ,\mathrm{\Sigma }\right)=\frac{1}{{\left(2\pi \right)}^{n/2}{\left|\mathrm{\Sigma }\right|}^{1/2}}\exp \left\{-\frac{1}{2}{\left(x-\mu \right)}^T{\mathrm{\Sigma }}^{-1}\left(x-\mu \right)\right\},$$

(21)

where $\mu$ and $\Sigma$ denote the mean and covariance matrices of the $n$-dimensional normal distribution, respectively.

Supposing $P_i(·)~N\left(x|{\mu }_i,{\mathrm{\Sigma }}_i\right)$ and $P_j(·)~N\left(x|{\mu }_j,{\mathrm{\Sigma }}_j\right)$, the KL distance between $n$-dimensional normal distributions can be obtained as

$$D\left(P_i\Vert P_j\right)=\frac{1}{2}\left[{\left({\mu }_i-{\mu }_j\right)}^T{\mathrm{\Sigma }}_j^{-1}\left({\mu }_i-{\mu }_j\right)+tr\left({\mathrm{\Sigma }}_i{\mathrm{\Sigma }}_j^{-1}\right)+\mathit{ln}\frac{\left|{\mathrm{\Sigma }}_j\right|}{\left|{\mathrm{\Sigma }}_i\right|}-n\right].$$

(22)

Supposing $p^i(·)~N\left(x|{\mu }^i,{\mathrm{\Sigma }}^i\right)$, $\overline{p}(·)~N\left(x|\overline{\mu }, \mathrm{\Sigma } ¯\right)$, and the probability density as an $n$-dimensional normal distribution, the result of Equation (20) can be expressed as

$$\{\begin{array}{c}{\overline{\mathrm{\Sigma }}}^{-1}={{\displaystyle \sum }}_{i=1}^N{\pi }^i{\left({\mathrm{\Sigma }}^i\right)}^{-1}\\ {\overline{\mathrm{\Sigma }}}^{-1}\overline{\mu }={{\displaystyle \sum }}_{i=1}^N{\pi }^i{\left({\mathrm{\Sigma }}^i\right)}^{-1}{\mu }^i\end{array}.$$

(23)

To achieve KLA information fusion, $k$ is set at a discrete point in time, ${\mathit{x}}_k\in R^n$ is the system state, and ${\mathit{w}}_k\in R^n$ is the process noise, where $R^n$ represents the set of all $n$-dimensional real vectors, and $R^{m\times n}$ represents the set of all $m\times n$-dimensional matrices. The positioning state equation of any vehicle is

$${\mathit{x}}_{k+1}=\mathit{A}{\mathit{x}}_k+{\mathit{w}}_k,$$

(24)

where $\mathit{A}$ is the coefficient matrix of the state equation of the system.

The measurement equation of the received positioning information of surrounding vehicles is

$${\mathit{y}}_k^i={\mathit{C}}^i{\mathit{x}}_k+{\mathit{v}}_k^i,$$

(25)

where ${\mathit{C}}^i$ is the measurement equation coefficient matrix of the $i$-th vehicle, ${\mathit{v}}_k^i\in R^{n\times y}$ represents zero-mean random white noise, and its probability density is $p_{v^i}(·)$.

Next, $p_l^i(·)$ is defined as the positioning result of the $i$-th vehicle at the $l$-th iteration, and the initial iteration value is $p_0^i(·)=p^i(·)$. The initial state of the system ${\mathit{x}}_0$ is unknown but can be assigned according to a known probability distribution $p_{0|-1}(·)$. The process disturbance and all measurement noise are set as a normal distribution. Then,

$$p_0\left(\mathit{x}\right)=N\left(\mathit{x};{\widehat{\mathit{x}}}_{0|-1},{\mathit{P}}_{0|-1}\right),$$

(26)

$$p_w\left(\mathit{x}\right)=N\left(\mathit{w};\mathbf{0},\mathit{Q}\right),$$

(27)

$$p_{v^i}\left(\mathit{x}\right)=N\left({\mathit{v}}^i;\mathbf{0},{\mathit{R}}^i\right), i=1,2,\cdots ,N.$$

(28)

At this point, the estimation of the geometric density function of the positioning information of the $i$-th vehicle can be obtained recursively by Bayesian filtering. Then,

$$p_{0|-1}^i\left(\mathit{x}\right)=p_{0|-1}\left(\mathit{x}\right),$$

(29)

$$p_{k|k}^i\left(\mathit{x}\right)=\frac{p_{v^i}\left[{\mathit{y}}_k^i-h^i\left(\mathit{x}\right)\right]p_{k|k-1}^i\left(\mathit{x}\right)}{{{\displaystyle \int }}^{ }{p}_{v^i}\left[{\mathit{y}}_k^i-h^i\left(\xi \right)\right]p_{k|k-1}^i\left(\xi \right)\mathrm{d}\xi },$$

(30)

$$p_{k+1|k}^i\left(\mathit{x}\right)={{\displaystyle \int }}^{ }{p}_{v^i}\left[\mathit{x}-f\left(\xi \right)\right]p_{k|k}^i\left(\xi \right)\mathrm{d}\xi ,$$

(31)

where ${\widehat{\mathit{x}}}_{0|-1}$ is the known vector, and ${\mathit{P}}_{0|-1}$ is the known positive definite matrix.

The iterative estimation of Equations (30) and (31) can be expressed as

$$p_{k|k}^i\left(\mathit{x}\right)=N\left(\mathit{x};{\widehat{\mathit{x}}}_{k|k}^i,{\mathit{P}}_{k|k}^i\right),$$

(32)

$$p_{k+1|k}^i\left(\mathit{x}\right)=N\left(\mathit{x};{\widehat{\mathit{x}}}_{k+1|k}^i,{\mathit{P}}_{k+1|k}^i\right).$$

(33)

To improve the positioning speed and stability of multivehicle cooperation, the information matrix is used to replace the mean vector and covariance matrix, which is expressed as follows:

$${\Omega }_{k|k}^i={\left({\mathit{P}}_{k|k}^i\right)}^{-1},$$

(34)

$${\Omega }_{k+1|k}^i={\left({\mathit{P}}_{k+1|k}^i\right)}^{-1}.$$

(35)

The information vector can be obtained as

$${\mathit{q}}_{k|k}^i={\Omega }_{k|k}^i{\widehat{\mathit{x}}}_{k|k}^i,$$

(36)

$${\mathit{q}}_{k+1|k}^i={\Omega }_{k+1|k}^i{\widehat{\mathit{x}}}_{k+1|k}^i.$$

(37)

Then, the update process can be expressed as

$${\mathit{q}}_{k|k}^i={\mathit{q}}_{k|k-1}^i+{\left({\mathit{C}}^i\right)}^T{\left({\mathit{R}}^i\right)}^{-1}{\mathit{y}}_k^i,$$

(38)

$${\Omega }_{k|k}^i={\Omega }_{k|k-1}^i+{\left({\mathit{C}}^i\right)}^T{\left({\mathit{R}}^i\right)}^{-1}{\mathit{C}}^i.$$

(39)

The prediction process can be expressed as

$${\mathit{q}}_{k+1|k}^i={\mathit{A}}^{-T}\left[1-{\Omega }_{k|k}^i{\left({\Omega }_{k|k}^i+{\mathit{A}}^T{\mathit{Q}}^{-1}\mathit{A}\right)}^{-1}\right]{\mathit{q}}_{k|k}^i,$$

(40)

$${\Omega }_{k+1|k}^i={\mathit{A}}^{-T}{\Omega }_{k|k}^i{\mathit{A}}^{-1}-{\mathit{A}}^{-T}{\Omega }_{k|k}^i{\left({\Omega }_{k|k}^i+{\mathit{A}}^T{\mathit{Q}}^{-1}\mathit{A}\right)}^{-1}{\Omega }_{k|k}^i{\mathit{A}}^{-1}.$$

(41)

Combined with the above equation, the below algorithm steps can be obtained.

(1)

Step 1

Through the vehicle measurement results ${\mathit{y}}_k^i$ and the updated local information group $\left({\mathit{q}}_{k|k-1}^i,{\Omega }_{k|k-1}^i\right)$, obtain the posterior information group $\left({\mathit{q}}_{k|k,0}^i,{\Omega }_{k|k,0}^i\right)$ using Equations (38) and (39).

(2)

Step 2

Execute the l-th iteration based on the KLA algorithm,

$${\Omega }_{k|k,l+1}^i={\displaystyle \sum }_{j\in N^i}{\pi }^{i,j}{\Omega }_{k|k,l}^i,l=0,1,2,\cdots ,L-1,$$

(42)

$${\mathit{q}}_{k|k,l+1}^i={\displaystyle \sum }_{j\in N^i}{\pi }^{i,j}{\mathit{q}}_{k|k,l}^i,l=0,1,2,\cdots ,L-1,$$

(43)

and obtain the fusion information group $\left({\mathit{q}}_{k|k}^i,{\Omega }_{k|k}^i\right)\triangleq \left({\mathit{q}}_{k|k,L}^i,{\Omega }_{k|k,L}^i\right)$.

(3)

Step 3

Calculate the posterior information group $\left({\mathit{q}}_{k+1|k}^i,{\Omega }_{k+1|k}^i\right)$ using Equations (42) and (43).

When the vehicle can obtain the initial positioning information through the wireless station or navigation satellite, the iterative initial value of the information matrix and the information vector is

$${\Omega }_{0|-1}^i={\left({\mathit{P}}_{0|-1}^i\right)}^{-1},$$

(44)

$${\mathit{q}}_{0|-1}^i={\left({\mathit{P}}_{0|-1}^i\right)}^{-1}{\widehat{\mathit{x}}}_{0|-1}^i.$$

(45)

When the vehicle cannot be positioned because of occlusion, set the initial iterative value of the vehicle’s information matrix and information vector as

$${\Omega }_{0|-1}^i=0,$$

(46)

$${\mathit{q}}_{0|-1}^i=0$$

(47)

.

The KLA fusion method has low computational complexity and can achieve vehicle plug-and-play fusion under the internet of vehicles. In addition, it can reduce the influence of sudden errors and effectively improve the accuracy and stability of multivehicle cooperative positioning by transforming the positioning information of each vehicle into the geometric density function of positioning information.

5. Simulation Results and Analysis

This paper used MATLAB 2018a to simulate and compare the performance of the MVCP-GW algorithm with the current mainstream multivehicle cooperative positioning algorithms, such as the second-order cone programming (SOCP) algorithm [24], factor graph cooperative positioning (FGCP) algorithm [25], and neural networks cooperative positioning (NNCP) algorithm [26], from three aspects: accuracy stability, applicability, and obstruction scenarios. Among them, the SOCP algorithm adopts the second-order cone optimization method to process the information of cooperative vehicles, and its convergence speed is fast, but its positioning accuracy is low, and its anti-interference ability is weak. The FGCP algorithm adopts the factor graph theory, regards the vehicle as the node of the factor graph, and completes the cooperative positioning through the confidence information transmission. Its positioning accuracy and robustness are improved, but the algorithm complexity is large, and the convergence speed is slow. The NNCP algorithm establishes the connection between vehicles through deep neural network (DNN) and blockchain technology, and designs the corresponding information selection, information sharing, and punishment mechanisms. Its positioning accuracy is high, and its stability is good, but there is also a problem of slow convergence time.

In this paper, all errors are finally reflected in the ranging error and positioning error; hence, in order to unify the quantification, we use the ranging error and positioning error to simulate the measurement. The mean square error (MSE) is used to evaluate the positioning accuracy.

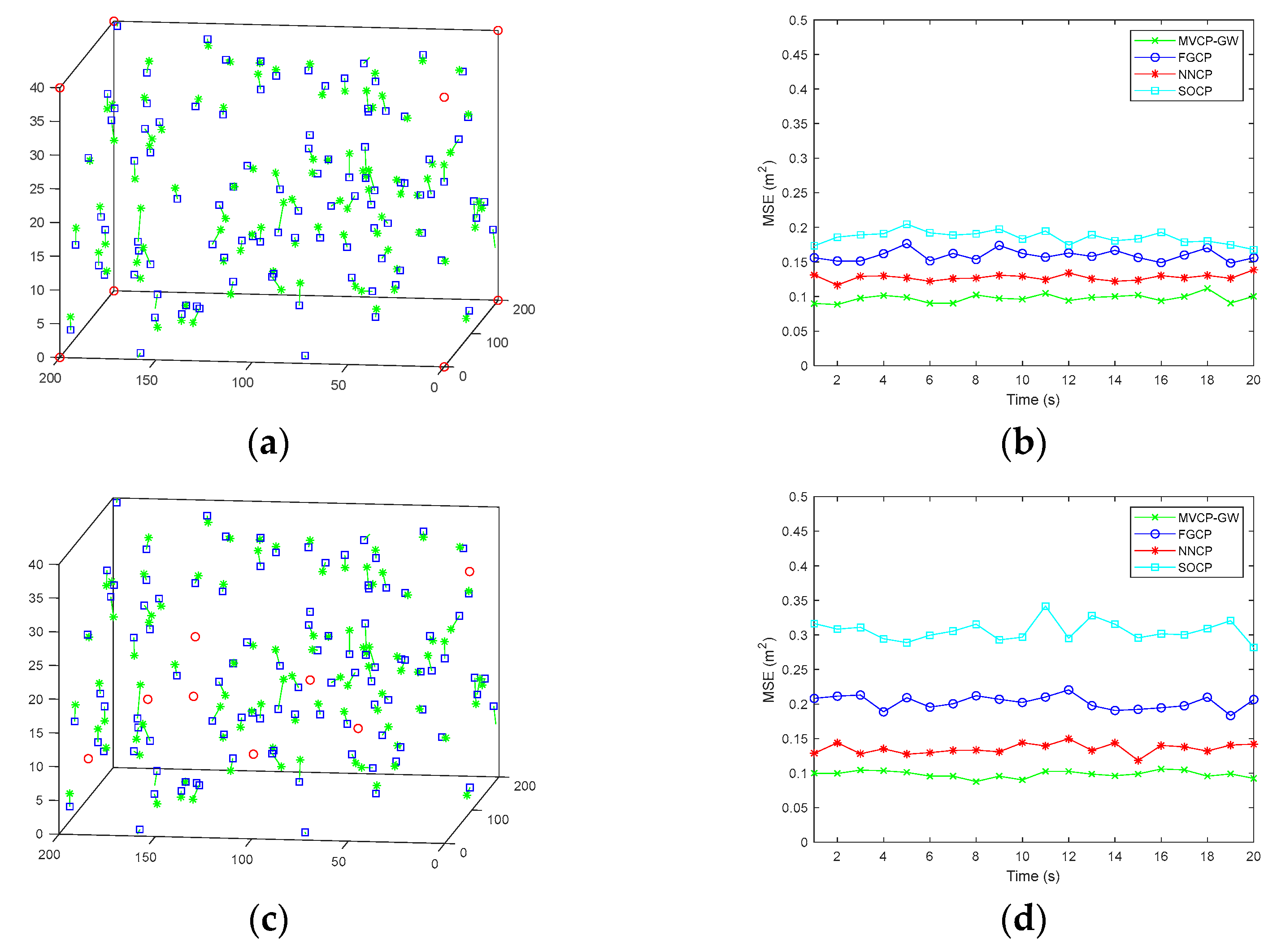
5.1. Simulation Analysis of Positioning Accuracy and Stability

In multivehicle cooperative positioning, the interactive ranging information between vehicles is the core foundation of cooperative positioning, and the ranging accuracy directly affects the accuracy of cooperative positioning. In this section, the effect of the ranging error variance ${\sigma }_1$ on the positioning accuracy is simulated. The range of ${\sigma }_1$ is set as $0~0.5 \mathrm{m}$, the size of the simulation scene is set as $200 \mathrm{m}\times 200 \mathrm{m}\times 40 \mathrm{m}$, the number of vehicles is set as $n=100$, whose positions are randomly distributed in the simulation scene, the number of base stations is set as $N=8$, which are arranged at the top of the simulation scene, the variance of satellite navigation positioning error is set as ${\sigma }_2=1 \mathrm{m}$, and the number of Monte Carlo simulations is set as 1000. The simulation results are shown in Figure 3.

As seen from Figure 3, with the increase in ${\sigma }_1$, the positioning accuracy of all algorithms was significantly reduced, among which the performance of the MVCP-GW algorithm was the best. When ${\sigma }_1=0.1 \mathrm{m}$, the positioning error was only 0.098 m. This result shows that the MVCP-GW algorithm can make use of ranging information between vehicles to realize cooperative positioning, and it can effectively suppress the influence of ranging error. The NNCP algorithm took second place. Under the same variance condition, the error was 0.126 m, indicating that the neural network can suppress the influence of ranging error well. Because the FGCP algorithm introduces ranging errors in the confidence calculation, its error was much higher than that of the NNCP algorithm when ${\sigma }_1$ was large. The performance of the SOCP algorithm had a large gap with the performance of other algorithms, indicating that the information cooperative ability of SOCP is weak.

In multivehicle cooperative positioning, the network topology of base stations has a great impact on the positioning results. To verify the stability of the MVCP-GW algorithm, this section conducted a simulation experiment on the relationship between the positioning error and the distribution of base stations. Thus, ${\sigma }_1=0.1 \mathrm{m}$ was considered, and the other simulation conditions were the same as above. First, this paper simulated the effect of network topology on positioning error under the ideal condition of base station distribution, in which base stations were distributed at the top of the simulation scene. The simulation conditions are shown in Figure 4a, in which the red circle denotes the base station, the blue square denotes the vehicle, the green asterisks connected to the blue square denote the node movement direction, and the length of the line between the square and the asterisks denotes the speed.

As seen in Figure 4b, the MVCP-GW algorithm had the best and most stable positioning effect under the ideal distribution of base stations, and the average positioning error was approximately 0.1 m. The positioning accuracy of the NNCP algorithm was lower than that of the MVCP-GW algorithm but higher than that of the FGCP and SOCP algorithms, and the error fluctuation amplitude was also smaller. The FGCP and SOCP algorithms had poor stability in this simulation experiment, and the FGCP algorithm outperformed the SOCP algorithm.

In fact, it is impossible to ensure that the base station distribution is always in an ideal condition. Under the condition that other simulation conditions remain unchanged, this paper conducted the simulation of a random situation in which the distribution of base stations was random. The simulation scenarios are shown in Figure 4c.

Figure 4d shows that, under the random distribution of base stations, the positioning accuracy of the MVCP-GW algorithm was still the best, and the positioning error still fluctuated approximately 0.1 m, which is consistent with the ideal distribution. The simulation results show that the MVCP-GW algorithm could eliminate the influence of base station distribution through the cooperative information among vehicles, and it could realize multivehicle cooperative positioning under various base station distribution topologies, revealing strong applicability. The positioning accuracy of the NNCP algorithm was also close to the ideal situation, and the positioning error and jitter of the FGCP and SOCP algorithms increased significantly, indicating that these two algorithms were greatly affected by the topology of the base station.

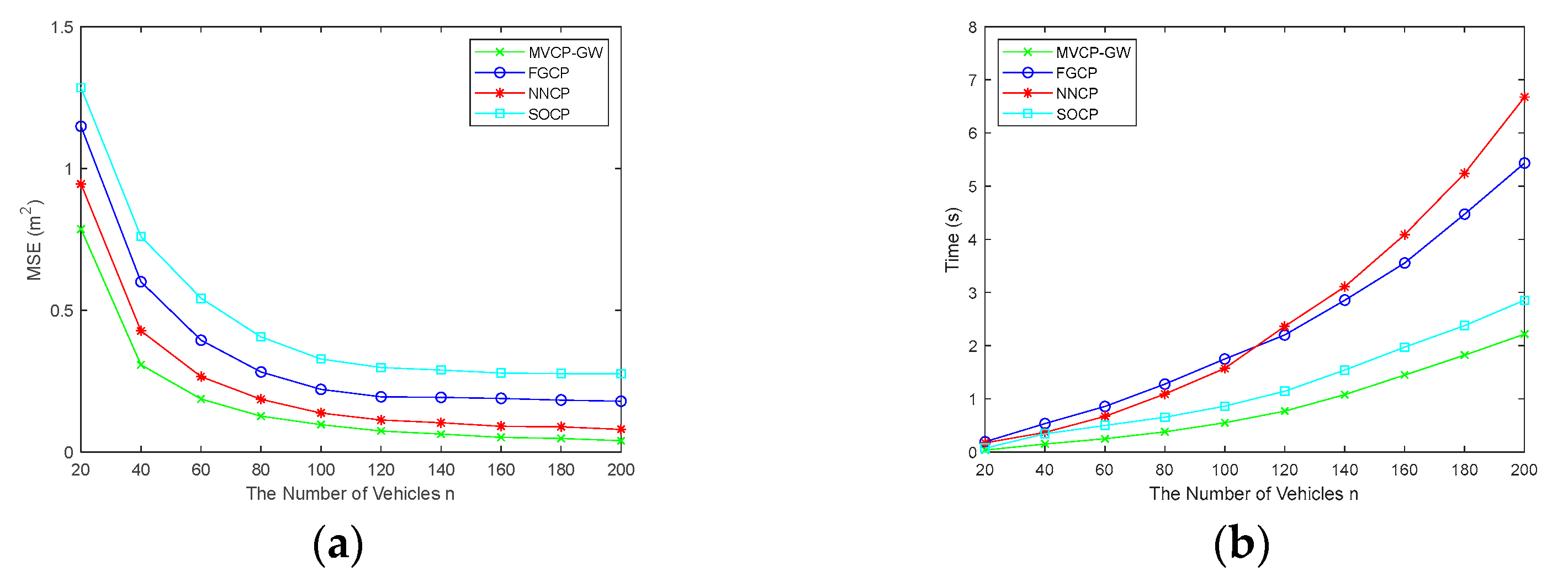
5.2. Simulation Analysis of Algorithm Applicability

In the real environment, the vehicle density directly affects the construction of the network topology and the accuracy of cooperative positioning. In addition, the demand for the plug-and-play characteristics of the internet of vehicles also necessitates good applicability of the multivehicle cooperative positioning algorithm, which can enable real-time high-precision positioning under different vehicle densities. In this section, the relationship between the multivehicle cooperative positioning error and the vehicle distribution density and the relationship between the multivehicle cooperative positioning time and the vehicle distribution density were simulated. The number of vehicles was set as $n=20~200$ with a random distribution of base stations, and ${\sigma }_1=0.1 \mathrm{m}$ was considered; other simulation conditions were consistent with Section 5.1.

In this scenario, the average speed of the positioning vehicle was 15 m/s, and it traveled in a random direction, which was used to simulate the actual positioning performance under real road conditions. In Figure 5b, the time on the vertical axis is the total running time $t_{all}$ of the algorithm, and $t_{all}/n$ is the average time of single-vehicle positioning. The simulation results are shown in Figure 5.

Figure 5a shows that, with increasing $n$, the errors of the four algorithms decreased rapidly and then tended to be stable. This result indicates that the sparse distribution of vehicles led to less cooperative information and low positioning accuracy; in contrast, if the vehicles were densely distributed, the positioning accuracy was improved, but there was a limit to the improvement. As seen in Figure 5b, the MVCP-GW algorithm had the fastest positioning time under the random distribution of base stations, which indicates that the MVCP-GW algorithm had lower computational complexity when compared with the other three algorithms.

Under different vehicle distribution densities, the performance of the MVCP-GW algorithm was always optimal, indicating that the MVCP-GW algorithm can adapt to the network topology of different vehicle densities and effectively meet the needs of plug-and-play characteristics under the internet of vehicles. These findings are due to the fact that the heterogeneous navigation source information is converted into information geometric probability, and then the navigation source is unified, which can effectively reduce the complexity of the algorithm and improve the scalability of the algorithm.

5.3. Simulation Analysis of Positioning in Obstruction Scenarios

In a real road environment, because of the influence of the urban canyon effect and a complex electromagnetic environment, the satellite navigation signal and the communication signal between vehicles is abnormal or even lost, and these sudden changes greatly affect the positioning accuracy. This section simulates the influence of sudden error in obstruction scenarios. The same simulation parameter settings were selected with a random distribution of base stations, the maximum number of times was set as $k_m=50$, and the sampling interval was set as $T=0.1 \mathrm{s}$. At the 10th moment, 20% of the vehicles lost satellite signals, and, at the 30th moment, 30% of the ranging information between vehicles changed suddenly, where we randomly selected 30% of the vehicles and changed their ranging error variance ${\sigma }_1$ from 0.1 m to 0.3 m. The simulation results are shown in Figure 6.

As seen from Figure 6, when satellite signal mutation occurred at the 10th moment, the error increment of the MVCP-GW algorithm was the smallest, approximately 0.04 m, and it could converge again after four moments. The other three algorithms needed $5~8$ moments, and the error increment was close to 0.06 m, 0.10 m, and 0.13 m for the NNCP algorithm, FGCP algorithm, and SOCP algorithm, respectively. When intervehicle ranging information mutation occurs at the 30th moment, the error increment and convergence time of the four algorithms increased, but the MVCP-GW algorithm was still optimal among the four algorithms.

The experimental results show that the MVCP-GW algorithm based on information geometry can rapidly fuse multiple types of navigation source information through the KLA method, effectively suppress the influence of sudden error on positioning results, ad improve the stability of the whole cooperative network, which can meet the needs of continuous, real-time, and high-precision positioning under the internet of vehicles.

5.4. Summary of Simulation Results

From the above experiments, we selected two groups of representative experimental data, positioning error and positioning time in the non-mutation scene, and error fluctuation and convergence time in the mutation scene, and we provide a comparison of algorithm performance in

Table 1. Comparison of algorithm performance in non-mutation scene (ranging error variance ${\sigma }_1=0.1 \mathrm{m}$, the number of vehicles $n=100$).

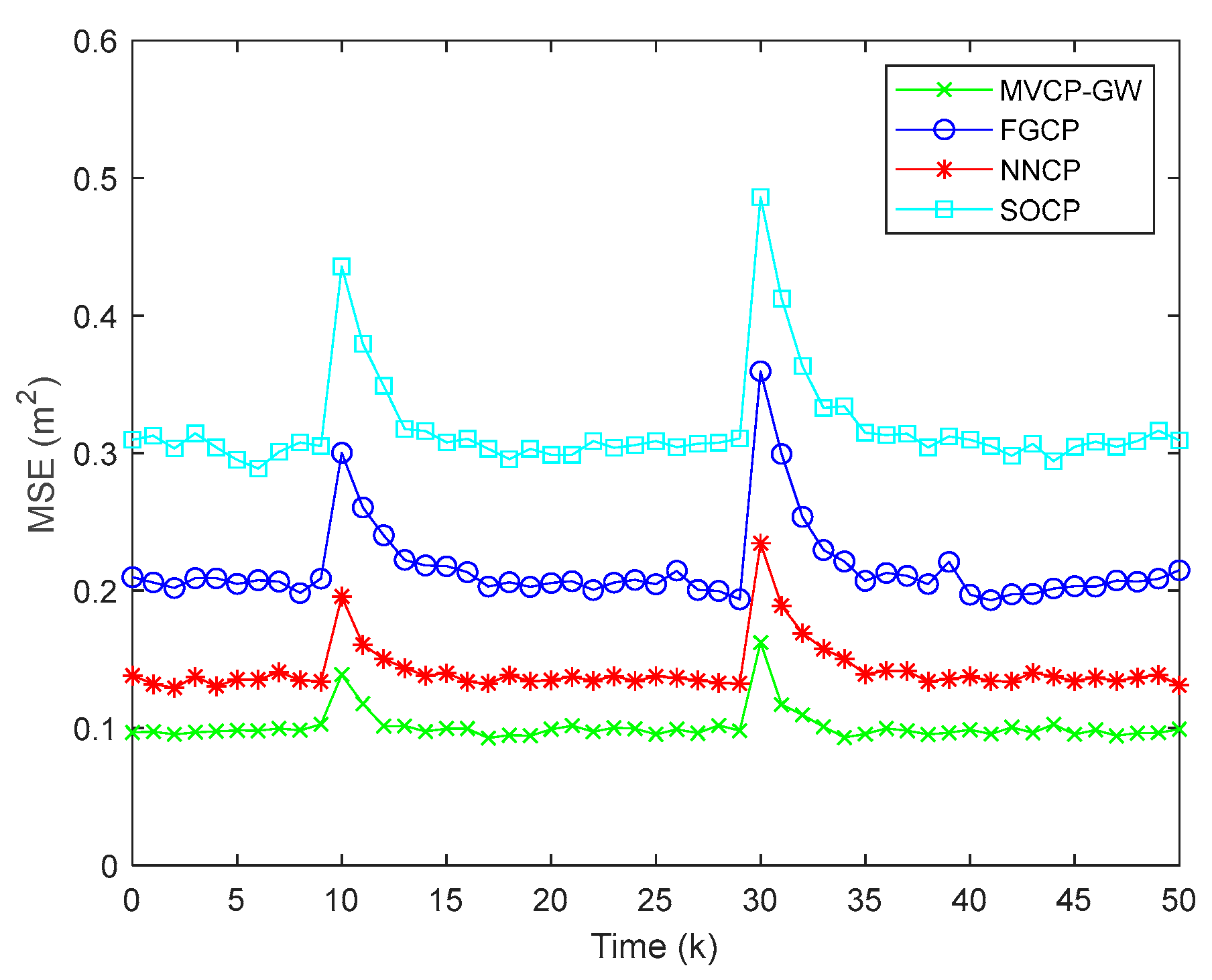
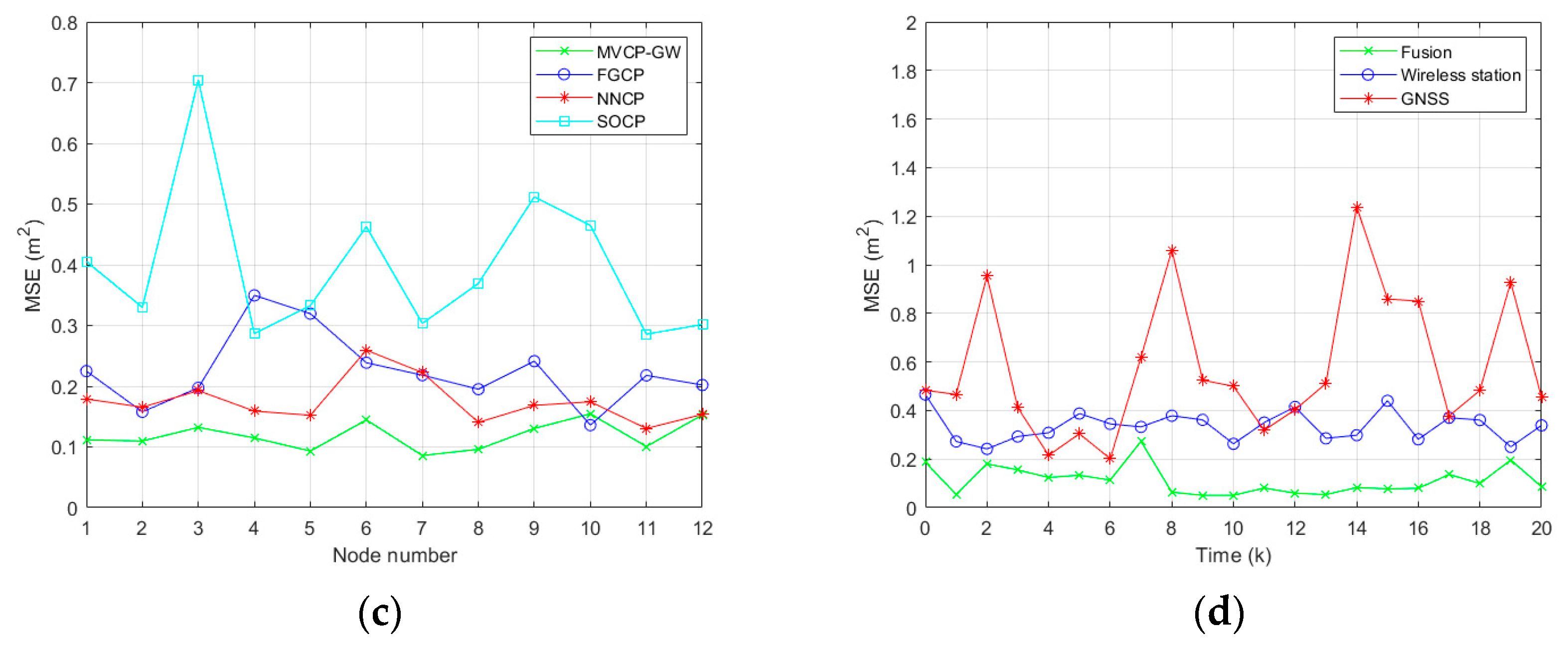
Algorithm	MSE (m2)	Positioning Time (s)
MVCP-GW	0.098	0.58
SOCP	0.317	0.94
FGCP	0.215	1.84
NNCP	0.126	1.62

and

Table 2. Comparison of algorithm performance in mutation scene (20% of the vehicles lost satellite signals).

Algorithm	MSE Fluctuation (m2)	Reconvergence Time (s)
MVCP-GW	0.04	0.4
SOCP	0.13	0.6
FGCP	0.10	0.8
NNCP	0.06	0.8

.

Through the comparison of the above experimental data, we can see that in the same environment, the MVCP-GW algorithm had the smallest positioning error, the highest positioning accuracy, and the shortest positioning time, which shows that the algorithm can meet the real-time and high-precision positioning requirements. In the face of abrupt interference, it had the strongest anti-interference ability and the fastest convergence speed, which shows that the algorithm can effectively reduce the influence of sudden error on positioning results. In addition, the MVCP-GW algorithm has strong scalability and can meet the positioning requirements of different vehicle densities under the internet of vehicles. All these show the superiority of MVCP-GW algorithm.

6. Physical Verification Platform Testing

The MVCP-GW algorithm was tested using sensor nodes to construct a cooperative positioning network. The DWM1000 module was adopted to construct the cooperative node, and the distance between the cooperative nodes was measured by the UWB communication of DWM1000. The range of the DWM1000 module was 3 km, and the measurement accuracy of the module was 0.1 m—roughly the size of a coin. The appearance is shown in Figure 7. To realize the positioning of the cooperative nodes, the STM32 development board designed by our team was utilized in the cooperative positioning system, as shown in Figure 8.

In order to verify the rationality and effectiveness of the proposed algorithm and architecture, we built a physical verification platform and randomly set up 12 cooperative nodes in the range of 6 m × 9 m × 3 m. The verification platform is shown in Figure 9.

The initial positioning error and ranging error depend on the node device. The physical simulation results are shown in Figure 10.

Figure 10a shows the static positioning results of 12 nodes, in which node 1 and node 2 are mobile cars. As can be seen from Figure 10c, in the actual test environment, the positioning accuracy of the MVCP-GW algorithm was still the highest, reaching 0.13 m on average in this scenario. Figure 10b shows the dynamic positioning results of two cars, in which the red line indicates the actual motion track, the blue line indicates the GNSS positioning results, the green line indicates the wireless station positioning results, and the yellow line indicates the MVCP-GW algorithm positioning results. It can be seen from Figure 10b that the positioning result of the MVCP-GW algorithm was basically consistent with the actual motion track. In Figure 10d, we compare the dynamic positioning error of node 1 among the MVCP-GW algorithm, GNSS, and wireless station navigation. The average positioning accuracy of the MVCP-GW algorithm was about 0.15 m, showing that the MVCP-GW algorithm can integrate the advantages of the two navigation sources and effectively improve the positioning accuracy.

From the analysis of Figure 10, it can be seen that the experimental results of the physical verification platform are in good agreement with the simulation results, which can effectively improve the positioning accuracy and stability. Furthermore, the algorithm processing module was implemented by the STM32 development board and could realize a real-time response, which proves that the MVCP-GW algorithm has low computational complexity.

The navigation source sensor used in our physical verification platform is consistent with the sensor used in the actual scene; thus, the test results of the physical verification platform can be successfully replicated in the actual application. Through the physical verification platform test results, we can see that the MVCP-GW algorithm can effectively improve the positioning accuracy, can reduce the positioning time, and has strong anti-interference ability. It can be widely used in actual positioning scenes such as large parking lots, multistory high-speed viaducts, and urban lane-level positioning.

7. Conclusions

Aiming at the problem that the multi-navigation source information has time–space–frequency asynchrony and the existing fusion positioning algorithms are limited to two dimensions and have poor real-time performance, this paper proposed a multivehicle three-dimensional cooperative positioning algorithm based on information geometric probability. From the perspective of information geometry, this paper deduced the information geometric probability model of wireless station positioning and satellite positioning by using the correlation between the information probability of the vehicle navigation source and positioning accuracy, and then proposed the KLA information fusion algorithm based on the geometric probability model, which solves the difficult problem of three-dimensional cooperative positioning of multiple vehicles. By comparing the MVCP-GW algorithm with the current main algorithms in four simulation tests of accuracy stability, applicability, obstruction scenarios, and physical verification, the results showed that the MVCP-GW algorithm is less affected by the ranging error, has good convergence and fast convergence speed, can adapt to the network topology of different vehicle densities, and meets the plug-and-play characteristics of the internet of vehicles. When some vehicle navigation information is lost, it can also effectively and quickly suppress the impact of sudden error on the whole network. As a supplement, when the number of vehicles in the internet of vehicles is small or the ranging information between vehicles cannot interact, the accuracy of the MVCP-GW algorithm is reduced. For this potential limitation, we are considering adding other navigation sources, such as INS, into the fusion of multiple navigation sources, which can effectively improve the problem of increase in positioning accuracy caused by the inability of cooperative positioning, as well as further enhance the applicability of this algorithm. Predictably, it has broad development prospects in automatic driving and unmanned transportation in smart cities.