Coordinate Frames and Transformations in GNSS Ray-Tracing for Autonomous Driving in Urban Areas
Abstract
1. Introduction
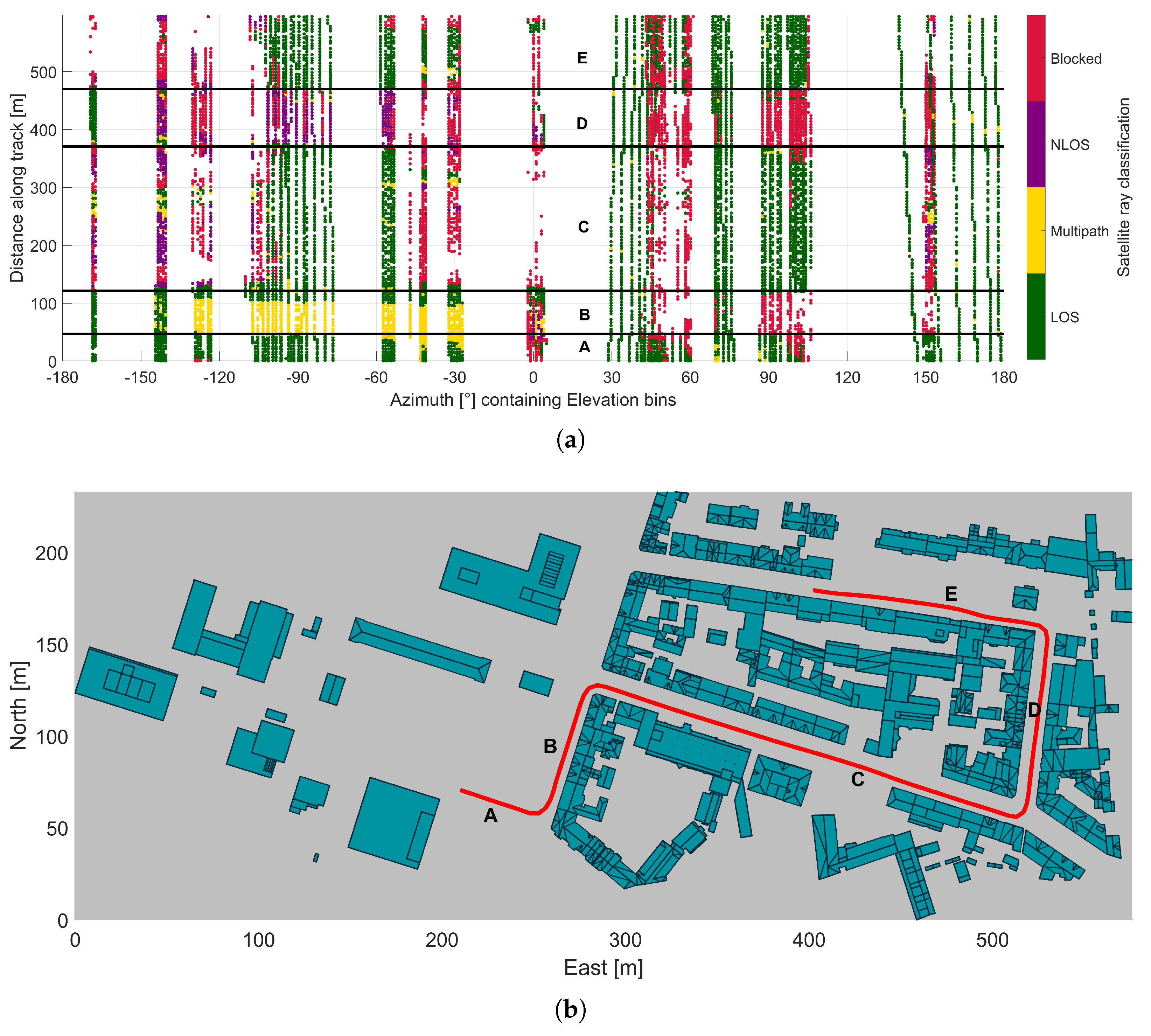
2. Ray Classification Algorithm
2.1. LOS/NLOS Classification
2.2. Determination of Signal Reflections
- 1.
- LOS: rays without obstruction and without any possible reflection points;
- 2.
- Multipath: satellite is in LOS and additionally a signal reflection is determined;
- 3.
- NLOS: the direct LOS is obstructed by a building but the signal can be received via reflection on a building surface;
- 4.
- Blocked: all other cases in which the direct LOS is obstructed and a single reflection does not suffice for the signal to reach the antenna.
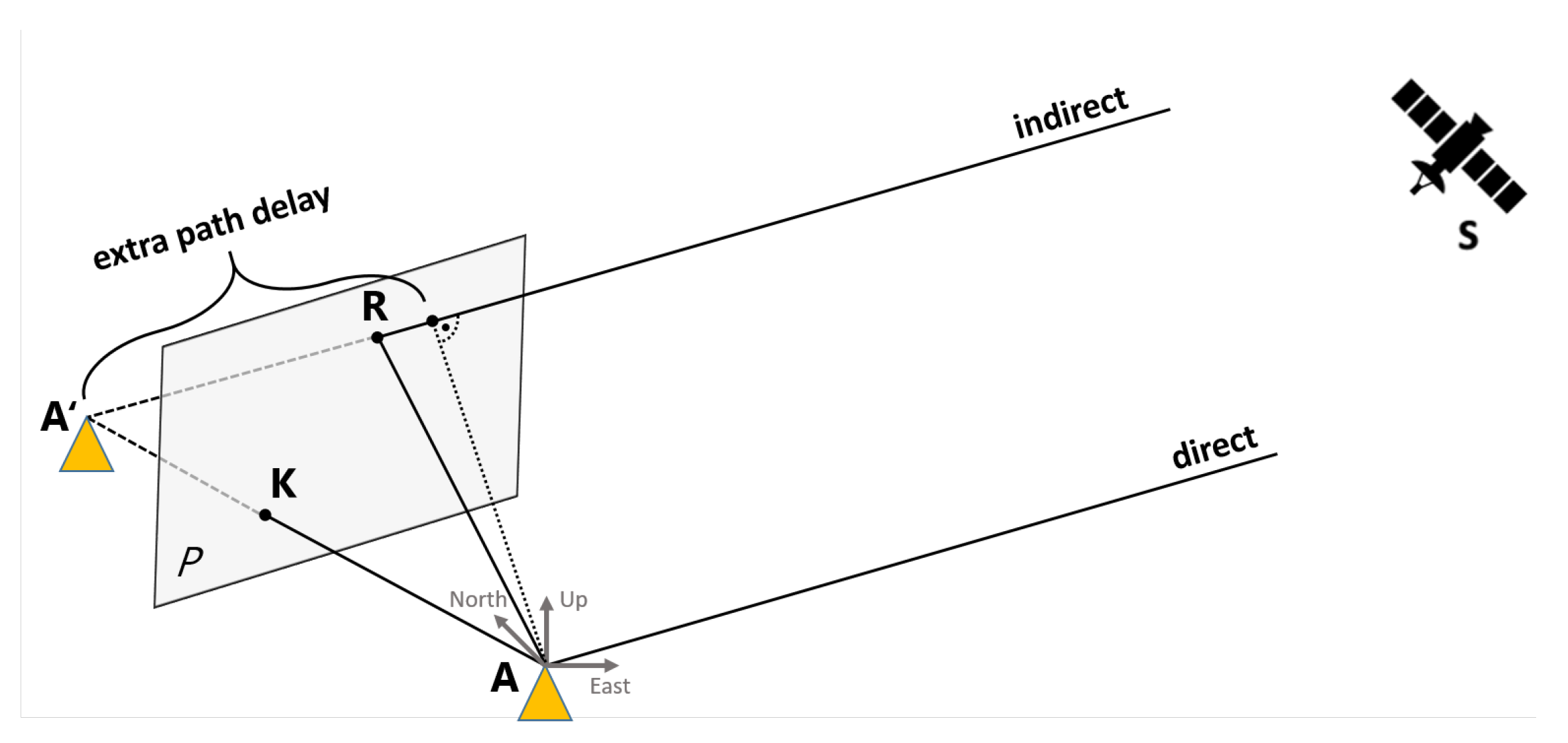
2.3. Extra Path-Delay Computation and Multipath Error
3. Coordinate Frames
3.1. Coordinate Frames and Datum Definitions for GNSS Satellite Orbits
3.2. Coordinate Frames and Datum Definitions for 3D Building Models
3.3. Coordinate Frames for User Positions
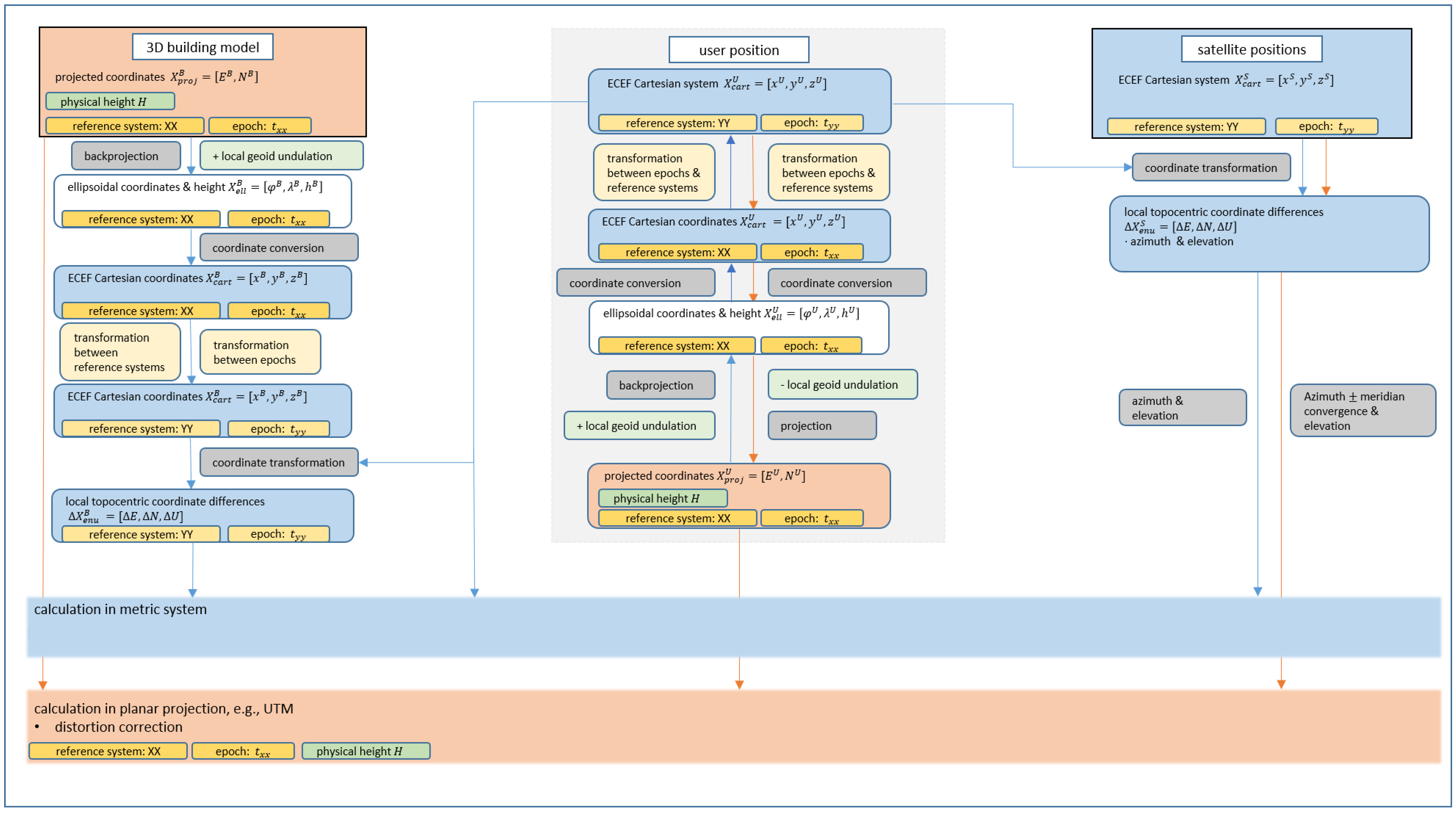
4. Transformation between Different Frames
4.1. Conversion from Map Projection into a 3D Cartesian System
4.2. Transformation between Plate-Fixed and Earth-Fixed Frames, Datum Transformation
4.3. Representation of Coordinate Differences in a Topocentric System
4.4. Conversion from 3D ECEF Cartesian Coordinates to a Map Projection
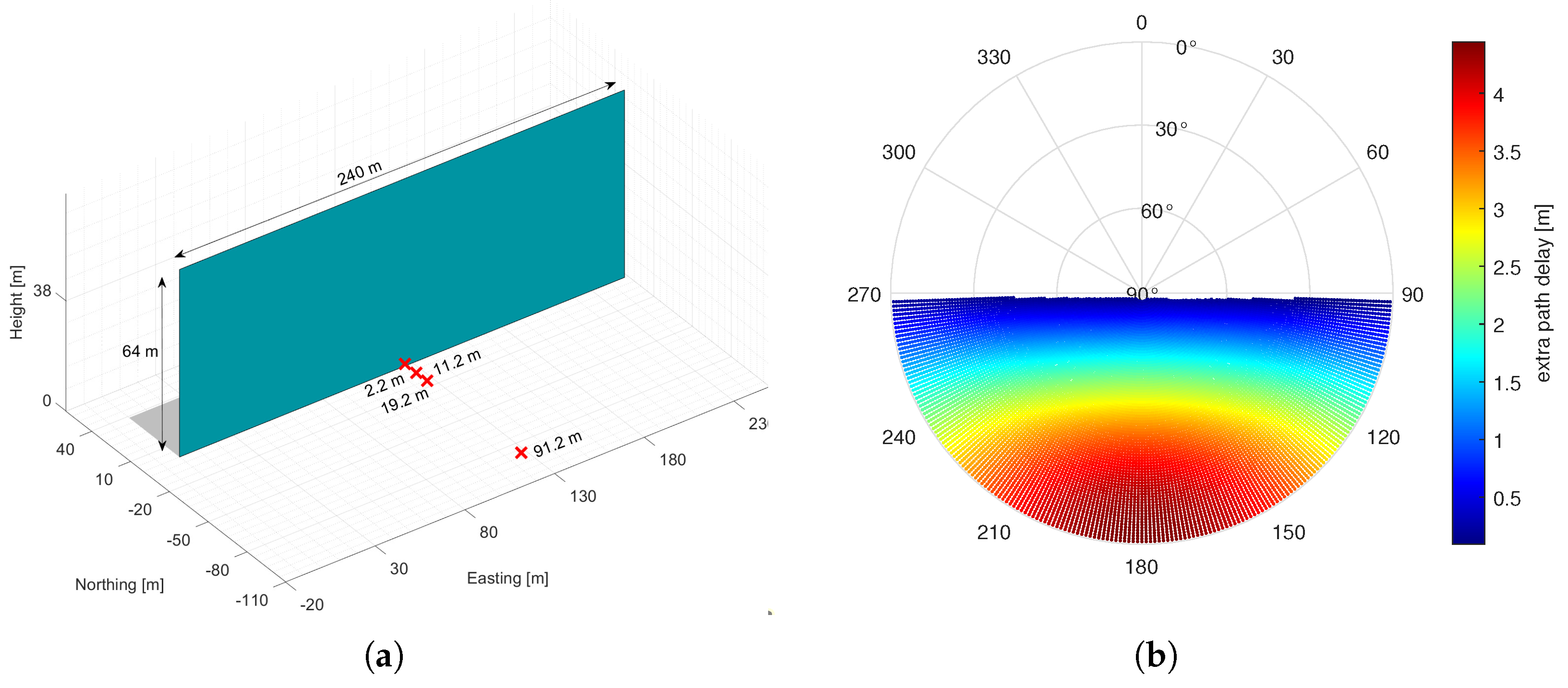
5. Simulation Set Up
6. Results
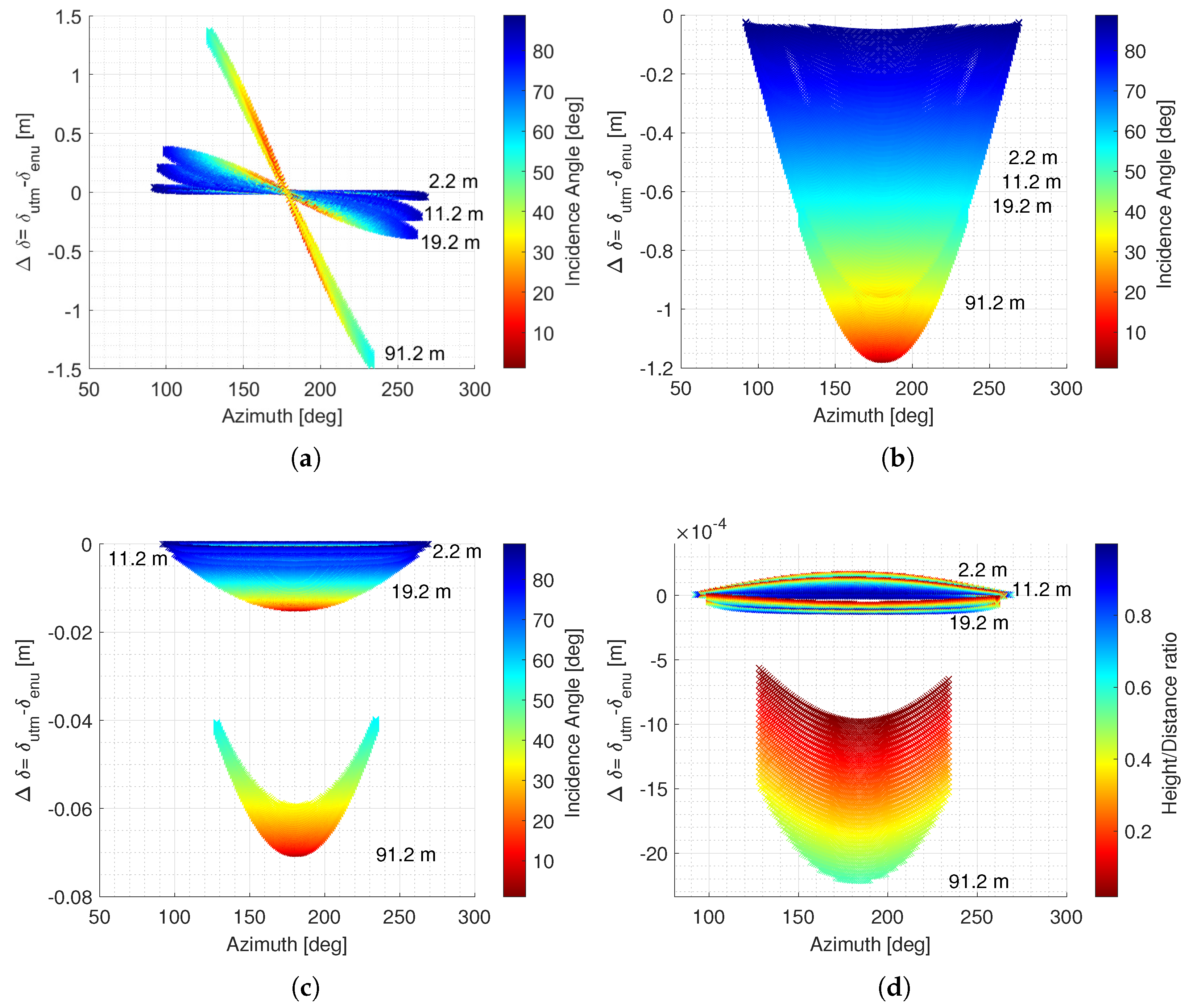
6.1. Impact of Neglecting Different Reference Frames and Meridian Convergence
6.2. Transformation to a Common Reference System
6.3. Different Frames but Consideration of the Meridian Convergence
6.4. Transformation to Common Reference Systems and Consideration of the Meridian Convergence
6.5. Transformation to Common Reference Systems, Consideration of the Meridian Convergence and Distortion Correction
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reid, T.G.; Houts, S.E.; Cammarata, R.; Mills, G.; Agarwal, S.; Vora, A.; Pandey, G. Localization Requirements for Autonomous Vehicles. SAE Int. J. Connect. Autom. Veh. 2019, 173–190. [Google Scholar] [CrossRef]
- Zhu, N.; Betaille, D.; Marais, J.; Berbineau, M. Extended Kalman Filter (EKF) Innovation-Based Integrity Monitoring Scheme with C/N0 Weighting. In Proceedings of the 2018 IEEE 4th International Forum on Research and Technology for Society and Industry (RTSI), Palermo, Italy, 10–13 September 2018. [Google Scholar] [CrossRef]
- Gottschalg, G.; Leinen, S. Comparison and Evaluation of Integrity Algorithms for Vehicle Dynamic State Estimation in Different Scenarios for an Application in Automated Driving. Sensors 2021, 21, 1458. [Google Scholar] [CrossRef] [PubMed]
- Bisnath, S. Relative Positioning and Real-Time Kinematic (RTK). In Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; Morton, Y.J., van Diggelen, F., Spilker, J.J., Jr., Parkinson, B.W., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2021; Chapter 19; pp. 481–502. [Google Scholar]
- Teunissen, P.J.G. Precise Point Positioning. In Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; Morton, Y.J., van Diggelen, F., Spilker, J.J., Jr., Parkinson, B.W., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2021; Chapter 20; pp. 503–528. [Google Scholar]
- Betaille, D.; Peyret, F.; Ortiz, M.; Miquel, S.; Fontenay, L. A New Modeling Based on Urban Trenches to Improve GNSS Positioning Quality of Service in Cities. IEEE Intell. Transp. Syst. Mag. 2013, 5, 59–70. [Google Scholar] [CrossRef]
- Icking, L.; Kersten, T.; Schön, S. Evaluating the Urban Trench Model For Improved GNSS Positioning in Urban Areas. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 631–638. [Google Scholar] [CrossRef]
- Icking, L.; Zhang, G.; Hsu, L.T.; Schön, S. Quantification of GNSS NLOS Spatial Correlation—A Case Study in Hong Kong’s Urban Canyon. In Proceedings of the 2022 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 19–23 September 2022; pp. 712–722. [Google Scholar] [CrossRef]
- Hsu, L.T. Analysis and modeling GPS NLOS effect in highly urbanized area. GPS Solut. 2017, 22, 7. [Google Scholar] [CrossRef]
- Braasch, M.S. Multipath. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Chapter 15; pp. 443–468. [Google Scholar]
- McGraw, G.A.; Groves, P.D.; Ashman, B.W. Robust Positioning in the Presence of Multipath and NLOS GNSS Signals. In Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; Jade Morton, Y.T., van Diggelen, F., Spilker, J.J.B.W.P., Jr., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2021; Chapter 22; pp. 551–589. [Google Scholar]
- Amt, J.H.; Raquet, J.F. Positioning for Range-Based Land Navigation Systems Using Surface Topography. In Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006), Fort Worth, TX, USA, 26–29 September 2006; pp. 1494–1505. [Google Scholar]
- Groves, P.D.; Jiang, Z. Height Aiding, C/N0 Weighting and Consistency Checking for GNSS NLOS and Multipath Mitigation in Urban Areas. J. Navig. 2013, 66, 653–669. [Google Scholar] [CrossRef]
- Ng, H.F.; Zhang, G.; Hsu, L.T. Robust GNSS Shadow Matching for Smartphones in Urban Canyons. IEEE Sens. J. 2021, 21, 18307–18317. [Google Scholar] [CrossRef]
- Groves, P.D. Shadow Matching: A New GNSS Positioning Technique for Urban Canyons. J. Navig. 2011, 64, 417–430. [Google Scholar] [CrossRef]
- Groves, P.D.; Wang, L.; Adjrad, M.; Ellul, C. GNSS Shadow Matching: The Challenges Ahead. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015; pp. 2421–2443. [Google Scholar]
- Obst, M.; Bauer, S.; Wanielik, G. Urban multipath detection and mitigation with dynamic 3D maps for reliable land vehicle localization. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 685–691. [Google Scholar] [CrossRef]
- Peyraud, S.; Bétaille, D.; Renault, S.; Ortiz, M.; Mougel, F.; Meizel, D.; Peyret, F. About Non-Line-Of-Sight Satellite Detection and Exclusion in a 3D Map-Aided Localization Algorithm. Sensors 2013, 13, 829–847. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Kubo, N. Correcting GNSS Multipath Errors Using a 3D Surface Model and Particle Filter. In Proceedings of the 26th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013; pp. 1583–1595. [Google Scholar]
- Hsu, L.T.; Gu, Y.; Kamijo, S. Sensor integration of 3D map aided GNSS and smartphone PDR in urban canyon with dense foliage. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016. [Google Scholar] [CrossRef]
- Ruwisch, F.; Schön, S. GNSS Feature Map: Representation of Signal Propagation-related Features in Urban Trenches. In Proceedings of the 2022 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 19–23 September 2022; pp. 701–711. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, B.; Ng, H.F.; Hsu, L.T. GNSS RUMS: GNSS Realistic Urban Multiagent Simulator for Collaborative Positioning Research. Remote Sens. 2021, 13, 544. [Google Scholar] [CrossRef]
- van Diggelen, F. End Game for Urban GNSS: Google’s Use of 3D Building Models. Inside GNSS 2021, 16, 42–49. [Google Scholar]
- Bugayevskiy, L.; Snyder, J.P. General Theory of Map Projections. In Map Projections—A Working Manual; CRC Press: Boca Raton, FL, USA, 1995; Chapter 1; pp. 1–49. [Google Scholar] [CrossRef]
- Jaud, Š.; Donaubauer, A.; Heunecke, O.; Borrmann, A. Georeferencing in the context of building information modelling. Autom. Constr. 2020, 118, 103211. [Google Scholar] [CrossRef]
- Landeshauptstadt Hannover, FB Planen und Stadtentwicklung, Bereich Geoinformation. In Produktinformation Digitales 3D-Stadtmodell, 3rd ed.; Landeshauptstadt Hannover: Hannover, Germany, 2017.
- Business Location Center. Berlin 3D—Download Portal. 2021. Available online: https://www.businesslocationcenter.de/en/economic-atlas/download-portal/ (accessed on 25 February 2022).
- van den Brink, L.; Stoter, J.E.; Zlatanova, S. Establishing a national 3D standard compliant to CityGML: Good practice of a national 3D SDI. Int. J. Geogr. Inf. Sci. 2013, 27, 92–113. [Google Scholar] [CrossRef]
- Department of Information Technology & Telecommunications (DoITT). NYC 3-D Building Model. Available online: https://www1.nyc.gov/site/doitt/initiatives/3d-building.page (accessed on 25 February 2022).
- Land Information Centre (LIC), Survey and Mapping Office (SMO), Lands Department. Information Sheet on 3D Spatial Data; Technical Report; The Government of the Hong Kong Special Administrative Region: Hong Kong, China, 2021.
- Wen, W.; Zhang, G.; Hsu, L.T. Correcting GNSS NLOS by 3D LiDAR and Building Height. In Proceedings of the 31st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24 – 28 September 2018; pp. 3156–3168. [Google Scholar] [CrossRef]
- Wen, W.; Hsu, L.T. 3D LiDAR Aided GNSS Real-time Kinematic Positioning. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MI, USA, 20 – 24 September 2021; pp. 2212–2220. [Google Scholar] [CrossRef]
- Hannah, B.M. Modelling and Simulation of GPS Multipath Propagation. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 2001. [Google Scholar]
- Smyrnaios, M. Carrier-Phase Multipath in Satellite-Based Positioning. Ph.D. Thesis, Leibniz Universität Hannover, Hanover, Germany, 2016. [Google Scholar]
- Icking, L.; Ruwisch, F.; Schön, S. Multipath Characterization using Ray-Tracing in Urban Trenches. In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Bradbury, J.; Ziebart, M.; Cross, P.; Boulton, P.; Read, A. Code Multipath Modelling in the Urban Environment Using Large Virtual Reality City Models: Determining the Local Environment. J. Navig. 2007, 60, 95–105. [Google Scholar] [CrossRef]
- Irsigler, M. Characterization of multipath phase rates in different multipath environments. GPS Solut. 2010, 14, 305–317. [Google Scholar] [CrossRef]
- Smyrnaios, M.; Schön, S.; Nicolàs, M.L. Multipath Propagation, Characterization and Model in GNSS. In Geodetic Sciences—Observations, Modeling and Applications; Jin, S., Ed.; License: CC BY 3.0—Open Access; Earth and Planetary Sciences, InTech: Rijeka, Croatia, 2013; Chapter 2; pp. 99–125. [Google Scholar] [CrossRef]
- Smyrnaios, M.; Schon, S.; Nicolas, M.L.; Kurner, T. Ray-tracing approach versus double difference, multipath characterization in a multiple ray scenario. In Proceedings of the 2012 6th ESA Workshop on Satellite Navigation Technologies (Navitec 2012) & European Workshop on GNSS Signals and Signal Processing, Noordwijk, The Netherlands, 5–7 December 2012. [Google Scholar] [CrossRef]
- Jekeli, C.; Montenbruck, O. Time and Reference Systems. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Chapter 2; pp. 25–58. [Google Scholar]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Kelly, K.M.; Dennis, M.L. Transforming between WGS84 realizations. J. Surv. Eng. 2022, 148, 04021031. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS) – Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Liu, P.; Tan, W.; Dong, D.; Qu, W. Comparison and Assessment of Three ITRS Realizations. Remote Sens. 2021, 13, 2304. [Google Scholar] [CrossRef]
- Altamimi, Z. EUREF Technical Note 1: Relationship and Transformation between the International and the European Terrestrial Reference Systems; Technical Report; EUREF: Berlin, Germany, 2018. [Google Scholar]
- Torge, W.; Müller, J. Methods of Positioning and Gravity Field Modeling. In Geodesy; Walter de Gruyter: Berlin, Germany, 2012; Volume 3, Chapter 6; pp. 223–304. [Google Scholar]
- Gröger, G.; Kolbe, T.H.; Nagel, C.; Häfele, K.H. OGC City Geography Markup Language (CityGML) Enconding Standard; Open Geospatial Consortium, 2.0.0 ed.: Arlington, VA, USA, 2012. [Google Scholar]
- 3D-Gebäudemodelle, Level of Detail 2 (LoD2) Produkt- und Formatbeschreibung; Technical Report; Landesamt für Geoinformation und Landesvermessung Niedersachsen (LGLN): Hannover, Germany, 2018.
- Krakiwsky, E.J. Computations on a Conformal Map Projection Plane. In Conformal Map Projections in Geodesy; Department of Surveying Engineering, University of New Brunswick: Fredericton, NB, Canada, 1977; Chapter II; pp. 109–136. [Google Scholar]
- Quasigeoid of the Federal Republic of Germany: German Combined Quasigeoid 2016; Technical Report; Federal Agency for Cartography and Geodesy: Frankfurt, Germany, 2021.
- Seeber, G. Fundamentals. In Satellite Geodesy: Foundations, Methods and Applications, 2nd ed.; de Gruyter: Berlin, Germany, 2003; Chapter 2; pp. 10–61. [Google Scholar] [CrossRef]
- Boucher, C.; Altamimi, Z. Terrestrial Reference System and its first realizations. VeröFfentlichung Bayer. Komm. Für Die Int. Erdmess. Astron.-Geodätische Arb. 1992, 52, 205–213. [Google Scholar]
- Bruyninx, C. The EPN CB Coordinate Transformation Tool. In Proceedings of the EUREF Tutorial, Riga, Latvia, 14–17 June 2016. [Google Scholar]
- Hooijberg, M. Symbology. In Practical Geodesy: Using Computers; Springer: Berlin/Heidelberg, Germany, 1997; Chapter 5.3; p. 78. [Google Scholar] [CrossRef]
- Krakiwsky, E.J. Transverse Mercator Projection. In Conformal Map Projections in Geodesy; Department of Surveying Engineering, University of New Brunswick: Fredericton, NB, Canada, 1977; Chapter 6; pp. 51–80. [Google Scholar]
- Moffitt, F.; Bossler, J. Application of the State Coordinate System. In Surveying, 10th ed.; Addison-Wesley: Boston, MA, USA, 1998; p. 411. [Google Scholar]

| Input Data | Coordinate Frame | Coordinates |
|---|---|---|
| GNSS satellite orbits | ITRF2014 | 3D Cartesian |
| 3D building model | ETRF2000 | UTM, physical height |
| Antenna position | ITRF2014 | 3D Cartesian |
| Distance to Reflector | 2.2 m | 11.2 m | 19.2 m | 91.2 m |
|---|---|---|---|---|
| Correction Steps | RMSE [cm] | |||
| None | 57 | 65 | 72 | 128 |
| Meridian convergence | 57 | 64 | 69 | 98 |
| Conformal system | 2 | 12 | 20 | 81 |
| Meridian convergence & conformal system | 0.08 | 0.5 | 0.9 | 6 |
| Meridian convergence & conformal system & distortion correction | 0.0089 | 0.006 | 0.0097 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baasch, K.-N.; Icking, L.; Ruwisch, F.; Schön, S. Coordinate Frames and Transformations in GNSS Ray-Tracing for Autonomous Driving in Urban Areas. Remote Sens. 2023, 15, 180. https://doi.org/10.3390/rs15010180
Baasch K-N, Icking L, Ruwisch F, Schön S. Coordinate Frames and Transformations in GNSS Ray-Tracing for Autonomous Driving in Urban Areas. Remote Sensing. 2023; 15(1):180. https://doi.org/10.3390/rs15010180
Chicago/Turabian StyleBaasch, Kai-Niklas, Lucy Icking, Fabian Ruwisch, and Steffen Schön. 2023. "Coordinate Frames and Transformations in GNSS Ray-Tracing for Autonomous Driving in Urban Areas" Remote Sensing 15, no. 1: 180. https://doi.org/10.3390/rs15010180
APA StyleBaasch, K.-N., Icking, L., Ruwisch, F., & Schön, S. (2023). Coordinate Frames and Transformations in GNSS Ray-Tracing for Autonomous Driving in Urban Areas. Remote Sensing, 15(1), 180. https://doi.org/10.3390/rs15010180






