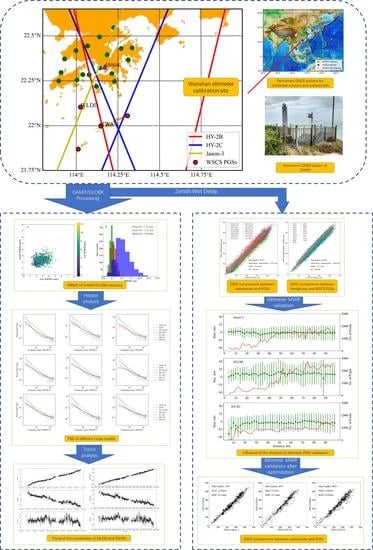
GNSS Data Processing and Validation of the Altimeter Zenith Wet Delay around the Wanshan Calibration Site
Abstract
1. Introduction
2. Dataset and Methods
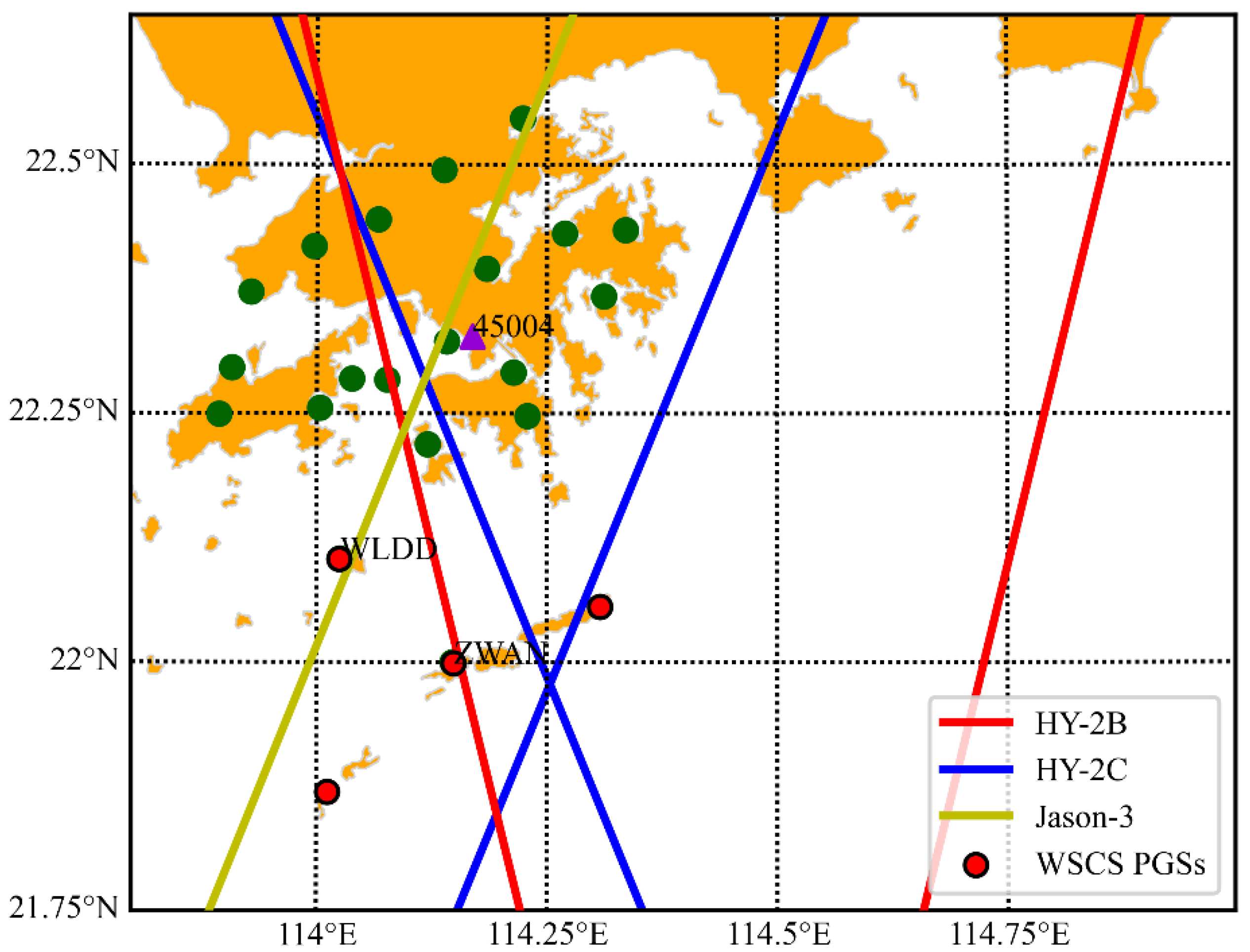
2.1. Dataset
2.2. Processing of GNSS Data
2.2.1. Processing Methods
2.2.2. Accuracy Assessment
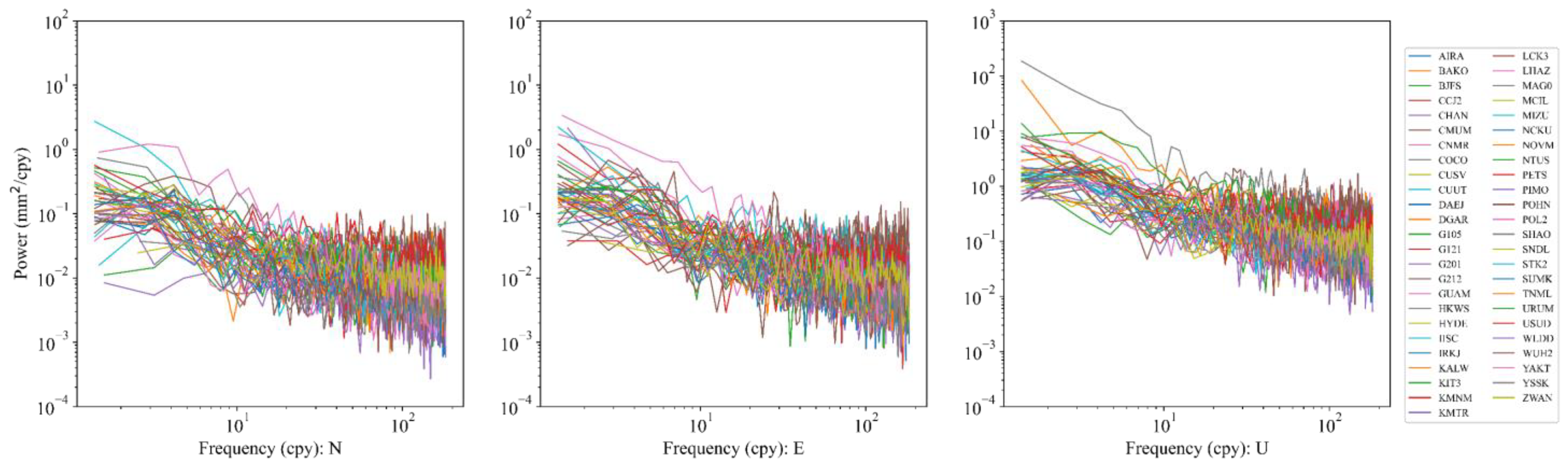
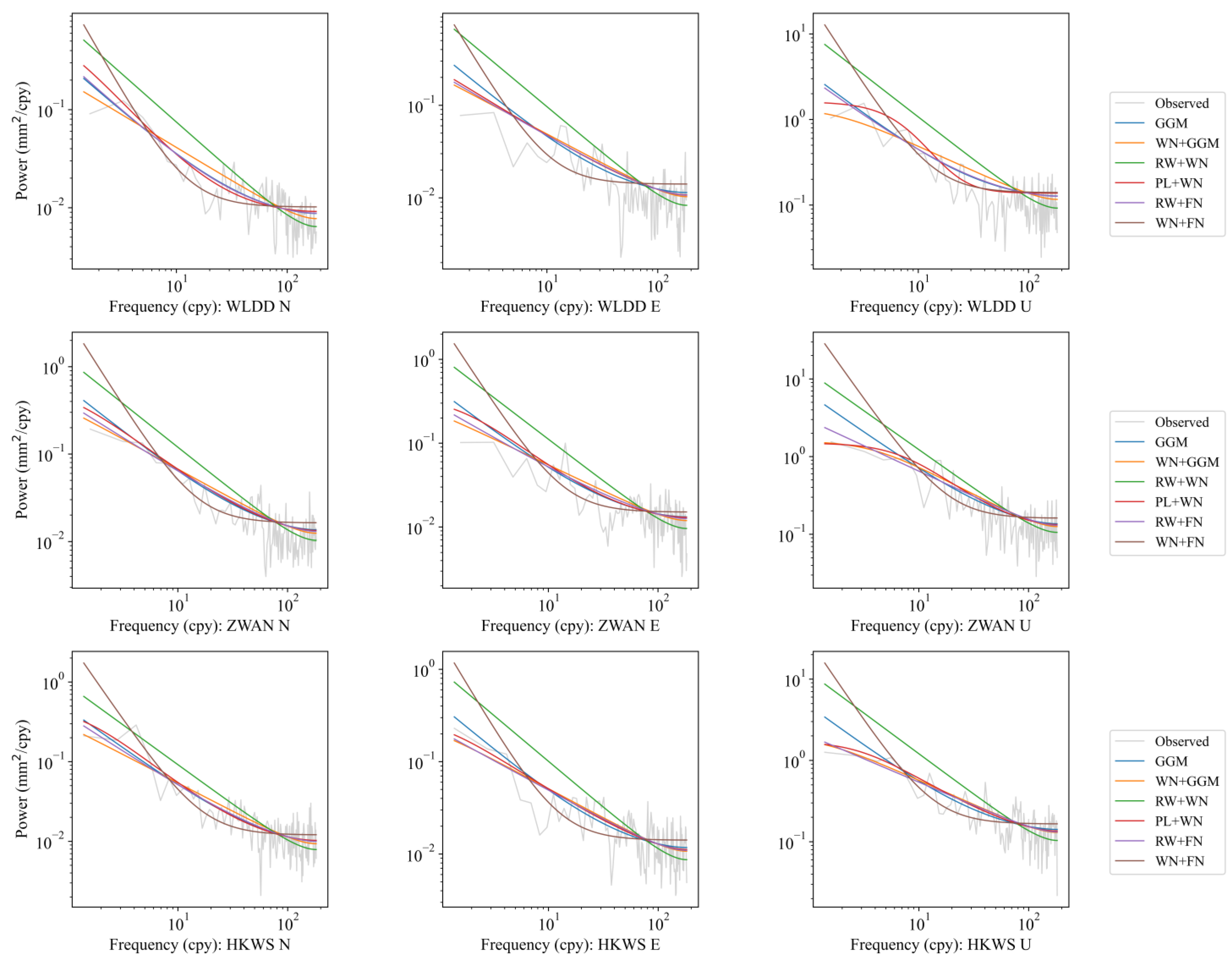
2.2.3. Noise Characteristics and Station Velocities
- Generalized Gauss–Markov noise (GGM);
- White noise + generalized Gauss–Markov noise (WN + GGM);
- Flicker noise + white noise (WN + FN);
- Random walk + flicker noise (RW + FN);
- White noise + random walk (WN + RW);
- White noise + Power law noise (WN + PL).
2.3. Validation of the Altimeter ZWD
2.3.1. ZWD from GNSS and Radiosonde
2.3.2. Validation of the Altimeter ZWD
3. GNSS Processing Results
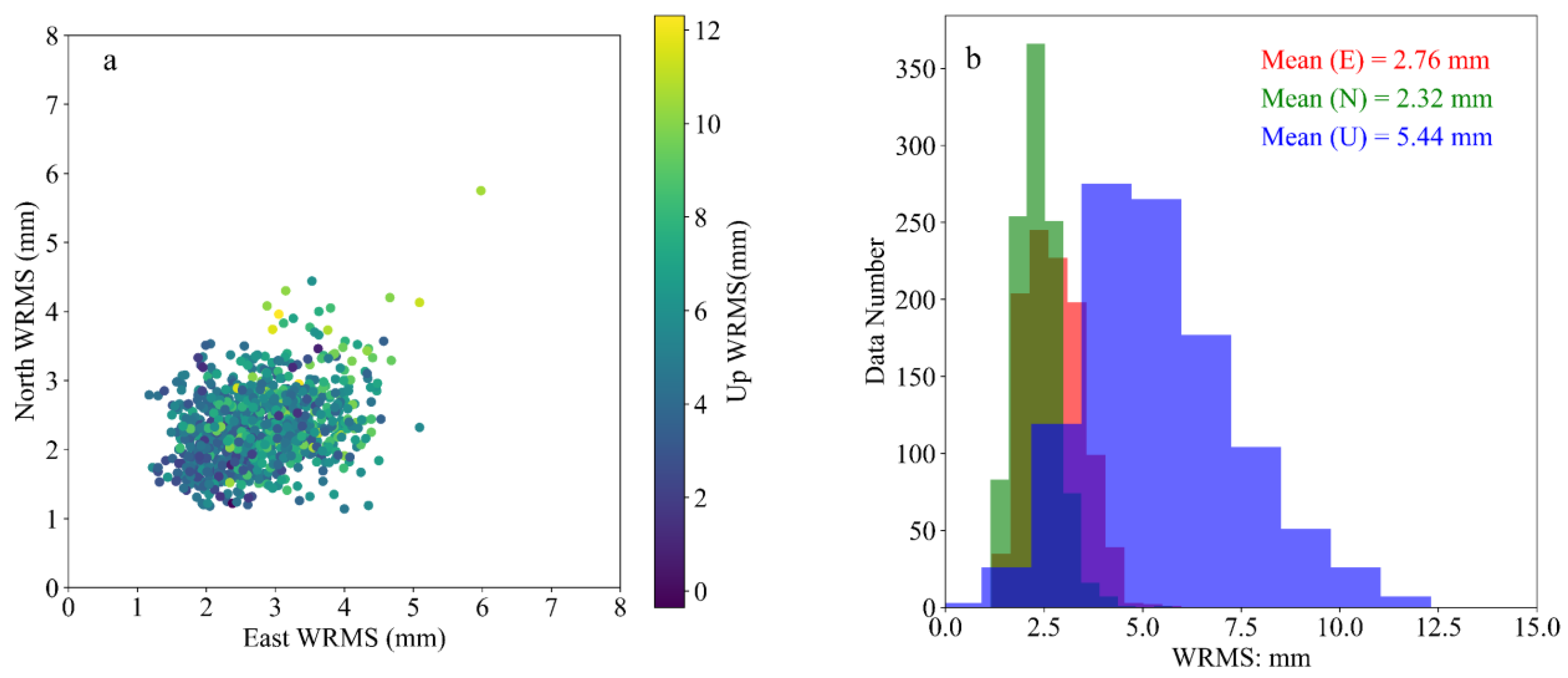
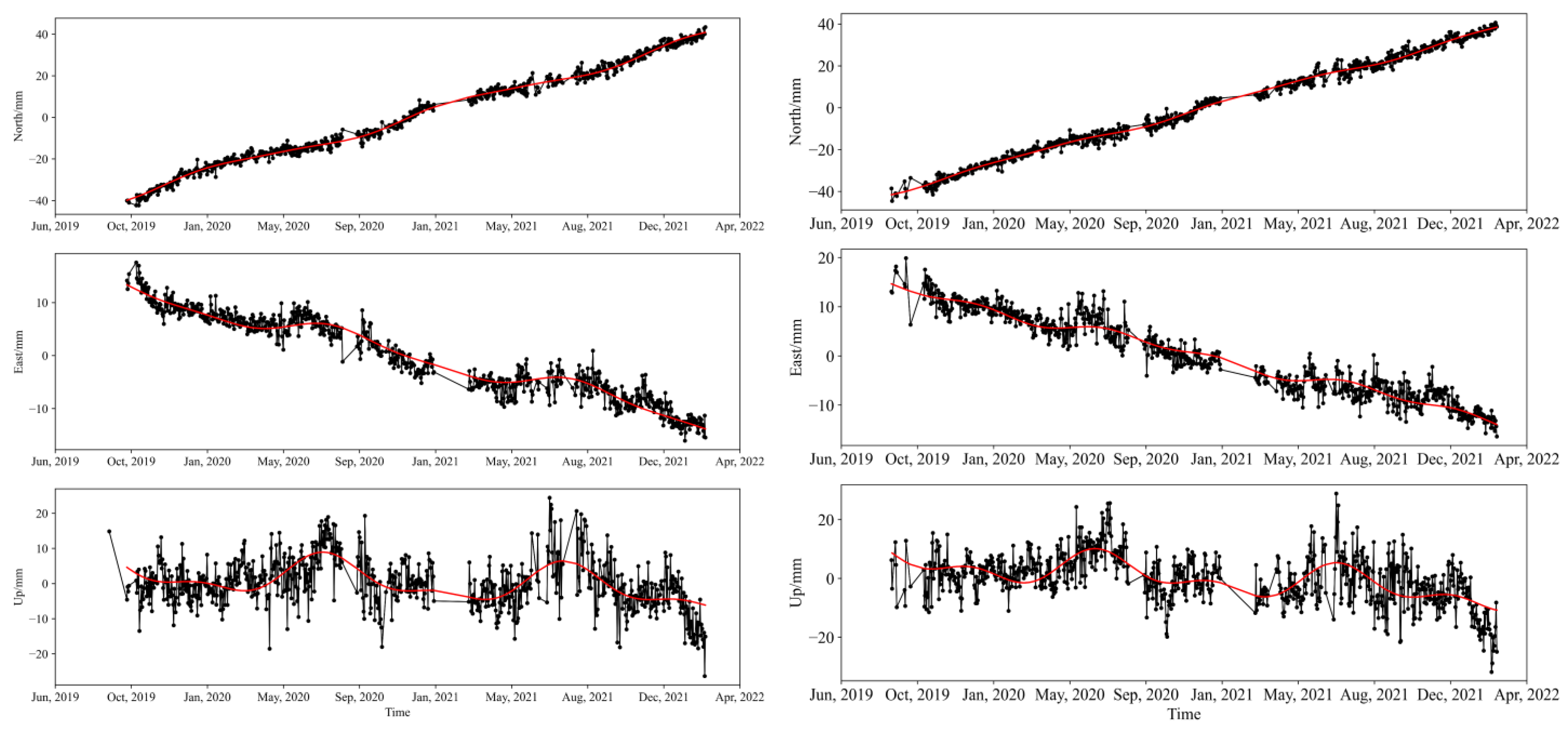
3.1. WRMS
3.2. Noise Properties
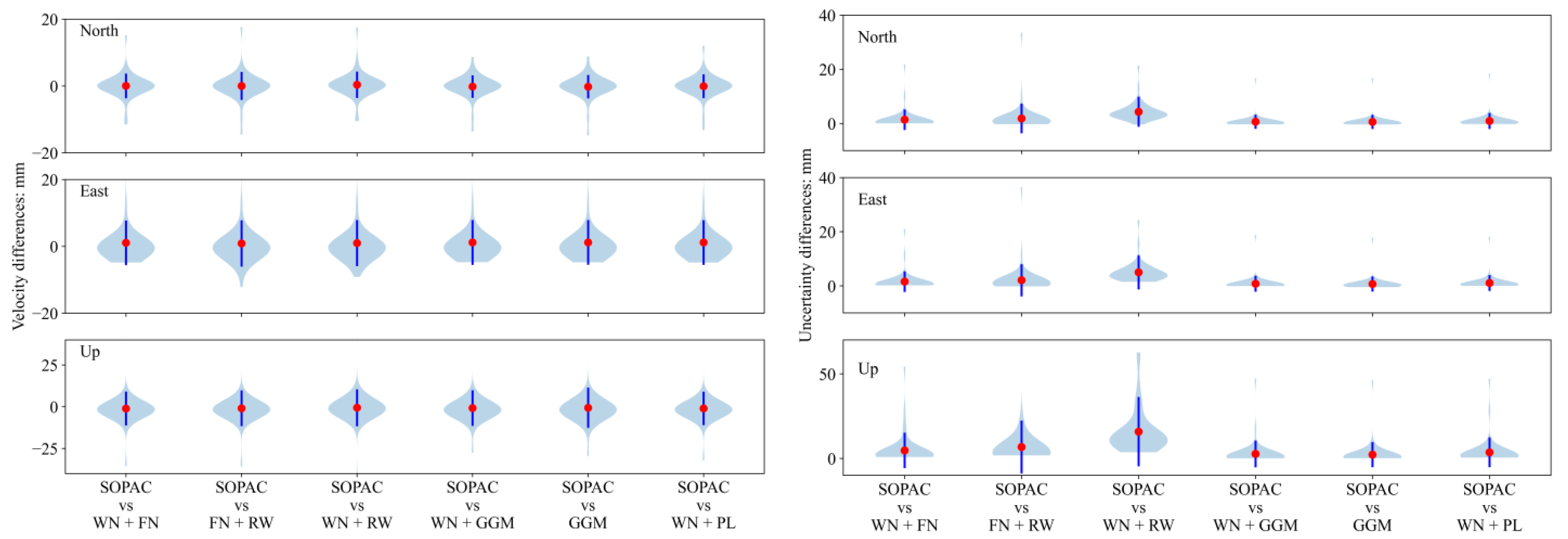
3.3. Velocity Estimation
4. Validation of ZWD
4.1. Comparisons between GNSS Stations and Radiosonde
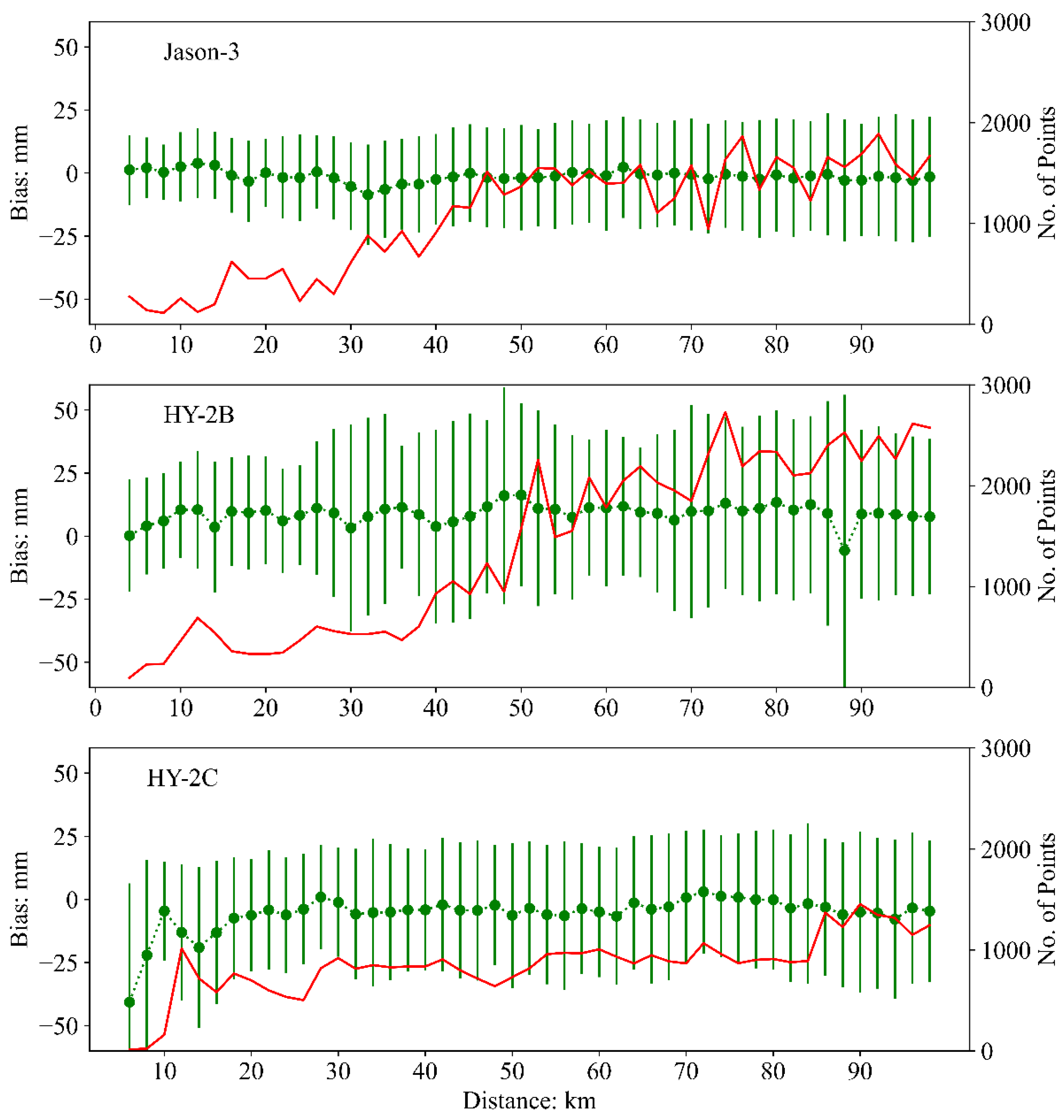
4.2. Validation of the ZWD Using PGSs
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, X.; Lin, M.; Song, Q. On the Construction of China’s Ocean Satellite Radar Altimetry Calibration Site. Ocean Dev. Manag. 2016, 5, 8–15. [Google Scholar]
- Quartly, G.D.; Chen, G.; Nencioli, F.; Morrow, R.; Picot, N. An Overview of Requirements, Procedures and Current Advances in the Calibration/Validation of Radar Altimeters. Remote Sens. 2021, 13, 125. [Google Scholar] [CrossRef]
- Bonnefond, P.; Exertier, P.; Laurain, O.; Guinle, T.; Féméniase, P. Corsica: A 20-Yr multi-mission absolute altimeter calibration site. Adv. Space Res. 2021, 68, 1171–1186. [Google Scholar] [CrossRef]
- Haines, B.; Desai, S.; Kubitschek, D.; Leben, R. A brief history of the Harvest experiment: 1989–2019. Adv. Space Res. 2021, 68, 1161–1170. [Google Scholar] [CrossRef]
- Mertikas, S.; Tripolitsiotis, A.; Donlon, C.; Mavrocordatos, C.; Féménias, P.; Borde, F.; Frantzis, X.; Kokolakis, C.; Guinle, T.; Vergos, G.; et al. The ESA Permanent Facility for altimetry calibration: Monitoring performance of radar altimeters for Sentinel3A, Sentinel-3B and Jason-3 using transponder and sea-surface calibrations with FRM standards. Remote Sens. 2020, 12, 2642. [Google Scholar] [CrossRef]
- Watson, C. Satellite Altimeter Calibration and Validation Using GPS Buoy Technology. Ph.D. Thesis, University of Tasmania, Hobart, Australia, July 2005. [Google Scholar]
- Chen, C.; Zhu, J.; Ma, C.; Lin, M.; Yan, L.; Huang, X.; Zhai, W.; Mu, B.; Jia, Y. Preliminary Calibration Results of the HY-2B Altimeter’s SSH at China’s Wanshan Calibration Site. Acta Oceanol. Sin. 2021, 40, 129–140. [Google Scholar] [CrossRef]
- Li, Y. Analysis of GAMIT/GLOBK in high-precision GNSS data processing for crustal deformation. Earthq. Res. Adv. 2021, 1, 100028. [Google Scholar] [CrossRef]
- Herring, T. MATLAB Tools for viewing GPS velocities and time-series. GPS Solut. 2003, 7, 194–199. [Google Scholar] [CrossRef]
- Herring, T.; King, R.; McClusky, S. Introduction to GAMIT/GLOBK (Release 10.7); Massachusetts Institute of Technology: Cambridge, MA, USA; Available online: http://geoweb.mit.edu/gg/Intro_GG.pdf (accessed on 22 June 2020).
- Li, W.; Li, Z.; Jiang, W.; Chen, Q.; Zhu, G.; Wang, J. A New Spatial Filtering Algorithm for Noisy and Missing GNSS Position Time Series Using Weighted Expectation Maximization Principal Component Analysis: A Case Study for Regional GNSS Network in Xinjiang Province. Remote Sens. 2022, 14, 1295. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Bouin, M.-N.; Collilieux, X.; Wöppelmann, G. Correlated errors in GPS position time series: Implications for velocity estimates. J. Geophys. Res. 2011, 116, B01405. [Google Scholar] [CrossRef]
- Wang, L.; Herring, T. Impact of Estimating Position Offsets on the Uncertainties of GNSS Site Velocity Estimates. J. Geophys. Res. Solid Earth 2019, 124, 13452–13467. [Google Scholar] [CrossRef]
- Lidberg, M.; Johansson, J.; Scherneck, H.; Davis, J. An improved and extended GPS-derived 3D velocity field of the glacial isostatic adjustment (GIA) in Fennoscandia. J. Geod. 2007, 81, 213–230. [Google Scholar] [CrossRef]
- Bonafoni, S.; Mazzoni, A.; Cimini, D.; Montopoli, M.; Pierdicca, N.; Basili, P.; Ciotti, P.; Carlesimo, G. Assessment of water vapor retrievals from a GPS receiver network. GPS Solut. 2013, 17, 475–484. [Google Scholar] [CrossRef]
- Haase, J.; Ge, M.; Vedel, H.; Calais, E. Accuracy and variability of GPS tropospheric delay measurements of water vapor in the western Mediterranean. J. Appl. Meteorol. 2003, 42, 154768. [Google Scholar] [CrossRef]
- Ablain, M.; Meyssignac, B.; Zawadzki, L.; Jugier, R.; Ribes, A.; Spada, G.; Benveniste, J.; Cazenave, A.; Picot, N. Uncertainty in satellite estimates of global mean sea-level changes, trend and acceleration. Earth Syst. Sci. Data 2019, 11, 1189–1202. [Google Scholar] [CrossRef]
- Pearson, C.; Moore, P.; Edwards, S. GNSS Assessment of Sentinel-3A ECMWF Tropospheric Delays over Inland Waters. Adv. Space Res. 2020, 66, 2827–2843. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, C.; Chen, B.; Dai, W. Consistency evaluation of precipitable water vapor derived from ERA5, ERA-Interim, GNSS, and radiosondes over China. Radio Sci. 2019, 54, 561–571. [Google Scholar] [CrossRef]
- Zhai, W.; Zhu, J.; Fan, X.; Yan, L.; Chen, C.; Tian, Z. Preliminary calibration results for Jason-3 and Sentinel-3 altimeters in the Wanshan Islands. J. Ocean. Limnol. 2021, 39, 458–471. [Google Scholar] [CrossRef]
- Wang, J.; Xu, H.; Yang, L.; Song, Q.; Ma, C. Cross-Calibrations of the HY-2B Altimeter Using Jason-3 Satellite During the Period of April 2019–September 2020. Front. Earth Sci. 2021, 9, 647583. [Google Scholar] [CrossRef]
- Lazaro, C.; Fernandes, J.; Vieira, T.; Vieira, E. A coastally improved global dataset of wet tropospheric corrections for satellite altimetry. Earth Syst. Sci. Data 2019, 12, 3205–3228. [Google Scholar] [CrossRef]
- Li, F.; Zhang, Q.; Zhang, S.; Lei, J.; Li, W. Evaluation of spatio-temporal characteristics of different zenith tropospheric delay models in Antarctica. Radio Sci. 2020, 55, 1–16. [Google Scholar] [CrossRef]
- Nischan, T. GFZRNX—RINEX GNSS Data Conversion and Manipulation Toolbox; Version 2.0-8219; GFZ Data Services: Potsdam, Germany, 2016. [Google Scholar] [CrossRef]
- Estey, L.; Meertens, C. TEQC: The Multi-Purpose Toolkit for GPS/GLONASS Data. GPS Solut. 1999, 3, 42–49. [Google Scholar] [CrossRef]
- Herring, T.; Melbourne, T.; Murray, M.; Floyd, M.; Szeliga, W.; King, R.; Phillips, D.; Puskas, C.; Santillan, M.; Wang, L. Plate Boundary Observatory and related networks: GPS data analysis methods and geodetic products. Rev. Geophys. 2016, 54, 759–808. [Google Scholar] [CrossRef]
- He, X.; Yu, K.; Montillet, J.P.; Xiong, C.; Lu, T.; Zhou, S.; Ma, X.; Cui, H.; Ming, F. GNSS-TS-NRS: An Open-Source MATLAB-Based GNSS Time Series Noise Reduction Software. Remote Sens. 2020, 12, 3532. [Google Scholar] [CrossRef]
- He, X.; Bos, M.; Montillet, J.; Fernandes, R. Investigation of the noise properties at low frequencies in long GNSS time series. J. Geod. 2019, 93, 1271–1282. [Google Scholar] [CrossRef]
- Williams, S. The effect of coloured noise on the uncertainties of rates estimated from geodetic time series. J. Geod. 2003, 76, 483–494. [Google Scholar] [CrossRef]
- Nikolaidis, R.M. Observation of Geodetic and Seismic Deformation with the Global Positioning System. Ph.D. Thesis, University of California, San Diego, CA, USA, 2022. [Google Scholar]
- Xia, P.; Xia, J.; Ye, S.; Xu, C. A New Method for Estimating Tropospheric Zenith Wet-Component Delay of GNSS Signals from Surface Meteorology Data. Remote Sens. 2020, 12, 3497. [Google Scholar] [CrossRef]
- Kouba, J. Implementation and testing of the gridded Vienna Mapping Function 1 (VMF1). J. Geod. 2008, 82, 193–205. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. 2006, 111, B02406. [Google Scholar] [CrossRef]
- Vieira, T.; Fernandes, M.J.; Lázaro, C. Independent Assessment of On-Board Microwave Radiometer Measurements in Coastal Zones Using Tropospheric Delays From GNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1804–1816. [Google Scholar] [CrossRef]
- Zhao, B.; Huang, Y.; Zhang, C.; Wang, W.; Tan, K.; Du, R. Crustal deformation on the Chinese mainland during 1998–2014 based on GPS data. Geod. Geodyn. 2015, 6, 7–15. [Google Scholar] [CrossRef]
- He, Y.; Zhang, S.; Wang, Q.; Liu, Q.; Qu, W.; Hou, X. HECTOR for Analysis of GPS Time Series. In China Satellite Navigation Conference (CSNC) 2018 Proceedings. CSNC 2018; Lecture Notes in Electrical Engineering; Sun, J., Yang, C., Guo, S., Eds.; Springer: Singapore, 2018; Volume 497. [Google Scholar]
- Li, Y.; Xu, C.; Yi, L.; Fang, R. A data-driven approach for denoising GNSS position time series. J. Geod. 2018, 92, 905–922. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time series and their error sources. J. Geodyn. 2017, 106, 12–29. [Google Scholar] [CrossRef]



| Noise Model | N (%) | E (%) | U (%) | Total (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MLE | AIC | BIC | MLE | AIC | BIC | MLE | AIC | BIC | MLE | AIC | BIC | |
| GGM | 4.67 | 13.33 | 19.33 | 4.67 | 13.33 | 19.33 | 4.67 | 13.33 | 19.33 | 4.67 | 13.33 | 19.33 |
| WN + GGM | 64.00 | 48.00 | 43.33 | 64.00 | 48.00 | 43.33 | 64.00 | 48.00 | 43.33 | 64.00 | 48.00 | 43.33 |
| WN + PL | 0 | 6.67 | 0.67 | 0 | 6.67 | 0.67 | 0 | 6.67 | 0.67 | 0 | 6.67 | 0.67 |
| WN + RW | 0 | 0.67 | 2.67 | 0 | 0.67 | 2.67 | 0 | 0.67 | 2.67 | 0 | 0.67 | 2.67 |
| FN + RW | 0 | 0.67 | 2.67 | 0 | 0.67 | 2.67 | 0 | 0.67 | 2.67 | 0 | 0.67 | 2.67 |
| WN + FN | 31.33 | 30.67 | 31.33 | 31.33 | 30.67 | 31.33 | 31.33 | 30.67 | 31.33 | 31.33 | 30.67 | 31.33 |
| PGS | Direction | WN + FN | FN + RW | WN + RW | WN + GGM | GGM | WN + PL |
|---|---|---|---|---|---|---|---|
| WLDD | N | −10.28 ± 0.69 | −10.07 ± 0.92 | −9.61 ± 3.38 | −10.22 ± 0.42 | −10.18 ± 0.35 | −10.05 ± 0.61 |
| E | 31.57 ± 0.74 | 30.98 ± 1.05 | 30.59 ± 3.39 | 31.08 ± 0.38 | 31.10 ± 0.34 | 31.07 ± 0.42 | |
| U | −3.40 ± 2.10 | −2.90 ± 3.42 | −5.68 ± 13.57 | −2.24 ± 0.69 | −2.24 ± 0.63 | −2.48 ± 1.79 | |
| ZWAN | N | −10.77 ± 0.81 | −10.71 ± 1.11 | −10.72 ± 4.92 | −10.87 ± 0.38 | −10.82 ± 0.38 | −10.75 ± 0.54 |
| E | 30.93 ± 0.67 | 30.54 ± 1.07 | 30.98 ± 4.52 | 30.69 ± 0.30 | 30.65 ± 0.30 | 30.59 ± 0.45 | |
| U | −4.86 ± 2.68 | −2.84 ± 3.55 | −0.95 ± 19.42 | −3.81 ± 0.65 | −3.81 ± 0.66 | −3.37 ± 1.36 | |
| HKWS | N | −10.21 ± 0.75 | −10.93 ± 1.09 | −10.21 ± 4.80 | −11.01 ± 0.34 | −10.93 ± 0.36 | −10.80 ± 0.58 |
| E | 31.08 ± 0.59 | 31.16 ± 1.02 | 31.87 ± 3.94 | 31.03 ± 0.27 | 31.02 ± 0.26 | 31.05 ± 0.37 | |
| U | −2.78 ± 2.11 | −1.46 ± 3.51 | 0.70 ± 14.45 | −2.17 ± 0.67 | −2.12 ± 0.71 | −1.80 ± 1.06 |
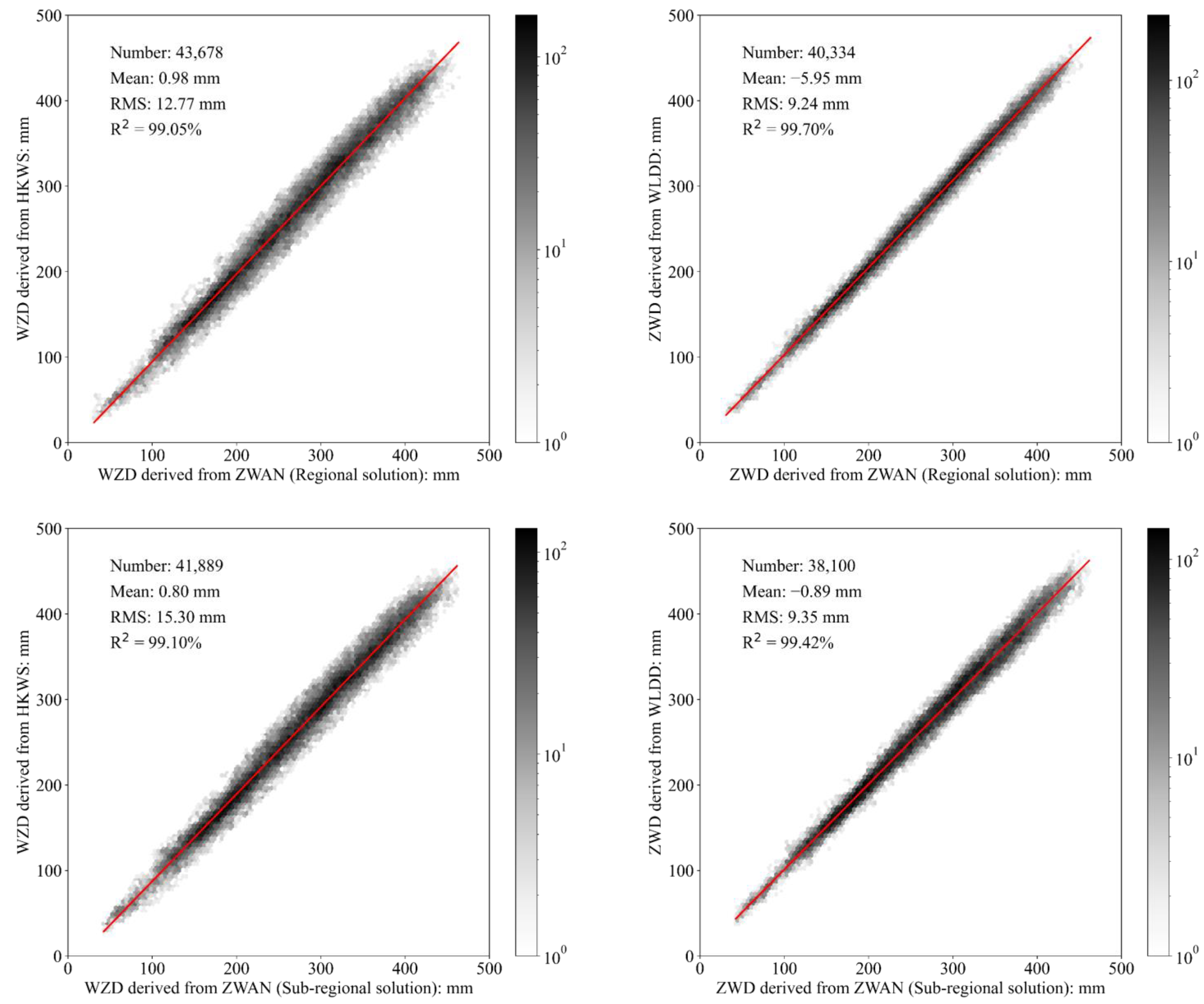
| Station Name | Data Number | Mean | Max | Min | RMS | |
|---|---|---|---|---|---|---|
| Regional solution | HKWS | 2014 | −6.66 | 48 | −61 | 15.18 |
| ZWAN | 1718 | 1.29 | 63.76 | −69.03 | 18.62 | |
| WLDD | 1656 | −0.54 | 60.94 | −63.38 | 14.98 | |
| Sub-regional solution | HKWS | 2014 | −7.72 | 34.83 | −58.38 | 14.53 |
| ZWAN | 1718 | 1.01 | 39.64 | −56.33 | 16.59 | |
| WLDD | 1656 | 2.79 | 40.12 | −53.62 | 15.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, W.; Zhu, J.; Lin, M.; Ma, C.; Chen, C.; Huang, X.; Zhang, Y.; Zhou, W.; Wang, H.; Yan, L. GNSS Data Processing and Validation of the Altimeter Zenith Wet Delay around the Wanshan Calibration Site. Remote Sens. 2022, 14, 6235. https://doi.org/10.3390/rs14246235
Zhai W, Zhu J, Lin M, Ma C, Chen C, Huang X, Zhang Y, Zhou W, Wang H, Yan L. GNSS Data Processing and Validation of the Altimeter Zenith Wet Delay around the Wanshan Calibration Site. Remote Sensing. 2022; 14(24):6235. https://doi.org/10.3390/rs14246235
Chicago/Turabian StyleZhai, Wanlin, Jianhua Zhu, Mingsen Lin, Chaofei Ma, Chuntao Chen, Xiaoqi Huang, Yufei Zhang, Wu Zhou, He Wang, and Longhao Yan. 2022. "GNSS Data Processing and Validation of the Altimeter Zenith Wet Delay around the Wanshan Calibration Site" Remote Sensing 14, no. 24: 6235. https://doi.org/10.3390/rs14246235
APA StyleZhai, W., Zhu, J., Lin, M., Ma, C., Chen, C., Huang, X., Zhang, Y., Zhou, W., Wang, H., & Yan, L. (2022). GNSS Data Processing and Validation of the Altimeter Zenith Wet Delay around the Wanshan Calibration Site. Remote Sensing, 14(24), 6235. https://doi.org/10.3390/rs14246235