Abstract
The delay caused by the troposphere is one of the major sources of errors limiting the accuracy of InSAR measurements. The tropospheric correction of InSAR measurements is important. The Weather Research and Forecasting (WRF) Model is a state-of-the-art mesoscale numerical weather prediction system designed for atmospheric research applications. It can be applied to InSAR tropospheric correction. Its parameters can be altered according to the requirements of the given application. WRF is usually initialized based on 3 h- or 6 h temporal resolution data in InSAR tropospheric correction studies, a lower temporal resolution compared to ERA5 data. A lower time resolution means a longer integration time for WRF to simulate from the initial time to the target time. Initialization with a higher resolution can shorten the integration time of the simulation theoretically and improve its accuracy. However, an evaluation of the effectiveness of ERA5_WRF for InSAR tropospheric correction is lacking. To evaluate the efficiency of WRF tropospheric correction, we used Reanalysis v5 (ERA5) from the European Centre for Medium-Range Weather Forecasts (ECMWF) for initialization to drive the WRF (ERA5_WRF) for efficient applications in InSAR. Three methods based on global atmospheric models—FNL_WRF (tropospheric correction method based on WRF driven by NCEP FNL), Generic Atmospheric Correction Online Service for InSAR (GACOS), and ERA5—were used to evaluate the corrective effects of ERA5_WRF. The reliability of ERA5_WRF in different scenarios with large tropospheric delay was evaluated from the spatial and temporal perspectives by considering seasonal, topographic, and climatic factors. Its applications in the local space showed that ERA5_WRF could adequately correct tropospheric delay. Benefits include its high-quality data sources and the simulation of WRF, and its application in different seasons had proven superior to other methods in terms of the corrective effects of elevation-related and spatially related delays in summer. By analyzing the data sources and downscaling methods of correction methods and weather conditions of cases, ERA5_WRF had superior performance under the condition of large content and hourly variation of tropospheric delay. Furthermore, WRF showed the potential for tropospheric correction when other higher-quality data appear in the future.
1. Introduction
Because of its advantages of high precision, high resolution, and capability of operating in all kinds of weather, space-borne Synthetic Aperture Radar Interferometry (InSAR) is one of the most commonly used techniques in geodetic surveys [1]. Research on removing atmospheric effects in InSAR applications has attracted considerable attention from researchers [2,3,4]. The propagation of SAR signals is affected by the troposphere and the ionosphere. The ionospheric effects are currently considered only in specific bands and regions [5,6]. A suitable method of correction for the troposphere can improve InSAR’s accuracy of measurement of deformations at the millimeter level [7]. It can also correctly identify atmospheric signals mistaken as deformation variables in the case of volcanic or earthquake-induced deformations to avoid the adverse effects of inaccurate judgments of volcanic or crustal movements [8]. Therefore, appropriate tropospheric correction is critical for InSAR measurements.
The accuracy of estimated tropospheric delays depends on the properties of the troposphere in the given area of interest, the spatial and temporal scale of the area, as well as the spatial/temporal resolution and accuracy of the correction dataset or model [6]. Therefore, the method of tropospheric correction should satisfy the following three requirements to ensure effective atmospheric correction: (1) The approach should be able to correct different components in the troposphere, including hydrostatic and wet delays [2,9,10,11,12]; (2) The time corresponding to the obtained tropospheric water vapor content should be as consistent as possible with the data acquisition time of the SAR [13,14]; and (3) The spatial scale of tropospheric correction should be able to accurately capture changes in the tropospheric delay in the horizontal direction [2,15].
Methods of tropospheric correction can be divided into four categories. The first is based on correlation analysis, and it cannot capture turbulence delays and lateral changes in the stratified components, and cannot achieve good results in flat areas [10,16,17,18,19,20]. The second assumes the spatiotemporal properties of multiple SAR images and removes the tropospheric atmospheric phase delay without relying on external data [5,21,22,23,24]. These methods generally ignore the correlation of the tropospheric delay in time. In addition, using only SAR data processing, it is generally difficult, or impossible, to quantitatively validate the parameters used and the residual phase screens produced [25]. The third category of methods includes new methods that combine machine learning with SAR images or other datasets. They are still being explored and are not widely available currently. The acquisition of training samples is a difficulty of this type of method. The corrective effects of these methods depend on the inputs and responses in the training model [26].
The fourth method of tropospheric correction is based on external data [6]. These data can be divided into two types according to their sources: externally measured data including the use of the Global Navigation Satellite System (GNSS), the Medium-Resolution Imaging Spectrometer (MERIS), and the Moderate-Resolution Imaging Spectro-Radiometer (MODIS) and Data based on global atmospheric numerical models, including analysis models (ERA5, NCEP, etc.) and numerical weather prediction models (MM5, WRF, etc.).
In addition to the above sources, special data are provided by the Generic Atmospheric Correction Online Service for InSAR (GACOS). This is an online data service based on the iterative tropospheric decomposition (ITD) model combined with GNSS, ECMWF, and methods of correlation analysis [27]. Because its features are user-friendly, many scholars have applied it to analyze disasters, such as earthquakes and volcanoes [28,29]. It eliminates topography-related delays as well as seasonal signals [30], improves the accuracy of InSAR measurements, and can be used for large-scale and near-real-time automatic volcanic monitoring [8].
The above methods are limited owing to the sparse distribution of GNSS data, the coarse temporal resolution of reanalysis data, and errors caused by the methods of interpolation used for correction. MERIS products can be synchronized with ENVISAT-ASAR but cannot be synchronized with data from other satellites. MODIS at the Infrared Band and MERIS are limited by weather and sunlight. Moreover, ENVISAT ceased service in 2012, and the synchronization of MODIS products, reanalysis data, and SAR satellites is relatively poor. They should be corrected by other data products when they are used for InSAR measurements. Although GACOS has performed well in some applications, it relies on assumptions about atmospheric properties and is limited by the resolution of ECMWF. When the corrective effects are not adequate, users do not have sufficient flexibility to replace the source of data or the model.
It is difficult to overcome the limitations of data acquisition or those of inflexible data and models. WRF is a state-of-the-art atmospheric modeling system designed for both meteorological research and numerical weather prediction. Using WRF, scholars can flexibly simulate meteorological parameters with different spatial and temporal resolutions according to application requirements. The initialization and microphysical schemes can be adjusted for various areas of research and different weather conditions. WRF data assimilation (WRFDA) can be used to integrate other observations during simulation. In early research, scholars explored the process of InSAR tropospheric correction based on WRF [31,32,33]. Since then, researchers improved the accuracy of tropospheric correction method based on WRF by means of data assimilation [34,35,36,37,38], WRF parameterization adjustment and evaluation [39,40], Ensemble Forecasting [41], and estimation of the effective resolution for InSAR tropospheric correction [42]. Four approaches to improving accuracy by using WRF results in Persistent Scattering Interferometry (PSI) have been summarized [43]. Applications such as the generation of DEM by InSAR [44], deformation measurements by D-InSAR [45,46,47], and the monitoring of ground deformation by TS-InSAR [7,32,48,49] have verified the reliability of the method for atmospheric correction based on WRF. Meanwhile, as an aid, the result of WRF can be used for parameter optimization of temporal filtering [50] and for understanding of mountain-wave phases [51]. However, its running time and accuracy are limited by the initial field, boundary conditions, and microphysical schemes. Accordingly, this paper focuses on the method of tropospheric correction based on WRF.
Instead of forecasting the meteorological parameters for a certain period in applications of meteorology and hydrology, InSAR atmospheric correction requires simulating the atmospheric parameters at a specific point in time. WRF is used to simulate the atmospheric parameters at the time of SAR image acquisition. During simulation, the initialization is the known atmosphere at the initial time. WRF predicts the atmospheric state by forward time integrating from the initial time to the target time and outputs meteorological parameters. Initializations with a higher resolution can shorten the run time of the simulation for the tropospheric delay of InSAR. A commonly used initialization is the NECP FNL.
Therefore, we improved the simulation efficiency of WRF in InSAR tropospheric correction from the perspective of initializations with ERA5 datasets. To determine whether this initialization can improve the operational efficiency of WRF simulations and lead to better tropospheric correction, WRF driven by ERA5 (ERA5_WRF) was used for the tropospheric correction of InSAR.
To evaluate the corrective effects of ERA5_WRF on the tropospheric components of different properties, three typical regions were chosen according to the type of climate and topography: Beijing, Taiwan, and Nyingchi. To macroscopically evaluate the corrective effects of ERA5_WRF, its corrective effects in different seasons were assessed. The RMS error and the semi-variograms of residuals after correction were used as the evaluation index for macroscopic evaluation
This manuscript is organized as follows: Section 2 describes the experimental design and the data used. Section 3 describes the methods used in this paper. Section 4 describes the results of the correction and analysis of regions with different tropospheric properties, and areas in different seasons of the year. Section 5 discusses and analyzes the experimental results, and Section 6 offers the conclusions of this paper.
2. Experiment Design and Materials
To select the representative research cases, the tropospheric delay conditions were analyzed and cases of different scenarios were selected for experiments.
According to atmospheric characteristics, tropospheric delays can be divided into systematic and stochastic components in space and time, represented in space as stratified components and turbulent components, and in time as seasonal and non-seasonal components [12]. Therefore, the corrective effects of ERA5_WRF were evaluated under the different influences of the tropospheric delay from the perspective of time and space.
In terms of time, considering the influence of monsoon circulation, the seasonal performances of the tropospheric corrective effects of ERA5_WRF were analyzed.
In terms of space, considering the influence of climatic conditions and local topography, the performance of the tropospheric corrective effects of ERA5_WRF in different locations was analyzed.
2.1. Local Space-Typical Regions with Different Tropospheric Properties
Tropospheric phase delays can be split into hydrostatic delay and wet delay. The hydrostatic delay is a function of pressure. The wet delay is dependent upon the water vapor content of the atmosphere [2]. Tropospheric wet delay is a function of temperature, pressure, specific humidity, and height [26].
Variations in interferograms in flat regions are mainly caused by the wet delay; the hydrostatic delay often appears as a smooth signal because of the large spatial scale of high- and low-pressure fields. In regions with significant topography, both the hydrostatic component and wet component will cause a correlation between the phase and topography [9]. Atmospheric circulation is a major factor in the formation of various climate types and weather variations.
Considering the above factors and the degree of variations, the study areas with different terrain and local atmospheric circulations were selected. Beijing, Taiwan, and Nyingchi were chosen as study areas. The variations in the elevations of Beijing and Taiwan are similar, ranging from 0 to 3000 m, and the elevation of Nyingchi ranges from 630 to 7300 m.
The study area in Beijing includes mountainous areas and urban areas, and the variation in meteorological elements is affected by the urban heat island circulation and the valley wind circulation. The study area in northern Taiwan includes urban areas and some mountainous areas. The variation in meteorological elements in Taiwan is affected by the coupling of sea–land breeze circulation, mountain–valley wind circulation, and urban heat island circulation. Beijing and Taiwan belong to monsoon climates with high temperatures and heavy rainfall in summer. SAR images in summer were used for this study. Beijing belongs to the temperate zone, whereas Taiwan belongs to the subtropical zone. Taiwan has a higher temperature and rainfall in summer.
Meanwhile, from the perspective of the application, the performance of ERA5_WRF under the scenarios of slow surface deformation and seismic deformation is evaluated. The study area of slow surface deformation is represented by Beijing and Taiwan, and the seismic deformation area is represented by Nyingchi. At the same time, to better compare our results with GACOS, research data and images in previous research [52] that have been proven to be effective at removing tropospheric delay by using GACOS were selected.
Beijing: Beijing is a city that suffers from regional land subsidence. Many scholars have used InSAR to monitor the subsidence in Beijing [53,54,55,56]. SAR and MERIS data from Envisat-ASAR (Table 1) were used, and the reference station was a GPS Continuously Operating Reference Station (CORS) (ZHAI). The study area was located in the northwest of Beijing and included the central city, suburbs, and mountains over an area covering 63 km (north–south) × 46 km (east–west) (Figure 1b).

Table 1.
Information in SAR images for Beijing Taiwan and Nyingchi.
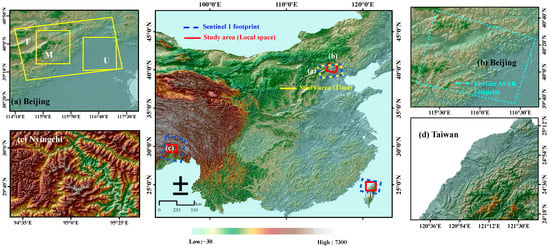
Figure 1.
Study area and SAR images used in the experiment of local space and time. The coverage of SAR data is shown by the dotted polygon. The study area is shown by the solid polygon. (a) Topographic map of Beijing for time experiment; F represents the coverage of the interferogram, M represents the mountainous area with complex terrain, and U is the urban area with flat terrain. (b) Topographic map of Beijing for local space experiment. (c) Topographic map of Nyingchi for local space experiment. (d) Topographic map of Taiwan for local space experiment.
Taiwan: Taiwan was chosen to explore the performance of the proposed method under more complicated tropospheric conditions. Sentinel-1 data were used in this case (Table 1). The study area was located in the northwest of Taiwan and included several cities, suburbs, and mountains (Figure 1d).
Nyingchi: Yu et al. used Sentinel-1 data (Table 1) to identify a strong atmospheric effect, and extracted the co-seismic surface displacement after removing the atmospheric effect by using GACOS [56]. At 22:34 (UTC) on 17 November 2017, an Mw 6.5 earthquake (epicenter at 29.75°N, 95.02°E) struck Mainling County in Nyingchi (referred to herein as the Nyingchi earthquake) with a focal depth of 10 km [57] (Figure 1c).
The Nyingchi earthquake occurred on the northern edge of the Namcha Barwa (altitude, 7784 m), the core of the eastern Himalayan tectonic junction, and the front edge of the collision and convergence of the Indian and Eurasian plates. The same study area and data were used as in the previous study [52].
2.2. Time-Seasonality Effects
Considering the seasonality of the atmosphere, the study area of Beijing was chosen in this case. It belongs to the monsoon climate of medium latitudes with characteristic seasonal changes.
Sentinel-1 images were acquired in the period from 1 January 2019–1 January 2020 (Table 2). The images covered Beijing and part of the Taihang and Yanshan Mountains (Figure 1a), and the acquisition time was 10:13 (UTC Time). Interferograms were obtained from two temporally adjacent images. The corresponding tropospheric phase delays based on FNL_WRF, ERA5_WRF, ERA5, and GACOS for the corresponding interferograms were calculated. To further analyze the corrective effects of ERA5_WRF in different seasons and different terrains, the corrective effects of the mountainous area in the northwest of Beijing (referred to as the mountain area hereinafter, Figure 1a M) and the flat urban area including the main part of Beijing (referred to as urban area, Figure 1a U) of the full interferograms (Figure 1a F) were evaluated.

Table 2.
Information in SAR images in different seasons in Beijing.
2.3. Correction Evaluation
- (1)
- Local space
The results of the interferogram correction of ERA5_WRF, FNL_WRF, ERA5, and GACOS were compared. ERA5_WRF was also compared with MERIS data where they were available.
Empirically, we believe that the theoretical deformation at short time intervals is very small in the absence of major crustal movements. For the interferograms involved in this paper, except for Nyingchi, the time intervals between master and slave images were less than three months, and most of them were less than one month. If the surface deformation was very small and other errors were ignored, the theoretical value of the phase residuals after removing the tropospheric delay error would be close to 0 rad. Meanwhile, the residual error was close to a normal distribution, and the coefficient of the phase–elevation relationship was close to zero.
To assess the overall corrective effects, the root mean square (RMS) and the standard deviation (STD) error were used in this paper. The RMS error of the corrected interferogram estimated over a sample window containing n pixels is given by [6]:
If the mean value of the sample is removed, the RMS is simply the STD of the sample. Apart from RMS/STD, the corrective effects were evaluated by analyzing the spatial distribution of the interferograms and histograms of the corrective residuals. The correlation coefficient of the phase elevation was also used to assess the correction of the topography-related delays. The semi-variogram function was used to explicitly separate the impact of the correction on different length scales. is the semi-variogram for distance , and it is calculated by [58]:
where is the separation distance in the specified direction between points () and (), is the number of pairs of samples with distance from each other, is the phase or residual phase at point (), and is the value at the point in the interferograms.
- (2)
- Time
The STD errors, semi-variogram, and phase–elevation correlation coefficients of were used in these cases. In addition, the number of interferograms with the reduction in STD error was analyzed to represent the probabilities of effective correction. The averages of the percentages of reduction/increase in the STD error () by different methods were analyzed to represent the overall degrees of effectiveness/deterioration of correction.
where is the number of interferograms, is the reduction in the STD error of the ith interferogram, and is the increase in the STD error of the ith interferogram.
3. Methods
3.1. Calculation Principle of Tropospheric Phase Delay
The phase of InSAR consists of four components [24]:
where is the topographic phase that can be removed by subtracting a simulated topographic phase from a digital elevation model (DEM), is the deformation phase along the line of sight (LOS) direction, is the phase resulting from the tropospheric delay, and is the phase error caused by thermal noise.
The LOS tropospheric delay is integral to the refractivity of air between the ground and the satellite. By using the incident angle of the radar (), the relationship between the zenith delay and the slant delay can be written as:
represent the total zenith delay, hydrostatic zenith delay, and wet zenith delay, respectively. is the refractivity at height :
can be calculated by the following formula [51]:
where KhPa−1 Jkg−1K−1 is the specific gas constant for dry air, and is the local gravity at the center of the atmospheric column ( ms−2). is the surface pressure and and and are the surface pressures of two SAR acquisitions, respectively [51].
For data for the numerical weather model [26], can be calculated by the temperature (), partial pressure of water vapor (hPa), and the specific difference in height at level :
where KhPa−1 and K2hPa−1.
Usually, cannot be obtained directly from the datasets and needs to be calculated by the following formula:
= 0.622 is the ratio of the gas constant of dry air and pure water vapor, and is the water vapor mixing ratio that is obtained from the datasets. If the specific humidity were obtained, can be calculated as:
For IWV data provided by MERIS, can be calculated from the conversion factor Π and the IWV:
is the density of water. The empirical conversion factor Π is typically ~6.2 [6].
Through the above calculation, the slant delay and thus the slant delay of the troposphere can be obtained:
where is the wavelength of the radar.
In this paper, the resolution of the interferograms is about 100 m. The resolution of using MERIS data is 300 m. For other datasets, was calculated at a resolution of 1 km. Therefore, spline interpolation was used to interpolate all the to the interferogram resolution.
3.2. WRF Model
3.2.1. WRF Configuration
NCEP FNL is a reanalysis dataset with a time resolution of 6 h. ERA5 datasets comprises the fifth-generation reanalysis data released by the ECMWF after the ERA-Interim. Compared with the ERA-Interim, ERA5 datasets assimilates more observational data. The spatial resolution of ERA5 datasets has been increased to 0.25° and the temporal resolution to 1 h. Researchers in meteorology and hydrology have conducted related experiments to compare the differences between the results of simulations of WRF driven by FNL (FNL_WRF) and ERA5 datasets (ERA5_WRF). Both types of data can adequately simulate changes in the meteorological elements [59,60]. To determine whether the new initialization can improve the operating efficiency of WRF simulations and better perform tropospheric correction, WRF was driven by FNL and ERA5 datasets to simulate tropospheric delays for InSAR tropospheric correction and assess its accuracy.
Both sets of experiments used the same parameterization scheme (Table 3). A two-way nested-grid technique was used with the configuration of a 9/3/1 km domain for ERA5_WRF and a 27/9/3/1 km domain for FNL_WRF. The domain in each case was centered on the latitude and longitude of the center of the study area. ERA5_WRF and FNL_WRF used the same boundary of the 9/3/1 km domain. For the 9/3/1 km domain, the inner domain precisely contained the study area, and the boundary distance between the second domain and the inner domain was about 2°. The distance between the outer domain and the boundary of the second domain was about 1°. In total, 40 vertical levels were used in each simulation, with the model top set to 50 hPa.

Table 3.
The parameterization scheme of WRF.
3.2.2. WRF Simulation
WRF simulated the meteorological data in two parts: WRF preprocessing and WRF simulation [68]:
- (1)
- WRF preprocessing
In WRF preprocessing, the static geographical data and initialization data were processed, and the input files for WRF simulation were prepared.
The processing of the initialization data was mainly as follows: First, the simulated spatial grid resolution (1 km in this paper) was defined during the parameter setting. The system read the initialization data and extracted the corresponding meteorological parameters. Then, the system interpolated the extracted meteorological data into the defined simulated grid (1 km) and generated the input file for WRF simulation.
According to the above description, the initialization data with different resolutions (ERA5 and FNL datasets) were interpolated into the model grid (1 km) before entering the simulation. Therefore, the spatial resolution of the two datasets did not affect the efficiency of the simulation.
- (2)
- WRF simulation
The essence of WRF simulation is to solve differential equations. WRF used Runge-Kutta time integration to integrate forward through initial values. That is, WRF simulated the meteorological parameters from the initial time to the corresponding SAR image acquisition time.
The time resolution of FNL is 6 h (00:00, 06:00, 12:00, and 18:00 each day), whereas the time resolution of ERA5 datasets is 1 h (hourly). For FNL_WRF, simulations could only start at 00:00, 06:00, 12:00, and 18:00, whereas ERA5_WRF simulations could start at any hour of the day (usually the time closest to the target time). Therefore, for any target time (X: 00-X: 59), the length of the simulation time of the FNL_WRF method was up to six times that of ERA5_WRF. When other simulation parameters are the same, we believe that a higher initial time resolution means a higher simulation efficiency.
The results of the simulation were output every 5 min. The results closest to the time of acquisition of the SAR images were selected to calculate the tropospheric phase.
During the WRF simulation of Nyingchi, due to the limitation of computing resources, for steep terrain or very strong convection cases, the solving process of differential equation in WRF is difficult to converge and causes the computation to sharply increase. A suitable domain size or a larger boundary band may solve the problem, but it was difficult for us to find the suitable one. For the sake of simplicity, the time step was reduced and the “epssm” value was increased (https://forum.mmm.ucar.edu/threads/what-is-the-most-common-reason-for-a-segmentation-fault.133/ (accessed on 1 June 2022)). The study area was divided into nine blocks of the same size and each of the nine areas was simulated with the same parameters. The nested domain was the same except for the innermost domain. After the simulation, the tropospheric delay of the nine regions was calculated, respectively, and the tropospheric phase delay of the whole study area was obtained by weighted average fusion.
3.3. Methods for Comparison
To demonstrate the effectiveness of the tropospheric correction method based on ERA5_WRF, the comparison between ERA5_WRF and other methods based on GACOS, ERA5, and FNL_WRF was conducted (Table 4).

Table 4.
The characteristics of different methods.
FNL_WRF and ERA5_WRF downscaled FNL and ERA5 datasets by means of WRF simulation. The two closest FNL and ERA5 datasets samples were used to drive WRF.
For ERA5, the data closest to SAR acquisition time were used for each case. Then, the meteorological parameters were interpolated before the calculation of . Vertically, the delay was interpolated every meter via the cubic spline method. Horizontally, the delay was interpolated to the resolution of 1 km by bilinear interpolation at the corresponding height.
GACOS provided the with a resolution of 1 km using HRES-ECMWF (High-Resolution ECMWF). It applied linear temporal interpolation using the two closest ECMWF ZTD samples. GACOS used an Iterative Tropospheric Decomposition (ITD) model to calculate the best model for the elevation-dependent tropospheric delay. The difference between the best elevation-dependent model and the tropospheric delay from HRES-ECMWF was interpolated by IDW to obtain the turbulence delay [27].
3.4. InSAR Processing
Interferograms were generated by using InSAR Scientific Computing Environment (ISCE) software, developed at the NASA Jet Propulsion Laboratory. The DEM of one arc-second (~30 m) from the Shuttle Radar Topography Mission (SRTM) was used to remove the topographic phase and calculate the correlation coefficient between the phase and the elevation. The SNAPHU method was used in the unwrapping step. PyAPS were used to generate ERA5-based tropospheric phase delays.
For processing, the GNSS point with the lowest deformation as the reference point in areas for which GNSS data were available was used, and the RMS error as the evaluation indicator was Used. The point with the highest coherence was used as the reference point in areas for which GNSS data were unavailable, and the STD error was used as the evaluation indicator. Severe geological activities occurred in Nyingchi. The areas with severe deformation were masked and the results of residuals for the other areas were evaluated before and after correction.
4. Results
4.1. Local Space-Typical Regions with Different Tropospheric Conditions
4.1.1. Beijing
The interferograms were corrected based on five datasets. MERIS data delivered the best performance in terms of the pattern of the overall interferogram. Of the remaining methods based on data from numerical weather models, methods based on ERA5_WRF and ERA5 performed better than the others in mountainous areas, whereas the interferogram corrected by GACOS was the best for urban areas.
- (1)
- RMS errors
The RMS errors after correction by ERA5-WRF, GACOS, ERA5, and MERIS decreased compared with those of the original interferogram by 26%, 2%, 26%, and 62%, respectively. However, the RMS error corrected by FNL_WRF was increased by 8%. The correction by using MERIS was the best, followed by ERA5-WRF and ERA5, GACOS, and FNL-WRF (Figure 2b, first row).
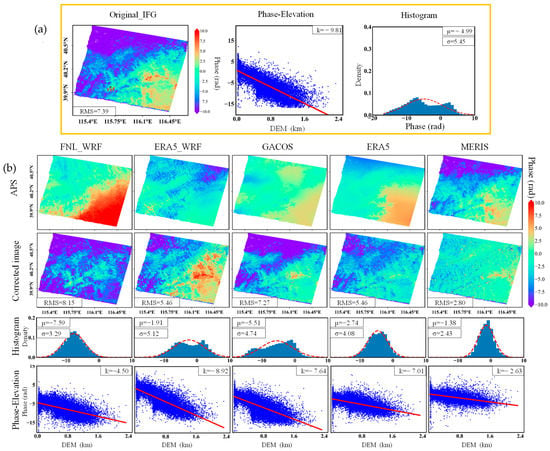
Figure 2.
Beijing: (a) Interferogram (left), phase–elevation relationship (middle), and histogram (right) for date pair 5 July 2010–13 September 2010. (b) Tropospheric delays modeled by different external datasets (first row), corrected interferograms for different types of correction (second row), histograms (third row), and phase–elevation relationship (fourth row) for each corrected interferogram.
- (2)
- Histogram
According to the original interferogram and the corresponding histogram distribution (Figure 2b, third row), compared with the original interferogram, the mean and variance of the corrected residuals of ERA5_WRF, ERA5, and MERIS were reduced, showing the effectiveness of the correction of ERA5_WRF, ERA5, and MERIS.
The histogram of residuals after correction by MERIS was the closest to the standard normal distribution, which means it is the best correction method (Figure 2b, third row).
- (3)
- The phase–elevation correlation coefficient
The phase–elevation relationship shows that MERIS significantly corrected the elevation-dependent tropospheric phase delay. Owing to its DEM-dependent method of interpolation and higher-quality sources of data, ERA5 exhibited better corrections for elevation-dependent tropospheric phase delays. FNL_WRF overestimated the troposphere in urban areas. ERA5_WRF underestimated it and was less effective than the other methods in correcting the tropospheric phase delay related to elevation. FNL_WRF overestimated the tropospheric phase delay in urban areas and failed to correct it in mountainous areas, which resulted in a high correlation coefficient. ERA5_WRF underestimated the tropospheric phase delay in urban areas, and its correlation coefficient was also high. GACOS corrected the tropospheric phase delay in urban areas well but failed to fully correct it in mountainous areas. Its correlation coefficient was better than those of FNL_WRF and ERA5_WRF, but worse than those of ERA5 and MERIS (Figure 2b, fourth row).
- (4)
- Semi-variogram
The results of semi-variograms (Figure 3) showed that ERA5 and GACOS yielded significant improvements, starting at values greater than approximately 30 km. On the contrary, the results of ERA5_WRF and FNL_WRF deteriorated, starting at values greater than approximately 30 km. The corrected residuals of ERA5_WRF and FNL_WRF were similar in the curve characteristics of semi-variograms.
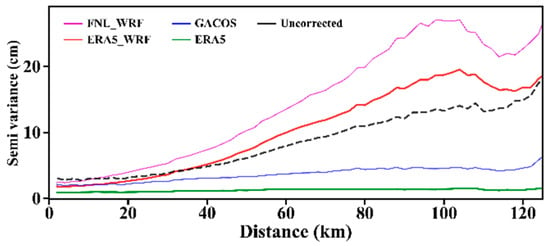
Figure 3.
Beijing: Semi-variograms of the residuals after correction by FNL_WRF, ERA5_WRF, GACOS, and ERA5.
- (5)
- Summary
The correction for data on Beijing showed that ERA5_WRF adequately corrected the tropospheric delay in mountainous areas, but its performance in urban areas was not satisfactory. ERA5 performed better than ERA5_WRF in urban areas. GACOS corrected the urban areas well, whereas the corrective effects in mountainous areas were poor. FNL_WRF showed the worst corrective effects.
4.1.2. Taiwan
- (1)
- RMS errors
The RMS errors after correction by the four methods decreased compared with those of the original interferogram by 33%, 49%, 62%, and 49% for FNL-WRF, ERA5-WRF, GACOS, and ERA5, respectively. The correction by GACOS was the best, followed by ERA5_WRF and ERA5, and corrections by FNL_WRF were the worst (Figure 4b, first row).
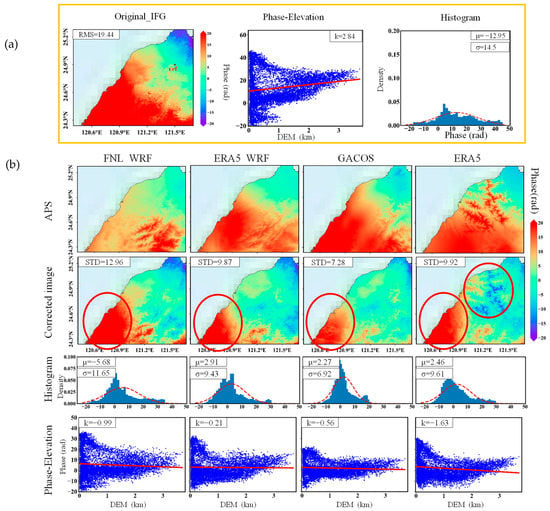
Figure 4.
Taiwan: (a) Interferogram (left), phase–elevation relationship (middle), and histogram (right) for the date pair 18 July 2019–30 July 2019. (b) Modeled tropospheric delays by using different external datasets (first row), corrected interferograms for different correction types (second row), histograms (third row), and phase–elevation relationships (fourth row) for each corrected interferogram.
- (2)
- Residuals distribution and histogram
The interferograms after correction showed that all four methods corrected the severe tropospheric delay in the southwest of the study area, but there were still residual errors. The mean and variance of the corrected residuals of the four methods were reduced compared with the original interferogram. Although the RMS of ERA5 and ERA5_WRF were similar, their residuals showed different textures after correction. ERA5 introduced errors related to elevation.
The histogram of residuals after correction by GACOS was the closest to the standard normal distribution, which means the best correction is provided. (Figure 4b, second row).
- (3)
- The phase–elevation correlation coefficient
The phase–elevation relationship showed that all four methods adequately corrected the tropospheric phase delay related to elevation (Figure 4b, fourth row). ERA5_WRF showed the best performance.
- (4)
- Semi-variograms
The results of semi-variograms (Figure 5) showed that all four methods led to significant improvements. ERA5_WRF had the same curve trend and similar values to ERA5, and FNL_WRF was almost the same as GACOS. The values of ERA5_WRF and ERA5 were higher than those of FNL_WRF and GACOS, which means a smaller error in the difference in spatial structure is provided.
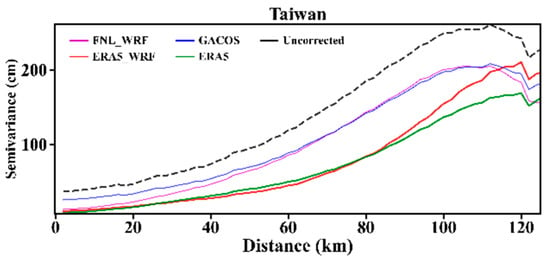
Figure 5.
Taiwan: Semi-variograms of the residuals after correction by FNL_WRF, ERA5_WRF, GACOS, and ERA5.
- (5)
- Summary
For the correction in Taiwan, the large residuals of the four methods in the same region (northwest of the study area) imply the limitations of the data sources. ERA5_WRF was superior to the correction of tropospheric delay related to elevation. The spatial structure function was almost identical to ERA5 and lower than GACOS. However, a higher RMS than GACOS indicated that ERA5_WRF and ERA5 had a poor correction for random errors.
4.1.3. Nyingchi
ERA5_WRF, FNL_WRF, GACOS, and ERA5 were used to correct the interferograms of 6 November 2017–18 November 2017. Figure 6 shows that corrections by FNL_WRF, ERA5_WRF, GACOS, and ERA5 reduced the STD error compared with the original interferogram by 40%, 34%, 18%, and 44%, respectively.
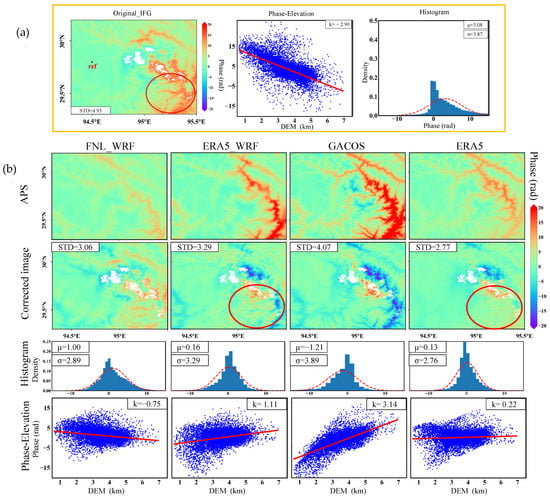
Figure 6.
Nyingchi: (a) Interferogram (left in the yellow box), phase–elevation relationship (middle in the yellow box), and histogram (right in the yellow box) for date pair 6 November 2017–18 November 2017. (b) Modeled tropospheric delays by using different external datasets (first row), corrected interferograms for different types of correction (second row), histograms (third row), and phase–elevation relationships (fourth row) for each corrected interferogram.
The histogram of the original interferogram was similar to a steep wall in shape and became closer in shape to a standard histogram after correction by each of the three methods.
After correction by ERA5_WRF and ERA5, the topographic texture of the area inside the red circle in the interferogram had been adequately corrected, indicating that the component of tropospheric phase delay related to elevation could be corrected. Although both ERA5_WRF and GACOS reduced the STD error of the original interferogram, their simulated tropospheric phase delays overestimated the water vapor in valleys. After correction by GACOS, the original red texture in the red circle turned blue, and the correlation coefficient between phase and elevation changed from negative to positive.
According to the results of the semi-variograms (Figure 7), FNL_WRF, ERA5_WRF, ERA5, and GACOS all yielded significant improvements, starting at values greater than approximately 40 km.
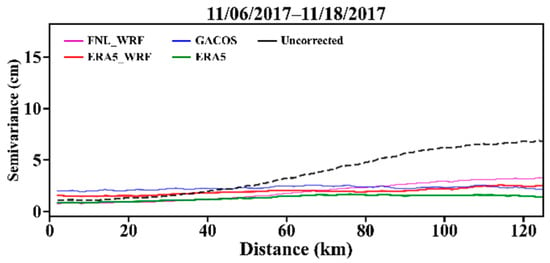
Figure 7.
Nyingchi: Semi-variograms of the residuals after correction by FNL_WRF, ERA5_WRF, GACOS, and ERA5.
The correction in Nyingchi showed that it can correct tropospheric delay in areas with a complex topography effectively. However, ERA5 shows the best correction. Although ERA5_WRF used the same data source as ERA5, ERA5 and showed better results.
This means that compared with the interpolation method of ERA5, the simulation method of ERA5_WRF in Nyingchi was not enough to accurately capture the changes in meteorological parameters.
Meanwhile, the domain of the WRF model in Nyingchi covered complex terrain with a large topographic gradient. The highest resolution in the simulation was 1 km, which increased the instability of WRF calculations and caused the program to easily crash. In this case, it was not sufficient to modify the related parameters such as the “epssm” value or the time step. It needed to be simulated in blocks, and this reduced the efficiency of correction and increased its complexity.
4.2. Time-Seasonality Effects
- (1)
- STD errors
The methods of tropospheric correction based on FNL_WRF, ERA5_WRF, ERA5, and GACOS were used to correct the interferograms of adjacent images for Beijing from 1 January 2019 to 1 January 2020. Figure 8 shows the original STD errors of Full (F) interferograms overall the for mountainous areas, and those for urban (U) areas as well as the corrected STD error for different methods of tropospheric correction.
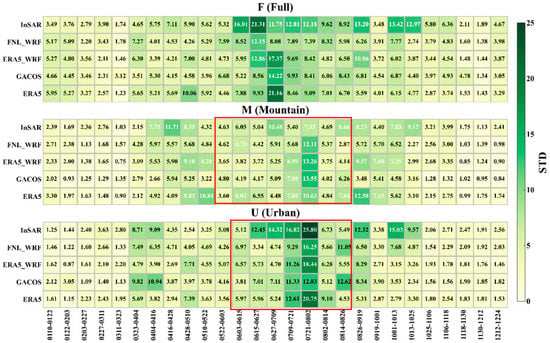
Figure 8.
Original STD errors in the interferograms of adjacent images obtained from Sentinel-1 for the period from 1 January 2019–1 January 2020, and STD errors of interferograms corrected by different methods in areas F (first row), M (second row), and U (third row).
Figure 8 shows that before and after correction by different methods, the STD errors in interferograms in the summer were significantly larger than those in the winter, and peaked around July. The STD errors of interferograms in mountainous (M) areas were significantly lower than those in urban (U) areas.
To highlight the corrective effects of different methods, Figure S1 shows the effects on the full interferogram (Study area F shown in Figure 1a), those for mountainous areas (Study area M shown in Figure 1a), and those for urban areas (Study area U shown in Figure 1a), owing to different methods (compared with the original interferogram, with the percentage of reduction or increase in the STD error). Table 5 shows the average of corrective effects (STD_Ravg and STD_Iavg) of different methods.

Table 5.
The average of STD error reduction after correction by different methods in different regions of Beijing in 2019 (%). The green color represents a reduction in STD error, dark green represents the greatest reduction, light orange represents an increase in STD error, and dark orange represents the greatest increase.
For the Full (F) interferograms, the corrective effects of the four methods exhibited little difference. Only six of the interferograms recorded an increase in the STD error after correction by FNL_WRF whereas eight recorded an increase after correction by ERA5 and GACOS. The sum of percentages of reductions in the STD error showed that the overall reductions by using the four methods were not significantly different. ERA5_WRF yielded the greatest reduction among the four methods, with the number of interferograms after reduction being smaller than those produced by using FNL_WRF. In terms of the percentage of increases in the STD error in the corrected results, the sum of the increase from using FNL_WRF was the smallest, and that by using ERA5 was slightly larger. The sums of the increase using ERA5 and GACOS were much larger.
For mountainous (M) areas, in interferograms for June–August, ERA5_WRF (values in the red box of mountain areas in Figure 8) had a smaller STD than the other three methods, showing a correction advantage when the tropospheric delay is large. Errors in nine interferograms increased after correction by FNL_WRF and ERA5_WRF.
In interferograms excluding from June–August, GACOS performed the best, followed by ERA5. The STD errors for only six interferograms increased after correction by GACOS, whereas twelve increased for ERA5. FNL_WRF performed the worst.
The sum of the corrected percentages of reduction in the STD error showed a significant difference among the four methods. GACOS recorded the greatest reduction, followed by ERA5_WRF, and ERA5 showed the worst corrective effects. The sum of the percentages of errors by using GACOS recorded the smallest increase, followed by FNL_WRF. The sums of the increase in errors from using ERA5 and ERA5_WRF were much larger, especially the former.
In urban (U) areas, in the interferograms for May–August (values in the red box of urban areas in Figure 8), FNL_WRF performed the best, and ERA5_WRF was slightly better than ERA5 and GACOS. However, in the remaining interferograms, the corrective effects of ERA5_WRF, ERA5, and GACOS were not significantly different, and FNL_WRF was worse than ERA5_WRF.
The STD errors of five interferograms increased after correction by ERA5_WRF and ERA5, and those of eight interferograms increased after correction by GACOS (Figure S1). The sum of the percentages of reduction in the STD error after interferogram correction showed that ERA5_WRF recorded the greatest reduction among the four methods, followed by GACOS, and FNL_WRF showed the worst correction. GACOS had the largest increases in the sum of the percentages of STD error and FNL_WRF had the smallest (Table 5).
- (2)
- The absolute value of the phase–elevation correlation coefficient
Figure 9 shows the original phase–elevation correlation coefficient of full (F) interferograms, those for mountainous (M) areas, and those for urban (U) areas, as well as the corrected phase–elevation correlation coefficient for different methods of tropospheric correction.
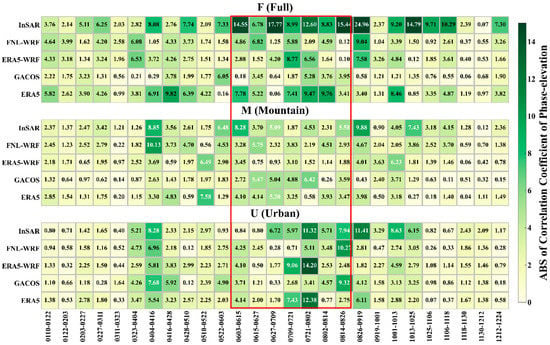
Figure 9.
The original absolute value of the correlation coefficient of phase–elevation in the interferograms of adjacent images obtained from Sentinel-1 for the period from 1 January 2019–1 January 2020, and the absolute value of correlation coefficient of phase–elevation of interferograms corrected by different methods in areas F (first row), M (second row), and U (third row).
Figure 9 shows that the absolute value of the correlation coefficient before and after correction by different methods is similar to the STD error. The corrected phase–elevation correlation coefficients in interferograms in the summer were significantly larger than those in the winter, and they peaked around July. The correlation coefficients of interferograms in mountainous (M) areas were significantly lower than those in urban (U) areas. ERA5_WRF showed the lowest correlation between the residual phases and elevation (values in the red box of mountain areas in Figure 9) in the full interferogram and mountainous (M) areas. However, in urban areas, FNL_WRF showed the best correction.
- (3)
- Semi-variograms
Functions of the spatial structure (semi-variogram) of the mountain (M) areas and urban (U) areas were calculated (Figures S2 and S3). The seasonality is clear in Figures S2 and S3. For a clearer analysis, 27 pairs of interferograms were divided into four sets corresponding to the four seasons.
Winter is the longest season in Beijing, followed by summer, whereas spring and autumn are shorter. Therefore, in our grouping, spring spanned from late March to late May, summer from late May to late August, autumn from late August to late October, and winter from late October to late March of the following year. Due to the short time in spring and autumn, only a few interferograms were included, and individual errors would lead to large changes in the normalized mean semi-variogram. The normalized mean semi-variograms of summer and winter were calculated separately (Figure 10).
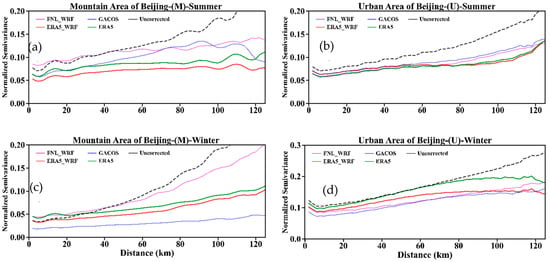
Figure 10.
Semi-variograms of residuals corrected by different methods of correction in: (a) summer of areas M; (b) summer of areas U; (c) winter of areas M; (d) winter of areas U.
The results (Figure 10) show that the four methods had good corrective effects in summer and winter at distances greater than 40 km.
ERA5_WRF and ERA5 had prominent corrective effects at distances greater than 20 km (Figure 10a–c) except for urban (U) areas in winter. The curve trends of ERA5 and ERA5_WRF were almost the same. However, the normalized mean semi-variogram value of ERA5 was higher than that of ERA5_WRF (reflecting the nugget of the semi-variogram), which means the error is larger than ERA5_WRF. ERA5_WRF had prominent corrective effects in urban (U) areas in winter at distances greater than 40 km, and at 70 km for ERA5.
Both GACOS and FNL_WRF have a data source time resolution of 6 h, and they showed a similar curve trend and values, except in Figure 10c. At distances greater than 20 km, GACOS had prominent corrective effects (Figure 10b–d), except for in mountainous (M) areas in summer. It had the best corrective effects for mountainous (M) areas in winter (Figure 10c).
GACOS and FNL_WRF had corrective effects at distances greater than 80 km in summer in mountainous (M) areas.
- (4)
- Summary
The residuals after correction of the four methods showed obvious seasonality. To analyze the reasons for this, and to consider the characterization of the monthly variations of tropospheric delay and data processing, MERRA2 (the Modern-Era Retrospective analysis for Research and Applications, Version 2) was used to calculate the tropospheric phase delay corresponding to the central location of Beijing (40.16°N, 115.94°E) in the C-band (Figure 11). The tropospheric phase delay peaked in July.
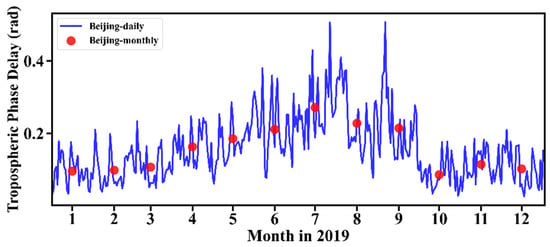
Figure 11.
Daily and monthly tropospheric delay in Beijing in 2019.
Therefore, the interferograms around July were greatly affected by the tropospheric delay, and the STD error was relatively large. The tropospheric delay can be corrected to some extent by using different correction methods. However, because of the large base, the residual error after correction is still large compared with other months. The same is true for the peak of the phase elevation relationship in July.
In conclusion, for the case of Beijing in different seasons, ERA5_WRF had the best corrective effects in mountain areas with a large effect of tropospheric delay, both for stratified delay (related to elevation) and spatially correlated delay.
5. Discussion and Analysis
ERA5_WRF was used for tropospheric correction and applied to different scenarios; local space-typical regions with different tropospheric conditions and time-seasonality effects were examined.
The performance of ERA5_WRF in the above cases showed that it can adequately correct the tropospheric phase delay. However, performance in a particular area is related to the quality of the data sources, the simulation process, and the tropospheric conditions of the case, and it did not always show the best results.
The correction results of ERA5_WRF in cases of the different seasons showed that, for the cases of severe tropospheric delay, ERA5_WRF can effectively correct the stratified delay and spatially correlated delay.
5.1. Local Space-Typical Regions with Different Tropospheric Conditions
- (1)
- Beijing
To explore the specific reasons for the performance of different methods, the synoptic conditions of the case were analyzed (Figure 12). The study area showed obvious urban heat island effects. On the evening of 5 July 2010, the wind was blowing from the suburbs to the city, and the atmospheric horizontal movement was dominated by synoptic winds of medium strength. On 13 September 2010, the urban heat island circulation and mountain–valley wind circulation had a great influence on the wind in the mountain areas. On both dates, the horizontal wind speeds in the mountain area were relatively high, and the water vapor content was high, which led to the rapid change in water vapor content. The temporal resolution of data sources used for FNL_WRF and GACOS were 6 h, which cannot capture its changes in time. Therefore, FNL_WRF and GACOS were less effective in mountainous areas. ERA5 and ERA5_WRF showed good results in mountainous areas.
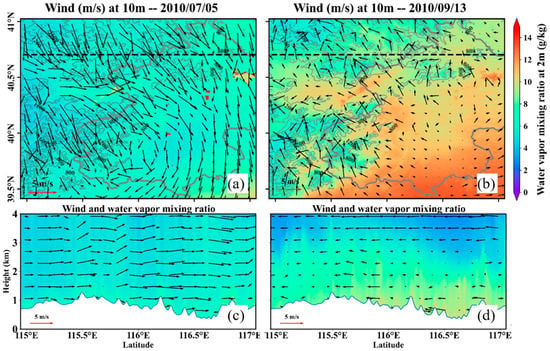
Figure 12.
Beijing: (a,b) Wind at 10 m and water vapor ratio at 2 m at 2:30 on the dates of 5 July 2010 and 13 September 2010. The gray thin solid line is the contour line, and the unit of the contour line elevation label is m. The gray thick solid line is the administrative boundary of Beijing. (c,d) Wind and water vapor ratio in black dotted profile at 2:30 on dates of 5 July 2010 and 13 September 2010.
Compared to ERA5, in urban areas of Beijing, the insufficient correction of ERA5_WRF may be due to the influence of land surface model as Beijing is a typical metropolis. For WRF, simply using a land surface model for simulation cannot accurately capture the changes in surface energy. The use of the single-layer urban canopy model (UCM), multi-layer urban canopy model (BEP), and urban building energy model (BEM), which are applied explicitly to cities, may improve the simulation of atmospheric parameters for urban areas. In addition, the setting of the cumulus parameterization may also have some influence on the results.
- (2)
- Taiwan
By analyzing the synoptic conditions of Taiwan (Figure 13), the sea–land breeze circulation and mountain–valley wind circulation were obvious in this case. The horizontal wind speed was low, and the water vapor content slowly. Therefore, the time resolution of the data sources had less influence on the correction results.
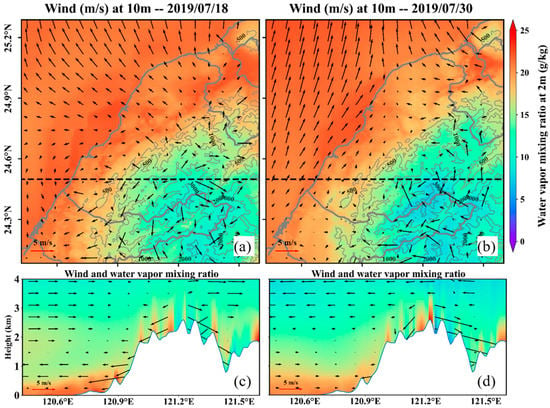
Figure 13.
Taiwan: (a,b) Wind at 10 m and water vapor ratio at 2 m at 22:00 on the dates of 18 July 2019 and 30 July 2019. The gray thin solid line is the contour line, and the unit of the contour line elevation label is m. The gray thick solid line is the administrative boundary of Taiwan. (c,d) Wind and water vapor ratio in black dotted profile at 22:00 on dates of 18 July 2019 and 30 July 2019.
The circulation structure in the mountainous area was relatively complex, and the distribution of water vapor had a significant correlation with the elevation. GACOS performed well, benefiting from the high spatial resolution of the data sources and the elevation dependence of the space downscaling method.
Although ERA5_WRF performed better than GACOS in the removal of the phase-related delay and spatial-correlated delay, GACOS provided the best benefits in the method of turbulence delay removal.
Since ERA5_WRF and ERA5 used the same dataset, they had similar performance in spatial structure. Downscaling by WRF provides better performance for ERA5_WRF.
5.2. Time-Seasonality Effects
The ERA5 datasets were used to calculate the mean diurnal variation of tropospheric phase delay in July and December for urban (U) and mountainous (M) areas in the case of seasonality effects (Figure 14).
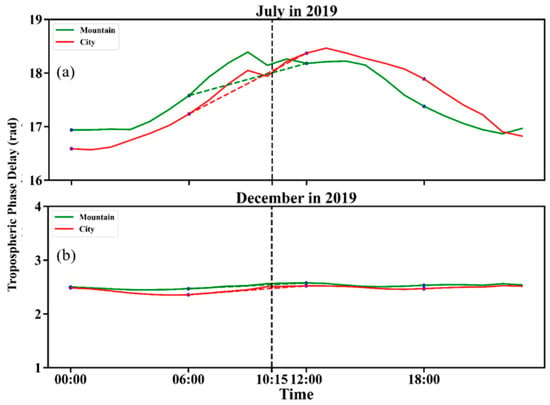
Figure 14.
Beijing: (a,b) Mean diurnal variation of tropospheric phase delay in July and December for urban (red line) and mountainous (green line) areas. The dotted line represents the time linear interpolation method of GACOS, and the intersection of the black dotted line with the red and green dotted lines is the time interpolation results of GACOS.
In summer, the variation of tropospheric delay is larger in the 6 h interval. The acquisition time difference between the data sources of the correction method and the SAR image data dominated the corrective effects. Meanwhile, the time downscaling methods had influences on their corrective effects. FNL_WRF and GACOS used FNL and HRES-ECMWF, respectively, at 6:00 and 12:00, as data sources. Therefore, the correlation between the corrected residuals and the elevation, as well as the residual semi-variogram showed similar characteristics. Additionally, neither of them can accurately capture the tropospheric delay at the acquisition time of the SAR image.
The data sources of ERA5_WRF and ERA5 were the same, but the spatial structure of the corrected residuals was quite different. The downscaling method of ERA5 was highly dependent on elevation. Therefore, ERA5 cannot capture the elevation-independent shortwave signal, which is smaller than the resolution scale of the data sources. Its corrective effects were poor where the atmospheric motion was complex and the water vapor content was high.
In winter, the tropospheric delay had a small variation in the 6h interval. The spatial resolution of the data sources and the spatial downscaling method determined the corrective effects. GACOS had better corrective effects in mountainous areas because of the data sources and the spatial downscaling method.
5.3. Effect of Duration of Simulation on Correction by ERA5_WRF
Most of the current data on atmospheric observations are for 00:00, 06:00, 12:00, and 18:00. If the WRF simulation started at these times, more observational data were used in the simulation. FNL_WRF started simulations at these times. To shorten the run time of the simulation, the probability that the ERA5_WRF simulation starts at exactly these time points is low, and fewer observations may lead to lower accuracy. To explore the impact of the run time, the Beijing area in Figure 1b was used as the study area, using ERA5 datasets as the initial field, and applying the same microphysical schemes to start the simulation at 00:00 and 02:00. The results were used for interferogram correction (Figure 15). The results showed that correction by using the WRF simulation starting at 00:00 was worse than that at 2:00. To simulate the tropospheric parameters at the time of acquisition of the SAR images, a longer simulation time may lead to the accumulation of errors such that better simulation results cannot be obtained.
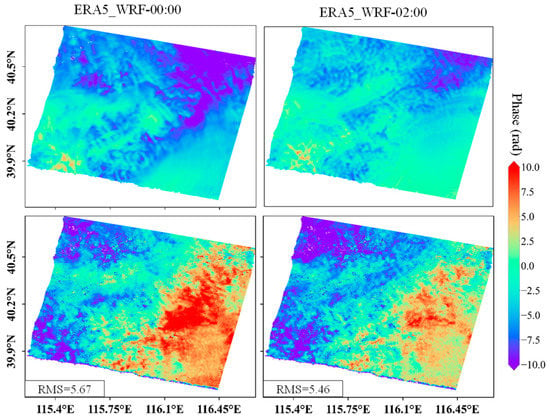
Figure 15.
Modeled tropospheric delays by using ERA5_WRF with start times of 00:00 and 02:00 (first row), and the corrected interferograms (second row).
6. Conclusions
In this study, the ERA5 datasets with a higher time and space resolution were used for initialization to drive WRF for tropospheric correction to improve the efficiency of the simulation. This reduced the run time of WRF simulation to up to one-sixth of that of FNL_WRF. To further assess the corrective effects, the performances of ERA5_WRF were evaluated by comparing them with FNL_WRF, ERA5, and GACOS in different scenarios.
Those approaches were applied in cases with different tropospheric conditions. We come to the following conclusions for ERA5_WRF:
- Regarding the benefits of the 1 h resolution of data sources, ERA5_WRF performed better in the case of large hourly variation.
- Effective simulation of WRF contributed to better performance of ERA5_WRF in terms of the corrective effects in interferograms with a large content of tropospheric delay, both for the elevation-dependent delay and spatially correlated delay.
- In areas with a highly complex topography, users need to consider the balance between improvement in accuracy and the complexity of the correction when using ERA5_WRF.
The same microphysical schemes were used for the simulation of WRF in this paper. The cumulus parameterization is turned on at 3 km, and it is controversial whether to use the cumulus parameterization below 4 km [69]. It depends on specific applications. In future research, for specific regions and atmospheric conditions, it is valuable for research and recommendation of the parameterization of microphysical schemes. Additionally, it is useful for higher precision correction and wider use of ERA5_WRF.
WRF can flexibly change data sources and conduct appropriate downscaling processing by simulating atmospheric motion. It is a good choice for tropospheric correction when other higher quality data appear in the future. The significantly improved efficiency of simulation and better overall performance reported here promise the widespread use of WRF in multi-temporal InSAR.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15010273/s1.
Author Contributions
Conceptualization, Q.L. and Q.Z.; methodology, Q.L. and Q.Z.; software, Q.L.; validation, Q.L. and Q.Z.; formal analysis, Q.L. and Zhang, Z.; investigation, Q.L.; resources, Q.L.; data curation, Q.L.; writing—original draft preparation, Q.L. and Z.Z.; writing—review and editing, Q.L.; visualization, Q.L.; supervision, Q.L.; project administration, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China, under grant 2017YFB0502703.
Acknowledgments
The authors thank ESA and JAXA for the MERIS, Sentinel-1, and ALOS PALSAR images archived at the European Space Agency (https://earth.esa.int/eogateway (accessed on 1 June 2022)). We also thank the University of Newcastle for providing data on tropospheric correction data through GACOS (2019) (http://www.gacos.net/ (accessed on 1 June 2022)). We thank the High-Performance Computing Platform of Peking University for providing their computational resources. We also thank the ISCE team in JPL for providing the ISCE software package.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cao, Y.; Jónsson, S.; Li, Z. Advanced InSAR Tropospheric Corrections from Global Atmospheric Models that Incorporate Spatial Stochastic Properties of the Troposphere. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020952. [Google Scholar] [CrossRef]
- Parker, A.L.; Biggs, J.; Walters, R.J.; Ebmeier, S.K.; Wright, T.J.; Teanby, N.A.; Lu, Z. Systematic assessment of atmospheric uncertainties for InSAR data at volcanic arcs using large-scale atmospheric models: Application to the Cascade volcanoes, United States. Remote Sens. Environ. 2015, 170, 102–114. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Liao, M.; Gong, J. Improved correction of seasonal tropospheric delay in InSAR observations for landslide deformation monitoring. Remote Sens. Environ. 2019, 233, 111370. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Triggered afterslip on the southern Hikurangi subduction interface following the 2016 Kaikōura earthquake from InSAR time series with atmospheric corrections. Remote Sens. Environ. 2020, 251, 112097. [Google Scholar] [CrossRef]
- Hanssen, R.F.; SpringerLink. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic Publishers: Hingham, MA, USA, 2001; Volume 2. [Google Scholar]
- Murray, K.D.; Bekaert, D.P.; Lohman, R.B. Tropospheric corrections for InSAR: Statistical assessments and applications to the Central United States and Mexico. Remote Sens. Environ. 2019, 232, 111326. [Google Scholar] [CrossRef]
- Jung, J.; Kim, D.-J.; Park, S.-E. Correction of Atmospheric Phase Screen in Time Series InSAR Using WRF Model for Monitoring Volcanic Activities. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2678–2689. [Google Scholar] [CrossRef]
- Albino, F.; Biggs, J.; Yu, C.; Li, Z. Automated Methods for Detecting Volcanic Deformation Using Sentinel-1 InSAR Time Series Illustrated by the 2017–2018 Unrest at Agung, Indonesia. J. Geophys. Res. Solid Earth 2020, 125, e2019JB017908. [Google Scholar] [CrossRef]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Hooper, A.; Wright, T.J. A spatially variable power law tropospheric correction technique for InSAR data. J. Geophys. Res. Solid Earth 2015, 120, 1345–1356. [Google Scholar] [CrossRef]
- Doin, M.-P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Fattahi, H.; Amelung, F. InSAR bias and uncertainty due to the systematic and stochastic tropospheric delay. J. Geophys. Res. Solid Earth 2015, 120, 8758–8773. [Google Scholar] [CrossRef]
- Hu, Z.; Mallorquí, J.J. An Accurate Method to Correct Atmospheric Phase Delay for InSAR with the ERA5 Global Atmospheric Model. Remote Sens. 2019, 11, 1969. [Google Scholar] [CrossRef]
- Kim, J.-R.; Lin, S.-Y.; Yun, H.-W.; Tsai, Y.-L.; Seo, H.-J.; Hong, S.; Choi, Y. Investigation of Potential Volcanic Risk from Mt. Baekdu by DInSAR Time Series Analysis and Atmospheric Correction. Remote Sens. 2017, 9, 138. [Google Scholar] [CrossRef]
- Yun, Y. Mitigating Atmospheric Effects in Repeat-Pass Spaceborne InSAR Measurement through Data Assimilation and Numerical Simulations with WRF Model; Peking University: Beijing, China, 2015. [Google Scholar]
- Welch, M.D.; Schmidt, D.A. Separating volcanic deformation and atmospheric signals at Mount St. Helens using Persistent Scatterer InSAR. J. Volcanol. Geotherm. Res. 2017, 344, 52–64. [Google Scholar] [CrossRef]
- Wicks, C.W.; Dzurisin, D.; Ingebritsen, S.; Thatcher, W.; Lu, Z.; Iverson, J. Magmatic activity beneath the quiescent Three Sisters volcanic center, central Oregon Cascade Range, USA. Geophys. Res. Lett. 2002, 29, 26-1–26-4. [Google Scholar] [CrossRef]
- Lin, Y.-N.N.; Simons, M.; Hetland, E.A.; Muse, P.; DiCaprio, C. A multiscale approach to estimating topographically correlated propagation delays in radar interferograms. Geochem. Geophys. Geosystems 2010, 11, Q09002. [Google Scholar] [CrossRef]
- Béjar-Pizarro, M.; Socquet, A.; Armijo, R.; Carrizo, D.; Genrich, J.; Simons, M. Andean structural control on interseismic coupling in the North Chile subduction zone. Nat. Geosci. 2013, 6, 462–467. [Google Scholar] [CrossRef]
- Shen, L.; Hooper, A.; Elliott, J. A Spatially Varying Scaling Method for InSAR Tropospheric Corrections Using a High-Resolution Weather Model. J. Geophys. Res. Solid Earth 2019, 124, 4051–4068. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Discrimination of geophysical phenomena in satellite radar interferograms. Geophys. Res. Lett. 1995, 22, 1537–1540. [Google Scholar] [CrossRef]
- González, P.J.; Fernandez, J. Error estimation in multitemporal InSAR deformation time series, with application to Lanzarote, Canary Islands. J. Geophys. Res. Earth Surf. 2011, 116, B10404. [Google Scholar] [CrossRef]
- Cao, Y.; Li, Z.; Wei, J.; Hu, J.; Duan, M.; Feng, G. Stochastic modeling for time series InSAR: With emphasis on atmospheric effects. J. Geodesy 2018, 92, 185–204. [Google Scholar] [CrossRef]
- Li, Z.; Cao, Y.; Wei, J.; Duan, M.; Wu, L.; Hou, J.; Zhu, J. Time-series InSAR ground deformation monitoring: Atmospheric delay modeling and estimating. Earth-Sci. Rev. 2019, 192, 258–284. [Google Scholar] [CrossRef]
- Foster, J.; Kealy, J.; Cherubini, T.; Businger, S.; Lu, Z.; Murphy, M. The utility of atmospheric analyses for the mitigation of artifacts in InSAR. J. Geophys. Res. Solid Earth 2013, 118, 748–758. [Google Scholar] [CrossRef]
- Shamshiri, R.; Motagh, M.; Nahavandchi, H.; Haghighi, M.H.; Hoseini, M. Improving tropospheric corrections on large-scale Sentinel-1 interferograms using a machine learning approach for integration with GNSS-derived zenith total delay (ZTD). Remote Sens. Environ. 2020, 239, 111608. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res.-Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Xiong, W.; Luo, S. InSAR Observation and Fault Rupture Study of the Jiuzhaigou M_S7.0Earthquake. J. Geod. Geodyn. 2019, 39, 452–457. [Google Scholar]
- Vaka, D.S.; Rao, Y.S.; Bhattacharya, A. Surface displacements of the 12 November 2017 Iran–Iraq earthquake derived using SAR interferometry. Geocarto Int. 2019, 36, 660–675. [Google Scholar] [CrossRef]
- Song, X.; Shan, X.; Qu, C. Interseismic strain accumulation across the zemuhe-daliangshan fault zone in heavily-vegetated southwestern China, From Alos-2 Interferometric Observation. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1490–1493. [Google Scholar]
- Mateus, P.; Nico, G.; Catalao, J. Uncertainty Assessment of the Estimated Atmospheric Delay Obtained by a Numerical Weather Model (NMW). IEEE Trans. Geosci. Remote Sens. 2015, 53, 6710–6717. [Google Scholar] [CrossRef]
- Jung, J.; Kim, D.-j. Correction of tropospheric phase delay in time series InSAR using WRF model for monitoring Shinmoedake volcano. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium, IEEE International Symposium on Geoscience and Remote Sensing IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 137–140. [Google Scholar]
- Mateus, P.; Nico, G.; Tome, R.; Catalao, J.; Miranda, P.M.A. Experimental Study on the Atmospheric Delay Based on GPS, SAR Interferometry, and Numerical Weather Model Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 6–11. [Google Scholar] [CrossRef]
- Zhang, Z.; Lou, Y.; Zhang, W.; Wang, H.; Zhou, Y.; Bai, J. On the Assessment GPS-Based WRFDA for InSAR Atmospheric Correction: A Case Study in Pearl River Delta Region of China. Remote Sens. 2021, 13, 3280. [Google Scholar] [CrossRef]
- Yun, Y.; Zeng, Q.; Green, B.W.; Zhang, F. Mitigating atmospheric effects in InSAR measurements through high-resolution data assimilation and numerical simulations with a weather prediction model. Int. J. Remote Sens. 2015, 36, 2129–2147. [Google Scholar] [CrossRef]
- Miranda, P.M.A.; Mateus, P.; Nico, G.; Catalão, J.; Tomé, R.; Nogueira, M. InSAR Meteorology: High-Resolution Geodetic Data Can Increase Atmospheric Predictability. Geophys. Res. Lett. 2019, 46, 2949–2955. [Google Scholar] [CrossRef]
- Mateus, P.; Miranda, P.M.A.; Nico, G.; Catalao, J. Continuous Multitrack Assimilation of Sentinel-1 Precipitable Water Vapor Maps for Numerical Weather Prediction: How Far Can We Go with Current InSAR Data? J. Geophys. Res. Atmos. 2021, 126, e2020JD034171. [Google Scholar] [CrossRef]
- Mateus, P.; Miranda, P.M.A. Using InSAR Data to Improve the Water Vapor Distribution Downstream of the Core of the South American Low-Level Jet. J. Geophys. Res. Atmos. 2022, 127, e2021JD036111. [Google Scholar] [CrossRef]
- Roukounakis, N.; Katsanos, D.; Briole, P.; Elias, P.; Kioutsioukis, I.; Argiriou, A.; Retalis, A. Use of GNSS Tropospheric Delay Measurements for the Parameterization and Validation of WRF High-Resolution Re-Analysis over the Western Gulf of Corinth, Greece: The PaTrop Experiment. Remote Sens. 2021, 13, 1898. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, Q.; Jiao, J.; Hao, Z. Evaluation of Weather Research and Forecast (WRF) microphysics schemes in simulating zenith total delay for InSAR atmospheric correction. Int. J. Remote Sens. 2021, 42, 3456–3473. [Google Scholar] [CrossRef]
- Dou, F.; Lv, X.; Chai, H. Mitigating Atmospheric Effects in InSAR Stacking Based on Ensemble Forecasting with a Numerical Weather Prediction Model. Remote Sens. 2021, 13, 4670. [Google Scholar] [CrossRef]
- Ulmer, F.-G.; Adam, N. Characterisation and improvement of the structure function estimation for application in PSI. ISPRS J. Photogramm. Remote Sens. 2017, 128, 40–46. [Google Scholar] [CrossRef]
- Adam, N. Methodology of a Troposphere Effect Mitigation Processor for SAR Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 5334–5344. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhang, X.; Jiao, J. Atmospheric correction of spaceborne repeat-pass InSAR DEM generation based on WRF. J. Remote Sens. 2016, 20, 1151–1160. [Google Scholar]
- Wang, X.; Zeng, Q.; Yun, Y.; Han, K.; Jiao, J. The reliability inspection of water vapor from WRF utilized for InSAR atmospheric correction in different areas. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium, IEEE International Symposium on Geoscience and Remote Sensing IGARSS, Fort Worth, TX, USA, 23–28 July 2017; pp. 3105–3108. [Google Scholar]
- Kinoshita, Y.; Furuya, M.; Hobiger, T.; Ichikawa, R. Are numerical weather model outputs helpful to reduce tropospheric delay signals in InSAR data? J. Geod. 2013, 87, 267–277. [Google Scholar] [CrossRef]
- Roukounakis, N.; Elias, P.; Briole, P.; Katsanos, D.; Kioutsioukis, I.; Argiriou, A.; Retalis, A. Tropospheric Correction of Sentinel-1 Synthetic Aperture Radar Interferograms Using a High-Resolution Weather Model Validated by GNSS Measurements. Remote Sens. 2021, 13, 2258. [Google Scholar] [CrossRef]
- Xiong, S.; Zeng, Q.; Jiao, J.; Zhang, X. PS-InSAR analysis for Radarsat-2 datasets in Guangdong Province to detect accurate land deformation. Dragon 3Mid Term Results 2014, 724, 111. [Google Scholar]
- Darvishi, M.; Cuozzo, G.; Bruzzone, L.; Nilfouroushan, F. Performance Evaluation of Phase and Weather-Based Models in Atmospheric Correction with Sentinel-1Data: Corvara Landslide in the Alps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1332–1346. [Google Scholar] [CrossRef]
- Gong, W.; Meyer, F.J.; Liu, S.; Hanssen, R.F. Temporal Filtering of InSAR Data Using Statistical Parameters from NWP Models. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4033–4044. [Google Scholar] [CrossRef]
- Yun, Y.; Zeng, Q.; Lv, X. Understanding Mountain-Wave Phases in ERS Tandem DInSAR Interferogram Using WRF Model Simulation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2762–2771. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Chen, J.; Hu, J.-C. Small Magnitude Co-Seismic Deformation of the 2017 Mw 6.4 Nyingchi Earthquake Revealed by InSAR Measurements with Atmospheric Correction. Remote Sens. 2018, 10, 684. [Google Scholar] [CrossRef]
- Chen, B.; Gong, H.; Chen, Y.; Lei, K.; Zhou, C.; Si, Y.; Li, X.; Pan, Y.; Gao, M. Investigating land subsidence and its causes along Beijing high-speed railway using multi-platform InSAR and a maximum entropy model. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102284. [Google Scholar] [CrossRef]
- Navarro-Hernández, M.; Tomás, R.; Lopez-Sanchez, J.; Cárdenas-Tristán, A.; Mallorquí, J. Spatial Analysis of Land Subsidence in the San Luis Potosi Valley Induced by Aquifer Overexploitation Using the Coherent Pixels Technique (CPT) and Sentinel-1 InSAR Observation. Remote Sens. 2020, 12, 3822. [Google Scholar] [CrossRef]
- Hu, L.; Dai, K.; Xing, C.; Li, Z.; Tomás, R.; Clark, B.; Shi, X.; Chen, M.; Zhang, R.; Qiu, Q.; et al. Land subsidence in Beijing and its relationship with geological faults revealed by Sentinel-1 InSAR observations. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101886. [Google Scholar] [CrossRef]
- Xu, H.; Luo, Y.; Yang, B.; Li, Z.; Liu, W. Tropospheric Delay Correction Based on a Three-Dimensional Joint Model for InSAR. Remote Sens. 2019, 11, 2542. [Google Scholar] [CrossRef]
- Jian, H.; Wang, L.; Gan, W.; Zhang, K.; Li, Y.; Liang, S.; Liu, Y.; Gong, W.; Yin, X. Geodetic Model of the 2017 Mw 6.5 Mainling Earthquake Inferred from GPS and InSAR Data. Remote Sens. 2019, 11, 2940. [Google Scholar] [CrossRef]
- Maroufpoor, S.; Bozorg-Haddad, O.; Chu, X. Chapter 9—Geostatistics: Principles and methods. In Handbook of Probabilistic Models; Samui, P., Tien Bui, D., Chakraborty, S., Deo, R.C., Eds.; Butterworth-Heinemann: Oxford, UK, 2020; pp. 229–242. [Google Scholar]
- Somos-Valenzuela, M.; Manquehual-Cheuque, F. Evaluating Multiple WRF Configurations and Forcing over the Northern Patagonian Icecap (NPI) and Baker River Basin. Atmosphere 2020, 11, 815. [Google Scholar] [CrossRef]
- Duzenli, E.; Yucel, I.; Pilatin, H.; Yilmaz, M.T. Evaluating the performance of a WRF initial and physics ensemble over Eastern Black Sea and Mediterranean regions in Turkey. Atmos. Res. 2021, 248, 105184. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Dudhia, J.; Chen, S.-H. A Revised Approach to Ice Microphysical Processes for the Bulk Parameterization of Clouds and Precipitation. Mon. Weather. Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch Convective Parameterization: An Update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather. Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather. Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Version 4; National Center for Atmospheric Research: Boulder, CO, USA, 2019. [Google Scholar]
- Liang, X.; Li, Q.; Mei, H.; Zeng, M. Multi-Grid Nesting Ability to Represent Convections Across the Gray Zone. J. Adv. Model. Earth Syst. 2019, 11, 4352–4376. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).