Quantifying the Reliability and Uncertainty of Satellite, Reanalysis, and Merged Precipitation Products in Hydrological Simulations over the Topographically Diverse Basin in Southwest China
Abstract
1. Introduction
2. Data and Methods
2.1. Study Area
2.2. Data
2.2.1. Rain Gauge Precipitation and Streamflow Data
2.2.2. Precipitation Products
2.2.3. Hydrological Model Input Datasets
2.3. Methods
2.3.1. Statistical Metrics
2.3.2. Hydrological Model and Calibration Schemes
2.3.3. Analysis of Variance (ANOVA) Method
3. Results
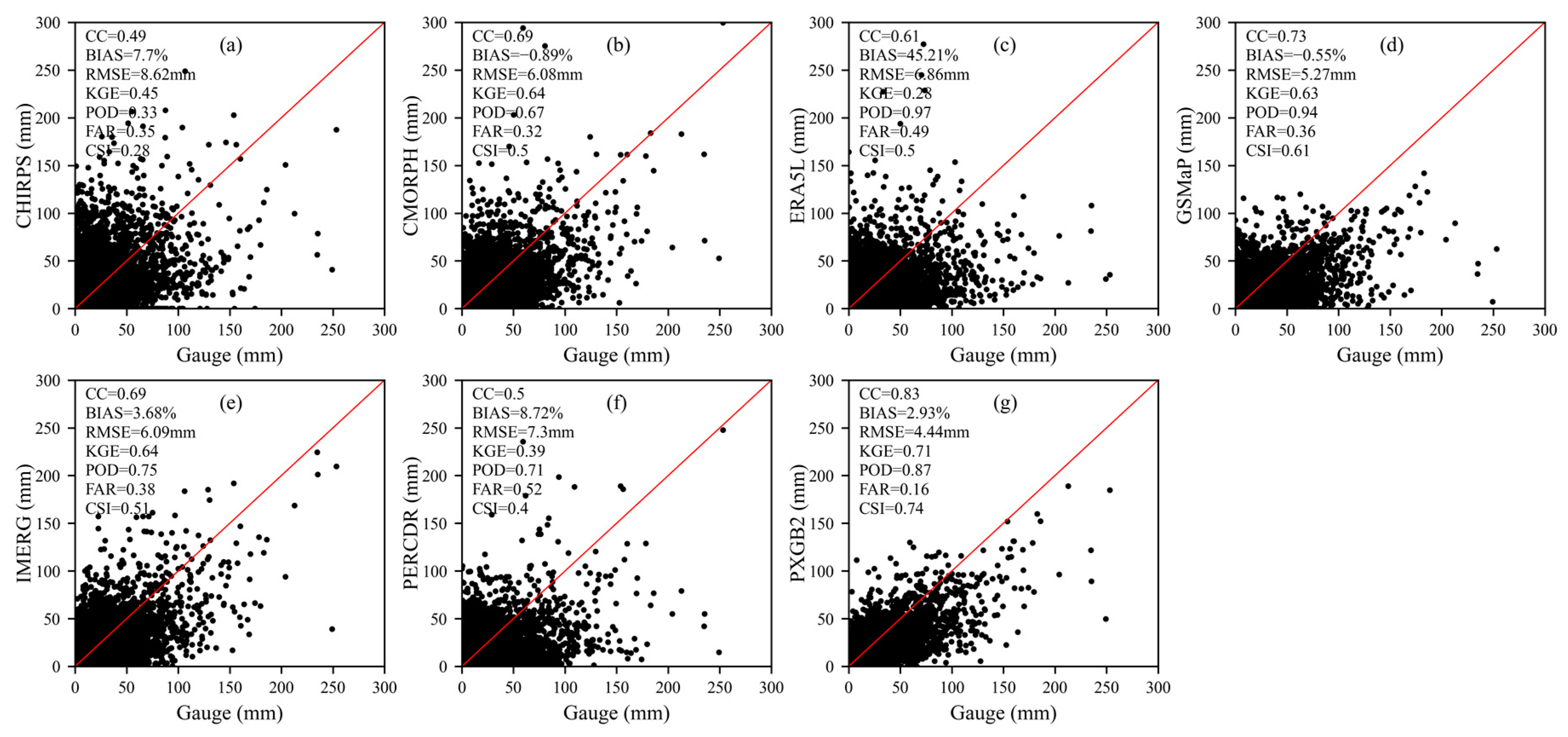
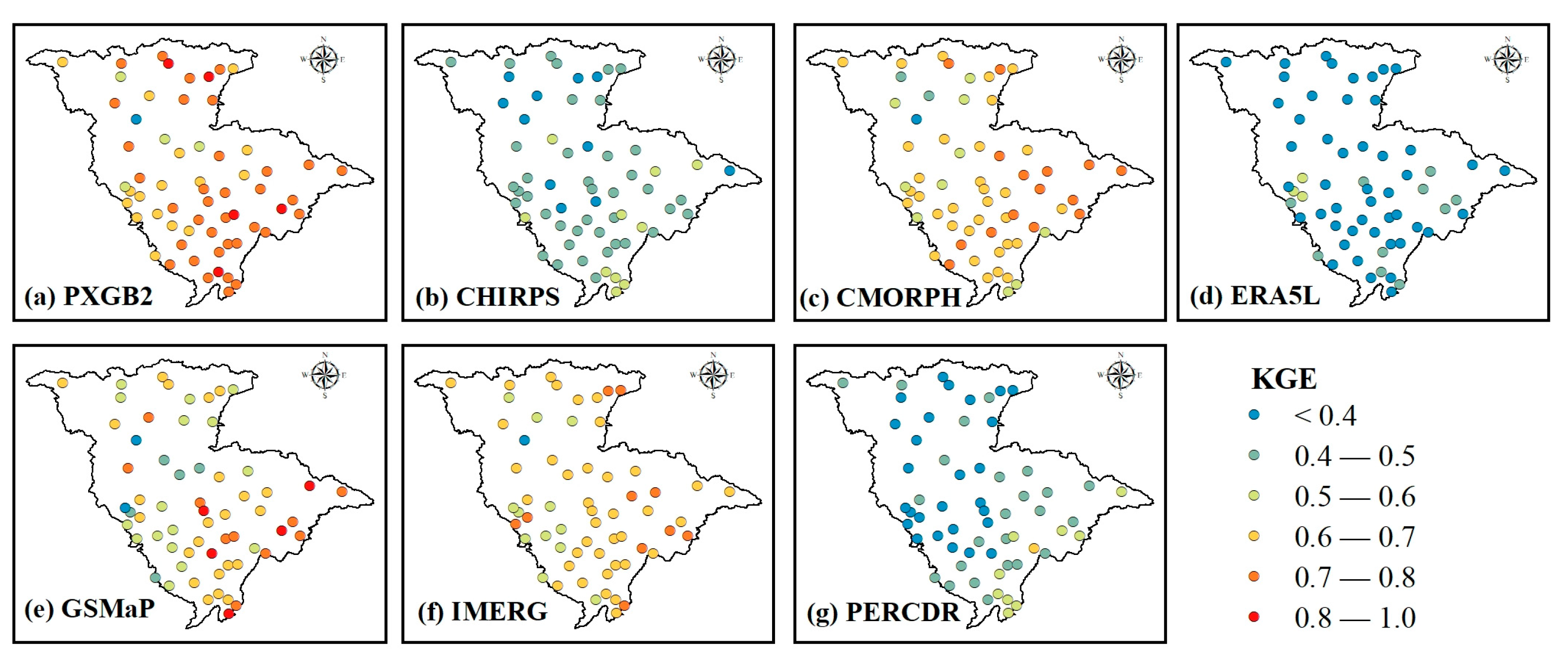
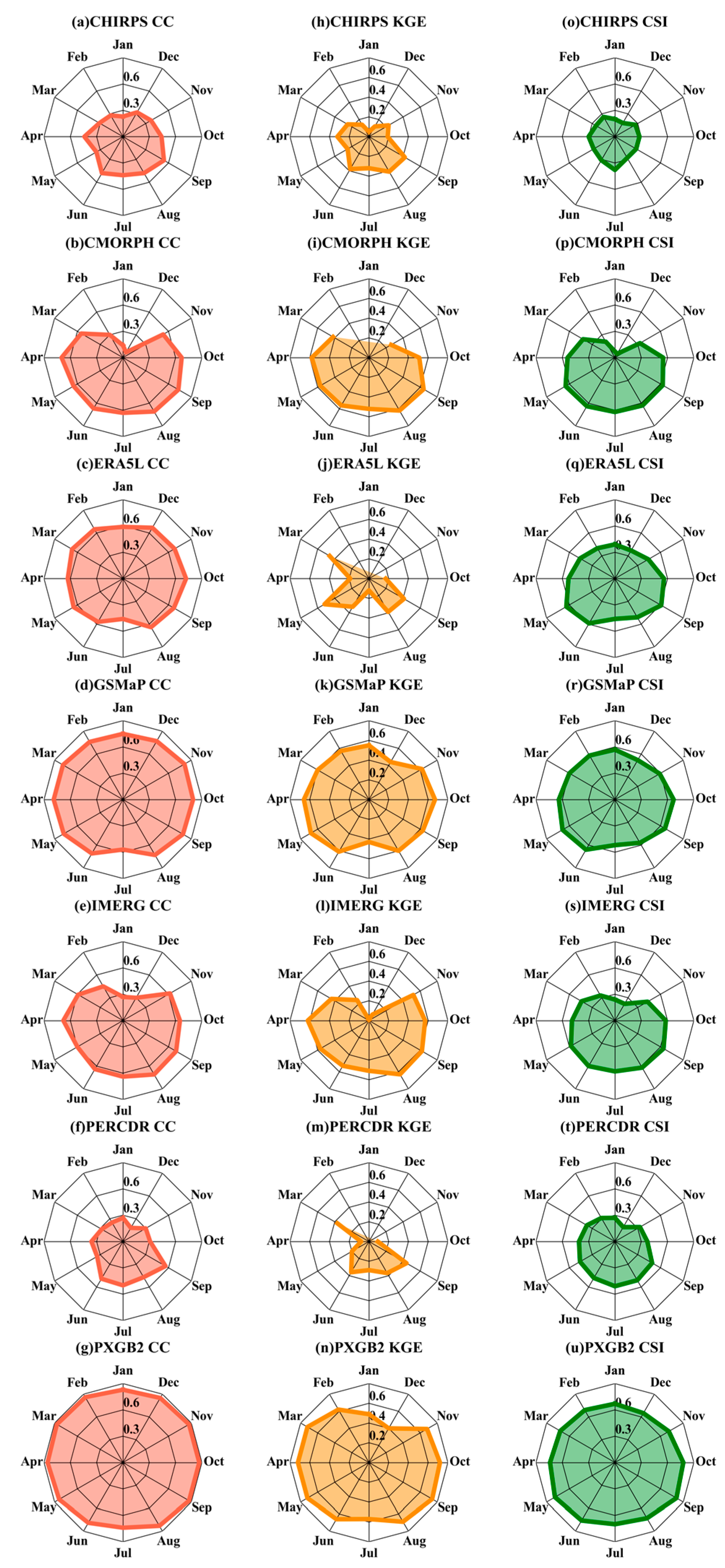
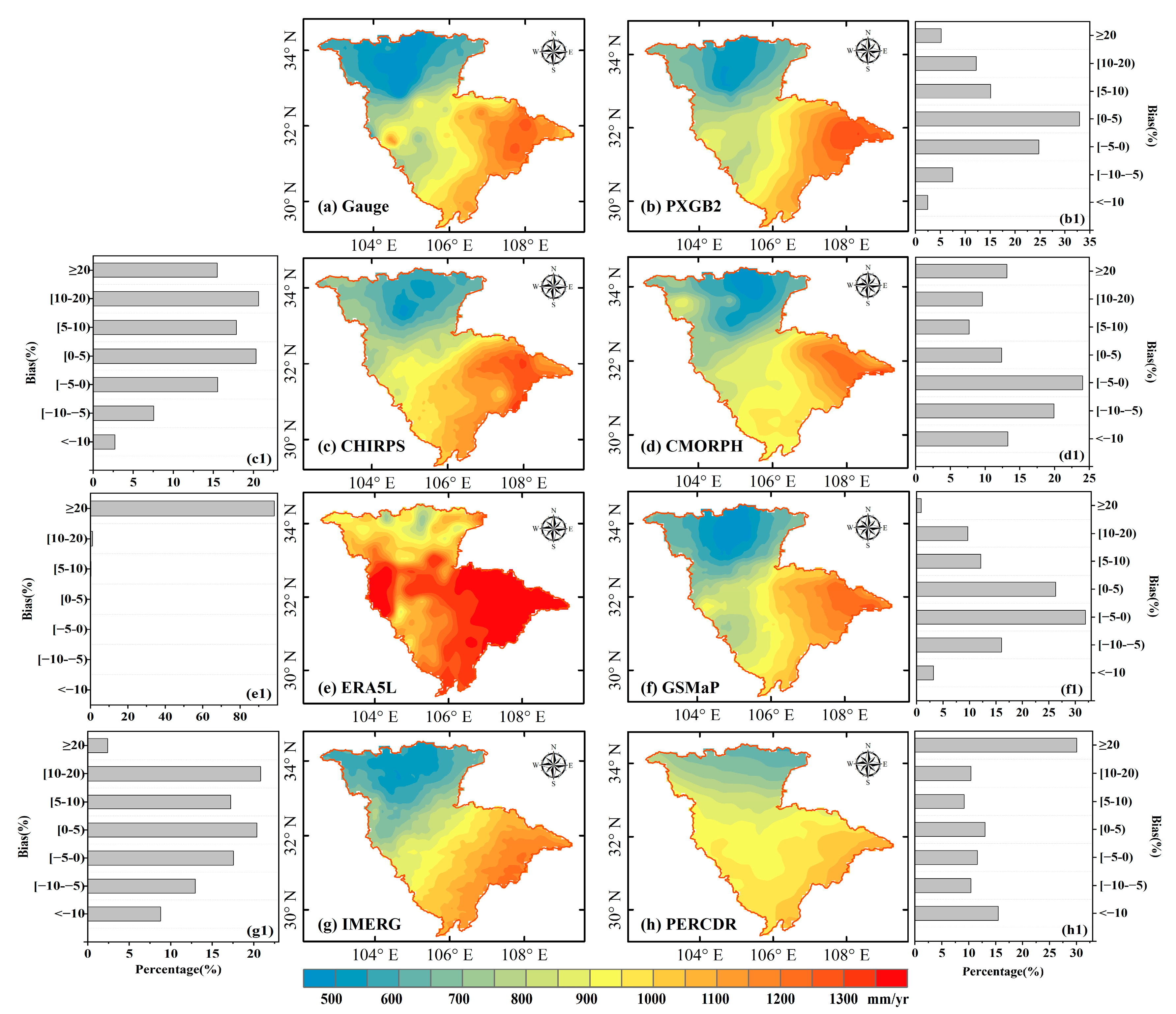
3.1. Precipitation Assessment
3.1.1. Grid Scale
3.1.2. Basin Scale
3.2. Evaluation and Comparison Streamflow Simulation
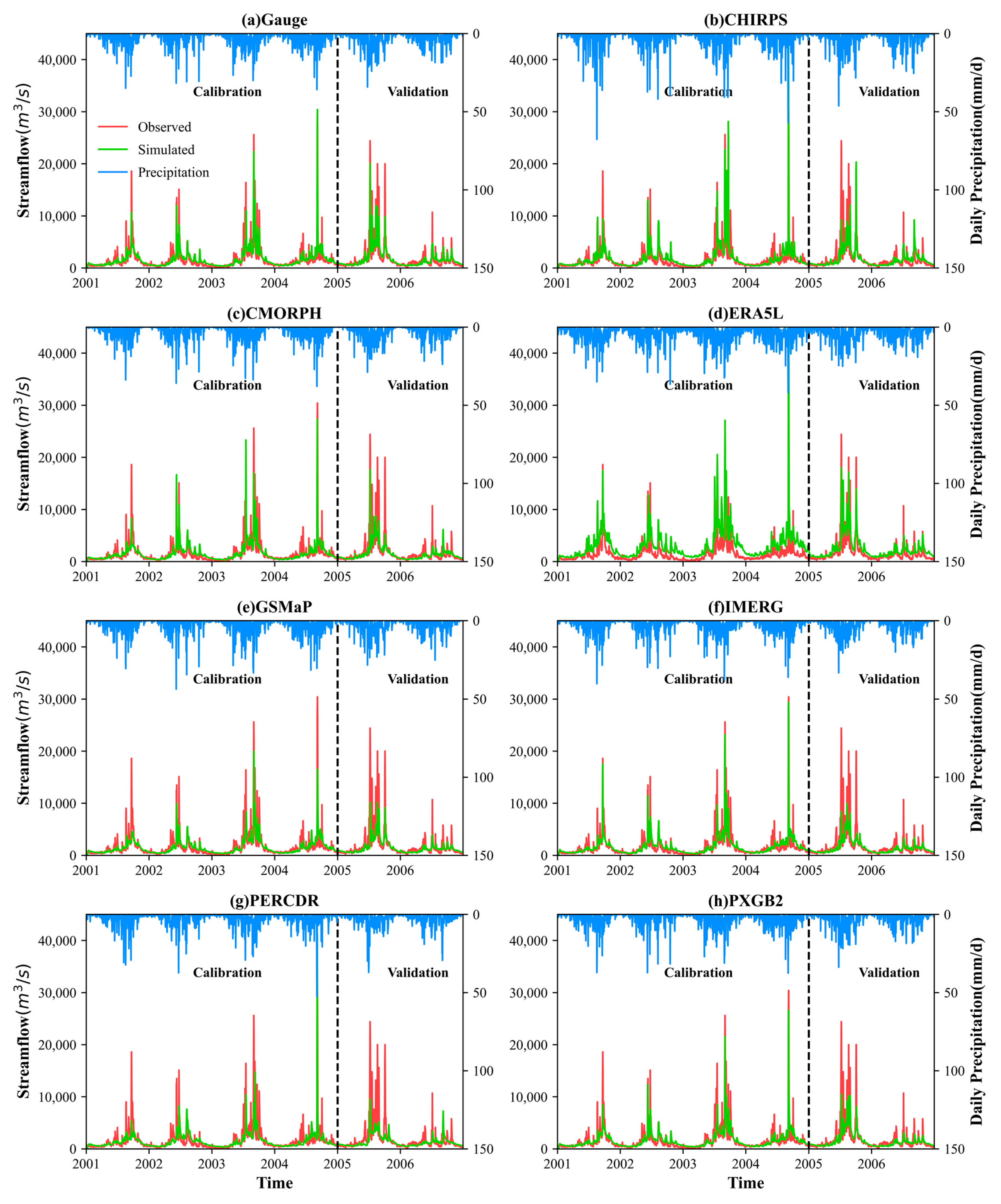
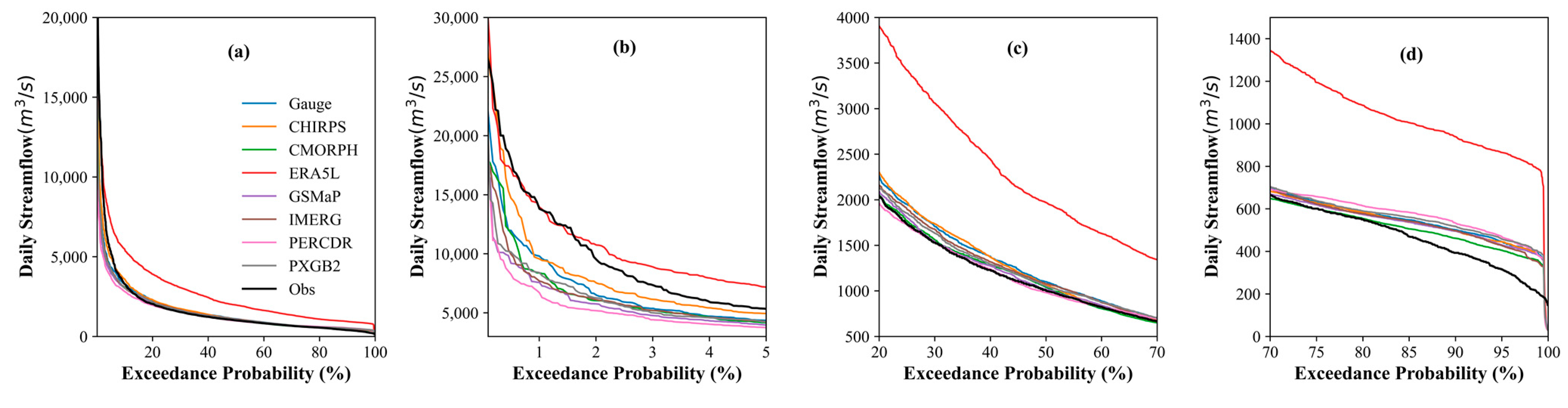
3.2.1. Streamflow Simulation under Scenario I: Gauge-Based Calibration Parameters
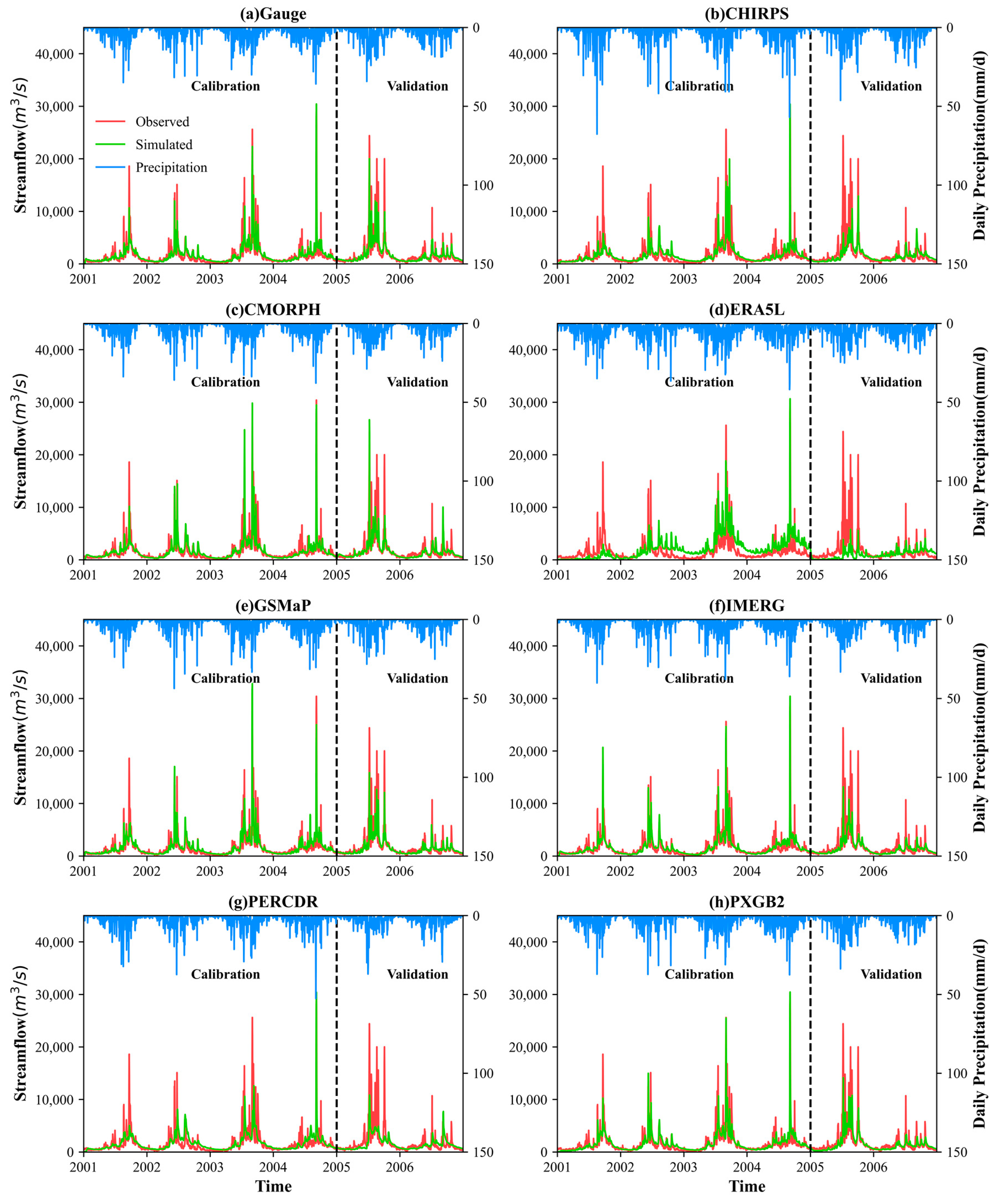
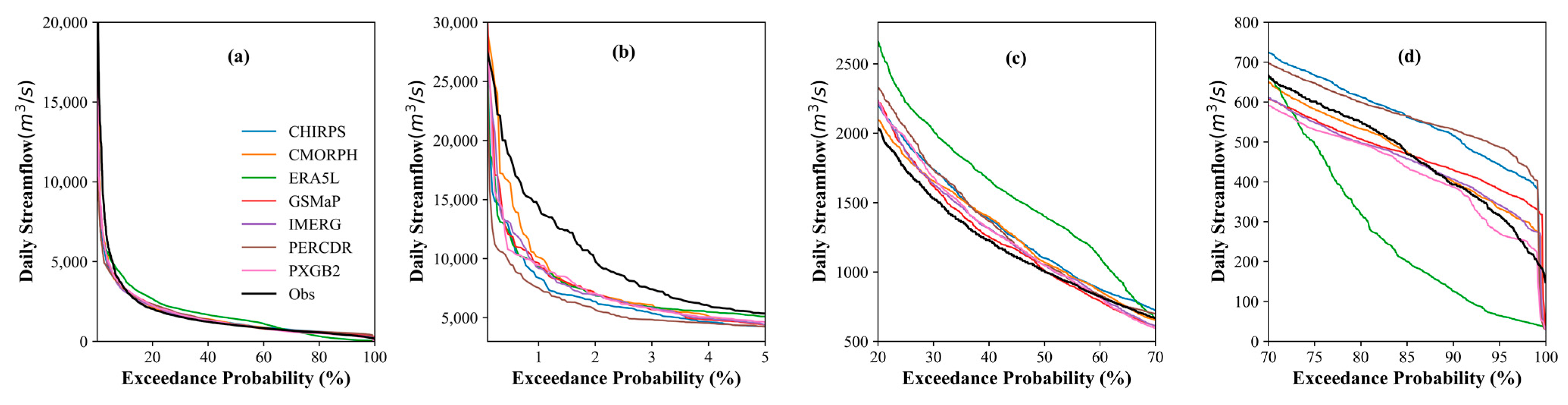
3.2.2. Streamflow Simulation under Scenario II: Product-Specific Calibration Parameters
3.3. Uncertainty Analysis of Hydrological Simulation
4. Discussion
4.1. Evaluation of MSPs and Its Uncertainties
4.2. Hydrological Evaluation and Its Uncertainties
5. Conclusions
- Compared to gauge observations, ensembled and satellite-based products reflect better precipitation capture ability and precipitation intensity than the reanalysis products used in this study. They have a similar spatial variation trend to the observations and have significant accuracy differences within the year. Generally, PXGB2 presents the best performance with the highest CC of 0.83, KGE of 0.71, and CSI of 0.74, followed by GSMaP and IMERG.
- The simulation results using gauge-calibrated parameters show that the simulation forced by observation precipitation performs best in both calibration and validation periods due to the robustness of the model and the relatively dense rain gauges in the JLR basin. Among the seven MSPs, PXGB2 presents better simulation with the highest R2 (0.73) and NSE (0.69), indicating that incorporating various precipitation information can effectively reduce the error caused by single sources. Generally, GSMaP, IMERG, and CMORPH show better hydrological performance than CHIRPS, PERCDR, and ERA5L.
- The model parameters calibrated based on individual products significantly enhance the simulation performance of most MSPs, suggesting that model calibration can mitigate the impact of precipitation errors on streamflow simulation. The simulations can better capture the variation trends of streamflow in both timing and magnitude. This improvement is most remarkable in GSMaP, with the largest R2 (0.76), NSE (0.75), and KGE (0.79). The most suitable performance rankings of MSPs are GSMaP, PXGB2, CMORPH, IMERG, CHIRPS, PERCDR, and ERA5L, which are slightly different from the gauge-calibrated simulation results.
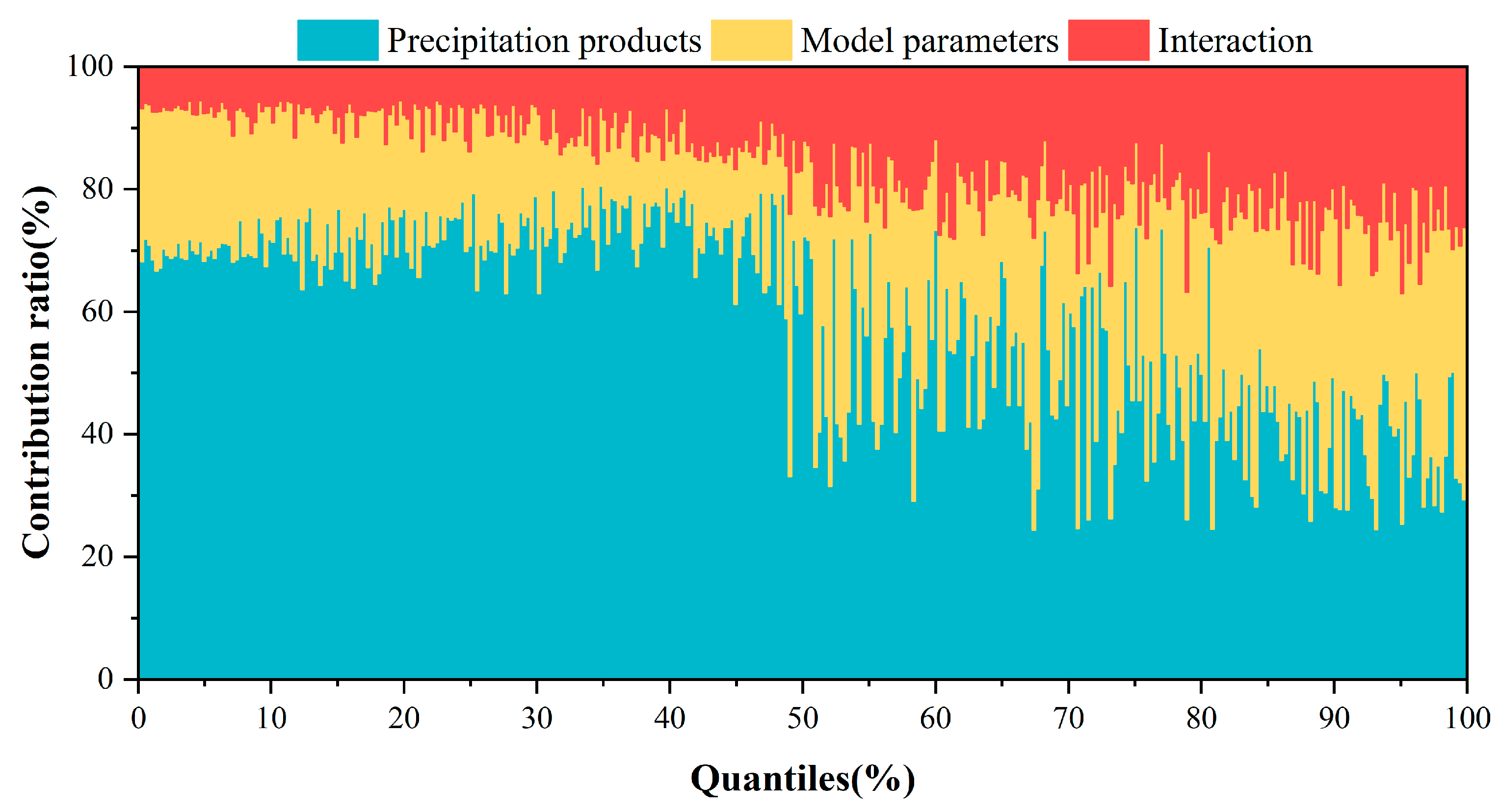
- The results based on the ANOVA method show that the precipitation products contribute most to the total uncertainty of streamflow simulation. The contribution ratio of precipitation products, model parameters, and their interactions is 59%, 25%, and 16% in this study, respectively, which is influenced by seasons and the magnitude of streamflow. Under the influence of interaction, it is easier to understand why good products may produce unsatisfactory results. The result demonstrates that an appropriate combination of precipitation products and model parameters is essential to produce a good streamflow simulation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Behrangi, A.; Khakbaz, B.; Jaw, T.C.; AghaKouchak, A.; Hsu, K.; Sorooshian, S. Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrol. 2011, 397, 225–237. [Google Scholar] [CrossRef]
- Ma, D.; Xu, Y.P.; Gu, H.; Zhu, Q.; Sun, Z.; Xuan, W. Role of satellite and reanalysis precipitation products in streamflow and sediment modeling over a typical alpine and gorge region in Southwest China. Sci. Total Environ. 2019, 685, 934–950. [Google Scholar] [CrossRef] [PubMed]
- Awange, J.; Hu, K.; Khaki, M. The newly merged satellite remotely sensed, gauge and reanalysis-based Multi-Source Weighted-Ensemble Precipitation: Evaluation over Australia and Africa (1981–2016). Sci. Total Environ. 2019, 670, 448–465. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Sun, X.; Chen, H.; Hong, Y.; Zhang, Y. A two-stage blending approach for merging multiple satellite precipitation estimates and rain gauge observations: An experiment in the northeastern Tibetan Plateau. Hydrol. Earth Syst. Sci. 2021, 25, 359–374. [Google Scholar] [CrossRef]
- Sun, R.; Yuan, H.; Liu, X.; Jiang, X. Evaluation of the latest satellite–gauge precipitation products and their hydrologic applications over the Huaihe River basin. J. Hydrol. 2016, 536, 302–319. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, B.; Ma, Z.; Chen, X.; Qiu, J.; Liu, D. Comprehensive comparisons of state-of-the-art gridded precipitation estimates for hydrological applications over southern China. Remote Sens. 2020, 12, 3997. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gao, X.; Sorooshian, S.; Gupta, H. Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Tan, J.K. Integrated Multi-satellite Retrievals for GPM (IMERG) Technical Documentation, NASA. 2019. Available online: https://gpm1.gesdisc.eosdis.nasa.gov/data/GPM_L3/GPM_3IMERGDF.06/ (accessed on 12 June 2022).
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global precipitation 30 map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations–a new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Chen, Y.; Guo, H.; Wang, Y.; Lian, L. Applicability Evaluation of Multisource Satellite Precipitation Data for Hydrological Research in Arid Mountainous Areas. Remote Sens. 2020, 12, 2886. [Google Scholar] [CrossRef]
- Lei, H.; Zhao, H.; Ao, T. Ground validation and error decomposition for six state-of-the-art satellite precipitation products over mainland China. Atmos. Res. 2022, 269, 106017. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Z.; Yan, S.; Peng, J. Do ERA5 and ERA5-land precipitation estimates outperform satellite-based precipitation products? A comprehensive comparison between state-of-the-art model-based and satellite-based precipitation products over mainland China. J. Hydrol. 2022, 605, 127353. [Google Scholar] [CrossRef]
- Khandu; Awange, J.L.; Forootan, E. An evaluation of high-resolution gridded precipitation products over Bhutan (1998–2012). Int. J. Climatol. 2016, 36, 1067–1087. [Google Scholar] [CrossRef]
- Duan, Z.; Liu, J.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of eight high spatial resolution gridded precipitation products in Adige Basin (Italy) at multiple temporal and spatial scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef] [PubMed]
- Tan, M.L.; Santo, H. Comparison of GPM IMERG, TMPA 3B42 and PERSIANN-CDR satellite precipitation products over Malaysia. Atmos. Res. 2018, 202, 63–76. [Google Scholar] [CrossRef]
- Kim, J.; Han, H. Evaluation of the CMORPH high-resolution precipitation product for hydrological applications over South Korea. Atmos. Res. 2021, 258, 105650. [Google Scholar] [CrossRef]
- Moazami, S.; Najafi, M.R. A comprehensive evaluation of GPM-IMERG V06 and MRMS with hourly ground-based precipitation observations across Canada. J. Hydrol. 2021, 594, 125929. [Google Scholar] [CrossRef]
- Alemohammad, S.H.; McColl, K.A.; Konings, A.G.; Entekhabi, D.; Stoffelen, A. Characterization of precipitation product errors across the United States using multiplicative triple collocation. Hydrol. Earth Syst. Sci. 2015, 19, 3489–3503. [Google Scholar] [CrossRef]
- Massari, C.; Crow, W.; Brocca, L. An assessment of the performance of global rainfall estimates without ground-based observations. Hydrol. Earth Syst. Sci. 2017, 21, 4347–4361. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, L.; Zheng, H.; Zhang, B.; Li, M. Hydroclimate assessment of gridded precipitation products for the Tibetan Plateau. Sci. Total Environ. 2019, 660, 1555–1564. [Google Scholar] [CrossRef] [PubMed]
- Lei, H.; Li, H.; Zhao, H.; Ao, T.; Li, X. Comprehensive evaluation of satellite and reanalysis precipitation products over the eastern Tibetan plateau characterized by ahigh diversity of topographies. Atmos. Res. 2021, 259, 105661. [Google Scholar] [CrossRef]
- Li, K.; Tian, F.; Khan, M.Y.A.; Xu, R.; He, Z.; Yang, L.; Lu, H.; Ma, Y. A high-accuracy rainfall dataset by merging multiple satellites and dense gauges over the southern Tibetan Plateau for 2014–2019 warm seasons. Earth Syst. Sci. Data 2021, 13, 5455–5467. [Google Scholar] [CrossRef]
- Wild, A.; Chua, Z.-W.; Kuleshov, Y. Evaluating accuracy of satellite precipitation estimates over the South West Pacific. Remote Sens. 2021, 13, 3929. [Google Scholar] [CrossRef]
- Wild, A.; Chua, Z.-W.; Kuleshov, Y. Triple Collocation Analysis of Satellite Precipitation Estimates over Australia. Remote Sens. 2022, 14, 2724. [Google Scholar] [CrossRef]
- Jiang, L.; Bauer-Gottwein, P. How do GPM IMERG precipitation estimates perform as hydrological model forcing? Evaluation for 300 catchments across Mainland China. J. Hydrol. 2019, 572, 486–500. [Google Scholar] [CrossRef]
- Su, J.; Li, X.; Ren, W.; Lü, H.; Zheng, D. How reliable are the satellite-based precipitation estimations in guiding hydrological modelling in South China? J. Hydrol. 2021, 602, 126705. [Google Scholar] [CrossRef]
- Tian, W.; Liu, X.; Wang, K.; Bai, P.; Liang, K.; Liu, C. Evaluation of six precipitation products in the Mekong River Basin. Atmos. Res. 2021, 255, 105539. [Google Scholar] [CrossRef]
- Dembélé, M.; Schaefli, B.; Van De Giesen, N.; Mariéthoz, G. Suitability of 17 gridded rainfall and temperature datasets for large-scale hydrological modelling in West Africa. Hydrol. Earth Syst. Sci. 2020, 24, 5379–5406. [Google Scholar] [CrossRef]
- Qi, W.; Zhang, C.; Fu, G.; Sweetapple, C.; Zhou, H. Evaluation of global fine-resolution precipitation products and their uncertainty quantification in ensemble discharge simulations. Hydrol. Earth Syst. Sci. 2016, 20, 903–920. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Mendoza, P.A.; McNamara, I.; Beck, H.E.; Thurner, J.; Nauditt, A.; Ribbe, L.; Thinh, N.X. On the selection of precipitation products for the regionalisation of hydrological model parameters. Hydrol. Earth Syst. Sci. 2021, 25, 5805–5837. [Google Scholar] [CrossRef]
- Satgé, F.; Pillot, B.; Roig, H.; Bonnet, M.P. Are gridded precipitation datasets a good option for streamflow simulation across the juruá river basin, amazon? J. Hydrol. 2021, 602, 126773. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resour. Res. 2010, 46, W05521. [Google Scholar] [CrossRef]
- Huard, D.; Mailhot, A. A Bayesian perspective on input uncertainty in model calibration: Application to hydrological model “abc”. Water Resour. Res. 2006, 42, W07416. [Google Scholar] [CrossRef]
- Sun, R.; Yuan, H.; Yang, Y. Using multiple satellite-gauge merged precipitation products ensemble for hydrologic uncertainty analysis over the Huaihe River basin. J. Hydrol. 2018, 566, 406–420. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Moradkhani, H.; Sorooshian, S. Uncertainty quantification of satellite precipitation estimation and Monte Carlo assessment of the error propagation into hydrologic response. Water Resour. Res. 2006, 42, W08421. [Google Scholar] [CrossRef]
- Mockler, E.M.; Chun, K.P.; Sapriza-Azuri, G.; Bruen, M.; Wheater, H.S. Assessing the relative importance of parameter and forcing uncertainty and their interactions in conceptual hydrological model simulations. Adv. Water Resour. 2016, 97, 299–313. [Google Scholar] [CrossRef]
- Bosshard, T.; Carambia, M.; Goergen, K.; Kotlarski, S.; Krahe, P.; Zappa, M.; Schär, C. Quantifying uncertainty sources in an ensemble of hydrological climate-impact projections. Water Resour. Res. 2013, 49, 1523–1536. [Google Scholar] [CrossRef]
- Ma, Q.; Xiong, L.; Liu, D.; Xu, C.Y.; Guo, S. Evaluating the temporal dynamics of uncertainty contribution from satellite precipitation input in rainfall-runoff modeling using the variance decomposition method. Remote Sens. 2018, 10, 1876. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, Y.; Li, Z.; Chang, J.; Guo, A. Quantifying the uncertainty interaction between the model input and structure on hydrological processes. Water Resour. Res. 2021, 35, 3915–3935. [Google Scholar] [CrossRef]
- Joyce, R.; Janowiak, J.; Arkin, P.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. Roy Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Lei, H.; Zhao, H.; Ao, T. A two-step merging strategy for incorporating multi-source precipitation products and gauge observations using machine learning classification and regression over China. Hydrol. Earth Syst. Sci. 2022, 26, 2969–2995. [Google Scholar] [CrossRef]
- Yuan, H.; Dai, Y.; Xiao, Z.; Ji, D.; Shangguan, W. Reprocessing the MODIS Leaf Area Index Products for Land Surface and Climate Modelling. Remote Sens. Environ. 2011, 115, 1171–1187. [Google Scholar] [CrossRef]
- Martens, B.; Gonzalez Miralles, D.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Takeuchi, K.; Ao, T.; Ishidaira, H. Introduction of block-wise use of TOPMODEL and Muskingum-Cunge method for the hydroenvironmental simulation of a large ungauged basin. Hydrol. Sci. J. 1999, 44, 633–646. [Google Scholar] [CrossRef]
- Takeuchi, K.; Hapuarachchi, P.; Zhou, M.; Ishidaira, H.; Magome, J. A BTOP model to extend TOPMODEL for distributed hydrological simulation of large basins. Hydrol. Process. 2008, 22, 3236–3251. [Google Scholar] [CrossRef]
- Ao, T.; Ishidaira, H.; Takeuchi, K. Study of distributed runoff simulation model based on block type TOPMODEL and Muskingum-Cunge method. Proc. Hydraulic Eng. 1999, 43, 7–12. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Masutani, K.; Magome, J. An Application of Modified Muskingum-Cunge Routing Method with Water Conservation Condition to a Distributed Runoff Model. J. Jpn. Soc. Hydrol. Water Res. 2009, 22, 294–300. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops—An energy combination theory. Q. J. Roy Meteor Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Zhou, M.C.; Ishidaira, H.; Hapuarachchi, H.P.; Magome, J.; Kiem, A.S.; Takeuchi, K. Estimating potential evapotranspiration using the Shuttleworth-Wallace model and NOAA-AVHRR NDVI to feed the hydrological modeling over the Mekong River Basin. J. Hydrol. 2006, 327, 151–173. [Google Scholar] [CrossRef]
- Georgievsky, M.; Ishidaira, H.; Takeuchi, K. Development of a distributed snow model coupled with a new method of degree-day factors estimation. Ann. J. Hydraul. Eng. JSCE 2006, 50, 49–54. [Google Scholar] [CrossRef]
- Duan, Q.; Soroosh, S.; Vijai, G. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, B.; Shi, C.; Cui, W.; Zhao, C.; Liu, Y.; Ren, L.; Zhang, L.; Zhu, Y.; Chen, T.; et al. Evaluation of hydrological utility of IMERG Final run V05 and TMPA 3B42V7 satellite precipitation products in the Yellow River source region, China. J. Hydrol. 2018, 567, 696–711. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Evaluation of satellite rainfall products through hydrologic simulation in a fully distributed hydrologic model. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and hydrological comparisons between TRMM and GPM level-3 products over a midlatitude basin: Is day-1 IMERG a good successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Gao, Z.; Long, D.; Tang, G.; Zeng, C.; Huang, J.; Hong, Y. Assessing the potential of satellite-based precipitation estimates for flood frequency analysis in ungauged or poorly gauged tributaries of China’s Yangtze River basin. J. Hydrol. 2017, 550, 478–496. [Google Scholar] [CrossRef]
- Senatore, A.; Fuoco, D.; Maiolo, M.; Mendicino, G.; Smiatek, G.; Kunstmann, H. Evaluating the uncertainty of climate model structure and bias correction on the hydrological impact of projected climate change in a Mediterranean catchment. J. Hydro-Reg. Stud. 2022, 42, 101120. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A process-based diagnostic approach to model evaluation: Application to the NWS distributed hydrologic model. Water Resour. Res. 2008, 44, W09417. [Google Scholar] [CrossRef]
- Sahraei, S.; Asadzadeh, M.; Unduche, F. Signature-based multi-modelling and multi-objective calibration of hydrologic models: Application in flood forecasting for Canadian Prairies. J. Hydrol. 2020, 588, 125095. [Google Scholar] [CrossRef]
- Xie, P.; Yatagai, A.; Chen, M.; Hayasaka, T.; Fukushima, Y.; Liu, C.; Yang, S. A Gauge-based analysis of daily precipitation over East Asia. J. Hydrometeorol. 2007, 8, 607–626. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A quasi-global precipitation time series for drought monitoring. U.S. Geol. Survey Data Ser. 2014, 832, 4p. [Google Scholar] [CrossRef]
- Ye, B.; Yang, D.; Ding, Y.; Han, T.; Koike, T. A bias-corrected precipitation climatology for China. J. Hydrometeorol. 2004, 5, 1147–1160. [Google Scholar] [CrossRef]
- Ma, J.; Li, H.; Wang, J.; Hao, X.; Shao, D.; Lei, H. Reducing the statistical distribution error in gridded precipitation data for the Tibetan Plateau. J. Hydrometeorol. 2020, 21, 2641–2654. [Google Scholar] [CrossRef]
- Hong, Z.; Han, X.; Li, D.; Long, G.; Tang, J. Wang. Generation of an improved precipitation dataset from multi-source information over the Tibetan Plateau. J. Hydrometeor. 2021, 22, 1275–1295. [Google Scholar] [CrossRef]
- Wang, Q.; Xia, J.; She, D.; Zhang, X.; Liu, J.; Zhang, Y. Assessment of four latest long-term satellite-based precipitation products in capturing the extreme precipitation and streamflow across a humid region of southern China. Atmos. Res. 2021, 257, 105554. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, Y.; Li, W.; Zhou, T. Evaluating the performance of satellite-based precipitation products using gauge measurement and hydrological modeling: A case study in a dry basin of Northwest China. J. Hydrometeorol. 2022, 23, 541–559. [Google Scholar] [CrossRef]
- Kunnath-Poovakka, A.; Ryu, D.; Renzullo, L.J.; George, B. The efficacy of calibrating hydrologic model using remotely sensed evapotranspiration and soil moisture for streamflow prediction. J. Hydrol. 2016, 535, 509–524. [Google Scholar] [CrossRef]
- Dile, Y.T.; Ayana, E.K.; Worqlul, A.W.; Xie, H.; Srinivasan, R.; Lefore, N.; You, L.; Clarke, N. Evaluating satellite-based evapotranspiration estimates for hydrological applications in data-scarce regions: A case in Ethiopia. Sci. Total Environ. 2020, 743, 140702. [Google Scholar] [CrossRef]


| Products | Resolution | Temporal Span | Reference | Retrieval Algorithm |
|---|---|---|---|---|
| GSMaP | 1 h; 0.1° | 2000–present | Kubota et al. [9] | Kalman filtering technique |
| IMERG | 0.5 h; 0.1° | 2000–present | Huffman et al. [8] | Goddard profiling algorithm |
| PERCDR | 3 h; 0.25° | 1983–2021 | Hsu et al. [7] | Adaptive ANN |
| CHIRPS | daily; 0.05° | 1981–present | Funk et al. [10] | ‘Smart’ interpolation techniques |
| CMORPH | 3 h; 0.25° | 1998–2019 | Joyce et al. [42] | Morphing technique |
| ERA5L | 1 h; 0.1° | 1950–present | Hersbach et al. [43] | IFS Cy41r2 4D-Var |
| PXGB2 | daily; 0.1° | 2000–2017 | Lei et al. [44] | XGBoost regression and classification |
| Statistical Metrics | Equation | Perfect Value |
|---|---|---|
| Pearson correlation coefficient (CC) | 1 | |
| Coefficient of Determination (R2) | 1 | |
| Root mean square error (RMSE) | 0 | |
| Probability of detection (POD) | 1 | |
| False alarm ratio (FAR) | 0 | |
| Critical success index (CSI) | 1 | |
| Relative bias (BIAS) | 0 | |
| Nash–Sutcliffe coefficient of efficiency (NSE) | 1 |
| Zone | Parameter (Unit) | Description | Value Range |
|---|---|---|---|
| Channel | n0 (s/m1/3) | Block average Manning’s coefficient | 0.0001–0.8 |
| Root | α | Drying function parameter | −10–10 |
| Unsaturated/saturated | m (m) | Decay factor of lateral transmissivity | 0.01–0.1 |
| Unsaturated | SDbar (m) | Block-average saturation deficit | 0.001–0.9 |
| Saturated | D0clay (m/Δt) | Coefficients of dischargeability for clay, sand, and silt | 0.01–2.0 |
| D0sand (m/Δt) | 0.01–2.0 | ||
| D0silt (m/Δt) | 0.01–2.0 |
| Period | Metrics | CHIRPS | CMORPH | ERA5L | GSMaP | IMERG | PERCDR | PXGB2 |
|---|---|---|---|---|---|---|---|---|
| Calibration | CC | 0.48 | 0.69 | 0.63 | 0.74 | 0.68 | 0.49 | 0.83 |
| BIAS (%) | 8.74 | −0.31 | 51.05 | 1.53 | 5.17 | 10.54 | 4.20 | |
| RMSE | 8.74 | 6.09 | 6.89 | 5.20 | 6.16 | 7.42 | 4.40 | |
| KGE | 0.43 | 0.64 | 0.25 | 0.64 | 0.64 | 0.38 | 0.72 | |
| Validation | CC | 0.50 | 0.70 | 0.60 | 0.72 | 0.70 | 0.53 | 0.83 |
| BIAS (%) | 6.63 | −1.49 | 34.84 | −3.81 | 1.31 | 6.17 | 1.14 | |
| RMSE | 8.30 | 5.99 | 6.75 | 5.31 | 5.91 | 7.00 | 4.47 | |
| KGE | 0.46 | 0.64 | 0.32 | 0.59 | 0.64 | 0.39 | 0.69 |
| Period | Gauge | CHIRPS | CMORPH | ERA5L | GSMaP | IMERG | PERCDR | PXGB2 |
|---|---|---|---|---|---|---|---|---|
| Average annual | 838.5 | 889.8 | 842.4 | 1280.9 | 837.8 | 850.1 | 886.7 | 858.7 |
| 2001 | 765.2 | 806.8 | 747.7 | 1297.4 | 743.7 | 776.9 | 817.8 | 778.9 |
| 2002 | 753.1 | 844.2 | 810.9 | 1198.9 | 768.8 | 792.5 | 875.0 | 797.8 |
| 2003 | 958.8 | 1038.1 | 961.4 | 1498.5 | 985.3 | 973.3 | 999.4 | 989.2 |
| 2004 | 854.1 | 870.6 | 835.8 | 1294.1 | 881.7 | 888.4 | 884.5 | 886.4 |
| 2005 | 963.3 | 948.7 | 966.0 | 1343.9 | 930.9 | 934.8 | 928.0 | 970.1 |
| 2006 | 736.4 | 830.4 | 732.7 | 1052.7 | 716.6 | 734.5 | 815.5 | 729.9 |
| Metrics | Gauge | CHIRPS | CMORPH | IMERG | GSMaP | ERA5L | PERCDR | PXGB2 |
|---|---|---|---|---|---|---|---|---|
| Calibration period (2001–2004) | ||||||||
| R2 | 0.80 | 0.55 | 0.63 | 0.65 | 0.68 | 0.75 | 0.46 | 0.75 |
| NSE | 0.79 | 0.44 | 0.63 | 0.65 | 0.65 | 0.13 | 0.46 | 0.73 |
| KGE | 0.78 | 0.73 | 0.72 | 0.70 | 0.64 | 0.10 | 0.62 | 0.70 |
| BIAS (%) | −0.02 | 7.28 | −4.99 | −0.97 | −7.49 | 85.81 | −9.37 | −3.14 |
| Validation period (2005–2006) | ||||||||
| R2 | 0.82 | 0.66 | 0.65 | 0.61 | 0.66 | 0.76 | 0.55 | 0.71 |
| NSE | 0.77 | 0.64 | 0.58 | 0.51 | 0.54 | 0.72 | 0.42 | 0.61 |
| KGE | 0.72 | 0.68 | 0.59 | 0.52 | 0.53 | 0.52 | 0.43 | 0.60 |
| BIAS (%) | −7.65 | −7.65 | −19.18 | −20.18 | −20.62 | 30.66 | −25.79 | −17.08 |
| Entire period (2001–2006) | ||||||||
| R2 | 0.80 | 0.56 | 0.62 | 0.61 | 0.66 | 0.70 | 0.45 | 0.73 |
| NSE | 0.79 | 0.52 | 0.61 | 0.60 | 0.61 | 0.35 | 0.44 | 0.69 |
| KGE | 0.76 | 0.74 | 0.68 | 0.65 | 0.61 | 0.27 | 0.56 | 0.67 |
| BIAS (%) | −2.75 | 1.93 | −10.07 | −7.85 | −12.19 | 66.07 | −15.21 | −8.13 |
| Metrics | CHIRPS | CMORPH | IMERG | GSMaP | ERA5L | PERCDR | PXGB2 |
|---|---|---|---|---|---|---|---|
| Calibration period (2001–2004) | |||||||
| R2 | 0.58 | 0.67 | 0.71 | 0.77 | 0.52 | 0.50 | 0.75 |
| NSE | 0.58 | 0.66 | 0.70 | 0.77 | 0.43 | 0.50 | 0.75 |
| KGE | 0.68 | 0.80 | 0.80 | 0.83 | 0.49 | 0.60 | 0.79 |
| BIAS (%) | 0.01 | −0.03 | 0.00 | −0.01 | 31.20 | 0.00 | 0.03 |
| Validation period (2005–2006) | |||||||
| R2 | 0.55 | 0.61 | 0.61 | 0.81 | 0.25 | 0.48 | 0.69 |
| NSE | 0.50 | 0.60 | 0.54 | 0.72 | 0.13 | 0.43 | 0.63 |
| KGE | 0.53 | 0.70 | 0.58 | 0.68 | 0.20 | 0.47 | 0.66 |
| BIAS (%) | −14.00 | −11.29 | −19.78 | −16.96 | −43.20 | −18.50 | −17.30 |
| Entire period (2001–2006) | |||||||
| R2 | 0.55 | 0.64 | 0.65 | 0.76 | 0.36 | 0.48 | 0.71 |
| NSE | 0.55 | 0.64 | 0.64 | 0.75 | 0.32 | 0.47 | 0.71 |
| KGE | 0.63 | 0.77 | 0.74 | 0.79 | 0.53 | 0.56 | 0.75 |
| BIAS (%) | −5.01 | −4.06 | −7.08 | −6.08 | 4.56 | −6.62 | −6.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, H.; Zhao, H.; Ao, T.; Hu, W. Quantifying the Reliability and Uncertainty of Satellite, Reanalysis, and Merged Precipitation Products in Hydrological Simulations over the Topographically Diverse Basin in Southwest China. Remote Sens. 2023, 15, 213. https://doi.org/10.3390/rs15010213
Lei H, Zhao H, Ao T, Hu W. Quantifying the Reliability and Uncertainty of Satellite, Reanalysis, and Merged Precipitation Products in Hydrological Simulations over the Topographically Diverse Basin in Southwest China. Remote Sensing. 2023; 15(1):213. https://doi.org/10.3390/rs15010213
Chicago/Turabian StyleLei, Huajin, Hongyu Zhao, Tianqi Ao, and Wanpin Hu. 2023. "Quantifying the Reliability and Uncertainty of Satellite, Reanalysis, and Merged Precipitation Products in Hydrological Simulations over the Topographically Diverse Basin in Southwest China" Remote Sensing 15, no. 1: 213. https://doi.org/10.3390/rs15010213
APA StyleLei, H., Zhao, H., Ao, T., & Hu, W. (2023). Quantifying the Reliability and Uncertainty of Satellite, Reanalysis, and Merged Precipitation Products in Hydrological Simulations over the Topographically Diverse Basin in Southwest China. Remote Sensing, 15(1), 213. https://doi.org/10.3390/rs15010213







