Abstract
Positioning error components related to tropospheric and ionospheric delays are caused by the atmosphere in positioning determined by global navigation satellite systems (GNSS). Depending on the user’s requirements, the position error caused by tropospheric influences, which is commonly referred to as zenith tropospheric delay (ZTD), must be estimated during position determination or determined later by external tropospheric corrections. In this study, a new approach was adopted based on the reduction of residual tropospheric error (RTE), i.e., the unmodeled part of the tropospheric error that remains included in the total geodetic position error, along with other unmodeled systematic and random errors. The study was performed based on Global Navigation Satellite System (GLONASS) positioning solutions and accompanying meteorological parameters in a defined and harmonized temporal-spatial frame of three locations in the Republic of Croatia. A multidisciplinary approach-based analysis from a navigational science aspect was applied. The residual amount of satellite positioning signal tropospheric delay was quantitatively reduced by employing statistical analysis methods. The result of statistical regression is a model which correlates surface meteorological parameters with RTE. Considering the input data, the model has a regional character, and it is based on the Saastamoinen model of zenith tropospheric delay. The verification results show that the model reduces the RTE and thus increases the geodetic accuracy of the observed GNSS stations (with horizontal components of position accuracy of up to 3.8% and vertical components of position of up to 4.37%, respectively). To obtain these results, the Root Mean Square Error (RMSE) was used as the fundamental parameter for position accuracy evaluation. Although developed based on GLONASS data, the proposed model also shows a considerable degree of success in the verification of geodetic positions based on Global Positioning System (GPS). The purpose of the research, and one of its scientific contributions, is that the proposed method can be used to quantitatively monitor the dynamics of changes in deviations of X, Y, and Z coordinate values along coordinate axes. The results show that there is a distinct interdependence of the dynamics of Y and Z coordinate changes (with almost mirror symmetry), which has not been investigated and published so far. The resultant position of the coordinates is created by deviations of the coordinates along the Y and Z axes—in the vertical plane of space, the deviations of the coordinate X (horizontal plane) are mostly uniform and independent of deviations along the Y and Z axes. The proposed model shows the realized state of the statistical position equilibrium of the selected GNSS stations which were observed using RTE values. Although of regional character, the model is suitable for application in larger areas with similar climatological profiles and for users who do not require a maximum level of geodetic accuracy achieved by using Satellite-Based Augmentation Systems (SBAS) or other more advanced, time-consuming, and equipment-consuming positioning techniques.
1. Introduction and Background
A total satellite positioning error budget can be decomposed in satellite, receiver, and propagation medium components. The latter refers to atmospheric layers that affect the path of satellite navigation signals, namely the ionosphere and the troposphere. In addition, other present errors with a measurable and significant impact on GNSS positioning include signal multipath errors, receiver noise error, satellite and receiver clock errors, and satellite orbital error [1,2,3].
Tropospheric error is caused by the propagation of a radio navigation signal through the lowest layer of the atmosphere. In general, the troposphere is divided into two layers: the wet (non-hydrostatic) layer (with a height of up to about 10 km above the Earth’s surface) and the dry (hydrostatic) layer (which is 10–40 km above the Earth’s surface) [4,5]. These layers cause delays in satellite navigation signals. The troposphere is a non-dispersive medium; therefore, the magnitude of this error component does not depend on signal frequency and cannot be determined as is the case with ionospheric delay. Tropospheric error (which is the reduction of radio navigation signal propagation speed and its deviation from the geometric path and is also commonly called tropospheric delay) can be modeled based on the fundamental meteorological parameters of the troposphere: temperature, humidity, and atmospheric pressure [6,7,8,9,10]. Various models have been developed to predict and reduce tropospheric delay with different scopes of application, including the following: the Two-Quartic Hopfield model (n/a) ((n/a)—not specified or valid for any elevation angle.) [11], the Saastamoinen model (10° and above) [12], the Modified Hopfield model (n/a) [13], the Marini model (10° and above) [14], the Davis et al. model (CfA) (5° and above) [15], the Ifadis model (2° and above) [16], and the Askne and Nordius model (n/a) [17], etc. The above models allow the value of the tropospheric delay to be estimated with varying degrees of accuracy depending on the input components of the model (including dry, wet, or total delay and with or without mapping function); therefore, they have different elevation angles of mapping function (given in the brackets). Tropospheric delay caused by the wet component is a consequence of the presence of water vapor in all its forms in the upper layer of the troposphere (up to 10 km). Tropospheric delay is partly caused by non-hydrostatic causes; as such, the zenith wet delay (ZWD) is much smaller in absolute terms (several millimeters) than the zenith hydrostatic delay (ZHD—which reaches several tens of centimeters) [4]. The ZWD cannot be accurately modeled using surface meteorological data due to the extreme space and time volatile features of water vapor. With existing tropospheric models, the error caused by ZWD can be reduced by up to 10–20% of its actual value [18]. The causes of the wet component are not in hydrostatic equilibrium; therefore, models based on the partial pressure of water vapor or relative surface humidity do not provide sufficient accuracy. They require empirical constants that vary spatially and temporally [19], although approaches and models for ZWD estimation are being developed based on surface meteorological parameters [20].
The causes of the hydrostatic component of the zenith delay (or atmospheric dry gasses and the non-dipole component of water vapor refraction [18]) are in hydrostatic equilibrium [19] and are therefore determined relatively simply and precisely using the Saastamoinen model. Both components form the ZTD. Approaches of existing tropospheric delay models for ZHD and ZWD differ, and certain models [21,22,23,24,25,26] of ZTD usually include a non-hydrostatic zenith component which depends primarily on the temporal-spatial distribution of water vapor and the height of the distribution, with the influence of water vapor being the most important. Considering that the insufficient modeling capabilities of the non-hydrostatic causes of tropospheric delay in the zenith direction limit the accuracy of the mapping function for other signal elevation angles, the separation of the mapping function from the zenith delay allowed the development of a number of new models of mapping functions [27,28,29,30,31,32]. Such models can combine hydrostatic and non-hydrostatic causes and can be combined with tropospheric delay in the zenith direction. This results in hybrid models separated by hydrostatic and non-hydrostatic causes. In general, tropospheric errors in GNSS measurement range from 2–2.4 m in the zenith direction and 25 m at horizontal elevation angles [33,34].
The new approach used in this study investigates the overall effect of tropospheric delay on the accuracy of the GNSS geodetic position of the selected area. Several studies [10,35] show the relationship between tropospheric delays based on radiosonde signal measurements and deviations from position accuracy where the main effect was found to be the atmospheric refraction expressed by the number of N units, which is a value that varies greatly in time and space [36,37,38]. In this way, it is possible to combine the influence of the tropospheric delays in radio signals (usually with peak values up to several tens of millimeters) with the amounts of slant tropospheric errors in the GNSS system which can reach several tens of meters.
A model of empirical character is proposed which combines the value of the non-modeled geodetic position RTE GNSS with the meteorological surface parameters of the observed positions. Rather than determining the appropriateness of a particular model of tropospheric delay (either in the zenith or slant direction), the goal of the presented research was to determine the existence of structural dynamics of deviations of x, y, and z coordinates based on the observed GNSS stations in the function of reducing the non-modeled tropospheric error based on relevant and real surface meteorological data.
The basis for determining tropospheric errors within GNSS position accuracy errors was the Saastamoinen model. The proposed model, together with the previously modeled part of the tropospheric error, reduces the tropospheric error of the GNSS position by correlating the unmodeled portion of the tropospheric error with real meteorological parameters, thereby increasing the overall geodetic accuracy of the determined position.
The following section presents the methodology used in the development of the proposed model, including data collection, statistical regression, and the proposed model validation. The obtained verification results for each location and time period are presented in the third section. The performance of the proposed model and the periodicity characteristics of RTE are presented and discussed in the fourth section, including its potential suitability with GPS. Concluding remarks and possible directions for further research are given in the final section.
2. Methodology
The development of the presented model is based on combined GLONASS positioning solutions and meteorological data from GNSS reference stations in the mid-latitudes of the Republic of Croatia. Positioning solutions were calculated based on position data in the Receiver Independent Exchange (RINEX) 2.0 compressed format [39]. Initial theories regarding the development of the model included the assumption that the propagation medium error, the user segment, and the microenvironment errors have a constant time–space character. Initial limitations of the proposed model include:
- The presented methodology implies the creation of the most mutual and frequent alignment of positional and meteorological parameters, and thus the choice of used regional GNSS stations is conditioned (the availability of regional meteorological records is within a 10-min frequency).
- In accordance with the initial spatial limitation, the selection of available GNSS positional data measurements was limited to the GPS and GLONASS, and there was no possibility of using records from other GNSS systems. As a full-fledged part of the GNSS, GLONASS data were used due to their relative underrepresentation in similar research.
- The main goal of the research was to determine a possible statistically significant correlation between realistic surface meteorological parameters and the geodetic accuracy of GNSS position deviations. Therefore, the model was developed based on positional and meteorological data with a geographical resolution of 3.7° × 2.9° (geographical grid) which declared as of regional character.
- The format of the available GNSS data limited the possibilities of their processing. Therefore, single-frequency (L1) positioning and the Klobuchar model for ionospheric delay were used. Input clock parameters and ephemerides are contained in the navigation message (including the broadcast ephemerides and clock parameters). Processing of solid tides and multipath corrections was not accessible.
- Other more accurate positioning techniques, such as PPP (Precise Point Positioning) or RTK (Real-time Kinematics), were not supported.
2.1. Time Frame of the Study
The time frame used for the creation and validation of the proposed model covers the year 2019. The model verification was performed using data from 2014 and 2015. Data from the same locations were analyzed since the model verification required the mutual compatibility of meteorological and GLONASS data at all stages of the study.
2.2. Meteorological Data Collection
The set of meteorological input data was determined based on the relationship between the propagation of radio signals through the neutral atmosphere and tropospheric dynamic processes. Hydrostatic and non-hydrostatic causes of tropospheric delay were identified. The independent input variables for the model were: pressure P (hPa), temperature T (°C), precipitation water PWV (mm), precipitation Pr (mm), and relative humidity Rh (percent). Meteorological data can be interpolated from existing numerical weather models (NWM), which is acceptable for analyzing existing tropospheric models, but not for developing a new model according to the selected regional model development. Therefore, in this study, meteorological data collected using automatic meteorological instruments at selected GNSS locations were used by the State Hydrometeorological Institute of the Republic of Croatia (DHMZ) [40] as a source of meteorological data. The time resolution of the meteorological data was 10 min.
Given the current limitations of available data sources, the study was based on the well-known approach of determining the tropospheric error by determining pseudoranges [10]. The used data delimit the area from 42.60° to 46.38° North latitude and from 15.22° to 18.11° East longitude with an altitude range from 64.3 m to 457.9 m above sea level (Figure 1).
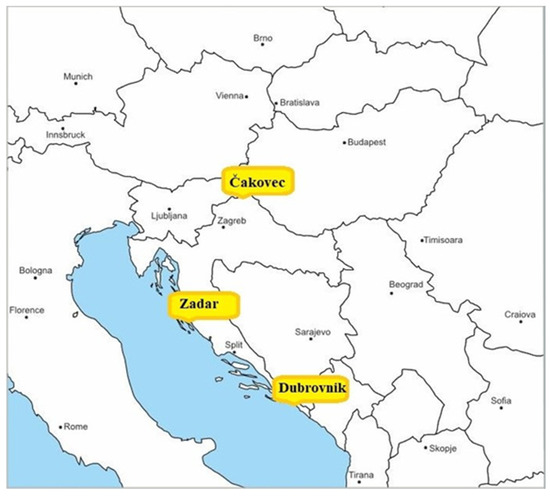
Figure 1.
The wide geographic area of selected GNSS measuring stations.
The climatological profiles of the observed locations differ. According to the Köppen climate classification, which is determined based on the average annual course of air temperature and precipitation, Čakovec is classified as Cb (which is a moderately warm, rainy climate with an average monthly temperature of the coldest month between −3 °C and 18 °C) [41]. At the same time, the warmest month of the year has an average temperature of less than 22 °C [40]. There are no particularly dry months in the year, and it is the area with the least precipitation in the cold season. Čakovec has a humid climate according to Thornthwaite’s climate classification which is based on the ratio of the amount of water needed for potential evapotranspiration and expressed by the humidity coefficient IP/E [41]. Zadar and Dubrovnik belong to areas with a temperate climate with long and hot summers (Ca-mark according to the Köppen climate classification), while Zadar belongs to an area with a subhumid (semi-humid) climate in terms of the humidity coefficient IP/E [42]. Dubrovnik has a humid climate due to heavier precipitation. Water vapor and precipitation amounts are the main meteorological input parameters for determining the non-hydrostatic zenith component of the GNSS position. The above measurement locations do not have significantly pronounced differences in their humidity coefficients; as such, they represent a suitable choice for creating the proposed model, which is also applicable to larger geographical areas with similar climate profiles.
2.3. Geographic GNSS Data Collection
The study was carried out based on data from locations equipped with GNSS stations that provided predicted meteorological parameters with adequate time resolution. Therefore, measuring stations in the Regional Reference Frame Sub-Commission for Europe (EUREF) in Čakovec, Zadar, and Dubrovnik were selected. The basic stations’ data are listed in Table 1 [43].

Table 1.
General data from the EUREF measuring stations used (made by authors according to [43]).
2.4. Model Development
The development of the model involves the harmonization of two parallel input components: the value of the geodetic deviation of the user’s position caused by the tropospheric error and the temporal-spatial harmonization of the corresponding meteorological input data.
2.4.1. Determination of the Size of the Tropospheric Error
Basically, the determination of the tropospheric error by measuring the pseudorange can be conducted in two ways:
(i) by determining and removing all systematic and random errors; and
(ii) by determining the deviation from the known position using a preselected tropospheric model and estimating the deviation residuals as unknown parameters [25].
In the first method, the pseudorange is calculated according to the general formula [10]:
where is the pseudorange from position A to satellite i; is the geometric distance; is l speed of light; is ionospheric and tropospheric delay; is the satellite orbit and clock error; is the multipath trajectories error; is relativistic error; and is the random error.
The multipath error can be determined programmatically, usually based on the receiver and antenna equipment manufacturer. Sources of ionospheric delay, relativistic errors, satellite orbit errors, and clock errors are included in the navigation message or, in the case of post-processing, from the appropriate ground truth data. In any case, it is necessary to perform software processing to ensure appropriate data sources are used for additional corrections. For additional verification, the values of the isolated and determined tropospheric delays of a known position were compared with the values determined using the radiosonde signals or another system [10].
The model development was based on the determination of the user’s position in accordance with the selected modeling approach and its initial limitations. It was obtained by determining the pseudoranges and isolating the accuracy deviation from the user’s position caused by the tropospheric error within the total positioning error. A position determined in this way can be defined in a simpler form as the difference between the signal reception time which is determined based on its clock and time (determined by the satellite clock), which can be represented with the following expression [4,44]:
where is the pseudorange of the i-th satellite; is the time of the signal reception determined by the receiver clock (s); and is the time of signal transmission determined by the satellite clock (s).
The misalignment of the satellite and receiver clocks (with input data contained in the navigation message), the ionospheric, tropospheric, and measurement error, and the expression (2) takes the form (3) by introducing the parameters of the geometric distance between the antennas of the satellite and the receiver:
where is the geometric distance between the satellite and receiver antenna; is the receiver and satellite clock offset; is the ionospheric error; is the tropospheric error; and is the measurement error.
The conversion of the geodetic position into a data set in ECEF ETRS89 format with values expressed in meters is expressed according to the following expressions:
where is the geodetic longitude; is the geodetic latitude; is the ellipsoidal height; is the semi-major axis of the reference Earth ellipsoid (6,378,137 m) is the first numerical eccentricity of the ellipsoid; and is the flattening coefficient of the reference Earth ellipsoid.
The Saastamoinen model of tropospheric zenith correction was used, and the present parameters were transmitted in the navigation message as a common source of input program corrections for all measuring stations and periods and for standardizing other program settings. The input program parameters for pressure, absolute temperature, and partial pressure are determined by the expressions of the standard atmosphere model [44]:
where is the total air pressure (hPa); is the temperature in degrees Kelvin; is the partial atmospheric pressure (hPa); is the geodetic altitude above sea level; and is the relative humidity. The applied Saastamoinen model uses a constant relative humidity value of 70%.
The tropospheric correction in this configuration was calculated using the following algorithms [45,46]. For the mapping function in the selected program setting, the Niell model is calculated according to the expression [47,48,49]:
where is the signal elevation angle; is the signal zenith angle; is the tropospheric gradient in the north direction; is the tropospheric gradient in the east direction; and is the non-hydrostatic mapping function of the non-hydrostatic Niell (New) Mapping Functions (NMF).
The total tropospheric delay was calculated according to the following expression:
where is the total tropospheric delay; is the hydrostatic component of zenith tropospheric delay (in meters and determined by the Saastamoinen model); is the tropospheric total zenithal retardation; and is the (NMF) hydrostatic mapping function. The parameters of tropospheric gradients and total tropospheric delay in zenith direction were estimated using the extended Kalman filter (EKF) [45]. The parameters for the correction of the ionospheric delay (A—the numerical coefficient of the maximum total free electron content in the ionospheric layer F2; F—the index of solar activity; and Ap—the daily index of geomagnetic activity) included in the GLONASS navigation message (broadcast ionosphere model) [47] have the following form:
The determination of ionospheric delay ^ (m) was performed using Klobuchar’s model due to single-frequency computing. Despite the efficiency of Klobuchar’s model, more effective reducing of the ionospheric delay would be achieved using an iono-free combination or dual-frequency receiver. However, considering the format of available input data, a single-frequency receiver with the Klobuchar model was used. Input data regarding clock parameters and ephemerides were sent in the navigation message (broadcast ephemerides and clock parameters) and used in calculations in the following form [44,46,50]:
In addition, the initial software setup included a single positioning mode and a 3° elevation mask value (due to the scope of applicability of the NMF mapping function) to isolate the deviation in the geodetic accuracy of the user’s position caused by the tropospheric error component.
2.4.2. Statistical Analysis and Model Development
The remaining value of the tropospheric error was determined based on the difference in the geodetic accuracy of the position determined both with and without tropospheric correction (using the Saastamoinen model). It is important to emphasize that, in addition to the tropospheric component, such determined deviations still contain several unmodeled systematic and random errors, including the residual ionospheric error, the satellite position and clock error, errors related to multipath, and solid tides. However, the only input difference when comparing the accuracy of the geodetic position was the application of the Saastamoinen model of tropospheric correction (as the other applied algorithms were identical); therefore, the effect of the resulting final difference between the two models can be deterministically attributed to the tropospheric component within the total geodetic position error.
The difference in geodetic accuracy of the user’s position can be analyzed as a function of the influence of the applied Saastamoinen model of tropospheric delay correction since all other parameters were set identically in both cases. This provided the theoretical basis for quantifying the effect of the Saastamoinen model on improving the geodetic accuracy of the observed GNSS positions.
The resulting RTE value of the known position caused by the non-modeled part of the tropospheric delay was subjected to a statistical regression procedure to determine the correlation with real meteorological surface parameters. Statistical correlation with its positive parameters are the basis for developing a mathematical model to reduce RTE as a function of surface meteorological parameters (as independent input variables).
The stages in the creation of the proposed model are shown in Figure 2.
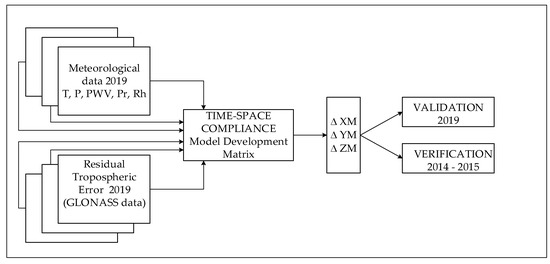
Figure 2.
The proposed model development.
Meteorological independent input variables are as follows: is the temperature (°C); is the precipitation (mm); is the relative humidity (percentage); is the precipitation water (mm); is the pressure (hPa); and , , and are deviations along the x, y, and z axes in the proposed model (m).
The proposed model contains a mathematical expression for each axis as the observed deviation from the exact geodetic position followed the ECEF coordinate system. The final form of the proposed model is shown as follows. The amounts of the coefficients of the input predictors are the result of the regression analysis that describes the form and intensity of the mutual connection between the meteorological input predictors and the output variable RTE. For the X axis, the model component has the form:
For the Y axis, the model component has the form:
For the Z axis, the model component has the form:
The final form of the proposed model () is based on an extension of the existing Saastamoinen model and represents the sum of the corrections made by the Saastamoinen model and the proposed model for each axis:
where is the correction value realized by the Saastamoinen model (in m).
2.4.3. Validation of the Proposed Model
Validation was performed using the cross-validation method with a 50:50 train-test ratio. Common statistical indicators of significance of the model components for a single coordinate axis include p value, multiple correlation coefficients, multiple determination, and adjusted determination coefficient. The results are shown in Table 2.

Table 2.
Statistical indicators of the proposed model validation.
The obtained results show statistically significant correlations (upper limit p = 0.05), i.e., there is a statistically significant correlation between the independent input variables (the meteorological parameters) and the dependent output variable (RTE) for each coordinate axis, expressed by the Equations (14)–(16). The obtained correlation coefficients show: (i) the presence of a statistically significant correlation between the input predictors and the dependent variable in all components of the proposed model; (ii) a statistically significant prediction of the criterion variable by the input predictors in all components of the proposed model; and (iii) a statistically significant relationship between the obtained correlation, the number of samples (the input records), and the number of input variables (the predictors) of all components of the proposed model. Although the existence of a statistically significant connection between the input predictors and the output RTE variable is shown, the realized adjusted determination coefficients show different connection intensities, which is evident considering the associated low values of the coefficients of the input predictors in the model component for the y axis.
3. Results and Findings
The verification of the proposed model was performed using independent input data and meteorological data from the same locations for the period of 2014–2015. The coordinates of the geodetic positions for the period of 2014–2015 were calculated in an identical way and with the same input algorithms as the geodetic positions for 2019. The proposed model was created on this basis. The fundamental parameter that highlights the success of the proposed model is the reduction of the RMSE deviation of the positional accuracy compared to the positional accuracy achieved exclusively by the Saastamoinen model. The verification process was performed separately for each location and period. The movement of the coordinates along the coordinate axes in the horizontal and vertical planes and the inversion of the deviation of individual coordinates were observed using the proposed validated and verified empirical model; for example, y and z are complexly and graphically shown on a series of diagrams provided in Appendix A of the paper.
3.1. Verification for Čakovec Location
The correction values generated by the proposed model are shown in Table 3.

Table 3.
Values of RTE corrections by the proposed model for Čakovec GNSS location (in m).
The proposed model generates negative RTE correction values for coordinate axes y and z for 2014 and 2015. For the x axis, corrections were made in the range of −0.65 m to 1.69 m (for both years). The absolute amounts of the corrections range from 0.04 m (y-axis in 2014) to 2.46 m (x-axis in 2015).
The values of the RMSE, the standard deviation (STD), and the associated statistical parameters for the Čakovec GNSS position are shown in Table 4.

Table 4.
Comparison of RMSE, STD, range, and median values for the Čakovec GNSS location obtained using the Saastamoinen model and the proposed model (in m).
Application of the proposed model shows that values of the minimum and maximum deviations do not change significantly with ranges remaining approximately within the usual scale. There was a noticeable tendency for one deviation value to decrease while the opposite value increased and their absolute range values remained the same. Moreover, both minimum and maximum deviation values of the z axis decreased in the proposed model for the observed year of 2014.
The 2014 results showed a simultaneous improvement in the accuracy of the position RMSE value, which is the basic parameter for the success of the proposed model. Improvements in accuracy were obtained for the x-axis (10.04 cm/2.73%), y-axis (0.09 cm/0.04%), and z-axis (15.85 cm/3.38%). At the same time, the parameter STD improved for the x- and z-axis, and the value STD decreased for the y-axis (−0.03 cm/−0.01%). An improvement of the measurement frequency distribution was also observed. In 2014, the median value obtained with the proposed model for all axes decreased and approached the initial value of the deviation (zero), and in 2015, an improvement of the median value of the x- and z-axes and a deterioration of the y-axis was observed. An improvement in position accuracy was seen when comparing the RMSE values over the indicated period. For 2015, the proposed model simultaneously improved the x-axis position accuracy (14.26 cm/3.87%) and the z-axis accuracy (7.56 cm/1.84%), but it simultaneously worsened the y-axis position accuracy (−0.75 cm/−0.32%). It is clear that an overall improvement in position accuracy was achieved when observing the ratio of improvement and the deterioration of the overall position accuracy at the same time.
3.2. Verification for Zadar Location
The correction values generated by the proposed model are shown in Table 5.

Table 5.
Values of RTE corrections based on the proposed model for Zadar GNSS location (in m).
It can also be seen that the values of generated RTE corrections for the GNSS station in Zadar were negative for the y and z axes in the observed period and ranged from −0.85 m to 0.9 m for the x axis. The absolute corrections’ values ranged from 0.055 m (y-axis in 2014) to 1.74 m (x-axis in 2015). The statistical parameters RMSE, STD, range, and median for the Zadar GNNSS position are shown in Table 6.

Table 6.
Comparison of the achieved values of RMSE, STD, minimum, maximum, and median values for the Zadar GNSS position obtained using the Saastamoinen model and the proposed model (in m).
Comparison of the parameters showed that the proposed model did not have a significant effect on the reduction of the final values of the accuracy deviations, and the range of the minimum and maximum values remained approximately the same. However, there was a significant change in the grouping values of the measurement frequencies for 2014 in all coordinate axes. For 2015, a positive shift of the median was obtained for the x and z axes, and an additional deviation from the zero value was registered for the y axis (0.26 m versus 0.10 m). The 2014 results showed an improvement in the accuracy of the RMSE value of the position at the same time for all axes. Accuracy improvements were obtained for the x-axis (3.33 cm/0.78%), the y-axis (0.9 cm/0.37%), and the z-axis (22.71 cm/4.33%). The parameter STD improved for the x-axis, and the value STD decreased for the y-axis (−0.03 cm/−0.01%) and the z-axis (−0.006 cm/−0.001%). For 2015, the results of the predictive model showed the RMSE values of the x-axis (11.21 cm/2.6%) and the z-axis (1.45 cm/0.35%), while the y-axis had a decrease in the RMSE value (−1.65 cm/−0.65%). The same tendency was seen in the parameter STD: the x-axis and z-axis obtained improvements, and a deterioration of the y-axis STD value (−0.03cm/−0.01%) was recorded.
3.3. Verification for Dubrovnik Location
The correction values generated by the proposed model for the Dubrovnik GNSS location are shown in Table 7.

Table 7.
Values of the RTE corrections based on the proposed model for the Dubrovnik GNSS location (in m).
The values shown indicated that the model generated negative correction amounts of RTE for the y- and z-axes over the observed two-year period and values within the limits of −0.96 m to 1.69 m for the x-axis. The values of the absolute correction amounts ranged from 0.047 m (y-axis in 2014) to 2.33 m (x-axis in 2014). The values of the RMSE, standard deviation (STD) and associated statistical parameters for Dubrovnik GNSS position are shown in Table 8.

Table 8.
Comparison of the realized values of RMSE, STD, range, and medians for the Dubrovnik GNNSS position obtained using the Saastamoinen model and the proposed model (in m).
Analysis of the presented accuracy parameters showed that the proposed model contributed to a deterioration of the RMSE value in 2014 for the x-axis (−1.35 cm/−0.3%), while it improved the accuracy of the other two axes, especially the z-axis (23.87 cm/4.37%), and also the y-axis (2.5 cm/0.92%). As for the two previously observed positions, there was no significant change in the value for the deviations range. An improvement in accuracy was observed for the median parameter in 2014 in the y and z axes, and an increase in the deviation was recorded for the x axis (from -0.17 m to 0.54 m). The parameter STD improved in the x-axis (1.78 cm/0.39%) and worsened in the y-axis (−0.004 cm/−0.001%) and z-axis (−0.12 cm/−0.02%).
For 2015, the proposed model improved the accuracy (parameter RMSE) of the x-axis (2.2 cm/0.57%), y-axis (0.3 cm/0.13%), and z-axis (11.15 cm /2.52%). The value of STD also improved for the x-axis, while it decreased for the y-axis (−0.03 cm/−0.01%) and the z-axis (−0.14 cm/−0.03%). At the same time, there were shifts in the median value toward the central value for all axes, with shifts on the y-axis (from −1.679 to 0.03 m) and the z-axis (from −3.84 to 0.53 m).
4. Discussion
Summary results of the verification procedure for the observed locations are presented in Table 9. The table contains data obtained by comparing the RMSE and STD parameters of the position accuracy obtained using the Saastamoinen model and the proposed model for all observed locations within the observed time frame.

Table 9.
Total results of RMSE and STD values achieved using the proposed model.
Positive values represented an increase in RMSE and STD values, i.e., a decrease in position accuracy, while negative values represented a decrease in the aforementioned statistical parameters, i.e., an increase in geodetic position accuracy. The graphical results of the performance of the proposed model are shown in Figure 3 and Figure 4 where the curve represents the relative value (in percentages) and the columns represent the absolute amount (in cm).
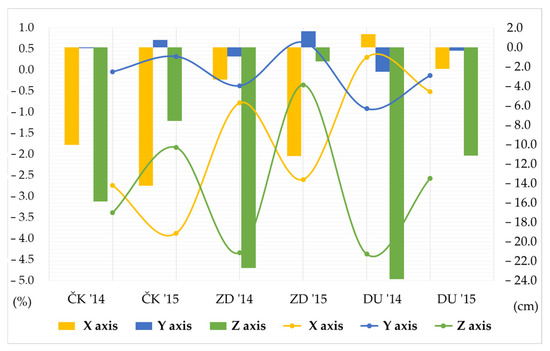
Figure 3.
Movement of RMSE deviation values using the proposed model from the exact geodetic position of the observed locations expressed in absolute (right y-axis) and relative (left y-axis) values.
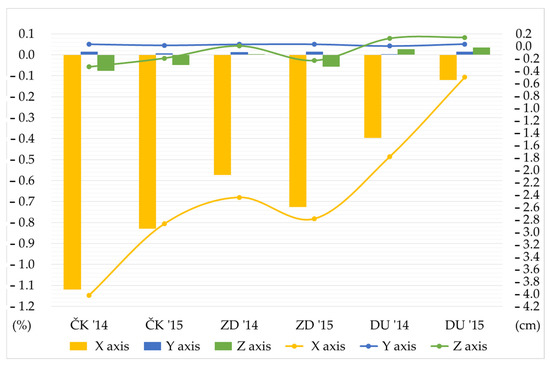
Figure 4.
Movement of the parameter STD using the proposed model of observed locations expressed in absolute (right y-axis) and relative (left y-axis) values.
The presented results of RMSE as the main performance parameter showed that the proposed model improved the overall geodetic accuracy of the observed positions. The x-axis position deviations decreased for five measurements, while the deviations in the y-axis and especially in the z-axis decreased simultaneously (Dubrovnik, 2014).
The model for the y-axis achieved a decrease in the deviation in four measurements, while where there was an increase in the deviation in the remaining measurements (Čakovec, 2014 and Zadar, 2015), and there improvement in the accuracy of the position along the second horizontal x-axis was achieved in addition to the improvement achieved along the vertical z-axis.
The results of the obtained STD values as measures of the variability of the obtained results were half-hearted (partial). Improvement was obtained in nine measurements and worse results were obtained in the other nine measurements, as shown in Figure 4. It is important to point out that the absolute amounts of the obtained worse results were within the limits of 0.0014 cm to 0.1448 cm, although they were nominally worse than the STD value obtained using the Saastamoinen model. Considering the mentioned amounts, the obtained worse results can be ignored in further interpretation of the results and evaluation of the study’s success.
4.1. Model Suitability for Application within the GPS
The proposed model shows a certain degree of success in the application within the GPS, although it was developed on the basis of GLONASS position records. The results showing the movement of the RMS parameter are shown in Figure 5.
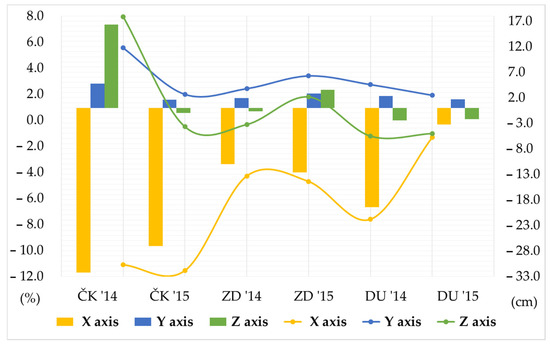
Figure 5.
Movement of the RMSE deviation value using the proposed model from the exact geodetic position of the observed locations obtained using a GPS system and expressed in absolute (right y-axis) and relative (left y-axis) values.
The proposed model generally increases geodetic accuracy throughout the verification period. The RMS value of the x-axis deviation for all cities in the entire verification period reduced with absolute reduction amounts ranging from 3.29 cm to 32.26 cm (1.32–11.08%). At the same time, the geodetic accuracy decreased along the y-axis for the absolute values from 1.64 cm to 4.77 cm (1.09% to 5.54%). In the z axis, the model showed a variable result: it achieved an improvement in four of the six measurements (in absolute amounts from 0.65 cm to 2.49 cm, i.e., 0.34% to 1.23%). In the remaining two measurements, the proposed model degraded geodetic accuracy (varying from 3.55 cm to 16.32 cm, i.e., 1.78% to 7.95%). Differences in the model’s ability to reduce the residual tropospheric delay of the satellite signal when compared to GPS are due to a number of reasons, including the different spatial constellation of systems, differences in modulations of the satellite navigation signals, etc. For adequate results within the GPS, a regression analysis should be performed as a function of the interdependence of meteorological input predictors and RTE output variables based on GPS positional data, which further observes and analyzes the dynamics and variations of RTE movements.
As expected, the results do not achieve an improvement as with the GLONASS system. Given the time and space limitations of the research, GLONASS was chosen as an affirmed part of the GNSS system since the main goal of the research was the development and adoption of a methodology based on statistical analysis. However, the verification of the proposed model using GPS data showed the potential of the adopted approach and the possibility of further development based on the input of multi-GNSS positioning data for a wider GNSS application.
4.2. Periodic Effect of the Proposed Model on the Positioning Accuracy
The proposed model showed the possibility of a quantitative influence on the reduction of the tropospheric error which increases the accuracy of GLONASS positions. The tropospheric error is a stochastic phenomenon due to natural causes; however, the conducted research proves the possibility of developing a statistically significant correlation between tropospheric dynamics (expressed as a set of meteorological parameters) and the improvement of GNSS position accuracy. The regularity of the movement of the absolute differences of the values of RTE according to the proposed and Saastamoinen models can be observed; thus, indirectly, the movement of the geodetic accuracy achieved via the GLONASS system can also be observed. The annual motions shown in Figure 6, Figure 7 and Figure 8 (see Appendix A for additional Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6 and Figure A7) show the annual oscillation for each position axis. The value for the x-axis is shown in the upper part of the graph, while the middle part of the graph shows the values for the z-axis, and the lower part of the graph shows the realized values for the z-axis. The property of periodicity of the motion manifests itself at smaller temporal resolutions—for example, at quarterly or monthly time frames—regardless of the selected GNSS position (see Appendix A: GNSS Position Zadar 2015).
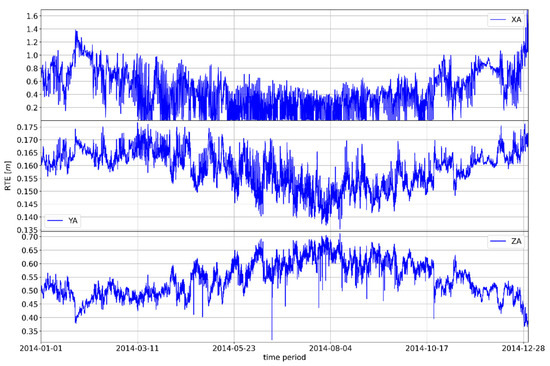
Figure 6.
Movement of the absolute difference of the parameter RTE at the GNSS position Čakovec in 2014.
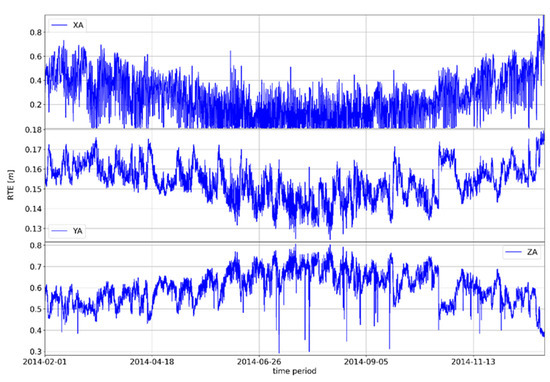
Figure 7.
Movement of the absolute difference of the parameter RTE at the GNSS position Zadar in 2014.
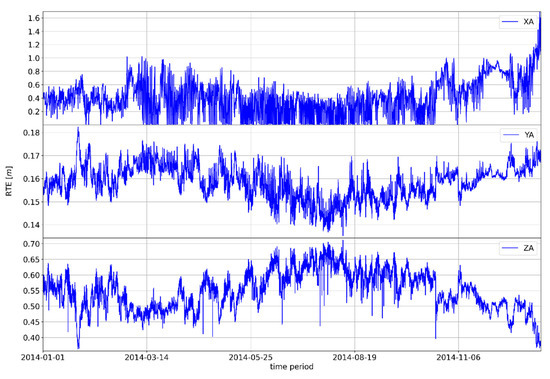
Figure 8.
Movement of the absolute difference of the parameter RTE at the GNSS position Dubrovnik in 2014.
The annual trends in the difference of shown absolute RTE deviations clearly indicate the seasonal nature of the tropospheric error. On the x-axis, the difference in absolute RTE deviations typically reaches a maximum in the winter months, although the upper values of the deviations may also occur in the later periods of spring or autumn, i.e., in summer in the case of climatological deviations for the mentioned seasons.
The same pattern of correlation of the differences in absolute deviations from RTE along the y and z axes is evident in the other two observed GNSS positions. There are differences in the absolute values (amounts) of the RTE deviation difference, but there are no differences in the general distribution of the measured RTE deviation difference.
4.3. Observations on the Specifics of the Conducted Research
The dynamic specificities of the presented relationship between the positioning accuracy and the absolute values of the RTE difference are shown in the vertical level in the direction of the z-axis (regarding the relationship with the zenith angle of the incoming radio navigation signal) and in the horizontal plane in the direction of the y-axis. The vertical plane is defined by the y- and z-axes; therefore, improvement in the positional accuracy is expressed in such a way that the increase in deviation along the y-axis is followed by a decrease in deviation along the z-axis and vice versa. At the horizontal level, the deviation along the x-axis is somewhat proportionally related to the value achieved along the y-axis. Simultaneous deviations along the y- and z-axis show the mutual relationship achieved at the vertical level which they jointly define in the observed space as the starting point.
It is possible to define the RTE vector using the origin in the center O of the coordinate space (Oxyz) based on analytical interpretation of the accuracy dynamics of GNSS positions (observed based on the movement of the difference of the absolute values of RTE realized by the Saastamoinen model and the proposed model where the reduction of the parameter RTE improves the geodetic accuracy of the GNSS position). The motion of the RTE vector within the stationary Oxyz system describes the translational motion of the RTE parameter/point within the available (six) degrees of freedom. The proposed model shows improvement of the RTE parameter within the observed Oxyz system of taking the position (or the reduction of the RTE parameter) independent of time where the specified property of the Oxyz system is also independent of time [51]. Therefore, it is justified to conclude that the observed GNSS system has reached a state of statistical position equilibrium. The original assumption was that a decrease in the RTE parameter leads to a decrease in the tropospheric error which increases the geodetic accuracy of the position. The observed GNSS GLONASS system also reaches this state due to the realized movement of the RTE parameter.
5. Conclusions
The proposed model showed its success by reducing deviations from exact GNSS geodetic positions by acting on the non-modeled part of the tropospheric error. The basis of the proposed model was the existing Saastamoinen model, and correction values (obtained using the proposed model) for each axis should have been added to this model. The proposed model needs meteorological input parameters which can be interpolated from a given standard weather model depending on availability; alternatively, standard predicted input values can be used (as is the case of the absence of meteorological parameters in the Saastamoinen model).
The proposed model was verified at the same GNSS stations within a two-year period. The proposed model showed an improvement in position accuracy achieved by reducing the residual tropospheric error when compared to the Saastamoinen model. The model did not achieve a simultaneous improvement in all axes for all locations during the entire verification period, but it demonstrated superiority over the Saastamoinen model. Improvements in the horizontal axes of the position up to a maximum of 3.87% were achieved (14.26 cm), while the accuracy of the second horizontal axis reduced by 0.65% (1.65 cm) for two measurements. At the same time, the accuracy of the height component of the position improved in all measurements to a maximum of 4.37% (23.87 cm).
The proposed model must be used programmatically (software) as a complement to the Saastamoinen model, although there are certain limitations in terms of the geographical area of application, i.e., the possibility of application in areas with similar climate profiles. At the same time, the optimal application areas of the proposed model are found in stationary and dynamic systems to determine the position of the user in real time with lower accuracy. Therefore, it is clear that the model can be used within the existing application areas of the Saastamoinen model with all existing limitations and advantages.
An additional result of the applied methodology and the use of the RTE parameter is the statistical position equilibrium of the observed GNSS GLONASS positions defined by the oscillation around the central position values within the Oxyz-space. The model was developed based on GLONASS position data; however, it also shows a certain level of success in the verification of geodetic positions based on GPS position. The possible continuation of this research includes applying this suggested approach to developing a model based on multi-GNSS positioning data and verifying its effectiveness with other available GNSS systems. Future research of this type will be focused on determining the positional statistical balance of the X, Y, and Z coordinates along the x, y, and z coordinate axes as a function of various satellite navigation arguments.
Author Contributions
Conceptualization, S.K. and M.B.; methodology, S.K. and M.B.; software, M.B.; validation, S.K., Z.M. and D.B.; formal analysis, M.B. and Z.M.; investigation, M.B.; resources, D.B.; data curation, M.B.; writing—original draft preparation, S.K. and M.B.; writing—review and editing, D.B.; visualization, M.B.; supervision, S.K. and D.B.; project administration, D.B.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The GNSS observation data are available at http://www.epncb.oma.be/index.php (accessed 29 August 2021). Meteorological data are available at https://meteo.hr/proizvodi.php?section=katalog_zahtjevi¶m=zahtjev_podaci_usluge upon request (accessed 29 August 2021).
Acknowledgments
This work was fully supported by the University of Rijeka under the project uniri-tehnic 18-66: Research of environmental impacts on satellite navigation systems.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations were used in the manuscript:
| DHMZ | Croatian Meteorological and Hydrological Service |
| ECEF | Earth Centered, Earth Fixed |
| EKF | Extended Kalman Filter |
| EUREF | Regional Reference Frame Sub-Commission for Europe |
| GLONASS | Global Navigation Satellite System |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| NMF | (New) Mapping Functions |
| NWM | Numerical Weather Models |
| PPP | Precise Point Positioning |
| PWV | Precipitable Water Vapor |
| RINEX | Receiver Independent Exchange |
| RMSE | Root Mean Square Error |
| RTE | Residual Tropospheric Error |
| RTK | Real-time Kinematics |
| SBAS | Satellite-based Augmentation Systems |
| STD | Standard Deviation |
| ZHD | Zenith Hydrostatic Delay |
| ZTD | Zenith Tropospheric Delay |
| ZWD | Zenith Wet Delay |
Appendix A
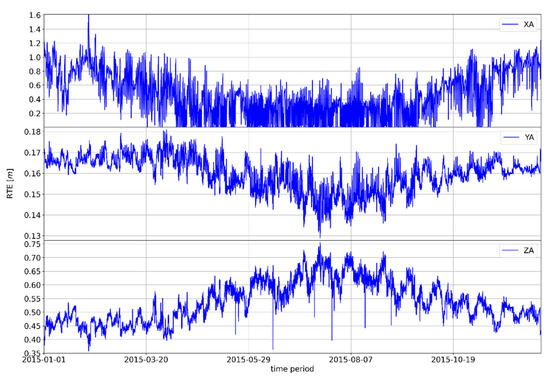
Figure A1.
Movement of the absolute difference of the RTE GNSS Čakovec position parameter in 2015.
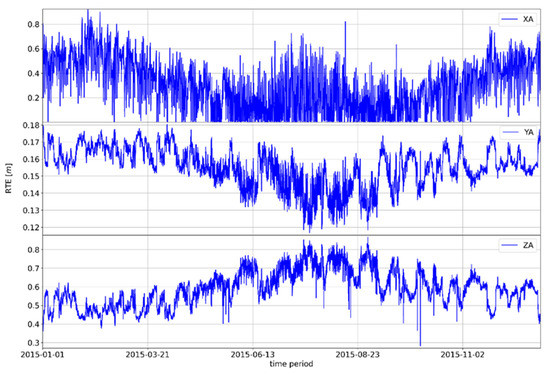
Figure A2.
Movement of the absolute difference of the RTE GNSS Zadar position parameter in 2015.
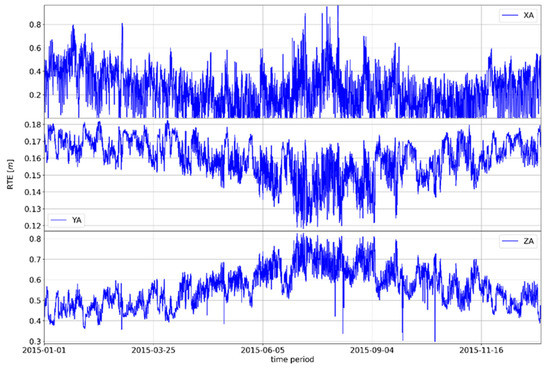
Figure A3.
Movement of the absolute difference of the RTE GNSS Zadar position parameter in 2015.
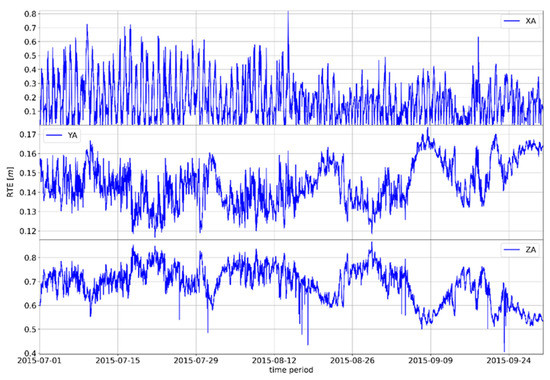
Figure A4.
Movement of the absolute difference of the RTE GNSS Zadar position parameter in the period July–September 2015.
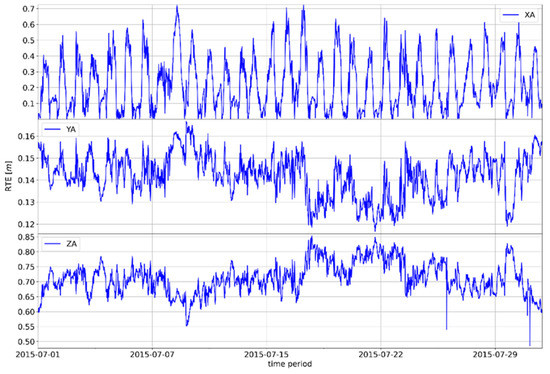
Figure A5.
Movement of the absolute difference of the RTE GNSS position parameter in Zadar, July 2015.
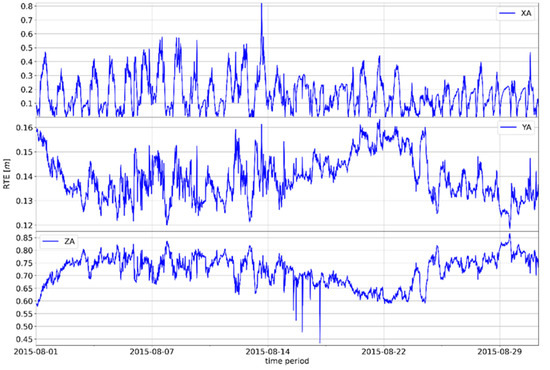
Figure A6.
Movement of the absolute difference of the RTE GNSS position in Zadar, August 2015.
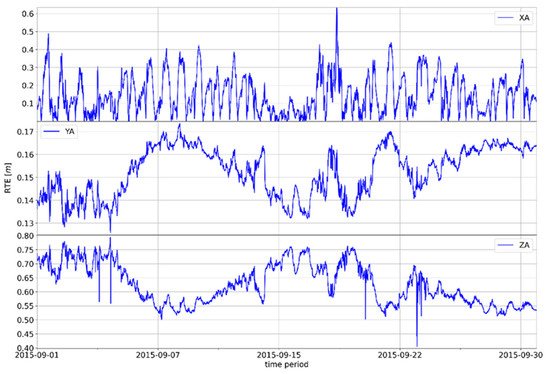
Figure A7.
Movement of the absolute difference of the RTE GNSS position parameter in Zadar, September 2015.
References
- Ansari, K.; Jamjareegulgarn, P. Effect of Weighted PDOP on Performance of Linear Kalman Filter for RTK Drone Data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3513504. [Google Scholar] [CrossRef]
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS: Principles and Application, 2nd ed.; Artech House: Boston, MA, USA, 2006. [Google Scholar]
- Brčić, D.; Ćelić, J.; Valčić, S. Reconstruction of Geomagnetic Event as Observed in Northern Adriatic Region and Its Correlation with GPS Single-frequency Positioning Deviations. Int. J. Mar. Navig. Saf. Sea Transp. 2020, 14, 349–357. [Google Scholar] [CrossRef]
- Subirana, J.S.; Zornoza, J.M.J.; Hernández-Pajares, M. GNSS DATA PROCESSING Volume I: Fundamentals and Algorithms Acknowledgements; ESA Communications ESTE: Leiden, The Netherlands, 2013. [Google Scholar]
- Elektronika, Uređaji. Širenje Valova. In Tehnička Enciklopedija; LZMIK: Zagreb, Croatia, 1998; pp. 623–627. [Google Scholar]
- Ustinov, U.M.; Afanasev, V.V.; Pripotnyuk, A.V.; Marinich, A.N. Судoвые Радиoлoкациoнные Системы, 3rd ed.; Веленара: Sankt-Petersburg, Russia, 2009. [Google Scholar]
- Jin, S.P.; Cardellach, E.; Xie, F. GNSS Atmospheric and Multipath Delays. In GNSS Remote Sensing; Springer: Dordrecht, The Netherlands, 2014; Volume 19, pp. 17–30. [Google Scholar]
- El-Arini, M.B. Tropospheric Effects on GNSS Bertram Arbesser-Rastburg. In Proceedings of the Atmosphere and its Effect on GNSS Systems, Santiago, Chile, 14–16 April 2018; pp. 146–165. [Google Scholar]
- Dodo, S.Y.; Ojigi, J.D.; Tsebeje, L.M. Determination of the best-fit Tropospheric Delay Model on the Nigerian Permanent GNSS Network. J. Geosci. Geomat. 2015, 3, 88–95. [Google Scholar]
- Katsougiannopoulos, S.; Pikridas, C.; Rossikopoulos, D.; Ifadis, I.M.; Fotiou, A. Tropospheric Refraction Estimation Using Various Models, Radiosonde Measurements and Permanent GPS Data. In Proceedings of the XXIII FIG Congress, Munich, Germany, 8–13 October 2006. [Google Scholar]
- Hopfield, H.S. Two-quartic tropospheric refractivity profile for correcting satellite data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géodésique 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Pershin, D.Y. Comparative analysis of tropospheric delay models in precise point positioning in satellite navigation systems GLONASS/GPS. Вестник Нoвoсибирскoгo Гoсударственнoгo Университета. Серия: Инфoрмациoнные Технoлoгии 2009, 7, 84–91. [Google Scholar]
- Marini, J.W. Correction of Satellite Tracking Data for an Arbitrary Tropospheric Profile. Radio Sci. 1972, 7, 223–231. [Google Scholar] [CrossRef]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Ifadis, I.M. The excess propagation path of radio waves: Study of the influence of the atmospheric parameters on its elevation dependence. Surv. Rev. 2013, 31, 289–298. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Shrestha, S.M. Investigations into the Estimation of Tropospheric Delay; University of Calgary: Calgary, AB, Canada, 2003. [Google Scholar]
- Kleijer, F. Troposphere Modeling and Filtering for Precise GPS Leveling; Delft University of Technology: Delft, The Netherlands, 2004. [Google Scholar]
- Xia, P.; Xia, J.; Ye, S.; Xu, C. A new method for estimating tropospheric zenith wet-component delay of gnss signals from surface meteorology data. Remote Sens. 2020, 12, 3497. [Google Scholar] [CrossRef]
- Dousa, J.; Elias, M. An improved model for calculating tropospheric wet delay. Geophys. Res. Lett. 2014, 41, 4389–4397. [Google Scholar] [CrossRef]
- Parameswaran, K.; Saha, K.; Raju, S.C. Development of a regional tropospheric delay model for GPS-based navigation with emphasis to the Indian Region. Radio Sci. 2008, 43, 1–10. [Google Scholar] [CrossRef]
- Parameswaran, K.; Raju, C.S.; Saha, K. Region-specific Tropospheric Delay Model for the Indian Subcontinent. In Proceedings of the ICG-Meeting, Bangalore, India, 5–7 September 2007. [Google Scholar]
- Isioye, O.A.; Combrinck, L.; Botai, J. Performance Evaluation of Blind Tropospheric Delay correction Models over Africa. S. Afr. J. Geomat. 2015, 4, 502. [Google Scholar] [CrossRef][Green Version]
- Hu, Y.; Yao, Y. A new method for vertical stratification of zenith tropospheric delay. Adv. Sp. Res. 2019, 63, 2857–2866. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Zhang, C.; Li, Y.; Li, J. A regional zenith tropospheric delay (Ztd) model based on Gpt3 and Ann. Remote Sens. 2021, 13, 838. [Google Scholar] [CrossRef]
- Morel, L.; Pottiaux, E.; Durand, F.; Fund, F.; Boniface, K.; Junior, P.S.d.; van Baelen, J. Validity and behaviour of tropospheric gradients estimated by GPS in Corsica. Adv. Sp. Res. 2015, 55, 135–149. [Google Scholar] [CrossRef]
- Deng, Z.; Bender, M.; Zus, F.; Ge, M.; Dick, G.; Ramatschi, M.; Wickert, J.; Löhnert, U.; Schön, S. Validation of tropospheric slant path delays derived from single and dual frequency GPS receivers. Radio Sci. 2011, 46, 6007. [Google Scholar] [CrossRef]
- Mohammed, A.N.; Abdelfatah, M.A.; Mousa, A.E.K.; El-Fiky, G.S. Regional Egypt tropospheric mapping function model. Alex. Eng. J. 2018, 57, 4157–4165. [Google Scholar] [CrossRef]
- Younes, S.A.M.; Afify, H.A. Accuracy improvement of tropospheric delay correction models in space geodetic data. Case study: Egypt. Geod. Cartogr. 2014, 40, 148–155. [Google Scholar] [CrossRef][Green Version]
- Yang, Y.F.; Chen, X.P.; Yao, M.H.; Zhou, C.L.; Liao, C.M. Research on zenith tropospheric delay modeling of regional cors network. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLII-3/W10, 1197–1200. [Google Scholar] [CrossRef]
- Dodo, J.D.; Ekeanyanwu, U.O.; Ono, M.N. Evaluation of Five Tropospheric Delay Models on Global Navigation Satellite System Measurements in Southern Nigeria. J. Geosci. Geomat. 2019, 7, 201–211. [Google Scholar] [CrossRef]
- Li, F.; Zhang, Q.; Zhang, S.; Lei, J.; Li, W. Evaluation of Spatio-Temporal Characteristics of Different Zenith Tropospheric Delay Models in Antarctica. Radio Sci. 2020, 55, e2019RS006909. [Google Scholar] [CrossRef]
- Krueger, E.; Schueler, T.; Arbesser-rastburg, B. The Standard Tropospheric Correction Model for the European Satellite Navi−Gation System Galileo. In Proceedings of the General As-sembly URSI, New Delhi, India, 2005; Available online: https://www.researchgate.net/profile/Bertram_Arbesser−Rastburg/publication/252717445_THE_STANDARD_TROPOSPHER-IC_CORRECTION_MODEL_FOR_THE_EUROPEAN_SATELLITE_NAVIGATION_SYSTEM_GALILEO/links/00b4952c318413b26d000000/THE−STANDARD−TROPOSPHERIC−CORRECTION−MODEL−FOR−THE−EUROPEAN−SATELLITE−NAVIGATION−SYSTEM−GALILEO.pdf (accessed on 30 November 2021).
- Snajdrova, K.; Boehm, J.; Willis, P.; Haas, R.; Schuh, H. Multi-technique comparison of tropospheric zenith delays derived during the CONT02 campaign. J. Geod. 2006, 79, 613. [Google Scholar] [CrossRef]
- Ajayi, G. Physics of the Tropospheric Radiopropagation; International Centre for Theoretical Physic: Trieste, Italy, 1989. [Google Scholar]
- Grabner, M.; Kvicera, V. Atmospheric Refraction and Propagation in Lower Troposphere. In Electromagnetic Waves; Prentice Hall: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Coleman, C.J. A direction-sensitive model of atmospheric noise and its application to the analysis of HF receiving antennas. Radio Sci. 2002, 37, 3-1–3-10. [Google Scholar] [CrossRef]
- Hatanaka, Y. A Compression Format and Tools for GNSS Observation Data. Bull. Geogr. Surv. Inst. 2008, 55, 21–30. [Google Scholar]
- DHMZ—Državni Hidrometeorološki Zavod. Available online: http://meteo.hr/index.php (accessed on 28 November 2021).
- Volarić, B.; Lisac, I. Klimatska podjela Hrvatske prema značajkama godišnjeg hoda temperature zraka. Acta Geogr. Croat. 1984, 19, 3–11. [Google Scholar]
- Tadić, M.P.; Čapka, G.M.; Zaninović, K.; Cindrić, K. Drought Vulnerability in Croatia. Agric. Conspec. Sci. 2014, 79, 31–38. [Google Scholar]
- EUREF Permanent GNSS Network. Available online: http://www.epncb.oma.be/index.php (accessed on 16 August 2021).
- RTKLIB: Documents. Available online: http://www.rtklib.com/rtklib_document.htm (accessed on 10 November 2021).
- Astudillo, M.J.; Lau, L.; Tang, Y.T.; Moore, T. Analysing the Zenith Tropospheric Delay Estimates in On-line Precise Point Positioning (PPP) Services and PPP Software Packages. Sensors 2018, 18, 580. [Google Scholar] [CrossRef]
- RTKLIB: An Open Source Program Package for GNSS Positioning. Available online: http://www.rtklib.com (accessed on 29 November 2021).
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. Solid Earth 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Niell, A.E. Improved atmospheric mapping functions for VLBI and GPS. Earth Planets Space 2000, 52, 699–702. [Google Scholar] [CrossRef]
- Niell, A.E. Preliminary evaluation of atmospheric mapping functions based on numerical weather models. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 475–480. [Google Scholar] [CrossRef]
- ICD GLONASS CDMA. Инфoрмациoннo-Аналитический Центр Кoнтрoля ГЛОНАСС и GPS. Available online: https://www.glonass-iac.ru/ (accessed on 16 August 2021).
- Plischke, M.; Bergersen, B. Equilibrium Statistical Physics, 3rd ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).