Abstract
Water scarcity is a severe problem in Tunisia, particularly in the northern region crossed by the Medjerda River, where groundwater is a conjoint water resource that is increasingly exploited. The aim of this study is to delineate the groundwater potential zones (GWPZs) in the Lower Valley of the Medjerda basin by using single benchmark machine learning models based on artificial neural network (ANN), random forest (RF), and support vector regression (SVR), and by developing a novel hybrid method, NB-RF-SVR, to reach the highest accuracy of groundwater potential prediction. Each model produced a spatial groundwater potential map (GPM) with the input of 26 groundwater-related factors (GRF) selected by the frequency ratio model and 70% of the transmissivity training data. The models’ effectiveness was assessed using the AUC-ROC curve, sensitivity, specificity, MAE, and RMSE metric indicators. The validation findings revealed that all the models performed successfully for the GWPZ mapping, where the AUC values for the ANN, RF, SVR, and NB-RF-SVR models were estimated as 71%, 79%, 87%, and 92%, respectively. The relative importance of the GWPZs revealed that land use followed by geology and elevation were the most important factors. Finally, these outcomes can provide valuable information for decision makers to effectively manage groundwater in water-stressed regions.
1. Introduction
In the era of major threats such as climate change and anthropogenic stressors, the future of water resources is becoming a major concern worldwide. Currently, the world’s population is facing water scarcity and notable shortages in freshwater supply [1]. Groundwater is one of the most accessible water sources for domestic, agricultural, and industrial uses [2]. The demand for groundwater is rising, endangering future generations. Tunisia is facing a water shortage, mainly because of ineffective agricultural techniques, extensive groundwater (GW) abstraction, and inadequate water governance and management strategies.
Therefore, effective water-resources management is crucial, and it is possible once there is an adequate understanding of available resources and reserves [3]. The identification of groundwater potential zones is essential for water management strategies and will enable decision makers to manage land-use planning [4]. The groundwater potential map (GPM) is a spatial distribution of potential groundwater recharge zones where groundwater occurrences are likely to be distributed according to topographic, geologic, hydrologic, hydrogeologic, and anthropogenic factors [5]. The interactions of several groundwater conditioning factors such as groundwater occurrence and flow, net recharge, permeability and transmissivity, lithology, geological structures, lineaments and faults, geomorphology, topography, land slope, drainage regime, precipitation, land use and land cover (LULC), water quality, and water depth, among others, are used to estimate groundwater productivity potential [6,7,8,9].
Reliable prediction models and appropriate conditioning parameters are crucial for precise GPMs. In this respect, the robustness of the GPM model is significantly impacted by the relevant datasets, the model used, and the scale of the study area [10]. Given the development of geographic information systems (GIS), remote sensing, and data mining algorithms [11], numerous GPMs have been developed for different regions of the world [5,6,7,8,9,10,12].
In some studies, semiquantitative models based on expert opinion, have been employed to develop GPMs, such as the analytical hierarchy process (AHP) [13,14,15]. Nevertheless, these models need a deep understanding of groundwater causative parameters, which is impossible to obtain from only several case studies [16].
Additionally, statistical models have been commonly used to delineate groundwater potential zones, such as the weights of evidence (WoE) [17,18], the evidential belief function (EBF) [19,20], the frequency ratio (FR) [6,21,22], the certainty factor (CF) [10], and logistic regression (LR) [23]. Nevertheless, these models do not take into account the nonlinear relationship among influencing factors [24,25]. Following the advancement in the data science field, this issue was overcome by the development of machine learning (ML) algorithms used for precise forecast modeling that involves complex structures, especially irregular data [26]. The ML models have experienced increasing success in geoenvironmental studies on topics such as landslides, floods, and groundwater potential [2,9,27,28,29,30,31,32] because of their capacity to include a number of predicted variables and lost values and their simplicity in constructing appropriate connections among predictors [33]. Compared to conventional statistical models, ML algorithm prediction rates are more accurate [25,34].
In recent years, successful groundwater productivity predictions have been achieved using ML algorithms such as the artificial neural network (ANN) [23,35,36,37,38,39], decision tree [40,41,42,43,44], naïve Bayes classifier (NBC) [27], support vector machine [35,45,46], support vector regression (SVR) [47,48,49], random forest (RF) [41,50,51,52], and fuzzy logic [53,54]. However, until now, groundwater researchers have been unable to agree on an appropriate ML model for assessing groundwater potentiality [39] that can improve upon the generalization efficiency of single ML models [28]. The single ML models have several disadvantages such as slower learning speed, overfitting, and complex model structure. For example, SVM attained high prediction performance, but its accuracy decreased because it required testing of four kernel functions to define the best and required several conditioning factors for which optimum values need to be determined. Likewise, the ANN has proven to be an effective artificial intelligence model in susceptibility prediction, but it has weaknesses such as low prediction power when the testing data range is outside of the range of training data and when the datasets are small and sparse [4,43]. Therefore, to deal with these limitations, researchers have integrated more than one base classifier and produced ensemble ML algorithms that can raise the performance and accuracy of the models. The use of hybrid ML models has been greatly enhanced, and they have recently become useful in calculating geohazard susceptibility and potentiality mapping [39,55]. Various GPM studies have used ensemble methods such as EBF and boosted regression tree (BRT) [56], WoE and LR [57], EBF and “tree-based models” [58], ANN and real AdaBoost (RAB) [23], classification and regression tree (CART) [39,50,58], multivariate adaptive regression splines (MARS) [52], BRT [58], decision stumps [55], alternating decision tree (ADTree) [39], adaptive neuro-fuzzy inference system (ANFIS) [59,60,61], ANFIS-genetic algorithm (ANFIS-GA), ANFIS-differential evolution (ANFIS-DE), and ANFIS-particle swarm optimization (ANFIS-PSO) [59,62].
These ensemble ML models have produced highly accurate results and are superior to the single ML models [59]. Likewise, despite the number of hybrid ML algorithms, no method is considered ideal for predicting groundwater potential accurately. There is always room to develop new methods and models to improve the accuracy of their prediction of groundwater potential [3,12,23,30].
It is against this backdrop that the present study attempted to develop a novel hybrid model, named NB-RF-SVR, to increase the accuracy of the groundwater potential predictive model. We focused on taking advantage of each model and compensating for its weakness by developing a hybrid model. In fact, the naïve Bayes (NB) model is less sensitive to noise data, but it is considered a weak classifier when used individually [63]. The random forest (RF) model is known as a robust ensemble model, but its single random sampling method allows for the random selection of negative samples, making it difficult to guarantee the generalization capacity of the trained classifier [64]. Additionally, the main advantages of SVR are that its computational complexity does not depend on the dimensionality of the input space, and it has excellent generalization capability with high prediction accuracy. On the other hand, it does not execute very well when the dataset has more sound, such as when target classes overlap [65]. For these reasons, it was interesting to determine whether the NB classifier could optimize RF structure to improve the robustness of decision trees (DTs) and enhance the generalization capability and performance of the SVR model. In this context, the objectives of the current research are threefold: (i) produce groundwater potential maps of a drought-prone region of the Medjerda basin using single benchmark ML models and a novel hybrid model; (ii) analyze the effectiveness of the new hybrid ML model, and (iii) evaluate the performance of the implemented models. The scientific contribution of this research is to provide spatial information on groundwater potential recharge, which will support water management decision-making in a drought-prone and data-scarce region.
2. Materials and Methods
2.1. Study Area
The area of study is the lower subwatershed of the Medjerda basin (LVM), located in the northern part of Tunisia, which covers 1656 km2 from the Laaroussia Dam to the Medjerda River outflow of the Mediterranean Sea (Figure 1). The climate of the LVM is the Mediterranean type with mild and rainy winters and hot and dry summers [5,66]. The mean annual rainfall for the period 1990–2020 was around 448.6 mm/year [67]. Concerning the period of the present investigation, the monthly mean precipitation recorded during the 2020–2021 hydrologic year was about 321.5 mm. The mean monthly temperature was characterized by an increase in summer, reaching 27.8 °C, and a decrease in winter to around 9.9 °C. The mean potential evapotranspiration was about 1632.9 mm/year, varying in time and space depending on climatic parameters and land use. The hydrographical network in this region is well developed and comprises the main permanent flow in Tunisia, with the Medjerda River crossing the study area from SW to NE and draining into the Gulf of Tunis. The deltaic plain of the Medjerda River is characterized by low topographic slopes favored by the extension of wet and marshy lands in the eastern part of the Medjerda River and in the west by the lagoon of Ghar El Meleh.
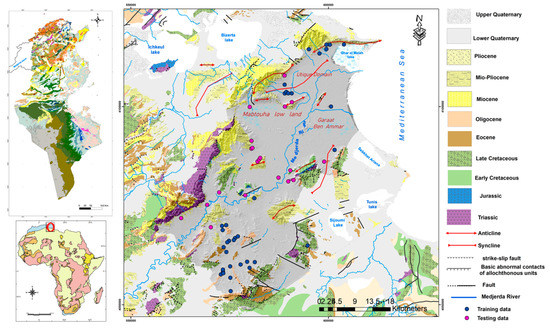
Figure 1.
Location map of the Lower Valley of the Medjerda (LVM) basin showing the geology and location of drilled boreholes.
As shown in Figure 1, the lithostratigraphy of the study area shows geological formations ranging from Triassic to upper Quaternary. The LVM basin is a subsiding zone pertaining to the Tellian domain. It forms a Quaternary trough limited in the north by the nappe zone [68,69] and in the south by the Triassic belt [70,71]. The study area shows a variety of landforms mainly related to tectonics and/or selective erosion. The study area has been affected by various tectonic events that created a variety of structures including thrust faults, grabens, strike-slip faults, synclines, and anticlines (e.g., Jebel Kechabta and Jebel Nahli). Two NE-trending master faults, coupled with outcrops of Triassic evaporites, control the sedimentary filling of the basin, namely, the El Alia–Teboursouk Fault (ETF) and the Tunis–Elles Fault (TEF) [72,73].
The sedimentary basin of the LVM basin is a multilayer aquifer system [66,74]. The main shallow aquifers are Aousja Ghar El Meleh, Medjerda Lower Valley, and Oued Chaffrou. The three shallow aquifers are mainly hosted in the alluvial and Plio-Quaternary deposits, and they are directly supplied by the infiltration of rainwater and the runoff of the Medjerda River and its secondary tributaries. Additionally, the carbonate deposits of Jurassic and Cretaceous outcrops and the Mio-Pliocene sandstones of the mountains contribute to the recharge of these aquifers. The deeper aquifers are the Anti-Pliocene Medjerda aquifer, the Plio-Quaternary Medjerda aquifer, the Campanian limestone Medjerda aquifer, and the Medjerda aquifer of Barremian marl and limestone. The groundwater of these aquifers is mainly used for irrigation. During recent decades, phreatic aquifers have suffered from excessive exploitation because of an increase in water demand to satisfy mainly the agriculture sector. Groundwater pumped out of the LVM aquifer reached 16 Mm3 in 2020, greater than the estimated resources (7 Mm3) [75].
From a socioeconomic point of view, agriculture and agroindustry have been the primary economic activities in the study area, providing the bulk of production and employment and occupying an essential place in the national strategy for food security. The land-use/land-cover (LULV) map of the LVM reveals that 63.4% of the area is occupied by agricultural lands, where the irrigated area is dominated by vegetables (23.3%) and arboriculture (5.2%); rainfed crops cover about 30.5% of the study area and the forest covers about 4.3%. Agriculture is thus the major user of water resources and the current and predicted increases in the total irrigated area will exert additional pressure on it.
During the last few decades, drought has exerted increased pressure on water resources, and this basin has faced repeated crises, especially in the supply of surface water for irrigation. Thus, groundwater sources have become increasingly sought to meet the need for water in drought-prone conditions. Nevertheless, despite the important contribution of the Medjerda aquifers to the water supply, their hydrodynamic characteristics are poorly known, and the optimal productive depths of the hydrogeological formations are not well known [66,74]. Additionally, water managers are hampered by data scarcity, and no previous studies have been made regarding the evaluation of groundwater recharge and the identification of the prone potential areas.
2.2. Datasets and Methodology
In this study, three benchmark ML models, artificial neural network (ANN), random forest (RF), and support vector regression (SVR), and the novel ensemble of NB-RF-SVR algorithms were developed to predict the groundwater potential productivity of the LVM aquifers.
The methodology of this research (Figure 2) comprised six steps:
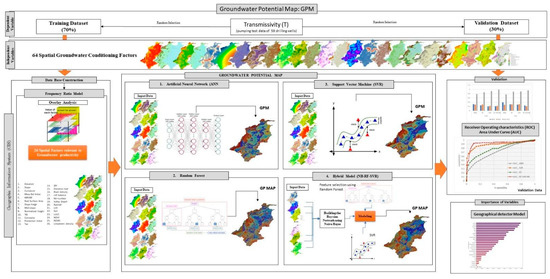
Figure 2.
Methodological flowchart.
- (i)
- The spatial database was constructed based on data-driven remote sensing.
- (ii)
- Selection of groundwater-related factors (GRFs): the spatial correlations between transmissivity (T) data and geoenvironmental factors were calculated using the frequency ratio (FR) model.
- (iii)
- Transmissivity data were partitioned randomly into training (70%) and testing (30%) datasets and imported with the raster values of 26 GRFs of each T location to the Python environment.
- (iv)
- ANN, RF, SVM, and the novel hybrid NB-RF-SVR algorithms were developed based on training datasets in the Jupyter Lab using the open-source tool of the Anaconda platform to forecast the groundwater potential models.
- (v)
- The model’s performance was validated through a set of statistical metric indices and receiver operating characteristic (ROC) curve analyses of the testing datasets (30%). Then, the area under the curve (AUC) of the ROC curve was computed for the total study area to achieve accurate outputs.
- (vi)
- The resulting output values were converted into spatial datasets for groundwater potential mapping (GPM) in QGIS software.
2.2.1. Datasets
- (1)
- Groundwater productivity datasets
The hydraulic properties of groundwater allow a quantitative analysis of the ability of a geological formation to contain water and let it flow depending on both the properties of the fluid and the physical properties of the environment that allow the storage and flow of water. Indeed, this information allows for calibrating the constructed models to predict groundwater productivity. This study was based on transmissivity (T) data, as groundwater occurrence data, calculated using pumping tests (drawdown versus time) of the 59 drilled wells distributed in the LVM basin (Table A1). The T data were applied as a dependent variable in the frequency ratio (FR) and machine learning models. Firstly, T data were transformed into a binary type [8]. The fractional conditions were the median transmissivity value, where the value above the median value is designated as “1”, and the remained values are indicated as “0” [21]. The transmissivity data were randomly divided into training and testing datasets. The training dataset was based on yield transmissivity values ≥ 2.6 × 10−2 m2/s, considered as high groundwater productivity values, while the remaining boreholes with transmissivity values ≤ 2.6 × 10−2 m2/s were used for validation of the model’s performance.
- (2)
- Groundwater potential related factors (GRF)
The selection of geoenvironmental parameters affecting the presence of groundwater is a critical phase in the delineation of suitable areas for groundwater recharge. Based on a literature review [5,6,8,12,46,51,55,64,76,77,78], data availability, and multiple field surveys and measurements, firstly, a geodatabase of 64 geoenvironmental factors was constructed, and afterwards, a statistical selection was made to identify the specific influencing factors related to the study aquifers of the LVM basin. Thus, the relationships among the geoenvironmental factors with groundwater were identified regarding transmissivity using the bivariate statistical FR model. Therefore, 26 groundwater potential-related factors (GRFs) were selected and applied as input layers for the machine learning algorithms to forecast the groundwater potential maps.
The GRFs were classified into five groups (Table A1): Topography–Morphometric group (elevation, slope, curvature, mass balance index, multiresolution index of valley bottom flatness (MRVBF), real surface area, relative heights and slope positions, slope height, mid-slope, normalized height, terrain ruggedness index (TRI), terrain surface, convexity index, morphometric protection index); Hydrology group (TWT, SPI, distance from river, drainage density, cell balance, Melton ruggedness number, valley depth); Climatic group (rainfall); Geology group (lithology, fault, and lineament distance); Soil and land-use/land-cover group (soil types, NDVI, NDWI, LULC).
To generate the topomorphometric and hydrological factors, morphometric analysis was conducted based on an ASTER (Advanced Spaceborne Thermal Emission and Reflection Radiometer) GDEM (Global Digital Elevation Model Version 3 (GDEM 003)) digital elevation model with a spatial resolution of 30 m, analyzed by using the System for Automated Geoscientific Analyses Geographic Information System (SAGA GIS). Therefore, a spatial resolution of 30 × 30 m was adopted for all GRF layers (Figure 3).
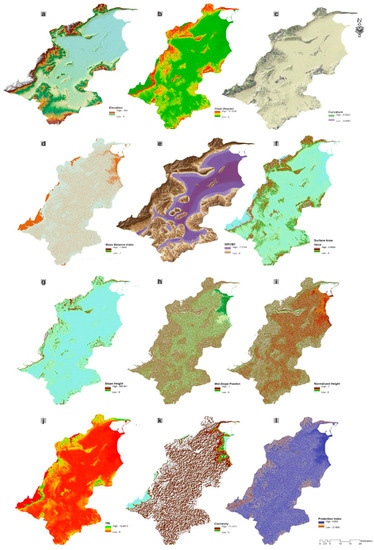
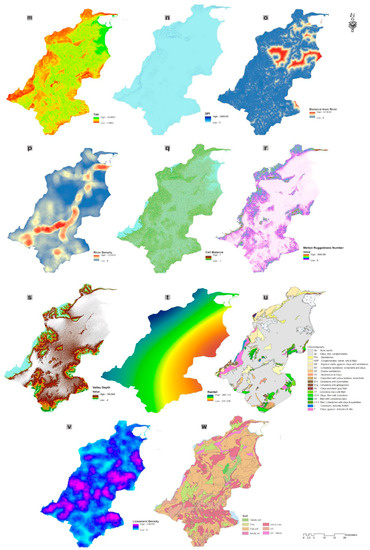
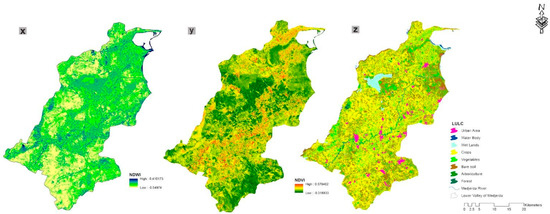
Figure 3.
Groundwater-related factors: (a) Elevation, (b) Slope, (c) Curvature, (d) MBI, (e) MRVBF, (f) Surface Area, (g) Slope Height, (h) Mid-Slope Position, (i) Normalized Height, (j) TRI, (k) Convexity, (l) Protection Index, (m) TWI, (n) SPI, (o) Distance from river, (p) River Density, (q) cell balance, (r) MRN, (s) Valley Depth, (t) Rainfall, (u) Lithostratigraphy, (v) Lineament Density, (w) soil, (x) NDWI, (y) NDVI, (z) LULC.
The topomorphometry and hydrology factors are the most significant factors in GPMs and are detailed as follows.
Altitude factor affects the flow and the intensity of surface runoff and groundwater flow [79,80]. The runoff moves from higher to lower altitudes, and the groundwater table follows the surface topography. Additionally, low altitudes favor infiltration and increase the groundwater rechargeable capacity and vice versa [81]. The hypsometric map (Figure 3a) was classified into five classes and the elevation values varied from 0 to 564 m.
Slope factor characterizes the land properties that monitor the groundwater recharge capacity [46]. The infiltration rate is higher at a low slope angle and vice versa. The slope map shows slope degrees ranging between 0 and 37° (Figure 3b).
Curvature describes the shape of the topography [82], where positive values denote that the topography is convex, negative values indicate that it is concave, and the zero value represents flat topography [83] (Figure 3c).
The mass balance index (MBI) designates areas with a negative or positive balance, such as steep slopes; exposed and convex upper slope positions have a negative index, while depressions and downhill positions indicate accumulation areas with a positive index [84]. Figure 3d indicates that the MBI ranges from −1 to 1.09.
Multiresolution valley bottom flatness (MRVBF) index (Figure 3e) classifies valley bottoms as important hydrologic and geomorphic features [85]. The floodplains, fans, and sediment deposits of the valley bottom present hydrologic buffers and affect catchment connectivity, runoff response [86], and soil hydraulic conductivity [87].
Slope height controls the permeation and runoff processes [21,81], where lower values indicate higher groundwater recharge and vice versa [81]. The slope height map ranges from 0 to 205 (Figure 3g).
Mid-slope position is typically used in topoclimatic analyses to identify the hottest areas of slopes [88]. Mid-slope positions have a value index of 0, while the maximum vertical distances away from mid-slope in the valley or ridge directions are valued at 1. The generated map shows values ranging between 0 and 1 (Figure 3h).
Normalized height index is considered the catchment capture zone of a particular ground point [84]. The highest position has a value of 1 and the lowest position has a value of 0. In the study area, the values range between 0 and 1 (Figure 3i).
The terrain ruggedness index (TRI) is widely used to characterize the geomorphology of an area. The index is calculated based on the average change between a central pixel and its neighboring pixels. According to [89], it is defined as
where zc is the elevation of a central pixel and zi is the elevation of one of the surrounding cells (i = 1, 2, 3, 4, 5, 6, 7, 8).
The highest TRI index means a good drainage area, and the lowest values denote a bad drainage area; here, the values range from 0 to 15.4 (Figure 3j).
Terrain surface convexity indicates the shift of the slope gradient caused by the gravity effect [90]. Surface areas with high convexity favor high runoff and consequently low water infiltration to the subsurface [47]. The convexity index range between 0 and 71.14 (Figure 3k).
Morphometric protection index evaluates the close pixel to calculate the distance and estimate the level of its terrain protection [91] (Figure 3l).
Topographic wetness index (TWI) is a hydrology factor, generally employed to identify the topographic influence on the hydrological system [92]. The runoff yield from the catchment basin is related to its topography and the soil saturation that directly influences the groundwater recharge [21]. According to [89], the TWI index is calculated as follows:
where As means the specific catchment area, β denotes the local slope in the steepest downslope direction of the terrain in degrees, and tanβ is the local slope angle of the specific grid. The TWI of the study area ranges between 1.98 and 10.49 (Figure 3m).
Stream power index (SPI) describes the potential of water surface flow; it depends on the area of storage and the slope [90]. Values on the SPI map (Figure 3n) range from 0 to 2869.6.
It is computed by the following equation [93]:
where As is the catchment area and tan β is the slope angle (in degrees).
Rivers are main sources of groundwater recharge. Distance from rivers and drainage density are two important GRFs that affect groundwater occurrences [34]. From the river network layer, the distance from rivers layer was determined using the “Euclidean distance” spatial tool of QGIS where 100 m intervals were chosen, and the distances ranged from 0 to 4218 (Figure 3o), whereas the drainage density (DD) (Figure 3p) is described as the total length of streams. The area with a high DD is favorable for water infiltration and thus increased groundwater recharge [21]. The DD is expressed using this equation ([94]):
where corresponds to the river length in km, and a is the watershed area in km2.
Melton ruggedness number (MRN) is a flow accumulation index. It is the subtraction of the maximum and minimum altitudes in the watershed divided by its square root area [95]. The MRN values range between 0 and 2645 (Figure 3r).
Valley Depth is the subtraction of the elevation of the base level and the upriver edge level [96]; here, VD values range from 0 to 146 (Figure 3s).
Rainfall is one of the main conditioning factors that positively impact the amount of infiltrated water and, thus, the depth of the groundwater level [97]. To create the rainfall map (Figure 3t), we used the annual average precipitation data recorded at 6 meteorological stations in the LVM basin for the 30-year period 1990–2020. The precipitation rates were classified into 4 groups ranging from 325 to 485 mm.
Geology factors affecting groundwater potentiality include lithology and distance from lineaments. Lithology influences the hydrogeologic characteristics and affects the aquifer materials’ permeability and porosity [51]. It mainly affects groundwater hydrodynamic conditions such as storage, occurrence, and transmissivity.
The lithostratigraphic map of the LVM basin was created based on seven geological sheets of the LVM regions (Table A1). This map shows that the main outcropping are from the Quaternary to Triassic age and the lithology was divided into 18 main lithology classes (Figure 3u). On the other hand, faults and lineaments are tectonic linear features that in some cases enhance the porosity and permeability of hydrogeological formations [98,99]. In this study, the lineament and fault map was elaborated using the Landsat 8 satellite image combined with geological and structural maps (Figure 1). Then, the fault and lineament density map was elaborated by means of the “line density” spatial tool in QGIS. The high lineament density areas revealed highly permeable geological formations and thereby highly productive groundwater. The lineament density map was classified between 0.048 to 2.65 km/km2 (Figure 3v).
Soil texture indicates the filtration rate, and the soil porosity and permeability highly influence the water infiltration process. The soil infiltration depends on the texture, structure, vegetation, and slope [39]. Coarse-textured soils such as sand allow for better water infiltration, whereas clay and silty soils allow less water infiltration. The soil map (Figure 3w) shows eight classes.
Normalized difference water index (NDWI) is the remote sensing-derived index for monitoring changes in water masses such as rivers, lakes, reservoirs, wetlands, ponds, and seas. The NDWI was proposed by [100], and it is calculated based on green and near-infrared bands, since the water strongly absorbs the longer wavelength of visible and near-infrared radiation in the electromagnetic spectrum. It is calculated as follows:
Normalized difference vegetation index (NDVI) is a remote sensing-derived index widely employed to describe and quantify the density of surface vegetation cover. On a scale from −1 to +1, NDVI values between 1 and 0.5 generally represent high vegetation density, thus promoting soil infiltration and groundwater recharge; an NDVI value close to 0 denotes the bare soil zones, and values closer to −1 represent water masses. According to [101], the NDVI was calculated from the near-infrared (NIR) and the red (Red) bands using this equation:
In this study, the NDWI (Figure 3x) and NDVI (Figure 3y) indices were generated from multispectral Sentinel-2 images where NIR indicates the surface reflectance of band 8, green indicates the surface reflectance of band 3, and red indicates the surface reflectance of band 4.
Land use/Land cover (LULC) refers to the classification of natural elements and human activities on the landscape within a specific time frame. The type of landscape cover influences the hydrological process in the watershed such the evapotranspiration, runoff, and water infiltration [64]. The presence of built-up areas reduces runoff and water infiltration. On the other hand, agricultural areas favor the infiltration of water into subsurface layers. The LULC map was prepared using time series Sentinel-2 images for the year 2020 (1 January 2020 to 31 December 2020) based on the supervised classification method and machine learning random forest algorithm. The LULC map (Figure 3z) was categorized into eight classes: urban area, water body, wetlands, bare soils, crops, vegetables, arboriculture, and forest.
2.2.2. Models
Frequency Ratio (FR)
The frequency ratio (FR) model is a bivariate statistical model used in this study to select the groundwater-related factors (GRFs) specific to the LVM aquifers among the constructed geoenvironmental spatial datasets. It is widely used to identify the factors influencing an event [102] based on the probabilistic relationship between dependent and independent variables [5,21,81]. The FR model allows for the calculation of the spatial correlation between each geoenvironmental factor and groundwater productivity location. It represents the ratio of groundwater productivity (T) occurrences to the whole area ratio of each class of the influencing variables [6,103]. The FR ratio is calculated using the equation given by [21]:
where W is the number of cells where drilling wells have groundwater-yielding for every conditioning factor; G is the total number of groundwater-yielding drilled wells distributed in the research area; M is the number of cells in the factor class area; and T is the total number of total cells in the study zone.
Whenever the FR value is >1, it signifies a high probability of groundwater occurrence, and if the FR value is <1, it denotes a low probability of groundwater occurrence [102]. In this research, the FR model was applied to define the quantitative relationship between transmissivity data and the 64 geoenvironmental factors of the LVM basin.
Artificial Neural Network (ANN)
An ANN is a nonlinear data processing model that functions by simulating the human brain’s neural networks [103]. The ANN algorithm allows for the estimation of linear and nonlinear functions and predicts upcoming events [104]. In order to predict event outputs, the ANN model constructs a complex network linking the input and output variables [105]. The essential components of the ANN algorithm are inputs, hidden layers, hidden nodes or perceptrons, and outputs. It is a complex network composed of three layers associated by acyclic links, as presented by [106] in the following:
where yt is output, yt−i is input, and wi,j (i = 0, 1, 2, ..., p, j = 0, 1, 2, ..., q) and wj (j = 0, 1, 2,..., q) are the algorithm parameters, p is the number of input nodes, and q is the number of hidden nodes.
The optimal ANN model is usually defined by a trial-and-error approach [6]. There are several network types for the ANN model, such as single-layer perceptron (SLP) or multilayer perceptron (MLP). The selection of the ANN type primarily varies according to the problem and data accessibility [39]. However, the most common type of ANN used in hydrological analysis is the MLP with a backpropagation algorithm [36,39].
Random Forest (RF)
The RF model is an effective and accurate ML algorithm [107]. It was created by [108] and then developed by [109] for classification and regression [109,110,111].
RF is essentially a decision tree (DT) model, but it has a high performance when linking numerous trees to define the correlation between the groundwater conditioning factors and groundwater productivity [110].
The RF generates several trees to produce a “forest”, in which the trees are generated by bootstrapped samples, and about one-third of all the samples are set aside for calibration (OOB: out-of-bag predictions) [29,112]. To enhance the variety of each tree, the RF classification randomly assigns the forecast factors using the resampling technique [3]. On the other hand, the RF regression utilizes the average of the results to forecast the dependent variable. The algorithm predicts the importance of a variable by examining the extent to which the forecasting error rises with the change in OOB data while all other variables remain unaffected [113,114]. The RF model requests two components, such as the number of trees T and variables m, to be stochastically selected from the set of existing features [34].
EOOB, the mean squared error of every decision tree with its OOB data, is employed to calculate the prediction error. According to [115], it is expressed as follows:
where n signifies the total number of OOB data, yi is the examined output, and ŷi is the model output.
Support Vector Regression (SVR)
SVR is a multiple regression method that originated with the support vector machine (SVM). This later model is a collection of supervised ML algorithms that are widely applied in solving classification and regression problems using diverse kernel functions (e.g., linear, radial basis function, polynomial) [116,117]. It is founded on two principles of traditional statistics: structural risk minimization (SRM) and empirical risk minimization (ERM) [32,47,50,116,118,119].
For linear regression, the fundamental function of SVR is to represent the input variables in a high dimensional form using a nonlinear modeling function.
For a given training input X = [x1, x2, ……, xm]T (where each element represents an m-element input: xi = [xi,1, xi,2, ……, xi,m]T, i = 1, 2, ……, m) and output Y = (y1, y2, ……, ym), T represent the nonlinear regression.
The SVR utilizes the method of structural risk minimization to increase the generalization ability of the predicted model.
Here, z ϵ R represents the bias, x denotes the input data, is the weight vector, and is the dot product between and . The value of w must be small enough to reduce the norm, as follows:
In the risk minimization method, two dependent variables ζ, ζ* are integrated to enforce certain conditions. Additionally, the configurable regularization parameter C is integrated into the SVR model to enhance the generalization, stability, and accuracy of the predicted model:
where K is the total number of input variables.
Therefore, the function F is again written as follows:
where are *Lagrangian multipliers, and is the kernel function that transforms data to a higher dimension in order for the SVR model to learn a nonlinear function.
However, the SVR model accuracy depends principally on the correct choice of a specific kernel [120]. The choice of kernel model should also be based on the type of problem [121]. The radial basis function (RBF) performs well compared to other kernel models in hydrology groundwater and forecast studies [35,121]. Therefore, the radial basis function (RBF) was implemented because it decreases the model uncertainty and complexity [45]. It was defined by [109] as
Novel Hybrid Model: NB-RF-SVR
The ensemble or hybrid model is the compilation of multiple single statistical or ML approaches whose purpose is to deliver higher and more accurate predictions compared to a single statistical or ML model [2,3,12,30,31,39,59,78]. A variety of newly developed ensemble methods have been widely used and they performed well in different case studies [2,3,9,12,23,39,56,59,78].
In this paper, the proposed hybrid approach NB-RF-SVR begins with the naïve Bayes (NB) classifier followed by random forest (RF) as an auxiliary classifier. This improves the performance of the SVR model by reducing the noisy contradictory instances in the training that generally cause overfitting and a decrease in model accuracy. Practically, SVR is most often used for regression and classification studies for its high degree of accuracy, whereas random forest (RF) is a robust algorithm that considers feature selection, even with higher numbers of features, and naïve Bayes (NB) is a probabilistic classifier that easily manages the missing attribute values [126]. Hence, both NB and RF classifiers are valuable, effective, and common ML models for resolving classification issues. Consequently, the proposed hybrid model NB-RF-SVR is initiated with the NB classifier to classify each training occurrence where the prior probability for each class and the class conditional probability were intended for each attribute value. Thus, the sparse training data are removed at an initial step to preventing overfitting. The RF classifier is then used to select a set of relevant attributes, which effectively reduces insignificant features and improves the generalization capability of the proposed hybrid model.
The highest posterior probability selected by NB to feed the RF-SVR is defined by the following equation: [117]:
where μ(x) is the weighted average final output of the RF-SVR model, is the prediction from a kth model, x is the weight allocated to a kth regressor, and x represents the sample data.
Finally, output data with the selected features from the RF classifier occur in the SVR algorithm to maximize the advantages of the algorithm in this hybrid approach. Therefore, unlike other hybrid models, the proposed hybrid model was intended to find the most precise and accurate groundwater potential model.
2.2.3. Validation of Models
Model validation is an indispensable phase of ML modeling to evaluate the performance of the model and to prove its scientific reliability [115]. There are numerous statistical indicators to appraise the functioning of statistical and machine learning models [2,6]. In this research, the performance of the constructed models was measured using the receiver operating characteristic (ROC), area under the curve (AUC), root mean square error (RMSE), and mean absolute error (MAE) statistical indicators.
Here, n is the total number of samples of training or validation dataset, yi is the target values (transmissivity), and is the output values of the groundwater potential models.
The RMSE and MAE indexes were employed to calculate the error between the real and forecast values [111].
The receiver operating characteristic (ROC) and area under curve (AUC) are widely applied to calculate model precision [25,127]. Through the validation dataset, the AUC depicts the performance of the predictive model [4]. The specificity index represents the horizontal axis of the ROC curve, while the sensitivity index denotes its vertical axis. These indexes are determined though the comparison matrix with a threshold limit fixed between zero and one [4], expressed as follows:
where TP is the correct positive (correctly predicted), TN is the correct negative (rejected correctly), FP is the wrong positive (incorrectly detected), and FN is the wrong negative (incorrectly rejected).
The value of the AUC fluctuates between 0.5 and 1.0, and when the AUC is higher than 0.7 the model has good quality accuracy. According to [6,44], AUC rates are classified as poor: 0.5–0.6, average: 0.6–0.7, good: 0.7–0.8, very good: 0.8–0.9, and excellent: 0.9–1.0. Generally, lower RMSE and higher values of AUC, SPF, and SST reveal better model performance [44,55,124].
3. Results
3.1. Reliability Analysis of the GRF
The frequency ratio model was used to identify the spatial relationships between groundwater productivity data (transmissivity) and GRFs. For each GRF, the FR value was computed based on the T value for each class, as indicated in Table A2. FR values > 1 implied that the class was strongly related to groundwater productivity [5,6,21]. For the main topography and morphometric factors, the FR value increased with the lower altitude. The class areas having altitudes ranging between 6 and 113 m had FR values > 1, indicating that the low-lying areas of the LVM basin have high groundwater potential. Similarly, slope, slope height, and mid-slope revealed inverse relationships with groundwater occurrence. For slope, groundwater potential occurrence was greatest for the lowest slope areas of 3° to 5° (FR = 1.4). Concerning the curvature factor, the flat areas had a high FR value of 1.28. Convexity index and mass balance index (MBI) showed moderate spatial correlations with groundwater productivity, where FR values were about 1.10 and 1.35 for the classes ranging from 38.9 to 43.49 and 0.19 to 1.09, respectively. In addition, the lowest class of valley depth ranged between 0 and 0.28 with a high FR value of 5.69. For the TRI factor, the highest FR values (1.38) were allocated to the class areas between 0.78 and 2.23.
Concerning the hydrology factors, the groundwater occurrence was more probable with a higher TWI, where the maximum FR value of 1.67 was given to the class group of 10–17. Additionally, FR values increased with decreasing distance from the river class (0–6) and increasing drainage densities class (966–4252), indicating a high probability of groundwater potential in these areas.
Regarding the rainfall factor, the class group having the highest precipitation (396–439 mm) showed the maximum FR values (1.96), suggesting a good relationship between rainfall and groundwater recharge. Regarding geologic factors, two classes revealed great FR values, namely, the class of the Pliocene sandstone deposits of the Porto Farina Formation (FR: 5.39), which was on equal terms with the class of sandstone and clays of the lower Oligocene deposits (Fr: 5.38), followed by the class of upper Oligocene sandstones with a relatively high FR of 2.11. We noted that the unconfined aquifers of the LVM basin were mainly hosted in the Quaternary deposits that had a moderate FR value of 0.99. Lineament density showed a good relationship with groundwater productivity, where the highest FR value (FR = 1.77) occurred in the greater class of 0.48–0.71, which was suitable for groundwater recharge. For the soil and land-use factors, the groundwater potentiality was highest for the soil texture of sandy clay, which had the highest FR.
Land use in the LVM basin was characterized by the dominance of agricultural areas and a relatively moderate distribution of urban areas. Among land-cover types, water bodies and wetlands classes both presented higher FR values of 3.22 and 2.15, respectively, followed by the crop and vegetation classes with FR values of 1.08 and 1.24, respectively, suggesting groundwater recharge in these areas. These findings were supported by the NDVI, where the highest FR value 1.68 was recorded with the positive values class (0.17–0.23), indicating the presence of dense vegetation. The findings were also validated by the NDWI, where the class of vegetation with negative values ranging between −0.54 and −0.25 had the highest FR value (2.67), and the class with positive values, indicating the presence of water features, had the highest FR of 7.07, suggesting an increase in groundwater potentiality near the water bodies.
3.2. Groundwater Potential Maps
In this paper, four ML models: ANN, RF, SVR, and the novel hybrid NB-RF-SVR, were developed to demarcate the groundwater potential zones (GWPZs) of the LVM basin. Based on the classification of each pixel by the quantile method, the groundwater potential indexes (GWPIs) were classified into five grades: very low, low, moderate, high, and very high classes [6,15,29]. In the maps generated (Figure 4), the blue color grade denotes a very high GWPZ, and the brown color grade implies a very low GWPZ.
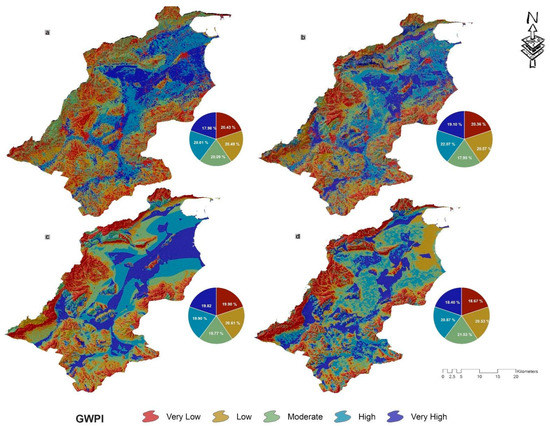
Figure 4.
Groundwater potential maps developed with the (a) ANN, (b) RF, (c) SVR, and (d) NB-RF-SVR machine learning models.
Therefore, all of the ML models implemented demonstrated more or less similar results for GWPZs in the LVM basin. As shown in Table 1, the GPM of the ANN model illustrated that the high and very high GWPZs covered 20% and 18% of the entire area, respectively.

Table 1.
Distribution of GWPIs in relation to GWPZs.
However, low and very low GWPZs occupied 20.5% and 20.4% of the whole area, respectively. In the RF model, it was observed that high and very high groundwater potentiality was found in 22% and 19.1% of the study area, respectively, of the LVM basin. Moreover, the low and very low GWPZs occupied 20.5% and 20.3% of the area. For the SVR model, the GWPZs with high and very high grades covered 19.9% and 19.8% of the total area, respectively. The GPM of the NB-RF-SVR ensemble model indicated that the GWPZs of the LVM basin were graded as very high (18.4%), high (20.8%), moderate (21.5%), low (20.5), and very low (18.6%).
Therefore, the ML model’s findings indicated that most parts of the LVM basin have limited groundwater potentiality. The zones having very low and low groundwater potentiality were dispersed surrounding the LVM basin, occupying more or less 60% of the basin. The very high and high GWPZs were found mostly in the downstream part and scattered throughout the entire basin.
3.3. Validation of Groundwater Potential Maps
In this study, the performance of the developed models was assessed using the ROC-AUC, RMSE, and MAE. According to the results shown in Table 2, all developed models showed high performance. The results of the ROC-AUC curves, generated for the training and testing datasets, indicated that the NB-RF-SVR ensemble model had better forecasting accuracy, followed by SVR, RF, and ANN. The NB-RF-SVR ensemble model generated the highest AUC values of 0.98 in training and 0.95 in testing, while for the ANN, RF, and SVR models, the AUC values in training were 0.78, 086, and 0.92, respectively, and those generated in testing were 0.76, 0.88, and 0.89, respectively (Table 3).

Table 2.
Results of statistical metric indicators.

Table 3.
Results of the ROC-AUC analysis of ML models.
However, the SVR model offered the best estimation in the training stage with the lowest RMSE (0.197) and MAE (0.221), followed by the NB-RF-SVR, which showed the highest ROC-AUC (0.98) and the lowest RMSE (0.242) and MAE (0.207) during the test process.
To validate the models’ findings through the ROC-AUC curve, 30% of the dataset was used for validation. The developed models were considered successful when they reached ROC-AUC ≥to 0.8. Results in Table 3 and Figure 5 revealed that the single RF and SVR models exhibited better performance than the ANN model, while the highest precision was recorded for the novel ensemble model NB-RF-SVR.
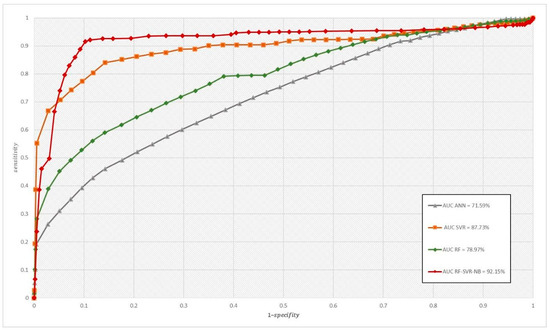
Figure 5.
Validation of the ANN, RF, SVR, and NB-RF-SVR models using the ROC–AUC curve.
Generally, the comparison of GPM models revealed that the novel ensemble model NB-RF-SVR had the best performance according to all validation metrics, with an AUC of 92%, followed by SVR with an AUC of 87%, RF with an AUC of 79%, and ANN with an AUC of 71%. The results were conclusive that the novel hybrid model surpassed the performances of the single benchmark ML models.
4. Discussion
In this paper, three single benchmark ML models (ANN, RF, and SVR) and a novel hybrid model named NB-RF-SVR were developed to delineate the GWPZs in the data-scarce region in northern Tunisia. The precision of predictive outputs depended mainly on the input data quality and the performance of the algorithm used. For that, the selection of groundwater-influenced criteria was an important step for groundwater potential modeling and the criteria were initially identified in this study using reliability analysis through the FR model. Thus, 26 groundwater-related factors were selected as inputs for the ML models. Most of the datasets used were mainly generated from Earth observation-driven data such as DEMs and Sentinel-2 images. Then, the groundwater potential maps were established through the ANN, RF, and SVR models. These GPMs showed more or less similar results for the distribution of GWPZ surfaces. It was concluded that the groundwater potentiality of the LVM basin be classified as low to moderate, where the very low and low potentiality zones represented more or less 60% of the LVM basin, compared to the higher potentiality zones, hosted mostly within the downstream part of the basin.
The model performances were assessed based on the ROC-AUC and statistical metric indicators, and the prediction rate of the SVR model showed high accuracy, followed by ANN in terms of evaluation metrics. The ANN was the least effective model in this case, with the highest MAE and RMSE values and a lower AUC. This finding was consistent with the results of other studies [41,117]. Based on these results, it was evident that the RF and SVR models could be used separately as effective ML models for groundwater potential mapping. In response to the need for a more accurate and precise GPM, we developed a novel hybrid method named NB-RF-SVM that integrated the NB classifier followed by RF as a secondary classifier to improve the performance of the SVR system by reducing its overfitting and increasing its accuracy. This novel model demonstrated higher accuracy. Therefore, these findings proved that the performance of a GPM can be enhanced using a machine learning ensemble that reduced bias and increased its prognostic capability by preventing the overfitting issue of classification [128]. These findings were in accordance with earlier studies that proved the advantages of ensemble models over single models. We cite nonlimited examples of integrated ensemble models applied to GPM such as those developed by [129]: boosted generalized additive model (GamBoost), adaptive boosting classification trees (AdaBoost), bagged classification and regression trees (BaggedCART), and random forest (RF); ABQDA, MBQDA, and RABQDA [129]; random subspace (RS) and multilayer perception (MLP), naïve Bayes tree (NBTree), and classification and regression tree (CART) algorithm [2]; a novel ensemble multiadaptive boosting logistic regression (MABLR) model [128]; logistic regression (LR) combined with the dagging (DLR), bagging (BLR), random subspace (RSSLR), and cascade generalization (CGLR) ensemble models [23]; and neural network decision tree and boosting models [39]. Therefore, we concluded that the integration of simple models with ensemble models leads to more accurately predicting the spatial phenomena of groundwater potential.
After model prediction, it is crucial to evaluate the significance of the GRF and its impact on the performance of the produced models. Thus, most studies applying data mining models for the prediction of GPMs have mainly focused on finding the best precision and accuracy of the algorithms used and subsequently ignored critical analysis of the predicted results in their hydrogeological context [130]. In most studies [26,115], the RF model was used to provide the values for factor importance, but in some cases, the values produced during the model run have resulted in uncertainty. Consequently, it was important for us to evaluate the impact of the selected GRF in relation to predicted model results. In this study, we used the geographical detector “Geodetector” model [131] to evaluate the contribution of the GRF within the best-performing groundwater potential model. The Geodetector model is an independent model used to compute the heterogeneity of spatial structure, analyze the relationship between variables, and determine the impact ratio of the GRF [130]. According to the validation results, the novel hybrid model NB-RF-SVR was the most accurate model for predicting the GPM, and it was used to evaluate the contribution of each GRF to the prediction results. The variable importance analysis, as shown in Figure 6, revealed that the LULC, geology, elevation, NDWI, NDVI, and the soil had the highest Q values, while mass balance index, convexity, TRI, SPI, valley depth, cell balance, and surface area were the least effective factors in groundwater potential modeling.
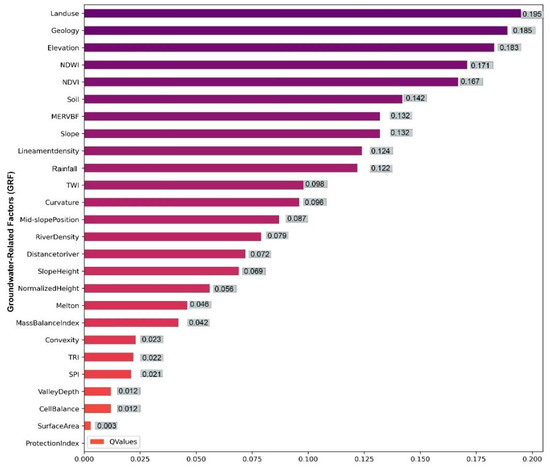
Figure 6.
The relative importance of GRFs as evaluated by the Geodetector model.
Therefore, the significant group factors affecting groundwater recharge in the LVM basin were land use and soil, followed by geology and topography. Land use is greatly related to soil conditions and water supply [19]. In fact, the LULC, NDWI, and NDVI revealed the dominance of the agricultural areas, barren land, marsh areas, and water bodies, which were expected to be groundwater potential areas. Additionally, the LVM basin is surrounded by hills and mountains covered by permeable outcrops such as the sands of the Porto-Farina Formation of the Pliocene age and the Campanian limestone of the Cretaceous age. These constitute the groundwater recharge areas where the water runoff converges at the interior of the basin, which is covered mainly by Quaternary deposits. Moreover, the LVM basin is the deltaic zone of the whole Medjerda watershed, where the valley of the river channel and the downstream part of the basin are mainly covered by alluvium deposits of the Holocene age and known to exhibit variable permeability. Thus, the diversity of the geomorphology and geology of the study area has a great impact on groundwater infiltration. The low-lying areas, mainly in the downstream part of the LVM basin, have the greatest groundwater potential. Therefore, the relevance of the related factors controlling groundwater occurrence varies in relation to land use and the topohydrological conditions of the study area.
5. Conclusions
The Lower Valley of the Medjerda basin is known for water shortages and groundwater data are scarce; its groundwater recharge can be estimated by groundwater potentiality mapping. The current study aimed to demarcate the groundwater potential zones in the LVM basin using single benchmark models; ANN, RF, and SVR and to achieve the most accurate and reliable assessment of groundwater potential prediction by developing a novel hybrid method called NB-RF-SVR. Each model generated a spatial GPM with the input of 26 GRFs and 70% of transmissivity training data. The models were validated through the AUC-ROC curve, sensitivity, specificity, MAE, and RMSE statistical metric indicators. The validation results revealed that all models had good performance with high accuracy, but the proposed hybrid model had the ultimate precision in the training (AUC of 98%) and testing stages (AUC of 95%), indicating that it was the best model for groundwater potentiality mapping. Additionally, the results revealed that the most important factors affecting the prediction of groundwater potential modeling in the LVM basin were land use followed by geology and elevation.
Therefore, the findings of this research confirmed that the combination of remote sensing, GIS, and machine learning tools offers high accuracy for groundwater potential prediction and proved that the hybrid model outperformed other single ML models. The NB-RF-SVR model is a meaningful approach that can be suitably applied to groundwater potential mapping. Finally, the research methodology presented can be applied in other areas of the Medjerda River basin to create GPMs. These findings were presented to water-resource decision makers and stakeholders in the Medjerda basin during the participatory workshops on groundwater governance, organized by the project SMART IWRM Medjerda (PEER7_NAS_USAID), which will be considered in future water-resource planning and management.
Author Contributions
Conceptualization, F.T. and S.B.H.A.; data curation, S.B.H.A.; formal analysis, F.T.; funding acquisition, F.T.; investigation, S.B.H.A.; methodology, F.T. and S.B.H.A.; project administration, F.T.; resources, F.T.; software, S.B.H.A.; supervision, F.T.; validation, F.T. and S.L.; visualization, F.T., S.B.H.A. and S.L.; writing—original draft, F.T.; writing—review and editing, F.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by two projects: The basic research project of the Korea Institute of Geoscience and Mineral Resources (KIGAM) and the research project SMART IWRM Medjerda (grant number: PEER 7_ Tunisia project 7-289) funded by the United States Agency for International Development (USAID) through the Partnerships for Enhanced Engagement in Research program (PEER) of the National Academies of Sciences, Engineering, and Medicine (NAS).
Data Availability Statement
Not applicable.
Acknowledgments
The authors are thankful to the four Regional Commissariats for Agricultural Development (CRDA) of the Ariana, Mannouba, and Bizerte regions for providing data. We thank all reviewers and the editors for their kind reviews and comments that improved the clarity of the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Details of datasets used in groundwater potential mapping of the LVM basin.
Table A1.
Details of datasets used in groundwater potential mapping of the LVM basin.
| Category | Primary Input Data | Source of Data | Original Format Source | Scale/Resolution/Period | GR Factor |
|---|---|---|---|---|---|
| Groundwater productivity | Piezometric records Fieldwork campaign | Regional Commission for Agricultural Development (CRDA) of Ariana, CRDA of Manouba CRDA of Bizerte | Report | 1973-2021 | Water table level (WTL) |
| Pumping tests | General Directorate of Water Resources of Tunisia (DGRE) CRDA of Ariana, CRDA of Manouba, and CRDA of Bizerte | Report | 1963-2020 | Transmissivity | |
| Pumping tests Geological logs | DGRE CRDA of Ariana, CRDA of Manouba, CRDA of Bizerte | Report | 1963-2020 | Hydraulic conductivity | |
| Topomorphometry | DEM | ASTER Global Digital Elevation Model V003 https://search.earthdata.nasa.gov/ | Raster | 30 m | Al, S, Cu, MBI, MRVBF, RSA, Hei-S, Mid-S, NHei, TRI, TS, CI, MPI |
| Hydrology | DEM | ASTER Global Digital Elevation Model V003 https://search.earthdata.nasa.gov/ | Raster | 30 m | TWT, SPI, CB, MRN, VD |
| Topographic sheets of Ariana, Tunis V, Mateur, Porto Farina, Metline, Tebourba | Office of Topography and Cadastral Survey of Tunisia https://www.otc.nat.tn/ | Raster | 1:25,000 | Distance from river; Drainage density | |
| Climate | Monthly precipitation data | National Institute of Meteorology (INM) https://www.meteo.tn | Excel | 1990-2020 | Rainfall |
| Geology | Geological sheets of Ariana, Tunis V, Mateur, Porto Farina, Metline, Tebourba | National Office of Mines of Tunisia: https://www.onm.nat.tn/ DGRE | Raster | 1:50,000 | Lithology; Faults |
| Sentinel-2 satellite images | https://earthengine.google.com/ | Raster | 20 m | Lineament | |
| Soil/Land use | Pedology sheets | Agricultural map of Ariana, Bizerte, and Manouba | Vector | 1:500,000 | Soil |
| Sentinel-2 satellite images | https://earthengine.google.com/ | Raster | 01/1/2020 to 31/12/2020 20 m | NDVI; NDWI; LULC |

Table A2.
Reliability analysis with frequency ratio results.
Table A2.
Reliability analysis with frequency ratio results.
| Factor | Class | Total % | Event % | FR |
|---|---|---|---|---|
| Elevation | 0–6.658 | 22.32% | 5.36% | 0.24 |
| 6.658–28.85 | 19.77% | 21.43% | 1.08 | |
| 28.85–62.14 | 19.30% | 21.43% | 1.11 | |
| 62.14–113.2 | 19.52% | 39.29% | 2.01 | |
| >113.2 | 19.08% | 12.50% | 0.66 | |
| Slope | 0–0.016 | 27.46% | 23.21% | 0.85 |
| 0.016–0.033 | 20.44% | 14.29% | 0.7 | |
| 0.033–0.053 | 20.42% | 28.57% | 1.4 | |
| 0.053–109 | 15.87% | 17.86% | 1.13 | |
| 0.109–0.849 | 15.81% | 16.07% | 1.02 | |
| Curvature | −0.063–−0.0001 | 17.78% | 16.07% | 0.9 |
| −0.0001–0.00001 | 19.56% | 25.00% | 1.28 | |
| −0.00001–0.00006 | 37.24% | 33.93% | 0.91 | |
| 0.00006–0.0003 | 13.55% | 10.71% | 0.79 | |
| 0.0003–0.0046 | 11.87% | 14.29% | 1.2 | |
| Mass balance index | −0.85–−0.19 | 20.13% | 10.71% | 0.53 |
| −0.19–−0.10 | 19.88% | 26.79% | 1.35 | |
| −0.10–−0.006 | 20.19% | 16.07% | 0.8 | |
| −0.006–0.19 | 20.82% | 25.00% | 1.2 | |
| 0.19–1.09 | 18.98% | 21.43% | 1.13 | |
| MRVBF | 0–0.47 | 19.92% | 23.21% | 1.17 |
| 0.47–1.87 | 20.28% | 33.93% | 1.67 | |
| 1.87–4.12 | 20.45% | 28.57% | 1.4 | |
| 4.12–5.94 | 17.41% | 8.93% | 0.51 | |
| 5.94–7.57 | 21.94% | 5.36% | 0.24 | |
| Real surface area | <812.93 | 27.46% | 23.21% | 0.85 |
| 812.93–814.56 | 20.44% | 14.29% | 0.7 | |
| 814.56–819.48 | 20.42% | 28.57% | 1.4 | |
| 819.48–829.31 | 15.87% | 17.86% | 1.13 | |
| 829.31–1230.70 | 15.81% | 16.07% | 1.02 | |
| Slope height | 0–1.34 | 0.01% | 0.00% | 0 |
| 1.341–2.01 | 10.27% | 1.79% | 0.17 | |
| 2.01–4.02 | 44.25% | 35.71% | 0.81 | |
| 4.02–9.37 | 26.41% | 44.64% | 1.69 | |
| 9.37–170.83 | 19.04% | 17.86% | 0.94 | |
| Mid-slope | 0–0.09 | 20.00% | 21.43% | 1.07 |
| 0.09–0.22 | 20.00% | 17.86% | 0.89 | |
| 0.22–0.39 | 20.01% | 32.14% | 1.61 | |
| 0.39–0.57 | 25.07% | 23.21% | 0.93 | |
| 0.58–0.99 | 14.92% | 5.36% | 0.36 | |
| Normalized height index | 0.02–0.22 | 20.01% | 7.14% | 0.36 |
| 0.23–0.34 | 20.02% | 23.21% | 1.16 | |
| 0.34–0.45 | 20.01% | 25.00% | 1.25 | |
| 0.45–0.54 | 19.98% | 21.43% | 1.07 | |
| 0.54–0.99 | 19.98% | 23.21% | 1.16 | |
| 0–0.43 | 21.47% | 19.64% | 0.91 | |
| TRI | 0.44–0.77 | 28.75% | 25.00% | 0.87 |
| 0.78–1.12 | 17.15% | 21.43% | 1.25 | |
| 1.13–2.23 | 16.82% | 23.21% | 1.38 | |
| 2.24–21.92 | 15.81% | 10.71% | 0.68 | |
| Convexity | 0–37.36 | 18.55% | 8.93% | 0.48 |
| 37.36–38.90 | 18.67% | 17.86% | 0.96 | |
| 38.90–40.43 | 21.09% | 30.36% | 1.44 | |
| 40.43–43.49 | 22.74% | 25.00% | 1.1 | |
| 43.49–78.10 | 18.96% | 17.86% | 0.94 | |
| Protection index | 0–0.012 | 20.03% | 6.98% | 0.35 |
| 0.013–0.02 | 20.21% | 20.93% | 1.04 | |
| 0.021–0.027 | 20.04% | 27.91% | 1.39 | |
| 0.028–0.043 | 19.93% | 25.58% | 1.28 | |
| 0.044–0.499 | 19.79% | 18.60% | 0.94 | |
| TWI | −10.32–3.86 | 18.97% | 19.64% | 1.04 |
| 3.87–4.83 | 20.61% | 19.64% | 0.95 | |
| 4.83–6.02 | 21.78% | 12.50% | 0.57 | |
| 6.02–10.21 | 11.96% | 3.57% | 0.3 | |
| 10.21–17.09 | 26.69% | 44.64% | 1.67 | |
| SPI | −408,344,80–−2,793,230.43 | 0.00% | 0.00% | 0 |
| −2,793,230.43–−658,748.48 | 0.00% | 0.00% | 0 | |
| −658,748.48–1,475,733.45 | 0.02% | 0.00% | 0 | |
| 1,475,733.46–5,744,697.34 | 99.98% | 100.00% | 1 | |
| 5,744,697.35–135,948,096 | 0.00% | 0.00% | 0 | |
| Distance to river | 0–16.63 | 21.33% | 28.57% | 1.34 |
| 16.63–83.18 | 21.05% | 26.79% | 1.27 | |
| 83.18–199.63 | 19.40% | 16.07% | 0.83 | |
| 199.64–549 | 19.17% | 26.79% | 1.4 | |
| 549–4242.32 | 19.05% | 1.79% | 0.09 | |
| River density | 0–966.499 | 19.85% | 7.14% | 0.36 |
| 966.5–2077.97 | 20.28% | 28.57% | 1.41 | |
| 2077.97–2996.14 | 19.72% | 25.00% | 1.27 | |
| 2996.14–4252.59 | 20.33% | 21.43% | 1.05 | |
| 4252.59–12,322.86 | 19.82% | 17.86% | 0.9 | |
| Cell balance | −1–−0.90 | 19.93% | 14.29% | 0.72 |
| −0.90–−0.49 | 19.93% | 21.43% | 1.08 | |
| −0.49–−0.15 | 19.93% | 28.57% | 1.43 | |
| −0.15–0.28 | 20.28% | 23.21% | 1.14 | |
| 0.28–7 | 19.93% | 12.50% | 0.63 | |
| Melton ruggedness number | 0–0.29 | 51.83% | 50.00% | 0.96 |
| 0.29–0.96 | 13.09% | 8.93% | 0.68 | |
| 0.96–1.88 | 13.85% | 19.64% | 1.42 | |
| 1.88–3.28 | 10.63% | 12.50% | 1.18 | |
| 3.28–9.41 | 10.61% | 8.93% | 0.84 | |
| Valley depth | 0–2.869 | 17.56% | 100.00% | 5.69 |
| 2.87–5.165 | 23.41% | 0.00% | 0 | |
| 5.16–8.60 | 21.21% | 0.00% | 0 | |
| 8.60–15.49 | 19.04% | 0.00% | 0 | |
| 15.49–146.33 | 18.77% | 0.00% | 0 | |
| Rainfall | 325.13–370.93 | 19.54% | 10.71% | 0.55 |
| 370.93—396.66 | 19.84% | 10.71% | 0.54 | |
| 396.66–417.36 | 20.08% | 39.29% | 1.96 | |
| 417.36–439.32 | 19.72% | 26.79% | 1.36 | |
| 439.32–485.13 | 20.82% | 12.50% | 0.6 | |
| Lithology | M3P—Conglomerates, sands, silts, and marl | 5.39% | 4.87% | 0.91 |
| M2—Gypsum marls, gypsum, clays, and sandstones | 5.24% | 2.44% | 0.46 | |
| Plm—Sandstones | 1.81% | 9.75% | 5.38 | |
| T—Clays, gypsum, dolomite, and silts | 3.33% | 2.44% | 0.73 | |
| C7—Limestone bars with marl | 1.09% | 0.00% | 0 | |
| C5-6—Clays, marl with limestone | 2.41% | 0.00% | 0 | |
| Pa—Clays and black-gray marl | 0.39% | 0.00% | 0 | |
| E1g—Limestone with globigerines | 0.32% | 0.00% | 0 | |
| E2—Clays, marl with yellow bubbles, lumachelle | 0.90% | 0.00% | 0 | |
| C4—Marl with limestones bars | 0.99% | 2.44% | 2.47 | |
| C1-3—Marl, limestones with clays and quartzites | 1.27% | 0.00% | 0 | |
| O2—Coarse sandstones | 1.16% | 2.44% | 2.11 | |
| O1—Sandstones and clays | 0.45% | 2.44% | 5.39 | |
| E1n—Limestone with nummulites | 0.65% | 0.00% | 0 | |
| J—Limestone, dolomite, and marl | 0.17% | 0.00% | 0 | |
| M1—Limestone sandstone, lumachelle, and clays | 0.37% | 0.00% | 0 | |
| Qe—Dune sands | 0.36% | 0.08% | 0.21 | |
| Qc—Clays, silts, conglomerates | 73.71% | 73.12% | 0.99 | |
| Lineament density | 0–0.48 | 20.00% | 23.21% | 1.16 |
| 0.48–0.71 | 20.00% | 33.93% | 1.7 | |
| 0.71–0.96 | 20.00% | 12.50% | 0.63 | |
| 0.96–1.32 | 20.00% | 16.07% | 0.8 | |
| 1.32–2.65 | 20.00% | 14.29% | 0.71 | |
| Soil texture | Clay–silt | 36.35% | 21.05% | 0.58 |
| Sandy clay | 29.85% | 22.81% | 0.76 | |
| Silt | 19.20% | 1.75% | 0.09 | |
| Clay | 0.48% | 8.77% | 18.26 | |
| Silt clayey | 3.22% | 0.00% | 0 | |
| Sandy soil; Sandy silt | 6.69% | 3.51% | 0.52 | |
| Sandy clay | 0.03% | 21.05% | 735.65 | |
| Sandy-silty | 0.04% | 21.05% | 587.29 | |
| NDWI | −0.54–−0.25 | 28.27% | 75.61% | 2.67 |
| −0.05 | 39.65% | 41.46% | 1.05 | |
| −0.20–−0.14 | 27.15% | 17.07% | 0.63 | |
| −0.14–0.02 | 4.24% | 2.44% | 0.57 | |
| 0.02–0.41 | 0.69% | 4.88% | 7.07 | |
| NDVI | −0.34–0.09 | 17.02% | 7.32% | 0.43 |
| 0.099–0.134 | 22.08% | 14.63% | 0.66 | |
| 0.135–0.177 | 21.19% | 24.39% | 1.15 | |
| 0.178–0.231 | 20.36% | 34.15% | 1.68 | |
| 0.232–0.571 | 19.34% | 19.51% | 1.01 | |
| LULC | Urban area | 8.74% | 8.06% | 0.92 |
| Water body | 2.14% | 6.91% | 3.22 | |
| Wetlands | 7.67% | 16.48% | 2.15 | |
| Crop | 30.54% | 32.99% | 1.08 | |
| Vegetables | 23.33% | 29.01% | 1.24 | |
| Bare soil | 18.03% | 3.29% | 0.18 | |
| Arboriculture | 5.18% | 2.77% | 0.53 | |
| Forest | 4.37% | 0.50% | 0.11 |
References
- IPCC. Climate Change and Land: An IPCC Special Report on Climate Change, Kimdesertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems; Shukla, P.R., Skea, J., Buendía, E.C., Eds.; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Lee, S.; Sohrabi, M. An ensemble model for landslide susceptibility mapping in a forested area. Geocarto Int. 2020, 35, 1680–1705. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Moghaddam, D.D.; Kalantar, B.; Pradhan, B.; Kisi, O. A comparative assessment of GIS-based data mining models and a novel ensemble model in groundwater well potential mapping. J. Hydrol. 2017, 548, 471–483. [Google Scholar] [CrossRef]
- Khosravi, K.; Panahi, M.; Tien Bui, D. Spatial prediction of groundwater spring potential mapping based on an adaptive neuro-fuzzy inference system and metaheuristic optimization. Hydrol. Earth Syst. Sci. 2018, 22, 4771–4792. [Google Scholar] [CrossRef]
- Trabelsi, F.; Lee, S.; Khlifi, S.; Arfaoui, A. Frequency Ratio Model for Mapping Groundwater Potential Zones Using GIS and Remote Sensing; Medjerda Watershed Tunisia. In Advances in Sustainable and Environmental Hydrology, Hydrogeology, Hydrochemistry and Water Resources; CAJG 2018, Advances in Science, Technology & Innovation; Chaminé, H., Barbieri, M., Kisi, O., Chen, M., Merkel, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 341–345. [Google Scholar]
- Lee, S.; Rezaie, F. Status of Groundwater Potential Mapping Research Using GIS and Machine Learning. Korean J. Remote Sens. 2020, 36, 14. [Google Scholar] [CrossRef]
- Adeyeye, O.; Ikpokonte, E.; Arabi, S.A. GIS-based groundwater potential mapping within Dengi area, North Central Nigeria Egypt. J. Remote. Sens. Space Sci. 2019, 22, 175–181. [Google Scholar]
- Arabameri, A.; Roy, J.; Saha, S.; Blaschke, T.; Ghorbanzadeh, O.; Bui, D.T. Application of Probabilistic and Machine Learning Models for Groundwater Potentiality Mapping in Damghan Sedimentary Plain, Iran. Remote Sens. 2019, 11, 3015. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Han, L.; Zhang, H.; Zhao, Y.-H.; Li, X.-A.; Zhao, L. GIS-based landslide susceptibility mapping using hybrid integration approaches of fractal dimension with index of entropy and support vector machine. J. Mt. Sci. 2019, 16, 1275–1288. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Trabelsi, F.; Tarhouni, J.; Mammou, A.B. GIS-based subsurface databases and 3-D geological modeling as a tool for the set up of hydrogeological framework: Nabeul–Hammamet coastal aquifer case study (Northeast Tunisia). Environ. Earth Sci. 2013, 70, 2087–2105. [Google Scholar] [CrossRef]
- Arabameri, A.; Pal, S.C.; Rezaie, F.; Nalivan, O.A.; Chowdhuri, I.; Saha, A.; Lee, S.; Moayedi, H. Modeling groundwater potential using novel GIS-based machine-learning ensemble techniques. J. Hydrol. Reg. Stud. 2021, 36, 100848. [Google Scholar] [CrossRef]
- Dar, T.; Rai, N.; Bhat, A. Delineation of potential groundwater recharge zones using analytical hierarchy process (AHP). Geol. Ecol. Landsc. 2020, 5, 292–307. [Google Scholar] [CrossRef]
- Saranya, T.; Saravanan, S. Groundwater potential zone mapping using analytical hierarchy process (AHP) and GIS for Kancheepuram District, Tamilnadu, India. Model. Earth Syst. Environ. 2020, 6, 1105–1122. [Google Scholar] [CrossRef]
- Rahmati, O.; Samani, A.N.; Mahdavi, M.; Pourghasemi, H.R.; Zeinivand, H. Groundwater potential mapping at Kurdistan region of Iran using analytic hierarchy process and GIS. Arab. J. Geosci. 2014, 8, 7059–7071. [Google Scholar] [CrossRef]
- Akgun, A. A comparison of landslide susceptibility maps produced by logistic regression, multi-criteria decision, and likelihood ratio methods: A case study at İzmir, Turkey. Landslides 2011, 9, 93–106. [Google Scholar] [CrossRef]
- Al-Abadi, A.M. Groundwater potential mapping at northeastern Wasit and Missan governorates, Iraq using a data-driven weights of evidence technique in framework of GIS. Environ. Earth Sci. 2015, 74, 1109–1124. [Google Scholar] [CrossRef]
- Tahmassebipoor, N.; Rahmati, O.; Noormohamadi, F.; Lee, S. Spatial analysis of groundwater potential using weights-of-evidence and evidential belief function models and remote sensing. Arab. J. Geosci. 2015, 9, 1–18. [Google Scholar] [CrossRef]
- Nampak, H.; Pradhan, B.; Manap, M.A. Application of GIS based data driven evidential belief function model to predict groundwater potential zonation. J. Hydrol. 2014, 513, 283–300. [Google Scholar] [CrossRef]
- Mogaji, K.A.; Omosuyi, G.O.; Adelusi, A.O.; Lim, H.S. Application of GIS-Based Evidential Belief Function Model to Regional Groundwater Recharge Potential Zones Mapping in Hardrock Geologic Terrain. Environ. Process. 2016, 3, 93–123. [Google Scholar] [CrossRef]
- Oh, H.-J.; Kim, Y.-S.; Choi, J.-K.; Park, E.; Lee, S. GIS mapping of regional probabilistic groundwater potential in the area of Pohang City, Korea. J. Hydrol. 2011, 399, 158–172. [Google Scholar] [CrossRef]
- Guru, B.; Seshan, K.; Bera, S. Frequency ratio model for groundwater potential mapping and its sustainable management in cold desert, India. J. King Saud Univ. Sci. 2017, 29, 333–347. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Ha, D.H.; Jaafari, A.; Nguyen, H.D.; Van Phong, T.; Al-Ansari, N.; Prakash, I.; Van Le, H.; Pham, B.T. Groundwater Potential Mapping Combining Artificial Neural Network and Real AdaBoost Ensemble Technique: The DakNong Province Case-study, Vietnam. Int. J. Environ. Res. Public Health 2020, 17, 2473. [Google Scholar] [CrossRef] [PubMed]
- Mallick, J.; Singh, C.K.; Al-Wadi, H.; Ahmed, M.; Rahman, A.; Shashtri, S.; Mukherjee, S. Geospatial and geostatistical approach for groundwater potential zone delineation. Hydrol. Process. 2014, 29, 395–418. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using GIS-based machine learning techniques for Chongren County, Jiangxi Province, China. Sci. Total. Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef] [PubMed]
- Rasool, U.; Yin, X.; Xu, Z.; Rasool, M.A.; Senapathi, V.; Hussain, M.; Siddique, J.; Trabucco, J.C. Mapping of groundwater productivity potential with machine learning algorithms: A case study in the provincial capital of Baluchistan, Pakistan. Chemosphere 2022, 303, 135265. [Google Scholar] [CrossRef] [PubMed]
- Ali, S.A.; Parvin, F.; Pham, Q.B.; Vojtek, M.; Vojteková, J.; Costache, R.; Linh, N.T.T.; Nguyen, H.Q.; Ahmad, A.; Ghorbani, M.A. GIS-based comparative assessment of flood susceptibility mapping using hybrid multi-criteria decision-making approach, naïve Bayes tree, bivariate statistics and logistic regression: A case of Topľa basin, Slovakia. Ecol. Indic. 2020, 117, 106620. [Google Scholar] [CrossRef]
- Truong, X.L.; Mitamura, M.; Kono, Y.; Raghavan, V.; Yonezawa, G.; Truong, X.Q.; Do, T.H.; Bui, D.T.; Lee, S. Enhancing Prediction Performance of Landslide Susceptibility Model Using Hybrid Machine Learning Approach of Bagging Ensemble and Logistic Model Tree. Appl. Sci. 2018, 8, 1046. [Google Scholar] [CrossRef]
- Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluation of different machine learning models for predicting and mapping the susceptibility of gully erosion. Geomorphology 2017, 298, 118–137. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Arabameri, A.; Saha, A.; Chakrabortty, R.; Blaschke, T.; Pradhan, B.; Band, S. Implementation of Artificial Intelligence Based Ensemble Models for Gully Erosion Susceptibility Assessment. Remote. Sens. 2020, 12, 3620. [Google Scholar] [CrossRef]
- Talukdar, S.; Roy, S.K.; Sarkar, S.K.; Mahato, S.; Pal, S.; Rahman, A.; Praveen, B.; Das, T. Application of Hybrid Machine Learning Algorithms for Flood Susceptibility Modeling. In Spatial Modelling of Flood Risk and Flood Hazards; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Friedman, J.H.; Meulman, J.J. Multiple additive regression trees with application in epidemiology. Stat. Med. 2003, 22, 1365–1381. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R. A Comparative Assessment Between Three Machine Learning Models and Their Performance Comparison by Bivariate and Multivariate Statistical Methods in Groundwater Potential Mapping. Water Resour. Manag. 2015, 29, 5217–5236. [Google Scholar] [CrossRef]
- Lee, S.; Hong, S.-M.; Jung, H.-S. GIS-based groundwater potential mapping using artificial neural network and support vector machine models: The case of Boryeong city in Korea. Geocarto Int. 2017, 33, 847–861. [Google Scholar] [CrossRef]
- Lee, S. Editorial for Special Issue: “Application of Artificial Neural Networks in Geoinformatics”. Appl. Sci. 2018, 8, 55. [Google Scholar] [CrossRef]
- Foddis, M.L.; Montisci, A.; Trabelsi, F.; Uras, G. An MLP-ANN-based approach for assessing nitrate contamination. J. Water Supply Res. Technol. 2019, 19, 1911–1917. [Google Scholar] [CrossRef]
- Tamiru, H.; Wagari, M. Comparison of ANN model and GIS tools for delineation of groundwater potential zones, Fincha Catchment, Abay Basin, Ethiopia. Geocarto Int. 2021, 37, 6736–6754. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, W.; Pal, S.C.; Saha, A.; Chowdhuri, I.; Adeli, B.; Janizadeh, S.; Dineva, A.A.; Wang, X.; Mosavi, A. Evaluation efficiency of hybrid deep learning algorithms with neural network decision tree and boosting methods for predicting groundwater potential. Geocarto Int. 2021, 37, 5564–5584. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.-W. Application of Decision-Tree Model to Groundwater Productivity-Potential Mapping. Sustainability 2015, 7, 13416–13432. [Google Scholar] [CrossRef]
- Chen, C.; He, W.; Zhou, H.; Xue, Y.; Zhu, M. A comparative study among machine learning and numerical models for simulating groundwater dynamics in the Heihe River Basin, northwestern China. Sci. Rep. 2020, 10, 3904. [Google Scholar] [CrossRef]
- Duan, H.; Deng, Z.; Deng, F.; Wang, D. Assessment of Groundwater Potential Based on Multicriteria Decision Making Model and Decision Tree Algorithms. Math. Probl. Eng. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Choubin, B.; Hosseini, F.S.; Fried, Z.; Mosavi, A. Application of Bayesian Regularized Neural Networks for Groundwater Level Modeling. In Proceedings of the 2020 IEEE 3rd International Conference and Workshop in Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 18–19 November 2020; pp. 209–212. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen-Thoi, T.; Ly, H.-B.; Nguyen, M.D.; Al-Ansari, N.; Tran, V.-Q.; Le, T.-T. Extreme Learning Machine Based Prediction of Soil Shear Strength: A Sensitivity Analysis Using Monte Carlo Simulations and Feature Backward Elimination. Sustainability 2020, 12, 2339. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Abbaspour, K. A comparison between ten advanced and soft computing models for groundwater qanat potential assessment in Iran using R and GIS. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2017, 131, 967–984. [Google Scholar] [CrossRef]
- Chen, W.; Tsangaratos, P.; Ilia, I.; Duan, Z.; Chen, X. Groundwater spring potential mapping using population-based evolutionary algorithms and data mining methods. Sci. Total Environ. 2019, 684, 31–49. [Google Scholar] [CrossRef] [PubMed]
- Panahi, M.; Sadhasivam, N.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of groundwater potential mapping based on convolutional neural network (CNN) and support vector regression (SVR). J. Hydrol. 2020, 588, 125033. [Google Scholar] [CrossRef]
- Fadhillah, M.F.; Lee, S.; Lee, C.W.; Park, Y.C. Application of Support Vector Regression and Metaheuristic Optimization Algorithms for Groundwater Potential Mapping in Gangneung-si, South Korea. Remote Sens. 2021, 13, 1196. [Google Scholar] [CrossRef]
- Al-Fugara, A.; Ahmadlou, M.; Al-Shabeeb, A.R.; AlAyyash, S.; Al-Amoush, H.; Al-Adamat, R. Spatial mapping of groundwater springs potentiality using grid search-based and genetic algorithm-based support vector regression. Geocarto Int. 2022, 37, 284–303. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Dashtpagerdi, M.M. Evaluation of four supervised learning methods for groundwater spring potential mapping in Khalkhal region (Iran) using GIS-based features. Hydrogeol. J. 2016, 25, 169–189. [Google Scholar] [CrossRef]
- Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluating the influence of geo-environmental factors on gully erosion in a semi-arid region of Iran: An integrated framework. Sci. Total. Environ. 2017, 579, 913–927. [Google Scholar] [CrossRef]
- Golkarian, A.; Naghibi, S.A.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using C5.0, random forest and multivariate adaptive regression spline models in GIS. Environ. Monit. Assess. 2018, 190, 149. [Google Scholar] [CrossRef]
- Rajasekhar, M.; Sudarsana Raju, G.; Sreenivasulu, Y.; Siddi Raju, R. Delineation of groundwater potential zones in semi-arid region of Jilledubanderu river basin, Anantapur District, Andhra Pradesh, India using fuzzy logic, AHP and integrated fuzzy-AHP approaches. HydroResearch 2019, 2, 97–108. [Google Scholar] [CrossRef]
- Ahmad, I.; Dar, M.A.; Teka, A.H.; Teshome, M.; Andualem, T.G.; Teshome, A.; Shafi, T. GIS and fuzzy logic techniques-based demarcation of groundwater potential zones: A case study from Jemma River basin, Ethiopia. J. Afr. Earth Sci. 2020, 169, 103860. [Google Scholar] [CrossRef]
- Pham, B.; Jaafari, A.; Prakash, I.; Singh, S.; Quoc, N.; Bui, D. Hybrid computational intelligence models for groundwater potential mapping. Catena 2019, 182, 104101. [Google Scholar] [CrossRef]
- Kordestani, M.D.; Naghibi, S.A.; Hashemi, H.; Ahmadi, K.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using a novel data-mining ensemble model. Hydrogeol. J. 2018, 27, 211–224. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Zhao, Z. A GIS-based comparative study of Dempster-Shafer, logistic regression and artificial neural network models for landslide susceptibility mapping. Geocarto Int. 2017, 32, 367–385. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Dolatkordestani, M.; Rezaei, A.; Amouzegari, P.; Heravi, M.T.; Kalantar, B.; Pradhan, B. Application of rotation forest with decision trees as base classifier and a novel ensemble model in spatial modeling of groundwater potential. Environ. Monit. Assess. 2019, 191, 248. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Panahic, M.; Khosravid, K.; Pourghasemie, H.R.; Rezaiec, F.; Parvinnejhad, D. Spatial prediction of groundwater potentiality using ANFIS ensembled with teaching-learning-based and biogeography-based optimization. J. Hydrol. 2019, 572, 435–448. [Google Scholar] [CrossRef]
- Termeh, S.V.R.; Khosravi, K.; Sartaj, M.; Keesstra, S.D.; Tsai, F.T.-C.; Dijksma, R.; Pham, B.T. Optimization of an adaptive neuro-fuzzy inference system for groundwater potential mapping. Hydrogeol. J. 2019, 27, 2511–2534. [Google Scholar] [CrossRef]
- Panahi, M.; Gayen, A.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of landslide susceptibility using hybrid support vector regression (SVR) and the adaptive neuro-fuzzy inference system (ANFIS) with various metaheuristic algorithms. Sci. Total. Environ. 2020, 741, 139937. [Google Scholar] [CrossRef]
- Milan, S.G.; Roozbahani, A.; Azar, N.A.; Javadi, S. Development of adaptive neuro fuzzy inference system –Evolutionary algorithms hybrid models (ANFIS-EA) for prediction of optimal groundwater exploitation. J. Hydrol. 2021, 598, 126258. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, Q.; Hsu, W.; Lee, M.L. Enhancing SNNB with Local Accuracy Estimation and Ensemble Techniques. In Database Systems for Advanced Applications; DASFAA 2005, Lecture Notes in Computer Science; Zhou, L., Ooi, B.C., Meng, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3453, pp. 523–535. [Google Scholar] [CrossRef]
- Miraki, S.; Zanganeh, S.H.; Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Pham, B.T. Mapping Groundwater Potential Using a Novel Hybrid Intelligence Approach. Water Resour. Manag. 2019, 33, 281–302. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support Vector Regression. In Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar] [CrossRef]
- Trabelsi, F.; Ali, S.B.H. Exploring Machine Learning Models in Predicting Irrigation Groundwater Quality Indices for Effective Decision Making in Medjerda River Basin, Tunisia. Sustainability 2022, 14, 2341. [Google Scholar] [CrossRef]
- National Institute of Meteorology, Tunisia 2021. Available online: https://www.meteo.tn/en/national-institute-meteorology (accessed on 1 September 2022).
- Ben Ayed, N. Les Décrochements—Chevauchements de la Tunisie Septentrionale: Géométrie et Essai de Reconstitution des Conditions de Déformations; ETAP: Aberdeen, UK, 1998. [Google Scholar]
- Rouvier, H. Géologie de l’Extrême Nord-Tunisien: Tectonique et Paléogéographie Superposées à l’Extrémité Orientale de la Chaine Nord-Maghrébine. Thèsed’Etat, Paris, France, 1977. [Google Scholar]
- Perthuisot, V. Dynamique et Pétrogenèse des Extrusions Triasiques en Tunisie Septentrionale. Thèse de Doctorat es-Sciences, Trav. Labo. Géol. (Ecole Normale Supérieure), Paris, France, 1978. [Google Scholar]
- Ghanmi, M. Étude Géologique du Djebel Kebbouch (Tunisie Septentrionale). Thèse Doct. 3e Cycle, Univ. Paul-Sabatier, Toulouse, France, 1980. [Google Scholar]
- Melki, F.; Zouaghi, T.; Harrab, S.; Sainz, A.C.; Bédir, M.; Zargouni, F. Structuring and evolution of Neogene transcurrent basins in the Tellian foreland domain, north-eastern Tunisia. J. Geodyn. 2011, 52, 57–69. [Google Scholar] [CrossRef]
- Bejaoui, H.; Aïfa, T.; Melki, F.; Zargouni, F. Structural evolution of Cenozoic basins in northeastern Tunisia, in response to sinistral strike-slip movement on the El Alia-Teboursouk Fault. J. Afr. Earth Sci. 2017, 134, 174–197. [Google Scholar] [CrossRef]
- Bouyahya, N.; Trabelsi, F. Caractérisation de la Géométrie du Système Aquifère de la Basse Vallée de la Medjerda. Mémoire de fin d’études de mastère de recherche, spécialité Changement Climatique et gestion de l’eau. ESIM/Université de Jendouba: Tunisie.
- Regional Commission for Agricultural Development Ariana, Tunisia. 2020. Available online: http://www.ctab.nat.tn/index.php/en/sector-situation/tunisia/structure-and-organization (accessed on 1 September 2022).
- Singh, A.; Panda, S.N.; Uzokwe, V.N.; Krause, P. An assessment of groundwater recharge estimation techniques for sustainable resource management. Groundw. Sustain. Dev. 2019, 9, 100218. [Google Scholar] [CrossRef]
- Choubin, B.; Rahmati, O. Groundwater potential mapping using hybridization of simulated annealing and random forest. In Water Engineering Modeling and Mathematic Tools; Elsevier: Amsterdam, The Netherlands, 2021; pp. 391–403. [Google Scholar] [CrossRef]
- Mallick, J.; Talukdar, S.; Ahmed, M. Combining high resolution input and stacking ensemble machine learning algorithms for developing robust groundwater potentiality models in Bisha watershed, Saudi Arabia. Appl. Water Sci. 2022, 12, 77. [Google Scholar] [CrossRef]
- Costache, R. Flash-Flood Potential assessment in the upper and middle sector of Prahova river catchment (Romania). A comparative approach between four hybrid models. Sci. Total. Environ. 2019, 659, 1115–1134. [Google Scholar] [CrossRef]
- Yousefi, S.; Avand, M.; Yariyan, P.; Pourghasemi, H.; Keesstra, S.; Tavangar, S.; Tabibian, S. A novel GIS-based ensemble technique for rangeland downward trend mapping as an ecological indicator change. Ecol. Indic. 2020, 117, 106591. [Google Scholar] [CrossRef]
- Manap, M.A.; Nampak, H.; Pradhan, B.; Lee, S.; Sulaiman, W.N.A.; Ramli, M.F. Application of probabilistic-based frequency ratio model in groundwater potential mapping using remote sensing data and GIS. Arab. J. Geosci. 2012, 7, 711–724. [Google Scholar] [CrossRef]
- Torcivia, C.E.G.; López, N.N.R. Preliminary Morphometric Analysis: Río Talacasto Basin, Central Precordillera of San Juan, Argentina Advances in Geomorphology and Quaternary Studies in Argentina; Springer: Cham, Switzerland, 2020; pp. 158–168. [Google Scholar]
- Costache, R.; Bui, D.T. Identification of areas prone to flash-flood phenomena using multiple-criteria decision-making, bivariate statistics, machine learning and their ensembles. Sci. Total. Environ. 2020, 712, 136492. [Google Scholar] [CrossRef]
- Böhner, J.; Selige, T. Spatial prediction of soil attributes using terrain analysis and climate regionalization. In SAGA—Analyses and Modelling Applications; Böhner, J., McCloy, K.R., Strobl, J., Eds.; Göttinger Geographische Abhandlungen: Göttingen, Germany, 2006; Volume 115, pp. 13–28 + 118–120. [Google Scholar]
- Gallant, J.C.; Dowling, T.I. A multiresolution index of valley bottom flatness for mapping depositional areas. Water Resour. Res. 2003, 39, 1347–1359. [Google Scholar] [CrossRef]
- Herron, N.; Wilson, C. A water balance approach to assessing the hydrologic buffering potential of an alluvial fan. Water Resour. Res. 2001, 37, 341–351. [Google Scholar] [CrossRef]
- Butterworth, R.; Wilson, C.J.; Herron, N.F.; Greene, R.S.B.; Cunningham, R.B. Geomorphic controls on the physical and hydrologic properties of soils in a valley floor. Earth Surf. Process. Landf. 2000, 25, 1161–1179. [Google Scholar] [CrossRef]
- Bendix, J. Geländeklimatologie. Meteorol. Z. 2004, 14, 282. [Google Scholar]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terain modelling: A review of hydrological.; geomorphological.; and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Beheshtirad, M. Assessment of a data-driven evidential belief function model and GIS for groundwater potential mapping in the Koohrang Watershed, Iran. Geocarto Int. 2014, 30, 662–685. [Google Scholar] [CrossRef]
- Olaya, V. A Gentle Introduction to SAGA GIS. 2001. Available online: http://www.saga-gis.uni-goettingen.de (accessed on 10 August 2022).
- Bourque, C.P.-A.; Bayat, M. Landscape Variation in Tree Species Richness in Northern Iran Forests. PLoS ONE 2015, 10, e0121172. [Google Scholar] [CrossRef]
- Moore, I.D.; Wilson, J.P. Length-slope factors for the revised universal soil loss equation: Simplified method of estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Horton, R.E. Drainage basin characteristics. Trans. Am. Geop. Union 1932, 14, 350–361. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Tahmasebipour, M.N. Haghizadeh networks from digital elevation data. Comput. Vis. Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Oikonomidis, D.; Dimogianni, S.; Kazakis, N.; Voudouris, K. A GIS/Remote Sensing-based methodology for groundwater potentiality assessment in Tirnavos area, Greece. J. Hydrol. 2015, 525, 197–208. [Google Scholar] [CrossRef]
- Travaglia, C.; Dianelli, N. Groundwater Search by Remote Sensing: A Methodological Approach; Author’s Personal Copy; Environment and Natural Earth Sci Inform, Resources Service Sustainable Development Department; FAO: Rome, Italy, 2003; p. 34. [Google Scholar]
- Adiat, K.; Nawawi, M.; Abdullah, K. Assessing the Accuracy of GIS-Based Elementary Multicriteria Decision Analysis as a Spatial Prediction Tool: A Case of Predicting Potential Zones of Sustainable Groundwater Resources. J. Hydrol. 2012, 440–441, 75–89. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite Symposium, Washington, DC, USA, 10–14 December 1973; NASA: Washington, DC, USA, 1973; Volume 1, pp. 309–331. [Google Scholar]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Delhi, India, 1994. [Google Scholar]
- Jain, S.K.; Das, A.; Srivastava, D.K. Application of ANN for reservoir infow prediction and operation. J. Water Resour. Plan. Manag. 1999, 125, 263–271. [Google Scholar] [CrossRef]
- Vadiati, M.; Yami, Z.R.; Eskandari, E.; Nakhaei, M.; Kisi, O. Application of artificial intelligence models for prediction of groundwater level fluctuations: Case study (Tehran-Karaj alluvial aquifer). Environ. Monit. Assess. 2022, 194, 1–21. [Google Scholar] [CrossRef]
- Khashei, M.; Bijari, M. An artificial neural network (p,d,q) model for timeseries forecasting. Expert Syst. Appl. 2010, 37, 479–489. [Google Scholar] [CrossRef]
- Hasanuzzaman, M.; Mandal, M.H.; Hasnine, M.; Shit, P.K. Groundwater potential mapping using multi-criteria decision, bivariate statistic and machine learning algorithms: Evidence from Chota Nagpur Plateau, India. Appl. Water Sci. 2022, 12, 1–16. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kim, J.-C.; Lee, S.; Jung, H.-S.; Lee, S. Landslide susceptibility mapping using random forest and boosted tree models in Pyeong-Chang, Korea. Geocarto Int. 2018, 33, 1000–1015. [Google Scholar] [CrossRef]
- Razavi-Termeh, S.V.; Sadeghi-Niaraki, A.; Choi, S.-M. Groundwater Potential Mapping Using an Integrated Ensemble of Three Bivariate Statistical Models with Random Forest and Logistic Model Tree Models. Water 2019, 11, 1596. [Google Scholar] [CrossRef]
- Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J.M. Modeling spatial patterns of fire occurrence in Mediterranean Europe using Multiple Regression and Random Forest. For. Ecol. Manag. 2012, 275, 117–129. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by random forest. R News 2002, 2, 18–22. [Google Scholar]
- Catani, F.; Lagomarsino, D.; Segoni, S.; Tofani, V. Landslide susceptibility estimation by random forests technique: Sensitivity and scaling issues. Nat. Hazards Earth Syst. Sci. 2013, 13, 2815–2831. [Google Scholar] [CrossRef]
- Prasad, P.; Loveson, V.J.; Kotha, M.; Yadav, R. Application of machine learning techniques in groundwater potential mapping along the west coast of India. GIScience Remote. Sens. 2020, 57, 735–752. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Kombo, O.H.; Kumaran, S.; Ndashimye, E.; Bovim, A. An Ensemble Mode Decomposition Combined with SVR-RF Model for Prediction of Groundwater Level: The Case of Eastern Rwandan Aquifers. In Cybernetics Perspectives in Systems; Lecture Notes in Networks and Systems; Silhavy, R., Ed.; CSOC: Singapore, 2022; pp. 312–328. [Google Scholar] [CrossRef]
- Yang, Z.R. Biological applications of support vector machines. Brief. Bioinform. 2004, 5, 328–338. [Google Scholar] [CrossRef]
- Sajedi-Hosseini, F.; Malekian, A.; Choubin, B.; Rahmati, O.; Cipullo, S.; Coulon, F.; Pradhan, B. A novel machine learning-based approach for the risk assessment of nitrate groundwater contamination. Sci. Total. Environ. 2018, 644, 954–962. [Google Scholar] [CrossRef]
- Yao, X.; Tham, L.G.; Dai, F.C. Landslide susceptibility mapping based on Support Vector Machine: A case study on natural slopes of Hong Kong, China. Geomorphology 2008, 101, 572–582. [Google Scholar] [CrossRef]
- Arabgol, R.; Sartaj, M.; Asghari, K. Predicting nitrate concentration and its spatial distribution in groundwater resources using support vector machines (SVMs) model. Environ. Model. Assess. 2016, 21, 71–82. [Google Scholar] [CrossRef]
- Soria, D.; Garibaldi, J.M.; Ambrogi, F.; Biganzoli, E.M.; Ellis, I.O. A ‘non-parametric’version of the naive Bayes classifier. Knowl. -Based Syst. 2011, 24, 775–784. [Google Scholar] [CrossRef]
- Li, G.; Liu, Q.; Zhao, S.; Qiao, W.; Ren, X. Automatic crack recognition for concrete bridges using a fully convolutional neural network and naive Bayes data fusion based on a visual detection system. Meas. Sci. Technol. 2020, 31, 075403. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Van Phong, T.; Mafi-Gholami, D.; Amiri, M.; Van Tao, N.; Duong, V.-H.; Prakash, I. Naïve Bayes ensemble models for groundwater potential mapping. Ecol. Inform. 2021, 64, 101389. [Google Scholar] [CrossRef]
- Bhargavi, P.; Jyothi, S. Applying naive bayes data mining technique for classification of agricultural land soils. Int. J. Comput. Sci. Netw. Secur. 2009, 9, 117–122. [Google Scholar]
- Chen, J.; Huang, H.; Tian, S.; Qu, Y. Feature selection for text classification with Naïve Bayes. Expert Syst. Appl. 2009, 36, 5432–5435. [Google Scholar] [CrossRef]
- Gayen, A.; Pourghasemi, H.R.; Saha, S.; Keesstra, S.; Bai, S. Gully erosion susceptibility assessment and management of hazard-prone areas in India using different machine learning algorithms. Sci. Total. Environ. 2019, 668, 124–138. [Google Scholar] [CrossRef]
- Rizeei, H.M.; Pradhan, B.; Saharkhiz, M.A.; Lee, S. Groundwater aquifer potential modeling using an ensemble multi-adoptive boosting logistic regression technique. J. Hydrol. 2019, 579, 124172. [Google Scholar] [CrossRef]
- Mosavi, A.; Sajedi Hosseini, F.; Choubin, B.; Goodarzi, M.; Dineva, A.; Sardooi, E.A. Ensemble Boosting and Bagging Based Machine Learning Models for Groundwater Potential Prediction. Water Resour. Manag. Int. J. 2021, 35, 23–37. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Han, J. Spatial prediction of groundwater potential and driving factor analysis based on deep learning and geographical detector in an arid endorheic basin. Ecol. Indic. 2022, 142, 109256. [Google Scholar] [CrossRef]
- Wang, J.-F.; Li, X.-H.; Christakos, G.; Liao, Y.-L.; Zhang, T.; Gu, X.; Zheng, X.-Y. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).