Enhancing Solar Energy Forecast Using Multi-Column Convolutional Neural Network and Multipoint Time Series Approach
Abstract
1. Introduction
- We propose the Gramian cloud field (GCF) matrix (Section 2.1.1) to understand the clouds’ impact on solar power generation from ground-measured spatial and temporal solar power components.
- We evaluated the performance of the proposed models in different domains, namely time series, temporal, spatial, and spatial–temporal.
- For the first time, the CNN was used to forecast solar PV power using the multipoint and GCF approaches.
- We designed the MCNN model for use with multi-resolution input images from satellite and ground data. However, the target was the ground (in situ) data only.
2. Methodology
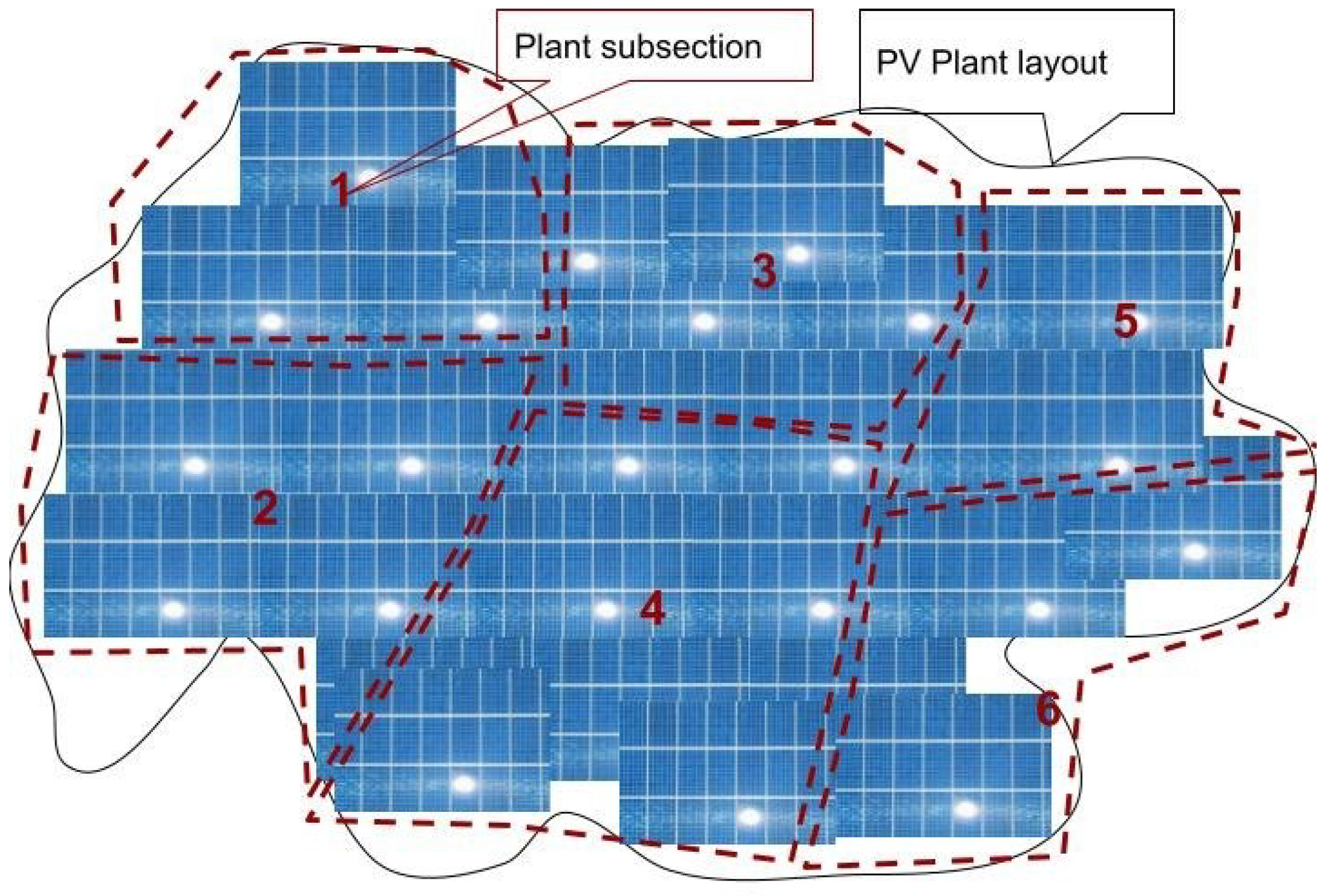
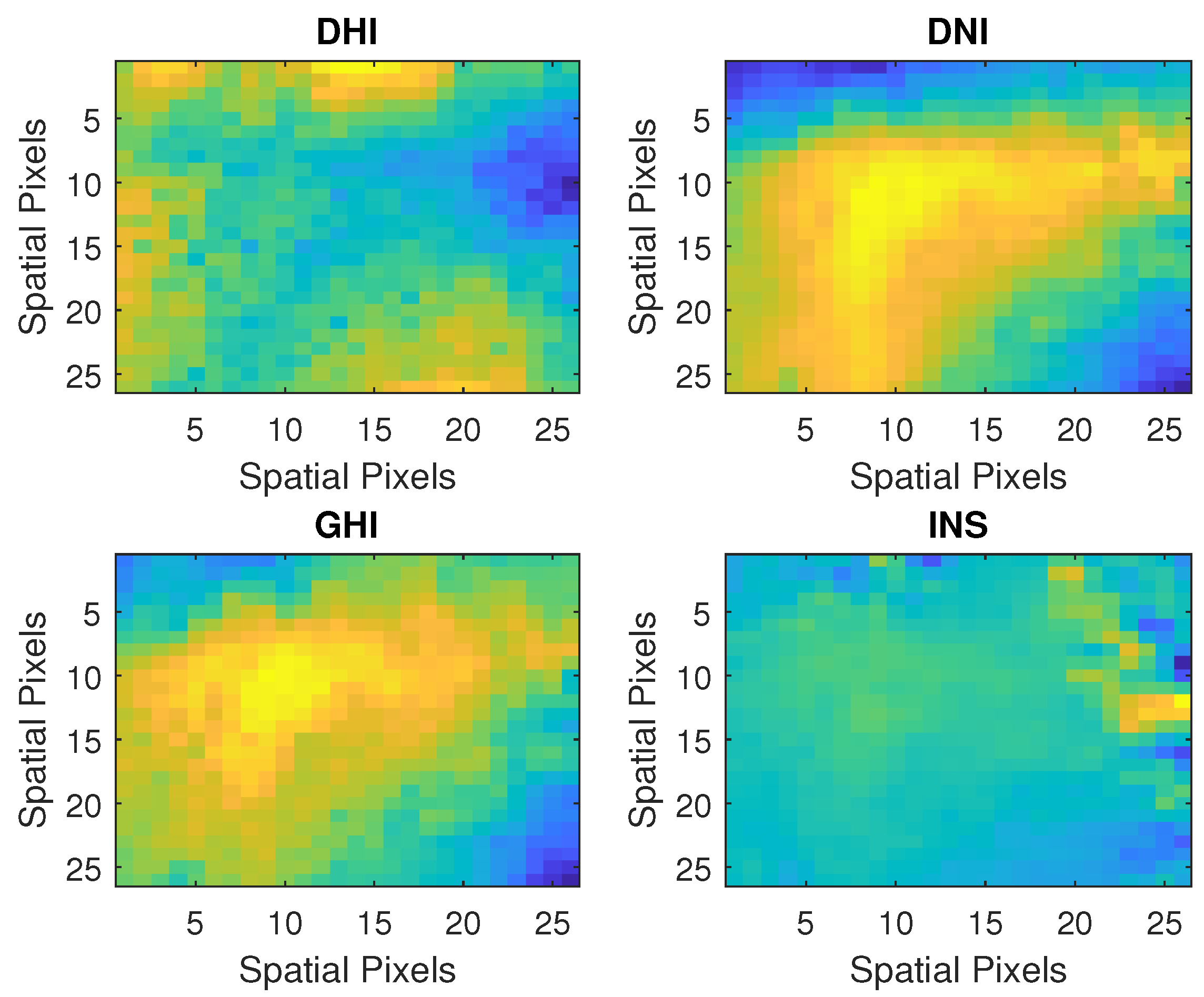
2.1. Data Processing
2.1.1. GCF Matrix
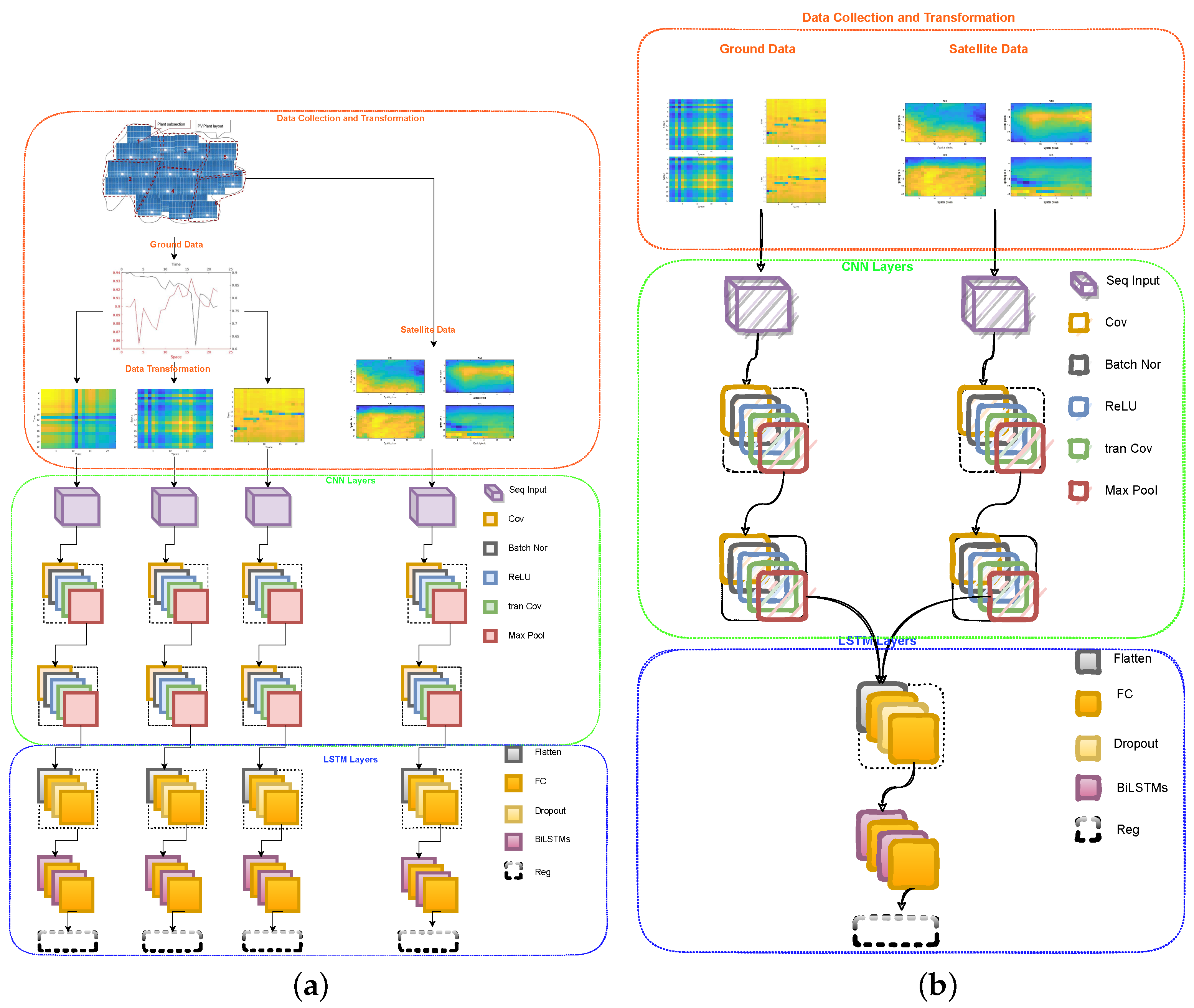
2.2. Deep Neural Network Structure
2.3. DNN Properties
2.3.1. DNN setup
2.3.2. DNN Settings
2.3.3. DNN Performance Parameters
- 1
- The validation of the proposed approach was performed by comparing with single and multiple inputs to match the single and multiple outputs on a typical time series dataset.
- 2
- The validation of the proposed approach is illustrated to reveal the effectiveness of the 2D input image metrics in the spatial domain to match the single and multiple outputs on a typical time series dataset.
- 3
- Similarly, the validation of the proposed approach is illustrated to reveal the effectiveness of the 2D input image metrics in the temporal domain to match the single and multiple outputs on a typical time series dataset.
- 4
- Finally, the validation of the proposed approach is illustrated to reveal the effectiveness of the 2D input image metrics in the spatiotemporal domain to match the single and multiple outputs on a typical time series dataset.
| Name | DI | Unit | Type | Sources | Category | Layers | M-Type | Outputs |
|---|---|---|---|---|---|---|---|---|
| M1 | 1D | MW | Ts | GD | CR+CD | 2 | LSTM | 1 |
| M2 | 1D | kW | Ts | GD | CR+CD | 2 | LSTM | 1 |
| M3 | 1D | kW | Ts | GD | CR+CD | 2 | LSTM | 22 |
| M4 | 2D | kW | Sp | GD | CR+CD | 2 | CNN | 1 |
| M5 | 2D | kW | Sp | GD | CR+CD | 2 | CNN | 22 |
| M6 | 2D | kW | Tp | GD | CR+CD | 2 | CNN | 1 |
| M7 | 2D | kW | Tp | GD | CR+CD | 2 | CNN | 22 |
| M8 | 2D | kW | Sp-Tp | GD | CR+CD | 2 | CNN | 1 |
| M9 | 2D | kW | Sp-Tp | GD | CR+CD | 2 | CNN | 22 |
| M10 | 1D | kW | Sp-Tp V | GD | CR+CD | 2 | LSTM | 1 |
| M11 | 1D | kW | Sp-Tp V | GD | CR+CD | 2 | LSTM | 22 |
| M12 | 2D | kW | Sp | GD | CR+CD | 4 | CNN-LSTM | 1 |
| M13 | 2D | kW | Sp | GD | CR+CD | 4 | CNN-LSTM | 22 |
| M14 | 2D | MW | Tp | GD | CR+CD | 4 | CNN-LSTM | 1 |
| M15 | 2D | kW | Tp | GD | CR+CD | 4 | CNN-LSTM | 22 |
| M16 | 2D | kW | Sp-Tp | GD | CR+CD | 4 | CNN-LSTM | 1 |
| M17 | 2D | kW | Sp-Tp | GD | CR+CD | 4 | CNN-LSTM | 22 |
| M18 | 2D | kW | Sp-Tp | GD | CR | 4 | CNN-LSTM | 22 |
| M19 | 2D | kW | Sp-Tp | GD | CD | 4 | CNN-LSTM | 22 |
| M20 | 2D | kW | Sp-Tp | Sat | CR | 4 | CNN-LSTM | 22 |
| M21 | 2D | kW | Sp-Tp | Sat | CD | 4 | CNN-LSTM | 22 |
| M22 | 2D | kW | Sp-Tp | Sat+GD | CR | 4 | CNN-LSTM | 22 |
| M23 | 2D | kW | Sp-Tp | Sat+GD | CD | 4 | CNN-LSTM | 22 |
| M24 | 2D | kW | Sp-Tp | GD | CR | 4 | MCNN | 22 |
| M25 | 2D | kW | Sp-Tp | GD | CD | 4 | MCNN | 22 |
| M26 | 2D | kW | Sp-Tp | Sat | CR | 4 | MCNN | 22 |
| M27 | 2D | kW | Sp-Tp | Sat | CD | 4 | MCNN | 22 |
| M28 | 2D | kW | Sp-Tp | Sat+GD | CR | 4 | MCNN | 22 |
| M29 | 2D | kW | Sp-Tp | Sat+GD | CD | 4 | MCNN | 22 |
3. Experimental Results and Evaluation
3.1. Comparisons of Methods
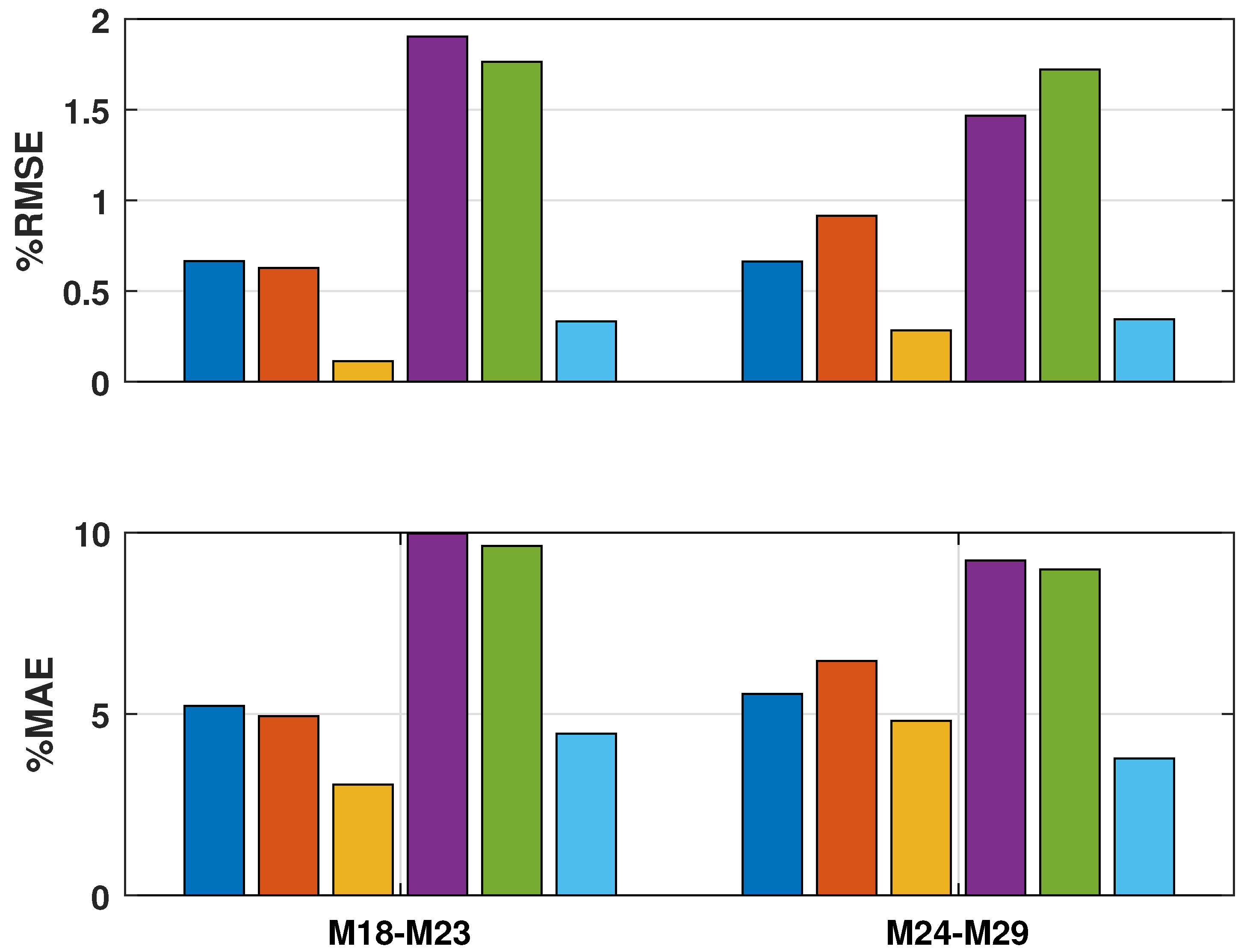
3.2. Effects of Multi-Column CNN-LSTM model
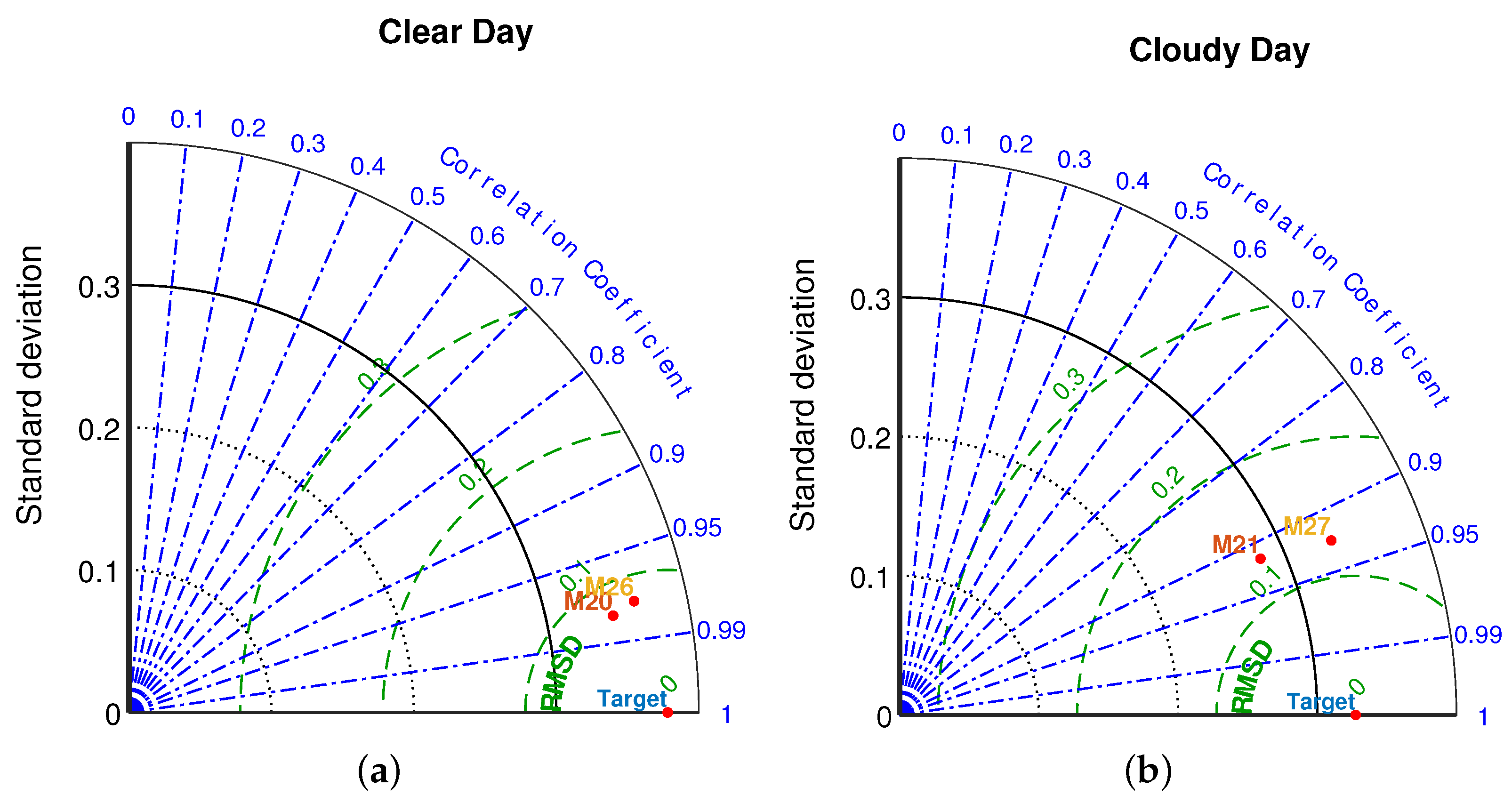
3.3. Effects of Cloudy Conditions
3.4. Effects of Satellite Inputs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature and Abbreviations
| Multi-column convolutional neural network | ||
| Multipoint time series | ||
| Gramian cloud field matrix | ||
| Photovoltaic | ||
| Convolutional neural network | ||
| Long short-term memory | ||
| Deep neural network | ||
| Fully connected layer | ||
| Regression | ||
| Cloud potential | ||
| Model-type | ||
| Input dimension | ||
| Time series | ||
| Spatial | ||
| Temporal | ||
| Spatial–temporal | ||
| Ground | ||
| Satellite | ||
| Satellite–ground | ||
| Clear | ||
| Cloudy | ||
| Clear–cloudy | ||
| Root-mean-squared error | ||
| Mean absolute error | ||
| Root-mean-squared deviation | ||
| Global horizontal irradiance | ||
| Direct normal irradiance | ||
| Diffuse horizontal irradiance | ||
| Insolation |
References
- Owusu, P.A.; Asumadu-Sarkodie, S. A review of renewable energy sources, sustainability issues and climate change mitigation. Cogent Eng. 2016, 3, 1167990. [Google Scholar] [CrossRef]
- Irfan, M.; Zhao, Z.Y.; Ahmad, M.; Mukeshimana, M.C. Solar energy development in Pakistan: Barriers and policy recommendations. Sustainability 2019, 11, 1206. [Google Scholar] [CrossRef]
- Das, L.; Habib, K.; Saidur, R.; Aslfattahi, N.; Yahya, S.M.; Rubbi, F. Improved thermophysical properties and energy efficiency of aqueous ionic liquid/mxene nanofluid in a hybrid pv/t solar system. Nanomaterials 2020, 10, 1372. [Google Scholar] [CrossRef]
- Chikh, M.; Berkane, S.; Mahrane, A.; Sellami, R.; Yassaa, N. Performance assessment of a 400 kWp multi-technology photovoltaic grid-connected pilot plant in arid region of Algeria. Renew. Energy 2021, 172, 488–501. [Google Scholar] [CrossRef]
- Yadav, H.K.; Pal, Y.; Tripathi, M.M. Photovoltaic power forecasting methods in smart power grid. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–6. [Google Scholar]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Kumler, A.; Xie, Y.; Zhang, Y. A Physics-based Smart Persistence model for Intra-hour forecasting of solar radiation (PSPI) using GHI measurements and a cloud retrieval technique. Sol. Energy 2019, 177, 494–500. [Google Scholar] [CrossRef]
- Hajirahimi, Z.; Khashei, M. Hybrid structures in time series modeling and forecasting: A review. Eng. Appl. Artif. Intell. 2019, 86, 83–106. [Google Scholar] [CrossRef]
- Nayak, A.; Heistrene, L. Hybrid machine learning model for forecasting solar power generation. In Proceedings of the 2020 International Conference on Smart Grids and Energy Systems (SGES), Perth, Australia, 23–26 November 2020; pp. 910–915. [Google Scholar]
- de Freitas Viscondi, G.; Alves-Souza, S.N. A Systematic Literature Review on big data for solar photovoltaic electricity generation forecasting. Sustain. Energy Technol. Assess. 2019, 31, 54–63. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Sikinioti-Lock, A.; Shah, N. Machine-learning methods for integrated renewable power generation: A comparative study of artificial neural networks, support vector regression, and Gaussian Process Regression. Renew. Sustain. Energy Rev. 2019, 108, 513–538. [Google Scholar] [CrossRef]
- Marquez, R.; Pedro, H.T.; Coimbra, C.F. Hybrid solar forecasting method uses satellite imaging and ground telemetry as inputs to ANNs. Sol. Energy 2013, 92, 176–188. [Google Scholar] [CrossRef]
- Chu, Y.; Pedro, H.T.; Nonnenmacher, L.; Inman, R.H.; Liao, Z.; Coimbra, C.F. A smart image-based cloud detection system for intrahour solar irradiance forecasts. J. Atmos. Ocean. Technol. 2014, 31, 1995–2007. [Google Scholar] [CrossRef]
- Peng, Z.; Yu, D.; Huang, D.; Heiser, J.; Yoo, S.; Kalb, P. 3D cloud detection and tracking system for solar forecast using multiple sky imagers. Sol. Energy 2015, 118, 496–519. [Google Scholar] [CrossRef]
- Caldas, M.; Alonso-Suárez, R. Very short-term solar irradiance forecast using all-sky imaging and real-time irradiance measurements. Renew. Energy 2019, 143, 1643–1658. [Google Scholar] [CrossRef]
- Joshi, J.C.; Kaur, P.; Kumar, B.; Singh, A.; Satyawali, P. HIM-STRAT: A neural network-based model for snow cover simulation and avalanche hazard prediction over North-West Himalaya. Nat. Hazards 2020, 103, 1239–1260. [Google Scholar] [CrossRef]
- Zamora, R.J.; Dutton, E.G.; Trainer, M.; McKeen, S.A.; Wilczak, J.M.; Hou, Y.T. The accuracy of solar irradiance calculations used in mesoscale numerical weather prediction. Mon. Weather Rev. 2005, 133, 783–792. [Google Scholar] [CrossRef]
- Lima, F.J.; Martins, F.R.; Pereira, E.B.; Lorenz, E.; Heinemann, D. Forecast for surface solar irradiance at the Brazilian Northeastern region using NWP model and artificial neural networks. Renew. Energy 2016, 87, 807–818. [Google Scholar] [CrossRef]
- Ji, W.; Chee, K.C. Prediction of hourly solar radiation using a novel hybrid model of ARMA and TDNN. Sol. Energy 2011, 85, 808–817. [Google Scholar] [CrossRef]
- Bhardwaj, S.; Sharma, V.; Srivastava, S.; Sastry, O.; Bandyopadhyay, B.; Chandel, S.; Gupta, J. Estimation of solar radiation using a combination of Hidden Markov Model and generalized Fuzzy model. Sol. Energy 2013, 93, 43–54. [Google Scholar] [CrossRef]
- Voyant, C.; Muselli, M.; Paoli, C.; Nivet, M.L. Hybrid methodology for hourly global radiation forecasting in Mediterranean area. Renew. Energy 2013, 53, 1–11. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, D.; Reindl, T.; Walsh, W.M. Short-term solar irradiance forecasting using exponential smoothing state space model. Energy 2013, 55, 1104–1113. [Google Scholar] [CrossRef]
- Hajihassani, M.; Jahed Armaghani, D.; Kalatehjari, R. Applications of particle swarm optimization in geotechnical engineering: A comprehensive review. Geotech. Geol. Eng. 2018, 36, 705–722. [Google Scholar] [CrossRef]
- Baser, F.; Demirhan, H. A fuzzy regression with support vector machine approach to the estimation of horizontal global solar radiation. Energy 2017, 123, 229–240. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Tong, C.W.; Arif, M.; Petković, D.; Ch, S. A new hybrid support vector machine–wavelet transform approach for estimation of horizontal global solar radiation. Energy Convers. Manag. 2015, 92, 162–171. [Google Scholar] [CrossRef]
- Deo, R.C.; Wen, X.; Qi, F. A wavelet-coupled support vector machine model for forecasting global incident solar radiation using limited meteorological dataset. Appl. Energy 2016, 168, 568–593. [Google Scholar] [CrossRef]
- Hussain, S.; Al Alili, A. A pruning approach to optimize synaptic connections and select relevant input parameters for neural network modelling of solar radiation. Appl. Soft Comput. 2017, 52, 898–908. [Google Scholar] [CrossRef]
- Lan, H.; Yin, H.; Hong, Y.Y.; Wen, S.; David, C.Y.; Cheng, P. Day-ahead spatio-temporal forecasting of solar irradiation along a navigation route. Appl. Energy 2018, 211, 15–27. [Google Scholar] [CrossRef]
- Davò, F.; Alessandrini, S.; Sperati, S.; Delle Monache, L.; Airoldi, D.; Vespucci, M.T. Post-processing techniques and principal component analysis for regional wind power and solar irradiance forecasting. Sol. Energy 2016, 134, 327–338. [Google Scholar] [CrossRef]
- Li, P.; Zhou, K.; Lu, X.; Yang, S. A hybrid deep learning model for short-term PV power forecasting. Appl. Energy 2020, 259, 114216. [Google Scholar] [CrossRef]
- de Jesús, D.A.R.; Mandal, P.; Chakraborty, S.; Senjyu, T. Solar PV Power Prediction Using A New Approach Based on Hybrid Deep Neural Network. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Al-Hajj, R.; Assi, A.; Fouad, M.M. Multi-level Stacking of Long Short Term Memory Recurrent Models for Time Series Forecasting of Solar Radiation. In Proceedings of the 2021 10th International Conference on Renewable Energy Research and Application (ICRERA), Ankara, Turkey, 26–29 September 2021; pp. 71–76. [Google Scholar]
- Munkhammar, J.; Widén, J.; Hinkelman, L.M. A copula method for simulating correlated instantaneous solar irradiance in spatial networks. Sol. Energy 2017, 143, 10–21. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhou, X.; Yang, T. Hetero-convlstm: A deep learning approach to traffic accident prediction on heterogeneous spatio-temporal data. In Proceedings of the Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 984–992. [Google Scholar]
- Drineas, P.; Mahoney, M.W. Approximating a gram matrix for improved kernel-based learning. In Proceedings of the International Conference on Computational Learning Theory, Paris, France, 3–6 July 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 323–337. [Google Scholar]
- Xiong, J.; Li, C.; Wang, C.D.; Cen, J.; Wang, Q.; Wang, S. Application of Convolutional Neural Network and Data Preprocessing by Mutual Dimensionless and Similar Gram Matrix in Fault Diagnosis. IEEE Trans. Ind. Inform. 2022, 18, 1061–1071. [Google Scholar] [CrossRef]
- Lim, S.C.; Huh, J.H.; Hong, S.H.; Park, C.Y.; Kim, J.C. Solar Power Forecasting Using CNN-LSTM Hybrid Model. Energies 2022, 15, 8233. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. The libRadtran software package for radiative transfer calculations-description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0. 1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Kosmopoulos, P.G.; Kazadzis, S.; Taylor, M.; Raptis, P.I.; Keramitsoglou, I.; Kiranoudis, C.; Bais, A.F. Assessment of surface solar irradiance derived from real-time modelling techniques and verification with ground-based measurements. Atmos. Meas. Tech. 2018, 11, 907–924. [Google Scholar] [CrossRef]
- Masoom, A.; Kosmopoulos, P.; Bansal, A.; Kazadzis, S. Solar energy estimations in India using remote sensing technologies and validation with sun photometers in urban areas. Remote Sens. 2020, 12, 254. [Google Scholar] [CrossRef]
- Ricchiazzi, P.; Yang, S.; Gautier, C.; Sowle, D. SBDART: A research and teaching software tool for plane-parallel radiative transfer in the Earth’s atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
- Kato, S.; Ackerman, T.P.; Mather, J.H.; Clothiaux, E.E. The k-distribution method and correlated-k approximation for a shortwave radiative transfer model. J. Quant. Spectrosc. Radiat. Transf. 1999, 62, 109–121. [Google Scholar] [CrossRef]
- Shettle, E. Models of aerosols, clouds and precipitation for atmospheric propagation studies, paper presented at Conference on Atmospheric Propagation in the UV, Visible, IR and MM-Region and Related System Aspects, NATO Adv. Group for Aerosp. Res. Dev. Cph. 1989. [Google Scholar]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Sainath, T.N.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, long short-term memory, fully connected deep neural networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Queensland, Australia, 19–24 April 2015; pp. 4580–4584. [Google Scholar]
- Yang, H.; Han, J.; Min, K. A multi-column CNN model for emotion recognition from EEG signals. Sensors 2019, 19, 4736. [Google Scholar] [CrossRef]
- Ouyang, X.; Xu, S.; Zhang, C.; Zhou, P.; Yang, Y.; Liu, G.; Li, X. A 3D-CNN and LSTM based multi-task learning architecture for action recognition. IEEE Access 2019, 7, 40757–40770. [Google Scholar] [CrossRef]
- Olmschenk, G.; Tang, H.; Zhu, Z. Improving dense crowd counting convolutional neural networks using inverse k-nearest neighbor maps and multiscale upsampling. arXiv 2019, arXiv:1902.05379. [Google Scholar]
- Xiao, M.; Wu, Y.; Zuo, G.; Fan, S.; Yu, H.; Shaikh, Z.A.; Wen, Z. Addressing Overfitting Problem in Deep Learning-Based Solutions for Next Generation Data-Driven Networks. Wirel. Commun. Mob. Comput. 2021, 2021. [Google Scholar] [CrossRef]
- Javid, A.M.; Das, S.; Skoglund, M.; Chatterjee, S. A ReLU Dense Layer to Improve the Performance of Neural Networks. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 2810–2814. [Google Scholar] [CrossRef]
- Xie, J.; Chen, B.; Gu, X.; Liang, F.; Xu, X. Self-attention-based BiLSTM model for short text fine-grained sentiment classification. IEEE Access 2019, 7, 180558–180570. [Google Scholar] [CrossRef]
- Aslan, M.F.; Unlersen, M.F.; Sabanci, K.; Durdu, A. CNN-based transfer learning–BiLSTM network: A novel approach for COVID-19 infection detection. Appl. Soft Comput. 2021, 98, 106912. [Google Scholar] [CrossRef]
- Yongsheng, D.; Fengshun, J.; Jie, Z.; Zhikeng, L. A short-term power output forecasting model based on correlation analysis and ELM-LSTM for distributed PV system. J. Electr. Comput. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Qu, J.; Qian, Z.; Pei, Y. Day-ahead hourly photovoltaic power forecasting using attention-based CNN-LSTM neural network embedded with multiple relevant and target variables prediction pattern. Energy 2021, 232, 120996. [Google Scholar] [CrossRef]
- Tovar, M.; Robles, M.; Rashid, F. PV power prediction, using CNN-LSTM hybrid neural network model. Case of study: Temixco-Morelos, México. Energies 2020, 13, 6512. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Liang, Z.; Wei, Z.; Sun, G. Hybrid method for short-term photovoltaic power forecasting based on deep convolutional neural network. IET Gener. Transm. Distrib. 2018, 12, 4557–4567. [Google Scholar] [CrossRef]
- Yan, R.; Liao, J.; Yang, J.; Sun, W.; Nong, M.; Li, F. Multi-hour and multi-site air quality index forecasting in Beijing using CNN, LSTM, CNN-LSTM, and spatiotemporal clustering. Expert Syst. Appl. 2021, 169, 114513. [Google Scholar] [CrossRef]
- Gao, B.; Huang, X.; Shi, J.; Tai, Y.; Zhang, J. Hourly forecasting of solar irradiance based on CEEMDAN and multi-strategy CNN-LSTM neural networks. Renew. Energy 2020, 162, 1665–1683. [Google Scholar] [CrossRef]







| Settings | Parameters |
|---|---|
| Solar dataset number | 22 |
| Training set size | 72,576 |
| LSTM network layer number | 6 |
| LSTM neuron number in each layer | 100 |
| CNN network layer number | 6 |
| CNN neuron number in each layer | 100 |
| LSTM-CNN network layer number | 12 |
| LSTM-CNN neuron number in each layer | 100 |
| Hidden dense layer number | 2 |
| Hidden neuron number | 200, 200 |
| Dropout rate | 0.2 |
| Training method | Adam optimizer |
| Loss function | RMSE, MAE |
| Forecast horizon (min) | 5–120 (2-h) |
| Model | MAE | RMSE | ||||
|---|---|---|---|---|---|---|
| 15 | 30 | 90 | 15 | 30 | 90 | |
| M1 | 27.2203 | 27.5405 | 24.7239 | 9.7590 | 10.3284 | 8.4229 |
| M2 | 9.5770 | 15.3224 | 25.2258 | 1.5453 | 3.1543 | 9.0886 |
| M3 | 17.3940 | 12.3964 | 20.9350 | 4.7824 | 2.2567 | 6.2924 |
| M4 | 26.2417 | 26.2595 | 26.3432 | 9.0746 | 9.0960 | 9.1694 |
| M5 | 25.8696 | 25.8866 | 25.9707 | 8.8227 | 8.8378 | 8.9141 |
| M6 | 26.2419 | 26.2598 | 26.3453 | 9.0777 | 9.0982 | 9.1745 |
| M7 | 8.4704 | 10.7054 | 19.9611 | 1.4691 | 2.1297 | 5.4158 |
| M8 | 25.9674 | 24.8605 | 26.3303 | 8.8689 | 8.0851 | 9.1643 |
| M9 | 13.7934 | 12.0208 | 20.1083 | 2.8352 | 2.2700 | 5.4955 |
| M10 | 20.6757 | 14.4866 | 20.8888 | 6.4844 | 3.1501 | 5.9975 |
| M11 | 13.9041 | 15.9961 | 22.4180 | 3.1708 | 3.8144 | 6.8712 |
| M12 | 8.9575 | 12.1475 | 20.9664 | 1.5873 | 2.4501 | 5.9187 |
| M13 | 9.0794 | 11.9933 | 20.9083 | 1.5672 | 2.3315 | 5.9165 |
| M14 | 9.2380 | 10.4488 | 15.7862 | 1.6760 | 2.0737 | 4.1134 |
| M15 | 8.9872 | 10.6592 | 15.3156 | 1.5511 | 1.9917 | 3.6687 |
| M16 | 8.9911 | 10.9749 | 15.3569 | 1.6573 | 2.2885 | 3.9627 |
| M17 | 8.7971 | 10.6773 | 14.8766 | 1.5922 | 2.1281 | 3.5232 |
| M18 | 3.0580 | 2.1712 | 5.0391 | 0.1135 | 0.1093 | 0.7463 |
| M19 | 4.4561 | 4.4877 | 9.9952 | 0.3324 | 0.3796 | 1.2174 |
| M20 | 4.9387 | 5.1428 | 10.9953 | 0.6260 | 0.8058 | 2.6585 |
| M21 | 9.6306 | 9.9354 | 13.2887 | 1.7636 | 1.8470 | 3.3160 |
| M22 | 5.2187 | 5.4727 | 11.4658 | 0.6640 | 0.8664 | 2.7936 |
| M23 | 9.9740 | 10.6457 | 15.4560 | 1.9031 | 2.5889 | 4.8156 |
| M24 | 4.8158 | 3.5540 | 5.5037 | 0.2826 | 0.2826 | 0.4237 |
| M25 | 5.0246 | 4.5348 | 9.3128 | 0.5826 | 0.5752 | 1.7748 |
| M26 | 5.8434 | 8.03844 | 19.6718 | 0.7357 | 1.8813 | 8.7471 |
| M27 | 8.9803 | 8.9398 | 19.0666 | 1.7213 | 1.7662 | 6.0082 |
| M28 | 5.5534 | 7.0940 | 18.9287 | 0.6613 | 1.1534 | 5.9412 |
| M29 | 9.2267 | 9.5179 | 18.3195 | 1.4669 | 1.8996 | 5.8551 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Kashyap, Y.; Kosmopoulos, P. Enhancing Solar Energy Forecast Using Multi-Column Convolutional Neural Network and Multipoint Time Series Approach. Remote Sens. 2023, 15, 107. https://doi.org/10.3390/rs15010107
Kumar A, Kashyap Y, Kosmopoulos P. Enhancing Solar Energy Forecast Using Multi-Column Convolutional Neural Network and Multipoint Time Series Approach. Remote Sensing. 2023; 15(1):107. https://doi.org/10.3390/rs15010107
Chicago/Turabian StyleKumar, Anil, Yashwant Kashyap, and Panagiotis Kosmopoulos. 2023. "Enhancing Solar Energy Forecast Using Multi-Column Convolutional Neural Network and Multipoint Time Series Approach" Remote Sensing 15, no. 1: 107. https://doi.org/10.3390/rs15010107
APA StyleKumar, A., Kashyap, Y., & Kosmopoulos, P. (2023). Enhancing Solar Energy Forecast Using Multi-Column Convolutional Neural Network and Multipoint Time Series Approach. Remote Sensing, 15(1), 107. https://doi.org/10.3390/rs15010107







