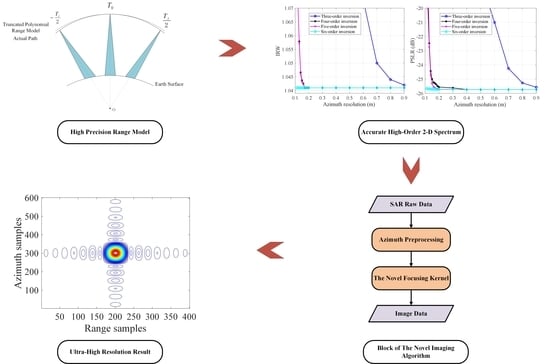
A Novel Ultra−High Resolution Imaging Algorithm Based on the Accurate High−Order 2−D Spectrum for Space−Borne SAR
Abstract
:1. Introduction
2. Infinite Polynomial Range Model and Signal Spectrum
3. Imaging Algorithm
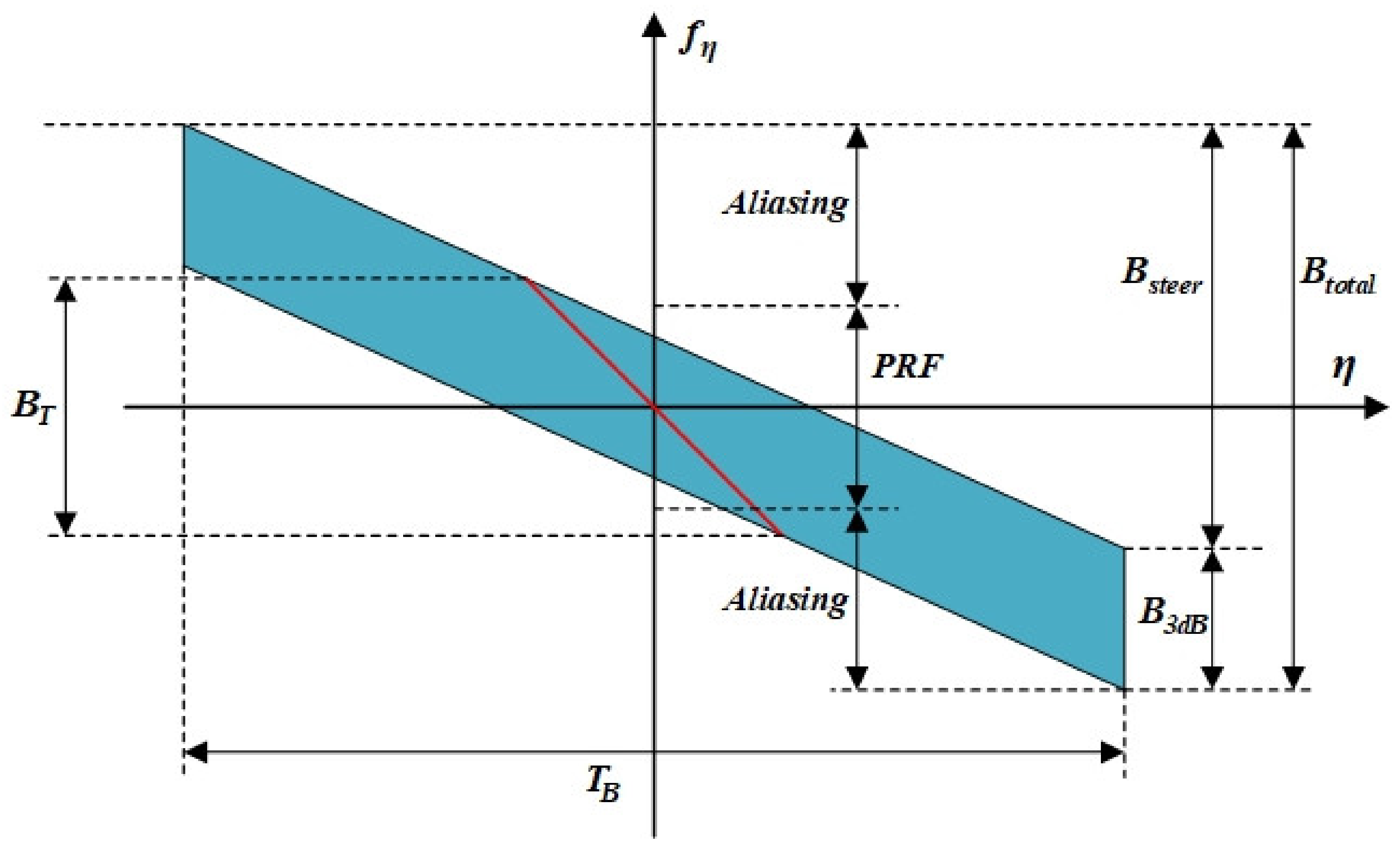
3.1. Azimuth Preprocessing
3.2. High−Order Phase Compensation
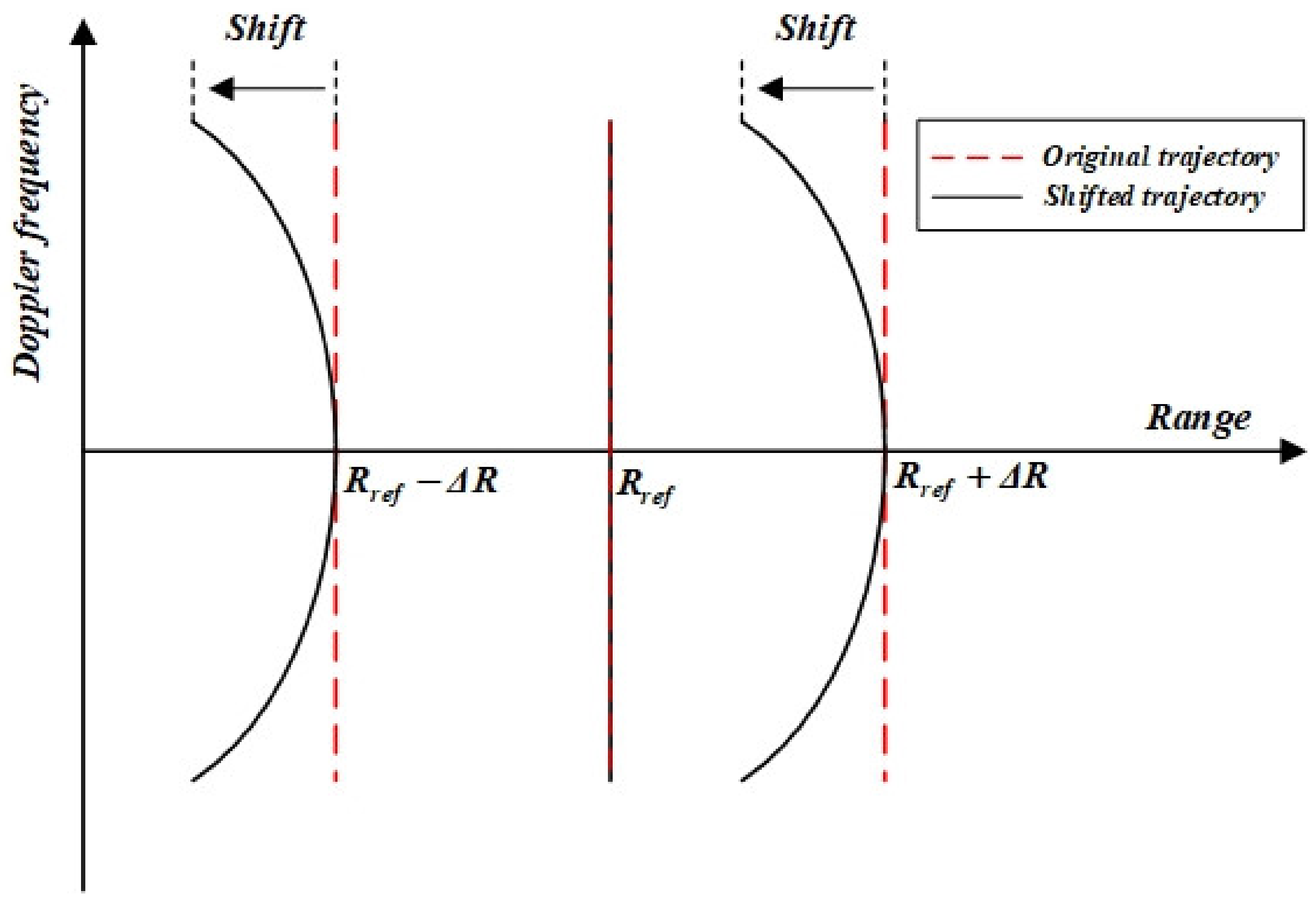
3.3. Linear RCMC
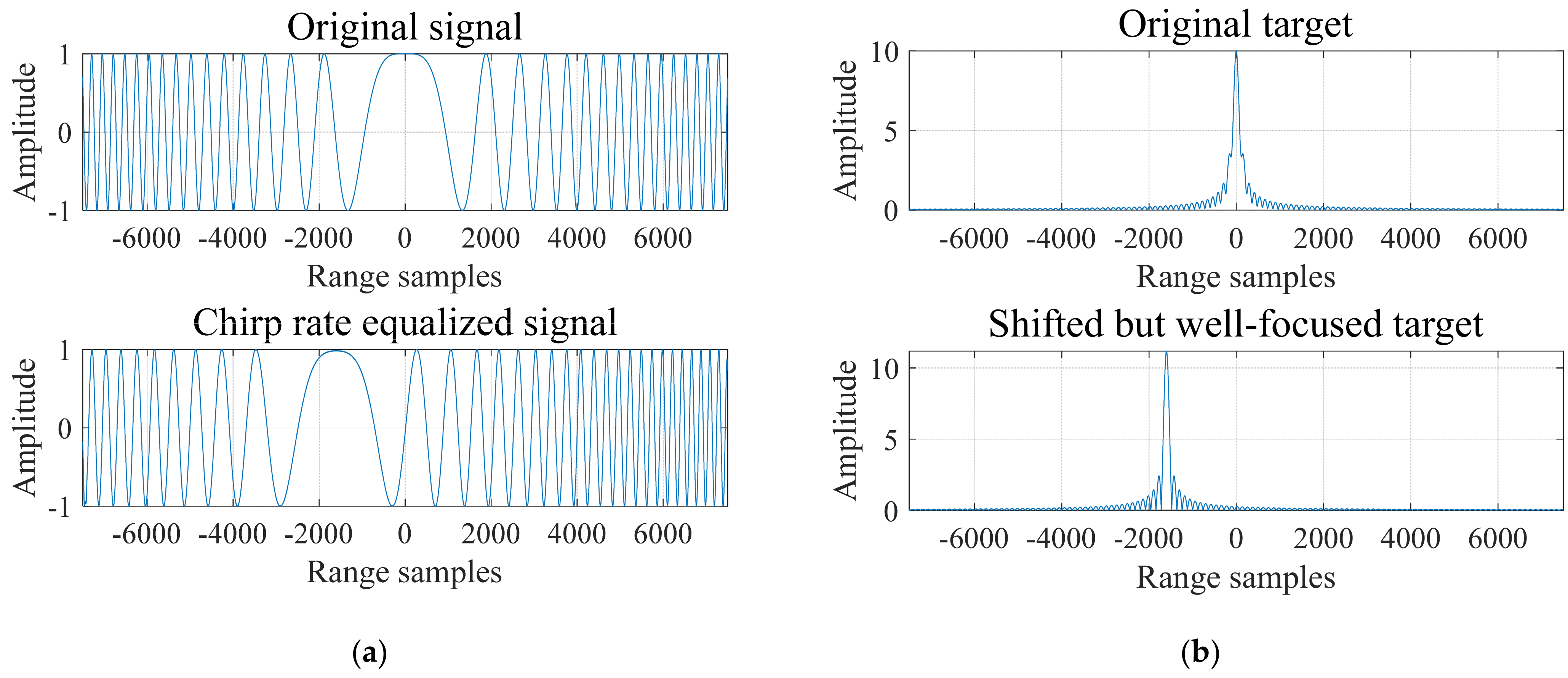
3.4. Chirp Rate Equalization and Quadratic RCMC
3.5. Azimuth Compression and Resampling
4. Discussion and Simulation Results
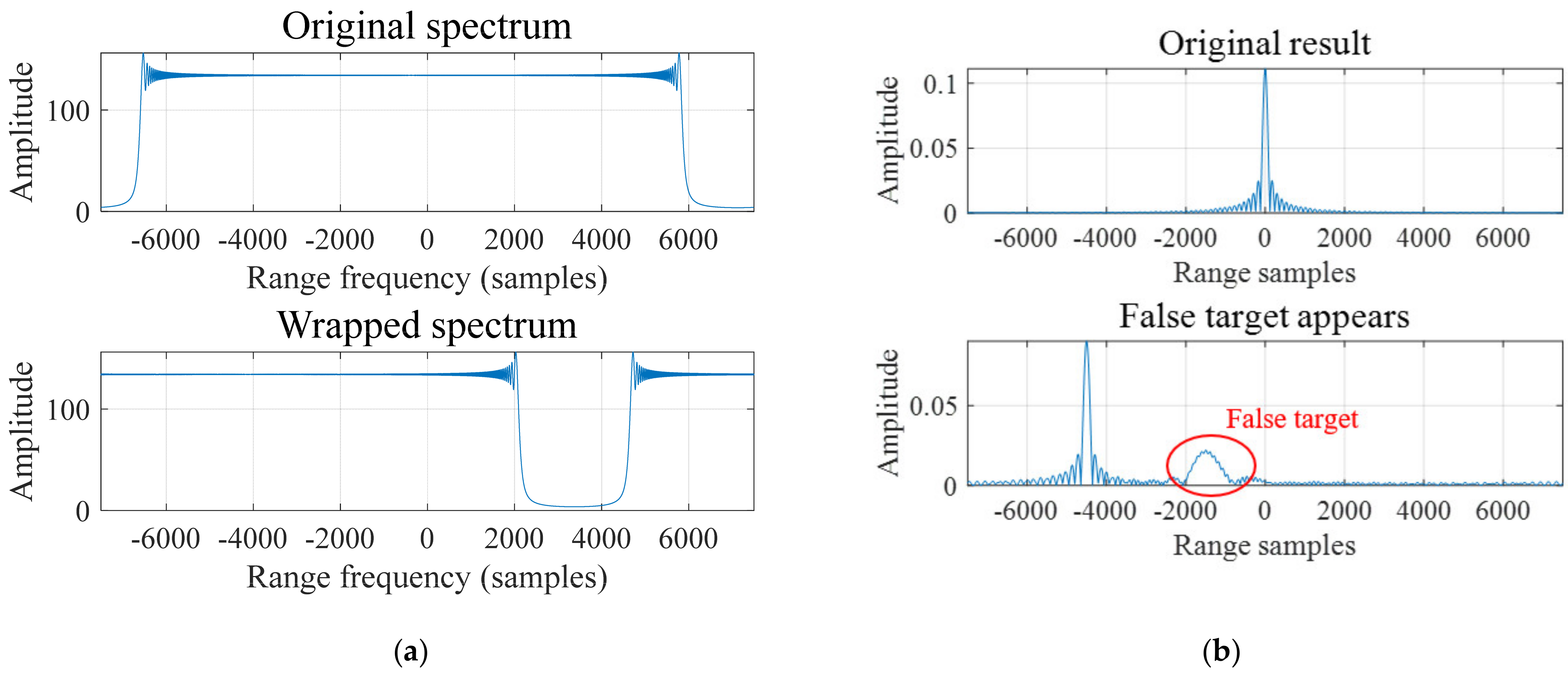
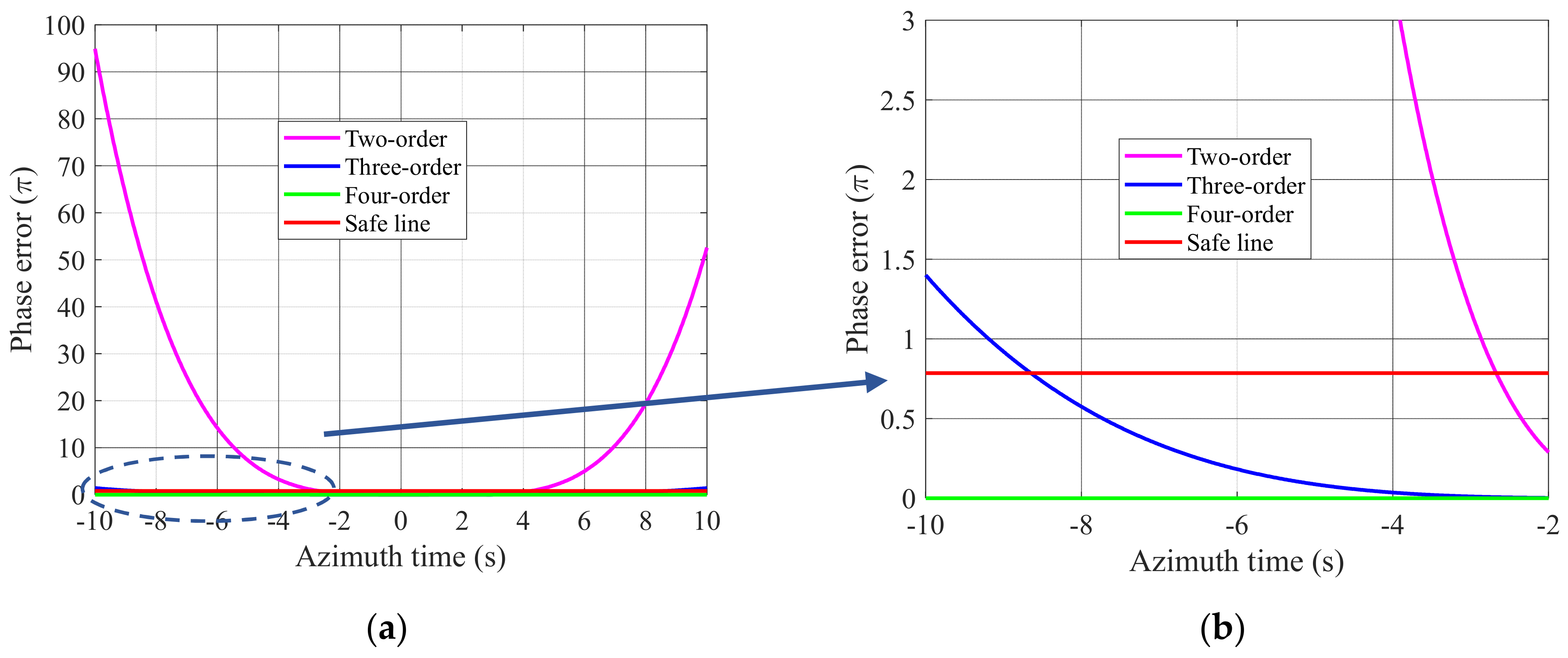
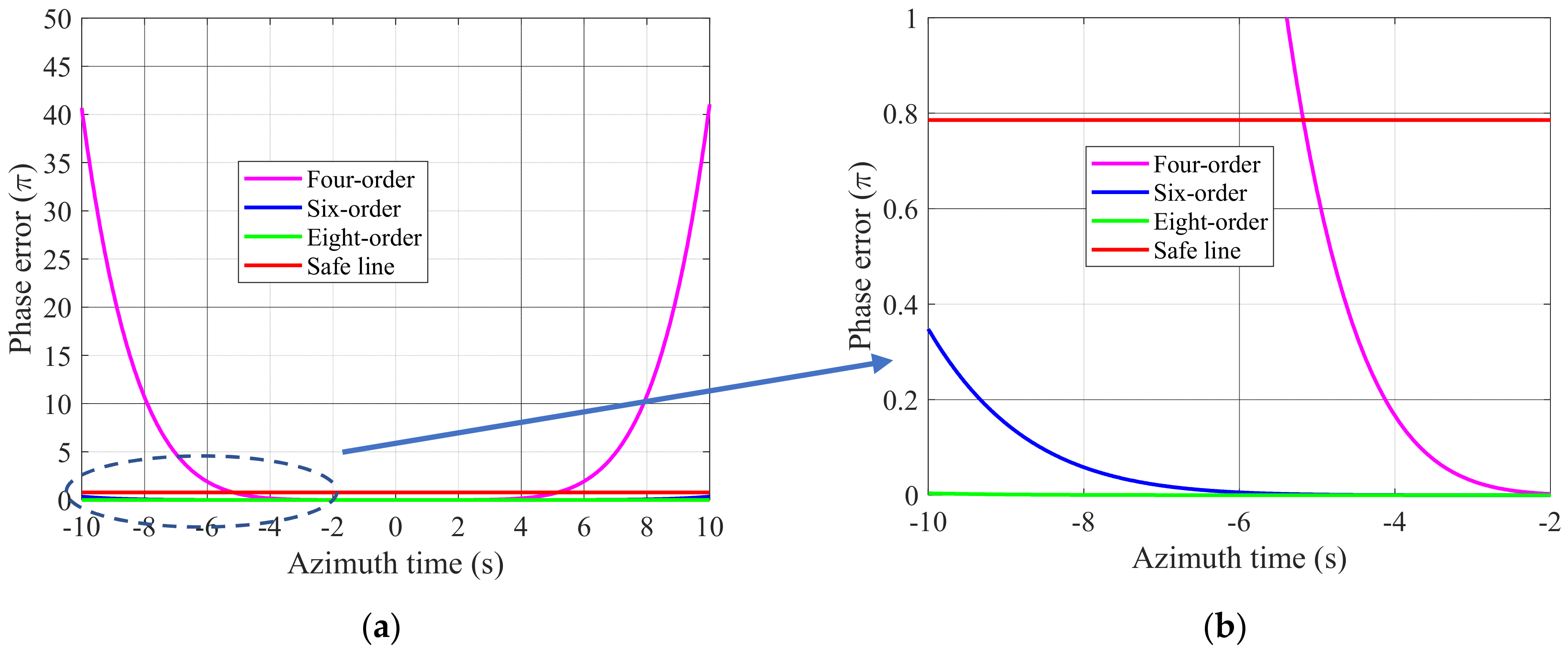
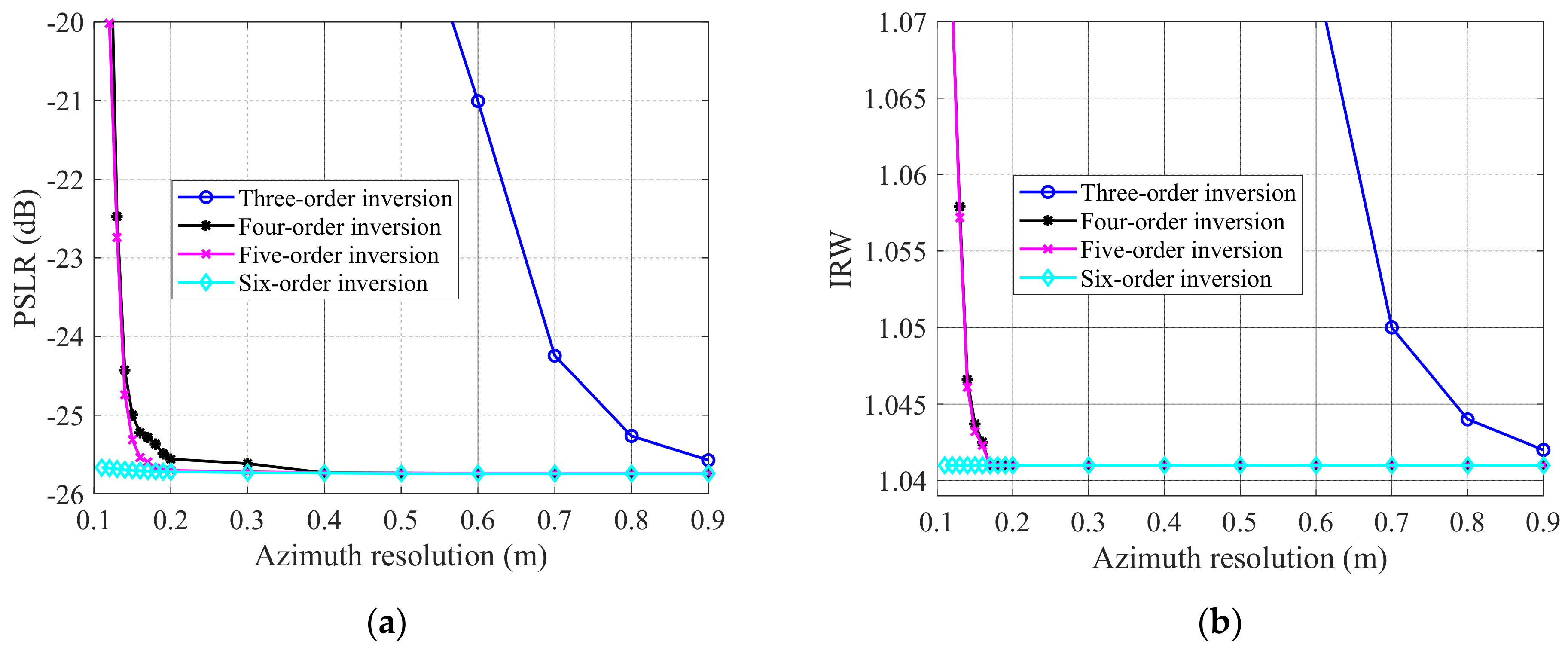
4.1. The Discussion of The Polynomial Range Model and High−Order 2−D Spectrum Analyses
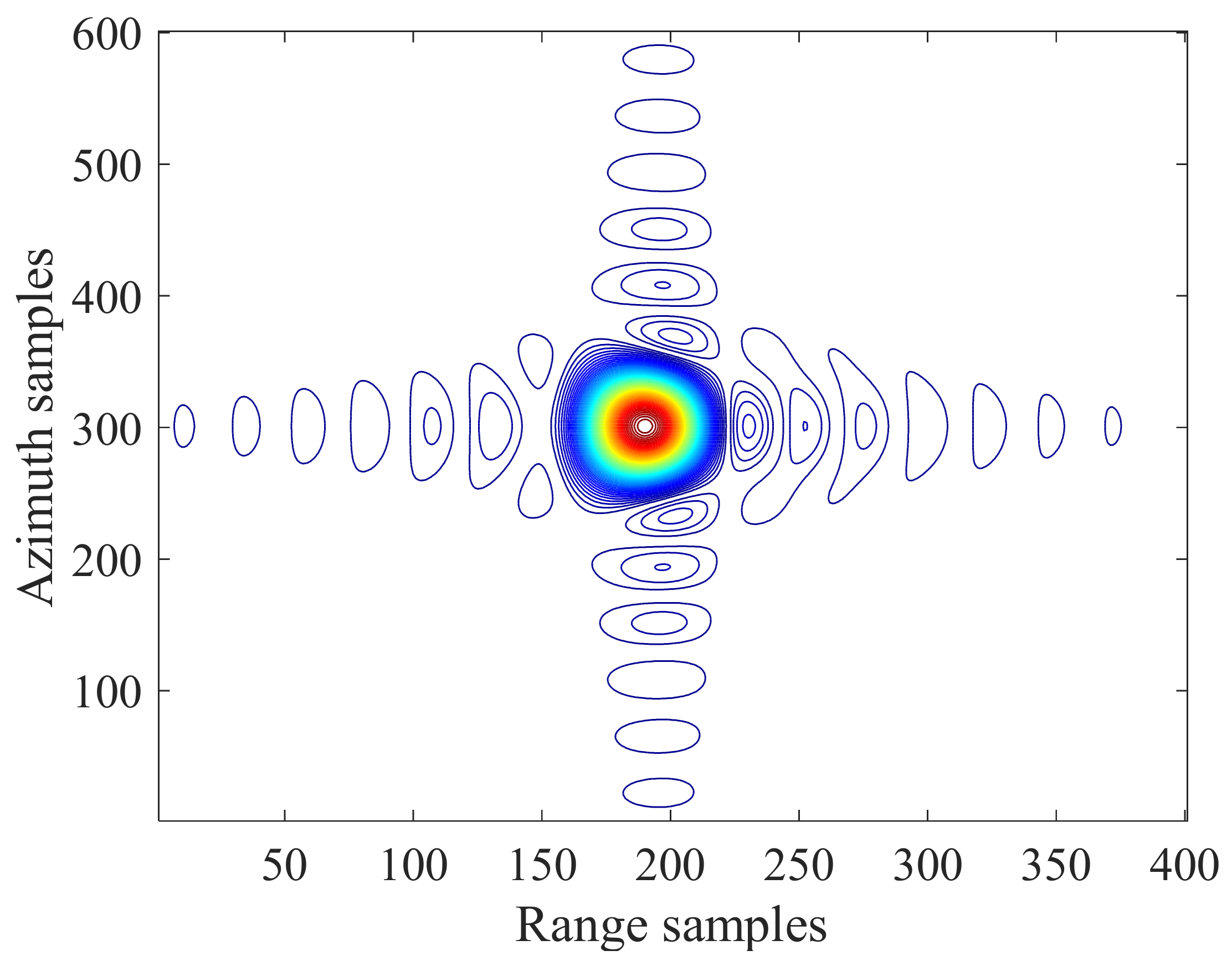
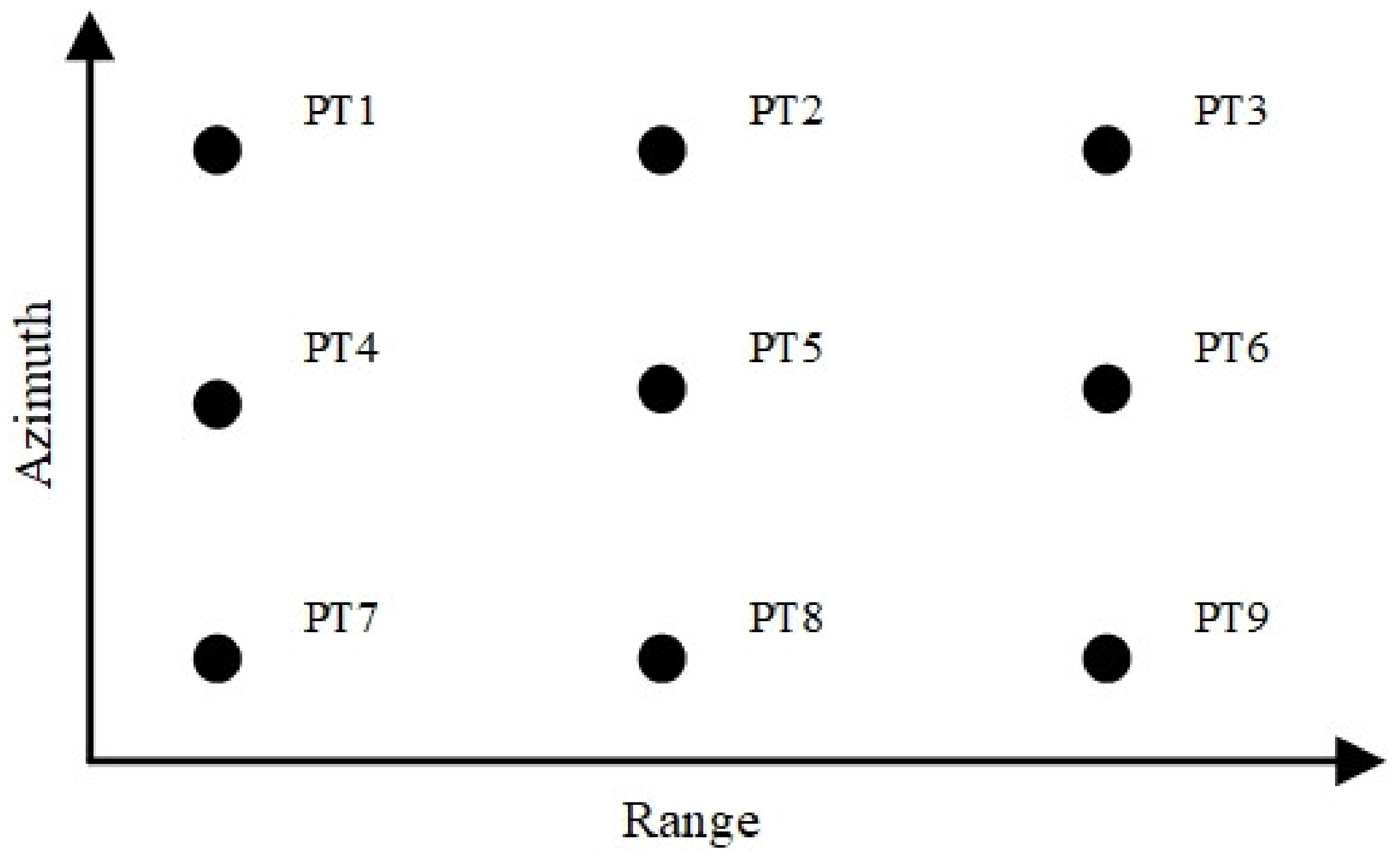
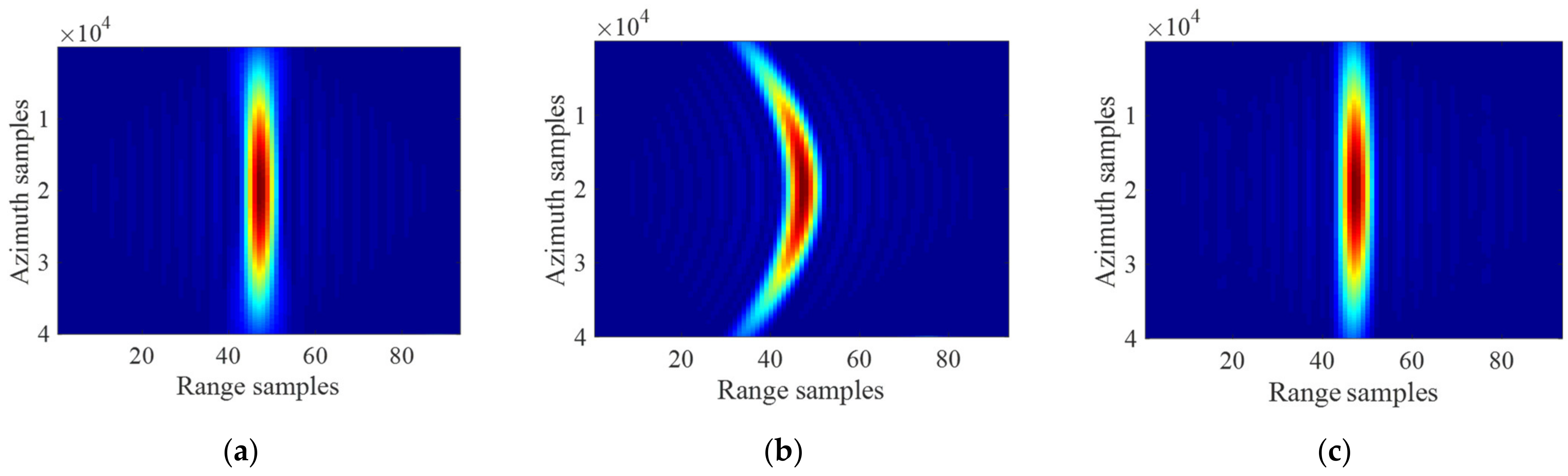
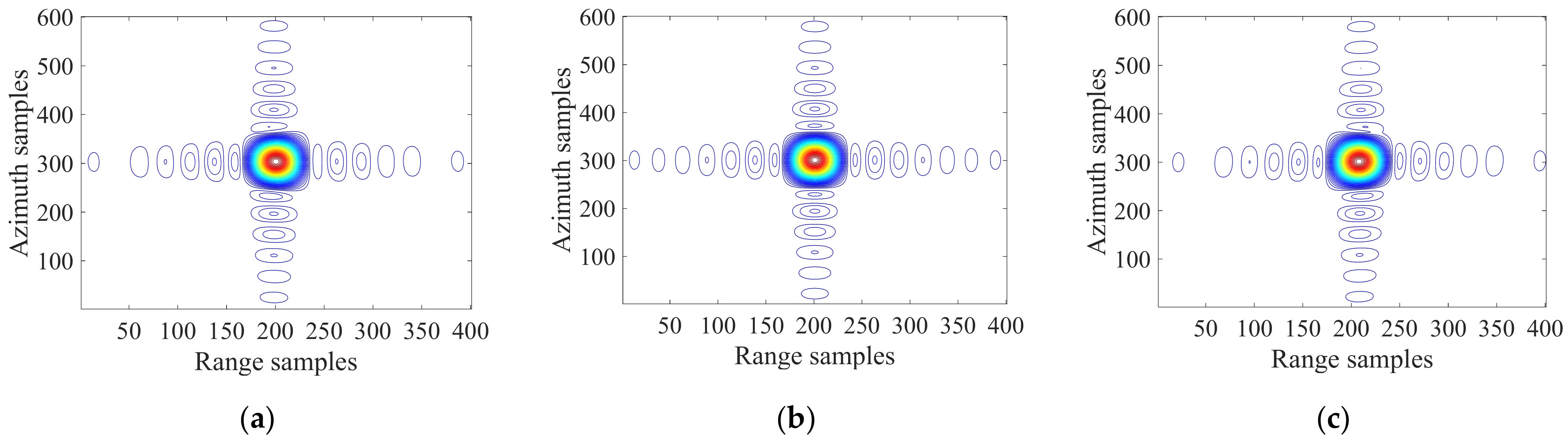
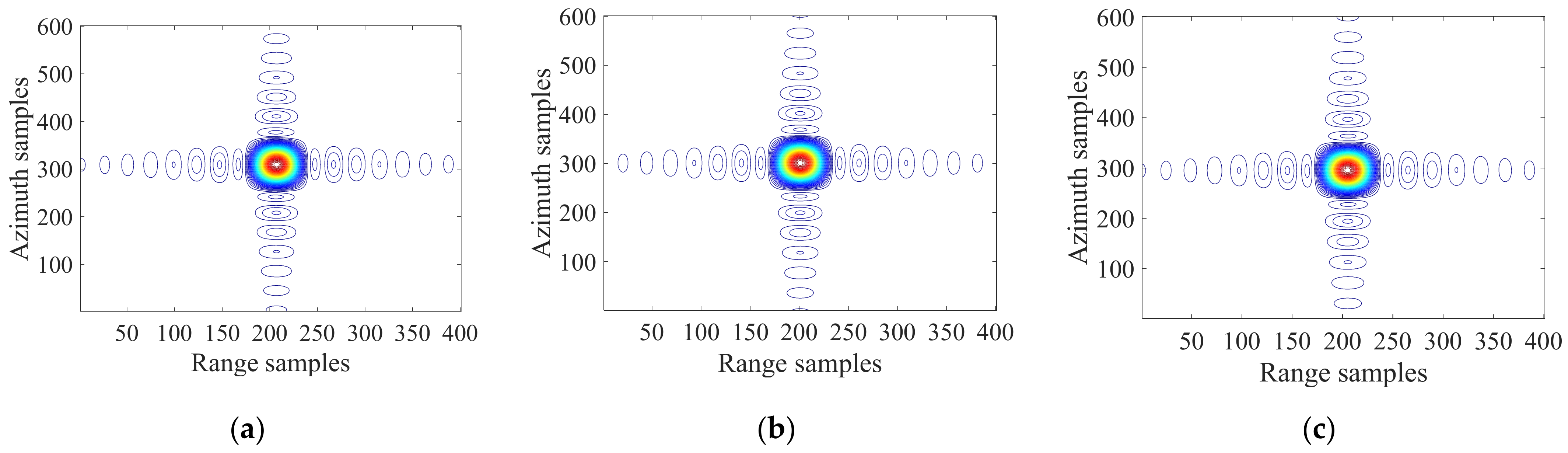
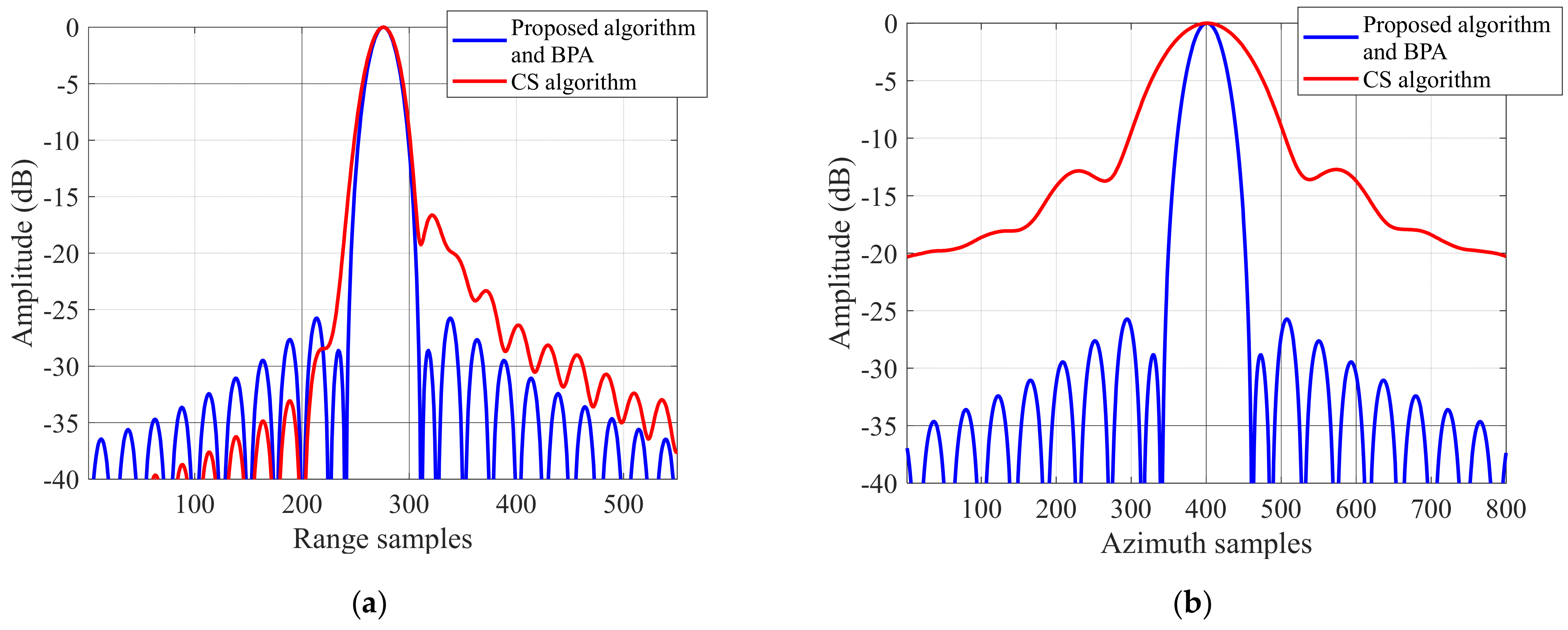
4.2. Image Quality Evaluation and Analysis
4.3. Geolocation Analysis
4.4. The Discussion of the LEO SAR Motion Error and Autofocus Algorithms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Werninghaus, R.; Buckreuss, S. The TerraSAR−X Mission and System Design. IEEE Trans. Geosci. Remote Sens. 2010, 48, 606–614. [Google Scholar] [CrossRef] [Green Version]
- Breit, H.; Fritz, T.; Balss, U.; Lachaise, M.; Niedermeier, A.; Vonavka, M. TerraSAR−X SAR Processing and Products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 727–740. [Google Scholar] [CrossRef]
- Pitz, W.; Miller, D. The TerraSAR−X Satellite. IEEE Trans. Geosci. Remote Sens. 2010, 48, 615–622. [Google Scholar] [CrossRef]
- Covello, F.; Battazza, F.; Coletta, A.; Lopinto, E.; Fiorentino, C.; Pietranera, L.; Valentini, G.; Zoffoli, S. COSMO−SkyMed an existing opportunity for observing the Earth. J. Geodyn. 2010, 49, 171–180. [Google Scholar] [CrossRef] [Green Version]
- Mezzasoma, S.; Gallon, A.; Impagnatiello, F.; Angino, G.; Fagioli, S.; Capuzi, A.; Caltagirone, F.; Leonardi, R.; Ziliotto, U. COSMO−SkyMed system commissioning: End−to−end system performance verification. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Janoth, J.; Gantert, S.; Schrage, T.; Kaptein, A. Terrasar next generation—Mission capabilities. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 2297–2300. [Google Scholar] [CrossRef]
- Smith, A.M. A new approach to range−Doppler SAR processing. Int. J. Remote Sens. 1991, 12, 235–251. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR processing using chirp scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Cafforio, C.; Prati, C.; Rocca, F. SAR data focusing using seismic migration techniques. IEEE Trans. Aerosp. Electron. Syst. 1991, 27, 194–207. [Google Scholar] [CrossRef]
- Sun, X.; Yeo, T.S.; Zhang, C.; Lu, Y.; Kooi, P.S. Time−varying step−transform algorithm for high squint SAR imaging. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2668–2677. [Google Scholar] [CrossRef]
- Bamler, R. A comparison of range−Doppler and wavenumber domain SAR focusing algorithms. IEEE Trans. Geosci. Remote Sens. 1992, 30, 706–713. [Google Scholar] [CrossRef]
- Yegulalp, F.A. Fast backprojection algorithm for synthetic aperture radar. In Proceedings of the 1999 IEEE Radar Conference. Radar into the Next Millennium (Cat. No.99CH36249), Waltham, MA, USA, 22 April 1999; pp. 60–65. [Google Scholar] [CrossRef]
- Ulander, L.M.H.; Hellsten, H.; Stenstrom, G. Synthetic−aperture radar processing using fast factorized back−projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.; Zhou, S.; Yang, L.; Deng, S.; Wang, Y.; Xing, M. Efficient Fast Time−Domain Processing Framework for Airborne Bistatic SAR Continuous Imaging Integrated With Data−Driven Motion Compensation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Xie, H.; Shi, S.; An, D.; Wang, G.; Wang, G.; Xiao, H.; Huang, X.; Zhou, Z.; Xie, C.; Wang, F.; et al. Fast Factorized Backprojection Algorithm for One−Stationary Bistatic Spotlight Circular SAR Image Formation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1494–1510. [Google Scholar] [CrossRef]
- Eldhuset, K. A new fourth−order processing algorithm for spaceborne SAR. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 824–835. [Google Scholar] [CrossRef] [Green Version]
- Eldhuset, K. Spaceborne Bistatic SAR Processing Using the EETF4 Algorithm. IEEE Geosci. Remote Sens. Lett. 2009, 6, 194–198. [Google Scholar] [CrossRef]
- Eldhuset, K. Ultra high resolution spaceborne SAR processing. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 370–378. [Google Scholar] [CrossRef]
- Wang, P.; Han, Y.; Chen, J.; Cui, Z.; Yang, W.; Li, S. A refined chirp scaling algorithm for high−resolution spaceborne SAR based on the fourth−order model. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 2051–2054. [Google Scholar] [CrossRef]
- Luo, Y.; Zhao, B.; Han, X.; Wang, R.; Song, H.; Deng, Y. A Novel High−Order Range Model and Imaging Approach for High−Resolution LEO SAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3473–3485. [Google Scholar] [CrossRef]
- Wang, P.; Liu, W.; Chen, J.; Niu, M.; Yang, W. A High−Order Imaging Algorithm for High−Resolution Spaceborne SAR Based on a Modified Equivalent Squint Range Model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1225–1235. [Google Scholar] [CrossRef] [Green Version]
- Vizitiu, I.; Anton, L.; Popescu, F.; Iubu, G. The synthesis of some NLFM laws using the stationary phase principle. In Proceedings of the 2012 10th International Symposium on Electronics and Telecommunications, Timisoara, Romania, 15–16 November 2012; pp. 377–380. [Google Scholar] [CrossRef]
- Li, C.; Zhang, H.; Deng, Y. Focus Improvement of Airborne High−Squint Bistatic SAR Data Using Modified Azimuth NLCS Algorithm Based on Lagrange Inversion Theorem. Remote Sens. 2021, 13, 1916. [Google Scholar] [CrossRef]
- Chen, X.; Yi, T.; He, F.; He, Z.; Dong, Z. An Improved Generalized Chirp Scaling Algorithm Based on Lagrange Inversion Theorem for High−Resolution Low Frequency Synthetic Aperture Radar Imaging. Remote Sens. 2019, 11, 1874. [Google Scholar] [CrossRef] [Green Version]
- Davidson, G.W.; Cumming, I.G.; Ito, M.R. A chirp scaling approach for processing squint mode SAR data. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 121–133. [Google Scholar] [CrossRef]
- Wong, F.H.; Cumming, I.G.; Neo, Y.L. Focusing Bistatic SAR Data Using the Nonlinear Chirp Scaling Algorithm. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2493–2505. [Google Scholar] [CrossRef] [Green Version]
- Jeffrey, D.J.; Kalugin, G.A.; Murdoch, N. Lagrange Inversion and Lambert W. In Proceedings of the 2015 17th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), Timisoara, Romania, 21–24 September 2015; pp. 42–46. [Google Scholar] [CrossRef]
- An, D.; Huang, X.; Jin, T.; Zhou, Z. Extended Two−Step Focusing Approach for Squinted Spotlight SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2889–2900. [Google Scholar] [CrossRef]
- Lanari, R.; Tesauro, M.; Sansosti, E.; Fornaro, G. Spotlight SAR data focusing based on a two−step processing approach. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1993–2004. [Google Scholar] [CrossRef]
- Pengbo, W.; Zhou, Y.; Chen, J.; Li, C.; Yu, Z.; Min, H. A Deramp Frequency Scaling Algorithm for Processing Space−Borne Spotlight SAR Data. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 3148–3151. [Google Scholar] [CrossRef]
- Deng, R.; Tian, X.; Kang, Z.−M.; Hong, B.; Wang, W.−Q. Linear Programming Based Sidelobe Suppression for SAR Image Optimization. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 3157–3160. [Google Scholar] [CrossRef]
- Li, J.; Wu, R.; Chen, V.C. Robust autofocus algorithm for ISAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1056–1069. [Google Scholar] [CrossRef]
- Pu, W. SAE−Net: A Deep Neural Network for SAR Autofocus. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5220714. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, S.; Feng, Z.; Gao, Q.; Wang, M. Fast SAR Autofocus Based on Ensemble Convolutional Extreme Learning Machine. Remote Sens. 2021, 13, 2683. [Google Scholar] [CrossRef]



| Description | Value | Units |
|---|---|---|
| Orbit Parameters | ||
| Semi−major | 514 | km |
| Eccentricity | 0.0011 | − |
| Inclination | 98 | deg |
| Longitude of ascend note | 0 | deg |
| Argument of perigee | 90 | deg |
| Radar Parameters | ||
| Carrier frequency | 9.6 | GHz |
| Bandwidth | 1.25 | GHz |
| Sampling frequency | 1.5 | GHz |
| Look angle | 30 | deg |
| Antenna width | 0.7 | m |
| Antenna Length | 6 | m |
| Target Parameters of Scene Center | ||
| Azimuth resolution | 0.25 | m |
| Hybrid factor | 0.075 | − |
| of scene center | 593.42 | km |
| of scene center | 4.969 | Hz |
| of scene center | 5909.132 | Hz/s |
| of scene center | 0.019894 | Hz/s2 |
| of scene center | 2.765661 | Hz/s3 |
| Target No. | Range | Azimuth | ||||
|---|---|---|---|---|---|---|
| (m) | PSLR(dB) | ISLR(dB) | (m) | PSLR(dB) | ISLR(dB) | |
| 1 | 0.1357 | −25.856 | −20.807 | 0.2433 | −25.901 | −21.327 |
| 2 | 0.1348 | −25.753 | −20.529 | 0.2427 | −25.729 | −21.123 |
| 3 | 0.1357 | −25.968 | −20.845 | 0.2437 | −25.789 | −21.035 |
| 4 | 0.1352 | −25.725 | −20.655 | 0.2428 | −25.721 | −21.225 |
| 5 | 0.1349 | −25.755 | −20.571 | 0.2427 | −25.737 | −21.195 |
| 6 | 0.1352 | −25.793 | −20.595 | 0.2428 | −25.725 | −21.228 |
| 7 | 0.1356 | −25.894 | −20.736 | 0.2435 | −25.897 | −21.050 |
| 8 | 0.1348 | −25.764 | −20.518 | 0.2427 | −25.729 | −21.138 |
| 9 | 0.1356 | −25.930 | −20.815 | 0.3435 | −25.794 | −21.322 |
| Target No. | X (m) | Y(m) | Z(m) |
|---|---|---|---|
| 1 | 0.000013 | −0.000237 | 0.000134 |
| 2 | 0.000013 | 0.000300 | −0.001480 |
| 3 | −0.000013 | 0.000232 | −0.000029 |
| 4 | 0.000013 | −0.000248 | −0.000050 |
| 5 | 0.000000 | 0.000000 | 0.000000 |
| 6 | −0.000013 | 0.000211 | 0.000043 |
| 7 | 0.000013 | −0.000249 | 0.000029 |
| 8 | 0.000013 | −0.000456 | 0.002241 |
| 9 | −0.000013 | 0.000244 | 0.000139 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, T.; Cui, L.; Wang, P.; Guo, Y.; Zhuang, L. A Novel Ultra−High Resolution Imaging Algorithm Based on the Accurate High−Order 2−D Spectrum for Space−Borne SAR. Remote Sens. 2022, 14, 2284. https://doi.org/10.3390/rs14092284
He T, Cui L, Wang P, Guo Y, Zhuang L. A Novel Ultra−High Resolution Imaging Algorithm Based on the Accurate High−Order 2−D Spectrum for Space−Borne SAR. Remote Sensing. 2022; 14(9):2284. https://doi.org/10.3390/rs14092284
Chicago/Turabian StyleHe, Tao, Lei Cui, Pengbo Wang, Yanan Guo, and Lei Zhuang. 2022. "A Novel Ultra−High Resolution Imaging Algorithm Based on the Accurate High−Order 2−D Spectrum for Space−Borne SAR" Remote Sensing 14, no. 9: 2284. https://doi.org/10.3390/rs14092284
APA StyleHe, T., Cui, L., Wang, P., Guo, Y., & Zhuang, L. (2022). A Novel Ultra−High Resolution Imaging Algorithm Based on the Accurate High−Order 2−D Spectrum for Space−Borne SAR. Remote Sensing, 14(9), 2284. https://doi.org/10.3390/rs14092284