Adaptive Subspace Signal Detection in Structured Interference Plus Compound Gaussian Sea Clutter

Abstract

This paper discusses the problem of detecting subspace signals in structured interference plus compound Gaussian sea clutter with persymmetric structure. The sea clutter is represented by a compound Gaussian process wherein the texture obeys the inverse Gaussian distribution. The structured interference lies in a known subspace, which is independent with the target signal subspace. By resorting to the two-step generalized likelihood ratio test, two-step Rao, and two-step Wald design criteria, three adaptive subspace signal detectors are proposed. Moreover, the constant false-alarm rate property of the proposed detectors is proved. The experimental results based on IPIX real sea clutter data and simulated data illustrate that the proposed detectors outperform their counterparts.

1. Introduction

In recent years, adaptive signal detection has received considerable attention in radar, sonar, and communications [1,2]. The most representative adaptive radar target detectors are Kelly’s generalized likelihood ratio test [3] (GLRT) and Robey’s two-step GLRT, which is also called the adaptive matched filter [4]. In the classical detectors, the signal is assumed as the product of the unknown amplitude and the completely known steering vector. However, the signal signature is always uncertain due to the beampointing error, uncalibrated arrays, sidelobe targets, etc. Subspace model is an effective way to deal with the steering vector uncertain [5]. In some other applications such as polarimetric detection [6], the signal can also be formulated by a subspace model.

To detect subspace signals, Kraut [7] derived the adaptive subspace detector in the partially homogeneous noise wherein the training data can accurately represent the noise structure but not the noise level. In [8], a new modified Rao test is proposed by introducing a tunable parameter, and the analytical expressions for the false-alarm and detection probabilities of the modified Rao test are also given. Kelly’s GLRT and the traditional Rao test are two special cases of the modified Rao test. Detection of subspace signals in the presence of the signal-dependent interference wherein the clutter depends on the transmit signal is considered in [9]. The problem of detecting subspace random signals in the compound Gaussian clutter is discussed in [10], and the optimum Neyman–Pearson detector, GLRT-based detector, and constant false-alarm rate (CFAR) detector have been proposed.

In practical radar target detection scenarios, besides clutter, radar echoes are often contaminated by unintentional or intentional interference released by civil broadcasting and electronic countermeasure systems [11,12,13,14]. Among them, coherent interference can deceive the radar by generating false targets and seriously degrade radar performance [15,16]. When prior information of coherent interference can be obtained by electronic support measures, etc.; it is also called subspace interference or structured interference. The point-like signals detection problem in Gaussian clutter and subspace interference was discussed in [17]. Two Wald-based detectors are designed in homogeneous and partially homogeneous environment under the condition that the interference belongs to a subspace with unknown coordinates. For the detection of distributed targets, one-step and two-step GLRT decision rules [18] were utilized to design detectors in subspace interference plus homogeneous and partially homogeneous clutter. In [19], persymmetric property was exploited to improve detection performance for multi-rank subspace signals detection in partially homogeneous clutter and structured interference. By modeling the texture as a random variable, Gao [20] et al. considered distributed targets detection problem in structured interference and pareto-distributed clutter.

Most of the above works assume that the clutter is Gaussian. The assumption is invalid for sea clutter especially when grazing angles are low, or high-resolution radars are used. The compound Gaussian clutter model is a popular model to describe sea clutter and has been demonstrated by experimental data and theoretical arguments. In [21], the authors discussed detection problem of radar targets in compound Gaussian with inverse Gaussian texture (CG-IG) clutter and showed that CG-IG can fit sea clutter better in some cases than pareto-distribution and K-distribution clutter. However, detectors in [21] were designed without taking into account the interference. Since there is no uniformly most powerful invariant test for the detection problem at hand, the GLRT may not be the best decision rule. In addition to GLRT, Rao and Wald tests only need to estimate unknown parameters under hypothesis $H_0$ or $H_1$, which usually has a smaller computational cost.

Thus, in this paper, we propose three adaptive subspace detectors for radar target detection by resorting to the two-step Rao test, two-step Wald test, and two-step GLRT decision rules in structured interference plus CG-IG clutter. In nonhomogeneous scenarios, sufficient training data that are independent and identically distributed with the primary data are difficult to obtain [22,23,24,25]. To reduce the requirement of training data, the persymmetric structure of the clutter covariance matrix (CM) is exploited in this paper. The persymmetric property holds if the radar array is symmetrically distributed about the phase center, or equally spaced pulse trains are utilized [26,27]. We also analyze the CFAR property of the proposed detectors. Experimental results illustrate that the proposed detectors can effectively suppress interference and exhibit good detection performance in the training-limited cases.

We organize the reminder of the paper as follows: In Section 2, we give the formula of the considered detection problem. We design three new subspace signal detectors in Section 3. In Section 4, we carry out experiments based on real data and simulated data to test the detection performance of the new detectors. We draw some conclusions in Section 5.

Notations: Matrices (vectors) are denoted by uppercase (lowercase) bold letters. $C^{A\times B}$ denotes the $A\times B$ dimensional complex matrix. Superscripts ${(\cdot )}^H$, ${(\cdot )}^T$, ${(\cdot )}^{\ast }$, and ${(\cdot )}^{-1}$ denote conjugate transpose, transpose, conjugate, and inverse. $\mathrm{real}(\cdot )$ is the real part of a complex matrix. $CN\left(\mathit{m},\mathit{R}\right)$ denotes the circularly symmetric complex normal distribution with mean $\mathit{m}$ and covariance matrix $\mathit{R}$.

Table 1 gives a list of acronyms used throughout the paper.

Table 1. Acronyms of the paper.

Acronym	Definition
CFAR	Constant false-alarm rate
CG-IG	Compound Gaussian with inverse Gaussian texture
CM	Covariance matrix
GLRT	Generalized likelihood ratio test
ICR	Interference to clutter ratio
MLE	Maximum likelihood estimate
PDF	Probability density function
PFP	Persymmetric fixed point
PMF	Persymmetric matched filter
PS-GLRT-CG-I	Persymmetric GLRT in the compound Gaussian clutter plus deterministic interference
PS-Rao-CG-I	Persymmetric Rao test in the compound Gaussian clutter plus deterministic interference
PS-Wald-CG-I	Persymmetric Wald test in the compound Gaussian clutter plus deterministic interference
ROC	Receiver operating characteristic
SCR	Signal to clutter ratio

2. Problem Formula

Assume that radar echoes are acquired from $N$ spatial or/and temporal channels. The primary data are denoted as an $N$-dimensional column vector ${\mathit{z}}_0$. The training data, which contain the disturbance only [16,20], are denoted by ${\mathit{z}}_k\in C^{N\times 1},k=1,\dots ,K$. We want to decide whether the received data contain the target signal or not. We express the detection problem to be solved as the binary hypothesis testing as follows:

$$\{\begin{array}{c}{H}_0:\{\begin{array}{l}{\mathit{z}}_0=\mathit{J}\mathit{\phi }+{\mathit{n}}_0,\hfill \\ \begin{array}{cc}{\mathit{z}}_k={\mathit{n}}_k,\hspace{0.17em}& k=1,\dots ,K\end{array}\hfill \end{array}\\ H_1:\{\begin{array}{c}{\mathit{z}}_0=\mathit{H}\mathit{\varphi }+\mathit{J}\mathit{\phi }+{\mathit{n}}_0,\\ {\mathit{z}}_k={\mathit{n}}_k,k=1,\dots ,K\end{array}\end{array}$$

(1)

where $\mathit{H}\mathit{\varphi }$ and $\mathit{J}\mathit{\phi }$ are the useful target signal and the interference. The interference and target signal belong to two linearly independent subspaces $\mathit{J}\in C^{N\times \mathit{Q}}$ and $\mathit{H}\in C^{N\times p}$, $p+q\le N$. $\mathit{H}$ and $\mathit{J}$ are both known full-column-rank matrices [11,17,18,19,20], $\mathit{\varphi }$ is unknown signal coordinate, and $\mathit{\phi }$ is unknown interference coordinate.

The clutter ${\mathit{n}}_0$ and ${\mathit{n}}_k$ follow the compound Gaussian distribution: ${\mathit{n}}_l=\sqrt{{\mathit{\tau }}_l}{\mathit{g}}^{\prime }$, $l=0,\dots ,K$. The speckle component ${\mathit{g}}^{\prime }$ satisfies: ${\mathit{g}}^{\prime }\sim CN\left(\mathit{0},\mathit{R}\right)$. Since the CG-IG clutter can describe sea clutter well and provide better fit than the K distribution or the pareto distribution for the sea clutter in some situations, we assume that ${\tau }_l$ obeys the inverse Gaussian distribution:

$$f\left({\tau }_l\right)=\sqrt{\frac{v_l}{2\pi }}{\tau }_l^{-3/2}\exp \left[-\frac{v_l{\left({\tau }_l-u_l\right)}^2}{2u_l^2{\tau }_l}\right],l=0,\dots ,K$$

(2)

where $u_l$ and $v_l$ are scale and shape parameters.

According to Proposition 1 in [28], we constructed a unitary matrix $\mathit{T}$ to exploit the persymmetric structure. The unitary matrix $\mathit{T}$ is defined as

$$\mathit{T}=\{\begin{array}{c}\begin{array}{ll}\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{\mathit{I}}_{N/2}& {\mathit{D}}_{N/2}\\ j{\mathit{I}}_{N/2}& -j{\mathit{D}}_{N/2}\end{array}\right)\hfill & for\hspace{0.17em}N\hspace{0.17em}even\hfill \end{array}\\ \begin{array}{ll}\frac{1}{\sqrt{2}}\left(\begin{array}{ccc}{\mathit{I}}_{\left(N-1\right)/2}& 0& {\mathit{D}}_{\left(N-1\right)/2}\\ 0& \sqrt{2}& 0\\ j{\mathit{I}}_{\left(N-1\right)/2}& 0& -j{\mathit{D}}_{\left(N-1\right)/2}\end{array}\right)\hfill & for\hspace{0.17em}N\hspace{0.17em}odd\hfill \end{array}\end{array}$$

where ${\mathit{I}}_N$ is an $N$-dimensional identity matrix; $\mathit{D}$ is a permute matrix whose antidiagonal elements are 1, and the other elements are 0. Multiplying by the unitary matrix $\mathit{T}$, the detection problem (1) can be reformulated as

$$\{\begin{array}{c}{H}_0:\{\begin{array}{l}{\mathit{x}}_0=\mathit{Q}\mathit{\phi }+{\mathit{c}}_0,\hfill \\ {\mathit{x}}_k={\mathit{c}}_k,k=1,\dots ,K\hspace{0.17em}\hfill \end{array}\\ H_1:\{\begin{array}{c}{\mathit{x}}_0=\mathit{S}\mathit{\varphi }+\mathit{Q}\mathit{\phi }+{\mathit{c}}_0,\\ {\mathit{x}}_k={\mathit{c}}_k,k=1,\dots ,K\end{array}\end{array}$$

(3)

where ${\mathit{x}}_0=\mathit{T}{\mathit{z}}_0$, ${\mathit{x}}_k=\mathit{T}{\mathit{z}}_k$, ${\mathit{c}}_0=\mathit{T}{\mathit{n}}_0$, ${\mathit{c}}_k=\mathit{T}{\mathit{n}}_k$, $\mathit{g}=\mathit{T}{\mathit{g}}^{\prime }$, $\mathit{S}=\mathit{T}\mathit{H}$, $\mathit{Q}=\mathit{T}\mathit{J}$, and $\mathit{\Sigma }=\mathit{T}\mathit{R}{\mathit{T}}^H$. From above definitions, the probability density functions (PDFs) of the primary data ${\mathit{x}}_0$ is

$$f\left({\mathit{x}}_0|{\tau }_0,\mathit{\varphi },\mathit{\phi },\mathit{\Sigma },H_{\sigma }\right)=\frac{1}{{\pi }^N{\tau }_0^N\det \left(\mathit{\Sigma }\right)}\exp \left[-\frac{1}{{\tau }_0}{\left({\mathit{x}}_0-\sigma \mathit{S}\mathit{\varphi }-\mathit{Q}\mathit{\phi }\right)}^H{\mathit{\Sigma }}^{-1}\left({\mathit{x}}_0-\sigma \mathit{S}\mathit{\varphi }-\mathit{Q}\mathit{\phi }\right)\right],$$

(4)

where $\sigma =0$ denotes null hypothesis $H_0$, and $\sigma =1$ denotes alternative hypothesis $H_1$.

3. Adaptive Persymmetric Detectors Design

Since it is mathematically intractable to derive one-step detectors in compound Gaussian clutter when the texture is random [29], we resort to the two-step Rao test, two-step Wald test, and two-step GLRT to detect targets.

3.1. Adaptive Two-Step Persymmetric GLRT

The GLRT based on the primary data with known speckle CM $\mathit{\Sigma }$ is

$$\frac{\underset{\mathit{\varphi },\mathit{\phi }}{\max }{\displaystyle \int f\left({\mathit{x}}_0|{\tau }_0,\mathit{\varphi },\mathit{\phi },\mathit{\Sigma },H_1\right)f\left({\tau }_0\right)d{\tau }_0}}{\underset{\mathit{\phi }}{\max }{\displaystyle \int f\left({\mathit{x}}_0|{\tau }_0,\mathit{\phi },\mathit{\Sigma },H_0\right)f\left({\tau }_0\right)d{\tau }_0}}\begin{array}{c}{H}_1\\ >\\ <\\ H_0\end{array}\eta$$

(5)

Plugging (2) and (4) into (5), we have the integration terms in the denominator:

$$\begin{array}{l}{\displaystyle \int f\left({\mathit{x}}_0|{\tau }_0,\mathit{\phi },\mathit{\Sigma },H_0\right)f\left({\tau }_0\right)d{\tau }_0}\\ ={\left(\pi u_0\right)}^{-N-\frac{1}{2}}{\left|\mathit{\Sigma }\right|}^{-1}\exp \left(\frac{v_0}{u_0}\right)\sqrt{2v_0}{\left(1+\frac{2T_0}{v_0}\right)}^{\left(-\frac{N}{2}-\frac{1}{4}\right)}{\left(\frac{1}{2}\right)}^{\left(N+3/2\right)}{\left(\frac{v_0^2+2v_0{T}_0}{u_0^2}\right)}^{\left(\frac{N}{2}+\frac{1}{4}\right)}\\ \times {\displaystyle \int {\left(\frac{v_0{\tau }_0}{2u_0^2}\right)}^{-\left(N+3/2\right)}}\exp \left\{-\frac{v_0{\tau }_0}{2u_0^2}-\left(v_0+2T_0\right)/2{\tau }_0\right\}d\left(\frac{v_0{\tau }_0}{2u_0^2}\right)\\ \propto {\left(1+\frac{2T_0}{v_0}\right)}^{-\frac{N}{2}-\frac{1}{4}}{K}_{N+\frac{1}{2}}\left(\frac{v_0}{u_0}\sqrt{1+2T_0/v_0}\right)\end{array}$$

(6)

where $T_0={\left({\mathit{x}}_0-\mathit{Q}\mathit{\phi }\right)}^H{\mathit{\Sigma }}^{\mathit{-}1}\left({\mathit{x}}_0-\mathit{Q}\mathit{\phi }\right)$, $K_n(\cdot )$ is the modified Bessel function of the second kind with order $n$. We get the integration results under $H_1$ in a similar way:

$${\displaystyle \int f\left({\mathit{x}}_0|{\tau }_0,\mathit{\varphi },\mathit{\phi },\mathit{\Sigma },H_1\right)f\left({\tau }_0\right)d{\tau }_0}\propto {\left(1+\frac{2T_1}{v_0}\right)}^{-\frac{N}{2}-\frac{1}{4}}{K}_{N+\frac{1}{2}}\left(\frac{v_0}{u_0}\sqrt{1+2T_1/v_0}\right)$$

(7)

where $T_1={\left({\mathit{x}}_0-\mathit{W}\mathit{\psi }\right)}^H{\mathit{\Sigma }}^{-1}\left({\mathit{x}}_0-\mathit{W}\mathit{\psi }\right)$, $\mathit{\psi }={\left[{\mathit{\varphi }}^T,{\mathit{\phi }}^T\right]}^T$, and $\mathit{W}=\left[\mathit{S},\mathit{Q}\right]$.

We obtain the maximum likelihood estimates (MLEs) of $\mathit{\phi }$ and $\mathit{\psi }$ by taking the derivative of (6) and (7) with respect to $\mathit{\phi }$ and $\mathit{\psi }$ and setting the results to zero. Let $y_1=\frac{v_0}{u_0}\sqrt{1+2T_1/v_0}$, $y_0=\frac{v_0}{u_0}\sqrt{1+2T_0/v_0}$. According to the property of the modified Bessel function of the second kind [30], we have

$$d_{\mathit{\phi }}{\left(y_0\right)}^{-\left(N+\frac{1}{2}\right)}{K}_{N+\frac{1}{2}}\left(y_0\right)=-{\left(y_0\right)}^{-\left(N+\frac{1}{2}\right)}{K}_{N+\frac{1}{2}+1}\left(y_0\right)d_{\mathit{\phi }}\left(y_0\right)$$

(8)

After some calculation, we can obtain the MLEs of $\mathit{\phi }$ and $\mathit{\psi }$

$$\widehat{\mathit{\phi }}={\left({\mathit{Q}}^H{\mathit{\Sigma }}^{-1}\mathit{Q}\right)}^{-1}{\mathit{Q}}^H{\mathit{\Sigma }}^{-1}{\mathit{x}}_0$$

(9)

$$\widehat{\mathit{\psi }}={\left({\mathit{W}}^H{\mathit{\Sigma }}^{-1}\mathit{W}\right)}^{-1}{\mathit{W}}^H{\mathit{\Sigma }}^{-1}{\mathit{x}}_0$$

(10)

In the compound Gaussian clutter, the estimate of the unknown speckle CM with persymmetric structure is persymmetric fixed point (PFP) CM ${\widehat{\mathit{\Sigma }}}_{\mathrm{PFP}}$. We obtain the fully adaptive persymmetric GLRT in the compound Gaussian clutter plus deterministic interference (PS-GLRT-CG-I) by inserting (6), (7), (9) and (10), and ${\widehat{\mathit{\Sigma }}}_{\mathrm{PFP}}$ into (5):

$${\left(v_0+2{\tilde{T}}_1\right)}^{-\frac{N}{2}-\frac{1}{4}}{K}_{N+\frac{1}{2}}\left(\frac{v_0}{u_0}\sqrt{1+2{\tilde{T}}_1/v_0}\right)/\left[{\left(v_0+2{\tilde{T}}_0\right)}^{-\frac{N}{2}-\frac{1}{4}}{K}_{N+\frac{1}{2}}\left(\frac{v_0}{u_0}\sqrt{1+2{\tilde{T}}_0/v_0}\right)\right]\begin{array}{c}{H}_1\\ >\\ <\\ H_0\end{array}\eta$$

(11)

where ${\tilde{T}}_0={\tilde{\mathit{x}}}_0^H{\mathit{P}}_{\tilde{\mathit{Q}}}^{\perp }{\tilde{\mathit{x}}}_0$, ${\tilde{T}}_1={\tilde{\mathit{x}}}_0^H{\mathit{P}}_{\tilde{\mathit{W}}}^{\perp }{\tilde{\mathit{x}}}_0$, ${\tilde{\mathit{x}}}_0={\widehat{\mathit{\Sigma }}}_{\mathrm{PFP}}^{-\frac{1}{2}}{\mathit{x}}_0$, $\tilde{\mathit{Q}}={\widehat{\mathit{\Sigma }}}_{\mathrm{PFP}}^{-\frac{1}{2}}\mathit{Q}$, ${\mathit{P}}_{\tilde{\mathit{Q}}}^{\perp }=\mathit{I}-\tilde{\mathit{Q}}{\left({\tilde{\mathit{Q}}}^H\tilde{\mathit{Q}}\right)}^{-1}{\tilde{\mathit{Q}}}^H$, $\tilde{\mathit{W}}={\widehat{\mathit{\Sigma }}}_{\mathrm{PFP}}^{-\frac{1}{2}}\mathit{W}$, ${\mathit{P}}_{\tilde{\mathit{W}}}^{\perp }=\mathit{I}-\tilde{\mathit{W}}{\left({\tilde{\mathit{W}}}^H\tilde{\mathit{W}}\right)}^{-1}{\tilde{\mathit{W}}}^H$, ${\widehat{\mathit{\Sigma }}}_{\mathrm{PFP}}=\mathrm{real}\left(\mathit{T}{\widehat{\mathit{\Sigma }}}_{\mathrm{FP}}{\mathit{T}}^H\right)$, ${\widehat{\mathit{\Sigma }}}_{\mathrm{FP}}=\frac{N}{K}{\displaystyle \underset{k=1}{\overset{K}{\Sigma }}\frac{{\mathit{c}}_k{\mathit{c}}_k^H}{{\mathit{c}}_k{\widehat{\mathit{\Sigma }}}_{\mathrm{FP}}^{-1}{\mathit{c}}_k^H}}$, ${\widehat{\mathit{\Sigma }}}_{\mathrm{FP}}\left(0\right)=\frac{N}{K}{\displaystyle \underset{k=1}{\overset{K}{\Sigma }}\frac{{\mathit{c}}_k{\mathit{c}}_k^H}{{\mathit{c}}_k^H{\mathit{c}}_k}}$.

3.2. Adaptive Two-Step Persymmetric Rao Test

Different from [21], we treat the complex-valued variable in the Rao test and Wald test as a single one to avoid the time-consuming problem of dividing it into real and imaginary parts. Since the interference can be nulled more effectively by setting the relative parameter to contain both the signal and interference coordinates [11], we set the relative parameter ${\mathit{\theta }}_r$ in the Rao test and Wald test as ${\mathit{\theta }}_r={\left[{\mathit{\varphi }}^T,{\mathit{\phi }}^T\right]}^T=\mathit{\psi }$.

The Rao test for complex-valued signals based on the primary data with known speckle CM is

$${\frac{\partial \ln f\left({\mathit{x}}_0|\mathit{\theta },\mathit{\Sigma },H_1\right)}{\partial {\mathit{\theta }}_r}|}_{\mathit{\theta }={\widehat{\mathit{\theta }}}_0}^{\mathrm{T}}{\left[{\mathit{J}}^{-1}\left({\widehat{\mathit{\theta }}}_0\right)\right]}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\times {\frac{\partial \ln f\left({\mathit{x}}_0|\mathit{\theta },\mathit{\Sigma },H_1\right)}{\partial {\mathit{\theta }}_r{}^{*}}|}_{\mathit{\theta }={\widehat{\mathit{\theta }}}_0}\begin{array}{c}{H}_1\\ >\\ <\\ H_0\end{array}\epsilon$$

(12)

where ${\mathit{\theta }}_r={\left[{\mathit{\varphi }}^T,{\mathit{\phi }}^T\right]}^T$ is a $\left(p+q\right)$-dimensional vector; ${\mathit{\theta }}_s={\tau }_0$, $\mathit{\theta }={\left[{\mathit{\theta }}_r^T,{\mathit{\theta }}_s^T\right]}^T$ is a $\left(p+q+1\right)$-dimensional vector. ${\widehat{\mathit{\theta }}}_0$ is the MLE of $\mathit{\theta }$ under $H_0$. $\mathit{J}\left(\mathit{\theta }\right)$ is Fisher information matrix, which can be partitioned as four block matrices ${\mathit{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\left(\mathit{\theta }\right)$, ${\mathit{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_s}\left(\mathit{\theta }\right)$, ${\mathit{J}}_{{\mathit{\theta }}_s,{\mathit{\theta }}_r}\left(\mathit{\theta }\right)$, and ${\mathit{J}}_{{\mathit{\theta }}_s,{\mathit{\theta }}_s}\left(\mathit{\theta }\right)$.

After some calculation, we obtain the following results

$$\frac{\partial \ln f\left({\mathit{x}}_0|\mathit{\theta },\mathit{\Sigma },H_1\right)}{\partial {\mathit{\theta }}_r{}^{*}}=\frac{1}{{\tau }_0}{\mathit{W}}^H{\mathit{\Sigma }}^{-1}\left({\mathit{x}}_0-\mathit{W}\mathit{\psi }\right)$$

(13)

$$\frac{\partial \ln f\left({\mathit{x}}_0|\mathit{\theta },\mathit{\Sigma },H_1\right)}{\partial {\mathit{\theta }}_r^T}=\frac{1}{{\tau }_0}{\left({\mathit{x}}_0-\mathit{W}\mathit{\psi }\right)}^H{\mathit{\Sigma }}^{-1}\mathit{W}$$

(14)

$${\mathit{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\left(\mathit{\theta }\right)=\frac{1}{{\tau }_0^2}{\mathit{W}}^H{\mathit{\Sigma }}^{-1}E\left[\left({\mathit{x}}_0-\mathit{W}\mathit{\psi }\right){\left({\mathit{x}}_0-\mathit{W}\mathit{\psi }\right)}^H\right]{\mathit{\Sigma }}^{-1}\mathit{W}=\frac{1}{{\tau }_0}{\mathit{W}}^H{\mathit{\Sigma }}^{-1}\mathit{W}$$

(15)

$${\mathit{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_s}\left(\mathit{\theta }\right)=0_{\left(p+q\right)\times 1}$$

(16)

$${\left\{{\left[{\mathit{J}}^{-1}\left(\mathit{\theta }\right)\right]}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\right\}}^{-1}={\mathit{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\left(\mathit{\theta }\right)-{\mathit{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_s}\left(\mathit{\theta }\right){\mathit{J}}_{{\mathit{\theta }}_s,{\mathit{\theta }}_s}^{-1}\left(\mathit{\theta }\right){\mathit{J}}_{{\mathit{\theta }}_s,{\mathit{\theta }}_r}\left(\mathit{\theta }\right)={\mathit{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\left(\mathit{\theta }\right)={\left[{\tau }_0{\left({\mathit{W}}^H{\mathit{\Sigma }}^{-1}\mathit{W}\right)}^{-1}\right]}^{-1}$$

(17)

The estimates of the unknown parameters are also needed. We obtain the ML estimate of $\mathit{\phi }$ by setting the derivative of (4) with respect to $\mathit{\phi }$ to zero.

$${\widehat{\mathit{\phi }}}_0={\left({\mathit{Q}}^H{\mathit{\Sigma }}^{-1}\mathit{Q}\right)}^{-1}{\mathit{Q}}^H{\mathit{\Sigma }}^{-1}{\mathit{x}}_0$$

(18)

Since the equation ${\mathit{\varphi }}_0=0_{p\times 1}$ holds under $H_0$, the ML estimate of ${\mathit{\theta }}_r$ is ${\widehat{\mathit{\theta }}}_{r,0}={\left[0^T,{\widehat{\mathit{\phi }}}_0^T\right]}^T$.

In the second step, we estimate the texture and speckle CM. The MAP estimate of the texture is

$${\widehat{\tau }}_0=\underset{{\tau }_0}{\arg \max }f\left({\mathit{x}}_0|{\tau }_0,{\widehat{\mathit{\phi }}}_0,\mathit{\Sigma },H_0\right)f\left({\tau }_0\right)=\frac{u_0^2}{v_0}\left[\sqrt{{\left(N+\frac{3}{2}\right)}^2+\frac{2v_0}{u_0^2}\left({\overline{\mathit{x}}}_0^H{\mathit{P}}_{\overline{\mathit{Q}}}^{\perp }{\overline{\mathit{x}}}_0+\frac{v_0}{2}\right)}-\left(N+\frac{3}{2}\right)\right]$$

(19)

where ${\overline{\mathit{x}}}_0={\mathit{\Sigma }}^{-\frac{1}{2}}{\mathit{x}}_0$, $\overline{\mathit{Q}}={\mathit{\Sigma }}^{-\frac{1}{2}}\mathit{Q}$, ${\mathit{P}}_{\overline{\mathit{Q}}}^{\perp }=\mathit{I}-\overline{\mathit{Q}}{\left({\overline{\mathit{Q}}}^H\overline{\mathit{Q}}\right)}^{-1}{\overline{\mathit{Q}}}^H$. By substituting (13)–(19) and PFP CM into (12) and ignoring the constants, the two-step persymmetric Rao test in compound Gaussian clutter plus deterministic interference (PS-Rao-CG-I) is

$$v_0{\tilde{\mathit{x}}}_0^H{\mathit{P}}_{\tilde{\mathit{Q}}}^{\perp }{\mathit{P}}_{\tilde{\mathit{W}}}{\mathit{P}}_{\tilde{\mathit{Q}}}^{\perp }{\tilde{\mathit{x}}}_0/\left\{u_0^2\left[\sqrt{{\left(N+\frac{3}{2}\right)}^2+2v_0\left({\tilde{\mathit{x}}}_0^H{\mathit{P}}_{\tilde{\mathit{Q}}}^{\perp }{\tilde{\mathit{x}}}_0+\frac{v_0}{2}\right)/u_0^2}-\left(N+\frac{3}{2}\right)\right]\right\}\begin{array}{c}{H}_1\\ >\\ <\\ H_0\end{array}\epsilon$$

(20)

where ${\mathit{P}}_{\tilde{\mathit{W}}}=\tilde{\mathit{W}}{\left({\tilde{\mathit{W}}}^H\tilde{\mathit{W}}\right)}^{-1}{\tilde{\mathit{W}}}^H$.

3.3. Adaptive Two-Step Persymmetric Wald Test

In this part, two-step design procedure is utilized to derive the Wald test. We first derive the Wald test with known $\mathit{\theta }$, $\mathit{\Sigma }$ and then replace them with their estimates. The Wald test for complex-valued signals is

$$\left({\widehat{\mathit{\theta }}}_{r,1}^H-{\mathit{\theta }}_{r,0}^H\right){\left({\left[{\mathit{J}}^{-1}\left({\widehat{\mathit{\theta }}}_1\right)\right]}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\right)}^{-1}\left({\widehat{\mathit{\theta }}}_{r,1}-{\mathit{\theta }}_{r,0}\right)\begin{array}{c}{H}_1\\ >\\ <\\ H_0\end{array}\zeta$$

(21)

where ${\mathit{\theta }}_{r,0}^H$ is the true value of ${\mathit{\theta }}_r$ under $H_0$, ${\widehat{\mathit{\theta }}}_{r,1}^H$ denotes the MLE of ${\mathit{\theta }}_r$ under $H_1$, and ${\widehat{\mathit{\theta }}}_1$ denotes the MLE of $\mathit{\theta }$ under $H_1$.

Substituting (17) into (21), we obtain the Wald test with known $\mathit{\theta }$, $\mathit{\Sigma }$:

$$\frac{1}{{\tau }_0}\left[{\mathit{\varphi }}^H,0^H\right]{\mathit{W}}^H{\mathit{\Sigma }}^{-1}\mathit{W}\left[\begin{array}{c}\begin{array}{l}\mathit{\varphi }\\ \end{array}\\ 0\end{array}\right]\begin{array}{c}{H}_1\\ >\\ <\\ H_0\end{array}\zeta$$

(22)

In the second step, we estimate $\mathit{\theta }$, $\mathit{\Sigma }$ under $H_1$. We take the derivative of (4) with respect to $\mathit{\psi }$ and set the result to zero to obtain the MLE of $\mathit{\psi }$ under $H_1$.

$${\widehat{\mathit{\psi }}}_1={\left[{\widehat{\mathit{\varphi }}}_1^T,{\widehat{\mathit{\phi }}}_1^T\right]}^T={\left({\mathit{W}}^H{\mathit{\Sigma }}^{-1}\mathit{W}\right)}^{-1}{\mathit{W}}^H{\mathit{\Sigma }}^{-1}{\mathit{x}}_0$$

(23)

We substitute $\mathit{W}=\left[\mathit{S},\mathit{Q}\right]$ to (23) and obtain the MLE of $\mathit{\varphi }$ under $H_1$ according to the partitioned matrix inversion lemma [31]

$${\widehat{\mathit{\varphi }}}_1={\left({\overline{\mathit{S}}}^H{\mathit{P}}_{\overline{\mathit{Q}}}^{\perp }\overline{\mathit{S}}\right)}^{-1}{\overline{\mathit{S}}}^H{\mathit{P}}_{\overline{\mathit{Q}}}^{\perp }{\overline{\mathit{x}}}_0$$

(24)

where $\overline{\mathit{S}}={\mathit{\Sigma }}^{-\frac{1}{2}}\mathit{S}$. The MAP estimate of $\tau$ under $H_1$ can be calculated as

$${\widehat{\tau }}_0=\underset{{\tau }_0}{\arg \max }f\left({\mathit{x}}_0|{\tau }_0,{\widehat{\mathit{\psi }}}_1,\mathit{\Sigma },H_1\right)f\left({\tau }_0\right)=\frac{u_0^2}{v_0}\left[\sqrt{{\left(N+\frac{3}{2}\right)}^2+\frac{2v_0}{u_0^2}\left({\overline{\mathit{x}}}_0^H{\mathit{P}}_{\overline{\mathit{W}}}^{\perp }{\overline{\mathit{x}}}_0+\frac{v_0}{2}\right)}-\left(N+\frac{3}{2}\right)\right]$$

(25)

where $\overline{\mathit{W}}={\mathit{\Sigma }}^{-\frac{1}{2}}\mathit{W}$, ${\mathit{P}}_{\overline{\mathit{W}}}^{\perp }=I-\overline{\mathit{W}}{\left({\overline{\mathit{W}}}^H\overline{\mathit{W}}\right)}^{-1}{\overline{\mathit{W}}}^H$.

Plugging (23)–(25) and the PFP CM ${\widehat{\mathit{\Sigma }}}_{\mathrm{PFP}}$ into (22), we obtain the adaptive two-step persymmetric Wald test in compound Gaussian clutter plus deterministic interference (PS-Wald-CG-I):

$$v_0{\tilde{\mathit{x}}}_0^H{\mathit{P}}_{\tilde{\mathit{S}}|\tilde{\mathit{Q}}}^H{\mathit{P}}_{\tilde{\mathit{S}}|\tilde{\mathit{Q}}}{\tilde{\mathit{x}}}_0/\left\{u_0^2\left[\sqrt{{\left(N+\frac{3}{2}\right)}^2+2v_0\left({\tilde{\mathit{x}}}_0^H{\mathit{P}}_{\tilde{\mathit{W}}}^{\perp }{\tilde{\mathit{x}}}_0+\frac{v_0}{2}\right)/u_0^2}-\left(N+\frac{3}{2}\right)\right]\right\}\begin{array}{c}{H}_1\\ >\\ <\\ H_0\end{array}\zeta$$

(26)

where $\tilde{\mathit{S}}={\widehat{\mathit{\Sigma }}}_{\mathrm{PFP}}^{-\frac{1}{2}}\mathit{S}$, ${\mathit{P}}_{\tilde{\mathit{W}}}^{\perp }=\mathit{I}-{\mathit{P}}_{\tilde{\mathit{W}}}$, ${\mathit{P}}_{\tilde{\mathit{S}}|\tilde{\mathit{Q}}}=\tilde{\mathit{S}}{\left({\tilde{\mathit{S}}}^H{\mathit{P}}_{\tilde{\mathit{Q}}}^{\perp }\tilde{\mathit{S}}\right)}^{-1}{\tilde{\mathit{S}}}^H{\mathit{P}}_{\tilde{\mathit{Q}}}^{\perp }$, ${\mathit{P}}_{\tilde{\mathit{Q}}|\tilde{\mathit{S}}}=\tilde{\mathit{Q}}{\left({\tilde{\mathit{Q}}}^H{\mathit{P}}_{\tilde{\mathit{S}}}^{\perp }\tilde{\mathit{Q}}\right)}^{-1}{\tilde{\mathit{Q}}}^H{\mathit{P}}_{\tilde{\mathit{S}}}^{\perp }$.

All the three proposed detectors have been proven to have the CFAR property. We give the detailed proof in the Appendix A.

4. Performance Assessment

The detection performance of the proposed detectors is assessed by utilizing Monte Carlo simulations in this section. We resort to $100/P_{fa}$ independent trials to compute the thresholds and detection probabilities. The $\left(i,j\right)$ element of speckle CM $\mathit{R}$ is $\mathit{R}\left(i,j\right)={\rho }^{\left|i-j\right|},\hspace{0.17em}\rho =0.9$. Unless otherwise specified, we set $\mathit{H}=\left[\mathit{h}\left(f_1\right),\dots ,\mathit{h}\left(f_p\right)\right]$, $\mathit{h}\left(f_s\right)={\left[1,{\mathrm{e}}^{-j2\pi f_s},\dots ,{\mathrm{e}}^{-j2\pi f_s\left(N-1\right)}\right]}^T$, $\mathit{J}=\left[\mathit{j}\left(f_1\right),\dots ,\mathit{j}\left(f_q\right)\right]$, $\mathit{j}\left(f_m\right)={\left[1,{\mathrm{e}}^{-\mathit{J}2\pi f_m},\dots ,{\mathrm{e}}^{-\mathit{J}2\pi f_m\left(N-1\right)}\right]}^T$, $f_s=0.2s$, $s=1,\dots ,p$, $m=1,\dots ,q$, and $f_m=-0.2+0.01m$. Other parameters of the simulated data are shown in Table 2. The interference to clutter ratio (ICR) and signal to clutter ratio (SCR) are defined as $\mathrm{ICR}=\mathrm{trace}\left({\mathit{\phi }}^H{\mathit{J}}^H\mathit{J}\mathit{\phi }\right)/Nu$ and $\mathrm{SCR}=\mathrm{trace}\left({\mathit{\varphi }}^H{H}^{H}H\mathit{\varphi }\right)/Nu$.

Table 2. Parameters of the simulated data.

Parameters	Values
Shape parameter	0.5
Scale parameter	1
False-alarm probability	10−3
$N$	8
$p$	1
$q$	3

4.1. Simulated Data Results

Figure 1 shows false-alarm probabilities of the proposed persymmetric detectors (PS-Rao-CG-I, PS-Wald-CG-I, and PS-GLRT-CG-I) versus correlation coefficients when $K=2N$. The detection threshold is obtained by setting $\rho =0.4$. The figure shows that probabilities of false alarm remain almost the same under different correlation coefficients. Thus, both theoretical analysis and simulation results verify that the PS-Rao-CG-I, PS-Wald-CG-I, and PS-GLRT-CG-I are CFAR detectors.

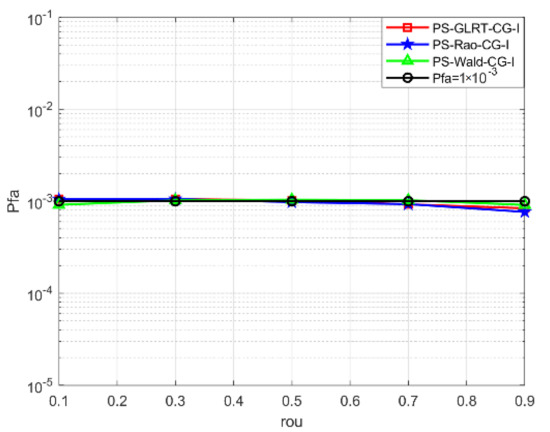
Figure 1. False-alarm probabilities versus correlation coefficients for $K=2N$.

In Figure 2a,b, we present probabilities of detection of the proposed PS-Rao-CG-I, PS-Wald-CG-I, and PS-GLRT-CG-I as a function of SCR for different $K$. For comparison, we give the performance of the PS-GLRT-I [19] proposed in partially homogeneous clutter plus subspace interference. The performance of the PS-GLRT-CG, PS-Rao-CG, PS-Wald-CG [21], and the GLRT-ML-CG [29], which are proposed in the compound Gaussian clutter but without considering the interference, is also given. Moreover, the performance of the persymmetric matched filter (PMF), which is derived with known covariance matrix $\mathit{R}$, is given just as a benchmark since $\mathit{R}$ is unknown in real applications [32,33].

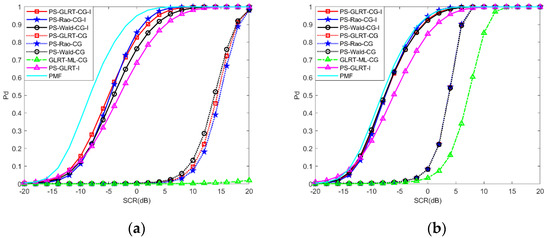
Figure 2. Detection performance of the detectors: (a) $K=N$; (b) $K=4N$.

Figure 2a,b indicate that the proposed PS-Rao-CG-I, PS-Wald-CG-I, and PS-GLRT-CG-I achieve better detection performance than the conventional detectors. The proposed detectors achieve about 14 dB and 6 dB performance gains compared to the PS-GLRT-CG, PS-Rao-CG, and PS-Wald-CG for $K=N$ and $K=4N$, respectively. The proposed detectors achieve about 2 dB performance gain at $P_d=0.9$ compared to the PS-GLRT-I. When $K=4N$, the performance of the proposed detectors approaches that of the PMF. This can be attributed to the reason that the proposed detectors exploit both the persymmetric structure of the speckle CM and prior distribution of the texture, while the PS-GLRT-I exploits persymmetric property of the speckle CM but assumes that the texture is a constant. Meanwhile, the PS-GLRT-CG, PS-Rao-CG, PS-Wald-CG, and GLRT-ML-CG do not consider the presence of the interference.

In Figure 3a,b, the receiver operating characteristic (ROC) of the detectors for $\mathrm{SCR}=-5\hspace{0.17em}\mathrm{dB}$, $K=2N$ and $\mathrm{SCR}=5\mathrm{dB},K=2N$ are displayed. The figures indicate that the proposed detectors are superior to conventional methods in a wide range of $P_{fa}$.

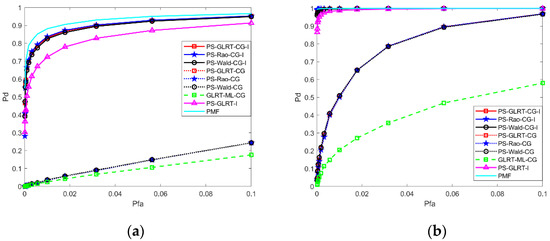
Figure 3. ROC of the detectors for $K=2N,\mathrm{INR}=10\mathrm{dB}$: (a) $\mathrm{SCR}=-5\mathrm{dB}$; (b) $\mathrm{SCR}=5\mathrm{dB}$.

The detection performance of the PS-Rao-CG-I, PS-Wald-CG-I, and PS-GLRT-CG-I under different ICRs is analyzed in Figure 4. We can see that the detection probabilities of the three proposed detectors remain almost the same under different ICRs. The detection performance does not vary with ICR.

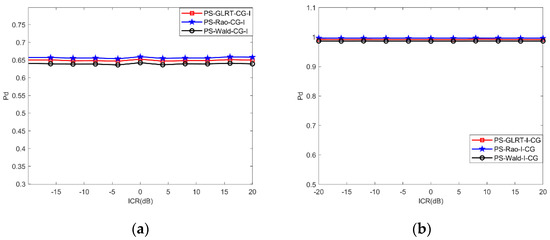
Figure 4. Detection performance of the detectors for $K=2N$: (a) $\mathrm{SCR}=-5\mathrm{dB}$; (b) $\mathrm{SCR}=5\mathrm{dB}$.

To see the detection performance of the PS-Rao-CG-I, PS-Wald-CG-I, and PS-GLRT-CG-I in the mismatched signal cases, we define mismatch angle as ${\cos }^2\mathit{\varphi }={\left|\mathrm{tr}\left({\mathit{H}}^H{\mathit{\Sigma }}^{-1}{\mathit{H}}_0\right)\right|}^2/\left[\mathrm{tr}\left({\mathit{H}}^H{\mathit{\Sigma }}^{-1}\mathit{H}\right)\mathrm{tr}\left({\mathit{H}}_0{\mathit{\Sigma }}^{-1}{\mathit{H}}_0\right)\right]$, where $\mathit{H}$ and ${\mathit{H}}_0$ denote the nominal and actual target subspaces. The smaller ${\cos }^2\mathit{\varphi }$, the more serious the mismatch between the nominal target subspaces and actual one. The SCR becomes $\mathrm{SCR}=\mathrm{Trace}\left({\mathit{\varphi }}^H{\mathit{H}}_0^H{\mathit{H}}_0\mathit{\varphi }\right)/Nu$. It can be seen from Figure 5 that when SCR is small, PS-Rao-CG-I is the most selective when the signal mismatch occurs. As SCR increases, the PS-Wald-CG-I is the most sensitive to mismatched signals, while the PS-Rao-CG-I is more robust than PS-Rao-CG-I and PS-GLRT-CG-I.

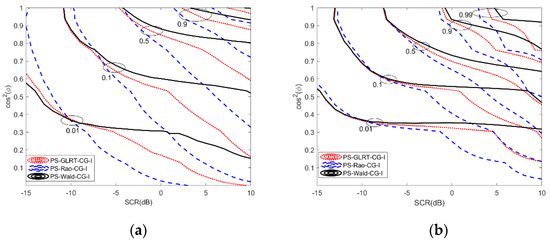
Figure 5. Contours of const $P_d$ for the proposed detectors: (a) $K=N$; (b) $K=4N$.

4.2. Real Data Results

For purpose of further demonstrating the effectiveness of the proposed PS-Rao-CG-I, PS-Wald-CG-I, and PS-GLRT-CG-I, real sea clutter data measured with IPIX radar in 1998 [34] are used to test the performance of the detectors. The selected data are dataset 85 in VV polarization. Table 3 shows the main parameters of the real sea data.

Table 3. Parameters of the real data.

Range Resolution	Range Cells	Range
15 m	34	3501–3996 m

The simulated target signal and interference signal are added in the 16th range bin wherein the data are chosen as the primary data. The training data are chosen from the data in range bins adjacent to the primary data. Figure 6a gives the amplitudes of the chosen primary data. The amplitude PDF of the real data is analyzed in Figure 6b. The results show that the real sea clutter can be fitted well with the inverse Gaussian distribution.

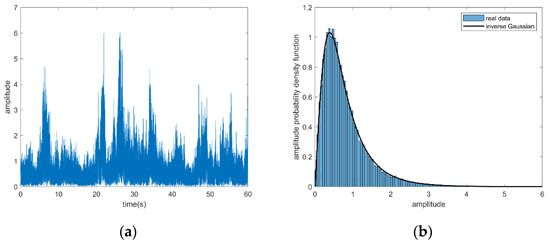
Figure 6. Clutter amplitude and amplitude probability density function for VV polarizations, 16th range cell, dataset 85: (a) clutter amplitude; (b) amplitude probability density function.

Since the amount of real data is limited, we set $N=6$. The detection probability versus SCR for $N=6$ and various $K$ is displayed in Figure 7. The figure shows that the proposed detectors achieve more than 2 dB detection performance gain compared to the PS-GLRT-I and more than 10 dB detection performance gain compared to the PS-GLRT-CG, PS-Rao-CG, and PS-Wald-CG. Thus, both the real data and simulated data results demonstrate that compared with conventional detectors, the proposed PS-GLRT-CG-I, PS-Rao-CG-I, and PS-Wald-CG-I can achieve better detection performance in deterministic interference plus compound Gaussian sea clutter environment.

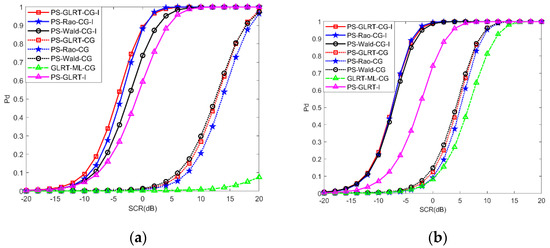
Figure 7. Detection performance of the detectors: (a) $K=N$; (b) $K=2N$.

5. Conclusions

The problem of adaptive subspace signal detection in compound Gaussian clutter plus deterministic interference were herein considered. The texture is random and follows the inverse Gaussian distribution. The target signal and interference occupy two independent known subspaces. Three new CFAR detectors, i.e., PS-Rao-CG-I, PS-Wald-CG-I, and PS-GLRT-CG-I, were proposed by utilizing the persymmetric structure of the clutter CM. Real sea clutter data and simulated data results have demonstrated that the proposed detectors can effectively suppress interference and exhibit good detection performance in complex environments. Since the PS-Rao-CG-I, PS-Wald-CG-I, and PS-GLRT-CG-I are proposed when the subspaces occupied by the target signal and interference are independent, future research may focus on the situation when the two subspaces overlap each other. Moreover, it would be interesting to investigate and design detectors based on other design criteria, such as gradient and Durbin tests.