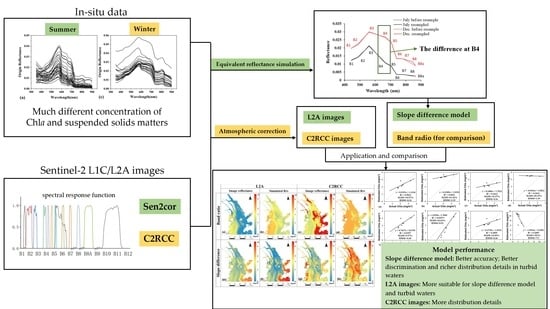
An Integrated Model of Summer and Winter for Chlorophyll-a Retrieval in the Pearl River Estuary Based on Hyperspectral Data
Abstract
:1. Introduction
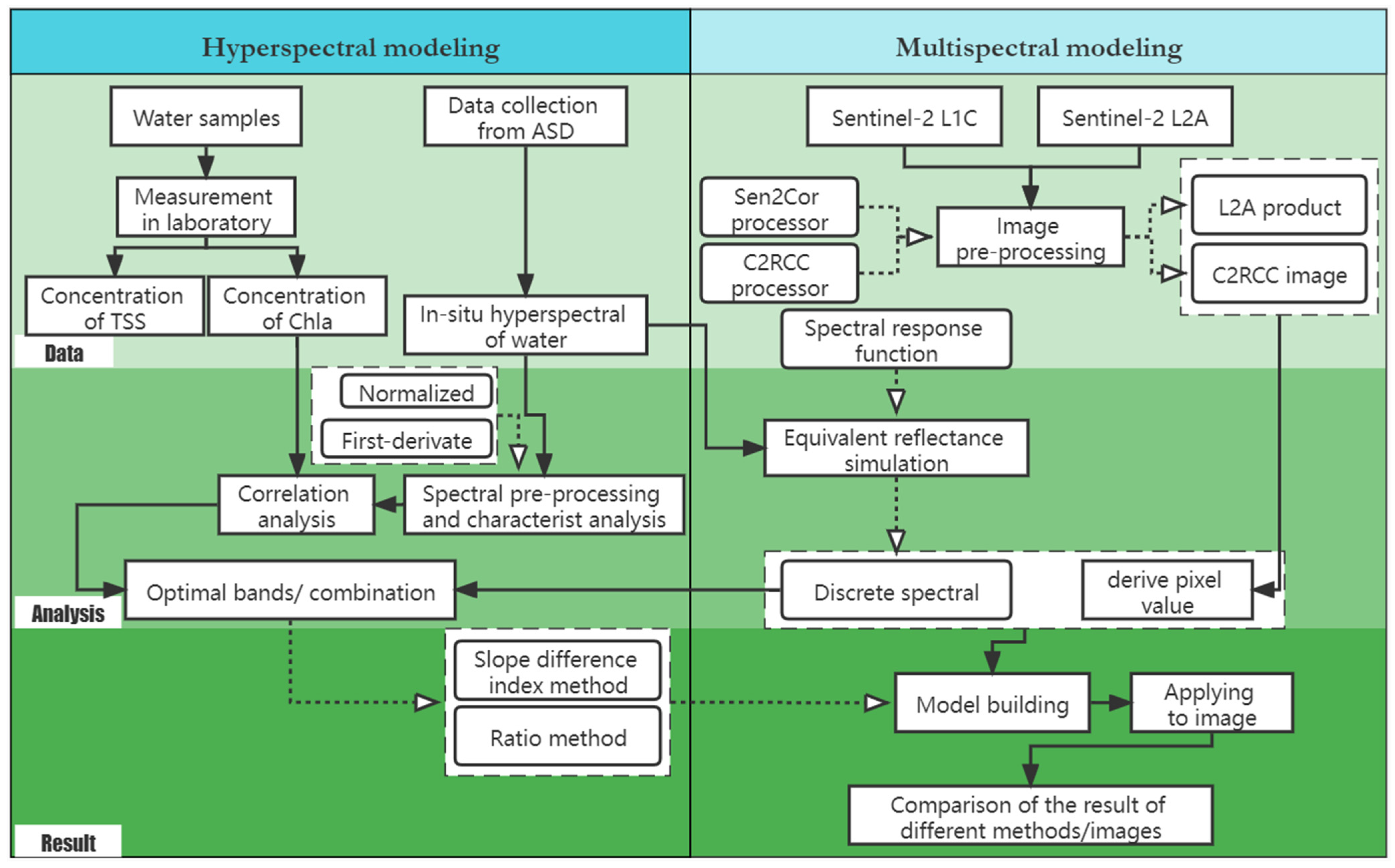
2. Materials and Methods
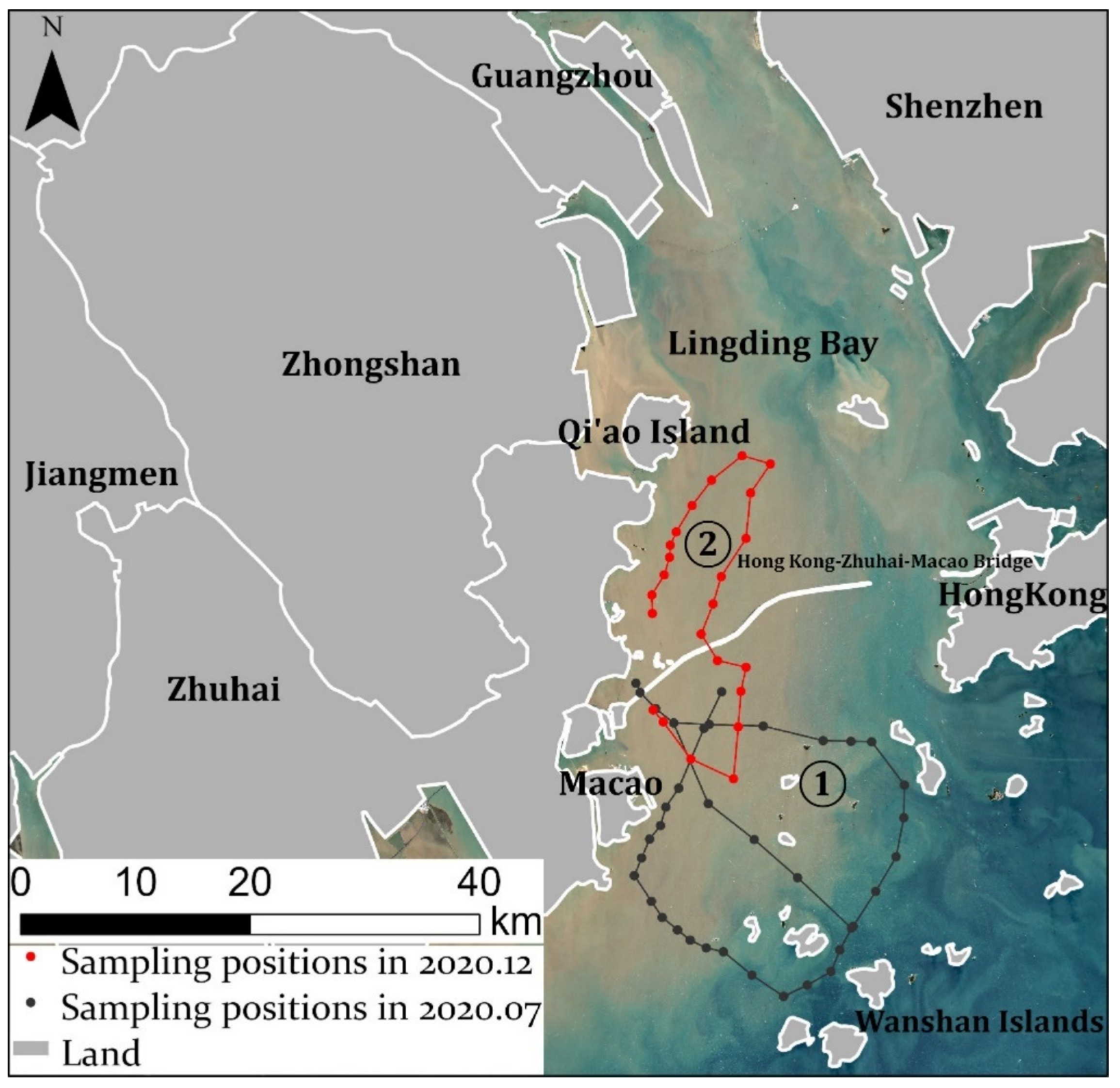
2.1. Study Area
2.2. Field Data Collection
2.3. Data Pre-Processing and Models
2.3.1. Normalization Processing
2.3.2. First-Derivate Processing
2.3.3. Equivalent Reflectance Simulation
2.3.4. The Slope Difference Index
2.3.5. Model Validation and Evaluation
3. Results
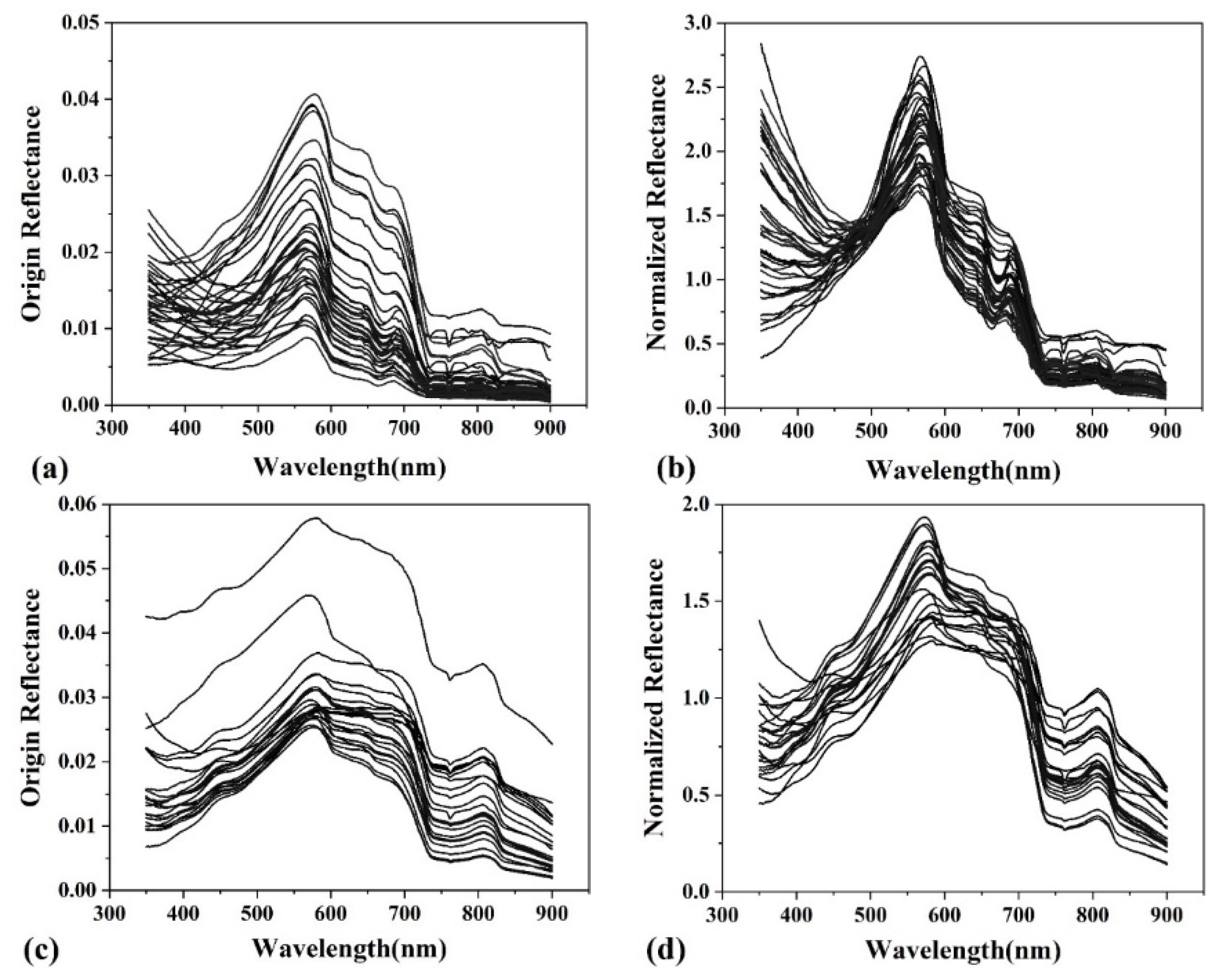
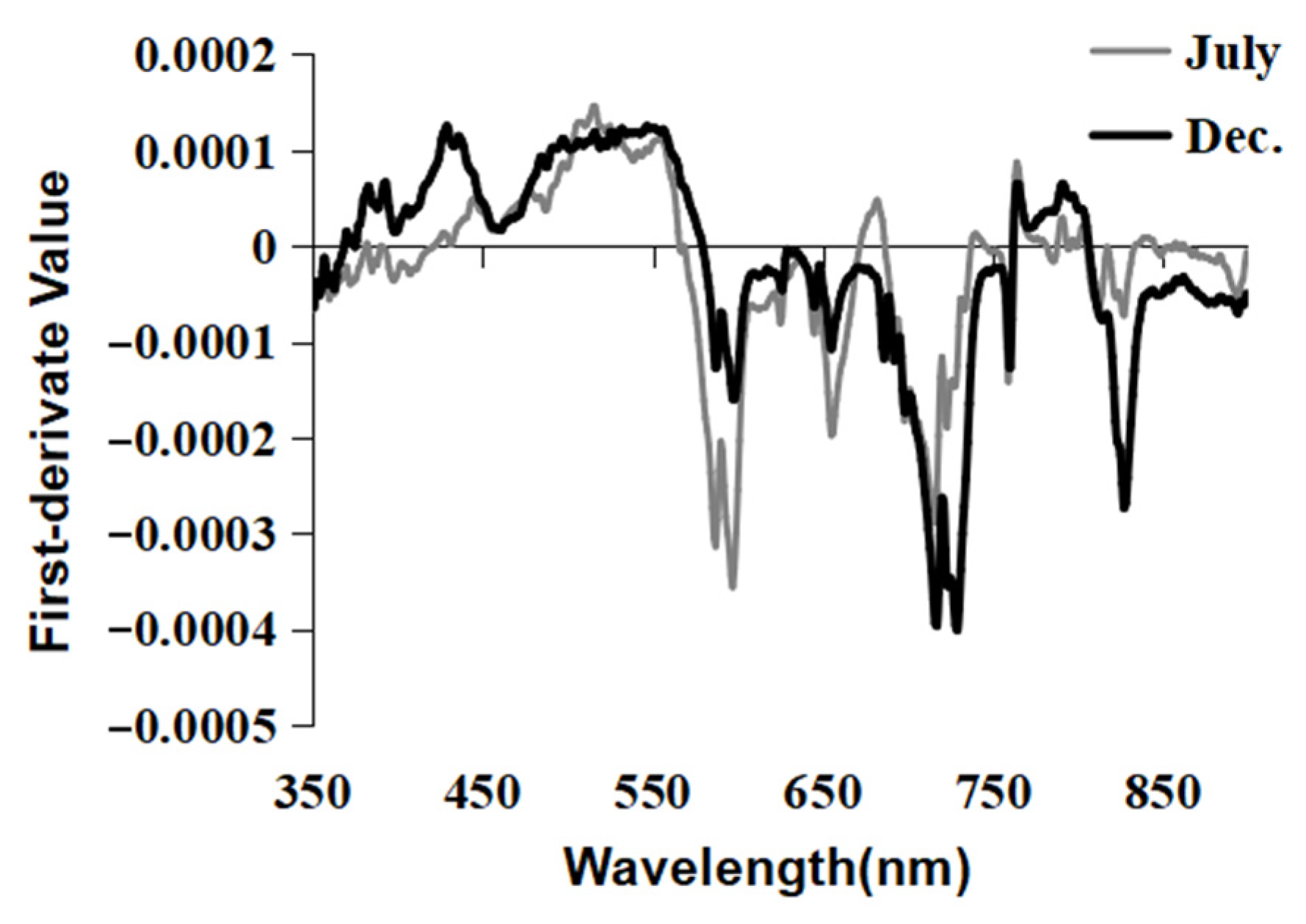
3.1. In-Situ Spectral Characteristics
3.2. Model of Normalized Reflectance
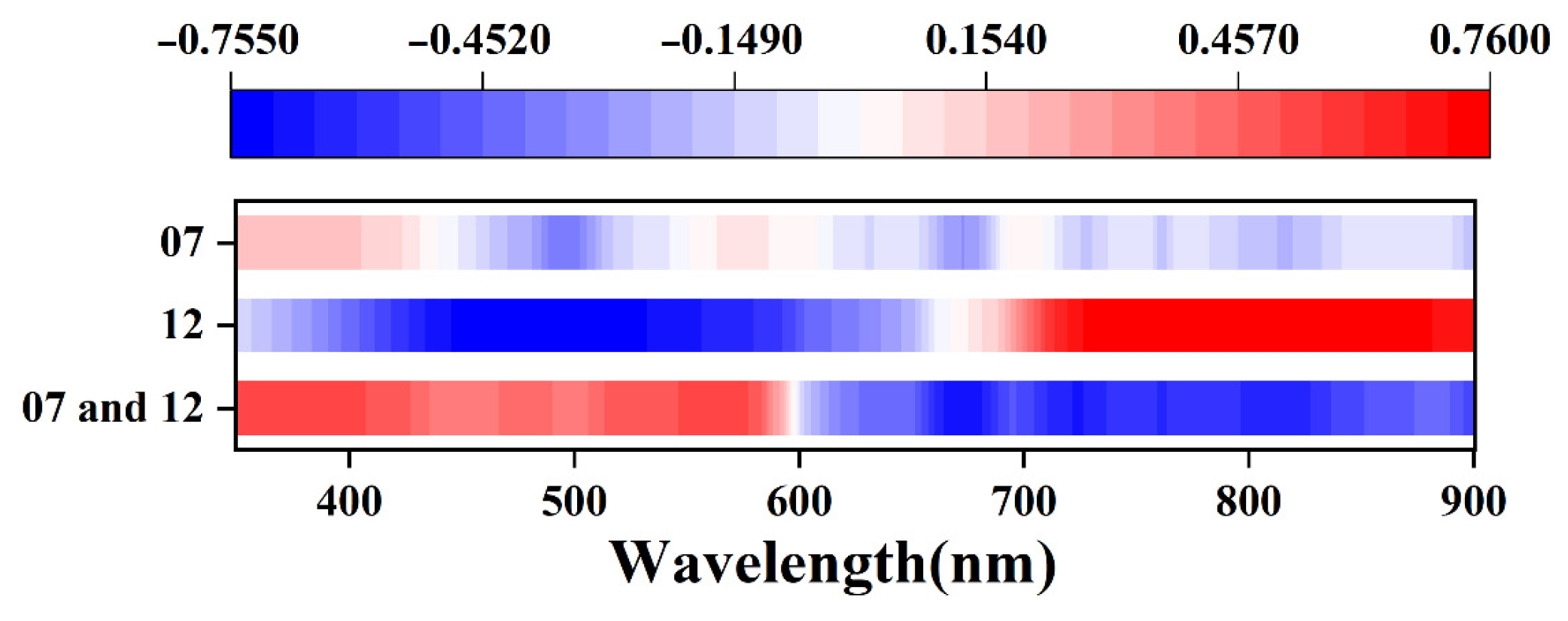
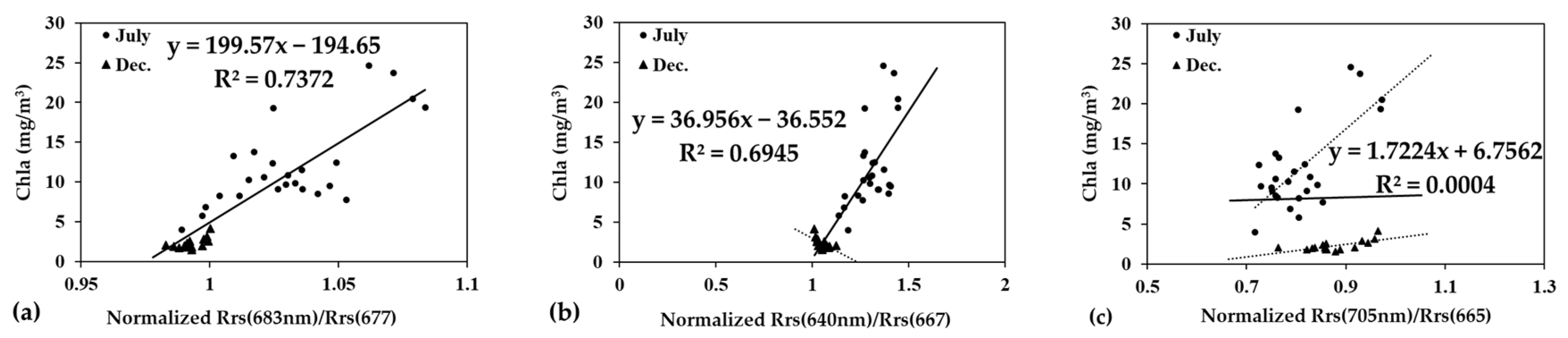
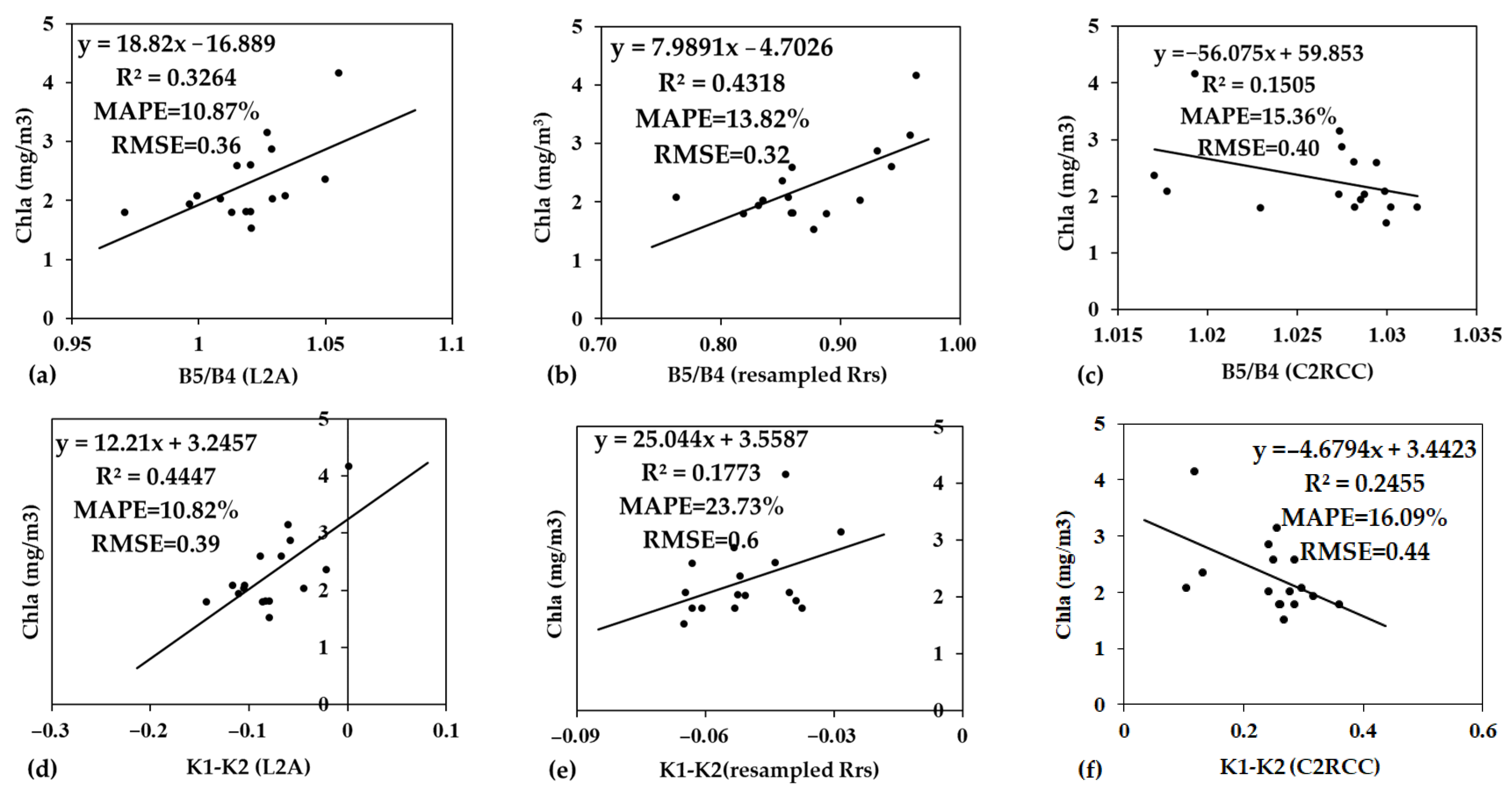
3.2.1. Correlation between Normalized Results and Chla
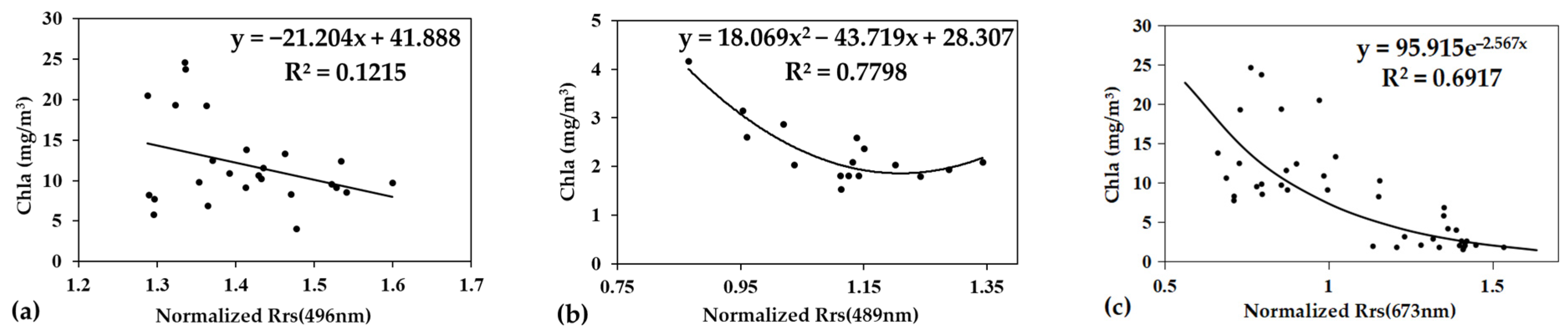
3.2.2. Established Single Band Model for Comparison
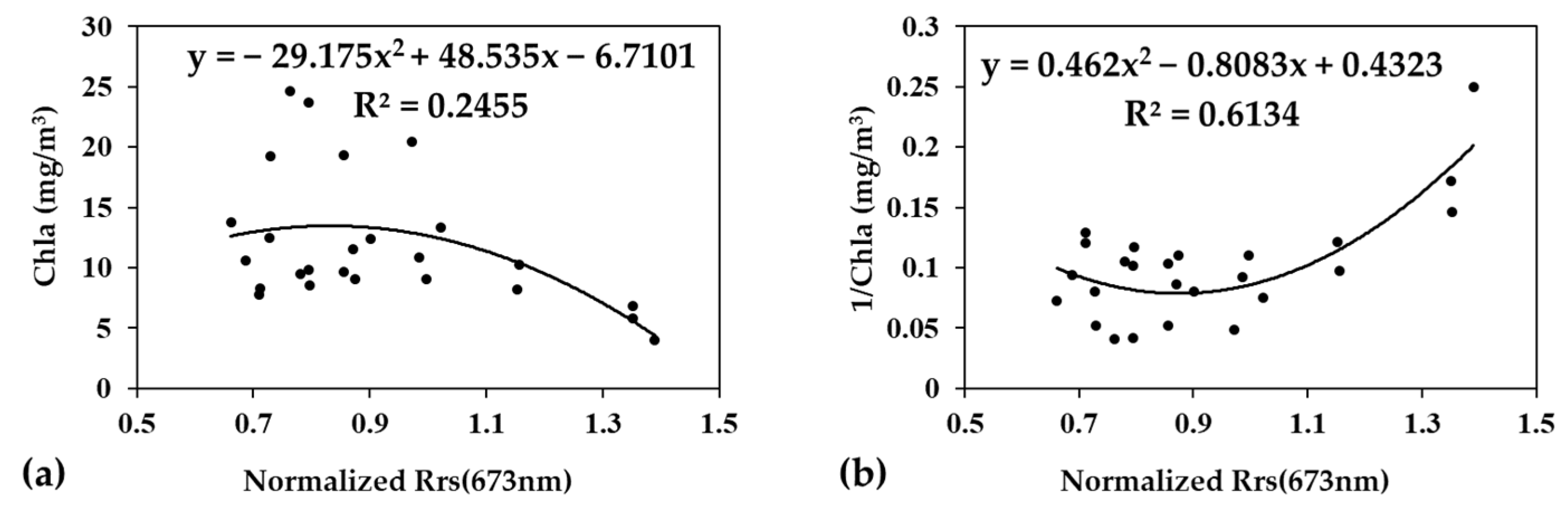
3.2.3. Established Ratio Model for Comparison
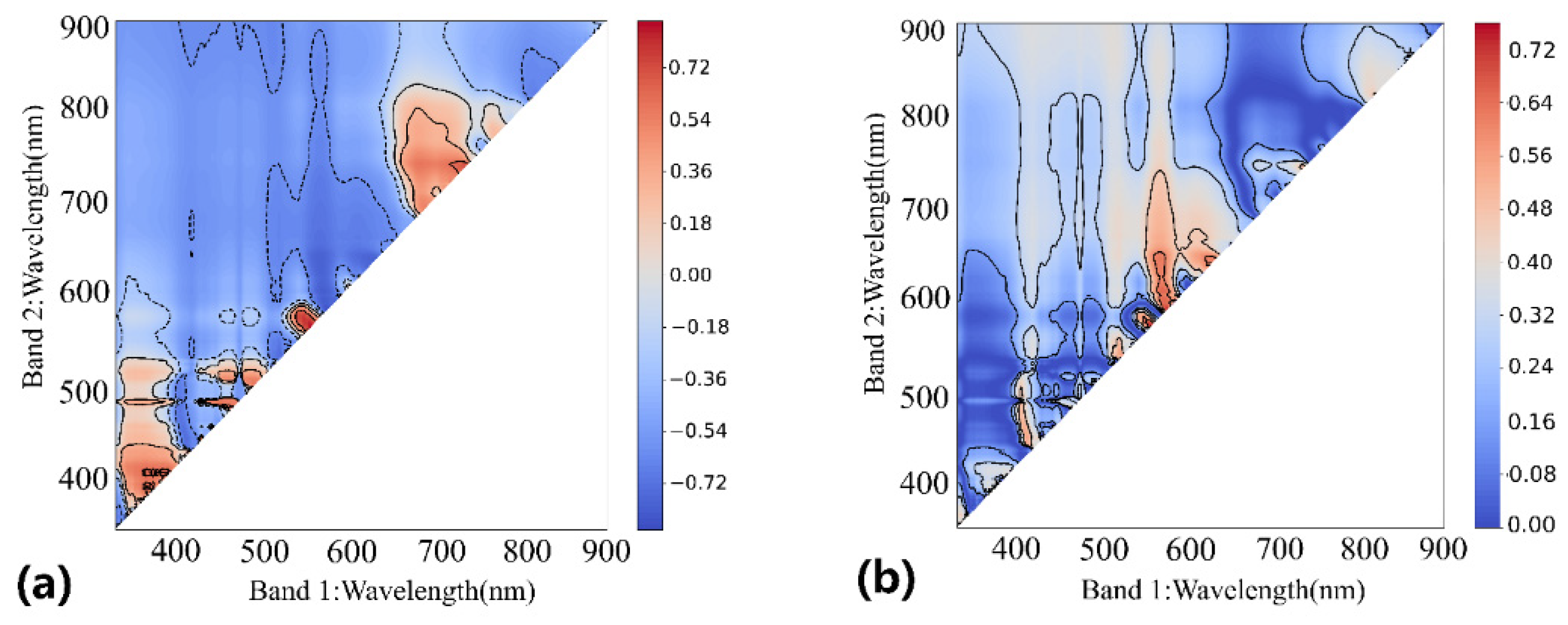
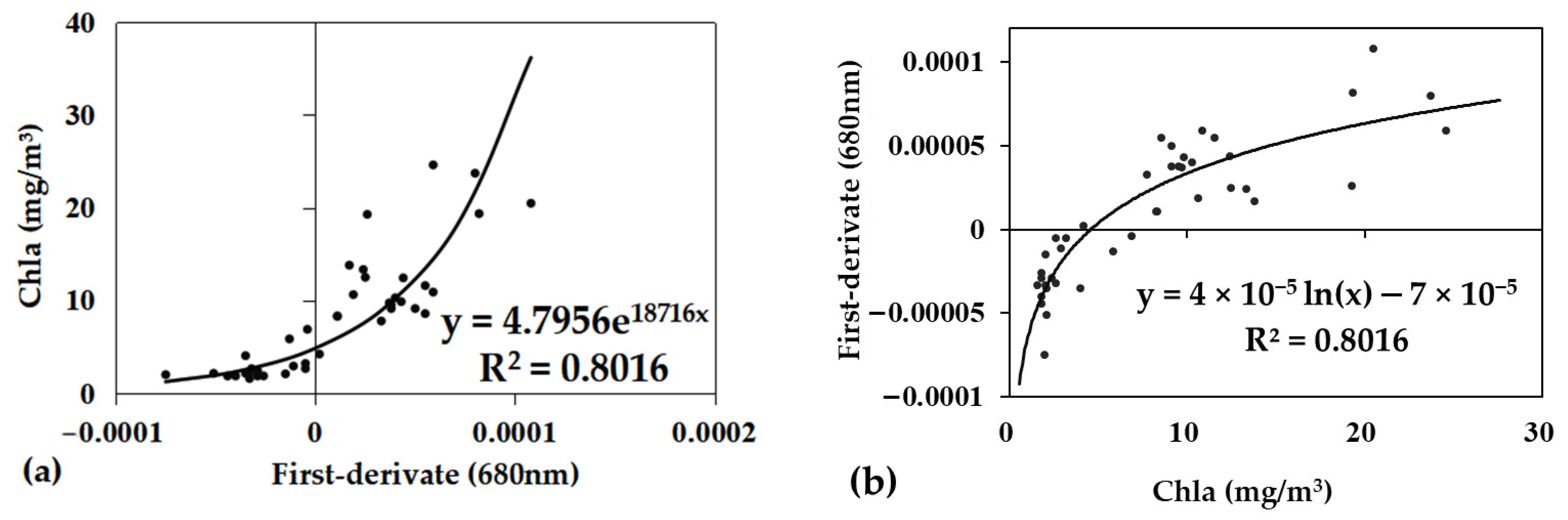
3.3. First-Derivate Model Exploration
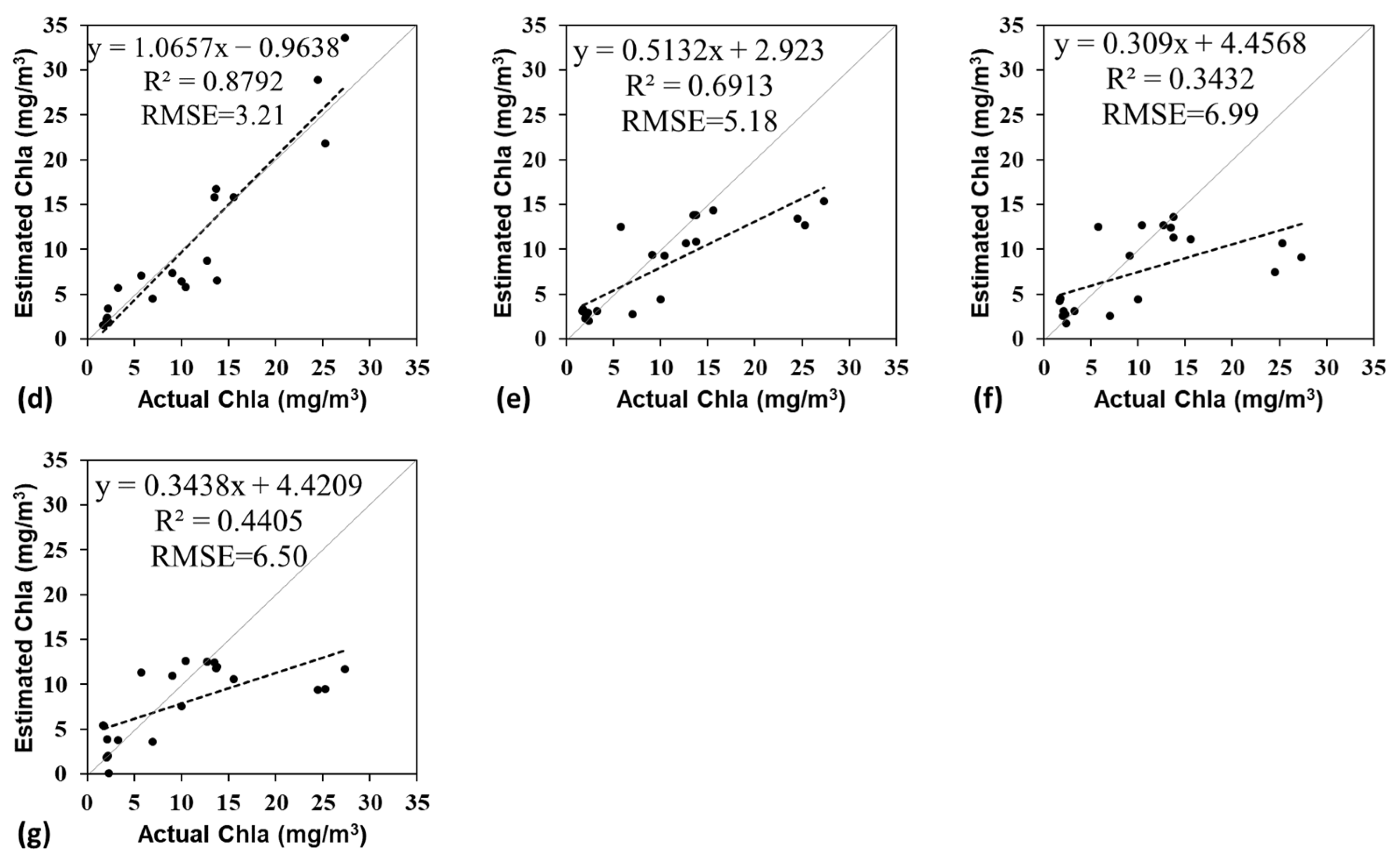
3.4. Discrete Spectral Model Based on Sentinel-2 Images
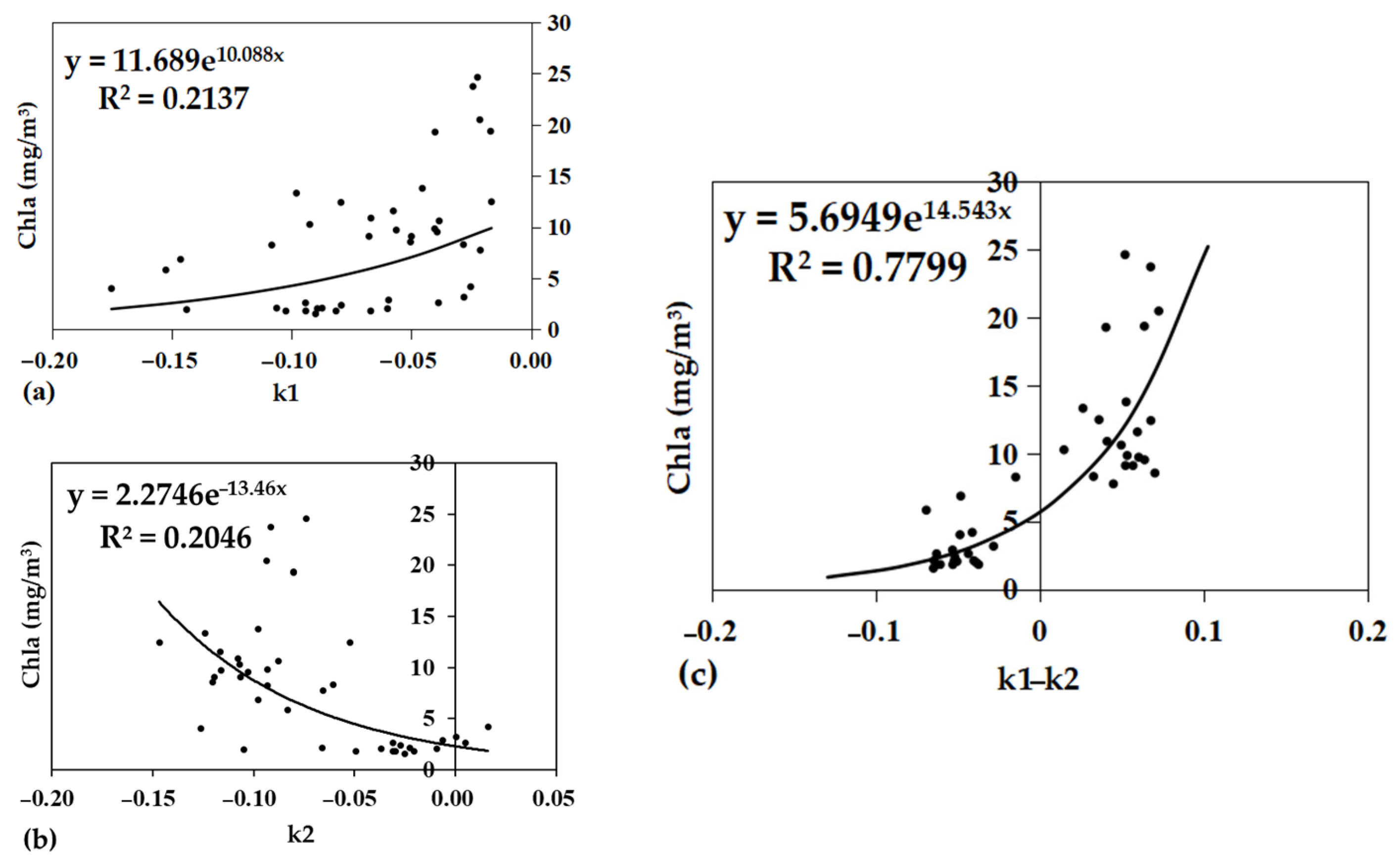
3.4.1. Slope Difference Index Model
3.4.2. Derivate Method of Discrete Spectral
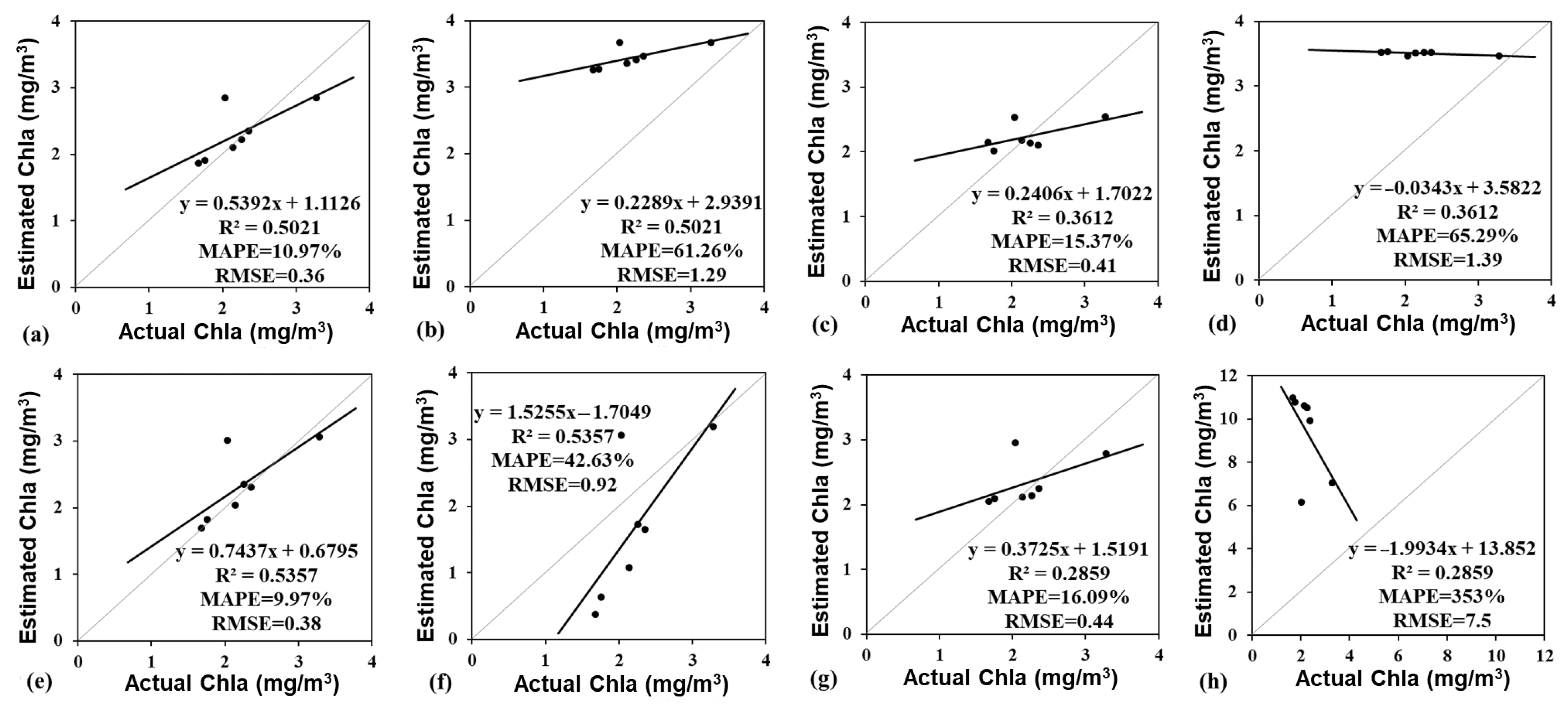
3.5. Model Summary and Validation
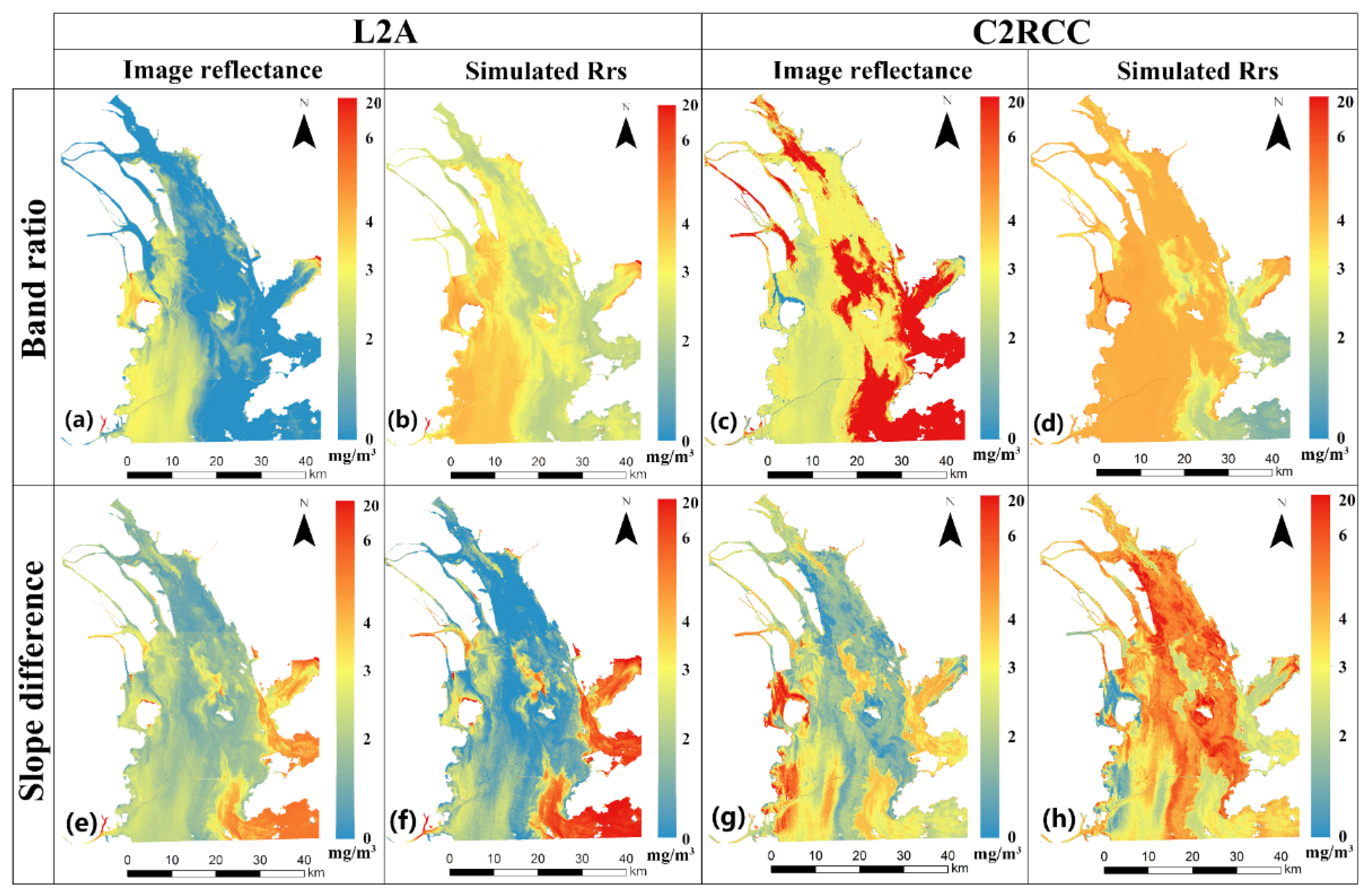
3.6. Applicability of the Model to the Satellite Images
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blondeau-Patissier, D.; Gower, J.F.R.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef] [Green Version]
- Palmer, S.C.J.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Duan, H.; Ma, R.; Hu, C. Evaluation of remote sensing algorithms for cyanobacterial pigment retrievals during spring bloom formation in several lakes of East China. Remote Sens. Environ. 2012, 126, 126–135. [Google Scholar] [CrossRef]
- Pirasteh, S.; Mollaee, S.; Fatholahi, S.N.; Li, J. Estimation of Phytoplankton Chlorophyll-a Concentrations in the Western Basin of Lake Erie Using Sentinel-2 and Sentinel-3 Data. Can. J. Remote Sens. 2020, 46, 585–602. [Google Scholar] [CrossRef]
- Arabi, B.; Salama, M.S.; Wernand, M.R.; Verhoef, W. MOD2SEA: A Coupled Atmosphere-Hydro-Optical Model for the Retrieval of Chlorophyll-a from Remote Sensing Observations in Complex Turbid Waters. Remote Sens. 2016, 8, 722. [Google Scholar] [CrossRef] [Green Version]
- IOCCG. Why Ocean Colour? The Societal Benefits of Ocean-Colour Technology; Platt, T., Hoepffner, N., Stuart, V., Brown, C., Eds.; Reports of the International Ocean-Colour Coordinating Group, No. 7; IOCCG: Dartmouth, NS, Canada, 2008. [Google Scholar]
- Härmä, P.; Vepsäläinen, J.; Hannonen, T.; Pyhälahti, T.; Kämäri, J.; Kallio, K.; Eloheimo, K.; Koponen, S. Detection of water quality using simulated satellite data and semi-empirical algorithms in Finland. Sci. Total Environ. 2001, 268, 107–121. [Google Scholar] [CrossRef]
- Politi, E.; Cutler, M.E.; Rowan, J.S. Evaluating the spatial transferability and temporal repeatability of remote-sensing-based lake water quality retrieval algorithms at the European scale: A meta-analysis approach. Int. J. Remote Sens. 2015, 36, 3005–3033. [Google Scholar] [CrossRef] [Green Version]
- Mobley, C.; Stramski, D.; Bissett, P.; Boss, E. Optical Modeling of Ocean Waters: Is the Case 1–Case 2 Classification Still Useful? Oceanography 2004, 17, 60–67. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chang, P.; Yang, F.; Fukushima, T. A simple method for distinguishing global Case-1 and Case-2 waters using SeaWiFS measurements. ISPRS J. Photogramm. Remote Sens. 2012, 69, 74–87. [Google Scholar] [CrossRef] [Green Version]
- Östlund, C.; Flink, P.; Strömbeck, N.; Pierson, D.; Lindell, T. Mapping of the water quality of Lake Erken, Sweden, from Imaging Spectrometry and Landsat Thematic Mapper. Sci. Total Environ. 2001, 268, 139–154. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Novel Spectra-Derived Features for Empirical Retrieval of Water Quality Parameters: Demonstrations for OLI, MSI, and OLCI Sensors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10285–10300. [Google Scholar] [CrossRef]
- Jinkun, Y.; Chu-qun, C. An Optimal Algorithm for the Retrieval of Chlorophyll, Suspended Sediments and Gelbstoff of Case Ⅱ Waters in the Pearl River Estuary. Mar. Sci. Bull. 2009, 11, 13–23. [Google Scholar]
- Dierssen, H.M.; Randolph, K. Remote Sensing of Ocean Color. In Earth System Monitoring; Springer: Berlin/Heidelberg, Germany, 2012; pp. 439–472. [Google Scholar]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, Q.; Pan, D.; Wu, X. Remote sensing estimation of chlorophyll-a concentration in east coastal water in China based on MAMS data. In Remote Sensing of the Ocean, Sea Ice, and Large Water Regions 2008; SPIE: Bellingham, DC, USA, 2008; Volume 7105. [Google Scholar]
- Zhang, Q.; Wu, Z.; Xie, X. Research progress of the inversion algorithm of chlorophyll-a concentration in estuaries and coastal waters. Ecol. Sci. 2017, 36, 215–222. [Google Scholar] [CrossRef]
- Chen, S.; Fang, L.; Li, H.; Chen, W.; Huang, W. Evaluation of a three-band model for estimating chlorophyll-a concentration in tidal reaches of the Pearl River Estuary, China. ISPRS J. Photogramm. Remote Sens. 2011, 66, 356–364. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A.; Rundquist, D.C. Towards a unified approach for remote estimation of chlorophyll-a in both terrestrial vegetation and turbid productive waters. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Son, S. VIIRS-derived chlorophyll-a using the ocean color index method. Remote Sens. Environ. 2016, 182, 141–149. [Google Scholar] [CrossRef]
- Tehrani, N.A.; Janalipour, M.; Babaei, H. Estimating Water Surface Chlorophyll-a Concentration by Big Remote Sensing Data in the Persian Gulf, Bushehr. Remote Sens. Earth Syst. Sci. 2021, 4, 87–95. [Google Scholar] [CrossRef]
- Wang, Z.; Sakuno, Y.; Koike, K.; Ohara, S. Evaluation of Chlorophyll-a Estimation Approaches Using Iterative Stepwise Elimination Partial Least Squares (ISE-PLS) Regression and Several Traditional Algorithms from Field Hyperspectral Measurements in the Seto Inland Sea, Japan. Sensors 2018, 18, 2656. [Google Scholar] [CrossRef] [Green Version]
- Odermatt, D.; Gitelson, A.; Brando, V.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Liu, F.; Tang, S. Estimation of heavy metal concentration in the Pearl River estuarine waters from remote sensing data. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2575–2578. [Google Scholar] [CrossRef]
- Mahasandana, S.; Tripathi, N.K.; Honda, K. Sea surface multispectral index model for estimating chlorophyllaconcentration of productive coastal waters in Thailand. Can. J. Remote Sens. 2009, 35, 287–296. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Schalles, J.F.; Hladik, C.M. Remote chlorophyll-a retrieval in turbid, productive estuaries: Chesapeake Bay case study. Remote Sens. Environ. 2007, 109, 464–472. [Google Scholar] [CrossRef]
- Gitelson, A.; Mayo, M.; Yacobi, Y.Z.; Parparov, A.; Berman, T. The use of high-spectral-resolution radiometer data for detection of low chlorophyll concentrations in Lake Kinneret. J. Plankton Res. 1994, 16, 993–1002. [Google Scholar] [CrossRef]
- Kallio, K.; Kutser, T.; Hannonen, T.; Koponen, S.; Pulliainen, J.; Vepsäläinen, J.; Pyhälahti, T. Retrieval of water quality from airborne imaging spectrometry of various lake types in different seasons. Sci. Total Environ. 2001, 268, 59–77. [Google Scholar] [CrossRef]
- Gao, C. Seasonal Remote Sensing Retrieval Matter and Chlorophyll-a Concentration in Poyang Lake; Jiangxi Normal University: Nanchang, China, 2018. [Google Scholar]
- Xing, Q.; Chen, C.; Shi, H.; Shi, P.; Zhang, Y. Estimation of Chlorophyll-a Concentrations in the Pearl River Estuary Using In Situ Hyperspectral Data: A Case Study. Mar. Technol. Soc. J. 2008, 42, 22–27. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.; Tian, Y.Q.; Yu, Q.; Zheng, Y.; Huang, L. Remote estimation of colored dissolved organic matter and chlorophyll-a in Lake Huron using Sentinel-2 measurements. J. Appl. Remote Sens. 2017, 11, 036007. [Google Scholar] [CrossRef]
- Han, M.-K.; Wu, L.; Liu, Y.-F.; Mimura, N. Impacts of sea-level rise and human activities on the evolution of the pearl River Delta, South China. Proc. Mar. Sci. 2000, 2, 237–246. [Google Scholar] [CrossRef]
- HUI CHI-CHIU. Water quality: Its practical implications to sustainable development in the Pearl river delta, China. Glob. Int. J. 2000, 2, 209–216. [Google Scholar]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef]
- Zhang, X.; He, S.; Shabani, A.; Zhai, P.-W.; Du, K. Spectral sea surface reflectance of skylight. Opt. Express 2017, 25, A1–A13. [Google Scholar] [CrossRef]
- Johan, F.; Jafri, M.Z.; Lim, H.S.; Maznah, W.O.W. Laboratory measurement: Chlorophyll-a concentration measurement with acetone method using spectrophotometer. In Proceedings of the 2014 IEEE International Conference on Industrial Engineering and Engineering Management, Selangor, Malaysia, 9–12 December 2014; pp. 744–748. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Han, X.; Chen, X.; Qi, L. Long-Term Distribution Patterns of Chlorophyll-a Concentration in China’s Largest Freshwater Lake: MERIS Full-Resolution Observations with a Practical Approach. Remote Sens. 2014, 7, 275–299. [Google Scholar] [CrossRef] [Green Version]
- Becker, B.L.; Lusch, D.P.; Qi, J. Identifying optimal spectral bands from in situ measurements of Great Lakes coastal wetlands using second-derivative analysis. Remote Sens. Environ. 2005, 97, 238–248. [Google Scholar] [CrossRef]
- Nadal, J.L.V.; Franch, B.; Roger, J.C.; Skakun, S.; Vermote, E.; Justice, C. Spectrally Adjusted Surface Reflectance and its Dependence with NDVI for pAssive Optical Sensors. In Proceedings of the GARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6452–6455. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.; Qin, B.; Van der Woerd, H.J.; Li, J.; Li, Y. Modeling Remote-Sensing Reflectance and Retrieving Chlorophyll-a Concentration in Extremely Turbid Case-2 Waters (Lake Taihu, China). IEEE Trans. Geosci. Remote Sens. 2009, 47, 1937–1948. [Google Scholar] [CrossRef]
- Loisel, H.; Vantrepotte, V.; Ouillon, S.; Ngoc, D.D.; Herrmann, M.; Tran, V.; Mériaux, X.; Dessailly, D.; Jamet, C.; Duhaut, T.; et al. Assessment and analysis of the chlorophyll-a concentration variability over the Vietnamese coastal waters from the MERIS ocean color sensor (2002–2012). Remote Sens. Environ. 2017, 190, 217–232. [Google Scholar] [CrossRef]
- Yuchun, W.; Guoxiang, W.; Huayun, S. A Logical Problem in the Building Linear Regression Model on Estimating Chlorophyll-a Concentration in Lake Based on the Measured Spectrum Data. Math. Pract. Theory 2010, 40, 100–110. [Google Scholar]
- Gitelson, A.A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.C.; Barrow, T.; Fisher, T.R.; Gurlin, D.; Holz, J. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar] [CrossRef]
- Sakuno, Y.; Yajima, H.; Yoshioka, Y.; Sugahara, S.; Elbasit, M.A.M.A.; Adam, E.; Chirima, J.G. Evaluation of Unified Algorithms for Remote Sensing of Chlorophyll-a and Turbidity in Lake Shinji and Lake Nakaumi of Japan and the Vaal Dam Reservoir of South Africa under Eutrophic and Ultra-Turbid Conditions. Water 2018, 10, 618. [Google Scholar] [CrossRef] [Green Version]
- Duan, H.; Ma, R.; Xu, J.; Zhang, Y.; Zhang, B. Comparison of different semi-empirical algorithms to estimate chlorophyll-a concentration in inland lake water. Environ. Monit. Assess. 2009, 170, 231–244. [Google Scholar] [CrossRef]
- Yadav, S.; Yamashiki, Y.; Susaki, J.; Yamashita, Y.; Ishikawa, K. Chlorophyll Estimation of Lake Water and Coastal Water Using Landsat-8 and Sentinel-2a Satellite. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-3/W7, 77–82. [Google Scholar] [CrossRef] [Green Version]
- Nazeer, M.; Nichol, J.E. Development and application of a remote sensing-based Chlorophyll-a concentration prediction model for complex coastal waters of Hong Kong. J. Hydrol. 2016, 532, 80–89. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Nõges, T. First Experiences in Mapping Lake Water Quality Parameters with Sentinel-2 MSI Imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef] [Green Version]
- Xiangsheng, K.; Anding, Z.; Yonggang, Q.; Yuyang, D. Teaching design and practice on reflectance measurement combined with the calculation of planetary reflectance. Sci. Surv. Mapp. 2011, 36, 234–236. [Google Scholar] [CrossRef]
- Chen, Q.; Yu, R.; Hao, Y.; Wu, L.; Zhang, W.; Zhang, Q.; Bu, X. A New Method for Mapping Aquatic Vegetation Especially Underwater Vegetation in Lake Ulansuhai Using GF-1 Satellite Data. Remote Sens. 2018, 10, 1279. [Google Scholar] [CrossRef] [Green Version]
- Brockmann, C.; Doerffer, R.; Peters, M.; Kerstin, S.; Embacher, S.; Ruescas, A. Evolution of the C2RCC Neural Network for Sentinel 2 and 3 for the Retrieval of Ocean Colour Products in Normal and Extreme Optically Complex Waters. ESASP 2016, 740, 54. [Google Scholar]
- Cui, T.; Zhang, J.; Wang, K.; Wei, J.; Mu, B.; Ma, Y.; Zhu, J.; Liu, R.; Chen, X. Remote sensing of chlorophyll a concentration in turbid coastal waters based on a global optical water classification system. ISPRS J. Photogramm. Remote Sens. 2020, 163, 187–201. [Google Scholar] [CrossRef]
- Lins, R.C.; Martinez, J.-M.; Marques, D.D.M.; Cirilo, J.A.; Fragoso, C.R. Assessment of Chlorophyll-a Remote Sensing Algorithms in a Productive Tropical Estuarine-Lagoon System. Remote Sens. 2017, 9, 516. [Google Scholar] [CrossRef] [Green Version]
- Pompêo, M.; Moschini-Carlos, V.; Bitencourt, M.D.; Sòria-Perpinyà, X.; Vicente, E.; Delegido, J. Water quality assessment using Sentinel-2 imagery with estimates of chlorophyll a, Secchi disk depth, and Cyanobacteria cell number: The Cantareira System reservoirs (São Paulo, Brazil). Environ. Sci. Pollut. Res. 2021, 28, 34990–35011. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L.; Gege, P. Inter-Comparison of Methods for Chlorophyll-a Retrieval: Sentinel-2 Time-Series Analysis in Italian Lakes. Remote Sens. 2021, 13, 2381. [Google Scholar] [CrossRef]




| Parameter | Time | Range | Mean Value | Median Value |
|---|---|---|---|---|
| Chla (mg/m3) | 2020.07 | 3.995~27.312 | 12.84 | 10.73 |
| 2020.12 | 1.527~4.168 | 2.27 | 2.08 | |
| Suspended solids (mg/L) | 2020.07 | 0.33~54 | 24.28 | 24.33 |
| 2020.12 | 25.2~278 | 112.31 | 84.60 |
| Bands | Central Wavelength (nm) | Resolution (m) | Bands | Central Wavelength (nm) | Resolution (m) |
|---|---|---|---|---|---|
| B1 | 443 | 60 | B8 | 842 | 10 |
| B2 | 490 | 10 | B8a | 865 | 20 |
| B3 | 560 | 10 | B9 | 945 | 60 |
| B4 | 665 | 10 | B10 | 1375 | 60 |
| B5 | 705 | 20 | B11 | 1610 | 20 |
| B6 | 740 | 20 | B12 | 2190 | 20 |
| B7 | 783 | 20 | B8 | 842 | 10 |
| Data | Pre-Processing | Time | Method | Bands | Model | R2 | RMSE | MAPE | MAE |
|---|---|---|---|---|---|---|---|---|---|
| Hyperspectral data from in-situ investigation | Normalization | July | Single band | 673 | y = 0.462x2 − 0.8083x + 0.4323 | 0.61 | 7.08 | 0.31 | 4.88 |
| Ratio | 705/665 | y = 53.531x − 31.291 | 0.49 | 4.71 | 0.30 | 4.08 | |||
| December | Single band | 489 | y = 18.069x2 − 43.719x + 28.307 | 0.78 | 0.46 | 0.19 | 0.40 | ||
| First-derivate | Both | Single band | 680 | y = 4.7956e18.716x | 0.80 | 3.21 | 0.26 | 2.48 | |
| Discrete spectral (simulated reflectance) | Slope | Both | Slope difference | 560~665~705 | y = 5.6949e14.543x | 0.78 | 5.18 | 0.35 | 3.26 |
| First-derivate | Subtraction | 665–705 | y = 10.45e−9.671x | 0.68 | 6.99 | 0.47 | 4.26 | ||
| Multiplication | 705 × 783 | y = 13.282e−398.4x | 0.70 | 6.50 | 0.55 | 4.20 |
| Data Used First | Area | Image Source | Method | Bands Involved | Model Validation (RMSE) and Chla Range (mg/m3) | Validation of Image Retrieval Result |
|---|---|---|---|---|---|---|
| In-situ hyperspectral | Bangpakong River estuary (Thailand) [25] | Landsat-5 | Empirical model | 435, 488, 692 | 1.13 (0.13~7.25) Figure 16e | 1.6 (0.13~7.25) Figure 18f |
| Lake Huron (USA) [31] | Sentinel2-L2A | Red–NIR Ratio Multiple regression | 705, 665 443, 490, 560, 665, 705, 740, 783 | 9.972 (1.62~51.68) Figure 15b and Figure 16b 3.127 (1.62~51.68) Figure 15e and Figure 16e | Did not show the validation, only discusses that it is similar to the real distribution | |
| The Bohai Sea (China) [52] | MODIS | OC4 OC3Mv6 Empirical model | 443, 490, 510, 555 443, 490, 555 443, 412, 555, 490 | 2.36 (0~13) Figure 16e | No specific figure was given, but compared with MODIS standard Chla product, it was found that the retrieval error is large, ranging from 3~5 mg/m3 | |
| Mundaú-Manguaba Estuarine-Lagoon System(Brazil) [53] | MODIS MERIS Sentinel-MSI/OLCI | Blue–Green Ratio NIR–Red Ratio Three-Band Four-Band | 645, 555 681, 709, 665 681, 709, 674 674, 709, 681,665 | 14.55 (5.99~117.54) 10.44 (0.97~117.54) 5.02 (average 27.6) 7.69 (average 27.6) | Discussed the performance of different algorithms before and after classification; no images application. | |
| Spectral from images directly | Lake Erie (USA) [4] | Sentinel2-L1C/L2A | MCI model and processor from SNAP | 665, 705, 740 | 9.6 (0.13~88) Figure 16a,d | Compared the modeling results, not applied to images |
| Some inland lakes (Brazil) [54] | Sentinel2-L1C/ C2RCC | C2RCC-C2X processor and its product from SNAP | Unclear, using the C2RCC NN model, possibly all bands | Did not build models by themselves, use the retrieval result calculated by C2RCC processor of SNAP | For different water: 1.84 (5~8) Figure 18e,g 2.26 (0~20) 2.91 (0~20) | |
| Three subalpine lakes and a turbid lake (Italy) [55] | Sentinel2- L1C/L2A | C2RCC MASI OC3 | No details for C2RCC and MASI; 443, 490 for OC3 | Compared the agreement (R2) between different algorithms | For different lakes: Subalpine (0~6); Turbid (1~25): C2RCC: 0.57; 3.2 MASI: 0.6; 2.6 OC3: 1.39; 4.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xie, X.; Yang, X.; Cao, B.; Xia, X. An Integrated Model of Summer and Winter for Chlorophyll-a Retrieval in the Pearl River Estuary Based on Hyperspectral Data. Remote Sens. 2022, 14, 2270. https://doi.org/10.3390/rs14092270
Li H, Xie X, Yang X, Cao B, Xia X. An Integrated Model of Summer and Winter for Chlorophyll-a Retrieval in the Pearl River Estuary Based on Hyperspectral Data. Remote Sensing. 2022; 14(9):2270. https://doi.org/10.3390/rs14092270
Chicago/Turabian StyleLi, Haitao, Xuetong Xie, Xiankun Yang, Bowen Cao, and Xuening Xia. 2022. "An Integrated Model of Summer and Winter for Chlorophyll-a Retrieval in the Pearl River Estuary Based on Hyperspectral Data" Remote Sensing 14, no. 9: 2270. https://doi.org/10.3390/rs14092270
APA StyleLi, H., Xie, X., Yang, X., Cao, B., & Xia, X. (2022). An Integrated Model of Summer and Winter for Chlorophyll-a Retrieval in the Pearl River Estuary Based on Hyperspectral Data. Remote Sensing, 14(9), 2270. https://doi.org/10.3390/rs14092270