Infrared Dim and Small Target Detection from Complex Scenes via Multi-Frame Spatial–Temporal Patch-Tensor Model
Abstract
1. Introduction
1.1. Related Works
- (1)
- The first kind of detection method is based on the assumption of background consistency. This idea assumes that the background is consistent and the targets are destructive pixels in the uniform background so that the target pixels can be extracted by filtering. Commonly used methods include Tophat filtering [9], maximum mean filtering and maximum median filtering, etc. [10]. The principle of this kind of method is relatively simple, but the robustness to noise is not strong, and the detection performance is relatively poor.
- (2)
- In order to improve the detection accuracy and robustness of traditional filtering methods, scholars have combined human visual system (HVS) [11] to infrared dim and small target detection. Chen and others [12] firstly utilized saliency feature extraction and proposed the local contrast measure (LCM), which is used to calculate the local contrast saliency map of each pixel and detect the small targets on the saliency map. On this basis, many methods have been subsequently developed. Han et al. [13] proposed an improved local contrast measure (ILCM) by changing the method of taking the slider in LCM, which improved the detection performance. Wei et al. [14] proposed a multiscale patch-based contrast measure (MPCM) under the assumption that the background is uniform and the target is bright. Bai et al. [15] proposed a detection method based on derivative entropy-based contrast measure (DECM). Shi et al. [16] proposed a high-boost-based multiscale local contrast measure (HB-MLCM) method based on high-boost-based contrast detection. Lu et al. [17] proposed a new small target detection method based on multidirectional derivative-based weighted contrast measures (MDWCM). Han et al. [18], who improved the filtering window and introduced a three-layer filtering window, proposed a new detection framework named multiscale tri-layer local contrast measure (TLLCM). Hao et al. [19] considered the brightness characteristics of the target and proposed a method based on multiple morphological profiles (MMP). Zhang et al. [20] detected infrared targets by improving pixel growth using two-dimensional density-distance space. HVS-based methods have been widely applied because they require less prior information and the time consumption is low. However, these approaches are as sensitive to noises as previous filtering methods and the detection results severely depend on the choice of parameters, whose performances are poor, especially in the face of complex backgrounds.
- (3)
- To solve the difficulties in extracting the target features and the adaptability to the scenes for previous algorithms, a method based on the low-rank and sparse decomposition (LRSD) framework is proposed. Based on the characteristics of infrared images, these methods avoid extracting the characteristics of the target itself. Instead, it makes low-rank and sparse assumptions for the background and the target as a whole, respectively, and models the image as consisting of noise, background, and target components. Through the establishment of the objective function and the optimization algorithm, the final detection result is obtained. Gao et al. [21] firstly proposed the method of infrared patch image (IPI), which assumes that the background is low-rank, and the target is sparse, using nuclear norm minimization (NNM) to replace the rank function of the matrix. However, NNM has a problem of excessive target shrinkage. To solve this problem, Dai et al. [22] introduced the concept of re-weighting each patch and proposed a weighted infrared patch image (WIPI), using singular value partial sum minimization [23] to approximate the image rank. By introducing the norm to approximate the rank of the non-convex function and adding the norm to reduce the false alarm of strong edges, the non-convex rank approximation minimization (NRAM) model was proposed [24]. Zhang et al. [25] also used the norm to approximate the rank and proposed NOLC model. Inspired by the total variation (TV) norm, Wang et al. [26] improved the robustness of the algorithm in non-uniform scenes by introducing the TV regularization term into the constructed model. Rawat et al. [27] replaced NNM with partial sum minimization (PSM) of singular values based on IPI and introduced the TV norm (TV-PSMSV) for infrared target detection. In addition, some subspace learning models have also been applied to the detection of small infrared targets, such as self-regularized weighted sparse (SRWS) [28], the stable multi-subspace learning (SMSL) [29] method and so on, which have also achieved good results.To further improve the computational efficiency and the detection effect, Dai et al. [30] introduced the theory of tensor into the low-rank sparse model by transforming the matrix construction method [31,32], and proposed a reweighted infrared patch tensor (RIPT) model. Because tensors can make better use of the structural information between pixels, the research on tensors has since received extensive attention. Zhang et al. [33] proposed an image-block model using the information between pictures. Through adding the prior weight information of the corner and edges and using the partial sum of tensor singular values to approximate the rank of the non-convex function, partial sum of tensor nuclear norm (PSTNN) was proposed [34]. The PSTNN model approximates the rank by preserving the summation of some singular values, while the reservation is defined by a fixed energy ratio, which should be different for different scenes so that the estimation of various images can be improved. Zhang et al. [35]. proposed an edge and corner awareness-based spatial–temporal tensor model (ECA-STT) by introducing an edge–corner awareness indicator and adding a tensor-based non-convex tensor low-rank approximation (NTLA) regularization term to the model. Liu [36] preserved more information in the spatial–temporal domain by giving different weights to the spatial TV norm and the temporal TV norm, and thus proposed a new model, which shows a better performance in complex scenes. Kong [37] used a Log operator to replace the norm to approximate the rank of the background, also adding the spatial–temporal TV norm and thus proposed infrared small-target detection via non-convex tensor-fibered nuclear norm rank approximation (LogTFNN).
1.2. Motivation
- (1)
- Tensor construction exploits spatial and temporal information. We propose an approach to combine both spatial information and temporal information to construct the tensor model. The constructed model satisfies the low-rank assumptions much better and can also help to remove the false alarm clutters.
- (2)
- Approximation of rank by the Laplace operator. The Laplace operator is introduced to approximate the rank that has better performance than other methods in this paper. It assigns different weights to each singular value, which helps us to obtain an accurate background estimation.
- (3)
- Weighted prior weights. We propose a method for computing prior weights by weighting, which can give different weights to the corner information and edge information. By adjusting the importance of two structures, it is better at dealing with dim and small targets.
- (4)
- We apply the tensor construction, the rank approximation and weighted prior weights to the IPT model for infrared small-target detection, and the process of applying alternating direction method of multipliers (ADMM) to solve the model are introduced in detail. Experimental results verify the superior performance of our method.
2. Notations
| Algorithm 1: Three-dimensional tensor decomposition by t-SVD. t-SVD of 3D tensors. |
|
Input: Output: U, S, V after tensor decomposition 1. 2. Count each front slice through for i =1, ⋯, , , = end for i = , ⋯, n3 end 3. Count |
3. Proposed Model
3.1. Image Patch Tensor (IPT) Model
3.2. Information of Local Structure Tensor
3.3. Spatial–Temporal Low-Rank Tensor Construction
3.4. Rank Approximation Based on Laplace Operator
3.5. Model Optimization
Model to Be Solved
| Algorithm 2: Optimization of problem (25). |
|
Input: Output: 1. Calculate 2. Compute each frontal slice by for i = 1, (1). (2). Calculated by (32) (3). end for i = end 3. Count |
| Algorithm 3: Model optimization by ADMM algorithm. |
|
Input: Output: Initialization: While and update by Formula (28); update by Algorithm 2; update by Formula (19); update Y by Formula (33); update by Formula (34); update k: k = k + 1; end While |
3.6. Infrared Dim and Small-Target Detection Algorithm Based on Multi-Frame Spatial–Temporal Patch-Tensor Decomposition
- Prior weighted saliency map extraction. The saliency map is obtained by calculating the prior weight between adjacent frames in the sequence by Formula (19);
- Construct a tensor. Through the sliding window of , as shown in Figure 5, the sliders are formed into a three-dimensional tensor X ∈ in order, and z is the number of sliders obtained. Similarly, the above operations are performed on the prior weighted saliency map, acquiring the prior weight ∈;
- The input tensor is decomposed into a low-rank background tensor B and a sparse target tensor T by the ADMM algorithm;
- Tensor reconstruction. Contrary to the construction process, the obtained sparse target tensor and low-rank background tensor are restored and reconstructed, and the overlapping position is sized by a one-dimensional median filter;
- Image post-processing. The recovered sparse target image is processed by adaptive thresholding to obtain the final target image.
4. Experiments and Results
4.1. Evaluation Metrics
- Background suppression factor (BSF). The background inhibitory factor is a measure of the prominence of the target and the inhibitory ability of the background. BSF is defined as [66]:and represent the standard deviation of the whole background area of the input image and the processed image, respectively.
- Signal-to-clutter ratio gain (SCRG) is a measure of the image before and after processing to suppress the noise and clutter. It is related to signal clutter ratio (SCR). SCR is defined as follows:and represent the mean value of pixels in the target area and the surrounding background area as shown in Figure 9. represents the variance in the background neighborhood pixels around the target. SCRG is then defined as:Among them, represents the SCR of the input image, and represents the SCR of the processed image.
- The detection probability and false alarm rate are used to measure the performance of the algorithm [36]. Detection probability is defined as:where DT represents the number of detected targets, and AT represents the number of targets that exist in the image sequence. Moreover, the false alarm rate is described as:where FP represents the number of pixels in the false alarm area, and NP represents the total number of pixels in the image sequence. Taking the detection probability as the abscissa and false-alarm probability as the ordinate, we can draw the receiver operation characteristic (ROC) curve and calculate the area between the curve and the coordinate axis to obtain the value of area under curve (AUC).
- Contrast gain (CG) [67] is used to evaluate the ability to enhance the grayscale contrast of the target and background. CG is calculated by:where is the contrast (CON) of the processed images, and is the contrast of the original images. The definition of the CON is:where and are defined as above. Among these metrics, the larger the SCRG, BSF, CG, and AUC, the better performance of the method is, and it should be noted that SCRG and CG are calculated in the local area, while BSF is computed in the whole image. Because the neighborhoods of the target that we use to evaluate the performance are varied, it is reasonable to consider multiple indicators at the same time.
4.2. Dataset Description
4.3. Parameters Analysis
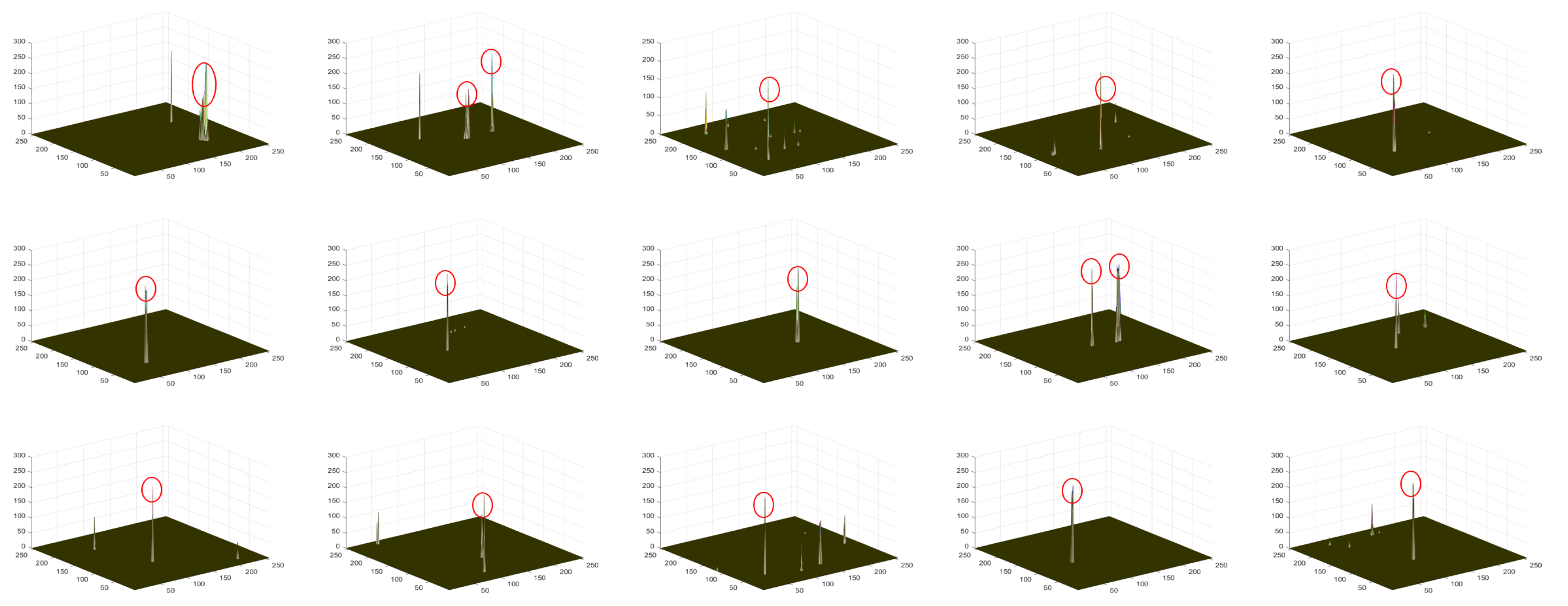
4.4. Detection Capability for Different Scenarios
Robustness to Noise
4.5. Comparison with Other Typical Methods
4.6. Quantitative Comparison of Eleven Methods
4.7. Computation Time
4.8. Validation Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luo, K. Space-Based Infrared Sensor Scheduling with High Uncertainty: Issues and Challenges. Syst. Eng. 2015, 18, 102–113. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Peng, Z.; Zhang, Q.; Guan, A. Extended target tracking using projection curves and matching pel count. Opt. Eng. 2007, 46, 066401. [Google Scholar]
- Kennedy, H.L. Multidimensional digital filters for point-target detection in cluttered infrared scenes. J. Electron. Imaging 2014, 23, 063019. [Google Scholar] [CrossRef][Green Version]
- Grossi, E.; Lops, M.; Venturino, L. A novel dynamic programming algorithm for track-before-detect in radar systems. IEEE Trans. Signal Process. 2013, 61, 2608–2619. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y. Robust infrared small target detection using local steering kernel reconstruction. Pattern Recognit. 2018, 77, 113–125. [Google Scholar] [CrossRef]
- Dong, X.; Huang, X.; Zheng, Y.; Bai, S.; Xu, W. A novel infrared small moving target detection method based on tracking interest points under complicated background. Infrared Phys. Technol. 2014, 65, 36–42. [Google Scholar] [CrossRef]
- Rawat, S.S.; Verma, S.K.; Kumar, Y. Review on recent development in infrared small target detection algorithms. Procedia Comput. Sci. 2020, 167, 2496–2505. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, C.; Liu, B.; Zhang, Y. A kernel-based nonparametric regression method for clutter removal in infrared small-target detection applications. IEEE Geosci. Remote Sens. Lett. 2010, 7, 469–473. [Google Scholar] [CrossRef]
- Reed, I.S.; Gagliardi, R.M.; Stotts, L.B. Optical moving target detection with 3-D matched filtering. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 327–336. [Google Scholar] [CrossRef]
- Dong, X.; Huang, X.; Zheng, Y.; Shen, L.; Bai, S. Infrared dim and small target detecting and tracking method inspired by human visual system. Infrared Phys. Technol. 2014, 62, 100–109. [Google Scholar] [CrossRef]
- Chen, C.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Han, J.; Ma, Y.; Zhou, B.; Fan, F.; Liang, K.; Fang, Y. A robust infrared small target detection algorithm based on human visual system. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2168–2172. [Google Scholar]
- Wei, Y.; You, X.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Bai, X.; Bi, Y. Derivative entropy-based contrast measure for infrared small-target detection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2452–2466. [Google Scholar] [CrossRef]
- Shi, Y.; Wei, Y.; Yao, H.; Pan, D.; Xiao, G. High-boost-based multiscale local contrast measure for infrared small target detection. IEEE Geosci. Remote Sens. Lett. 2017, 15, 33–37. [Google Scholar] [CrossRef]
- Lu, R.; Yang, X.; Li, W.; Fan, J.; Li, D.; Jing, X. Robust infrared small target detection via multidirectional derivative-based weighted contrast measure. IEEE Geosci. Remote Sens. Lett. 2020, 19, 7000105. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Liu, C.; Zhang, H.; Zhao, Q. A local contrast method for infrared small-target detection utilizing a tri-layer window. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1822–1826. [Google Scholar] [CrossRef]
- Zhao, M.; Li, L.; Li, W.; Tao, R.; Li, L.; Zhang, W. Infrared small-target detection based on multiple morphological profiles. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6077–6091. [Google Scholar] [CrossRef]
- Zhang, C.; Li, D.; Qi, J.; Liu, J.; Wang, Y. Infrared Small Target Detection Method with Trajectory Correction Fuze Based on Infrared Image Sensor. Sensors 2021, 21, 4522. [Google Scholar] [CrossRef]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared patch-image model for small target detection in a single image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Song, Y. Infrared small target and background separation via column-wise weighted robust principal component analysis. Infrared Phys. Technol. 2016, 77, 421–430. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Song, Y.; Guo, J. Non-negative infrared patch-image model: Robust target-background separation via partial sum minimization of singular values. Infrared Phys. Technol. 2017, 81, 182–194. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, L.; Zhang, T.; Cao, S.; Peng, Z. Infrared small target detection via non-convex rank approximation minimization joint l2, 1 norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, H.; Liu, Y.; Peng, L.; Yang, C.; Peng, Z. Infrared small target detection based on non-convex optimization with Lp-norm constraint. Remote Sens. 2019, 11, 559. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Z.; Kong, D.; Zhang, P.; He, Y. Infrared dim target detection based on total variation regularization and principal component pursuit. Image Vis. Comput. 2017, 63, 1–9. [Google Scholar] [CrossRef]
- Rawat, S.S.; Alghamdi, S.; Kumar, G.; Alotaibi, Y.; Khalaf, O.I.; Verma, L.P. Infrared small target detection based on partial sum minimization and total variation. Mathematics 2022, 10, 671. [Google Scholar] [CrossRef]
- Zhang, T.; Peng, Z.; Wu, H.; He, Y.; Li, C.; Yang, C. Infrared small target detection via self-regularized weighted sparse model. Neurocomputing 2021, 420, 124–148. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Z.; Kong, D.; He, Y. Infrared dim and small target detection based on stable multisubspace learning in heterogeneous scene. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5481–5493. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y. Reweighted infrared patch-tensor model with both nonlocal and local priors for single-frame small target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3752–3767. [Google Scholar] [CrossRef]
- Goldfarb, D.; Qin, Z. Robust low-rank tensor recovery: Models and algorithms. SIAM J. Matrix Anal. Appl. 2014, 35, 225–253. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Q.; Jin, J.; Shen, Y. Structure tensor total variation-regularized weighted nuclear norm minimization for hyperspectral image mixed denoising. Signal Process. 2017, 131, 202–219. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, Q.; Luo, H.; Hui, B.; Chang, Z.; Zhang, J. Infrared small target detection based on an image-patch tensor model. Infrared Phys. Technol. 2019, 99, 55–63. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, Z. Infrared small target detection based on partial sum of the tensor nuclear norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, L.; Wang, X.; Shen, F.; Pu, T.; Fei, C. Edge and Corner Awareness-Based Spatial–Temporal Tensor Model for Infrared Small-Target Detection. IEEE Trans. Geosci. Remote Sens. 2020, 59, 10708–10724. [Google Scholar] [CrossRef]
- Liu, T.; Yang, J.; Li, B.; Xiao, C.; Sun, Y.; Wang, Y.; An, W. Non-Convex Tensor Low-Rank Approximation for Infrared Small Target Detection. arXiv 2021, arXiv:2105.14974. [Google Scholar]
- Kong, X.; Yang, C.; Cao, S.; Li, C.; Peng, Z. Infrared Small Target Detection via Nonconvex Tensor Fibered Rank Approximation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–21. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Zhou, F.; Barnard, K. Attentional local contrast networks for infrared small target detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9813–9824. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.; Wang, L. Miss detection vs. false alarm: Adversarial learning for small object segmentation in infrared images. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 8509–8518. [Google Scholar]
- Qi, G.; Zhang, Y.; Wang, K.; Mazur, N.; Liu, Y.; Malaviya, D. Small Object Detection Method Based on Adaptive Spatial Parallel Convolution and Fast Multi-Scale Fusion. Remote Sens. 2022, 14, 420. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Zhou, F.; Barnard, K. Asymmetric contextual modulation for infrared small target detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 950–959. [Google Scholar]
- Pang, D.; Shan, T.; Ma, P.; Li, W.; Liu, S.; Tao, R. A novel spatiotemporal saliency method for low-altitude slow small infrared target detection. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Its Appl. 2011, 435, 641–658. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 925–938. [Google Scholar] [CrossRef] [PubMed]
- Martin, C.D.; Shafer, R.; LaRue, B. An order-p tensor factorization with applications in imaging. SIAM J. Sci. Comput. 2013, 35, A474–A490. [Google Scholar] [CrossRef]
- Liu, H.K.; Zhang, L.; Huang, H. Small target detection in infrared videos based on spatio-temporal tensor model. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8689–8700. [Google Scholar] [CrossRef]
- Fang, H.; Chen, M.; Liu, X.; Yao, S. Infrared Small Target Detection with Total Variation and Reweighted Regularization. Math. Probl. Eng. 2020, 2020, 1529704. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, J.; Long, Y.; Shang, Z.; An, W. Infrared patch-tensor model with weighted tensor nuclear norm for small target detection in a single frame. IEEE Access 2018, 6, 76140–76152. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, Y.; Dai, Y. Infrared small target detection via incorporating spatial structural prior into intrinsic tensor sparsity regularization. Digit. Signal Process. 2021, 111, 102966. [Google Scholar] [CrossRef]
- Gao, C.Q.; Tian, J.W.; Wang, P. Generalised-structure-tensor-based infrared small target detection. Electron. Lett. 2008, 44, 1349–1351. [Google Scholar] [CrossRef]
- Brown, M.; Szeliski, R.; Winder, S. Multi-image matching using multi-scale oriented patches. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 510–517. [Google Scholar]
- Liu, J.; He, Z.; Chen, Z.; Shao, L. Tiny and dim infrared target detection based on weighted local contrast. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1780–1784. [Google Scholar] [CrossRef]
- Nie, C.; Wang, H.; Lu, A. Infrared Small Target Detection Based on Prior Constraint Network and Efficient Patch-Tensor Model. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV); Springer: Berlin/Heidelberg, Germany, 2020; pp. 504–517. [Google Scholar]
- Zhou, F.; Wu, Y.; Dai, Y.; Wang, P. Detection of small target using schatten 1/2 quasi-norm regularization with reweighted sparse enhancement in complex infrared scenes. Remote Sens. 2019, 11, 2058. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted L1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Wang, H.; Yang, F.; Zhang, C.; Ren, M. Infrared small target detection based on patch image model with local and global analysis. Int. J. Image Graph. 2018, 18, 1850002. [Google Scholar] [CrossRef]
- Zhu, H.; Ni, H.; Liu, S.; Xu, G.; Deng, L. Tnlrs: Target-aware non-local low-rank modeling with saliency filtering regularization for infrared small target detection. IEEE Trans. Image Process. 2020, 29, 9546–9558. [Google Scholar] [CrossRef] [PubMed]
- Nie, Y.; Li, W.; Zhao, M.; Ran, Q.; Ma, P. Infrared small target detection in image sequences based on temporal low-rank and sparse decomposition. In Proceedings of the Twelfth International Conference on Graphics and Image Processing (ICGIP 2020); International Society for Optics and Photonics: Bellingham, WA, USA, 2021; Volume 11720, p. 117200A. [Google Scholar]
- Xu, W.H.; Zhao, X.L.; Ji, T.Y.; Miao, J.Q.; Ma, T.H.; Wang, S.; Huang, T.Z. Laplace function based nonconvex surrogate for low-rank tensor completion. Signal Process. Image Commun. 2019, 73, 62–69. [Google Scholar] [CrossRef]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3842–3849. [Google Scholar]
- Guan, X.; Zhang, L.; Huang, S.; Peng, Z. Infrared small target detection via non-convex tensor rank surrogate joint local contrast energy. Remote Sens. 2020, 12, 1520. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, Y.; Dai, Y.; Wang, P.; Ni, K. Graph-regularized laplace approximation for detecting small infrared target against complex backgrounds. IEEE Access 2019, 7, 85354–85371. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends. Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Hale, E.T.; Yin, W.; Zhang, Y. Fixed-point continuation for ℓ1-minimization: Methodology and convergence. SIAM J. Optim. 2008, 19, 1107–1130. [Google Scholar] [CrossRef]
- Lu, C.; Tang, J.; Yan, S.; Lin, Z. Generalized nonconvex nonsmooth low-rank minimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 4130–4137. [Google Scholar]
- Guan, X.; Peng, Z.; Huang, S.; Chen, Y. Gaussian scale-space enhanced local contrast measure for small infrared target detection. IEEE Geosci. Remote Sens. Lett. 2019, 17, 327–331. [Google Scholar] [CrossRef]
- Gao, C.; Wang, L.; Xiao, Y.; Zhao, Q.; Meng, D. Infrared small-dim target detection based on Markov random field guided noise modeling. Pattern Recognit. 2018, 76, 463–475. [Google Scholar] [CrossRef]



























| Notation | Instruction |
|---|---|
| X//x/x | Tensor/matrix/vector/scalar |
| X | its th element |
| or | k-th frontal/m-th lateral/n-th horizontal slice |
| the i-th iteration of X | |
| the mode-i unfolding matrix of X | |
| The zero norm of X is the number of non-zero elements | |
| The sum of all non-zero elements in X | |
| The kernel norm of is the sum of all singular values in the matrix | |
| The Frobenius norm of X is the sum of the squares of all values in the tensor and then the square root | |
| Fourier transform of X | |
| Inverse fourier transform of |
| DATA | Total Number of Frames | Average SCR | Data Introduction |
|---|---|---|---|
| DATA 1 (g) | 399 | 6.01 | From far to near, single target, ground background |
| DATA 2 (h) | 399 | 6.29 | From near to far, single target, ground background |
| DATA 3 (n) | 399 | 2.98 | Target by far and near, single target, extended target, target maneuver, ground background |
| DATA 4 (e) | 399 | 1.09 | Low signal-to-noise ratio, target from far to near, single target, ground background |
| DATA 5 (o) | 400 | 3.01 | Single target, target maneuver, open space background |
| Methods | Parameter Settings |
|---|---|
| Top-Hat [9] | Structure size: square, size: 3 × 3 |
| LCM [12] | Window size: 3 × 3 |
| HB-MLCM [16] | Window size: 3 × 3, 5 × 5, 7 × 7, 9 × 9 |
| TLLCM [18] | Window size: 3 × 3 |
| IPI [21] | patch size: 50 × 50, sliding step: 10, |
| RIPT [30] | patch size: 30 × 30, sliding step: 10,, h = 1 |
| NRAM [24] | patch size: |
| PSTNN [34] | patch size: 40 × 40, step: 40, |
| NOLC [25] | patch size: 30 × 30, Slide step: 10, |
| ECA-STT [35] | |
| LOGTNN [37] | patch size: 40 × 40, step: 40, |
| Proposed | patch size: 60 × 60, step: 60, |
| Methods | Seq.1 | Seq.2 | Seq.3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BSF | SCRG | CG | BSF | SCRG | CG | BSF | SCRG | CG | |
| TOPHAT | 1.161 | 2.070 | 36.609 | 1.766 | 1.664 | 0.741 | 2.866 | 1.496 | 11.931 |
| LCM | 0.910 | 1.755 | 0.924 | 0.962 | 0.404 | 26.159 | 1.818 | 1.226 | 7.829 |
| HB-MLCM | 4.437 | 4.577 | 34.967 | 16.089 | 2.192 | 7.018 | 56.681 | 1.472 | 12.021 |
| TLLCM | 6.214 | 1.493 | 3.617 | 22.339 | 2.022 | 8.461 | 28.455 | 1.539 | 9.364 |
| IPI | 8.736 | 3.352 | 20.871 | 11.527 | 2.272 | 28.227 | 19.255 | 1.699 | 21.354 |
| RIPT | 7.452 | 4.714 | 89.268 | 11.124 | 2.537 | 56.258 | 12.982 | 2.343 | 18.282 |
| NRAM | 15.920 | 5.045 | 82.644 | 23.164 | 2.230 | 60.592 | 29.559 | 2.176 | 54.072 |
| PSTNN | 16.424 | 5.056 | 98.977 | 44.915 | 2.315 | 65.115 | 26.359 | 2.594 | 39.214 |
| NOLC | 11.942 | 4.970 | 81.366 | 16.596 | 2.457 | 57.563 | 18.563 | 2.116 | 27.737 |
| ECA-STT | 13.355 | 4.359 | 54.090 | 34.858 | 1.999 | 9.346 | 46.425 | 1.550 | 7.126 |
| LogTFNN | 8.961 | 4.395 | 66.518 | 16.596 | 2.117 | 52.880 | 32.031 | 2.160 | 69.964 |
| Proposed | 33.017 | 5.207 | 101.415 | inf | 3.156 | 72.488 | 134.267 | 2.262 | 64.312 |
| Methods | Seq.4 | Seq.5 | ||||
|---|---|---|---|---|---|---|
| BSF | SCRG | CG | BSF | SCRG | CG | |
| TOPHAT | 2.026 | 1.806 | 26.217 | 3.310 | 1.544 | 7.131 |
| LCM | 1.473 | 0.775 | 15.414 | 1.630 | 0.546 | 21.853 |
| HB-MLCM | 36.361 | 2.177 | 1.016 | 10.049 | 1.887 | 15.365 |
| TLLCM | 30.425 | 2.240 | 6.940 | 27.922 | 1.995 | 23.396 |
| IPI | 26.342 | 2.287 | 0.647 | 14.562 | 1.693 | 4.035 |
| RIPT | 17.980 | 2.712 | 21.021 | 15.258 | 1.594 | 31.900 |
| NRAM | 68.585 | 2.828 | 48.054 | 22.962 | 1.791 | 38.960 |
| PSTNN | inf | 3.304 | 78.458 | 24.206 | 1.956 | 45.227 |
| NOLC | 26.973 | 2.665 | 56.447 | 18.036 | 2.561 | 34.274 |
| ECA-STT | 136.212 | 2.382 | 19.495 | 30.791 | 1.968 | 34.779 |
| LogTFNN | inf | 2.482 | 72.915 | 15.693 | 1.659 | 54.820 |
| Proposed | inf | 2.981 | 78.793 | 134.572 | 1.994 | 55.687 |
| Methods | Seq.1 | Seq.2 | Seq.3 | Seq.4 | Seq.5 |
|---|---|---|---|---|---|
| TOPHAT | 0.0576 | 0.6162 | 0.1894 | 0.5597 | 0.6216 |
| LCM | 0.0179 | 0.0372 | 0.0162 | 0.0048 | 0.0280 |
| HB-MLCM | 0.0969 | 0.9012 | 0.2360 | 0.9709 | 0.3513 |
| TLLCM | 0.0502 | 0.7259 | 0.9241 | 0.9839 | 0.9006 |
| IPI | 0.9687 | 0.7817 | 0.4418 | 0.7609 | 0.8576 |
| RIPT | 0.9668 | 0.7518 | 0.2290 | 0.5082 | 0.6450 |
| NRAM | 0.9596 | 0.6091 | 0.2471 | 0.7530 | 0.8658 |
| PSTNN | 0.9818 | 0.7539 | 0.4552 | 0.7858 | 0.9021 |
| NOLC | 0.9678 | 0.7552 | 0.4214 | 0.7650 | 0.7487 |
| ECA-STT | 0.8631 | 0.6031 | 0.2883 | 0.8489 | 0.8545 |
| LogTFNN | 0.6373 | 0.6519 | 0.6214 | 0.7247 | 0.6299 |
| Proposed | 0.9828 | 0.9092 | 0.9605 | 0.9970 | 0.9999 |
| Methods | Seq.1 | Seq.2 | Seq.3 | Seq.4 | Seq.5 |
|---|---|---|---|---|---|
| TOPHAT | 0.0137 | 0.6162 | 0.1894 | 0.5597 | 0.6216 |
| LCM | 0.0636 | 0.0545 | 0.0463 | 0.0452 | 0.0491 |
| HB-MLCM | 0.0172 | 0.0174 | 0.0145 | 0.0157 | 0.0155 |
| TLLCM | 1.0336 | 1.0293 | 1.0761 | 1.0164 | 0.9962 |
| IPI | 5.5765 | 6.1107 | 6.3536 | 6.0694 | 6.1535 |
| RIPT | 1.6991 | 1.5782 | 1.5513 | 1.5445 | 1.5946 |
| NRAM | 8.2516 | 7.7308 | 7.4015 | 7.4239 | 8.4935 |
| PSTNN | 0.0937 | 0.1420 | 0.0943 | 0.0935 | 0.1005 |
| NOLC | 4.8856 | 5.225 | 2.8089 | 2.5513 | 6.3097 |
| ECA-STT | 3.0169 | 3.1745 | 2.9984 | 3.0237 | 3.0713 |
| LogTFNN | 4.5226 | 4.6316 | 4.5990 | 4.5665 | 4.4655 |
| Proposed | 17.7711 | 17.8345 | 16.0337 | 13.7015 | 14.6458 |
| Methods | Seq.6 | Seq.7 |
|---|---|---|
| TOPHAT | 0.8402 | 0.6381 |
| LCM | 0 | 0.2680 |
| HB-MLCM | 0.0528 | 0.4581 |
| TLLCM | 0.3354 | 0.9694 |
| IPI | 0.9706 | 0.9971 |
| RIPT | 0.9636 | 0.9974 |
| NRAM | 0.9787 | 0.9974 |
| PSTNN | 0.9734 | 0.9967 |
| NOLC | 0.9694 | 0.9974 |
| ECA-STT | 0.9148 | 0.9685 |
| LogTFNN | 0.3695 | 0.9838 |
| Proposed | 0.9928 | 0.9998 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Ma, Y.; Pan, Z.; Liu, Y. Infrared Dim and Small Target Detection from Complex Scenes via Multi-Frame Spatial–Temporal Patch-Tensor Model. Remote Sens. 2022, 14, 2234. https://doi.org/10.3390/rs14092234
Hu Y, Ma Y, Pan Z, Liu Y. Infrared Dim and Small Target Detection from Complex Scenes via Multi-Frame Spatial–Temporal Patch-Tensor Model. Remote Sensing. 2022; 14(9):2234. https://doi.org/10.3390/rs14092234
Chicago/Turabian StyleHu, Yuxin, Yapeng Ma, Zongxu Pan, and Yuhan Liu. 2022. "Infrared Dim and Small Target Detection from Complex Scenes via Multi-Frame Spatial–Temporal Patch-Tensor Model" Remote Sensing 14, no. 9: 2234. https://doi.org/10.3390/rs14092234
APA StyleHu, Y., Ma, Y., Pan, Z., & Liu, Y. (2022). Infrared Dim and Small Target Detection from Complex Scenes via Multi-Frame Spatial–Temporal Patch-Tensor Model. Remote Sensing, 14(9), 2234. https://doi.org/10.3390/rs14092234







