Bayesian Cloud Detection over Land for Climate Data Records
Abstract
:1. Introduction
2. Bayesian Cloud Detection over Land
2.1. Radiative Transfer and Numerical Weather Prediction (NWP) Data
2.2. Uncertainty Specification
2.3. Gaussian Mixed Model
2.4. Surface Characterisation
2.5. Cloudy Probability Distribution Functions (PDFs)
2.6. Aerosol Characterisation
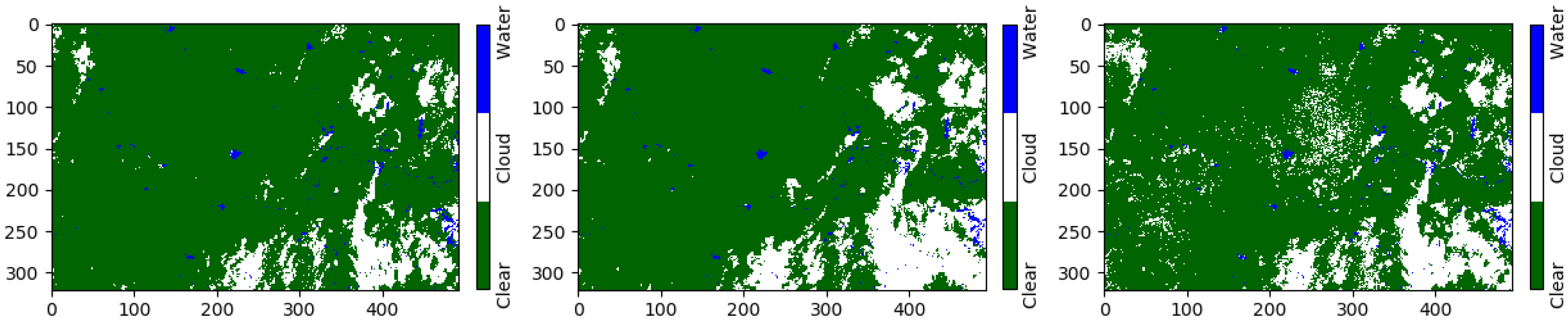
3. Results
4. Application to CDR Generation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Meteorological Organisation. The Global Observing System for Climate: Implementation Needs. GCOS-200. 2016. Available online: https://library.wmo.int/doc_num.php?explnum_id=3417 (accessed on 13 March 2022).
- Plummer, S.; Lecomte, P.; Doherty, M. The ESA Climate Change Initiative (CCI): A European contribution to the generation of the Global Climate Observing System. Remote Sens. Environ. 2017, 203, 2–8. [Google Scholar] [CrossRef]
- Hollmann, R.; Merchant, C.J.; Saunders, R.; Downy, C.; Buchwitz, M.; Cazenave, A.; Chuvieco, E.; Defourny, P.; de Leeuw, G.; Forsberg, R.; et al. THE ESA CLIMATE CHANGE INTIATIVE Satellite Data Records for Essential Climate Variables. Bull. Am. Meteorol. Soc. 2013, 94, 1541–2663. [Google Scholar] [CrossRef] [Green Version]
- Legeais, J.F.; Ablain, M.; Zawadzki, L.; Zuo, H.; Johannessen, J.A.; Scharffenberg, M.G.; Fenoglio-Marc, L.; Fernandes, M.J.; Andersen, O.B.; Rudenko, S.; et al. An improved and homogeneous altimeter sea level record from the ESA Climate Change Initiative. Earth Syst. Sci. Data 2018, 10, 281–301. [Google Scholar] [CrossRef] [Green Version]
- Mousivand, A.; Arsanjani, J.J. Insights on the historical and emerging global land cover changes: The case of ESA-CCI-LC datasets. Appl. Geogr. 2019, 106, 82–92. [Google Scholar] [CrossRef]
- Popp, T.; de Leeuw, G.; Bingen, C.; Bruhl, C.; Capelle, V.; Chedin, A.; Clarisse, L.; Dubovik, O.; Grainger, R.; Heckel, A.; et al. Development, Production and Evaluation of Aerosol Climate Data Records from European Satellite Observations (Aerosol_cci). Remote Sens. 2016, 8, 421. [Google Scholar] [CrossRef] [Green Version]
- Merchant, C.J.; Embury, O.; Bulgin, C.E.; Block, T.; Corlett, G.K.; Fiedler, E.; Good, S.A.; Mittaz, J.; Rayner, N.A.; Berry, D.; et al. Satellite-based time-series of sea-surface temperature since 1981 for climate applications. Sci. Data 2019, 6, 223. [Google Scholar] [CrossRef] [Green Version]
- Sogacheva, L.; Kolmonen, P.; Virtanen, T.H.; Rodriguez, E.; Saponaro, G.; de Leeuw, G. Post-processing to remove residual clouds from aerosol optical depth retrieved using the Advanced Along Track Scanning Radiometer. Atmos. Meas. Tech. 2017, 10, 491–505. [Google Scholar] [CrossRef] [Green Version]
- Lattanzio, A.; Fell, F.; Bennartz, R.; Trigo, I.F.; Schulz, J. Quality assessment and improvement of the EUMETSAT Meteosat Surface Albedo Climate Data Record. Atmos. Meas. Tech. 2015, 8, 4561–4571. [Google Scholar] [CrossRef] [Green Version]
- Wilson, A.M.; Parmentier, B.; Jetz, W. Systematic land cover bias in Collection 5 MODIS cloud mask and derived products—A global overview. Remote Sens. Environ. 2014, 141, 149–154. [Google Scholar] [CrossRef]
- Preimmesberger, W.; Scanlin, T.; Su, C.H.; Gruber, A.; Dorigo, W. Homogenization of Structural Breaks in the Global ESA CCI Soil Moisture Multisatellite Climate Data Record. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2845–2862. [Google Scholar] [CrossRef]
- Melin, F.; Vantrepotte, V.; CChuprin, A.; Grant, M.; Jackson, T.; Sathyendranath, S. Assessing the fitness-for-purpose of satellite multi-mission ocean color climate data record: A protocol to OC-CCI chlorophyll-a data. Remotes Sens. Environ. 2017, 203, 139–151. [Google Scholar] [CrossRef] [PubMed]
- Merchant, C.J.; Harris, A.R.; Maturi, E.; MacCallum, S. Probabilistic physically-based cloud screening of satellite infra-red imagery for operational sea surface temperature retrieval. Q. J. R. Meteorol. Soc. 2005, 131, 2735–2755. [Google Scholar] [CrossRef] [Green Version]
- Bulgin, C.E.; Mittaz, J.P.D.; Embury, O.; Eastwood, S.; Merchant, C.J. Bayesian Cloud Detection for 37 Years of Advanced Very High Resolution Radiometer (AVHRR) Global Area Coverage (GAC) Data. Remote Sens. 2018, 10, 97. [Google Scholar] [CrossRef] [Green Version]
- Zavody, A.M.; Mutlow, C.T.; Llewellyn-Jones, D. Cloud Clearing over the Ocean in the Processing of Data from the Along-Track Scanning Radiometer (ATSR). J. Atmos. Ocean. Technol. 2000, 17, 595–615. [Google Scholar] [CrossRef]
- Frey, R.A.; Ackerman, S.A.; Liu, Y.; Strabala, K.I.; Zhang, H.; Key, J.R.; Wang, Z. Cloud Detection with MODIS. Part I: Improvements in the MODIS Cloud Mask for Collection 5. J. Atmos. Ocean. Tech. 2008, 25, 1057–1072. [Google Scholar] [CrossRef]
- Bulgin, C.E.; Eastwood, S.; Embury, O.; Merchant, C.J.; Donlon, C. Sea surface temperature climate change initiative: Alternative image classification algorithms for sea-ice affected oceans. Remote Sens. Environ. 2015, 162, 396–407. [Google Scholar] [CrossRef]
- Simpson, J.J.; Gobat, J.I. Improved cloud detection for daytime AVHRR scenes over land. Remote Sens. Environ. 1996, 55, 21–49. [Google Scholar] [CrossRef]
- Bulgin, C.E.; Sembhi, H.; Ghent, D.; Remedios, J.J.; Merchant, C.J. Cloud-clearing techniques over land for land-surface temperature retrieval from the Advanced Along-Track Scanning Radiometer. Int. J. Remote Sens. 2014, 35, 3594–3615. [Google Scholar] [CrossRef]
- Herbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on single levels from 1979 to present. Copernic. Clim. Chang. Serv. (C3S) Clim. Data Store (CDS) 2018. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A.; et al. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef] [Green Version]
- Mackie, S.; Embury, O.; Old, C.; Merchant, C.J.; Francis, P. Generalized Bayesian Cloud Detection for Satellite Imagery: Part 1: Technique and Validation for Night-Time Imagery Over Land and Sea. Int. J. Remote Sens. 2010, 31, 2573–2594. [Google Scholar] [CrossRef]
- ECMWF. RTTOV v12 Coefficient File Downloads. EUMETSAT NWP SAF. 2021. Available online: https://nwp-saf.eumetsat.int/site/software/rttov/download/coefficients/coefficient-download/ (accessed on 20 May 2019).
- Hocking, J.; Rayer, P.; Rundle, D.; Saunders, R.; Matricardi, M.; Geer, A.; Brunel, P.; Vidot, J. RTTOV v12 Users Guide. NWP SAF. 2019. NWPSAF-MO-UD-037. Available online: https://nwp-saf.eumetsat.int/site/download/documentation/rtm/docs_rttov12/users_guide_rttov12_v1.3.pdf (accessed on 20 May 2019).
- Borbas, E.; Feltz, M. The RTTOV CAMEL Module: Updating the CAMEL Surface Emissivity Atlas for RTTOV. EUMETSAT NWP SAF NWP-MO-VS-058. 2019. Available online: https://nwp-saf.eumetsat.int/publications/vs_reports/nwpsaf-mo-vs-058.pdf (accessed on 20 May 2019).
- Vidot, J.; Borbas, E. Land surface VIS/NIR BRDF atlas for RTTOV-11: Model and Validation against SEVIRI Land SAF Albedo product. Q. J. R. Meteorol. Soc. 2013, 140, 2186–2196. [Google Scholar] [CrossRef]
- Abrams, M.; Crippen, R.; Fujisada, H. ASTER Global Digital Elevation Model (GDEM) and ASTER Global Water Body Dataset (ASTWBD). Remote Sens. 2020, 12, 1156. [Google Scholar] [CrossRef] [Green Version]
- Santoro, M.; Kirches, G.; Wevers, J.; Boettcher, M.; Brockmann, C.; Lamarche, C.; Bontemps, S. Land Cover CCI, Product User Guide Version 2.0. CCI-LC-PUGv2. 2017. Available online: https://www.esa-landcover-cci.org/?q=webfm_send/84 (accessed on 20 May 2019).
- Ghent, D.J.; Corlett, G.K.; Göttsche, F.-M.; Remedios, J.J. Global land surface temperatures from the Along-Track Scanning Radiometers. J. Geophys. Res. Atmos. 2017, 122, 12167–12193. [Google Scholar] [CrossRef] [Green Version]
- Eresmaa, R.; McNally, A.P. Diverse profile datasets from the ECMWF 137-level short-range forecasts. NWP SAF NWPSAF-EC-TR-017. 2014. Available online: https://nwpsaf.eu/site/download/documentation/rtm/nwpsaf-ec-tr-017.pdf (accessed on 31 March 2021).
- Inness, A.; Ades, M.; Agustí-Panareda, A.; Barré, J.; Benedictow, A.; Blechschmidt, A.-M.; Dominguez, J.J.; Engelen, R.; Eskes, H.; Flemming, J.; et al. The CAMS reanalysis of atmospheric composition. Atmos. Chem. Phys. 2019, 19, 3515–3556. [Google Scholar] [CrossRef] [Green Version]
- Bozzo, A.; Benedetti, A.; Flemming, J.; Kipling, Z.; Rémy, S. CAMS Monthly Mean Aerosol Climatology for Global Models. Available online: https://confluence.ecmwf.int/display/CKB/CAMS+Monthly+Mean+Aerosol+Climatology+for+global+models (accessed on 31 March 2021). [CrossRef]
- Bozzo, A.; Benedetti, A.; Flemming, J.; Kipling, Z.; Rémy, S. An aerosol climatology for global models based on the tropospheric aerosol scheme in the Integrated Forecasting System of ECMWF. Geosci. Model Dev. 2020, 13, 1007–1034. [Google Scholar] [CrossRef]
- Gomez-Chova, L.; Camps-Valls, G.; Calpe-Maravilla, J.; Guanter, L.; Moreno, J. Cloud-Screening Algorithm for ENVISAT/MERIS Multispectral Images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4105–4118. [Google Scholar] [CrossRef]
- Gomez-Chova, L.; Munnoz-Mari, J.; Izquierdo-Verdiguier, E.; Camps-Valls, G.; Calpe, J.; Moreno, J. Cloud Screening with Combined MERIS and AATSR Images. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; p. 761. [Google Scholar] [CrossRef]
- Bulgin, C.E.; Merchant, C.J.; Ghent, D.; Klüser, L.; Popp, T.; Poulsen, C.; Sogacheva, L. Quantifying Uncertainty in Satellite-Retrieved Land Surface Temperature from Cloud Detection Errors. Remote Sens. 2018, 10, 616. [Google Scholar] [CrossRef] [Green Version]
- Birks, A.R. Improvements to the AATSR IPF Relating to Land Surface Temperature Retrieval and Cloud Clearing over Land; AATSR Technical Note; Rutherford Appleton Laboratory: Chilton, UK, 2007. [Google Scholar]
- Závody, A.M.; Mutlow, C.T.; Llewellyn-Jones, D.T. A Radiative Transfer Model for Sea Surface Temperature Retrieval for the Along-Track Scanning Radiometer. J. Geophys. Res. Oceans 1995, 100, 937–952. [Google Scholar] [CrossRef]
- Atmospheric Radiation Measurement (ARM) User Facility. Ceilometer (CEIL). In Southern Great Plains (SGP) Central Facility, Lamont, OK (C1); Morris, V., Zhang, D., Ermold, B., Eds.; 01-09-2002 to 30-07-2017; ARM Data Centre, 1997. Available online: https://www.osti.gov/dataexplorer/biblio/dataset/1181954 (accessed on 20 May 2019).
- Maturilli, M.; Herber, A. Ceilometer Cloud Base Height from Station Ny-Alesund from August 1992 to July 2017, Reference List of 290 Datasets. PANGAEA. 2017. Available online: https://doi.pangaea.de/10.1594/PANGAEA.880300 (accessed on 13 March 2022). [CrossRef]
- Atmospheric Radiation Measurement (ARM) User Facility. Ceilometer (CEIL). In North Slope Alaska (NSA) Central Facility, Barrow AK (C1); Morris, V., Zhang, D., Ermold, B., Eds.; 01-09-2002 to 30-07-2017; ARM Data Centre, 1997. Available online: https://www.osti.gov/dataexplorer/biblio/dataset/1181954 (accessed on 20 May 2019).
- Atmospheric Radiation Measurement (ARM) User Facility. Ceilometer (CEIL). In ARM Mobile Facility (OLI) Oliktok Point, Alaska; AMF3 (M1, C1); Morris, V., Zhang, D., Ermold, B., Eds.; 01-06-2016 to 30-07-2017; ARM Data Centre, 2013. Available online: https://www.osti.gov/dataexplorer/biblio/dataset/1181954 (accessed on 20 May 2019).
- Atmospheric Radiation Measurement (ARM) User Facility. Ceilometer (CEIL). In Tropical Wester Pacific (TWP) Central Facility, Manus I. PNG (C1); Morris, V., Zhang, D., Ermold, B., Eds.; 03-09-2002 to 28-03-2012; ARM Data Centre, 1996. Available online: https://www.osti.gov/dataexplorer/biblio/dataset/1181954 (accessed on 20 May 2019).
- Haeffelin, M.; Barthós, L.; Bock, O.; Baitel, C.; Bony, S.; Bounial, D.; Chepfer, H.; Chiriaco, M.; Cuesta, J.; Delanoö, J.; et al. SIRTA, a ground-based atmospheric observatory for cloud and aerosol research. Ann. Geophys. 2005, 23, 253–275. [Google Scholar] [CrossRef] [Green Version]
- González, G. LCZO—Metrology—ceilometer and meteorological data—Sabana, Bisley—(2000–2016). Hydroshare. 2019. Available online: https://www.hydroshare.org/resources/4a5f560d20004213acf3eb52cca93f67 (accessed on 17 April 2020).
- Ackerman, S.A.; Menzel, P.; Frey, R.; Baum, B. MODIS Atmosphere L2 Cloud Mask Product; NASA MODIS Adaptive Processing System, Goddard Space Flight Centre: Greenbelt, MD, USA, 2017. [Google Scholar] [CrossRef]
- ACRI-ST IPF Team. Product Data Format Specification—SLSTR Level 1 Products. In Preparation and Operations of the Mission Performance Centre (MPC) for the Copernicus Sentinel-3 Mission; ACRI-ST IPF Team, 2019; Available online: https://sentinels.copernicus.eu/web/sentinel/user-guides/sentinel-3-slstr/document-library/-/asset_publisher/fgeRuiak1n39/content/id/3402065 (accessed on 17 April 2020).



| Channels (μm) | Dimension | Range | No. of Bins | Time | |
|---|---|---|---|---|---|
| 1 | 11.0, 12.0 | Biome | 1–8 | 7 | Day |
| Solar zenith angle | 0–180° | 2 | |||
| Atmospheric path length | 1–2.4 | 4 | |||
| NWP surface temperature | 240–330 K | 90 | |||
| 11.0–12.0 μm channel difference | −1–6 K | 35 | |||
| 11.0 μm-NWP surface temperature | −15–15 K | 30 | |||
| 2 | 3.7, 11.0, 12.0 | Biome | 1–8 | 7 | Night |
| Solar zenith angle | 90–180° | 1 | |||
| Atmospheric path length | 1–2.4 | 4 | |||
| NWP surface temperature | 240–330 K | 90 | |||
| 3.7–11.0 μm channel difference | −6–10 K | 80 | |||
| 11.0–12.0 μm channel difference | −1–6 K | 35 | |||
| 11.0 μm-NWP surface temperature | −15–15 K | 30 | |||
| 3 | 0.6, 0.8, 1.6 | Biome | 1–8 | 7 | Day |
| Solar zenith angle | 0–95° | 38 | |||
| Atmospheric path length | 1–2.4 | 4 | |||
| 1.6 μm channel | 0–1 | 50 | |||
| 0.8 μm channel | 0–1 | 50 | |||
| 0.6–0.8 μm channel difference | −0.5–0.2 | 35 |
| Biome | Name | Land Cover CCI Classes | ALB2 Classes |
|---|---|---|---|
| 1 | Cropland | 10, 11, 12, 20, 30, 40, 100, 110 | - |
| 2 | Forest | 50, 60, 61, 62, 70, 71, 72, 80, 81, 82, 90 | - |
| 3 | Shrubland | 120, 121, 122, 130, 140, 150, 151, 152, 153 | - |
| 4 | Flooded | 160, 170, 180 | - |
| 5 | Urban | 190 | - |
| 6 | Bare Soil | 200, 201, 202 | 20, 21, 22, 23, 24, 25 |
| 7 | Snow and Ice | 220 | - |
| Scene | Location | Date | Orbit Number | Day/Night | Project |
|---|---|---|---|---|---|
| 1 | China | 21/05/2007 | 27304 | Night | GlobT |
| 2 | Russia | 22/05/2007 | 27314 | Day | GlobT |
| 3 | Florida, USA | 23/05/2007 | 27333 | Day | GlobT |
| 4 | UK | 23/08/2007 | 28647 | Day | GlobT |
| 5 | Algeria | 11/06/2010 | 43290 | Day | GlobT |
| 6 | Ukraine | 05/08/2010 | 44083 | Night | GlobT |
| 7 | Antarctica | 08/08/2010 | 44121 | Night | GlobT |
| 8 | Mauritania | 08/08/2010 | 44128 | Night | GlobT |
| 9 | Canada | 07/06/2011 | 48474 | Day | GlobT |
| 10 | Uruguay | 11/11/2009 | 40250 | Night | GlobT |
| 11 | Brazil | 06/06/2004 | 11858 | Day | SYNERGY |
| 12 | Brazil | 26/05/2005 | 17369 | Day | SYNERGY |
| 13 | Oklahoma, USA | 09/08/2004 | 12776 | Day | SYNERGY |
| 14 | Oklahoma, USA | 16/05/2005 | 16784 | Day | SYNERGY |
| 15 | Oklahoma, USA | 25/07/2005 | 17786 | Day | SYNERGY |
| 16 | Oklahoma, USA | 05/06/2006 | 22295 | Day | SYNERGY |
| 17 | Oklahoma, USA | 08/10/2007 | 29309 | Day | SYNERGY |
| 18 | Burkina Faso | 28/11/2002 | 03897 | Day | SYNERGY |
| 19 | Burkina Faso | 01/12/2002 | 03941 | Day | SYNERGY |
| 20 | Burkina Faso | 02/01/2003 | 04398 | Day | SYNERGY |
| 21 | Burkina Faso | 21/01/2003 | 04670 | Day | SYNERGY |
| 22 | Burkina Faso | 15/07/2003 | 07176 | Day | SYNERGY |
| 23 | Zambia | 15/01/2003 | 04583 | Day | SYNERGY |
| 24 | Zambia | 09/07/2003 | 07088 | Day | SYNERGY |
| 25 | Zambia | 17/11/2003 | 08090 | Day | SYNERGY |
| 26 | Russia | 03/06/2004 | 11810 | Day | SYNERGY |
| 27 | Russia | 12/08/2004 | 12812 | Day | SYNERGY |
| 28 | Russia | 23/06/2005 | 17321 | Day | SYNERGY |
| 29 | Russia | 06/10/2005 | 18824 | Day | SYNERGY |
| 30 | Russia | 21/09/2006 | 23834 | Day | SYNERGY |
| 31 | Russia | 02/08/2007 | 28343 | Day | SYNERGY |
| Performance Metric | Bayesian Cloud Detection (%) | Operational Cloud Detection (%) |
|---|---|---|
| Percentage of Perfect Classification | 86.6 | 81.0 |
| Hit Rate | 93.9 | 86.0 |
| False Alarm Rate | 16.7 | 21.6 |
| True Skill Score | 77.2 | 64.7 |
| Confusion Matrix | Manual Mask Cloud | Manual Mask Clear |
|---|---|---|
| Bayesian Cloud | 1,437,732 | 570,659 |
| Bayesian Clear | 93,099 | 2,856,615 |
| Operational Cloud | 1,316,944 | 729,595 |
| Operational Clear | 213,887 | 2,697,679 |
| Station | Country | Latitude (Degrees) | Longitude (Degrees) | Frequency of Observations |
|---|---|---|---|---|
| Bingley | UK | 53.8 | −1.9 | 1 min |
| Coleshill | UK | 52.5 | −1.7 | 1 min |
| North Slope | Alaska | 71.3 | −156.6/−156.7 | 35 s |
| Ny Alesund | Norway | 78.9 | 11.9 | 5 min |
| Oliktok Point | Greenland | 70.5 | −149.9 | 30 s |
| Paris | France | 48.7 | 2.2 | 3 s |
| Sabana | Puerto Rico | 18.3 | −65.7 | 1 h |
| Southern Great Plains | USA | 36.6 | −97.5 | 1 min |
| Tropical West Pacific | Papua New Guinea | −2.1 | 147.4 | 1 min |
| University of Reading | UK | 51.4 | 0.9 | 1 min |
| Location | ATSR-2 | AATSR | AATSR | MODIS | MODIS | SLSTR |
|---|---|---|---|---|---|---|
| Bingley, UK | - | - | 94.4 | 92.8 | 93.3 | 96.1 |
| Coleshill, UK | - | - | 89.7 | 90.9 | 92.4 | 92.7 |
| North Slope Alaska | 77.5 | 83.3 | 78.8 | 95.2 | 95.0 | 91.4 |
| Ny Alesund | 86.1 | 87.2 | 88.9 | 95.2 | 94.6 | 96.0 |
| Oliktok Point Alaska | - | - | - | - | 95.7 | 94.5 |
| Paris | - | - | - | - | 96.2 | 98.5 |
| Puerto Rico | - | - | - | - | 100.0 | 100.0 |
| Southern Great Plains | 91.9 | 96.3 | 90.1 | 87.4 | 89.9 | 97.2 |
| Tropical West Pacific | 76.5 | 70.0 | 83.9 | 84.8 | - | - |
| University of Reading, UK | - | - | - | - | 91.9 | 95.5 |
| Location | ATSR-2 | AATSR | AATSR | MODIS | MODIS | SLSTR |
|---|---|---|---|---|---|---|
| Bingley, UK | - | - | 36 | 125 | 570 | 563 |
| Coleshill, UK | - | - | 29 | 110 | 542 | 547 |
| North Slope Alaska | 120 | 102 | 170 | 673 | 686 | 455 |
| Ny Alesund | 532 | 501 | 973 | 2147 | 2156 | 2231 |
| Oliktok Point Alaska | - | - | - | - | 515 | 327 |
| Paris | - | - | - | - | 292 | 326 |
| Puerto Rico | - | - | - | - | 10 | 11 |
| Southern Great Plains | 62 | 54 | 81 | 174 | 189 | 290 |
| Tropical West Pacific | 17 | 30 | 87 | 151 | - | - |
| University of Reading, UK | - | - | - | - | 405 | 445 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulgin, C.E.; Embury, O.; Maidment, R.I.; Merchant, C.J. Bayesian Cloud Detection over Land for Climate Data Records. Remote Sens. 2022, 14, 2231. https://doi.org/10.3390/rs14092231
Bulgin CE, Embury O, Maidment RI, Merchant CJ. Bayesian Cloud Detection over Land for Climate Data Records. Remote Sensing. 2022; 14(9):2231. https://doi.org/10.3390/rs14092231
Chicago/Turabian StyleBulgin, Claire E., Owen Embury, Ross I. Maidment, and Christopher J. Merchant. 2022. "Bayesian Cloud Detection over Land for Climate Data Records" Remote Sensing 14, no. 9: 2231. https://doi.org/10.3390/rs14092231
APA StyleBulgin, C. E., Embury, O., Maidment, R. I., & Merchant, C. J. (2022). Bayesian Cloud Detection over Land for Climate Data Records. Remote Sensing, 14(9), 2231. https://doi.org/10.3390/rs14092231






