An AR Geo-Registration Algorithm for UAV TIR Video Streams Based on Dual-Antenna RTK-GPS
Abstract
:1. Introduction
2. Related Research
3. Method
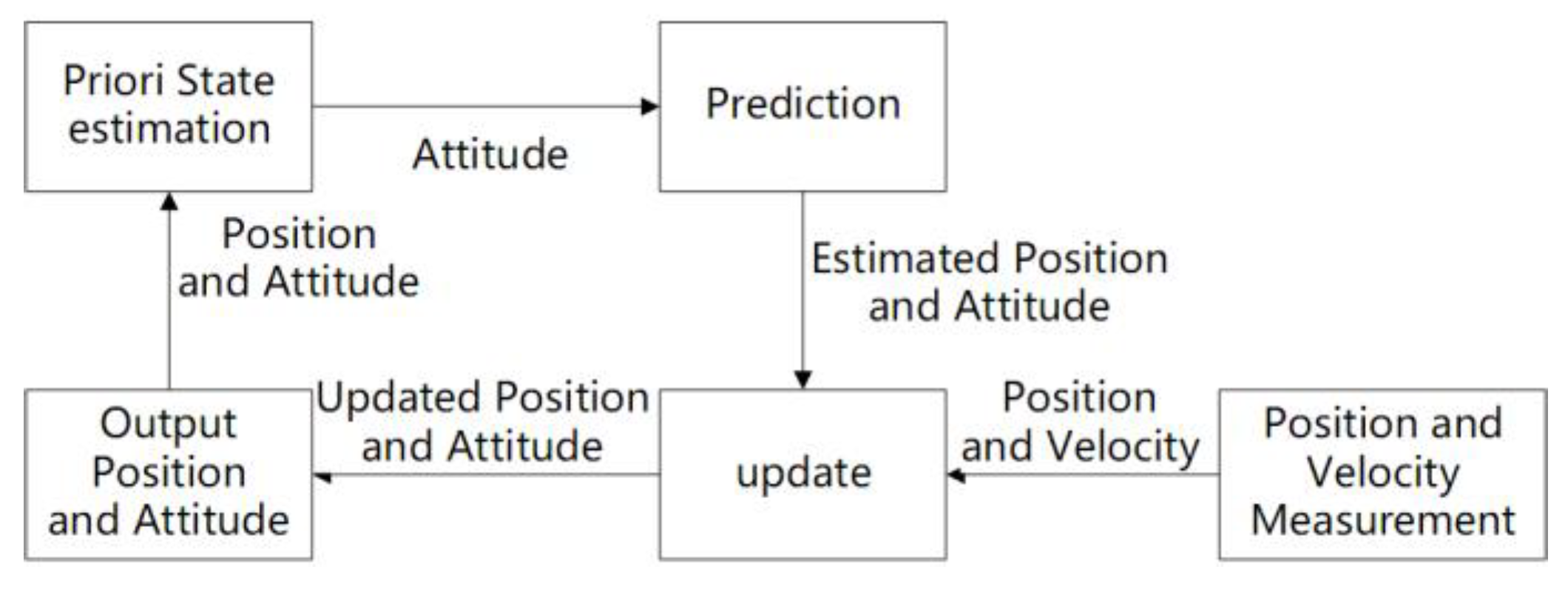
3.1. Augmented Reality Geo-Registration Based on Position and Posture Sensor Data
3.2. The Basic Principle of Extended Kalman Filtering
3.3. An Improved Extended Kalman Filter Algorithm with RTK Heading
3.4. Camera Pose Calculation for Geo-Registration
3.5. Error Analysis of Position and Attitude Sensor Data for Geo-Registration
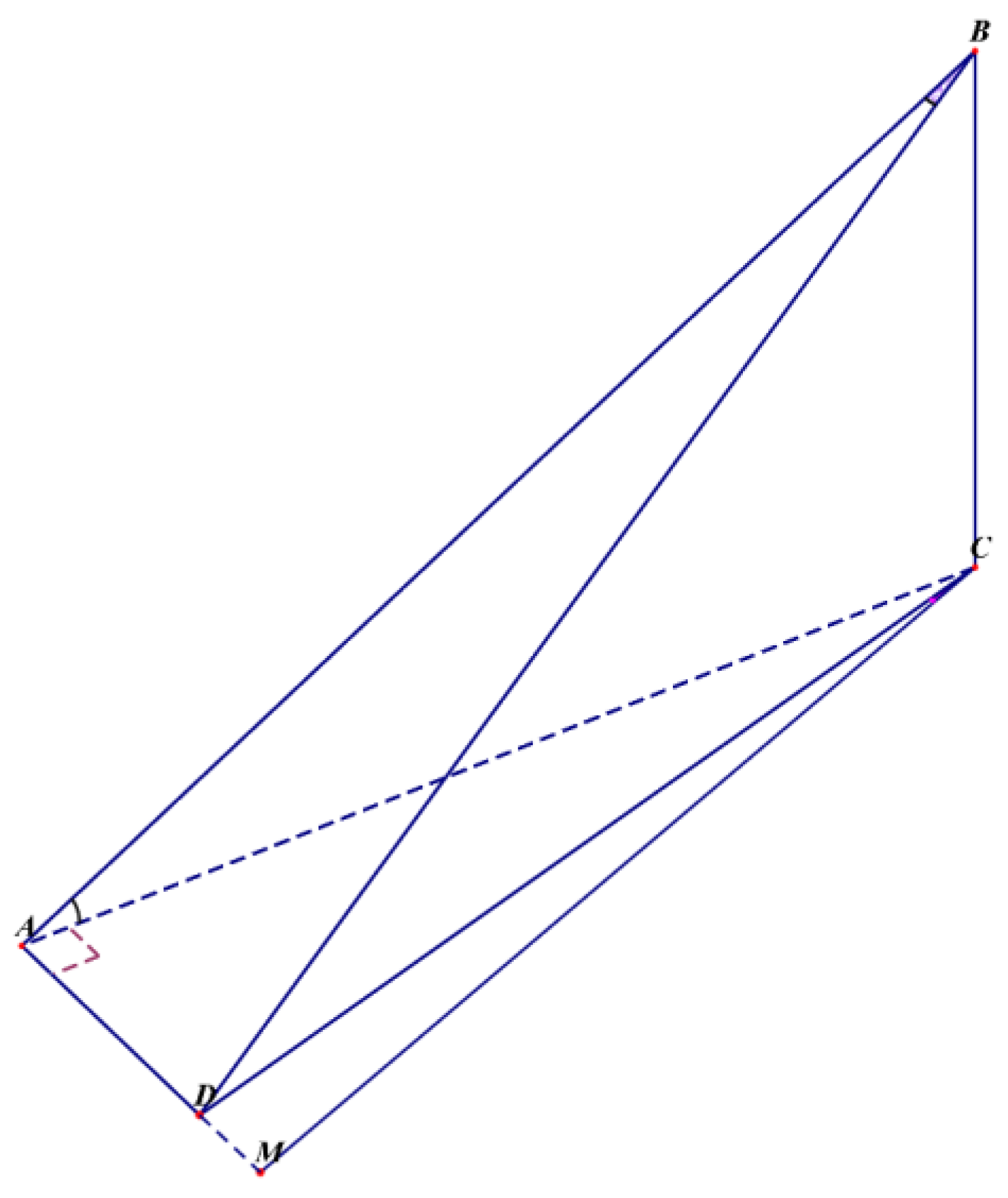
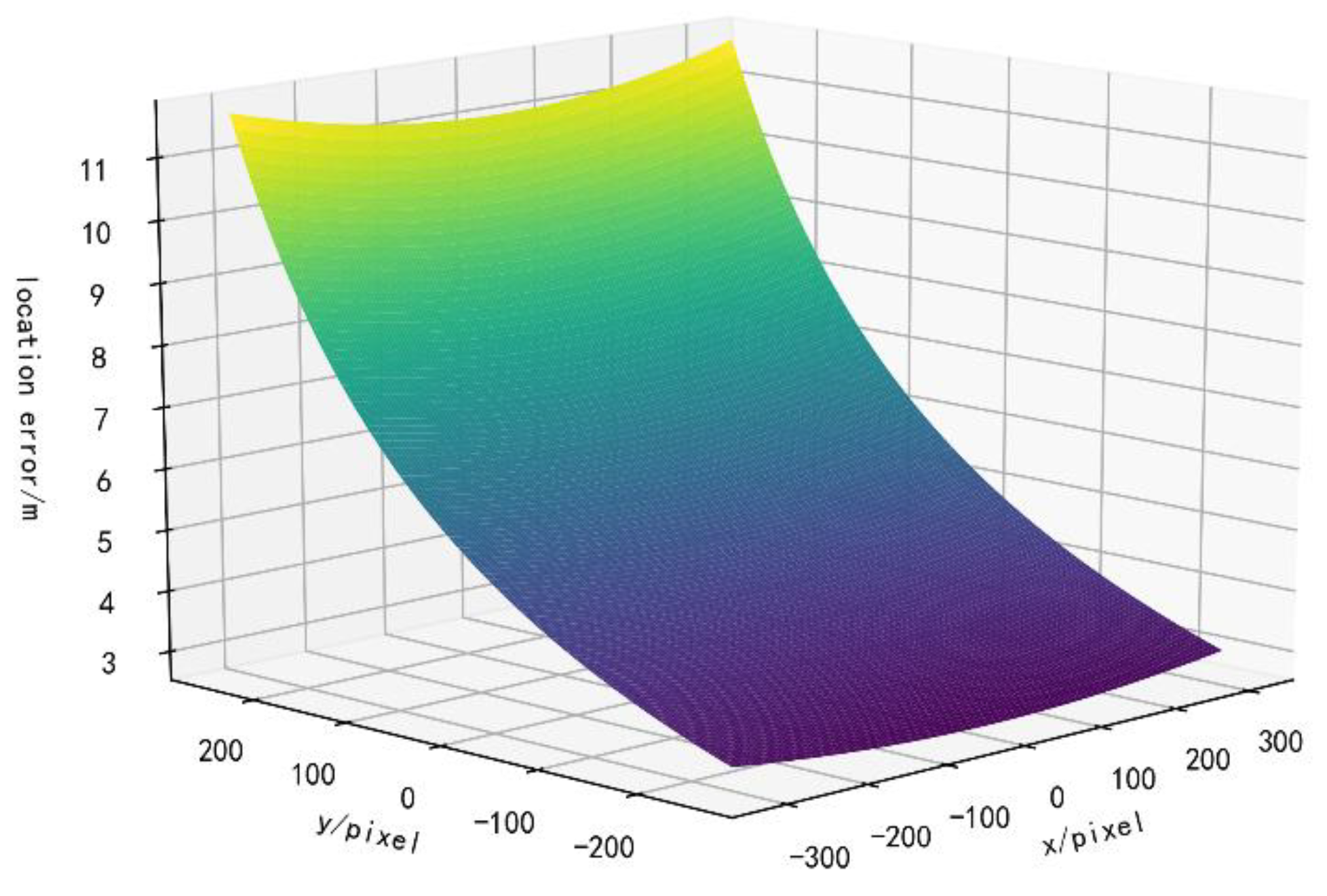
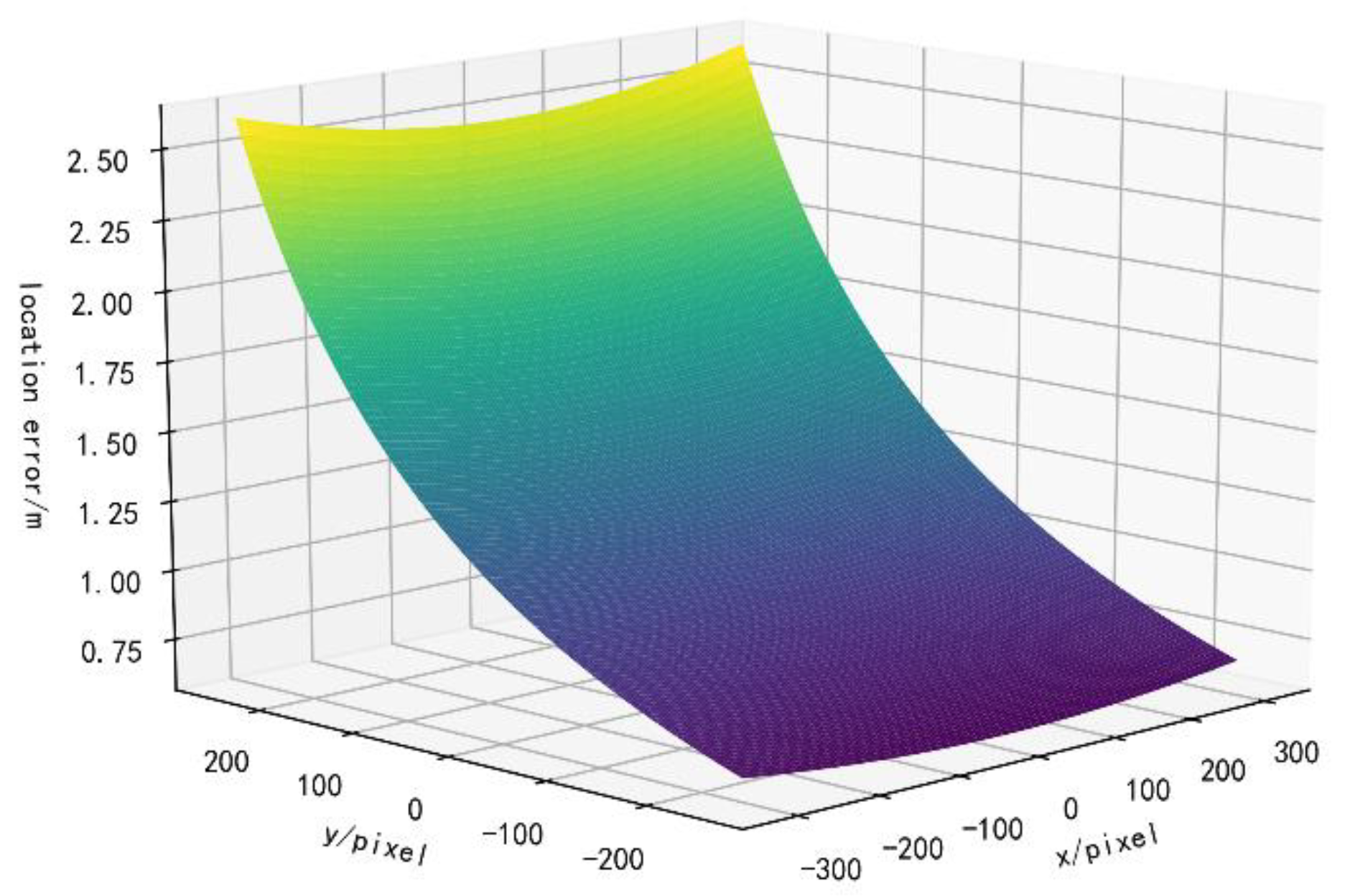
3.5.1. The Effect of the Camera Position Error on the Registration Accuracy
3.5.2. The Effect of the Camera Height Error on the Registration Accuracy
3.5.3. Effect of the Camera Attitude Error on the Registration Accuracy
4. Experiments
4.1. Experimental Platform
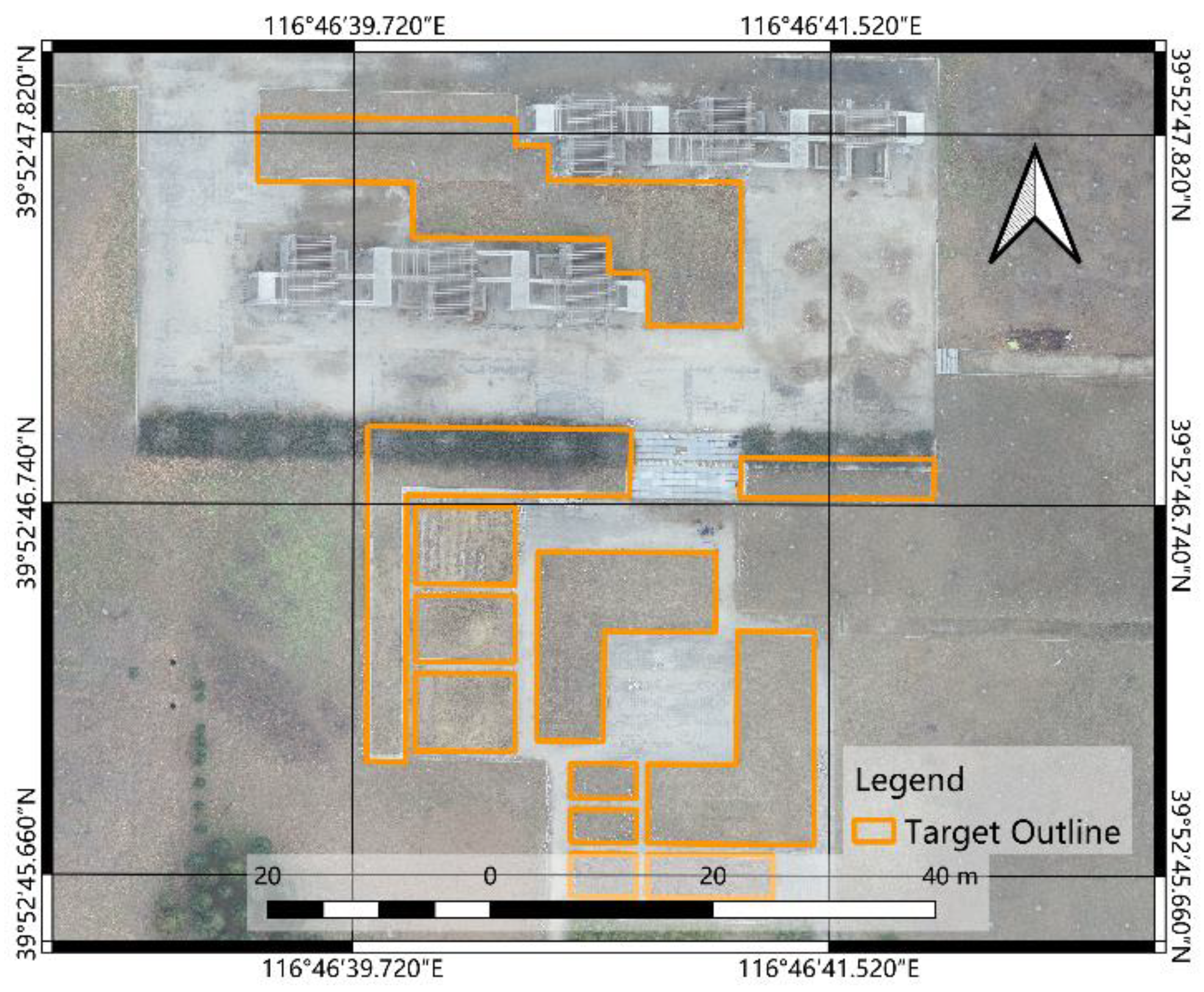
4.2. Experimental Area and Geographic Data Collection
4.3. TIR Video and UAV Flight Data Acquisition
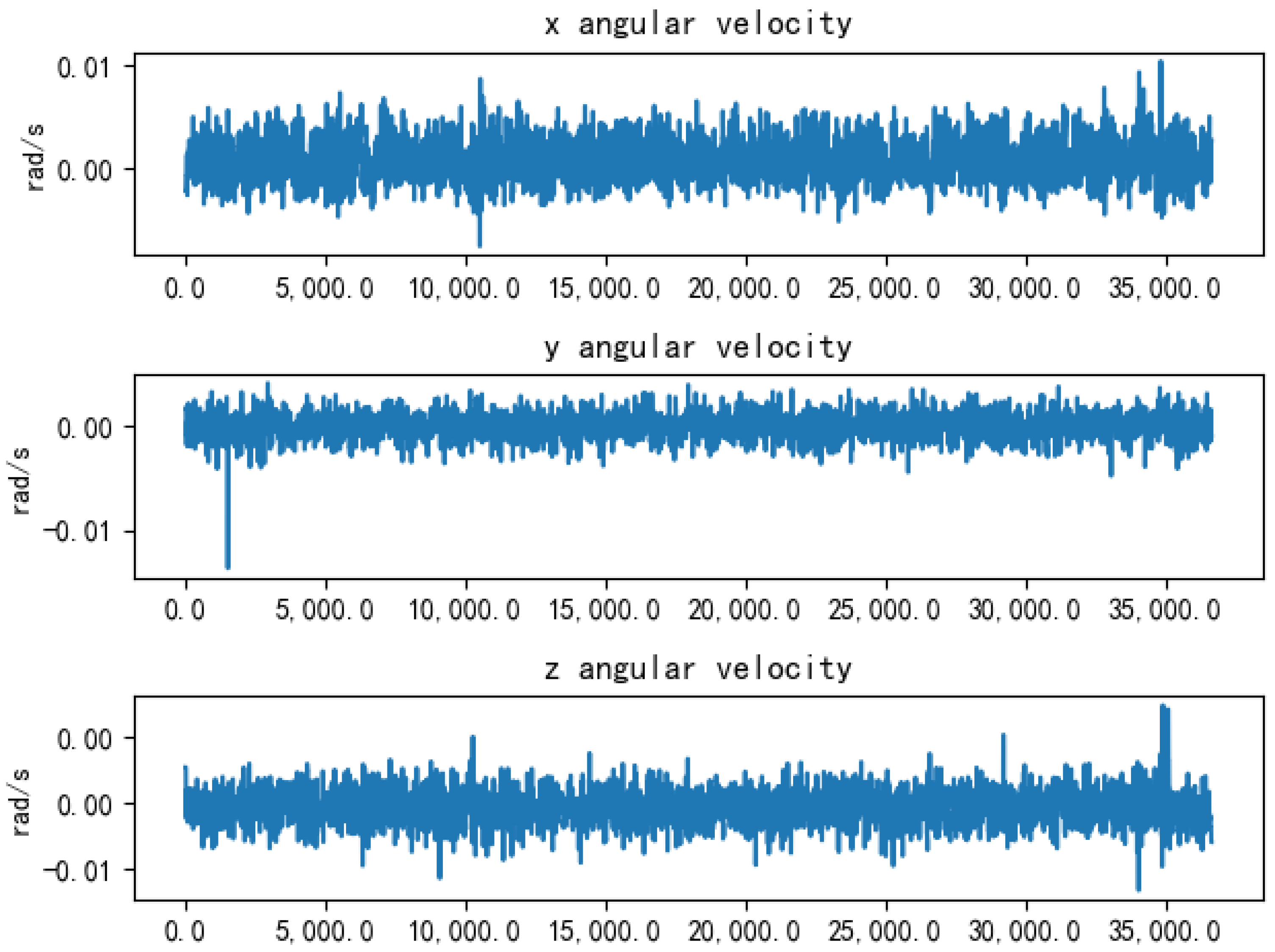
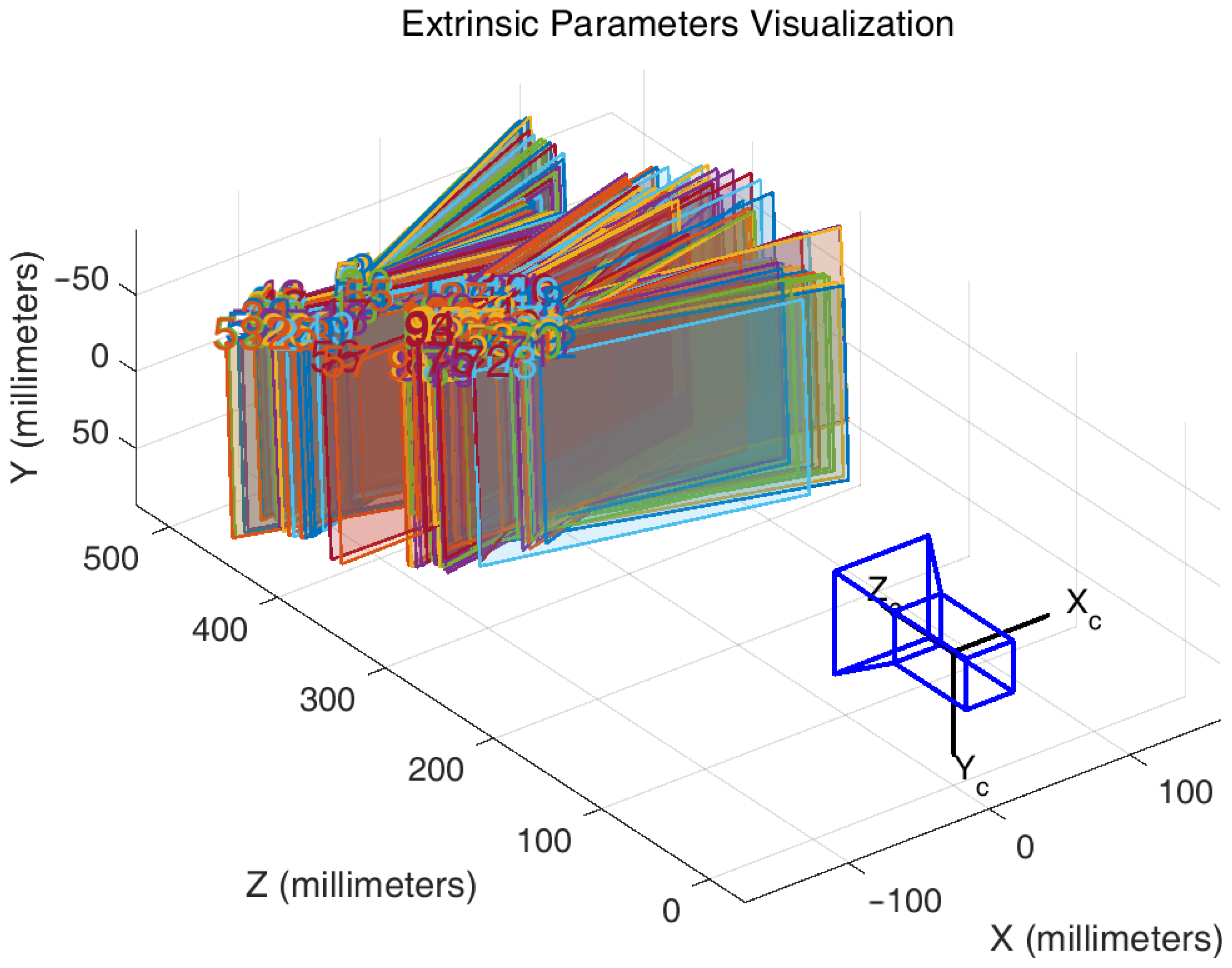
4.4. IMU Error Parameter Acquisition
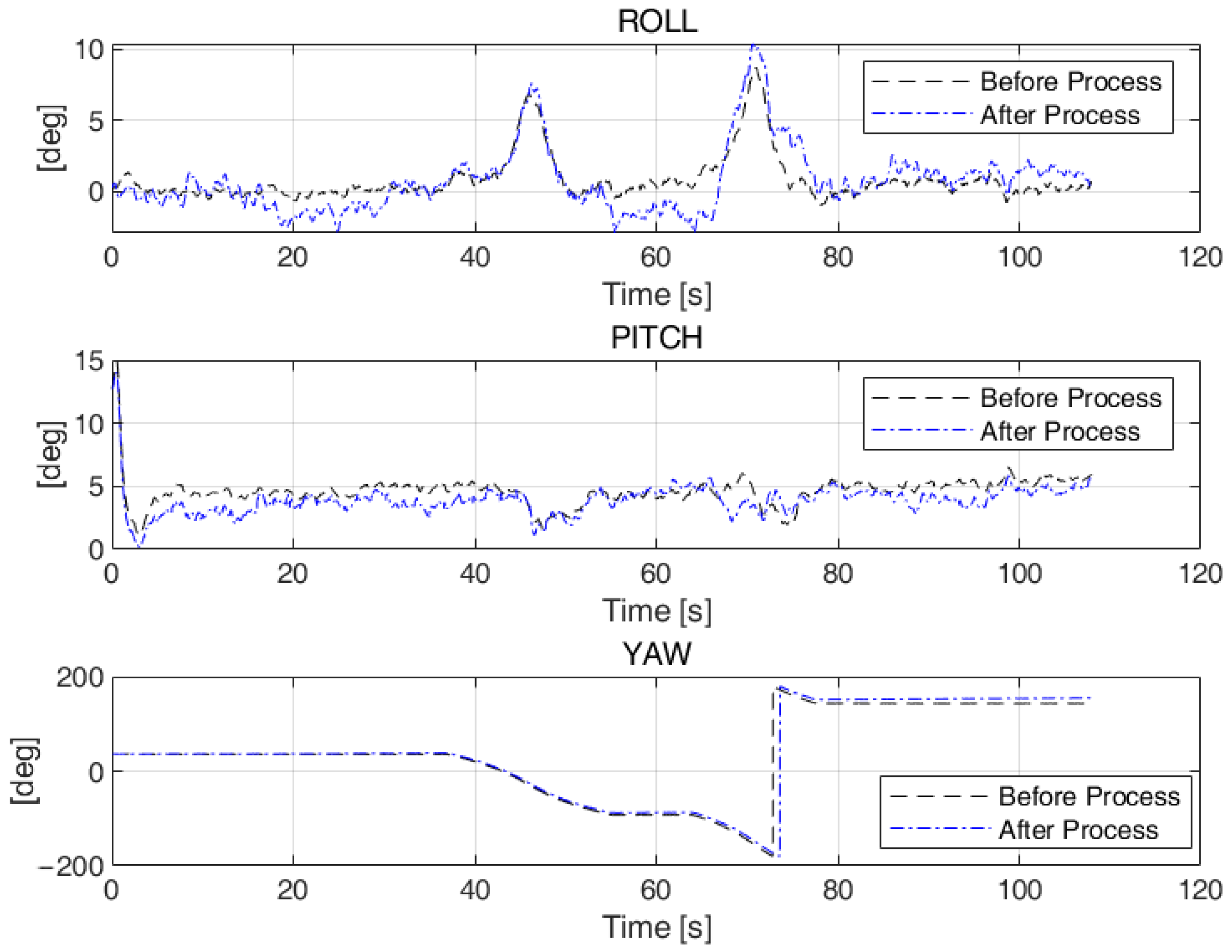
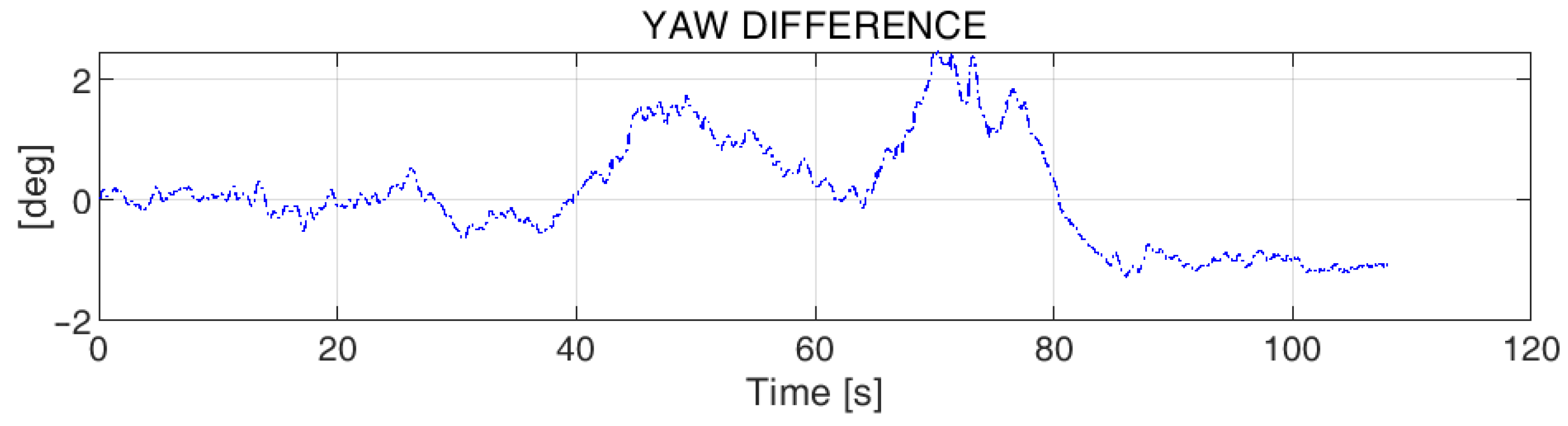
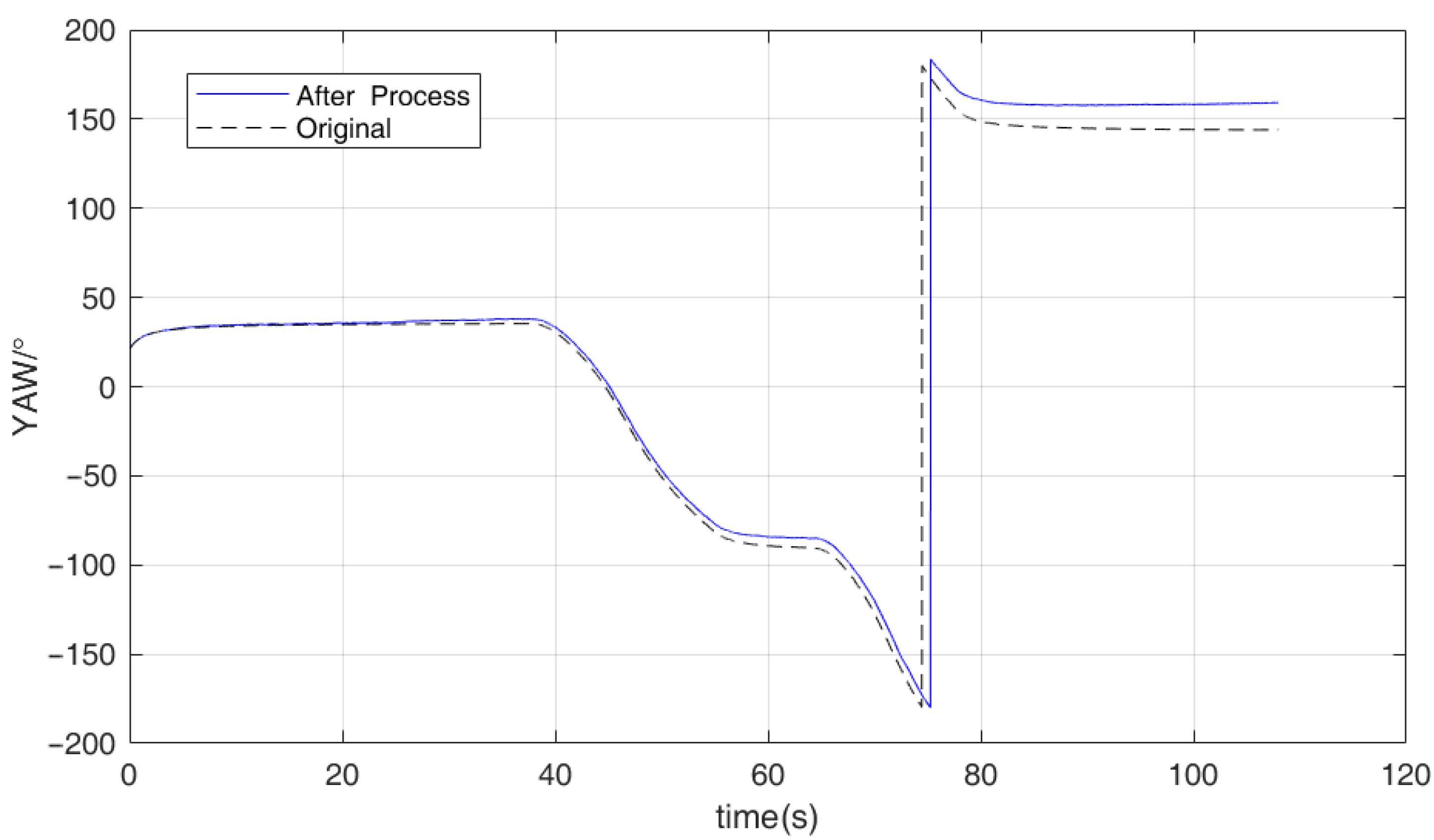
4.5. UAV Attitude Data Enhancement Results
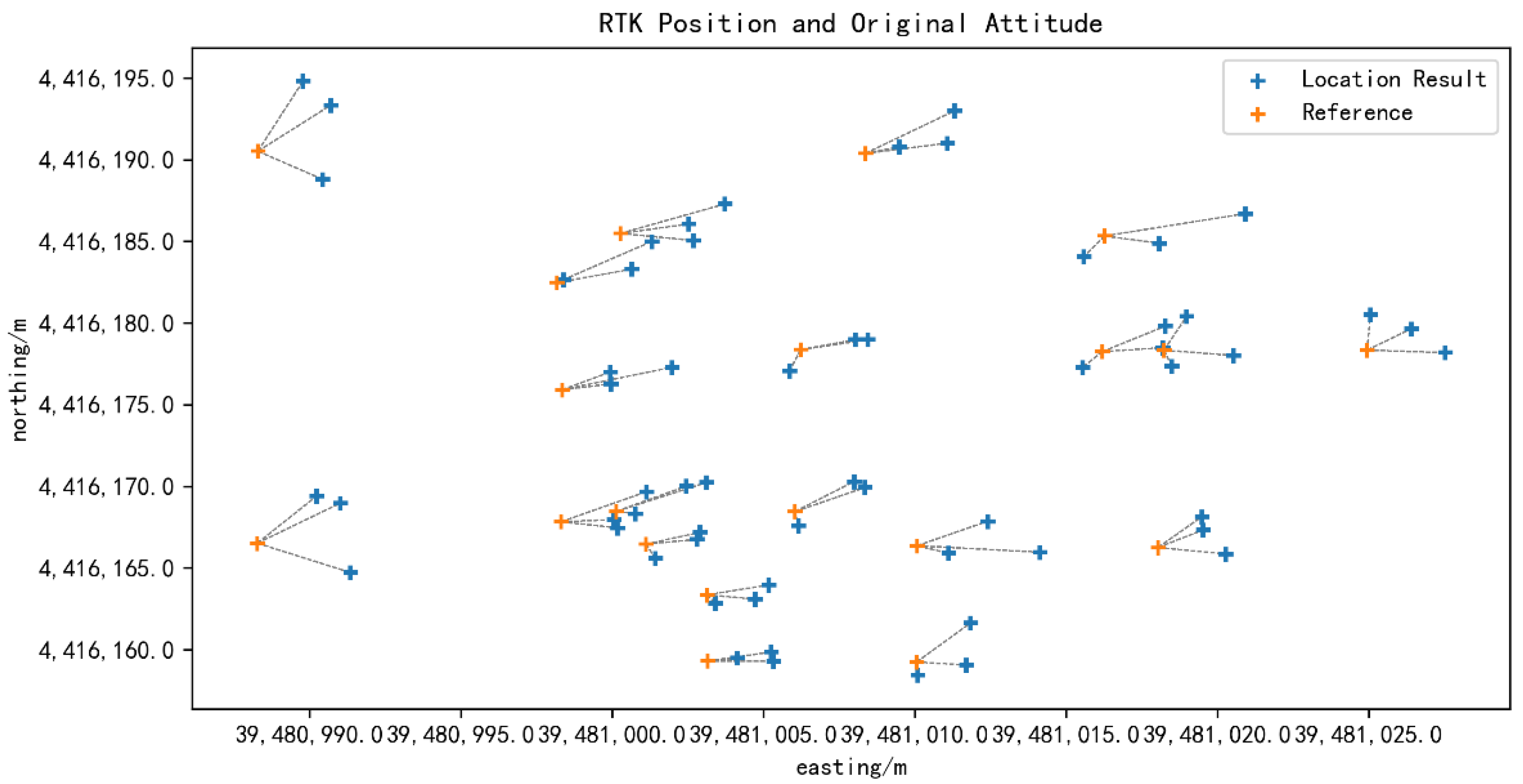
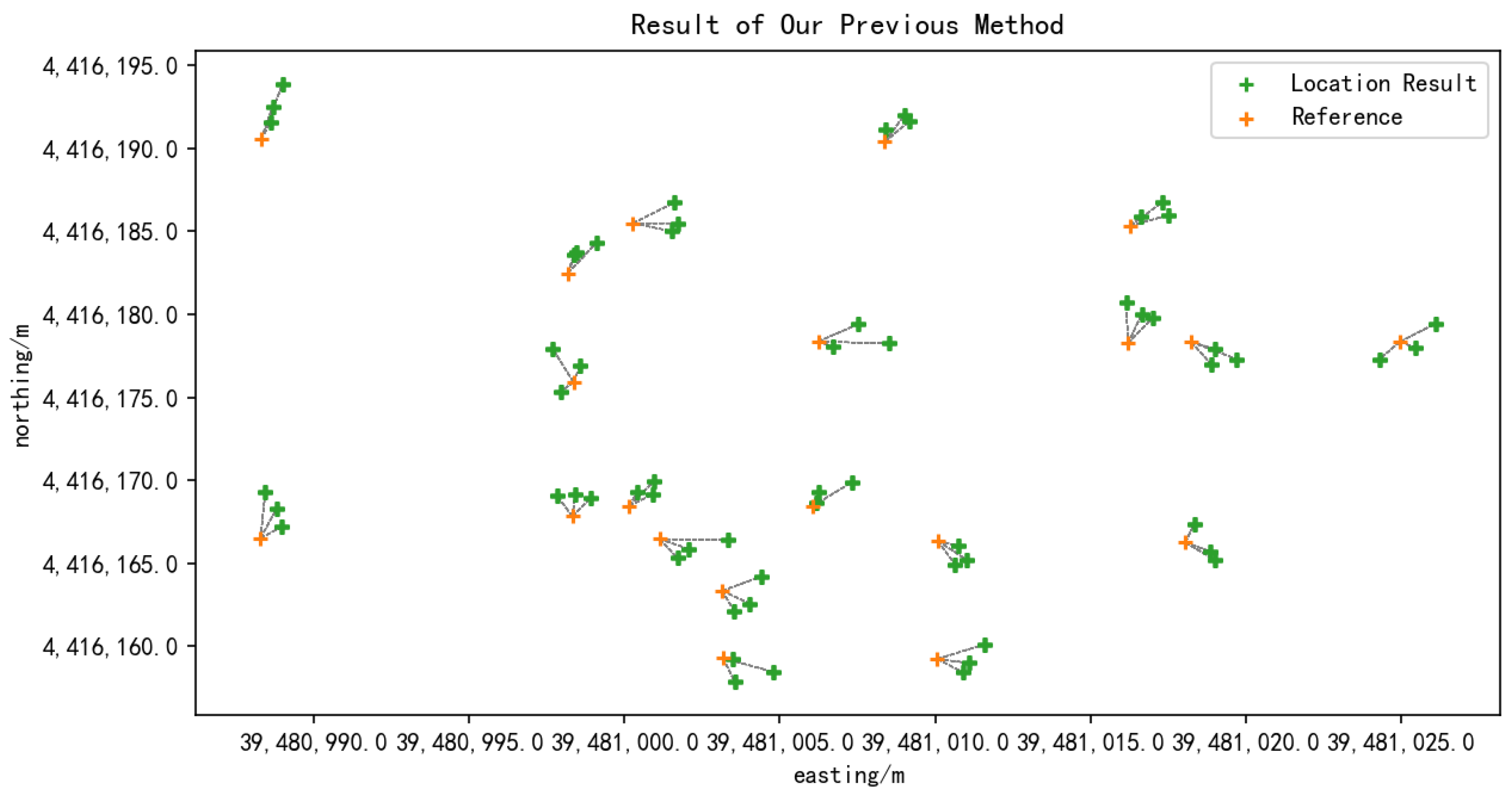
4.6. High-Precision Geo-Registration Results of UAV TIR Video
5. Assessment and Discussion
5.1. Geo-Registration Accuracy Assessment
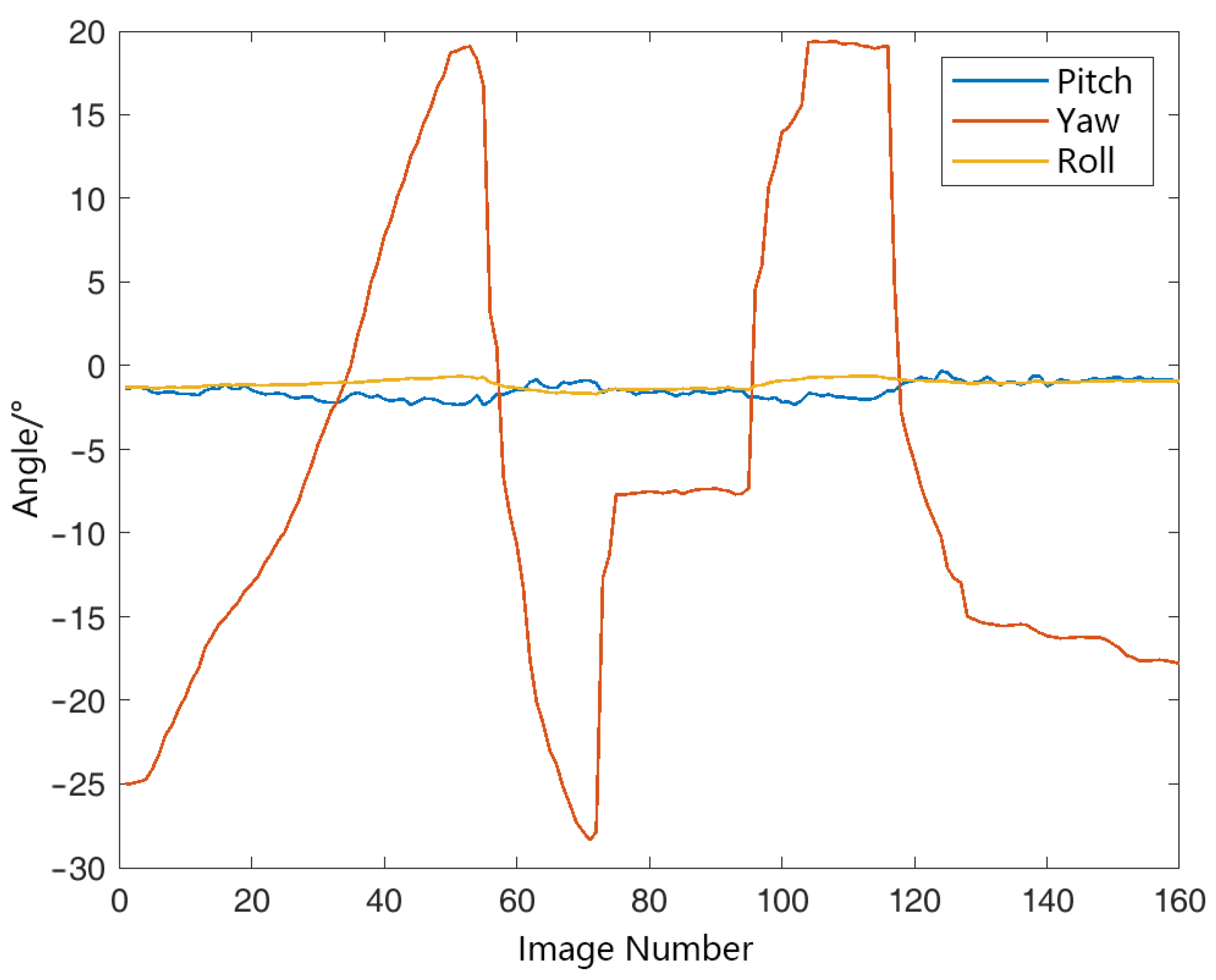
5.2. Evaluation of the Airborne Gimbal Stabilization Effect
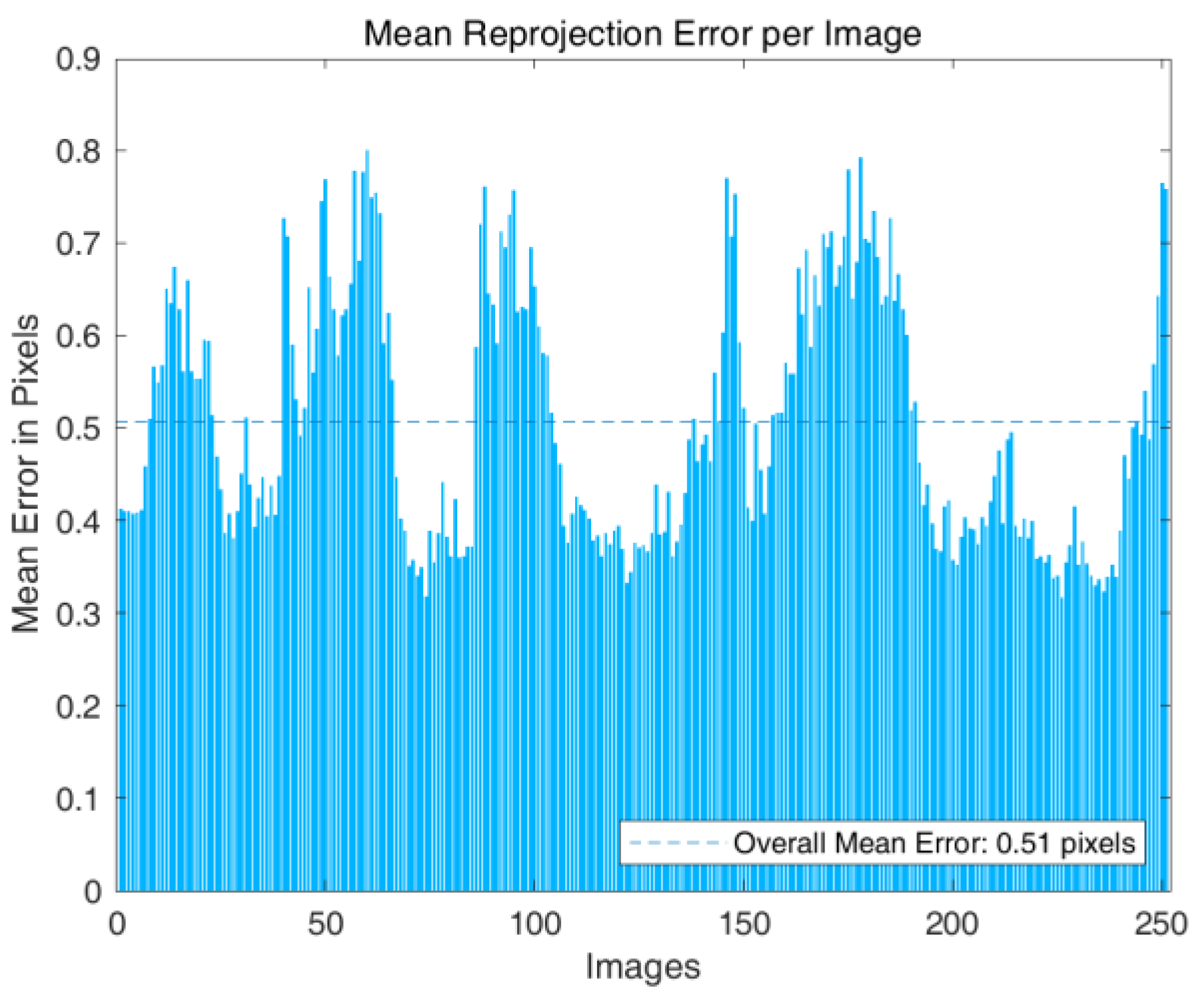
5.3. Assessment and Correction of Lens Distortion
5.4. The Effect of a Sudden Change in the Body Attitude
- As mentioned in Section 3, the input GNSS position has a median filter to deal with a sudden position change in the UAV body.
- A sudden change means that the effect may have a short impact time. Thus, the error caused by the sudden change may also last for a very short time, which means that the working state of the EKF will quickly return to being steady. In our consideration, this can be tolerated during the process. The registration can quickly return to normal and continue to provide accurate results.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Han, Y.; Hao, D.; Lv, Z. ARGIS-based outdoor underground pipeline information system. J. Vis. Commun. Image Represent. 2016, 40, 779–790. [Google Scholar] [CrossRef]
- Agrawal, A.; Cleland-Huang, J. RescueAR: Augmented reality supported collaboration for UAV driven emergency response systems. arXiv 2021, arXiv:2110.00180. Available online: https://arxiv.org/abs/2110.00180 (accessed on 16 March 2022).
- Ribeiro, R.; Ramos, J.; Safadinho, D.; Reis, A.; Rabadão, C.; Barroso, J.; Pereira, A. Web AR solution for UAV pilot training and usability testing. Sensors 2021, 21, 1456. [Google Scholar] [CrossRef] [PubMed]
- Misse, E.S.; Villacrés, S.A.; Velasco, P.M.; Andaluz, V.H. Augmented reality system for the assistance of unmanned aerial vehicles. In Proceedings of the 2020 15th Iberian Conference on Information Systems and Technologies (CISTI), Seville, Spain, 24–27 June 2020; pp. 1–6. [Google Scholar]
- Jill, L.D.; Justin, R.; Nathan, R.; Michael, A.G. Comparing situation awareness for two unmanned aerial vehicle human interface approaches. In Proceedings of the IEEE International Workshop on Safety, Security and Rescue Robotics (SSRR), Undefined, 22–24 August 2006. [Google Scholar]
- Foyle, D.C.; Andre, A.D.; Hooey, B.L. Situation awareness in an augmented reality cockpit: Design, viewpoints and cognitive glue. In Proceedings of the 11th International Conference on Human Computer Interaction, Las Vegas, NV, USA, 22–27 July 2005; pp. 3–9. [Google Scholar]
- Sadeghi-Niaraki, A.; Choi, S.-M. A survey of marker-less tracking and registration techniques for health & Environmental applications to augmented reality and ubiquitous geospatial Information systems. Sensors 2020, 20, 2997. [Google Scholar]
- Liu, W.; Wang, C.; Zang, Y.; Lai, S.H.; Weng, D.; Bian, X.; Lin, X.; Shen, X.; Li, J. Ground camera images and UAV 3D model registration for outdoor augmented reality. In Proceedings of the 2019 IEEE Conference on Virtual Reality and 3D User Interfaces (VR), Osaka, Japan, 23–27 March 2019; pp. 1050–1051. [Google Scholar]
- Hiroyuki, H. AR-marker/IMU hybrid navigation system for tether-powered UAV. J. Robot. Mechatron. 2018, 30, 76–85. [Google Scholar]
- Colleu, T.; Sourimant, G.; Morin, L. Automatic initialization for the registration of GIS and video data. In Proceedings of the 2008 3DTV Conference: The True Vision-Capture, Transmission and Display of 3D Video, Istanbul, Turkey, 28–30 May 2008; pp. 49–52. [Google Scholar]
- Ho, C.C.; Ho, M.C.; Chang, C.Y. Markerless indoor/outdoor augmented reality navigation device based on ORB-visual-odometry positioning estimation and wall-floor-boundary image registration. In Proceedings of the 2019 Twelfth International Conference on Ubi-Media Computing (Ubi-Media), Bali, Indonesia, 5–8 August 2019; pp. 199–204. [Google Scholar]
- Li, S.; Cai, H.; Kamat, V.R. Uncertainty-aware geospatial system for mapping and visualizing underground utilities. Autom. Constr. 2015, 53, 105–119. [Google Scholar] [CrossRef]
- Huang, W.; Sun, M.; Li, S. A 3D GIS-based interactive registration mechanism for outdoor augmented reality system. Expert Syst. Appl. 2016, 55, 48–58. [Google Scholar] [CrossRef]
- Ren, X.; Sun, M.; Jiang, C.; Liu, L.; Huang, W. An augmented reality Geo-registration method for ground target localization from a low-cost UAV platform. Sensors 2018, 18, 3739. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stilla, U.; Kolecki, J.; Hoegner, L. Texture mapping of 3d building models with oblique direct geo-referenced airborne IR image sequences. In Proceedings of the ISPRS Workshop: High-Resolution Earth Imaging for Geospatial Information, Hannover, Germany, 2–5 June 2009; pp. 4–7. [Google Scholar]
- Angelino, C.V.; Baraniello, V.R.; Cicala, L. UAV position and attitude estimation using IMU, GNSS and camera. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 735–742. [Google Scholar]
- Chen, J.; Cao, R.; Wang, Y. Sensor-Aware Recognition and Tracking for Wide-Area Augmented Reality on Mobile Phones. Sensors 2015, 15, 31092–31107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W.; Lai, B.; Wang, C.; Bian, X.; Yang, W.; Xia, Y.; Lin, X.; Lai, S.; Weng, D.; Li, J. Learning to match 2D images and 3D LiDAR point clouds for outdoor augmented reality. In Proceedings of the 2020 IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW), Atlanta, GA, USA, 22–26 March 2020; pp. 654–655. [Google Scholar]
- Nagy, B. A New method of improving the azimuth in mountainous terrain by skyline matching. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2020, 88, 121–131. [Google Scholar] [CrossRef] [Green Version]
- Schneider, J.; Eling, C.; Klingbeil, L.; Kuhlmann, H.; Förstner, W.; Stachniss, C. Fast and effective online pose estimation and mapping for UAVs. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4784–4791. [Google Scholar]
- Nakata, Y.; Hayamizu, M.; Koshimizu, K.i.; Takeuchi, F.; Masuto, E.; Sato, H. Accuracy assessment of topographic measurements and monitoring of topographic changes using RTK-UAV in landslide area caused by 2018 Hokkaido Eastern Iburi EarthquakeRTK-UAV. Landsc. Ecol. Manag. 2020, 25, 43–52. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry using UAV-mounted GNSS RTK: Georeferencing strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Svedin, J.; Bernland, A.; Gustafsson, A. Small UAV-based high resolution SAR using low-cost radar, GNSS/RTK and IMU sensors. In Proceedings of the 2020 17th European Radar Conference (EuRAD), Utrecht, The Netherlands, 10–15 January 2021; pp. 186–189. [Google Scholar]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems; Artech House: Norfolk County, MA, USA, 2013. [Google Scholar]
- Gonzalez, R.; Giribet, J.I.; Patino, H.D. NaveGo: A simulation framework for low-cost integrated navigation systems. Control Eng. Appl. Inform. 2015, 17, 110–120. [Google Scholar]
- DJI. DJI Matrice 600 Pro-DJI. Available online: https://www.dji.com/matrice600-pro (accessed on 16 March 2022).
- DJI. Zenmuse XT2-DJI. Available online: https://www.dji.com/zenmuse-xt2 (accessed on 16 March 2022).
- DJI. D-RTK GNSS-Specs-DJI. Available online: https://www.dji.com/d-rtk/info#specs (accessed on 10 September 2021).
- Gonzalez, R.; Dabove, P. Performance assessment of an ultra low-cost inertial measurement unit for GROUND vehicle navigation. Sensors 2019, 19, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DJI. DJI Lightbridge 2-Professional Quality Live Streaming From the Sky. 2018. Available online: https://www.dji.com/cn/downloads/products/lightbridge-2 (accessed on 16 March 2022).
- MathWorks. Computer Vision Toolbox-MATLAB & Simulink. Available online: https://www.mathworks.cn/products/computer-vision.html#camera-calibration (accessed on 10 September 2021).





















| Numerical Name | ||||
|---|---|---|---|---|
| Numerical results | 1.2846 m | 0.9342 m | 2.8017 m | 1.7972° |
| Numerical Name | ||||
|---|---|---|---|---|
| Numerical results | 1.5884 m | 5.6036 m | 5.8243 m | 1.2497 m |
| Parameter | Value |
|---|---|
| Diagonal Wheelbase | 1133 mm |
| Weight (with six TB47S batteries) | 9.5 kg |
| Max Takeoff Weight Recommended | 15.5 kg |
| Hovering Accuracy (P-GPS) | Vertical: ±0.5 m, Horizontal: ±1.5 m |
| Max Angular Velocity | Pitch: 300°/s, Yaw: 150°/s |
| Max Pitch Angle | 25° |
| Max Ascent Speed | 5 m/s |
| Max Descent Speed | 3 m/s |
| Hovering Time (with six TB47S batteries) | No payload: 32 min, 6 kg payload: 16 min |
| Flight Control System | A3 Pro |
| Operating Temperature | −10 °C to 40 °C |
| Parameter | Value |
|---|---|
| Thermal Imager | Uncooled VOx Microbolometer |
| FPA/Digital Video Display Formats | 640 × 512 |
| Spectral Band | 7.5–13.5 μm |
| Field of View | 45° × 37° |
| Exportable Frame Rates | <9 Hz |
| Sensitivity (NETD) | <50 mk @ f/1.0 |
| Scene Range (High Gain) | −25 °C to 135 °C |
| Scene Range (Low Gain) | −40 °C to 550 °C |
| Parameter Name | x-Axis | y-Axis | z-Axis |
|---|---|---|---|
| Angular Random Walk () | 1.6828 | 1.9601 | 1.6542 |
| Speed Random Walk | 1.2917 | 1.2996 | 1.2921 |
| Gyro Dynamic Bias () | 1.5289 | 37.010 | 2.2793 |
| Acceleration Meter Dynamic Bias () | 6.0546 | 2.8561 | 7.9284 |
| Gyro Correlation Cycle | 7000 | 100 | 9000 |
| Acceleration Meter Correlation Cycle | 20 | 600 | 10,000 |
| Data Number | Original GPS and Original Attitude (m) | RTK GPS and Original Attitude (m) | Our Previous Method (m) | The Proposed Method (m) |
|---|---|---|---|---|
| 1 | 4.15 | 2.86 | 1.37 | 1.02 |
| 2 | 4.84 | 3.74 | 2.38 | 1.17 |
| 3 | 3.18 | 3.59 | 2.00 | 1.40 |
| 4 | 2.93 | 2.45 | 1.32 | 0.95 |
| 5 | 1.92 | 2.67 | 1.40 | 0.93 |
| 6 | 2.37 | 2.78 | 1.53 | 0.80 |
| 7 | 2.96 | 2.99 | 1.55 | 0.55 |
| 8 | 3.83 | 3.11 | 1.34 | 1.06 |
| 9 | 1.93 | 2.01 | 2.03 | 0.93 |
| 10 | 3.30 | 1.90 | 1.67 | 0.87 |
| 11 | 2.70 | 2.27 | 1.23 | 1.39 |
| 12 | 2.77 | 2.58 | 1.24 | 0.95 |
| 13 | 3.46 | 1.58 | 1.61 | 0.87 |
| 14 | 2.82 | 1.58 | 1.35 | 1.41 |
| 15 | 2.42 | 1.86 | 1.37 | 1.56 |
| 16 | 4.03 | 2.03 | 1.35 | 1.23 |
| 17 | 4.32 | 2.92 | 1.30 | 1.52 |
| 18 | 2.62 | 2.17 | 1.20 | 0.77 |
| 19 | 3.90 | 1.93 | 1.46 | 1.20 |
| 20 | 3.84 | 2.26 | 1.22 | 1.25 |
| average | 3.21 | 2.46 | 1.50 | 1.09 |
| Original GPS and Original Attitude | RTK GPS and Original Attitude | Our Previous Method | The Proposed Method | |
|---|---|---|---|---|
| Original GPS and Original Attitude | - | 0.0008 | - | - |
| RTK GPS and Original Attitude | 0.0008 | - | 0.0001 | 0.0001 |
| Our Previous Method | - | 0.0001 | - | 0.0005 |
| The Proposed Method | - | 0.0001 | 0.0005 | - |
| Direction | Pitch | Yaw | Roll |
|---|---|---|---|
| std (°) | 0.4839 | 13.8857 | 0.2704 |
| Parameter Name | Parameter Value |
|---|---|
| Radial distortion | 0.0540, 0.3462 |
| tangential distortion | −0.0037, 0.0076 |
| Principle point location | 349.3325, 251.8215 |
| Lens focal distance | 803.5593, 797.6270 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Sun, M.; Zhang, X.; Liu, L.; Wang, X.; Zhou, H. An AR Geo-Registration Algorithm for UAV TIR Video Streams Based on Dual-Antenna RTK-GPS. Remote Sens. 2022, 14, 2205. https://doi.org/10.3390/rs14092205
Ren X, Sun M, Zhang X, Liu L, Wang X, Zhou H. An AR Geo-Registration Algorithm for UAV TIR Video Streams Based on Dual-Antenna RTK-GPS. Remote Sensing. 2022; 14(9):2205. https://doi.org/10.3390/rs14092205
Chicago/Turabian StyleRen, Xiang, Min Sun, Xianfeng Zhang, Lei Liu, Xiuyuan Wang, and Hang Zhou. 2022. "An AR Geo-Registration Algorithm for UAV TIR Video Streams Based on Dual-Antenna RTK-GPS" Remote Sensing 14, no. 9: 2205. https://doi.org/10.3390/rs14092205
APA StyleRen, X., Sun, M., Zhang, X., Liu, L., Wang, X., & Zhou, H. (2022). An AR Geo-Registration Algorithm for UAV TIR Video Streams Based on Dual-Antenna RTK-GPS. Remote Sensing, 14(9), 2205. https://doi.org/10.3390/rs14092205






