Using Ensemble-Based Systems with Near-Infrared Hyperspectral Data to Estimate Seasonal Snowpack Density
Abstract
:1. Introduction
2. Materials and Methods
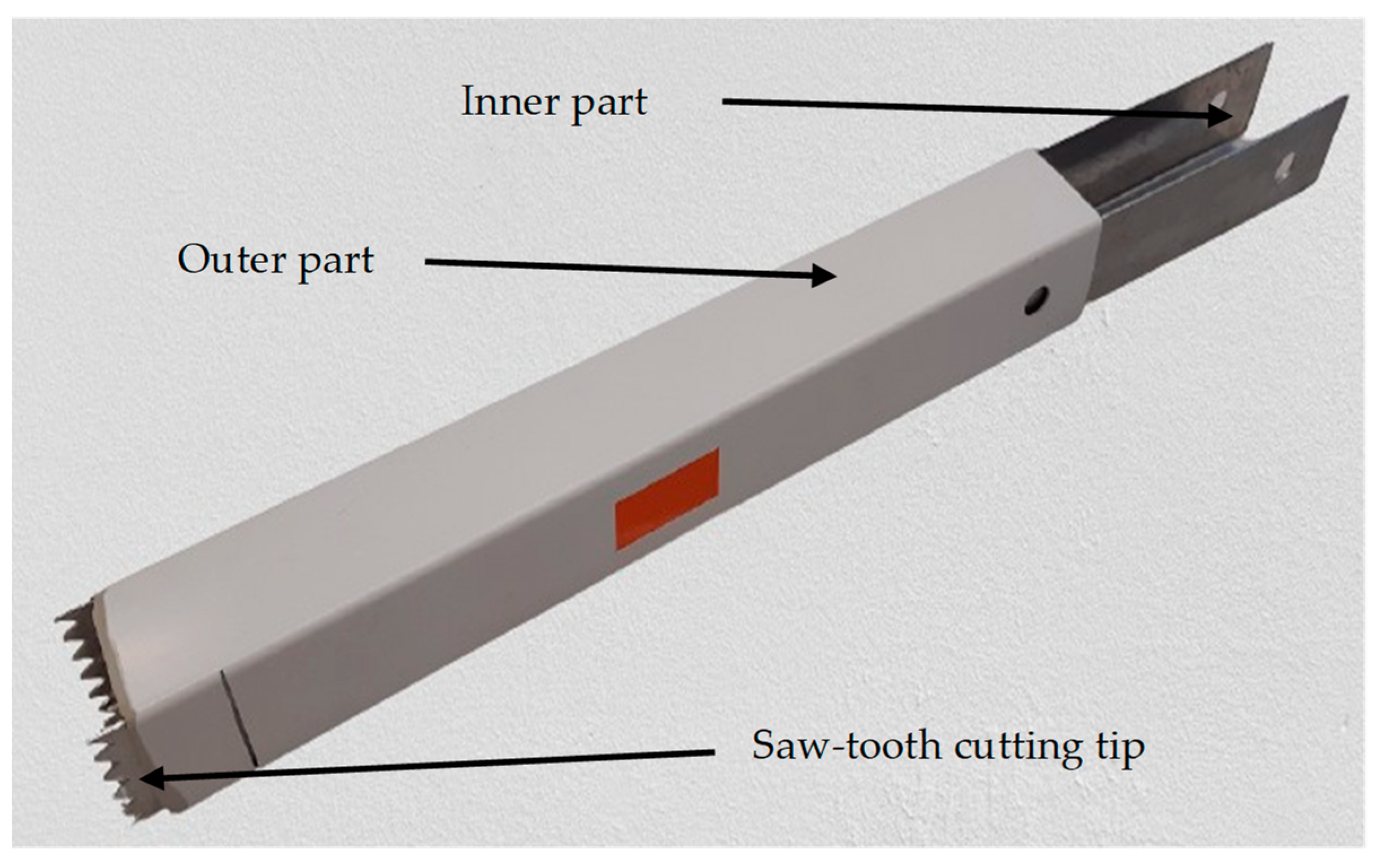
2.1. In Situ Measurements for the Calibration and Validation Database
2.2. Algorithm Development
2.2.1. The Hybrid Model
- ❖
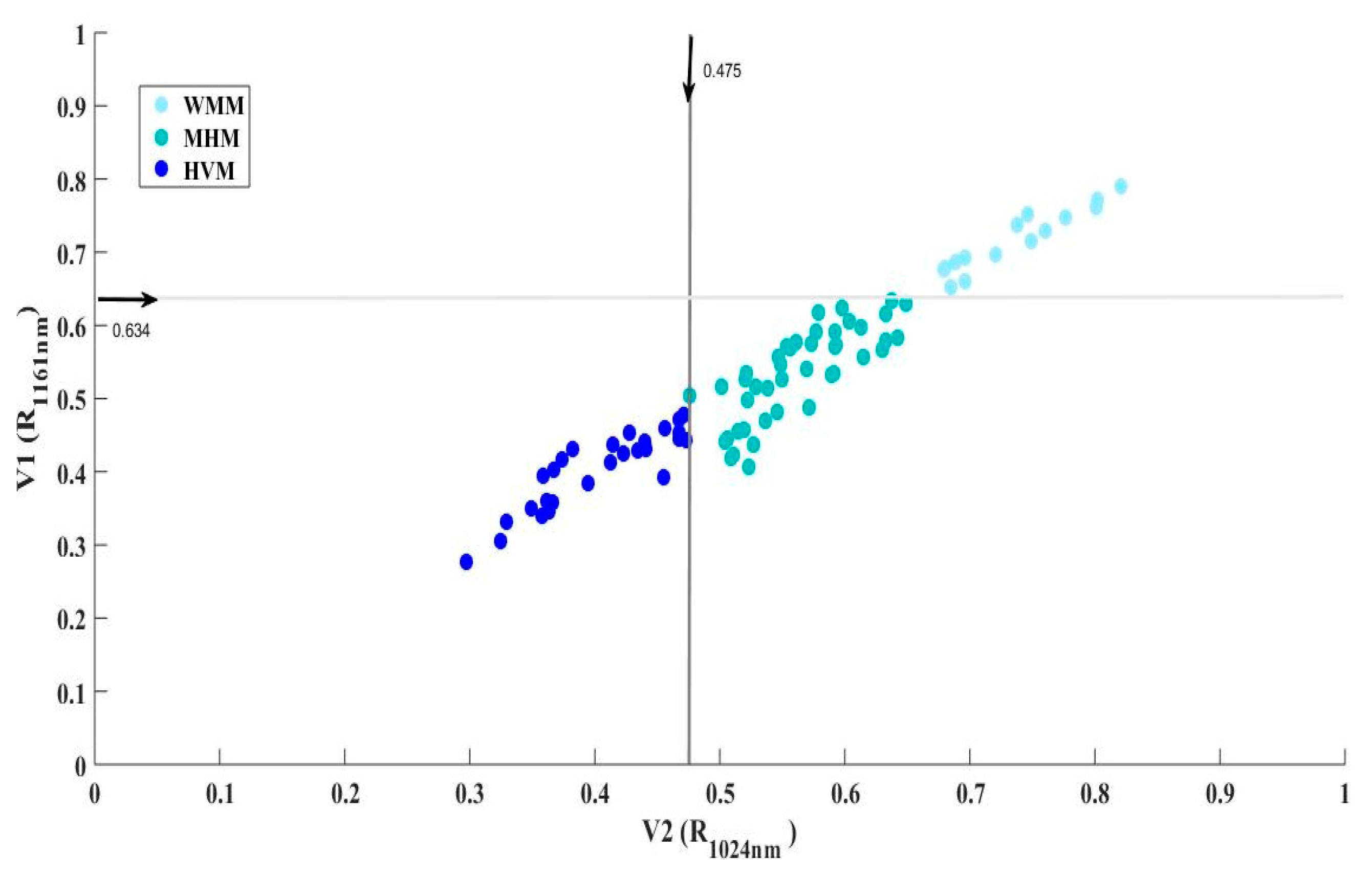
- Classification of the snow samples into one of the three snow classes using the classifier of the HM;
- ❖
- Estimation of each class’s density using the corresponding specific estimator [19].
2.2.2. Development of the Ensemble-Based System
- ➢
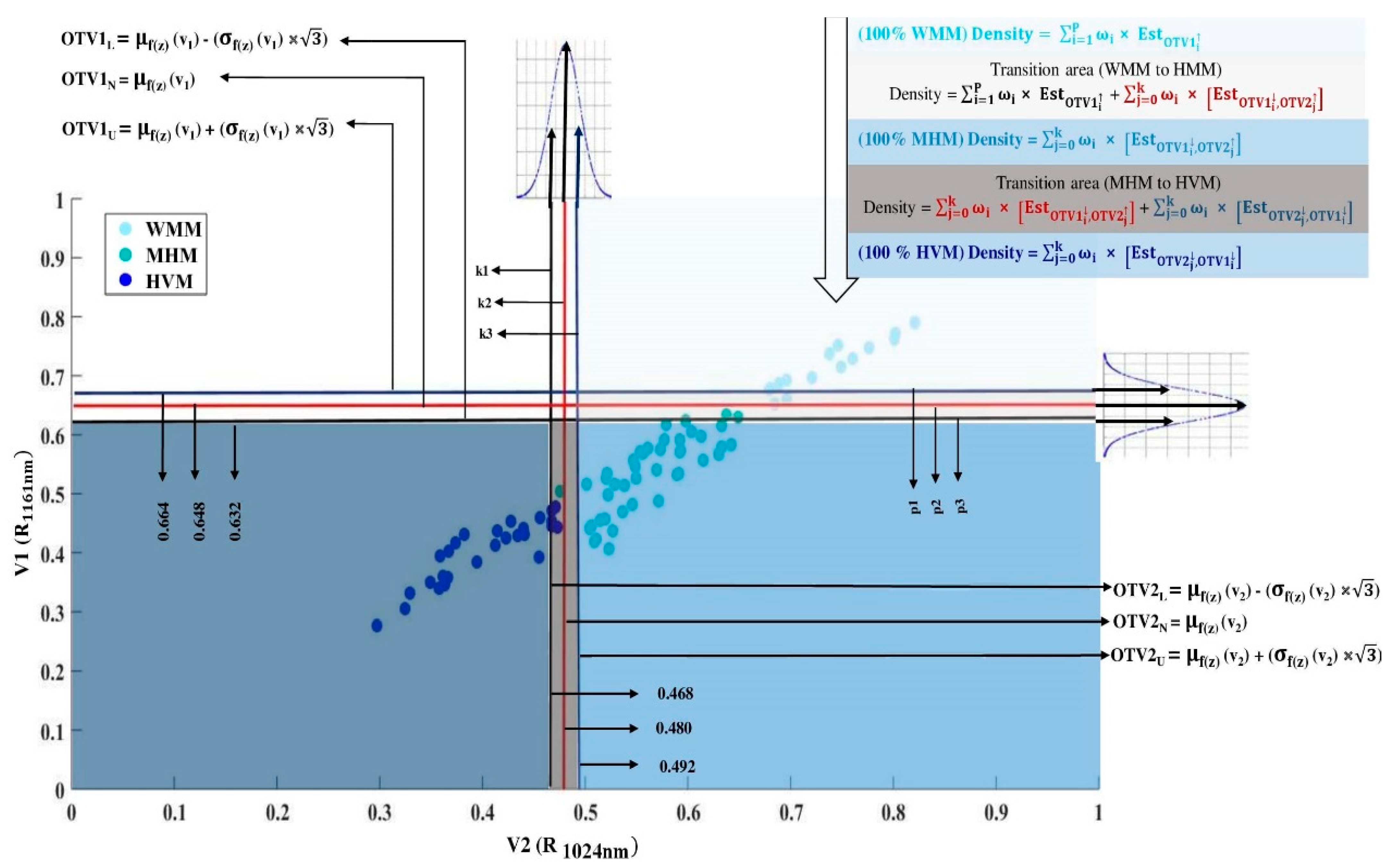
- Parameterization of classifiers based on ensembles
- ➢
- Parameterization of estimators based on ensembles
2.3. Accuracy Assessment
3. Results and Discussion
3.1. Analysis of In Situ Snow Data
3.2. Estimator Calibration
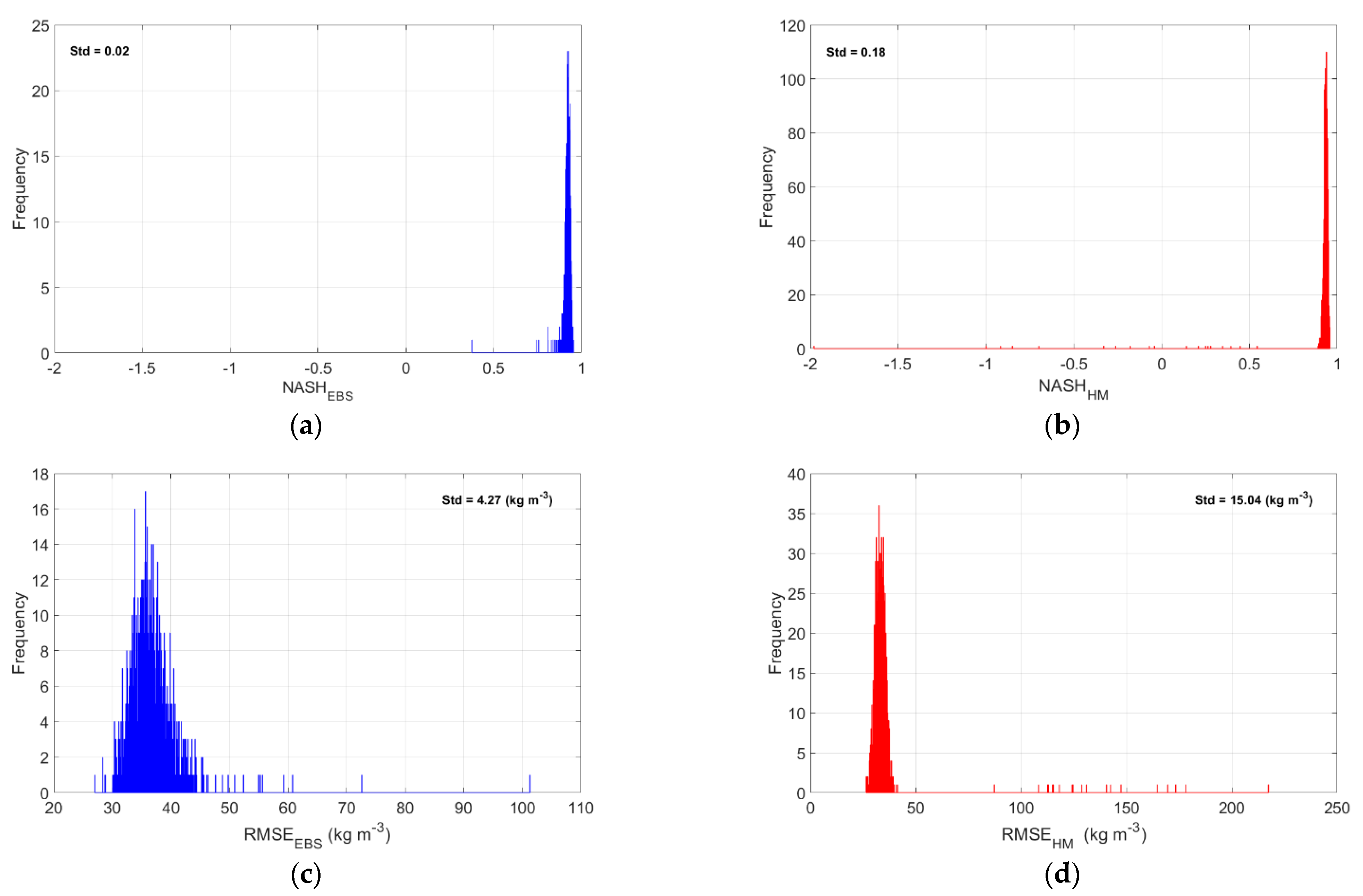
3.3. Evaluation and Validation of the Ensemble-Based System
3.4. Reliability Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
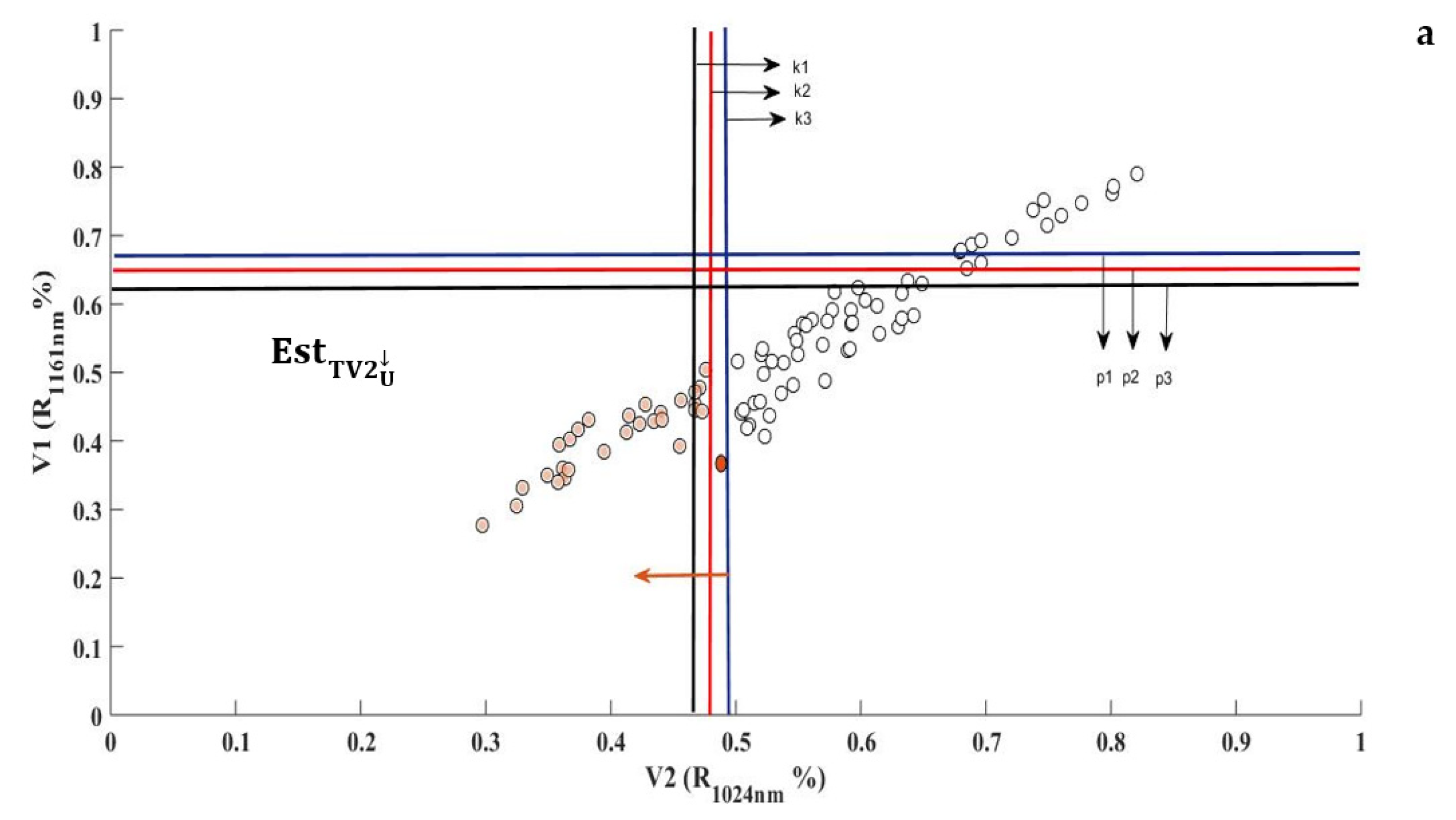

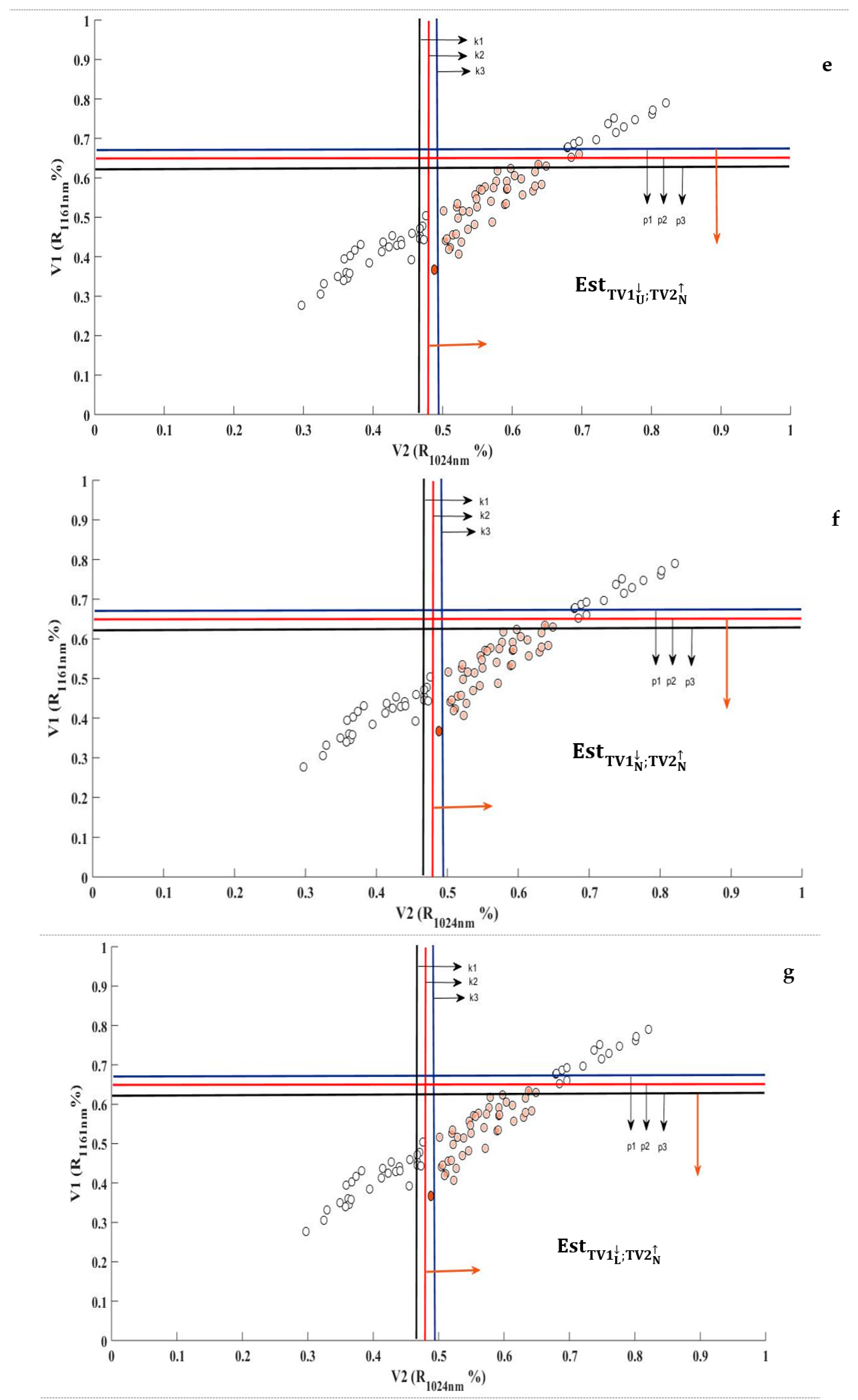
Appendix B
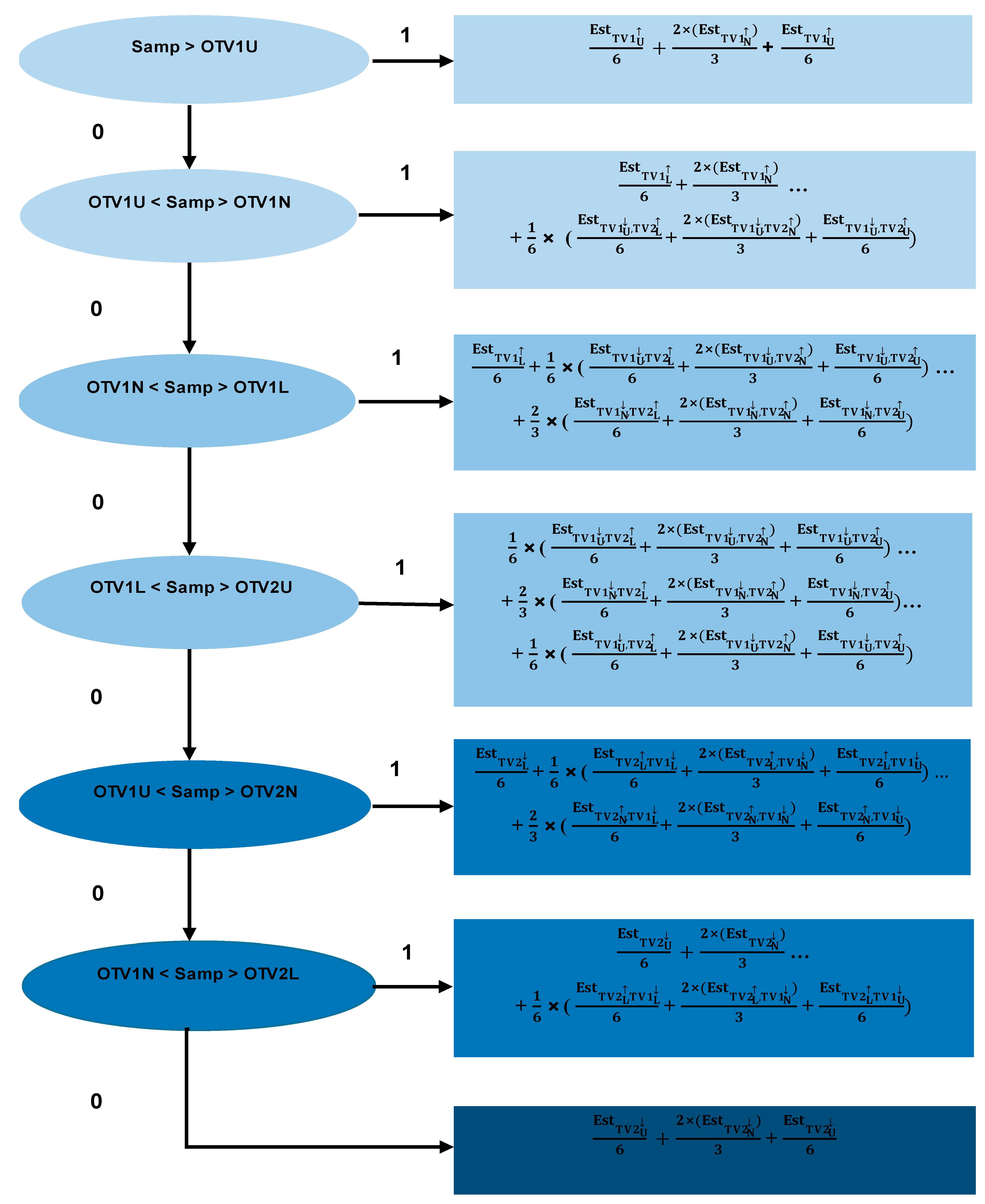
References
- Schweizer, J.; Bruce Jamieson, J.; Schneebeli, M. Snow avalanche formation. Rev. Geophys. 2003, 41, 4. [Google Scholar] [CrossRef] [Green Version]
- Gray, D.; Landine, P. An energy-budget snowmelt model for the Canadian Prairies. Can. J. Earth Sci. 1988, 25, 1292–1303. [Google Scholar] [CrossRef]
- McKay, G.; Blackwell, S. Plains snowpack water equivalent from climatological records. In Proceedings of the 29th Annual Western Snow Conference, Spokane, WA, USA, 11–13 April 1961; pp. 2–43. [Google Scholar]
- Matzl, M.; Schneebeli, M. Measuring specific surface area of snow by near-infrared photography. J. Glaciol. 2006, 52, 558–564. [Google Scholar] [CrossRef] [Green Version]
- Pielmeier, C.; Schneebeli, M. Stratigraphy and changes in hardness of snow measured by hand, ramsonde and snow micro penetrometer: A comparison with planar sections. Cold Reg. Sci. Technol. 2003, 37, 393–405. [Google Scholar] [CrossRef]
- Kinar, N.; Pomeroy, J. Measurement of the physical properties of the snowpack. Rev. Geophys. 2015, 53, 481–544. [Google Scholar] [CrossRef]
- Berisford, D.F.; Molotch, N.P.; Durand, M.T.; Painter, T.H. Portable spectral profiler probe for rapid snow grain size stratigraphy. Cold Reg. Sci. Technol. 2013, 85, 183–190. [Google Scholar] [CrossRef]
- Zuanon, N. IceCube, a portable and reliable instruments for snow specific surface area measurement in the field. In Proceedings of the International Snow Science Workshop, Grenoble-Chamonix, Mont-Blance, France, 7–11 October 2013; pp. 1020–1023. [Google Scholar]
- Domine, F.; Salvatori, R.; Legagneux, L.; Salzano, R.; Fily, M.; Casacchia, R. Correlation between the specific surface area and the short wave infrared (SWIR) reflectance of snow. Cold Reg. Sci. Technol. 2006, 46, 60–68. [Google Scholar] [CrossRef]
- Varade, D.; Maurya, A.K.; Sure, A.; Dikshit, O. Supervised classification of snow cover using hyperspectral imagery. In Proceedings of the 2017 International Conference on Emerging Trends in Computing and Communication Technologies (ICETCCT), Dehradun, India, 17–18 November 2017; pp. 1–7. [Google Scholar]
- ElMasry, G.; Sun, D.-W.; Allen, P. Near-infrared hyperspectral imaging for predicting colour, pH and tenderness of fresh beef. J. Food Eng. 2012, 110, 127–140. [Google Scholar] [CrossRef]
- Lorente, D.; Aleixos, N.; Gómez-Sanchis, J.; Cubero, S.; García-Navarrete, O.L.; Blasco, J. Recent advances and applications of hyperspectral imaging for fruit and vegetable quality assessment. Food Bioprocess Technol. 2012, 5, 1121–1142. [Google Scholar] [CrossRef]
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef]
- Donahue, C.; Skiles, S.M.; Hammonds, K. In situ effective snow grain size mapping using a compact hyperspectral imager. J. Glaciol. 2021, 67, 49–57. [Google Scholar] [CrossRef]
- El Oufir, M.K.; Chokmani, K.; El Alem, A.; Agili, H.; Bernier, M. Seasonal Snowpack Classification Based on Physical Properties Using Near-Infrared Proximal Hyperspectral Data. Sensors 2021, 21, 5259. [Google Scholar] [CrossRef]
- Gallet, J.-C.; Domine, F.; Zender, C.; Picard, G. Measurement of the specific surface area of snow using infrared reflectance in an integrating sphere at 1310 and 1550 nm. Cryosphere 2009, 3, 167–182. [Google Scholar] [CrossRef] [Green Version]
- Painter, T.H.; Molotch, N.P.; Cassidy, M.; Flanner, M.; Steffen, K. Contact spectroscopy for determination of stratigraphy of snow optical grain size. J. Glaciol. 2007, 53, 121–127. [Google Scholar] [CrossRef] [Green Version]
- Eppanapelli, L.K.; Lintzen, N.; Casselgren, J.; Wåhlin, J. Estimation of Liquid Water Content of Snow Surface by Spectral Reflectance. J. Cold Reg. Eng. 2018, 32, 05018001. [Google Scholar] [CrossRef]
- Negi, H.; Singh, S.; Kulkarni, A.; Semwal, B. Field-based spectral reflectance measurements of seasonal snow cover in the Indian Himalaya. Int. J. Remote Sens. 2010, 31, 2393–2417. [Google Scholar] [CrossRef]
- Gergely, M.; Schneebeli, M.; Roth, K. First experiments to determine snow density from diffuse near-infrared transmittance. Cold Reg. Sci. Technol. 2010, 64, 81–86. [Google Scholar] [CrossRef]
- El Oufir, M.K.; Chokmani, K.; El Alem, A.; Bernier, M. Estimating Snowpack Density from Near-Infrared Spectral Reflectance Using a Hybrid Model. Remote Sens. 2021, 13, 4089. [Google Scholar] [CrossRef]
- Alpak, F.O.; Vink, J.C.; Gao, G.; Mo, W. Techniques for effective simulation, optimization, and uncertainty quantification of the in-situ upgrading process. J. Unconv. Oil Gas Resour. 2013, 3, 1–14. [Google Scholar] [CrossRef]
- Chan, J.C.-W.; Paelinckx, D. Evaluation of Random Forest and Adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Hansen, L.K.; Salamon, P. Neural network ensembles. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 993–1001. [Google Scholar] [CrossRef] [Green Version]
- Ismail, R.; Mutanga, O. A comparison of regression tree ensembles: Predicting Sirex noctilio induced water stress in Pinus patula forests of KwaZulu-Natal, South Africa. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S45–S51. [Google Scholar] [CrossRef]
- Jacobs, R.A.; Jordan, M.I.; Nowlan, S.J.; Hinton, G.E. Adaptive mixtures of local experts. Neural Comput. 1991, 3, 79–87. [Google Scholar] [CrossRef]
- Jordan, M.I.; Jacobs, R.A. Hierarchical mixtures of experts and the EM algorithm. Neural Comput. 1994, 6, 181–214. [Google Scholar] [CrossRef] [Green Version]
- Oza, N.C.; Tumer, K. Classifier ensembles: Select real-world applications. Inf. Fusion 2008, 9, 4–20. [Google Scholar] [CrossRef]
- Wang, S.-j.; Mathew, A.; Chen, Y.; Xi, L.-f.; Ma, L.; Lee, J. Empirical analysis of support vector machine ensemble classifiers. Expert Syst. Appl. 2009, 36, 6466–6476. [Google Scholar] [CrossRef] [Green Version]
- Polikar, R. Ensemble based systems in decision making. IEEE Circuits Syst. Mag. 2006, 6, 21–45. [Google Scholar] [CrossRef]
- Kelly, K.; Krzysztofowicz, R. A bivariate meta-Gaussian density for use in hydrology. Stoch. Hydrol. Hydraul. 1997, 11, 17–31. [Google Scholar] [CrossRef]
- Tørvi, H.; Hertzberg, T. Estimation of uncertainty in dynamic simulation results. Comput. Chem. Eng. 1997, 21, S181–S185. [Google Scholar] [CrossRef]
- Fierz, C.; Armstrong, R.L.; Durand, Y.; Etchevers, P.; Greene, E.; McClung, D.M.; Nishimura, K.; Satyawali, P.K.; Sokratov, S.A. The International Classification for Seasonal Snow on the Ground; UNESCO/IHP: Paris, France, 2009; Volume 25. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Springer: Monterey, CA, USA; Wadsworth, OH, USA, 1984. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Pahaut, E. Les Cristaux de Neige et Leurs Métamorphoses; Direction de la Météorologie Nationale: Sarcenas, France, 1975. [Google Scholar]
- Dozier, J. Spectral signature of alpine snow cover from the Landsat Thematic Mapper. Remote Sens. Environ. 1989, 28, 9–22. [Google Scholar] [CrossRef]
- Warren, S.G. Optical properties of snow. Rev. Geophys. 1982, 20, 67–89. [Google Scholar] [CrossRef]
- Wiscombe, W.J. Improved Mie scattering algorithms. Appl. Opt. 1980, 19, 1505–1509. [Google Scholar] [CrossRef] [PubMed]
- Colbeck, S. An overview of seasonal snow metamorphism. Rev. Geophys. 1982, 20, 45–61. [Google Scholar] [CrossRef]




| Optimal Threshold (OT) | Abscissa (Zi) | |
|---|---|---|
| 1 | 0 | 1 |
| 2 | −1, +1 | |
| 3 |
| Snow Class | Type of Grain | Grain Size (mm) | Number of Samples (N) | Density (kg m−3) |
|---|---|---|---|---|
| WMM | <1 mm | 19 | 100–250 | |
| MHM | 1–2 mm | 59 | 150–400 | |
| HVM | >2 mm | 36 | 350–650 |
| Snow Class | Estimator ID | Specific Estimator | Calibration Equation | R2 | Samp | |
|---|---|---|---|---|---|---|
| WMM | 1 | −1119.75 × SISUB (1,282,941) − 167.59 | 0.91 | 17 | 1282–941 | |
| 2 | −877.36 × SISUB (1,452,968) − 433.25 | 0.95 | 15 | 1452–968 | ||
| 3 | −967.69 × SISUB (1,666,935) − 425.24 | 0.97 | 13 | 1666–935 | ||
| MHM | 4 | −1491.40 × SINOR (1,600,946) − 951.09 | 0.83 | 45 | 1600–946 | |
| 5 | −1491.40 × SINOR (1,600,946) − 951.09 | 0.83 | 45 | 1600–946 | ||
| 6 | −1432.65 × SINOR (1,617,946) − 880.87 | 0.84 | 48 | 1617–946 | ||
| 7 | −1397.68 × SINOR (1,617,941) − 854.96 | 0.80 | 43 | 1617–941 | ||
| 8 | −1397.68 × SINOR (1,617,941) − 854.96 | 0.80 | 43 | 1617–941 | ||
| 9 | −1427.73 × SINOR (1,617,941) − 877.38 | 0.82 | 46 | 1617–941 | ||
| 10 | −1480.06 × SINOR (1,600,946) − 940.11 | 0.80 | 41 | 1600–946 | ||
| 11 | −1480.06 × SINOR (1,600,946) − 940.11 | 0.80 | 41 | 1600–946 | ||
| 12 | −1419.73 × SINOR (1,617,946) − 868.75 | 0.82 | 44 | 1617–946 | ||
| HVM | 13 | −26,859.26 × SINOR (979,974) + 82.90 | 0.77 | 28 | 979–974 | |
| 14 | −26,859.26 × SINOR (979,974) + 82.90 | 0.77 | 28 | 979–974 | ||
| 15 | −1378.90 × SISUB (14,411,122) + 1207.81 | 0.86 | 22 | 1441–1122 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Oufir, M.K.; Chokmani, K.; El Alem, A.; Bernier, M. Using Ensemble-Based Systems with Near-Infrared Hyperspectral Data to Estimate Seasonal Snowpack Density. Remote Sens. 2022, 14, 1089. https://doi.org/10.3390/rs14051089
El Oufir MK, Chokmani K, El Alem A, Bernier M. Using Ensemble-Based Systems with Near-Infrared Hyperspectral Data to Estimate Seasonal Snowpack Density. Remote Sensing. 2022; 14(5):1089. https://doi.org/10.3390/rs14051089
Chicago/Turabian StyleEl Oufir, Mohamed Karim, Karem Chokmani, Anas El Alem, and Monique Bernier. 2022. "Using Ensemble-Based Systems with Near-Infrared Hyperspectral Data to Estimate Seasonal Snowpack Density" Remote Sensing 14, no. 5: 1089. https://doi.org/10.3390/rs14051089
APA StyleEl Oufir, M. K., Chokmani, K., El Alem, A., & Bernier, M. (2022). Using Ensemble-Based Systems with Near-Infrared Hyperspectral Data to Estimate Seasonal Snowpack Density. Remote Sensing, 14(5), 1089. https://doi.org/10.3390/rs14051089







