Spatial Structure of an Urban Park System Based on Fractal Theory: A Case Study of Fuzhou, China

Abstract

The rationality and efficiency of the spatial structure of an urban park system are critical in building a livable urban environment. Fractal theory is currently treated as the frontier theory for exploring the law of complex systems; however, it has rarely been applied to urban park systems. This study applied the aggregation, grid and correlation dimension models of fractal theory in Fuzhou, China. The spatial structure and driving factors of the urban park system were analyzed and an innovative model was proposed. The evidence shows that the spatial structure of the park system has fractal characteristics, although self-organization and optimization have not yet been fully formed, revealing a multi-core nesting pattern. Moreover, the core is cluster of four popular parks with weakening adsorption, and the emerging Baima River Park is located at the geometric center, which is likely to be further developed. The system structure is primarily driven by geographical conditions, planning policies, and transportation networks. Against this backdrop, an innovative model for the park system was proposed. The central park has heterogeneity and synergistic development, relying on the kinds of flow which can lead to the formation of a park city, a variation of a garden city. At the regional scale, relying on the geographical lines, the formation of a regional park zone could be realized. These findings provide new perspectives to reveal the spatial structure of urban park systems. The information derived can assist policy makers and planners in formulating more scientific plans, and may contribute to building a balanced and efficient urban park system.

1. Introduction

Urban parks in the modern sense originated from the Industrial Revolution, with a goal of solving the deterioration of human settlements caused by rapid urbanization. Currently, urban parks play an essential role in enhancing the public health of urban residents, supporting ecological integrity within urban areas, and carrying out additional functions [1,2,3,4] which are of crucial significance for the livability of modern cities and well-being of urban dwellers [5,6]. Furthermore, a practical urban park’ spatial structure plays an important role in controlling urban sprawl and has attracted extensive academic interest in the context of rapid urbanization. Previous studies on the spatial structure of parks can be roughly divided into three categories: (1) statistical research on park growth and the usage of parks. Zhang et al. (2021) studied the dynamic evolution of all urban parks in Beijing for 2005, 2010, and 2017, concluding the presence of significant and sustained park growth [7], whereas comparing 2014 to 2000, the total urban green space in China shrank with core urban expansion [8]. Based on six medium-sized urban parks in Tokyo, significant seasonal variations in park visitor volume, visitor behavior, and park service area were observed [9]; (2) research on parks’ landscape and aesthetic structures, such as the landscape shape index [10], vegetation coverage [11,12], and human emotion [13]; and (3) the accessibility and fairness of service demands. For example, Dony et al. (2015) used the two-step floating catchment area (2SFCA) method to establish a function of park attractiveness and the number of amenities to promote consistency in the way parks are planned and used [14]. Guan et al. (2020) utilized cell phone big data to determine urban park catchment areas under the behavioral orientation of residents, noting that park catchment areas are influenced by park size and significant differences in spatial patterns of visitors at the same scale [15]. Other scholars have employed social media data to provide a new understanding of the spatial use and preferences of urban parks [16], and have also focused on the park needs of minority groups [17,18] to realize the value of parks in terms of social equity.

A series of achievements have been made in past studies regarding the spatial layout of parks. Nevertheless, such studies usually consider macro control in a statistical sense, proposing rigid rules for the number and scale of parks. Or they are keen on reducing the spatial distribution of park systems to simple geometry and applying classical forms of spatial layout. For instance, the concentric circle model, based on the concept of urban green space integration, was a plan in Beijing proposed to build three levels of park rings, including, “the ring of city wall ruins park”, “the ring of green partition city park” and “the ring of green partition country park ring” [19]. The construction of park rings is indeed conducive to stabilizing the ecological structure of the city and limiting urban sprawl. However, whether or not the ring-shaped spatial structure is the optimal form for the spatial layout of the park system is still in question. In addition, one of the most important indicators in the spatial layout of parks is the service radius, which ensures the rationality of the spatial layout to a certain extent. Inevitably, there are overlaps and gaps in the service area, and the synergy between park elements remains weak, which is not conducive to the realization of urban ecological and economic values. How to promote the optimal efficiency of the spatial layout of the park system is a problem that has been neglected in past studies. The functional zoning and structural settings of parks under the current logical thinking have formed a seemingly well-organized urban spatial structure. Nevertheless, the generative logic that simplifies the functions and features of the park system often leads to the mechanization of the exterior of the spatial layout and the lack of organic connections within. Therefore, there is an urgent need for theoretical guidance on the combination of external pluralism and internal order of the spatial layout of the park system.

With the development of modern mathematics, fractal theory, known as the geometry of nature, brings a quantitative description and new language for the discovery of new laws in various disciplines, providing a new world outlook and methodology for the additional development of science. Fractal theory was founded by Mandelbrot (1967) and it considers the fractal to be the performance of the optimized structure of nature [20]. Applications of this theory will continuously fill and optimize the fixed space during the process of self-organization. The self-organization evolutionary process will ultimately achieve the maximum efficiency for occupation and utilization. The most fundamental characteristic of fractals is “self-similarity”, i.e., the statistical similarity between the local and the whole in terms of form, function and information. Scholars use “Dimension” to describe the core characteristics of the object of study. Fractal theory refines dimensionality from one-, two-, and three-dimensional to fractions, and explains the inherent spatial laws of objective things in a more scientific way. However, fractals are not self-similar at any scale, and the range for which fractal features exist is called the “scaleless range”. Especially for natural random fractals, the determination of the scaleless range is the basic condition for calculating the fractal dimension. The non-scaleless range, meaning that the system does not have fractal characteristics in that range, does not generally exist in the case of mathematical models, and the natural object would more probably have an imperfect fractal. Additionally, it requires a goodness of fit determination, and most of the studies have chosen the coefficient of determination (R²) as the indicator.

Fractal theory is among the three pillars of contemporary nonlinear science for complex systems, and has become a frontier research area in many disciplines. Fractal theory has been closely related to urban planning since it was founded, and numerous studies have shown that cities have fractal characteristics. Moreover, the fractal cities theory is established, which enables the use of fractal theory to simulate and model the research object. This study addresses urban systems [21,22], urban forms [23,24,25], and urban elements [26,27,28,29]. By simulating and modeling cities with the help of fractal theory, scholars have concluded that urban systems are at optimal efficiency when cities have fractal characteristics.

Urban parks are one of the key subsystems of cities, but limited research has been conducted on the fractalization of park systems. Kaligarič et al. (2008) took Goričko Landscape Park in Slovenia as an example, and used fractal dimensions to classify habitat types, and concluded that patches showed slightly higher fractal dimensions in areas with higher intensity [30]. Wang et al. (2011) used fractal dimensions to analyze the dynamic change in construction land, and concluded that because the amount of land under construction and green space was not proportional, there should be an increase in the green space area of the urbanized area [31]. Liang et al. (2013) proved the feasibility of applying fractal theory to urban square green space design, indicating that a continuous hierarchical scale is essential for the essential analysis of the built environment [32]. Gong et al. (2020) used the fractal dimension model to compare the average scale range of green space and to determine the spatial characteristic range of urban green space to evaluate the rationality of urban green space layouts [33]. These studies merely emphasize the interpretive mathematical structure and theoretical applications of the park system space structure, while failing to address the core mining, driving mechanism and actual developmental strategy of the structure.

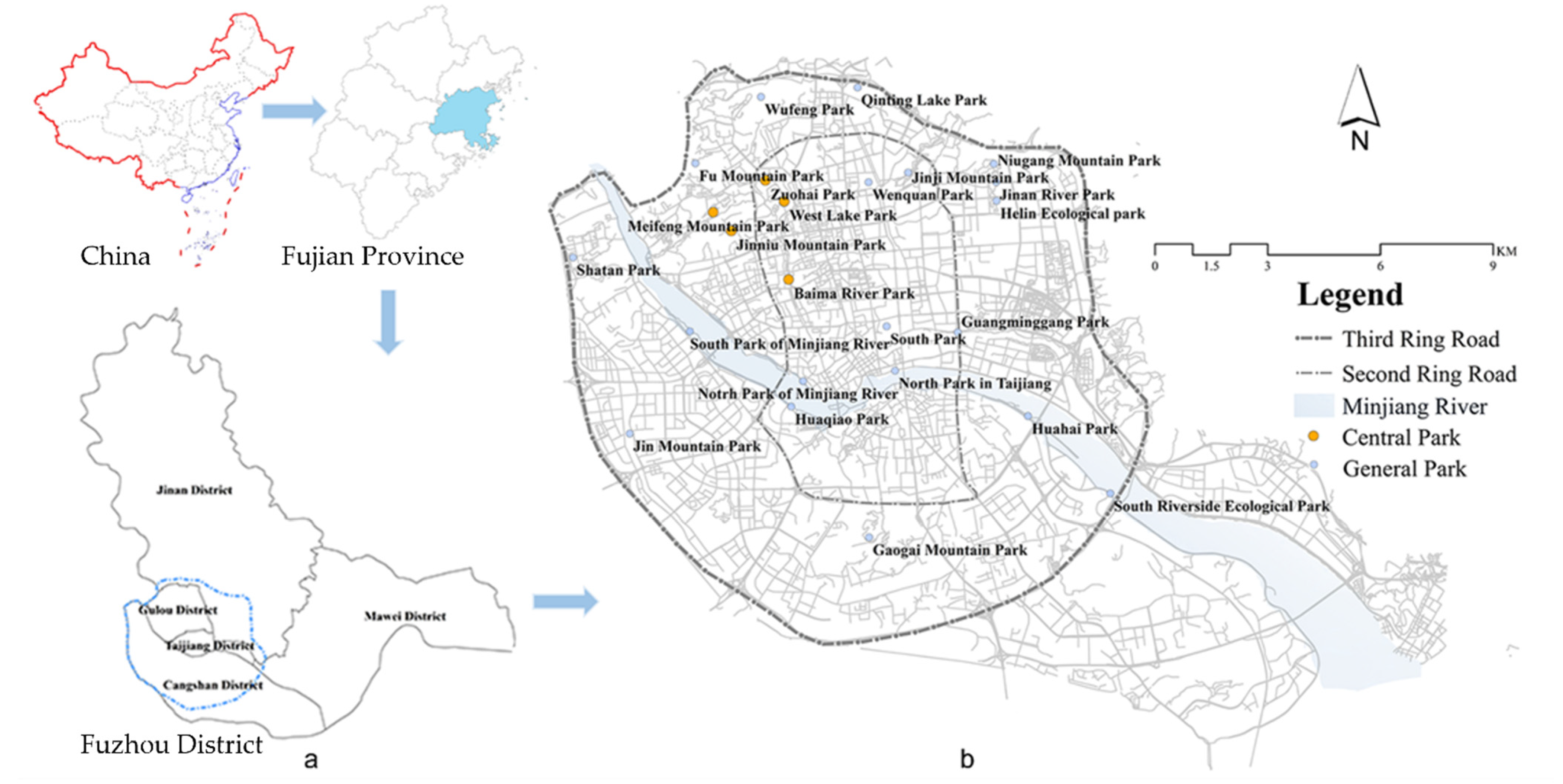
Against this backdrop, based on the fractal theory, a correct understanding of the degree of development, spatial characteristics and driving mechanisms is highly significant for the creation of a healthy and comfortable city and to enhance the comprehensive competitiveness. To this end, the parks in the main urban areas of Fuzhou were used as an example. The spatial structure and phylogeny of the parks were quantitatively analyzed using the fractal dimension index, including the aggregation fractal dimension, grid dimension and correlation dimension. Given this context, the objectives of this study were to (1) analyze the spatial structure distribution characteristics of the park system; (2) explore the evolutionary mechanism of park systems, and (3) propose a development model of the park system to provide theoretical support for the optimal planning and management of the park spatial layout.

The remainder of this paper is organized in the following order. First, we hypothesize that the park system had fractal characteristics, selected the central park, and investigated the developmental level and characteristics of the system. The Section 2 focuses on how to establish the connection between fractal theory and the park system, and the fractal dimension calculation method. The Section 3 introduces how to use the dimensional results to evaluate the current developmental stage of the park system. The Section 4 further proposes the method for determining the spatial structure and development model of the park systems. The Section 5 summarizes the contributions of the paper.

2. Materials and Methods

2.1. Overview of the Study Area

2.1.1. Study Scope: The Fuzhou Central Area, China

Our study was undertaken in the city of Fuzhou, a metropolitan city on the southeast coast of China. It is the capital of Fujian Province, which has a rapidly developing economy and increasing urbanization (25°15′~26°39′N, 118°08′~120°31′E; Figure 1a). The study area has a subtropical monsoon climate with long summers and short winters [34]. Fuzhou is surrounded by mountains and the Minjiang River runs through the city, flowing into the ocean in the East. The Fuzhou Statistical Yearbook 2018 indicated that the city has a park green area of 4094.38 hm, and a per capita park green area of 15.05 m². To ensure the availability and representativeness of data acquisition, we selected the Fuzhou Main Districts as the study area, including Gulou, Cangshan, Taijiang and part of the Jin’an District, in which the total area is approximately 248.3 km².

2.1.2. Park Selection

The self-similarity of fractals has no interaction with the level of structure of the fractal itself, but it is closely related to the Euclidean measure of objects, which primarily refers to the Euclidean area. Hence, the selection of target parks should keep the area and function of parks as similar as possible. China divided park green space into comprehensive parks, regional comprehensive parks and specialized parks [35]. A comprehensive urban park is the “core” of the park green space, is generally large in area, rich in content and many services, suitable for urban residents of all ages and professions to have a day or half a day of rewarding activities in, and plays an essential role in the urban landscape, environmental protection and social lives. To some extent, comprehensive urban parks can reflect the development level of urban parks more closely and they have similar areas. Therefore, 24 urban comprehensive parks that are similar in scale and type in the main urban areas were selected as the samples to study the spatial structure system (Figure 1b).

2.2. Data Preparation

The data from this study include information on urban park names and coordinates, and administrative boundaries. The administrative division data were collected from the network of Fuzhou Urban and Rural Planning Bureau [36], and the designation and scale data of the 24 parks stem from the Fuzhou Landscape Bureau [37]. Furthermore, the coordinate data for the parks were obtained from the Baidu Map Application Programming Interface [38] and confirmed by GPS-measured positioning data. All the point data from the parks are reliable. The data were imported into ArcMap 10.5 to integrate the geospatial information and attributes of parks and projected to WGS-84 UTM 50N as the basic data for the next step of spatial analysis. The calculation of fractal dimension was based on ArcGIS10.5 software and combined with MATLAB software (MathWorks, Inc., Natick, MA, USA) in the park distribution map.

2.3. Methodology

Many samples are statistically ‘‘self-similar”, indicating that each portion can be considered to be a reduced-scale image of the whole, and are characterized by an exponent of similarity D, which could be described as the degree of complication [20]. In essence, this is a hierarchical system that is connected with the cascade structure of complex networks [39]. For the purposes of this study, one must assume that the Fuzhou urban park system utilizes a condensed matter distribution around the central park according to the self-similarity law, and the fractal changes uniformly. The park system is discussed with the assistance of the essential indicators in the theory, aggregation dimension, grid dimension and correlation dimension. The framework is shown as Figure 2.

2.3.1. Aggregation Dimension

The aggregation dimension represents the aggregation of individual parks around the central park and reflects the compactness of spatial structure of the park system. On the basis of the evolution model of fractal theory, the relationship between the number of parks “$N\left(r\right)$” in a circle with radius “$r$” and the corresponding radius can be determined using a geometric measure, as follows:

$${N\left(r\right)\propto r}^{D_f}$$

(1)

where $D_f$ is the fractal dimension. To avoid the influence of unit of radius $r$ on the value of fractal dimension, it was converted to the mean radius $R_s$ as follows:

$$R_s\equiv \langle {\left(\frac{1}{S}{\displaystyle \sum }_{i=1}^s{r}^2\right)}^{\frac{1}{2}}\rangle$$

(2)

$R_s$ represents the average radius; $r_i$ denotes the Euclidean distance from the urban park $i$ to the central park; $s$ is the number of scenic spots, and 〈 〉 is the average radius. Furthermore,

$$R_s\propto S^{\frac{1}{D}}$$

(3)

The $D$ value utilizes 2 as the critical point, which indicates that the park system is evenly distributed in the study area. Lower than 2 indicates a concentrated distribution, and the park spatial distribution decays from the center to the periphery. Higher than 2 indicates in a centrifugal distribution, and its density increases from the center to periphery.

2.3.2. Grid Dimension

The grid dimension $D_1$ is primarily used to reflect the balance of distribution of parks in the region. When investigating the spatial distribution of the system, the number of grids $N\left(\epsilon \right)$ occupied by the park is related to the grid size $\epsilon$. Assuming that the distribution of parks is a scaleless property, the relationship holds:

$${N\left(\epsilon \right)\propto r}^{\alpha }$$

(4)

where ${\alpha =D}_0$ is the capacity dimension, $\epsilon$ is the grid size. When $0<D<2$, it means that the parks in the system are relatively evenly distributed; when $D$ tends to be closer to 0, the parks tend to be concentrated in one place; when $D=2$, it means that the parks are extremely well-distributed, which is compatible with the central place model. Afterwards, we can ignore the difference in number of parks in the grid, assuming that the number of “Parks” in the grid of row $i$ and column $j$ is $N_{ij}$, and the total number of parks in the whole domain is $N$. Its formula is as follows:

$$P_{ij}=\frac{N_{ij}}{N}$$

(5)

Next, we can obtain information dimensions, whose expression is as follows:

$$I\left(\epsilon \right)=-{\displaystyle \sum }_i^k{\displaystyle \sum }_j^k{P}_{ij\left(\epsilon \right)}{\ln P}_{ij\left(\epsilon \right)}$$

(6)

In the formula, $K=\frac{1}{\epsilon }$ represents the number of segments on each side of the region. If the park system is fractal, the expression is as follows:

$${I\left(\epsilon \right)=I}_0-D_1\ln \epsilon$$

(7)

where $I_0$ is a constant, and $D_1$ is an information dimension.

$$K=\frac{D_1}{D_0}$$

(8)

where the geographical significance of the $K$ value is that connectivity increases as the $K$ value grows closer to 1. When $K=1$, the traffic line between the parks is a straight line, and the connectivity worsens as the value grows closer to 0.

2.3.3. Correlation Dimension

However, during the process of studying the park system, it was not enough to only discuss the attraction of the central park. In addition to the relationship between central parks and non-central parks, the regularity of the spatial interaction between individuals also requires clarification. In fractal theory, the correlation dimension is often used to explain the regularity of spatial interaction between elements, whose expression is as follows:

$$C\left(r\right)=\frac{1}{N^2}{\displaystyle \sum }_{i,j=1}^N{H(r-d}_{ij})$$

(9)

$$H\left(x\right)=\left\{\begin{array}{c}1,x>0\\ 0,x<0\end{array}\right.$$

(10)

where $r$ is the yardstick, $d_{ij}$ denotes the crow distance (or the cow distance) between park $i$ and park $j$ in the park system and $H\left(x\right)$ represents the Heaviside step function. If the spatial distribution of the park system has fractal characteristics, it has the following formula:

$$C\left(r\right)\propto r^{\alpha }$$

(11)

where ${\alpha =D}_0$ is designated the crow (cow) correlation dimension. The crow–cow dimension ratio value reflects the accessibility of actual network. The accessibility increases as the value grows closer to 1.

3. Results

3.1. Fractal Aggregation Dimension Analysis of Park System under Different Centers

Fuzhou City is crossed by the Min River, and park resources show a clear distribution along geographical lines. Therefore, this study followed the principle of geometric center and chose the Baima River Park, which is adjacent to the Min River (geographical line), as the central park to carry out the aggregation dimension calculation. The fractal dimension $D_1$ (

Table 1. The determining data of fractal dimension of Fuzhou’s park system.

Central Park	Baima River Park	West Lake Park	Jinniu Mountain Park	Zuohai Park	Meifeng Mountain Park
D	1.8372	1.2912	1.2840	1.2005	1.1554
R2	0.9649	0.9712	0.9575	0.9817	0.9931

) was obtained by calculating the center distance and average radius of the spatial structure distribution of the park using Formula (2), and drawn $\left(\ln S,\ln R_s\right)$ into a double logarithmic coordinate map (Please see Appendix A of

Table A1. Park system aggregation dimensions based on White Horse River Park.

S	RS	Park	lnS	lnRS
1	0	White Horse Park’	0	0
2	1474.13	West Lake Park’	0.69315	7.29583
3	1941.51	Jinniu Mountain Park’	1.09861	7.57122
4	2153.91	Meifeng Mountain Park’	1.38629	7.67504
5	2276.38	Zuohai Park’	1.60944	7.73034
6	2364.84	North Park of Minjiang Park ‘	1.79176	7.76847
7	2447.13	South Park’	1.94591	7.80267
8	2518.85	South Park of Minjiang Park’	2.07944	7.83156
9	2624.57	Hot Spring Park’	2.19723	7.87267
10	2711.06	Overseas Chinese Park’	2.30259	7.90509
11	2819.10	North Riverside Ecological Park ‘	2.3979	7.94417
12	2967.16	Jinji Mountain Park’	2.48491	7.99536
13	3136.19	Guangming Harbor Park’	2.56495	8.05076
14	3283.30	Wufeng Country Park’	2.63906	8.09661
15	3417.10	Wufeng Park’	2.70805	8.13655
16	3576.8	Qinting Lake Park’	2.77259	8.18223
17	3741.52	Beach Park’	2.83321	8.22725
18	3891.04	Helin Ecological Park’	2.89037	8.26643
19	4021.57	Jinshan Park’	2.94444	8.29943
20	4148.29	Jinan River Park’	2.99573	8.33045
21	4271.01	Niugang Mountain Park’	3.04452	8.35961
22	4446.12	Gaogai Mountain Park’	3.09104	8.39979
23	4609.77	Sea of Flower Park ‘	3.13549	8.43593
24	4977.19	South Riverside Ecological Park’	3.17805	8.51262

for supporting data). The spatial structure of the park system centered on Baima River Park is two-stage (Figure 3) and has a scaleless range ($\ln S$: 1.79~3.18). The aggregation dimension value $D=1.8372<2$, and R² = 0.9649, with a good fit of the regression line to the observation. The hypothesis that the park system has fractal characteristics stands, and showed that the spatial aggregation pattern and self-organization evolution have a centripetal trend. The central park has some attraction to the surrounding parks, and the attraction follows the law of spatial distance attenuation.

If the park system evolution follows a Diffusion-Limited Cluster Aggregation (DLCA) model, i.e., the system at the state with the best structural effects, the ideal aggregation dimension is 1.78. Referring to the division of model structure stage from a previous study,” 0 < D ≤ 0.90” changes into the primary stage of system evolution; “0.90 < D < 1.50” is regarded as the middle stage, “1.50 ≤ D < 1.78” is considered to be the late stage, and “1.78 ≤ D ≤ 2” is the advanced stage [40]. Furthermore, in the scaleless range, the park system (D = 1.8372) has entered the advanced stage of DLCA, indicating that the whole system had matured and spatial structure effects were significant. Here, as the system entered an advanced stage and there was a non-scaleless range, we assumed that there might be multiple central parks in the system.

To ensure the rigor of the argument, we analyzed parks in the non-scaleless range, which include: West Lake Park, Zuohai Park, Jinniu Mountain Park and Meifeng Mountain Park. These four parks are among the most popular parks in Fuzhou, with high frequencies of visitation, comprehensive infrastructure and well-organized spatial layout. Therefore, we hypothesized that the above four parks were also the central parks of the park system, meaning that the Fuzhou park system has a double-center structure. Next, we calculated the aggregation fractal dimension “D” with the above four parks as park centers, respectively, and the corresponding results are shown in Table 1 and Figure 4 (Please see Appendix A of

Table A2. Park system aggregation dimensions based on Zuohai Park.

S	RS	Park	lnS	lnRS
1	0	Zuohai Park’	0	0
2	530.152	West Lake Park’	0.69315	6.27316
3	1034.87	Meifeng Mountain Park’	1.09861	6.94203
4	1430.40	Wufeng Park’	1.38629	7.26571
5	1657.61	Jinniu Mountain Park’	1.60944	7.41313
6	1871.19	Wufeng Country Park’	1.79176	7.53433
7	2012.82	White Horse Park’	1.94591	7.60729
8	2118.25	Hot Spring Park’	2.07944	7.65834
9	2310.41	Qinting Lake Park’	2.19722	7.74518
10	2500.14	Jinji Mountain Park’	2.30259	7.8241
11	2742.74	South Park of Minjiang Park’	2.3979	7.91671
12	3004.12	South Park’	2.48491	8.00774
13	3260.22	North Park of Minjiang Park ‘	2.56495	8.08955
14	3470.56	Beach Park’	2.63906	8.15207
15	3701.10	Overseas Chinese Park’	2.70805	8.21638
16	3892.5	Helin Ecological Park’	2.77259	8.26681
17	4056.81	Jinan River Park’	2.83321	8.30815
18	4199.17	North Riverside Ecological Park’	2.89037	8.34264
19	4324.73	Niugang Mountain Park’	2.94444	8.3721
20	4460.55	Guangming Harbor Park’	2.99573	8.40303
21	4662.46	Jinshan Park’	3.04452	8.4473
22	4976.44	Sea of Flower Park’	3.09104	8.51247
23	5287.15	Gaogai Mountain Park’	3.13549	8.57304
24	5761.86	South Riverside Ecological Park’	3.17805	8.65901

,

Table A3. Park system aggregation dimensions based on Jinniu Mountain Park.

S	RS	Park	lnS	lnRS
1	0	Jinniu Mountain Park’	0	0
2	564.385	Meifeng Mountain Park’	0.69315	6.33574
3	1436.58	Zuohai Park’	1.09861	7.27002
4	1758.20	West Lake Park’	1.38629	7.47205
5	1927.32	South Park of Minjiang Park’	1.60944	7.56389
6	2062.97	White Horse Park’	1.79176	7.6319
7	2157.37	Wufeng Country Park’	1.94591	7.67665
8	2345.12	Beach Park’	2.07944	7.76009
9	2602.71	Wufeng Park’	2.19722	7.86431
10	2881.62	North Park of Minjiang Park’	2.30259	7.96611
11	3100.69	Hot Spring Park’	2.3979	8.03938
12	3316.53	Overseas Chinese Park’	2.48491	8.10667
13	3534.85	Jinshan Park’	2.56495	8.17043
14	3713.13	South Park ‘	2.63906	8.21963
15	3891.03	Qinting Lake Park’	2.70805	8.26643
16	4041.18	Jinji Mountain Park’	2.77259	8.30429
17	4208.53	North Riverside Ecological Park’	2.83321	8.34487
18	4440.69	Guangming Harbor Park’	2.89037	8.39857
19	4688.97	Helin Ecological Park’	2.94444	8.45297
20	4910.55	Jinan River Park’	2.99573	8.49914
21	5110.36	Niugang Mountain Park’	3.04452	8.53903
22	5362.23	Gaogai Mountain Park’	3.09104	8.58714
23	5641.31	Sea of Flower Park’	3.13549	8.63787
24	6117.97	South Riverside Ecological Park’	3.17805	8.71898

,

Table A4. Park system aggregation dimensions based on Meifeng Mountain Park.

S	RS	Park	lnS	lnRS
1	0	Meifeng Mountain Park’	0	0
2	564.385	Jinniu Mountain Park’	0.69315	6.33574
3	1046.87	Zuohai Park’	1.09861	6.95356
4	1317.61	West Lake Park’	1.38629	7.18358
5	1525.22	Wufeng Country Park’	1.60944	7.32989
6	1773.90	White Horse Park’	1.79176	7.48094
7	2047.94	South Park of Minjiang Park’	1.94591	7.62459
8	2247.79	Wufeng Park’	2.07944	7.7177
9	2489.96	Beach Park’	2.19722	7.82002
10	2711.74	Hot Spring Park’	2.30259	7.90535
11	3005.24	Qinting Lake Park’	2.3979	8.00811
12	3231.29	North Park of Minjiang Park’	2.48491	8.08064
13	3434.28	Jinji Mountain Park’	2.56495	8.14156
14	3624.32	South Park’	2.63906	8.19542
15	3786.70	Overseas Chinese Park’	2.70805	8.23925
16	3990.95	Jinshan Park’	2.77259	8.29178
17	4173.46	North Riverside Ecological Park’	2.83321	8.3365
18	4401.31	Guangming Harbor Park’	2.89037	8.38966
19	4613.62	Helin Ecological Park’	2.94444	8.43677
20	4802.81	Jinan River Park’	2.99573	8.47696
21	4973.57	Niugang Mountain Park’	3.04452	8.51189
22	5273.37	Gaogai Mountain Park’	3.09104	8.57043
23	5562.07	Sea of Flower Park’	3.13549	8.62373
24	6053.29	South Riverside Ecological Park’	3.17805	8.70836

and

Table A5. Park system aggregation dimensions based on West Lake Park.

S	RS	Park	lnS	lnRS
1	0	West Lake Park’	0	0
2	530.152	Zuohai Park’	0.69315	6.27316
3	1185.86	Meifeng Mountain Park’	1.09861	7.07822
4	1463.29	White Horse Park’	1.38629	7.28844
5	1665.16	Hot Spring Park’	1.60944	7.41768
6	1827.46	Jinniu Mountain Park’	1.79176	7.51068
7	2006.36	Wufeng Park’	1.94591	7.60408
8	2225.99	Wufeng Country Park’	2.07944	7.70796
9	2382.90	Jinji Mountain Park’	2.19723	7.77608
10	2532.37	Qinting Lake Park’	2.30259	7.83691
11	2737.79	South Park of Minjiang Park’	2.3979	7.91491
12	2900.95	South Park’	2.48491	7.9728
13	3094.55	North Park of Minjiang Park’	2.56495	8.0374
14	3311.80	North Riverside Ecological Park’	2.63906	8.10525
15	3497.93	Overseas Chinese Park’	2.70805	8.15993
16	3661.50	Helin Ecological Park’	2.77259	8.20563
17	3805.99	Jinan River Park’	2.83321	8.24433
18	3936.16	Niugang Mountain Park’	2.89037	8.27796
19	4054.69	Guangming Harbor Park’	2.94444	8.30763
20	4160.57	Beach Park’	2.99573	8.33341
21	4372.10	Jinshan Park’	3.04452	8.383
22	4652.91	Sea of Flower Park ‘	3.09104	8.44525
23	4941.29	Gaogai Mountain Park’	3.13549	8.50538
24	5390.86	South Riverside Ecological Park’	3.17805	8.59246

for supporting data).

The results indicated that the D values of the park systems centered on the above four parks were in the range of [1.1554, 1.2912], which were all in the middle stage of the DLCA model, indicating that the four parks were also the centers of the park systems. The spatial distribution of the park system followed a density decay from the center to the periphery, accompanied by a gradual decrease in the attractiveness of the center. Since the aggregation dimension D can reflect the development level of the system, we suggested that by assuming different parks as the center of the system, if the assumptions all hold, D can reflect the attractiveness level and dominance of the park. Therefore, the order of the adsorption effect of the central park on the general park was: Fuzhou West Lake Park ($D=1.2912$) > Jinniushan Park ($D=1.82840$) > Zuohai Park ($D=1.2005$) > Meifeng Mountain Park ($D=1.1554$). Since the four parks are closely distributed and have similar development levels, we deem that the four parks form a central cluster, which has been referred to as the Four-Park Cluster. There is a construction principle for all classical fractals, which has a self-similar infinite nested structure. Combined with the aggregation fractal dimension values of the five parks, we concluded that the hypothesis that there are multiple centers in the Fuzhou comprehensive park system holds true, with the centers being Baima River Park and the Four-Park Cluster, respectively.

3.2. Analysis of System Spatial Balance Based on Grid Dimension

The grid dimension reflects the rate of coverage of parks in the city, and the increase indicates that the balance degree and filling degree of the parks increased. The selection of a rectangle on the vector map of the spatial distribution of the park system, which contains 24 park samples, changes the visible rectangular area into a unit, and each side of K is divided equally. The calculation of the probability $P_{ij}\left(r\right)$, with a change in the $r$ value, enables the determination of the corresponding $K\left(r\right)$ and P_i values, and the corresponding $I\left(r\right)$ can be obtained using Formula (5) (

Table 2. The determining dates of grid dimension of the Fuzhou park system.

K	2	3	4	5	6	7	8	9	10	11	12
N	4	9	12	13	17	17	18	17	16	18	19
I(r)	1.319	1.896	2.196	2.181	2.550	2.528	2.586	2.550	2.470	2.608	2.665

). Next, the grid dimension calculation data were obtained from Formulas (5) and (6), and $\left(\right(\ln K,\ln N)$ and $(\ln K,\ln I(r\left)\right)$ were drawn, leading to the transformation of $(\ln K,\ln N)$ and $(\ln K,\ln I(r\left)\right)$ into a double logarithmic coordinate map (please see Appendix B of

Table A6. Measurements for park system grid capacity dimension.

lnK	ε	lnε	N	lnN	I
0.69315	0.5000	−0.6932	4	1.386294	1.318569
1.09861	0.33333	−1.0986	9	2.197225	1.896191
1.38629	0.25000	−1.3863	12	2.484907	2.195531
1.60944	0.20000	−1.6094	13	2.564949	2.181372
1.79176	0.16667	−1.7918	17	2.833213	2.549748
1.94591	0.14286	−1.9459	17	2.833213	2.527946
2.07944	0.12500	−2.0794	18	2.890372	2.585708
2.19723	0.11111	−2.1972	17	2.833213	2.549748
2.30259	0.10000	−2.3026	16	2.772589	2.470184
2.3979	0.09091	−2.3979	18	2.890372	2.60751
2.48491	0.08333	−2.4849	19	2.944439	2.665273

and

Table A7. Measurements for park system grid information dimension.

lnK	ε	lnε	N	lnN	I
0.693	0.500	−0.693	4	1.386	1.319
1.099	0.333	−1.099	9	2.197	1.896
1.386	0.25	−1.386	12	2.485	2.196
1.609	0.200	−1.609	13	2.565	2.181
1.792	0.167	−1.792	17	2.833	2.55
1.946	0.143	−1.946	17	2.833	2.528
2.079	0.125	−2.079	18	2.89	2.586
2.197	0.111	−2.197	17	2.833	2.55
2.303	0.1	−2.303	16	2.773	2.47
2.398	0.091	−2.398	18	2.89	2.608
2.485	0.083	−2.485	19	2.944	2.665

for supporting data). The grid capacity dimension $D_0$ and grid information dimension $D_1$ are then determined (

Table 3. The determining data of grid dimension of Fuzhou park system.

Type	Capacity Dimension	Information Dimension
D	0.7785	0.7198
R2	0.9559	0.9076

).

Figure 5 indicates that the spatial structure of the park system is mathematically significant when measured on a scaleless range ($\ln K$ 1.0986–1.9459) with grid dimension $D$. The capacity dimension $D_0$ = 0.7785, $R_0^2$ = 0.90, the grid information dimension $D_1$ = 0.7198, $R_0^2$ = 0.9076. $D_0$ and $D_1$ are less than 1, which states that the self-organization evolution is not balanced, and the spatial distribution has some frequency bias. In addition, similar values of $D_0$ and $D_1$ indicate that the probabilities of park distribution in the region are relatively similar, and the system has a high degree of spatial distribution uniformity and a relatively simple overall fractal structure. The formation of such fractal characteristics is the result of the self-organization evolution of the park system. Fuzhou has a complex topography with numerous mountains and rivers, a high degree of reliance on geographical lines for park development and construction, and a simple spatial arrangement of the system.

3.3. Exploration of Connectivity of System Space by Correlation Dimension

The crow distance and dairy cow distance between the 24 parks were calculated using ArcGIS 10.5 Point Analysis and OD Cost Matrix Tool of Network Analysis to form the distance matrix table. The use of Formulas (9) and (10) resulted in a step length of 1 km; $r$ was changed to obtain a series of $N\left(r\right)$, and the double logarithm of $(r,C(r\left)\right)$ point pair series and the $\mathrm{In}C\left(r\right)$ coordinate diagram were drawn (Please see Appendix C of

Table A8. Measurements for park system cow correlation dimension.

r	lnr	C	lnC
1	0	0.00521	−5.2575
2	0.69315	0.01389	−4.2767
3	1.09861	0.03472	−3.3604
4	1.38629	0.07465	−2.5949
5	1.60944	0.1059	−2.2452
6	1.79176	0.16146	−1.8235
7	1.94591	0.21701	−1.5278
8	2.07944	0.25868	−1.3522
9	2.19722	0.31424	−1.1576
10	2.30259	0.35243	−1.0429
11	2.39790	0.38715	−0.9489
12	2.48491	0.41667	−0.8755

and

Table A9. Measurements for park system crow correlation dimension.

r	lnr	C	lnC
1	0	0.01042	−4.5643
2	0.69315	0.02083	−3.8712
3	1.09861	0.06944	−2.6672
4	1.38629	0.11285	−2.1817
5	1.60944	0.17014	−1.7711
6	1.79176	0.24132	−1.4216
7	1.94591	0.29514	−1.2203
8	2.07944	0.34896	−1.0528
9	2.19722	0.38715	−0.9489
10	2.30259	0.42361	−0.8589
11	2.39790	0.43924	−0.8227
12	2.48491	0.46007	−0.7764

for supporting data). Finally, the crow and cow dimension were obtained (

Table 4. The determining data of correlation dimension of the Fuzhou park system.

Type	Crow Dimension		Cow Dimension
Scaleless Range	I	II	I	II
D	1.8366	0.9293	1.9641	1.2308
R2	0.9742	0.9661	0.9883	0.9879

).

There are obvious scaleless ranges in the system, whether in the crow dimension or cow dimension (Figure 6), which provides additional evidence that the spatial structure of the park system in Fuzhou is fractal, and the system manifests as multi-fractal. During the wide interval scaleless range I ($\ln C_{\left(r\right)}:$ 0–1.7917), the crow dimension $D_{0-1}$ is 1.8366 (correlation coefficient $R_{0-1}^2$ = 0.9742) and cow correlation dimension $D_{1-1}$ is 1.9641 ($R_{1-1}^2$ = 0.9883). When the spatial correlation dimension $D\to 2$, it indicates that the spatial distribution of parks within the park system is quite balanced. At this point, the crow–cow dimension $d$ = 1.0694, close to 1, indicates that the accessibility of the transportation network tends to be ideal for the parks in Fuzhou within a distance of 1 km to 7 km, with strong spatial coherence between each park.

During the relatively narrow scaleless range II ($\ln C_{\left(r\right)}:$ 1.9459–2.2849), the crow dimension $D_{0-2}$ is 0.9293 (correlation coefficient $R_{0-2}^2$ = 0.9661) and cow correlation dimension $D_{1-2}$ is 1.2308 ($R_{1-2}^2$ = 0.9879). The correlation dimension D → 1 means that the park system is relatively evenly clustered along the geographical line, which makes the spatial distribution conducive to the construction of the park system and the development of the park portfolio series. By now, crow–cow dimension D = 1.5181, with a d value farther away from 1 relative to the scaleless range I, indicating that the accessibility of the traffic road system within this range is relatively weak. The large difference between the results of the two UBN ratios indicates that the agglomeration of parks in the central city of Fuzhou results in good accessibility and spatial connections between parks for daily distances (within 1–7 km). For long-distance trips of 7–12 km, inter-park connections are weak and the construction of large-scale inter-park transport networks still needs to be enhanced.

4. Discussion

4.1. Methodological Contributions

A growing amount of evidence shows that it is feasible to reveal the internal laws of complex systems using the fractal theory [41,42], which can provide a better analysis of the order and regularity of the internal structure of the system from the perspective of the nature, characteristics and laws of the phenomenon itself. Our study states that it is feasible to apply fractal theory to the study of urban park system spaces, and provides a new perspective to explain the spatial structure of park systems. The fractal dimension model no longer simplifies the spatial layout of the park system into a linear problem for processing [43,44,45]. It can describe the degree of development of the spatial structure of the park system and correct the issue that it is difficult to quantitatively describe the developmental status and trends of the park systems in previous research. These findings prove that the park system is a hierarchical system connected with the cascade structure of complex networks, which is in the middle and advanced stage of Diffusion-Limited Cluster Aggregation. The self-organization optimization of the system has not yet been fully formed, which indicates that there is still room for optimization. On the one hand, these findings are conducive to exploring a deeper internal spatial operation mechanism, improving the efficiency of spatial structure, and promoting the system to continue toward fractal optimization. Alternatively, they are helpful for planners and policy makers to provide theoretical support regarding the spatial layout of parks.

4.2. The Judgment Method and Cause of the Multiple Core Space Structure

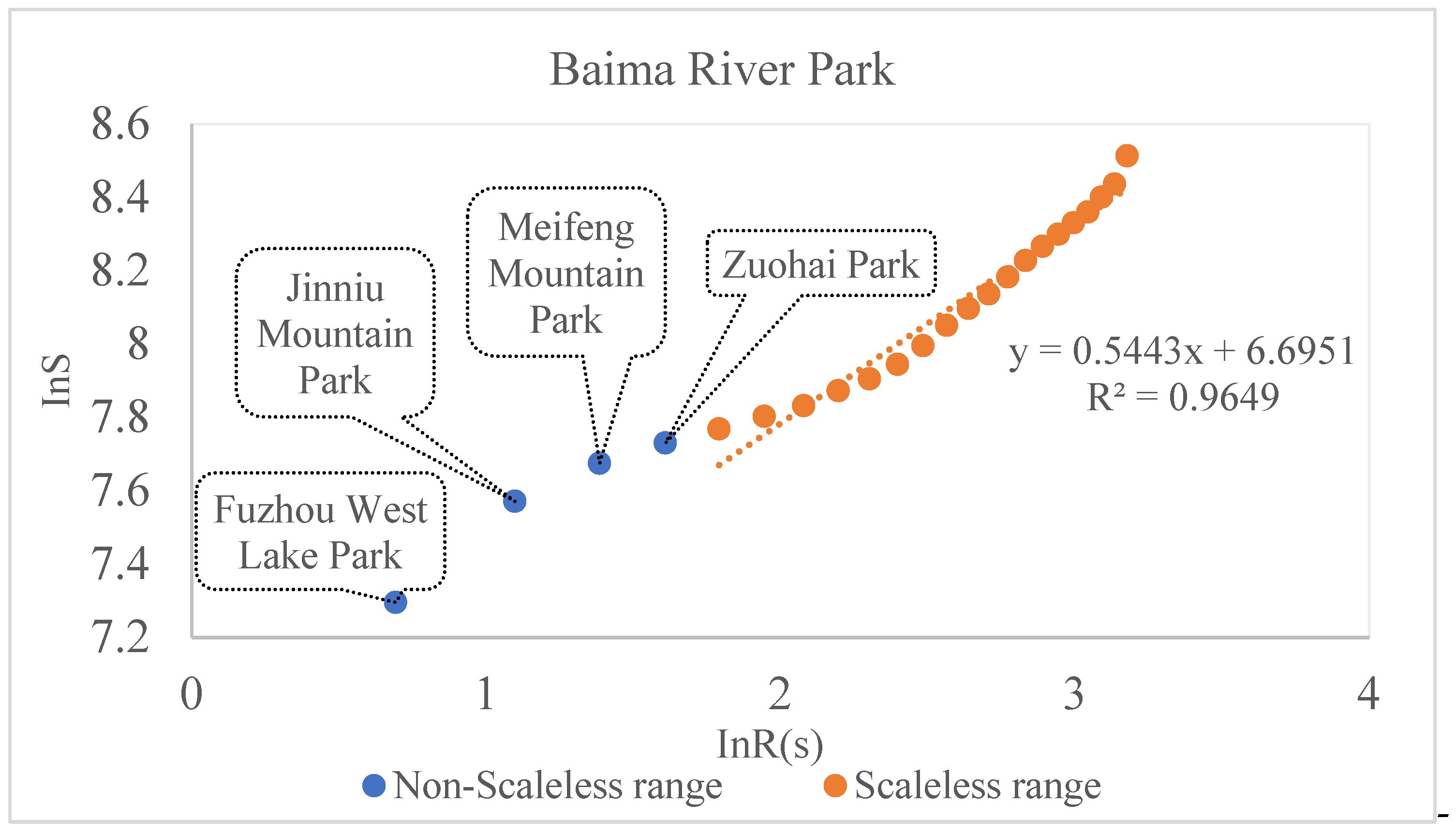
Significantly, this study concluded that the spatial structure of the Fuzhou Park system is a multi-center-level mode, including combination-center parks (Four-Park Cluster) and single-center park (Baima River Park). Our findings demonstrate a method for exploring polycentric spatial patterns. When the aggregated fractal model of the system represents a local fractal or multi-fractal, it should not only determine the scaleless range, but also further analyze the non-scaleless range. The scaleless range indicates that the park system has fractal characteristics, and the non-scaleless range may be another center of the system or an element deviating from the system. The aggregation dimension is calculated by centering on the elements of the non-scaleless range. If the aggregation dimension is lower than 2, the system has multiple centers. In subsequent system center research based on aggregation dimension, the analysis of the non-scaleless range and perfect logic of spatial pattern analysis should be the focus of intensive study.

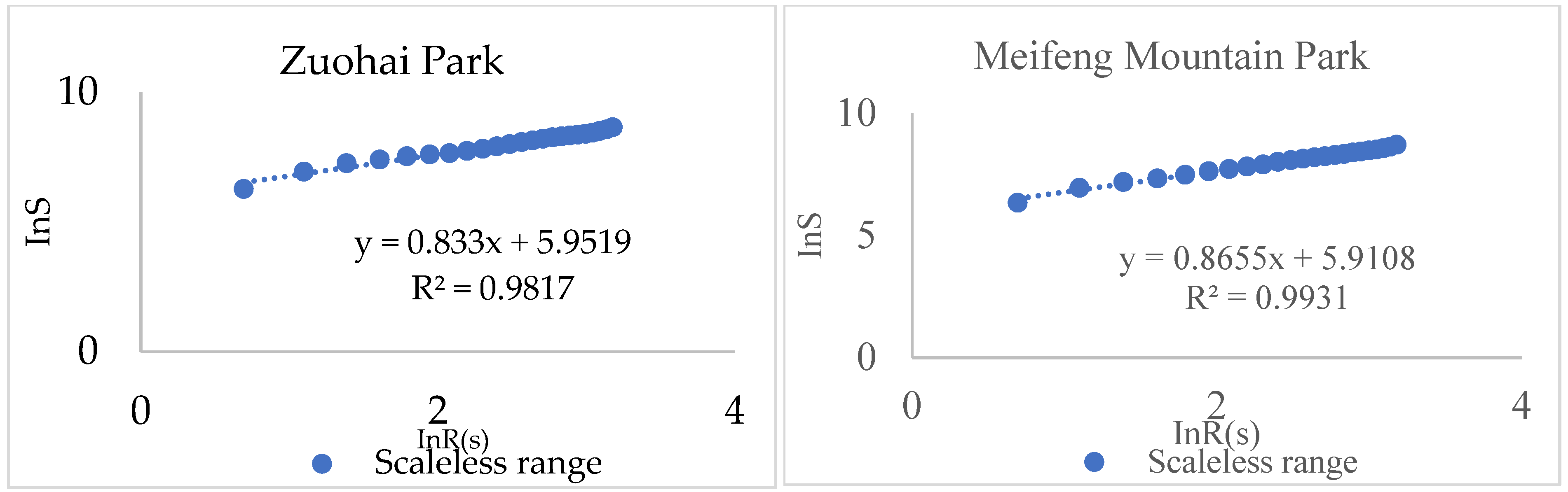
Remarkably, a new understanding of aggregation fractal dimension D has been introduced. Within the same system, it is assumed that different parks are the center of the system. When the system has fractal characteristics, a higher D value indicates a stronger adsorption and better degree of development of the central park. Among the Four-Park Cluster, the order of the degree of central park development is Fuzhou West Lake Park > Jinniu Mountain Park > Zuohai Park > Meifeng Mountain Park. Subsequently, the system space formed by the two centers is compared. The width of the scaleless range indicates that the core of the Four-Park Cluster has a wider range, which indicates that it is more mature. However, in terms of the geographical location and overall urban development strategies to the south and west, compared with the Four-Park Clusters located in the northwest of the region, Baima River Park has a larger adsorption radius and stronger control over the overall the Fuzhou Park system. Combined with the ideal stage of system development represented by the aggregation dimension values, Baima River Park, as the center of the system, has more structural advantages and development potential, and the multi-level nested center structure will be more stable. As a result, after the system development process, we suggest that the two centers’ linkage be strengthened, spatial integration be conducted, and the optimization of system structure be promoted.

4.3. The Characteristics and Driving Force of the Park System

The urban park system has formed a complex fractal structure and is in the process of continuous spatial evolution. It is extremely significant to explore the structural characteristics and driving mechanism of evolution for the optimization of the system. Based on the fractal results, the driving mechanism of park spatial layout behind the numerical value is explained in more detail.

There are two reasons why the system evolves into a multi-center nested spatial pattern. On the one hand, the Four-Park Cluster is located in the old town (Gulou district, Figure 2), which has a stable service population and earlier formation of its center. Baima River Park is relatively far away from the old urban area in space and is geographically obstructed, so it recieved little absorption and shielding effects during its evolution. Alternatively, with the development of the city southwards and along the river, a number of parks have been built in Taijiang District and Changshan District (mainly in the southern part of the Baima River Park), enhancing the radius of absorption and influence of the Baima River Park. The natural and human conditions of the new park are substantially different from those of the earlier parks in historical urban areas in the north. Therefore, geographical location and policy planning should enable the possibility of having them evolve into a relatively independent center, forming a dual center in the overall system space. Considering the Fuzhou City Master Plan (Appendix D), the dynamics of the spatial structure of the park system has a strong similarity to urbanization development [46]. Fuzhou’s planning concept of green space coordination and development along the river will enhance the status of the Baima River Park.

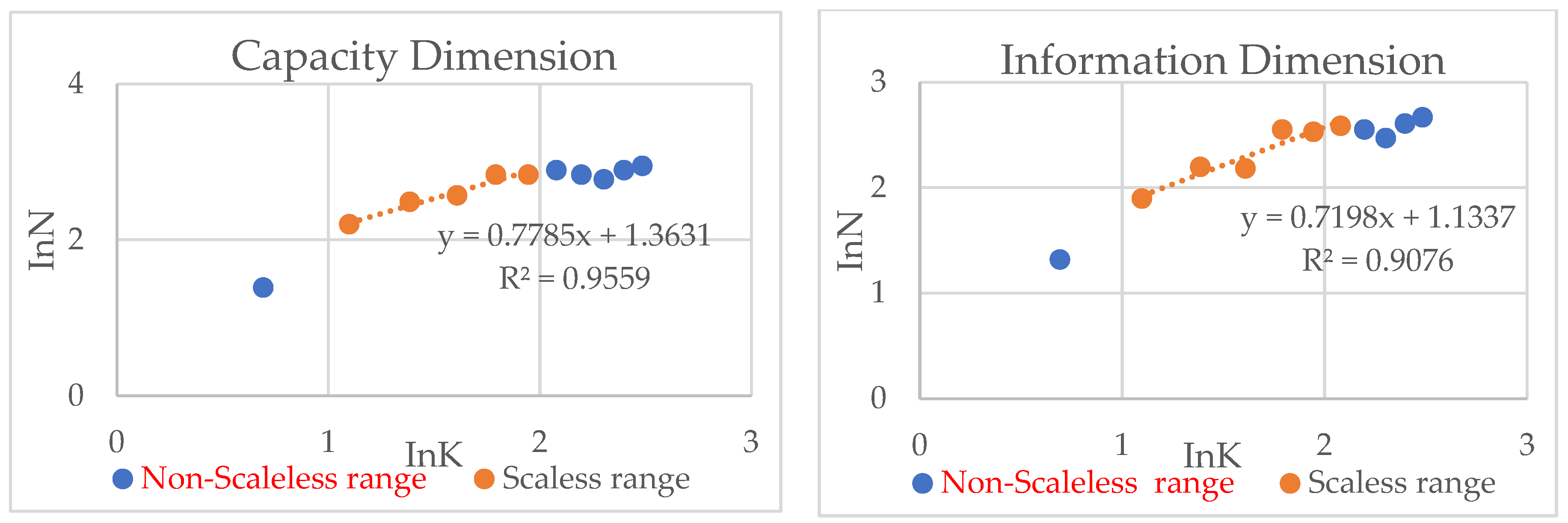
Further, the equilibrium and filling of the park system were analyzed based on the grid dimension. Both the grid information dimension and the grid capacity dimension tend to be close to one. Additionally, the results of the spatial distribution indicate a certain extent of bias. Fuzhou’s comprehensive parks are mainly located in close proximity to mountains and rivers in the territory, with distinct regional characteristics. The clustering of parks in areas with good natural resource endowments demonstrates that park planning follows nature, preserves the landscape pattern and builds a regional park system with a spatial layout. The similar values of the capacity dimension and information dimension demonstrate the simplicity of the spatial pattern of the park system in terms of fractal structure. The results show that the existing spatial pattern of the park system in Fuzhou is characterized by a simple generative logic and a mechanistic external structure. Therefore, we suggest that, based on the ecological network of “one city and two rings” [46], we should emphasize the plurality and integrity of parkland from a holistic systemic perspective, and highlight the organic connection of parks, rather than as viewing them as simple urban spatial fillers.

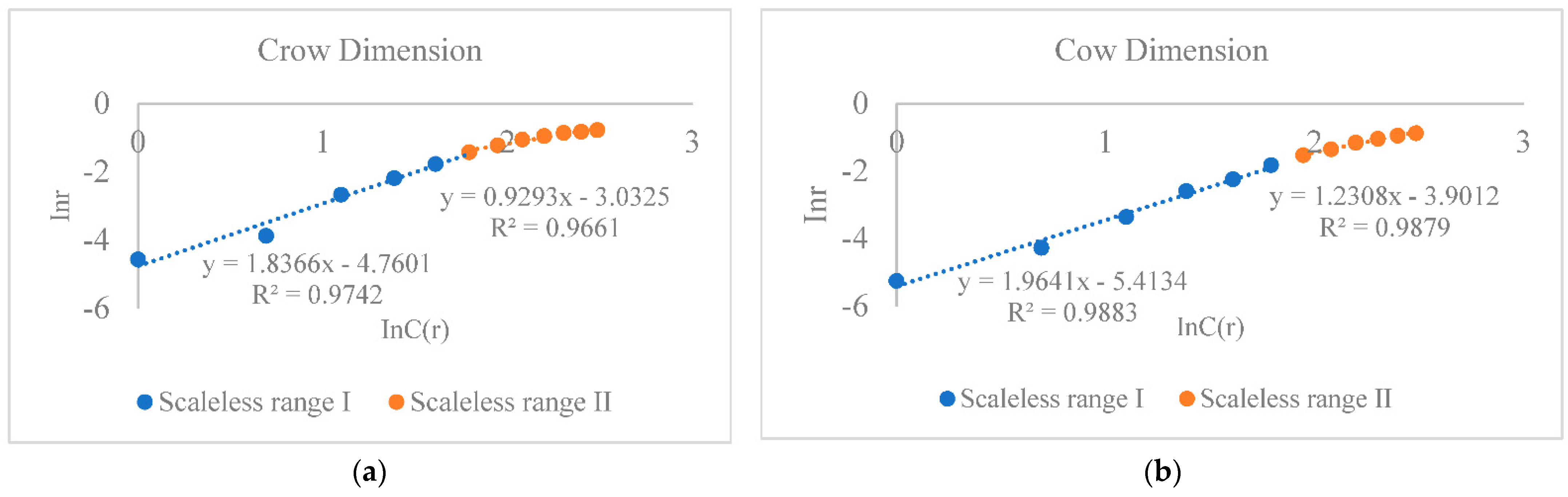
Lastly, the two-part correlation dimension demonstrated the spatial variability in the accessibility of the park system’s transportation network. Both the correlation dimension and the grid dimension reflect the spatial distribution of the park system to some extent, but the former focuses more on the degree of correlation between each park. Park distances within 1 km–7 km, crow correlation dimension and cow correlation dimension are both close to 2, showing a good accessibility of spatial distribution and an ideal transportation network for the system. Observing the distribution of the parks, it was found that most of the parks are located along roads (Figure 1), with good accessibility and relatively good transport network support facilities. Similar results were found in previous studies in other cities [47,48]. In addition, good connectivity between parks contributes to the structure of the park network, which will be discussed in the next sub-section. The crow–cow dimension ration = 1.5181 within a park distance of 7–12 km, indicating that the connectivity of the park system within this range is not promising and that more attention needs to be paid to the systematization and networking of urban green spaces at a large scale. Huang et al. (2021) used a spatial synthesis method and a geographical regression weighting method, and it was concluded that the accessibility of parks in Fuzhou City decreases from the central urban area to the peripheral areas and is related to the high level of street integration [49]. The high density of the road network in the center of the map (Gulou District and Taijiang District) and the low accessibility of most streets in the peripheral Jin’an District and Cangshan District led to a high accessibility of the network of the internal transport system of the park system. As a result, the internal transport network of the park system is highly accessible, while the external transport network is poorly accessible.

In short, the multi-scale correlation dimension of the park system shows a transformation in measurement geometry, reflecting spatial differences in the accessibility of the system’s transport network, in line with the results of spatial syntax studies reflecting pedestrian orientation. We therefore suggest that emphasis should be placed on park development in peripheral areas or that the construction of a transport network which is centered on development axes should be studied in more depth. The results of the three dimensions indicate that the multidimensional nature of Fuzhou’s park system and the interwoven nature of the city dictate that its planning layout is influenced by multiple factors. These include, but are not limited to, geographic location, policies and transport networks, and analyzing the influence of these factors on spatial patterns allows the essential causes of the fractal dimensionality of the park system to be dissected at different scales [50].

4.4. Implications for Urban Park Planning and Management

The garden city is the original exploration of urban–ecological harmony and integration, advocating for the breaking of the urban–rural dichotomy. However, due to the simple geometry of the spatial composition and the low economy of operation, its application is still somewhat limited in the context of the contradiction between human and land and compact cities. The park city is a variation of the garden city, and is in line with the Chinese philosophy of “Heaven and Man” and “Taoism and Nature”. The park city emphasizes the systematic, functional and orderly nature of parks, aiming at the organic integration of natural ecology with the city, forming a structured and complete system. Further, the influence of the city has broken through the original administrative boundaries as a result of the polarizing effect of the metropolitan area. As an important carrier of the spatial connection between urban and rural areas, how to create a park system at the regional scale is also one of the key development propositions for the future. The urban system forms an orderly, self-organized spatial structure supported by material, information and human flows [51,52], and with the change in spatial scale, expanding the main subject into an urban subsystem (in this case, the park system) is still adaptable with urban agglomeration. Based on the calculation of the fractal dimension of the park system above, this study proposed an evolutionary model of the park system and related development strategies through the extraction and analysis of spatial fractals, at the city and regional levels, in the expectation of moving from urban parks to a park city and then to a regional park zone.

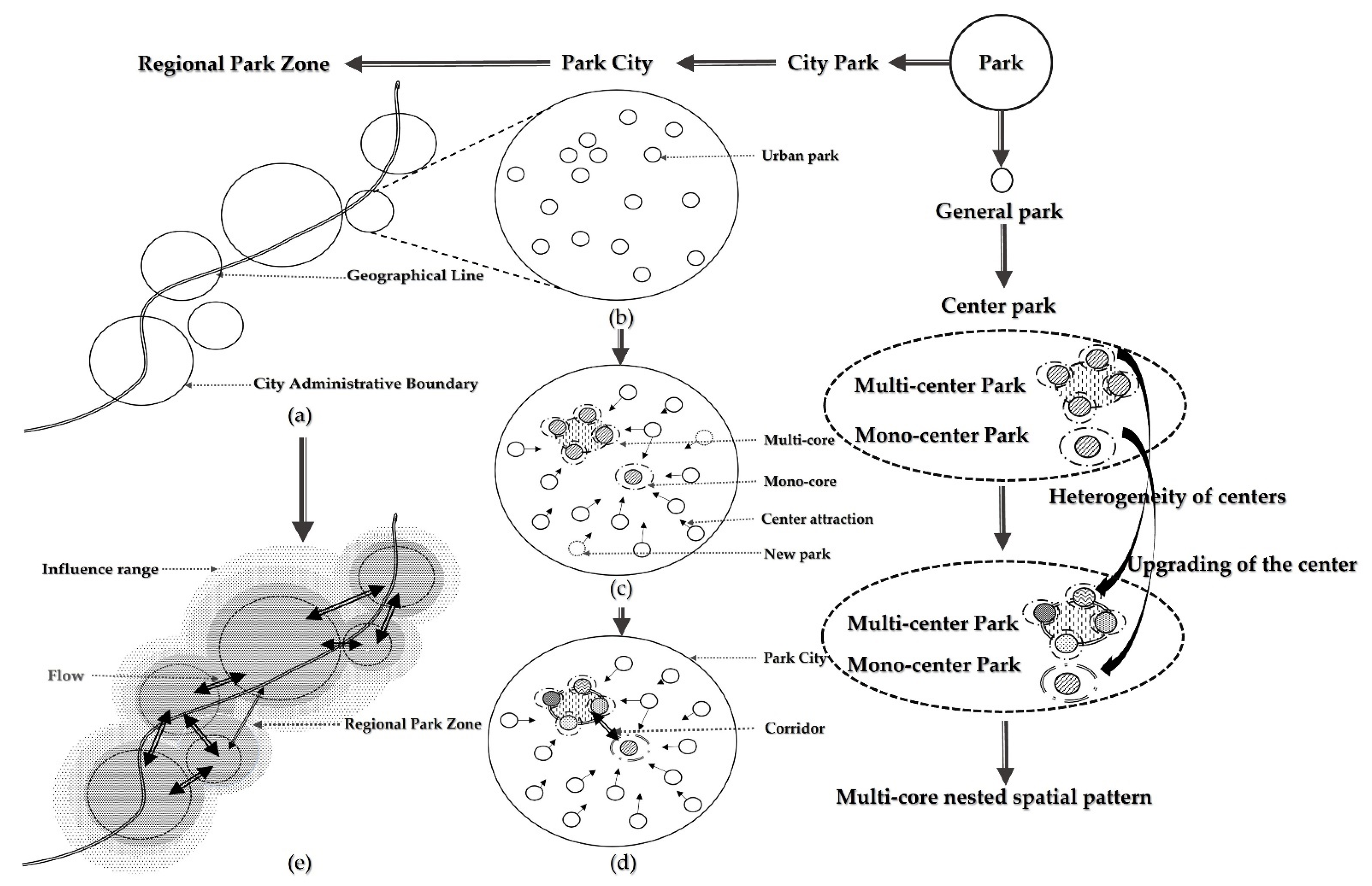
Firstly, at the regional scale, urban agglomeration basically develops along geographical lines (Figure 7a), for example, Shanghai, Suzhou and Nanjing form the Yangtze River Delta urban agglomeration based on the Yangtze River. At the urban level, the early spatial arrangement of parks has not been very structured (Figure 7b), but as the park system develops, two types of parks gradually emerge: the center park and the general park. In our study, the central park of the park system was determined by calculating and comparing the agglomeration dimension, which avoids the influence of subjective selection bias on the results and is an effective method for objectively measuring spatial morphological characteristics.

The above-mentioned background can serve as a consensus for the case studies. The following model description takes the Fuzhou city park system as an example. Our findings indicated that the park system in Fuzhou is currently in a multi-center nested spatial pattern (Figure 7c). The center is a combination of Baima River Park (a single center) and the Four-Park Cluster, which is located in the old town, was developed relatively early and has a mature range of infrastructure and services. Our findings currently show that the park system is in the spatial pattern of multi-core nesting, and the aggregation fractal dimension of Baima River Park is higher than that of the Four-Park Cluster, which indicates that the developmental degree of the system centered on it is more effective, and the self-organization optimization ability is stronger. In addition, the more concentrated distribution of parks in the vicinity of the Four-Park Cluster has resulted in homogeneity and intense competition for resources in the area. For this reason, we suggest that parks can integrate cultural and social elements into the system through differentiated development (heterogeneity of centers), reduce the shielding effect within the system, and build functional themes that reflect human characteristics, natural endowments and life interests. For the Baima River Park, which has great potential for development, our research indicated that further developing and upgrading the functional structure (upgrading of the center) and increasing the radiating power of the central park is a priority (center attraction). Our study shows that it is a priority to further develop and upgrade the functional structure (upgrading of the center), which will help to fully exploit the advantages of the fractal structure and enhance the system’s ability to self-organize and evolve. Moreover, the capacity and information dimensions indicate that the urban park system is not sufficiently populated and that the number and spatial balance of parks needs to be further improved in the future.

In the process of upgrading from urban parks to a park city, it is not enough to rely on the self-organised optimisation of the park system by enhancing the central park individually. The two-stage correlation dimension suggests that there are spatially disconnected differences in accessibility between the parks. The corridor can be understood as a belt park and green transportation infrastructure at different scales. The concept of a corridor is reflected in some studies as an ecological network of green spaces, which is an important part of modern metropolitan regional planning [53], such as in Stockholm [54], Shanghai [55], Sheffield [56] and so on. Fuzhou Park planners have strengthened the development and connection between the parks through the construction of Fu Forest Trail, which serves as an urban forest trail that connects Zuohai Park, Jinniu Mountain Park, National Light Park and Meifeng Mountain Park. A study on Fu Forest Trail conducted a comprehensive evaluation of tourists [57], and showed that the tourists are satisfied with the trails, which to some extent supports the validity of the conclusion that the Four-Park Cluster has a core linkage. However, Fu Forest Trail may contain better park elements and more streamlined designs based on the result of aggregation fractal dimension, changing National Light Park to West Lake Park, and then establishing a two-center corridor (Four-Park Cluster–Single Park), which may make more sense in terms of spatial integration and efficiency gains for the whole system. In addition, Lin et al. (2019) also used the Fu Forest Trail skyline evaluated by fractal dimension to draw the conclusion that a skyline with a higher fractal dimension is not necessarily equivalent to a satisfactory contour and should be designed in combination with subjective aesthetics [44]. This is also a point worthy of attention when fractal dimension theory is applied to the guidance of park spatial layout, and the shaping of urban three-dimensional space aesthetics should be studied more intensively. Qian et al. (2018) proposed the potential index of a greenway to guide the construction of one in Wuhan that could enrich the landscape type and improve the suitability of land, which is of merit for the planners of Fu Forest Trail [58].

Because the system is under the continuous development of self-organizational optimization and external driving forces, when the core level of multicenter spatial mode is similar and subsystems are closely connected, the system will evolve further into a relatively even spatial pattern and a highly efficient collaborative system (Figure 7e). When the spatial distance between parks in a self-organized state is smaller than a critical degree, the attraction between them abruptly increases, in the non-typical sense of functional convergence. This can also be understood as the First Law of Geography [59], that any objects in close proximity are correlated. When both the spatial scale and its own attractiveness reach a certain threshold, the influence of the park system will break through the limits of administrative boundaries. We consider the regional park zone to be a manifestation of the combined effect of parks and the overall characteristics of the park system. At the urban scale, we used corridors to express the connectivity of the system, while at the regional scale we call it flow, which includes physical flow, information flow and human flow. Flow emphasizes morphology less than corridors, just as cities evolve into urban agglomerations bordering zones through flow. A mature and complete regional park zone will attract more urban residents to the city and create a more progressive urban image. It is considered that the coordinated development model of the park system is beyond the geometric scope in form, breaking the limits of maintaining the administrative boundaries. It is an exploration of the spatial development pattern of the park system at a regional scale, aiming to make it easier for residents to return to nature and to give them more accessibility, life and production.

4.5. Limitations and Further Research

Even though this study intended to use more scientific and advanced fractal theory to analyze the spatial structure, driving forces and development model of the Fuzhou park system, there are still some limitations regarding the research target and translation of results. Only the comprehensive parks with a greater influence on the park system were analyzed in terms of spatial structure, and the number of samples was limited. Therefore, subsequent studies could add block parks, community parks and pocket parks, calculating the weighted fractal dimension according to the degree of the park, which can more accurately reflect the spatial structure of the system. Moreover, since the study was only conducted in Fuzhou, it lacks a cross-city comparison. A complete spatiotemporal analysis in other cities would further increase the generalizability and depth of the study. In addition, understanding the self-organized structure of the park system from a macroscopic perspective deepens the knowledge of the park system, however, the research model is still in a relatively preliminary conceptualization stage. In this case, it is not possible to determine the threshold of the spatial extent of the self-organization effect, and thus, there is still a long way to go before the theory can be applied to actual park system planning.

5. Conclusions

The rationality of the spatial layout of the urban park system is a crucial reflection of the construction of urban residential environments. A radical understanding of the characteristics of the spatial structure and its internal mechanism will help to optimize the spatial pattern and increase social and economic benefits. In this study, the degree of development of the park system, its aggregation, balance, relevance and driving force of the spatial characteristics were analyzed with the aid of theory of fraction, which is a new perspective to explain the spatial structure and the inner law of the park system. The results indicate that the park system of Fuzhou has fractal characteristics, and it is in the middle and senior developmental stages of Diffusion-Limited Cluster Aggregation. According to the law of self-similarity, the park is distributed in a cohesive state around a central park, and the self-organization optimization of the system has not yet been fully formed. Remarkably, the degree of development of the central park can be determined by comparing the values of the aggregation dimension, using different parks as the center of the system. The spatial structure of the Fuzhou park system is a polycentric nested model with a newly emerging park center (Baima River Park) and a relatively mature Four-Park Cluster. The results of the correlation dimension show that the current system has good accessibility in a short distance (1 km to 7 km), but the accessibility in a long distance (7 km to 12 km) still requires improvement. In addition, the findings prove that the complex characteristics of the park system are primarily driven by physical and geographical conditions, policy trends and transportation networks. Finally, the research proposed a conceptual model for the development of the park system, which will move from the multi-center nested model to the community development model. Relying on the heterogeneity and upgrading of central parks, corridors between parks are established to increase the totality of the park system, thus forming a park city. When the self-organized structure of this park system is further optimized, a Park Regional Zone will be formed through flows at the regional scale. These findings provide theoretical guidance to policy makers and planners for scientific planning and efficient evolution of the park system.