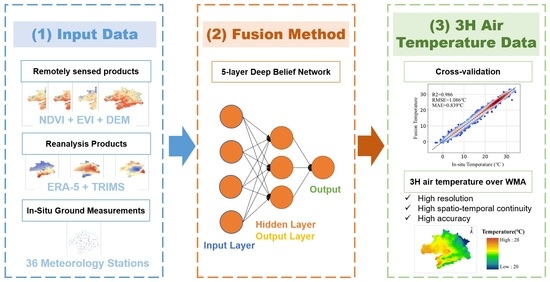
Deep Learning-Based 500 m Spatio-Temporally Continuous Air Temperature Generation by Fusing Multi-Source Data
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
2.2.1. Remotely Sensed Product
2.2.2. Reanalysis Products
2.2.3. In Situ Measurement
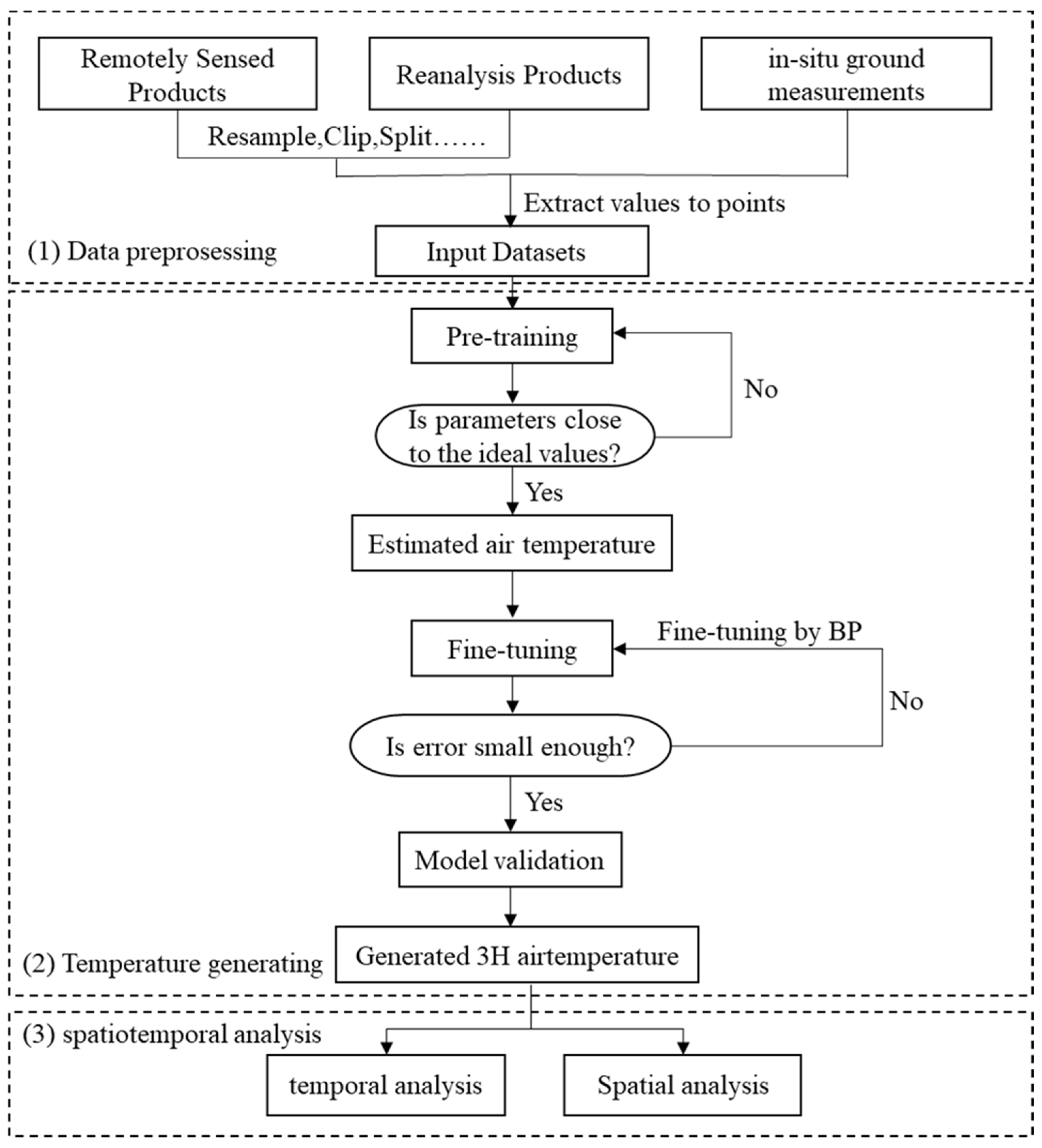
3. Methods
3.1. Deep Belief Network Model
3.2. Model Validation
4. Results
4.1. Correlation Analysis of Input Variables
4.2. Evaluation of Multi-Source Data Fusion Algorithm
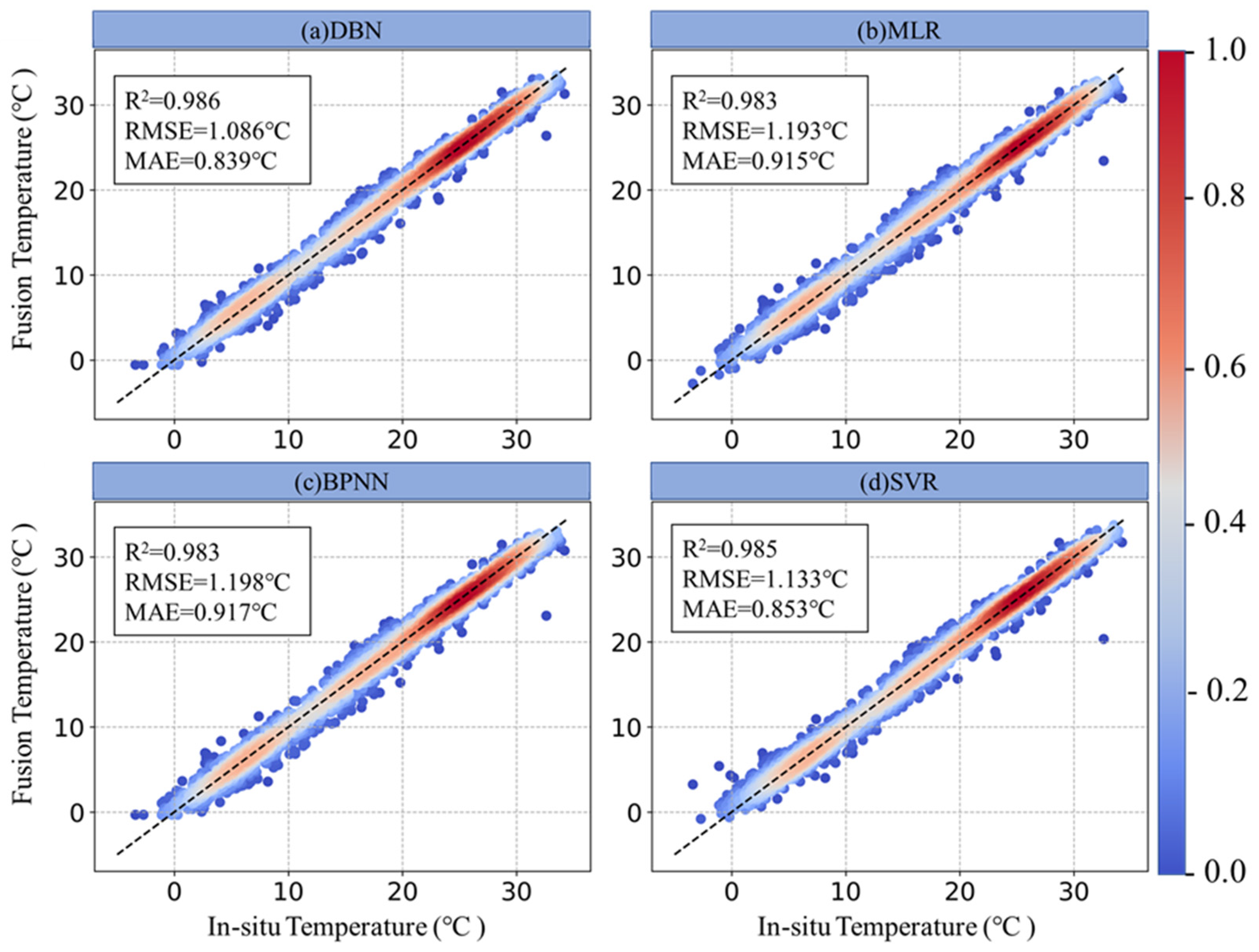
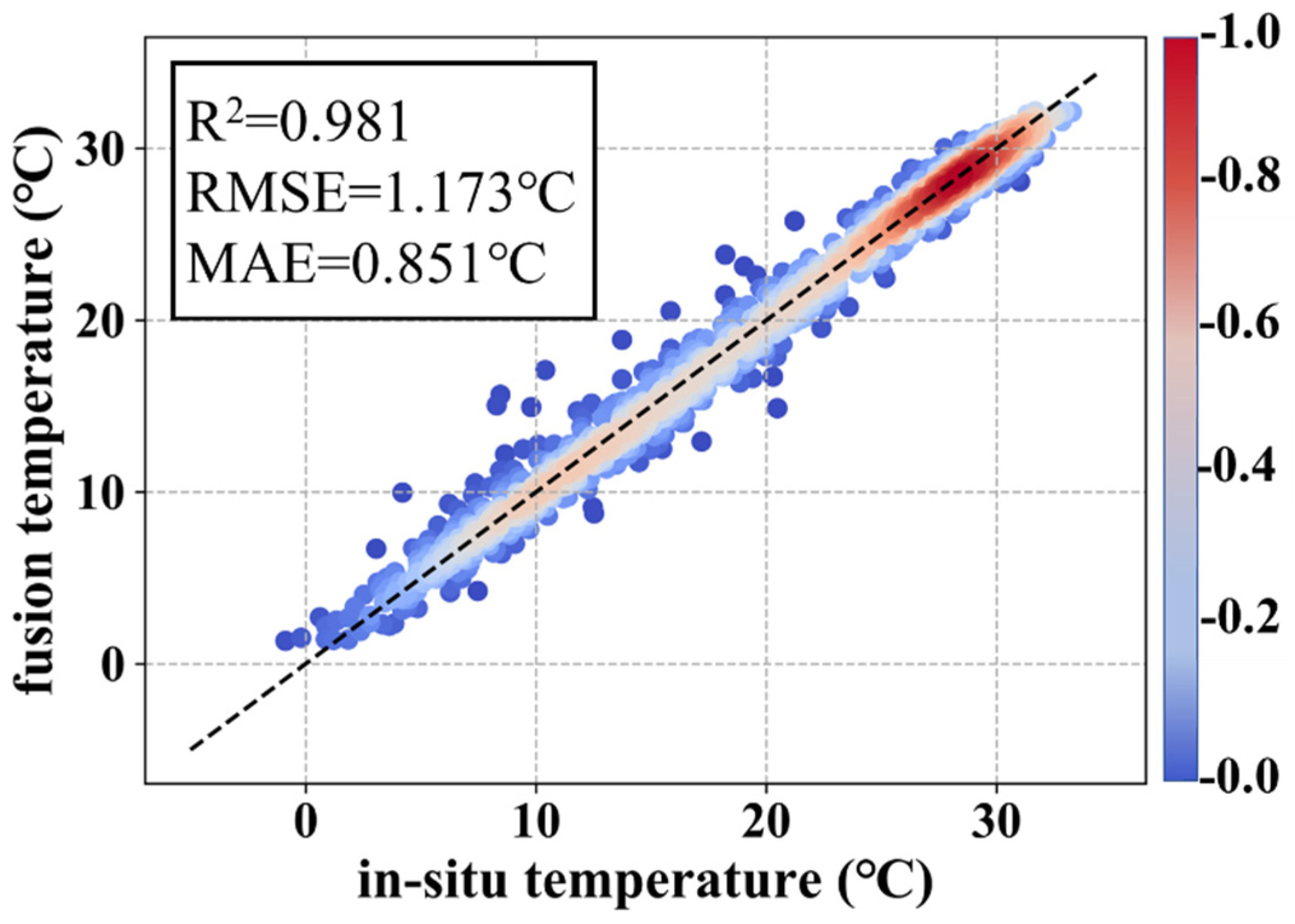
4.2.1. Evaluation of the Overall Accuracy of the DBN Model
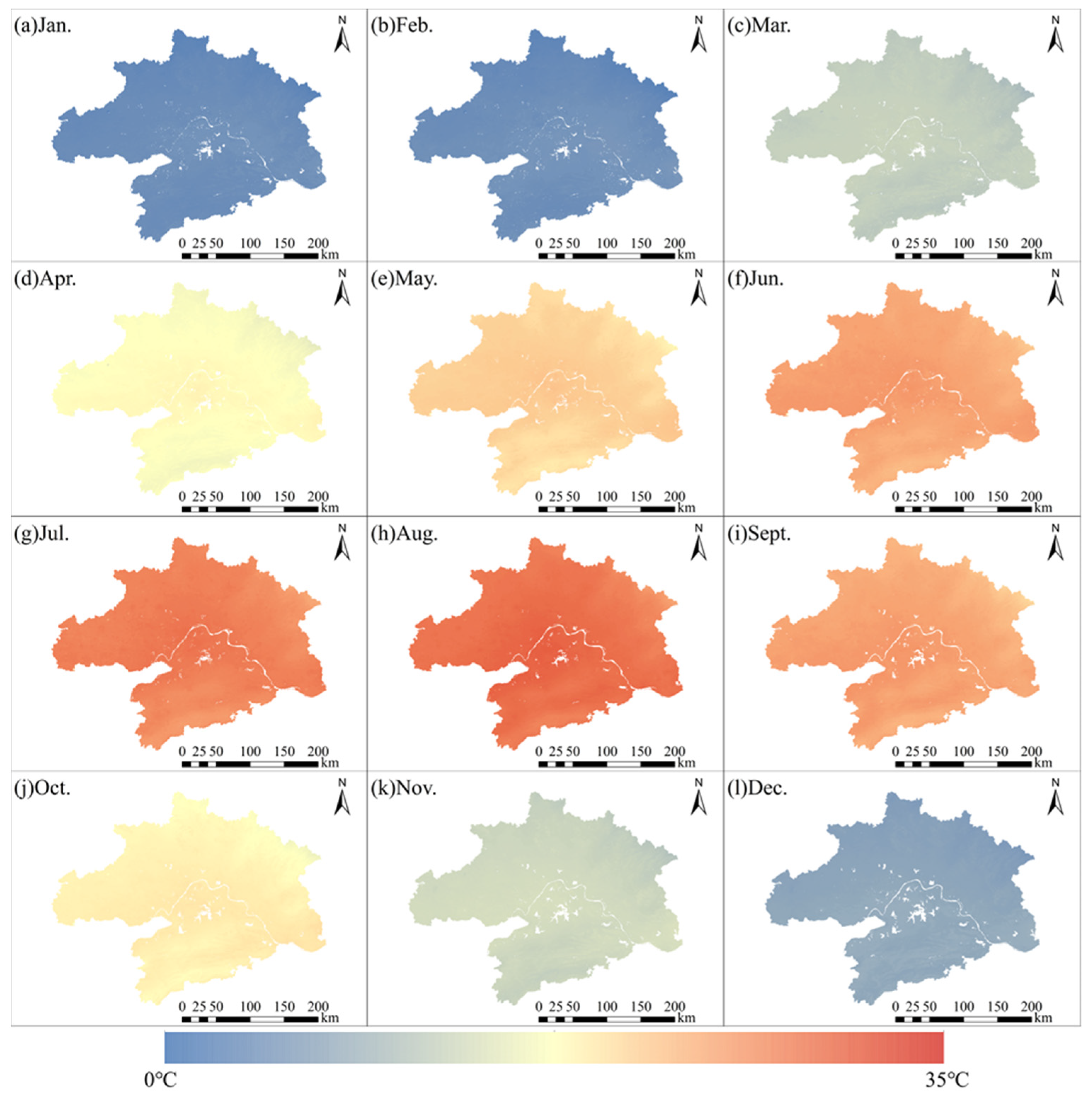
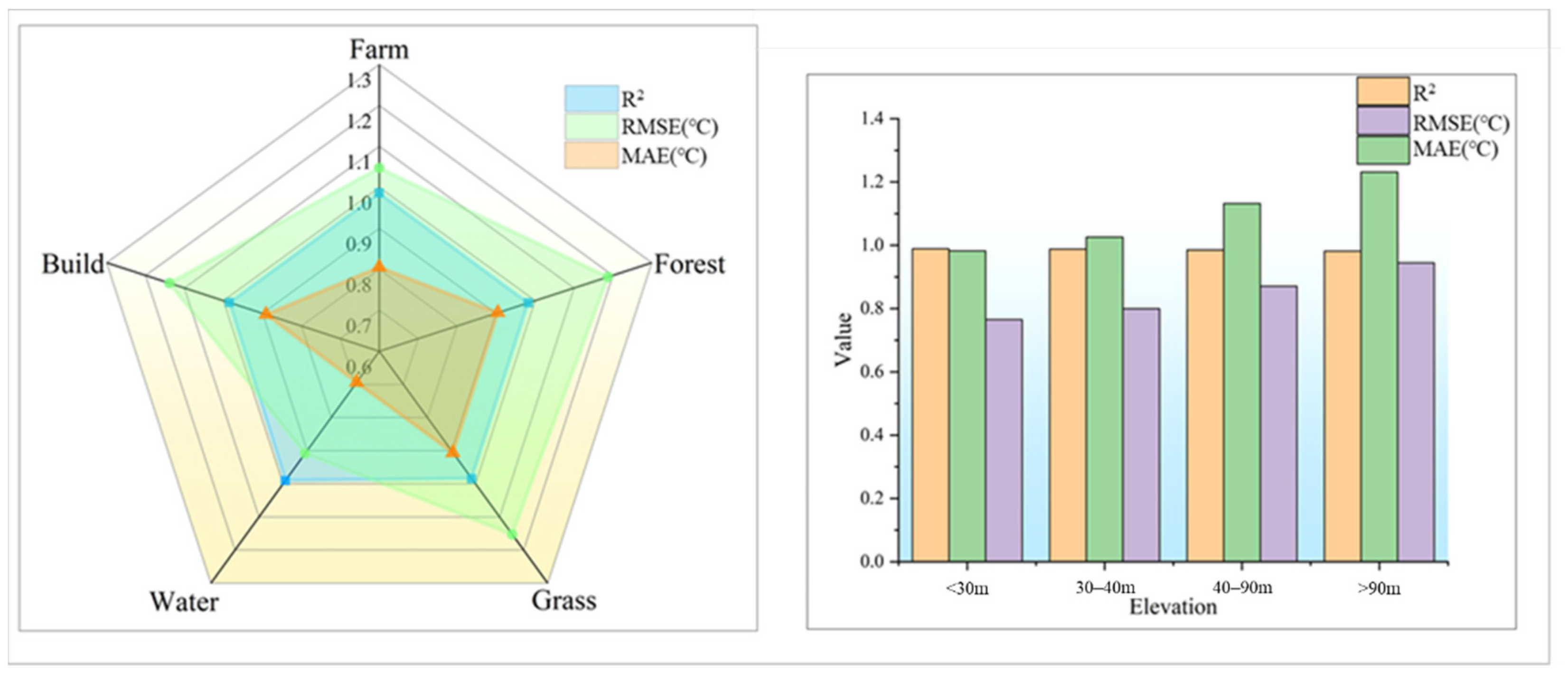
4.2.2. Spatial Evaluation of Model Performance
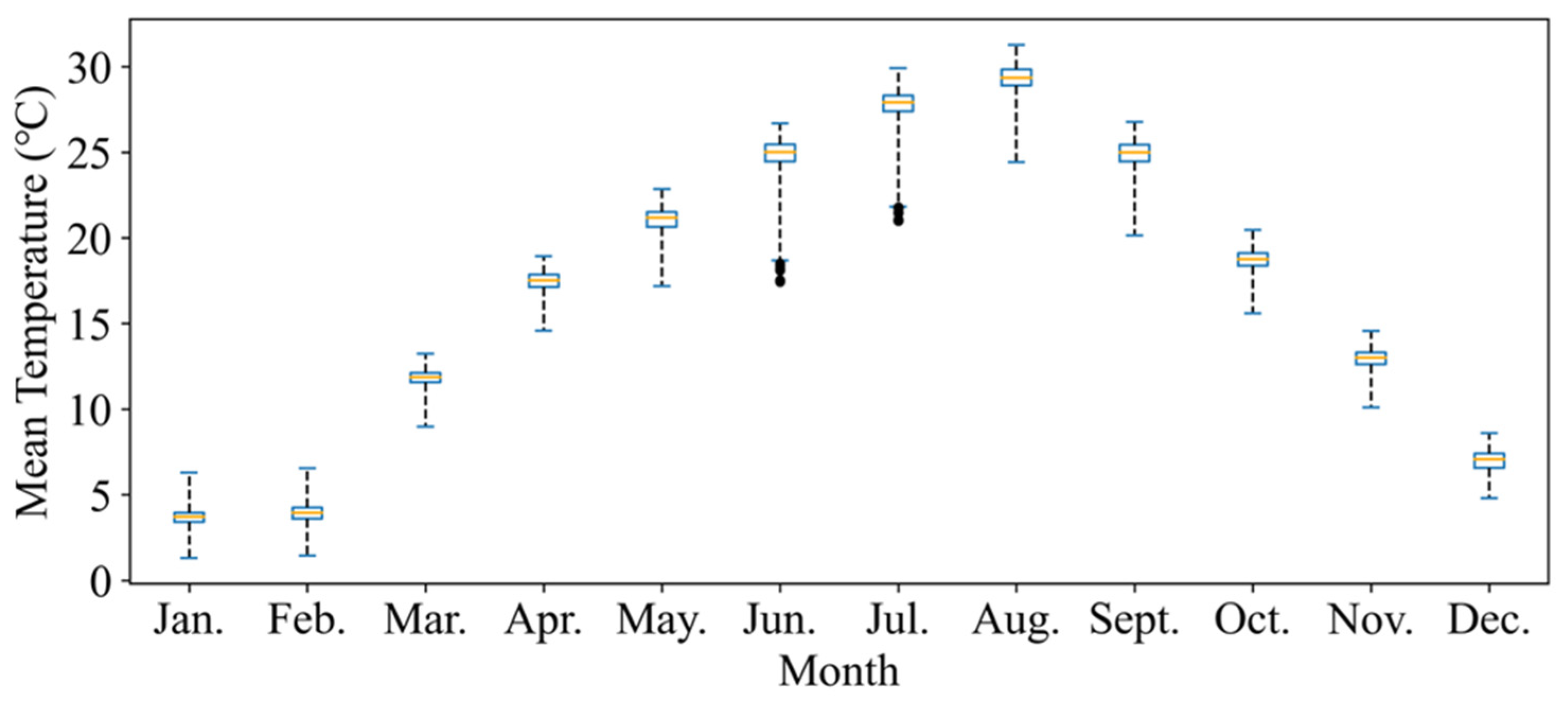
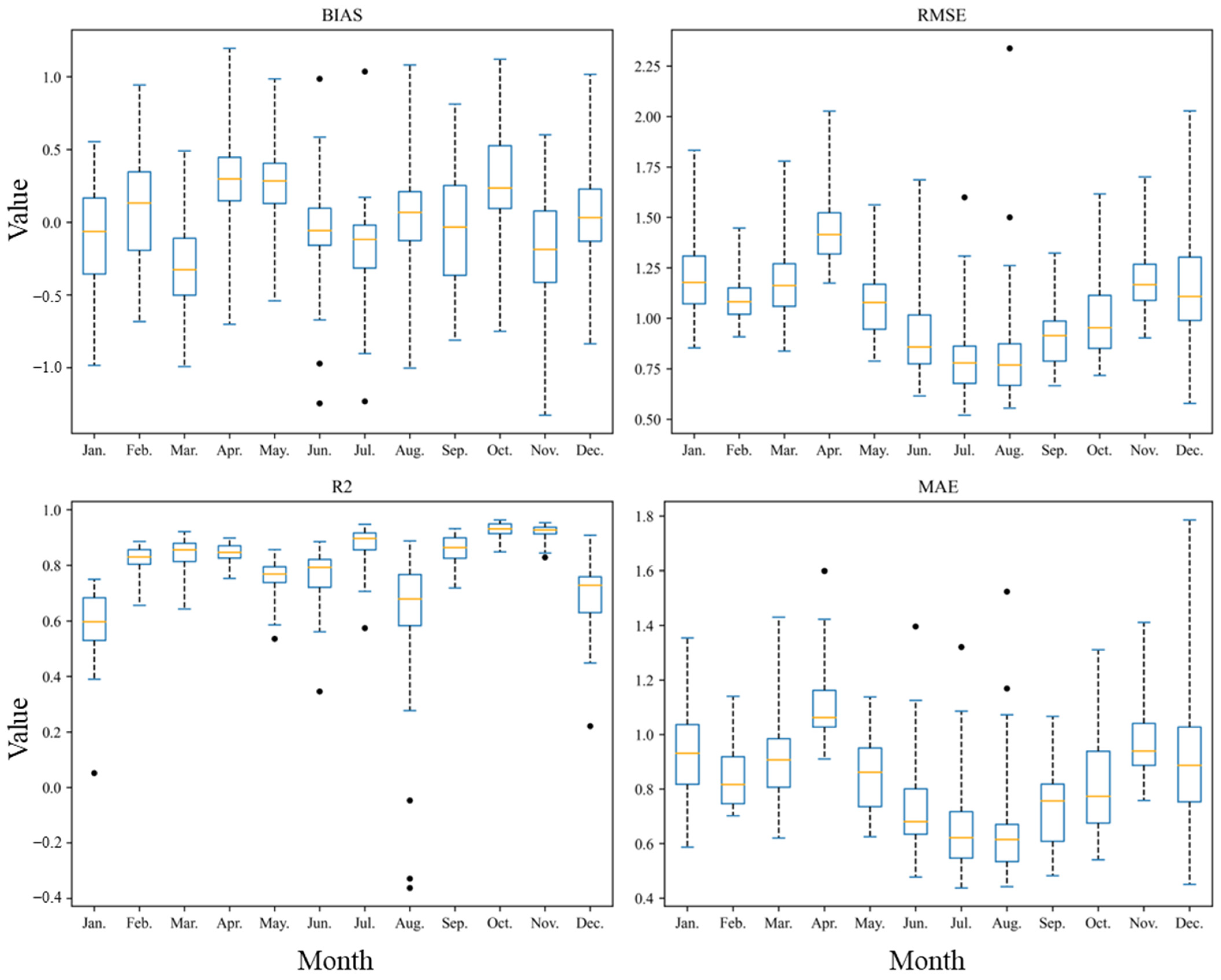
4.2.3. Temporal Evaluation of Model Performance
5. Discussion
5.1. DBN Structure Comparison
5.2. DBN Performance with Different Variables
5.3. Spatio-Temporal Evaluation of the Fusion Accuracy
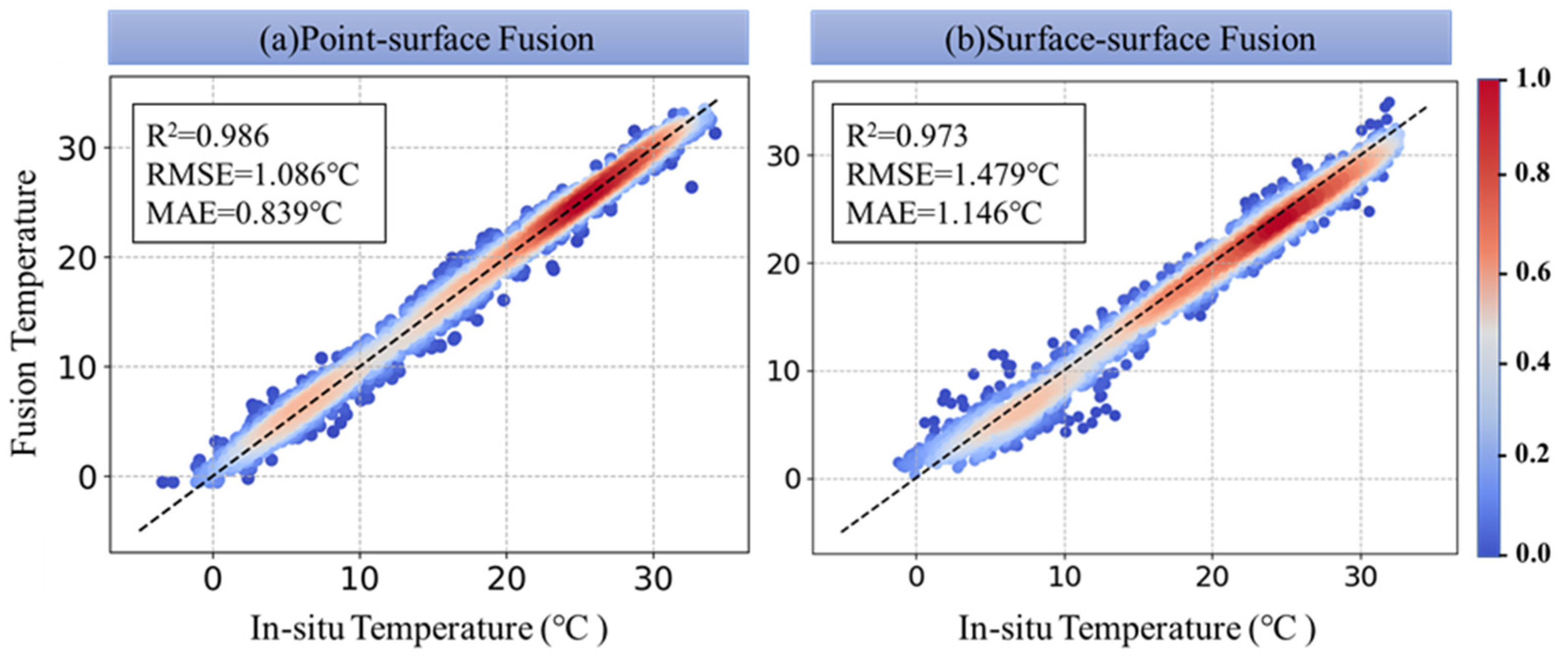
5.4. Role of Point-Surface Fusion in Generating 3H Temperature Data
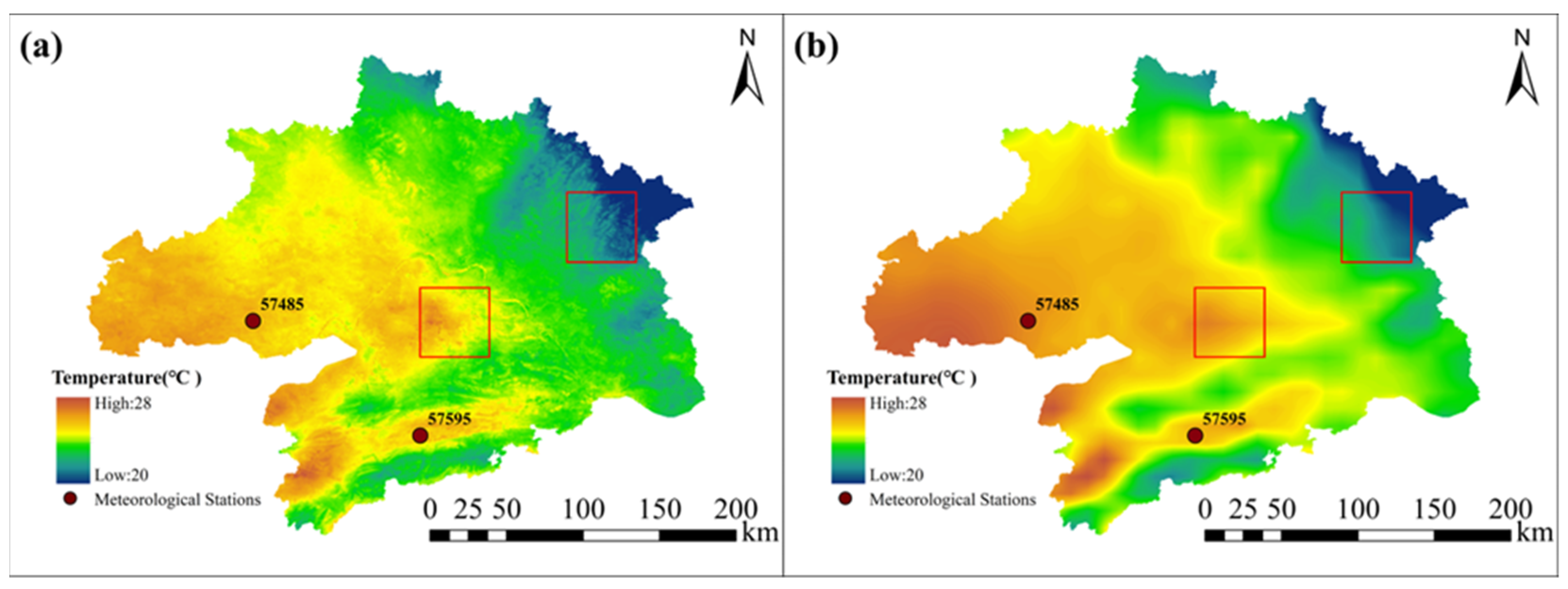
5.5. Spatial Transferability of the Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Osborn, T.J.; Jones, P.D.; Lister, D.H.; Morice, C.P.; Simpson, I.R.; Winn, J.P.; Hogan, E.; Harris, I.C. Land surface air temperature variations across the globe updated to 2019: The CRUTEM5 data set. J. Geophys. Res.-Atmos. 2021, 126, e2019JD032352. [Google Scholar] [CrossRef]
- Cox, P.M.; Huntingford, C.; Williamson, M.S. Emergent constraint on equilibrium climate sensitivity from global temperature variability. Nature 2018, 553, 319. [Google Scholar] [CrossRef] [PubMed]
- Niaz, R.; Zhang, X.; Iqbal, N.; Almazah, M.M.A.; Hussain, T.; Hussain, I.; Li, F. Logistic regression analysis for spatial patterns of drought persistence. Complexity 2021, 2021, 3724919. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.; Chen, N.; Wang, W. Classifying diurnal changes of cyanobacterial blooms in Lake Taihu to identify hot patterns, seasons and hotspots based on hourly GOCI observations. J. Environ. Manag. 2022, 310, 114782. [Google Scholar] [CrossRef]
- Yu, X.; Gu, X.; Kong, D.; Zhang, Q.; Cao, Q.; Slater, L.J.; Ren, G.; Luo, M.; Li, J.; Liu, J.; et al. Asymmetrical shift toward less light and more heavy precipitation in an urban agglomeration of East China: Intensification by urbanization. Geophys. Res. Lett. 2022, 49, e2021GL097046. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef]
- Zhao, Z.; Sharifi, A.; Dong, X.; Shen, L.; He, B.-J.J.R.S. Spatial variability and temporal heterogeneity of surface urban heat island patterns and the suitability of local climate zones for land surface temperature characterization. Remote Sens. 2021, 13, 4338. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, X.; Chen, N.; Li, B.; Ma, H.; Xu, L.; Li, R.; Niyogi, D. Drought propagation modification after the construction of the three gorges dam in the Yangtze river basin. J. Hydrol. 2021, 603, 127138. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Asrar, G.R.; Zhu, Z. Developing a 1 km resolution daily air temperature dataset for urban and surrounding areas in the conterminous United States. Remote Sens. Environ. 2018, 215, 74–84. [Google Scholar] [CrossRef]
- Yang, J.; Xin, J.; Zhang, Y.; Xiao, X.; Xia, J.C. Contributions of sea–land breeze and local climate zones to daytime and nighttime heat island intensity. Npj Urban Sustain. 2022, 2, 1–11. [Google Scholar] [CrossRef]
- Schwarz, N.; Lautenbach, S.; Seppelt, R. Exploring indicators for quantifying surface urban heat islands of European cities with MODIS land surface temperatures. Remote Sens. Environ. 2011, 115, 3175–3186. [Google Scholar] [CrossRef]
- Lu, Y.; Yue, W.; He, T.; Shan, Z.J. Urban form centrality and thermal environment: An empirical study of Chinese megacities. Sustain. Cities Soc. 2022, 83, 103955. [Google Scholar]
- Lu, Y.; Yue, W.; Liu, Y.; Huang, Y. Investigating the spatiotemporal non-stationary relationships between urban spatial form and land surface temperature: A case study of Wuhan, China. Sustain. Cities Soc. 2021, 72, 103070. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Oltra-Carrió, R.; Sòria, G.; Bianchi, R.; Paganini, M. Impact of spatial resolution and satellite overpass time on evaluation of the surface urban heat island effects. Remote Sens. Environ. 2012, 117, 50–56. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Zhang, X.; Fu, P.; Zheng, D.; Wigneron, J.-P.; Chen, N.; Niyogi, D. Evaluation of six satellite- and model-based surface soil temperature datasets using global ground-based observations. Remote Sens. Environ. 2021, 264, 112605. [Google Scholar] [CrossRef]
- Decker, M.; Brunke, M.A.; Wang, Z.; Sakaguchi, K.; Zeng, X.B.; Bosilovich, M.G. Evaluation of the reanalysis products from GSFC, NCEP, and ECMWF using flux tower observations. J. Clim. 2012, 25, 1916–1944. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Munoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.Q.; Ren, G.Y.; Ren, Y.Y.; Sun, X.B. Comparison of surface air temperature between observation and reanalysis data over eastern china for the last 100 years. J. Meteorol. Soc. Jpn. 2019, 97, 89–103. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zhou, Z.J.; Liu, Z.Q.; Li, Q.L.; Zhang, X.L. Bias adjustment and analysis of chinese daily historical radiosonde temperature data. J. Meteorol. Res. 2021, 35, 17–31. [Google Scholar] [CrossRef]
- Li, R.; Huang, T.; Song, Y.; Huang, S.; Zhang, X. Generating 1 km spatially seamless and temporally continuous air temperature based on deep learning over Yangtze river basin, China. Remote Sens. 2021, 13, 3904. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, H.; Hagen, S.C.; Ye, M.; Wang, D.; Gui, D.; Zeng, C.; Tian, L.; Liu, J. Snow cover and runoff modelling in a high mountain catchment with scarce data: Effects of temperature and precipitation parameters. Hydrol. Process. 2015, 29, 52–65. [Google Scholar] [CrossRef]
- Shi, Y.; Jiang, Z.; Dong, L.; Shen, S. Statistical estimation of high-resolution surface air temperature from MODIS over the Yangtze river delta, China. J. Meteorol. Res. 2017, 31, 448–454. [Google Scholar] [CrossRef]
- Wang, F.; Tian, D.; Lowe, L.; Kalin, L.; Lehrter, J. Deep learning for daily precipitation and temperature downscaling. Water Resour. Res. 2021, 57, e2020WR029308. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, X.; Chen, N.; Ma, H.; Fu, P.; Dong, J.; Gu, X.; Nam, W.H.; Xu, L.; Rab, G.; et al. A novel fusion method for generating surface soil moisture data with high accuracy, high spatial resolution, and high spatio-temporal continuity. Water Resour. Res. 2022, 58, e2021WR030827. [Google Scholar] [CrossRef]
- Zeng, L.; Hu, Y.; Wang, R.; Zhang, X.; Peng, G.; Huang, Z.; Zhou, G.; Xiang, D.; Meng, R.; Wu, W.; et al. 8-Day and Daily Maximum and Minimum Air Temperature Estimation via Machine Learning Method on a Climate Zone to Global Scale. Remote Sens. 2021, 13, 2355. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X.; Moradkhani, H.; Zhang, C.; Hu, C. In-situ and triple-collocation based evaluations of eight global root zone soil moisture products. Remote Sens. Environ. 2021, 254, 112248. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Petersen, L.; Ragettli, S.; Pellicciotti, F. The importance of observed gradients of air temperature and precipitation for modeling runoff from a glacierized watershed in the Nepalese Himalayas. Water Resour. Res. 2014, 50, 2212–2226. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; Moore, N.J.; Messina, J.P.; DeVisser, M.H.; Wu, J. Evaluation of estimating daily maximum and minimum air temperature with MODIS data in east Africa. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 128–140. [Google Scholar] [CrossRef]
- Chen, H.R.; Qin, H.W.; Dai, Y.W. FC-ZSM: Spatiotemporal downscaling of rain radar data using a feature constrained zooming slow-mo network. Front. Earth Sci. 2022, 10, 887842. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Zheng, W.; Yin, W.J.; Lei, W.W. Improving the resolution and accuracy of groundwater level anomalies using the machine learning-based fusion model in the north China plain. Sensors 2021, 21, 46. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.L.; Zhang, Y.H.; Wang, J.G.; Tian, W.; Liu, Q.; Ma, G.Y.; Kan, X.; Chu, Y. Downscaling snow depth mapping by fusion of microwave and optical remote-sensing data based on deep learning. Remote Sens. 2021, 13, 584. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, X.; Zhang, L. Estimating ground-level PM2.5 by fusing satellite and station observations: A geo-intelligent deep learning approach. Geophys. Res. Lett. 2017, 44, 11985–11993. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Jiang, Y.; Li, T.; Cheng, Q.; Zeng, C.; Zhang, L. Deep learning-based air temperature mapping by fusing remote sensing, station, simulation and socioeconomic data. Remote Sens. Environ. 2020, 240, 111692. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Zhang, A.L.; Sun, Z.L. How regional economic integration influence on urban land use efficiency? A case study of Wuhan metropolitan area, China. Land Use Policy 2020, 90, 104329. [Google Scholar] [CrossRef]
- Zhang, J.F.; Zhang, A.L.; Dong, J.J.R.; Basin, E.I.T.Y. Carbon emission effect of land use and influencing factors decomposition of carbon emission in Wuhan urban agglomeration. Yangtze Basin 2014, 23, 595–602. [Google Scholar]
- Chen, J.; Gao, C.; Zeng, X.; Xiong, M.; Wang, Y.; Jing, C.; Krysanova, V.; Huang, J.; Zhao, N.; Su, B. Assessing changes of river discharge under global warming of 1.5 °C and 2 °C in the upper reaches of the Yangtze River Basin: Approach by using multiple-GCMs and hydrological models. Quat. Int. 2017, 453, 63–73. [Google Scholar] [CrossRef]
- Su, L.L.; Gao, X.Y.; Liu, Y.F. Study on dynamic change of land utilization in Wuhan metropolitan area. In Proceedings of the 1st International Workshop on Database Technology and Applications, Wuhan, China, 25–26 April 2009; p. 642. [Google Scholar]
- Wang, K.; Wang, J.; Wang, P.; Sparrow, M.; Yang, J.; Chen, H. Influences of urbanization on surface characteristics as derived from the moderate-resolution imaging spectroradiometer: A case study for the Beijing metropolitan area. J. Geophys. Res. 2007, 112, D22S06. [Google Scholar] [CrossRef]
- Shen, H.; Huang, L.; Zhang, L.; Wu, P.; Zeng, C. Long-term and fine-scale satellite monitoring of the urban heat island effect by the fusion of multi-temporal and multi-sensor remote sensed data: A 26-year case study of the city of Wuhan in China. Remote Sens. Environ. 2016, 172, 109–125. [Google Scholar] [CrossRef]
- Amiri, R.; Weng, Q.H.; Alimohammadi, A.; Alavipanah, S.K. Spatial-temporal dynamics of land surface temperature in relation to fractional vegetation cover and land use/cover in the Tabriz urban area, Iran. Remote Sens. Environ. 2009, 113, 2606–2617. [Google Scholar] [CrossRef]
- Goward, S.N.; Xue, Y.K.; Czajkowski, K.P. Evaluating land surface moisture conditions from the remotely sensed temperature/vegetation index measurements-An exploration with the simplified simple biosphere model. Remote Sens. Environ. 2002, 79, 225–242. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Du, L.T.; Song, N.P.; Liu, K.; Hou, J.; Hu, Y.; Zhu, Y.G.; Wang, X.Y.; Wang, L.; Guo, Y.G. Comparison of two simulation methods of the temperature vegetation dryness index (TVDI) for drought monitoring in semi-arid regions of China. Remote Sens. 2017, 9, 177. [Google Scholar] [CrossRef] [Green Version]
- Long, M.; Ying, L.; IEEE. Evaluation of SRTM DEM over China. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Denver, CO, USA, 31 July–4 August 2006; pp. 2977–2980. [Google Scholar]
- Liu, G.; Chen, J.M.; Ji, L.R.; Sun, S.Q. Relationship of summer soil moisture with early winter monsoon and air temperature over eastern China. Int. J. Climatol. 2012, 32, 1513–1519. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Wang, X.P.; Pan, Y.X.; Hu, R. Diurnal relationship between the surface albedo and surface temperature in revegetated desert ecosystems, northwestern China. Arid. Land Res. Manag. 2012, 26, 32–43. [Google Scholar] [CrossRef]
- He, B.J.; Ding, L.; Prasad, D. Wind-sensitive urban planning and design: Precinct ventilation performance and its potential for local warming mitigation in an open midrise gridiron precinct. J. Build. Eng. 2020, 29. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Zhang, B.; Yao, Y.B. An ERA5-based model for estimating tropospheric delay and weighted mean temperature over China with improved spatiotemporal resolutions. Earth Space Sci. 2019, 6, 1926–1941. [Google Scholar] [CrossRef]
- Meyer, H.; Katurji, M.; Appelhans, T.; Muller, M.U.; Nauss, T.; Roudier, P.; Zawar-Reza, P. Mapping daily air temperature for antarctica based on MODIS LST. Remote Sens. 2016, 8, 732. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.D.; Zhou, J.; Gottsche, F.M.; Zhan, W.F.; Liu, S.M.; Cao, R.Y. A method based on temporal component decomposition for estimating 1-km all-weather land surface temperature by merging satellite thermal infrared and passive microwave observations. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4670–4691. [Google Scholar] [CrossRef]
- Zhang, X.D.; Zhou, J.; Liang, S.L.; Wang, D.D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Du, L.T.; Tian, Q.J.; Yu, T.; Meng, Q.Y.; Jancso, T.; Udvardy, P.; Huang, Y. A comprehensive drought monitoring method integrating MODIS and TRMM data. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 245–253. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Wong, T.T.; Yeh, P.Y. Reliable accuracy estimates from k-fold cross validation. IEEE Trans. Knowl. Data Eng. 2020, 32, 1586–1594. [Google Scholar] [CrossRef]
- Song, J.; Wang, Z.H.; Myint, S.W.; Wang, C.Y. The hysteresis effect on surface-air temperature relationship and its implications to urban planning: An examination in Phoenix, Arizona, USA. Landsc. Urban Plan. 2017, 167, 198–211. [Google Scholar] [CrossRef]
- Tomlinson, C.J.; Chapman, L.; Thornes, J.E.; Baker, C.J.; Prieto-Lopez, T. Comparing night-time satellite land surface temperature from MODIS and ground measured air temperature across a conurbation. Remote Sens. Lett. 2012, 3, 657–666. [Google Scholar] [CrossRef]
- Marzban, F.; Sodoudi, S.; Preusker, R. The influence of land-cover type on the relationship between NDVI-LST and LST-T-air. Int. J. Remote Sens. 2018, 39, 1377–1398. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, N.C. Reconstruction of GF-1 soil moisture observation based on satellite and in situ sensor collaboration under full cloud contamination. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5185–5202. [Google Scholar] [CrossRef]
- Deng, K.Q.; Ting, M.F.; Yang, S.; Tan, Y.H. Increased frequency of summer extreme heat waves over Texas area tied to the amplification of pacific zonal SST gradient. J. Clim. 2018, 31, 5629–5647. [Google Scholar] [CrossRef]
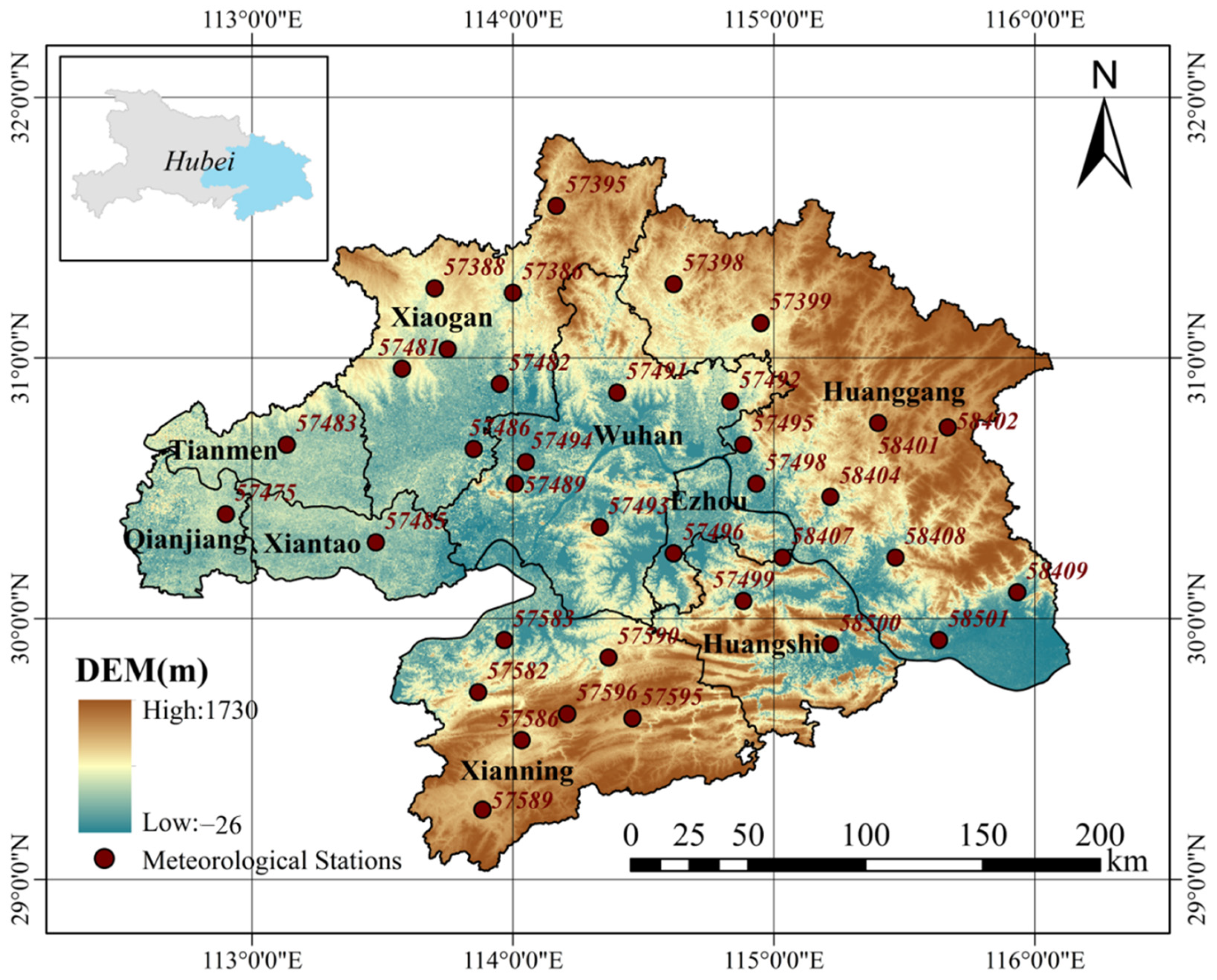
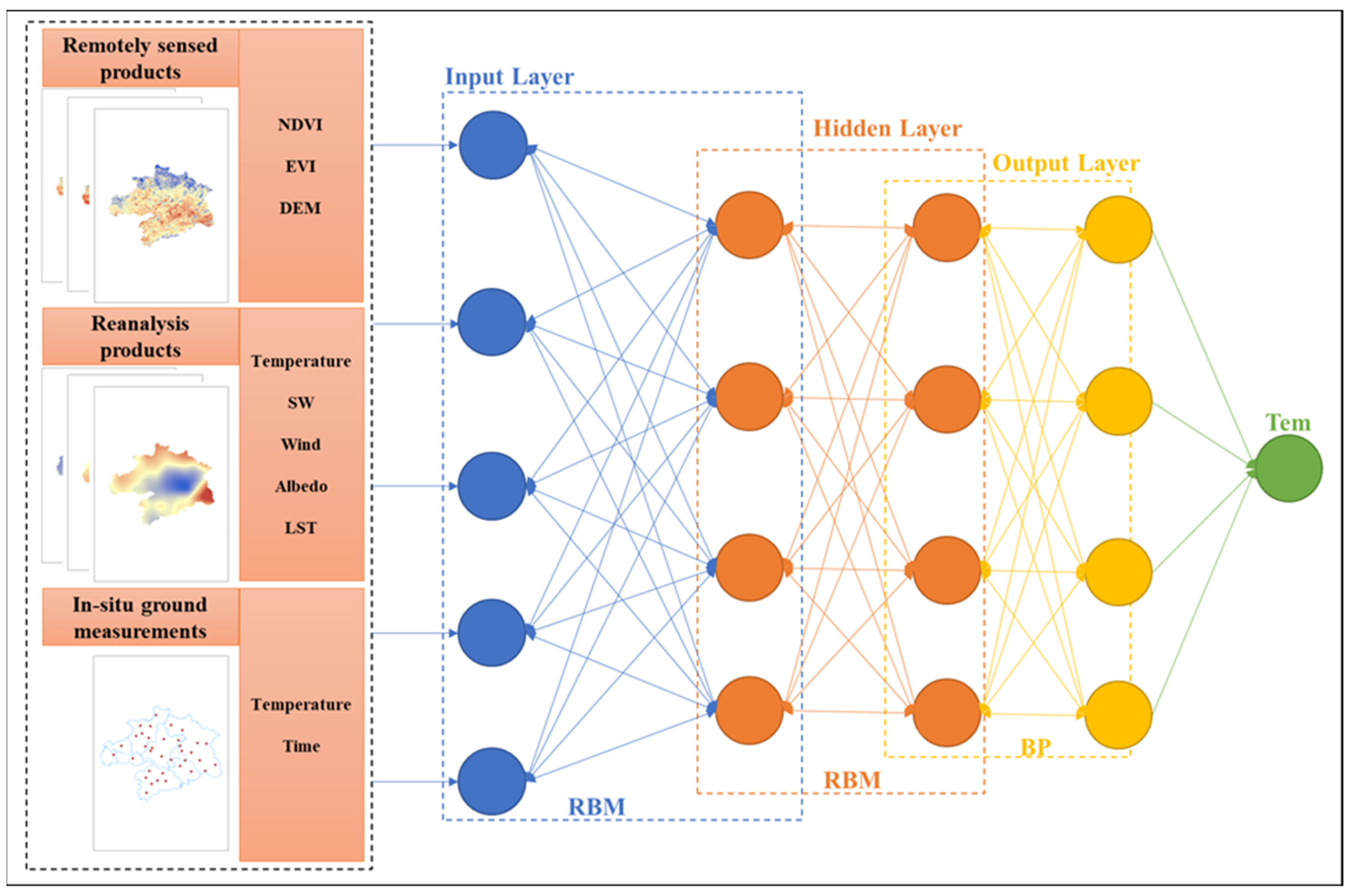





| Category | Product | Variable | Spatial Resolution | Temporal Resolution | Temporal Span |
|---|---|---|---|---|---|
| Remotely Sensed Products | MOD13Q1 | NDVI | 250 m | 16 Days | |
| EVI | |||||
| SRTM | DEM | 30 m | - | ||
| Reanalysis Products | ERA5-Land | 2 m Temperature | 0.1° | Hourly | 2019 |
| Soil moisture | |||||
| Wind Speed | |||||
| Albedo | |||||
| TRIMS LST | LST | 1 km | Daily | ||
| In Situ Measurements | In Situ Station | Mean Temperature | - | Daily |
| Metric | Equation | Unit |
|---|---|---|
| PCC | - | |
| R2 | - | |
| RMSE | °C | |
| MAE | °C | |
| BIAS | °C |
| City | Max Elevation (m) | Mean Elevation (m) | Min Temperature (°C) | Max Temperature (°C) | Mean Temperature (°C) |
|---|---|---|---|---|---|
| Wuhan | 726 | 37.00 | 16.40 | 18.24 | 17.42 |
| Huangshi | 776 | 108.98 | 16.40 | 17.88 | 17.10 |
| Ezhou | 445 | 31.41 | 16.92 | 18.18 | 17.48 |
| Xiaogan | 818 | 75.37 | 15.59 | 17.84 | 16.81 |
| Huanggang | 1674 | 174.69 | 13.82 | 18.05 | 16.65 |
| Xianning | 1555 | 189.72 | 15.62 | 17.94 | 16.79 |
| Xiantao | 83 | 26.26 | 16.83 | 17.84 | 17.41 |
| Qianjiang | 127 | 28.09 | 14.28 | 17.52 | 17.13 |
| Tianmen | 144 | 31.19 | 15.04 | 17.53 | 16.95 |
| DBN Hidden Layer | Hidden Layer Neurons | RMSE (°C) | MAE (°C) | R2 |
|---|---|---|---|---|
| 2 | 25, 20 | 1.117 | 0.864 | 0.985 |
| 3 | 25, 15, 10 | 1.086 | 0.839 | 0.986 |
| 3 | 25, 20, 15 | 1.087 | 0.844 | 0.986 |
| 4 | 25, 20, 15, 10 | 1.085 | 0.839 | 0.986 |
| Dataset Combinations | RMSE (°C) | MAE (°C) | R2 |
|---|---|---|---|
| E | 1.219 | 0.922 | 0.982 |
| E + L | 1.244 | 0.941 | 0.982 |
| E + R | 1.124 | 0.876 | 0.985 |
| E + R + T | 1.106 | 0.858 | 0.986 |
| E + L + R | 1.134 | 0.875 | 0.985 |
| E + L + R + T | 1.086 | 0.839 | 0.986 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Huang, T.; Gulakhmadov, A.; Song, Y.; Gu, X.; Zeng, J.; Huang, S.; Nam, W.-H.; Chen, N.; Niyogi, D. Deep Learning-Based 500 m Spatio-Temporally Continuous Air Temperature Generation by Fusing Multi-Source Data. Remote Sens. 2022, 14, 3536. https://doi.org/10.3390/rs14153536
Zhang X, Huang T, Gulakhmadov A, Song Y, Gu X, Zeng J, Huang S, Nam W-H, Chen N, Niyogi D. Deep Learning-Based 500 m Spatio-Temporally Continuous Air Temperature Generation by Fusing Multi-Source Data. Remote Sensing. 2022; 14(15):3536. https://doi.org/10.3390/rs14153536
Chicago/Turabian StyleZhang, Xiang, Tailai Huang, Aminjon Gulakhmadov, Yu Song, Xihui Gu, Jiangyuan Zeng, Shuzhe Huang, Won-Ho Nam, Nengcheng Chen, and Dev Niyogi. 2022. "Deep Learning-Based 500 m Spatio-Temporally Continuous Air Temperature Generation by Fusing Multi-Source Data" Remote Sensing 14, no. 15: 3536. https://doi.org/10.3390/rs14153536
APA StyleZhang, X., Huang, T., Gulakhmadov, A., Song, Y., Gu, X., Zeng, J., Huang, S., Nam, W.-H., Chen, N., & Niyogi, D. (2022). Deep Learning-Based 500 m Spatio-Temporally Continuous Air Temperature Generation by Fusing Multi-Source Data. Remote Sensing, 14(15), 3536. https://doi.org/10.3390/rs14153536