1. Introduction
Integrity of Global Navigation Satellite System (GNSS) service has been the primary concern of GNSS users in the Safety-of-Life (SoL) domain. Models of each error source are necessary inputs for integrity monitoring, especially for protection level calculation. Multipath error is the ranging error caused by reflected GNSS signal that distorts correlation peaks of receiver. It remains one of the dominant error sources for GNSS applications. Therefore, it is essential to include multipath error in error budget of GNSS integrity.
In recent years, multipath modeling has been a hotspot in GNSS integrity monitoring research. Systematic research of multipath error modeling was implemented in the United States and Europe to promote GNSS application in civil aviation. For example, researchers from the Boeing Company and the Collins Aerospace performed multipath modeling tests with flight test data collected at a prototype Collins Dual-Frequency Multi-Constellation (DFMC) receiver [
1]. Moreover, the European Commission, combined with renowned institutes and companies, e.g., German Aerospace Center (DLR) and Airbus, started the Dual-Frequency Multipath Model for Aviation (DUFMAN) project. Researchers of the project aimed at developing new multipath error models recommended for aviation users of GPS L5 and Galileo E1, E5a [
2,
3,
4] and is promoting standardization of their modeling methodology [
5].
Some independent research has focused on multipath error modeling according to physical analysis. For instance, Refs [
6,
7] aimed at handling the multipath obstacles faced by automatic airport surface operation. They modeled all possible reflection sources in region and simulated multipath error for modeling with a receiver model. Others committed to multipath error modeling via mass observation data analysis. For example, Ref [
8] proposed a piecewise multipath error model for BDS-2 satellites, which bounds multipath samples from satellites whose elevation is less than 15° while fitting samples in other elevation bins to maximize availability of integrity monitoring. Ref [
9] proposed dedicated time parameters to the existing error model to enable multipath model applicable before convergence of smoothing filter.
In summary, the algorithm for data processing and error bounding is mature and widely accepted. Similar methodologies are well-recognized in available literatures. These studies usually obtain multipath data from the method of MP (MultiPath) combination at first [
10], and then sort out multipath samples according to elevation. After that, the strategy of Cumulative Distribution Function (CDF) overbounding is widely used to bound error and derive model parameters. Nevertheless, it is strange to find out that how the CDF overbounding strategy is managed was hardly involved. Since multipath effect is elevation-dependent, it is challenging to effectively bound multipath error while limiting the model’s conservatism at each elevation bin manually. Notably, this problem remains a challenge, which is also raised in Ref [
1].
Focusing on the above question, we proposed a new automatic multipath error modeling methodology utilizing the CDF overbounding strategy and the multiobjective genetic algorithm (GA). Primary contribution of this study is twofold. At first, we proposed quantifying considerations of bounding error and avoiding modeling results from being too conservative in the objective function of GA. Therefore, iterative weighing between effectiveness and conservatism can be managed automatically. Second, we introduced a new model form with two inflation factors to generate less-conservative models, which means tighter boundaries and thus less availability loss of integrity monitoring. Moreover, it is worth mentioning that our method is not designed for specific dataset. Therefore, it is independent of data source and data smoothing.
To validate the effects, we initially demonstrated our methodology with a large ground-based dataset of BDS-3 Medium Earth Orbit (MEO) satellites’ B1I and B3I observations. The remainder of our paper is structured as follows.
Section 2 introduces our data collection and processing strategy. Next, we illustrate our methodology of multipath modeling in
Section 3.
Section 4 displays constructed multipath models and verifications of modeling results with multiple analyses in terms of error overbounding, and model conservatism. Finally, the last section draws the conclusion.
2. Data Collection, Processing and Analysis
2.1. Data Collection and Processing
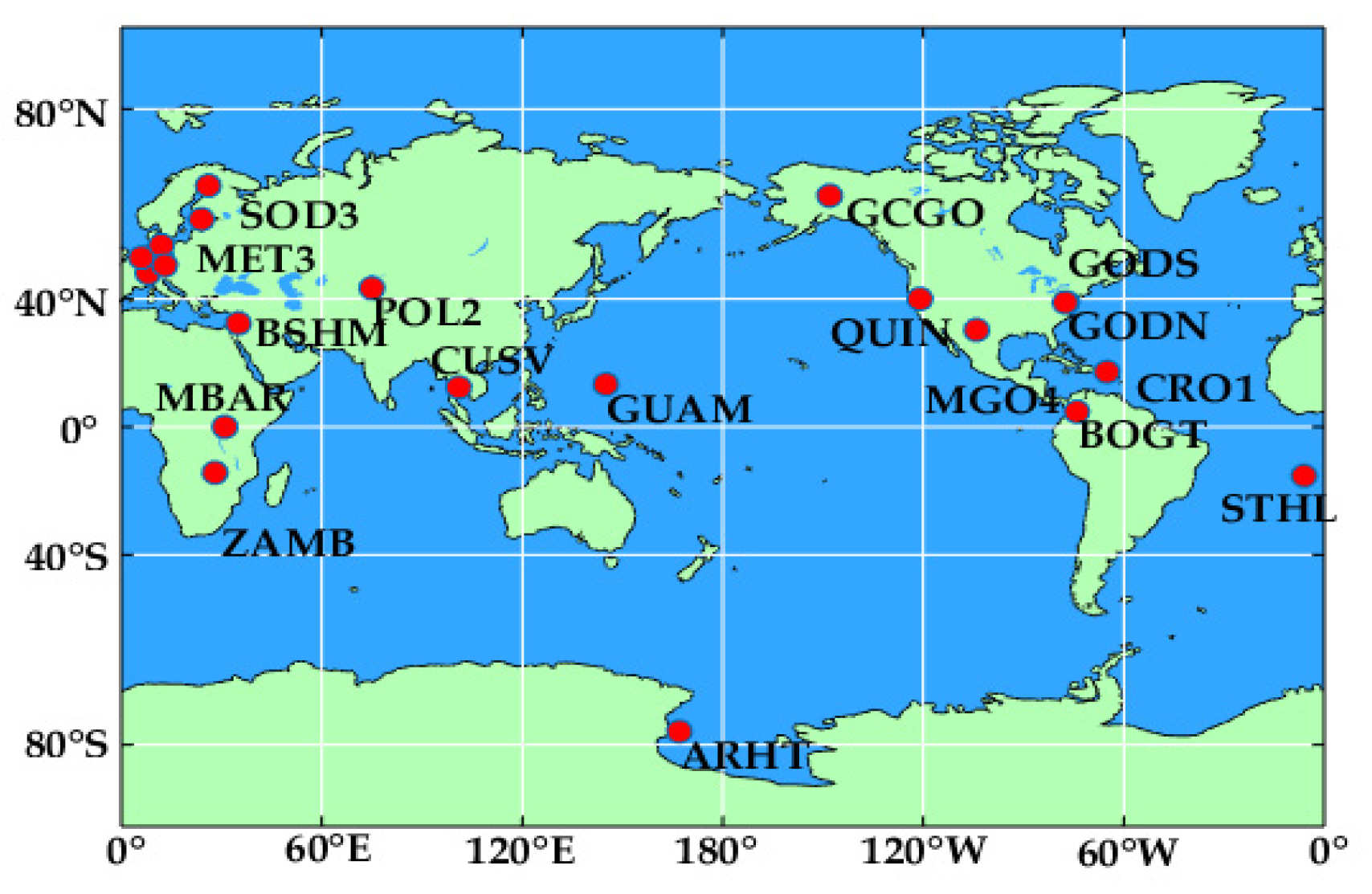
A large-scale dataset of multipath error was used for modeling in this work. The period was DOY (Day Of Year) 70–190, 2020. To maximize dataset for modeling, we collected the classical 30s-interval unsmoothed observations of the B1I and B3I signals broadcast by BDS-3 MEO satellites. Observations were from 23 IGS MGEX stations that are shown in
Figure 1. These stations are all equipped with JAVAD TRE_3 DELTA receivers in which data of all BDS-3 MEO working satellites are available.
Moreover, scholars of multipath modeling always mind the influence of antenna-induced error on multipath data [
11]. It is worth explaining that since the Phase Center Variation (PCV) of users’ BeiDou antenna is not available in public files, the PCV was not corrected in this study. And to obtain the multipath samples for modeling, we used the widely adopted multipath combination to characterize multipath characteristics. Details of the process can be referred in [
10].
To improve data processing efficiency, we grouped and counted multipath error samples according to value and elevation at the first step. The finite data value range shown in
Table 1 was selected according to the maximum data value in dataset while reserving necessary redundancy for unexpected extreme cases. The mask angle is 5°, which is consistent with that of the error model for Galileo in ARAIM Interim Report Annex B [
12]. Moreover, to precisely reflect the distribution characteristic of multipath error, small intervals of data value and elevation were chosen. They were 0.03 m and 1°, respectively. After grouping and counting, the counts in each bin were generalized using the total number of samples in the corresponding elevation bin so that multipath CDFs were generated.
2.2. Distribution of Multipath Error
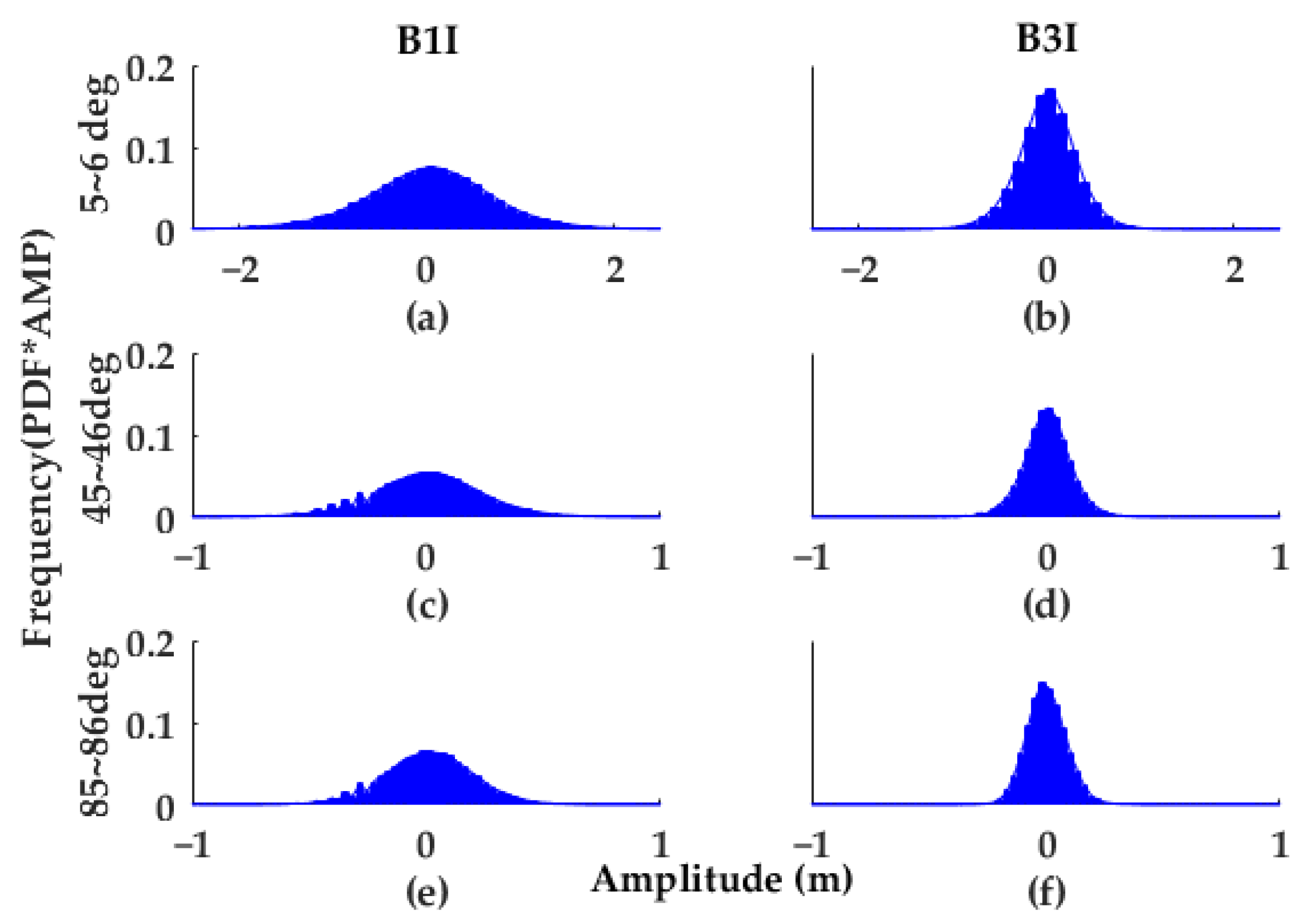
Concerning the heavy-tail problem of multipath error, DeCleene of the Federal Aviation Administration (FAA) proposed the CDF overbounding strategy to model error that is not strictly Gaussian. Nevertheless, as stressed by DeCleene, unimodality, zero mean value, and well symmetry of error distribution are the prerequisites for using CDF overbounding strategy [
13]. As a consequence, this part focuses on analyzing unimodality, mean value, and symmetry of multipath error distribution.
Figure 2 presents multipath error distribution for BDS-3 MEO satellites at B1I and B3I. The x-axis denotes amplitude whose unit is meter. The y-axis whose unit is one represents the product of Probability Density Function (PDF) and corresponding × coordinate. In theory, unimodality and symmetry of our graphs are consistent with that of PDFs. Notably, subfigures below show that all distributions are unimodal and of good symmetry.
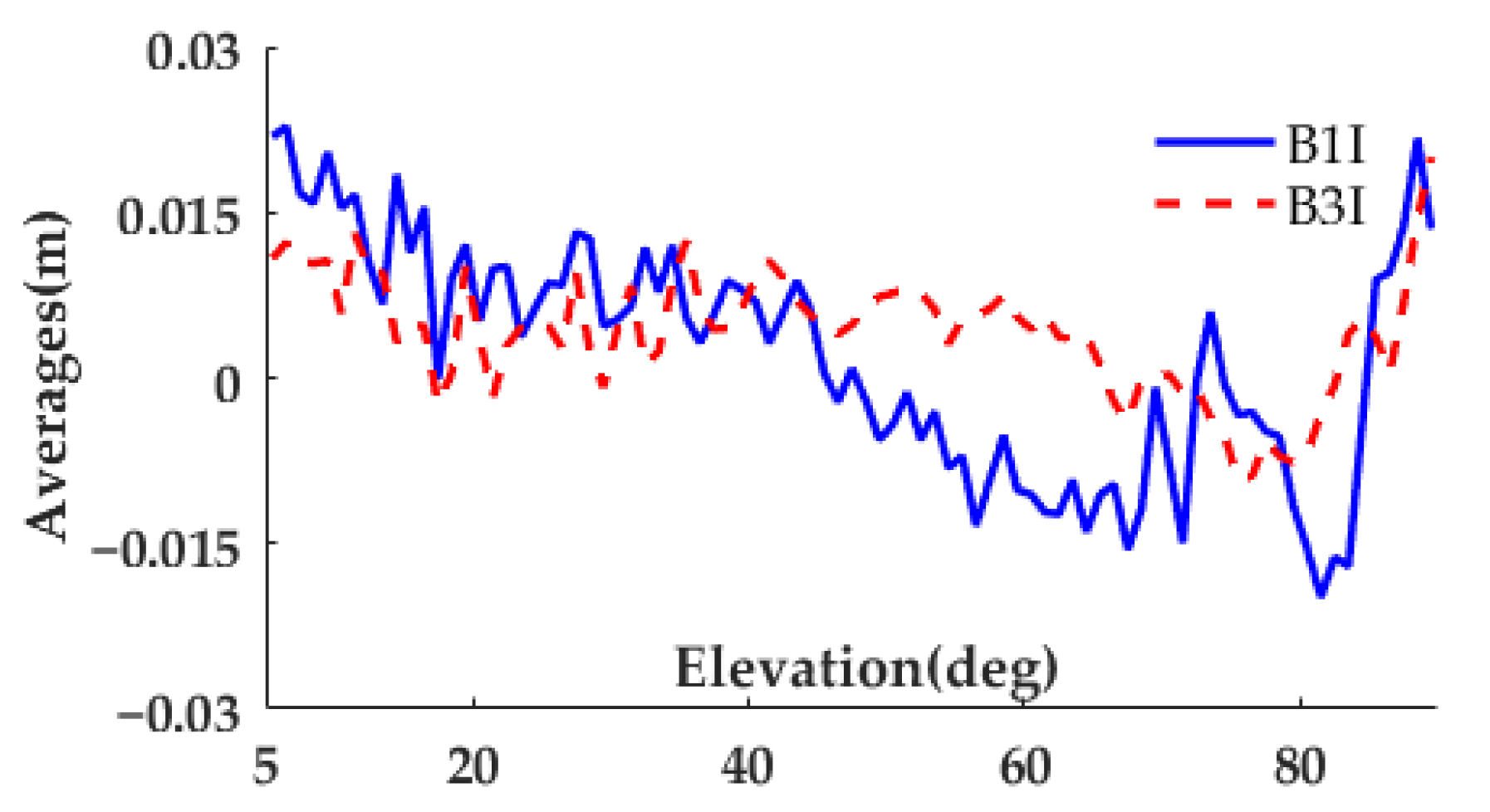
Figure 3 shows averages of multipath error in different elevation bins. As shown in the figure, none of the mean value curves show pronounced characteristics related to elevation like BDS-2, and the maximum amplitude is two orders of magnitude smaller than that of BDS-2 found in Ref [
14]. With the above analysis, we presumed the multipath data for modeling is zero-mean. Moreover, if our method is used for BDS-2 satellites, the satellite-induced bias can be modeled, which is referred in the work of Ref [
15].
3. Methodology of Modeling
Based on multipath dataset and analyses derived in the preceding section, we modeled multipath error based on the CDF overbounding strategy. Two inflation factors rather than the previous single factor were used to produce a tighter boundary. Then, we estimated all of the model parameters with a global optimization process using multiobjective GA.
3.1. Model Form
Considering the non-Gaussian tails and the near-Gaussian peaks of multipath error distribution [
13], we follow the strategy introduced in Ref [
8] (pp. 54–55) and assume that the multipath error comprises three stochastic components, which is to precisely express characteristics of multipath error. Namely, the elevation-independent Gaussian component
(
), the elevation-dependent Gaussian component
(
) and an additional Gaussian component
that is used to overbound heavy tail error:
As shown in (2), with two inflation factors
and
,
is assumed to be a linear combination of
and
:
It should be mentioned that single inflation factor in (3) was widely used [
16,
17]. The symbol
in (3) denotes inflation factor.
Nevertheless, we used two inflation factors in (2) to improve the fit of model to the multipath error and thus reducing model’s conservatism. After that, the new model form is shown in (4).
It is worthwhile here to explain the reason why such intuitive improvement is not available previously. Since the multipath model for integrity monitoring must bound real error well, classical algorithms that solely fits samples, e.g., the least square, are not able to generate qualified results. Moreover, the number of inflation factors should be based on rational presumption. As a result, two rather than more inflation factors are used.
Then, the standard deviation of
can be expressed as:
With reference to the exponential form of current multipath error models, the form of
is set as follows in (6).
where
El is the elevation value in degrees. At this point, there are six unknown parameters, namely,
. Furthermore, the multiobjective GA will be used for estimating these parameters.
3.2. Strategy of Model Parameter Estimation
Based on the proposed model, the strategy of CDF overbounding together with multiobjective GA was used to derive model parameters. In this part, principle of the CDF overbounding strategy and the multiobjective GA is introduced.
3.2.1. Principle of CDF Overbounding
For error modeling in the field of integrity monitoring, heavy tails of multipath error should be bounded by a more conservative function whose characteristics are known a priori. As a result, it can be ensured that multipath error in the worst case is still in the integrity budget. In practice, these requirements are always managed with the strategy of overbounding [
13] or the extreme value theory [
18].
To construct suitable multipath error models for integrity monitoring, we used the strategy of CDF overbounding. It is worth noting that the strategy of CDF overbounding was also recommended in Section 3.6.8.3.2 of ICAO Annex 10, Volume I [
19]. The principle is listed as follows:
where the subscript “o” means “overbounding” and denotes constructed models. The subscript “a” means “actual” and represents actual distribution of multipath error. In (9),
and
respectively represent CDF and PDF. The distribution form of the CDF model is not limited, and multipath error modeling in this work was implemented with a Gaussian distribution. Nevertheless, to validate the range-to-position conversion, distribution of constructed CDF models must be unimodal, zero-mean, and symmetric [
20], which accounts for the analysis introduced in previous sections.
3.2.2. Overview of the Multiobjective Genetic Algorithm
In this work, the multiobjective GA was used for estimating multipath error model parameters (
). It simulates the evolution process in nature and derives a better solution to the problem through generation evolution [
21]. The GA is efficient in handling global optimization problems and is much easier to implement compared to other complex AI algorithms. In this work, our multiobjective GA is based on the random-weight approach [
22,
23], which avoids fixed search direction of GA by assigning a random weight value to each objective [
24].
The multiobjective GA in our work aims at dealing with the multiple requirements for multipath modeling, namely ensuring the integrity of constructed models while avoiding modeling results from being too conservative. Specifically, the integrity performance of modeling results is guaranteed by complying with the integrity requirements of CDF overbounding defined in (7) to (9). And the consideration of integrity monitoring conservatism is managed by reducing the difference between the CDF of constructed model and actual data. Since the increase of error model value would lead to increasing conservatism of constructed protection level [
25], establishing an error model that is as precise as possible can effectively improve the availability of integrity monitoring.
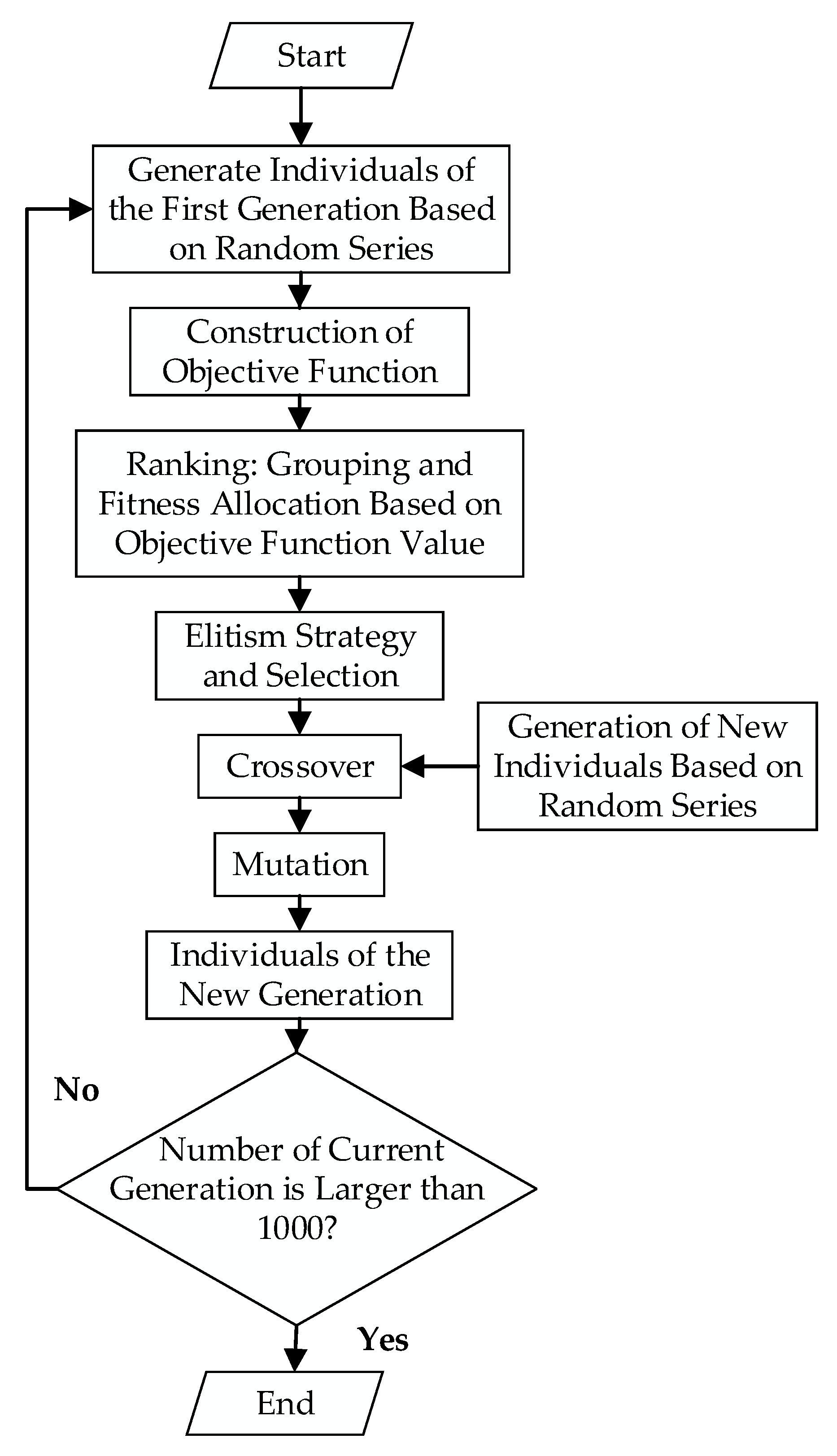
Based on the above-mentioned strategy, configuration of GA is illustrated in
Table 2. Furthermore, a flowchart of our GA algorithm is summarized in
Figure 4. Details of the table will be further illustrated. As for coding, we abstracted each unknown parameter into a chromosome of the individual and encoded it into a binary sequence then. Concerning the distribution in
Figure 2, variation range of B1I for unknown parameters was set to 0 to 1.5 m, and B3I was set to 0 to 1 m. The coding strategy can be summarized as follows:
where
CA means Coding Accuracy, Value denotes decimal value.
N is the length of binary sequences. The subscripts End and Start correspond to the a priori search range of unknown parameters.
Para denotes an unknown parameter.
BS means Binary Sequence. After coding, every unknown parameter was transformed into a binary sequence and evolved with GA.
3.2.3. Determination of Objective Function
This section introduces the core of our GA. Through constructing objective function, the multiobjective genetic algorithm was specified as a minimization problem in this work. Namely, individuals with lower objective function values are considered to be more competitive. These leading individuals will be assigned a larger fitness value in ranking, which means their genes are more likely to survive into the next generation. Definition of our objective function is illustrated with details as follows:
where
p and
q are numbers of elevation and value bins, respectively.
,
k and
are all weighting factors.
is a value between 0 and 1 that is randomly determined to avoid single-direction search.
k is a constant that defines the weight of integrity requirements. The choice of k determines the conservatism of modeling results. In this paper, a less conservative value of 1 is arranged for k. It means that the two modeling targets shown in (13) and (14) are equally important in this case. Under extreme conditions where k equals 0, the multipath modeling problem is essentially a least-square problem without considering integrity requirements. The adaptive sine function of elevation is utilized to adjust the weight of different elevation bins, namely, assigning a large weight value to low-elevation cases where “heavy tail error” primarily occurs while reduces as elevation increases. The choice of the adaptive function would affect shape of the constructed model. and are objective functions of minimization targets and integrity targets. Their definitions are given in (13) and (14).
For , it measures the difference between the CDFs of constructed model and actual data. is a penalty function. When the overbounding requirements depicted in (7) and (8) are satisfied, it corresponds to “success” in (14) and vice versa to “fail”. As a result, genes of individuals that fail to overbound the error are less likely to enter the next generation.
3.2.4. Ranking
Premature convergence is one of the most challenging problems for GA. The problem brings the random search process of GA to an early end without converging to a satisfactory solution. Ranking is one of the efficient methods to mitigate this problem. It works by preventing the domination of a few individuals with strong competitiveness at early stages of evolution so that genetic diversity is ensured [
26,
27].
Specifically, this strategy divides individuals with similar objective function values into the same group. Each group is called a rank, and individuals within the same rank share a same fitness value, i.e., the same probability of being selected into the next generation. In practices, fitness value of each rank is determined according to a specified rule then. In this work, we set the maximum fitness value to the number of individuals within a generation and the minimal value to one. Then, the fitness of each rank is assigned linearly.
3.2.5. Selection, Crossover and Mutation Operators
In this part, we briefly illustrate our selection, crossover, and mutation operators. Corresponding parameters are displayed in
Table 2. The roulette selection operator was adopted to select individuals for a new generation [
21]. The process abstracts the population of GA into a roulette wheel in which a sector denotes an individual. The area of each sector is proportional to the fitness value. Every time the wheel stops spinning, an individual is selected randomly to construct the next generation. As illustrated in (15), the probability of an individual being selected into the next generation is proportional to the corresponding fitness value.
where
N is the number of individuals. Besides, to retain competitive genotypes, a certain number of elites with maximum fitness values are permitted to the next generation directly without selection. The number of elites for each generation is specified in
Table 2.
In terms of chromosome crossover, the principle of the two-point crossover strategy is illustrated as follows in
Figure 5. The location of cross points is determined randomly.
As for mutation, for each bit of binary gene sequence, we generated a random Boolean number whose probability of being true equals the value specified in
Table 2. Once the random number is true, the corresponding binary digit shall be flipped, namely zero to one or one to zero.
4. Experiment and Analysis
After illustrating our methodology in previous sections, this part displays our modeling result. Then, their performance of bounding multipath error was evaluated using actual data. We also compared conservatism of constructed model that was from our modeling method and that with the classic one. All of our experiments were performed on a laptop with Intel i7-8750H CPU, and the RAM was 16 GB. Calculation time of each generation for GA can be managed within 1.4 s with no additional efficiency promotion. This fact indicates the efficiency of the algorithm.
4.1. Validation of Constructed Models
This part validates our modeling results in terms of bounding error. Model parameters for the two-inflation-factor and single-inflation-factor model form are shown in
Table 3 and
Table 4, respectively. At first, we compared modeled standard deviation with that of actual error at each elevation bin in
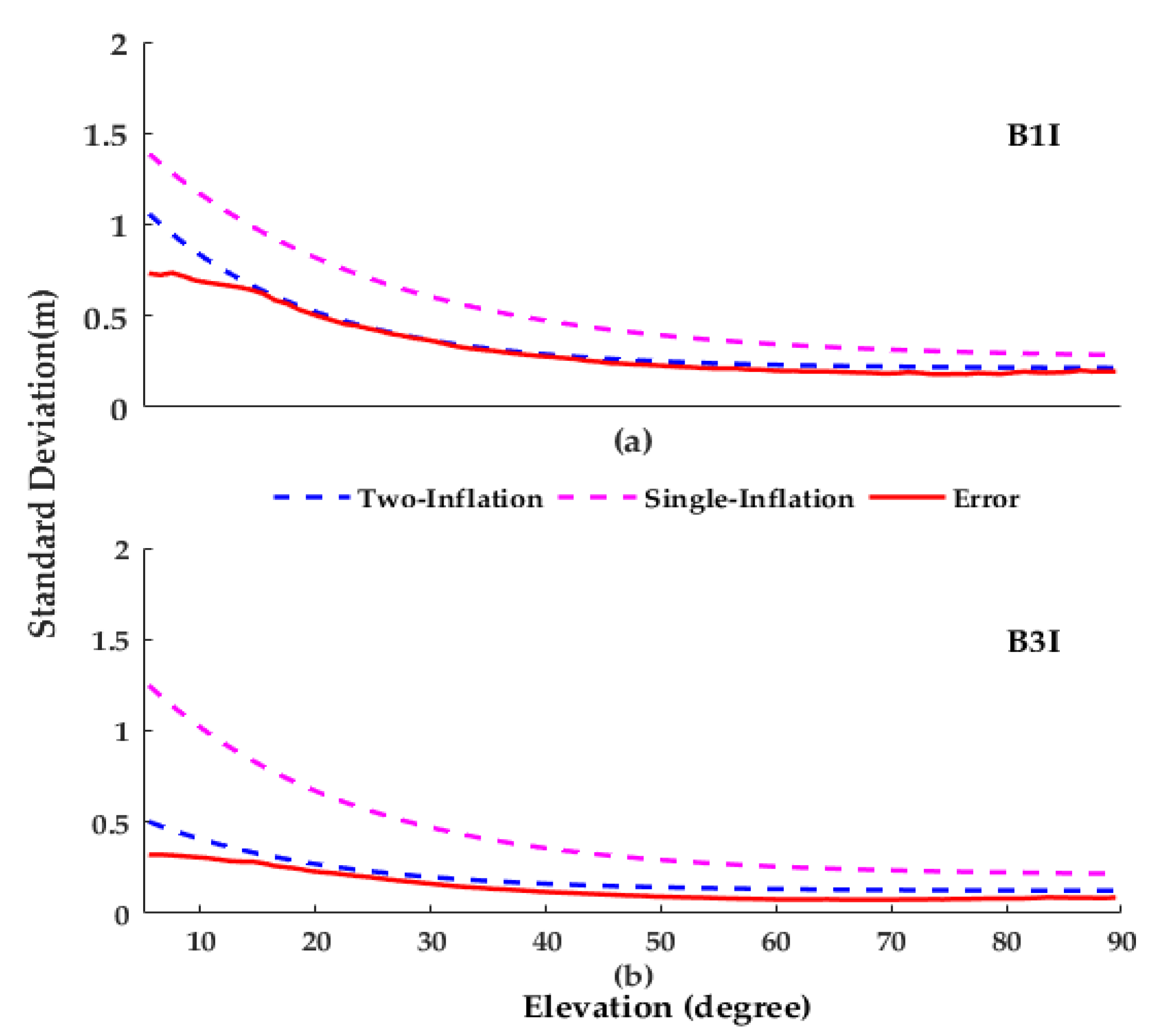
Figure 6. The x-axis denotes elevation angle whose unit is degree. It can be seen that our models successfully bound multipath error, and the standard deviation differences between model and error reduces as elevation increases. This fact demonstrates the utility of our modeling methodology in bounding multipath error as well as in preserving integrity monitoring availability in high-elevation cases, which was primarily managed by designating the sine function weight in (12).
As depicted in previous sections, meeting CDF overbounding requirements is our direct modeling target to ensure model’s integrity performance. To validate our algorithm, we also compared CDFs of constructed models and multipath error in
Figure 7. The dashed lines represent CDF model while red lines denote multipath error. As shown in the graphs, the expected modeling targets of CDF overbounding were achieved and well reflected.
4.2. Improvement Compared to Previous Methods
Effects of our multipath error modeling methodology are illustrated with comparison of previous methods.
Section 4.2.1 validates the effect of quantifying integrity requirements in GA’s objective function.
Section 4.2.2 demonstrates the contribution of the proposed two-inflation-factor model form.
4.2.1. Effective Boundary
As we know, it is the work of Ref [
8,
16] that first modeled multipath error for integrity monitoring with GA. They estimated model parameters by minimizing the CDF difference between model and actual error. Nevertheless, the requirement of bounding error was not directly considered in their design. To illustrate effects of our method, we calculated a set of models with the previous algorithm for comparison. Despite integrity considerations in the objective function of GA, other conditions were all the same.
The following analysis is based on a method called Sigma Analysis. It plots constructed multipath standard deviation model of a certain multiple in time series. Then, the performance of modeling result is evaluated by judging whether the Sigma series tightly bound real multipath error time series. As the knowledge of statistics indicates that the probability of Gaussian random variable value exceeding more than three times its standard deviation is small, the overbounded Sigma series demonstrates to some extent the performance of error model to bound multipath error.
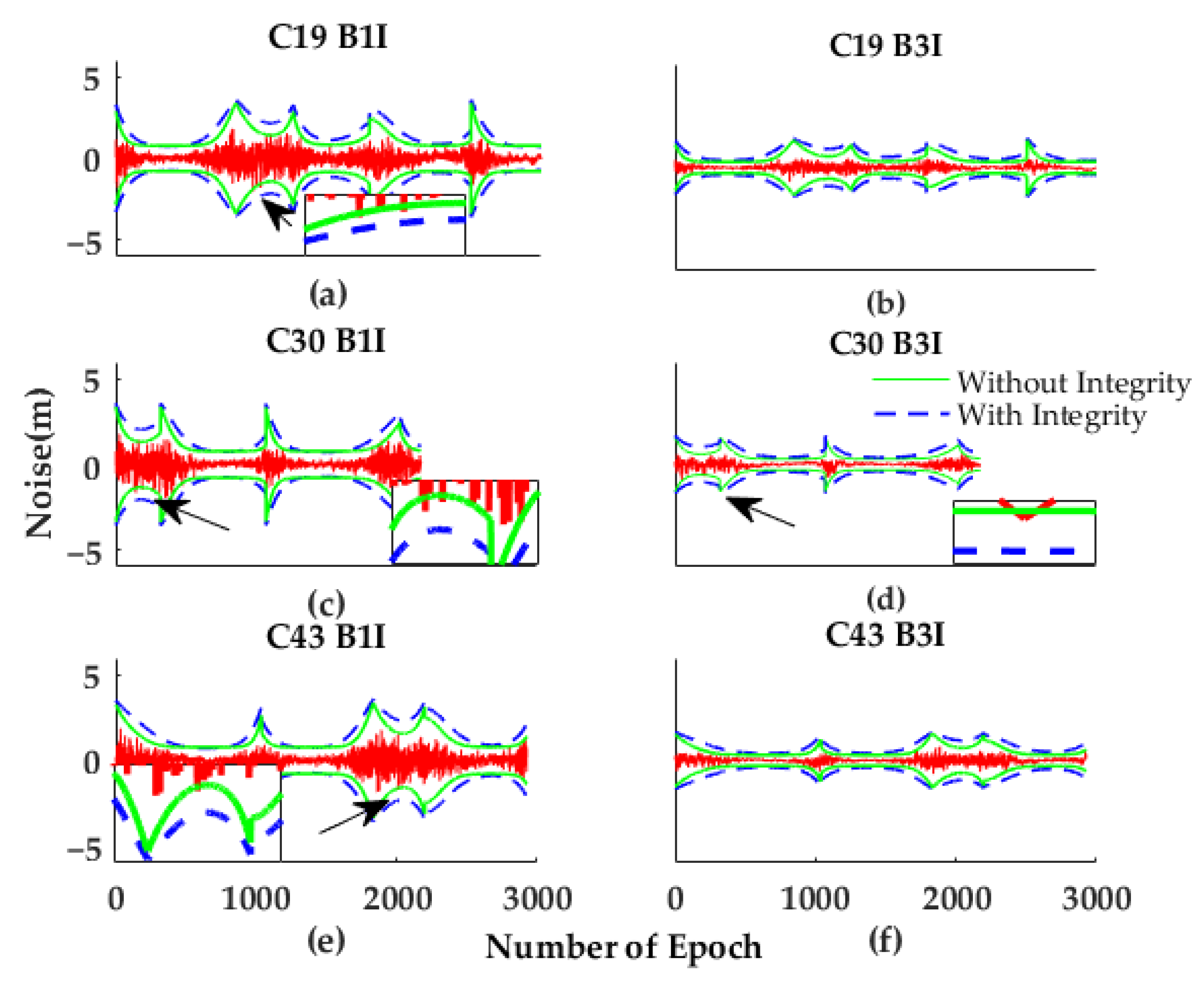
Figure 8 plots a three-day time series of multipath error and the corresponding 3.29-Sigma series of our constructed models. The value 3.29 is the standard Gaussian quantile corresponding to 99.9%. To verify the effectiveness of the model for various satellites, three satellites from different platforms (
http://en.beidou.gov.cn/SYSTEMS/Officialdocument/, accessed on 20 April 2022) were selected. The period without observation was removed in the figure. Since the B3I signal has a larger code rate [
28], it suffers obviously less from multipath effect [
29] than B1I.
It can be seen in
Figure 8 that raw models from the previous algorithm cannot bound multipath error well. As we mentioned in
Section 3.2.3, although GA’s output is random, modeling without considering integrity requirement is essentially a least-square problem. Under such cases, additional method may be required to further inflat the modeling result, which would limit the effect of algorithm. This fact indicates the advantage of our algorithm in producing effective boundaries.
4.2.2. Less Conservative Models
With the support of GA, the effect of a new model form is utilized to obtain a better fit of multipath error and thus generate tighter boundaries. In this section, effect of the proposed two-inflation-factor model is evaluated through the average CDF difference comparison with the commonly-used single-inflation-factor model. Definition of the average CDF difference is presented as follows. The smaller the converged CDF difference, the tighter the boundary.
where
N is the number of individuals in each generation.
p and
q are numbers of elevation bins and value bins, respectively.
F denotes the CDF. The subscript “
o” denotes modeling result and “
a” denotes actual data.
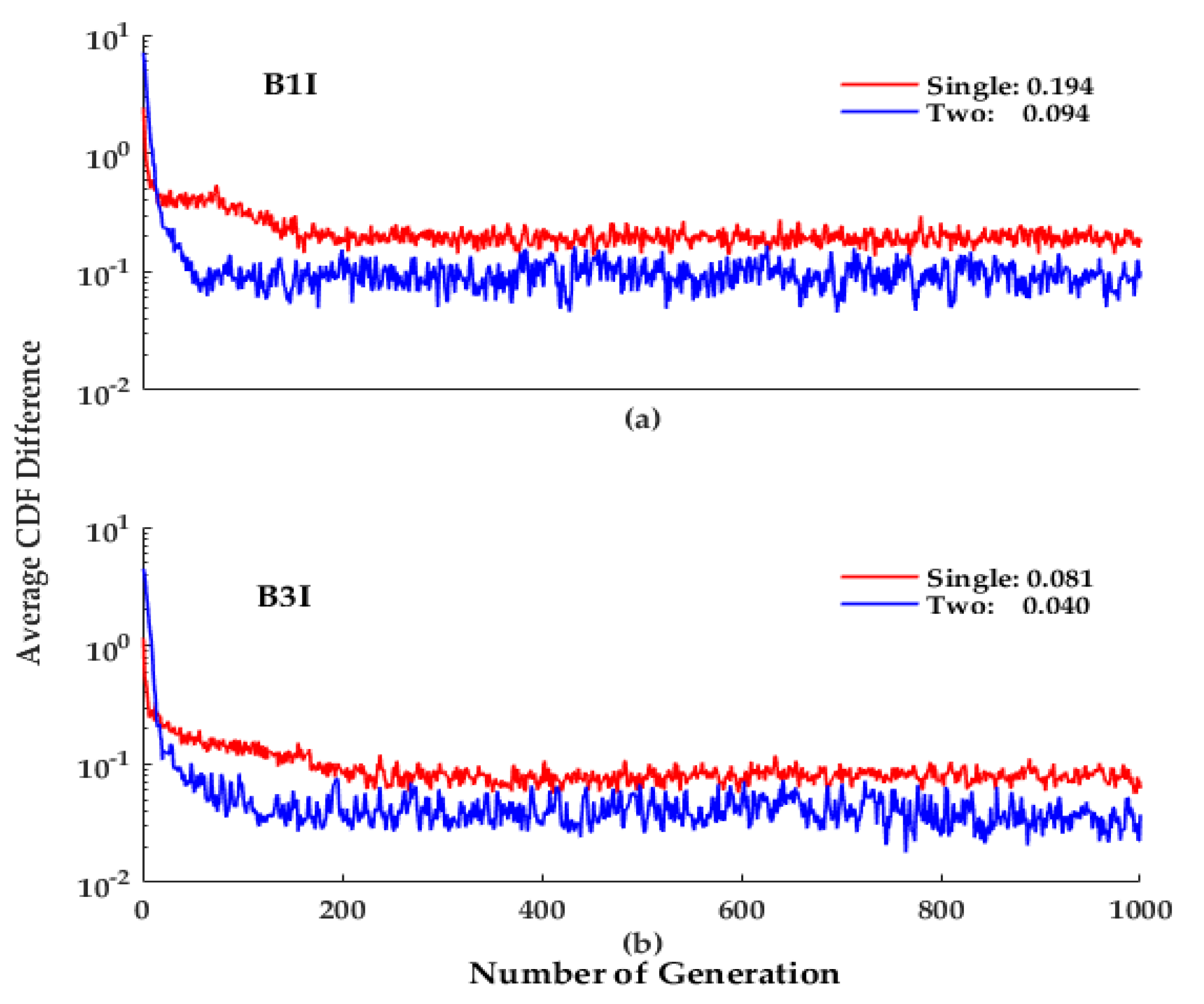
Figure 9 plots average CDF difference after taking logarithm. The x-axis denotes the number of generations. And the converged CDF difference value without taking logarithm is given in legend. It is worth explaining that the converged CDF difference is set as the average CDF difference of GA’s last 100 generation. For B1I, the converged values are 0.193 and 0.063 for the classic single-inflation-factor model and our two-inflation-factor model, respectively. And for B3I, the values are 0.081 and 0.040, respectively. Compared to the previous one, our new model brings a 67.4% improvement to the B1I signal and a 50.6% improvement to the B3I signal. This fact validates the effect of our two-inflation-factor model in producing a less-conservative multipath model.
5. Discussion
With the promotion of dual-frequency and even multi-frequency applications, the ionospheric residual is no longer the primary concern of GNSS integrity monitoring. This fact results in the growing popularity of multipath error modeling research. Nevertheless, rare literature provides valid solution to producing effective boundary while reducing the conservatism. The proposed strategy utilizes the random search characteristic of multiobjective GA. It quantifies considerations of bounding error and avoiding modeling result being too conservative in the objective function of GA. Therefore, manual iterative weighing can be replaced and multipath modeling for GNSS integrity monitoring can be managed automatically. Moreover, a new model form based on two inflation factors is proposed to improve the fitting and thus reducing the conservatism. Experiments have validated its effect.
6. Conclusions
In this work, a new automatic multipath error modeling methodology based on the CDF overbounding strategy and multiobjective GA is proposed. We generated multipath data for modeling with the widely-used method of MP combination for demonstration. The raw data was from a 4-month dataset of ground-based BDS-3 MEO observations. Since the cruise phase at high altitude takes up the majority of the flight time, and surface surrounding the runway and taxiway is open and unobstructed, it is rational to believe ground-based BDS-3 observations from IGS stations suffers no less multipath effect than actual airborne cases and our initial demonstration with ground measurement is acceptable.
The new methodology quantifies considerations of bounding error and avoiding modeling result being too conservative in the objective function of GA. Therefore, multipath modeling for GNSS integrity monitoring can be managed automatically. Multiple analysis on the performance of bounding multipath error indicates that modeling results based on our methodology are of good quality. Moreover, we introduced a new two-inflation-factor model form to reduce conservatism of modeling results. Experiments on the average CDF difference show that compared to the previous single-inflation-factor model, our two-inflation-factor model improves average CDF difference of B1I model by 67.4% and that of B3I model by 50.6%.
Author Contributions
Conceptualization, X.F. and D.S.; methodology and software, X.F.; validation, L.F. and Z.H.; writing—review and editing, X.F., D.S. and C.S.; supervision, C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (Project No.2020YFB0505601), National Natural Science Foundation of China (Grant No. 41931075, 41804024).
Data Availability Statement
Raw BDS-3 observations used in this study were provided by the International GNSS Service (IGS). The observation dataset is available on the website of IGS analysis centers.
Acknowledgments
We are sincerely grateful for the data support of IGS, the effort of respectful reviewers and academic editor in improving this article, and the timely assistance of assistant editor.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Harris, M.; Schlais, P.; Murphy, T.; Joseph, A.; Kazmierczak, J. Gps and Galileo Airframe Multipath Error Bounding Method and Test Results. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2020), Online, 21–25 September 2020. [Google Scholar] [CrossRef]
- Circiu, M.; Caizzone, S.; Felux, M.; Enneking, C.; Rippl, M.; Meurer, M. Development of the Dual-Frequency Dual-Constellation Airborne Multipath Models. Navigation 2019, 67, 61–81. [Google Scholar] [CrossRef] [Green Version]
- Circiu, M.-S.; Felux, M.; Caizzone, S.; Enneking, C.; Fohlmeister, F.; Rippl, M.; Gulie, I.; Rüegg, D.; Griggs, J.; Lazzerini, R.; et al. Airborne Multipath Models for Dual-Constellation Dual-Frequency Aviation Applications. In Proceedings of the 2020 International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 21–24 January 2020; pp. 162–173. [Google Scholar] [CrossRef]
- Felux, M.; Circiu, M.-S.; Caizzone, S.; Enneking, C.; Fohlmeister, F.; Rippl, M. Towards Airborne Multipath Models for Dual Constellation and Dual Frequency Gnss. In Proceedings of the 2019 International Technical Meeting of the Institute of Navigation, Reston, VA, USA, 28–31 January 2019; pp. 62–68. [Google Scholar] [CrossRef] [Green Version]
- Felux, M.; Circiu, M.-S.; Caizzone, S.; Rippl, M.; Sgammini, M.; Durel, P. Standardization of New Airborne Multipath Models. In Proceedings of the 2020 International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 21–25 January 2020; pp. 146–153. [Google Scholar] [CrossRef]
- Amielh, C.; Chabory, A.; Macabiau, C.; Azoulai, L. Gnss Multipath Error Model for Aircraft Surface Navigation Based on Canonical Scenarios for Class F Airports. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 1418–1437. [Google Scholar] [CrossRef] [Green Version]
- Montloin, L.; Azoulai, L.; Chen, A.; Martineau, A.; Milner, C.; Chabory, A.; Macabiau, C. Gnss Multipath Error Model for Airport Surface Operations. In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 210–228. [Google Scholar]
- Fan, G. Research on Receiver Autonomous Integrity Monitoring in Typical Urban Canyon and Simulation System Design. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2018. [Google Scholar]
- Blanch, J.; Walter, T.; Phelts, R. Development and Evaluation of Airborne Multipath Error Bounds for L1-L5. In Proceedings of the 2019 International Technical Meeting of the Institute of Navigation, Reston, VA, USA, 28–31 January 2019; pp. 53–61. [Google Scholar] [CrossRef]
- Hauschild, A. Basic Observation Equations. In Springer Handbook of Global Navigation Satellite Systems; Peter, J., Teunissen, G., Oliver Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 561–582. [Google Scholar]
- Caizzone, S.; Circiu, M.-S.; Elmarissi, W.; Enneking, C.; Felux, M.; Yinusa, K. Effect of Antenna Pattern Uniformity on the Pseudorange Tracking Error. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 16–20 September 2017; pp. 3460–3470. [Google Scholar] [CrossRef]
- ARAIM. Interim Report Issue 1.0; EU-U.S. In Cooperation on Satellite Navigation Working Group C, ARAIM Technical Subgroup; 2012. Available online: https://www.gps.gov/policy/cooperation/europe/2013/working-group-c/ARAIM-report-1.0.pdf (accessed on 20 April 2022).
- De Cleene, B. Defining Pseudorange Integrity—Overbounding. In Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000; pp. 1916–1924. [Google Scholar]
- Wanninger, L.; Beer, S. Beidou Satellite-Induced Code Pseudorange Variations: Diagnosis and Therapy. GPS Solut. 2015, 19, 639–648. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.; Li, X.; Liu, W. Mitigating Beidou Satellite-Induced Code Bias: Taking into Account the Stochastic Model of Corrections. Sensors 2016, 16, 909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, G.; Xu, C.; Zhao, J.; Zheng, X. A distribution model of the GNSS code noise and multipath error considering both elevation angle and orbit type. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 233, 1900–1915. [Google Scholar] [CrossRef]
- Niu, F.; Chen, J.; Gao, W.; Zhang, Y. Calculation and Analysis on Integrity Threshold Based on Non-Gaussian Distributing. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 1429–1433. [Google Scholar] [CrossRef]
- Azais, J.-M.; Gadat, S.; Lévy, J.C.; Rols, B.; Mercadier, C.; Jordan, C.; Suard, N. Gnss Integrity Achievement by Using Extreme Value Theory. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 1281–1287. [Google Scholar]
- International Civil Aviation Organization (ICAO). International Standards and Recommended Practices, Aeronautical Telecommunications—Volume I (Radio Navigation Aids); Annex 10; ICAO: Montreal, QC, Canada, 2006. [Google Scholar]
- Rife, J.; Walter, T.; Blanch, J. Overbounding Sbas and Gbas Error Distributions with Excess-Mass Functions. In Proceedings of the International Symposium on GNSS/GPS, Sydney, Australia, 6–8 December 2004. [Google Scholar]
- Whitley, D. A Genetic Algorithm Tutorial. In Statistics and Computing; Springer: Berlin/Heidelberg, Germany, 1994; pp. 65–85. [Google Scholar]
- Ishibuchi, H.; Murata, T. A Multiobjective Genetic Local Search Algorithm and Its Application to Flowshop Scheduling. IEEE Trans. Syst. Man Cybern. 1998, 28, 392–403. [Google Scholar] [CrossRef]
- Murata, T.; Ishibuchi, H.; Tanaka, H. Multiobjective Genetic Algorithm and Its Application to Flowshop Scheduling. Comput. Eng. 1996, 30, 957–968. [Google Scholar]
- Zhao, R. Analysis About the Application of the Multiobjective Genetic Algorithm. Master’s Thesis, Tianjin University, Tianjin, China, 2005. [Google Scholar]
- Bhattacharyya, S. Performance and Integrity Analysis of the Vector Tracking Architecture of Gnss Receivers. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2012. [Google Scholar]
- Fonseca, C.; Fleming, P. Genetic Algorithms for Multiobjective Optimization: Formulation Discussion and Generalization. In Proceedings of the 5th International Conference on Genetic Algorithms, San Mateo, CA, USA; 1999. [Google Scholar]
- Grefenstette, J.J. Optimization of Control Parameters for Genetic Algorithms. IEEE Trans. Syst. Man Cybern. 1986, 16, 122–128. [Google Scholar] [CrossRef]
- Lu, M.; Li, W.; Yao, Z.; Cui, X. Overview of BDS III new signals. Navigation 2019, 66, 19–35. [Google Scholar] [CrossRef] [Green Version]
- Avila-Rodriguez, J.A.; Wallner, S.; Hein, G.W. How to Optimize Gnss Signals and Codes for Indoor Positioning. In Proceedings of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2006), Fort Worth, TX, USA, 26–29 September 2006; pp. 2418–2426. [Google Scholar]
Figure 1.
Distribution of the 23 selected IGS MGEX stations.
Figure 1.
Distribution of the 23 selected IGS MGEX stations.
Figure 2.
Distribution of multipath error at three elevation bins. The sub-figures (a,c,e) are distributions of B1I and (b,d,f) are distributions of B3I, respectively. The symbol “*” means “multiply”.
Figure 2.
Distribution of multipath error at three elevation bins. The sub-figures (a,c,e) are distributions of B1I and (b,d,f) are distributions of B3I, respectively. The symbol “*” means “multiply”.
Figure 3.
Averages of multipath error at B1I and B3I in each elevation bin.
Figure 3.
Averages of multipath error at B1I and B3I in each elevation bin.
Figure 4.
Flow chart of multiobjective genetic algorithm.
Figure 4.
Flow chart of multiobjective genetic algorithm.
Figure 5.
Principle of the two-point crossover operator used in this work.
Figure 5.
Principle of the two-point crossover operator used in this work.
Figure 6.
The modeled and the actual standard deviations of multipath error. The sub-figure (a,b) are results of B1I and B3I respectively.
Figure 6.
The modeled and the actual standard deviations of multipath error. The sub-figure (a,b) are results of B1I and B3I respectively.
Figure 7.
CDF of constructed models and multipath error. The sub-figures (a,c,e) are results of B1I and (b,d,f) are results of B3I, respectively. The red lines are CDF of actual multipath error, the dashed blue lines are that of constructed models based on two inflation factors, and the dashed magenta lines are that of constructed models based on single inflation factor.
Figure 7.
CDF of constructed models and multipath error. The sub-figures (a,c,e) are results of B1I and (b,d,f) are results of B3I, respectively. The red lines are CDF of actual multipath error, the dashed blue lines are that of constructed models based on two inflation factors, and the dashed magenta lines are that of constructed models based on single inflation factor.
Figure 8.
Range domain validation (CUSV, DOY 201–203, 2020). The sub-figures (a,c,e) are results of B1I and (b,d,f) are results of B3I, respectively. The red curves are multipath time series. The blue boundaries are from models based on two-inflation factors. And the green boundaries are from models based on single inflation factor.
Figure 8.
Range domain validation (CUSV, DOY 201–203, 2020). The sub-figures (a,c,e) are results of B1I and (b,d,f) are results of B3I, respectively. The red curves are multipath time series. The blue boundaries are from models based on two-inflation factors. And the green boundaries are from models based on single inflation factor.
Figure 9.
Average CDF difference comparison. The sub-figures (a,b) are results of B1I and B3I respectively.
Figure 9.
Average CDF difference comparison. The sub-figures (a,b) are results of B1I and B3I respectively.
Table 1.
Details of data division.
Table 1.
Details of data division.
| Items | Description |
|---|
| Range of data value | [−6 m, 6 m] |
| Range of elevation | [5°, 90°] |
| Interval of value bins | 0.03 m |
| Interval of elevation bins | 1° |
| Number of value bins | 400 |
| Number of elevation bins | 85 |
Table 2.
Configuration of multiobjective genetic algorithm parameters.
Table 2.
Configuration of multiobjective genetic algorithm parameters.
| Items | Description |
|---|
| Size of population | 150 |
| Number of generations | 1000 |
| Number of ranks | 30 |
| Coding | Binary; 14 bits |
| Number of elites per generation | 5 |
| Probability of crossover | 0.6 |
| Probability of mutation | 0.01 |
Table 3.
Parameters of constructed models with two inflation factors.
Table 3.
Parameters of constructed models with two inflation factors.
| Orbit | Signal | | | | | | |
|---|
| BDS-3MEO | B1I | 0.039 | 0.186 | 1.168 | 0.069 | 0.900 | 0.069 |
| B3I | 0.035 | 0.099 | 0.546 | 0.063 | 0.961 | 0.024 |
Table 4.
Parameters of constructed models with single inflation factor.
Table 4.
Parameters of constructed models with single inflation factor.
| Orbit | Signal | | | | | |
|---|
| BDS-3MEO | B1I | 0.043 | 0.259 | 1.444 | 0.049 | 1.018 |
| B3I | 0.112 | 0.182 | 1.481 | 0.055 | 0.972 |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).