Accounting for Almond Crop Water Use under Different Irrigation Regimes with a Two-Source Energy Balance Model and Copernicus-Based Inputs
Abstract
:1. Introduction
2. Materials and Methods
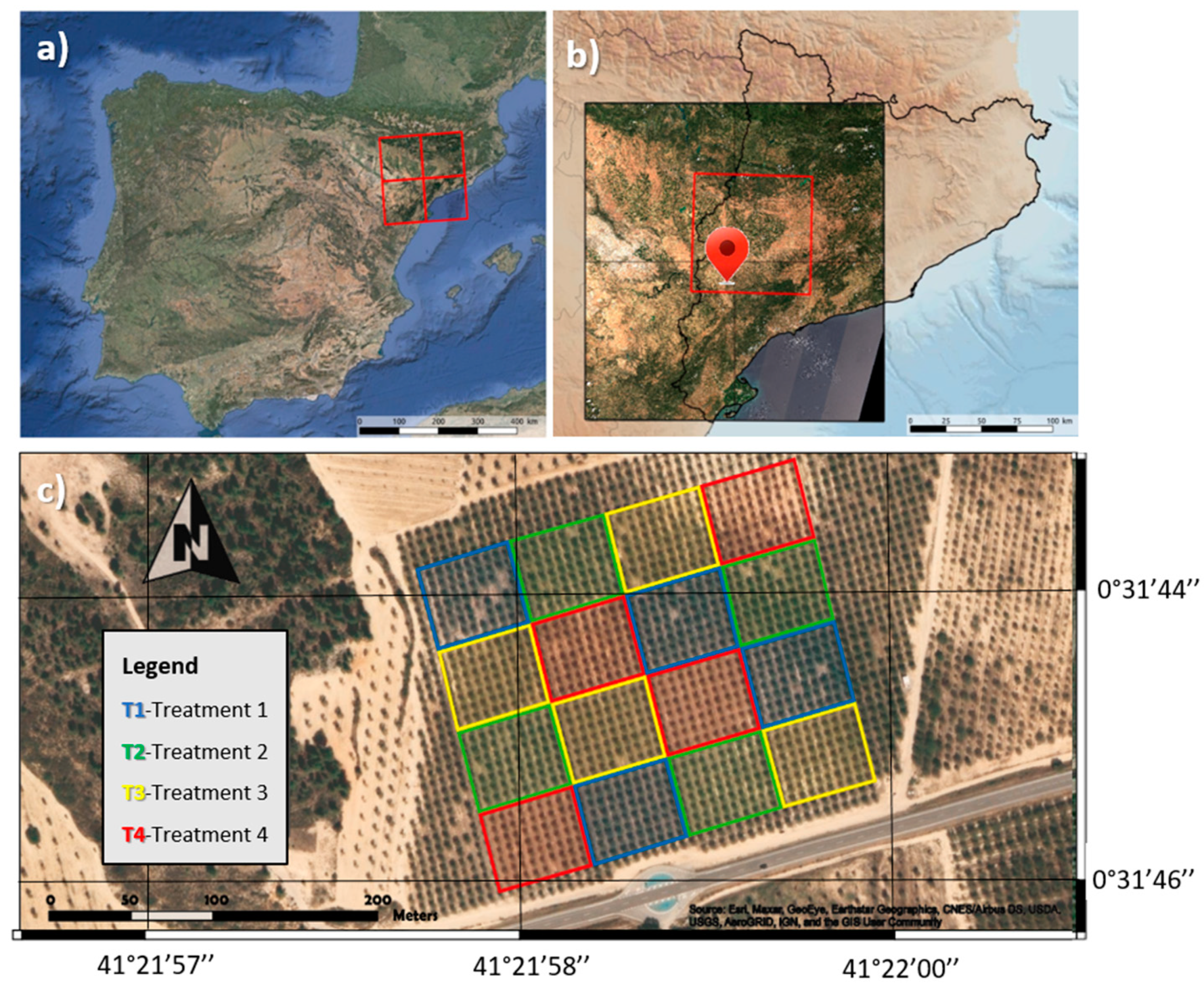
2.1. Study Site
2.2. Field Experimental Design
2.3. TSEB Scheme

2.4. Input Data
2.4.1. Image Acquisition
2.4.2. Sentinel-2 Biophysical Parameters of the Vegetation
2.4.3. Sharpening Land Surface Temperature (LST)
2.4.4. Meteorological Data
2.4.5. Ancillary Data
2.5. Daily ET Upscaling
2.6. Gap Filling
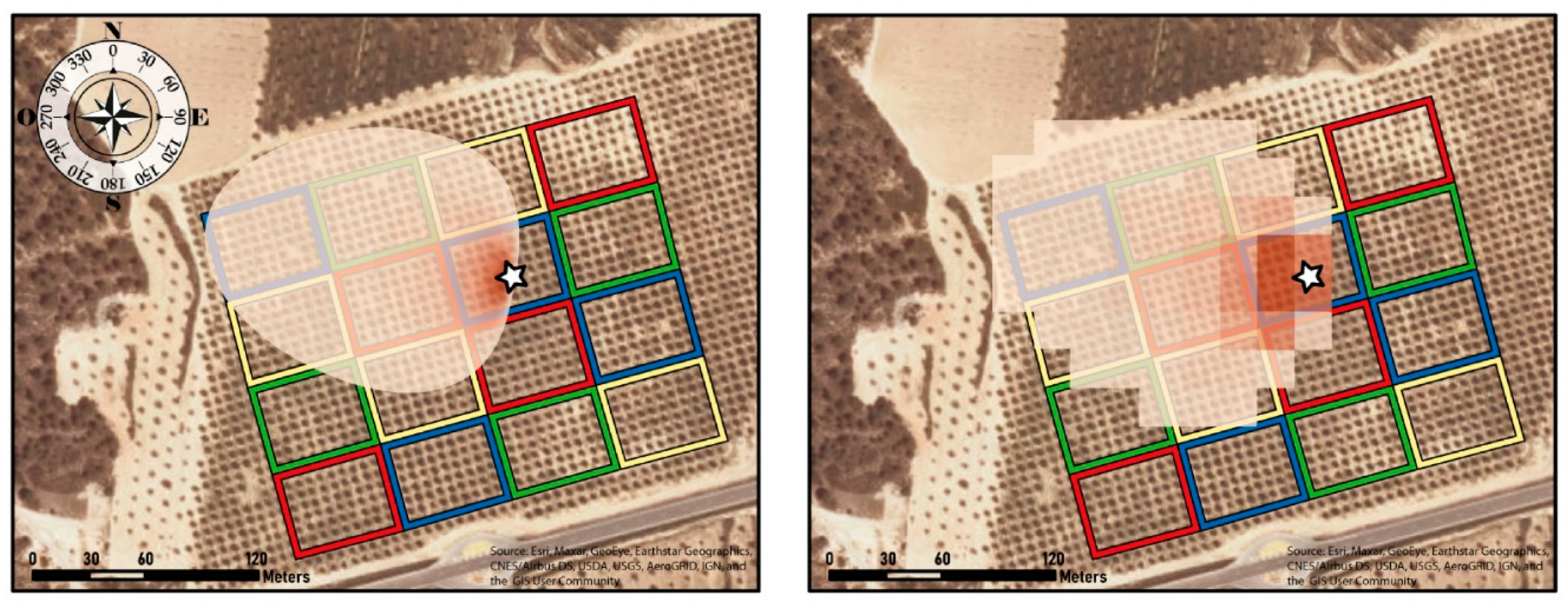
2.7. Eddy Covariance (EC) Fluxes
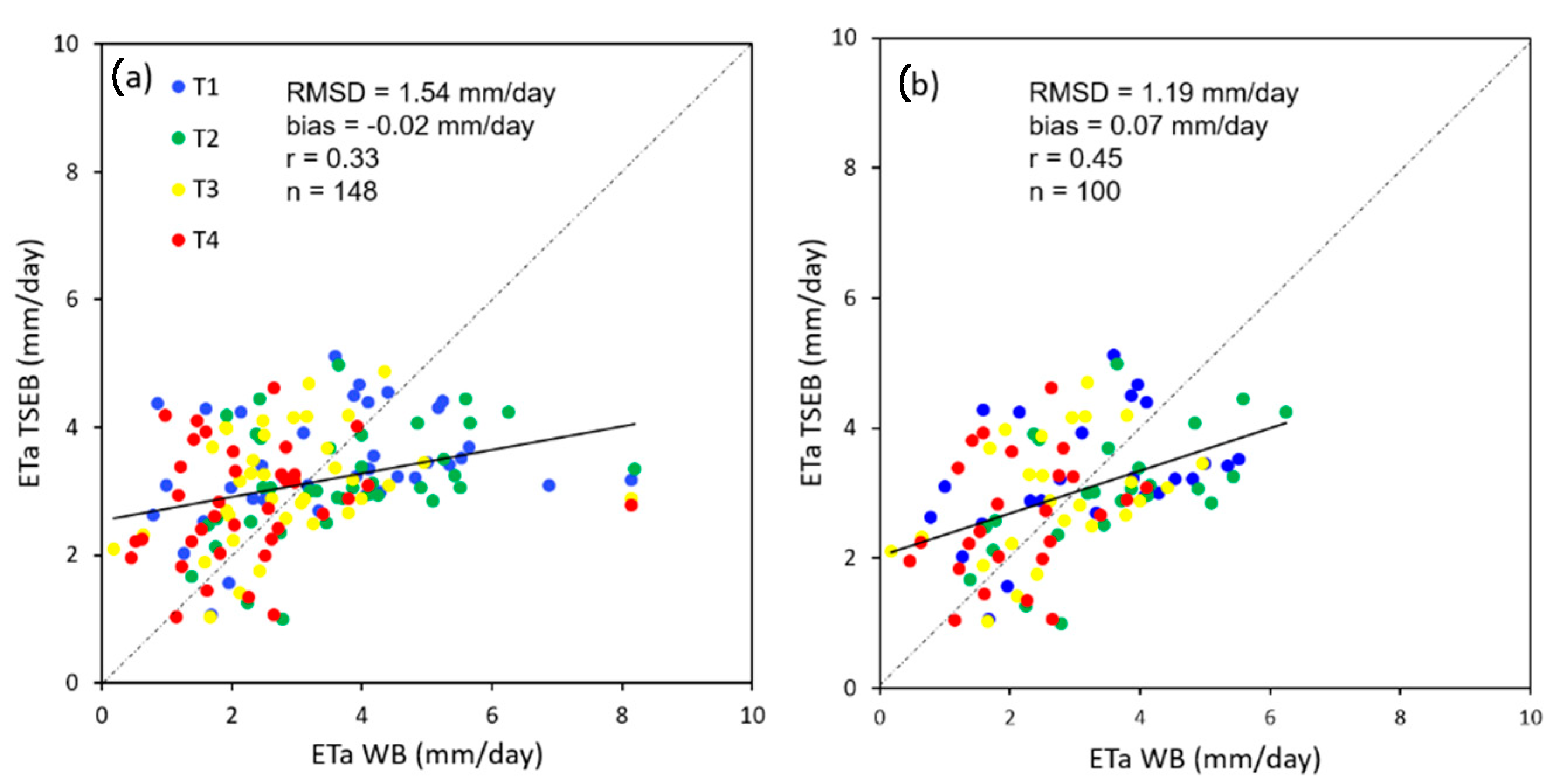
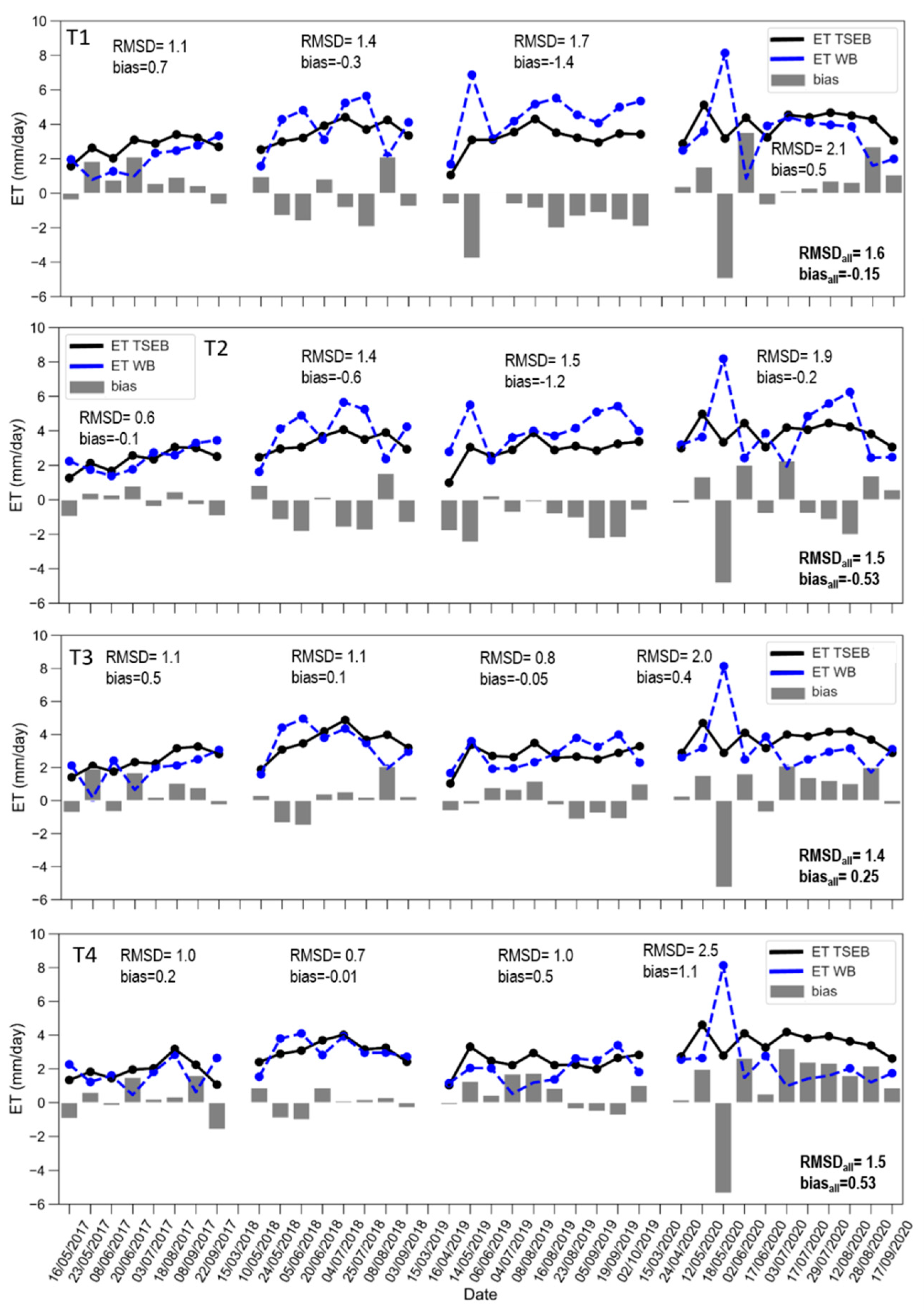
2.8. Model ETa Intercomparison through a Soil Water Balance Approach
3. Results
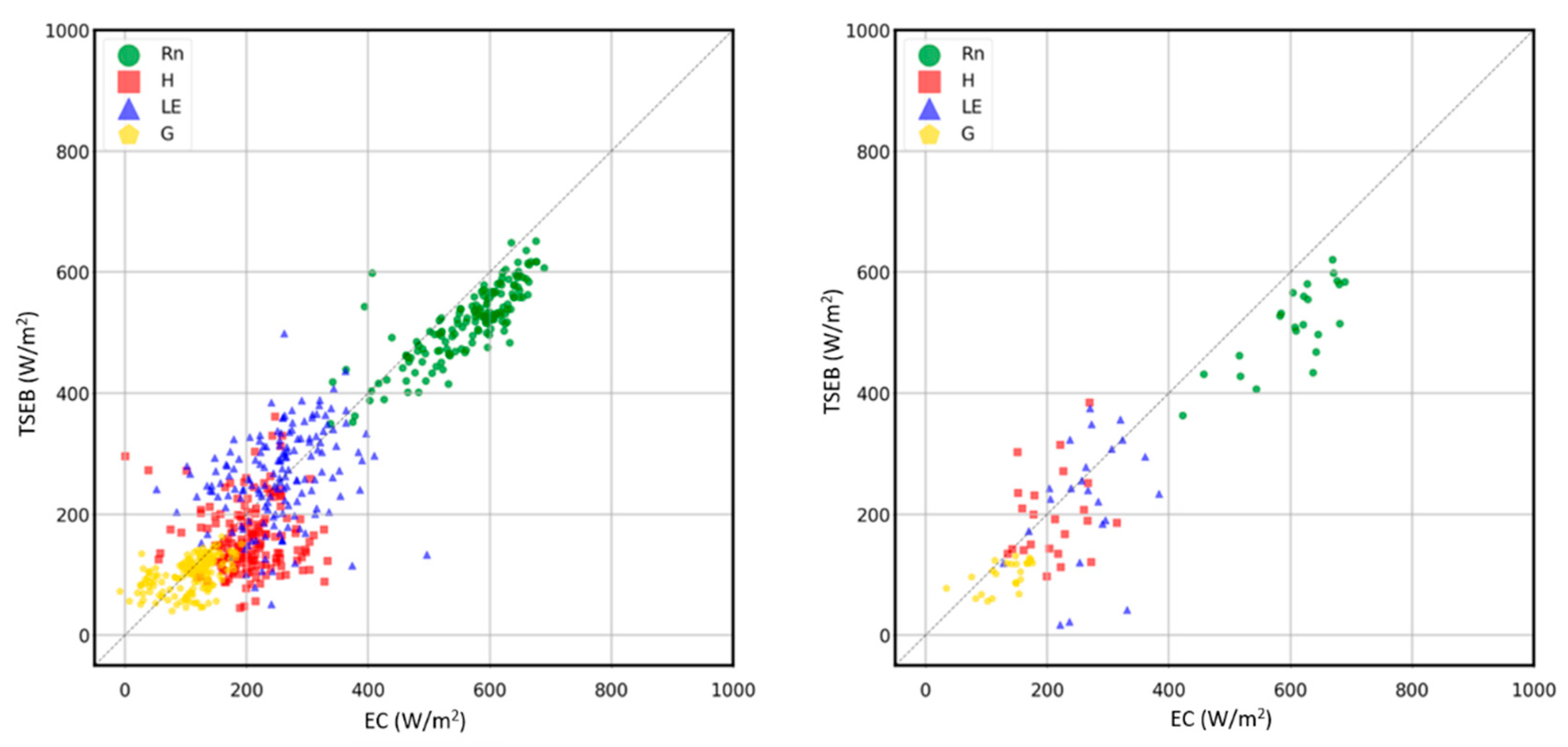
3.1. Validation with the Eddy Covariance Flux Tower
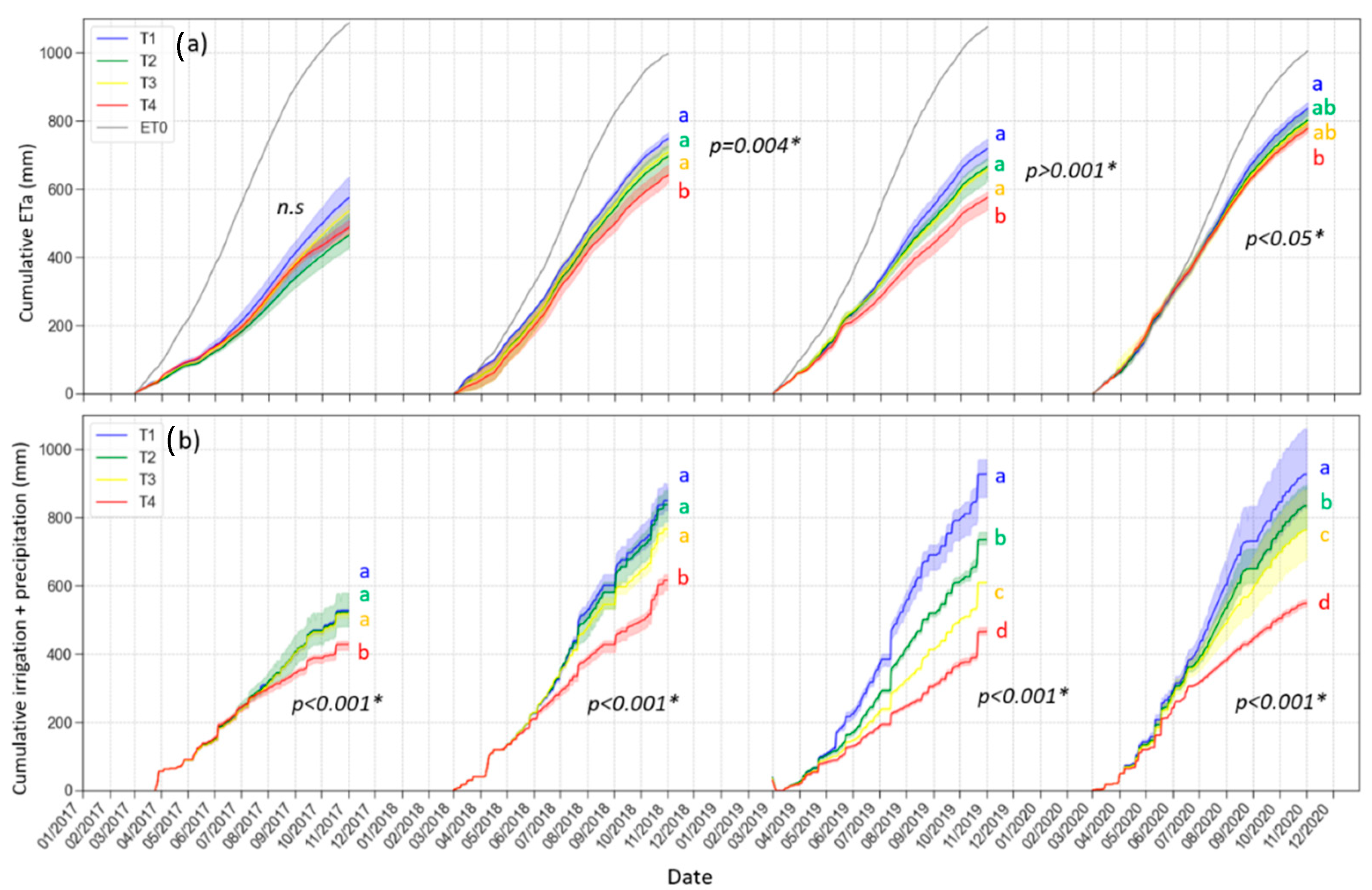
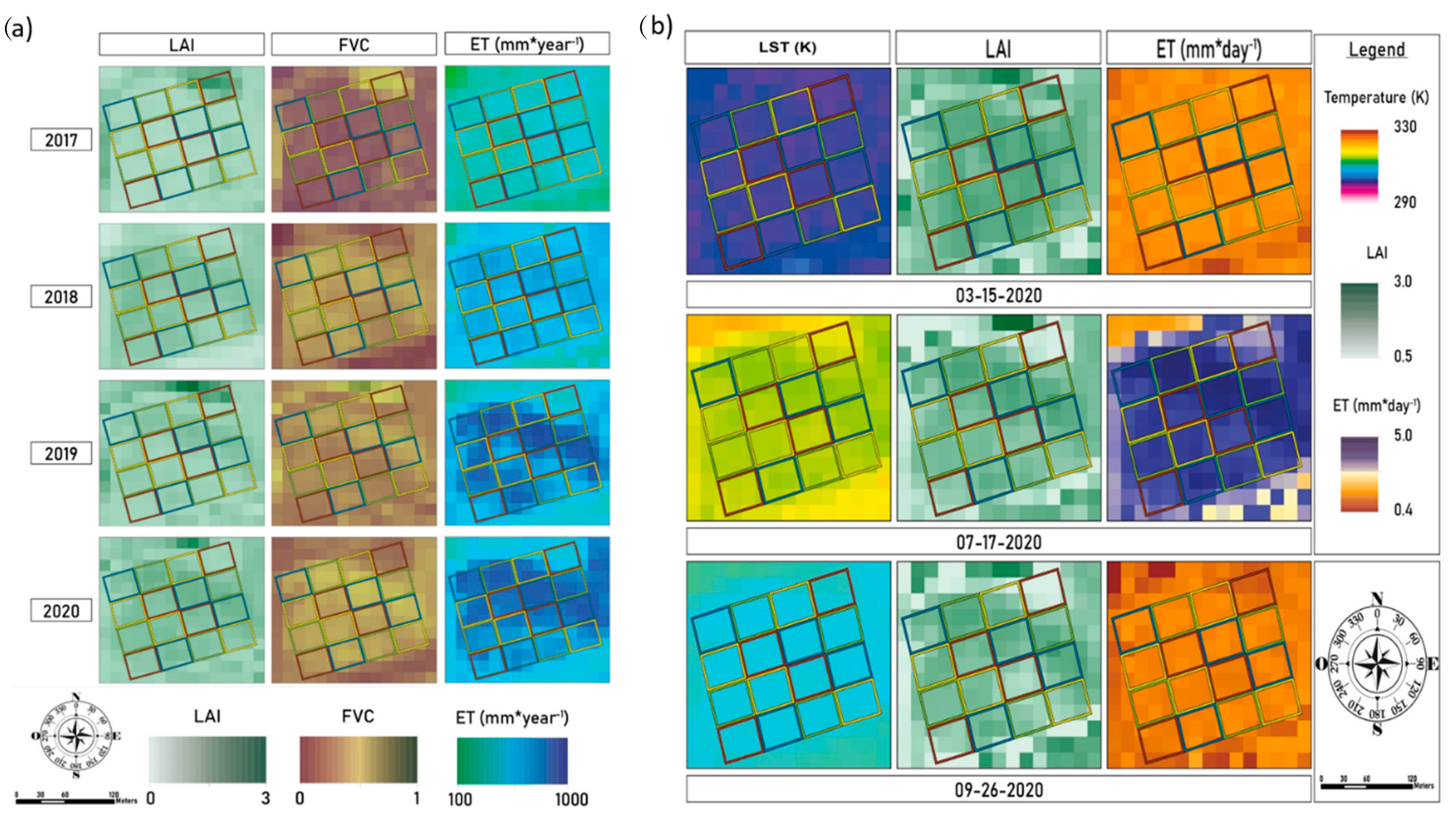
3.2. Water Applied and Biophysical Parameters of the Vegetation
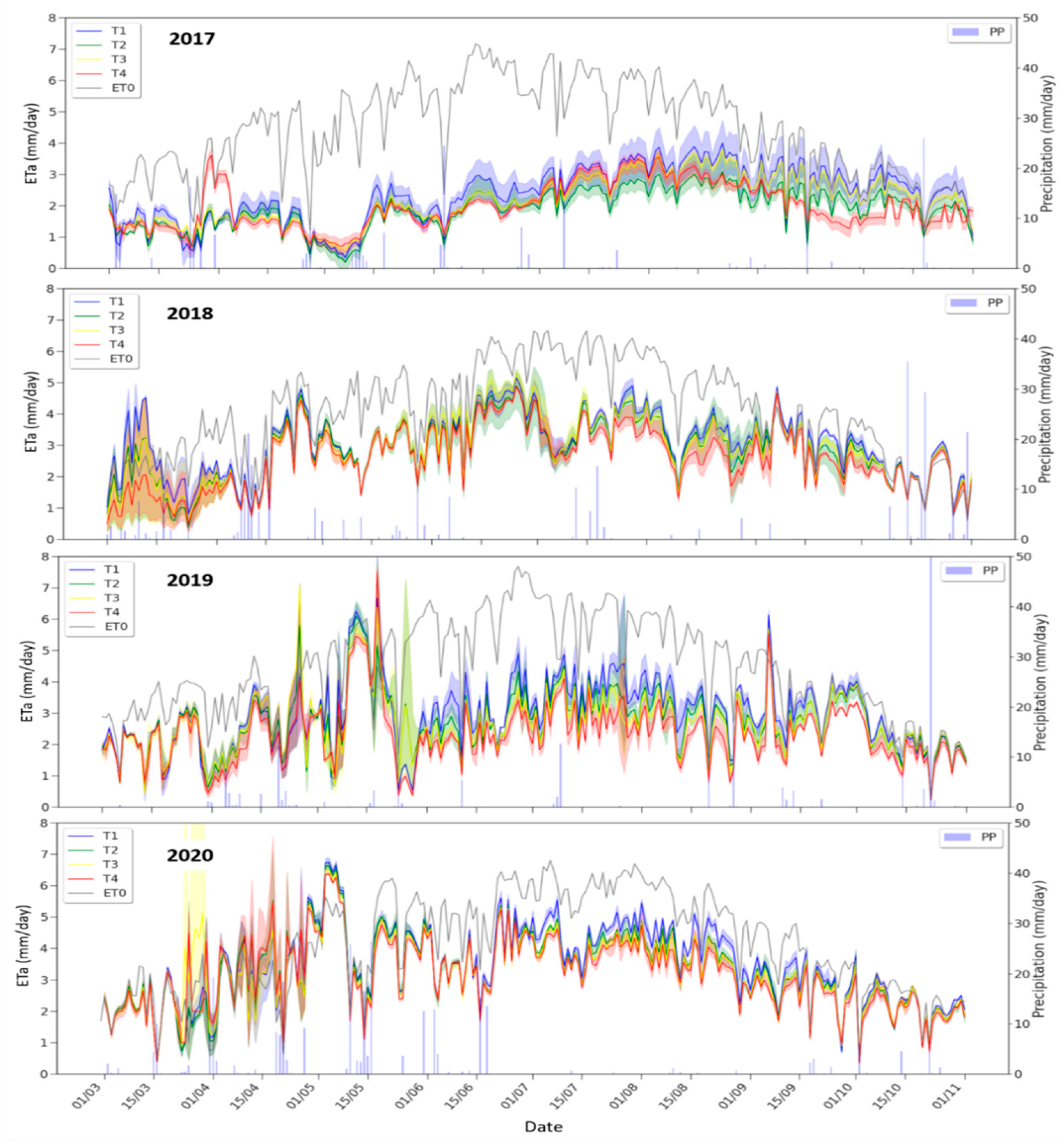
3.3. Seasonal Trend of Actual Crop Evapotranspiration
3.4. Comparison of ETa Estimates with TSEBS2+S3 and a Soil Water Balance Approach
4. Discussion
4.1. Validation of Energy Fluxes
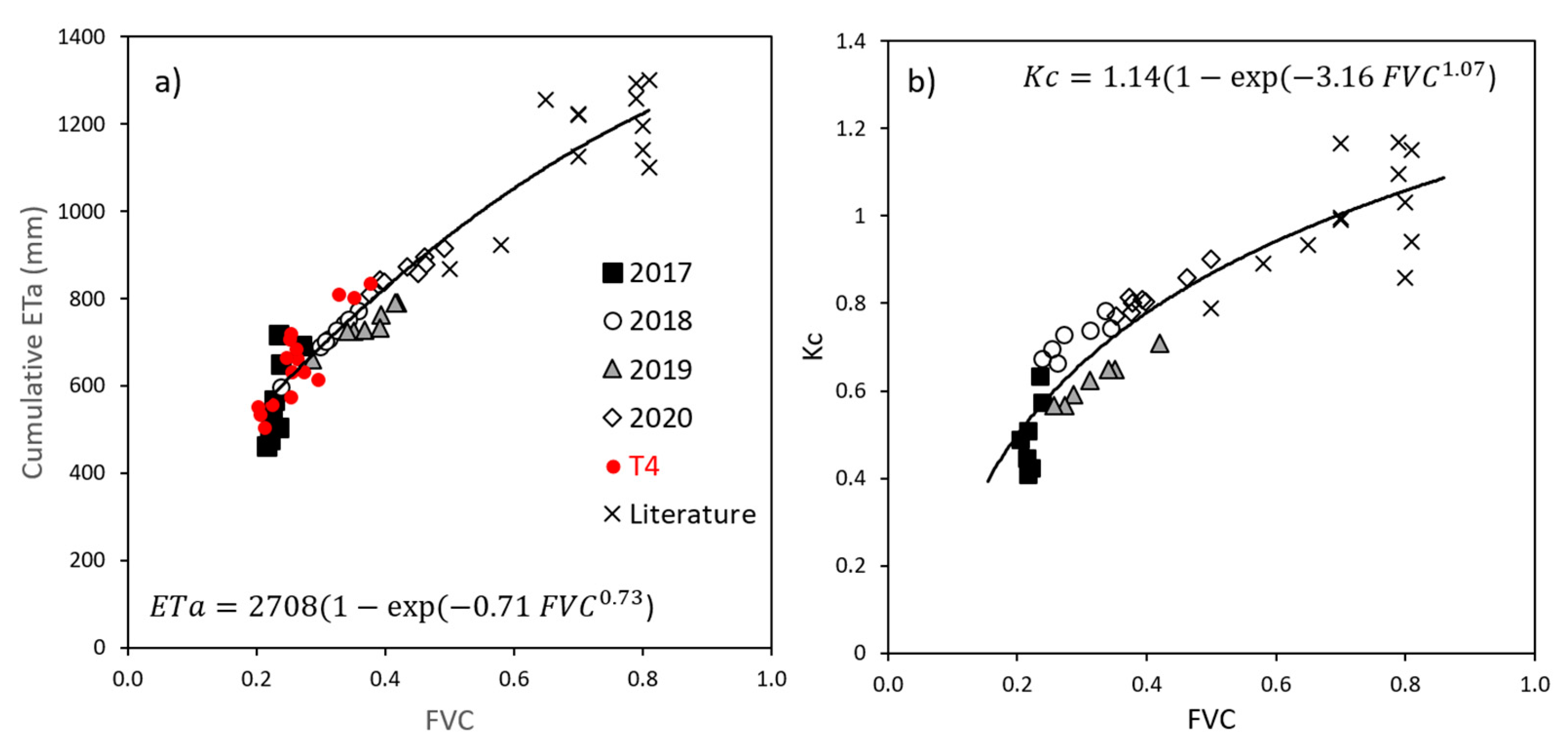
4.2. Land Surface Temperature (LST) and Biophysical Parameters of the Vegetation
4.3. Seasonal Actual Evapotranspiration (ETa)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAOSTAT. FAO Statistical Database. 2018. Available online: http://www.fao.org/faostat/en/#data/QC (accessed on 13 October 2021).
- MAPA. Ministerio de Agricultura, Pesca y Alimentación. 2020. Available online: https://www.mapa.gob.es/es/estadistica/temas/estadisticas-agrarias/agricultura/superficies-producciones-anuales-cultivos/ (accessed on 10 September 2021).
- Egea, G.; Nortes, P.; González-Real, M.M.; Baille, A.; Domingo, R. Agronomic response, and water productivity of almond trees under contrasted deficit irrigation regimes. Agric. Water Manag. 2010, 97, 171–181. [Google Scholar] [CrossRef]
- López-López, M.; Espadafor, M.; Testi, L.; Lorite, I.; Orgaz, F.; Fereres, E. Water requirements of mature almond trees in response to atmospheric demand. Irrig. Sci. 2018, 36, 271–280. [Google Scholar] [CrossRef]
- Moldero, D.; López-Bernal, Á.; Testi, L.; Lorite, I.; Fereres, E.; Orgaz, F. Long-term almond yield response to deficit irrigation. Irrig. Sci. 2021, 39, 409–420. [Google Scholar] [CrossRef]
- Spinelli, G.M.; Snyder, R.L.; Sanden, B.L.; Shackel, K.A. Water stress causes stomatal closure but does not reduce canopy evapotranspiration in almond. Agric. Water Manag. 2016, 168, 11–22. [Google Scholar] [CrossRef]
- Goldhamer, D.A.; Fereres, E. Establishing an almond water production function for California using long-term yield response to variable irrigation. Irrig. Sci. 2017, 35, 169–179. [Google Scholar] [CrossRef]
- Bellvert, J.; Adeline, K.; Baram, S.; Pierce, L.; Sanden, B.L.; Smart, D.R. Monitoring Crop Evapotranspiration and Crop Coefficients over an Almond and Pistachio Orchard Throughout Remote Sensing. Remote Sens. 2018, 10, 2001. [Google Scholar] [CrossRef] [Green Version]
- López-López, M.; Espadafor, M.; Testi, L.; Lorite, I.J.; Orgaz, F.; Fereres, E. Yield response of almond trees to transpiration déficits. Irrig. Sci. 2018, 36, 111–120. [Google Scholar] [CrossRef]
- Confederación Hidrográfica del Guadalquivir (CHG). Plan Hidrológico de la Demarcación del Guadalquivir 2015–2021, R.D. 1/2016; Confederación Hidrográfica del Guadalquivir: Sevilla, Spain, 2016. [Google Scholar]
- Fereres, E.; Soriano, M.A. Deficit irrigation for reducing agricultural water use. J. Exp. Bot. 2007, 58, 147–159. [Google Scholar] [CrossRef] [Green Version]
- Expósito, A.; Berbel, J. The economics of irrigation in almond orchards. Application to southern Spain. Agronomy 2020, 10, 796. [Google Scholar] [CrossRef]
- Goldhamer, D.A.; Viveros, M. Effects of preharvest irrigation cutoff durations and postharvest water deprivation on almond tree performance. Irrig. Sci. 2000, 19, 125–131. [Google Scholar] [CrossRef]
- Esparza, G.; DeJong, T.M.; Weinbaum, S.A.; Klein, I. Effects of irrigation deprivation during the harvest period on yield determinants in mature almond trees. Tree Physiol. 2001, 21, 1073–1079. [Google Scholar] [CrossRef] [PubMed]
- Girona, J.; Mata, M.; Marsal. Regulated deficit irrigation during the kernel-filling period and optimal irrigation rates in almond. Agric. Water Manag. 2005, 75, 152–167. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration. Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; 300p. [Google Scholar]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of ground cover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef] [Green Version]
- García-Tejero, I.F.; Hernández, A.; Rodríguez, V.M.; Ponce, J.R.; Ramos, V.; Muriel, J.L.; Durán-Zauzo, V.H. Estimating almond crop coefficients and physiological response to water stress in semiarid environments (SW Spain). J. Agric. Sci. Technol. 2015, 17, 1255–1266. [Google Scholar]
- Espadafor, M.; Orgaz, F.R.; Testi, L.; Lorite, I.J.; Villalobos, F.J. Transpiration of Young almond trees in relation to intercepted radiation. Irrig. Sci. 2015, 33, 265–275. [Google Scholar] [CrossRef] [Green Version]
- Stevens, R.M.; Ewenz, C.M.; Grigson, G.; Conner, S.M. Water use by an irrigated almond orchard. Irrig. Sci. 2012, 30, 189–200. [Google Scholar]
- Girona, J.; del Campo, J.; Mata, M.; Lopez, G.; Marsal, J.A. comparative study of apple and pear tree water consumption measured with two weighing lyismeters. Irrig. Sci. 2011, 29, 55–63. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Ezzahar, J.; Khabba, S.; Boulet, G.; Hanich, L.; Williams, D. Evapotranspiration Partitioning from Sap Flow and Eddy Covariance Techniques for Olive Orchards in Semi-Arid Region. Acta Hortic. 2009, 846, 201–208. [Google Scholar] [CrossRef]
- Testi, L.; Villalobos, F.J.; Orgaz, F. Evapotranspiration of a young irrigated olive orchard in southern Spain. Agric. Meteorol. 2004, 121, 1–18. [Google Scholar] [CrossRef]
- Ferreira, M.I. Stress Coefficients for Soil Water Balance Combined with Water Stress Indicators for Irrigation Scheduling of Woody Crops. Horticulturae 2017, 3, 38. [Google Scholar] [CrossRef] [Green Version]
- Garnier, E.; Berger, A.; Rambal, S. Water balance and pattern of soil water uptake in a peach orchard. Agric. Water Manag. 1986, 11, 145–158. [Google Scholar] [CrossRef]
- Ahumada, L.; Ortega-Farias, S.; Poblete-Echevarría, C.; Peter, S. Estimation of stomatal conductance and stem water potential threshold values for water stress in olive trees (cv. Arbequina). Irrig. Sci. 2019, 37, 461–467. [Google Scholar] [CrossRef]
- Domínguez-Niño, J.M.; Oliver-Manera, J.; Girona, J.; Casadesús, J. Differential irrigation scheduling by an automated algorithm of water balance tuned by capacitance-type soil moisture sensors. Agric. Water Manag. 2020, 228, 105880. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Model. J. Irrig. Drain. Eng.-Asce 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.; Humes, K. A two-source approach for estimating soil and vegetation energy fluxes from observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Prueger, J.H.; Diak, G.R. Surface flux estimation using radiometric temperature: A dual-temperature-difference method to minimize measurement errors. Water Resour. Res. 2000, 36, 2263. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Torn, R.D.; Kustas, W.P.; Basara, J.B. A multiscale remote sensing model for disaggregating regional fluxes to micrometeorological scales. J. Hydrometeorol. 2004, 5, 343–363. [Google Scholar] [CrossRef]
- Boulet, G.; Mougenot, B.; Lhomme, J.-P.; Fanise, P.; Lili-Chabaane, Z.; Olioso, A.; Bahir, M.; Rivalland, V.; Jarlan, L.; Merlin, O.; et al. The SPARSE model for the prediction of water stress and evapotranspiration components from thermal infra-red data and its evaluation over irrigated and rainfed wheat. Hydrol. Earth Syst. Sci. 2015, 19, 4653–4672. [Google Scholar] [CrossRef] [Green Version]
- He, R.; Jin, Y.; Kandelous, M.M.; Zaccaria, D.; Sanden, B.L.; Snyder, R.L.; Jiang, J.; Hopmans, J.W. Evapotranspiration estimate over an almond orchard using Landsat satellite observations. Remote Sens. 2017, 9, 436. [Google Scholar] [CrossRef] [Green Version]
- Xue, J.; Bali, K.M.; Light, S.; Hessels, T.; Kisekka, I. Evaluation of remote sensing-based evapotranspiration models against surface renewal in almonds, tomatoes and maize. Agric. Water Manag. 2020, 238, 106228. [Google Scholar] [CrossRef]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Senay, G.B.; Friedrichs, M.; Singh, R.K.; Velpuri, N.M. Evaluating landsat 8 evapotranspiration for water use mapping in the Colorado River Basin. Remote Sens. Environ. 2016, 185, 171–185. [Google Scholar] [CrossRef] [Green Version]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef] [Green Version]
- Knipper, K.R.; Kustas, W.P.; Anderson, M.C.; Alfieri, J.G.; Prueger, J.H.; Hain, C.R.; Gao, F.; Yang, Y.; McKee, L.G.; Nieto, H.; et al. Evapotranspiration estimates derived using thermal-based satellite remote sensing and data fusion for irrigation management in California vineyards. Irrig. Sci. 2019, 37, 431–449. [Google Scholar] [CrossRef]
- Knipper, K.R.; Kustas, W.P.; Anderson, M.C.; Nieto, H.; Alfieri, J.; Prueger, J.; Hain, C.; Gao, F.; McKee, L.; Alsina, M.M.; et al. Using high-spatiotemporal thermal satellite ET retrievals to monitor water use over California vineyards of different climate, vine variety and trellis design. Agric. Water Manag. 2020, 241, 106361. [Google Scholar] [CrossRef]
- Fisher, J.B.; Lee, B.; Purdy, A.J.; Halverson, G.H.; Dohlen, M.B.; Cawse-Nicholson, K.; Wang, A.; Anderson, R.G.; Aragon, B.; Arain, M.A.; et al. ECOSTRESS: NASA’s Next GenerationMission to measure evapotranspirationfrom the International Space Station. Water Resour. Res. 2020, 56, e2019WR026058. [Google Scholar] [CrossRef]
- Anderson, M.C.; Yang, Y.; Xue, J.; Knipper, K.R.; Yang, Y.; Gao, F.; Hain, C.R.; Kustas, W.P.; Cawse-Nicholson, K.; Hulley, G.; et al. Interoperability of ECOSTRESS and Landsat for mapping evapotranspiration time series at sub-field scales. Remote Sens. Environ. 2021, 252, 112189. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H. Evaluating the feasibility of using Sentinel-2 and Sentinel-3 satellites for high-resolution evapotranspiration estimations. Remote Sens. Environ. 2019, 221, 157–172. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H.; Sandholt, I.; Karamitilios, G. Modelling High-Resolution Actual Evapotranspiration through Sentinel-2 and Sentinel-3 Data Fusion. Remote Sens. 2020, 12, 1433. [Google Scholar] [CrossRef]
- Gao, F.; Kustas, W.P.; Anderson, M.C. A data mining approach for sharpening thermal satellite imagery over land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef] [Green Version]
- Guzinski, R.; Nieto, H.; Sánchez, J.M.; López-Urrea, R.; Boujnah, D.M.; Boulet, G. Utility of Copernicus-Based Inputs for Actual Evapotranspiration Modeling in Support of Sustainable Water Use in Agriculture. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11466–11484. [Google Scholar] [CrossRef]
- Bellvert, J.; Jofre-Ĉekalović, C.; Pelechá, A.; Mata, M.; Nieto, H. Feasibility of Using the Two-Source Energy Balance Model (TSEB) with Sentinel-2 and Sentinel-3 Images to Analyze the Spatio-Temporal Variability of Vine Water Status in a Vineyard. Remote Sens. 2020, 12, 2299. [Google Scholar] [CrossRef]
- BOE. Real decreto 1201/2002, de 20 de Noviembre, por el que se Regula la Producción Integrada de Productos Agrícolas. Madrid: Boletin Oficial del Estado. 2002. Available online: https://www.boe.es/buscar/doc.php?id=BOE-A-2002-23340 (accessed on 25 April 2022).
- Goldhamer, D.A.; Girona, J. Crop yield response to water: Almond. In FAO Irrigation and Drainage; Steduto, P., Hsiao, T.C., Fereres, E., Raes, D., Eds.; Food and Agriculture Organization of the United Nations: Rome, Italy, 2012; Volume 66, pp. 358–373. [Google Scholar]
- Fereres, E. Drip Irrigation Management; Leaflet No. 21259; Cooperative Ext., Univ.: Berkeley, CA, USA, 1981. [Google Scholar]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Idso, S.B.; Reginato, R.J. Analysis of an empirical model for soil heat flux under a growing wheat crop for estimating evaporation by an infrared-temperature based energy balance equation. Agric. For. Meteorol. 1987, 38, 283–297. [Google Scholar] [CrossRef]
- Santanello, J.A.; Friedl, M. Diurnal covariation in soil heat flux and net radiation. J. Appl. Meteorol. 2003, 42, 851–862. [Google Scholar] [CrossRef]
- McNaughton, K.G.; van den Hurk, B.J.J.M. A Lagrangian revision of the resistors in the 2-layer model for calculation the energy budget of a plant canopy. Bound.-Layer Meteor. 1995, 74, 261–288. [Google Scholar] [CrossRef]
- Choudhury, B.; Monteith, J. A four-layer model for the heat budget of homogeneous land surfaces. Q. J. R. Meteorol. Soc. 1988, 114, 373–398. [Google Scholar] [CrossRef]
- Kustas, W.P.; Nieto, H.; Morillas, L.; Anderson, M.C.; Alfieri, J.G.; Hipps, L.E.; Villagarcía, L.; Domingo, F.; Garcia, M. Revisiting the paper Using radiometric Surface temperature for Surface energy flux estimation in Mediterranean drylands from a two-source perspective. Remote Sens. Environ. 2016, 184, 645–653. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F. S2ToolBox Level 2 products: LAI, FAPAR, FCOVER—Version 1.1. Sentin. ToolBox Level2 Prod. 2016, 53. Available online: https://step.esa.int/docs/extra/ATBD_S2ToolBox_L2B_V1.1.pdf (accessed on 19 May 2021).
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M.U. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Parry, C.K.; Nieto, H.; Guillevic, P.; Agam, N.; Kustas, W.P.; Alfieri, J.; McKee, L.; McElrone, A.J. An intercomparison of radiation partitioning models in vineyard canopies. Irrig. Sci. 2019, 37, 239–252. [Google Scholar] [CrossRef]
- Campbell, G.S. Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle Distribution. Agric. For. Meteorol. 1986, 36, 317–321. [Google Scholar] [CrossRef]
- Raupach, M.R. Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Bound.-Layer Meteorol. 1994, 71, 211–216. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Kustas, W.P. Upscaling of evapotranspiration fluxes from instantaneous to daytime scales for thermal remote sensing applications. Hydrol. Earth Syst. Sci. 2014, 18, 1885–1894. [Google Scholar] [CrossRef] [Green Version]
- Foken, T.; Aubinet, M.; Finnigan, J.J.; Leclerc, M.Y.; Mauder, M.; Paw U, K.T. Results of a panel discussion about the energy balance closure correction for trace gases. Bull. Am. Meteorol. Soc. 2011, 92, 13–18. [Google Scholar] [CrossRef] [Green Version]
- Barr, A.G.; King, K.M.; Gillespie, T.J.; den Hartog, G.; Neumann, H.H. A comparison of Bowen ratio and eddy correlation sensible and latent heat flux measurements above deciduous forest. Bound.-Layer Meteorol. 1994, 71, 21–41. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–3000. [Google Scholar] [CrossRef] [Green Version]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for flux footprint prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef] [Green Version]
- Baldocchi, D.D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2435. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, J.M.; Simón, L.; González-Piqueras, J.; Montoya, F.; López-Urrea, R. Monitoring Crop Evapotranspiration and Transpiration/Evaporation Partitioning in a Drip-Irrigated Young Almond Orchard Applying a Two-Source Surface Energy Balance Model. Water 2021, 13, 2073. [Google Scholar] [CrossRef]
- Foken, T.; Wimmer, F.; Mauder, M.; Thomas, C.; Liebethal, C. Some aspects of the energy balance closure problem. Atmos. Chem. Phys. 2006, 6, 4395–4402. [Google Scholar] [CrossRef] [Green Version]
- Alfieri, J.G.; Kustas, W.P.; Prueger, J.H.; Hipps, L.E.; Evett, S.R.; Basara, J.B.; Neale, C.M.; French, A.N.; Colaizzi, P.; Agam, N.; et al. On the discrepancy between eddy covariance and lysimetry-based surface flux measurements under strongly advective conditions. Adv. Water Resour. 2012, 50, 62–78. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.P.; Nieto, H.; García-Tejera, O.; Bambach, N.; McElrone, A.J.; Gao, F.; Alfieri, J.G.; Hipps, L.E.; Prueger, J.H.; Torres-Rua, A.; et al. Impact of advection on two-source energy balance (TSEB) canopy transpiration parameterization for vineyards in the California Central Valley. Irrig. Sci. 2022. [Google Scholar] [CrossRef]
- Massman, W. A comparative study of some mathematical models of the mean wind structure and aerodynamic drag of plant canopies. Bound.-Lay. Meteorol. 1987, 40, 179–197. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.; Ciraolo, G.; D’Urso, G.; Kustas, W.P.; la Loggia, G.; Minacapilli, M. The impact of in-canopy wind profile formulations on heat flux estimation using the remote sensing-based two-source model for an open orchard canopy in southern Italy. Hydrol. Earth Syst. Sci. 2010, 7, 4687. [Google Scholar]
- Nieto, H.; Kustas, W.P.; Torres-Rúa, A.; Alfieri, J.G.; Gao, F.; Anderson, M.C.; White, W.A.; Song, L.; Alsina, M.; Prueger, J.H.; et al. Evaluation of TSEB turbulent fluxes using different methods for the retrieval of soil and canopy component temperatures from UAV thermal and multispectral imagery. Irrig. Sci. 2019, 37, 389–406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goudriaan, J. Crop Micrometeorology: A Simulation Study; Center Agricoltural Publications and Documentation, Wageningen Universitait: Wageningen, The Netherlands, 1977. [Google Scholar]
- Ghosh, A.; Joshi, P.K. Hyperspectral imagery for disaggregation of land surface temperature with selected regression algorithms over different land use land cover scenes. ISPRS J. Photogramm. Remote Sens. 2014, 96, 76–93. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Q.; Yin, K.; He, G.; Zhang, Z.; Wang, G.; Wen, M.; Zhang, N. Spatial Downscaling of Land Surface Temperature Based on a Multi-Factor Geographically Weighted Machine Learning Model. Remote Sens. 2021, 13, 1186. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu., T.-Y. LightGMB: A high eficient gradient boosting decision tree. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Burchard-Levine, V.; Nieto, H.; Riaño, D.; Migliavacca, M.; El-Madany, T.S.; Perez-Priego, O.; Carrara, A.; Martín, M.P. Seasonal Adaptation of the Thermal-Based Two-Source Energy Balance Model for Estimating Evapotranspiration in a Semiarid Tree-Grass Ecosystem. Remote Sens. 2020, 12, 904. [Google Scholar] [CrossRef] [Green Version]
- Goward, S.N.; Markham, B.; Dye, D.G.; Dulaney, W.; Yang, J. Normalized difference vegetation index measurements from the advanced very high resolution radiometer. Remote Sens. Environ. 1991, 35, 257–277. [Google Scholar] [CrossRef]
- Cai, Z.; Jönsson, P.; Jin, H.; Eklundh, L. Performance of Smoothing Methods for Reconstructing NDVI Time-Series and Estimating Vegetation Phenology from MODIS Data. Remote Sens. 2017, 9, 1271. [Google Scholar] [CrossRef] [Green Version]
- North, P.R.J. Three-dimensional forest light interaction model using a Monte Carlo method. IEEE Trans. Geosci. Remote Sens. 1996, 34, 946–956. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.-P.; Demarez, V.; Pinel, V.; Zagolski, F. Modeling radiative transfer in heterogeneous 3-D vegetation canopies. Remote Sens. Environ. 1996, 58, 131–156. [Google Scholar] [CrossRef] [Green Version]
- Yingjie, W.; Gastellu-Etchegorry, J.-P. Accurate and Fast Simulation of Remote Sensing Images at Top of Atmosphere with Dart-lux. Remote Sens. Environ. 2021, 256, 112311. [Google Scholar]
- Gonzalez-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prieger, J.H.; Anderson, M.C.; Li, F. A comparison of operational remote sensing-based models for estimating crop evapotranspiration. Agric. For. Meteorol. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]


| TSEBs2+s3 | TSEBLandsat | |||||||
|---|---|---|---|---|---|---|---|---|
| Rn | H | LE | G | Rn | H | LE | G | |
| RMSE | 63 | 90 | 87 | 37 | 103 | 80 | 108 | 43 |
| MAE | 54 | 73 | 69 | 29 | 92 | 66 | 76 | 38 |
| Bias | −46 | −43 | 9 | −7 | −92 | −12 | −42 | −32 |
| % diff | −8.2 | −20.1 | 3.7 | −6.5 | −15.1 | −5.8 | −15.9 | −24.1 |
| NRMSE | 0.11 | 0.44 | 0.35 | 0.34 | 0.17 | 0.38 | 0.41 | 0.33 |
| NMAE | 0.09 | 0.36 | 0.27 | 0.26 | 0.15 | 0.32 | 0.29 | 0.29 |
| Variable | Treatment | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|
| ET0 | - | 1130.8 | 1029.9 | 1113.0 | 1039.3 |
| Precipitation | - | 226 | 394 | 224.0 | 350.2 |
| Irrigation | T1 | 313.2 a | 512.7 a | 730.7 a | 634.1 a |
| T2 | 311.9 a | 521.6 a | 542.6 b | 573.3 b | |
| T3 | 307.74 a | 458.45 a | 413.3 c | 474.7 c | |
| T4 | 219.3 b | 319.0 b | 272.2 d | 284.2 d | |
| Prob > F | 0.0002 * | 0.0001 * | <0.0001 * | <0.0001 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jofre-Čekalović, C.; Nieto, H.; Girona, J.; Pamies-Sans, M.; Bellvert, J. Accounting for Almond Crop Water Use under Different Irrigation Regimes with a Two-Source Energy Balance Model and Copernicus-Based Inputs. Remote Sens. 2022, 14, 2106. https://doi.org/10.3390/rs14092106
Jofre-Čekalović C, Nieto H, Girona J, Pamies-Sans M, Bellvert J. Accounting for Almond Crop Water Use under Different Irrigation Regimes with a Two-Source Energy Balance Model and Copernicus-Based Inputs. Remote Sensing. 2022; 14(9):2106. https://doi.org/10.3390/rs14092106
Chicago/Turabian StyleJofre-Čekalović, Christian, Héctor Nieto, Joan Girona, Magi Pamies-Sans, and Joaquim Bellvert. 2022. "Accounting for Almond Crop Water Use under Different Irrigation Regimes with a Two-Source Energy Balance Model and Copernicus-Based Inputs" Remote Sensing 14, no. 9: 2106. https://doi.org/10.3390/rs14092106
APA StyleJofre-Čekalović, C., Nieto, H., Girona, J., Pamies-Sans, M., & Bellvert, J. (2022). Accounting for Almond Crop Water Use under Different Irrigation Regimes with a Two-Source Energy Balance Model and Copernicus-Based Inputs. Remote Sensing, 14(9), 2106. https://doi.org/10.3390/rs14092106







