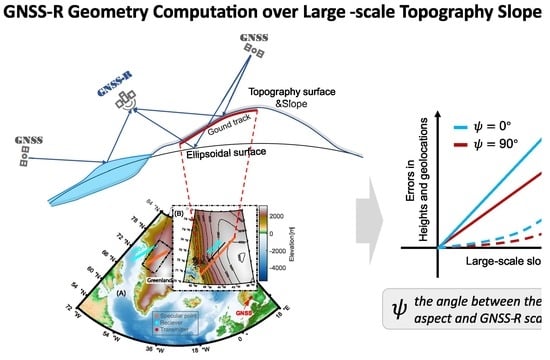
Investigation on Geometry Computation of Spaceborne GNSS-R Altimetry over Topography: Modeling and Validation
Abstract
:1. Introduction
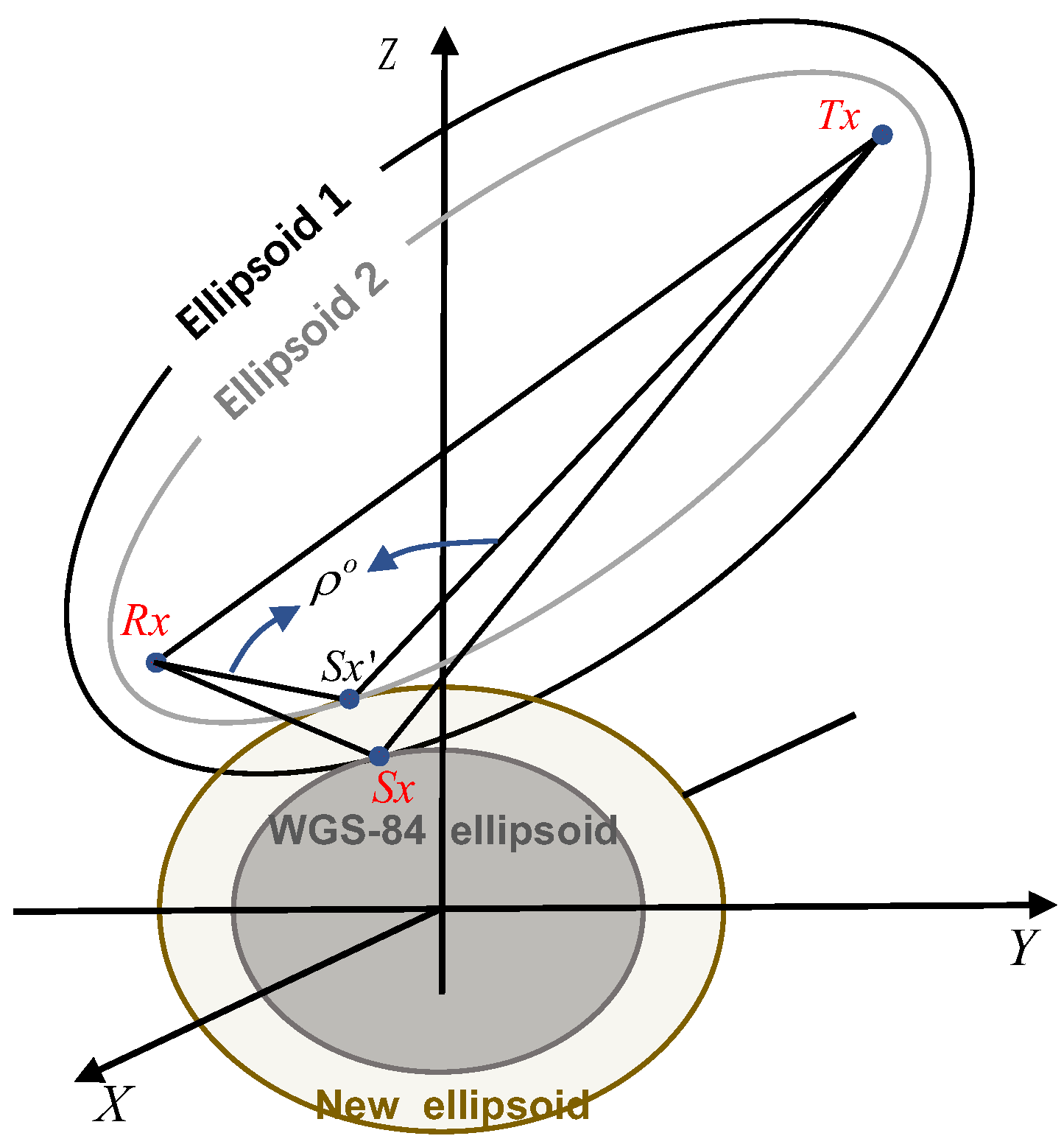
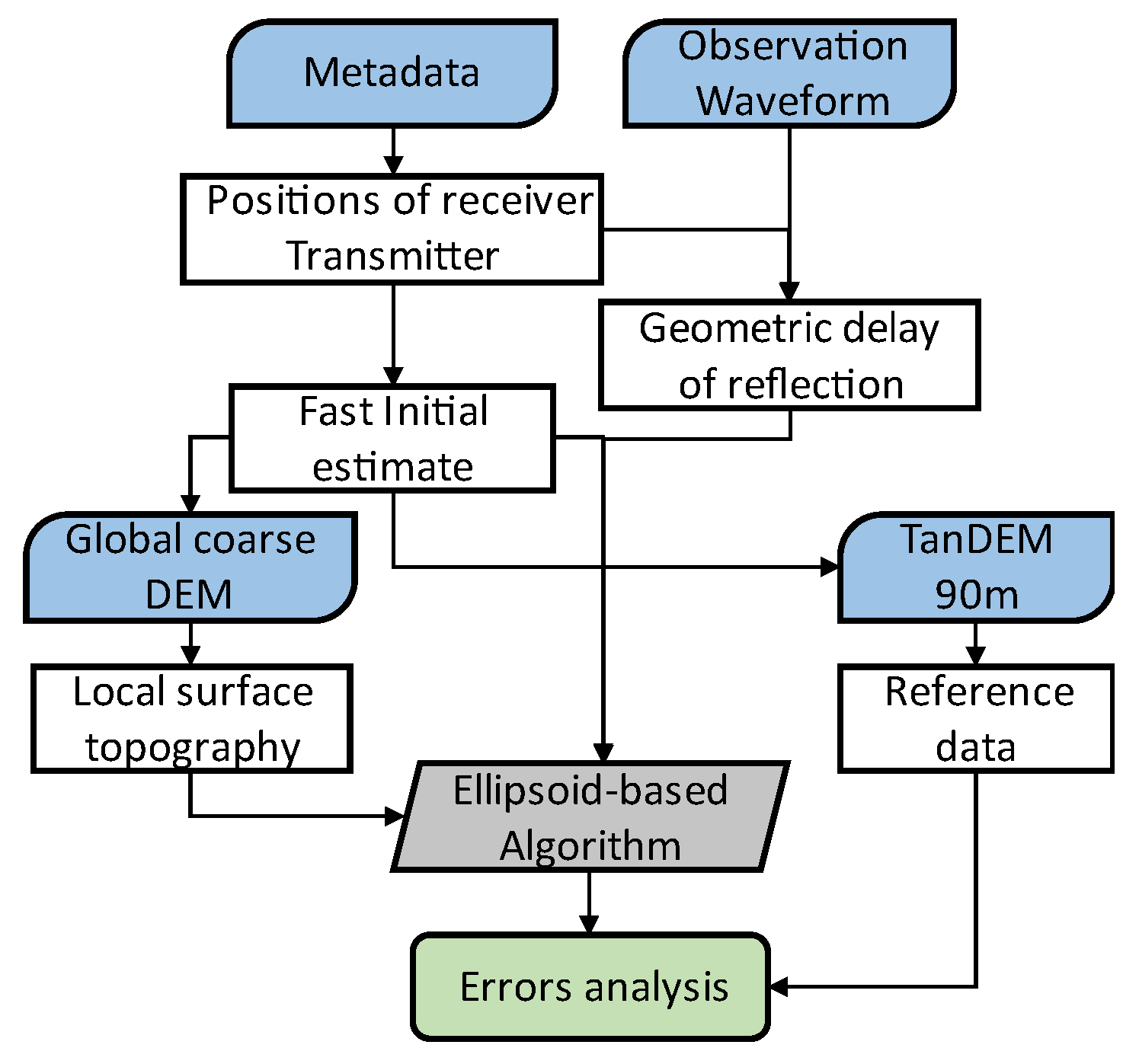
2. Ellipsoid-Based Geometry Computation Strategy
2.1. Observation-Driven GNSS-R Geometry Computation
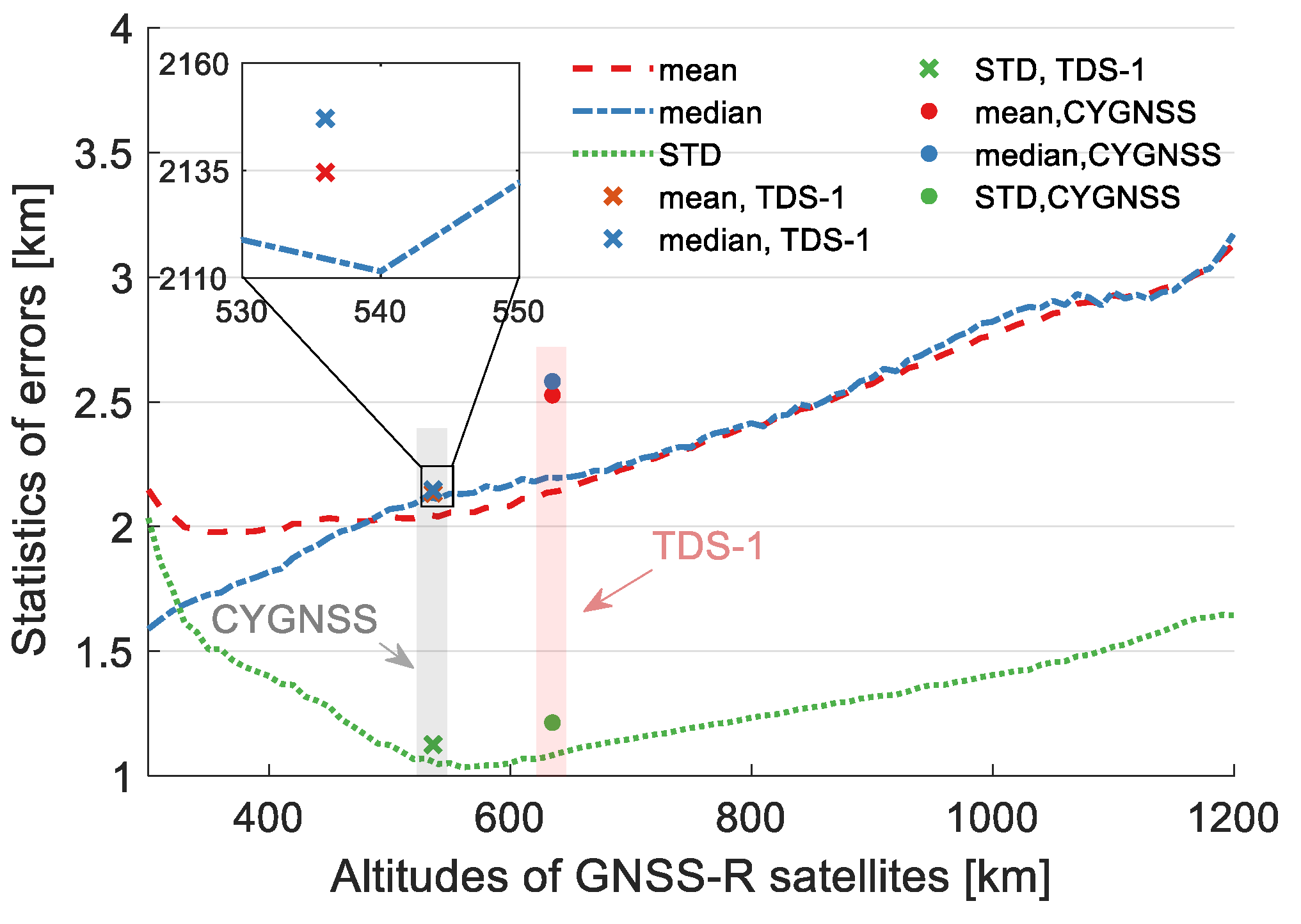
2.2. Comparisons of the Specular Point Calculation Performance
3. Geometry Computation Based on Topography
3.1. True Specular Area Determination Based on Topography
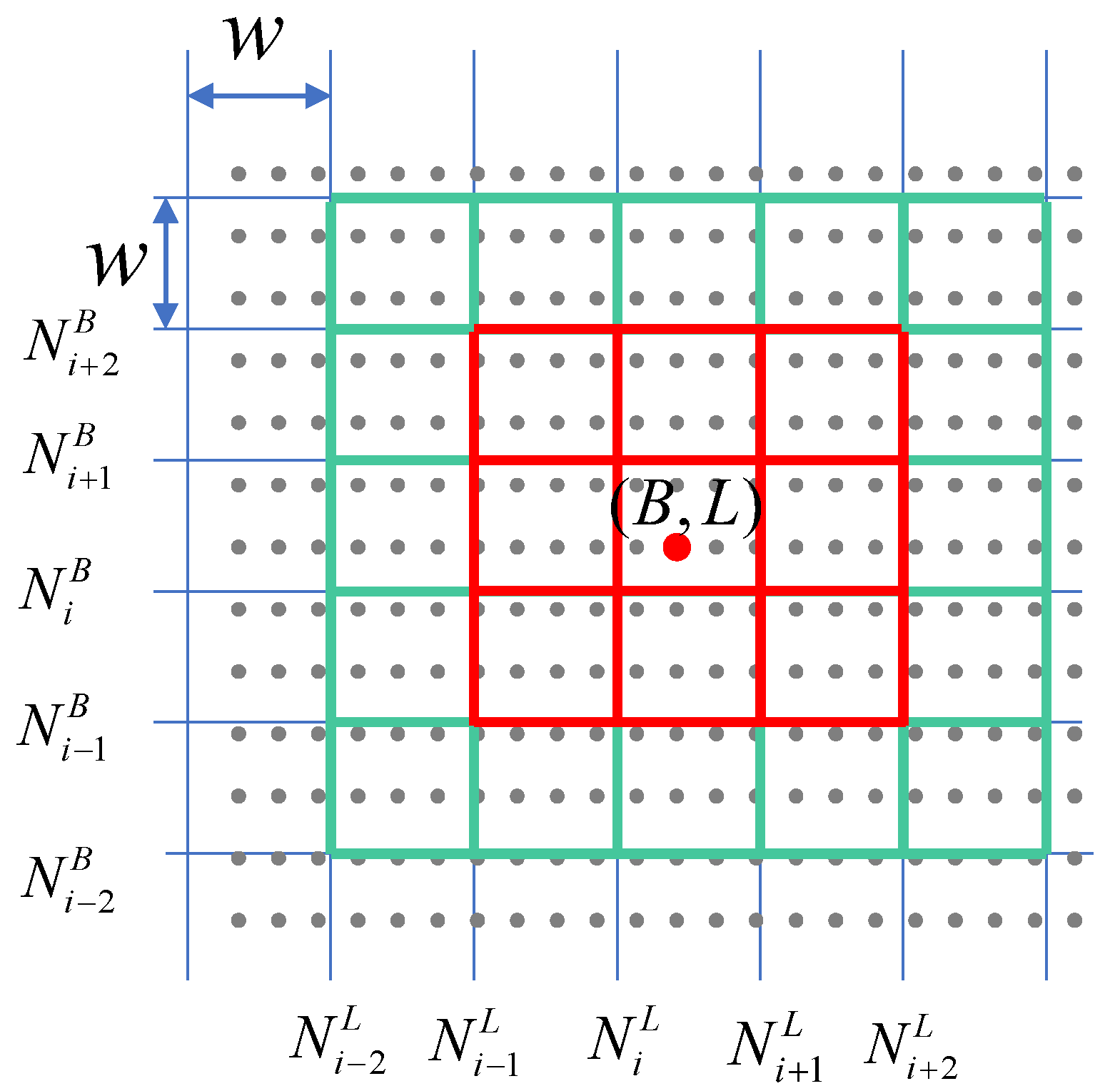
3.1.1. Local Area Searching Based on the Initial Specular Point
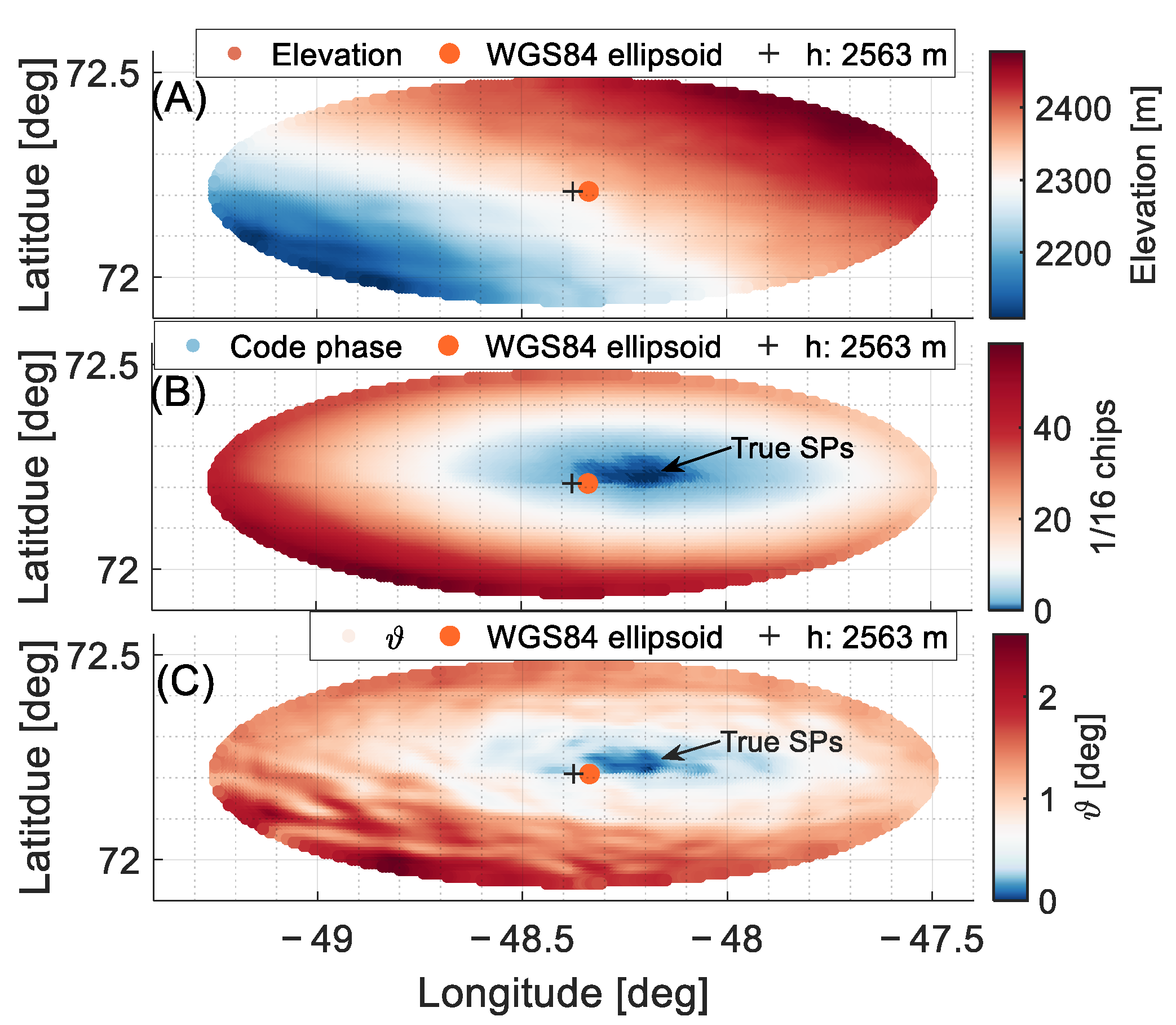
3.1.2. Analysis of the Topography Impact on the Geometry
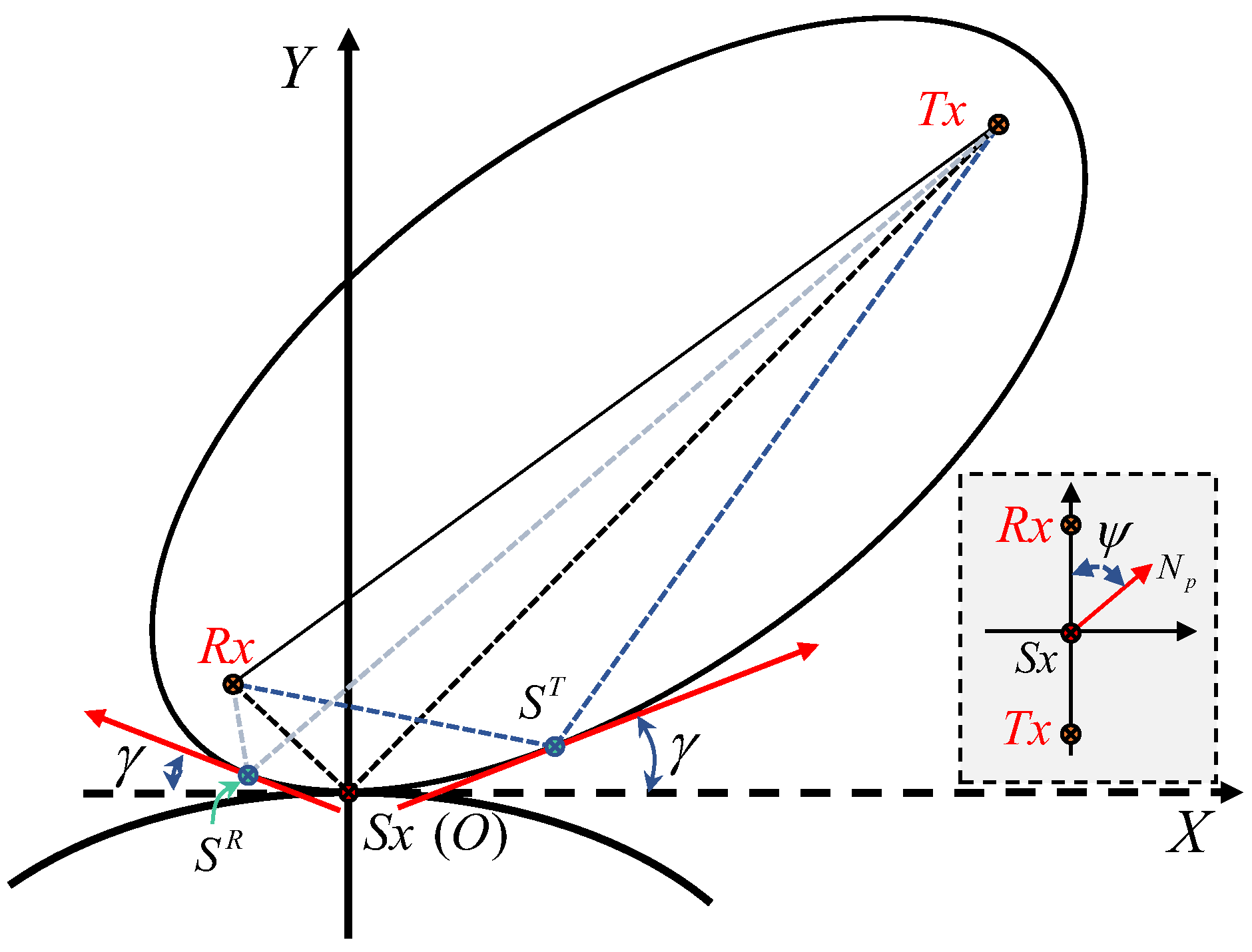
3.2. Geometry Computation over Slopes
3.3. Analysis of Errors Based on Simulations
4. Datasets and Results
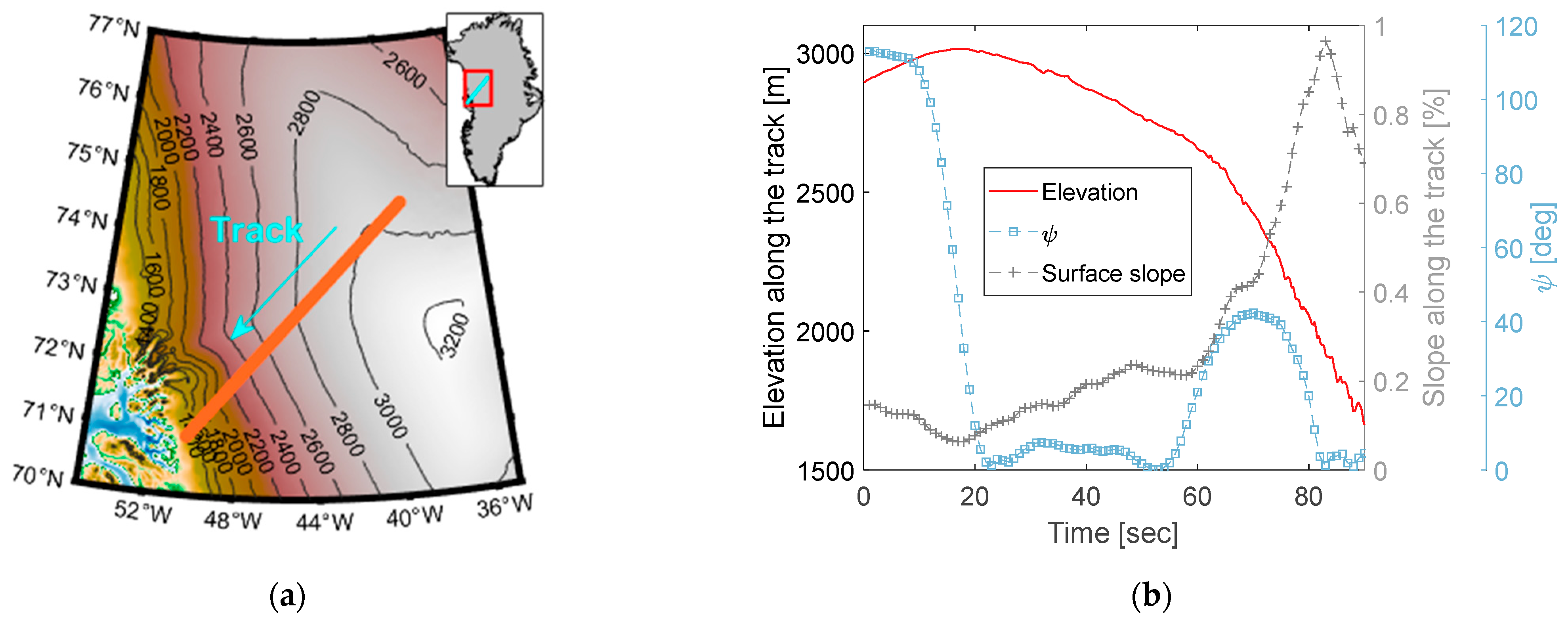
4.1. Datasets
4.2. Data Processing
4.3. Results and Analysis
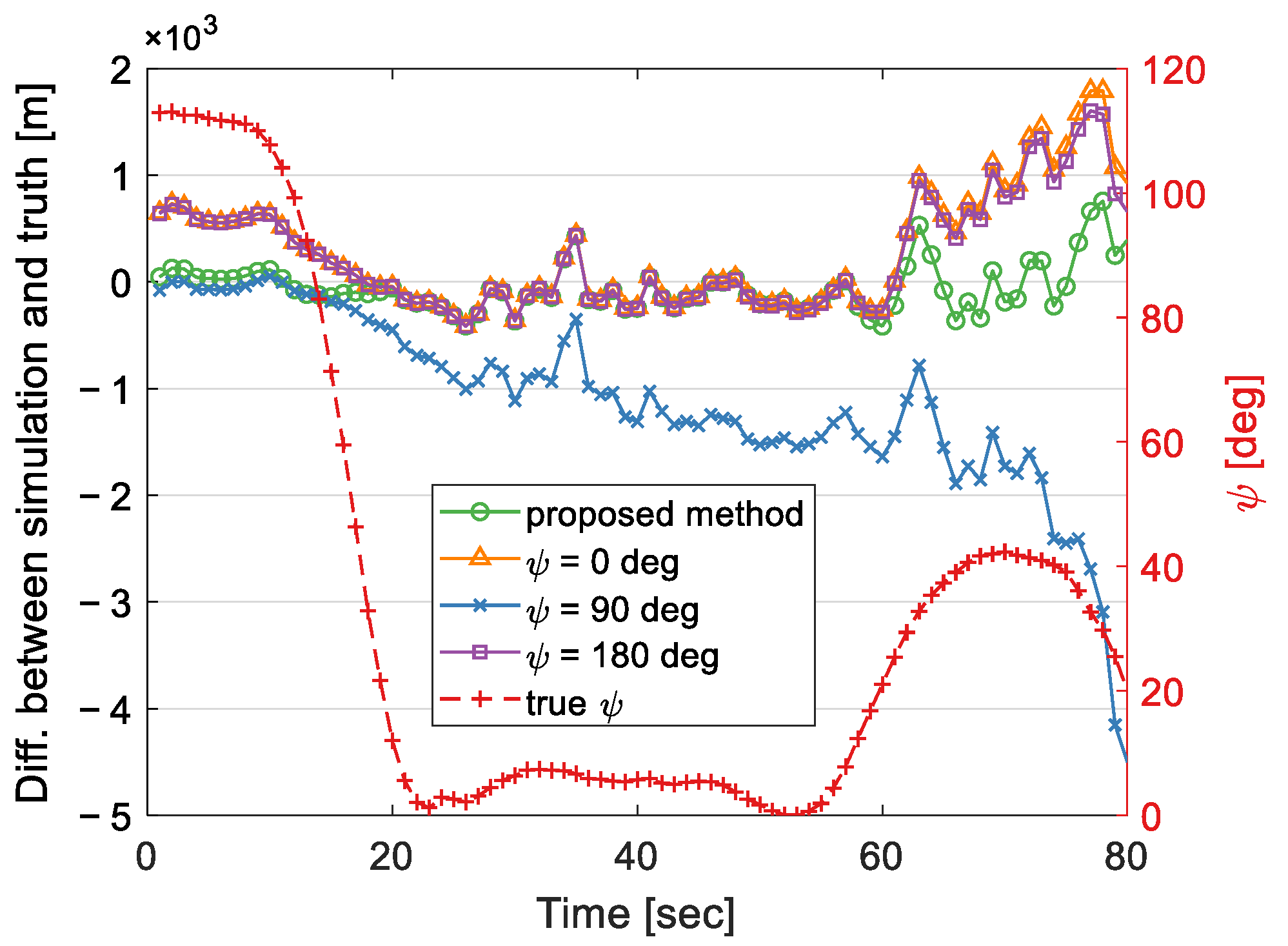
4.3.1. Effects of the Slope Angle
4.3.2. Effect of the Slope Aspect
5. Discussions
5.1. Surface Fitting Model
5.2. Selection of Fitting Data in the Local Area
5.3. Selection of the Coarse DEM Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
A New Empirical Model for Initialization

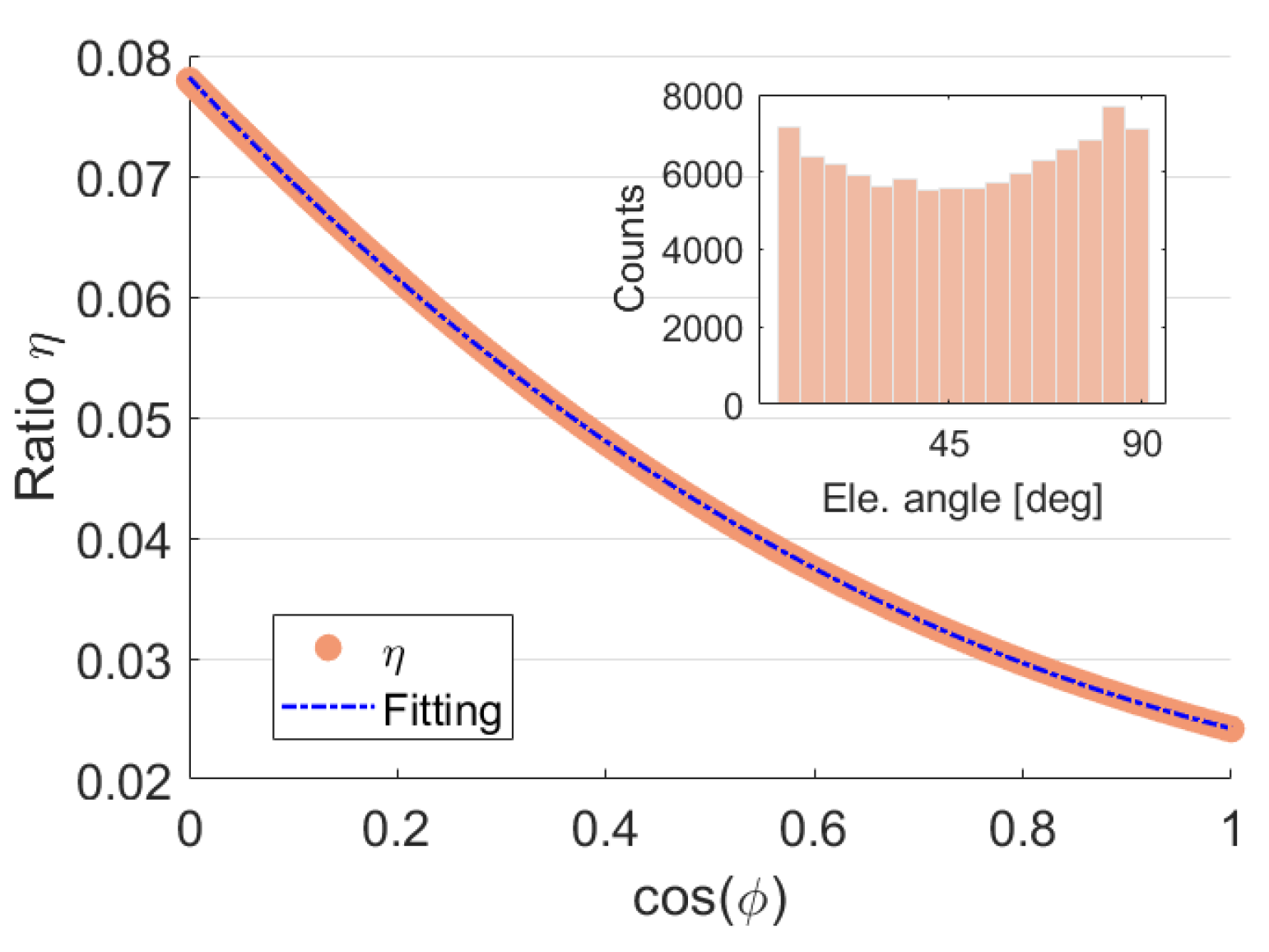
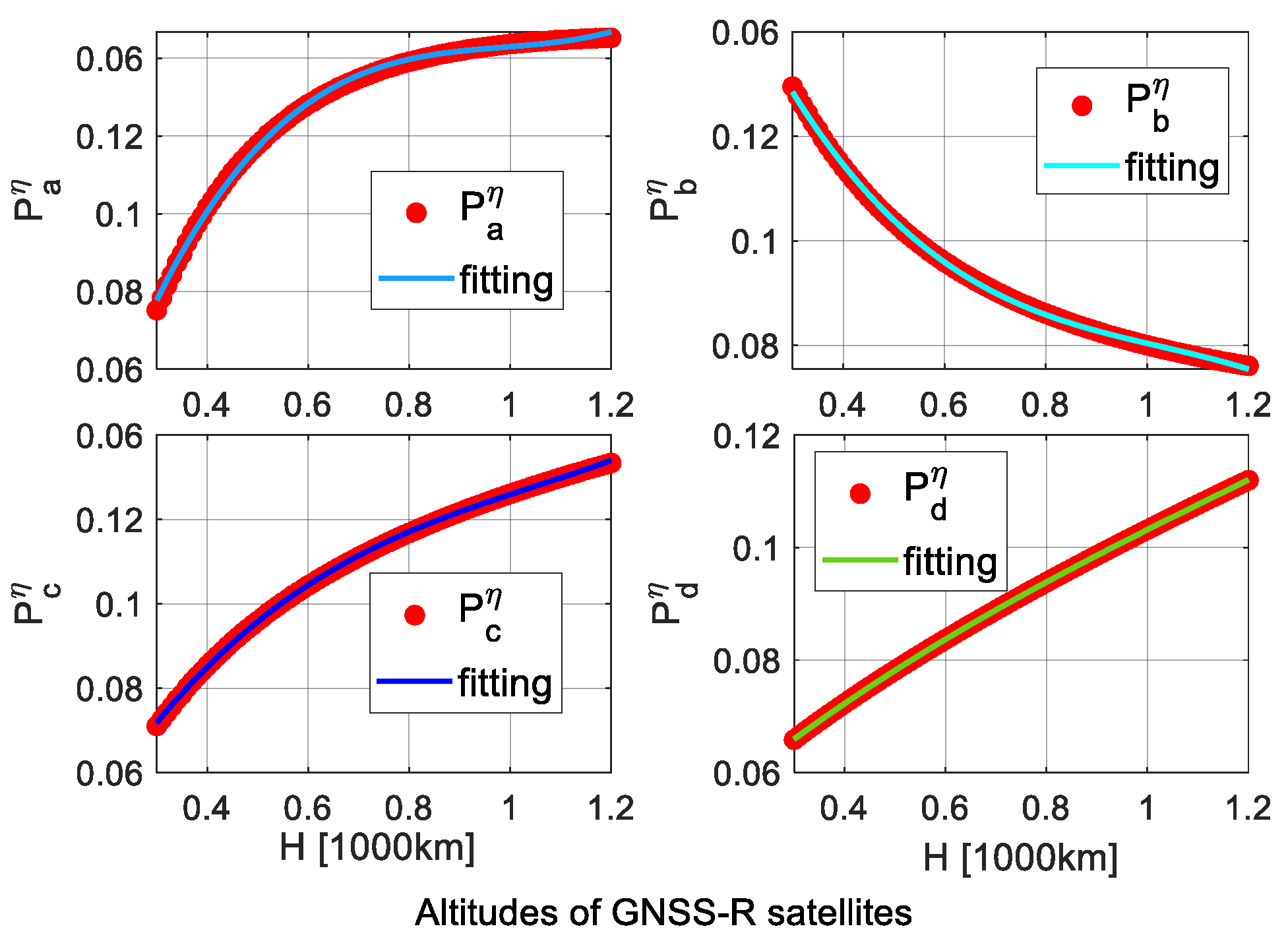
| 0.04478 | −0.1325 | 0.1333 | −0.04484 | |
| −0.08442 | 0.2599 | −0.2892 | 0.1341 | |
| 0.03152 | −0.09935 | 0.1240 | −0.1332 | |
| 0.008292 | −0.03064 | 0.08151 | 0.04403 |
| 0.0695 | −0.1987 | 0.1874 | −0.05558 | |
| −0.1316 | 0.387 | −0.3958 | 0.1581 | |
| 0.05733 | −0.1688 | 0.1838 | −0.1515 | |
| 0.005163 | −0.02294 | 0.07767 | 0.049 |
| 0.05364 | −0.1556 | 0.1507 | −0.04809 | |
| −0.09738 | 0.2902 | −0.3043 | 0.1306 | |
| 0.03784 | −0.1125 | 0.125 | −0.1199 | |
| 0.006253 | −0.02476 | 0.07224 | 0.03729 |
| 0.05879 | −0.1698 | 0.1631 | −0.05077 | |
| −0.1085 | 0.322 | −0.335 | 0.1403 | |
| 0.04405 | −0.1306 | 0.1443 | −0.1308 | |
| 0.005997 | −0.02447 | 0.07456 | 0.04127 |
References
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on remote sensing using GNSS bistatic radar of opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Cardellach, E.; Fabra, F.; Ribo, S.; Rius, A. Assessment of Spaceborne GNSS-R Ocean Altimetry Performance Using CYGNSS Mission Raw Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 238–250. [Google Scholar] [CrossRef]
- Hajj, G.A.; Zuffada, C. Theoretical description of a bistatic system for ocean altimetry using the GPS signal. Radio Sci. 2003, 38, 10-1–10-19. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, P.; Lowe, S.T.; Larson, K.M. Global Ocean Altimetry with GNSS Reflections from TechDemoSat-1. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4088–4097. [Google Scholar] [CrossRef]
- Huang, F.; Garrison, J.L.; Rodriguez-Alvarez, N.; O’Brien, A.J.; Schoenfeldt, K.M.; Ho, S.C.; Zhang, H. Sequential processing of GNSS-R delay-doppler maps to estimate the ocean surface wind field. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10202–10217. [Google Scholar] [CrossRef]
- Katzberg, S.J.; Dunion, J.; Ganoe, G.G. The use of reflected GPS signals to retrieve ocean surface wind speeds in tropical cyclones. Radio Sci. 2013, 48, 359–370. [Google Scholar] [CrossRef]
- Asgarimehr, M.; Wickert, J.; Reich, S. TDS-1 GNSS Reflectometry: Development and Validation of Forward Scattering Winds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4534–4541. [Google Scholar] [CrossRef]
- Strandberg, J.; Hobiger, T.; Haas, R. Coastal Sea Ice Detection Using Ground-Based GNSS-R. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1552–1556. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A.; Weiqiang, L.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A.; et al. Measuring Greenland Ice Sheet Melt Using Spaceborne GNSS Reflectometry From TechDemoSat-1. Geophys. Res. Lett. 2020, 47, e2019GL086477. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.W.; Judge, J. Sensitivity of GNSS-R Spaceborne Observations to Soil Moisture and Vegetation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4730–4742. [Google Scholar] [CrossRef] [Green Version]
- Al-Khaldi, M.M.; Johnson, J.T.; O’Brien, A.J.; Balenzano, A.; Mattia, F. Time-Series Retrieval of Soil Moisture Using CYGNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4322–4331. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. Above-ground biomass retrieval over tropical forests: A novel GNSS-R approach with CYGNSS. Remote Sens. 2020, 12, 1368. [Google Scholar] [CrossRef]
- Asgarimehr, M.; Hoseini, M.; Semmling, M.; Ramatschi, M.; Camps, A.; Nahavandchi, H.; Haas, R.; Wickert, J. Remote Sensing of Precipitation Using Reflected GNSS Signals: Response Analysis of Polarimetric Observations. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Asgarimehr, M.; Zavorotny, V.; Wickert, J.; Reich, S. Can GNSS Reflectometry Detect Precipitation Over Oceans? Geophys. Res. Lett. 2018, 45, 12585–12592. [Google Scholar] [CrossRef] [Green Version]
- Martín-Neira, M.; Martin-Neira, M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Rodriguez-Alvarez, N.; Camps, A.; Vall-llossera, M.; Bosch-Lluis, X.; Monerris, A.; Ramos-Perez, I.; Valencia, E.; Marchan-Hernandez, J.F.; Martinez-Fernandez, J.; Baroncini-Turricchia, G.; et al. Land Geophysical Parameters Retrieval Using the Interference Pattern GNSS-R Technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 71–84. [Google Scholar] [CrossRef]
- Cardellach, E.; Fabra, F.; Nogués-Correig, O.; Oliveras, S.; Ribó, S.; Rius, A. GNSS-R ground-based and airborne campaigns for ocean, land, ice, and snow techniques: Application to the GOLD-RTR data sets. Radio Sci. 2011, 46, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Mashburn, J.; Axelrad, P.; Lowe, S.T.; Larson, K.M.; Lowe, S.T.; Larson, K.M. An Assessment of the Precision and Accuracy of Altimetry Retrievals for a Monterey Bay GNSS-R Experiment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4660–4668. [Google Scholar] [CrossRef]
- Semmling, A.M.; Beckheinrich, J.; Wickert, J.; Beyerle, G.; Schön, S.; Fabra, F.; Pflug, H.; He, K.; Schwabe, J.; Scheinert, M. Sea surface topography retrieved from GNSS reflectometry phase data of the GEOHALO flight mission. Geophys. Res. Lett. 2014, 41, 954–960. [Google Scholar] [CrossRef] [Green Version]
- Cardellach, E.; Li, W.; Rius, A.; Semmling, M.; Wickert, J.; Zus, F.; Ruf, C.S.; Buontempo, C. First Precise Spaceborne Sea Surface Altimetry with GNSS Reflected Signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 102–112. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface height using GPS-Reflectometry. Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar] [CrossRef] [Green Version]
- Gleason, S.; O’Brien, A.; Russel, A.; Al-Khaldi, M.M.; Johnson, J.T. Geolocation, calibration and surface resolution of CYGNSS GNSS-R land observations. Remote Sens. 2020, 12, 1317. [Google Scholar] [CrossRef] [Green Version]
- Southwell, B.J.; Dempster, A.G. A New Approach to Determine the Specular Point of Forward Reflected GNSS Signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 639–646. [Google Scholar] [CrossRef]
- Gleason, S. A Real-Time On-Orbit Signal Tracking Algorithm for GNSS Surface Observations. Remote Sens. 2019, 11, 1858. [Google Scholar] [CrossRef] [Green Version]
- Jales, P. Spaceborne Receiver Design for Scatterometric GNSS Reflectometry. Ph.D. Thesis, University of Surrey, Guildford, UK, 2012. [Google Scholar]
- Gleason, S.; Gebre-Egziabher, D.; Egziabher, D.G.; Gleason, S. GNSS Applications and Methods; Balint, G., Antala, B., Carty, C., Mabieme, J.-M.A., Amar, I.B., Kaplanova, A., Eds.; Artech House: Norwood, MA, USA, 2009; ISBN 1596933305. [Google Scholar]
- Roussel, N.; Frappart, F.; Ramillien, G.; Darrozes, J.; Desjardins, C.; Gegout, P.; Pérosanz, F.; Biancale, R. Simulations of direct and reflected wave trajectories for ground-based GNSS-R experiments. Geosci. Model Dev. 2014, 7, 2261–2279. [Google Scholar] [CrossRef] [Green Version]
- Semmling, A.M.; Schmidt, T.; Wickert, J.; Schn, S.; Fabra, F.; Cardellach, E.; Rius, A.; Schön, S.; Fabra, F.; Cardellach, E.; et al. On the retrieval of the specular reflection in GNSS carrier observations for ocean altimetry: Reflection retrieval for ocean altimetry. Radio Sci. 2012, 47, 1–13. [Google Scholar] [CrossRef]
- Semmling, A.M.; Leister, V.; Saynisch, J.; Zus, F.; Heise, S.; Wickert, J. A Phase-Altimetric Simulator: Studying the Sensitivity of Earth-Reflected GNSS Signals to Ocean Topography. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6791–6802. [Google Scholar] [CrossRef]
- Wu, S.-C.; Meehan, T.; Young, L.; Wu, S.-C.; Mcchan, T. The Potential Use of GPS Signals as Ocean Altimetry Observables. In Proceedings of the 1997 National Technical Meeting of the Institute of Navigation, Santa Monica, CA, USA, 14 January 1997; pp. 543–550. [Google Scholar]
- Wu, F.; Zheng, W.; Li, Z.; Liu, Z. Improving the GNSS-R Specular Reflection Point Positioning Accuracy Using the Gravity Field Normal Projection Reflection Reference Surface Combination Correction Method. Remote Sens. 2018, 11, 33. [Google Scholar] [CrossRef] [Green Version]
- Gleason, S.; Ruf, C.S.; Orbrien, A.J.; McKague, D.S. The CYGNSS Level 1 Calibration Algorithm and Error Analysis Based on On-Orbit Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 37–49. [Google Scholar] [CrossRef]
- Rius, A.; Cardellach, E.; Martín-Neira, M. Altimetric analysis of the sea-surface GPS-reflected signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2119–2127. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A.; Weiqiang, L.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A.; et al. Lake Level and Surface Topography Measured With Spaceborne GNSS-Reflectometry From CYGNSS Mission: Example for the Lake Qinghai. Geophys. Res. Lett. 2018, 45, 13332–13341. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Rius, A.; Ribó, S.; Martín-Neira, M.; Weiqiang, L.; Cardellach, E.; Fabra, F.; Rius, A.; et al. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals. Geophys. Res. Lett. 2017, 44, 8369–8376. [Google Scholar] [CrossRef]
- Song, M.; He, X.; Wang, X.; Jia, D.; Xiao, R.; Shi, H.; Wu, Y. Study on the Exploration of Spaceborne GNSS-R Raw Data Focusing on Altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6142–6154. [Google Scholar] [CrossRef]
- Nguyen, V.A.; Nogués-Correig, O.; Yuasa, T.; Masters, D.; Irisov, V. Initial GNSS Phase Altimetry Measurements From the Spire Satellite Constellation. Geophys. Res. Lett. 2020, 47, e2020GL088308. [Google Scholar] [CrossRef]
- Yu, K.; Rizos, C.; Dempster, A.G. GNSS-based model-free sea surface height estimation in unknown sea state scenarios. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1424–1435. [Google Scholar] [CrossRef]
- Hu, C.; Benson, C.; Rizos, C.; Qiao, L. Single-Pass Sub-Meter Space-Based GNSS-R Ice Altimetry: Results From TDS-1. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3782–3788. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Smith, W.H.F. Slope correction for ocean radar altimetry. J. Geod. 2014, 88, 765–771. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. First Evaluation of Topography on GNSS-R: An Empirical Study Based on a Digital Elevation Model. Remote Sens. 2019, 11, 2556. [Google Scholar] [CrossRef] [Green Version]
- Dente, L.; Guerriero, L.; Comite, D.; Pierdicca, N. Space-Borne GNSS-R Signal over a Complex Topography: Modeling and Validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1218–1233. [Google Scholar] [CrossRef]
- Cartwright, J.; Banks, C.J.; Srokosz, M. Improved GNSS-R bi-static altimetry and independent digital elevation models of Greenland and Antarctica from TechDemoSat-1. Cryosphere 2020, 14, 1909–1917. [Google Scholar] [CrossRef]
- Cartwright, J.; Clarizia, M.P.; Cipollini, P.; Banks, C.J.; Srokosz, M. Independent DEM of Antarctica Using GNSS-R Data From TechDemoSat-1. Geophys. Res. Lett. 2018, 45, 6117–6123. [Google Scholar] [CrossRef]
- Nilsson, J.; Gardner, A.; Sørensen, L.S.; Forsberg, R. Improved retrieval of land ice topography from CryoSat-2 data and its impact for volume-change estimation of the Greenland Ice Sheet. Cryosphere 2016, 10, 2953–2969. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Zhang, S.; Liang, S.; Zhu, J. Elevation and Volume Changes in Greenland Ice Sheet From 2010 to 2019 Derived From Altimetry Data. Front. Earth Sci. 2021, 9, 362. [Google Scholar] [CrossRef]
- Zus, F.; Bender, M.; Deng, Z.; Dick, G.; Heise, S.; Shang-Guan, M.; Wickert, J. A methodology to compute GPS slant total delays in a numerical weather model. Radio Sci. 2012, 47, 1–15. [Google Scholar] [CrossRef] [Green Version]
- CYGNSS Level 1 Science Data Record Version 3.0|PO.DAAC/JPL/NASA. Available online: https://podaac.jpl.nasa.gov/dataset/CYGNSS_L1_V3.0 (accessed on 7 March 2022).
- Jorge, N.; Stephen, J. Numerical Optimization; USA (TB/HAM): Waltham, MA, USA, 2006; ISBN 978-0-387-30303-1. [Google Scholar]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef] [Green Version]
- Schaffer, J.; Timmermann, R.; Arndt, J.; Steinhage, D. RTopo-2: A global dataset of ice sheet topography, cavity geometry and ocean bathymetry to study ice-ocean interaction in Northeast Greenland. In Proceedings of the REKLIM Conference “Our Climate—Our Future”, Berlin, Germany, 6–9 October 2014. [Google Scholar]
- Cardellach, E.; Wickert, J.; Baggen, R.; Benito, J.; Camps, A.; Catarino, N.; Chapron, B.; Dielacher, A.; Fabra, F.; Flato, G.; et al. GNSS Transpolar Earth Reflectometry exploriNg System (G-TERN): Mission Concept. IEEE Access 2018, 6, 13980–14018. [Google Scholar] [CrossRef]
- Wickert, J.; Cardellach, E.; Martin-Neira, M.; Bandeiras, J.; Bertino, L.; Andersen, O.B.; Camps, A.; Catarino, N.; Chapron, B.; Fabra, F.; et al. GEROS-ISS: GNSS REflectometry, Radio Occultation, and Scatterometry Onboard the International Space Station. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4552–4581. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Cardellach, E.; Ribó, S.; Oliveras, S.; Rius, A. Exploration of Multi-Mission Spaceborne GNSS-R Raw IF Data Sets: Processing, Data Products and Potential Applications. Remote Sens. 2022, 14, 1344. [Google Scholar] [CrossRef]
- Available online: https://download.geoservice.dlr.de/TDM90 (accessed on 10 September 2021).
- Martín-Neira, M.; Caparrini, M.; Font-Rossello, J.; Lannelongue, S.; Vallmitjana, C.S.; Martm-Neira, M.; Caparrini, M.; Font-Rossello, J.; Lannelongue, S.; Vallmitjana, C.S. The paris concept: An experimental demonstration of sea surface altimetry using gps reflected signals. IEEE Trans. Geosci. Remote Sens. 2001, 39, 142–150. [Google Scholar] [CrossRef] [Green Version]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Orús, R.; Hernández-Pajares, M.; Juan, J.M.; Sanz, J. Improvement of global ionospheric VTEC maps by using kriging interpolation technique. J. Atmos. Sol.-Terr. Phys. 2005, 67, 1598–1609. [Google Scholar] [CrossRef]
- Leandro, R.; Santos, M.; Langley, R.B. UNB Neutral Atmosphere Models: Development and Performance. In Proceedings of the 2006 National Technical Meeting of The Institute of Navigation, Monterey, CA, USA, 18–20 January 2006; pp. 564–573. [Google Scholar]
- Xing, Z.; Chi, Z.; Yang, Y.; Chen, S.; Huang, H.; Cheng, X.; Hui, F. Accuracy evaluation of four greenland digital elevation models (Dems) and assessment of river network extraction. Remote Sens. 2020, 12, 3429. [Google Scholar] [CrossRef]
- Porter, C.; Morin, P.; Howat, I.; Noh, M.-J.; Bates, B.; Peterman, K.; Keesey, S.; Schlenk, M.; Gardiner, J.; Tomko, K.; et al. ArcticDEM 2018, Harvard Dataverse, V1. Available online: https://doi.org/10.7910/DVN/OHHUKH (accessed on 1 October 2021).
- Amante, C.; Eakins, B.W. ETOPO1 1 arc-minute global relief model: Procedures, data sources and analysis. NOAA technical memorandum NESDIS NGDC-24. Natl. Geophys. Data Cent. NOAA 2009, 10, V5C8276M. [Google Scholar]


| Methods | Time(s) | 5° < θ < 30° | θ > 30° | ||||
|---|---|---|---|---|---|---|---|
| Iterations | TPL (m) | SPs (m) | Iterations | TPL (m) | SPs (m) | ||
| S#1 | 31.65 | 2.77 | <1 × 10−7 m | <1 × 10−7 m | 2.72 | <1 × 10−7 m | <1 × 10−7 m |
| S#2 | 76.93 | 282.03 | 3.93 | 6059.59 | 29.15 | 4.71 | 2227.61 |
| S#3 | 1.53 | 1.02 | 2392.05 | 3.89 | 1811.24 | ||
| S#4 | 13.20 | 1 | 0.92 | 4.13 | 1 | 3.63 | 2.51 |
| No. | Method Description | Horizontal/Geolocation | Vertical/Height |
|---|---|---|---|
| M#1 | Typical method with equation given in Equations (1) and (2) [15,34] | Specular points at WGS84 ellipsoid | Calculated by Equations (1) and (2) |
| M#2 | Ellipsoid-based method given in Section 2 | Specular points considered Earth curvature and height | Derived from specular points |
| M#3 | Ellipsoid-based method with slope considered given in Section 3 | Specular points considered local topography | Derived from specular points |
| Topography | Resolution | |||||
|---|---|---|---|---|---|---|
| RTopo-2.0.1 | 30 arc- second | 1845 m | 466 m | 367 m | 512 m | 642 m |
| ArcticDEM | 100 m | 1024 m | 443 m | 386 m | 496 m | 607 m |
| ArcticDEM | 500 m | 1022 m | 434 m | 382 m | 494 m | 606 m |
| ArcticDEM | 1000 m | 1025 m | 413 m | 372 m | 493 m | 603 m |
| ETOPO1 | 1 arc-minute | 1358 m | 577 m | 513 m | 577 m | 738 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, M.; He, X.; Asgarimehr, M.; Li, W.; Xiao, R.; Jia, D.; Wang, X.; Wickert, J. Investigation on Geometry Computation of Spaceborne GNSS-R Altimetry over Topography: Modeling and Validation. Remote Sens. 2022, 14, 2105. https://doi.org/10.3390/rs14092105
Song M, He X, Asgarimehr M, Li W, Xiao R, Jia D, Wang X, Wickert J. Investigation on Geometry Computation of Spaceborne GNSS-R Altimetry over Topography: Modeling and Validation. Remote Sensing. 2022; 14(9):2105. https://doi.org/10.3390/rs14092105
Chicago/Turabian StyleSong, Minfeng, Xiufeng He, Milad Asgarimehr, Weiqiang Li, Ruya Xiao, Dongzhen Jia, Xiaolei Wang, and Jens Wickert. 2022. "Investigation on Geometry Computation of Spaceborne GNSS-R Altimetry over Topography: Modeling and Validation" Remote Sensing 14, no. 9: 2105. https://doi.org/10.3390/rs14092105
APA StyleSong, M., He, X., Asgarimehr, M., Li, W., Xiao, R., Jia, D., Wang, X., & Wickert, J. (2022). Investigation on Geometry Computation of Spaceborne GNSS-R Altimetry over Topography: Modeling and Validation. Remote Sensing, 14(9), 2105. https://doi.org/10.3390/rs14092105