Abstract
Precise delineation of individual tree crowns is critical for accurate forest biophysical parameter estimation, species classification, and ecosystem modelling. Multispectral optical remote sensors mounted on low-flying unmanned aerial vehicles (UAVs) can rapidly collect very-high-resolution (VHR) photogrammetric optical data that contain the spectral, spatial, and structural information of trees. State-of-the-art tree crown delineation approaches rely mostly on spectral information and underexploit the spatial-contextual and structural information in VHR photogrammetric multispectral data, resulting in crown delineation errors. Here, we propose the spectral, spatial-contextual, and structural information-based individual tree crown delineation (S3-ITD) method, which accurately delineates individual spruce crowns by minimizing the undesirable effects due to intracrown spectral variance and nonuniform illumination/shadowing in VHR multispectral data. We evaluate the performance of the S3-ITD crown delineation method over a white spruce forest in Quebec, Canada. The highest mean intersection over union (IoU) index of 0.83, and the lowest mean crown-area difference (CAD) of 0.14 , proves the superior crown delineation performance of the S3-ITD method over state-of-the-art methods. The reduction in error by 2.4 cm and 1.0 cm for the allometrically derived diameter at breast height (DBH) estimates compared with those from the WS-ITD and the BF-ITD approaches, respectively, demonstrates the effectiveness of the S3-ITD method to accurately estimate biophysical parameters.
1. Introduction
Spruce trees are important conifers in the temperate and boreal regions of the Northern hemisphere. They display the highest gross primary productivity in global forest ecosystems [1,2]. They are critical entities in mitigating the anthropogenically induced carbon imbalance between the atmosphere and the Earth’s land surface [3]. Efforts to preserve and/or generate a climate-resilient forest ecosystem include sustainable forest management [4], precision forestry [5], and pest- and climate-resilient species and genotype selection [6,7]. However, such efforts demand accurate estimates of forest parameters such as tree height [8], biomass [9], leaf area index [10], and foliar pigment concentration [11], which are crucial inputs in activities such as tree-health monitoring [12], ecosystem modelling [13], and carbon-cycle studies [14]. Traditional field-surveying approaches for collecting tree-level parameters in large forests is time-consuming, low-throughput, and costly in terms of human labour. Alternatively, remote sensing data collected using optical light detection and ranging (LiDAR) and radio detection and ranging (RADAR) sensors offers a cost-effective, highly repeatable and high-throughput solution for tree-level parameter estimation [4]. Although both LiDAR and RADAR remote sensors provide comprehensive canopy structural information, the higher data-acquisition costs and complex data-processing requirements are key drawbacks when performed over large forest areas. In the case of optical sensors, the low and medium spatial-resolution optical data collected from remote sensors onboard high-altitude platforms such as satellite and aeroplanes are often associated with a limited spatial and spectral resolution that is not enough to accurately estimate tree parameters such as biomass, leaf area index, leaf water content, and chlorophyll concentration at the tree level. In fact, the limited data resolution allows only a blockwise (i.e., on a group of trees) estimation of forest parameters. On the contrary, very-high-resolution (VHR) optical remote sensing data from optical sensors on low-flying (<200 m) unmanned aerial vehicles (UAVs) is a promising data acquisition strategy to capture individual-tree-level data [12,15].
The low operational cost together with the unprecedentedly high payload carrying capacity of state-of-the-art UAVs have enabled forest managers to perform periodic optical data collection using multispectral and/or hyperspectral remote sensors [16]. In addition, the relatively short flight time associated with UAVs over other remote sensing platforms allows to quickly capture forest data with large swath overlap. This enables accurate retrieval of two-dimensional (2D) and three-dimensional (3D) crown structural information from VHR optical remote sensing data using photogrammetric techniques. The conical geometry of spruce trees causes the most brilliant pixels in their VHR optical data to be associated with the crown apex (which also aligns with the stem location for a straight stem). Hence, tree detection and localization in VHR optical data is usually performed by detecting the centroid of the region spanned by the set of brilliant pixel(s). Local Maxima (LM) algorithm [17] is one of the most popular approaches, which exploits the conical geometry of spruce crowns to detect individual trees in VHR optical data. However, the LM algorithm is often affected by undesirable intracrown spectral variance induced by local crown components and the nonuniform illumination/shadowing caused by the crown geometry and the sun’s angle [18]. The effects of intracrown spectral variance are usually minimized using smoothing filters employed in multiscale [19] and morphological analysis [20] of VHR data. However, such smoothening often results in omission errors as the local maxima corresponding to smaller spruce-tree apexes are lost in the process [21]. Object-oriented approaches such as template matching, which jointly consider shape, size, and texture of crowns, achieve improved accuracy by mapping crown pixels based on spatial and spectral similarity [22]. Nevertheless, treetop localization using only the spectral component in optical data is limited in its ability to quantify crown structural attributes such as height and geometry. Thus, photogrammetric techniques such as structure-from-motion [23] and multiview stereopsis [24] approaches are employed to derive a 3D point cloud of the visible canopy from optical data stereo pairs (i.e., images of the canopy taken from different flight-path locations).
The canopy height model (CHM) derived from the 3D point cloud represents the tree-canopy structure and is minimally affected by crown spectral variance and nonuniform illumination and shadowing. Hence, tree detection using CHM is reliably preformed using LM detection [25] and the pouring algorithm [26], under the assumption that the treetops correspond to the local maxima in CHM. Tree detection is generally followed by crown delineation (i.e., tree-crown perimeter demarcation). In the case of optical remote sensing data, individual crown delineation refers to identifying the set of pixels that corresponds to an individual spruce tree. A plethora of approaches for delineating tree crowns from medium- and high-resolution multispectral data has been described in the literature, including valley following [27], watershed segmentation [28], region growing [29], multiscale [30], and object-oriented analysis [25]. However, most of the delineation approaches assume homogeneous crowns, i.e., there is minimal variance between the reflectance spectrum of individual crown pixels. Unfortunately, the spectral homogeneity assumption in tree crowns is valid only in low and medium-resolution data, which are less affected by heterogeneity and shadowing within an individual crown. In contrast, VHR multispectral data contain details of crown components, including branches, twigs, and leaves, resulting in an undesirably large variation in pixel values within individual tree crowns [31]. Thus, a preprocessing step that minimizes crown heterogeneity (i.e., intracrown pixel variance) is critical to delineate tree crowns reliably in the case of VHR multispectral data. Employing techniques such as the Gaussian smoothening mitigates the spectral heterogeneity in the data at the cost of losing crown edge information [32]. By grouping pixels based on spectral similarity and being subjected to geometric constraints, object-oriented crown delineation approaches use template matching [22], multiresolution analysis [30], and hierarchical segmentation [33] to mitigate the effect of spectral heterogeneity in crown delineation. Huang et al. (2018) mitigated the crown spectral heterogeneity problem in VHR multispectral data by performing marker-controlled watershed segmentation on the morphologically smoothened bias field estimate [25]. However, deriving edge-mask (i.e., image representing the edges) using an edge-detection filter often results in inaccurate boundary delineation of tree crowns in forests with proximal and/or overlapping crowns. In addition, it does not exploit the potential of the 3D crown structural information in VHR multispectral data to accurately delineate tree crowns. Thus, it is essential to develop a crown delineation approach that jointly exploits both the spectral, spatial-contextual, and 3D crown structural characteristics to address the undesirable effects of intracrown spectral heterogeneity and nonuniform illumination/shadowing.
This paper describes a novel approach to delineate individual spruce crowns by combining spectral, spatial-contextual, and crown structural information in VHR photogrammetric multispectral data. The proposed crown delineation method, referred to as the S3-ITD, achieves accurate crown delineation by: (a) minimizing the undesirable effect of intracrown spectral variance and nonuniform illumination/shadowing by exploiting the noise robustness of the fuzzy framework and (b) jointly exploiting the spectral, spatial-contextual, and 3D structural information in VHR photogrammetric multispectral data.
In the following Section 2, we will first describe the study area and the data collected. Section 3 elaborates on the proposed crown delineation approach. The experiments that validate the performance of the method are reported in Section 4. Section 5 discusses the experimental results in addition to highlighting merits and limitations of the proposed method. The paper is concluded in Section 6.
2. Study Area and Data Description
The study area is a mature planned white spruce (Picea glauca) forest located in Saint-Casimir in the province of Quebec in southern Canada, with an approximate centre at 46°72′N–46°11′E. The forest stand is at the centre of a Canada-wide research project investigating white-spruce tolerance in response to a changing climate and includes individuals of 180 different white-spruce genotypic families, differing in their physiological and phenological characteristics [34].
2.1. Reference Data
In the experiments, we use two different sets of reference data collected for trees in eight carefully selected plots with different levels of crown complexity and overlap. The former set of reference data includes field-collected tree height and stem diameter at breast height (DBH) for all the trees in the eight plots, obtained in August 2018. The latter set consists of crown boundary/span (in the form of vector shape files) of the individual trees in the eight plots which were manually derived by an expert operator by visual interpretation of the photogrammetrically generated 3D dense point cloud and the image orthomosaic. The manual approach to crown span/boundary collection was preferred as it was challenging to derive crown span/boundary from the field due to factors such as the proximity to neighbouring trees, crown overlaps, and irregular conical shape of the spruce crowns. The plotwise basic statistics of the tree height and the DBH for all the trees in the eight plots are shown in Table 1.

Table 1.
Basic statistics of the reference height, the reference crown diameter, and reference stem diameter breast height (DBH) of trees in the eight circular plots with varying degree of complexity, considered for the performance evaluation of the S3-ITD.
We compare the reference DBH with estimated DBH to evaluate the performance of the ITD approaches. Optical data provides only the canopy-level information of trees and, hence, we indirectly estimate the stem DBH of a delineated tree in the experiments by using the allometric equation
where is the estimated DBH of the ith tree in millimetres, and and are the tree height in decimetres and the crown diameter (in decimeter), respectively. The model coefficients specific to spruce trees used are = −3.524, = 0.729, and = 1.345 [35]. We correct the bias in the DBH estimate resulting from the nonlinear transformation on the dependent variables in (1) by the method described in [36]. The estimated stem DBH is compared with the reference stem DBH measured on the field to evaluate the biophysical parameter estimation performance of the respective delineation tree method.
2.2. Remote Sensing Data
The VHR multispectral images of the forest area were acquired on 10 October 2018 using a modified MicaSense RedEdge multispectral camera (Micasense, Seattle, WA, USA) mounted on a DJI Matrice 100 quadrocopter (DJI Technology Co., Ltd., Shenzhen, China) with Autonomous mode with the global positioning system (GPS)-based waypoint navigation. The custom-filter camera captures near-simultaneous images in five narrow bands in the visible and the near-infrared regions of the electromagnetic spectrum (Table 2).

Table 2.
Micasense custom-filter camera specifications and unmanned aerial vehicle (UAV) flight mission parameters used in the mission planner software PRECISIONFLIGHT v.1.4.3 (PrecisionHawk, Toronto, ON, Canada). Here, CW is centre wavelengths, FWHM is full width at half maximum, HFOV is horizontal field of view, and GSD is ground sampling distance.
Images were acquired for a 0.11 square km area (Figure 1) on 10 August 2017 within two hours of local solar noon to minimize shadowed area and in stable illumination conditions (i.e., clear skies or fully overcast). The data acquisition was made with more than 75% swath overlap and sidelap to facilitate accurate detection of tie-points critical for accurate photogrammetric processing.

Figure 1.
The orthomosiac (a) of the St. Casimir forest generated from the VHR multispectral data collected in October 2018. The reference data including the diameter at breast height (represented by coloured dots) and the crown spans (dotted-white-lines) were obtained for every tree in all eight circular plots (b–i).
3. Methodology
The proposed method exploits the spectral, spatial-contextual, the 3D crown structural information in the VHR photogrammetric multispectral data to perform accurate crown delineation in a fuzzy framework. Figure 2 shows the block scheme of the proposed S3-ITD tree crown delineation approach. The 3D point cloud P and the orthomosaic O derived from the UAV optical data are the sources of the geometric and spectral/spatial-contextual information in the S3-ITD approach.
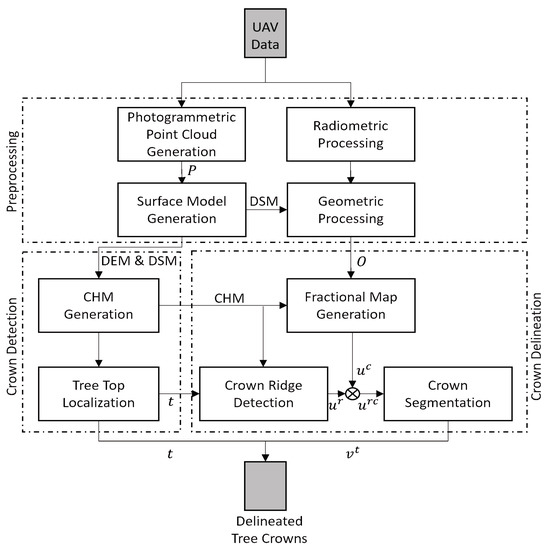
Figure 2.
Block scheme of the spectral, spatial-contextual, and structural information-based individual tree crown delineation method (S3-ITD), crown detection, and delineation method for VHR multispectral data. The geometric and radiometric corrections of the VHR data are performed using the photogrammetrically derived digital surface model (DSM) and the known reflectance panel parameters, respectively. The set of treetops t corresponding to local maxima in the canopy height model (CHM) are detected using the local maxima detection (LM) algorithm. The crown-fractional map () generated using the Markov random field based spatial-contextual model (FCM-MRF) classifier is integrated with the ridge map () obtained using the marker-controlled watershed segmentation in order to derive the ridge-integrated fractional map (). Spruce crown delineation is achieved by performing region growing on the ridge-integrated fractional map () using the gradient vector field (GVF) snake algorithm.
3.1. Preprocessing
Radiometric preprocessing of the raw VHR multispectral data is performed separately for individual bands to transform respective pixel values to physically meaningful radiance value L. The transformation compensates for sensor black level, the sensitivity of the sensor, the sensor gain, the exposure settings, and the lens vignette effects, using (2).
where p is the normalized raw DN number, is the normalized dark pixel value, , and are the radiometric calibration coefficients, is the exposure time, g is the sensor gain, is the pixel coordinate set, and L is the radiance. The reflectance conversion is performed by multiplying the radiance image by a scaling factor that is determined by measuring the radiance of a surface with known reflectance [12]. In this study, the radiometric processing to convert raw digital numbers (DN) to radiance and then to reflectance is performed in the AgiSoft Metashape Professional commercial software (version 1.5.5) using the radiance derived from a 61% reflectance panel that is imaged right before the data acquisition [12,37]. The reflectance (i.e., radiometrically corrected) images are also geometrically preprocessed to (a) estimate the camera and sensor orientation at the imaging instance, (b) determine the 3D crown geometric models from images, and (c) remove spatial distortions in the images. We perform all the geometric preprocessing steps using the Agisoft Metashape Professional commercial software for its excellent performance in feature detection, tie-point matching, and photo-based 3D reconstruction using the structure from motion (SfM) photogrammetric technique [38]. The camera and the sensor orientation parameters required for the image alignment and sparse point cloud generation were estimated using Agisoft with high accuracy by selecting 40,000 and 4000 key and tie points, respectively. An automatic outlier removal is performed on the sparse 3D cloud by removing 10% of the points with the largest reprojection errors. The alignment and location errors were estimated based on 14 widely spaced control points, for which the accurate geographic location is collected using the Trimble Geo XT GPS (Trimble Inc., Sunnyvale, CA, USA). A 3D dense point cloud representing the 3D canopy structure and underlying ground topography was generated with the quality attribute set to medium. The dense point cloud data are used to derive the digital surface model (DSM) and digital elevation model (DEM) that represent the crown surface geometry and underlying Earth surface geometry, respectively [39]. The canopy height model (CHM) representing the local tree canopy height is obtained by subtracting the DEM from the DSM. Effects of canopy/ground surface relief on the reflectance images are compensated for by performing orthorectification using the DSM. The output of the geometric processing is referred to as the image orthomosaic, where all crown geometric distortions are minimized, if not removed, for the individual trees.
3.2. Crown Detection
The individual spruce crowns are detected and localized by (a) performing Gaussian smoothening using a × spatial mask on the CHM to remove artifacts caused due to vertical branches proximal to the treetop, where is the the kernel size of the Gaussian filter that is chosen in an empirical way to minimize both omission and commission errors in detecting tree crowns; (b) detecting and localizing peaks in the CHM using the LM algorithm on the assumption that treetops manifest themselves as local maxima in the CHM; and (c) selecting only the apexes points that have an apex-height greater than a threshold in order to minimize the commission error caused by other shorter vegetation such as shrubs in the scene [40]. The value of is selected using a sensitivity analysis that aims to maximizes the overall crown detection accuracy by varying between 0 m and 3 m with increments of 0.25 m. Based on the assumption that treetops in CHM, which are very proximal to one another, are very likely to be part of the same tree (e.g., false peaks resulting from protruding branches), we merge the treetops that are less than a threshold Euclidean distance of from each other. Considering the approximate conical shape of spruce crowns, we define to be equal to one-fourth of the average distance of individual treetops to its nearest neighbour. The locations of treetops which remains after merging are used as the seed points to perform spruce crown delineation.
3.3. Crown Delineation
For each detected spruce crown, the S3-ITD approach performs crown delineation by performing region growing on a fuzzy crown-spectral map integrated with ridge-location information.
3.3.1. Fractional Map Generation
VHR multispectral images contain pixels which are often not pure but mixed in nature due to the presence of more than one object/land-cover class in the scene and, hence, the relative composition of each class in a pixel can be better represented by a class membership value rather than digital numbers. In our case, the membership value of the ith image pixel to belong to jth class is estimated by jointly considering the information in both the multispectral spectral bands and the CHM. We use the fuzzy C-means classifier integrated with the Markov random field based spatial-contextual model (FCM-MRF) [41] to generate noise-robust fractional maps and which contain estimates of the class membership values of each pixel. Here, N and are the total number pixels and classes, respectively. The fractional maps generated by the FCM-MRF classifier are the least affected by spectral variance and nonuniform illumination/shadowing, as the class membership values of a pixel is estimated by jointly considering the spectral (i.e., DN) value, CHM value, and spatial-context of the pixel. Here, the study focuses only on two broad object/land-cover classes: (a) the crown and (b) the background. The former class is composed of stem, branches, and leaves, and the latter class is composed of the remaining background objects in the scene, including soil and shadowed regions/objects. We refer to the factional maps generated against the crown and the background class as and , respectively. The objective function (3) of the FCM-MRF is a minimization problem that minimizes the posterior energy E of each image pixel by considering both the spectral similarity with respective class reference spectrum, local crown height, and spatial context of pixels.
Here, N is the number of pixels, m is the fuzzification index, and D is the Euclidean distance between the data point and the cluster centre . The optimal m is estimated by a sensitivity analysis that aims to maximize classification performance while minimizing the loss of edge information in the data measured using image entropy. Here, m is varied between 1.2 and 3.0 with increments of 0.2 [42]. We initialize the crown class with the average spectral response of the 25 brightest pixels that are located within a distance of 1 m from the 10 randomly selected treetop locations (i.e., local maxima in the CHM), while the ground class is initialized with the average spectral response of the 25 darkest pixels that are located within a distance of 1 m from 10 randomly selected local minima locations in the CHM. All parameter updates are subjected to the constraint , which ensures that the class membership values are effectively relaxed. Here, is the pixel neighbourhood defined as + + where , and represent the potential function corresponding to the single-site , pair-site , and triple-site cliques, respectively. A clique is a neighborhood pixel subset where individual members are mutual neighbours [41]. The first term in (3) estimates the spectral similarity of a pixel to individual classes, while the second term is an adaptive potential function that estimates the influence of a pixel with its neighbours in , where is the pixel value variance in . A larger results in lower neighbourhood influence, and a higher neighbour influence can be generated from smaller . It is worth saying that higher occurs at the crown boundaries and, hence, causes minimum neighbourhood influence in the estimation of the corresponding class membership values. The influence of the first and the second components in determining the class membership value is controlled by . The smoothening strength at the boundaries is controlled by . The global posterior energy E for the ith pixel and jth class in (3) is minimized using the simulated annealing optimization algorithm (Goffe, 1996) by iteratively modifying and using (4) and (5), respectively.
The optimized fractional maps and represent the likelihood of a pixel to belong to the crown and the background class, respectively. Here, is identified as the one which has its mean spectral value most proximal to the mean spectral value of the reference-crown-class spectral value. The class membership associated with a class is often never zero, even in regions dominated by other classes. For example, the vegetation membership value associated with a soil pixel is not often zero. This low membership value is a source of noise and, hence, is undesirable for our analysis. Thus, we remove the undesirable variance in by assigning zero to all membership values where .
3.3.2. Crown Ridge Detection
Crown delineation using only becomes challenging when there is no detectable variation in the likelihood values at the crown boundaries. Such challenges occur at those sections of tree crowns which overlap or touch the neighbouring crown(s). In this case, we exploit the canopy surface information in the CHM to identify ridges that correspond to the lowest height contour in the local valley around tree crowns. It is worth noting that the ridges only define the section of boundaries where tree crowns overlap or touch and not the boundary sections, which are already separated from neighbouring crown(s) by another class (e.g., the ground class). Individual pixels in CHM, represent the ith pixel height and, hence, a binary ridge map derived from the CHM is used to locate the crown boundaries at the overlapping regions. We derive by (a) performing the marker-controlled watershed algorithm with the treetop locations as the markers/seeds, (b) assigning maximum membership value (i.e., 1) to all the watershed pixels in , and minimum membership value (i.e., 0) to all the ridge pixels in . We perform a pixelwise multiplication of the ridge map and the to generate the ridge-integrated fractional map , which is used to perform the crown delineation. The ridges occur at the crown boundaries of all proximal trees with overlapping or touching crowns, and the pixelwise multiplication forces all the pixels at the watershed ridges to have the minimum membership value (i.e., 0). To this point, we assume that canopy overlap/fusion does not occur below the height of the local crown valley, as both branch and foliage density below the height is likely to be very low due to the minimal availability of sunlight.
3.3.3. Crown Segmentation
Delineation of individual tree crowns is performed on the ridge-integrated fractional map . Here, the gradient vector Ffow (GVF) snake region-growing algorithm [43,44] is used to perform crown delineation in VHR multispectral data for its (a) tolerance to pixel heterogeneity (i.e., abrupt changes or edges) within a crown area and (b) ability to map complex crown shapes without causing overestimation of crown area. The GVF snake algorithm detects tree-crown boundaries by iteratively minimizing the energy of a seed curve , in the spatial domain of the input tree-crown image. The objective energy function of the GVF snake algorithm is given by (6),
This can be viewed as a force balance equation , where − and are the internal and external forces acting on the input seed curve. On the one hand, the internal force resists the stretching and bending of the curve, while on the other hand, the external force pulls the curve towards the image edges/boundary. Here, the edge map , derived from the image , is used as the .
The gradient vector field (GVF) is the vector field , which minimizes the energy function (8).
where, the first and second terms represent the partial derivatives of the vector field, and the gradient field of the edge map where , respectively. The regularization parameter controls the contributions from the first and the second terms. The GVF can be iteratively solved by treating v and w as time-variant parameters, using (9) and (10)
The parametric curve that solves (11) is referred to as the GVF snake contour. We initialize the parametric curve corresponding to the ith tree crown as a set of uniformly spaced 100 points at a distance of 0.1 m from the respective treetop (i.e., in a circular pattern). The assumption here is that the region most proximal to the treetop is very likely to be part of the respective tree crown. The thin-plate energy , membrane energy , and balloon force are estimated in an empirical way to minimize crown segmentation error. Over a finite number of iterations, the vertices of the seed curve (which is has a circular shape in our case) shifts toward the crown boundary based on the membership values of the crown pixels. However, the shifting is constrained at the crown edges as the membership values abruptly fall to a minimum at the ridges. The boundary point updation is stopped when the average shift in vertices over successive iteration is less than 1 unit. The resulting contour captures the 2D crown boundary/span of a tree crown in the VHR multispectral data. The output of the GVF-snake-based region growing on a tree is a polygon vector shape that defines the crown boundary of the tree.
4. Results
The alignment of individual UAV images was performed using the AgiSoft Metashape Professional software and had a mean standard deviation error of 3 m for the camera locations and a mean error of 3.2 pixels for the tie points. The reprojection errors were approximately 0.35 pixels, and the root mean square error (RMSE) values of the GPS position residuals is 1.2 m. In our case, the point cloud P generated (Figure 3a) was of medium quality with a mean density of 96 points/, and is in turn used to generate the image orthomsaic (Figure 3b). The apex-height threshold that maximizes the crown detection accuracy is estimated to be 2 m. For all experiments, treetops are automatically detected by performing local-maxima detection on the CHM (Figure 4c) that is Gaussian smoothened using the 3 × 3 spatial mask. The kernel size is estimated to be 3 for the considered plots. We merged treetops detected by the local-maxima algorithm, which are more proximal than equal to 1 m to prevent multiple treetops for the same tree.

Figure 3.
The 3D point cloud (a) and orthomosaic (b) corresponding to a plot are used as the source of structural and spectral information, respectively, by the S3-ITD method.

Figure 4.
The digital elevation model (a) representing the ground surface height is subtracted from the digital surface model (b) representing the canopy surface height to derive the canopy height model (c) representing the real height of canopy in meters.
Both and are derived from the FCM-MRF classifier with the optimal fuzzification factor m as 2 and the number of clusters C set to 2. Figure 5a,b shows the fractional maps derived without and with the incorporation of the MRF-based spatial-contextual term in FCM, respectively. It can be clearly seen that the generated by the FCM-MRF classifier has relatively less intraclass membership variance. The thin-plate energy , membrane energy , and balloon force for the dataset are estimated as 1.5, 0.2, and 0.8, respectively. Figure 6a shows the marker-controlled watershed segments (coloured areas) obatined using the detected treetops (red dots) as markers, and ridges (white lines) in the CHM, for a sample plot. The fractional image of the crown class and the ridge-intergrated fractional map for the sample plot are show in Figure 6b,c, respectively. Figure 7a,b show the iterative region growing (starting from the seed circle placed around the treetop) performed by GVF snake on a fractional image with and without ridge integration, respectively. It can be clearly seen (Figure 7b) that crown span is overestimated when the ridge integration is not performed on the crown fractional map. This is because (a) the GVF snake can smoothly expand the seed curve as the intracrown class membership values tend to be more homogeneous, and (b) the abrupt fall in membership values at the crown boundary constrain the expansion of the seed curve. In other words, crown delineation error is maximum when considering only the spectral information but ignoring the spatial contextual and structural crown information. Figure 8 shows the crowns detected and delineated by the proposed method for the eight reference plots with various levels of complexities in terms of crown proximity, tree height, and crown span.
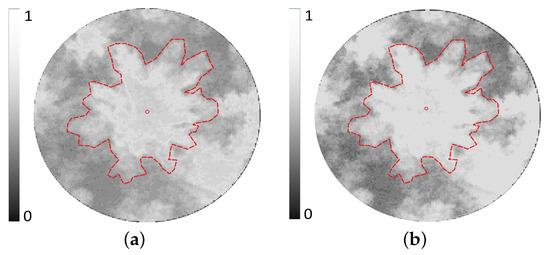
Figure 5.
The fractional image ∈ [0, 1] obtained for a sample crown using (a) the fuzzy C-means (FCM) without spatial contextual term and (b) FCM with the spatial-contextual term (i.e., FCM-MRF classifier). The manually extracted reference treetop and crown boundary are shown as red dot and dotted-red line, respectively.

Figure 6.
(a) Marker-controlled watershed segmentation using the treetops (red dots) as markers, used to detect the watershed regions (coloured areas) and ridges (white lines) in the canopy height model (CHM); (b) fractional map of the crown class ∈ [0, 1] with all pixels with set to 0; (c) ridge-integrated fractional map generated by element-wise multiplication of the and .
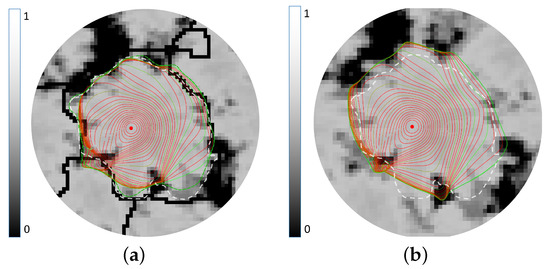
Figure 7.
The crown delineation by the gradient vector field snake (GVF snake) on fractional images with and without ridge integration are shown in (a,b), respectively. A circular seed contour whose centre is placed at the treetop (red dot) is iteratively grown (red lines) using the GVF snake to detect crown boundary (dotted-green line). The reference crown boundary is shown in white-dotted lines.

Figure 8.
The crown polygons (black lines) were derived using the spectral, spatial-contextual, and structural information-based individual tree crown delineation (S3-ITD) approach for the eight reference plots (Plot 1–Plot 8 (a–h)). The manually delineated reference crown boundaries and treetops are shown using dotted white lines and red dots, respectively.
4.1. Assessing Crown Delineation Accuracy
We assessed the performance of the S3-ITD method on the eight circular forest plots and also compared it with the performance of two other state-of-the-art (SoA) methods. The first SoA method considered is the widely used marker-controlled watershed segmentation (WS-ITD), which uses treetop locations in the image as the seeds for crown segmentation [20]. The second SoA method is the bias-field segmentation algorithm (BF-ITD), which performs watershed segmentation on the bias-field image generated by modelling the variance in the local neighbourhood of a pixel [25]. The absolute accuracy of individual crown polygons is obtained by comparing it with the reference crown polygons. The trees proximal to the plot boundaries with incomplete crowns were not considered for the accuracy assessment. The accuracy of delineation is quantified using two indices: (a) The intersection over union (IoU) , which is the ratio of the common area and the total area, between the estimated and the reference crown polygons, respectively. The IoU value of less than 1 occurs when the estimated crown polygon does not exactly overlap the reference crown area, and an IoU value equal to 0 corresponds to no crown overlap. (b) The crown-area difference (CAD) ∈ (, ∞), which is the difference in area between delineated crown polygons and reference polygons. A crown polygon larger than the reference polygon results in positive CAD values, and a polygon smaller than the reference polygon results in negative CAD values. The CAD value provides a quantitative estimate of the underestimation (i.e., positive CAD values) or overestimation (i.e., negative CAD values) in the crown area. The IoU and CAD for an accurately delineated crown are 1 and 0 , respectively. Table 3 shows the mean IoU and mean CAD for trees in the eight reference plots. It can be seen that the S3-ITD method delineated crowns with high IoU and small CAD for all the eight reference plots, compared with the WS-ITD and the BF-ITD methods. This shows the ability of the S3-ITD method to accurately delineate tree crowns by addressing issues resulting from large crown spectral variance and nonuniform illumination/shadowing. In the case of WS-ITD, the low IoU and high CAD occur due to overestimation of the crown boundaries by the watershed algorithm. This is because the watershed algorithm assigns all the pixels including the noisy and the shadowed ones to one of the nearest crown segments, and the background is selected by performing binary thresholding on the input image. The BF-ITD attempts to address the problem of large crown spectral variance with the help of field-bias maps. However, the algorithm relies only on the spectral crown data to achieve crown delineation, and, hence fails to distinguish crowns of neighbouring trees, where there is no or little difference in crown spectral properties. Although the BF-ITD method performs better than the WS-ITD methods, its limited ability to accurately delineate proximal and or overlapping crowns affects the delineation performance. Figure 9 shows the IoU and CAD distribution for all the trees in the eight reference plots represented as boxplots.

Table 3.
The mean intersection over union (IoU) and mean crown-area difference (CAD) for trees in the eight reference plots. For an accurately delineated crown, the IoU ∈ (0, 1) and CAD ∈ (, ∞) will be 1 and 0 , respectively.
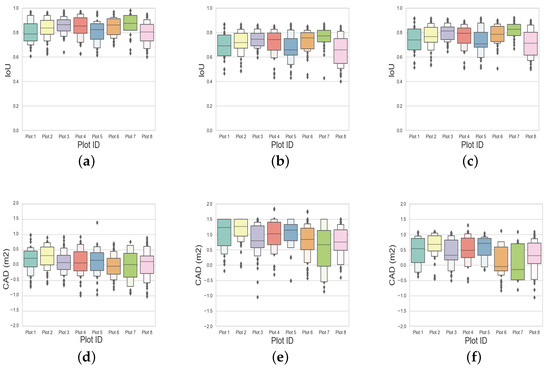
Figure 9.
The intersection over union (IoU) and crown-area difference (CAD) distribution for all the trees in the eight circular plots are represented as boxplots for the spectral, spatial, and structural information-based individual tree crown delineation (a,d), the marker-controlled watershed segmentation (b,e), and the bias-field segmentation algorithm (c,f), respectively.
4.2. Performance Validation Using DBH Estimates
We validate the performance of crown delineation approaches based on its ability to accurately estimate the stem DBH. The crown parameters derived from the S3-ITD, WS-ITD, and BF-ITD methods are separately used to estimate the stem DBH in an allometric fashion using (1) and comparing with the field-collected reference DBH to qualify the DBH estimation performance. The input parameters of (1) include the crown diameter and tree height and are taken as the maximum span of crown boundary of polygon shape vector derived from the respective crown delineation method and the field-collected tree height, respectively. The DBH estimation accuracy quantifies the ability of the considered approach to accurately delineate spruce crowns. We also evaluate the DBH estimation accuracy of trees based on the spectral homogeneity within tree crown in order to quantify the effect of intracrown spectral variance in crown delineation. Thus, we divide the 383 trees from the eight plots into three spectral groups with different ranges of pixel homogeneity represented in terms of image entropy. The Group 1 and the Group 3 consist of trees with the lowest (i.e., homogeneous) and the highest (i.e., heterogeneous) intracrown spectral variance, while Group 2 has trees with intermediate intracrown spectral variance. Table 4 shows the mean error (ME), mean absolute error (MAE), and root mean squared error (RMSE) in DBH estimates for the three different groups. In all the investigated cases, increasing heterogeneity in the crown affected the crown delineation accuracy and is reflected as higher RMSE (see Table 4). In general, the lower DBH estimation error associated with the S3-ITD approach proves its ability to accurately delineate tree crowns in very-high-resolution multispectral data. This is evident from the minimum RMSE in DBH for S3-ITD in all three entropy groups compared with the WS-ITD and the BF-ITD methods. The ME provides an estimate of the underestimation or overestimation associated with the individual methods. i.e., a negative ME value implies that the DBH values for most of the trees in a plot were underestimated, and a positive ME corresponds to overestimation. The WS-ITD often results in large inaccurate segments and is evident from its positive ME in DBH estimation, obtained on the plots (Table 3). It is also worth noting that the ME is found to be minimum and the closest to zero for the S3-ITD method compared with the other methods for all the three groups. This infers the ability of the S3-ITD method to accurately estimated stem DBH.

Table 4.
The mean error (ME), mean absolute error (MAE), and root mean squared error (RMSE) accuracy of estimated DBH for the proposed and state-of-the-art methods for different image entropy groups. Each entropy group contains the set of trees with similar intracrown pixel variance.
5. Discussion
The proposed S3-ITD method merges the spectral, spatial-contextual and structural information derived from the photogrammetric multispectral data into to a fuzzy membership map, where trees are delineated using the GVF-snake-based region-growing technique. The MRF-based estimation of membership values based on the context of pixels minimizes the intracrown spectral variance resulting from nonuniform illumination/shadowing in VHR optical data. Such an estimation forces the membership values within a class (i.e., crown or ground) to be homogeneous, and this allows the GVF snake region-growing algorithm to detect tree crowns accurately. In addition, the crown ridges/boundaries (detected using the marker-controlled watershed algorithm) integrated into the fuzzy map restricts the growth of the GVF snake algorithm and prevents associating sections of spectrally similar neighbouring crown sections to the considered crown, while the WS-ITD and the BF-ITD rely on the Gaussian smoothing technique to minimize the undesirable effects of nonuniform illumination/shadowing on crown delineation. However, such smoothing results in loss of edge information in the optical data and causes delineation errors. It is evident from Table 3 that the S3-ITD method delineates crowns with high IoU and small CAD for all the eight reference plots, compared with the WS-ITD and the BF-ITD methods. Despite the improved performance of the S3-ITD method over the WS-ITD and the BF-ITD methods, the crown delineation performance of the S3-ITD method is found to vary across the eight plots. This variance in performance is attributed to the difference in forest complexity within these plots, largely in terms of crown proximity and tree density. In particular, plots with a lower number of trees (Plots 1, 5, and 7) are shown to have higher delineation errors compared with denser plots. This is because regions along the boundary of individual tree crowns, which are defined by the ridge lines, becomes small when (a) the trees’ crowns are further apart from one another and (b) there is a fewer number of neighbouring trees. It is also worth noting that ridge lines act as good attractors of the GVF snake contour (as they produce prominent edges in the edge map), and thereby reduce both over and underestimation of crown span/boundary. For example, there are more ridge lines in Plots 2, 3, 4, 6, and 8 (due to the presence of relatively more trees and high crown proximity) and they are associated with higher performance in crown delineation. The proposed S3-ITD approach resulted in the highest average IoU of 0.83, while the average IoU for the WS-ITD and the BF-ITD are only 0.73 and 0.77, respectively. In addition, the lowest average CAD of 0.13 proves the ability of the S3-ITD approach to minimize both the under and overestimation of crowns compared with the WS-ITD and the BF-ITD approaches. In addition, it is a fact that the camera location and reprojection errors induce geometric distortions in tree crowns, and consequently result in tree parameter estimation errors. In our case, the average variance camera location and reprojection errors are as low as 3 m and 0.35 pixels, respectively. This means that that the average distortion in crown shape is also as low as 1.4 cm (for a GSD of 4 cm) and, hence, results in minimal or no impact on the estimated crown parameters.
We also evaluated the potential of the S3-ITD method to estimate stem DBH. The lowest mean error (ME), mean absolute error (MAE), and root mean squared error (RMSE) accuracy of estimated DBH in Table 4 proves the potential of the S3-ITD method to accurately estimate stem DBH over the state-of-the-art counterparts. The S3-ITD method achieves accurate DBH estimation by minimizing the errors associated with the crown-span and crown-height measurements. In forestry, low errors in the estimation of biophysical parameters such as DBH is very advantageous for effective monitoring and analysis of large forests. Most state-of-the-art ITD algorithms fail to maximally exploit spatial and spectral information, resulting in parameter estimation errors. In this context, the S3-ITD method has great potential to be used as a fully automatic parameter estimation approach in operational forestry.
Nevertheless, it is also important to note that the proposed approach performs well only with conifers where the crown shape is approximately symmetrical and, hence, it is open to improvements. Thus, prospective future research directions include enabling the method to be used for deciduous tree-crown delineation as well maximally exploiting the textural and spatial information in tree point clouds.
6. Conclusions
An approach for spruce crown delineation was developed by exploiting spectral, spatial-contextual, and structural information in very-high-resolution (VHR) photogrammetric multispectral remote sensing data. We refer to this approach as the S3-ITD method. Fractional images of the crown class are derived using the Markov random field based fuzzy C-means classifier (FCM-MRF) to minimize the effect of intracrown spectral variance and the crown illumination/shadowing. Region growing performed using the gradient Vector field snake (GVF snake) algorithm on the ridge-integrated fractional map enabled precise crown delineation by allowing the joint exploitation of the spectral, spatial-contextual, and structural information in the photogrammetric VHR multispectral data. The improved average intersection over union (IoU) of 0.1 and 0.05 and the lower average absolute crown-area difference (CAD) of 0.8 and 0.2 , respectively, compared with the marker-controlled watershed segmentation (WS-ITD) and the bias-field segmentation algorithm (BF-ITD) methods on the eight white-spruce forest plots proves the ability of the S3-ITD approach to accurately delineate individual crowns in the VHR multispectral data. The S3-ITD method reduces the overall RMSE in diameter at breast height (DBH) estimates by 2.95 cm and 1.5 cm over the WS-ITD and the BF-ITD methods. The DBH estimation accuracy decreased with an increase in intracrown spectral variance and shadowing effects. However, the S3-ITD method minimizes the inaccuracies in crown delineation compared with its WS-ITD and BF-ITD counterparts.
Author Contributions
Conceptualization, A.H. and I.E.; methodology, A.H.; software, A.H.; validation, A.H., P.D. and I.E.; formal analysis, A.H. and I.E.; investigation, I.E.; resources, I.E.; data curation, A.H.; writing—original draft preparation, A.H.; writing—review and editing, P.D. and I.E.; visualisation, A.H.; supervision, P.D. and I.E.; project administration, I.E.; funding acquisition, I.E. All authors have read and agreed to the published version of the manuscript.
Funding
Funds were received by Ingo Ensminger from National Science and Engineering Council (NSERC), Grant/AwardNumber: RGPIN-2020-06928; and Genome Canada, Genome Quebec, and Genome Bristish Columbia for the Spruce-Up (243FOR) Project (www.spruce-up.ca, accessed on 10 March 2022).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We are grateful for field support and access to the field site provided by the Forest and Environmental Genomics group of the Canadian Forest Service, Quebec, in particular to Nathalie Isabel, Daniel Plourde, Eric Dussault, Ernest Earon and colleagues from PrecisionHawk for kindly provided hardware and training during the initial phases of the project at their Toronto facility.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Burley, J. Encyclopedia of Forest Sciences; Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Jahan, N.; Gan, T.Y. Developing a gross primary production model for coniferous forests of northeastern USA from MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 11–20. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, L.; Shao, G. Drone remote sensing for forestry research and practices. J. For. Res. 2015, 26, 791–797. [Google Scholar] [CrossRef]
- Dyck, B. Precision forestry—The path to increased profitability. In Proceedings of the 2nd International Precision Forestry Symposium, Seattle, WA, USA, 15–17 July 2003; pp. 3–8. [Google Scholar]
- D’Odorico, P.; Besik, A.; Wong, C.Y.; Isabel, N.; Ensminger, I. High-throughput drone-based remote sensing reliably tracks phenology in thousands of conifer seedlings. New Phytol. 2020, 226, 1667–1681. [Google Scholar] [CrossRef]
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T.; Yu, X.; Hyyppä, J.; Saari, H.; Pölönen, I.; Imai, N.N.; et al. Individual tree detection and classification with UAV-based photogrammetric point clouds and hyperspectral imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef] [Green Version]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Peña, J.M.; de Castro, A.; Torres-Sánchez, J.; Andújar, D.; Martín, C.S.; Dorado, J.; Fernández-Quintanilla, C.; López-Granados, F. Estimating tree height and biomass of a poplar plantation with image-based UAV technology. AIMS Agric. Food 2018, 3, 313–326. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, J.; Ni, W.; Sun, G.; Zhang, Z.; Liu, Q.; Wang, Q. Estimation of Forest Leaf Area Index Using Height and Canopy Cover Information Extracted From Unmanned Aerial Vehicle Stereo Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 471–481. [Google Scholar] [CrossRef]
- Wong, C.Y.; D’Odorico, P.; Arain, M.A.; Ensminger, I. Tracking the phenology of photosynthesis using carotenoid-sensitive and near-infrared reflectance vegetation indices in a temperate evergreen and mixed deciduous forest. New Phytol. 2020, 226, 1682–1695. [Google Scholar] [CrossRef] [PubMed]
- Näsi, R.; Honkavaara, E.; Lyytikäinen-Saarenmaa, P.; Blomqvist, M.; Litkey, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Tanhuanpää, T.; Holopainen, M. Using UAV-based photogrammetry and hyperspectral imaging for mapping bark beetle damage at tree-level. Remote Sens. 2015, 7, 15467–15493. [Google Scholar] [CrossRef] [Green Version]
- De Araujo Barbosa, C.C.; Atkinson, P.M.; Dearing, J.A. Remote sensing of ecosystem services: A systematic review. Ecol. Indic. 2015, 52, 430–443. [Google Scholar] [CrossRef]
- Isabel, N.; Holliday, J.A.; Aitken, S.N. Forest genomics: Advancing climate adaptation, forest health, productivity, and conservation. Evol. Appl. 2020, 13, 3–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohan, M.; Silva, C.A.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.T.; Dia, M. Individual tree detection from unmanned aerial vehicle (UAV) derived canopy height model in an open canopy mixed conifer forest. Forests 2017, 8, 340. [Google Scholar] [CrossRef] [Green Version]
- Wallace, L.; Lucieer, A.; Watson, C.S. Evaluating tree detection and segmentation routines on very high resolution UAV LiDAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7619–7628. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 2003, 29, 564–577. [Google Scholar] [CrossRef]
- Gougeon, F.A. A crown-following approach to the automatic delineation of individual tree crowns in high spatial resolution aerial images. Can. J. Remote Sens. 1995, 21, 274–284. [Google Scholar] [CrossRef]
- Brandtberg, T.; Walter, F. Automated delineation of individual tree crowns in high spatial resolution aerial images by multiple-scale analysis. Mach. Vis. Appl. 1998, 11, 64–73. [Google Scholar] [CrossRef]
- Meyer, F.; Maragos, P. Multiscale morphological segmentations based on watershed, flooding, and eikonal PDE. In Proceedings of the International Conference on Scale-Space Theories in Computer Vision, Corfu, Greece, 26–27 September 1999; pp. 351–362. [Google Scholar]
- Wulder, M.; Niemann, K.O.; Goodenough, D.G. Local maximum filtering for the extraction of tree locations and basal area from high spatial resolution imagery. Remote Sens. Environ. 2000, 73, 103–114. [Google Scholar] [CrossRef]
- Hung, C.; Bryson, M.; Sukkarieh, S. Multi-class predictive template for tree crown detection. ISPRS J. Photogramm. Remote Sens. 2012, 68, 170–183. [Google Scholar] [CrossRef]
- Schonberger, J.L.; Frahm, J.M. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Harwin, S.; Lucieer, A. Assessing the accuracy of georeferenced point clouds produced via multi-view stereopsis from unmanned aerial vehicle (UAV) imagery. Remote Sens. 2012, 4, 1573–1599. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Li, X.; Chen, C. Individual tree crown detection and delineation from very-high-resolution UAV images based on bias field and marker-controlled watershed segmentation algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2253–2262. [Google Scholar] [CrossRef]
- Kattenborn, T.; Sperlich, M.; Bataua, K.; Koch, B. Automatic single tree detection in plantations using UAV-based photogrammetric point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 139. [Google Scholar] [CrossRef] [Green Version]
- Leckie, D.; Gougeon, F.; Hill, D.; Quinn, R.; Armstrong, L.; Shreenan, R. Combined high-density lidar and multispectral imagery for individual tree crown analysis. Can. J. Remote Sens. 2003, 29, 633–649. [Google Scholar] [CrossRef]
- Wang, L.; Gong, P.; Biging, G.S. Individual tree-crown delineation and treetop detection in high-spatial-resolution aerial imagery. Photogramm. Eng. Remote Sens. 2004, 70, 351–357. [Google Scholar] [CrossRef] [Green Version]
- Erikson, M. Segmentation of individual tree crowns in colour aerial photographs using region growing supported by fuzzy rules. Can. J. For. Res. 2003, 33, 1557–1563. [Google Scholar] [CrossRef]
- Jing, L.; Hu, B.; Noland, T.; Li, J. An individual tree crown delineation method based on multi-scale segmentation of imagery. ISPRS J. Photogramm. Remote Sens. 2012, 70, 88–98. [Google Scholar] [CrossRef]
- Gomes, M.F.; Maillard, P. Detection of Tree Crowns in Very High Spatial Resolution Images; InTech: London, UK, 2016. [Google Scholar]
- Brandtberg, T.; Warner, T. High-spatial-resolution remote sensing. In Computer Applications in Sustainable Forest Management; Springer: Berlin/Heidelberg, Germany, 2006; pp. 19–41. [Google Scholar]
- Suárez, J.C.; Ontiveros, C.; Smith, S.; Snape, S. Use of airborne LiDAR and aerial photography in the estimation of individual tree heights in forestry. Comput. Geosci. 2005, 31, 253–262. [Google Scholar] [CrossRef]
- Bousquet, J.; Gérardi, S.; de Lafontaine, G.; Jaramillo-Correa, J.P.; Pavy, N.; Prunier, J.; Lenz, P.; Beaulieu, J. Spruce Population Genomics; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Kalliovirta, J.; Tokola, T. Functions for estimating stem diameter and tree age using tree height, crown width and existing stand database information. Silva Fenn. 2005, 39, 227–248. [Google Scholar] [CrossRef] [Green Version]
- Lappi, J. Metsäbiometrian Menetelmiä [Methods of Forest Biometrics, in Finnish]; Silva Carelica 24; University of Joensuu: Kuopio, Finland, 1993. [Google Scholar]
- Eltner, A.; Schneider, D. Analysis of different methods for 3D reconstruction of natural surfaces from parallel-axes UAV images. Photogramm. Rec. 2015, 30, 279–299. [Google Scholar] [CrossRef]
- Ullman, S. The interpretation of structure from motion. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1979, 203, 405–426. [Google Scholar]
- Puliti, S.; Ørka, H.O.; Gobakken, T.; Næsset, E. Inventory of small forest areas using an unmanned aerial system. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef] [Green Version]
- Monnet, J.M.; Mermin, E.; Chanussot, J.; Berger, F. Tree top detection using local maxima filtering: A parameter sensitivity analysis. In Proceedings of the 10th International Conference on LiDAR Applications for Assessing Forest Ecosystems, Freiburg, Germany, 14–17 September 2010. [Google Scholar]
- Dutta, A. Fuzzy c-Means Classification of Multispectral Data Incorporating Spatial Contextual Information by Using Markov Random Field; ITC: Enschede, The Netherlands, 2009. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Processing Using MATLAB; Pearson Education: Chennai, India, 2004; Chapter 11. [Google Scholar]
- Lürig, C.; Kobbelt, L.; Ertl, T. Hierarchical solutions for the deformable surface problem in visualization. Graph. Model. 2000, 62, 2–18. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Prince, J.; Flow, G.V. A new external force for snakes. In Proceedings of the 1997 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 66–71. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).