Atmosphere and Terrain Coupling Simulation Framework for High-Resolution Visible-Thermal Spectral Imaging over Heterogeneous Land Surface
Abstract
:1. Introduction
2. Methods and Materials
2.1. Signal Component of At-Sensor Radiance
2.2. Atmospheric and Terrain Effects Modeling
2.2.1. Topographic Irradiance
2.2.2. Trapping Effect
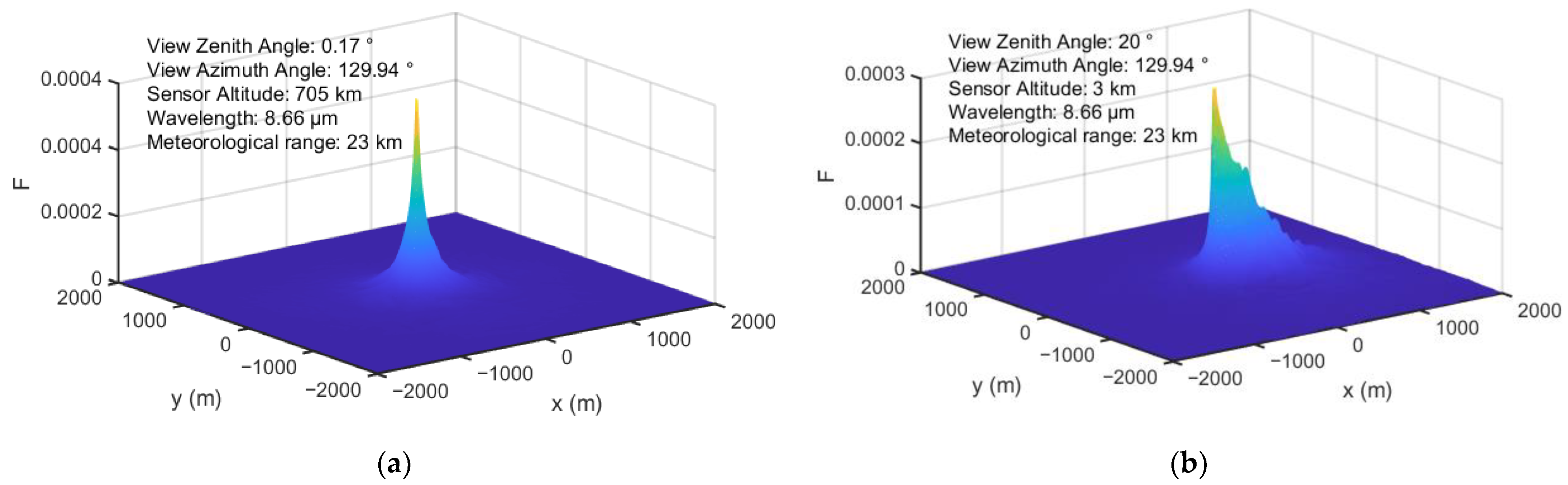
2.2.3. Atmospheric Adjacency Effect
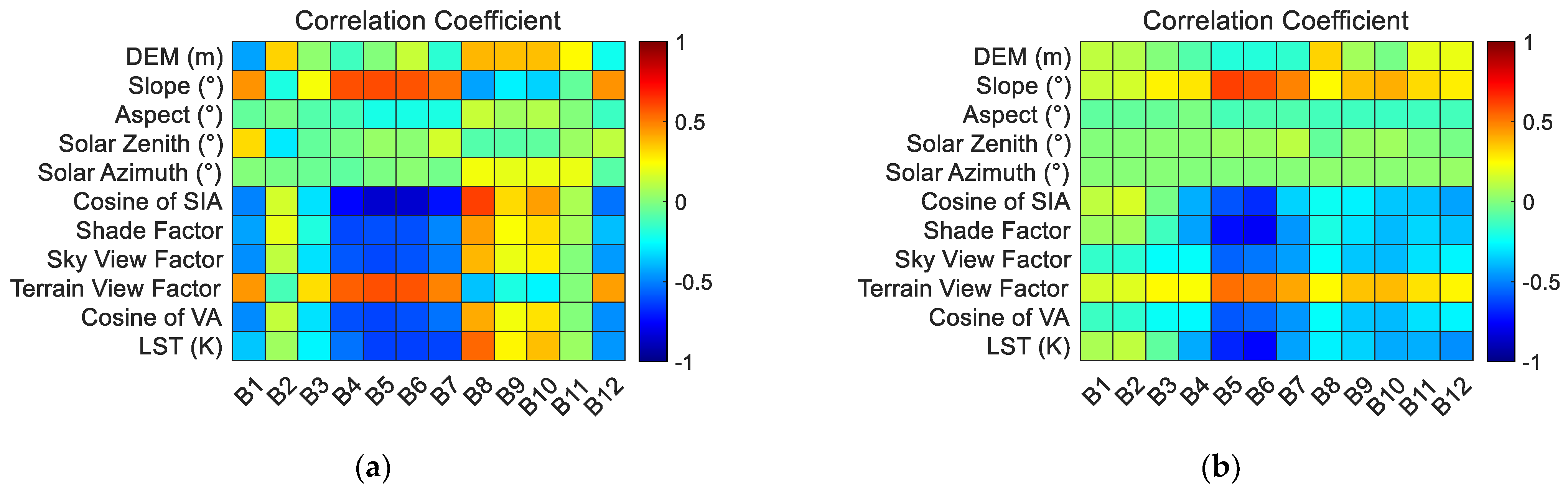
2.2.4. Atmospheric and Topographic Parameter Generation
2.3. Materials for Simulation Case Study
3. Results
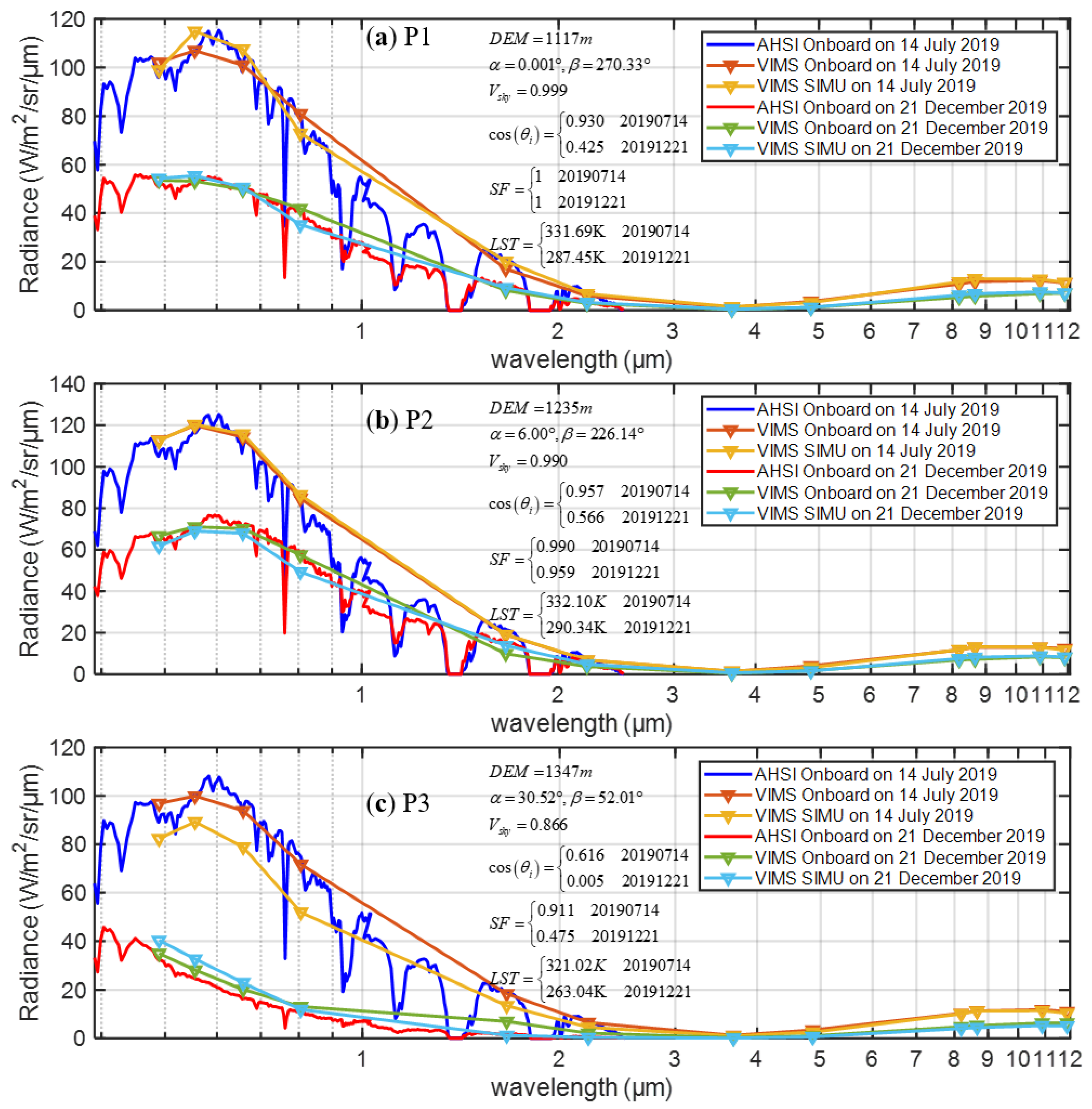
3.1. Validation of the Simulation Results
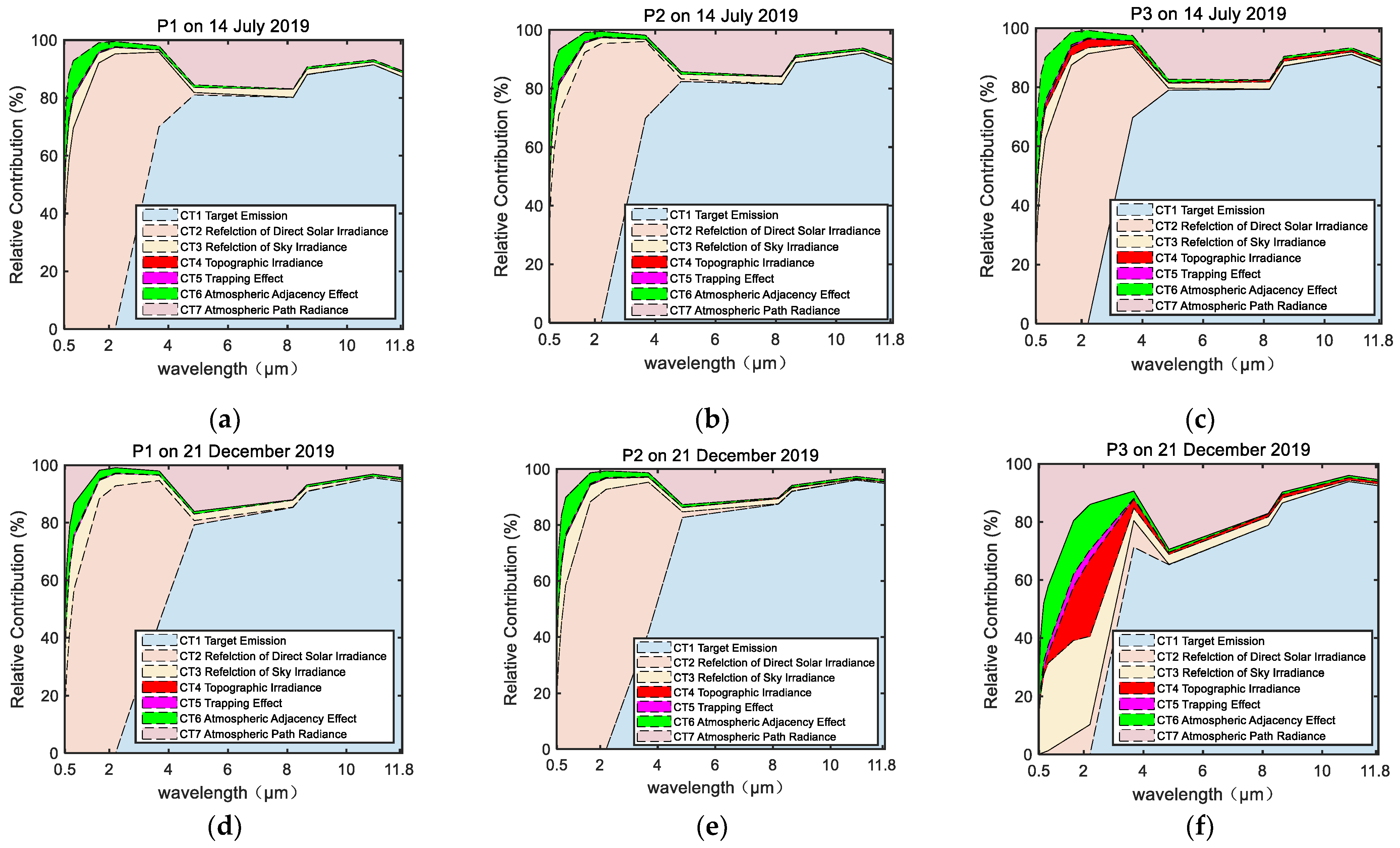
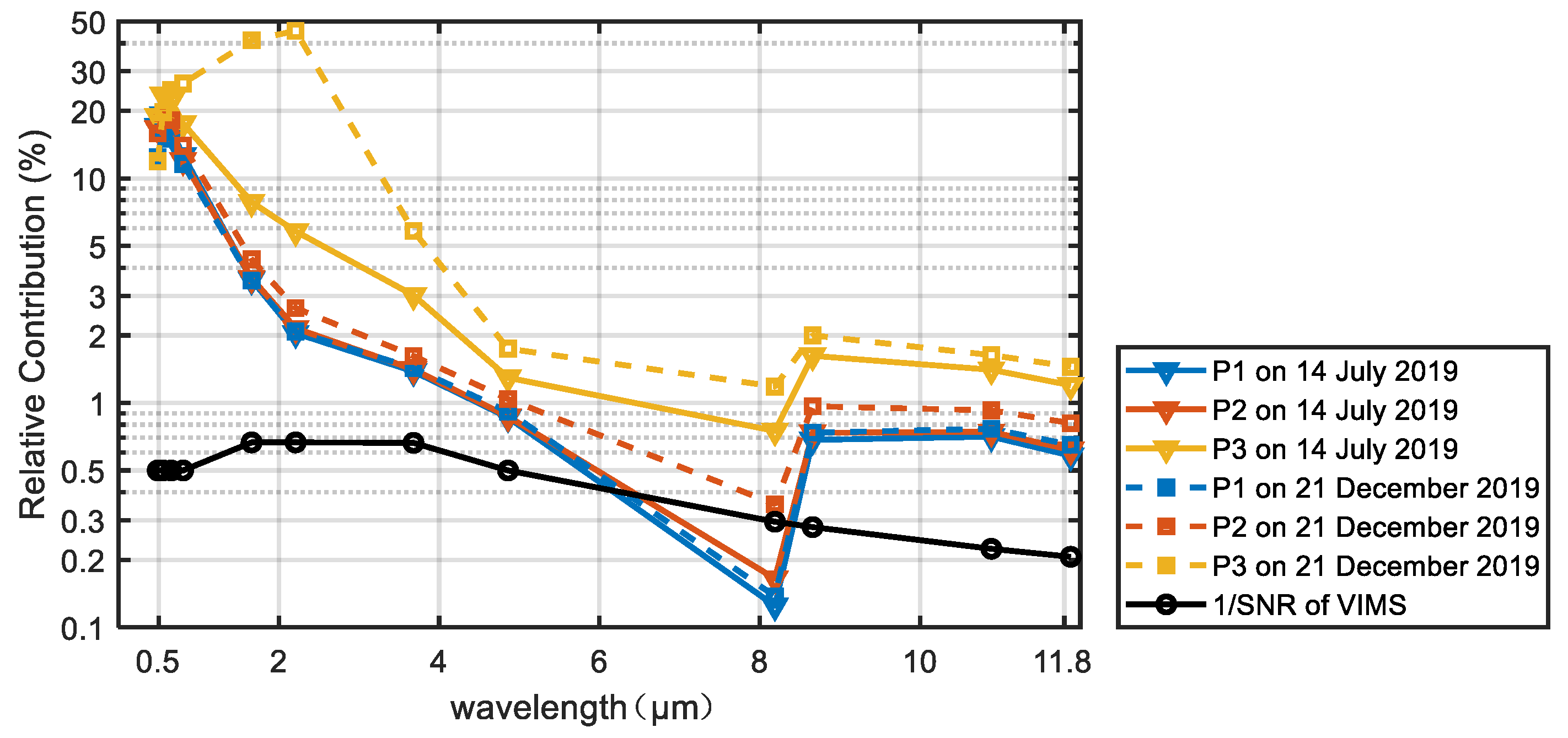
3.2. Evaluation of Atmospheric and Topographic Contributions
4. Discussion
4.1. Topographic Error Accumulation
4.2. The Angle and Scale Effects
4.3. Challenges for Retrieval Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, S. Quantitative Remote Sensing of Land Surfaces; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; ISBN 0-471-28166-2. [Google Scholar]
- Kuenzer, C.; Dech, S. Thermal Infrared Remote Sensing; Springer: Dordrecht, The Netherlands, 2013; ISBN 978-94-007-6638-9. [Google Scholar]
- Fahlen, J.E.; Brodrick, P.G.; Thompson, D.R.; Herman, R.L.; Hulley, G.; Cawse-Nicholson, K.; Green, R.O.; Green, J.J.; Hook, S.J.; Miller, C.E. Joint VSWIR-TIR retrievals of earth’s surface and atmosphere. Remote Sens. Environ. 2021, 267, 112727. [Google Scholar] [CrossRef]
- Liu, Y.-N.; Zhang, J.; Sun, W.-W.; Jiao, L.-L.; Sun, D.-X.; Hu, X.-N.; Ye, X.; Li, Y.-D.; Liu, S.-F.; Cao, K.-Q.; et al. The Advanced Hyperspectral Imager: Aboard China’s GaoFen-5 Satellite. IEEE Geosci. Remote Sens. Mag. 2019, 7, 23–32. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, J.; Zhou, S. Retrieving Land Surface Temperature from High Spatial Resolution Thermal Infrared Data of Chinese Gaofen-5. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar] [CrossRef]
- Zhao, Y.; Dai, L.; Bai, S.; Liu, J.; Peng, H.; Wang, H. Design and Implementation of Full-spectrum Spectral Imager System. Spacecr. Recovery Remote Sens. 2018, 39, 38–50. (In Chinese) [Google Scholar] [CrossRef]
- Schott, J.R. Remote Sensing: The Image Chain Approach; Oxford University Press: New York, NY, USA, 2007; ISBN 978-0-19-517817-3. [Google Scholar]
- Richter, R. Correction of atmospheric and topographic effects for high spatial resolution satellite imagery. Int. J. Remote Sens. 1997, 18, 1099–1111. [Google Scholar] [CrossRef]
- Shepherd, J.D.; Dymond, J.R. Correcting satellite imagery for the variance of reflectance and illumination with topography. Int. J. Remote Sens. 2003, 24, 3503–3514. [Google Scholar] [CrossRef]
- Santini, F.; Palombo, A. Physically Based Approach for Combined Atmospheric and Topographic Corrections. Remote Sens. 2019, 11, 1218. [Google Scholar] [CrossRef] [Green Version]
- Yan, G.; Wang, T.; Jiao, Z.; Mu, X.; Zhao, J.; Chen, L. Topographic radiation modeling and spatial scaling of clear-sky land surface longwave radiation over rugged terrain. Remote Sens. Environ. 2016, 172, 15–27. [Google Scholar] [CrossRef]
- Zheng, X.; Li, Z.-L.; Zhang, X.; Shang, G. Quantification of the Adjacency Effect on Measurements in the Thermal Infrared Region. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9674–9687. [Google Scholar] [CrossRef]
- Yan, G.; Jiao, Z.-H.; Wang, T.; Mu, X. Modeling surface longwave radiation over high-relief terrain. Remote Sens. Environ. 2020, 237, 111556. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Gao, C.; Zhao, W.; Wu, H.; Qian, Y.; Leng, P.; Gao, M. Influence of adjacency effect on high-spatial-resolution thermal infrared imagery: Implication for radiative transfer simulation and land surface temperature retrieval. Remote Sens. Environ. 2020, 245, 111852. [Google Scholar] [CrossRef]
- Zhu, X.; Duan, S.-B.; Li, Z.-L.; Zhao, W.; Wu, H.; Leng, P.; Gao, M.; Zhou, X. Retrieval of Land Surface Temperature with Topographic Effect Correction from Landsat 8 Thermal Infrared Data in Mountainous Areas. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6674–6687. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K. MODTRAN 5.3.2 User’s Manual; Spectral Sciences, Inc.: Burlington, MA, USA; Air Force Research Laboratory, Hanscom AFB: Albuquerque, NM, USA, 2013. [Google Scholar]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second Simulation of the Satellite Signal Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An Overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef] [Green Version]
- Clough, S.A.; Iacono, M.J.; Moncet, J.-L. Line-by-line calculations of atmospheric fluxes and cooling rates: Application to water vapor. J. Geophys. Res. 1992, 97, 15761–15785. [Google Scholar] [CrossRef]
- Clough, S.; Shephard, M.; Mlawer, E.; Delamere, J.; Iacono, M.; Cady-Pereira, K.; Boukabara, S.A.; Brown, P. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Schott, J.R.; Brown, S.D.; Raqueno, R.V.; Gross, H.N.; Robinson, G. Advanced synthetic image generation models and their application to multi/hyperspectral algorithm development. In Proceedings of the 27th AIPR Workshop: Advances in Computer-Assisted Recognition, Washington, DC, USA, 14 October 1998; Mericsko, R.J., Ed.; pp. 211–220. [Google Scholar]
- Goodenough, A.A.; Brown, S.D. DIRSIG5: Next-Generation Remote Sensing Data and Image Simulation Framework. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4818–4833. [Google Scholar] [CrossRef]
- Sundberg, R.L.; Berk, A.; Richtsmeier, S.; Adler-Golden, S.M.; Haren, R. Hyperspectral scene simulation from the visible through the LWIR. Proc. SPIE 2004, 5234, 252–261. [Google Scholar] [CrossRef]
- Grau, E.; Gastellu-Etchegorry, J.-P. Radiative transfer modeling in the Earth–Atmosphere system with DART model. Remote Sens. Environ. 2013, 139, 149–170. [Google Scholar] [CrossRef]
- Wu, S.; Wen, J.; You, D.; Hao, D.; Lin, X.; Xiao, Q.; Liu, Q.; Gastellu-Etchegorry, J.-P. Characterization of Remote Sensing Albedo Over Sloped Surfaces Based on DART Simulations and In Situ Observations. J. Geophys. Res. Atmos. 2018, 123, 8599–8622. [Google Scholar] [CrossRef]
- Spurr, R.; Kurosu, T.P.; Chance, K.V. A linearized discrete ordinate radiative transfer model for atmospheric remote-sensing retrieval. J. Quant. Spectrosc. Radiat. Transf. 2001, 68, 689–735. [Google Scholar] [CrossRef]
- Borel, C.C.; Gerstl, S.A.W.; Powers, B.J. The radiosity method in optical remote sensing of structured 3-D surfaces. Remote Sens. Environ. 1991, 36, 13–44. [Google Scholar] [CrossRef]
- Borel, C.C.; Gerstl, S.A.W. Simulation of partially obscured scenes using the radiosity method. In Proceedings of the Orlando ‘91, Characterization, Propagation, and Simulation of Sources and Backgrounds, Orlando, FL, USA, 1 April 1991; Watkins, W.R., Clement, D., Eds.; pp. 271–277. [Google Scholar]
- Borel, C.C.; Gerstl, S.A.W. Adjacency-blurring-effect of scenes modeled by the radiosity method. In Proceedings of the SPIE Aerospace Sensing, Atmospheric Propagation and Remote Sensing, Orlando, FL, USA, 20 April 1992; Kohnle, A., Miller, W.B., Eds.; pp. 620–624. [Google Scholar]
- Zhao, H.; Jia, G.; Li, N. Transformation from Hyperspectral Radiance Data to Data of Other Sensors Based on Spectral Superresolution. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3903–3912. [Google Scholar] [CrossRef]
- Florio, C.J.; Cota, S.A.; Gaffney, S.K. Predicting top-of-atmosphere radiance for arbitrary viewing geometries from the visible to thermal infrared: Generalization to arbitrary average scene temperatures. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 1–5 August 2010. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Zhang, B. Top-of-Atmosphere Image Simulation in the 4.3-μm Mid-infrared Absorption Bands. IEEE Trans. Geosci. Remote Sens. 2016, 54, 452–456. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Simulation of hyperspectral and directional radiance images using coupled biophysical and atmospheric radiative transfer models. Remote Sens. Environ. 2003, 87, 23–41. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Simulation of Sentinel-3 images by four-stream surface–atmosphere radiative transfer modeling in the optical and thermal domains. Remote Sens. Environ. 2012, 120, 197–207. [Google Scholar] [CrossRef]
- Mousivand, A.; Verhoef, W.; Menenti, M.; Gorte, B. Modeling Top of Atmosphere Radiance over Heterogeneous Non-Lambertian Rugged Terrain. Remote Sens. 2015, 7, 8019–8044. [Google Scholar] [CrossRef] [Green Version]
- Shi, H.; Xiao, Z.; Wen, J.; Wu, S. An Optical–Thermal Surface–Atmosphere Radiative Transfer Model Coupling Framework With Topographic Effects. IEEE Trans. Geosci. Remote Sensing 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, C.; Jia, G.; Tao, D. Simulation of hyperspectral radiance images with quantification of adjacency effects over rugged scenes. Meas. Sci. Technol. 2013, 24, 5405. [Google Scholar] [CrossRef]
- Goel, N.S.; Rozehnal, I.; Thompson, R.L. A computer graphics based model for scattering from objects of arbitrary shapes in the optical region. Remote Sens. Environ. 1991, 36, 73–104. [Google Scholar] [CrossRef]
- Miesch, C.; Briottet, X.; Kerr, Y.H. Phenomenological Analysis of Simulated Signals Observed Over Shaded Areas in an Urban Scene. IEEE Trans. Geosci. Remote Sens. 2004, 42, 434–442. [Google Scholar] [CrossRef]
- Miesch, C.; Briottet, X.; Kerr, Y.H.; Cabot, F. Monte Carlo approach for solving the radiative transfer equation over mountainous and heterogeneous areas. Appl. Opt. 1999, 38, 7419–7430. [Google Scholar] [CrossRef]
- Sanders, L.C.; Schott, J.R.; Raqueño, R. A VNIR/SWIR atmospheric correction algorithm for hyperspectral imagery with adjacency effect. Remote Sens. Environ. 2001, 78, 252–263. [Google Scholar] [CrossRef]
- Diner, D.; Martonchik, J. Influence of Aerosol Scattering on Atmospheric Blurring of Surface Features. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 618–624. [Google Scholar] [CrossRef]
- Santer, R.; Schmechtig, C. Adjacency effects on water surfaces: Primary scattering approximation and sensitivity study. Appl. Opt. 2000, 39, 361–375. [Google Scholar] [CrossRef] [PubMed]
- Liou, K.-N. An introduction to Atmospheric Radiation, 2nd ed.; Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2002; ISBN 0080491677. [Google Scholar]
- Guanter, L.; Richter, R.; Kaufmann, H. On the application of the MODTRAN4 atmospheric radiative transfer code to optical remote sensing. Int. J. Remote Sens. 2009, 30, 1407–1424. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Analysis of errors of derived slope and aspect related to DEM data properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Wang, J.; Robinson, G.J.; White, K. A Fast Solution to Local Viewshed Computation Using Grid-Based Digital Elevation Models. Photogramm. Eng. Remote Sens. 1996, 62, 1157–1164. [Google Scholar] [CrossRef]
- Dozier, J.; Frew, J. Rapid calculation of terrain parameters for radiation modeling from digital elevation data. IEEE Trans. Geosci. Remote Sens. 1990, 28, 963–969. [Google Scholar] [CrossRef]
- Karra, K.; Kontgis, C.; Statman-Weil, Z.; Mazzariello, J.C.; Mathis, M.; Brumby, S.P. Global land use / land cover with Sentinel 2 and deep learning. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021. [Google Scholar] [CrossRef]
- ASF Data Search. Available online: https://search.asf.alaska.edu (accessed on 20 February 2022).
- Qiu, X.; Jia, G.; Zhao, H.; Zhang, C. Antinoise Estimation of Temperature and Emissivity for FTIR Spectrometer Data Using Spectral Polishing Filters: Design and Comparison. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3292–3308. [Google Scholar] [CrossRef]
- Salisbury, J.W.; Wald, A.; D’Aria, D.M. Thermal-infrared remote sensing and Kirchhoff’s law: 1 Laboratory measurements. J. Geophys. Res. Earth Surf. 1994, 99, 11897–11911. [Google Scholar] [CrossRef]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Copernicus Climate Data Store | Copernicus Climate Data Store. Available online: https://cds.climate.copernicus.eu (accessed on 20 February 2022).
- EUMETSAT NWP SAF IR_SRF of GF5 VIMS. Available online: https://nwp-saf.eumetsat.int/downloads/rtcoef_rttov13/ir_srf/rtcoef_gf5_1_vims_srf.html (accessed on 20 February 2022).
- Tao, D.; Jia, G.; Yuan, Y.; Zhao, H. A digital sensor simulator of the pushbroom Offner hyperspectral imaging spectrometer. Sensors 2014, 14, 23822–23842. [Google Scholar] [CrossRef] [PubMed] [Green Version]
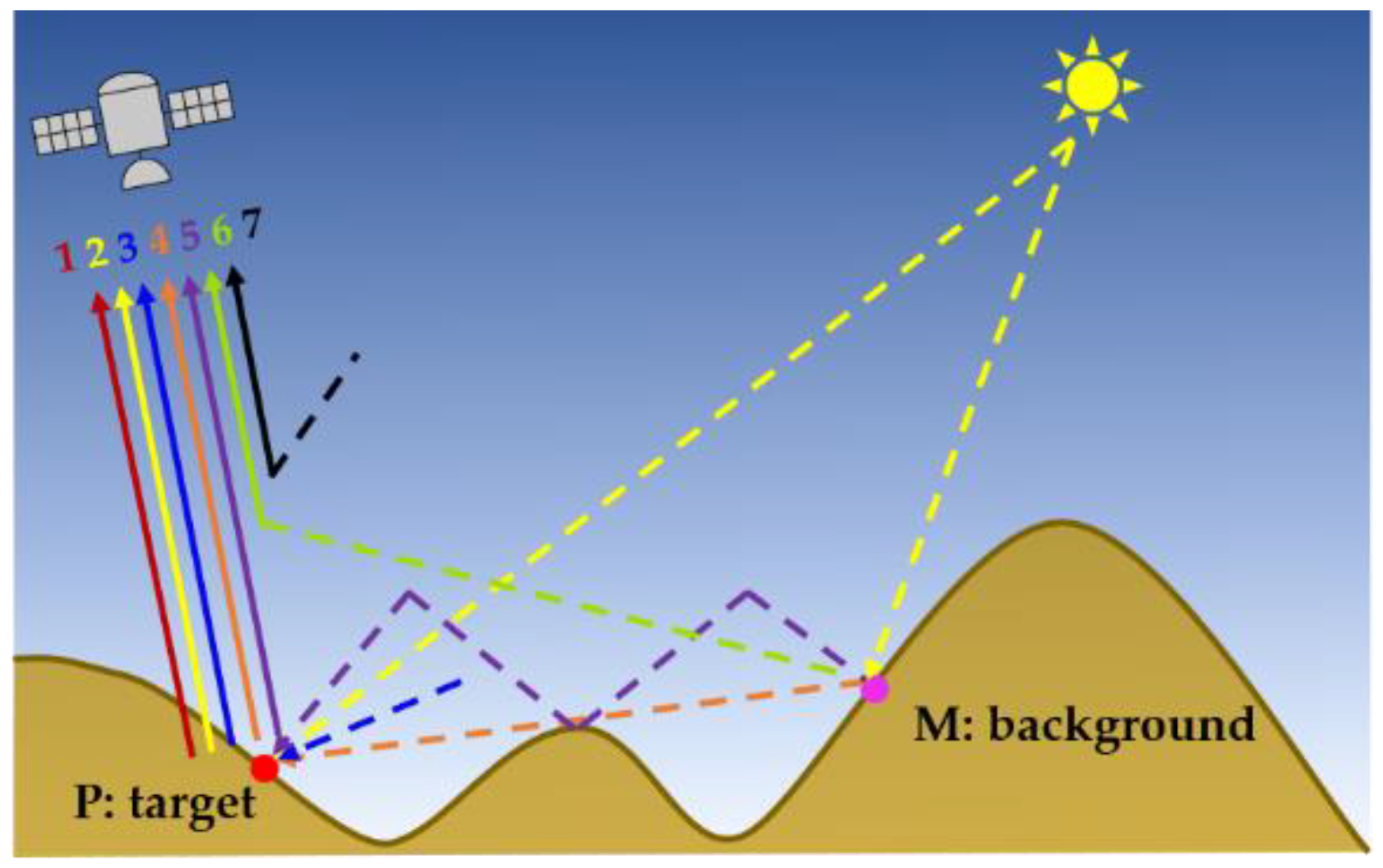
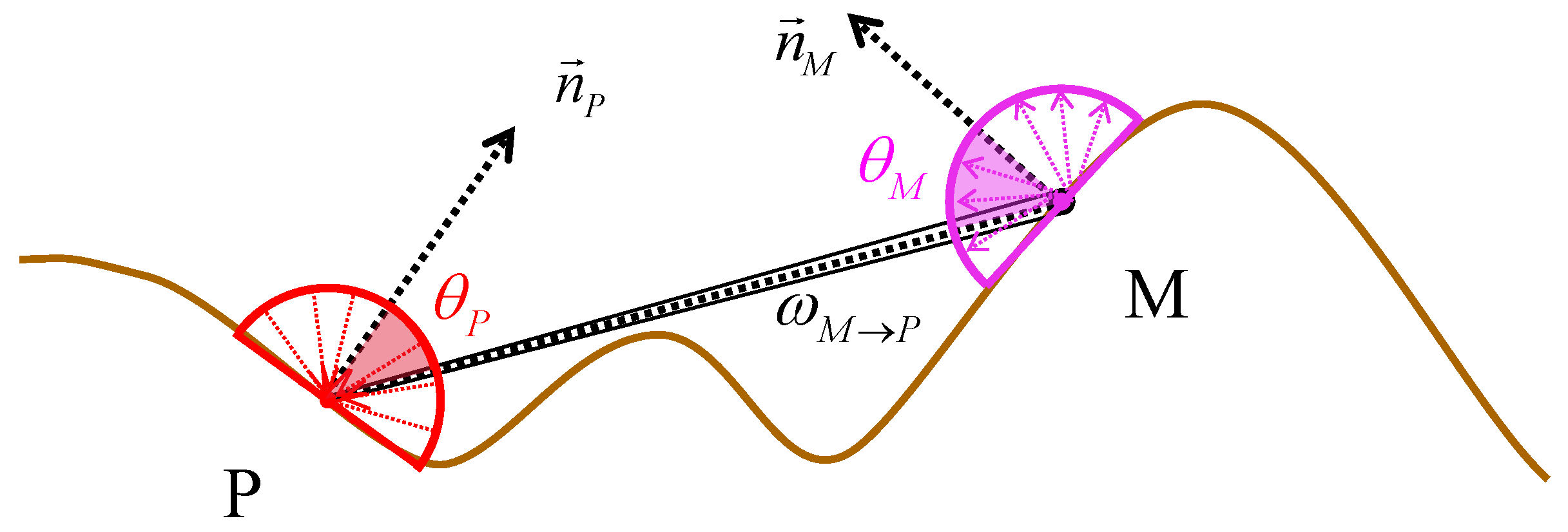
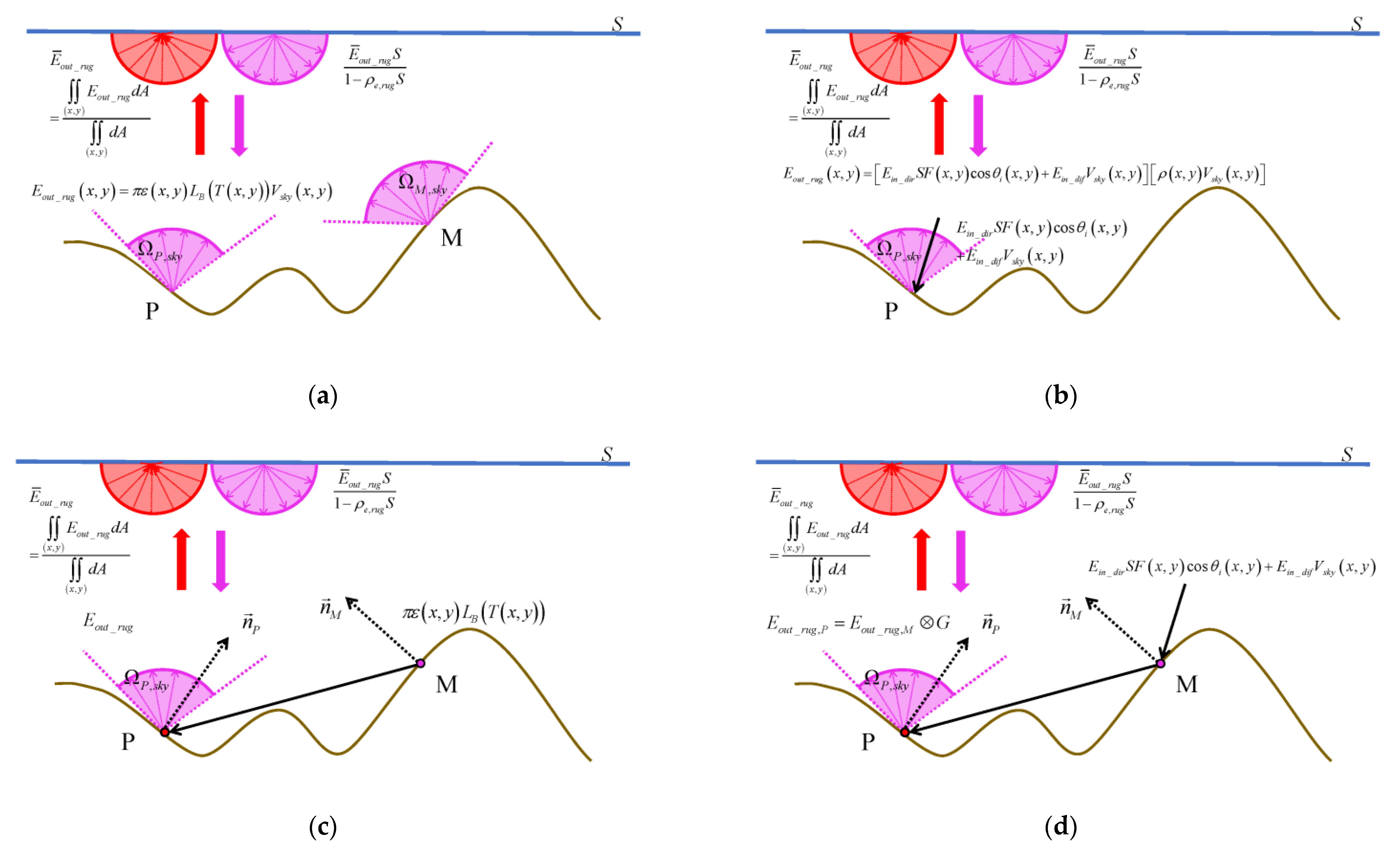









| Terrain Parameter | Symbol | Calculation Method |
|---|---|---|
| Slope angle | where the inverse square distance weighted spatial interpolation of DEM [45], was used to calculate, and along a west–east and south–north direction, respectively. | |
| Aspect angle | ||
| Cosine of SIA | ||
| Shade factor | SF | Shade factor was calculated using the depth buffer method. |
| Sky view Factor | where is defined as the angle between the zenith and the horizon surface at a given orientation direction [46,47]. |
| Atmospheric Coefficients | Symbol | Calculation Using the MODTRAN Output Data |
|---|---|---|
| Hemispherical scattering albedo of BOA 1 | ||
| Direct transmittance 1 | ||
| Diffuse transmittance 1 | ||
| Path radiance 2 | ||
| Direct solar irradiance 3 | ||
| Diffused solar irradiance 3 | ||
| Diffused thermal irradiance from sky 3 | ||
| Extinction coefficient of layers 3 | where is the height interval of the ith layer. | |
| Scattering coefficient of layers 4 |
| Scene Number | Scene 1 | Scene 2 | ||
|---|---|---|---|---|
| Imaging time (UTC) | 14 July 2019 6:38:45 | 21 December 2019 6:36:20 | ||
| Average solar zenith angle (°) | 21.40 | 64.90 | ||
| Solar azimuth (°) | 214.43 | 194.44 | ||
| View zenith angle (°) | 0.16 | 0.17 | ||
| View azimuth angle (°) | 131.04 | 129.94 | ||
| Quick view(true color) |  |  | ||
| Instrument performance parameters of VIMS | ||||
| Band number | B1-B4 | B5-B6 | B7-B8 | B9-B12 |
| Band range | B1: 0.44–0.51 μm B2: 0.51–0.58 μm B3: 0.62–0.68 μm B4: 0.76–0.87 μm | B5: 1.54–1.70 μm B6: 2.06–2.35 μm | B7: 3.45–3.90 μm B8: 4.76–4.96 μm | B9: 8.05–8.45 μm B10: 8.57–8.93 μm B11: 10.5–11.3 μm B12: 11.4–12.5 μm |
| GSD (m) | 20 | 20 | 40 | 40 |
| SNR | 200 | 150 | - | - |
| NEΔT (K) | - | - | 0.15K@300K | 0.15K@300K |
| MTF | 0.2 | 0.3 | 0.15 | 0.15 |
| Band (Central Wavelength) | 14 July 2019 | 21 December 2019 |
|---|---|---|
| B1 (0.49 μm) | 6.94 % | 11.73% |
| B2 (0.56 μm) | 9.93% | 19.55% |
| B3 (0.66 μm) | 7.89% | 20.99 % |
| B4 (0.81 μm) | 15.64% | 30.44 % |
| B5 (1.66 μm) | 11.64% | 37.15% |
| B6 (2.21 μm) | 15.15% | 37.31% |
| B7 (3.68 μm) | 9.58% | 22.28% |
| B8 (4.86 μm) | 16.49% | 16.61% |
| B9 (8.19 μm) | 5.57% | 7.27% |
| B10 (8.66 μm) | 6.69% | 6.78% |
| B11 (10.89 μm) | 7.72 % | 10.19% |
| B12 (11.88 μm) | 3.35% | 11.47% |
| Typical Point | Imaging Time | Relative Deviation | |||||
|---|---|---|---|---|---|---|---|
| B1 | B2 | B3 | B4 | B5 | B6 | ||
| P1 | 14 July 2019 | −3.00% | 0.15% | 2.08% | −5.97% | 18.37% | 17.57% |
| 21 December 2019 | −2.49% | −1.27% | 0.46% | −6.30% | 20.92% | 21.36% | |
| P2 | 14 July 2019 | −4.17% | −2.78% | −2.70% | −5.19% | 11.90% | 12.23% |
| 21 December 2019 | −1.99% | 0.24% | 2.30% | 0.22% | 35.85% | 31.89% | |
| P3 | 14 July 2019 | −2.95% | −0.52% | 1.66% | −3.07% | −3.34% | 4.75% |
| 21 December 2019 | −4.50% | −9.31% | −12.46% | −15.90% | −150.20% | −156.96% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, X.; Zhao, H.; Jia, G.; Li, J. Atmosphere and Terrain Coupling Simulation Framework for High-Resolution Visible-Thermal Spectral Imaging over Heterogeneous Land Surface. Remote Sens. 2022, 14, 2043. https://doi.org/10.3390/rs14092043
Qiu X, Zhao H, Jia G, Li J. Atmosphere and Terrain Coupling Simulation Framework for High-Resolution Visible-Thermal Spectral Imaging over Heterogeneous Land Surface. Remote Sensing. 2022; 14(9):2043. https://doi.org/10.3390/rs14092043
Chicago/Turabian StyleQiu, Xianfei, Huijie Zhao, Guorui Jia, and Jiyuan Li. 2022. "Atmosphere and Terrain Coupling Simulation Framework for High-Resolution Visible-Thermal Spectral Imaging over Heterogeneous Land Surface" Remote Sensing 14, no. 9: 2043. https://doi.org/10.3390/rs14092043
APA StyleQiu, X., Zhao, H., Jia, G., & Li, J. (2022). Atmosphere and Terrain Coupling Simulation Framework for High-Resolution Visible-Thermal Spectral Imaging over Heterogeneous Land Surface. Remote Sensing, 14(9), 2043. https://doi.org/10.3390/rs14092043







