Estimation of Daily and Instantaneous Near-Surface Air Temperature from MODIS Data Using Machine Learning Methods in the Jingjinji Area of China
Abstract
:1. Introduction
- Statistical methods such as linear regression models are commonly used to explore the relationship between Ta and other variables [35,36,37,38,39]. Cresswell et al. [40] estimated instantaneous Ta through a multiple regression model; the model used Solar Zenith Angle (SZA) as the only auxiliary variable and achieved an accuracy of mean deviation less than 3 °C for over 70% of the cases. Chen et al. [27] retrieved monthly average temperature (RMSE between 1.29 and 1.45 °C) and eight-day average temperature (RMSE between 0.8 and 1.29 °C) for China in 2010 using a model based on remote sensing data and a geographically weighted regression (GWR) algorithm; the elevation was the only secondary auxiliary variable; the results show that the GWR method performs better than the multiple linear regression method and the regression Kriging method.
- The temperature–vegetation index (TVX) method is based on the characteristics of plant canopy temperature that is close to the Ta; this method can be used to calculate the Ta by the relationship between a vegetation index and LST and has also been widely used [31,41,42]. The TVX method was tested in many areas of the world; the resulting RMSE was between 1–3 °C [41,42,43,44,45]. Due to the principle of the method, the TVX method is more suitable for areas with more vegetation coverage. The TVX method shows significant uncertainties while applied to the area with sparse vegetation [43].
- The energy balance method based on the surface heat flux balance equation, incoming net radiation flux, and anthropogenic heat fluxes equals the sum of outgoing land surface heat flux (sensible and latent heat flux) [46,47,48]. Zaksek et al. [49] carried out an estimation of Ta in Slovenia and Germany using the energy balance method, having the root mean square deviation (RMSD) of the results at 2 °C. The method can well describe the physical mechanism of the near-surface energy balance process [50]. The main drawback of the method is that many environmental data (usually in hourly intervals) were needed to force the model and not all data were easy to obtain, especially in a large scale [48].
- Machine learning (ML) methods (such as neural networks, decision trees, support vector machine) are based on nonlinear machine learning algorithms. ML methods greatly improve the computational efficiency and simplify the exploration process of nonlinear and highly interactive relationships compared with the traditional statistical method, the TVX method, and the energy balance method [51,52,53].
2. Study Area and Data
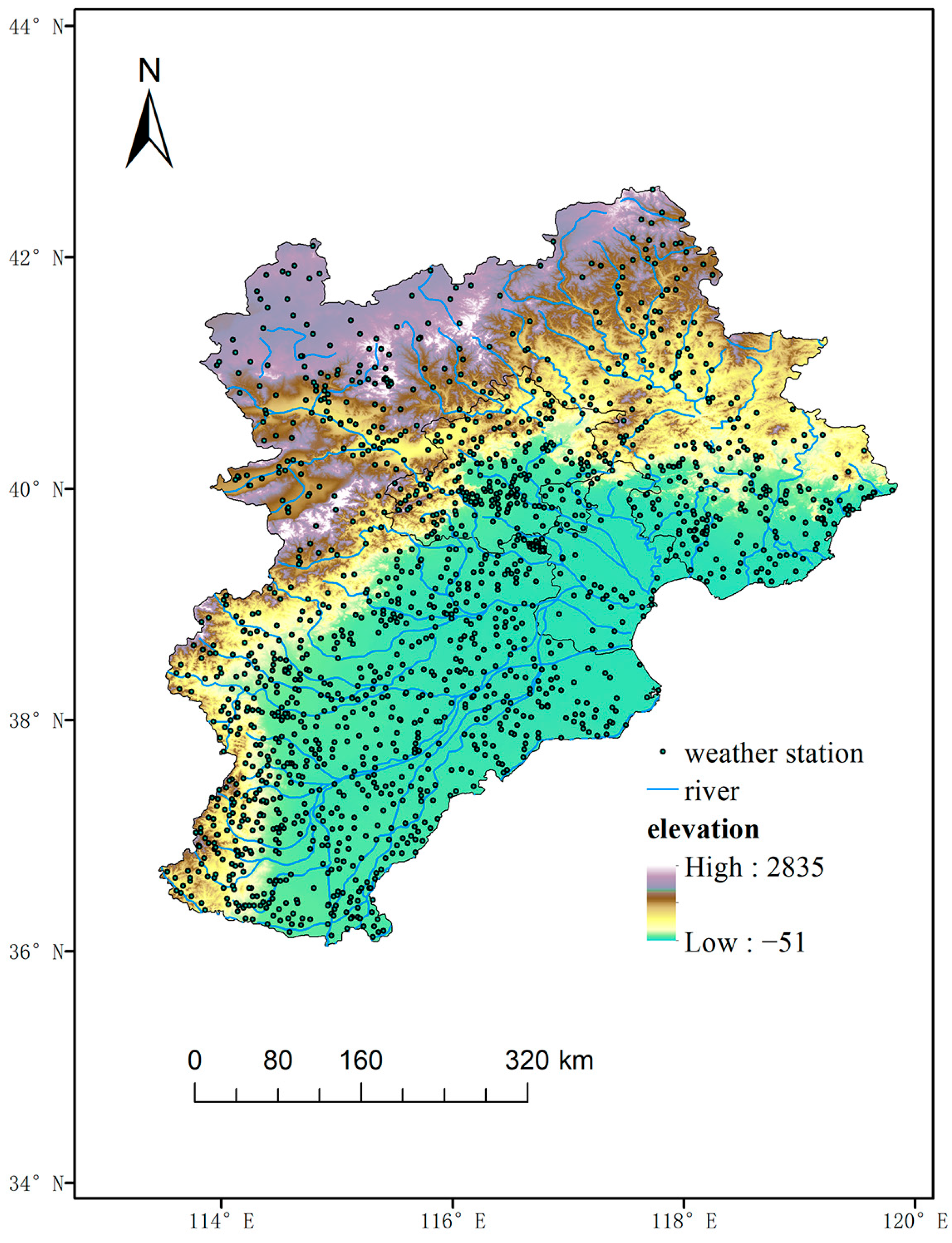
2.1. Study Area
2.2. Ground-Based Weather Data
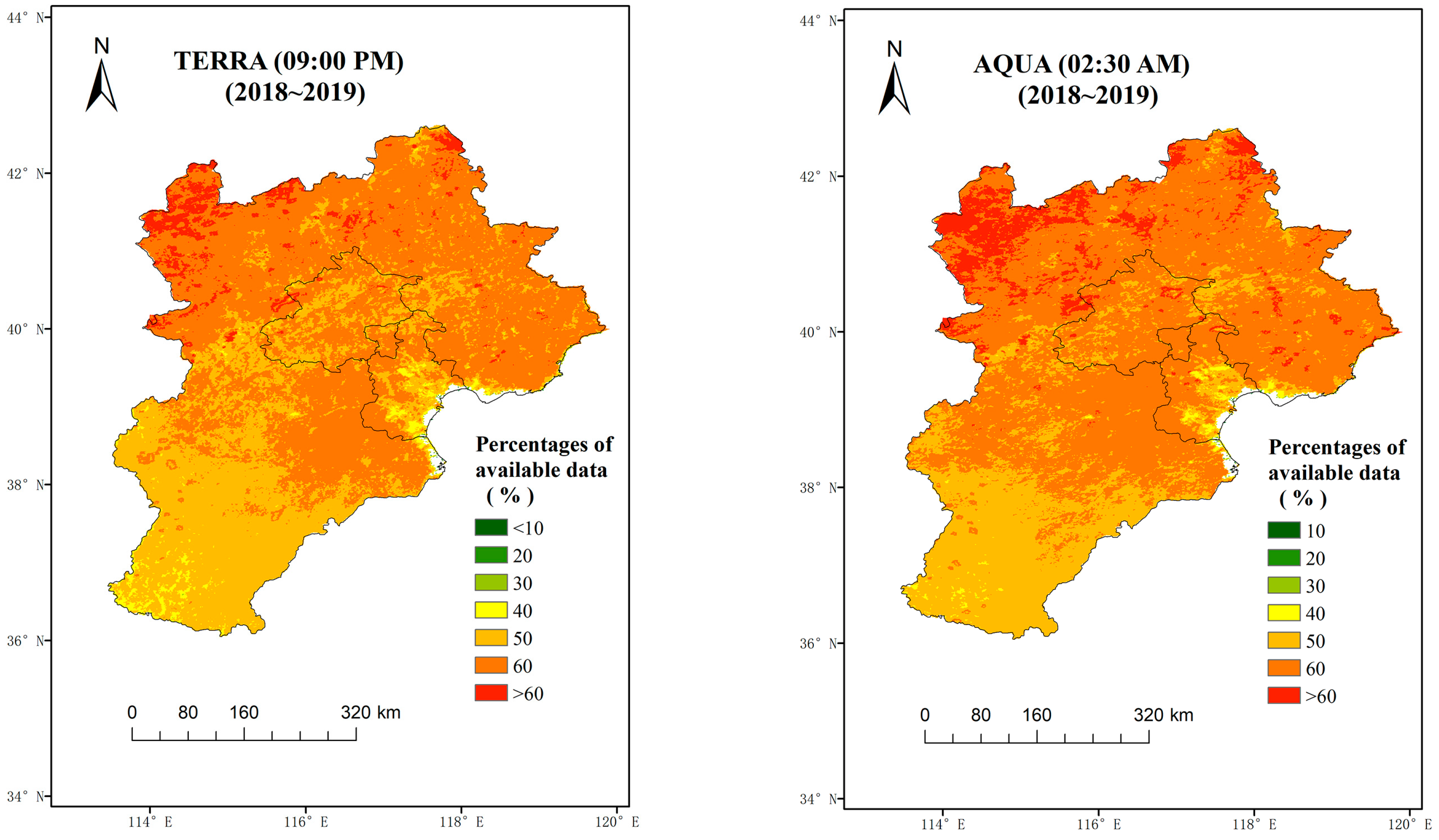
2.3. Remotely Sensed Data
3. Methods
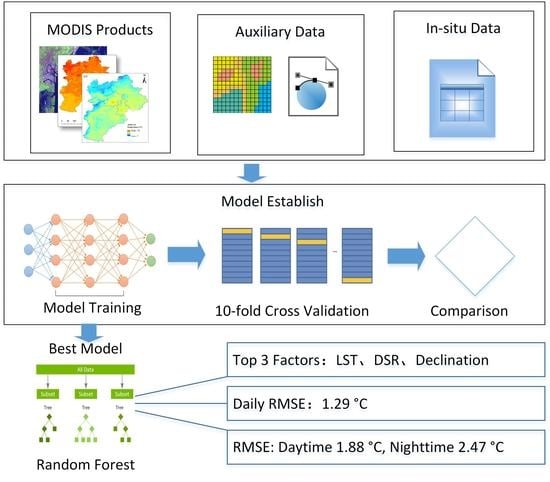
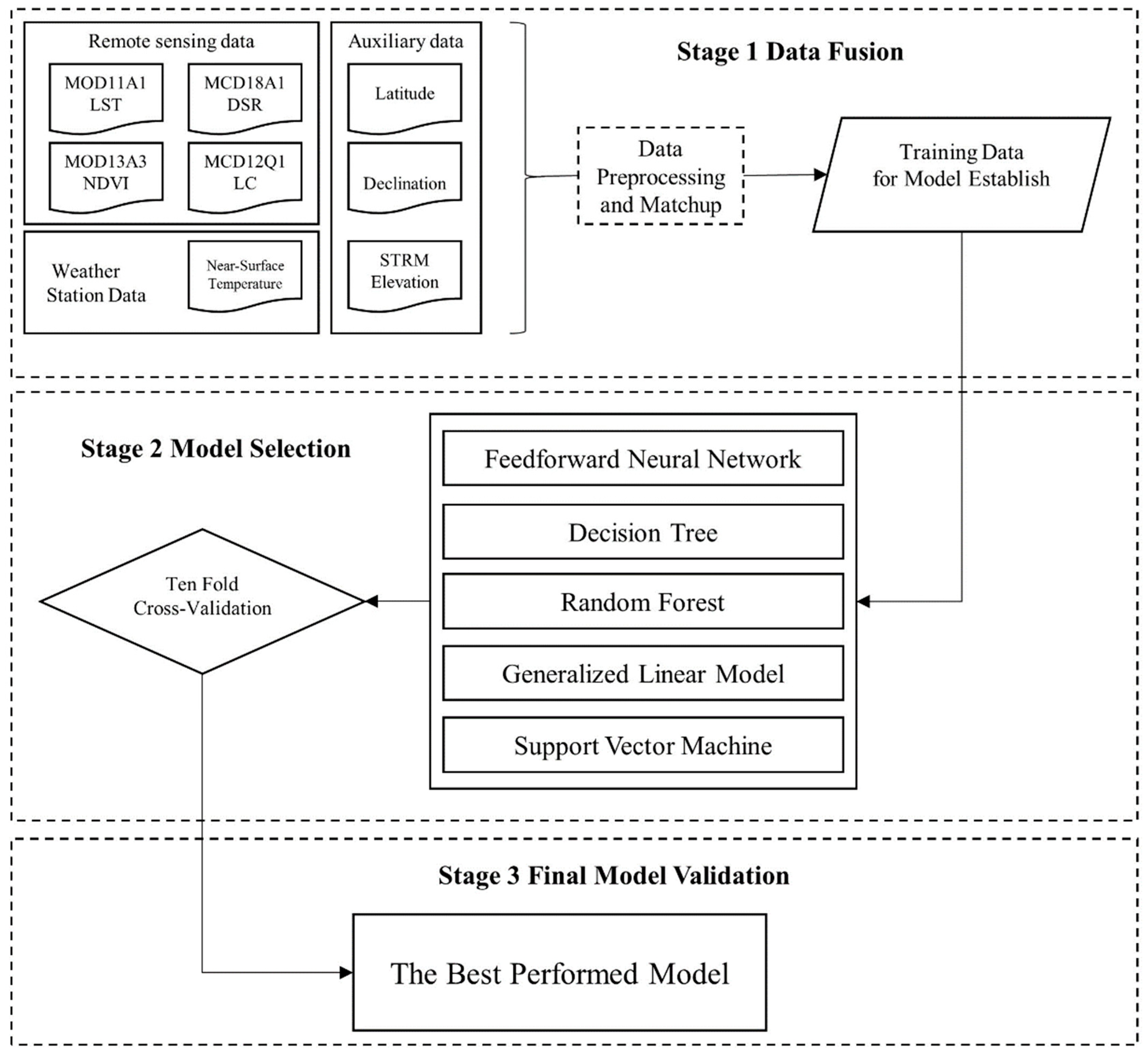
3.1. Variable Selection and Research Framework
3.2. Models
3.2.1. Feedforward Neural Network
3.2.2. Decision Tree
3.2.3. Random Forest
3.2.4. Generalized Linear Model
3.3. Variable Importance Analysis
3.4. Model Training and Validation
4. Results
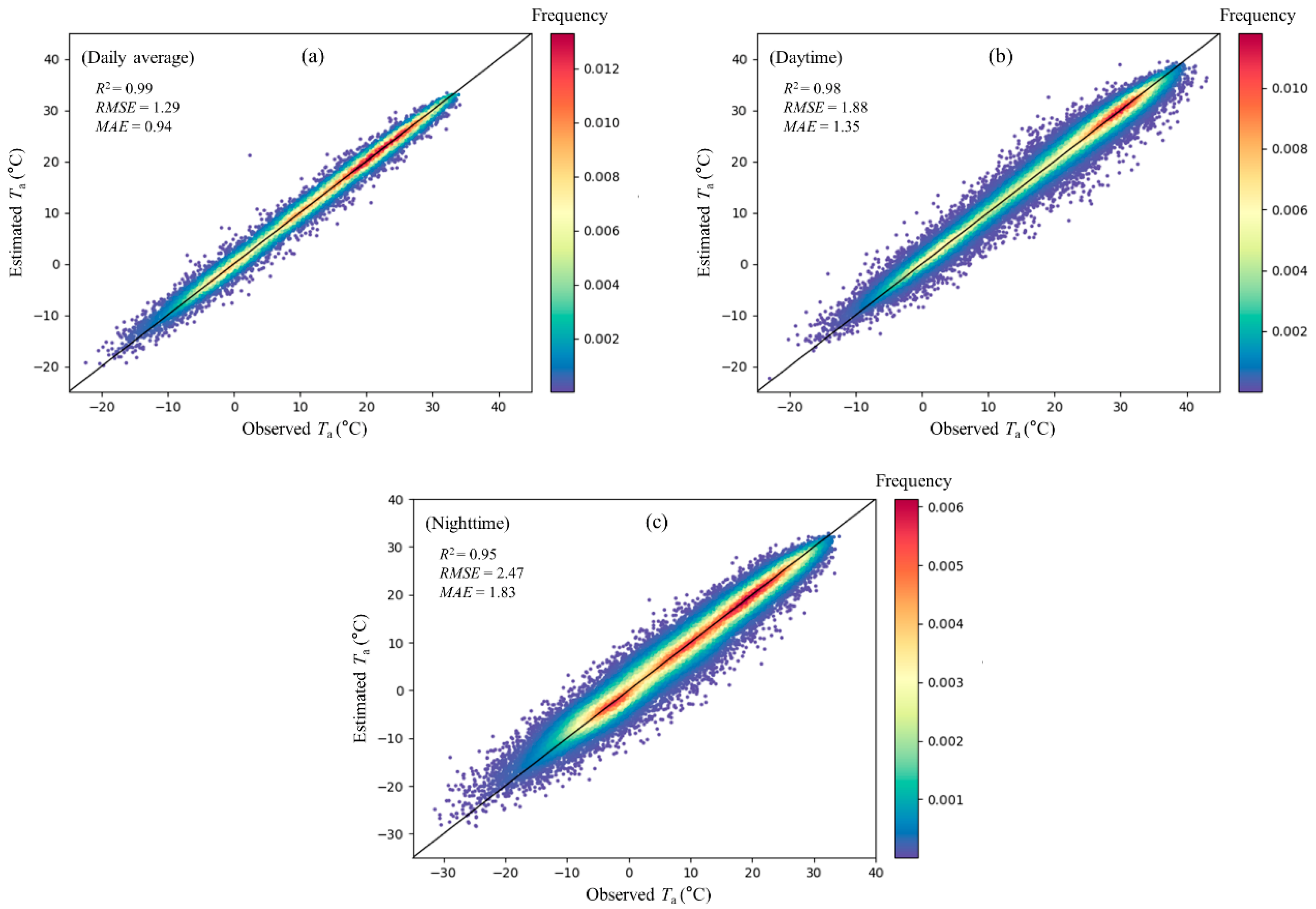
4.1. Comparison of Results of Different Models
4.2. Analysis of the Importance of Model Variables
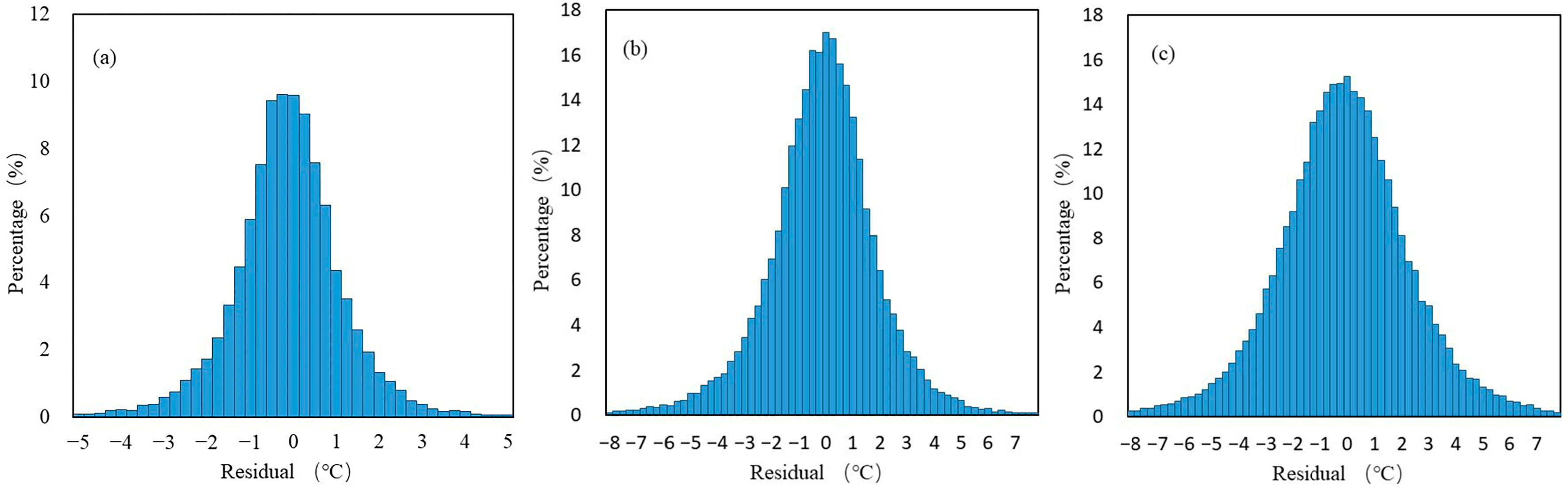
4.3. Evaluation of Random Forest Performance
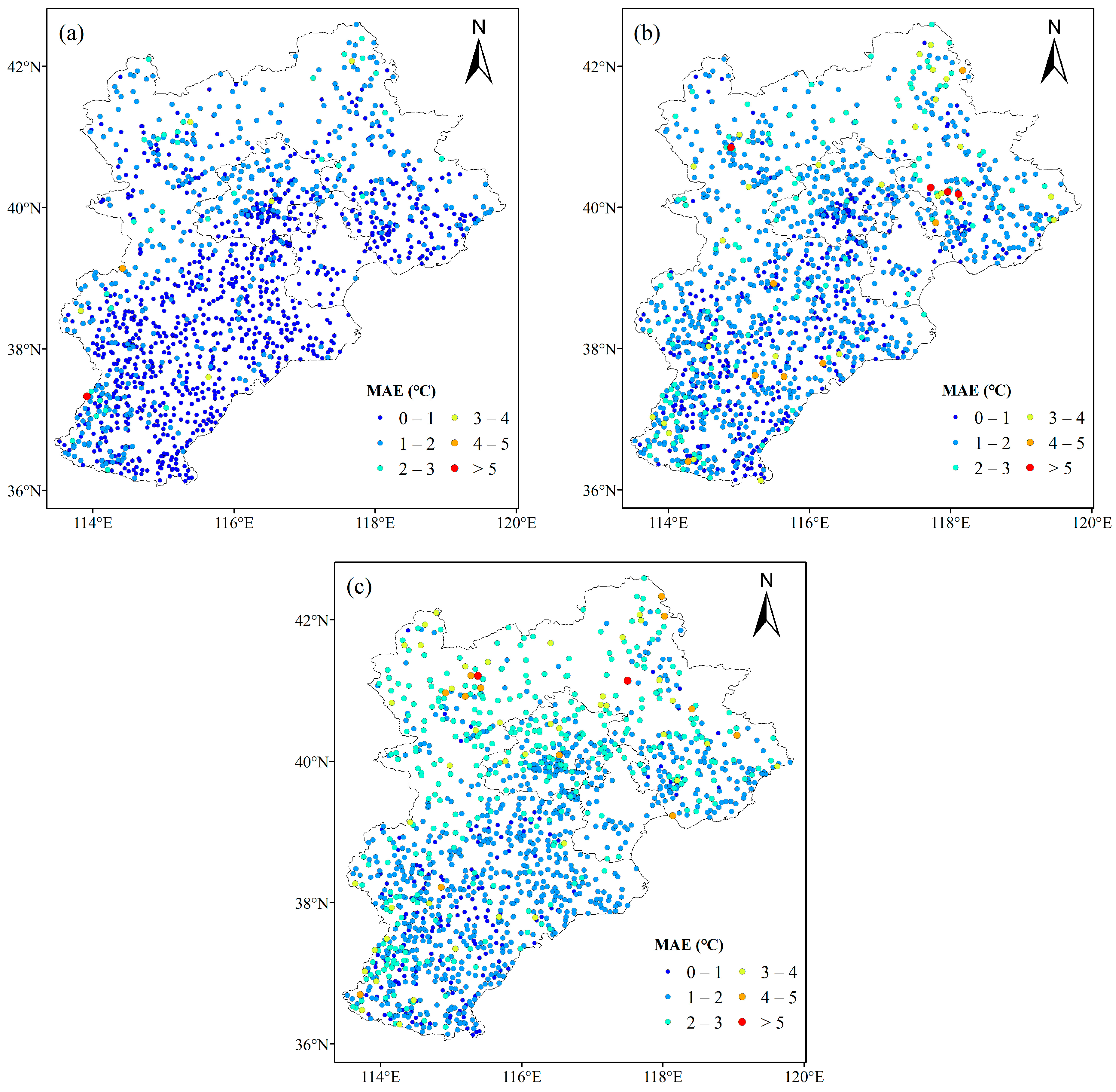
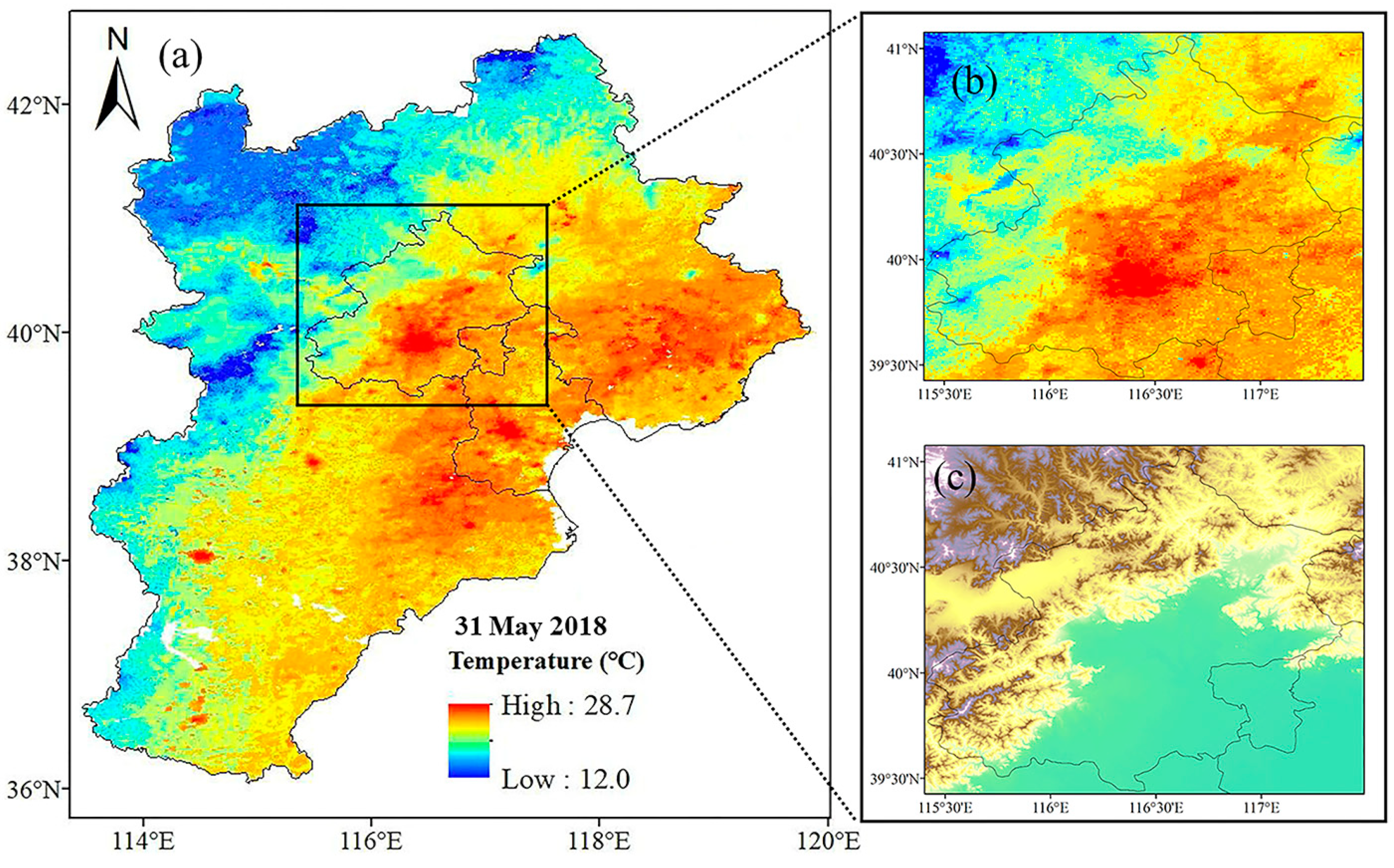
4.4. Spatial Distribution of Ta
5. Discussion
5.1. The Performance of RF Model
5.2. Comparison with Recent Studies
5.3. The Importance of Model Variables
5.4. Limitations and Future Perspectives
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Katsouyanni, K.; Pantazopoulou, A.; Touloumi, G.; Tselepidaki, I.; Moustris, K.; Asimakopoulos, D.; Poulopoulou, G.; Trichopoulos, D. Evidence for interaction between air pollution and high temperature in the causation of excess mortality. Arch. Environ. Health Int. J. 1993, 48, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Harvell, C.D.; Mitchell, C.E.; Ward, J.R.; Altizer, S.; Dobson, A.P.; Ostfeld, R.S.; Samuel, M.D. Climate warming and disease risks for terrestrial and marine biota. Science 2002, 296, 2158–2162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koken, P.J.; Piver, W.T.; Ye, F.; Elixhauser, A.; Olsen, L.M.; Portier, C.J. Temperature, air pollution, and hospitalization for cardiovascular diseases among elderly people in Denver. Environ. Health Perspect. 2003, 111, 1312–1317. [Google Scholar] [CrossRef] [PubMed]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Lofgren, B.M.; Hunter, T.S.; Wilbarger, J. Effects of using air temperature as a proxy for potential evapotranspiration in climate change scenarios of Great Lakes basin hydrology. J. Great Lakes Res. 2011, 37, 744–752. [Google Scholar] [CrossRef]
- Izady, A.; Davary, K.; Alizadeh, A.; Ziaei, A.; Akhavan, S.; Alipoor, A.; Joodavi, A.; Brusseau, M. Groundwater conceptualization and modeling using distributed SWAT-based recharge for the semi-arid agricultural Neishaboor plain, Iran. Hydrogeol. J. 2015, 23, 47–68. [Google Scholar]
- Smith, W.; Leslie, L.; Diak, G.; Goodman, B.; Velden, C.; Callan, G.; Raymond, W.; Wade, G. The integration of meteorological satellite imagery and numerical dynamical forecast models. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1988, 324, 317–323. [Google Scholar]
- Willmott, C.J.; Robeson, S.M. Climatologically aided interpolation (CAI) of terrestrial air temperature. Int. J. Climatol. 1995, 15, 221–229. [Google Scholar] [CrossRef]
- Prince, S.; Goetz, S.; Dubayah, R.; Czajkowski, K.; Thawley, M. Inference of surface and air temperature, atmospheric precipitable water and vapor pressure deficit using Advanced Very High-Resolution Radiometer satellite observations: Comparison with field observations. J. Hydrol. 1998, 212, 230–249. [Google Scholar] [CrossRef]
- Robeson, S.M. Relationships between mean and standard deviation of air temperature: Implications for global warming. Clim. Res. 2002, 22, 205–213. [Google Scholar] [CrossRef]
- Xu, Z.; Etzel, R.A.; Su, H.; Huang, C.; Guo, Y.; Tong, S. Impact of ambient temperature on children’s health: A systematic review. Environ. Res. 2012, 117, 120–131. [Google Scholar] [PubMed] [Green Version]
- Li, L.; Zha, Y. Satellite-based regional warming hiatus in China and its implication. Sci. Total Environ. 2019, 648, 1394–1402. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zha, Y. Satellite-based spatiotemporal trends of canopy urban heat islands and associated drivers in China’s 32 major cities. Remote Sens. 2019, 11, 102. [Google Scholar] [CrossRef] [Green Version]
- Muller, C.L.; Chapman, L.; Grimmond, C.; Young, D.T.; Cai, X. Sensors and the city: A review of urban meteorological networks. Int. J. Climatol. 2013, 33, 1585–1600. [Google Scholar] [CrossRef]
- Yan, H.; Fan, S.; Guo, C.; Wu, F.; Zhang, N.; Dong, L. Assessing the effects of landscape design parameters on intra-urban air temperature variability: The case of Beijing, China. Build. Environ. 2014, 76, 44–53. [Google Scholar] [CrossRef]
- Pepin, N.; Fowler, H.; Greenwood, G.; Hashmi, M.; Liu, X. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Chang. 2015, 5, 424–430. [Google Scholar]
- Rao, Y.; Liang, S.; Yu, Y. Land surface air temperature data are considerably different among BEST-LAND, CRU-TEM4v, NASA-GISS, and NOAA-NCEI. J. Geophys. Res. Atmos. 2018, 123, 5881–5900. [Google Scholar] [CrossRef]
- Boyer, D.G. Estimation of Daily Temperature Means Using Elevation and Latitude in Mountainous Terrain 1. JAWRA J. Am. Water Resour. Assoc. 1984, 20, 583–588. [Google Scholar] [CrossRef]
- De Beurs, K. Evaluation of Spatial Interpolation Techniques for Climate Variables: Case Study of Jalisco, Mexico. Master’s Thesis, Wageningen Agricultural University, Wageningen, The Netherlands, 1998. [Google Scholar]
- Ishida, T.; Kawashima, S. Use of cokriging to estimate surface air temperature from elevation. Theor. Appl. Climatol. 1993, 47, 147–157. [Google Scholar] [CrossRef]
- Hudson, G.; Wackernagel, H. Mapping temperature using kriging with external drift: Theory and an example from Scotland. Int. J. Climatol. 1994, 14, 77–91. [Google Scholar] [CrossRef]
- Monestiez, P.; Courault, D.; Allard, D.; Ruget, F. Spatial interpolation of air temperature using environmental context: Application to a crop model. Environ. Ecol. Stat. 2001, 8, 297–309. [Google Scholar] [CrossRef]
- Stahl, K.; Moore, R.; Floyer, J.; Asplin, M.; McKendry, I. Comparison of approaches for spatial interpolation of daily air temperature in a large region with complex topography and highly variable station density. Agric. For. Meteorol. 2006, 139, 224–236. [Google Scholar] [CrossRef]
- Wu, T.; Li, Y. Spatial interpolation of temperature in the United States using residual kriging. Appl. Geogr. 2013, 44, 112–120. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Nanni, T.; Simolo, C.; Spinoni, J. High-resolution temperature climatology for Italy: Interpolation method intercomparison. Int. J. Climatol. 2014, 34, 1278–1296. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.M.; Saz-Sánchez, M.A.; Cuadrat, J.M. Comparative analysis of interpolation methods in the middle Ebro Valley (Spain): Application to annual precipitation and temperature. Clim. Res. 2003, 24, 161–180. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Liu, Y.; Liu, Q.; Qin, F. A statistical method based on remote sensing for the estimation of air temperature in China. Int. J. Climatol. 2015, 35, 2131–2143. [Google Scholar] [CrossRef]
- Sun, Y.-J.; Wang, J.-F.; Zhang, R.-H.; Gillies, R.; Xue, Y.; Bo, Y.-C. Air temperature retrieval from remote sensing data based on thermodynamics. Theor. Appl. Climatol. 2005, 80, 37–48. [Google Scholar] [CrossRef]
- Hachem, S.; Duguay, C.; Allard, M. Comparison of MODIS-derived land surface temperatures with ground surface and air temperature measurements in continuous permafrost terrain. Cryosphere 2012, 6, 51–69. [Google Scholar] [CrossRef] [Green Version]
- Kloog, I.; Chudnovsky, A.; Koutrakis, P.; Schwartz, J. Temporal and spatial assessments of minimum air temperature using satellite surface temperature measurements in Massachusetts, USA. Sci. Total Environ. 2012, 432, 85–92. [Google Scholar] [CrossRef] [Green Version]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Good, E. Daily minimum and maximum surface air temperatures from geostationary satellite data. J. Geophys. Res. Atmos. 2015, 120, 2306–2324. [Google Scholar] [CrossRef]
- An, S.; Zhu, X.; Shen, M.; Wang, Y.; Cao, R.; Chen, X.; Yang, W.; Chen, J.; Tang, Y. Mismatch in elevational shifts between satellite observed vegetation greenness and temperature isolines during 2000–2016 on the Tibetan Plateau. Glob. Chang. Biol. 2018, 24, 5411–5425. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Mostovoy, G.V.; King, R.L.; Reddy, K.R.; Kakani, V.G.; Filippova, M.G. Statistical estimation of daily maximum and minimum air temperatures from MODIS LST data over the state of Mississippi. GIScience Remote Sens. 2006, 43, 78–110. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Huang, Y.; Yu, Y.; Sun, W. Empirical models for estimating daily maximum, minimum and mean air temperatures with MODIS land surface temperatures. Int. J. Remote Sens. 2011, 32, 9415–9440. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.; Nunes, J.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Noi, P.T.; Kappas, M.; Degener, J. Estimating daily maximum and minimum land air surface temperature using MODIS land surface temperature data and ground truth data in Northern Vietnam. Remote Sens. 2016, 8, 1002. [Google Scholar] [CrossRef] [Green Version]
- Shi, L.; Liu, P.; Kloog, I.; Lee, M.; Kosheleva, A.; Schwartz, J. Estimating daily air temperature across the Southeastern United States using high-resolution satellite data: A statistical modeling study. Environ. Res. 2016, 146, 51–58. [Google Scholar] [CrossRef] [Green Version]
- Cresswell, M.; Morse, A.; Thomson, M.; Connor, S. Estimating surface air temperatures, from Meteosat land surface temperatures, using an empirical solar zenith angle model. Int. J. Remote Sens. 1999, 20, 1125–1132. [Google Scholar] [CrossRef]
- Nieto, H.; Sandholt, I.; Aguado, I.; Chuvieco, E.; Stisen, S. Air temperature estimation with MSG-SEVIRI data: Calibration and validation of the TVX algorithm for the Iberian Peninsula. Remote Sens. Environ. 2011, 115, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Wloczyk, C.; Borg, E.; Richter, R.; Miegel, K. Estimation of instantaneous air temperature above vegetation and soil surfaces from Landsat 7 ETM+ data in northern Germany. Int. J. Remote Sens. 2011, 32, 9119–9136. [Google Scholar] [CrossRef]
- Czajkowski, K.P.; Goward, S.N.; Stadler, S.J.; Walz, A. Thermal remote sensing of near surface environmental variables: Application over the Oklahoma Mesonet. Prof. Geogr. 2000, 52, 345–357. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sens. Environ. 2007, 110, 262–274. [Google Scholar] [CrossRef]
- Zhu, W.; Lű, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Pape, R.; Löffler, J. Modelling spatio-temporal near-surface temperature variation in high mountain landscapes. Ecol. Model. 2004, 178, 483–501. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Li, K.; Dickerson, R.R.; Pinker, R.T.; Wang, J.; Liu, X.; Sun, L.; Xue, W.; Cribb, M. Full-coverage mapping and spatiotemporal variations of ground-level ozone (O3) pollution from 2013 to 2020 across China. Remote Sens. Environ. 2022, 270, 112775. [Google Scholar] [CrossRef]
- Keramitsoglou, I.; Kiranoudis, C.T.; Sismanidis, P.; Zakšek, K. An online system for nowcasting satellite derived temperatures for urban areas. Remote Sens. 2016, 8, 306. [Google Scholar] [CrossRef] [Green Version]
- Zakšek, K.; Schroedter-Homscheidt, M. Parameterization of air temperature in high temporal and spatial resolution from a combination of the SEVIRI and MODIS instruments. ISPRS J. Photogramm. Remote Sens. 2009, 64, 414–421. [Google Scholar] [CrossRef]
- Moran, M.S.; Kustas, W.P.; Vidal, A.; Stannard, D.I.; Blanford, J.H.; Nichols, W.D. Use of ground-based remotely sensed data for surface energy balance evaluation of a semiarid rangeland. Water Resour. Res. 1994, 30, 1339–1349. [Google Scholar] [CrossRef]
- Emamifar, S.; Rahimikhoob, A.; Noroozi, A.A. Daily mean air temperature estimation from MODIS land surface temperature products based on M5 model tree. Int. J. Climatol. 2013, 33, 3174–3181. [Google Scholar] [CrossRef]
- Noi, P.T.; Degener, J.; Kappas, M. Comparison of multiple linear regression, cubist regression, and random forest algorithms to estimate daily air surface temperature from dynamic combinations of MODIS LST data. Remote Sens. 2017, 9, 398. [Google Scholar] [CrossRef] [Green Version]
- Yao, R.; Wang, L.; Huang, X.; Li, L.; Sun, J.; Wu, X.; Jiang, W. Developing a temporally accurate air temperature dataset for Mainland China. Sci. Total Environ. 2020, 706, 136037. [Google Scholar] [CrossRef] [PubMed]
- Yoo, C.; Im, J.; Park, S.; Quackenbush, L.J. Estimation of daily maximum and minimum air temperatures in urban landscapes using MODIS time series satellite data. ISPRS J. Photogramm. Remote Sens. 2018, 137, 149–162. [Google Scholar] [CrossRef]
- Zhou, B.; Erell, E.; Hough, I.; Rosenblatt, J.; Just, A.C.; Novack, V.; Kloog, I. Estimating near-surface air temperature across Israel using a machine learning based hybrid approach. Int. J. Climatol. 2020, 40, 6106–6121. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Álvarez, M.; Alonso-Sarria, F.; Gomariz-Castillo, F. Interpolation of instantaneous air temperature using geographical and MODIS derived variables with machine learning techniques. ISPRS Int. J. Geo-Inf. 2019, 8, 382. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Knudby, A.; Shen, Y.; Liu, Y. Mapping monthly air temperature in the Tibetan Plateau from MODIS data based on machine learning methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 345–354. [Google Scholar] [CrossRef]
- Hrisko, J.; Ramamurthy, P.; Yu, Y.; Yu, P.; Melecio-Vázquez, D. Urban air temperature model using GOES-16 LST and a diurnal regressive neural network algorithm. Remote Sens. Environ. 2020, 237, 111495. [Google Scholar] [CrossRef]
- Li, L.; Zha, Y. Estimating monthly average temperature by remote sensing in China. Adv. Space Res. 2019, 63, 2345–2357. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Asrar, G.R.; Zhu, Z. Developing a 1 km resolution daily air temperature dataset for urban and surrounding areas in the conterminous United States. Remote Sens. Environ. 2018, 215, 74–84. [Google Scholar] [CrossRef]
- Phan, T.N.; Kappas, M.; Nguyen, K.T.; Tran, T.P.; Tran, Q.V.; Emam, A.R. Evaluation of MODIS land surface temperature products for daily air surface temperature estimation in northwest Vietnam. Int. J. Remote Sens. 2019, 40, 5544–5562. [Google Scholar] [CrossRef]
- Mira, M.; Ninyerola, M.; Batalla, M.; Pesquer, L.; Pons, X. Improving mean minimum and maximum month-to-month air temperature surfaces using satellite-derived land surface temperature. Remote Sens. 2017, 9, 1313. [Google Scholar] [CrossRef] [Green Version]
- Golkar, F.; Sabziparvar, A.A.; Khanbilvardi, R.; Nazemosadat, M.J.; Zand-Parsa, S.; Rezaei, Y. Estimation of instantaneous air temperature using remote sensing data. Int. J. Remote Sens. 2018, 39, 258–275. [Google Scholar] [CrossRef]
- Chen, P.; Chen, Z.; Yang, X.; Li, B.; Zhang, B. High-resolution land-use mapping in Beijing-Tianjin-Hebei region based on convolutional neural network. In Proceedings of the China High Resolution Earth Observation Conference, Chengdu, China, 1 September 2019; Springer: Singapore, 2019; pp. 213–222. [Google Scholar]
- Bavarian, B. Introduction to neural networks for intelligent control. IEEE Control Syst. Mag. 1988, 8, 3–7. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Nelder, J.A.; Wedderburn, R.W. Generalized linear models. J. R. Stat. Soc. Ser. A 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Saunders, C. Support Vector Machine. Comput. Sci. 2002, 1, 1–28. [Google Scholar]
- Raeesi, M.; Mesgari, M.; Mahmoudi, P. Traffic time series forecasting by feedforward neural network: A case study based on traffic data of Monroe. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 219. [Google Scholar] [CrossRef] [Green Version]
- Tran, D.; Tan, Y.K. Sensorless illumination control of a networked LED-lighting system using feedforward neural network. IEEE Trans. Ind. Electron. 2013, 61, 2113–2121. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X.; Shi, H.; Cui, J.; Wang, W.; Ma, H.; Chen, N. Modeling salinized wasteland using remote sensing with the integration of decision tree and multiple validation approaches in Hetao irrigation district of China. CATENA 2022, 209, 105854. [Google Scholar] [CrossRef]
- Vieira, R.M.d.S.P.; Tomasella, J.; Barbosa, A.A.; Polizel, S.P.; Ometto, J.P.H.B.; Santos, F.C.; da Cruz Ferreira, Y.; de Toledo, P.M. Land degradation mapping in the MATOPIBA region (Brazil) using remote sensing data and decision-tree analysis. Sci. Total Environ. 2021, 782, 146900. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Skinner, K.R.; Montgomery, D.C.; Runger, G.C. Process monitoring for multiple count data using generalized linear model-based control charts. Int. J. Prod. Res. 2003, 41, 1167–1180. [Google Scholar] [CrossRef]
- Sahani, N.; Ghosh, T. GIS-based spatial prediction of recreational trail susceptibility in protected area of Sikkim Himalaya using logistic regression, decision tree and random forest model. Ecol. Inform. 2021, 64, 101352. [Google Scholar] [CrossRef]
- Han, H.; Guo, X.; Yu, H. Variable selection using mean decrease accuracy and mean decrease gini based on random forest. In Proceedings of the 2016 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 26–28 August 2016; pp. 219–224. [Google Scholar]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar] [CrossRef]
- Xu, Y.; Knudby, A.; Ho, H.C. Estimating daily maximum air temperature from MODIS in British Columbia, Canada. Int. J. Remote Sens. 2014, 35, 8108–8121. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F.; Ye, M.; Che, T.; Zhang, G. Estimating daily air temperatures over the Tibetan Plateau by dynamically integrating MODIS LST data. J. Geophys. Res. Atmos. 2016, 121, 11425–11441. [Google Scholar] [CrossRef] [Green Version]
- Cao, Q.; Luan, Q.; Liu, Y.; Wang, R. The effects of 2D and 3D building morphology on urban environments: A multi-scale analysis in the Beijing metropolitan region. Build. Environ. 2021, 192, 107635. [Google Scholar] [CrossRef]
- Khesali, E.; Mobasheri, M. A method in near-surface estimation of air temperature (NEAT) in times following the satellite passing time using MODIS images. Adv. Space Res. 2020, 65, 2339–2347. [Google Scholar] [CrossRef]
- Zhao, P.; Xiao, H.; Liu, C.; Zhou, Y.; Xu, X.; Hao, K. Evaluating a simple proxy for climatic cloud-to-ground lightning in Sichuan Province with complex terrain, Southwest China. Int. J. Climatol. 2021. [Google Scholar] [CrossRef]
- Colombi, A.; De Michele, C.; Pepe, M.; Rampini, A.; Michele, C.D. Estimation of daily mean air temperature from MODIS LST in Alpine areas. EARSeL Eproceedings 2007, 6, 38–46. [Google Scholar]
- Sun, D.; Kafatos, M. Note on the NDVI-LST relationship and the use of temperature-related drought indices over North America. Geophys. Res. Lett. 2007, 34, L24406. [Google Scholar] [CrossRef] [Green Version]
- Crosson, W.L.; Al-Hamdan, M.Z.; Hemmings, S.N.; Wade, G.M. A daily merged MODIS Aqua–Terra land surface temperature data set for the conterminous United States. Remote Sens. Environ. 2012, 119, 315–324. [Google Scholar] [CrossRef]
- Kloog, I.; Nordio, F.; Coull, B.A.; Schwartz, J. Predicting spatiotemporal mean air temperature using MODIS satellite surface temperature measurements across the Northeastern USA. Remote Sens. Environ. 2014, 150, 132–139. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, C.; Huang, J.; Zhu, D.; Wang, L.; Liu, J. Mapping of daily mean air temperature in agricultural regions using daytime and nighttime land surface temperatures derived from TERRA and AQUA MODIS data. Remote Sens. 2015, 7, 8728–8756. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Jiang, Y.; Li, T.; Cheng, Q.; Zeng, C.; Zhang, L. Deep learning-based air temperature mapping by fusing remote sensing, station, simulation and socioeconomic data. Remote Sens. Environ. 2020, 240, 111692. [Google Scholar] [CrossRef] [Green Version]
- Rao, Y.; Liang, S.; Wang, D.; Yu, Y.; Song, Z.; Zhou, Y.; Shen, M.; Xu, B. Estimating daily average surface air temperature using satellite land surface temperature and top-of-atmosphere radiation products over the Tibetan Plateau. Remote Sens. Environ. 2019, 234, 111462. [Google Scholar] [CrossRef]
- Park, S. Integration of satellite-measured LST data into cokriging for temperature estimation on tropical and temperate islands. Int. J. Climatol. 2011, 31, 1653–1664. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Quan, J.; Zhan, W.; Guo, Z. Enhanced statistical estimation of air temperature incorporating nighttime light data. Remote Sens. 2016, 8, 656. [Google Scholar] [CrossRef] [Green Version]
- Janatian, N.; Sadeghi, M.; Sanaeinejad, S.H.; Bakhshian, E.; Farid, A.; Hasheminia, S.M.; Ghazanfari, S. A statistical framework for estimating air temperature using MODIS land surface temperature data. Int. J. Climatol. 2017, 37, 1181–1194. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Cai, W.H.; Yang, J. Evaluation of MODIS land surface temperature data to estimate near-surface air temperature in Northeast China. Remote Sens. 2017, 9, 410. [Google Scholar] [CrossRef] [Green Version]
- Zeng, L.; Wardlow, B.D.; Tadesse, T.; Shan, J.; Hayes, M.J.; Li, D.; Xiang, D. Estimation of daily air temperature based on MODIS land surface temperature products over the corn belt in the US. Remote Sens. 2015, 7, 951–970. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Xiao, H.; Liu, C.; Zhou, Y. Dependence of Warm Season Cloud-to-Ground Lightning Polarity on Environmental Conditions over Sichuan, Southwest China. Adv. Meteorol. 2021, 2021, 1500470. [Google Scholar] [CrossRef]
- Zhao, P.; Xiao, H.; Liu, J.; Zhou, Y. Precipitation efficiency of cloud and its influencing factors over the Tibetan plateau. Int. J. Climatol. 2022, 42, 416–434. [Google Scholar] [CrossRef]



| Variable | Dataset/MODIS Product Number | Resolution | Data Source |
|---|---|---|---|
| Elevation | STRM | 1 km/Unique | www.resdc.cn (accessed on 15 February 2020) |
| LST | MOD11A1/MYD11A1 | 1 km/Daily | NASA LP DAAC (accessed on 5 April 2020) |
| DSR | MCD18A1 | 5.6 km/Daily | NASA LP DAAC (accessed on 5 April 2020) |
| NDVI | MOD13A3 | 1 km/Monthly | NASA LP DAAC (accessed on 5 April 2020) |
| LC | MCD12Q1 | 0.5 km/Yearly | NASA LP DAAC (accessed on 5 April 2020) |
| Scenarios | Model Input Variables |
|---|---|
| Daily average | LAT, ELEVATION, DECLINATION, NDVI, LC, DSR (Daily average), LST (Daily average) |
| Daytime instantaneous | LAT, ELEVATION, DECLINATION, NDVI, LC, DSR, LST (Daytime instantaneous) |
| Nighttime instantaneous | LAT, ELEVATION, DECLINATION, NDVI, LC, LST (Nighttime instantaneous) |
| Scenarios | Model | Model Fitting | Model Validation | ||||
|---|---|---|---|---|---|---|---|
| MAE (°C) | RMSE (°C) | R2 | MAE (°C) | RMSE (°C) | R2 | ||
| Daily average | FNN | 1.29 | 1.66 | 0.98 | 1.29 | 1.66 | 0.98 |
| DT | 0.67 | 0.88 | 0.99 | 1.17 | 1.66 | 0.98 | |
| RF | 0.48 | 0.71 | 0.99 | 0.94 | 1.29 | 0.99 | |
| GLM | 1.54 | 1.97 | 0.97 | 1.53 | 1.97 | 0.97 | |
| SVM | 0.96 | 1.22 | 0.99 | 1.07 | 1.41 | 0.98 | |
| Daytime instantaneous | FNN | 2.02 | 2.63 | 0.95 | 2.02 | 2.63 | 0.95 |
| DT | 1.05 | 1.4 | 0.99 | 1.63 | 2.35 | 0.96 | |
| RF | 0.69 | 1.04 | 0.99 | 1.35 | 1.88 | 0.98 | |
| GLM | 2.84 | 3.59 | 0.91 | 2.84 | 3.58 | 0.91 | |
| SVM | 1.79 | 2.37 | 0.96 | 1.84 | 2.44 | 0.96 | |
| Nighttime instantaneous | FNN | 2.21 | 2.93 | 0.94 | 2.21 | 2.93 | 0.94 |
| DT | 1.32 | 1.74 | 0.98 | 2.14 | 2.97 | 0.94 | |
| RF | 0.98 | 1.42 | 0.99 | 1.83 | 2.47 | 0.95 | |
| GLM | 2.32 | 3.08 | 0.93 | 2.31 | 3.08 | 0.93 | |
| SVM | 2.06 | 2.79 | 0.94 | 2.08 | 2.83 | 0.94 | |
| Variables | Daily Average | Daytime Instantaneous | Nighttime Instantaneous | |||
|---|---|---|---|---|---|---|
| IncMSE (°C) | Weight (%) | IncMSE (°C) | Weight (%) | IncMSE (°C) | Weight (%) | |
| LAT | 2.34 | 12.55 | 2.09 | 7.14 | 3.72 | 21.10 |
| ELEVATION | 0.12 | 0.67 | 0.43 | 1.45 | 0.27 | 1.52 |
| LC | 0.04 | 0.23 | 0.35 | 1.18 | 1.42 | 8.03 |
| DECLINATION | 2.23 | 11.93 | 5.89 | 20.07 | 4.86 | 27.58 |
| NDVI | 0.26 | 1.40 | 1.66 | 5.67 | 0.49 | 2.77 |
| DSR | 1.24 | 6.63 | 4.38 | 14.93 | - | - |
| LST | 12.43 | 66.60 | 14.54 | 49.57 | 6.88 | 39.00 |
| Terrain | Plains (Elevation < 260 m) | Mountainous Area | Urban Area | Rural Area | |
|---|---|---|---|---|---|
| Daily average | MAE (°C) | 0.79 | 1.24 | 0.83 | 0.97 |
| RMSE (°C) | 1.07 | 1.66 | 1.12 | 1.34 | |
| R2 | 0.99 | 0.98 | 0.99 | 0.99 | |
| MD (°C) | 9.04 | 8.08 | 8.9 | 8.98 | |
| SD (°C) | 10.52 | 10.28 | 10.35 | 10.47 | |
| Daytime instantaneous | MAE (°C) | 1.19 | 1.70 | 1.19 | 1.42 |
| RMSE (°C) | 1.67 | 2.27 | 1.67 | 1.96 | |
| R2 | 0.98 | 0.97 | 0.98 | 0.97 | |
| MD (°C) | 9.92 | 9.94 | 10.04 | 9.89 | |
| SD (°C) | 11.45 | 11.44 | 11.56 | 11.41 | |
| Nighttime instantaneous | MAE (°C) | 1.69 | 2.20 | 1.75 | 1.87 |
| RMSE (°C) | 2.26 | 2.94 | 2.33 | 2.54 | |
| R2 | 0.96 | 0.94 | 0.96 | 0.95 | |
| MD (°C) | 9.01 | 8.95 | 9.03 | 8.98 | |
| SD (°C) | 10.51 | 10.49 | 10.51 | 10.5 | |
| Season | Spring | Summer | Autumn | Winter | |
|---|---|---|---|---|---|
| Daily average | MAE (°C) | 0.93 | 0.81 | 0.93 | 1.06 |
| RMSE (°C) | 1.32 | 1.11 | 1.25 | 1.43 | |
| R2 | 0.96 | 0.91 | 0.98 | 0.91 | |
| MD (°C) | 4.97 | 2.08 | 5.79 | 2.42 | |
| SD (°C) | 6.01 | 2.45 | 6.80 | 2.96 | |
| Daytime instantaneous | MAE (°C) | 1.61 | 1.35 | 1.25 | 1.19 |
| RMSE (°C) | 2.21 | 1.84 | 1.72 | 1.67 | |
| R2 | 0.92 | 0.77 | 0.96 | 0.90 | |
| MD (°C) | 5.65 | 2.25 | 6.76 | 3.36 | |
| SD (°C) | 6.75 | 2.8 | 8.01 | 4.14 | |
| Nighttime instantaneous | MAE (°C) | 2.02 | 1.48 | 1.76 | 1.98 |
| RMSE (°C) | 2.72 | 1.99 | 2.39 | 2.62 | |
| R2 | 0.87 | 0.83 | 0.91 | 0.78 | |
| MD (°C) | 5.20 | 2.68 | 5.56 | 2.82 | |
| SD (°C) | 6.29 | 3.21 | 6.59 | 3.50 | |
| Method | Resolution | Number of Ground Stations | Input Variables | Ta Type | Model Validation | Literature | ||
|---|---|---|---|---|---|---|---|---|
| MAE (°C) | RMSE (°C) | R2 | ||||||
| Random Forest | Daily/1 km | 1527 | LST, DSR, NDVI, LC, LAT, ELEVATION, DECLINATION | Daily mean | 0.94 | 1.29 | 0.99 | This study |
| Daytime instantaneous | 1.35 | 1.88 | 0.98 | |||||
| Nighttime instantaneous | 1.83 | 2.47 | 0.95 | |||||
| Statistical methods | Daily/1 km | 538 | LST, NDVI, PERCENT OF URBAN AREAS, ELEVATION, DISTANCE TO WATER BODY | Daily mean | - | 1.38 | 0.97 | [39] |
| Random Forest | Daily/1 km | 85 | LST, NDVI, ROAD AND POPULATION DENSITY, DISTANCE TO LARGE BODIES OF WATER, ELEVATION, SLOPE, ASPECT, URBAN FRACTIONS, VEGETATION FRACTIONS | Intra-daily instantaneous | 1.12 | 1.58 | 0.96 | [55] |
| Daily max | 1.27 | 1.89 | 0.97 | |||||
| Random Forest | Daily/1 km | 53 | LST, ALBEDO, NDVI, ELEVATION, DISTANCE TO THE SEA, POTENTIAL INSOLATION, TOPOGRAPHIC WETNESS INDEX | Daytime instantaneous | 3.01 | 0.89 | [56] | |
| Geographically weighted regression | Daily/1 km | 10,141 | LST, ELEVATION | Daily min | 1.54 | 2.14 | 0.95 | [60] |
| Linear regression | Daily/1 km | 23 | LST | Daily mean | 1.84 | 2.41 | [89] | |
| Deep belief network | Daily/0.01° | 829 | LST, NDVI, LC, ELEVATION, LATITUDE, LONGITUDE, DAY OF YEAR, MONTH OF YEAR, VIEW ZENITH ANGLE OF DAY, ROAD AND POPULATION DENSITY, WIND SPEED, SOIL MOISTURE CONTENT, ALBEDO | Daily max | 1.54 | 2.00 | 0.99 | [90] |
| Cubist | Daily/0.05° | 135 | LST, ISR, OLR, TOAALB, SFCALB, NDVI, NDSI | Daily mean | - | 1.87 | 0.96 | [91] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Bi, X.; Luan, Q.; Li, Z. Estimation of Daily and Instantaneous Near-Surface Air Temperature from MODIS Data Using Machine Learning Methods in the Jingjinji Area of China. Remote Sens. 2022, 14, 1916. https://doi.org/10.3390/rs14081916
Wang C, Bi X, Luan Q, Li Z. Estimation of Daily and Instantaneous Near-Surface Air Temperature from MODIS Data Using Machine Learning Methods in the Jingjinji Area of China. Remote Sensing. 2022; 14(8):1916. https://doi.org/10.3390/rs14081916
Chicago/Turabian StyleWang, Chunling, Xu Bi, Qingzu Luan, and Zhanqing Li. 2022. "Estimation of Daily and Instantaneous Near-Surface Air Temperature from MODIS Data Using Machine Learning Methods in the Jingjinji Area of China" Remote Sensing 14, no. 8: 1916. https://doi.org/10.3390/rs14081916
APA StyleWang, C., Bi, X., Luan, Q., & Li, Z. (2022). Estimation of Daily and Instantaneous Near-Surface Air Temperature from MODIS Data Using Machine Learning Methods in the Jingjinji Area of China. Remote Sensing, 14(8), 1916. https://doi.org/10.3390/rs14081916