Landslide Displacement Prediction via Attentive Graph Neural Network
Abstract
:1. Introduction
- We present a GNN-based landslide prediction model using accurate InSAR data. It shows superiority compared with traditional and deep learning methods in predicting land deformation.
- We propose a variant of the typical self-attention mechanism, which we call locally historical Transformer, to simultaneously utilize spatial and temporal dependencies.
- We provide a new real-world dataset collected from a critical area prone to landslides, based on which extensive experiments were conducted, evaluating and demonstrating the effectiveness of LandGNN.
2. Related Work
2.1. Land Displacement Prediction
2.2. InSAR Technology
2.3. Graph Neural Networks
2.4. Transformers
3. Methodology
3.1. Problem Definition
3.2. LandGNN
3.2.1. Spatial Graph
3.2.2. Spatial Feature Fusion
3.2.3. Locally Historical Transformer
| Algorithm 1 Predicting via LandGNN. |
Input: Adjacency matrix , reachability on h heads , N monitored sites S, displacement observations , convolution layers Y.
|
3.2.4. Objective
4. Experiments
4.1. Dataset
4.2. Baselines and Experimental Settings
4.3. Evaluation Metrics
- Root Mean Squared Error (RMSE):
- Mean Absolute Error (MAE):
- Accuracy:
- Coefficient of Determination (R):
- Explained Variance Score (var):where and represent the true and predicted measurement at time and iff x is true. Threshold for determining the correct prediction is 0.01. , and are real deformations, predicted deformations and average deformations, respectively.
4.4. Overall Performance Comparison
4.5. Parameter Sensitivity
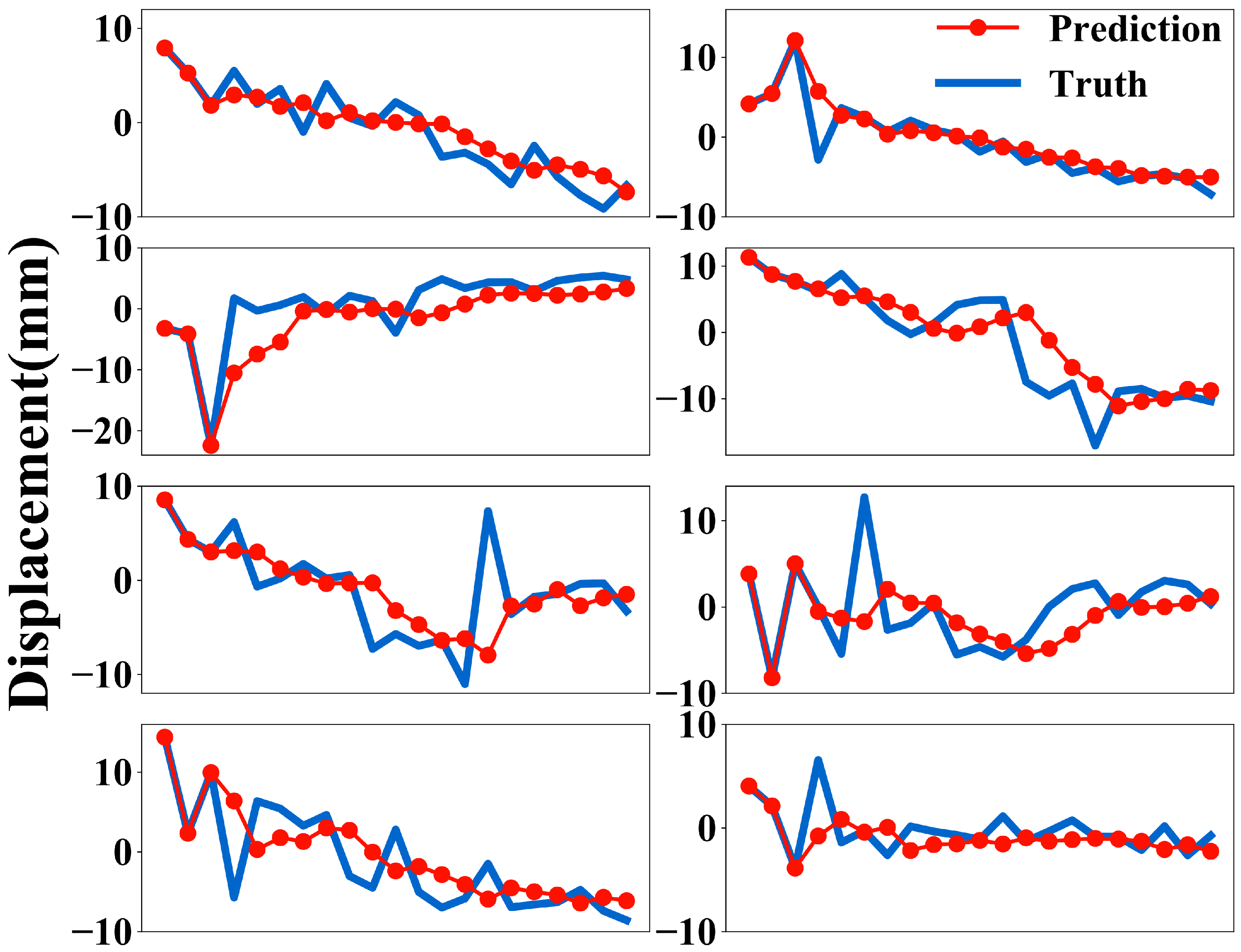
4.6. Visualizations
5. Discussion
6. Conclusions
- We apply graph convolution to aggregate spatial features on the defined graph structure and exploit transformer architecture to capture the locally historical dependencies between monitored nodes. Compared to traditional and deep learning-based methods, LandGNN explicitly models the spatio-temporal interactions between different locations and thus achieves better forecast performance.
- The experiments conducted on real-world datasets show that LandGNN is superior to previous approaches due to the capability of considering the evolution of local interactions. We also report the sensitivity of two important hyperparameters to explore the effectiveness of adjacency relations. Meanwhile, the visualization study indicates how the attention mechanism works, further validating our motivation.
- Our ongoing work aims to explore more information, such as the azimuth between monitored locations and the weather conditions to improve the accuracy and robustness of LandGNN. In addition, incorporating the data uncertainty and understanding the details of interactions between different areas while explaining the model prediction results are worthy of further investigation, which could benefit the development of prediction approaches useful for various safety-critical applications.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, C.; Lu, Z. Remote Sensing of Landslides—A Review. Remote Sens. 2018, 10, 279. [Google Scholar] [CrossRef] [Green Version]
- Tsironi, V.; Ganas, A.; Karamitros, I.; Efstathiou, E.; Koukouvelas, I.; Sokos, E. Kinematics of Active Landslides in Achaia (Peloponnese, Greece) through InSAR Time Series Analysis and Relation to Rainfall Patterns. Remote Sens. 2022, 14, 844. [Google Scholar] [CrossRef]
- Huang, R.; Fan, X. The landslide story. Nat. Geosci. 2013, 6, 325–326. [Google Scholar] [CrossRef]
- Bozzano, F.; Cipriani, I.; Mazzanti, P.; Prestininzi, A. Displacement patterns of a landslide affected by human activities: Insights from ground-based InSAR monitoring. Nat. Hazards 2011, 59, 1377–1396. [Google Scholar] [CrossRef]
- Gao, W.; Dai, S.; Chen, X. Landslide prediction based on a combination intelligent method using the GM and ENN: Two cases of landslides in the Three Gorges Reservoir, China. Landslides 2020, 17, 111–126. [Google Scholar] [CrossRef]
- Hajimoradlou, A.; Roberti, G.; Poole, D. Predicting Landslides Using Locally Aligned Convolutional Neural Networks. In Proceedings of the International Joint Conference on Artificial Intelligence, Jokohoma, Japan, 7–15 January 2021; pp. 3342–3348. [Google Scholar]
- Liu, S.; Yin, K.; Zhou, C.; Gui, L.; Liang, X.; Lin, W.; Zhao, B. Susceptibility Assessment for Landslide Initiated along Power Transmission Lines. Remote Sens. 2021, 13, 5068. [Google Scholar] [CrossRef]
- Jiang, Y.; Luo, H.; Xu, Q.; Lu, Z.; Liao, L.; Li, H.; Hao, L. A Graph Convolutional Incorporating GRU Network for Landslide Displacement Forecasting Based on Spatiotemporal Analysis of GNSS Observations. Remote Sens. 2022, 14, 1016. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, X.; Tu, R.; Chen, G.; Luo, T.; Xue, D. Prediction of Landslide Displacement Based on the Combined VMD-Stacked LSTM-TAR Model. Remote Sens. 2022, 14, 1164. [Google Scholar] [CrossRef]
- Kang, Y.; Zhao, C.; Zhang, Q.; Lu, Z.; Li, B. Application of InSAR Techniques to an Analysis of the Guanling Landslide. Remote Sens. 2017, 9, 1046. [Google Scholar] [CrossRef] [Green Version]
- Zhu, A.X.; Wang, R.; Qiao, J.; Qin, C.Z.; Chen, Y.; Liu, J.; Du, F.; Lin, Y.; Zhu, T. An expert knowledge-based approach to landslide susceptibility mapping using GIS and fuzzy logic. Geomorphology 2014, 214, 128–138. [Google Scholar] [CrossRef]
- Vakhshoori, V.; Zare, M. Landslide susceptibility mapping by comparing weight of evidence, fuzzy logic, and frequency ratio methods. Geomat. Nat. Hazards Risk 2016, 7, 1731–1752. [Google Scholar] [CrossRef]
- Zhou, J.W.; Lu, P.Y.; Yang, Y.C. Reservoir Landslides and Its Hazard Effects for the Hydropower Station: A Case Study. In Proceedings of the World Landslide Forum, Ljubljana, Slovenia, 30 May–1 June 2017; pp. 699–706. [Google Scholar]
- Gan, B.R.; Yang, X.G.; Zhou, J.W. GIS-based remote sensing analysis of the spatial-temporal evolution of landslides in a hydropower reservoir in southwest China. Geomat. Nat. Hazards Risk 2019, 10, 2291–2312. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Wang, J.; Duan, Z.; Hong, H. GIS-based landslide susceptibility modelling: A comparative assessment of kernel logistic regression, Naïve-Bayes tree, and alternating decision tree models. Geomat. Nat. Hazards Risk 2017, 8, 950–973. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Wang, Y.; Niu, R.; Peng, L. Integration of Information Theory, K-Means Cluster Analysis and the Logistic Regression Model for Landslide Susceptibility Mapping in the Three Gorges Area, China. Remote Sens. 2017, 9, 938. [Google Scholar] [CrossRef] [Green Version]
- Kalantar, B.; Pradhan, B.; Naghibi, S.A.; Motevalli, A.; Mansor, S. Assessment of the effects of training data selection on the landslide susceptibility mapping: A comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN). Geomat. Nat. Hazards Risk 2018, 9, 49–69. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in Lianhua County (China): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Jebur, M.N.; Bui, D.T.; Xu, C.; Akgun, A. Spatial prediction of landslide hazard at the Luxi area (China) using support vector machines. Environ. Earth Sci. 2016, 75, 40. [Google Scholar] [CrossRef]
- Liu, R.; Peng, J.; Leng, Y.; Lee, S.; Panahi, M.; Chen, W.; Zhao, X. Hybrids of Support Vector Regression with Grey Wolf Optimizer and Firefly Algorithm for Spatial Prediction of Landslide Susceptibility. Remote Sens. 2021, 13, 4966. [Google Scholar] [CrossRef]
- Jiang, P.; Chen, J. Displacement prediction of landslide based on generalized regression neural networks with K-fold cross-validation. Neurocomputing 2016, 198, 40–47. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of different machine learning methods and deep-learning convolutional neural networks for landslide detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef] [Green Version]
- Lei, T.; Zhang, Y.; Lv, Z.; Li, S.; Liu, S.; Nandi, A.K. Landslide inventory mapping from bitemporal images using deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2019, 16, 982–986. [Google Scholar] [CrossRef]
- Hua, Y.; Wang, X.; Li, Y.; Xu, P.; Xia, W. Dynamic development of landslide susceptibility based on slope unit and deep neural networks. Landslides 2020, 18, 281–302. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Liao, M.; Gong, J. Improved correction of seasonal tropospheric delay in InSAR observations for landslide deformation monitoring. Remote Sens. Environ. 2019, 233, 111370. [Google Scholar] [CrossRef]
- Carlà, T.; Intrieri, E.; Raspini, F.; Bardi, F.; Farina, P.; Ferretti, A.; Colombo, D.; Novali, F.; Casagli, N. Perspectives on the prediction of catastrophic slope failures from satellite InSAR. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. IJCAI 2018, 3634–3640. [Google Scholar]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2019. [Google Scholar]
- Wang, X.; Ma, Y.; Wang, Y.; Jin, W.; Wang, X.; Tang, J.; Jia, C.; Yu, J. Traffic flow prediction via spatial temporal graph neural network. In Proceedings of the Web Conference, Online, 20–24 April 2020; pp. 1082–1092. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Yuan, Z.; Liu, H.; Liu, Y.; Zhang, D.; Yi, F.; Zhu, N.; Xiong, H. Spatio-temporal dual graph attention network for query-poi matching. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 629–638. [Google Scholar]
- Park, C.; Lee, C.; Bahng, H.; Tae, Y.; Jin, S.; Kim, K.; Ko, S.; Choo, J. ST-GRAT: A Novel Spatio-temporal Graph Attention Networks for Accurately Forecasting Dynamically Changing Road Speed. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, New York, NY, USA, 19–23 October 2020; pp. 1215–1224. [Google Scholar]
- Liu, J.; Guang, Y.; Rojas, J. Gast-net: Graph attention spatio-temporal convolutional networks for 3d human pose estimation in video. arXiv 2020, arXiv:2003.14179. [Google Scholar]
- Cui, W.; He, X.; Yao, M.; Wang, Z.; Hao, Y.; Li, J.; Wu, W.; Zhao, H.; Xia, C.; Li, J.; et al. Knowledge and Spatial Pyramid Distance-Based Gated Graph Attention Network for Remote Sensing Semantic Segmentation. Remote Sens. 2021, 13, 1312. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Y.; Gao, X.; Zhang, X. A Simple Method of Mapping Landslides Runout Zones Considering Kinematic Uncertainties. Remote Sens. 2022, 14, 668. [Google Scholar] [CrossRef]
- Piacentini, D.; Troiani, F.; Torre, D.; Menichetti, M. Land-Surface Quantitative Analysis to Investigate the Spatial Distribution of Gravitational Landforms along Rocky Coasts. Remote Sens. 2021, 13, 5012. [Google Scholar] [CrossRef]
- Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow landslide susceptibility assessment using a novel hybrid intelligence approach. Environ. Earth Sci. 2017, 76, 60. [Google Scholar] [CrossRef]
- Lizama, E.; Morales, B.; Somos-Valenzuela, M.; Chen, N.; Liu, M. Understanding Landslide Susceptibility in Northern Chilean Patagonia: A Basin-Scale Study Using Machine Learning and Field Data. Remote Sens. 2022, 14, 907. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Ju, Y.; Xu, Q.; Jin, S.; Li, W.; Su, Y.; Dong, X.; Guo, Q. Loess Landslide Detection Using Object Detection Algorithms in Northwest China. Remote Sens. 2022, 14, 1182. [Google Scholar] [CrossRef]
- Jepsen, T.S.; Jensen, C.S.; Nielsen, T.D. Relational fusion networks: Graph convolutional networks for road networks. IEEE Trans. Intell. Transp. Syst. 2020, 23, 418–429. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.; Ding, X.; Zhu, J.; Zhang, L.; Sun, Q. Resolving three-dimensional surface displacements from InSAR measurements: A review. Earth-Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Osmanoğlu, B.; Sunar, F.; Wdowinski, S.; Cabral-Cano, E. Time series analysis of InSAR data: Methods and trends. ISPRS J. Photogramm. Remote Sens. 2016, 115, 90–102. [Google Scholar] [CrossRef]
- Solari, L.; Del Soldato, M.; Raspini, F.; Barra, A.; Bianchini, S.; Confuorto, P.; Casagli, N.; Crosetto, M. Review of Satellite Interferometry for Landslide Detection in Italy. Remote Sens. 2020, 12, 1351. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neur. Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, J.; Liu, H.; Zhu, H.; Xiong, H.; Dou, D. Joint Air Quality and Weather Prediction Based on Multi-Adversarial Spatiotemporal Networks. In Proceedings of the 35th AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; pp. 4081–4089. [Google Scholar]
- Liu, J.; Li, T.; Ji, S.; Xie, P.; Du, S.; Teng, F.; Zhang, J. Urban flow pattern mining based on multi-source heterogeneous data fusion and knowledge graph embedding. IEEE Trans. Knowl. Data Eng. 2021. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Wan, H.; Li, X.; Cong, G. Learning dynamics and heterogeneity of spatial-temporal graph data for traffic forecasting. IEEE Trans. Knowl. Data Eng. 2021. [Google Scholar] [CrossRef]
- Shi, W.; Ragunathan, R. Point-GNN: Graph Neural Network for 3D Object Detection in a Point Cloud. arXiv 2020, arXiv:2003.01251. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. NeurIPS 2020, 33, 1877–1901. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual Event, 3–7 May 2021. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 213–229. [Google Scholar]
- Liang, Y.; Zhou, P.; Zimmermann, R.; Yan, S. DualFormer: Local-Global Stratified Transformer for Efficient Video Recognition. arXiv 2021, arXiv:2112.04674. [Google Scholar]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 922–929. [Google Scholar]
- Cheng, W.; Shen, Y.; Zhu, Y.; Huang, L. A neural attention model for urban air quality inference: Learning the weights of monitoring stations. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LU, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. arXiv 2019, arXiv:1907.00235. [Google Scholar]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable spatio-temporal attention LSTM model for flood forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
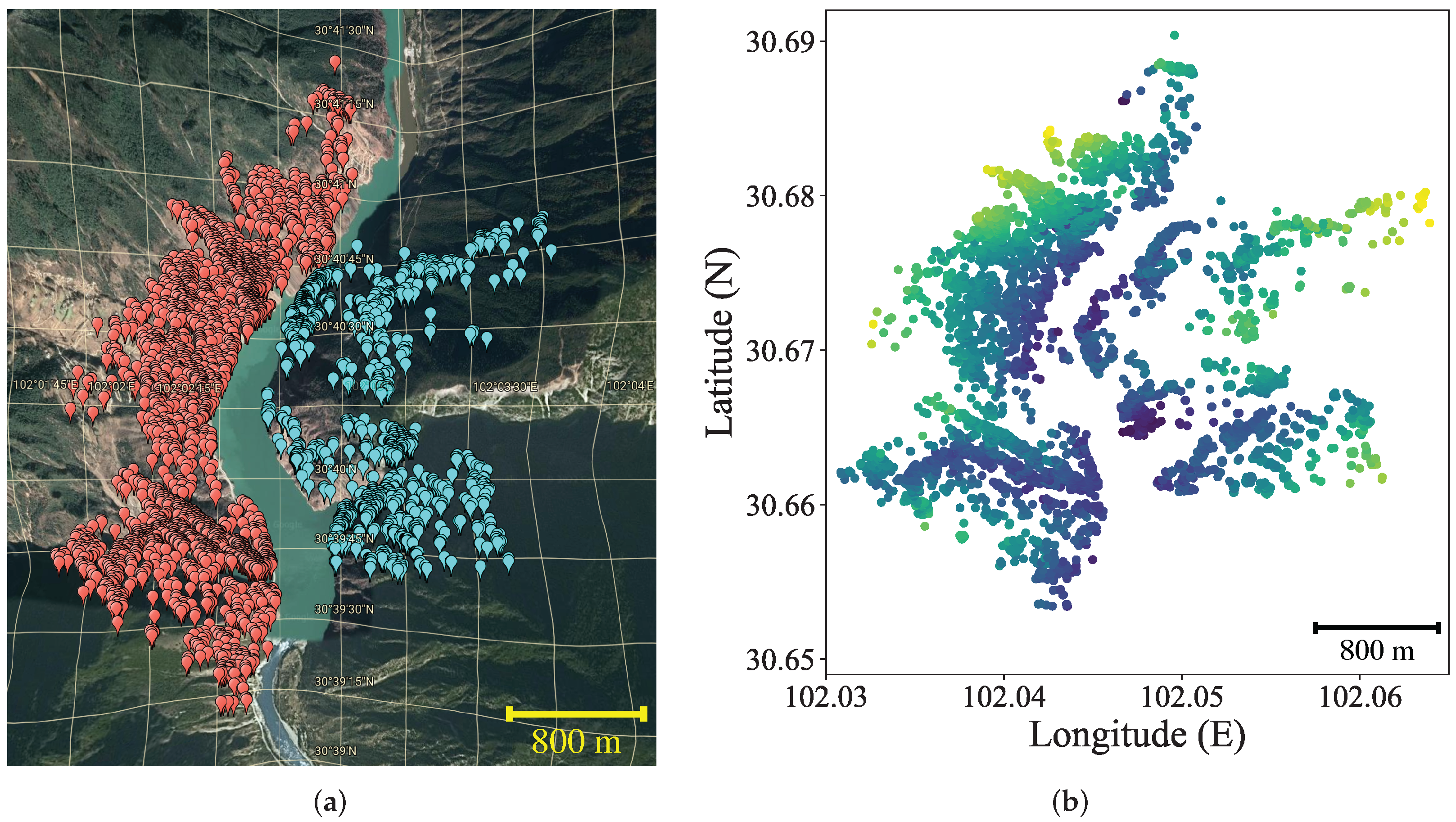

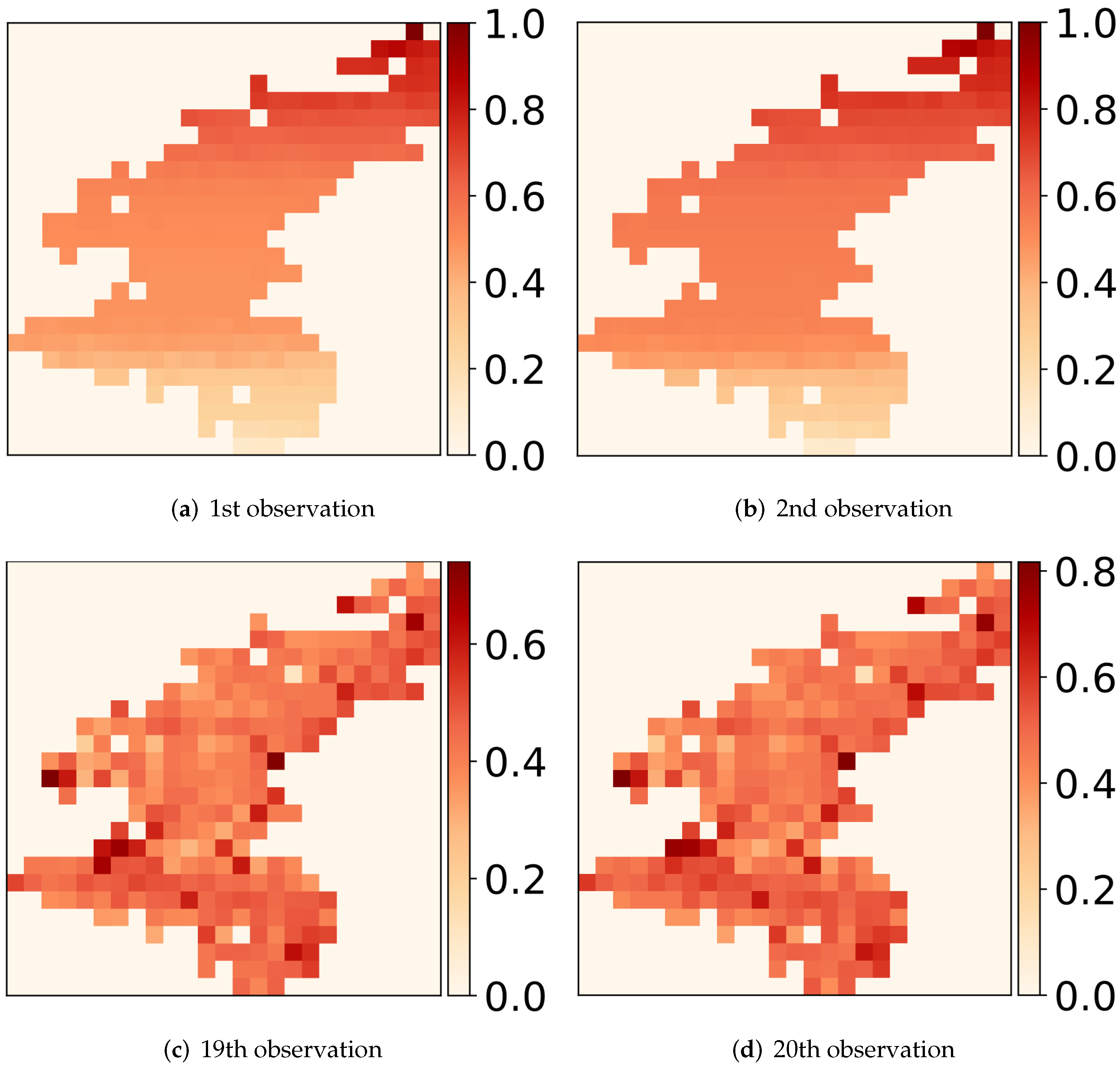
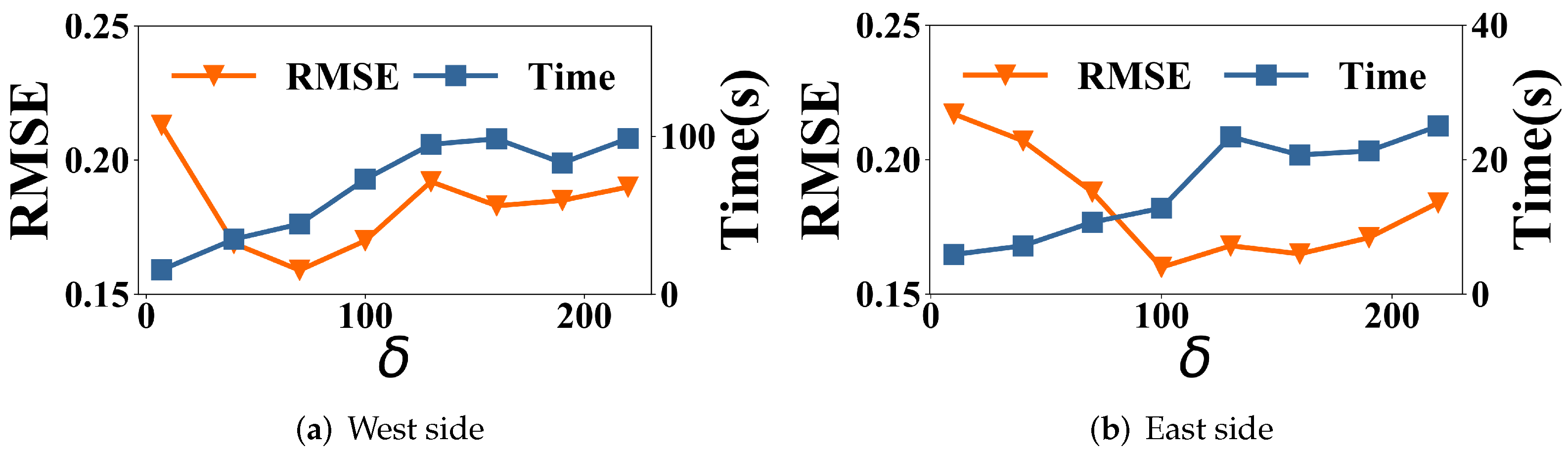
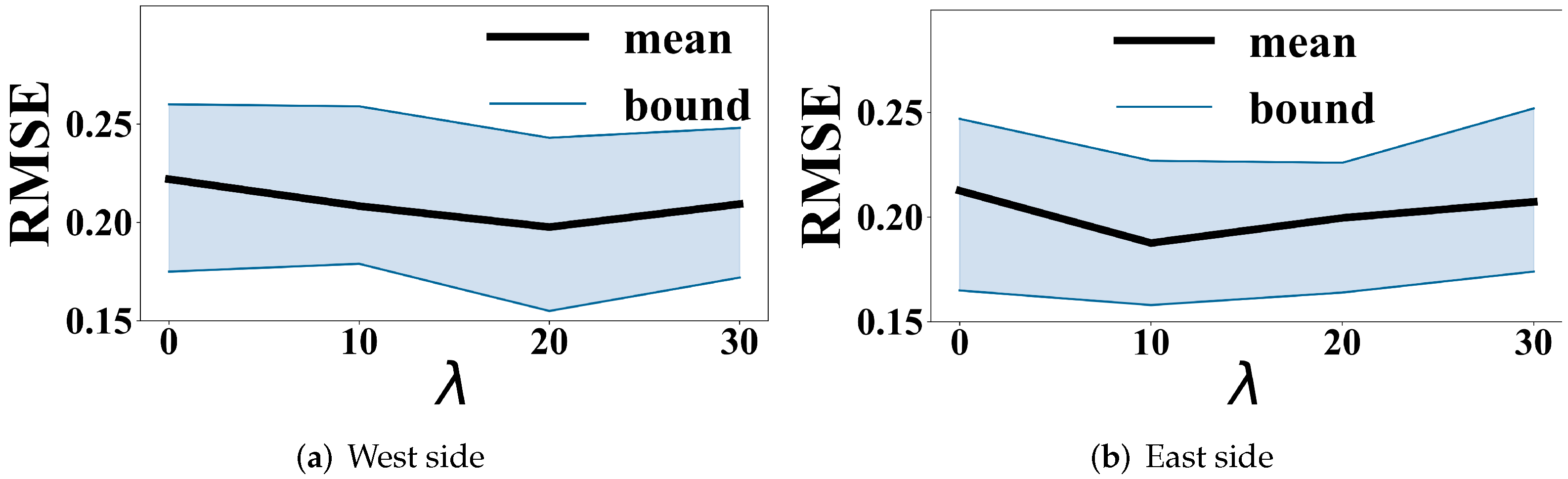

| Dataset | West Side | East Side |
|---|---|---|
| Nodes | 4569 | 2164 |
| Displacement range | [−27.58, 28.03] | [−29.06, 30.50] |
| Method | West Side | East Side | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | ACC | R | EVS | RMSE | MAE | ACC | R | EVS | |
| HA | 3.144 | 2.454 | 0.047 | 0.134 | 0.262 | 3.858 | 2.870 | 0.046 | 0.224 | 0.288 |
| SVR | 6.872 | 5.528 | 0.018 | 0.036 | 0.025 | 8.735 | 6.749 | 0.016 | 0.021 | 0.017 |
| ARIMA | 4.764 | 3.947 | 0.041 | 0.072 | 0.157 | 8.326 | 6.865 | 0.021 | 0.052 | 0.185 |
| LSTM | 0.254 | 0.218 | 0.490 | 0.038 | 0.094 | 0.254 | 0.210 | 0.518 | 0.077 | 0.086 |
| GRU | 0.254 | 0.217 | 0.491 | 0.040 | 0.095 | 0.250 | 0.207 | 0.526 | 0.078 | 0.092 |
| STGCN | 0.177 | 0.148 | 0.725 | 0.121 | 0.409 | 0.174 | 0.142 | 0.749 | 0.298 | 0.324 |
| DCRNN | 0.152 | 0.125 | 0.824 | 0.134 | 0.491 | 0.157 | 0.124 | 0.838 | 0.359 | 0.515 |
| STAL | 0.141 | 0.111 | 0.863 | 0.285 | 0.530 | 0.146 | 0.109 | 0.858 | 0.385 | 0.488 |
| LandGNN | 0.132 | 0.106 | 0.892 | 0.348 | 0.567 | 0.137 | 0.103 | 0.878 | 0.412 | 0.566 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuang, P.; Li, R.; Huang, Y.; Wu, J.; Luo, X.; Zhou, F. Landslide Displacement Prediction via Attentive Graph Neural Network. Remote Sens. 2022, 14, 1919. https://doi.org/10.3390/rs14081919
Kuang P, Li R, Huang Y, Wu J, Luo X, Zhou F. Landslide Displacement Prediction via Attentive Graph Neural Network. Remote Sensing. 2022; 14(8):1919. https://doi.org/10.3390/rs14081919
Chicago/Turabian StyleKuang, Ping, Rongfan Li, Ying Huang, Jin Wu, Xucheng Luo, and Fan Zhou. 2022. "Landslide Displacement Prediction via Attentive Graph Neural Network" Remote Sensing 14, no. 8: 1919. https://doi.org/10.3390/rs14081919
APA StyleKuang, P., Li, R., Huang, Y., Wu, J., Luo, X., & Zhou, F. (2022). Landslide Displacement Prediction via Attentive Graph Neural Network. Remote Sensing, 14(8), 1919. https://doi.org/10.3390/rs14081919






