Coastal Wetland Responses to Sea Level Rise: The Losers and Winners Based on Hydro-Geomorphological Settings
Abstract
:1. Introduction
2. Methods
2.1. Study Area

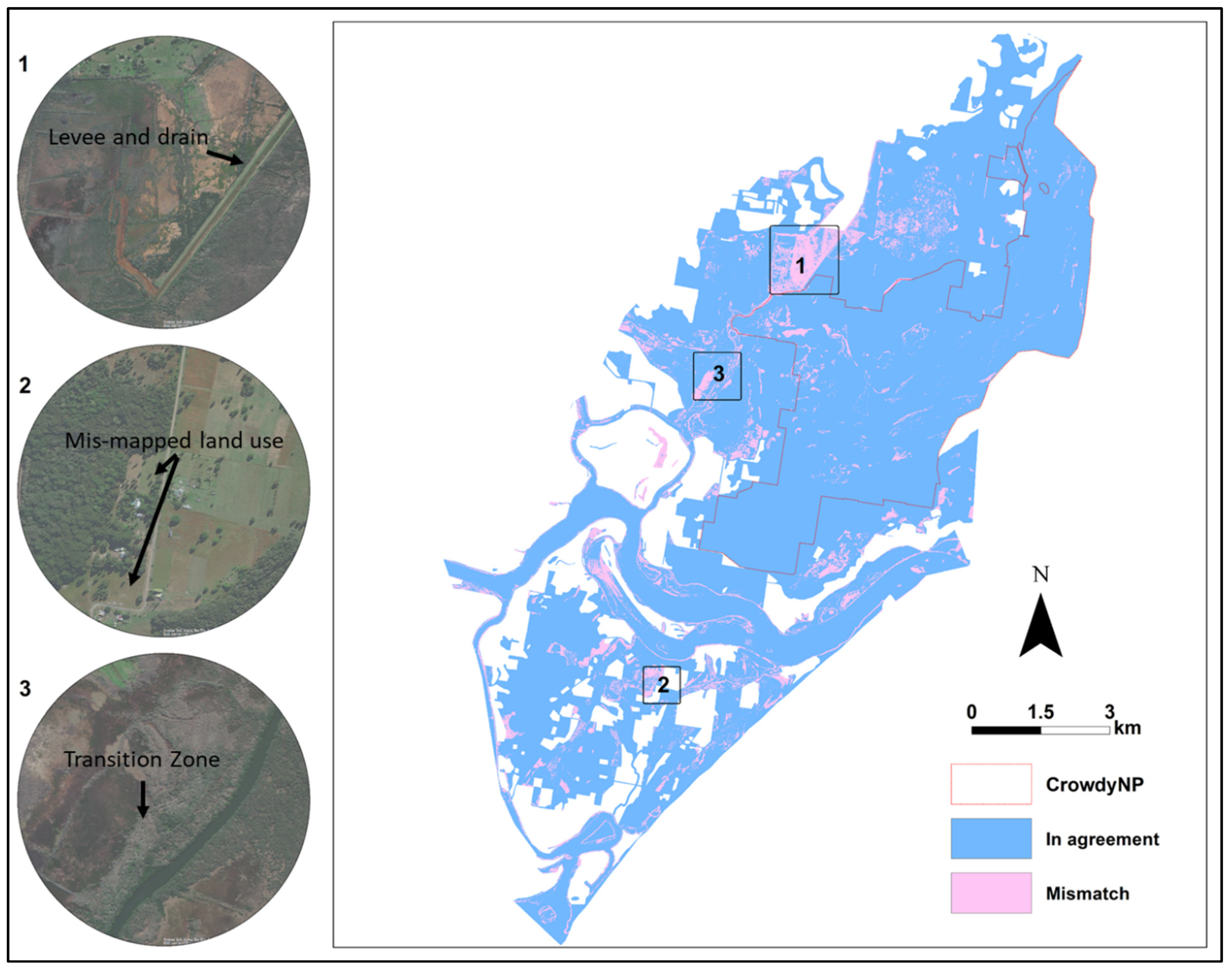
2.2. Data Sources and Preparation
2.2.1. Responsible Variable
2.2.2. Predictor Variables and Pre-Processing
- TPI (Topographic Position Index): The difference between the value of a grid cell and the mean value of its 8 surrounding cellswhere h is the elevation in meters. The positive or negative values of the TPI indicate that the central point is located higher or lower than its average surroundings, respectively.
- The Terrain Ruggedness Index (TRI) can be expresses as:where Zc is the elevation of the central grid cell and Zi is the elevation of one through to eight neighboring cells. The Terrain Ruggedness Index (TRI) is a topographic measurement developed by [50] to quantify topographic irregularities in a region.
- The Topographic Wetness Index (TWI), according to Kirkby and Beven [51], can be expressed as:where α is the catchment area [(flow accumulation + 1) × (pixel area in m2)], and θ is the ground slope angle in radians. It is assumed that topography controls the movement of the water in a sloped terrain, and thus the soil moisture level, which, in turn, affects the distribution of plant species. High TWI values are found in converging flat areas and low values are typical for steep diverging terrains.
- The calculated Wind Exposition Index (WEI), as proposed by Böhner and Antonić [52], can be expressed as:where N is the angle step (we used 24, i.e., each 15 degrees). The horizon angle φ for any given grid in the DEM (with the elevation z) is defined as the maximum angle toward any other grid in a given azimuth, within a selected search distance d (we used 10 km in this study), determined by:where d is the distance to the point with a higher elevation z + . The WEI is a non-dimensional index used to quantify wind exposure at the land surface. A value < 1 indicates more covered areas, and a value > 1 indicates the areas exposed to wind.
- Slope according to Horn [53] using the elevation of eight neighboring grid cells. Slope is one of the basic topographical parameters of the terrain. The slope angle is an important contributing factor to flooding and soil erosion, and the slope aspect affects sunlight, humidity, and temperature, which are all important for plant colonization and establishment.
2.3. A Random Forest Model for the Current Wetland Distributions
2.4. Predicting the Wetland Distribution under Sea Level Rise Scenarios
2.5. Wetland Changes under Three SLR Scenarios
3. Results
3.1. A Model Accuracy Assessment
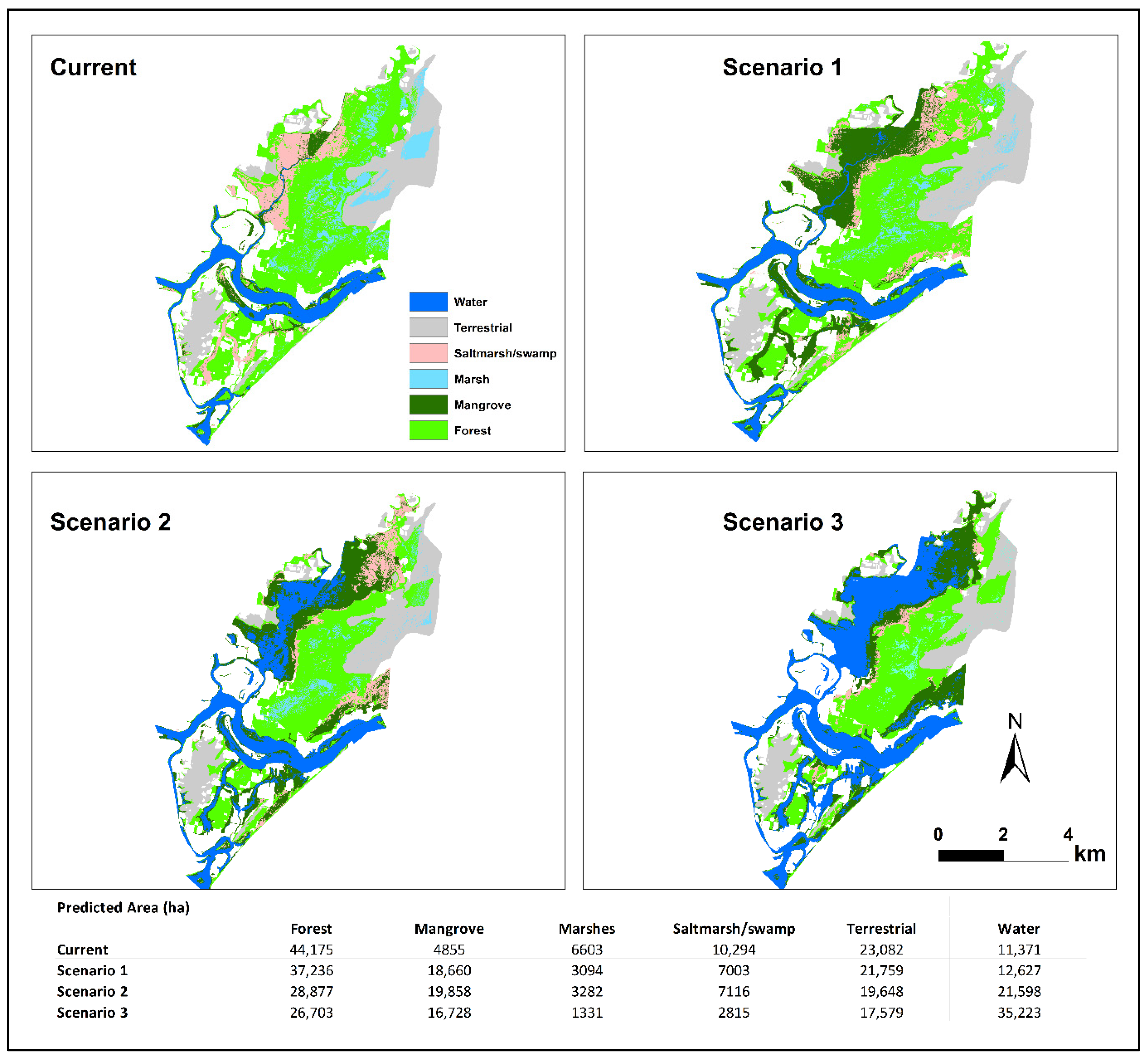
3.2. The Spatial Extent and Wetland Transitions under the SLR Scenarios
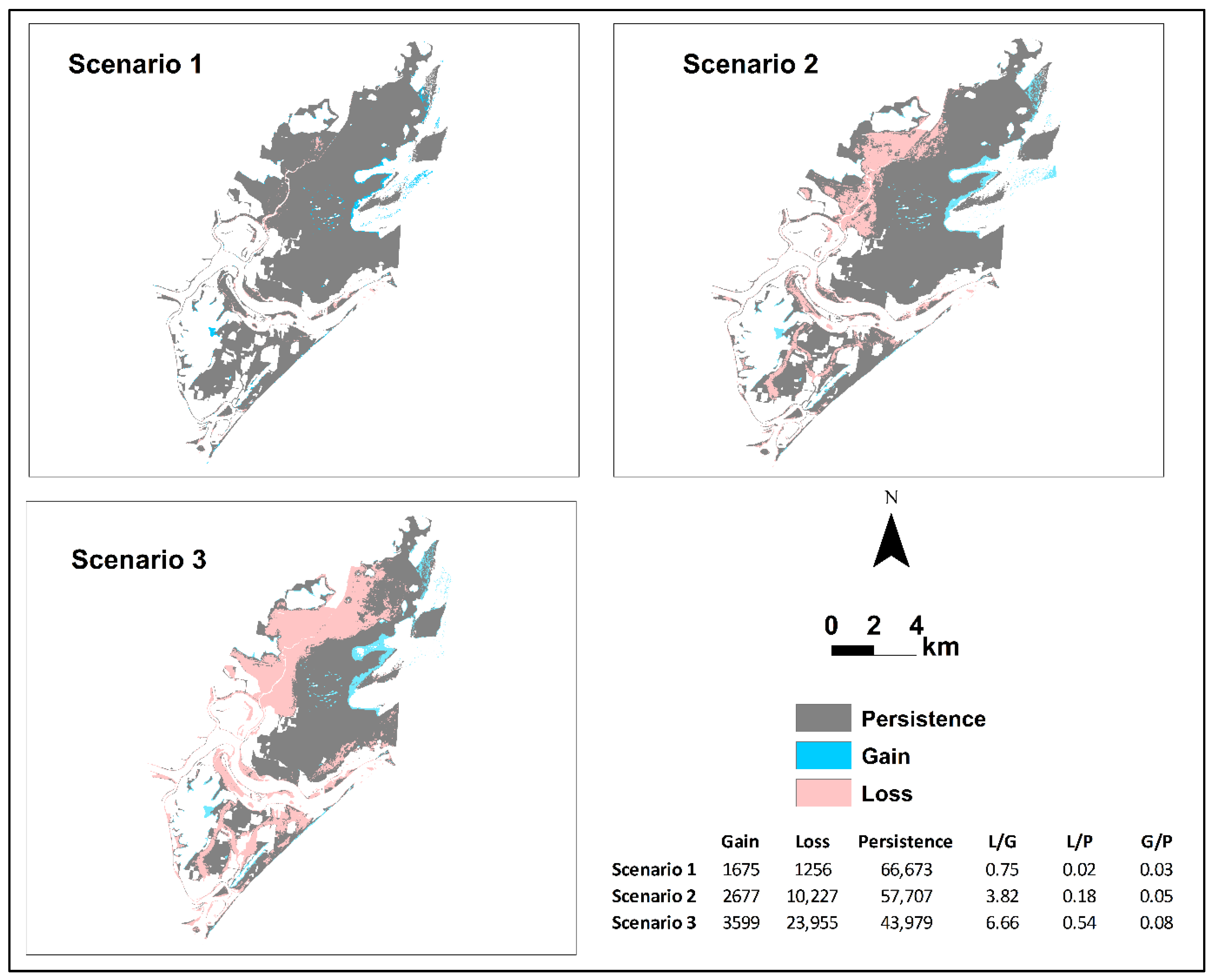
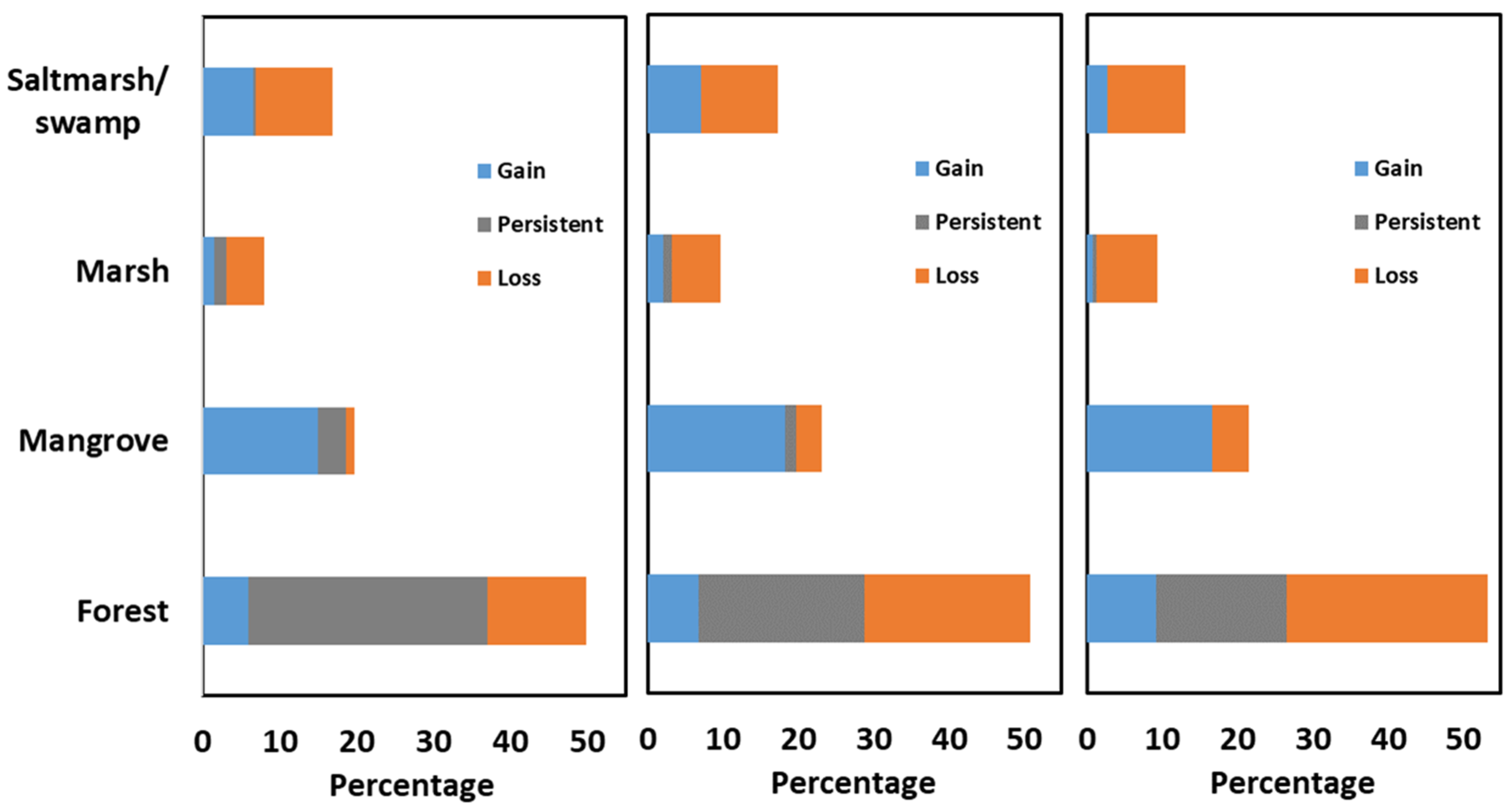
3.3. The Gains, Losses, Net Change, and Swap Change at the Category Levels
3.3.1. Forest Transitions
3.3.2. Mangrove Transitions
3.3.3. Saltmarsh/Swamp Transitions
3.3.4. Marsh Transitions
4. Discussion
4.1. Mangrove Has the Largest Horizontal Accommodation Space
4.2. Natural Coastal Squeeze Limited the Upland Migration of Other Wetland Types
4.3. Hydro-Geomorphology Alone Might Not Explain the Transitions among Current Freshwater Wetlands
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ewel, K.C. Appreciating tropical coastal wetlands from a landscape perspective. Front. Ecol. Environ. 2010, 8, 20–26. [Google Scholar] [CrossRef]
- Grieger, R.; Capon, S.J.; Hadwen, W.L.; Mackey, B. Spatial variation and drivers of vegetation structure and composition in coastal freshwater wetlands of subtropical Australia. Mar. Freshw. Res. 2021, 72, 1746–1759. [Google Scholar] [CrossRef]
- Hopkinson, C.S.; Wolanski, E.; Cahoon, D.R.; Perillo, G.M.; Brinson, M.M. Coastal wetlands: A synthesis. In Coastal Wetlands; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–75. [Google Scholar]
- Cowardin, L.M. Classification of Wetlands and Deepwater Habitats of the United States; Fish and Wildlife Service, US Department of the Interior: Washington, DC, USA, 1979.
- Barbier, E.B. The Protective Value of Estuarine and Coastal Ecosystem Services in a Wealth Accounting Framework. Environ. Resour. Econ. 2016, 64, 37–58. [Google Scholar] [CrossRef]
- Barbier, E.B.; Hacker, S.D.; Kennedy, C.; Koch, E.W.; Stier, A.C.; Silliman, B.R. The value of estuarine and coastal ecosystem services. Ecol. Monogr. 2011, 81, 169–193. [Google Scholar] [CrossRef]
- Saintilan, N.; Rogers, K.; Kelleway, J.J.; Ens, E.; Sloane, D.R. Climate change impacts on the coastal wetlands of Australia. Wetlands 2019, 39, 1145–1154. [Google Scholar] [CrossRef]
- Woodruff, J.D.; Irish, J.L.; Camargo, S.J. Coastal flooding by tropical cyclones and sea-level rise. Nature 2013, 504, 44–52. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Silliman, B.R. Climate Change, Human Impacts, and Coastal Ecosystems in the Anthropocene. Curr. Biol. 2019, 29, R1021–R1035. [Google Scholar] [CrossRef]
- IPCC. Climate change 2014: Synthesis report. In Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2014; pp. 1–151. [Google Scholar]
- Enwright, N.M.; Griffith, K.T.; Osland, M.J. Barriers to and opportunities for landward migration of coastal wetlands with sea-level rise. Front. Ecol. Environ. 2016, 14, 307–316. [Google Scholar] [CrossRef]
- Schuerch, M.; Spencer, T.; Temmerman, S.; Kirwan, M.L.; Wolff, C.; Lincke, D.; McOwen, C.J.; Pickering, M.D.; Reef, R.; Vafeidis, A.T.; et al. Future response of global coastal wetlands to sea-level rise. Nature 2018, 561, 231–234. [Google Scholar] [CrossRef]
- Grieger, R.; Capon, S.J.; Hadwen, W.L.; Mackey, B. Between a bog and a hard place: A global review of climate change effects on coastal freshwater wetlands. Clim. Chang. 2020, 163, 161–179. [Google Scholar] [CrossRef]
- Cahoon, D.R.; Lynch, J.C.; Perez, B.C.; Segura, B.; Holland, R.D.; Stelly, C.; Stephenson, G.; Hensel, P. High-Precision Measurements of Wetland Sediment Elevation: II. The Rod Surface Elevation Table. J. Sediment. Res. 2002, 72, 734–739. [Google Scholar] [CrossRef]
- Krauss, K.W.; Cahoon, D.R.; Allen, J.A.; Ewel, K.C.; Lynch, J.C.; Cormier, N. Surface elevation change and susceptibility of different mangrove zones to sea-level rise on Pacific high islands of Micronesia. Ecosystems 2010, 13, 129–143. [Google Scholar] [CrossRef]
- Rogers, K.; Wilton, K.M.; Saintilan, N. Vegetation change and surface elevation dynamics in estuarine wetlands of southeast Australia. Estuar. Coast. Shelf Sci. 2006, 66, 559–569. [Google Scholar] [CrossRef]
- Webb, E.L.; Friess, D.A.; Krauss, K.W.; Cahoon, D.R.; Guntenspergen, G.R.; Phelps, J. A global standard for monitoring coastal wetland vulnerability to accelerated sea-level rise. Nat. Clim. Chang. 2013, 3, 458–465. [Google Scholar] [CrossRef] [Green Version]
- Spalding, M.D.; Blasco, F.; Field, C.D. World Mangrove Atlas; International Society for Mangrove Ecosystems: Okinawa, Japan, 1997. [Google Scholar]
- Cole, L.E.S.; Bhagwat, S.A.; Willis, K.J. Long-term disturbance dynamics and resilience of tropical peat swamp forests. J. Ecol. 2015, 103, 16–30. [Google Scholar] [CrossRef] [Green Version]
- Cherry, J.A.; Battaglia, L.L. Tidal Wetlands in a Changing Climate: Introduction to a Special Feature. Wetlands 2019, 39, 1139–1144. [Google Scholar] [CrossRef]
- Saintilan, N.; Williams, R.J. Mangrove transgression into saltmarsh environments in south-east Australia. Glob. Ecol. Biogeogr. 1999, 8, 117–124. [Google Scholar] [CrossRef] [Green Version]
- Doyle, T.W.; Krauss, K.W.; Conner, W.H.; From, A.S. Predicting the retreat and migration of tidal forests along the northern Gulf of Mexico under sea-level rise. For. Ecol. Manag. 2010, 259, 770–777. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Gedan, K.B. Sea-level driven land conversion and the formation of ghost forests. Nat. Clim. Chang. 2019, 9, 450–457. [Google Scholar] [CrossRef] [Green Version]
- Bowman, D.M.J.S.; Prior, L.D.; De Little, S.C. Retreating Melaleuca swamp forests in Kakadu National Park: Evidence of synergistic effects of climate change and past feral buffalo impacts. Austral Ecol. 2010, 35, 898–905. [Google Scholar] [CrossRef]
- Reed, D.; Wang, Y.; Meselhe, E.; White, E. Modeling wetland transitions and loss in coastal Louisiana under scenarios of future relative sea-level rise. Geomorphology 2020, 352, 106991. [Google Scholar] [CrossRef]
- White, E.; Kaplan, D. Restore or retreat? Saltwater intrusion and water management in coastal wetlands. Ecosyst. Health Sustain. 2017, 3, e01258. [Google Scholar] [CrossRef] [Green Version]
- Kirwan, M.L.; Walters, D.C.; Reay, W.G.; Carr, J.A. Sea level driven marsh expansion in a coupled model of marsh erosion and migration. Geophys. Res. Lett. 2016, 43, 4366–4373. [Google Scholar] [CrossRef] [Green Version]
- Thorne, K.; MacDonald, G.; Guntenspergen, G.; Ambrose, R.; Buffington, K.; Dugger, B.; Freeman, C.; Janousek, C.; Brown, L.; Rosencranz, J.; et al. U.S. Pacific coastal wetland resilience and vulnerability to sea-level rise. Sci. Adv. 2018, 4, eaao3270. [Google Scholar] [CrossRef] [Green Version]
- Pontee, N. Defining coastal squeeze: A discussion. Ocean Coast. Manag. 2013, 84, 204–207. [Google Scholar] [CrossRef]
- OEH. Threatened Ecological Communities Strategy; NSW Office of Environment and Heritage: Sydney, Australia, 2017.
- Roy, P.S.; Williams, R.J.; Jones, A.R.; Yassini, I.; Gibbs, P.J.; Coates, B.; West, R.J.; Scanes, P.R.; Hudson, J.P.; Nichol, S. Structure and function of south-east Australian estuaries. Estuar. Coast. Shelf Sci. 2001, 53, 351–384. [Google Scholar] [CrossRef]
- Kopp, R.E.; Horton, R.M.; Little, C.M.; Mitrovica, J.X.; Oppenheimer, M.; Rasmussen, D.J.; Strauss, B.H.; Tebaldi, C. Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earth’s Future 2014, 2, 383–406. [Google Scholar] [CrossRef]
- Braimoh, A.K. Random and systematic land-cover transitions in northern Ghana. Agric. Ecosyst. Environ. 2006, 113, 254–263. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Shusas, E.; McEachern, M. Detecting important categorical land changes while accounting for persistence. Agric. Ecosyst. Environ. 2004, 101, 251–268. [Google Scholar] [CrossRef]
- West, R.J.; Thorogood, C.A.; Walford, T.R.; Williams, R.J. Estuarine Inventory of NSW Fisheries: Bulletin 2; NSW Department of Agriculture: Orange, Australia, 1985.
- Kench, P.S. Geomorphology of Australian estuaries: Review and prospect. Austral. J. Ecol. 1999, 24, 367–380. [Google Scholar] [CrossRef]
- Williams, R.E.; Wyllie, S. The retention of pollutants and the related tidal characteristics of the Manning river. In Proceedings of 12th Federal Convention; Australian Water & Wastewater Association: Adelaide, Australia, 1987; pp. 458–465. [Google Scholar]
- Bucher, D.J. Spatial and Temporal Patterns of Recreational Angling Effort in a Warm-Temperate Australian Estuary. Geogr. Res. 2006, 44, 87–94. [Google Scholar] [CrossRef]
- Manly Hydraulics Laboratory. OEH NSW Estuaries Salinity Data Compilation 1992 to 2011. In Report MHL 1812; Manly Hydraulics Laboratory: Manly Vale, Australia, 2012. [Google Scholar]
- Eco Logical Australia. Manning River Wetlands Mapping. Prepared for MidCoast Council. 2019. Available online: https://www.midcoast.nsw.gov.au/files/assets/public/document-resources/environment-docs/manning-river-catchment-wetland-mapping.pdf (accessed on 4 August 2020).
- MidCoast Council. Manning River Estuary and Catchment Management Program. 2021. Available online: https://haveyoursay.midcoast.nsw.gov.au/our-manning-river (accessed on 4 August 2021).
- Neyman, J. On the Two Different Aspects of the Representative Method: The Method of Stratified Sampling and the Method of Purposive Selection. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 123–150. [Google Scholar]
- Morzaria-Luna, L.; Callaway, J.C.; Sullivan, G.; Zedler, J.B. Relationship between topographic heterogeneity and vegetation patterns in a Californian salt marsh. J. Veg. Sci. 2004, 15, 523–530. [Google Scholar] [CrossRef]
- Schlesinger, W.H. On the Relative Dominance of Shrubs in Okefenokee Swamp. Am. Nat. 1978, 112, 949–954. [Google Scholar] [CrossRef]
- Huenneke, L.F.; Sharitz, R.R. Microsite abundance and distribution of woody seedlings in a South Carolina cypress-tupelo swamp. Am. Midl. Nat. 1986, 115, 328–335. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Alexander, C.; Deák, B.; Heilmeier, H. Micro-topography driven vegetation patterns in open mosaic landscapes. Ecol. Indic. 2016, 60, 906–920. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef] [Green Version]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA spatial modeling of plant species distribution. Plant Ecol. 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. Index that quantifies topographic heterogeneity. Intermt. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Böhner, J.; Antonić, O. Land-Surface Parameters Specific to Topo-Climatology. Dev. Soil Sci. 2009, 33, 195–226. [Google Scholar] [CrossRef]
- Horn, B.K. Hill shading and the reflectance map. Proc. IEEE 1981, 69, 14–47. [Google Scholar] [CrossRef] [Green Version]
- Hughes, M.G.; Rogers, K.; Wen, L. Saline wetland extents and tidal inundation regimes on a micro-tidal coast, New South Wales, Australia. Estuar. Coast. Shelf Sci. 2019, 227, 106297. [Google Scholar] [CrossRef]
- Hanslow, D.J.; Morris, B.D.; Foulsham, E.; Kinsela, M. A Regional Scale Approach to Assessing Current and Potential Future Exposure to Tidal Inundation in Different Types of Estuaries. Sci. Rep. 2018, 8, 7065. [Google Scholar] [CrossRef] [PubMed]
- Khojasteh, D.; Glamore, W.; Heimhuber, V.; Felder, S. Sea level rise impacts on estuarine dynamics: A review. Sci. Total Environ. 2021, 780, 146470. [Google Scholar] [CrossRef]
- Hughes, M.G.; Glasby, T.M.; Hanslow, D.J.; West, G.J.; Wen, L. Random forest classification method for predicting intertidal wetland migration under sea level rise. Front. Environ. Sci. 2022; in press. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- O’Brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J.M.C. Modeling spatial patterns of fire occurrence in Mediterranean Europe using Multiple Regression and Random Forest. For. Ecol. Manag. 2012, 275, 117–129. [Google Scholar] [CrossRef]
- Wen, L.; Hughes, M. Coastal Wetland Mapping Using Ensemble Learning Algorithms: A Comparative Study of Bagging, Boosting and Stacking Techniques. Remote Sens. 2020, 12, 1683. [Google Scholar] [CrossRef]
- Tyagi, S.; Mittal, S. Sampling Approaches for Imbalanced Data Classification Problem in Machine Learning. In Proceedings of ICRIC 2019; Springer: Cham, Switzerland, 2020; pp. 209–221. [Google Scholar]
- Forkel, M.; Wutzler, T. Greenbrown—Land Surface Phenology and Trend Analysis; Version 2.2, 15 April 2015; A Package for the R Software: Vienna, Austria, 2015. [Google Scholar]
- Rogers, K.; Boon, P.I.; Branigan, S.; Duke, N.C.; Field, C.D.; Fitzsimons, J.A.; Kirkman, H.; Mackenzie, J.R.; Saintilan, N. The state of legislation and policy protecting Australia’s mangrove and salt marsh and their ecosystem services. Mar. Policy 2016, 72, 139–155. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data Principles and Practices; CRS Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Anderson, J.R.; Hardy, E.E.; Roach, J.T.; Witmer, R.E. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; Survey Prof. Paper; United State Department of Interior: Washington, DC, USA, 1976; Volume 964, p. 28.
- Woodroffe, C.D.; Rogers, K.; McKee, K.L.; Lovelock, C.E.; Mendelssohn, I.A.; Saintilan, N. Mangrove Sedimentation and Response to Relative Sea-Level Rise. Annu. Rev. Mar. Sci. 2016, 8, 243–266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alizad, K.; Hagen, S.C.; Medeiros, S.C.; Bilskie, M.V.; Morris, J.T.; Balthis, L.; Buckel, C.A. Dynamic responses and implications to coastal wetlands and the surrounding regions under sea level rise. PLoS ONE 2018, 13, e0205176. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Anisfeld, S.C.; Blum, L.K.; Long, E.V.; Feagin, R.A.; Fernandes, A.; Kearney, W.S.; Williams, K. Sea Level Rise and the Dynamics of the Marsh-Upland Boundary. Front. Environ. Sci. 2019, 7, 25. [Google Scholar] [CrossRef]
- Waltham, N.J.; Burrows, D.; Wegscheidl, C.; Buelow, C.; Ronan, M.; Connolly, N.; Groves, P.; Marie-Audas, D.; Creighton, C.; Sheaves, M. Lost Floodplain Wetland Environments and Efforts to Restore Connectivity, Habitat, and Water Quality Settings on the Great Barrier Reef. Front. Mar. Sci. 2019, 6, 71. [Google Scholar] [CrossRef]
- Glick, P.; Clough, J.; Polaczyk, A.; Couvillion, B.; Nunley, B. Potential Effects of Sea-Level Rise on Coastal Wetlands in Southeastern Louisiana. J. Coast. Res. 2013, 63, 211–233. [Google Scholar] [CrossRef]
- Morris, J.T.; Sundareshwar, P.V.; Nietch, C.T.; Kjerfve, B.; Cahoon, D.R. Responses of coastal wetlands to rising sea level. Ecology 2002, 83, 2869–2877. [Google Scholar] [CrossRef]
- Brinson, M.M.; Christian, R.R.; Blum, L.K. Multiple States in the Sea-Level Induced Transition from Terrestrial Forest to Estuary. Estuaries 1995, 18, 648–659. [Google Scholar] [CrossRef]
- Smith, R.L. Ecology and Field Biology, 2nd ed.; Harper & Row: New York, NY, USA, 1974; p. 251. [Google Scholar]
- Noble, I.R. A Model of the Responses of Ecotones to Climate Change. Ecol. Appl. 1993, 3, 396–403. [Google Scholar] [CrossRef]
- White, E.E.; Ury, E.A.; Bernhardt, E.S.; Yang, X. Climate Change Driving Widespread Loss of Coastal Forested Wetlands throughout the North American Coastal Plain. Ecosystems 2021, 1–16. [Google Scholar] [CrossRef]
- Whitt, A.A.; Coleman, R.; Lovelock, C.E.; Gillies, C.; Ierodiaconou, D.; Liyanapathirana, M.; Macreadie, P.I. March of the mangroves: Drivers of encroachment into southern temperate saltmarsh. Estuar. Coast. Shelf Sci. 2020, 240, 106776. [Google Scholar] [CrossRef]
- Adam, P. Saltmarshes in a time of change. Environ. Conserv. 2002, 29, 39–61. [Google Scholar] [CrossRef]
- Leonardi, N.; Carnacina, I.; Donatelli, C.; Ganju, N.; Plater, A.J.; Schuerch, M.; Temmerman, S. Dynamic interactions between coastal storms and salt marshes: A review. Geomorphology 2018, 301, 92–107. [Google Scholar] [CrossRef] [Green Version]
- Fitzgerald, D.M.; Hughes, Z. Marsh Processes and Their Response to Climate Change and Sea-Level Rise. Annu. Rev. Earth Planet. Sci. 2019, 47, 481–517. [Google Scholar] [CrossRef] [Green Version]
- Di Nitto, D.; Neukermans, G.; Koedam, N.; Defever, H.; Pattyn, F.; Kairo, J.G.; Dahdouh-Guebas, F. Mangroves facing climate change: Landward migration potential in response to projected scenarios of sea level rise. Biogeosciences 2014, 11, 857–871. [Google Scholar] [CrossRef] [Green Version]
- Cavanaugh, K.C.; Kellner, J.R.; Forde, A.J.; Gruner, D.S.; Parker, J.D.; Rodriguez, W.; Feller, I.C. Poleward expansion of mangroves is a threshold response to decreased frequency of extreme cold events. Proc. Natl. Acad. Sci. USA 2014, 111, 723–727. [Google Scholar] [CrossRef] [Green Version]
- Eslami-Andargoli, L.; Dale, P.E.R.; Sipe, N.; Chaseling, J. Mangrove expansion and rainfall patterns in Moreton Bay, Southeast Queensland, Australia. Estuar. Coast. Shelf Sci. 2009, 85, 292–298. [Google Scholar] [CrossRef] [Green Version]
- Molino, G.D.; Defne, Z.; Aretxabaleta, A.L.; Ganju, N.K.; Carr, J.A. Quantifying Slopes as a Driver of Forest to Marsh Conversion Using Geospatial Techniques: Application to Chesapeake Bay Coastal-Plain, United States. Front. Environ. Sci. 2021, 9, 149. [Google Scholar] [CrossRef]
- Doody, J.P. ‘Coastal squeeze’—An historical perspective. J. Coast. Conserv. 2004, 10, 129–138. [Google Scholar] [CrossRef]
- Grieger, R.; Capon, S.; Hadwen, W. Resilience of coastal freshwater wetland vegetation of subtropical Australia to rising sea levels and altered hydrology. Reg. Environ. Chang. 2019, 19, 279–292. [Google Scholar] [CrossRef]
| Observed | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Forest | Mangrove | Marsh | Saltmarsh/Swamp | Terrestrial | Water | Total | PA (%) | UA (%) | ||
| Modeled | Forest | 34,754 | 0 | 1315 | 0 | 141 | 0 | 36,210 | 96.1 | 86.3 |
| Mangrove | 0 | 5435 | 0 | 2459 | 0 | 624 | 8518 | 63.9 | 91.1 | |
| Marsh | 5297 | 0 | 9848 | 0 | 1029 | 0 | 16,174 | 61.1 | 87.9 | |
| Saltmarsh/Swamp | 10 | 455 | 0 | 18,484 | 0 | 0 | 18,949 | 97.5 | 88.3 | |
| Terrestrial | 254 | 0 | 82 | 0 | 45,851 | 0 | 46,187 | 99.2 | 97.5 | |
| Water | 0 | 80 | 0 | 0 | 0 | 28,901 | 28,981 | 99.8 | 97.9 | |
| Total | 40,315 | 5970 | 11,245 | 20,943 | 47,021 | 29,525 | ||||
| Kappa | 0.90 | |||||||||
| OA (%) | 92.4 | |||||||||
| Wetland Type | Gain | Persistent | Loss | NC | SC | TC | G/P | L/P | L/G | |
|---|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | Forest | 5.94 | 31.16 | 12.85 | −6.91 | 11.87 | 18.78 | 0.19 | 0.41 | 2.16 |
| Mangrove | 15.00 | 3.59 | 1.25 | 13.75 | 2.49 | 16.25 | 4.18 | 0.35 | 0.08 | |
| Marsh | 1.49 | 1.59 | 6.98 | −5.50 | 2.98 | 8.47 | 0.93 | 4.38 | 4.69 | |
| Saltmarsh/Swamp | 6.62 | 0.36 | 9.90 | −3.28 | 13.24 | 16.52 | 18.55 | 27.74 | 1.50 | |
| Terrestrial | 2.28 | 19.40 | 1.60 | 0.68 | 3.19 | 3.88 | 0.12 | 0.08 | 0.70 | |
| Water | 1.25 | 11.33 | 0 | 1.25 | 0 | 1.25 | 0.11 | 0 | 0 | |
| Scenario 2 | Forest | 6.73 | 22.03 | 21.97 | −15.24 | 13.47 | 28.71 | 0.31 | 1.00 | 3.26 |
| Mangrove | 18.29 | 1.49 | 3.34 | 14.95 | 6.68 | 21.63 | 12.23 | 2.24 | 0.18 | |
| Marsh | 2.11 | 1.16 | 7.42 | −5.31 | 4.22 | 9.53 | 1.82 | 6.39 | 3.52 | |
| Saltmarsh/Swamp | 7.09 | 0 | 10.25 | −3.17 | 14.18 | 17.34 | 1.45 | |||
| Terrestrial | 1.25 | 18.33 | 2.67 | −1.42 | 2.49 | 3.91 | 0.07 | 0.15 | 2.14 | |
| Water | 10.19 | 11.33 | 0 | 10.19 | 0 | 10.19 | 0.90 | 0 | 0 | |
| Scenario 3 | Forest | 9.16 | 17.44 | 26.57 | −17.41 | 18.32 | 35.73 | 0.53 | 1.52 | 2.90 |
| Mangrove | 16.61 | 0.06 | 4.78 | 11.83 | 9.56 | 21.39 | 290.2 | 83.50 | 0.29 | |
| Marsh | 0.82 | 0.50 | 8.07 | −7.25 | 1.64 | 8.90 | 1.63 | 16.02 | 9.82 | |
| Saltmarsh/Swamp | 2.80 | 0 | 10.25 | −7.45 | 5.61 | 13.06 | 3.66 | |||
| Terrestrial | 0.10 | 17.41 | 3.59 | −3.48 | 0.21 | 3.69 | 0.01 | 0.21 | 34.80 | |
| Water | 23.76 | 11.33 | 0 | 23.76 | 0 | 23.76 | 2.10 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, L.; Hughes, M.G. Coastal Wetland Responses to Sea Level Rise: The Losers and Winners Based on Hydro-Geomorphological Settings. Remote Sens. 2022, 14, 1888. https://doi.org/10.3390/rs14081888
Wen L, Hughes MG. Coastal Wetland Responses to Sea Level Rise: The Losers and Winners Based on Hydro-Geomorphological Settings. Remote Sensing. 2022; 14(8):1888. https://doi.org/10.3390/rs14081888
Chicago/Turabian StyleWen, Li, and Michael G. Hughes. 2022. "Coastal Wetland Responses to Sea Level Rise: The Losers and Winners Based on Hydro-Geomorphological Settings" Remote Sensing 14, no. 8: 1888. https://doi.org/10.3390/rs14081888
APA StyleWen, L., & Hughes, M. G. (2022). Coastal Wetland Responses to Sea Level Rise: The Losers and Winners Based on Hydro-Geomorphological Settings. Remote Sensing, 14(8), 1888. https://doi.org/10.3390/rs14081888








