Automatic Relative Radiometric Normalization of Bi-Temporal Satellite Images Using a Coarse-to-Fine Pseudo-Invariant Features Selection and Fuzzy Integral Fusion Strategies
Abstract
:1. Introduction
- A coarse-to-fine approach is designed to efficiently extract reliable and well-spatially distributed PIFs from distinct ground surface clusters. Moreover, a hypothesis-based outlier detection was developed and embedded in this approach toefficiently refine the PIF candidates by taking advantage of the probability contour of the bivariate normal (BVN) joint distribution.
- The cluster-wise-RLR (CRLR) is proposed for better modeling the complex relationship between target and reference images with different LULC types. This model also contains a weight matrix defined based on the distance to PIFs that can reduce the potential bias in the results of RRN.
- A novel fusion-based framework is presented for RRN modeling that can integrate multiple normalized images using the Choquet integral as well as handle potential uncertainties, such as discontinues and bias in the final results.
2. Materials and Methods
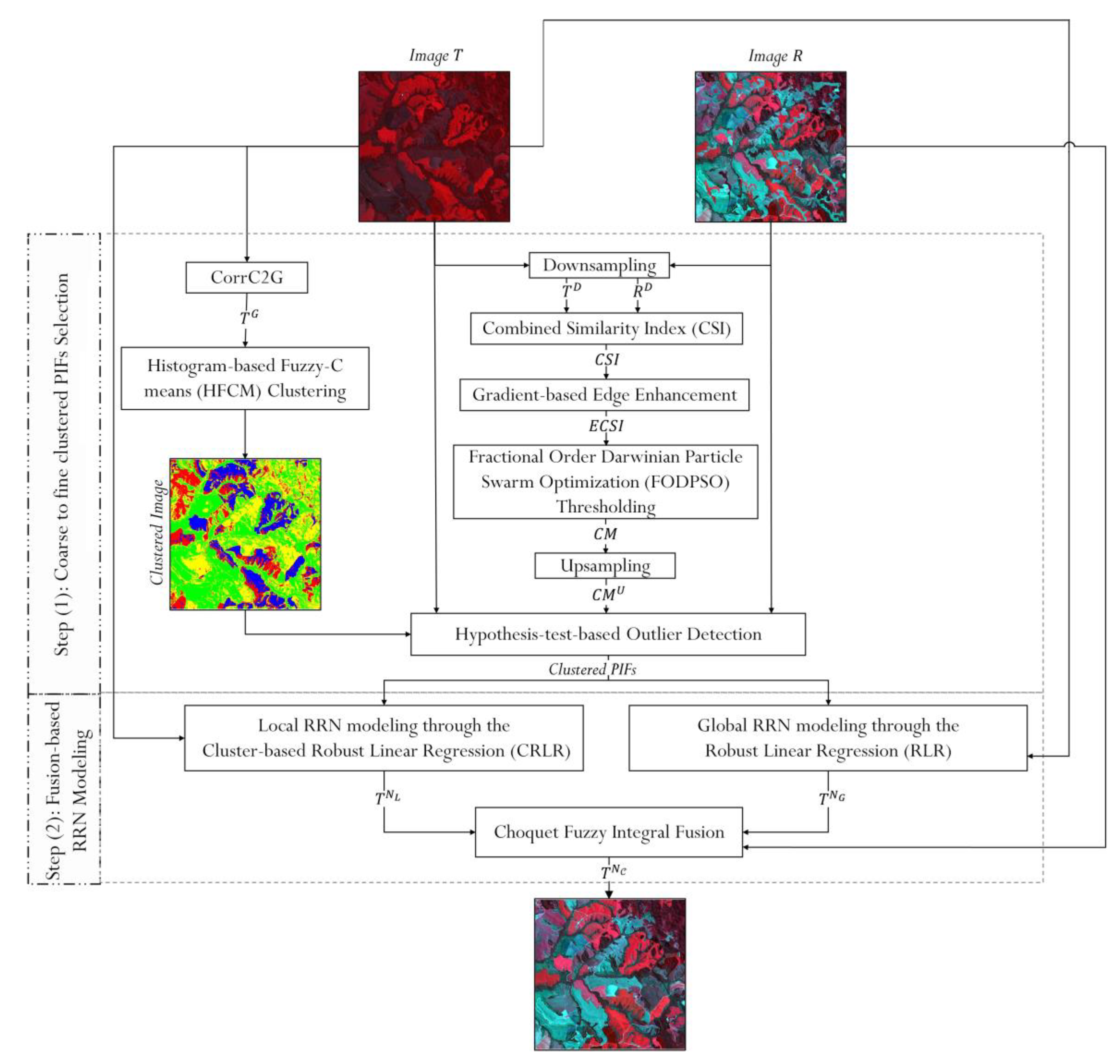
2.1. Proposed SRRN Method
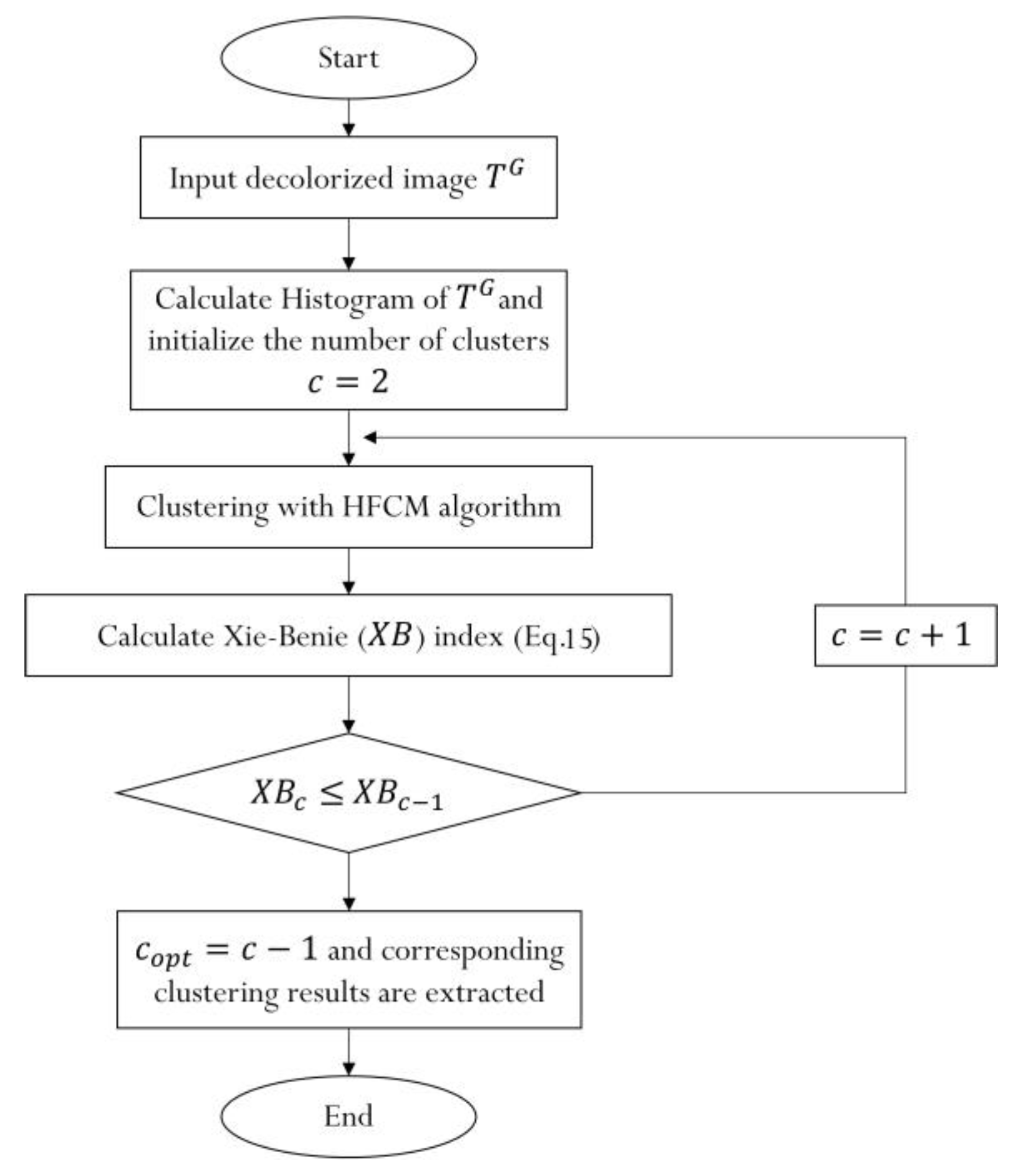
2.1.1. Step 1: Coarse-to-Fine Clustered PIFs Selection
2.1.2. Step 2: Fusion-Based RRN Modeling
2.2. Datasets
2.3. Evaluation Metrics
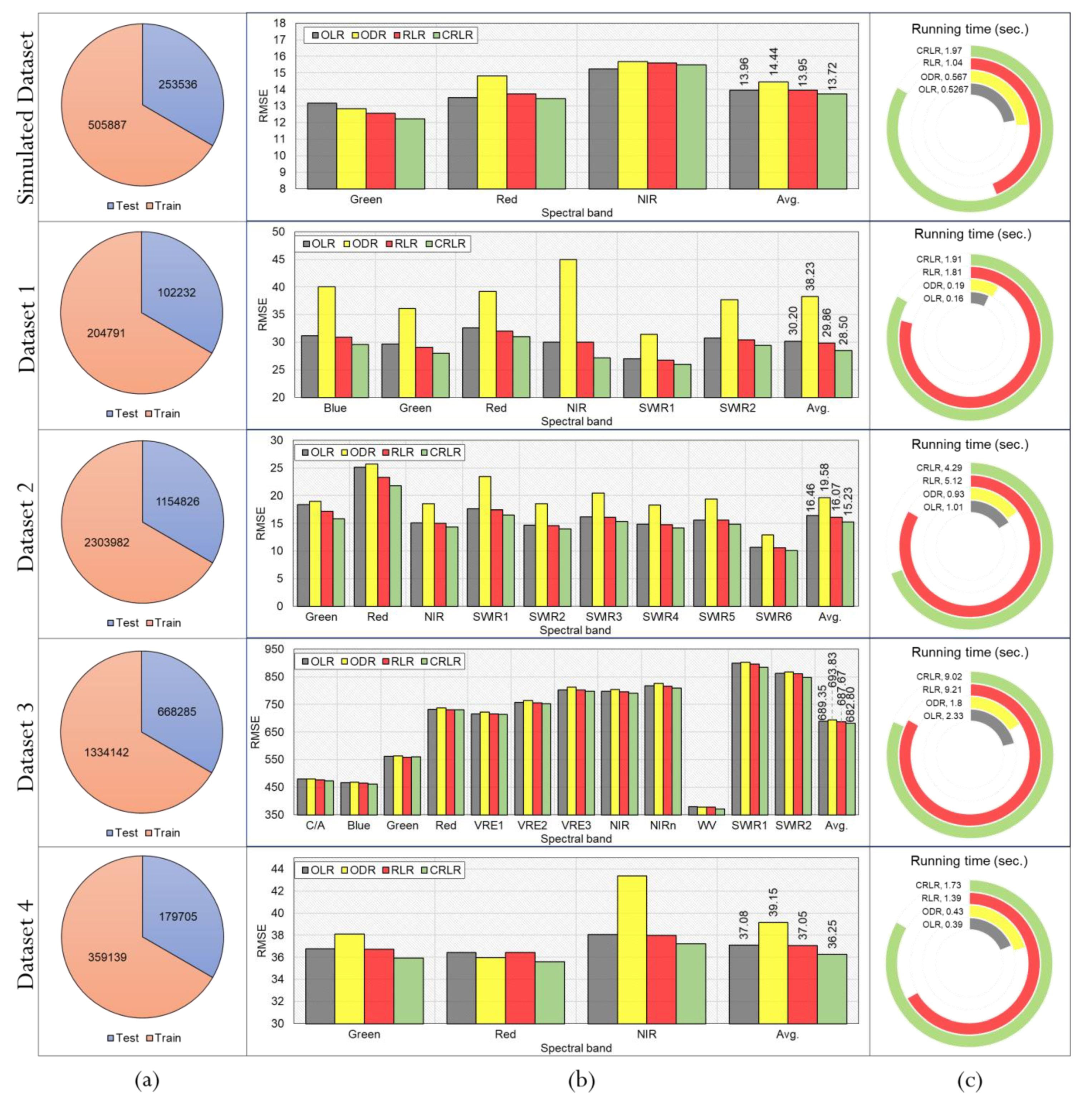
3. Experimental Results
3.1. Analysis of the Coarse-to-Fine PIFs Selection
3.2. Comparative Results of the RRN Modelling
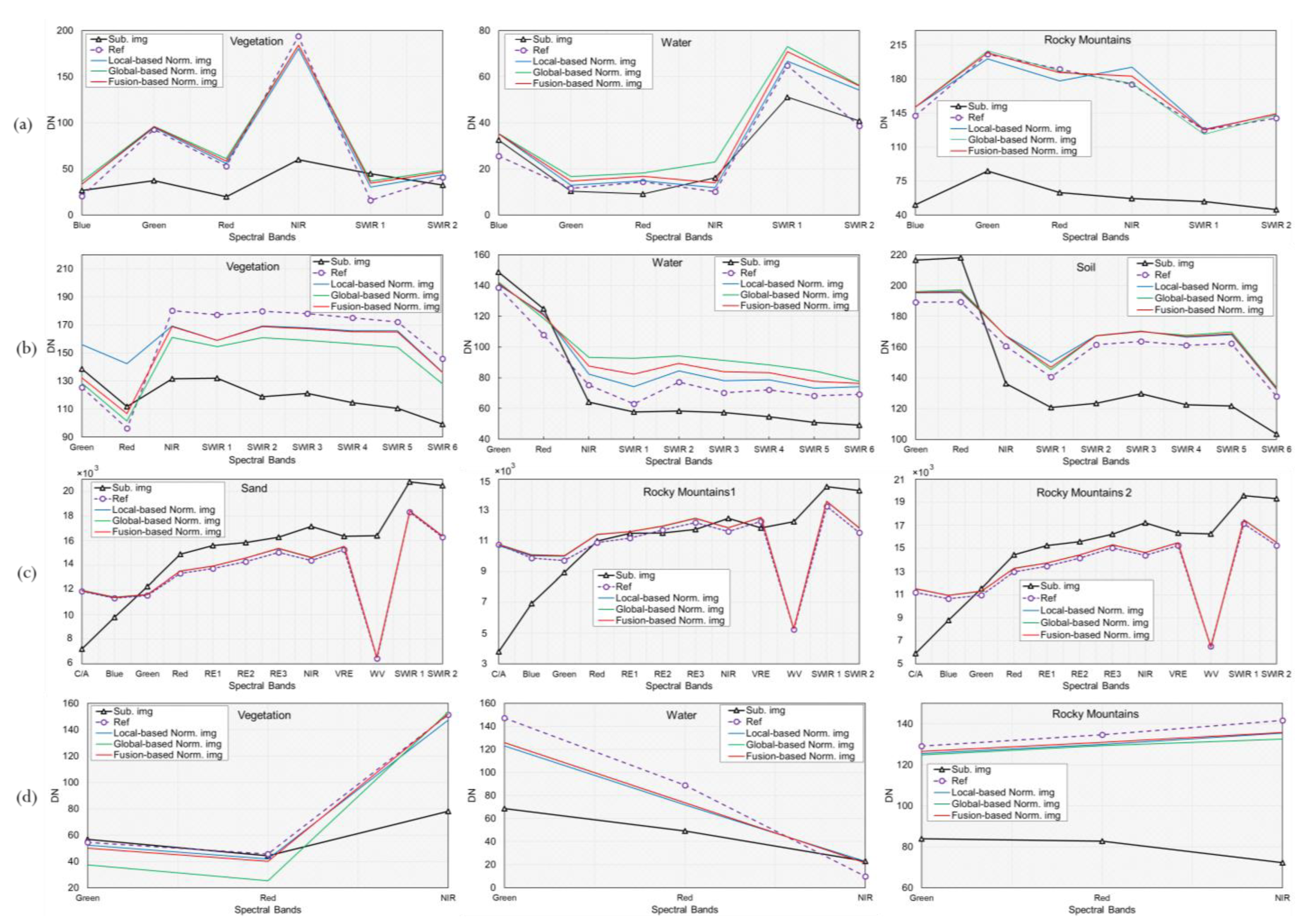
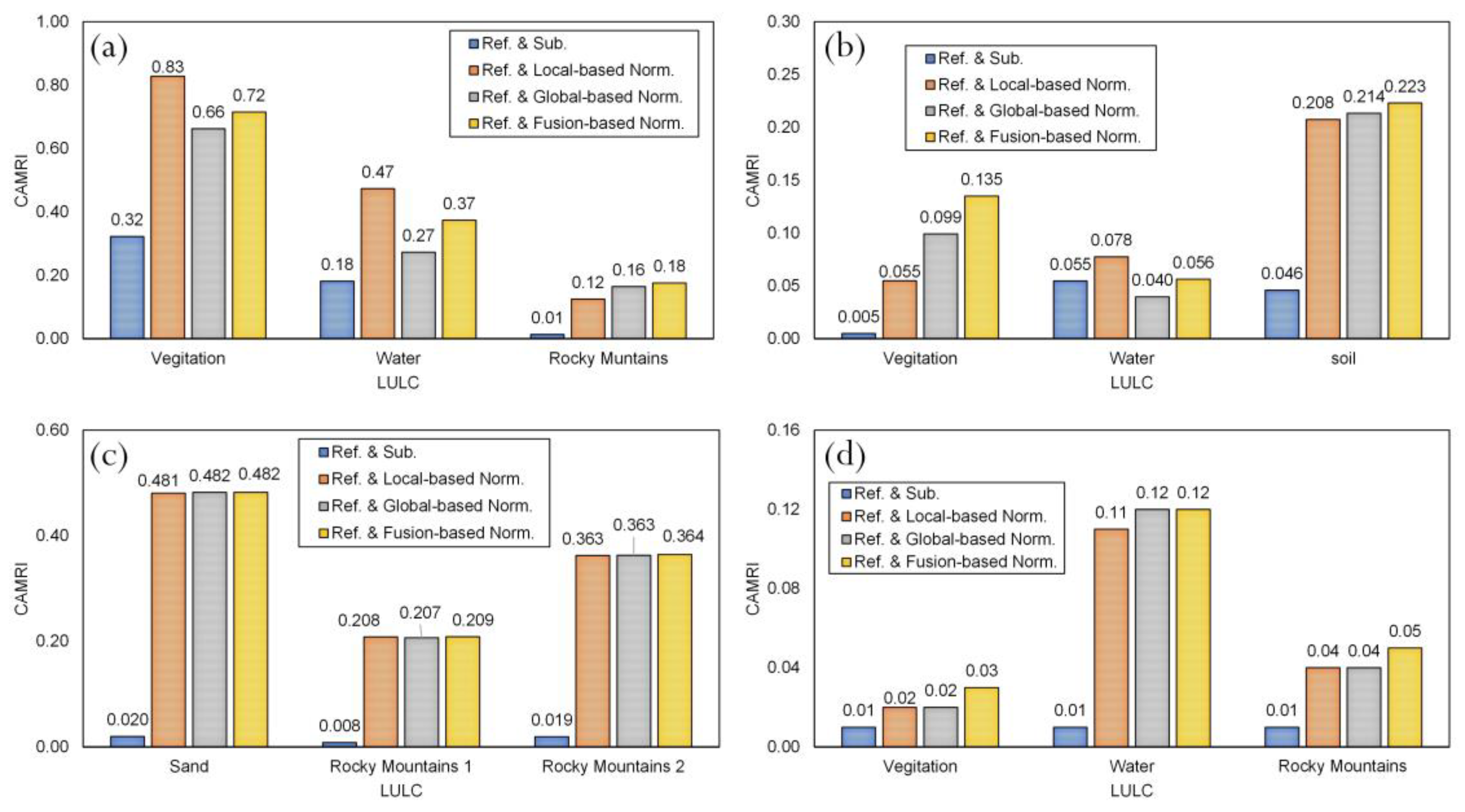
3.3. Effects of the Fusion-Based RRN Modelling
3.4. Comparative Results of the SRRN Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hall, F.G.; Strebel, D.E.; Nickeson, J.E.; Goetz, S.J. Radiometric Rectification: Toward a Common Radiometric Response among Multidate, Multisensor Images. Remote Sens. Environ. 1991, 35, 11–27. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Ding, Y.; Weerackoon, R.D.; Lunetta, R.S. Relative Radiometric Normalization of Landsat Multispectral Scanner (MSS) Data Using an Automatic Scattergram-Controlled Regression. Photogramm. Eng. Remote Sens. 1995, 61, 1255–1260. [Google Scholar]
- Moghimi, A.; Mohammadzadeh, A.; Celik, T.; Amani, M. A Novel Radiometric Control Set Sample Selection Strategy for Relative Radiometric Normalization of Multitemporal Satellite Images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2503–2519. [Google Scholar] [CrossRef]
- Moghimi, A.; Celik, T.; Mohammadzadeh, A.; Kusetogullari, H. Comparison of Keypoint Detectors and Descriptors for Relative Radiometric Normalization of Bitemporal Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4063–4073. [Google Scholar] [CrossRef]
- Yuan, D.; Elvidge, C.D. Comparison of Relative Radiometric Normalization Techniques. ISPRS J. Photogramm. Remote Sens. 1996, 51, 117–126. [Google Scholar] [CrossRef]
- Mohsenifar, A.; Mohammadzadeh, A.; Moghimi, A.; Salehi, B. A Novel Unsupervised Forest Change Detection Method Based on the Integration of a Multiresolution Singular Value Decomposition Fusion and an Edge-Aware Markov Random Field Algorithm. Int. J. Remote Sens. 2021, 42, 9376–9404. [Google Scholar] [CrossRef]
- Bazi, Y.; Melgani, F.; Al-Sharari, H.D. Unsupervised Change Detection in Multispectral Remotely Sensed Imagery with Level Set Methods. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3178–3187. [Google Scholar] [CrossRef]
- Wei, J.; Tang, W.; He, C. Enblending Mosaicked Remote Sensing Images with Spatiotemporal Fusion of Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5891–5902. [Google Scholar] [CrossRef]
- Yang, X.; Lo, C.P. Relative Radiometric Normalization Performance for Change Detection from Multi-Date Satellite Images. Photogramm. Eng. Remote Sens. 2000, 66, 967–980. [Google Scholar]
- Sadeghi, V.; Ebadi, H.; Ahmadi, F.F. A New Model for Automatic Normalization of Multitemporal Satellite Images Using Artificial Neural Network and Mathematical Methods. Appl. Math. Model. 2013, 37, 6437–6445. [Google Scholar] [CrossRef]
- Moghimi, A.; Sarmadian, A.; Mohammadzadeh, A.; Celik, T.; Amani, M.; Kusetogullari, H. Distortion Robust Relative Radiometric Normalization of Multitemporal and Multisensor Remote Sensing Images Using Image Features. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–20. [Google Scholar] [CrossRef]
- Du, Y.; Teillet, P.M.; Cihlar, J. Radiometric Normalization of Multitemporal High-Resolution Satellite Images with Quality Control for Land Cover Change Detection. Remote Sens. Environ. 2002, 82, 123–134. [Google Scholar] [CrossRef]
- Canty, M.J.; Nielsen, A.A.; Schmidt, M. Automatic Radiometric Normalization of Multitemporal Satellite Imagery. Remote Sens. Environ. 2004, 91, 441–451. [Google Scholar] [CrossRef]
- Nielsen, A.A.; Conradsen, K.; Simpson, J.J. Multivariate Alteration Detection (MAD) and MAF Postprocessing in Multispectral, Bitemporal Image Data: New Approaches to Change Detection Studies. Remote Sens. Environ. 1998, 64, 1–19. [Google Scholar] [CrossRef]
- Canty, M.J.; Nielsen, A.A. Automatic Radiometric Normalization of Multitemporal Satellite Imagery with the Iteratively Re-Weighted MAD Transformation. Remote Sens. Environ. 2008, 112, 1025–1036. [Google Scholar] [CrossRef]
- Nielsen, A.A. The Regularized Iteratively Reweighted MAD Method for Change Detection in Multi- and Hyperspectral Data. IEEE Trans. Image Process. 2007, 16, 463–478. [Google Scholar] [CrossRef]
- Ma, L.; Zhenhong, J.; Yang, J.; Kasabov, N. Multi-Spectral Image Change Detection Based on Single-Band Iterative Weighting and Fuzzy C-Means Clustering. Eur. J. Remote Sens. 2020, 53, 1–13. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, Z.; Li, F.; Yang, M.; Ren, H. The Regularized Iteratively Reweighted Object-Based MAD Method for Change Detection in Bi-Temporal, Multispectral Data. In Proceedings of the Hyperspectral Remote Sensing Applications and Environmental Monitoring and Safety Testing Technology, Beijing, China, 25 October 2016; Volume 10156. [Google Scholar] [CrossRef]
- Bai, Y.; Tang, P.; Hu, C. KCCA Transformation-Based Radiometric Normalization of Multi-Temporal Satellite Images. Remote Sens. 2018, 10, 432. [Google Scholar] [CrossRef]
- Liu, K.; Ke, T.; Tao, P.; He, J.; Xi, K.; Yang, K. Robust Radiometric Normalization of Multitemporal Satellite Images via Block Adjustment without Master Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6029–6043. [Google Scholar] [CrossRef]
- Byun, Y.; Han, D. Relative Radiometric Normalization of Bitemporal Very High-Resolution Satellite Images for Flood Change Detection. J. Appl. Remote Sens. 2018, 12, 26021. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, S.; He, J.; Wen, Q.; Song, L.; Ma, Y. A New Model for the Automatic Relative Radiometric Normalization of Multiple Images with Pseudo-Invariant Features. Int. J. Remote Sens. 2016, 37, 4554–4573. [Google Scholar] [CrossRef]
- Xu, H.; Wei, Y.; Li, X.; Zhao, Y.; Cheng, Q. A Novel Automatic Method on Pseudo-Invariant Features Extraction for Enhancing the Relative Radiometric Normalization of High-Resolution Images. Int. J. Remote Sens. 2021, 42, 6153–6183. [Google Scholar] [CrossRef]
- Ghanbari, H.; Homayouni, S.; Ghamisi, P.; Safari, A. Radiometric Normalization of Multitemporal and Multisensor Remote Sensing Images Based on a Gaussian Mixture Model and Error Ellipse. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4526–4533. [Google Scholar] [CrossRef]
- Yan, L.; Yang, J.; Zhang, Y.; Zhao, A.; Li, X. Radiometric Normalization for Cross-Sensor Optical Gaofen Images with Change Detection and Chi-Square Test. Remote Sens. 2021, 13, 3125. [Google Scholar] [CrossRef]
- Seo, D.K.; Kim, Y.H.; Eo, Y.D.; Park, W.Y.; Park, H.C. Generation of Radiometric, Phenological Normalized Image Based on Random Forest Regression for Change Detection. Remote Sens. 2017, 9, 1163. [Google Scholar] [CrossRef]
- Seo, D.K.; Eo, Y.D. Multilayer Perceptron-Based Phenological and Radiometric Normalization for High-Resolution Satellite Imagery. Appl. Sci. 2019, 9, 4543. [Google Scholar] [CrossRef]
- Denaro, L.G.; Lin, C.H. Hybrid Canonical Correlation Analysis and Regression for Radiometric Normalization of Cross-Sensor Satellite Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 976–986. [Google Scholar] [CrossRef]
- Sadeghi, V.; Ahmadi, F.F.; Ebadi, H. A New Automatic Regression-Based Approach for Relative Radiometric Normalization of Multitemporal Satellite Imagery. Comput. Appl. Math. 2017, 36, 825–842. [Google Scholar] [CrossRef]
- Ya’allah, S.M.; Saradjian, M.R. Automatic Normalization of Satellite Images Using Unchanged Pixels within Urban Areas. Inf. Fusion 2005, 6, 235–241. [Google Scholar] [CrossRef]
- He, H.; Liu, X.; Shen, Y. Relative Radiometric Correction of High-Resolution Remote Sensing Images Based on Feature Category. Cluster Comput. 2019, 22, 7933–7941. [Google Scholar] [CrossRef]
- Lo, C.-C.; Wang, S.-J. Video Segmentation Using a Histogram-Based Fuzzy c-Means Clustering Algorithm. Comput. Stand. Interfaces 2001, 23, 429–438. [Google Scholar] [CrossRef]
- Murofushi, T.; Sugeno, M. An Interpretation of Fuzzy Measures and the Choquet Integral as an Integral with Respect to a Fuzzy Measure. Fuzzy sets Syst. 1989, 29, 201–227. [Google Scholar] [CrossRef]
- Du, X.; Zare, A. Multiple Instance Choquet Integral Classifier Fusion and Regression for Remote Sensing Applications. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2741–2753. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The Spectral Image Processing System (SIPS)—Interactive Visualization and Analysis of Imaging Spectrometer Data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Ghamisi, P.; Couceiro, M.S.; Martins, F.M.L.; Benediktsson, J.A. Multilevel Image Segmentation Based on Fractional-Order Darwinian Particle Swarm Optimization. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2382–2394. [Google Scholar] [CrossRef]
- Teng, S.P.; Chen, Y.K.; Cheng, K.S.; Lo, H.C. Hypothesis-Test-Based Landcover Change Detection Using Multi-Temporal Satellite Images–A Comparative Study. Adv. Space Res. 2008, 41, 1744–1754. [Google Scholar] [CrossRef]
- Nafchi, H.Z.; Shahkolaei, A.; Hedjam, R.; Cheriet, M. CorrC2G: Color to Gray Conversion by Correlation. IEEE Signal Process. Lett. 2017, 24, 1651–1655. [Google Scholar] [CrossRef]
- Ghosh, A.; Mishra, N.S.; Ghosh, S. Fuzzy Clustering Algorithms for Unsupervised Change Detection in Remote Sensing Images. Inf. Sci. 2011, 181, 699–715. [Google Scholar] [CrossRef]
- Sadeghi, V.; Etemadfard, H. Optimal Cluster Number Determination of FCM for Unsupervised Change Detection in Remote Sensing Images. Earth Sci. Inform. 2022, 1–13. [Google Scholar] [CrossRef]
- Xie, X.L.; Beni, G. A Validity Measure for Fuzzy Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 841–847. [Google Scholar] [CrossRef]
- Holland, P.W.; Welsch, R.E. Robust Regression Using Iteratively Reweighted Least-Squares. Commun. Stat. Methods 1977, 6, 813–827. [Google Scholar] [CrossRef]
- Gross, A.M. Confidence Intervals for Bisquare Regression Estimates. J. Am. Stat. Assoc. 1977, 72, 341–354. [Google Scholar] [CrossRef]
- Abdullah, L.; Awang, N.A.; Othman, M. Application of Choquet Integral-Fuzzy Measures for Aggregating Customers’ Satisfaction. Adv. Fuzzy Syst. 2021, 2021, 2319004. [Google Scholar] [CrossRef]
- Wei, P.; Ball, J.E.; Anderson, D.T. Fusion of an Ensemble of Augmented Image Detectors for Robust Object Detection. Sensors 2018, 18, 894. [Google Scholar] [CrossRef] [PubMed]
- Shah, V.P.; Younan, N.H.; King, R.L. An Efficient Pan-Sharpening Method via a Combined Adaptive PCA Approach and Contourlets. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1323–1335. [Google Scholar] [CrossRef]
- Brodu, N. Super-Resolving Multiresolution Images with Band-Independent Geometry of Multispectral Pixels. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4610–4617. [Google Scholar] [CrossRef]
- Goldberger, A.S. Classical Linear Regression. Econom. Theory 1964, 156–212. [Google Scholar]
- Boggs, P.T.; Rogers, J.E. Orthogonal Distance Regression. Contemp. Math. 1990, 112, 183–194. [Google Scholar]




| Dataset | Reference/Target | Satellite (Sensor) | Band Type | Resolution | Image Size (Pixels) | Date | Study Area | |
|---|---|---|---|---|---|---|---|---|
| Spatial (m) | Radiometric (Bits) | |||||||
| # 1 | Reference | Landsat 7 (ETM+) | Blue, Green, Red, NIR *, SWIR * 1, SWIR 2 | 30 | 8 | 591 × 591 | September 2002 | Lago Mulargia lake, Cagliari, Italy |
| Target | May 2003 | |||||||
| # 2 | Reference | Terra (ASTER) | Green/Yellow, Red, NIR SWIR 1, SWIR 2, SWIR 3, SWIR 4, SWIR 5, SWIR 6, | 15/30 | 8 | 2000 × 2000 | July 2002 | Ahwaz, Khuzestan, Iran |
| Target | July 2003 | |||||||
| # 3 | Reference | Sentinel 2 (MSI) | C/A *, Blue, Green, Red, VRE * 1, VRE 2, VRE 3, NIR, NIRn *, WV *, SWIR 1, SWIR 2 | 10/20/60 | 12 | 1500 × 1500 | April 2016 | Hamoon wetland, Iran-Afghanistan border |
| Target | April 2018 | |||||||
| # 4 | Reference | IRS (LISSIII) | Green, Red, NIR | 23.5 | 8 | 900 × 900 | July 1998 | Varzaqan, East Azerbaijan Province, Iran |
| Target | May 2007 | |||||||
| Method | RMSE | Comp. Time (s) | |||
|---|---|---|---|---|---|
| Green | Red | NIR | Avg. | ||
| Raw 1 | 87.50 | 65.49 | 54.41 | 69.13 | ---- |
| IRMAD [15] | 22.07 | 28.84 | 21.01 | 23.97 | 8.16 |
| Multi-Otsu-based [29] | 34.97 | 46.85 | 41.33 | 41.05 | 7.83 |
| MPIF [22] | 18.09 | 29.80 | 28.80 | 25.56 | 8.77 |
| ASCR-RF-based [27] | 13.28 | 13.81 | 19.32 | 15.47 | 15.96 |
| GMM-EE [24] | 14.28 | 16.71 | 19.44 | 16.81 | 11.03 |
| HOG-based [31] | 12.59 | 16.51 | 9.36 | 12.82 | ---- |
| FLSM-based [3] | 16.19 | 16.92 | 12.31 | 15.14 | 14.44 |
| Proposed Method | 8.69 | 10.52 | 8.71 | 9.31 | 7.54 |
| Method | RMSE | Comp. Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|
| Blue | Green | Red | NIR | SWIR1 | SWIR2 | Avg. | ||
| Raw 1 | 63.84 | 80.96 | 79.80 | 121.17 | 95.41 | 91.72 | 88.82 | ---- |
| IRMAD [15] | 29.69 | 26.30 | 29.00 | 29.00 | 20.14 | 25.78 | 26.65 | 10.44 |
| Multi-Otsu-based [29] | 36.21 | 33.95 | 41.73 | 24.19 | 24.71 | 32.44 | 32.20 | 09.61 |
| MPIF [22] | 32.50 | 27.56 | 30.28 | 35.25 | 21.34 | 26.90 | 28.97 | 17.21 |
| ASCR-RF-based [27] | 58.39 | 40.29 | 37.91 | 25.58 | 23.93 | 29.00 | 35.85 | 21.02 |
| GMM-EE [24] | 30.81 | 28.57 | 31.50 | 23.44 | 22.61 | 28.52 | 27.57 | 14.94 |
| HOG-based [31] | 36.84 | 30.51 | 32.95 | 27.97 | 22.70 | 28.93 | 29.98 | ---- |
| FLSM-based [3] | 30.83 | 27.18 | 29.83 | 23.82 | 21.02 | 27.06 | 26.62 | 26.19 |
| Proposed Method | 26.60 | 23.53 | 25.76 | 21.59 | 18.78 | 23.68 | 23.32 | 10.04 |
| Method | RMSE | Comp. Time (s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Green | Red | NIR | SWIR1 | SWIR2 | SWIR3 | SWIR4 | SWIR5 | SWIR6 | Avg. | ||
| Raw 1 | 21.02 | 25.33 | 34.17 | 31.23 | 45.37 | 42.22 | 45.73 | 47.65 | 32.38 | 36.12 | ---- |
| IRMAD [15] | 14.54 | 19.99 | 15.84 | 19.53 | 15.74 | 16.44 | 15.20 | 15.34 | 12.44 | 16.12 | 30.12 |
| Multi-Otsu-based [29] | 19.06 | 26.21 | 20.47 | 22.84 | 20.14 | 21.36 | 19.88 | 20.20 | 15.38 | 20.62 | 29.11 |
| MPIF [22] | 14.92 | 21.39 | 18.45 | 22.37 | 18.08 | 19.05 | 17.59 | 17.80 | 14.05 | 18.19 | 40.01 |
| ASCR-RF-based [27] | 14.41 | 19.73 | 18.94 | 21.81 | 18.72 | 19.48 | 18.17 | 18.32 | 14.85 | 18.27 | 79.23 |
| GMM-EE [24] | 14.08 | 19.18 | 15.06 | 17.69 | 14.99 | 15.65 | 14.65 | 14.86 | 12.03 | 15.36 | 58.24 |
| HOG-based [31] | 14.49 | 18.83 | 13.44 | 16.24 | 13.25 | 14.20 | 13.13 | 13.58 | 10.26 | 14.16 | ---- |
| FLSM-based [3] | 14.35 | 19.48 | 16.30 | 18.72 | 16.19 | 16.98 | 15.85 | 16.17 | 12.90 | 16.33 | 95.26 |
| Proposed Method | 11.44 | 15.46 | 13.98 | 16.63 | 13.89 | 14.43 | 13.49 | 13.47 | 10.86 | 13.74 | 33.26 |
| Method | RMSE | Comp. Time (s) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C/A | Blue | Green | Red | VRE1 | VRE2 | VRE3 | NIR | NIRn | WV | SWIR1 | SWIR2 | Avg. | ||
| Raw 1 | 5500.07 | 2252.14 | 1067.89 | 1462.33 | 1633.91 | 1370.60 | 1229.10 | 2394.21 | 1141.94 | 9264.19 | 2160.05 | 3676.26 | 2762.72 | ----- |
| IRMAD [15] | 452.08 | 416.01 | 496.92 | 630.05 | 603.69 | 638.38 | 678.13 | 670.13 | 675.69 | 320.18 | 699.54 | 675.56 | 579.70 | 49.13 |
| Multi-Otsu-based [29] | 425.76 | 395.79 | 483.96 | 624.07 | 600.28 | 637.34 | 676.82 | 668.39 | 673.77 | 316.34 | 698.23 | 674.20 | 572.91 | 38.52 |
| MPIF [22] | 571.85 | 431.84 | 526.36 | 688.72 | 660.53 | 679.83 | 734.87 | 727.90 | 733.21 | 550.00 | 1132.36 | 784.99 | 685.21 | 42.94 |
| ASCR-RF-based [27] | 466.67 | 433.55 | 538.84 | 703.77 | 686.28 | 734.56 | 783.50 | 763.71 | 789.24 | 364.08 | 845.11 | 814.73 | 660.34 | 91.64 |
| GMM-EE [24] | 476.98 | 452.91 | 526.46 | 653.95 | 631.63 | 668.90 | 706.77 | 699.98 | 703.79 | 381.20 | 730.77 | 707.50 | 611.74 | 62.01 |
| HOG-based [31] | 1321.10 | 706.17 | 635.19 | 745.97 | 707.52 | 772.86 | 809.06 | 806.86 | 832.37 | 393.73 | 810.76 | 724.95 | 772.21 | ---- |
| FLSM-based [3] | 432.02 | 402.04 | 485.44 | 628.45 | 606.96 | 647.15 | 686.70 | 678.78 | 685.01 | 328.16 | 711.78 | 686.10 | 581.55 | 114.23 |
| Proposed Method | 421.15 | 389.92 | 482.63 | 621.99 | 598.18 | 634.77 | 673.96 | 664.97 | 669.78 | 312.80 | 693.43 | 668.66 | 569.35 | 45.88 |
| Method | RMSE | Comp. Time (s) | |||
|---|---|---|---|---|---|
| Green | Red | NIR | Avg. | ||
| Raw 1 | 55.60 | 58.83 | 76.86 | 63.77 | ---- |
| IRMAD [15] | 40.08 | 40.20 | 42.14 | 40.81 | 6.15 |
| Multi-Otsu-based [29] | 46.18 | 45.91 | 48.39 | 46.82 | 6.08 |
| MPIF [22] | 44.36 | 43.73 | 42.93 | 43.67 | 6.19 |
| ASCR-RF-based [27] | 41.14 | 47.32 | 49.62 | 46.02 | 8.96 |
| GMM-EE [24] | 37.54 | 37.42 | 39.07 | 38.01 | 8.29 |
| HOG-based [31] | 38.20 | 38.56 | 42.31 | 39.69 | --- |
| FLSM-based [3] | 40.61 | 39.13 | 41.78 | 40.51 | 13.65 |
| Proposed Method | 34.22 | 34.18 | 36.26 | 34.88 | 5.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moghimi, A.; Mohammadzadeh, A.; Celik, T.; Brisco, B.; Amani, M. Automatic Relative Radiometric Normalization of Bi-Temporal Satellite Images Using a Coarse-to-Fine Pseudo-Invariant Features Selection and Fuzzy Integral Fusion Strategies. Remote Sens. 2022, 14, 1777. https://doi.org/10.3390/rs14081777
Moghimi A, Mohammadzadeh A, Celik T, Brisco B, Amani M. Automatic Relative Radiometric Normalization of Bi-Temporal Satellite Images Using a Coarse-to-Fine Pseudo-Invariant Features Selection and Fuzzy Integral Fusion Strategies. Remote Sensing. 2022; 14(8):1777. https://doi.org/10.3390/rs14081777
Chicago/Turabian StyleMoghimi, Armin, Ali Mohammadzadeh, Turgay Celik, Brian Brisco, and Meisam Amani. 2022. "Automatic Relative Radiometric Normalization of Bi-Temporal Satellite Images Using a Coarse-to-Fine Pseudo-Invariant Features Selection and Fuzzy Integral Fusion Strategies" Remote Sensing 14, no. 8: 1777. https://doi.org/10.3390/rs14081777
APA StyleMoghimi, A., Mohammadzadeh, A., Celik, T., Brisco, B., & Amani, M. (2022). Automatic Relative Radiometric Normalization of Bi-Temporal Satellite Images Using a Coarse-to-Fine Pseudo-Invariant Features Selection and Fuzzy Integral Fusion Strategies. Remote Sensing, 14(8), 1777. https://doi.org/10.3390/rs14081777









