A Remotely Sensed Framework for Spatially-Detailed Dryland Soil Organic Matter Mapping: Coupled Cross-Wavelet Transform with Fractional Vegetation and Soil-Related Endmember Time Series
Abstract
:1. Introduction
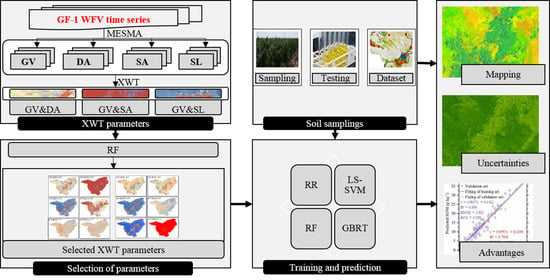
2. Materials and Methods
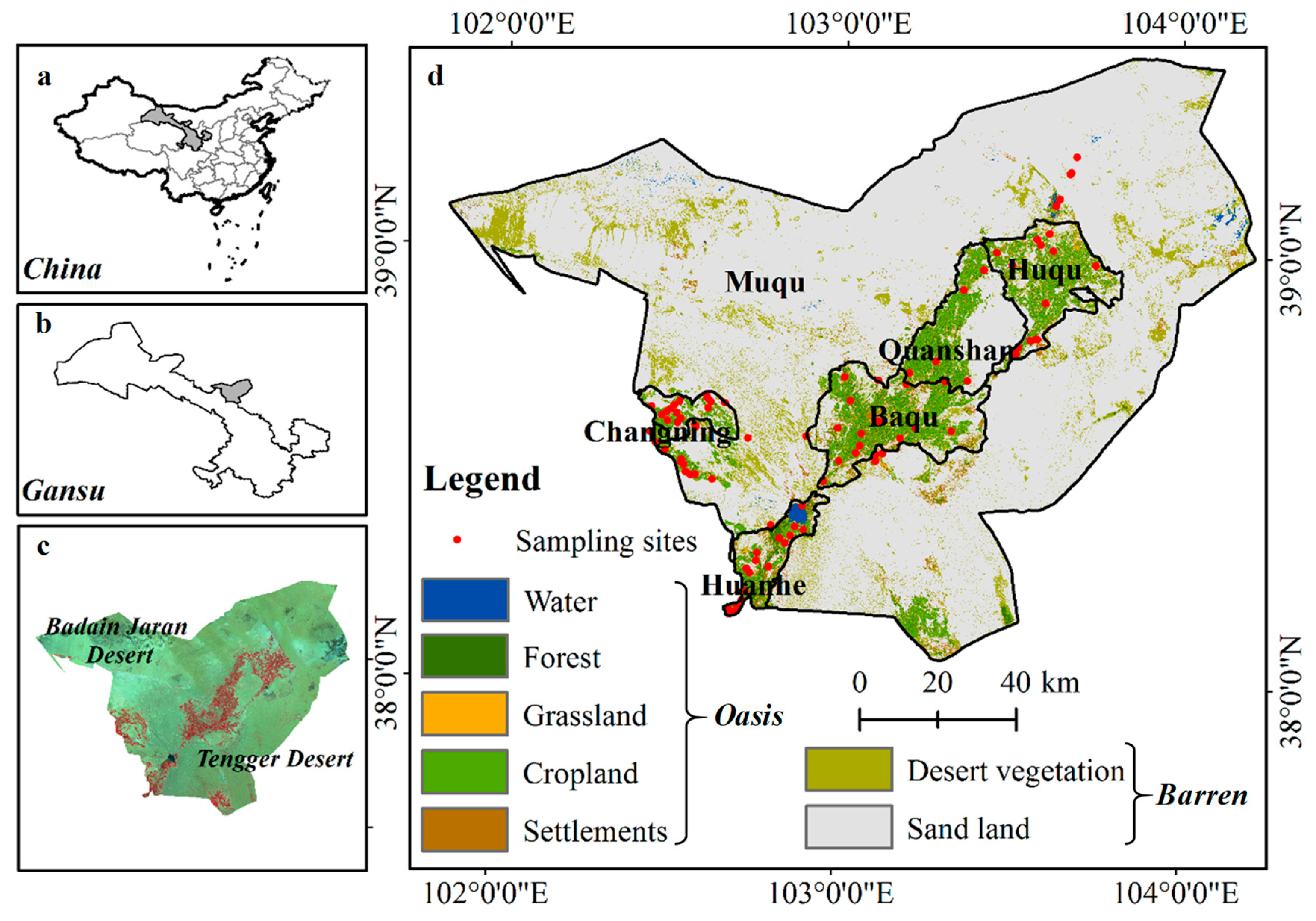
2.1. Study Area
2.2. Methods
2.2.1. Soil Sampling
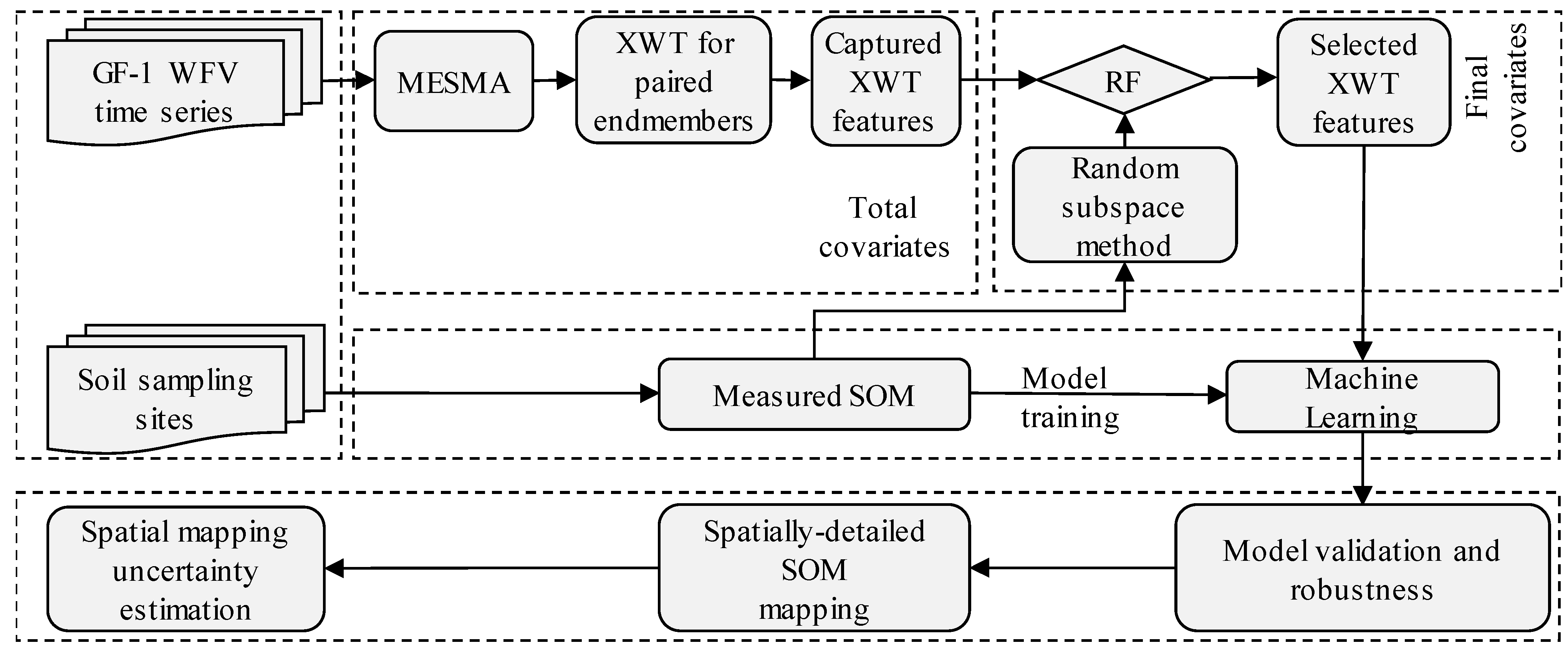
2.2.2. XWT Features Extraction from Endmember Sequences
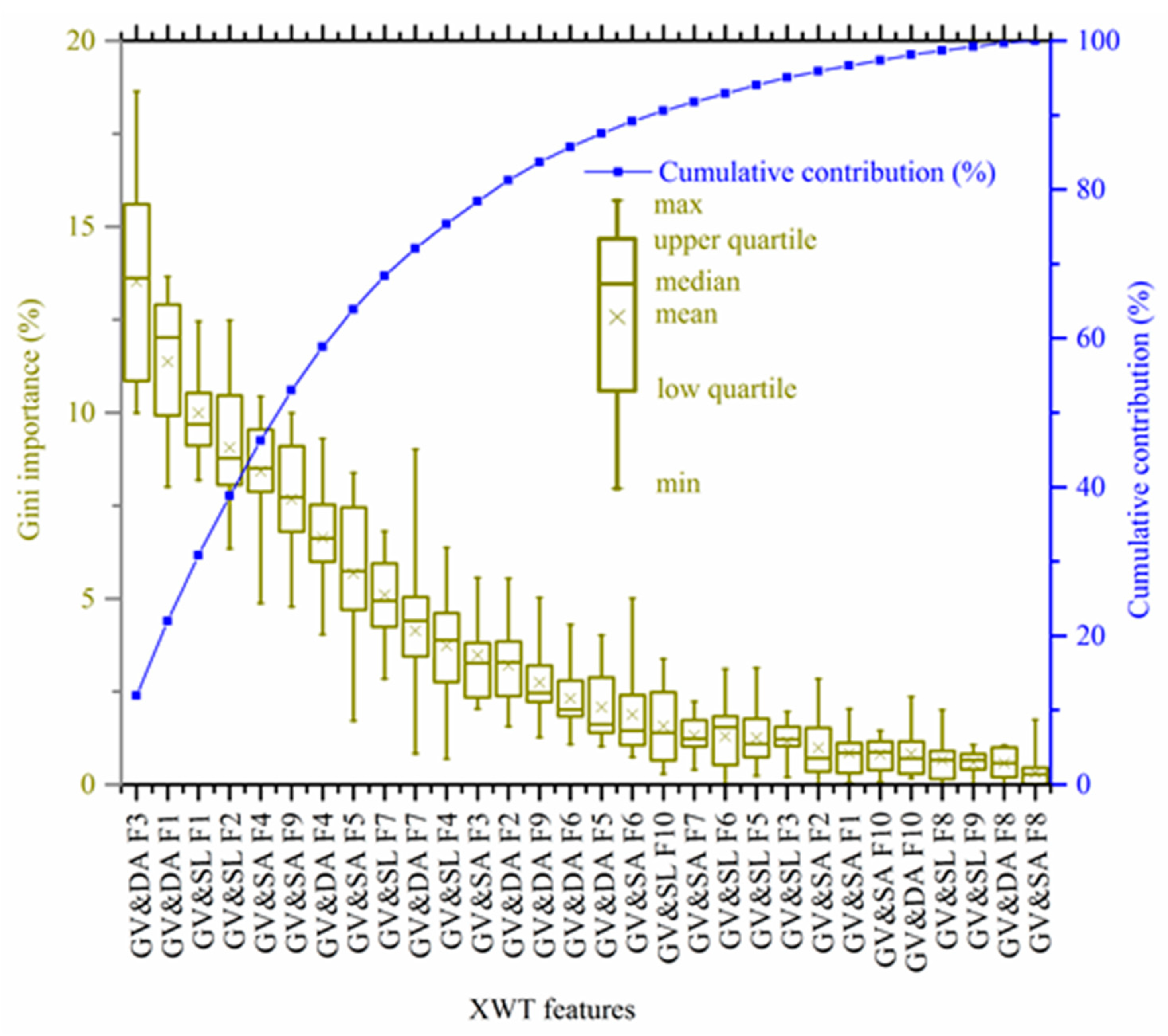
2.2.3. SOM Exploratory Covariates Selection
2.2.4. State-of-the-Art Machine Learning Approaches for SOM Mapping
2.2.5. Model Training and Validation
2.2.6. Spatially-Detailed SOM Mapping and Mapping Uncertainty Evaluation
2.3. Comparisons with Conventional Methods
3. Results
3.1. Selected XWT Features as SOM Covariates
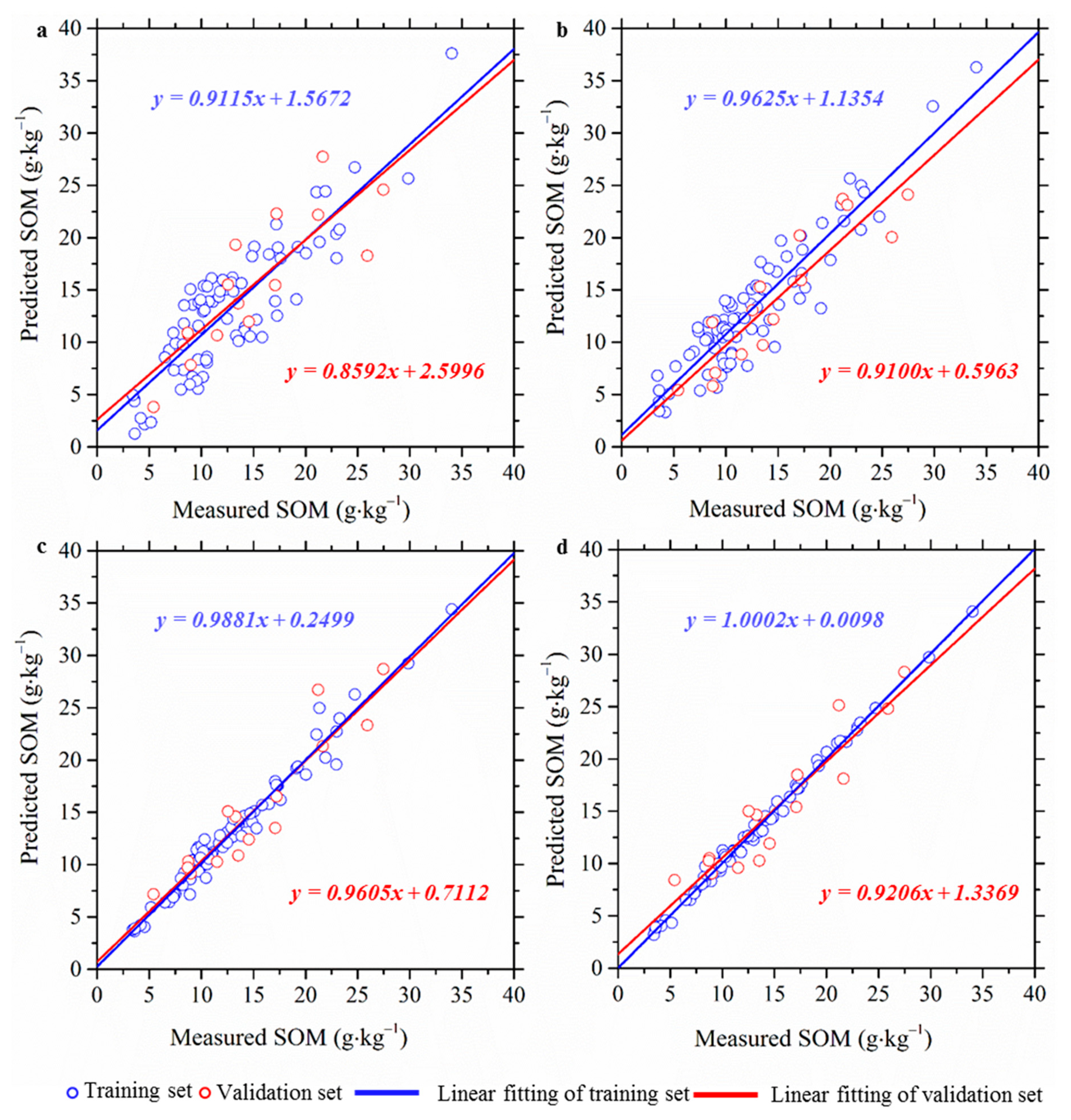
3.2. Performances of XWT-Based Framework
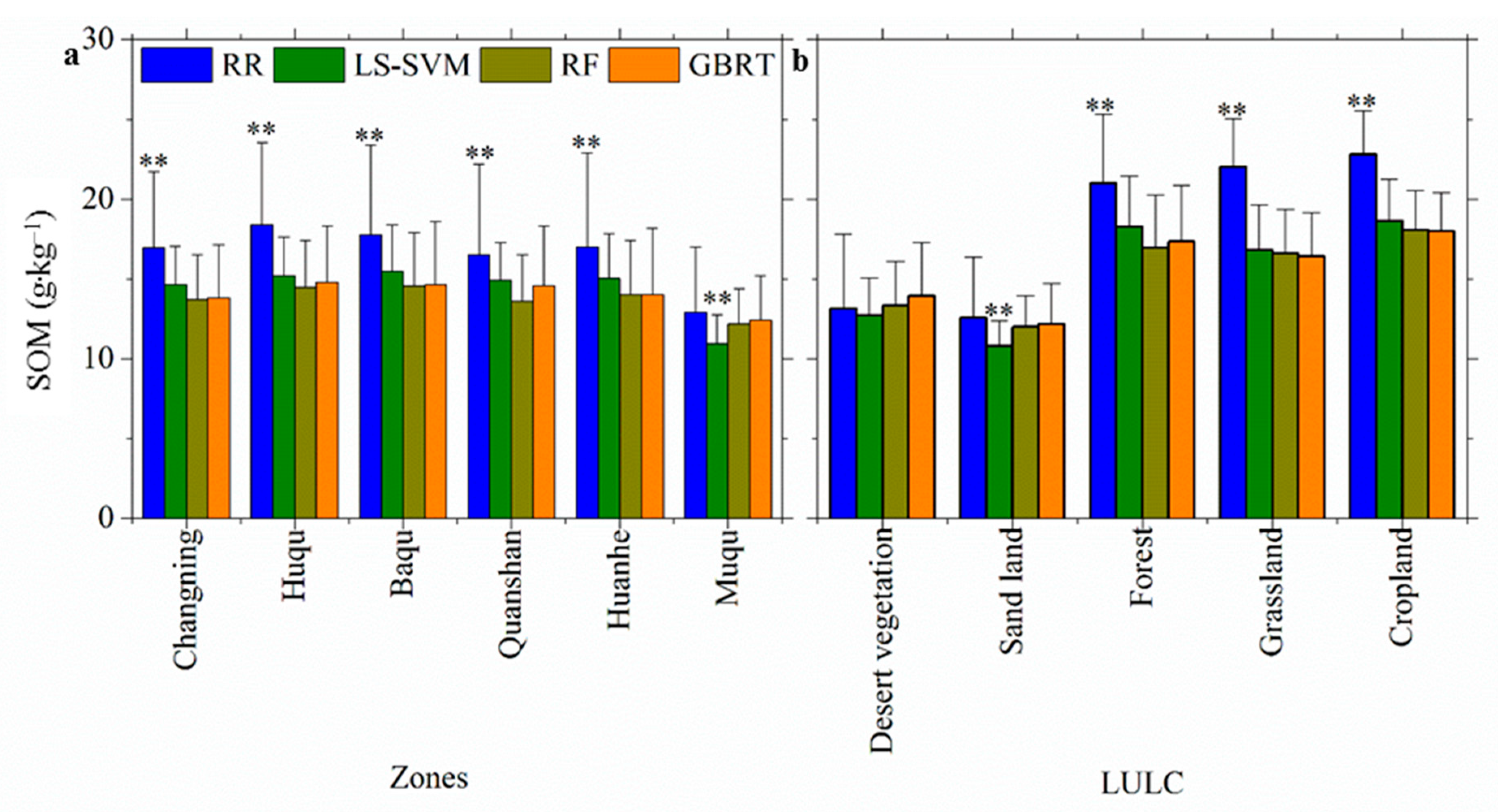
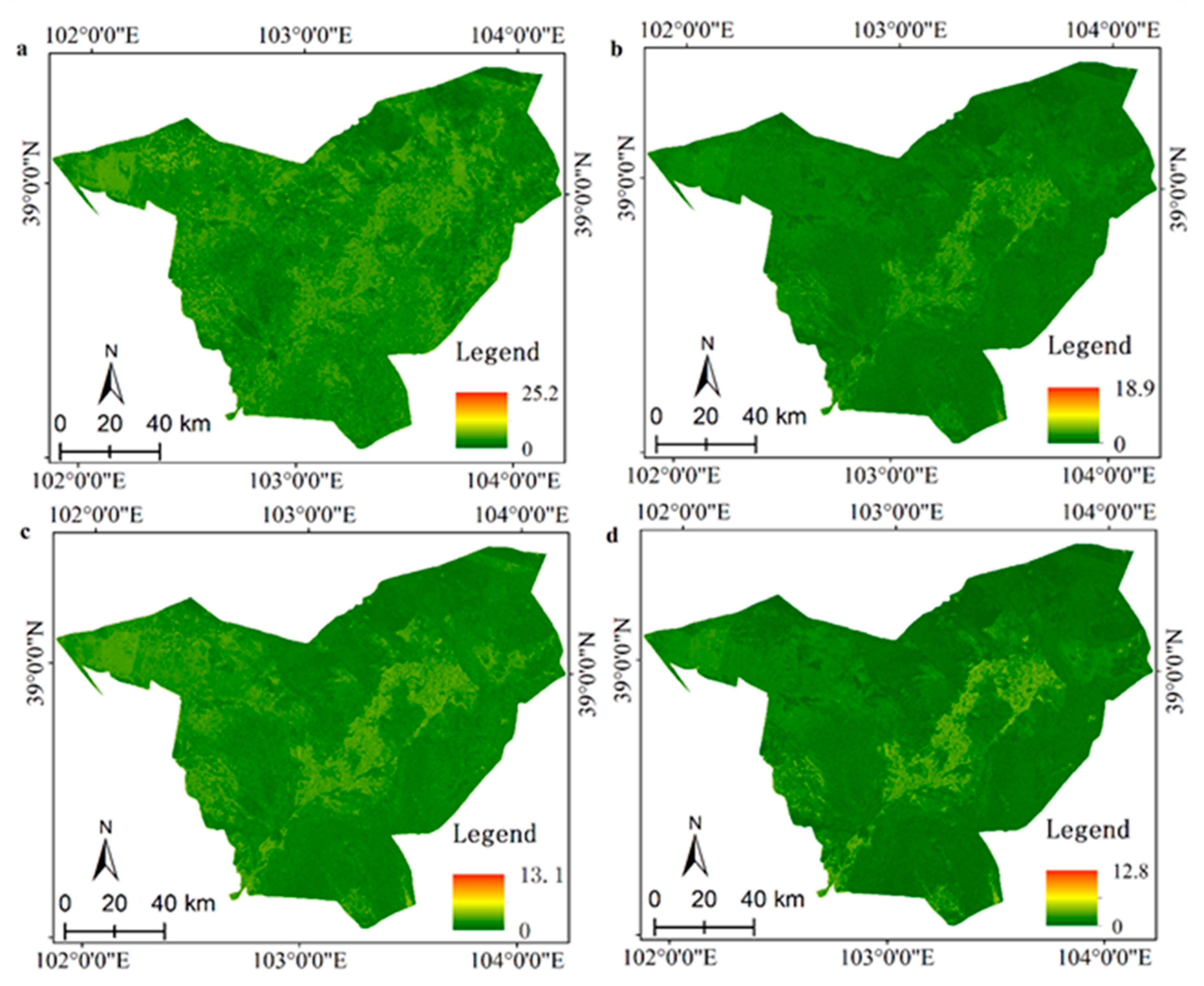
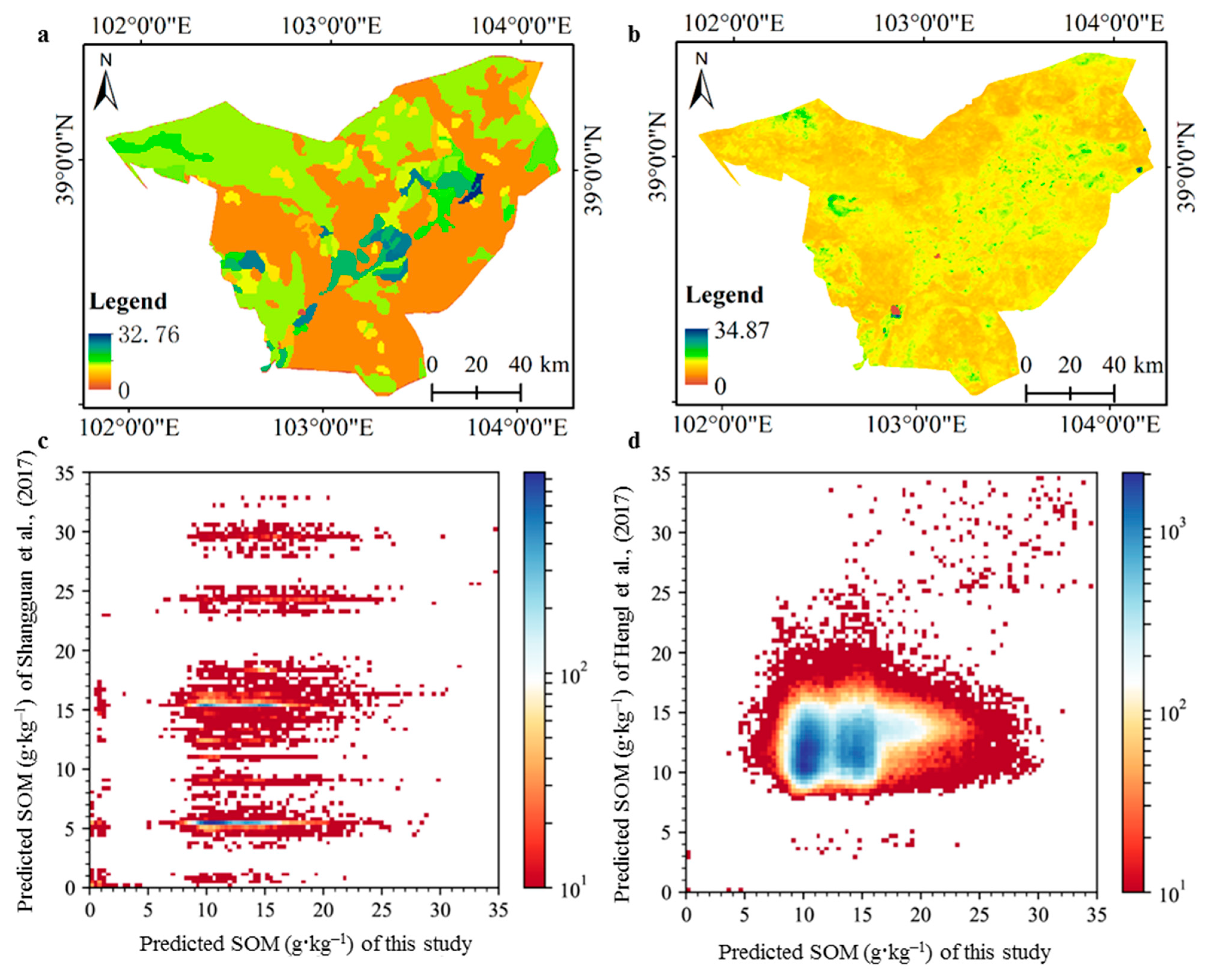
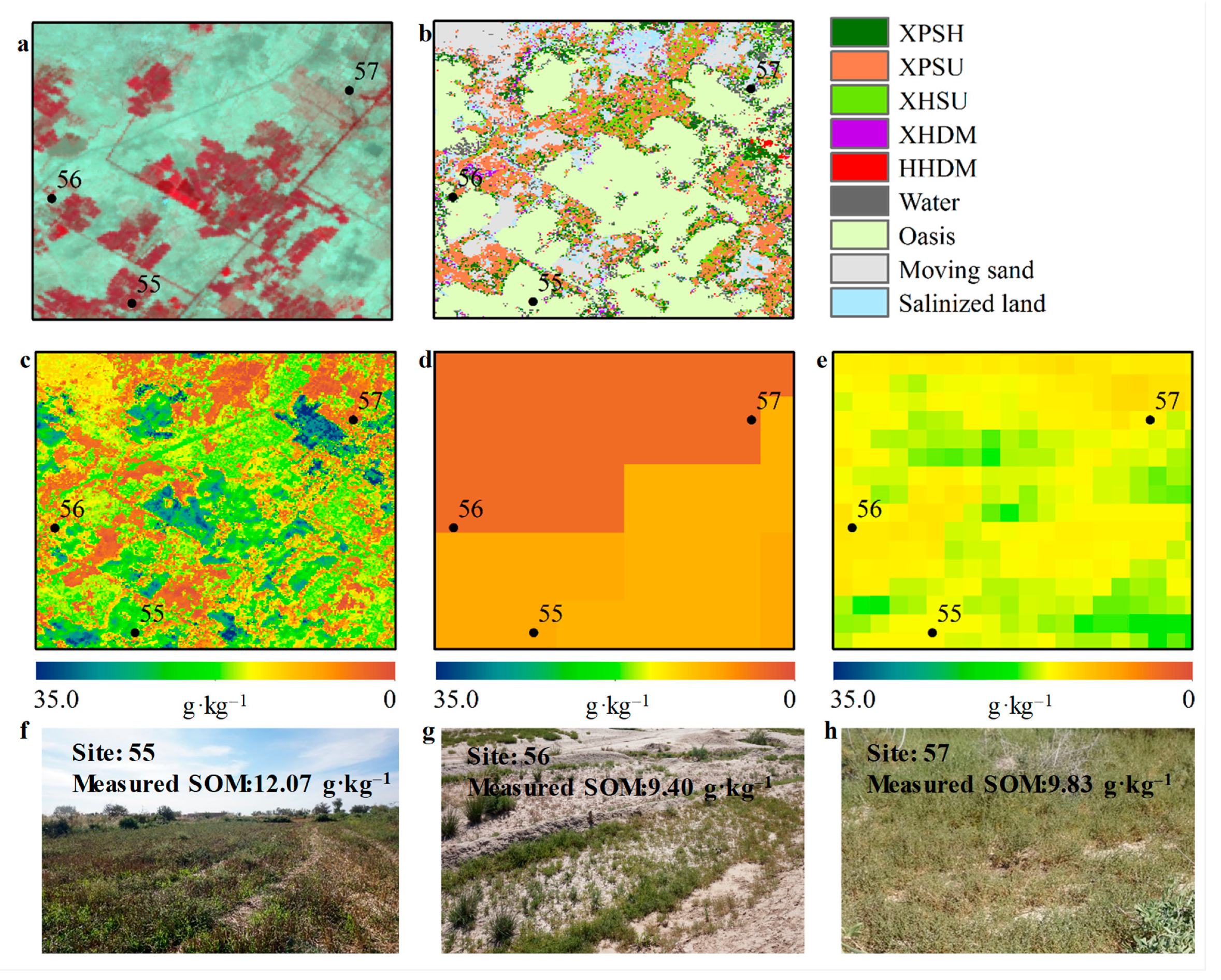
3.3. Spatially-Detailed SOM Mapping and Mapping Uncertainty Evaluation
3.4. Comparisons with Other Features and Existing Datasets
4. Discussion
4.1. Remotely Sensed Soil–Vegetation Interaction with XWT for Digital Soil Mapping
4.1.1. Soil–Vegetation Interaction Contributed to Digital Soil Mapping
4.1.2. XWT-Based Time-Series Features Extraction for Digital Soil Mapping
4.2. Future Applications and Outlook
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Middleton, N.; Thomas, D. World Atlas of Desertification; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Reynolds, J.F.; Smith, D.M.S.; Lambin, E.F.; Turner, B.L.; Mortimore, M.; Batterbury, S.P.; Downing, T.E.; Dowlatabadi, H.; Fernández, R.J.; Herrick, J.E.; et al. Global Desertification: Building a Science for Dryland Development. Science 2007, 316, 847–851. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Safriel, U.; Adeel, Z.; Niemeijer, D.; Puigdefabregas, J.; White, R.; Lal, R.; Winslow, M.; Ziedler, J.; Prince, S.; Archer, E.; et al. Dryland Systems, Ecosystems and Human Well-Being: Current State and Trends. Findings of the Condition and Trends Working Group; Island Press: Washington, DC, USA, 2020; pp. 623–662. [Google Scholar]
- Giuliani, G.; Mazzetti, P.; Santoro, M.; Nativi, S.; Van Bemmelen, J.; Colangeli, G.; Lehmann, A. Knowledge generation using satellite earth observations to support sustainable development goals (SDG): A use case on Land degradation. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102068. [Google Scholar] [CrossRef]
- UN Convention to Combat Desertification (UNCCD). A Stronger UNCCD for a Land-Degradation Neutral World; Issue Brief; UNCCD: Bonn, Germany, 2013. [Google Scholar]
- Orr, B.J.; Cowie, A.L.; Castillo Sanchez, V.M.; Chasek, P.; Crossman, N.D.; Erlewein, A.; Louwagie, G.; Maron, M.; Metternicht, G.I.; Minelli, S. Scientific conceptual framework for land degradation neutrality. In A Report of the Science-Policy Interface; United Nations Convention to Combat Desertification (UNCCD): Bonn, Germany, 2017. [Google Scholar]
- Cowie, A.L.; Orr, B.J.; Sanchez, V.M.C.; Chasek, P.; Crossman, N.D.; Erlewein, A.; Louwagie, G.; Maron, M.; Metternicht, G.I.; Minelli, S.; et al. Land in balance: The scientific conceptual framework for Land Degradation Neutrality. Environ. Sci. Policy 2018, 79, 25–35. [Google Scholar] [CrossRef]
- Altieri, M.A. The ecological role of biodiversity in agroecosystems. Agric. Ecosyst. Environ. 1999, 74, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, J.; Kleber, M. The contentious nature of soil organic matter. Nature 2015, 528, 60–68. [Google Scholar] [CrossRef]
- Parry, M.; Parry, M.L.; Canziani, O.; Palutikof, J.; Van der Linden, P.; Hanson, C. Climate Change 2007-Impacts, Adaptation and Vulnerability: Working Group II Contribution to the Fourth Assessment Report of the IPCC; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Pan, G.; Smith, P.; Pan, W. The role of soil organic matter in maintaining the productivity and yield stability of cereals in China. Agric. Ecosyst. Environ. 2009, 129, 344–348. [Google Scholar] [CrossRef]
- Schmidt, M.W.I.; Torn, M.S.; Abiven, S.; Dittmar, T.; Guggenberger, G.; Janssens, I.A.; Kleber, M.; Kögel-Knabner, I.; Lehmann, J.; Manning, D.A.C.; et al. Persistence of soil organic matter as an ecosystem property. Nature 2011, 478, 49–56. [Google Scholar] [CrossRef] [Green Version]
- Tiessen, H.; Cuevas, E.; Chacón, P. The role of soil organic matter in sustaining soil fertility. Nature 1994, 371, 783–785. [Google Scholar] [CrossRef]
- Sun, D.; Zhang, P.; Sun, Q.; Jiang, W. A dryland cover state mapping using catastrophe model in a spectral endmember space of OLI: A case study in Minqin, China. Int. J. Remote Sens. 2019, 40, 5673–5694. [Google Scholar] [CrossRef]
- Minasny, B.; Malone, B.P.; McBratney, A.; Angers, D.A.; Arrouays, D.; Chambers, A.; Chaplot, V.; Chen, Z.-S.; Cheng, K.; Das, B.S.; et al. Soil carbon 4 per mille. Geoderma 2017, 292, 59–86. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Chabrillat, S.; Demattê, J.A.M.; Taylor, G.R.; Hill, J.; Whiting, M.L.; Sommer, S. Using imaging spectroscopy to study soil properties. Remote Sens. Environ. 2009, 113 (Suppl. 1), S38–S55. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, H.; Zhang, M.; Yang, H.; Jin, Y.; Han, Y.; Tang, H.; Zhang, X.; Zhang, X. Mapping Soil Organic Matter and Analyzing the Prediction Accuracy of Typical Cropland Soil Types on the Northern Songnen Plain. Remote Sens. 2021, 13, 5162. [Google Scholar] [CrossRef]
- Mulder, V.; de Bruin, S.; Schaepman, M.; Mayr, T. The use of remote sensing in soil and terrain mapping—A review. Geoderma 2011, 162, 1–19. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, M.; Yang, H.; Jin, Y.; Zhang, X.; Liu, H. Mapping Regional Soil Organic Matter Based on Sentinel-2A and MODIS Imagery Using Machine Learning Algorithms and Google Earth Engine. Remote Sens. 2021, 13, 2934. [Google Scholar] [CrossRef]
- Shangguan, W.; Dai, Y.; Liu, B.; Zhu, A.; Duan, Q.; Wu, L.; Ji, D.; Ye, A.; Yuan, H.; Zhang, Q.; et al. A China data set of soil properties for land surface modeling. J. Adv. Model. Earth Syst. 2013, 5, 212–224. [Google Scholar] [CrossRef]
- Hengl, T.; De Jesus, J.M.; Heuvelink, G.B.M.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, L.; Fu, P.; Shi, T.; Chen, Y.; Zhang, H.; Meng, R.; Wang, S. Mapping field-scale soil organic carbon with unmanned aircraft system-acquired time series multispectral images. Soil Tillage Res. 2020, 196, 104477. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, X.; Meng, X.; Zhu, H.; Ni, C.; Chen, M.; Liu, H. Regional mapping of soil organic matter content using multitemporal synthetic Landsat 8 images in Google Earth Engine. CATENA 2022, 209, 105842. [Google Scholar] [CrossRef]
- Guo, P.-T.; Li, M.-F.; Luo, W.; Tang, Q.-F.; Liu, Z.-W.; Lin, Z.-M. Digital mapping of soil organic matter for rubber plantation at regional scale: An application of random forest plus residuals kriging approach. Geoderma 2015, 237, 49–59. [Google Scholar] [CrossRef]
- Luo, C.; Wang, Y.; Zhang, X.; Zhang, W.; Liu, H. Spatial prediction of soil organic matter content using multiyear synthetic images and partitioning algorithms. CATENA 2022, 211, 106023. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, S.; Yang, Y.; Zhao, R.; Shi, Z.; Viscarra, R.R.A. Baseline map of soil organic matter in china and its associated uncertainty. Geoderma 2019, 335, 47–56. [Google Scholar] [CrossRef]
- Wang, S.; Fan, J.; Zhong, H.; Li, Y.; Zhu, H.; Qiao, Y.; Zhang, H. A multi-factor weighted regression approach for estimating the spatial distribution of soil organic carbon in grasslands. CATENA 2019, 174, 248–258. [Google Scholar] [CrossRef]
- Tayebi, M.; Rosas, J.F.; Mendes, W.; Poppiel, R.; Ostovari, Y.; Ruiz, L.; dos Santos, N.; Cerri, C.; Silva, S.; Curi, N.; et al. Drivers of Organic Carbon Stocks in Different LULC History and along Soil Depth for a 30 Years Image Time Series. Remote Sens. 2021, 13, 2223. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Sankey, T.T.; Weber, K.T. Rangeland Assessments Using Remote Sensing: Is NDVI Useful. Final Report: Comparing Effects of Management Practices on Rangeland Health with Geospatial Technologies; NNX06AE47G: Pocatello, ID, USA, 2009; p. 168. [Google Scholar]
- Smith, W.K.; Dannenberg, M.P.; Yan, D.; Herrmann, S.; Barnes, M.L.; Barron-Gafford, G.A.; Biederman, J.A.; Ferrenberg, S.; Fox, A.M.; Hudson, A.; et al. Remote sensing of dryland ecosystem structure and function: Progress, challenges, and opportunities. Remote Sens. Environ. 2019, 233, 111401. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modeling: A new analysis of rock and soil types at the Viking Lander 1 Site. J. Geophys. Res. Earth Surf. 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
- Roberts, D.; Smith, M.; Adams, J. Green vegetation, nonphotosynthetic vegetation, and soils in AVIRIS data. Remote Sens. Environ. 1993, 44, 255–269. [Google Scholar] [CrossRef]
- Small, C. The Landsat ETM+ spectral mixing space. Remote Sens. Environ. 2004, 93, 1–17. [Google Scholar] [CrossRef]
- Van Der Meer, F. Spectral unmixing of Landsat Thematic Mapper data. Int. J. Remote Sens. 1995, 16, 3189–3194. [Google Scholar] [CrossRef]
- Dawelbait, M.; Morari, F. Monitoring desertification in a Savannah region in Sudan using Landsat images and spectral mixture analysis. J. Arid Environ. 2012, 80, 45–55. [Google Scholar] [CrossRef]
- Sun, D.; Liu, N. Coupling spectral unmixing and multiseasonal remote sensing for temperate dryland land-use/land-cover mapping in Minqin County, China. Int. J. Remote Sens. 2015, 36, 3636–3658. [Google Scholar] [CrossRef]
- Sun, D. Detection of dryland degradation using Landsat spectral unmixing remote sensing with syndrome concept in Minqin County, China. Int. J. Appl. Earth Obs. Geoinf. 2015, 41, 34–45. [Google Scholar] [CrossRef]
- Sun, D.; Jiang, W. Agricultural Soil Alkalinity and Salinity Modeling in the Cropping Season in a Spectral Endmember Space of TM in Temperate Drylands, Minqin, China. Remote Sens. 2016, 8, 714. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Waters, C.; Orgill, S.; Cowie, A.; Clark, A.; Liu, D.L.; Simpson, M.; McGowen, I.; Sides, T. Estimating soil organic carbon stocks using different modelling techniques in the semi-arid rangelands of eastern Australia. Ecol. Indic. 2018, 88, 425–438. [Google Scholar] [CrossRef]
- Stavros, E.N.; Schimel, D.; Pavlick, R.; Serbin, S.; Swann, A.; Duncanson, L.; Fisher, J.B.; Fassnacht, F.; Ustin, S.; Dubayah, R.; et al. ISS observations offer insights into plant function. Nat. Ecol. Evol. 2017, 1, 194. [Google Scholar] [CrossRef] [PubMed]
- Maynard, J.J.; Levi, M.R. Hyper-temporal remote sensing for digital soil mapping: Characterizing soil-vegetation response to climatic variability. Geoderma 2017, 285, 94–109. [Google Scholar] [CrossRef] [Green Version]
- Wilson, C.H.; Caughlin, T.T.; Rifai, S.W.; Boughton, E.H.; Mack, M.C.; Flory, S.L. Multi-decadal time series of remotely sensed vegetation improves prediction of soil carbon in a subtropical grassland. Ecol. Appl. 2017, 27, 1646–1656. [Google Scholar] [CrossRef]
- Yang, R.-M.; Guo, W.-W. Modelling of soil organic carbon and bulk density in invaded coastal wetlands using Sentinel-1 imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101906. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, L.; Chen, Y.; Shi, T.; Luo, M.; Ju, Q.; Zhang, H.; Wang, S. Prediction of Soil Organic Carbon based on Landsat 8 Monthly NDVI Data for the Jianghan Plain in Hubei Province, China. Remote Sens. 2019, 11, 1683. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Zhang, P.; Sun, D.; Liu, A.; Dai, J. Desert vegetation-habitat complexes mapping using Gaofen-1 WFV (wide field of view) time series images in Minqin County, China. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 522–534. [Google Scholar] [CrossRef]
- Fayyad, U.; Piatesky-Shapiro, G.; Smyth, P.; Uthurusamy, R. Advances in Knowledge Discovery and Data Mining; MIT Press: Cambridge, MA, USA, 1996; p. 560. [Google Scholar] [CrossRef]
- Gullo, F.; Ponti, G.; Tagarelli, A.; Greco, S. A time series representation model for accurate and fast similarity detection. Pattern Recognit. 2009, 42, 2998–3014. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Processes Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Sun, X.-L.; Wang, Y.; Wang, H.-L.; Zhang, C.; Wang, Z.-L. Digital soil mapping based on empirical mode decomposition components of environmental covariates. Eur. J. Soil Sci. 2019, 70, 1109–1127. [Google Scholar] [CrossRef]
- Soon, W.; Herrera, V.M.V.; Selvaraj, K.; Traversi, R.; Usoskin, I.; Chen, C.-T.A.; Lou, J.-Y.; Kao, S.-J.; Carter, R.M.; Pipin, V.; et al. A review of Holocene solar-linked climatic variation on centennial to millennial timescales: Physical processes, interpretative frameworks and a new multiple cross-wavelet transform algorithm. Earth-Sci. Rev. 2014, 134, 1–15. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, P.; Wei, H.; Liu, A.; You, S.; Sun, D. Improved mapping and understanding of desert vegetation-habitat complexes from intraannual series of spectral endmember space using cross-wavelet transform and logistic regression. Remote Sens. Environ. 2020, 236, 111516. [Google Scholar] [CrossRef]
- Fang, J.; Yu, G.; Liu, L.; Hu, S.; Chapin, F.S. Climate change, human impacts, and carbon sequestration in China. Proc. Natl. Acad. Sci. USA 2018, 115, 4015–4020. [Google Scholar] [CrossRef] [Green Version]
- Bao, S. Soil Agricultural Chemistry Analysis; China Agriculture Press: Beijing, China, 1999. (In Chinese) [Google Scholar]
- Van Der Meer, F.; De Jong, S.; De Jong, S. Improving the results of spectral unmixing of Landsat Thematic Mapper imagery by enhancing the orthogonality of end-members. Int. J. Remote Sens. 2000, 21, 2781–2797. [Google Scholar] [CrossRef]
- Dey, D.; Chatterjee, B.; Chakravorti, S.; Munshi, S. Rough-granular approach for impulse fault classification of transformers using cross-wavelet transform. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1297–1304. [Google Scholar] [CrossRef]
- Freedman, D.; Pisani, R.; Purves, R. Statistics: Fourth International Student Edition; W.W. Norton & Company: New York, NY, USA, 2007. [Google Scholar]
- Grus, J. Data Science from Scratch; O’Reilly: Sebastopol, CA, USA, 2015; pp. 99–100. [Google Scholar]
- Keskin, H.; Grunwald, S.; Harris, W.G. Digital mapping of soil carbon fractions with machine learning. Geoderma 2019, 339, 40–58. [Google Scholar] [CrossRef]
- Calle, M.L.; Urrea, V. Letter to the Editor: Stability of Random Forest importance measures. Brief. Bioinform. 2011, 12, 86–89. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, H.; Guo, X.; Yu, H. Variable selection using Mean Decrease Accuracy and Mean Decrease Gini based on Random Forest. In Proceedings of the 2016 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 26–28 August 2016; pp. 219–224. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.L.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Verikas, A.; Gelzinis, A.; Bacauskiene, M. Mining data with random forests: A survey and results of new tests. Pattern Recognit. 2011, 44, 330–349. [Google Scholar] [CrossRef]
- Wang, H.; Yang, F.; Luo, Z. An experimental study of the intrinsic stability of random forest variable importance measures. BMC Bioinform. 2016, 17, 60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bryll, R.; Gutierrez-Osuna, R.; Quek, F. Attribute bagging: Improving accuracy of classifier ensembles by using random feature subsets. Pattern Recognit. 2003, 36, 1291–1302. [Google Scholar] [CrossRef]
- Sammut, C.; Webb, G.I. Encyclopedia of Machine Learning and Data Mining; Springer: Boston, MA, USA, 2017. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 2000, 12, 55–67. [Google Scholar] [CrossRef]
- Kang, J.; Jin, R.; Li, X.; Zhang, Y.; Zhu, Z. Spatial Upscaling of Sparse Soil Moisture Observations Based on Ridge Regression. Remote Sens. 2018, 10, 192. [Google Scholar] [CrossRef] [Green Version]
- Mcdonald, G.C. Ridge regression. Wiley Interdiscip. Rev. Comput. Stat. 2010, 1, 93–100. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Gestel, T.V.; Brabanter, J.D.; Moor, B.D.; Vandewalle, J. Least Squares Support Vector Machines; World Scientific Publishing Co.: Singapore, 2002. [Google Scholar]
- Zhang, H.; Chen, L.; Qu, Y.; Zhao, G.; Guo, Z. Support Vector Regression Based on Grid-Search Method for Short-Term Wind Power Forecasting. J. Appl. Math. 2014, 2014, 835791. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Schapire, R.E. The Boosting Approach to Machine Learning: An Overview. In Nonlinear Estimation and Classification. Lecture Notes in Statistics; Denison, D.D., Hansen, M.H., Holmes, C.C., Mallick, B., Yu, B., Eds.; Springer: New York, NY, USA, 2003; Volume 171, pp. 149–171. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wijewardane, N.; Ge, Y.; Morgan, C.L. Moisture insensitive prediction of soil properties from VNIR reflectance spectra based on external parameter orthogonalization. Geoderma 2016, 267, 92–101. [Google Scholar] [CrossRef] [Green Version]
- GlobalSoilMap Science Committee Specifications. Tiered GlobalSoilMap.net Products Release, Version 2.3; GlobalSoilMap: Wageningen, The Netherlands, 2013. [Google Scholar]
- Odgers, N.P.; McBratney, A.; Minasny, B. Digital soil property mapping and uncertainty estimation using soil class probability rasters. Geoderma 2015, 237, 190–198. [Google Scholar] [CrossRef]
- Ballabio, C.; Fava, F.P.; Rosenmund, A. A plant ecology approach to digital soil mapping, improving the prediction of soil organic carbon content in alpine grasslands. Geoderma 2012, 187, 102–116. [Google Scholar] [CrossRef]
- Quintano, C.; Fernández-Manso, A.; Shimabukuro, Y.E.; Pereira, G. Spectral unmixing. Int. J. Remote Sens. 2012, 33, 5307–5340. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Bradshaw, G.A.; Spies, T.A. Characterizing Canopy Gap Structure in Forests Using Wavelet Analysis. J. Ecol. 1992, 80, 205–215. [Google Scholar] [CrossRef]
- He, Y.; Guo, X.; Si, B. Detecting grassland spatial variation by a wavelet approach. Int. J. Remote Sens. 2007, 28, 1527–1545. [Google Scholar] [CrossRef]
- Oades, J.M. The retention of organic matter in soils. Biogeochemistry 1988, 5, 35–70. [Google Scholar] [CrossRef]
- Preston, C.M.; Schmidt, M.W.I. Black (pyrogenic) carbon: A synthesis of current knowledge and uncertainties with special consideration of boreal regions. Biogeosciences 2006, 3, 397–420. [Google Scholar] [CrossRef] [Green Version]
- Heimann, M.; Reichstein, M. Terrestrial ecosystemcarbon dynamics and climate feedbacks. Nature 2008, 451, 289–292. [Google Scholar] [CrossRef] [PubMed]
- Feller, C.; Beare, M. Physical control of soil organic matter dynamics in the tropics. Geoderma 1997, 79, 69–116. [Google Scholar] [CrossRef]
- Dose, V.; Menzel, A. Bayesian analysis of climate change impacts in phenology. Glob. Chang. Biol. 2010, 10, 259–272. [Google Scholar] [CrossRef]
- Edwards, M.; Richardson, A. Impact of climate change on marine pelagic phenology and trophic mismatch. Nature 2004, 430, 881–884. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Zhang, Y.; Dong, J.; Xiao, X. Green-up dates in the Tibetan Plateau have continuously advanced from 1982 to 2011. Proc. Natl. Acad. Sci. USA 2013, 110, 4309–4314. [Google Scholar] [CrossRef] [Green Version]
- Minasny, B.; McBratney, A. Digital soil mapping: A brief history and some lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, B.; Song, H. A robust adaptive spatial and temporal image fusion model for complex land surface changes. Remote Sens. Environ. 2018, 208, 42–62. [Google Scholar] [CrossRef]
- Hill, J.; Stellmes, M.; Udelhoven, T.; Röder, A.; Sommer, S. Mediterranean desertification and land degradation: Mapping related land use change syndromes based on satellite observations. Glob. Planet. Chang. 2008, 64, 146–157. [Google Scholar] [CrossRef]
- Zhang, P.; Sun, Q.; Sun, D.; Sun, M.; Liu, H.; You, S.; Liu, A. Establishment of land degradation assessment system in arid region based on remote sensing spectrum. Trans. Chin. Soc. Agric. Eng. 2019, 9, 228–237. [Google Scholar] [CrossRef]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef] [Green Version]
- Huenneke, L.F.; Anderson, J.P.; Remmenga, M.; Schlesinger, W.H. Desertification alters patterns of aboveground net primary production in Chihuahuan ecosystems. Glob. Chang. Biol. 2010, 8, 247–264. [Google Scholar] [CrossRef]
- Unruh, J.D.; Akhobadze, S.; Ibrahim, H.O.; Karapinar, B.; Kusum, B.S.; Montoiro, M.; Santivane, M.S. Land Tenure in Support of Land Degradation Neutrality; FAO: Rome, Italy, 2019. [Google Scholar]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
| Land Use/Land Cover | Sample Numbers | Measured SOM (g·kg−1) | |||
|---|---|---|---|---|---|
| Minimum | Maximum | Average | Standard Error | ||
| Desert vegetation | 12 | 3.614 | 29.853 | 10.092 | 7.200 |
| Sand land | 16 | 3.450 | 11.043 | 6.112 | 3.099 |
| Forest | 21 | 4.183 | 34.029 | 12.842 | 7.069 |
| Grassland | 6 | 8.985 | 17.623 | 13.237 | 3.505 |
| Cropland | 39 | 6.938 | 27.474 | 14.340 | 5.534 |
| Total | 94 | 3.450 | 34.029 | 11.992 | 6.037 |
| Models | Training Set (n = 79) | Validation Set (n = 15) | ||||
|---|---|---|---|---|---|---|
| RMSE | R2 | RPD | RMSE | R2 | RPD | |
| RR | 3.148 (2.002) | 0.751 (0.401) | 1.860 (1.232) | 3.635 (2.926) | 0.706 (0.321) | 1.733 (1.411) |
| LS-SVM | 2.457 (0.987) | 0.851 (0.365) | 2.385 (1.454) | 2.825 (1.354) | 0.823 (0.426) | 2.231 (1.874) |
| RF | 0.991 (0.051) | 0.888 (0.056) | 5.913 (0.859) | 2.277 (0.621) | 0.875 (0.212) | 2.729 (1.456) |
| GBRT | 0.427 (0.026) | 0.879 (0.012) | 13.731 (1.231) | 2.309 (0.798) | 0.873 (0.198) | 2.768 (1.324) |
| Models | Training Set (N = 79) | Validation Set (N = 15) | ||||
|---|---|---|---|---|---|---|
| RMSE | R2 | RPD | RMSE | R2 | RPD | |
| RR | 3.288 (2.961) | 0.731 (0.624) | 1.782 (1.222) | 4.001 (4.565) | 0.689 (0.671) | 1.575 (1.687) |
| LS-SVM | 2.493 (1.824) | 0.795 (0.599) | 1.991 (1.416) | 3.258 (3.954) | 0.770 (0.610) | 1.836 (1.600) |
| RF | 1.299 (0.141) | 0.831 (0.242) | 3.458 (1.211) | 2.406 (1.645) | 0.845 (0.492) | 2.325 (1.723) |
| GBRT | 1.202 (0.107) | 0.856 (0.190) | 6.459 (1.200) | 2.655 (2.470) | 0.828 (0.666) | 2.307 (1.820) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Zhang, P.; Jiao, X.; Lun, F.; Dong, S.; Lin, X.; Li, X.; Sun, D. A Remotely Sensed Framework for Spatially-Detailed Dryland Soil Organic Matter Mapping: Coupled Cross-Wavelet Transform with Fractional Vegetation and Soil-Related Endmember Time Series. Remote Sens. 2022, 14, 1701. https://doi.org/10.3390/rs14071701
Sun Q, Zhang P, Jiao X, Lun F, Dong S, Lin X, Li X, Sun D. A Remotely Sensed Framework for Spatially-Detailed Dryland Soil Organic Matter Mapping: Coupled Cross-Wavelet Transform with Fractional Vegetation and Soil-Related Endmember Time Series. Remote Sensing. 2022; 14(7):1701. https://doi.org/10.3390/rs14071701
Chicago/Turabian StyleSun, Qiangqiang, Ping Zhang, Xin Jiao, Fei Lun, Shiwei Dong, Xin Lin, Xiangyu Li, and Danfeng Sun. 2022. "A Remotely Sensed Framework for Spatially-Detailed Dryland Soil Organic Matter Mapping: Coupled Cross-Wavelet Transform with Fractional Vegetation and Soil-Related Endmember Time Series" Remote Sensing 14, no. 7: 1701. https://doi.org/10.3390/rs14071701
APA StyleSun, Q., Zhang, P., Jiao, X., Lun, F., Dong, S., Lin, X., Li, X., & Sun, D. (2022). A Remotely Sensed Framework for Spatially-Detailed Dryland Soil Organic Matter Mapping: Coupled Cross-Wavelet Transform with Fractional Vegetation and Soil-Related Endmember Time Series. Remote Sensing, 14(7), 1701. https://doi.org/10.3390/rs14071701