HD Camera-Equipped UAV Trajectory Planning for Gantry Crane Inspection
Abstract
:1. Introduction
2. Methodology and Problem Statement
2.1. Methodology
2.2. Problem Statement
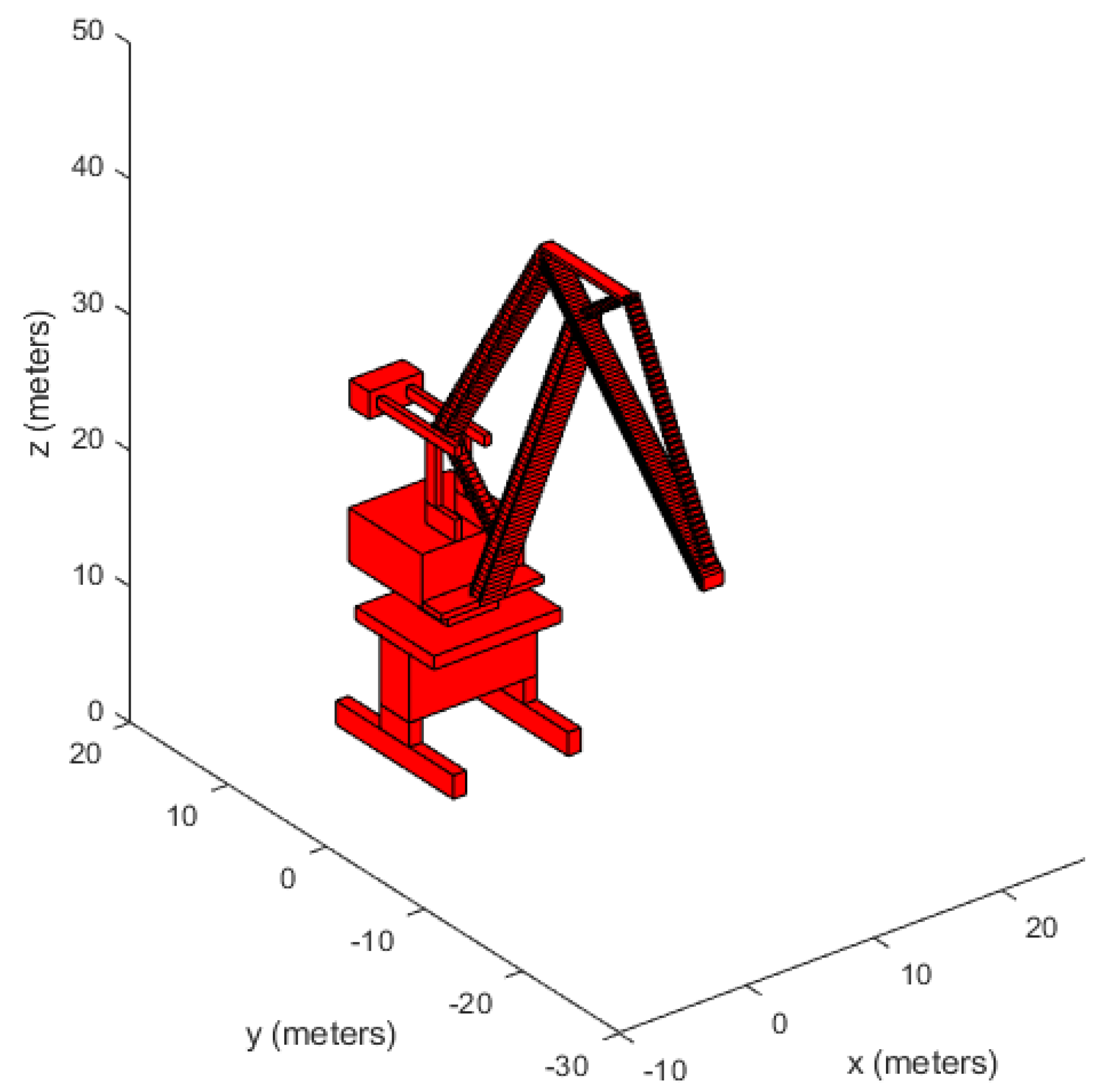
2.2.1. Gantry Crane Vulnerable Parts
2.2.2. A* Algorithm Overview
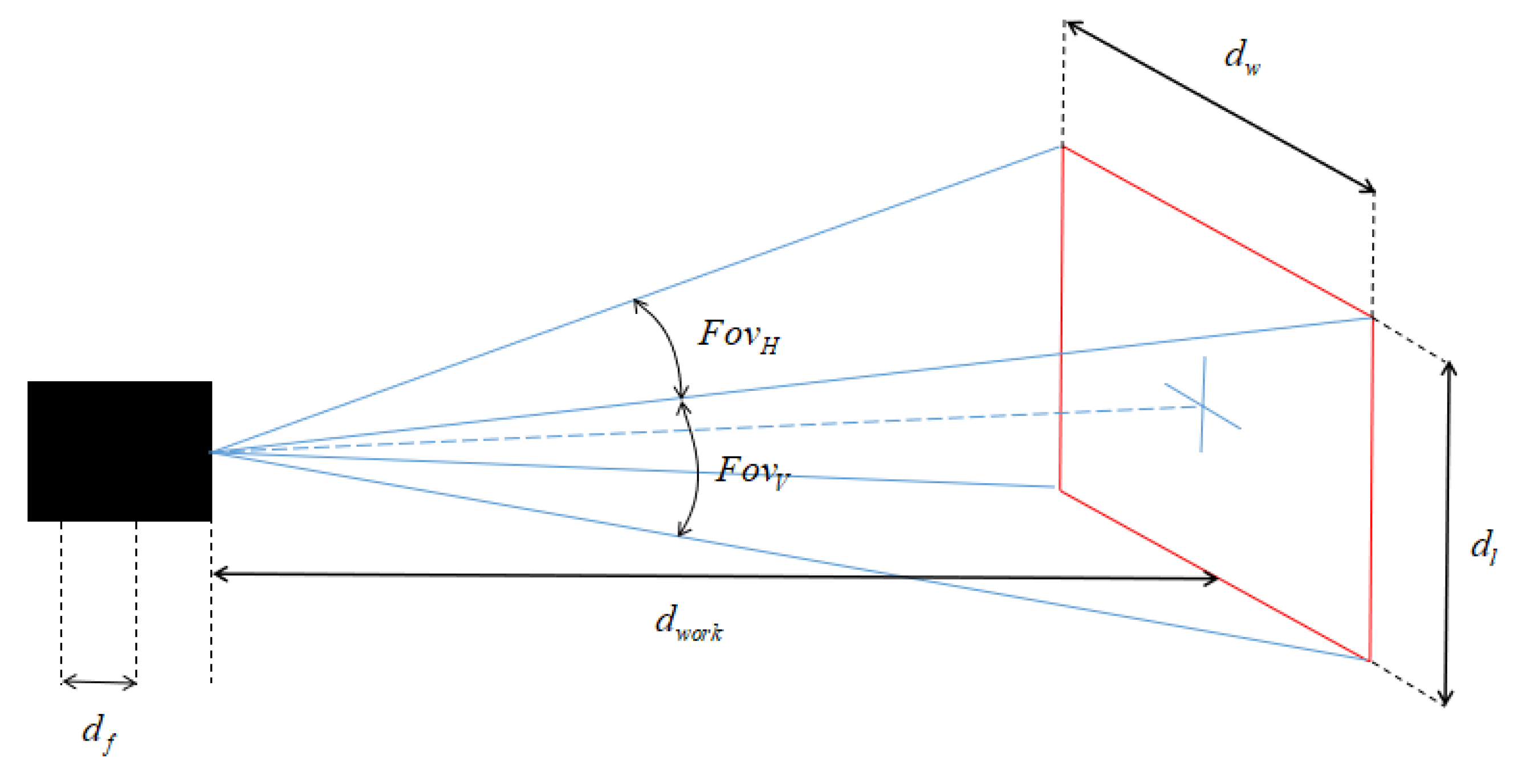
2.2.3. HD Camera Model
3. Simulation Results
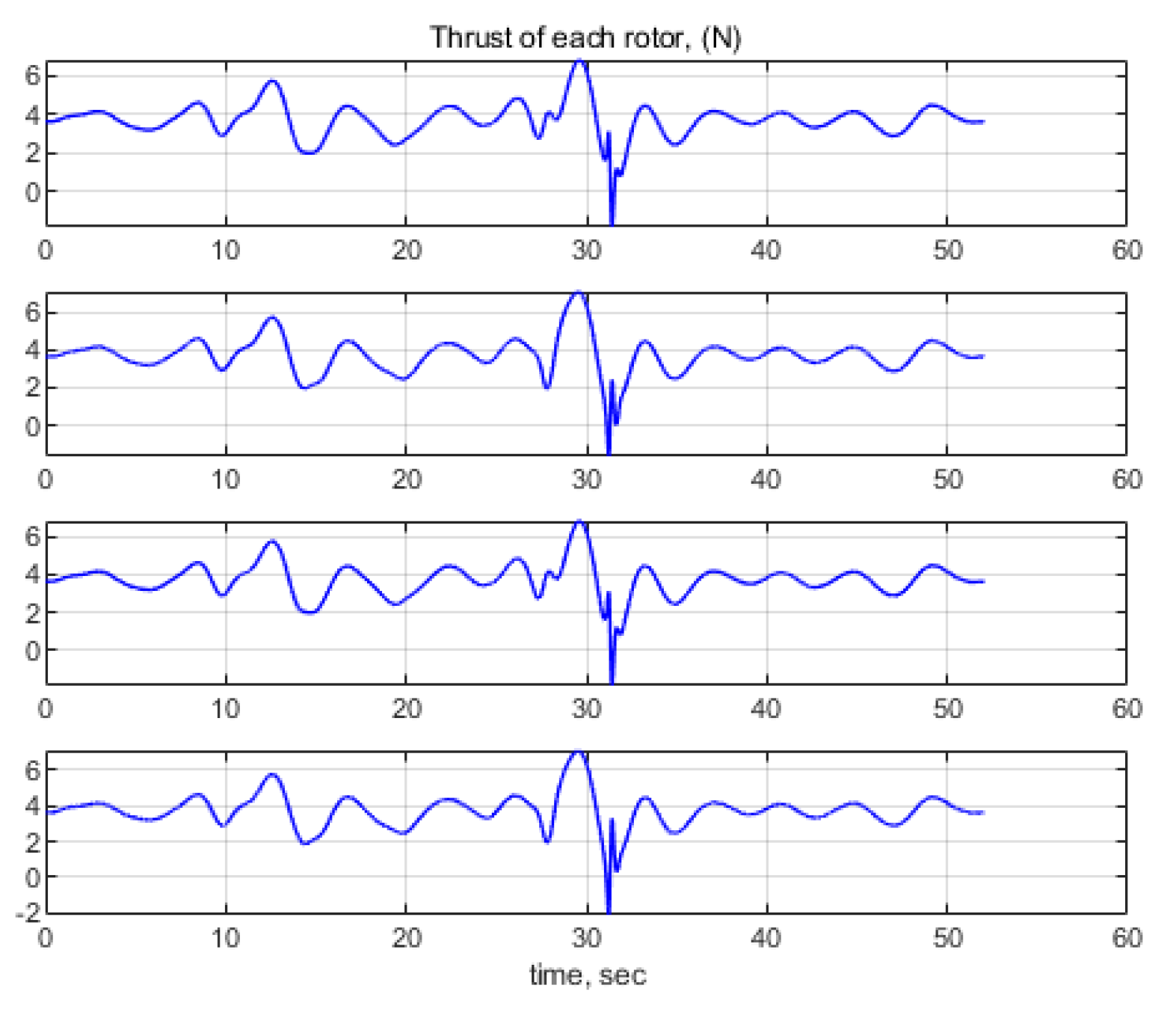
3.1. Motion Model and UAV Controller
3.2. Construct an Objective Function Based on Minimum Snap
3.3. Trajectory Deviationt Optimization
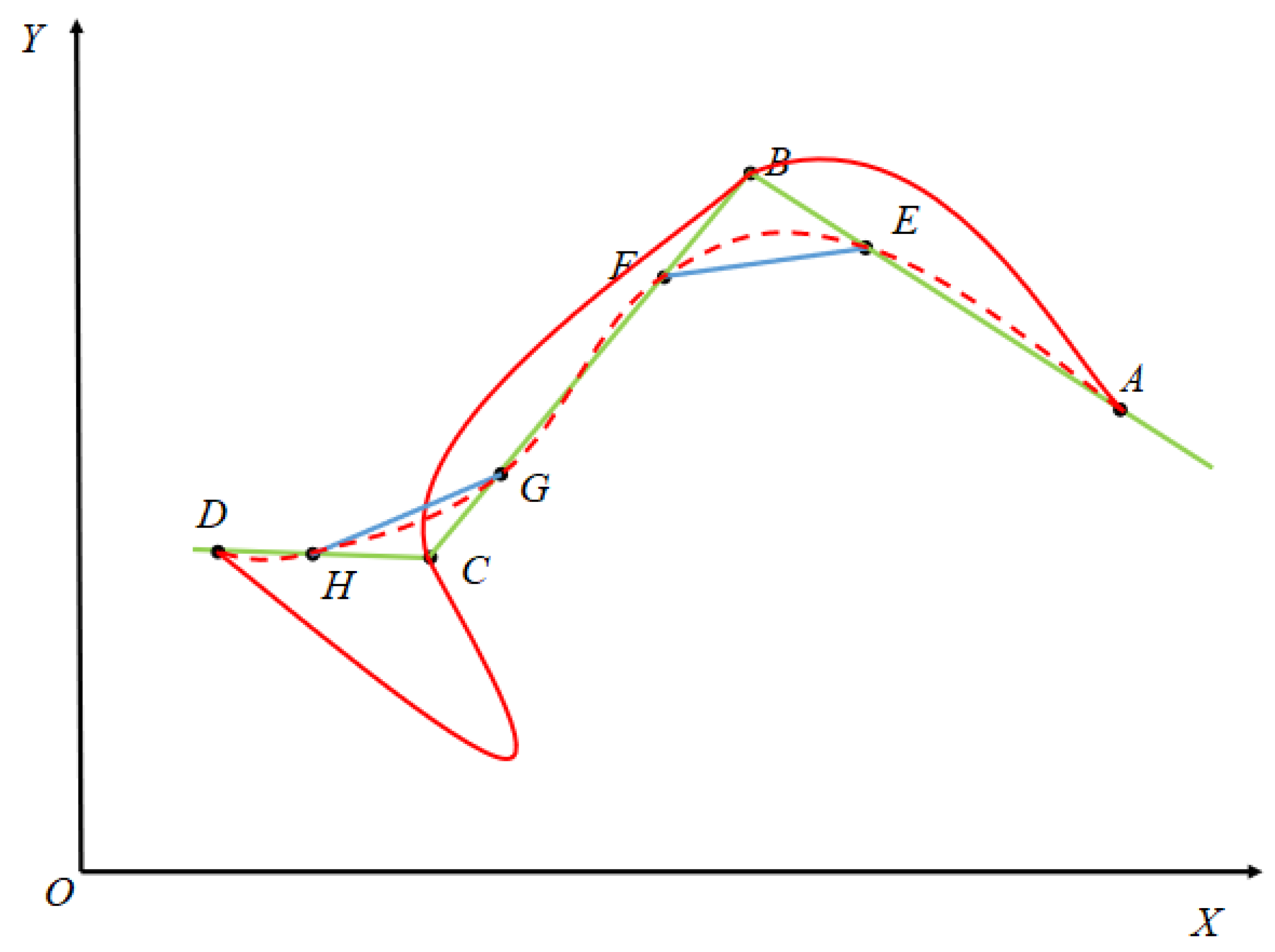
3.3.1. Trajectory Correction Method
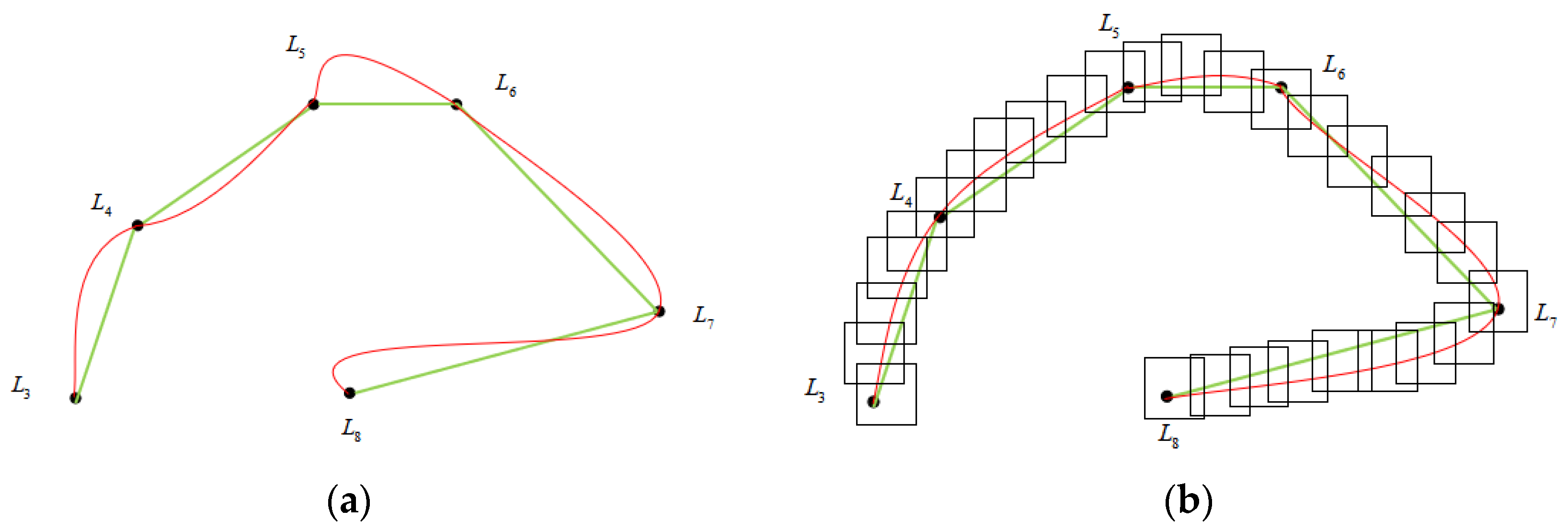
3.3.2. Trajectory Optimization Method with Corridor Constraints
3.4. Simulation Experiments
3.4.1. Simulation Experiments Comparison
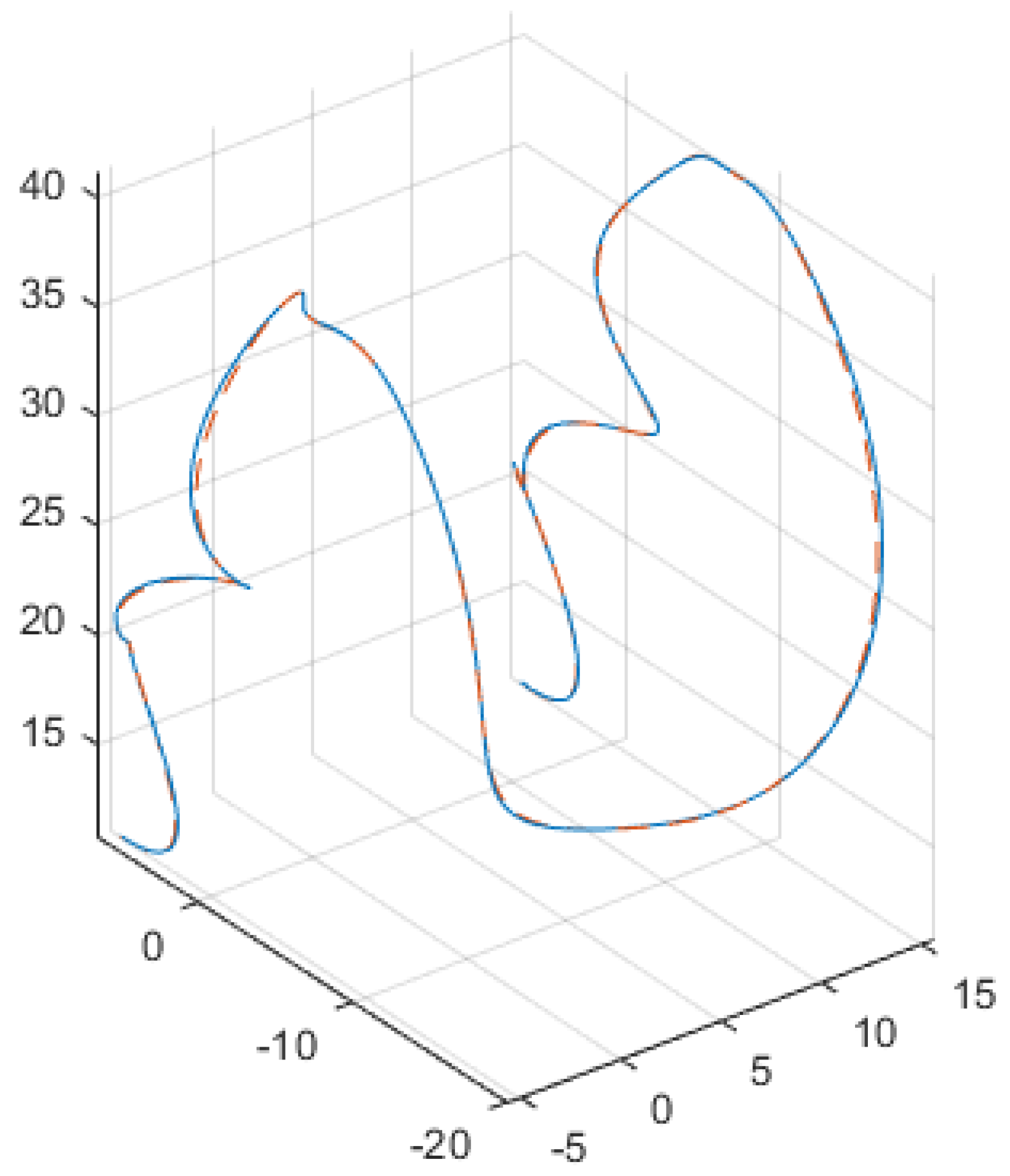
3.4.2. Trajectory Tracking Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bircher, A.; Kamel, M.; Alexis, K.; Burri, M.; Oettershagen, P.; Omari, S.; Mantel, T.; Siegwart, R. Three-dimensional coverage path planning via viewpoint resampling and tour optimization for aerial robots. Auton. Robot. 2016, 40, 1059–1078. [Google Scholar] [CrossRef]
- Adhikari, R.S.; Moselhi, O.; Bagchi, A. Image-based retrieval of concrete crack properties for bridge inspection. Autom. Constr. 2014, 39, 180–194. [Google Scholar] [CrossRef]
- Hampel, U.; Maas, H.G. Cascaded image analysis for dynamic crack detection in material testing. ISPRS J. Photogramm. Remote Sens. 2009, 64, 345–350. [Google Scholar] [CrossRef]
- Tang, G.; Hou, Z.; Claramunt, C.; Hu, X. UAV Trajectory Planning in a Port Environment. J. Mar. Sci. Eng. 2020, 8, 592. [Google Scholar] [CrossRef]
- Seo, J.; Duque, L.; Wacker, J. Drone-enabled bridge inspection methodology and application. Autom. Constr. 2018, 94, 112–126. [Google Scholar] [CrossRef]
- Zhang, D.; Watson, R.; Dobie, G.; MacLeod, C.; Khan, A.; Pierce, G. Quantifying impacts on remote photogrammetric inspection using unmanned aerial vehicles. Eng. Struct. 2020, 209, 109940. [Google Scholar] [CrossRef]
- Poksawat, P.; Wang, L.; Mohamed, A. Gain scheduled attitude control of fixed-wing UAV with automatic controller tuning. IEEE Trans. Control Syst. Technol. 2017, 26, 1192–1203. [Google Scholar] [CrossRef]
- Cohen, M.R.; Abdulrahim, K.; Forbes, J.R. Finite-Horizon LQR Control of Quadrotors on SE2(3). IEEE Robot. Autom. Lett. 2020, 5, 5748–5755. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, P.; Wang, Z.; Guo, L.; Yang, H. Active disturbance rejection control for the ranger neutral buoyancy vehicle: A delta operator approach. IEEE Trans. Ind. Electron. 2017, 64, 9410–9420. [Google Scholar] [CrossRef]
- Xian, B.; Hao, W. Nonlinear robust fault-tolerant control of the tilt trirotor UAV under rear servo’s stuck fault: Theory and experiments. IEEE Trans. Ind. Inform. 2018, 15, 2158–2166. [Google Scholar] [CrossRef]
- Liu, H.; Xi, J.; Zhong, Y. Robust attitude stabilization for nonlinear quadrotor systems with uncertainties and delays. IEEE Trans. Ind. Electron. 2017, 64, 5585–5594. [Google Scholar] [CrossRef]
- Das, A.; Lewis, F.; Subbarao, K. Backstepping approach for controlling a quadrotor using Lagrange form dynamics. J. Intell. Robot. Syst. 2009, 56, 127–151. [Google Scholar] [CrossRef]
- Mellinger, D.; Shomin, M.; Kumar, V. Control of quadrotors for robust perching and landing. In Proceedings of the International Powered Lift Conference, Philadelphia, PA, USA, 5–7 October 2010; pp. 205–225. [Google Scholar]
- Zhao, B.; Xian, B.; Zhang, Y.; Zhang, X. Nonlinear robust adaptive tracking control of a quadrotor UAV via immersion and invariance methodology. IEEE Trans. Ind. Electron. 2014, 62, 2891–2902. [Google Scholar] [CrossRef]
- Zhu, W.A.N.G.; Li, L.I.U.; Teng, L.O.N.G.; Yonglu, W.E.N. Multi-UAV reconnaissance task allocation for heterogeneous targets using an opposition-based genetic algorithm with double-chromosome encoding. Chin. J. Aeronaut. 2018, 31, 339–350. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner Jr, J.J. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, F.; Fang, X.; Lan, Z. Improved bat algorithm for UAV path planning in three-dimensional space. IEEE Access 2021, 9, 20100–20116. [Google Scholar] [CrossRef]
- Chen, Y.B.; Luo, G.C.; Mei, Y.S.; Yu, J.Q.; Su, X.L. UAV path planning using artificial potential field method updated by optimal control theory. Int. J. Syst. Sci. 2016, 47, 1407–1420. [Google Scholar] [CrossRef]
- Li, H.; Luo, Y.; Wu, J. Collision-free path planning for intelligent vehicles based on Bézier curve. IEEE Access 2019, 7, 123334–123340. [Google Scholar] [CrossRef]
- Wu, Z.; Su, W.; Li, J. Multi-robot path planning based on improved artificial potential field and B-spline curve optimization. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 4691–4696. [Google Scholar]
- Iskander, A.; Elkassed, O.; El-Badawy, A. Minimum snap trajectory tracking for a quadrotor UAV using nonlinear model predictive control. In Proceedings of the 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 24–26 October 2020; pp. 344–349. [Google Scholar]
- Ding, H.; Li, Y.; Chai, Y.; Jian, Q. Path planning for 2-DOF manipulator based on Bezier curve and A* algorithm. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 670–674. [Google Scholar]
- Ding, W.; Gao, W.; Wang, K.; Shen, S. An efficient b-spline-based kinodynamic replanning framework for quadrotors. IEEE Trans. Robot. 2019, 35, 1287–1306. [Google Scholar] [CrossRef] [Green Version]
- Richter, C.; Bry, A.; Roy, N. Polynomial trajectory planning for aggressive quadrotor flight in dense indoor environments. In Robotics Research; Springer: Cambridge, MA, USA, 2016; pp. 649–666. [Google Scholar]
- Duchoň, F.; Babinec, A.; Kajan, M.; Beňo, P.; Florek, M.; Fico, T.; Jurišica, L. Path planning with modified a star algorithm for a mobile robot. Procedia Eng. 2014, 96, 59–69. [Google Scholar] [CrossRef] [Green Version]
- Van Nieuwstadt, M.J.; Murray, R.M. Real-time trajectory generation for differentially flat systems. Int. J. Robust Nonlinear Control IFAC-Affil. J. 1998, 8, 995–1020. [Google Scholar] [CrossRef]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar]



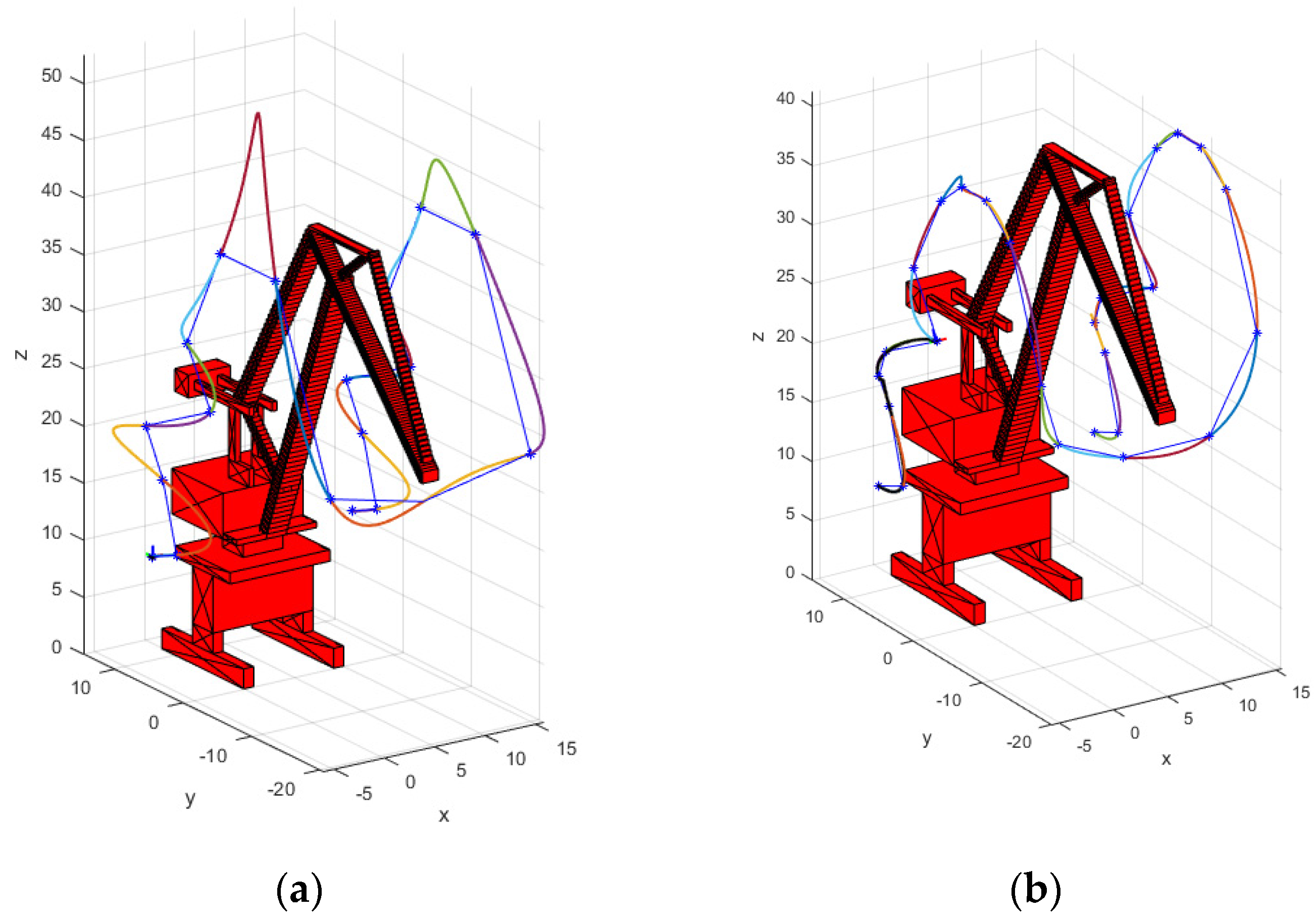
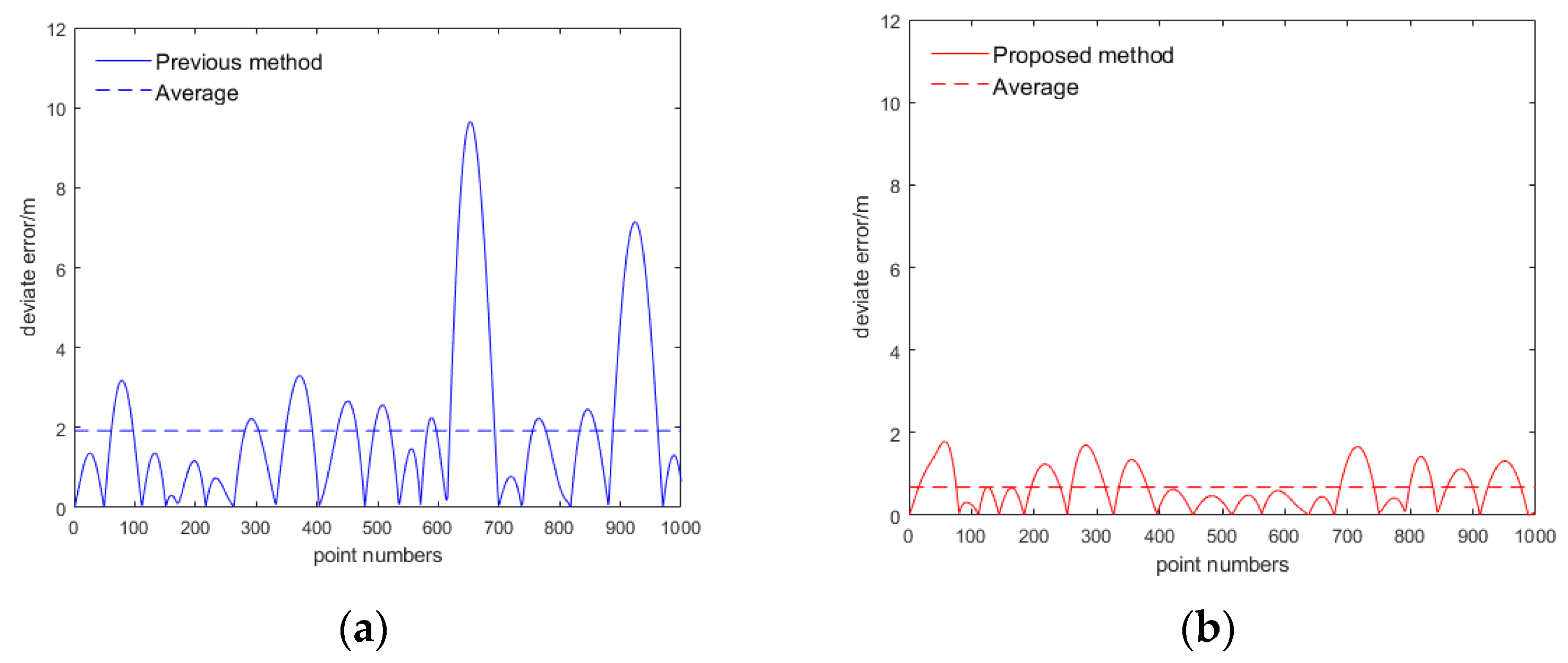

| Average Deviation Distance (m) | Maximum Deviation Distance (m) | Trajectory Length (m) | |
|---|---|---|---|
| Experiment 1 | 2.08 | 10.07 | 216.67 |
| Experiment 2 | 1.98 | 9.92 | 204.62 |
| Experiment 3 | 1.92 | 9.27 | 201.04 |
| Experiment 4 | 1.89 | 9.01 | 199.19 |
| Experiment 5 | 1.95 | 9.66 | 202.89 |
| Average Deviation Distance (m) | Maximum Deviation Distance (m) | Trajectory Length (m) | |
|---|---|---|---|
| Experiment 1 | 0.39 | 2.01 | 173.56 |
| Experiment 2 | 0.36 | 1.97 | 170.01 |
| Experiment 3 | 0.41 | 1.22 | 175.55 |
| Experiment 4 | 0.30 | 1.90 | 168.71 |
| Experiment 5 | 0.37 | 2.11 | 177.09 |
| Before Improvement | After Improvement | |
|---|---|---|
| Average deviation distance/m | 1.98 | 0.30 |
| Maximum deviation distance/m | 9.92 | 1.90 |
| Track length/m | 204.62 | 168.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, G.; Gu, J.; Zhu, W.; Claramunt, C.; Zhou, P. HD Camera-Equipped UAV Trajectory Planning for Gantry Crane Inspection. Remote Sens. 2022, 14, 1658. https://doi.org/10.3390/rs14071658
Tang G, Gu J, Zhu W, Claramunt C, Zhou P. HD Camera-Equipped UAV Trajectory Planning for Gantry Crane Inspection. Remote Sensing. 2022; 14(7):1658. https://doi.org/10.3390/rs14071658
Chicago/Turabian StyleTang, Gang, Jiaxu Gu, Weidong Zhu, Christophe Claramunt, and Peipei Zhou. 2022. "HD Camera-Equipped UAV Trajectory Planning for Gantry Crane Inspection" Remote Sensing 14, no. 7: 1658. https://doi.org/10.3390/rs14071658
APA StyleTang, G., Gu, J., Zhu, W., Claramunt, C., & Zhou, P. (2022). HD Camera-Equipped UAV Trajectory Planning for Gantry Crane Inspection. Remote Sensing, 14(7), 1658. https://doi.org/10.3390/rs14071658








