Predicting Species and Structural Diversity of Temperate Forests with Satellite Remote Sensing and Deep Learning
Abstract
1. Introduction
- To build and test a consistent modeling method for predicting different facets of forest structure relevant to biodiversity research and forest management planning.
- To examine the predictive power of DL models for different types of predictors extracted from radar and optical image data.
- To produce spatially explicit DL models that can generalize forest structural attributes across temperate forest types.
2. Materials and Methods
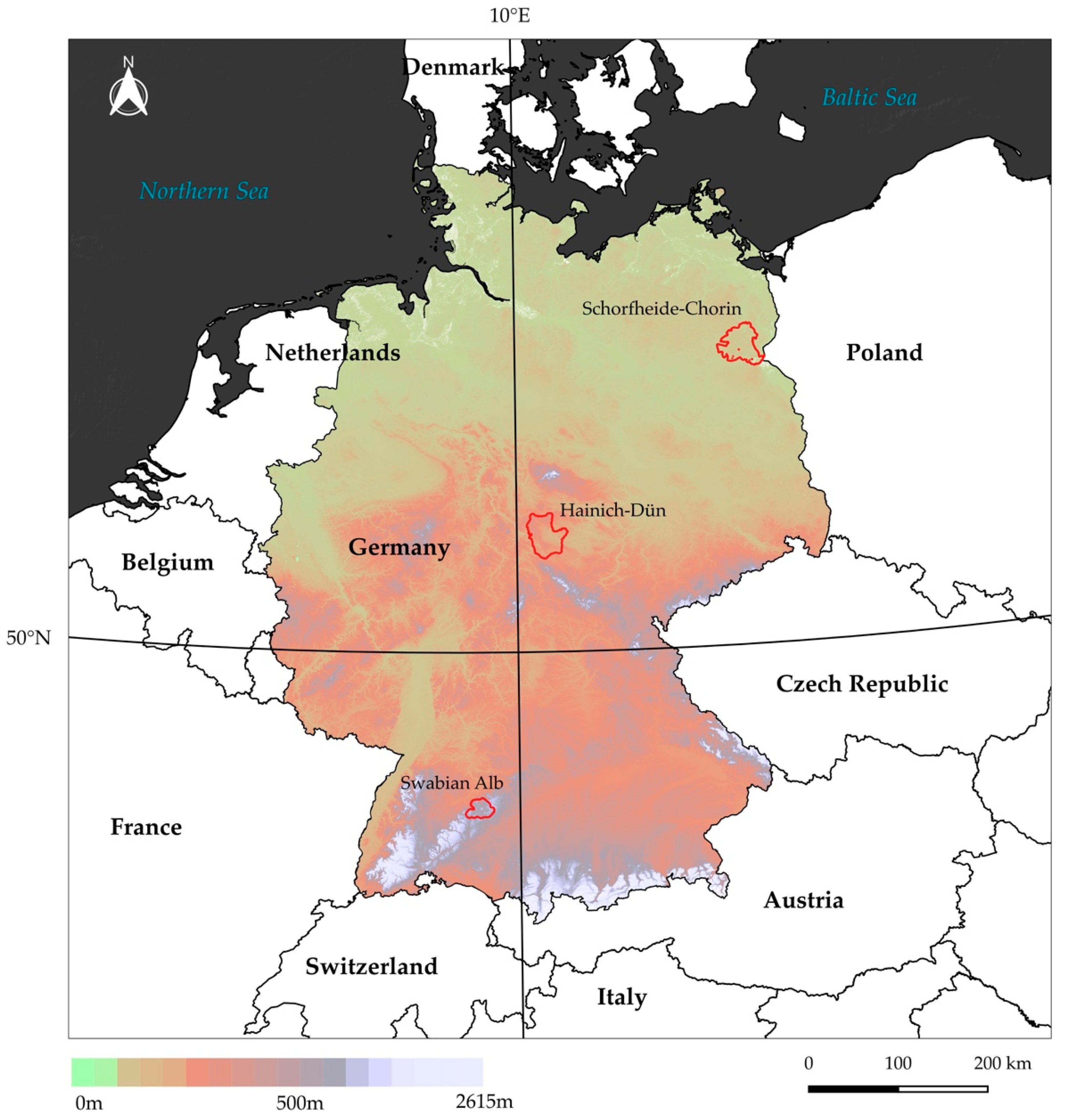
2.1. Study Sites
2.1.1. Schorfheide-Chorin
2.1.2. Hainich-Dün
2.1.3. Swabian Alb
2.2. Data
2.2.1. Sampling Design
2.2.2. Forest Management Types
2.2.3. Selection of Study Variables
2.2.4. Selection of Predictors Extracted from Satellite Data
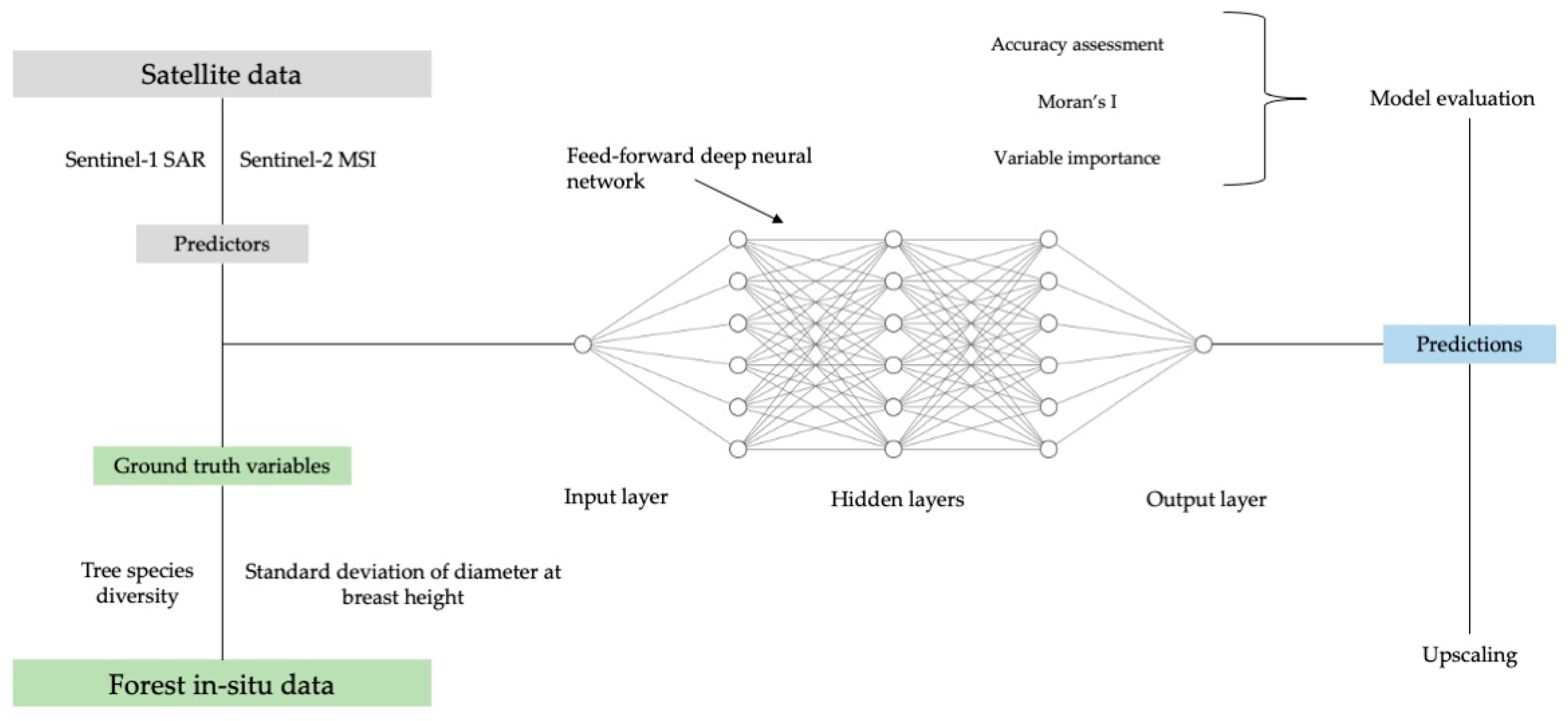
2.3. Deep Neural Network Regression
3. Results
3.1. Tree Species Diversity
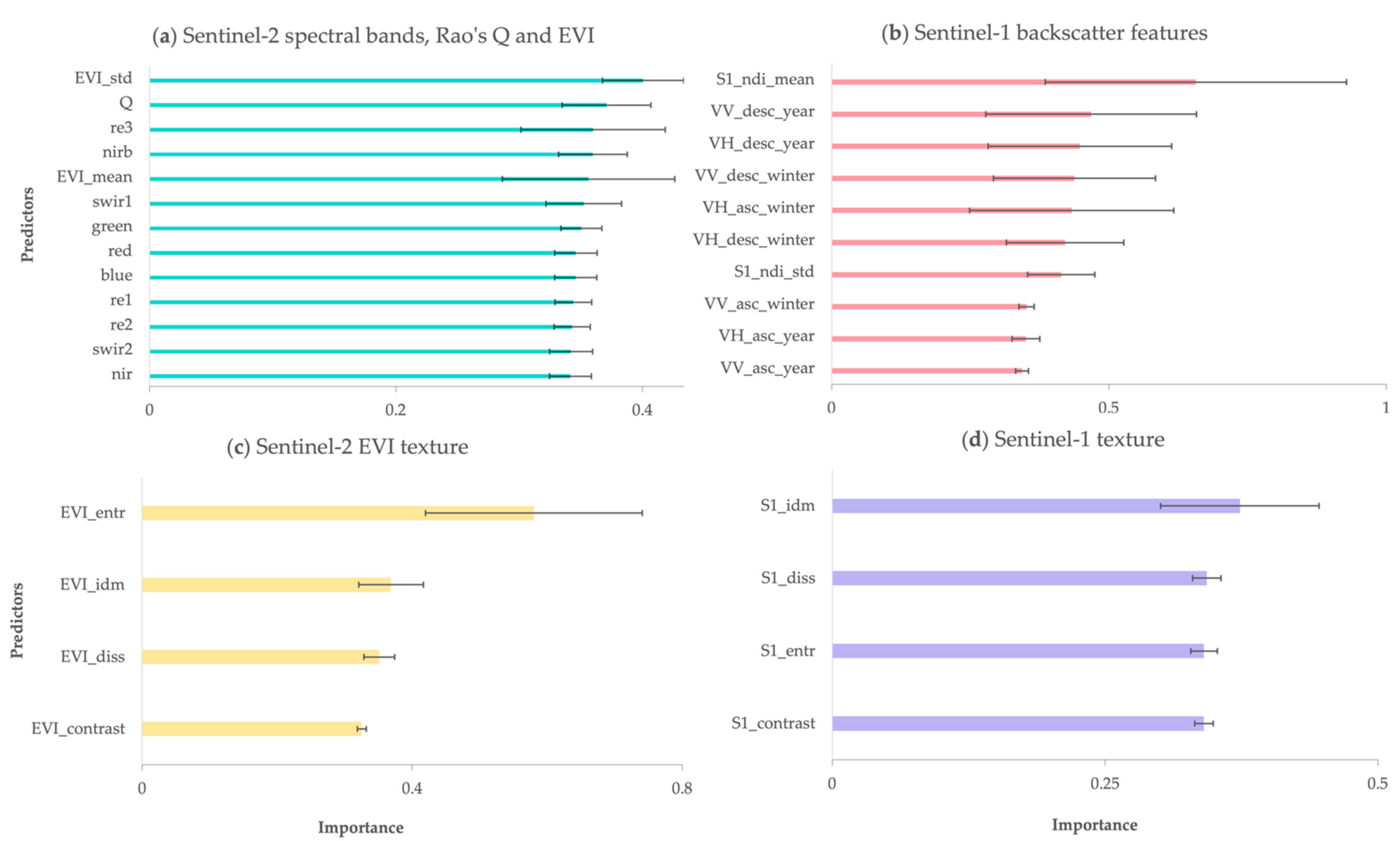
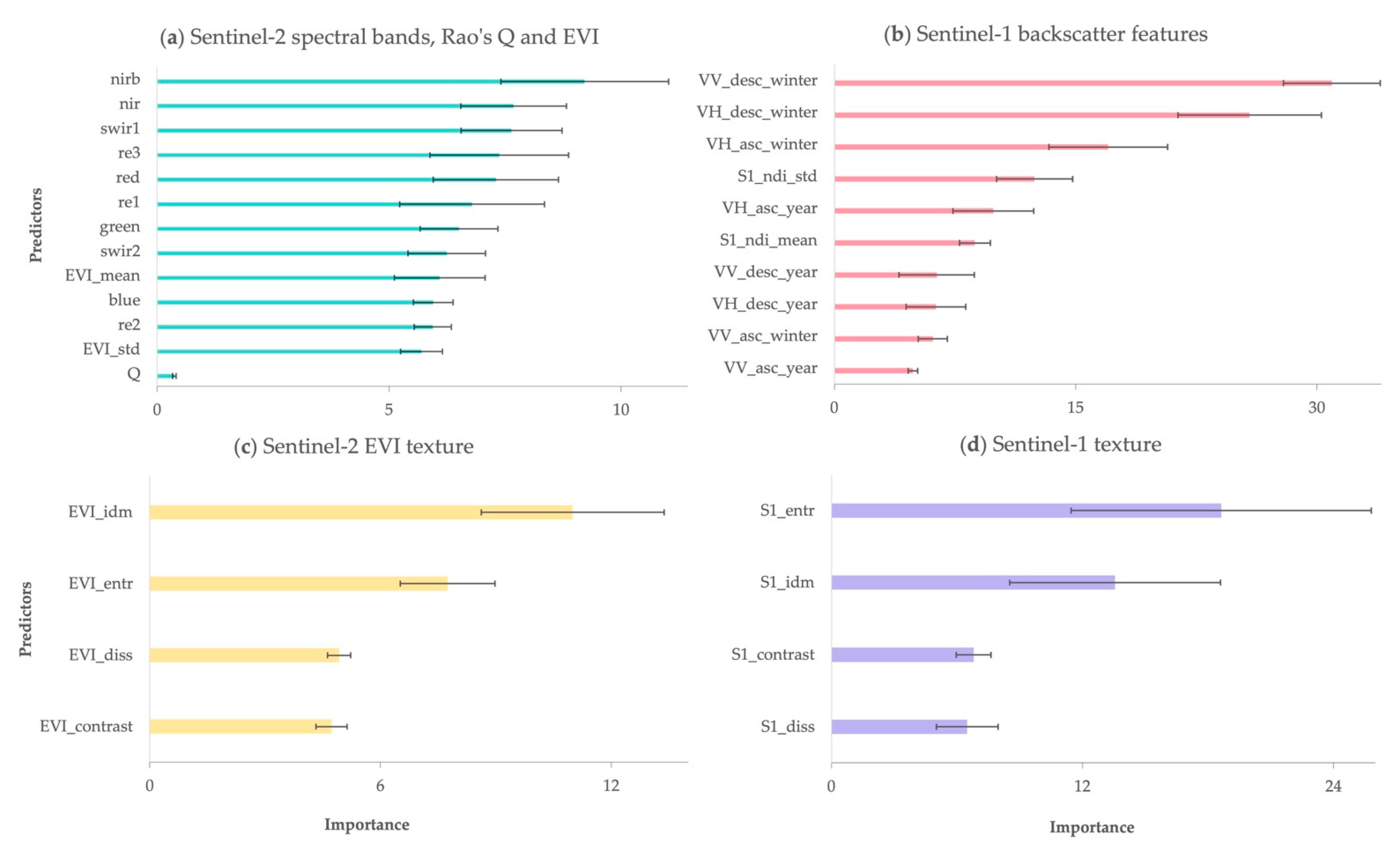
3.1.1. Predictors Importance
3.1.2. Model Accuracies
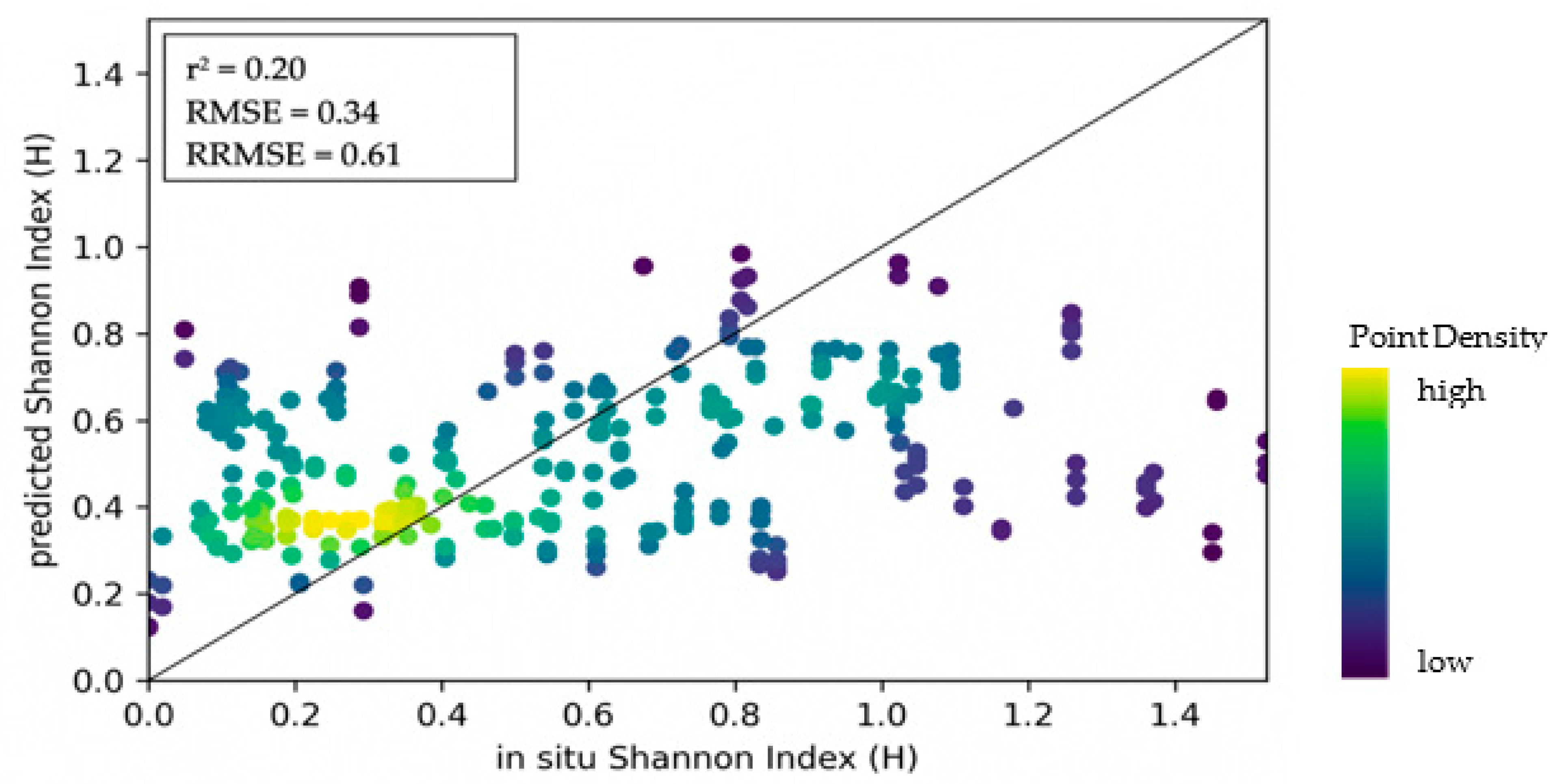
3.2. Structural Diversity
3.2.1. Predictors Importance
3.2.2. Model Accuracies
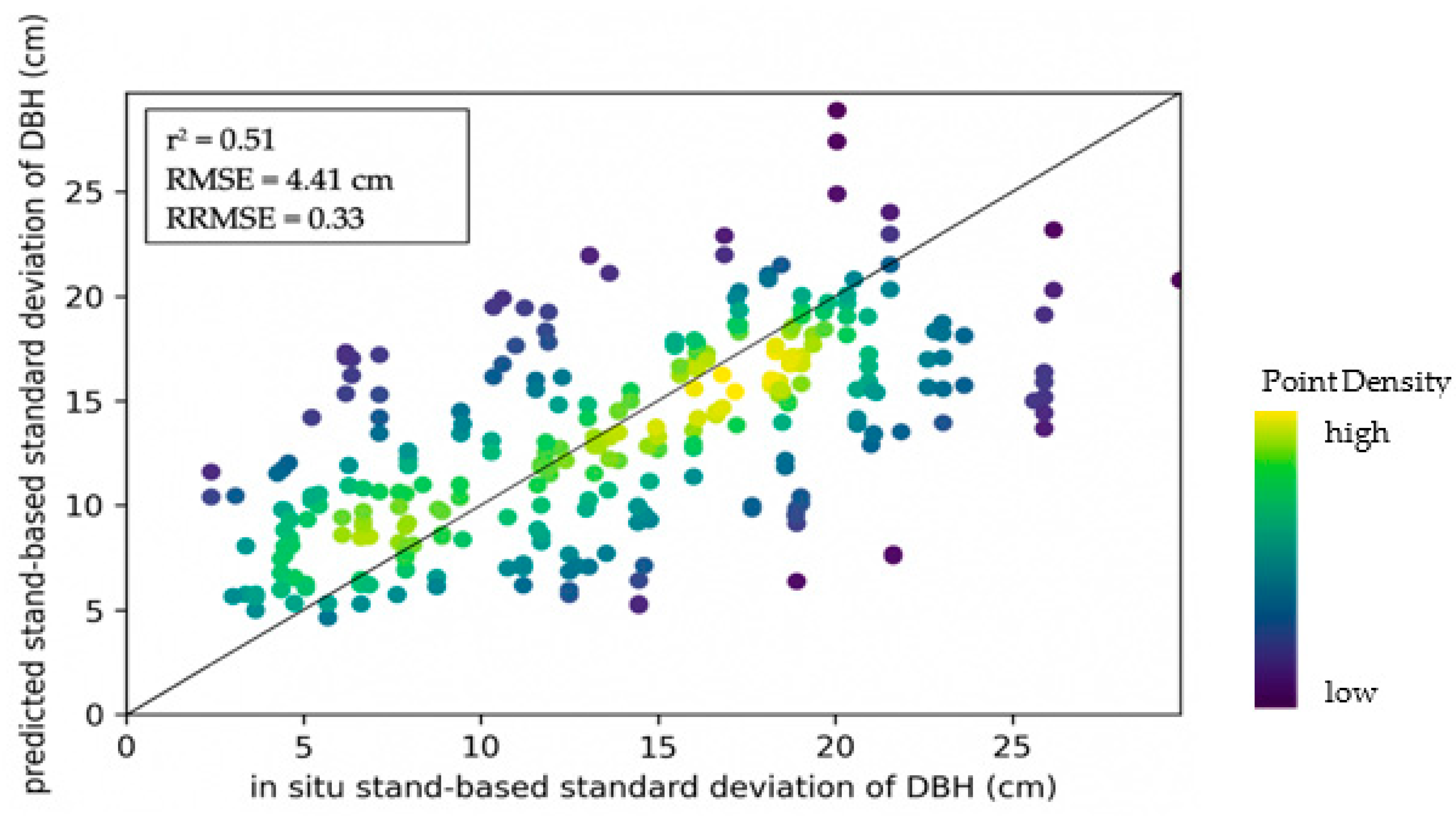
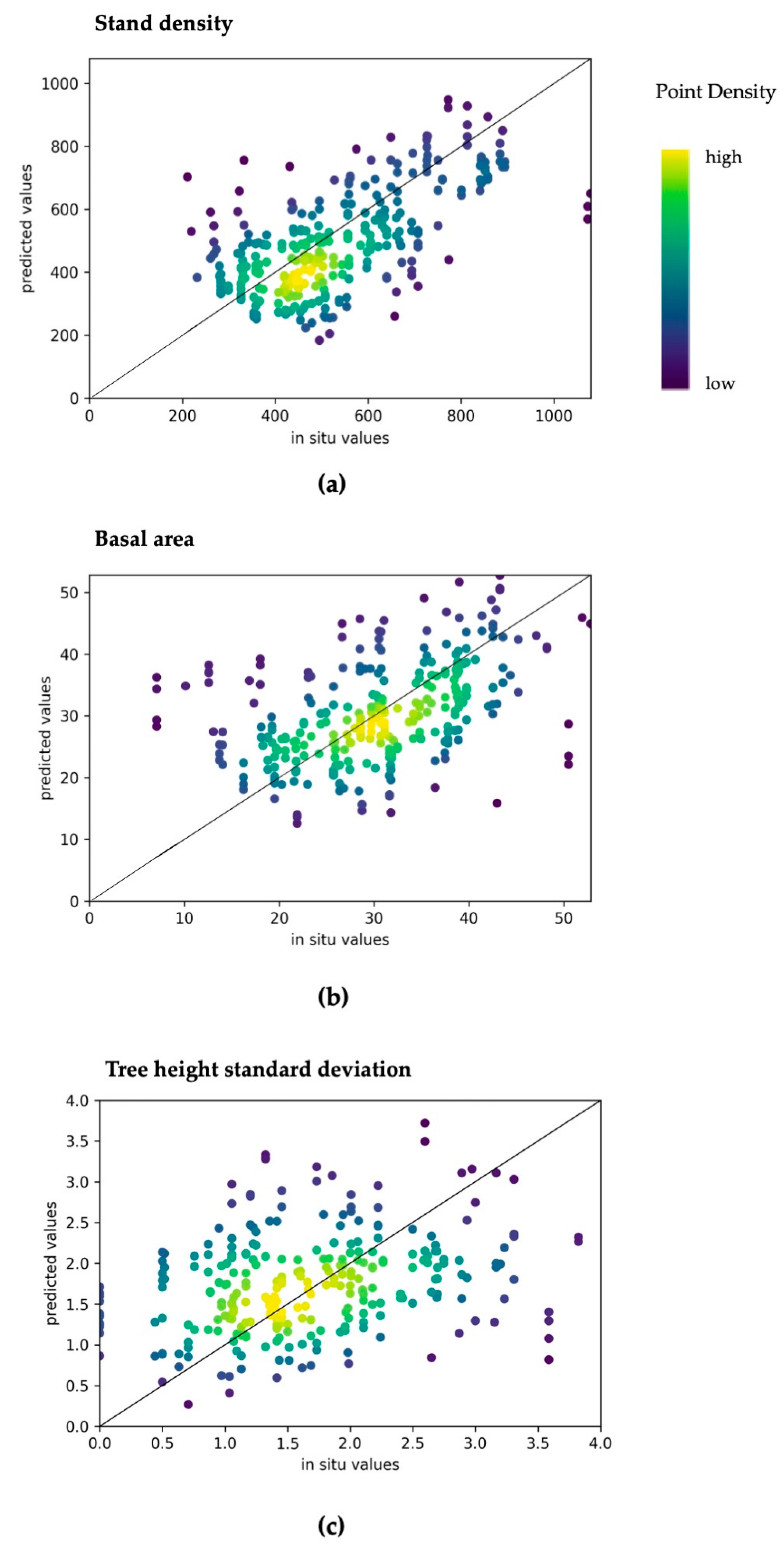
3.3. Model Accuracies for Other Structural Variables
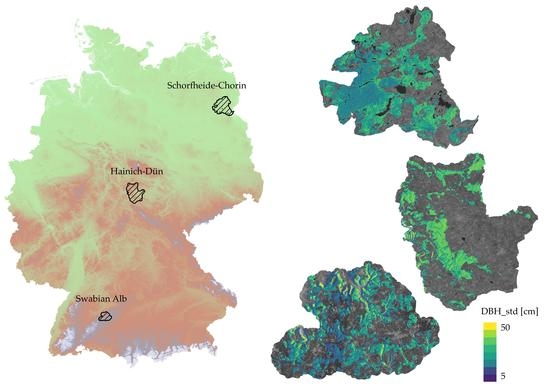
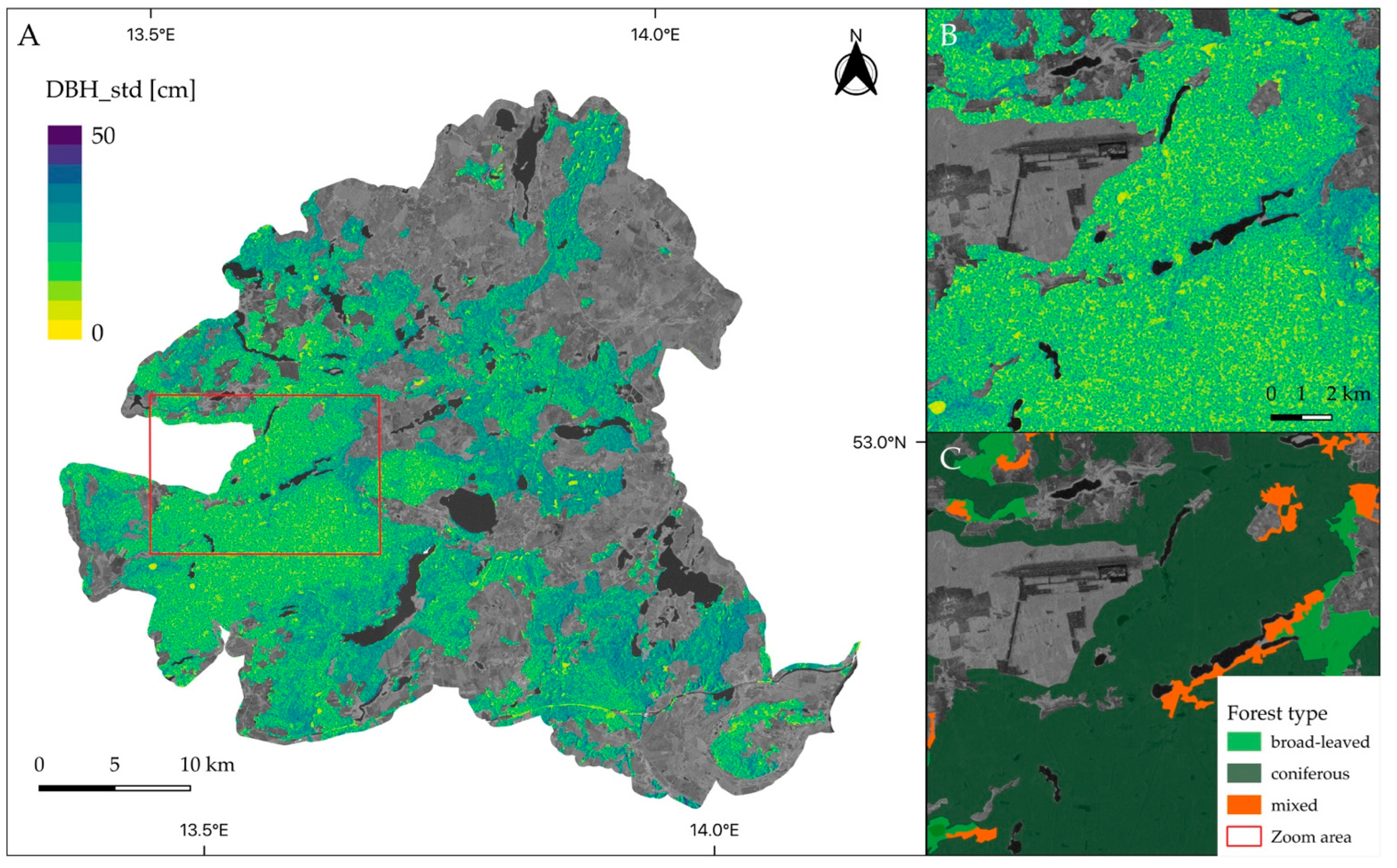
3.4. Spatial Patterns of Predicted Tree Diameter Variation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO; UNEP. The state of the world’s forests. In Forests, Biodiversity and People; United Nations Food and Agriculture Organization: Rome, Italy, 2020. [Google Scholar]
- Bauhus, J.; Forrester, D.I.; Pretzsch, H. From Observations to Evidence about Effects of Mixed-Species Stands. In Mixed-Species Forests: Ecology and Management, 1st ed.; Pretzsch, H., Forrester, D.I., Bauhus, J., Eds.; Springer: Berlin, Germany, 2017; pp. 27–73. [Google Scholar]
- Austin, Z.; McVittie, A.; McCracken, D.; Moxey, A.; Moran, D.; White, P.C.L. Integrating quantitative and qualitative data in assessing the cost-effectiveness of biodiversity conservation programmes. Biodivers. Conserv. 2015, 24, 1359–1375. [Google Scholar] [CrossRef][Green Version]
- Pereira, H.M.; Ferrier, S.; Walters, M.; Geller, G.N.; Jongman, R.H.G.; Scholes, R.J.; Bruford, M.W.; Brummitt, N.; Butchart, S.H.M.; Cardoso, A.C.; et al. Essential Biodiversity Variables. Science 2013, 339, 277–278. [Google Scholar] [CrossRef] [PubMed]
- Skidmore, A.K.; Coops, N.C.; Neinavaz, E.; Ali, A.; Schaepman, M.E.; Paganini, M.; Kissling, W.D.; Vihervaara, P.; Darvishzadeh, R.; Feilhauer, H.; et al. Priority list of biodiversity metrics to observe from space. Nat. Ecol. Evol. 2021, 5, 896–906. [Google Scholar] [CrossRef]
- Holzwarth, S.; Thonfeld, F.; Abdullahi, S.; Asam, S.; Da Ponte Canova, E.; Gessner, U.; Huth, J.; Kraus, T.; Leutner, B.; Kuenzer, C. Earth Observation based Monitoring of Forests in Germany: A Review. Remote Sens. 2020, 12, 3570. [Google Scholar] [CrossRef]
- Skidmore, A.K.; Pettorelli, N.; Coops, N.C.; Geller, G.N.; Hansen, M.; Lucas, R.; Mücher, C.A.; O’Connor, B.; Paganini, M.; Pereira, H.M.; et al. Environmental science: Agree on biodiversity metrics to track from space. Nature 2015, 523, 403–405. [Google Scholar] [CrossRef]
- Morin, D.; Planells, M.; Guyon, D.; Villard, L.; Mermoz, S.; Bouvet, A.; Thevenon, H.; Dejoux, J.; Le Toan, T.; Dedieu, G. Estimation and Mapping of Forest Structure Parameters from Open Access Satellite Images: Development of a generic method with a Study Case on Coniferous Plantation. Remote Sens. 2019, 11, 1275. [Google Scholar] [CrossRef]
- Sun, H.; Hu, J.; Wang, J.; Zhou, J.; Lv, L.; Nie, J. RSPD: A Novel Remote Sensing Index of Plant Biodiversity Combining Spectral Variation Hypothesis and Productivity Hypothesis. Remote Sens. 2021, 13, 3007. [Google Scholar] [CrossRef]
- Mallinis, G.; Chrysafis, I.; Korakis, G.; Pana, E.; Kyriazopoulos, A.P. A Random Forest Modeling Procedure for a Multi-Sensor Assessment of Tree Species Diversity. Remote Sens. 2020, 12, 1210. [Google Scholar] [CrossRef]
- Chrysafis, I.; Korakis, G.; Kyriazopoulos, A.P.; Mallinis, G. Predicting Tree Species Diversity Using Geodiversity and Sentinel-2 Multi Seasonal Spectral Information. Sustainability 2020, 12, 9250. [Google Scholar] [CrossRef]
- Grabska, E.; Hostert, P.; Pflugmacher, D.; Ostapowicz, K. Forest Stand Species Mapping Using the Sentinel-2 Time Series. Remote Sens. 2019, 11, 1197. [Google Scholar] [CrossRef]
- Torresani, M.; Rocchini, D.; Sonnenschein, R.; Zebisch, M.; Marcantonio, M.; Ricotta, C.; Tonon, G. Estimating tree species diversity from space in an alpine conifer forest: The Rao’s Q diversity index meets the spectral variation hypothesis. Ecol. Inform. 2019, 52, 26–34. [Google Scholar] [CrossRef]
- Gyamfi-Ampadu, E.; Gebreslasie, M.; Mendoza-Ponce, A. Evaluating Multi-Sensors Spectral and Spatial Resolutions for Tree Species Diversity. Remote Sens. 2021, 13, 1033. [Google Scholar] [CrossRef]
- Fagua, J.C.; Jantz, P.; Burns, P.; Massey, R.; Buitrago, J.Y.; Saatchi, S.; Hakkenberg, C.; Goetz, S.J. Mapping tree diversity in the tropical forest region of Chocó-Colombia. Environ. Res. Lett. 2021, 16, 054024. [Google Scholar] [CrossRef]
- Bruggisser, M.; Dorigo, W.; Dostálová, A.; Hollaus, M.; Navacchi, C.; Schlaffer, S.; Pfeifer, N. Potential of Sentinel-1 C-Band Time Series to Derive Structural Parameters of Temperate Deciduous Forests. Remote Sens. 2021, 13, 798. [Google Scholar] [CrossRef]
- Madonsela, S.; Cho, M.A.; Ramoelo, A.; Mutanga, O. Investigating the Relationship between Tree Species Diversity and Landsat-8 Spectral Heterogeneity across Multiple Phenological Stages. Remote Sens. 2021, 13, 2467. [Google Scholar] [CrossRef]
- Khare, S.; Latifi, H.; Rossi, S. Forest beta-diversity analysis by remote sensing: How scale and sensors affect the Rao’s Q index. Ecol. Indic. 2019, 106, 105520. [Google Scholar] [CrossRef]
- Rocchini, D.; Luque, S.; Pettorelli, N.; Bastin, L.; Doktor, D.; Faedi, N.; Feilhauer, H.; Féret, J.; Foody, G.M.; Gavish, Y.; et al. Measuring ß-diversity by remote sensing: A challenge for biodiversity monitoring. Methods Ecol. Evol. 2018, 9, 1787–1798. [Google Scholar] [CrossRef]
- Torresani, M.; Rocchini, D.; Zebisch, M.; Sonnenschein, R.; Giustino, T. Testing the spectral variation hypothesis by using the RAO-Q index to estimate forest biodiversity: Effect of spatial resolution. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2019. [Google Scholar]
- Thom, D.; Taylor, A.R.; Seidl, R.; Thuiller, W.; Wang, J.; Robideau, M.; Keeton, W.S. Forest structure, not climate, is the primary driver of functional diversity in northeastern North America. Sci. Total Environ. 2020, 762, 143070. [Google Scholar] [CrossRef]
- Del Río, M.; Pretzsch, H.; Alberdi, I.; Bielak, K.; Bravo, F.; Brunner, A.; Condés, S.; Ducey, M.J.; Fonseca, T.; von Lüpke, N.; et al. Characterization of the structure, dynamics and productivity of mixed-species stands: A review and perspectives. Eur. J. For. Res. 2016, 135, 23–49. [Google Scholar] [CrossRef]
- Storch, F.; Dormann, C.F.; Bauhus, J. Quantifying forest structural diversity based on large-scale inventory data: A new approach to support biodiversity monitoring. For. Ecosyst. 2018, 5, 34. [Google Scholar] [CrossRef]
- Ehbrecht, M.; Seidel, D.; Annighöfer, P.; Kreft, H.; Köhler, M.; Zemp, D.C.; Puettmann, K.; Nilus, R.; Babweteera, F.; Willim, K.; et al. Global patterns and climatic controls of forest structural complexity. Nat. Commun. 2021, 12, 519. [Google Scholar] [CrossRef] [PubMed]
- Castaño-Villa, G.J.; Estevez, J.V.; Guevara, G.; Bohado-Murilla, M.; Fontúrbel, F. Differential effects of forestry plantations on bird diversity: A global assessment. For. Ecol. Manag. 2019, 440, 202–207. [Google Scholar] [CrossRef]
- Bae, S.; Levick, S.R.; Heidrich, L.; Magdon, P.; Leutner, B.J.; Wöllauer, S.; Serebryanyk, A.; Nauss, T.; Krzystek, P.; Gossner, M.M.; et al. Radar vision in the mapping of forest biodiversity from space. Nat. Commun. 2019, 10, 4757. [Google Scholar] [CrossRef] [PubMed]
- Mura, M.; McRoberts, R.E.; Chirici, G.; Marchetti, M. Estimating and mapping forest structural diversity using airborne laser scanning data. Remote Sens. Environ. 2015, 170, 133–142. [Google Scholar] [CrossRef]
- Tello, A.; Cazcarra-Bes, V.; Pardini, M.; Papathanassiou, K. Forest Structure Characterization From SAR Tomography at L-Band. IEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3402–3414. [Google Scholar] [CrossRef]
- Farwell, L.S.; Gudex-Cross, D.; Anise, I.A.; Bosch, M.J.; Olah, A.M.; Radeloff, V.C.; Razenkova, E.; Rogova, N.; Silveira, E.M.O.; Smith, M.M.; et al. Satellite image texture captures vegetation heterogeneity and explains patterns of bird richness. Remote Sens. Environ. 2021, 253, 112175. [Google Scholar] [CrossRef]
- Wallner, A.; Elatawneh, A.; Schneider, T.; Knoke, T. Estimation of forest structural information using RapidEye satellite data. Forestry 2015, 88, 96–107. [Google Scholar] [CrossRef]
- Meng, J.; Li, S.; Wang, W.; Liu, Q.; Xie, S.; Ma, W. Estimation of Forest Structural Diversity Using the Spectral and Textural Information Derived from SPOT-5 Satellite Images. Remote Sens. 2016, 8, 125. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest aboveground biomass estimation using Landsat 8 and Sentinel-1A data with machine learning algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef] [PubMed]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 imagery for forest variable prediction in boreal region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Fischer, M.; Bossdorf, O.; Gockel, S.; Hänsel, F.; Hemp, A.; Hessenmöller, D.; Korte, G.; Nieschulze, J.; Pfeiffer, S.; Prati, D.; et al. Implementing large-scale and long-term functional biodiversity research: The Biodiversity Exploratories. Basic Appl. Ecol. 2013, 11, 473–485. [Google Scholar] [CrossRef]
- Hessenmöller, D.; Nieschulze, J.; von Lüpke, N.; Schulze, E. Identification of forest management types from ground-based and remotely sensed variables and the effects of forest management on forest structure and composition. Forstarchiv 2011, 13, 171–183. [Google Scholar]
- Schall, P.; Schulze, E.-D.; Fischer, M.; Ayasse, M.; Ammer, C. Relations between forest management, stand structure and productivity across different types of Central European forests. Basic Appl. Ecol. 2018, 32, 39–52. [Google Scholar] [CrossRef]
- Rocchini, D.; Boyd, D.S.; Féret, J.-B.; Foody, G.M.; He, K.S.; Lausch, A.; Nagendra, H.; Wegmann, M.; Pettorelli, N. Satellite remote sensing to monitor species diversity: Potentials and pitfalls. Remote Sens. Ecol. Conserv. 2016, 2, 25–36. [Google Scholar] [CrossRef]
- Pretzsch, H.; Schütze, G. Effect of tree species mixing on the size structure, density, and yield of forest stands. Eur. J. For. Res. 2015, 135, 1–22. [Google Scholar] [CrossRef]
- GEE. Sentinel-1 Algorithms in Google Earth Engine. Available online: https://developers.google.com/earth-engine/guides/sentinel1 (accessed on 29 December 2021).
- EO Research. Cloud Masks at Your Service. State-of-the-Art Cloud Masks now Available on Sentinel Hub. Available online: https://medium.com/sentinel-hub/cloud-masks-at-your-service-6e5b2cb2ce8a (accessed on 29 December 2021).
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Hofmann, S.; Everaars, J.; Schweiger, O.; Frenzel, M.; Bannehr, L. Modeling patterns of pollinator species richness and diversity using satellite image texture. PLoS ONE 2017, 12, e0185591. [Google Scholar] [CrossRef]
- Tuanmu, M.-N.; Jetz, W. A global, remote sensing-based characterization of terrestrial habitat heterogeneity for biodiversity and ecosystem modeling. Glob. Ecol. Biogeogr. 2015, 24, 1329–1339. [Google Scholar] [CrossRef]
- Rocchini, D.; Marcantonio, M.; Ricotta, C. Measuring Rao’s Q diversity index from remote sensing: An open source solution. Ecol. Indic. 2017, 72, 234–238. [Google Scholar] [CrossRef]
- Khare, S.; Latifi, H.; Rossi, S. A 15-year spatio temporal analysis of plant ß-diversity using Landsat time series derived Rao’s Q index. Ecol. Indic. 2021, 121, 107105. [Google Scholar] [CrossRef]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 2nd ed.; O’Reilly Media, Inc.: Beijing, China, 2016. [Google Scholar]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Hoeser, T.; Kuenzer, C. Object Detection and Image Segmentation with Deep Learning on Earth Observation Data: A Review-Part I: Evolution and Recent Trends. Remote Sens. 2020, 12, 1667. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- McElhinny, C.; Gibbons, P.; Brack, C.; Bauhus, J. Forest and woodland stand structural complexity: Its definition and measurement. For. Ecol. Manag. 2005, 218, 1–24. [Google Scholar] [CrossRef]
- Bellis, L.M.; Pidgeon, A.M.; Radeloff, V.C.; St-Louis, V.; Navarro, J.L.; Martella, M.B. Modeling habitat suitability for greater rheas based on satellite image texture. Ecol. Appl. 2008, 18, 1956–1966. [Google Scholar] [CrossRef]
- Joshi, N.; Mitchard, E.T.A.; Brolly, M.; Schumacher, J.; Fernández-Landa, A.; Johannsen, V.K.; Marchamalo, M.; Fensholt, R. Understanding ‘saturation’ of radar signals over forests. Sci. Rep. 2017, 7, 3505. [Google Scholar] [CrossRef]
- Chang, T.; Rasmussen, B.P.; Dickson, B.G.; Zachmann, L.J. Chimera: A Multi-Task Recurrent Convolutional Neural Network for Forest Classification and Structural Estimation. Remote Sens. 2019, 11, 768. [Google Scholar] [CrossRef]
- Astola, H.; Seitsonen, L.; Halme, E.; Molinier, M.; Lönnqvist, A. Deep Neural Networks with Transfer Learning for Forest Variable Estimation Using Sentinel-2 Imagery in Boreal Forest. Remote Sens. 2021, 13, 2392. [Google Scholar] [CrossRef]
- Marzialetti, F.; Di Febbraro, M.; Malavasi, M.; Giulio, S.; Rosario Acosta, A.T.; Carranza, L.M. Mapping Coastal Dune Landscape through Spectral Rao’s Q Temporal Diversity. Remote Sens. 2020, 12, 2315. [Google Scholar] [CrossRef]
- Geller, G.N.; Halpin, P.N.; Helmuth, B.; Hestir, E.L.; Skidmore, A.; Abrams, M.J.; Aguirre, N.; Blair, M.; Botha, E.; Colloff, M.; et al. Remote Sensing of Biodiversity. In The GEO Handbook on Biodiversity Observation Networks, 1st ed.; Walters, M., Scholes, R.J., Eds.; Springer: Berlin, Germany, 2017; pp. 187–210. [Google Scholar]
- Neumann, M.; Starlinger, F. The significance of different indices of stand structure and diversity in forests. For. Ecol. Manag. 2001, 145, 91–106. [Google Scholar] [CrossRef]
- Ma, X.; Mahecha, M.D.; Migliavacca, M.; van der Plas, F.; Benavides, R.; Ratcliffe, S.; Kattge, J.; Richter, R.; Musavi, T.; Baeten, L.; et al. Inferring plant functional diversity from space: The potential of Sentinel-2. Remote Sens. Environ. 2019, 233, 111368. [Google Scholar] [CrossRef]
- Chaves, P.P.; Zuquim, G.; Ruokolainen, K.; Van Doninck, J.; Kalliola, R.; Gómez Rivero, E.; Tuomisto, H. Mapping Floristic Patterns of Trees in Peruvian Amazonia Using Remote Sensing and Machine Learning. Remote Sens. 2020, 12, 1523. [Google Scholar] [CrossRef]
- Kampouri, M.; Kolokoussis, P.; Argialas, D.; Karathanassi, V. Mapping of forest tree distribution and estimation of forest biodiversity using Sentinel-2 imagery in the University Research Forest Taxiarchis in Chalkidiki, Greece. Geocarto Int. 2019, 34, 1273–1285. [Google Scholar] [CrossRef]
- Ploton, P.; Mortier, F.; Réjou-Méchain, F.; Barbier, M.; Picard, N.; Rossi, V.; Dormann, C.; Cornu, G.; Viennois, G.; Bayol, N.; et al. Spatial validation reveals poor predictive performance of large-scale ecological mapping models. Nat. Commun. 2020, 11, 4540. [Google Scholar] [CrossRef]
- Neff, F.; Brändle, M.; Ambarli, D.; Ammer, C.; Bauhus, J.; Boch, S.; Hölzel, N.; Klaus, V.H.; Kleinebecker, T.; Gossner, M.M. Changes in plant-herbivore network structure and robustness along land-use intensity gradients in grasslands and forests. Sci. Adv. 2021, 7, eabf3985. [Google Scholar] [CrossRef]
- Felipe-Lucia, M.R.; Soliveres, S.; Penone, C.; Fischer, M.; Ammer, C.; Bolch, S.; Boeddinghaus, R.S.; Bonkrowski, M.; Buscot, F.; Fiore-Donno, A.M.; et al. Land-use intensity alters networks between biodiversity, ecosystem functions and services. Proc. Natl. Acad. Sci. USA 2020, 117, 28140–28149. [Google Scholar] [CrossRef]
- Tomppo, E.; Olsson, H.; Ståhl, G.; Nilsson, M.; Hagner, O.; Katila, M. Combining national forest inventory field plots and remote sensing data for forest databases. Remote Sens. Environ. 2008, 112, 1982–1999. [Google Scholar] [CrossRef]
- Wallner, A.; Friedrich, S.; Geier, E.; Meder-Hokamp, C.; Wei, Z.; Kindu, M.; Tian, J.; Döllerer, M.; Schneider, T.; Knoke, T. A remote sensing-guided forest inventory concept using multispectral 3D and height information from ZiYuan-3 satellite data. Forestry 2021, 88, 1–16. [Google Scholar] [CrossRef]
- Thonfeld, F.; Gessner, U.; Holzwarth, S.; Kriese, J.; da Ponte, E.; Huth, J.; Kuenzer, C. A First Assessment of Canopy Cover Loss in Germany’s Forests after the 2018–2020 Drought Years. Remote Sens. 2022, 14, 562. [Google Scholar] [CrossRef]
- Schall, P.; Ammer, C. Stand Structural Attributes Based on 2nd Forest Inventory, All Forest EPs, 2014–2018. Biodiversity Exploratories Information System (BexIS). Dataset ID = 22766. Available online: https://www.bexis.uni-jena.de/ (accessed on 29 December 2021).
- Schall, P.; Ammer, C. Stand Composition Based on 2nd Forest Inventory, All Forest EPs, 2014–2018. Biodiversity Exploratories Information System (BexIS). Dataset ID = 22907. Available online: https://www.bexis.uni-jena.de/ (accessed on 29 December 2021).
- Schall, P.; Ammer, C. New Forest Type Classification of All Forest EPs, 2008–2014. Biodiversity Exploratories Information System (BexIS). Dataset ID = 17706. Available online: https://www.bexis.uni-jena.de/ (accessed on 29 December 2021).
- Ehbrecht, M.; Ammer, C.; Schall, P. Effective Number of Layers from LiDAR, Forest, EP, 2014. Biodiversity Exploratories Information System (BexIS). Dataset ID = 19986. Available online: https://www.bexis.uni-jena.de/ (accessed on 29 December 2021).
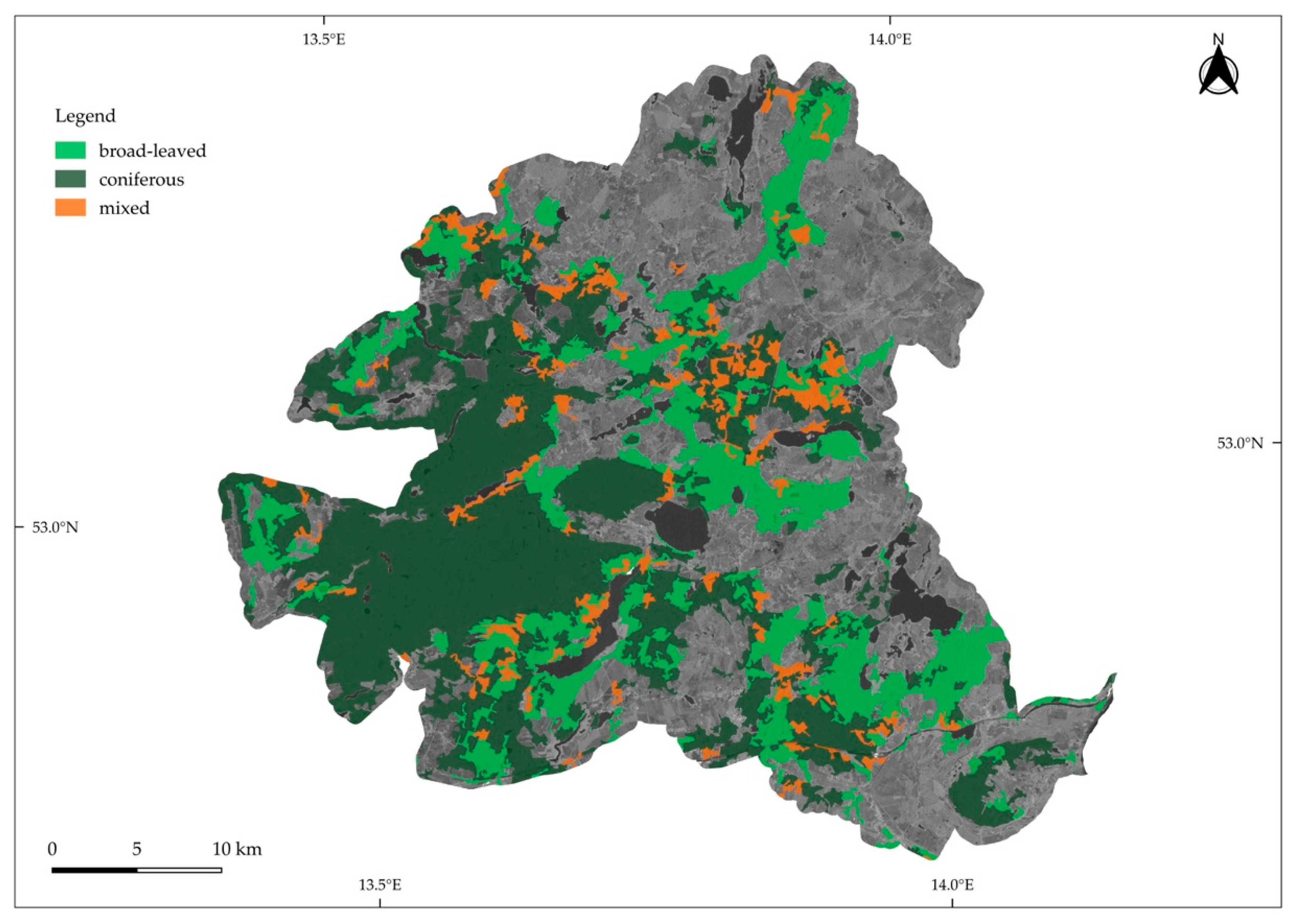



| Geographic Characteristics | Schorfheide-Chorin | Hainich-Dün | Swabian Alb |
|---|---|---|---|
| Location | NE Germany | Central Germany | SW Germany |
| Size | 1300 km2 | 1300 km2 | 422 km2 |
| Geology | Young glacial landscape | Calcareous bedrock | Calcareous bedrock |
| Dominant forest type | Pine and beech | Beech | Beech and spruce |
| Main soil type | Cambisol, Albeluvisol | Luvisol, Stagnosol | Cambisol, Leptisol |
| Altitude a.s.l. | 3–140 m | 285–550 m | 480–860 m |
| Annual mean temperature | 8–8.5 °C | 6.5–8 °C | 6–7 °C |
| Annual mean precipitation | 500–600 mm | 500–800 mm | 700–1000 mm |
| Feature Group | Feature Name | Wavelength [nm] | Abbreviation |
|---|---|---|---|
| Sentinel-2 spectral bands | Band 2—blue | 443 | blue |
| Band 3—green | 490 | green | |
| Band 4—red | 560 | red | |
| Band 5—vegetation red edge | 665 | re1 | |
| Band 6—vegetation red edge | 705 | re2 | |
| Band 7—vegetation red edge | 740 | re3 | |
| Band 8—near infrared | 842 | nir | |
| Band 8A—narrow near infrared | 865 | nirb | |
| Band 11—short wave infrared | 1610 | swir1 | |
| Band 12—short wave infrared | 2190 | swir2 | |
| Sentinel-2 EVI | EVI median | EVI_mean | |
| EVI std.dev. | EVI_std | ||
| Sentinel-2 Rao’s Q diversity index | Rao’s Q index | Q | |
| Sentinel-2 EVI texture | EVI contrast | EVI_contrast | |
| EVI dissimilarity | EVI_diss | ||
| EVI entropy | EVI_entr | ||
| EVI homogeneity | EVI_idm | ||
| Sentinel-1 C-Band backscatter | VH ascending (year) | VH_asc_year | |
| VH descending (year) | VH_desc_year | ||
| VV ascending (year) | VV_asc_year | ||
| VV descending (year) | VV_desc_year | ||
| VH ascending (winter) | VH_asc_winter | ||
| VH descending (winter) | VH_desc_winter | ||
| VV ascending (winter) | VV_asc_winter | ||
| VV descending (winter) | VV_desc_winter | ||
| normalized difference of winter VV and VH median | S1_ndi_mean | ||
| normalized difference of winter VV and VH std.dev. | S1_ndi_std | ||
| Sentinel-1 VV VH normalized difference texture | Sentinel-1 contrast | S1_contrast | |
| Sentinel-1 dissimilarity | S1_diss | ||
| Sentinel-1 entropy | S1_entr | ||
| Sentinel-1 homogeneity | S1_idm |
| Texture Metric | Description | Formula 1 |
| Contrast | Exponentially weighted difference in adjacent pixels. Measure of local variations in Digital Numbers (DN) within an image region. | |
| Inverse Difference Moment (Homogeneity) | Similarity of features between adjacent pixels or smoothness of the image. | |
| Entropy | “Randomness” in spatial distribution of pixels. | |
| Dissimilarity | Linear difference in values of adjacent pixels. |
| Feature Group | Predictors | RMSE | Std | RRMSE | Std | r2 | Std |
|---|---|---|---|---|---|---|---|
| S2 spectral bands, Rao’s Q, EVI | 13 | 0.37 | 0.05 | 0.71 | 0.10 | 0.09 | 0.09 |
| S1 backscatter features + NDI | 10 | 0.39 | 0.03 | 0.69 | 0.07 | 0.04 | 0.07 |
| S2 EVI texture | 4 | 0.34 | 0.04 | 0.61 | 0.09 | 0.20 | 0.11 |
| S1 texture winter-based NDI | 4 | 0.37 | 0.05 | 0.70 | 0.06 | 0.03 | 0.03 |
| All predictors | 31 | 0.34 | 0.05 | 0.60 | 0.11 | 0.25 | 0.10 |
| Only S2 features | 16 | 0.35 | 0.04 | 0.68 | 0.11 | 0.15 | 0.14 |
| Best predictors from each group | 4 | 0.35 | 0.02 | 0.66 | 0.07 | 0.16 | 0.08 |
| Spatial Autocorrelation | ALB | HAI | SCH | ALB, HAI, SCH |
|---|---|---|---|---|
| Moran’s I | −0.0003 | 0.03 | 0.09 | 0.06 |
| Z score | 0.10 | 0.21 | 0.49 | 0.38 |
| Feature Group | Predictors | RMSE | Std | RRMSE | Std | r2 | Std |
|---|---|---|---|---|---|---|---|
| S2 spectral bands, Rao’s Q, EVI | 13 | 6.06 | 0.68 | 0.43 | 0.05 | 0.09 | 0.06 |
| S1 backscatter features + NDI | 10 | 4.90 | 0.62 | 0.35 | 0.07 | 0.45 | 0.09 |
| S2 EVI texture | 4 | 4.98 | 0.54 | 0.37 | 0.05 | 0.35 | 0.09 |
| S1 texture winter-based NDI | 4 | 5.57 | 0.67 | 0.42 | 0.04 | 0.16 | 0.06 |
| All predictors | 31 | 4.30 | 0.85 | 0.31 | 0.05 | 0.49 | 0.12 |
| Only S1 features | 16 | 4.41 | 0.47 | 0.33 | 0.05 | 0.51 | 0.13 |
| Best predictors from each group | 4 | 4.91 | 0.55 | 0.36 | 0.06 | 0.45 | 0.08 |
| Spatial Autocorrelation | ALB | HAI | SCH | ALB, HAI, SCH |
|---|---|---|---|---|
| Moran’s I | −0.01 | 0.32 | 0.16 | 0.21 |
| Z score | 0.05 | 1.42 | 0.78 | 1.25 |
| Structure Variable | RMSE | Std | RRMSE | Std | r2 | Std |
|---|---|---|---|---|---|---|
| Height standard deviation (m) | 0.97 | 0.32 | 0.50 | 0.13 | 0.02 | 0.07 |
| Tree basal area (m) | 7.76 | 0.78 | 0.25 | 0.03 | 0.29 | 0.08 |
| Stand density (count) | 178 | 22.94 | 0.33 | 0.04 | 0.47 | 0.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffmann, J.; Muro, J.; Dubovyk, O. Predicting Species and Structural Diversity of Temperate Forests with Satellite Remote Sensing and Deep Learning. Remote Sens. 2022, 14, 1631. https://doi.org/10.3390/rs14071631
Hoffmann J, Muro J, Dubovyk O. Predicting Species and Structural Diversity of Temperate Forests with Satellite Remote Sensing and Deep Learning. Remote Sensing. 2022; 14(7):1631. https://doi.org/10.3390/rs14071631
Chicago/Turabian StyleHoffmann, Janik, Javier Muro, and Olena Dubovyk. 2022. "Predicting Species and Structural Diversity of Temperate Forests with Satellite Remote Sensing and Deep Learning" Remote Sensing 14, no. 7: 1631. https://doi.org/10.3390/rs14071631
APA StyleHoffmann, J., Muro, J., & Dubovyk, O. (2022). Predicting Species and Structural Diversity of Temperate Forests with Satellite Remote Sensing and Deep Learning. Remote Sensing, 14(7), 1631. https://doi.org/10.3390/rs14071631