Abstract
Lack of instrument sensitivity to low electron density (Ne) concentration makes it difficult to measure sharp Ne vertical gradients (four orders of magnitude over 30 km) in the D/E-region. A robust algorithm is developed to retrieve global D/E-region Ne from the high-rate GNSS radio occultation (RO) data, to improve spatiotemporal coverage using recent SmallSat/CubeSat constellations. The new algorithm removes F-region contributions in the RO excess phase profile by fitting a linear function to the data below the D-region. The new GNSS-RO observations reveal many interesting features in the diurnal, seasonal, solar-cycle, and magnetic-field-dependent variations in the Ne morphology. While the D/E-region Ne is a function of solar zenith angle (χ), it exhibits strong latitudinal variations for the same χ with a distribution asymmetric about noon. In addition, large longitudinal variations are observed along the same magnetic field pitch angle. The summer midlatitude Ne and sporadic E (Es) show a distribution similar to each other. The distribution of auroral electron precipitation correlates better with the pitch angle from the magnetosphere than from one at 100 km. Finally, a new TEC retrieval technique is developed for the high-rate RO data with a top reaching at least 120 km. For better characterization of the E- to F-transition in Ne and more accurate TEC retrievals, it is recommended to have all GNSS-RO acquisition routinely up to 220 km.
1. Introduction
The D- (60–90 km) and E-region (90–150 km) ionosphere play important roles in radio wave propagation because of their effective absorption of short-wave signals (e.g., high-frequency, HF, radio) [1] and reflection of long-wave communication and navigation radios (e.g., very low frequency, or VLF) [2]. It overlaps with the neutral atmosphere, known as the mesosphere, and is associated with large variability. The atmospheric temperature decreases with height in the mesosphere (or the D-region ionosphere), and the atmospheric thermal and density structures can be significantly perturbed by the atmospheric forcings from below (e.g., tides, planetary and gravity waves) [3].
The D-region is arguably one of the most critical interface layers between the lower atmosphere and the ionosphere. It is the layer where the electrical coupling takes place between the ionosphere and the phenomena such as sprites, elves, and blue jets from tropospheric thunderstorms occur. The D/E-region conductivity is important to complete a so-called global electric circuit (GEC), an electrical coupling between the ionosphere and the planetary surface with a DC current driven by tropospheric thunderstorms [4,5]. Because the D/E-layer conductivity can vary substantially between day and night, as well as between solar minimums and maximums over the 11-year cycle, it can short-circuit the F-region dynamo during the day [6,7,8] and modulate the GEC with the atmosphere throughout the day. However, it remains unclear if GEC has a significant feedback effect on thunderstorms, electrified clouds, or even on global cloud cover. If this feedback exists, the coupling between the ionosphere and the troposphere would act an important process to change Earth’s radiation and climate system [9,10,11].
The D-region plasma is weakly ionized during daytime, mainly from photoionization of nitric oxide (NO) by the solar Lyman-α (Ly-α) radiation [12]. When the photoionization is absent at night, the D-region electron density (Ne) decreases substantially but is maintained at a low level from complex sources [13]. During the quiet time, the daytime D-region Ne is balanced largely by positive molecular and cluster ions, where the upper D-layer mostly consists of molecular ions and the lower is dominated by cluster ions [14]. A strong solar activity can bring hard X-rays (wavelength < 1 nm) to ionize mesospheric N2 and O2, but even in this situation, the recombination rates are so high in the D-region that the environment tends to relax back to the neutral condition quickly once the ionization sources are gone. Hence, the number concentration in this altitude region is dominant by neutral molecules.
The D/E-region ionosphere can be often perturbed by irregular small-scale dynamic and electromagnetic variability and instability. In the E-region, for instance, sporadic E (Es) can occur as a transient disturbance to the background Ne profile at 90–120 km altitudes [15]. The wind shear is thought to play a critical role in Es formation by converging the plasma density via the v × B drift in this region [16,17]. Global distribution and seasonal variation of Es have been obtained and studied extensively with global navigation satellite system radio occultation (GNSS-RO) [18,19,20] and ground-based observations [21]. These sporadic layers can even occur in the D-layer [22]. At high latitudes, influences on the D/E-region come from magnetospheric disturbances through polar electron precipitation with enhanced ionization. This process is thought to play a role in increasing HOx and NOx productions through atmospheric chemical chain reactions involving electrons and positive and negative ions [23,24]. The short-lived HOx tends to produce direct effects on the O3 loss that are localized in space (i.e., the mesosphere) and time (i.e., precipitation events) [25,26], whereas the long-lived NOx can be transported down to the stratosphere to produce indirect effects on the O3 loss [27,28].
The D/E-region Ne data are rare and limited, largely because of poor instrument sensitivity to low Ne concentration and incapability of remote sensing from space to profile a sharp Ne vertical gradient (i.e., four orders of magnitude over 30 km). Inconvenient and costly access to this altitude region makes in situ measurements infrequent and sparse. Thus, the majority of lower-ionospheric Ne measurements were obtained from sounding rockets (D/E-region) and ionosondes (E/F-region), which constitute the basis of empirical models such as FIRI (Faraday-International Reference Ionosphere) [29] and IRI-2016 (International Reference Ionosphere 2016) [30].
The objective of this study is to develop a robust algorithm to retrieve global D/E-region Ne from the high-rate GNSS-RO data that have been increasing in spatiotemporal sampling from a large number of SmallSat/CubeSat constellations. An improved spatiotemporal coverage is critical for studying the lower ionosphere because of substantial and complex diurnal variations and influences from both the lower atmosphere and upper ionosphere. As in the algorithm developed previously for the E-region by Wu [31], the new retrieval method removes F-region contributions in the excess phase profile with a linear function fit to the data before they are input for the D/E-region Ne retrieval. The GNSS-RO Ne retrievals tend to produce a lower Ne in the E-region compared to the IRI-2016 but in a general agreement with FIRI [32]. Similar results are found in the GNSS-RO Ne retrieval from this study through a brief comparison with ionosonde observations at the Hermanus site. The paper is organized to describe the improved algorithm of Ne retrieval with examples in Section 2, followed by the retrieval results and climatology of the GNSS-RO D/E-region Ne in Section 3. Brief evaluations of the GNSS-RO Ne with ionosonde observations at the Hermanus site and a novel retrieval technique for total electron content (TEC) are discussed in Section 4, before it is concluded in Section 5.
2. Data and Methods
The algorithm developed in this study is an extension of the earlier attempt to retrieve the Ne profile in the lower ionosphere from the GNSS-RO excess phase () profile [31]. The RO excess phase is the difference between the measured and the free-space straight-line distance of GNSS (transmitter) and LEO (receiver) satellites. In the so-called “bottom-up” technique, a linear function is fitted to the profile over a narrow ht range below the D-region to remove the F-region effects before the data are input for the D/E-region Ne retrieval. The F-region effects need to be removed first as cleanly as possible on a profile-by-profile basis, because a small residual from the F-region variability can induce large errors in the D/E-region retrieval. The bottom-up method, self-sufficient in removing F-region effects, is specially designed for retrieving low Ne concentrations in the lower ionosphere (Appendix A). It has several important differences from the conventional onion-peeling or top-down approach.
First, the top-down method assumes spherical homogeneity for all Ne layers along the RO path and requires absolute calibration of the excess phase () measurements, whereas the bottom-up method assumes only homogeneity in the D/E-region. The homogeneity assumption on the F-region Ne is not required, because it can become problematic for retrieving the Ne below it, as a small error in the F-region Ne retrieval can induce a large effect on the D/E-region Ne. This error propagation is caused by a long tail of the Abel weighting function, which does not vanish even at the RO tangent height (ht) far below the F-region [31]. As a result, small residual errors of the F-region Ne retrieval can propagate down to the D/E-region Ne in the data inversion process and generate a large error there [33,34]. A manifestation of this error propagation is clearly seen in the Ne profiles retrieved from the onion-peeling approach, which often exhibit large oscillatory, sometimes negative, values in the lower ionosphere [35,36,37]. On the other hand, the bottom-up method shows little contribution from the F-region in its weighting function in the D/E-region, and therefore its Ne retrieval is less impacted by the F-region error. The differences between the Abel and bottom-up weighting functions are detailed in Section 2.3.
Second, the bottom-up method is resilient to complex F-region variability with capability to cope with most of the F-region effects (e.g., inhomogeneity, structural variations) on a profile-by-profile basis. It is a self-sufficient approach, without relying on any auxiliary data. In other words, the algorithm contains a standalone data process using the same measurement profile for both E-region Ne retrieval and F-region effect removal. Previous studies found that the E-region Ne retrieval using an auxiliary model or constrained to an assimilated 3D Ne distribution had limited improvements for mitigating unrealistic F-region Ne features [38] and gradient effects on the derived E-region Ne [39]. These model-aided approaches are prone to ionospheric variability and tend to bias towards the quiet-time condition, not working reliably for a disturbed ionosphere.
Third, the bottom-up algorithm does not require absolute calibration that is needed to derive a line-of-sight (LOS) or horizontal TEC (hTEC) profile prior to the Ne inversion. It uses a differential profile, or the hTEC difference (), with respect to a linear function fitted to the or hTEC data below the D/E-region. Thus, the linear fit serves a reference of each individual measurement profile, and the derived is used for the Ne retrieval. The algorithm assumes that the F-region contributions to the hTEC in the D/E-region vary linearly over a narrow ht range, and this linear variation can be estimated and removed using the hTEC measurements below the D-region. As a result, the new algorithm is perhaps more sensitive to residual ionospheric errors (RIEs) and phase scintillations that are uncorrectable with the dual-frequency GNSS RO receivers, but these residual errors are relatively smaller than the systematic error from the spherical homogeneity assumption about the F-region.
Fourth, the bottom-up retrieval should not be used to replace the Abel inversion for the whole ionospheric Ne. Because the linear function used to remove F-region effects is a fit to the lower-ionospheric data, its uncertainty tends to increase with height and causes a large error in the Ne retrieval in the upper ionosphere. Thus, the Abel inversion from hTEC, which requires absolute calibration of the profile, still works better for the whole-ionospheric Ne retrieval.
2.1. RO Excess Phase () Measurements
As a key variable for the Ne retrieval, hTEC(ht) is the integral of Ne along the RO path at each ht. It is related to excess phase profile by
Errors in hTEC can come from higher-order dependence (e.g., ) and multi-path propagation. In the E-region ht, the hTEC error contains contributions from both the F- and E-region, of which the former is much larger because its residual effects cannot be fully removed. Thus, any small error from the F-region Ne retrieval would cause a large error in the E-region Ne retrieval. The hTEC profile can be derived from the L1 ( = 1.57542 GHz) and L2 ( = 1.22760 GHz) excess phase ( and in meters) by
In the previous algorithm, Wu [31] used only the measurements to derive hTEC. Therefore, the linear fit for F-region effect removal had to be carried out at ht = 50–80 km to avoid the atmospheric bending () at ht < 60 km. Because the contribution is same in the L1 () and L2 () profiles, Equation (2) uses both L1 and L2 measurements to cancel the contribution, such that the linear fit can be carried out from lower ht. In this study, we fit the hTEC data at ht = 30–60 km to a linear function and extrapolate it up and subtract it from hTEC to yield for the D/E-region Ne retrieval. Hence, the use of hTEC data at ht = 30–60 km allows the Ne retrieval extended to the D-region.
To better understand and evaluate error sources and their contributions to hTEC, we broke down into the ionospheric and atmospheric components. First, the neutral atmospheric component () in the profile is defined by
Here, includes the atmospheric bending and the residual ionospheric effect (RIE), or , that cannot be accounted for by the assumption from Equation (1):
Because is not from the neutral atmosphere and is not negligible at ht > 80 km, it should be considered as a measurement error of hTEC in Equation (2). With the dual-frequency approach, one would hope to correct the -dependent ionospheric effects in radio propagation. However, multi-path propagation and higher-order frequency dependence may induce the RIEs at these altitudes [40,41]. In Figure 1a, the contribution is obtained from fitting an exponential function to the data at ht = 20–50 km and extrapolated to the heights above.
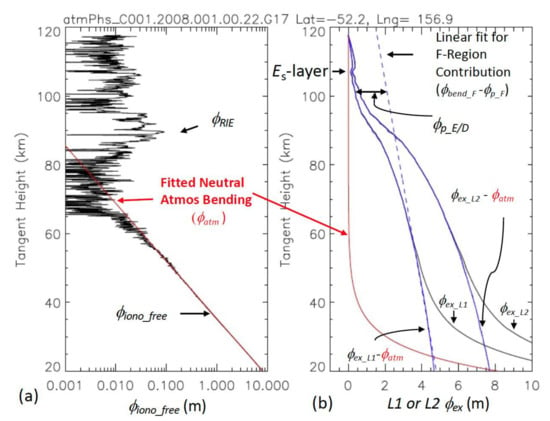
Figure 1.
(a) GNSS-RO excess phase profile from COSMIC-1 superimposed by the neutral atmospheric bending (in red) component derived from fitting the data ht = 30–60 km; (b) Illustration of different excess phase components in GNSS-RO for L1 excess phase , L2 excess phase , atmospheric bending , ionospheric component ( ) for L1 and L2, F-region contributions , and D/E-region phase advance . A thin sporadic-E (Es) layer is identified at 107 km with an enhanced excess phase in both and data.
Furthermore, it is important to understand the contributions to induced by ionospheric bending () and phase advance () effects as radio wave propagates in the ionosphere. The contributions from these processes are significant in the profile shown in Figure 1b, and these components have the opposite sign to each other.
This is because bending delay (due to a longer pathlength) and phase advance (due to faster phase speed) in the ionosphere produce the opposite effects in the measured excess phase . These components are defined by
where RO and SL in the integral represent the RO and straight-line (SL) path of radio propagation, and n is refractive index of the ionosphere. Although the RO is dominated by , ionospheric bending effects are not negligible because of the long pathlength in RO wave propagation. On the other hand, phase advance results from a faster phase speed of wave propagation in the ionospheric plasma, which will shorten . The two competing effects both manifest themselves in the GNSS-RO profile shown in Figure 1b.
The number of Ne retrievals may decrease with the dual-frequency approach, to some extent, compared to the -only approach. Data quality control is obviously more demanding from the joint use of and profiles, because large spikes in either measurement can cause a bad Ne retrieval. Because GNSS-RO measurements generally have better signal-to-noise ratio (SNR) for than for from GPS (Global Positioning System), the required calculation may be subject to the additional error induced from the profile, which can lead to an unsuccessful Ne retrieval. In addition, the relative signal strengths between L1 and L2 transmitters may vary with the GNSS systems. For example, GLONASS (Global Navigation Satellite System) satellites sometimes transmit stronger signals at the L2 frequency than L1.
The linear fitting for the F-region effect removal is similar between this study and one developed by Wu [31], except for slightly different height ranges. In this study, a linear function is fitted to the hTEC profile at ht = 30–60 km on a profile-by-profile basis:
The derived linear fit is extrapolated to the heights above at ht > 60 km, as estimated F-region contributions. By subtracting it from , we can obtain the D/E-region profile (in TECu):
where 1 TECu = 1016 m−3. Note that the conversion in Equation (9) neglects higher-order frequency dependence and ionospheric bending effects.
In essence, the bottom-up approach uses the difference with respect to the empirical reference (i.e., a linear function derived from ht = 30–60 km), instead of absolute values, for the D/E-region Ne retrieval. As shown in the next section, the at the D/E-region ht have much smaller contributions from the F-region Ne compared to the Abel weighting functions, which allows to yield a more reliable inversion for the D/E-region Ne.
2.2. Low-Rate (1 Hz) POD and High-Rate (50–100 Hz) RO Data
Both precise orbit determination (POD) and RO antennas can track GNSS signals at negative elevation angles or, in other words, at below the LEO receiver altitude. Generally speaking, the POD antennas have a wider field of view (FOV), lower SNR, and a coarser sampling resolution, compared to the RO antennas. Depending on the POD receiver design, receiver satellite altitude, and data acquisition schedule, the POD 1 Hz occultations usually have a smaller number of profiles (10–30% in COSMIC-1 podTEC) reaching the D/E-region. There are slightly more POD occultation profiles reaching the D/E-region when the satellite is in a lower orbital altitude. Thus, the higher RO cutoff tangent height and noisier hTEC measurements make the POD data less attractive for the D/E-region study.
In this study, we focus mainly on utilizing the high-rate (50–100 Hz) RO data, of which the sampling and spatiotemporal coverage are much higher than the POD data. The dense spatiotemporal sampling is critically needed to characterize the lower ionosphere variability. In addition, the high-rate data have advantages to detect and correct measurement errors such as clock time and cycle slips in the presence of ionospheric scintillations [42]. Smaller measurement errors help to retrieve a low Ne concentration in the lower ionosphere.
In recognition of the high-rate RO measurements for ionospheric observations, the MetOp-A operation conducted a short experiment with the high-rate RO acquisition up to ht ~ 290 km during 2020d161–2020d254 (9 June–10 September 2020). The success of the experiment allows the extended acquisition mode to continue from 2021d201 to the decommission in December 2021. As shown later in Section 3, the high-rate provides a significant benefit to the Ne retrievals in the E- to F-region transition and the retrieval of TEC. In addition to the extended high-rate profile from MetOp-A, the Spire GNSS-RO constellation, which NOAA uses to fill the polar latitudes outside the COSMIC-2 coverage, has been routinely acquiring the high-rate RO profile up to ht ~ 175 km. Among the earlier missions, the C/NOFS (Communications/Navigation Outage Forecasting System) had a frequent high-rate RO data reaching up to ht ~ 165 km from a low-inclination (13°) elliptical orbit.
The high-rate data in the D/E/F-region also provide a valuable diagnostic for better understanding and quantifying the RIEs of measurements in the ionosphere. The high-rate data help to reduce some of the scintillation-induced measurement noise, but the high-order frequency dependence and multi-path effects remain as a source of the errors in Equation (9) [31]. As shown in Figure 2, Es-induced phase scintillation can become a large random error source of at ht below the Es layer. An RIE from the F-region can sometimes induce a bias. If the bias is confined in a narrow height region, its impact on the Ne retrieval is generally small. But if the bias is present at all heights, the induced bias can be significant in the retrieved Ne.
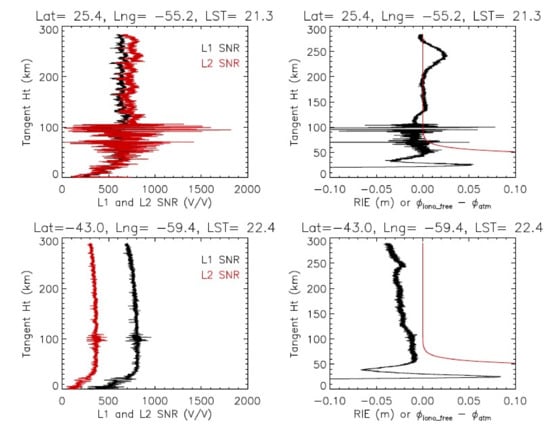
Figure 2.
Two examples of the RIE in the MetOp-A RO profiles from 2020d162: SNR profiles (left panels) and RIE profiles (right panels). The red line in the right panels is . The F-region and Es-induced RIEs are evident in the first case (top panels), whereas the sloped RIE profile is shown in the second case (bottom panels). The vertical gradient profile from RIEs is ~1.25 × 10−4 m/km, or ~1.25 × 10−7 in radians, along with a bias of 0.03 m.
RIEs can also have a non-negligible impact on the neutral atmospheric refractivity retrieval. Bending angle (), which is used to derive the atmospheric refractivity, is essentially a vertical derivative of the profile, i.e., . Therefore, a bias from RIEs would not be a problem for the retrieval, but a slope or vertical gradient of RIEs would. The RIE-induced error has been a major issue in the climate-quality data analysis of the upper stratosphere [43,44]. As shown in the second case in Figure 2, a vertical gradient (~1.25 × 10−7 radians) and bias (~0.03 m) are evident in the RIE profile. For this study, therefore, we simply allow a 0.3 m uncertainty for these RIEs in the D/E-region retrieval algorithm. Full characterization and correction for RIEs is an ongoing area of research and will be reported in a separate study.
2.3. Ne Retrievals
2.3.1. Inversion from
The inversion algorithm for the Ne retrieval in this study uses the optimal estimation inversion method [45]. The measurement vector y is the derived from Equations (3)–(8) as a function of ht, i.e., y , where is the maximum ht in the RO profile. The state vector x is Ne profile, i.e., x . When the measurement vector is changed from to , the weighting functions of the bottom-up algorithm are also transformed from the Abel functions to a new set of functions, as shown in red in Figure 3d. Unlike the Abel function, the new weighting functions for have a very small contribution from higher altitudes, which provide the advantage of minimizing F-region impacts.
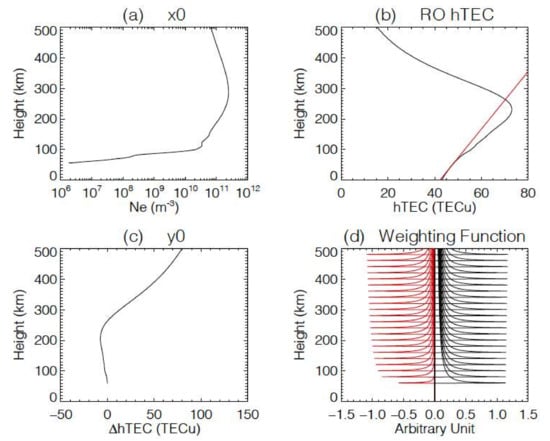
Figure 3.
(a) State vector , (b) measurement vector ( ), (c) in the linearization model, and (d) the associated weighting functions K (red) and their comparison with the Abel functions (black) for selected tangent heights between 50 and 500 km. The weighting functions K are flipped in sign purposely, to help the comparison. The intermediate step for the calculated RO hTEC and its linear fit (red line) from ht = 30–60 km is illustrated in (b), from which is derived as their difference. See text for more discussions.
The linearized forward model for the measurement vector () is related to the state vector () through a weighting function K, or the Jacobians as in , as follows:
where the linearization is based on the state vector (Ne in m−3) and the measurement vector ( in TECu). A single Ne profile is used for the in Equation (10), which is a merged profile from the annual mean of IRI-2016 from 2008 for the F-region [30] and the mean FIRI E-region profile for the solar minimum condition [29]. We assume that the weighting function K is invariant with the coefficient (i.e., the slope of the linear function in Equation (8)). The linearization model , , and K are depicted in Figure 3. The measurement uncertainty of y, or , is 0.3 m for the , or 1.9 TECu for , to account for multipath, RIE, scintillation, neglection of ionospheric bending, and other measurement errors. The multipath error from reflections off the spacecraft structure is estimated to <0.2 m for COSMIC-2 [46] and <1 m for COSMIC-1 [38]. The RIE error, as shown in Figure 1, is on the order of ~0.1 m but can be larger in a strong scintillation condition. The inversion in the optimal estimation method [45] can be expressed by
where is an optimal solution to x in Equation 10 and a is the a priori of x, which is set to be same as in this study. and are covariance matrices for a and y, respectively. Note that is a height-dependent parameter, which is empirically determined for stable Ne inversion over a large dynamic range and variability in the D/E-region altitudes. The detailed data flow diagram of the new algorithm and changes can be found in Appendix A.
For computation efficiency of the inversion from to Ne, we employ a variable height range for the state vector such that + 10 km. Because does not have much information on Ne at altitudes above , it would waste resources to carry out the Ne retrieval at extra levels above . This adaptive height range in the retrieval helps to reduce the number of Ne levels in the state vector, and therefore save CPU time for the inversion calculation in Equation (11).
2.3.2. D/E-Region
The bottom-up algorithm is developed to enable and optimize the D/E-region Ne retrieval in the situations where the F-region hTEC measurements are unavailable for correcting their effects on the lower-ionospheric retrieval. It is difficult to make this correction with the onion-peeling method when the entire hTEC profile is not available. An example from Equations (9) and (10) is shown in Figure 4, where the Ne profile is retrieved up to the RO top. Since most of the COSMIC 50-Hz RO data have a top height around ht ~ 125 km (see Appendix B), the D-region and a good portion of the E-region can be resolved, but the number of COSMIC-1 ROs started to decrease after 2017. The sampling reduction creates a problem for uniform local time coverage during the later years of COSMIC-1 mission. On the other hand, the operation from Sun-synchronous MetOp satellites has been stable throughout the mission, acquiring 100 Hz ROs up to ht ~ 90 km for the D-region. Therefore, the MetOp-A/B/C data are quite useful for studying long-term D-region Ne variations at two Sun-synchronous local times (8–11 h and 20–23 h).
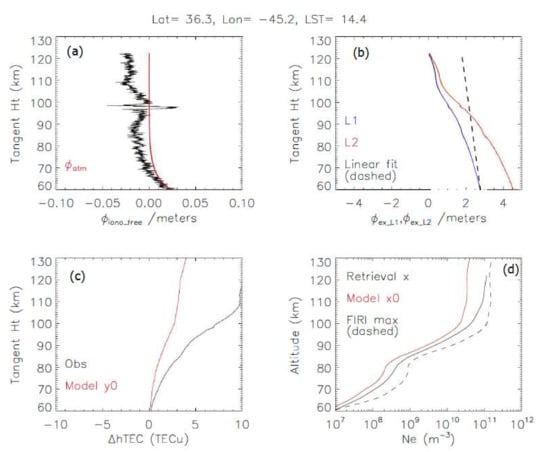
Figure 4.
(a–d) Illustration of a COSMIC-1 RO Ne profile retrieved from 1 January 2008. Differences between the measurement profile and the linearized model are inverted to produce a new state vector x for Ne.
Figure 4 is a relatively quiet case where the RIE component in the profile has an amplitude of ~3 cm with a small (~5 cm) Es residual at ht ~ 100 km. The D/E-region component () in is ~2 m (Figure 4b), significantly greater than the RIE and Es errors. This corresponds to ~10 TECu in (Figure 4c). Because the observed is larger than the linearization profile () from the state vector (), the retrieval yields an inverted Ne greater than , as seen in Figure 4d.
The D/E-region Ne. retrievals show a good sensitivity to the diurnal variations (Figure 5), since a constant linearization profile is used in Equation 11 without any a priori information on solar zenith angle (χ). As expected for the low Ne. concentration, the retrieval result is noisier at lower altitudes. More scatters are evident in the early evening hours, especially in the E-region, suggesting the potential impacts from ionospheric scintillations [47]. The local time coverage from the COSMIC-2 is fairly uniform on a single day. By the time of this day (i.e., 1 January 2021), the six-satellite constellation had spread out in local time sampling from their initial launch orbits on 25 June 2019. The low inclination (24°) orbit also helps to cover the tropical diurnal cycle in a relatively shorter period compared to those higher-inclination orbiters.
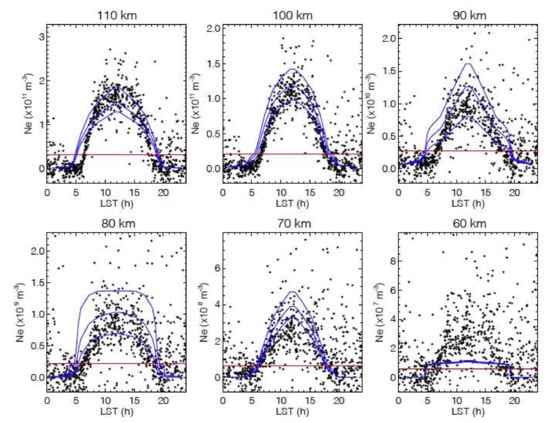
Figure 5.
COSMIC-2 Ne retrievals in the tropics (5°S–5°N) as a function of local time from 1 January 2021. The Ne value in the linearization state vector is the red line, and the FIRI models for three tabulated F10.7 (75, 130, 200 sfu) levels are the blue curves.
The diurnal variation of the retrieved D/E-region Ne is generally consistent with FIRI, although it exhibits a large deviation at 60 km (Figure 5). Unlike FIRI, which is symmetric about the local noon, the RO Ne retrievals are skewed slightly toward the afternoon hours. It is clear that the morning-hour onset of the daytime RO Ne lags the FIRI curve, while the retreat from the RO in the evening hours appears lagging behind the noon-symmetric FIRI model. The daytime RO Ne retrievals are slightly higher than the FIRI at 110 km. Given that F10.7 is at 77.7 solar flux unit (sfu) on 1 January 2021, the RO Ne retrievals are generally higher, compared to the FIRI prediction for F10.7 = 75 sfu.
2.3.3. Lower F-Region
The bottom-up algorithm can be extended to retrieve the Ne in the lower F-region if the RO hTEC profile reaches a higher altitude. However, most of the high-rate RO measurements do not go above ht ~ 120 km in the normal operation. On the other hand, MetOp-A has acquired some high-rate RO data with a top up to ~290 km, allowing to test the new algorithm for the lower F-region retrieval. Figure 6 shows the extended Ne retrievals from the ascending (nighttime) and descending (daytime) orbits in October 2021, revealing the E- to F-region transition across the meridional plane at two local times (8–11 h and 20–23 h). Because the E- and F-region dynamos are electrically connected, this global coverage in the lower ionosphere with a high spatiotemporal sampling is critically needed for studying and understanding their coupling processes.
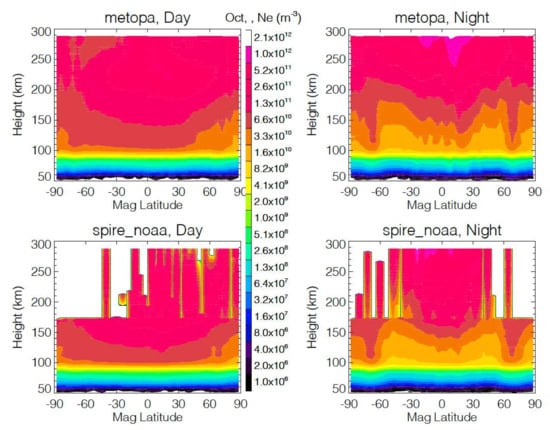
Figure 6.
Zonal mean Ne profile from MetOp-A (top panels) and Spire (bottom panels) as a function of magnetic latitude for October 2021.
In addition to MetOp-A, the Spire constellation also produces ROs with a top routinely up to ~175 km, higher than most of the GNSS-RO operations. The Spire’s high-rate data occasionally go up to an even higher altitude for large scintillation cases. As shown in Figure 6, these high profiles provide only sparse sampling at altitudes above 175 km, not enough to produce a reliable climatology. Below that altitude, the Spire sampling seems to be uniform. Different from MetOp-A, the Spire constellation covers all local times. In other words, the Spire zonal mean is truly daytime and nighttime from all local times, whereas the MetOp-A zonal means are from two Sun-synchronous local times (Appendix B). Nevertheless, the Spire daytime and nighttime climatologies below 175 km exhibit the distributions similar to those from MetOp-A.
2.3.4. TEC and Vertical Gradient of
The vertical gradient of profiles at the lower ionospheric ht contains quantitative information on TEC and can be used to retrieve TEC without requiring absolute calibration of . In this section we further analyzed the TEC information using the synthetic data from the January 2008 IRI-2016 Ne profiles for different geolocation and solar local time conditions. We compute TEC and from these Ne profiles and applied the same retrieval algorithm as in Equation (8) to the modeled and coefficient . As illustrated in Figure 7a, the coefficient from the synthetic data and TEC are highly correlated. There is a clear difference between the daytime and nighttime -TEC relationships, showing a smaller slope from the daytime profiles. On the other hand, TEC appears to correlate well the hTEC difference or ΔhTEC between ht = 200 and ht = 60 km. These sensitivities have an important application for the TEC remote sensing, because the hTEC differencing (ΔhTEC) approach does not require absolute calibration about hTEC measurements. It can be simply achieved by using the with respect to the value at a reference ht. In a broader sense, it is a similar technique to the measurement vector as formulated in Equations (7) and (8).
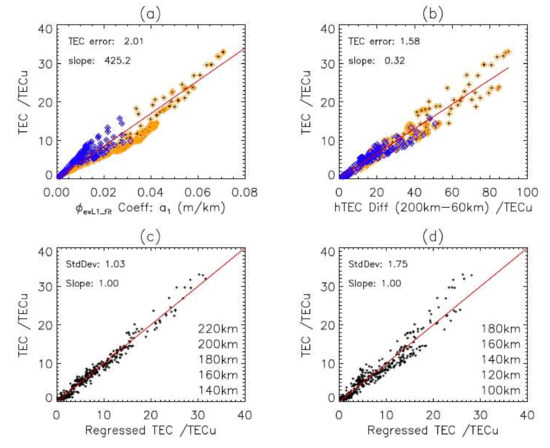
Figure 7.
Simulated TEC relationships with (a) coefficient in Equation (8), (b) hTEC difference between ht = 200 km and ht = 60 km, (c) TEC values regressed from the hTEC differences at five levels between 140–220 km, and (d) TEC values regressed from five levels between 100–180 km.
The model simulation shows that TEC can be retrieved from the lower-ionospheric measurements with the reference at ht = 60 km. The technique appears to work best for the measurements with the top reaching ht = 200 km, the altitude slightly below the F2 peak. Assuming a measurement uncertainty of 1 TECu, we test this idea with the synthetic IRI-2016 data and derive a set of regression coefficients for the TEC retrieval. The synthetic and TEC data represent all variabilities from 2008, and the linear regression is used to develop the retrieval coefficients for . Figure 7c,d show two TEC retrieval methods from different five-level data. The regressed coefficients for the five-level data are given by Equations (12) and (13) for the RO top reaching 220 km and 180 km, respectively,
where TEC’ is the TEC retrieval from the five-level measurements. Figure 7c produces a mean standard deviation of 1.03 TECu of the retrieved TEC from five ht levels at 140, 160, 180, 200, and 220 km, whereas in Figure 7d the retrieved TEC error increases to 1.75 TECu if the lower levels (100, 120, 140, 160, and 180 km) are used. The measurements near the F2 peak (ht = 180–220 km) are generally weighted more than those from other heights, as indicated by the regression coefficients in the simulated data. The weight coefficient decreases for the measurements at ht above the F2 peak (not shown), as expected for the measurements not going through the bulk of the ionosphere.
In summary, the TEC retrieval method demonstrated in Figure 7c is practically useful for the high-rate RO data with the top above 220 km. On the other hand, the method in Figure 7d is applicable to the Spire near-real-time (NRT) data when the top of RO profiles reaches ht ~ 175 km. For accurate TEC retrievals, these high-ht RO observations (close to the F2 peak) are more desirable. Thus, it is recommended in future GNSS-RO operations to extend the RO acquisition up to at least ht = 220 km.
2.4. GNSS-RO Data
Global Navigation Satellite System (GNSS) provides continuous broadcast of positioning and time data from space to the ground and other satellite receivers that can be used to determine their location. There are six major GNSS constellations either in operation or development: U.S. Global Positioning System (GPS), Russian Global Navigation Satellite System (GLONASS), European Navigation Satellite System Galileo (Galileo), Japanese Quasi Zenith Satellite System (QZSS), Chinese BeiDou System (BDS), and Indian Regional Navigation Satellite System (IRNSS). In addition, civil Satellite-based Augmentation System (SBAS) for aviation safety uses geostationary (GEO) satellites to improve the accuracy and reliability of GNSS information by broadcasting the augmentation data with signal measurement error corrections. Each of these GNSS constellations is assigned with a satellite system code: G: GPS, R: GLONASS, E: Galileo, J: QZSS, C: BDS, I: IRNSS, and S: SBAS, which is used in naming every GNSS-LEO link for the RO data.
The GNSS-RO data used in this study are summarized in Appendix B (Table A1), which lists different RO missions with information such as operation period, LEO (low Earth orbit) satellite initial and final altitude, orbital precession, latitude coverage, RO top height, and number of daily RO profiles. The majority of GNSS-RO data is obtained from the COSMIC Data Analysis and Archive Center (CDAAC) distribution, which processes the data to Level-2. The Level-1b data are processed with different versions of software, namely, NRT, postprocessing (postProc), and reprocessing (e.g., with subfix “2016”). The satellites that contribute to the global GNSS-RO acquisition include CHAMP (Challenging Minisatellite Payload), SAC-C (Satellite de Aplicaciones Cientifico-C), COSMIC-1/2 (Constellation Observing System for Meteorology, Ionosphere, and Climate 1 or 2), METOP-A/B/C (Meteorological Operational Polar Satellite A/B/C), GRACE (Gravity Recovery and Climate Experiment), C/NOFS, TSX (TerraSAR-X), TDX (TanDEM-X), Korean KOMPSAT-5, Spanish PAZ, and Chinese Fengyun-3 (FY3).
3. Results
3.1. Diurnal Variations
The D/E-region Ne is a strong function of χ as the lower ionosphere is largely influenced by the Ly-α ionization of mesospheric species such as NO. To characterize the Ne morphology, we averaged all the COSMIC-1 RO retrievals from 2006–2020 to generate a monthly climatology for each 2-hourly local time, 4° latitude, and 2 km altitude bin. As shown in Figure 8 for four selected months and four selected altitudes, the new Ne data reveal several interesting features and variations in the lower ionosphere. A complete set of monthly climatology can be found in Figure S1.
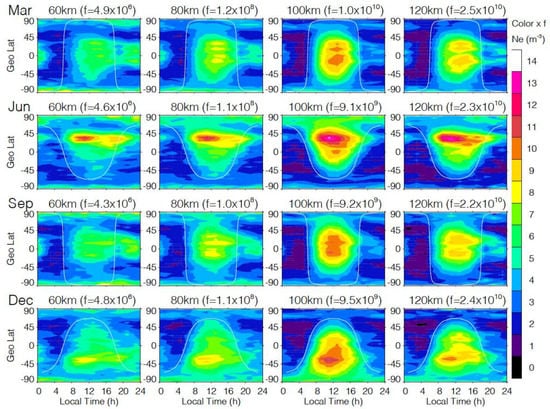
Figure 8.
COMSIC-1 Ne at 60, 80, 100, and 120 km as a function of LST and latitude for March, June, September, and December. The scaling factor for the color bar is indicated by the number in the parenthesis. The solid line denotes solar zenith angle χ = 90°.
Although the D/E-region Ne shows a clear χ-dependence, it exhibits strong latitudinal variations for the same χ. For example, at almost at all altitudes there is an enhanced daytime peak at the summer midlatitude during the solstice months (e.g., June and December). This peak occurs at a late morning hour slightly before noon. For the months near equinox (e.g., March and September), a dip at the magnetic equator is evident in the daytime Ne, especially at 100 and 120 km. This low Ne band, known as the “fountain effect” in the F-region, is likely an imprint of an upward plasma draft induced by the equatorial electrojet (EEJ). As expected for an eastward electric field build-up from EEJ, the E × B force could create an upward plasma drift [48]. Because of the strong vertical gradient in the D/E-region Ne, this vertical drift would manifest itself as a low Ne value compared to those at nearby latitudes without the drift.
Another noticeable feature is the asymmetry of Ne distribution about the noon. The D/E-region Ne climatology clearly shows that Ne arises slightly late in the morning with a lagged decay into the evening. The D-region Ne asymmetry about noon was also reported in ground-based observations [49]. In all monthly climatologies, the extended Ne enhancement from evening to midnight is observed. During the months near the equinox, such a prolonged Ne enhancement in the tropics is punctuated by a short decrease around LST = 19 h.
3.2. D-Region H′ and 𝛽 Parameters
The D-region (60–90 km) ionosphere is poorly characterized due to lack of Ne observations. In situ (e.g., sounding rockets) [50,51], remote sensing from incoherence scattering radar (ISR) [52], and radio wave propagation [53] are the common methods for measuring the D-region Ne [54], but their locations are sparse and the operation cost can be high. In addition, low electron concentrations in the D-region requires high power, large-sized antenna radars to obtain useful Ne measurements, which makes such systems unaffordable for wide deployment. On the other hand, high-frequency radio waves, although useful for the Ne sounding in the E-region and above, tend to pass through the D-region. At very low frequency (VLF, 3–30 kHz) and extremely low frequency (ELF, 0.3–3 kHz), radio waves are completely reflected by the D-layer and the ground surface, of which the two conducting boundaries act as an Earth–ionosphere waveguide (EIWG) to allow a low-loss long-range radio propagation. As a result, the VLF/ELF technique has been increasingly used for remote sensing of the D-region properties, including Ne [55,56,57].
To characterize the D-region Ne, the VLF/ELF observation community often uses a two-parameter D-region Ne model. As described by Wait and Spies [1964], the formula has characteristic reference height H′ (km) and exponential growth rate of Ne with height or 𝛽 (km−1), i.e.,
The model parameters from fitting to VLF/ELF observations yield a typical H′ value of 65–90 km and 𝛽 of 0.3–0.5 km−1 with a lower H′ value and slightly higher 𝛽 value during daytime [58,59,60,61,62,63,64]. Recently, an update was proposed to characterize a height split in the D-region Ne profiles with a four-parameter scheme, which appears to represent the daytime profiles better [65].
We used the same two-parameter model (Equation (14)) to fit the D-region Ne retrieved from COSMIC-1 (Figure 9). The H′ parameters derived from COSMIC-1 are slightly lower than those derived from the VLF observations [59,60], showing a daytime variation of 70–73 km, compared to 71–77 km from VLF. The COSMIC-1 𝛽 parameters exhibit a little variation around 0.31 km−1 during the day, compared to 0.25–0.4 km−1 reported from the VLF observations. For nighttime, the COSMIC-1 H′ and 𝛽 values are also lower, with H′ varying between 71 and 76 km compared to 82–86 km from VLF, and 𝛽 varying between 0.29 and 0.30 km−1 compared to 0.4–0.6 km−1 from VLF [61,62].
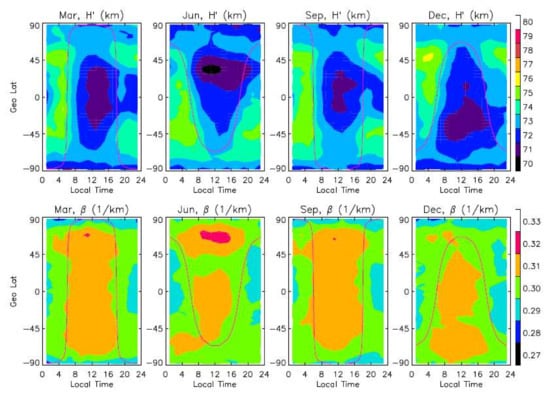
Figure 9.
The model parameters (H′ and 𝛽) for September and December as a function of magnetic latitude and local time from the fitting of COSMIC-1 D-region (60–80 km) Ne to Equation (14). The solid line is the terminator where the solar zenith angle χ at 100 km is equal to 90°.
3.3. Magnetic-Field Dependence
In addition to the diurnal variation, the D/E-region Ne can be significantly modulated by the magnetic field. To illustrate the magnetic-field effect, we averaged the COSMIC-1 Ne data from all LSTs and produced a monthly map for each altitude as a function of geographical longitude and latitude. Because the Ne at low and midlatitudes is dominated by the daytime climatology, the all-time averages appear similar to the daytime maps except for high latitudes. Figure 10 shows the 70 km maps, but the Ne distributions at the E-region altitudes are similar. A complete monthly climatology of all-LST maps can be found in Figure S2. The features observed below are generally applicable to the COSMIC-1 data at 70–120 km.
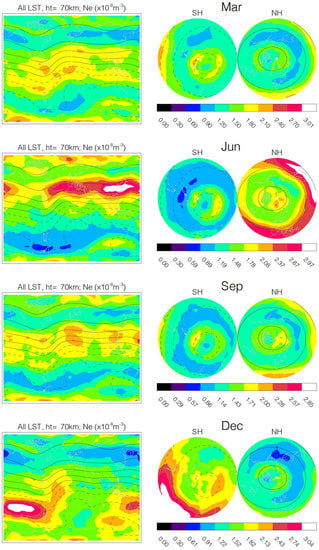
Figure 10.
COSMIC-1 monthly Ne maps at 70 km from all local times for March, June, September, and December. Magnetic field-line pitch angles (a.k.a., dip angles) are contoured at an interval of 20°. The pitch angles on the cylindrical-projection map (left) are derived from the magnetic field at a 100 km altitude, whereas the ones on the azimuthal polar maps are from the field at one Earth radius above the surface. The longitude–latitude grid size is 8° × 4° for these maps.
As shown in Figure 10, magnetic-field modulation of the D/E-region Ne is present in all months where the longitudinal variations follow the field line at most latitudes. There is an important distinction between the high-latitude and low- and midlatitude variations on what magnetic fields are in control. At high latitudes, as expected for the domination of auroral electron precipitation, the Ne distribution is correlated better with the magnetic field in the magnetosphere (e.g., at one Earth radius, Re). As seen Figure 10 (left panels), the correlation appears worse if it is compared to the magnetic pitch angles from the field at 100 km, but the distribution of auroral electron precipitation correlates better with the pitch angle derived from the magnetic field in the magnetosphere. In addition to the direct contribution from electron precipitation, the winter polar vortex is capable of transporting the aurora-produced NO down to the mesosphere and further enhancing the nighttime D-region Ne [66]. The fact that the polar Ne enhancements are closely associated with the magnetic pitch angle implies that such vertical transport from the polar vortex only plays a secondary role in the polar winter anomaly. As shown in the RO observations, the auroral electron precipitation does not produce a very strong polar Ne distribution as simulated under different hypothesized scenarios for the D-region ion chemistry [67].
It is worth noting that the summer-midlatitude Ne distributions in Figure 10 (June and December) bear a striking resemblance to the global Es morphology reported in the earlier studies with GNSS-RO [18,19,20]. As stressed by Wu [31], the new D/E-region Ne data will allow a more comprehensive study of the Es formation and its connection to the background E-region Ne concentration. The similar distribution between Es and Ne suggests that a common process is modulating their longitudinal variations in the summertime midlatitudes.
It remains challenging to fully understand what processes drive large longitudinal variations along the same field pitch angle (Figure 10). Planetary waves, such as the migrating and non-migrating tidal waves, can perturb the D/E-region Ne distribution by modulating the NO density and temperature in the upper mesosphere. In addition, some observations show that the lightning from tropospheric thunderstorms can induce a direct decrease in the D-region Ne [68] or sharpening in the Ne vertical gradient [69,70]. The lightning-induced Ne reduction may explain the relatively lower Ne values (along the same pitch angle) in June over the American and Indian Monsoon regions where deep convection and lightning activity are likely higher than elsewhere. It remains challenging with the GNSS-RO Ne observations to separate the direct lightning effect from others, as the D/E-region Ne is strongly coupled with other processes (e.g., solar radiation, planetary waves).
3.4. Seasonal Variations
To characterize the Ne seasonal variations, we divided the monthly data into daytime, post-sunset (LST = 19 h), and nighttime bins, and plotted these binned data as a function of time and magnetic latitude. Figure 11 shows the time series of Ne at 60, 80, 100, and 120 km. To the first order, the seasonal variation of daytime Ne at these altitudes is driven by solar radiation as the χ maximum moves around the equator with season. The midlatitude maximums near the solstice months are clearly seen in the time series, whereas the seasonal minimums at the midlatitudes appear to be quite different. The minimum in the SH winter is much lower than that in the northern winter. The seasonal asymmetry in Ne is extended to the nighttime time series where the χ effect can still be seen. The nighttime time series provides a better view of the seasonal variation of polar Ne. Similar to the post-sunset result, the polar Ne has a larger concentration in the summer month, as expected for a stronger field-aligned current from the sunlit hemisphere [71,72].
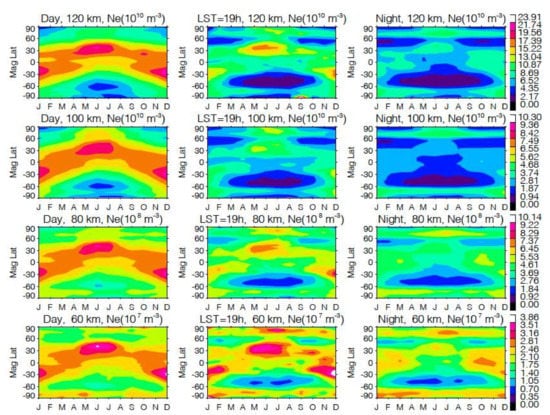
Figure 11.
Seasonal variations of daytime (left), post-sunset (middle), and nighttime (right) Ne (in 1010 m−3) at 70, 90, and 110 km.
A strong semiannual variation is observed in the nighttime D-region Ne with peaks near the equinox months. Several studies have suggested that the semiannual variation in the D-region could be induced by the NO concentration modulated by dynamic transport processes in the mesosphere and lower thermosphere [73,74]. In this case, the modulated NO concentration and the enhanced nighttime ionization in the D-region are correlated with a peak around the equinox. Consistent with the semiannual variation reported in these earlier studies, the COSMIC-1 observations seem to have two peaks in the tropics, but with a slightly higher concentration in October than that in March.
3.5. E- to F-Region Transition
The onion-peeling approach often produces negative or large oscillatory Ne values in the lower ionosphere [38]. These large errors make the onion-peeling retrieval unsuitable for studying the E- to F-region transition. The new Ne data, such as those with a higher RO top (e.g., Spire), can be used to describe the plasma transition from the E- to F-region with continuous height coverage and high spatiotemporal sampling. Figure 12 presents an example of monthly Ne statistics from such observations where high-RO-top (e.g., Spire) RO data are used. The retrieval covers an altitude range between 60 and 170 km and the data are averaged to 2-hourly bins in local time. More displays of Spire monthly climatology can be found in Figure S3 for the zonal mean and in Figure S4 for diurnal variations at the magnetic equator. One of the interesting features in the 2-hourly zonal mean (Figure 12) is the shift of the daytime Ne maximum from the SH E-region to the NH lower F-region. This shift implies a height-varying χ dependence of the Ne morphology in the lower F-region. Again, the equatorial dip in Ne is obvious in the late afternoon and early evening hours (i.e., LST = 15 h, 17 h, and 19 h), continuing through all altitudes in the E- to lower F-region.
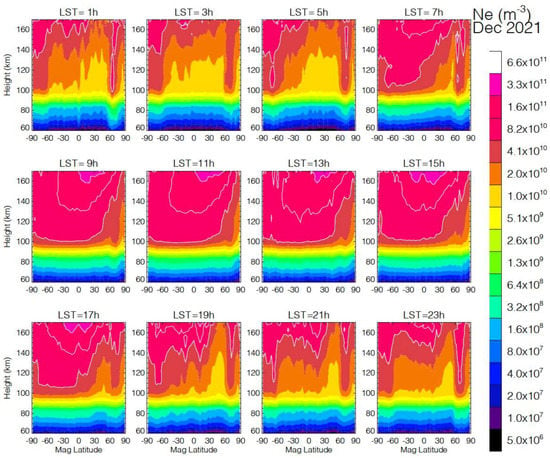
Figure 12.
E- to F-region transition in Ne for December 2021 from the Spire constellation. The Spire receivers acquire GNSS-RO routinely with a top up to ~175 km, allowing the Ne retrieval to be extended to the F1-region.
The polar features from auroral electron precipitation are more pronounced in the nighttime zonal mean in Figure 12. It is also known as the polar winter anomaly where ionospheric absorption of radio waves becomes extraordinarily strong [75]. Relatively speaking, they have a nearly uniform concentration in the lower F-region, but with a greater extension to the E-region compared to the low- to midlatitude Ne. The penetration to the D/E-region seems to be deeper around the midnight hours in the NH. Compared to the D/E-region, the nighttime Ne distribution in the lower F-region is less symmetric about the equator. In the early evening hours, the lower F-region appears to have a higher Ne in the winter subtropics, but the distribution peak shifts to the summer subtropics during the predawn hours.
The results presented in Figure 12 are based on the sampling from a subset of the Spire constellation data provided to the NOAA’s CWDP program, which have ~4000 daily RO profiles. Processed by the same COSMIC software to Level-1 and Level-2, these data have only become available on CDAAC for the research community since September 2021. As the constellation continues to expand, it is anticipated that more RO profiles will yield a further improved diurnal coverage on a monthly basis, perhaps to enable one-hour intervals in local time and a spatial resolution better than the 8° × 4° longitude–latitude grid used in this study. One of the advantages with dense spatial sampling is to allow a tomographic retrieval of Ne, which can help to mitigate the horizontal inhomogeneity problem associated with the poor horizontal resolution of the GNSS-RO technique.
3.6. Solar-Cycle Variations
Characterizing the long-term D/E-region Ne variations requires stable satellite operation and uniform sampling/quality in GNSS-RO observations. Because of the strong diurnal variability in the D/E-region Ne, a non-uniform or variable sampling of local times would make the observed Ne variation difficult to interpret and prone to the sampling error from aliasing to the diurnal variation. Although COSMIC-1 had a full diurnal coverage during the early period of mission, its sampling degraded over time as several of its operating satellites stopped working. As a result, the COSMIC-1 data are not ideal for studying the solar-cycle variation. On the other hand, the MetOp observations have been stable with the longest record at two Sun-synchronous local times around 8–10 a.m. and 8–10 p.m. Since the routine GNSS-RO acquisition from MetOp goes up to ~90 km, this long record is only available for the D-region Ne. To fill in the early period (2007–2008) of the MetOp record, we added the SACC data when they had the sampling at the similar equator-crossing time (see Appendix B).
The daytime and nighttime solar-cycle variations at 70 km from the MetOp/SACC observations are highlighted in Figure 13 as a function of magnetic latitude. As expected for the sunlight-driven ionization in the D-region, the D-region Ne correlates well with the Ly-α flux in terms of the solar-cycle variation. In addition, there is a strong semiannual modulation in the magnetic tropics from both daytime and nighttime time series. Because of the presence of the dominating solar-cycle and semiannual variations, it is not straightforward to discern a quasi-biennial oscillation (QBO) modulation in the D-region Ne, which was reported in some of the early studies [76,77].
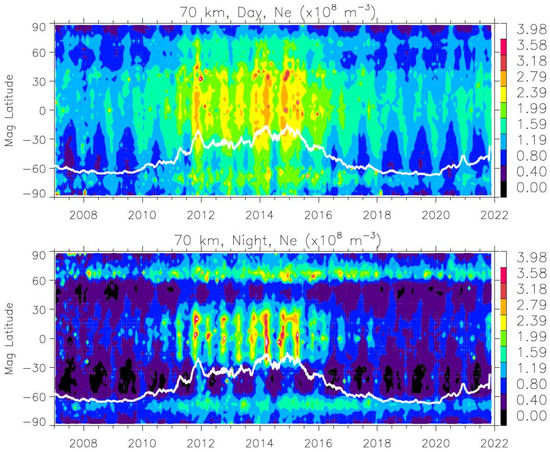
Figure 13.
Solar cycle variations of daytime (top) and nighttime (bottom) Ne at 70 km as a function of magnetic latitude from the combined MetOp-A/B/C and SAC-C (before 2008) monthly averages. The longterm variations at other altitudes (60 and 80 km) can be found in Figure S5. The time series of daily Ly-α is the overplotted white line. The Ly-α data are obtained from the GSFC’s Space Physics Data Facility (SPDF) OMNIweb service.
4. Discussions
4.1. Comparisons with Ionosonde Data at Hermanus
As a preliminary validation effort, the GNSS-RO E-region Ne profiles are compared against ionosonde Ne. The Hermanus (HE13N), South Africa (34.4°S, 19.2°E) ionosonde site was selected for the comparison because of the low fmin (minimum return frequency observed by the ionosondes) values over the period of interest: July 2008–August 2010. A low fmin value in the ionogram measurement is vital to derive the E-region Ne profiles. To collocate the GNSS-RO observations, RO tangent points were required to be within 2° of the Hermanus site and within 30 min of an ionosonde measurement that has an fmin below 1.2 MHz. The ionosonde data were obtained from the Digital Ionogram Database (DIDBASE, accessed 17 January 2022, https://giro.uml.edu/didbase/), and all ionograms were hand-scaled using the SAO Explorer application for ionosondes (https://ulcar.uml.edu/SAO-X/SAO-X.html, accessed 1 March 2022) to eliminate uncertainties caused by automatic scaling and ensure the quality of ionograms used in the comparison. The ionogram with sporadic-E or an uncertain E-region profile was excluded in the comparison. Over this two-year period, a total of 60 ionograms were hand-scaled for the comparison against the RO profiles.
Two examples of the ionosonde vs. RO Ne comparisons are displayed in Figure 14. The vertical line corresponds to the minimum return frequency measured by the ionosonde, fmin. The ionograms show E-region returns from fmin up to foE, but no measurements are obtained for the E- to F-region valley. Therefore, this comparison is limited to the altitude range between the fmin altitude and hmE, which varies with the time of day, location, and ionospheric conditions. As shown in Figure 14, the typical starting height for ionosonde measurements is 90 km, while GNSS-RO is capable of measuring densities at D-region altitudes (see Section 3). The NmE estimated from the RO and ionosonde techniques are in close agreement for these two examples, and the bottomside E-layer Ne gradients with respect to altitude (dNe/dz) are also in agreement.
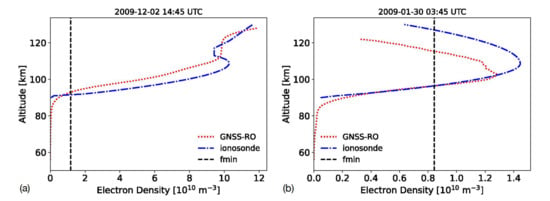
Figure 14.
Example electron density profiles for the GNSS-RO and ionosonde measurements. The vertical line corresponds to the minimum return frequency observed by ionosondes, fmin. Plot (a) corresponds to a daytime profile, while (b) shows a nighttime profile.
While many of the profiles show agreement in dNe/dz and NmE, the profiles are shifted in altitude with RO profiles being slightly higher, by 2 km on average, above the ionosonde profiles. This relatively small altitude difference may be due to the “internal uncertainty of the starting height of the profile” for ionosonde measurements [78]. The ionogram inversion assumptions and uncertainties were described in detail in several studies [79,80,81], revealing challenges in converting measured virtual heights to real heights for Ne. On the other hand, errors from ionospheric bending and derivation of the Earth ellipsoid model may also induce an uncertainty in the GNSS-RO HSL, but it is expected to be km.
For this comparison, we show the results obtained for both unshifted (original) and shifted profiles. The shifted profiles are obtained by adjusting the ionosonde Ne altitude to minimize the altitude difference between profiles at fmin. GNSS-RO and ionosonde-derived Ne at each height within the fmin altitude and hmE for the 60 profiles analyzed in this comparison are displayed in Figure 15. Here, the ionosonde Ne profiles are interpolated at each GNSS-RO altitude for a direct comparison. While the R2 and slope values for the linear regressions are nearly equal for the shifted and unshifted profiles, the y-intercept is closer to zero for the shifted profiles, closer to the 1:1 line that represents a perfect match between the two techniques. Overall, the densities show reasonable agreement with a larger variation for elevated densities.
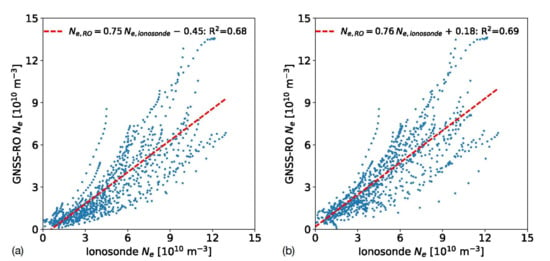
Figure 15.
Scatter plot of the electron densities predicted for each GNSS-RO altitude within the ionosonde fmin altitude and hmE. The ionosonde profiles are interpolated at each RO altitude for comparison. Unshifted profiles are compared in (a), while the ionosonde profiles shifted in altitude are displayed in (b). The linear regression parameters are also shown for both panels.
Histograms of the differences in density (Ne,GNSS-RO–Ne,ionosonde) as a function of altitude are displayed in Figure 16. The altitude bias in the unshifted profiles results in an underestimation of the electron densities by the GNSS-RO technique for the altitude range of roughly 90–110 km. However, when the ionosonde profiles are shifted in altitude, this underestimation bias is mostly removed, and the density differences are slightly less than zero for most altitudes. The mean absolute error (MAE) for the unshifted profiles is 1.9 × 1010 m−3, while the shifted profiles’ MAE is reduced to 1.4 × 1010 m−3.
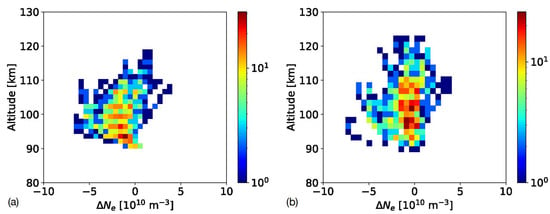
Figure 16.
Histograms of the Ne difference (Ne,GNSS-RO–Ne,ionosonde) at each GNSS-RO altitude between the fmin altitude and hmE. Plot (a) shows the unshifted Ne differences, while (b) shows the shifted profile differences. The color bar corresponds to the number of measurements within each bin.
Finally, the averaged daytime Ne for both techniques are displayed in Figure 17 for the shifted and unshifted profiles. Daytime profiles are constrained between 0800–1600 in LST, providing a total of 22 profiles for comparison. The altitude bias is obvious in the unshifted profiles and shifting the ionosonde profiles up in altitude helps to improve agreement. While the shifted ionosonde densities are larger than the RO-derived densities on average, the mean Ne profiles agree within their estimated uncertainty at E-region altitudes. Encouraged by the preliminary comparison, we plan to carry out a further, larger validation study to include more ionosonde sites from different latitudes. The new GNSS-RO Ne data at the altitudes near the ionosonde fmin may provide an alternative pathway for pinning the starting heights during ionogram inversion.
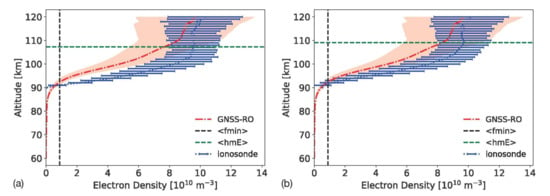
Figure 17.
Average daytime (LST = 0800–1600) Ne for the GPS-RO and ionosonde techniques for (a) unshifted and (b) shifted profiles. The average fmin is displayed as a vertical line, while the average hmE is displayed as a horizontal line.
4.2. TEC Comparisons and Maps
The TEC retrieval methods described in Figure 7 are applied to the real RO data and compared with the TEC measurements from ground-based GPS receivers. To validate the TEC retrieval methods, we use the MetOp-A data from 9–18 June 2020 when it acquired the high-rate RO data with the top up to ~290 km. To find collocated RO profiles with ground-based TEC observations, the RO TEC measurements are required within 1° × 1° latitude–longitude and 5 min windows. Figure 18 shows the RO TEC retrievals for the same four methods as illustrated in Figure 7. Similar to the conclusion in Figure 7, the method from Equation (12) works best, showing the lowest bias and standard deviation. The RO-TEC and ground-TEC are in generally good agreement along the 1:1 line. The standard deviations from the MetOp-A retrieval are higher than the simulation from the synthetic data, which may be caused by additional variability and differences in their observing times and spatial averaging where horizontal inhomogeneity can play a role.
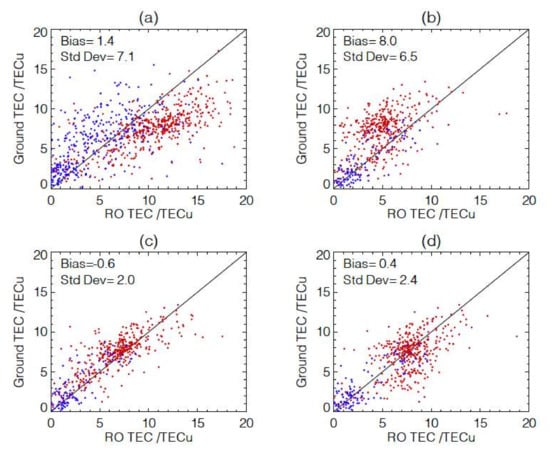
Figure 18.
(a–d) RO-TEC retrievals using the methods as labeled for the same panels as in Figure 7 and Equations (11) and (12), and their comparison with Ground-TEC. The MetOp-A RO data from 9–18 June 2020 are used because its high-rate ROs had a top up to ht ~ 290 km. The 1:1 line is plotted to guide the comparisons where daytime and nighttime measurements are in red and blue, respectively.
To develop a generalized method beyond Equations (11) and (12), we obtained a set of regression coefficients for the TEC retrieval from the RO profiles with different top cutoffs, using the synthetic IRI-2016 data. This method uses all measurements below the RO top, and the retrieval coefficients for different RO top cutoffs are stored in a lookup table. For the RO profiles with the top below 180 km, the TEC retrieval error tends to increase. We found that the RO profiles with a top above 120 km can still produce a scientifically useful TEC retrieval, but the retrieval error becomes too large if the top reaches only to 90 km, such as in the normal operation with MetOp-A/B/C.
One of the advantages with the high-rate RO data is to provide a better spatiotemporal coverage for the TEC measurement. Spatiotemporal sampling is critical for characterizing the ionosphere with large diurnal and geographical variabilities. Because of the recent high number of high-rate RO profiles (see Appendix B), the 2-hourly sampling of global TEC maps can be obtained on a monthly basis from GNSS-RO observations. Figure 19 demonstrates the latest capability of dense sampling from the combined Spire and COSMIC-2 constellations, plus a few additional GNSS-RO satellites in October 2021. More examples of monthly TEC maps can be found in Figure S6. While the daily sampling from the GNSS-RO observations is still sparse, the monthly sampling from these RO observations can provide nearly global coverage over a 4° × 8° latitude–longitude grid every 2 h. Thanks to the COSMIC-2 constellation, there is little data gap in the tropical/subtropical latitudes (<45°N/S). In addition, a small number of gaps are found in extratropical and polar latitudes largely because of the coverage from the Spire constellation. FY3D helps to fill in a small sampling gap in the Spire constellation around noontime at mid- to high latitudes (Appendix B). Further reduction in data gaps at high latitudes is a benefit from other polar-orbiting satellites (MetOp-A, TSX, Kompsat-3, FY3C, PAZ).
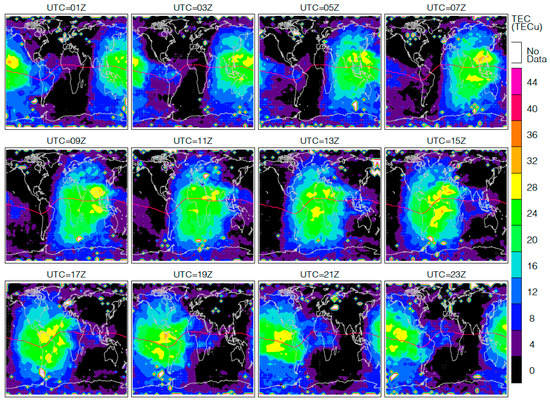
Figure 19.
TEC maps from multiple GNSS-RO satellites/constellations (Spire, Metop-A, COSMIC-2, FY3-C/D, Kompsat-5, TSX, and PAZ) for October 2021. Satellite data with the high-rate RO acquisition top < 100 km are excluded in this TEC climatology. The monthly data are aggregated into a 4° × 8° latitude–longitude and 2-hourly local time bins. The grid boxes without any measurements are colored in white.
Compared to the recent large number of RO profiles, the sampling from the COSMIC-1 constellation plus a few additions still had many regional data gaps in the 2-hourly maps for August 2008 when they were in a mission prime time (Figure 20). The unsampled regions are clearly more than in the case for October 2021. The regions with missing data appear to be randomly distributed, as the COSMIC-1 constellation had been fully deployed and spread in local time coverage. More “apparent” data gaps in the polar region are partly due to the reduced equivalent area from the 4° × 8° latitude–longitude grid.
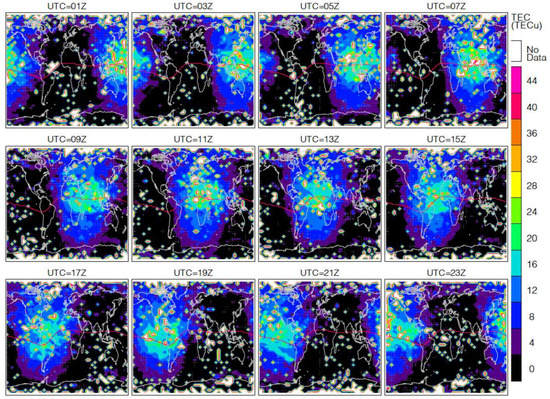
Figure 20.
As in Figure 20, but for August 2008, observed by COSMIC-1, GRACE, TSX, and SAC-C.
A few salient features emerge from the 2-hourly TEC maps from October 2021 (Figure 19). First, there appears to be a trough in the NH mid-latitude that evolves with time. October 2021 was generally a quiet month, but this trough feature is absent in the background TEC model [82]. Second, an auroral contribution to TEC is evident in the nighttime SH during UTC = 11Z–17Z. The auroral contribution is generally too weak to observe in TEC except from the enhancement during substorms [83]. Third, there is UTC-dependent symmetry in the subtropical TEC about the magnetic equator. Asymmetric distributions are more pronounced for the UTC time before 07Z.
Current global TEC nowcast and forecast rely primarily on the data analyses from ground-based measurements at the International GNSS Service for Geodynamics (IGS) stations. Because the ground stations are mostly over lands, the IGS-associated analysis centers, including GFZ (GeoForschungsZentrum), JPL (Jet Propulsion Laboratory), and USNO (U.S. Naval Observatory), use various interpolation-filtering methods to fill the data-sparse regions in producing a global TEC map [82,84,85]. Thus, a large TEC uncertainty is expected over the data-sparse regions. Over oceans, satellite altimeters may fill sampling voids with a better sensitivity to TEC measurements [86]. Nevertheless, dense spatiotemporal sampling is needed to provide globally uniform quality for the TEC measurement. As demonstrated in this study, the high-rate RO data can provide such sampling and contribute to the Global Ionosphere Map (GIM) analysis for improved accuracy over data-sparse regions.
4.3. Further Improvements for the Bottom-Up Inversion
As described Section 2, in the Ne inversion the modified measurement vector is a differential hTEC profile relative to its linear variation determined from ht = 20–50 km. This change yields two advantages: (1) significantly reducing the impact of F-region residuals on the D/E-region Ne retrieval; and (2) making the D/E-region Ne retrieval less dependent on absolute error or accuracy of the hTEC measurement. Apart from these changes, the core inversion formulation (i.e., Equation (11)) is the same in both approaches.
The same principle is applied to the TEC retrieval using hTEC differences between the measurement at ht = 60 km and those at ht < 220 km (Section 2.3.4). This ΔhTEC-based TEC retrieval will allow a full use of the high-rate RO data for both neutral atmospheric and ionospheric applications, and the retrieved TECs agree reasonably well with the ground-based observations in the case where the RO profile top reaches 220 km. Because the number of RO profiles is generally greater and the RO data quality (i.e., SNR and hTEC) is better than POD measurements, the high-rate RO profiles with a higher top will attract more attention in the dual applications for atmospheric and ionospheric sciences.
The bottom-up inversion algorithm has several similarities to the Abel inversion in formulation. A further development with this algorithm will be to apply the inversion technique to the 1 Hz POD measurements, some of which have the RO profile reaching to ht = 100 km or lower. Although these hTEC profiles may not have the same quality as the high-rate RO data, they can serve as a surrogate to verify the D/E-region Ne and TEC retrievals from the bottom-up method. If both POD and RO data can be used independently for the TEC retrieval, it will increase the sampling and coverage by a significant amount. Previous Ne retrievals from the POD hTEC have been struggling in the lower ionosphere, showing large oscillations in the Ne profile [38]. Preliminary results show that the sequential optimization inversion performs better than the onion-peeling approach for retrieving Ne retrieval without artificial oscillations in the lower ionosphere.
Although it is feasible to jointly retrieve the Ne profile from the 1 Hz POD and high-rate RO hTEC measurements, the LEO–PRN pair in both observations needs to be consistent. For COSMIC-2, there are ~50% of the POD profiles that can be paired to the high-rate RO profile. Out of these matches, approximate 50% are overlapped in tangent heights. As a result, there are only ~25% of the RO profiles that may be used for jointly retrieving Ne from the D-region to F-region.
5. Conclusions and Future Work
We have extended the bottom-up Ne retrieval to the D-region (60–90 km) using the ΔhTEC measurement derived from high-rate GNSS-RO data. The new algorithm can produce an Ne profile up to 180 km if the high-rate RO top reaches this height. The optimal estimation inversion has been updated to handle both measurement vectors hTEC with the Abel weighting function and ΔhTEC with the “bottom-up” weighting function. This flexibility allows the algorithm to process the podTEC data, if needed, for the Ne retrieval. In addition to the D/E-region Ne, a new TEC retrieval technique was developed using the high-rate RO data with a top above 120 km. For better characterizing the E- to F- Ne transition and the novel TEC retrieval, it is recommended to have the routine GNSS-RO acquisition up to ht = 220 km.
The RO Ne retrieval was compared briefly with the ionosonde observations at the Hermanus, South Africa site. A generally good agreement was found in the E-region, with the RO Ne profile being lower in density and shifted upwards slightly in altitude. Encouraged by the preliminary comparison, a greater validation effort is planned to include more ionosonde sites from different latitudes.
The morphology of new GNSS-RO Ne data revealed many interesting features in the diurnal, seasonal, solar-cycle, and magnetic-field-dependent variations. While the D/E-region Ne is a strong function of solar zenith angle (χ), it exhibits strong latitudinal variations for the same χ, and its distribution is asymmetric about noon. The magnetic-field modulation of Ne varies from month to month. There are large longitudinal variations along the same pitch angle of magnetic field. The summer-midlatitude Ne distributions in June and December closely resemble the global Es morphology, suggesting that the same processes likely drive these geophysical variations. In the polar region, the Ne distribution correlates better with the pitch angle derived from the magnetic field in the magnetosphere than from the 100 km, as expected for the magnetosphere-driven auroral electron precipitation. There is a clear semiannual variation in the nighttime zonal mean Ne in the D-region with peaks near the equinox months. We were able to derive the daytime and nighttime solar-cycle variations in the D-region Ne from the MetOp RO data that had stable operation and uniform sampling at ~9 a.m. and ~9 p.m. local times. There is a good correlation between the long-term Ne variations and the F10.7 flux during 2007–2021.
Spatiotemporal sampling is critical to characterize large diurnal and geographical variabilities in the ionosphere. Because there are more high-rate RO measurements than podTEC, it provides a clear advantage to sample the D/E-region ionosphere better with the high-rate RO observations. The combined spatiotemporal observations from COSMIC-2 and Spire constellations have provided an unprecedented coverage for studying the ionosphere since 2021. As the constellation continues to expand, it is feasible to improve the diurnal sampling to one-hour intervals and a spatial sampling better than the 8° × 4° longitude-latitude grid, as used in this study. The dense spatial sampling will perhaps allow a tomographic retrieval of Ne, to improve the horizontal resolution of the GNSS-RO technique.
For future algorithm developments, we plan to apply the retrieval to the podTEC and ionPhs data to obtain a full Ne profile in the ionosphere. The podTEC data from CDAAC contain the hTEC profile with absolute calibration that can be readily processed with the algorithm developed in this study for an Abel inversion of Ne. The Abel inversion can be further improved to include the podTEC data from both positive and negative elevation angles, making it less dependent on the orbital altitude of the RO receiver. It is also feasible to develop an algorithm for the joint retrievals of TEC and Ne using the profile, which should work in the cases where the absolute hTEC calibration is challenging. Finally, we will conduct a retrieval exercise for the tomographic inversion of TEC and Ne once the GNSS-RO constellations begin to provide a sufficient sampling density.
Supplementary Materials
The following are available online at https://zenodo.org/record/6057919#.YlOdhtNBzy1, Figure S1: As in Figure 10 but for COMSIC-1 monthly Ne in the D/E-region as a function of local solar time (LST) and latitude from 2006–2020. Figure S2: As in Figure 12 but for COSMIC-1 Ne maps at 70 and 110 km from all months in 2006–2020. Figure S3: As in Figure 13 but for the 2-hourly zonal mean from Spire data in Sep, Oct, and Nov 2021, and in Jan 2022. Figure S4: Spire Ne monthly climatology at the magnetic equator (6°S–6°N) as a function of local time and height from September, October, November, December of 2021, January of 2022. The NOAA CWDP NRT data delivered to CDAAC for September 2021 have 17 days, and the other months are complete. Figure S5: As in Figure 14 but for the solar-cycle variations at 60 and 80 km. Figure S6: As in Figure 20 but for TEC maps from November and December 2021 and January 2022.
Author Contributions
Conceptualization, D.L.W.; methodology, D.L.W.; software, D.L.W.; validation, D.J.E. and N.S.; formal analysis, D.L.W.; investigation, D.L.W.; resources, D.L.W.; writing, D.L.W. and D.J.E.; funding acquisition, D.L.W. All authors have read and agreed to the published version of the manuscript.
Funding
The work is supported by NASA’s Living with Star (WBS 936723.02.01.12.48) and Sun-Climate research (WBS 509496.02.03.01.17.04) funds to Goddard Space Flight Center (GSFC).
Data Availability Statement
The RO data used in this study were obtained from UCAR COSMIC Data Analysis and Archive Center (CDAAC) except for Fengyun-3 (FY3). The FY3 RO Level-1 profiles were obtained from the published NRT data at Fengyun Satellite Data Center (FSDC). The F10.7 data were obtained from the GSFC/SPDF OMNIWeb interface at https://omniweb.gsfc.nasa.gov (accessed 1 March 2022).
Acknowledgments
UCAR CDAAC services for data processing and distribution are acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Algorithm Flow Diagram
The algorithm developed in this study shares the similar flow to one published by Wu [31] in terms of data processing and retrieval modules. As shown in Figure A1, in this study we leveraged many modules from the previous development, including data quality control, F-region component estimation, and optimal estimation inversion, while the algorithm is extended to use of both and profiles. Slightly different thresholds for quality control are used in the new algorithm. Because of the need of quality control for both and profiles, the total number of Ne retrievals is slightly lower than the algorithm that uses the profile only.
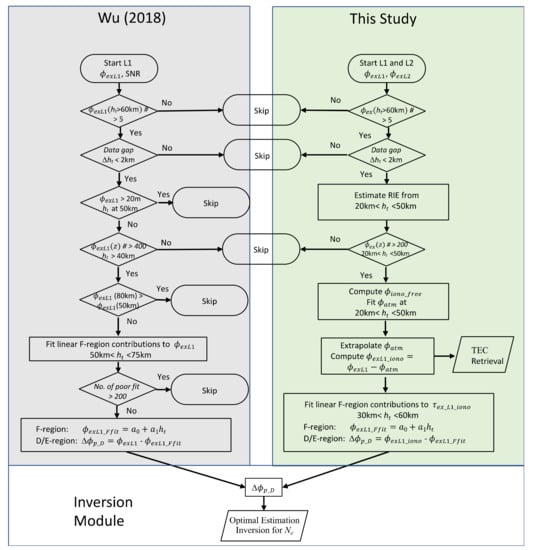
Figure A1.
Algorithm flow diagram in this study in comparison with the algorithm developed earlier by Wu [2018].
Although the inversion module bears essentially the same architecture, the weighting functions and linearization vectors are somewhat different. The new algorithm is linearized on a climatological profile derived from the IRI and FIRI models, instead of zero values. The weighting functions in the new algorithm are extended to a higher altitude such that it can handle the measurement and state vector up to 800 km. Both “bottom-up” and Abel weighting functions are computed and stored in the new algorithm, making it flexible to retrieve Ne from different input measurement vectors, namely (without absolute calibration) and hTEC (with absolute calibration) profiles. The capability of retrieving the entire ionospheric Ne from hTEC allows the new algorithm to process the podTEC data produced at CDAAC for COSMIC-1 and COSMIC-2. Initial testing of the retrieval from podTEC data shows that the optimal estimation inversion with the Abel weighting function produces better quality (much less oscillations) Ne in the lower ionosphere than the inversion from the onion-peeling approach [33,38,87]. The algorithm architecture in this study can readily accommodate further extensions of the Ne retrieval from the podTEC data, such as the use of podTEC from both positive and negative elevation angles.
This study added a new module to retrieve TEC from the high-rate RO data with a top up to 120 km. Preliminary results from this module were presented in Section 4.2, revealing scientifically-useful TEC measurements on a global basis. Unlike the TEC retrieval derived from the Ne profile retrieved from the podTEC data, this TEC retrieval method does not require absolute calibration in the hTEC or profile, as in most of the high-rate RO measurements. However, it does require the RO top to reach at least 120 km in order to observe a sufficient vertical gradient in the hTEC profile. This added TEC retrieval capability will significantly improve the spatiotemporal sampling of global ionosphere on a daily basis. Thus, further development and refinement are expected for this TEC module as the GNSS-RO constellations produce more the high-quality high-rate RO profiles.
Appendix B. GNSS-RO Data Availability and Statistics
The global GNSS-RO observations can be perhaps divided into three periods in terms of the total number of daily RO profiles (Figure A2): CHAMP-period (2001–2006), COSMIC1-period (2006–2019), and COSMIC2-commercial-period (2019–). Advanced satellite RO receiver technologies play a critical role in the increase of the number of RO acquisitions from space. The BlackJack RO receiver on CHAMP, developed by NASA Jet Propulsion Laboratory (JPL), was able to track a dual-frequency GPS signals for precise (cm accuracy range) orbit determination and continuous coverage [88]. In its occultation mode, the receiver software was also able to schedule every 50 Hz tracking of setting occultations of up to four GPS satellites. The BlackJack on CHAMP has only aft antennas for the RO sounding, which yielded ~250 profiles per day. The sampling was further improved by tracking rising occultations with the open-loop (OL) tracking successfully demonstrated on the SAC-C and later COMSIC-1 satellites. This advance led to the dual-antenna (aft and fore) and OL tracking IGOR (Integrated GPS and Occultation Receiver) implemented by the COMSIC-1 constellation [89], which produced ~700 daily ROs per satellite, or an average total of ~4000 daily ROs from the six-satellite constellation. A recent boost in RO acquisitions comes from the combination of a new four-antenna TriG (tri-band GNSS) receiver [90] implemented by the COSMIC-2 constellation and commercial CubeSat constellations (e.g., Spire) [91].

Table A1.
Summary of GNSS-RO data in this study.
Table A1.
Summary of GNSS-RO data in this study.
| LEO Satellites | Mission Lifetime | Init, Final Alt (km) | Sun-Syn (Asc ECT (1)) | Lat Coverage | Top RO Ht (km) | Tracked GNSS | Max No. ROs/day |
|---|---|---|---|---|---|---|---|
| CHAMP | 2001–2008 | 450,330 | varying | 90°S/N | 140 | G | ~250 |
| COSMIC-1 (2) constellation | 2006–2020 | 525,810 | varying | 90°S/N | 130 | G | ~4000 |
| SAC-C | 2000–2013 | 705 | 10:30 | 90°S/N | 90 | G | ~300 |
| MetOp-A | 2006–2021 | 820 | 19:00 (3) | 90°S/N | 90 | G | ~720 |
| MetOp-B | 2012– | 820 | 19:00 | 90°S/N | 90 | G | ~700 |
| MetOp-C | 2018– | 820 | 19:00 | 90°S/N | 90 | G | ~650 |
| C/NOPS | 2008–2015 | 850,350 | varying | 37°S/N | 170 | G | ~320 |
| KOMPSAT-5 | 2015– | 560 | 06:00 | 90°S/N | 135 | G | ~600 |
| TSX | 2009– | 520 | 18:00 | 90°S/N | 135 | G | ~320 |
| TDX | 2016– | 520 | 18:00 | 90°S/N | 135 | G | ~320 |
| GRACE | 2007–2017 | 475,300 | varying | 90°S/N | 140 | G | ~230 |
| FY-3C (4) | 2013– | 838,850 | 22:00 | 90°S/N | 135 | G | ~530 |
| FY-3D | 2017– | 838 | 13:30 | 90°S/N | 135 | G | ~600 |
| FY-3E | 2021– | 830 | 05:30 | 90°S/N | - | G | - |
| COSMIC-2 (5) constellation | 2019– | 715,545 | varying | 44°S/N | 90–130 | G,R | ~6500 |
| PAZ | 2018– | 520 | 18:00 | 90°S/N | 135 | G | ~320 |
| Sentinel-6A | 2020– | 1336 | varying | 90°S/N | 80 | G,R | ~830 |
| Spire (6) Constellation | 2018– | varying | varying | 90°S/N | 170–400 | G,R,E,J | ~4000 (7) ~12,000 (8) |
| Other (9) Constellations | 2020– | varying | varying | varying | varying | varying | varying |
(1) Ascending-orbit equator crossing time (Asc ECT). (2) The COSMIC1-3 spacecraft never reached the intended orbital altitude and was operated at 725 km for the rest of its mission. (3) The spacecraft started to drift away from the Sun-sync orbit since ~2021. A scan experiment with the high-rate data up to ht = 300 km was conducted between 2020.161 and 2020.254. (4) The FY-3C spacecraft started to drift away from the Sun-sync orbit (SSO) from 2016 (see Appendix B). (5) The COMSIC2 NRT data contain GNSS-RO profiles from GPS and GLONASS. (6) The Spire constellation acquires RO profiles from GPS, GLONASS, Galileo, and QZSS before 2021, and BDS since 2022. (7) NOAA’s Commercial Weather Data Pilot (CWDP) NRT data published by CDAAC from September 2021 to the present. The daily RO number is from November 2021 statistics. (8) NASA’s Commercial SmallSat Data Acquisition (CSDA) data from November 2019 to the present. The daily RO number is from November 2021 statistics, of which approximately 880 are overlapped with the NOAA CWDP profile. (9) Other commercial GNSS-RO data include the constellations such as GeoOptics and PlanetIQ.
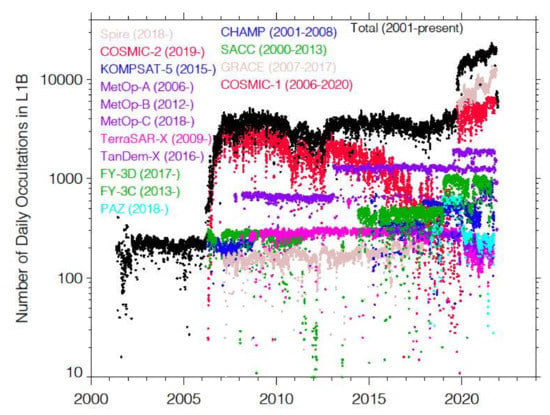
Figure A2.
Number of daily GNSS-RO profiles since the CHAMP mission. Recent rising numbers are mainly from the COSMIC-2 and Spire constellations. The Spire RO numbers are based on the data archived under NASA’s CSDA program.
The full diurnal coverage with GNSS-RO was not achieved on a monthly basis until the COSMIC-1 constellation was launched. Prior to COSMIC-1, CHAMP made a diurnal sampling through a single orbital precession from multi-month or seasonal composites. The lengthy averaging for ionospheric observations can create aliasing problems between diurnal and seasonal variations, whereas the averaging over the same month from different years may bring interannual variability to the diurnal characteristics. Hence, a dense spatiotemporal sampling on a monthly basis is needed and critical for characterizing ionospheric variability.
While COSMIC-1 achieved the needed monthly diurnal coverage initially, the six-satellite constellation degraded after 2016 with fewer satellites in operation. As seen in Figure A3, large gaps appeared in the GNSS-RO LST sampling. This creates a challenge to use the COSMIC-1 data for studying solar-cycle variations of the ionosphere. As a result, the long-term monitoring of ionospheric variability is limited to the observations at a few LSTs such as the 9AM and 21AM at which the combined operation from MetOp-A/B/C has provided more than 14 years of RO data.
A great boost in diurnal coverages comes from the recent COSMIC-2 and Spire constellation. Both constellations are capable of sampling a full LST range within a month, but COSMIC-2 covers only low latitudes (<44°S/N) with a good longitudinal sampling. On the other hand, the Spire constellation has a good pole-to-pole coverage with a smaller number of longitudinal samples at low latitudes, which was a similar situation to COSMIC-1. The combined COSMIC-2/Spire constellation, therefore, will provide an unprecedented spatiotemporal coverage for studying the ionosphere in the years to come.
Figure A3.
Time series of daily mean equator-crossing LSTs of the RO measurement from different missions. The LSTs from satellite’s ascending and descending orbits are separated roughly by 12 h. Each orbit node has two close LSTs separated by ~1.5 h, which comes from the RO measurements made by the fore and aft viewing antennas. Most of the modern RO instruments have at least two receivers to take measurements from the fore and aft directions.
In ionospheric limb sounding, the orbit altitude of RO receivers can have a significant effect on the retrieval, because of the extensive vertical range of ionosphere. Satellites are often orbiting inside the ionosphere. Depending on the orbital altitude, a significant portion of the ionosphere can reside above the satellite. Although the orbit altitude may affect little on the bending angle measurement for the atmosphere, the retrieval algorithms for TEC and Ne need to take into account the ionosphere portion that is not in the RO line-of-sight, which is dependent on orbit altitude.
As shown in Figure A4, the GNSS-RO satellite altitude varies widely between 300 and 800 km. The orbit of satellites such as CHAMP, GRACE, and C/NOFS decreased gradually during their mission lifetime, whereas others (e.g., operational weather satellites) were able to keep the orbital altitude nearly constant. To form their constellation with a uniform LST coverage, COSMIC-1 and COSMIC-2 had to raise and lower the altitude of its member satellites, respectively. After more than one year of the constellation formation, the COSMIC-2 satellites are now all operating in 525–540 km altitudes. Its companion polar-orbiting constellation from Spire, under contract with NOAA CWDP, is also operating at the similar orbital altitude. Other operational features, such as the raised orbit by FY3C after 2018 and the MetOp-A decommission toward the end of 2021, are also evident.
Figure A4.
Daily average orbital altitude of the past and current GNSS-RO missions. The altitudes are estimated from the LEO satellite position in the level-1b data. The Spire data contain only satellites (cubesats) from NOAA CWDP.
References
- Eccles, J.V.; Hunsucker, R.D.; Rice, D.; Sojka, J.J. Space weather effects on midlatitude HF propagation paths: Observations and a data-driven D region model. Space Weather 2005, 3, S01002. [Google Scholar] [CrossRef]
- Taylor, W.L. VLF attenuation for east-west and west-east daytime propagation using atmospherics. J. Geophys. Res. 1960, 65, 1933–1938. [Google Scholar] [CrossRef]
- Forbes, J.M. The equatorial electrojet. Rev. Geophys. 1981, 19, 469–504. [Google Scholar] [CrossRef]
- Hays, P.B.; Roble, R.G. A quasi-static model of global atmospheric electricity 1: The lower atmosphere. J. Geophys. Res. 1979, 84, 3291–3305. [Google Scholar] [CrossRef]
- Harrison, R.G. The Carnegie curve. Surv. Geophys. 2013, 34, 209–232. [Google Scholar] [CrossRef]
- Rishbeth, H. The ionospheric E-layer and F-layer dynamos—A tutorial review. J. Atmos. Sol.-Terr. Phys. 1997, 59, 1873–1880. [Google Scholar] [CrossRef]
- Heelis, R.A. Electrodynamics in the low and middle latitude ionosphere: A tutorial. J. Atmos. Sol.-Terr. Phys. 2004, 66, 825–838. [Google Scholar] [CrossRef]
- Kelly, M.C. E-region dynamo theory and the daytime equatorial electrojet. In The Earth’s Ionosphere; Academia Press: New York, NY, USA, 2009; pp. 89–99. [Google Scholar]
- Rycroft, M.J.; Israelsson, S.; Price, C. The global atmospheric electric circuit, solar activity and climate change. J. Atmos. Sol.-Terr. Phys. 2000, 62, 1563–1576. [Google Scholar] [CrossRef]
- Aplin, K.L.; Harrison, R.G.; Rycroft, M.J. Investigating Earth’s atmospheric electricity: A role model for planetary studies. Space Sci. Rev. 2008, 137, 11–27. [Google Scholar] [CrossRef]
- Lucas, G.M.; Baumgaertner, A.J.G.; Thayer, J.P. A global electric circuit model within a community climate model. J. Geophys. Res. Atmos. 2015, 120, 12054–12066. [Google Scholar] [CrossRef]
- Nicolet, M.; Aikin, A.C. The formation of the D region of the ionosphere. J. Geophys. Res. 1960, 65, 1469–1483. [Google Scholar] [CrossRef]
- Reid, G.C. The production of water-cluster positive ions in the quiet daytime D Region. Planet. Space Sci. 1977, 25, 275–290. [Google Scholar] [CrossRef]
- Brasseur, G.; Solomon, S. Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere, 3rd ed.; Springer: Dordrecht, The Netherlands, 2005; p. 646. [Google Scholar]
- Mathews, J.D. Sporadic E: Current views and recent progress. J. Atmos. Sol.-Terr. Phys. 1998, 60, 413–435. [Google Scholar] [CrossRef]
- Whitehead, J.D. Formation of the sporadic E layer in the temperate zones. Nature 1960, 188, 567. [Google Scholar] [CrossRef]
- Haldoupis, C. A tutorial review on sporadic E layers. In Aeronomy of the Earth’s Atmosphere and Ionosphere. IAGA Special Sopron Book Series; Springer: Berlin, Germany, 2011. [Google Scholar] [CrossRef]
- Wu, D.L.; Ao, C.O.; Hajj, G.A.; de La Torre Juarez, M.; Mannucci, A.J. Sporadic E morphology from GPS-CHAMP radio occultation. J. Geophys. Res. 2005, 110, A01306. [Google Scholar] [CrossRef]
- Arras, C.; Wickert, J.; Jacobi, C.; Heise, S.; Beyerle, G.; Schmidt, T. A global climatology of ionospheric irregularities derived from GPS radio occultation. Geophys. Res. Lett. 2008, 35, L14809. [Google Scholar] [CrossRef]
- Chu, Y.H.; Wang, C.Y.; Wu, K.H.; Chen, K.T.; Tzeng, K.J.; Su, C.L.; Feng, W.; Plane, J.M.C. Morphology of sporadic E layer retrieved from COSMIC GPS radio occultation measurements: Wind shear theory examination. J. Geophys. Res. Space Phys. 2014, 119, 2117–2136. [Google Scholar] [CrossRef]
- Yuan, T.; Wang, J.; Cai, X.; Sojka, J.; Rice, D.; Oberheide, J.; Criddle, N. Investigation of the seasonal and local time variations of the high-altitude sporadic Na layer (Nas) formation and the associated midlatitude descending E layer (Es) in lower E region. J. Geophys. Res. Space Phys. 2014, 119, 5985–5999. [Google Scholar] [CrossRef]
- Hoppe, U.P.; Eriksen, T.; Thrane, E.V.; Blix, T.A.; Fiedler, J.; Lübken, F.J. Observations in the polar middle atmosphere by rocket-borne Rayleigh lidar: First results. Earth Planets Space 1999, 51, 815–824. [Google Scholar] [CrossRef]
- Rusch, D.; Gerard, G.-C.; Solomon, S.; Crutzen, P.; Reid, G. The effect of particle precipitation events on the neutral and ion chemistry of the middle atmosphere. 1. Odd nitrogen. Planet. Space Sci. 1981, 29, 767–774. [Google Scholar] [CrossRef]
- Solomon, S.; Rusch, D.W.; Gerard, J.-C.; Reid, G.C.; Crutzen, P.J. The effect of particle precipitation events on the neutral and ion chemistry of the middle atmosphere, II, Odd hydrogen. Planet. Space Sci. 1981, 29, 885–892. [Google Scholar] [CrossRef]
- Verronen, P.T.; Rodger, C.J.; Clilverd, M.A.; Wang, S. First evidence of mesospheric hydroxyl response to electron precipitation from the radiation belts. J. Geophys. Res. 2011, 116, D07307. [Google Scholar] [CrossRef]
- Andersson, M.E.; Verronen, P.T.; Rodger, C.J.; Seppälä, A. Missing driver in the Sun-Earth connection from energetic electron precipitation impacts mesospheric ozone. Nat. Commun. 2014, 5, 5197. [Google Scholar] [CrossRef] [PubMed]
- Siskind, D.E.; Nedoluha, G.E.; Randall, C.E.; Fromm, M.; Russell, J.M., III. An assessment of Southern Hemisphere stratospheric NOx enhancements due to transport from the upper atmosphere. Geophys. Res. Lett. 2000, 27, 329–332. [Google Scholar] [CrossRef]
- Randall, C.E.; Harvey, V.L.; Singleton, C.S.; Bailey, S.M.; Bernath, P.F.; Codrescu, M.; Nakajima, H.; Russell, J.M. Energetic particle precipitation effects on the Southern Hemi-sphere stratosphere in 1992–2005. J. Geophys. Res.-Atmos. 2007, 112, D08308. [Google Scholar] [CrossRef]
- Friedrich, M.; Pock, C.; Torkar, K. FIRI-2018, an updated empirical model of the lower ionosphere. J. Geophys. Res. Space Phys. 2018, 123, 6737–6751. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Wu, D.L. New global electron density observations from GPS-RO in the D- and E-Region ionosphere. J. Atmos. Sol.-Terr. Phys. 2018, 171, 36–59. [Google Scholar] [CrossRef]
- Swarnalingam, N.; Wu, D.L.; Themens, D.R. Comparison and evaluation of a bottom-up GPS-RO electron density retrieval for D and E regions using radar observations and models. J. Atmos. Sol.-Terr. Phys. 2020, 207, 105333. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Sokolovskiy, S.V.; Rocken, C.; Hunt, D.C. Analysis and validation of GPS/MET radio occultation data in the ionosphere. Radio Sci. 1999, 34, 949–966. [Google Scholar] [CrossRef]
- Chu, Y.-H.; Wu, K.-H.; Su, C.-L. A new aspect of ionospheric E region electron density morphology. J. Geophys. Res. 2009, 114, A12314. [Google Scholar] [CrossRef]
- Nicolls, M.J.; Rodrigues, F.S.; Bust, G.S.; Chau, J.L. Estimating E region density profiles from radio occultation measurements assisted by IDA4D. J. Geophys. Res. 2009, 114, A10316. [Google Scholar] [CrossRef]
- Yue, X.; Schreiner, W.S.; Lei, J.; Sokolovskiy, S.V.; Rocken, C.; Hunt, D.C.; Kuo, Y.H. Error analysis of Abel retrieved electron density profiles from radio occultation measurements. Ann. Geophys. 2010, 28, 217–222. [Google Scholar] [CrossRef]
- Pedatella, N.M.; Yue, X.; Schreiner, W.S. An improved inversion for FORMOSAT-3/COSMIC ionosphere electron density profiles. J. Geophys. Res. Space Phys. 2015, 120, 8942–8953. [Google Scholar] [CrossRef]
- Yue, X.; Schreiner, W.S.; Lin, Y.-C.; Rocken, C.; Kuo, Y.-H.; Zhao, B. Data assimilation retrieval of electron density profiles from radio occultation measurements. J. Geophys. Res. 2011, 116, A03317. [Google Scholar] [CrossRef]
- Nicolls, M.J.; Rodrigues, F.S.; Bust, G.S. Global observations of E region plasma density morphology and variability. J. Geophys. Res. 2012, 117, A01305. [Google Scholar] [CrossRef]
- Syndergaard, S. On the ionospheric calibration in GPS radio occultation measurements. Radio Sci. 2000, 35, 865–883. [Google Scholar] [CrossRef]
- Hoque, M.M.; Jakowski, N. Ionospheric bending correction for GNSS radio occultation signals. Radio Sci. 2011, 46, RS0D06. [Google Scholar] [CrossRef]
- Schreiner, W.; Sokolovskiy, S.; Hunt, D.; Rocken, C.; Kuo, Y.-H. Analysis of GPS radio occultation data from the FORMOSAT-3/COSMIC and Metop/GRAS missions at CDAAC. Atmos. Meas. Tech. 2011, 4, 2255–2272. [Google Scholar] [CrossRef]
- Danzer, J.; Healy, S.B.; Culverwell, I.D. A simulation study with a new residual ionospheric error model for GPS radio occultation climatologies. Atmos. Meas. Tech. 2015, 8, 3395–3404. [Google Scholar] [CrossRef]
- Healy, S.B.; Culverwell, I.D. A modification to the standard ionospheric correction method used in GPS radio occultation. Atmos. Meas. Tech. 2015, 8, 3385–3393. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding-Theory and Practice; World Scientific: Singapore; Hackensack, NJ, USA; London, UK; Hong Kong, China, 2000. [Google Scholar] [CrossRef]
- Pedatella, N.M.; Zakharenkova, I.; Braun, J.J.; Cherniak, I.; Hunt, D.; Schreiner, W.S.; Straus, P.R.; Valant-Weiss, B.L.; Vanhove, T.; Weiss, J.; et al. Processing and validation of FORMOSAT-7/COSMIC-2 GPS total electron content observations. Radio Sci. 2021, 56, e2021RS007267. [Google Scholar] [CrossRef]
- Wu, D.L. Ionospheric S4 Scintillations from GNSS Radio Occultation (RO) at Slant Path. Remote Sens. 2020, 2, 2373. [Google Scholar] [CrossRef]
- Fang, T.W.; Richmond, A.D.; Liu, J.Y.; Maute, A. Wind dynamo effects on ground magnetic perturbations and vertical drifts. J. Geophys. Res. 2008, 113, A11313. [Google Scholar] [CrossRef]
- Mathews, J.D.; Breakall, J.K.; Ganguly, S. The measurement of diurnal variations of electron concentration in the 60–100 km ionosphere at Arecibo. J. Atmos. Terr. Phys. 1982, 44, 441. [Google Scholar] [CrossRef]
- Aikin, A.C.; Kane, J.A.; Troim, J. Some results of rocket experiments in the quiet D region. J. Geophys. Res. 1964, 69, 4621–4628. [Google Scholar] [CrossRef]
- Smith, L.G. Langmuir probes in the ionosphere. In Small Rocket Instrumentation Techniques; Maeda, K., Ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1969; pp. 1–15. [Google Scholar]
- Gordon, W.E. Arecibo ionospheric observatory: Studies of the upper atmosphere and planets are made with the aid of a huge reflector in Puerto Rico. Science 1964, 146, 26–30. [Google Scholar] [CrossRef]
- Wait, J.R.; Spies, K.P. Characteristics of Earth-Ionosphere Waveguide for VLF Radio Waves; U.S. Department of Commerce, National Bureau of Standards: Colo, IA, USA, 1964. [Google Scholar]
- Sechrist, C.F., Jr. Comparisons of techniques for measurement of D region electron densities. Radio Sci. 1974, 9, 137. [Google Scholar] [CrossRef]
- Fraser-Smith, A.C.; Helliwell, R.A. The Stanford University ELF/VLF radiometer project: Measurement of the global distribution of ELF/VLF electromagnetic noise. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Wakefield, MA, USA, 20–22 August 1985. [Google Scholar]
- Cummer, S.A.; Inan, U.S.; Bell, T.F. Ionospheric D region remote sensing using VLF radio atmospherics. Radio Sci. 1998, 33, 1781–1792. [Google Scholar] [CrossRef]
- Cohen, M.B.; Said, R.K.; Paschal, E.W.; McCormick, J.C.; Gross, N.C.; Thompson, L.; Higginson-Rollins, M.; Inan, U.S.; Chang, J. Broadband longwave radio remote sensing instrumentation. Rev. Sci. Instrum. 2018, 89, 94501. [Google Scholar] [CrossRef]
- Thomson, N.R. Experimental daytime VLF ionospheric parameters. J. Atmos. Terr. Phys. 1993, 55, 173–184. [Google Scholar] [CrossRef]
- McRae, W.M.; Thomson, N.R. VLF phase and amplitude: Daytime ionospheric parameters. J. Atmos. Sol.-Terr. Phys. 2000, 62, 609–618. [Google Scholar] [CrossRef]
- Han, F.; Cummer, S.A.; Li, J.; Lu, G. Daytime ionospheric D region sharpness derived from VLF radio atmospherics. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Han, F.; Cummer, S.A. Midlatitude nighttime D region ionosphere variability on hourly to monthly time scales. J. Geophys. Res. 2010, 115, A09323. [Google Scholar] [CrossRef]
- Maurya, A.K.; Veenadhari, B.; Singh, R.; Kumar, S.; Cohen, M.B.; Selvakumaran, R.; Inan, U.S. Nighttime D region electron density measurements from ELF-VLF tweek radio atmospherics recorded at low latitudes. J. Geophys. Res. 2012, 117, A11308. [Google Scholar] [CrossRef]
- Gross, N.C.; Cohen, M.B. VLF remote sensing of the D region ionosphere using neural networks. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027135. [Google Scholar] [CrossRef]
- Xu, W.; Marshall, R.A.; Bortnik, J.; Bonnell, J.W. An electron density model of the D- and E-region ionosphere for transionospheric VLF propagation. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029288. [Google Scholar] [CrossRef]
- McCormick, J.C.; Cohen, M.B. A new four-parameter D-region ionospheric model: Inferences from lightning-emitted VLF signals. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029849. [Google Scholar] [CrossRef]
- Garcia, R.R.; Solomon, S.; Avery, S.K.; Reid, G.C. Transport of nitric oxide and the D region winter anomaly. J. Geophys. Res. 1987, 92, 977–994. [Google Scholar] [CrossRef]
- Verronen, P.T.; Andersson, M.E.; Marsh, D.R.; Kovacs, T.; Plane, J.M.C. WACCM-D—Whole Atmosphere Community Climate Model with D-region ion chemistry. J. Adv. Model. Earth Syst. 2016, 8, 954–975. [Google Scholar] [CrossRef]
- Shao, X.-M.; Lay, E.H.; Jacobson, A.R. Reduction of electron density in the night-time lower ionosphere in response to a thunderstorm. Nat. Geosci. 2013, 6, 29–33. [Google Scholar] [CrossRef]
- Pasko, V.P.; Inan, U.S.; Bell, T.F.; Taranenko, Y.N. Sprites produced by quasi-electrostatic heating and ionization in the lower ionosphere. J. Geophys. Res. 1997, 102, 4529. [Google Scholar] [CrossRef]
- Cheng, Z.; Cummer, S.A. Broadband VLF measurements of lightning-induced ionospheric perturbations. Geophys. Res. Lett. 2005, 32, L08804. [Google Scholar] [CrossRef]
- Liou, K.; Newell, P.T.; Meng, I.C. Seasonal effects on auroral particle acceleration and precipitation. J. Geophys. Res. 2001, 106, 2643. [Google Scholar] [CrossRef]
- Wiltberger, M.; Weigel, R.S.; Lotko, W.; Fedder, J.A. Modeling seasonal variations of auroral particle precipitation in a global-scale magnetosphere-ionosphere simulation. J. Geophys. Res. 2009, 114, A01204. [Google Scholar] [CrossRef]
- Silber, I.; Price, C.; Rodger, C.J. Semi-annual oscillation (SAO) of the nighttime ionospheric D-region as detected through ground-based VLF receivers. Atmos. Chem. Phys. 2016, 16, 3279–3288. [Google Scholar] [CrossRef]
- Siskind, D.E.; Zawdie, K.; Sassi, F.; Drob, D.; Friedrich, M. Global modeling of the low and mid latitude ionospheric D and lower E regions and implications for HF radio wave absorption. Space Weather 2017, 15, 115–130. [Google Scholar] [CrossRef]
- Appleton, E.V.; Pigott, W.R. Ionospheric absorption measurements during a sunspot cycle. J. Atmos. Terr. Phys. 1954, 5, 141–172. [Google Scholar] [CrossRef]
- Kurschner, D.; Jacobi, C. Quasi-biennial and decadal variability obtained from long-term measurements of nighttime radio wave reflection heights over central Europe. Adv. Space Res. 2003, 32, 1701–1706. [Google Scholar] [CrossRef]
- Jacobi, C.; Kürschner, D. Long-term Measurements of Nighttime LF Radio Wave Reflection Heights over Central Europe. Adv. Radio Sci. 2005, 3, 427–430. [Google Scholar] [CrossRef][Green Version]
- Galkin, I.A.; Reinisch, B.W. The new ARTIST 5 for all Digisondes. Ionosonde Netw. Advis. Group Bull. 2008, 69, 1–8. [Google Scholar]
- McNamara, L.F. Model starting heights for N (h) analyses of ionograms. J. Atmos. Terr. Phys. 1979, 41, 543–547. [Google Scholar] [CrossRef]
- Titheridge, J.E. Starting models for the real height analysis of ionograms. J. Atmos. Terr. Phys. 1986, 48, 435–446. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Xueqin, H. Automatic calculation of electron density profiles from digital ionograms: 3. Processing of bottomside ionograms. Radio Sci. 1983, 18, 477–492. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Weygand, J.M.; Wing, S. Temporal and spatial development ofTEC enhancements during substorms. J. Geophys. Res. Space Phys. 2020, 125, e2019JA026985. [Google Scholar] [CrossRef]
- Mannucci, A.J.; Wilson, B.D.; Yuan, D.N.; Ho, C.M.; Lindqwister, U.J.; Runge, T.F. A global mapping technique for GPS derived ionospheric total electron content measurements. Radio Sci. 1998, 33, 565–582. [Google Scholar] [CrossRef]
- Brack, A.; Männel, B.; Wickert, J.; Schuh, H. Operational multi-GNSS global ionosphere maps at GFZ derived from uncombined code and phase observations. Radio Sci. 2021, 56, e2021RS007337. [Google Scholar] [CrossRef]
- Alizadeh, M.M.; Schuh, H.; Todorova, S.; Schmidt, M. Global ionosphere maps of VTEC from GNSS, satellite altimetry, and FORMOSAT-3/COSMIC data. J. Geod. 2011, 85, 975–987. [Google Scholar] [CrossRef]
- Tsai, L.C.; Tsai, W.H.; Schreiner, W.S.; Berkey, F.T.; Liu, J.Y. Comparisons of GPS/MET retrieved ionospheric electron density and ground based ionosonde data. Earth Planet Space 2001, 53, 193–205. [Google Scholar] [CrossRef]
- Hajj, G.A.; Ao, C.O.; Iijima, B.A.; Kuang, D.; Kursinski, E.R.; Mannucci, A.J.; Meehan, T.K.; Romans, L.J.; Juarez, M.D.; Yunck, T.P. CHAMP and SAC-C atmospheric occultation results and intercomparisons. J. Geophys. Res. 2004, 109, D06109. [Google Scholar] [CrossRef]
- BRE. Integrated GPS occultation receiver IGOR. In Data Sheet; Broadreach Engineering: Tempe, AZ, USA, 2003. [Google Scholar]
- Esterhuizen, S.; Franklin, G.; Hurst, K.; Mannucci, A.; Meehan, T.; Webb, F.; Young, L. TriG-A GNSS Precise Orbit and Radio Occultation Space Receiver. In Proceedings of the 22nd International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 1442–1446. [Google Scholar]
- Angling, M.J.; Nogués-Correig, O.; Nguyen, V.; Vetra-Carvalho, S.; Bocquet, F.X.; Nordstrom, K.; Melville, S.E.; Savastano, G.; Mohanty, S.; Masters, D. Sensing the ionosphere with the Spire radio occultation constellation. J. Space Weather Space Clim. 2021, 11, 56. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).