Filling Temporal Gaps within and between GRACE and GRACE-FO Terrestrial Water Storage Records: An Innovative Approach
Abstract
:1. Introduction
2. Filling Temporal Gaps in TWSGRACE Record: An Overview
| Reference | Scale/Region | Approach † | Inputs * |
|---|---|---|---|
| Becker et al. [38] | Grid (Amazon) | Correlation | GRACE, Water level |
| Pan et al. [36] | Basin (global) | Data assimilation | GRACE, LSM, P, ET |
| De Linage et al. [35] | Basin (Amazon) | MLR | Pacific and Atlantic SST |
| Long et al. [33] | Basin (Southwest China) | ANN | SMS, P, T |
| Forootan et al. [29] | Basin/Grid (West Africa) | ICA, ARX | SST, P |
| Sośnica et al. [46] | Grid (global) | LR | SLR, GRACE |
| Zhang et al. [64] | Basin (Yangtze) | ANN | SMS |
| Nie et al. [65] | Basin (Amazon) | LR | GRACE, GLDAS |
| Talpe et al. [43] | Grid (Greenland and Antarctica) | PCA | SLR, GRACE |
| Humphrey et al. [30] | Grid (global) | MLR | P, T |
| Yang et al. [41] | Basin (NW China) | ANN, GLM, RF, SVM | GRACE, GLDAS |
| Chen et al. [28] | Basin (Northeast China) | GRNN | P, T |
| Ahmed et al. [25] | Basin (Africa) | NARX | P, ET, NDVI, T |
| Hasan et al. [39] | Basin (Africa) | ARX | GLDAS, ENSO |
| Yin et al. [34] | Basin (China) | MLR | P, ET, runoff |
| Meyer et al. [49] | Grid (Arctic and Antarctic) | LR | SLR, Swarm,GRACE |
| Humphrey and Gudmundsson [66] | Grid (global) | MLR | GRACE, P |
| Ferreira et al. [67] | Grid (West Africa) | NARX | P, ET, T, SMS, climate indices |
| Sun et al. [68] | Grid (India) | CNN | GRACE, GLDAS |
| Li et al. [53] | Basin (China) | SSA, ARIMA | GRACE, GLDAS |
| Jing et al. [69] | Basin (Nile) | RF, XGB | GRACE, GLDAS |
| Kenea et al. [31] | Basin (Ethiopia) | ESM | SST, P |
| Jing et al. [40] | Basin (China) | RF, LR | GRACE, GLDAS |
| Zhu et al. [70] | Grid (global) | SSA | GRACE |
| Li et al. [32] | Grid/Basin (global) | MLR, ANN, ARX | P, T, SST, climate indices |
| Forootan et al. [48] | Grid/Basin (global) | ICA | GRACE, Swarm |
| Sun et al. [71] | Grid/Basin (global) | DNN, MLR, SARIMAX | GRACE, GLDAS, P, T |
| Sohoulande et al. [72] | Grid (United States) | MVS | P, T, potential ET |
| Jing et al. [73] | Basin (regional) | RF, XGB | CRU,GLDAS |
| Sun et al. [42] | Grid/Basin (United States) | AutoML | GLDAS, climate indices, P, T |
| Li et al. [37] | Grid (global) | ANN, ARX, MLR | P, SST, T, climate indices |
| Jeon et al. [74] | Grid/Basin (global) | CNN | T, ET, P |
| Yu et al. [75] | Grid (Canada) | CNN | GRACE,EALCO-TWS |
| Tang et al. [76] | Basin (Lancang-Mekong) | RF | GLDAS,CRU |
| Yang et al. [77] | Grid (Australia) | LSR | GRACE, modeled TWS |
| Wang et al. [55] | Basin (Global) | SSA | GRACE, Swarm |
| Löcher and Kusche [45] | Grid (global) | EOF | SLR |
| Yi and Sneeuw [52] | Grid/Basin (global) | SSA | Swarm, GRACE |
| Gyawali et al. [20] | Basin (Texas coast) | ANN, MLR | P, T, NLDAS-TWS |
| Mo et al. [78] | Grid/Basin (Global) | BCNN | P, T, ERA5L-TWSA, CWSC |
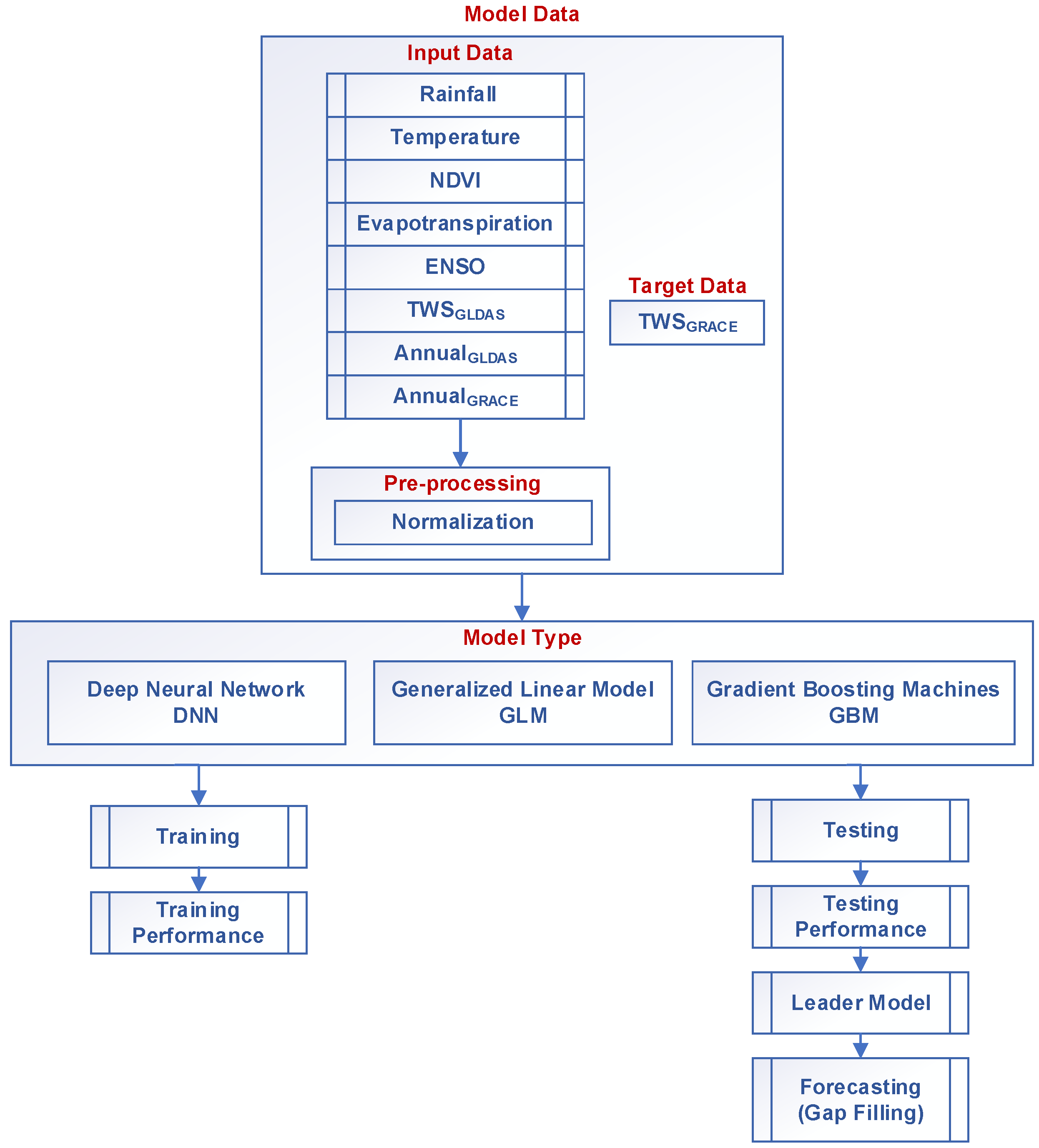
3. Innovative Approach to Fill Gaps in TWSGRACE Record
3.1. Machine Learning Models
3.1.1. Generalized Linear Model (GLM)
3.1.2. Gradient Boosting Machine (GBM)
3.1.3. Deep Neural Network (DNN)
3.2. Input and Target Data
3.2.1. GRACE-Derived TWS (TWSGRACE)
3.2.2. GLDAS-Derived TWS (TWSGLDAS)
3.2.3. Rainfall
3.2.4. Temperature
3.2.5. Evapotranspiration
3.2.6. Normalized Difference Vegetation Index (NDVI)
3.2.7. Climate Indices
3.3. Performance Measures
4. Results
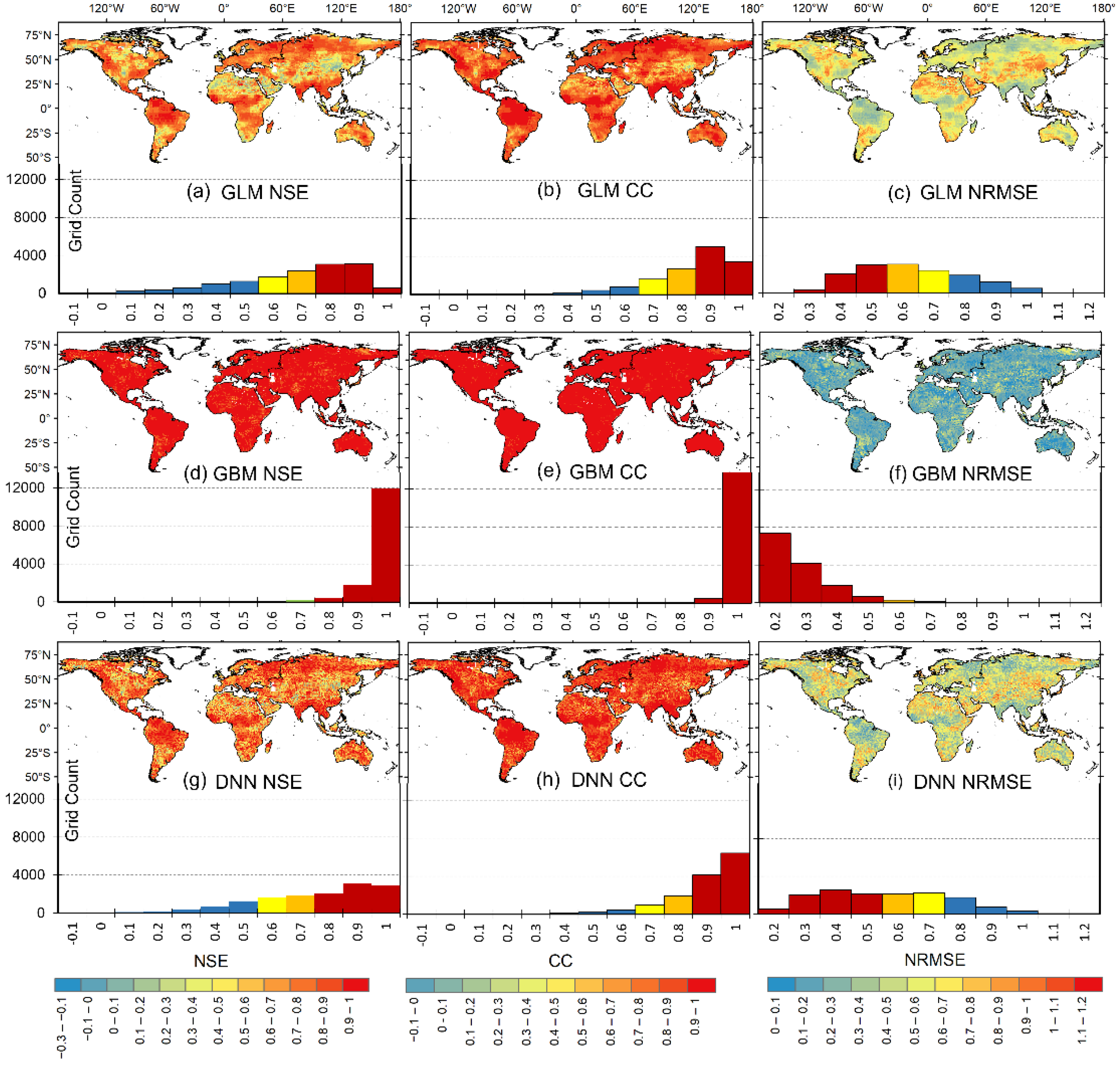
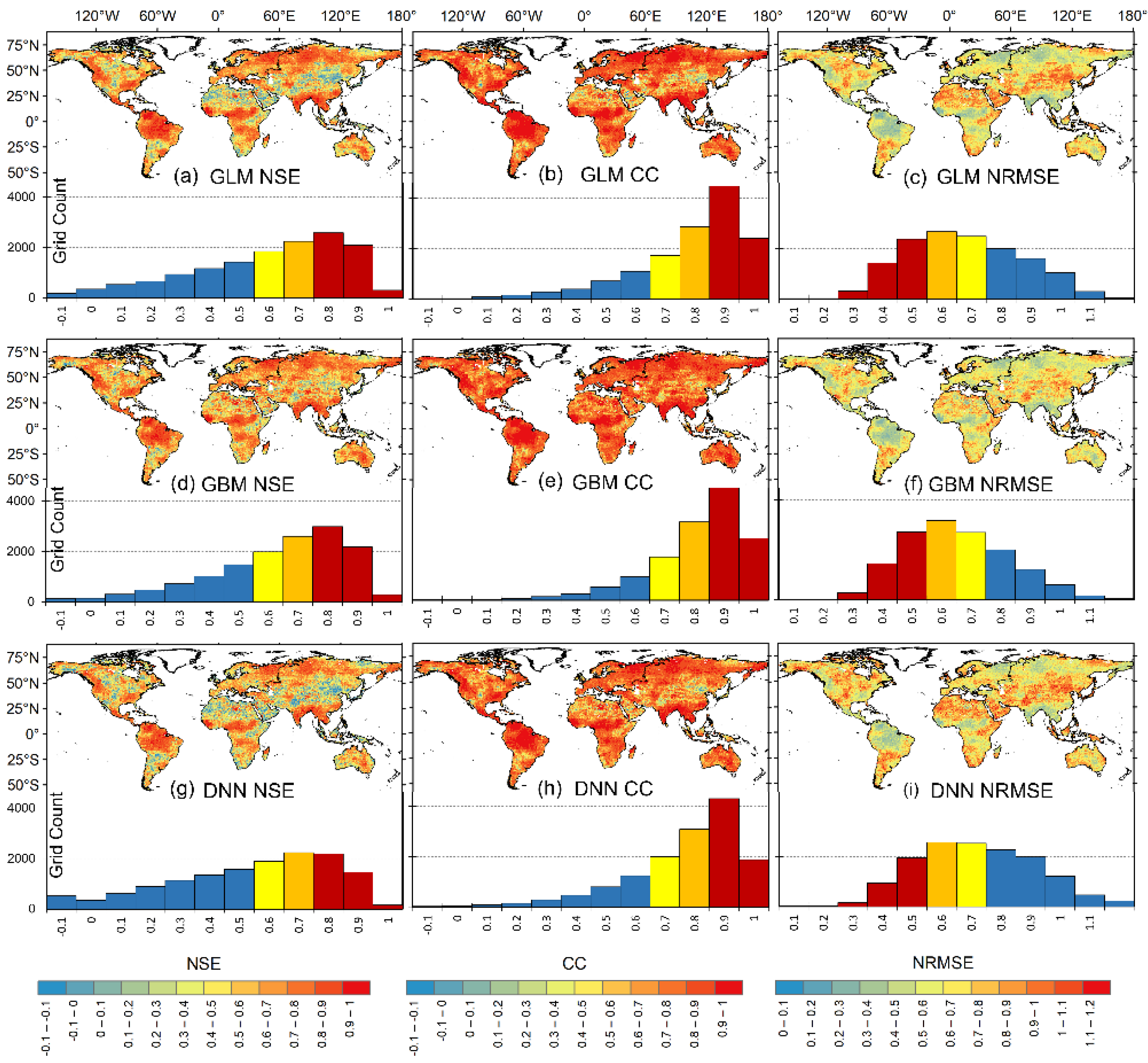
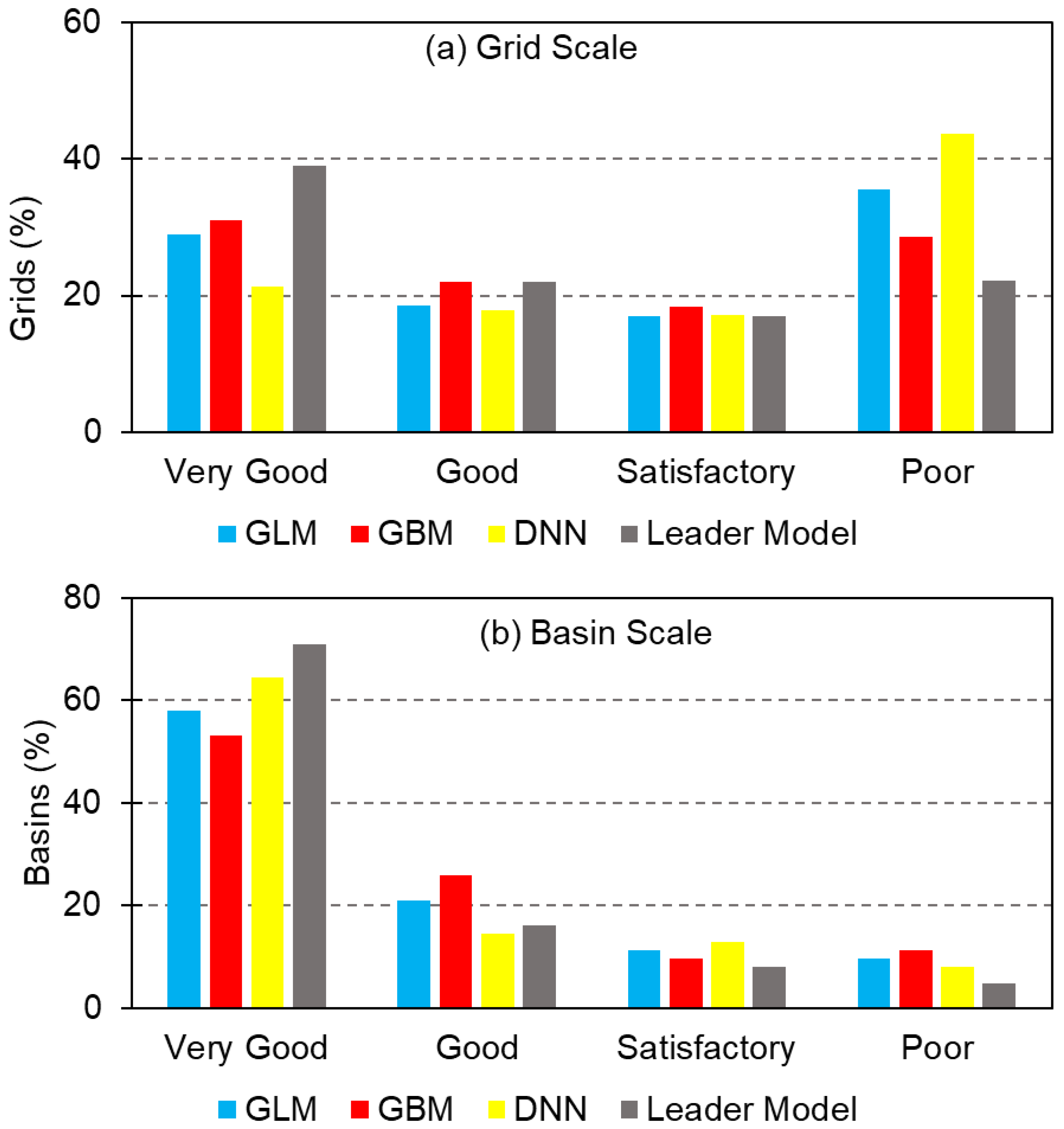
4.1. Model Performance: Grid Scale
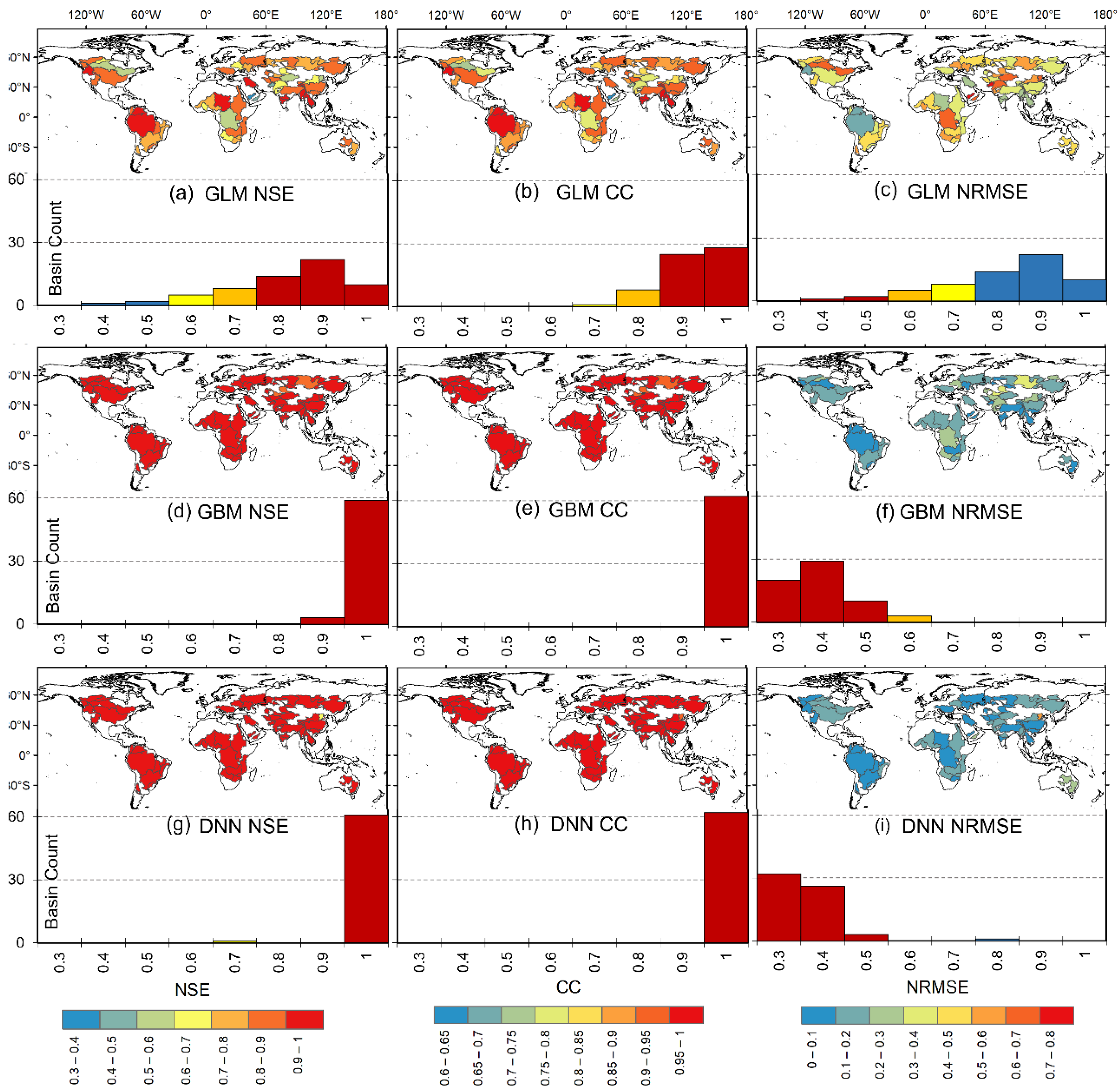
4.2. Model Performance: Basin Scale
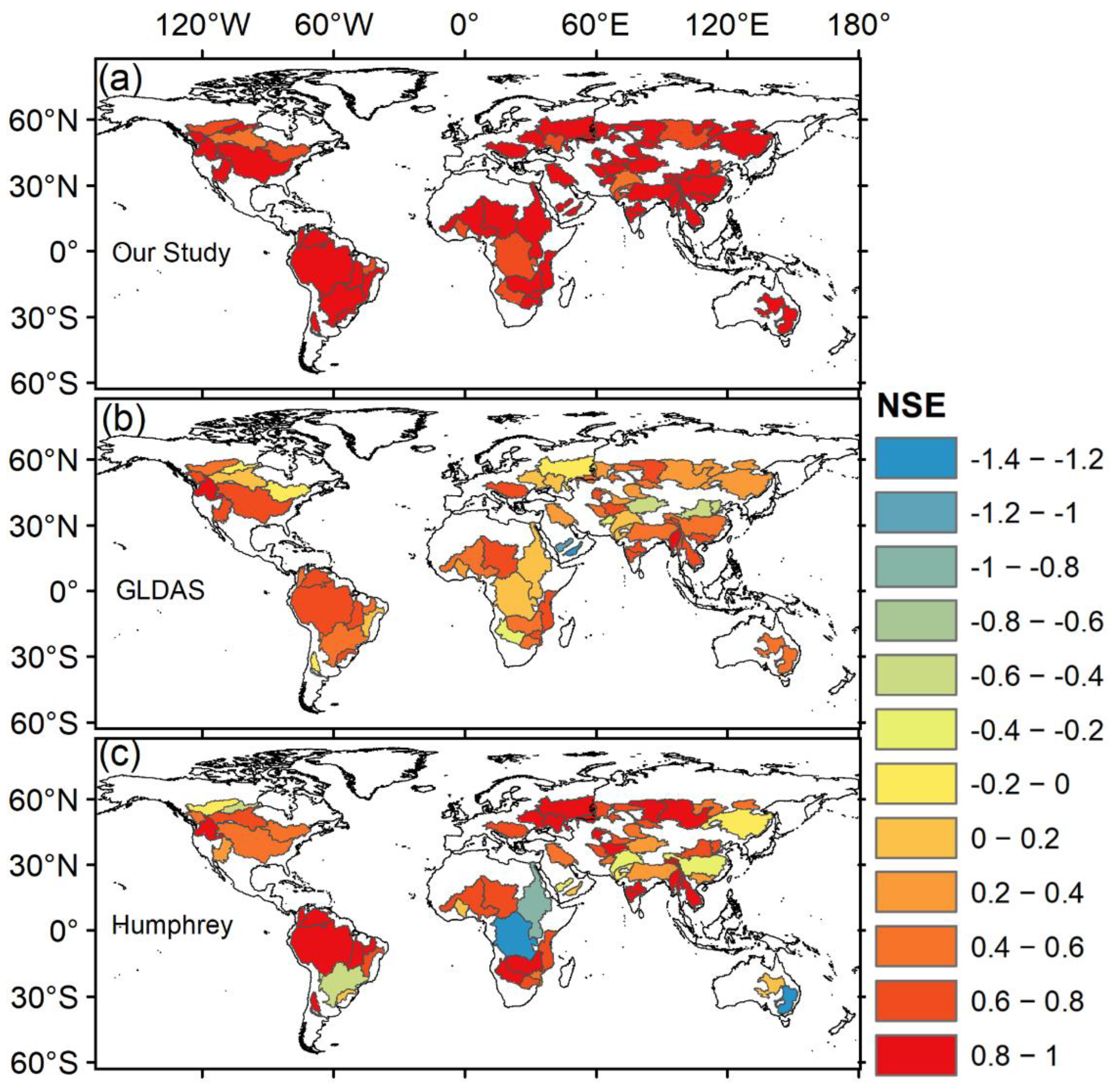
4.3. TWSGRACE Reconstruction Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
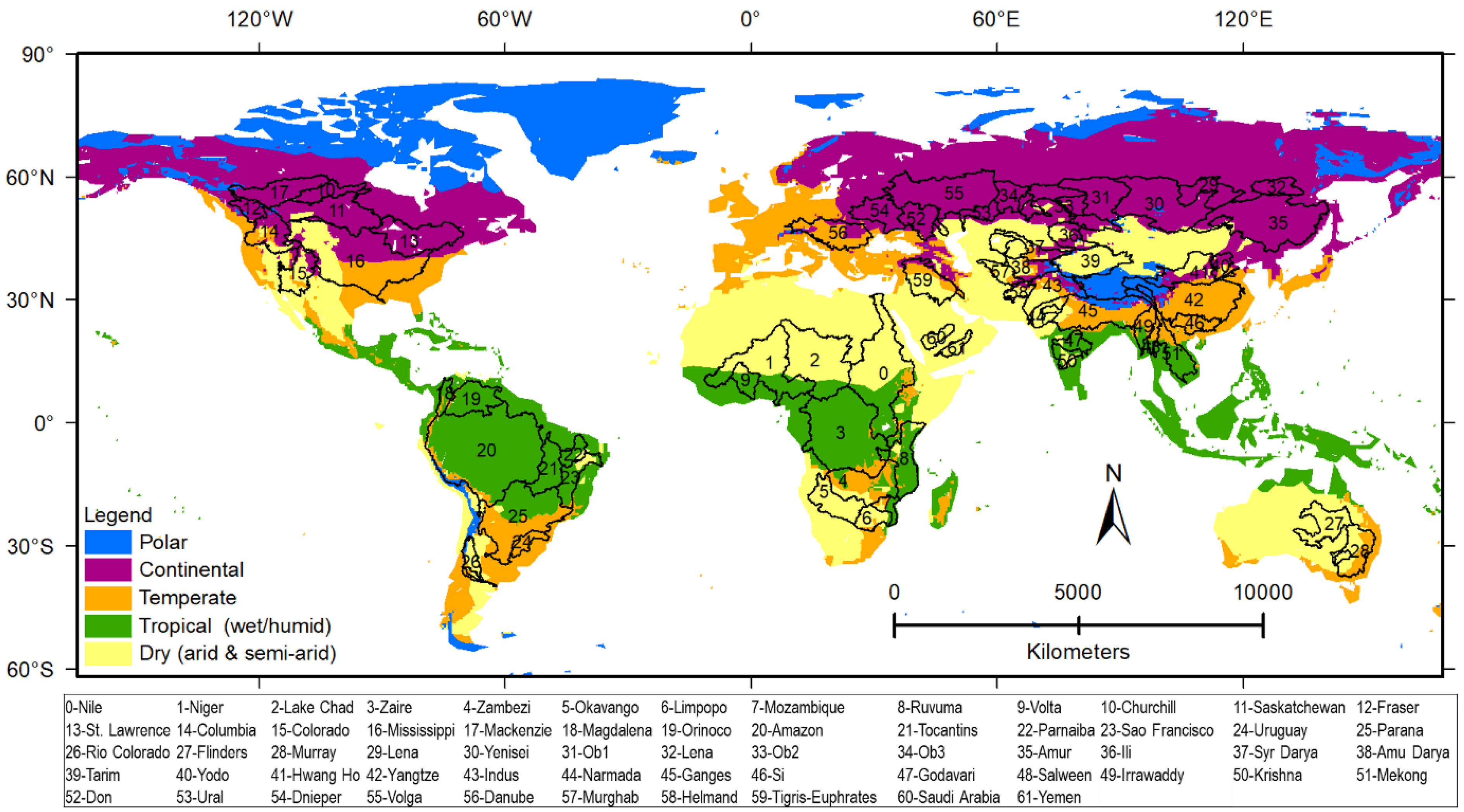
| Basin ID | Basin Name | Continent | Precipitation (mm/yr) | Area (km2) | Climate Zone |
|---|---|---|---|---|---|
| 0 | Nile | Africa | 704 | 3,271,155 | Dry |
| 1 | Niger | Africa | 704 | 2,277,159 | Dry |
| 2 | Lake Chad | Africa | 396 | 2,660,764 | Dry |
| 3 | Zaire | Africa | 1556 | 3,735,917 | Tropical |
| 4 | Zambezi | Africa | 980 | 1,472,701 | Temperate |
| 5 | Okavango | Africa | 561 | 971,144 | Dry |
| 6 | Limpopo | Africa | 537 | 487,829 | Dry |
| 7 | Mozambique NE Coast | Africa | 833 | 278,592 | Tropical |
| 8 | Ruvuma | Africa | 1017 | 1,071,358 | Tropical |
| 9 | Volta | Africa | 1016 | 425,491 | Tropical |
| 10 | Churchill | North America | 499 | 981,996 | Continental |
| 11 | Saskatchewan-Nelson | North America | 548 | 2,836,224 | Continental |
| 12 | Fraser | North America | 706 | 620,355 | Continental |
| 13 | St. Lawrence | North America | 1051 | 2,149,625 | Continental |
| 14 | Columbia | North America | 613 | 1,367,203 | Continental |
| 15 | Colorado | North America | 320 | 978,636 | Dry |
| 16 | Mississippi | North America | 884 | 5,625,053 | Temperate/Continental |
| 17 | Mackenzie | North America | 481 | 1,992,763 | Continental |
| 18 | Magdalena | South America | 2342 | 263,197 | Tropical |
| 19 | Orinoco | South America | 2374 | 944,775 | Tropical |
| 20 | Amazon | South America | 2263 | 6,025,286 | Tropical |
| 21 | Tocantins | South America | 1663 | 803,661 | Tropical |
| 22 | Parnaiba | South America | 1047 | 337,411 | Tropical |
| 23 | Sao Francisco | South America | 976 | 673,366 | Tropical |
| 24 | Uruguay | South America | 1795 | 347,840 | Temperate |
| 25 | Parana | South America | 1309 | 3,065,761 | Tropical |
| 26 | Rio Colorado | South America | 332 | 434,140 | Dry |
| 27 | Flinders | Australia | 286 | 971,231 | Dry |
| 28 | Murray | Australia | 521 | 1,040,403 | Dry/Temperate |
| 29 | Lena | Asia | 457 | 1,453,767 | Continental |
| 30 | Yenisei | Asia | 451 | 4,177,460 | Continental |
| 31 | Ob1 | Asia | 668 | 2,221,313 | Continental |
| 32 | Lena | Asia | 575 | 898,935 | Continental |
| 33 | Ob2 | Asia | 529 | 1,681,026 | Continental |
| 34 | Ob3 | Asia | 560 | 921,174 | Continental |
| 35 | Amur | Asia | 622 | 4,776,036 | Continental |
| 36 | Ili | Asia | 370 | 846,829 | Continental/Dry |
| 37 | Syr Darya | Asia | 387 | 596,945 | Dry |
| 38 | Amu Darya | Asia | 324 | 1,050,574 | Dry |
| 39 | Tarim (Yarkand) | Asia | 112 | 1,539,641 | Dry |
| 40 | Yodo | Asia | 531 | 346,578 | Continental |
| 41 | Hwang Ho | Asia | 490 | 1,251,658 | Continental/Dry |
| 42 | Yangtze | Asia | 1094 | 2,584,657 | Temperate |
| 43 | Indus | Asia | 535 | 1,202,195 | dry |
| 44 | Narmada | Asia | 409 | 401,453 | Dry |
| 45 | Ganges-Brahmaputra | Asia | 1293 | 2,001,344 | Temperate |
| 46 | Si | Asia | 1502 | 486,550 | Temperate |
| 47 | Godavari | Asia | 1165 | 347,993 | Tropical |
| 48 | Salween | Asia | 1113 | 327,489 | Temperate |
| 49 | Irrawaddy | Asia | 1802 | 447,888 | Tropical/Temperate |
| 50 | Krishna | Asia | 932 | 280,322 | Tropical/Dry |
| 51 | Mekong | Asia | 1581 | 871,453 | Tropical |
| 52 | Don | Europe | 722 | 1,055,369 | Continental |
| 53 | Ural | Europe | 489 | 540,152 | Continental |
| 54 | Dnieper | Europe | 786 | 1,308,031 | Continental |
| 55 | Volga | Europe | 777 | 4,535,995 | Continental |
| 56 | Danube | Europe | 917 | 1,653,884 | Temperate |
| 57 | Murghab/Hari Rud | Asia | 257 | 465,732 | Dry |
| 58 | Helmand | Europe | 241 | 285,431 | Dry |
| 59 | Tigris-Euphrates | Asia | 380 | 1,253,767 | Dry |
| 60 | Saudi Arabia | Asia | 80 | 275,525 | Dry |
| 61 | Yemen | Asia | 66 | 232,406 | Dry |
References
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the earth’s gravity field: Hydrological and oceanic effects and their possible detection using grace. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Ahmed, M.; Sultan, M.; Yan, E.; Wahr, J. Assessing and Improving Land Surface Model Outputs Over Africa Using GRACE, Field, and Remote Sensing Data. Surv. Geophys. 2016, 37, 529–556. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.M.; Pfeffer, W.T.; Swenson, S.C. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Rodel, M. Water in the balance. Science 2013, 340, 1300–1301. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Riva, R.; Sauber, J.; Okal, E. Source parameter inversion for recent megathrust earthquakes from global gravity field observations. J. Geophys. Res. 2013, 118, 1240–1267. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.; Abdelmohsen, K. Quantifying Modern Recharge and Depletion Rates of the Nubian Aquifer in Egypt. Surv. Geophys. 2018, 39, 729–751. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.-H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.-S.; Zhang, Q.; Zhao, C.-Y.; Wang, Q.-L.; Ji, L.-Y. Monitoring land subsidence and fault deformation using the small baseline subset InSAR technique: A case study in the Datong Basin, China. J. Geodyn. 2014, 75, 34–40. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Change 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.; Sultan, M.; Wahr, J.; Yan, E.; Milewski, A.; Sauck, W.; Becker, R.; Welton, B. Integration of GRACE (Gravity Recovery and Climate Experiment) data with traditional data sets for a better understanding of the time-dependent water partitioning in African watersheds. Geology 2011, 39, 479–482. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.; Wiese, D.N. Short-term trends in africa’s freshwater resources: Rates and drivers. Sci. Total Environ. 2019, 695, 133843. [Google Scholar] [CrossRef] [PubMed]
- Niyazi, B.A.; Ahmed, M.; Basahi, J.M.; Masoud, M.Z.; Rashed, M.A. Spatiotemporal trends in freshwater availability in the Red Sea Hills, Saudi Arabia. Arab. J. Geosci. 2018, 11, 702. [Google Scholar] [CrossRef]
- Fallatah, O.A.; Ahmed, M.; Cardace, D.; Boving, T.; Akanda, A.S. Assessment of modern recharge to arid region aquifers using an integrated geophysical, geochemical, and remote sensing approach. J. Hydrol. 2019, 569, 600–611. [Google Scholar] [CrossRef]
- Fallatah, O.A.; Ahmed, M.; Save, H.; Akanda, A.S. Quantifying temporal variations in water resources of a vulnerable middle eastern transboundary aquifer system. Hydrol. Process. 2017, 31, 4081–4091. [Google Scholar] [CrossRef]
- Ahmed, M. Sustainable management scenarios for northern Africa’s fossil aquifer systems. J. Hydrol. 2020, 589, 125196. [Google Scholar] [CrossRef]
- Gafurov, A.; Yapiyev, V.; Ahmed, M.; Sagin, J.; Haghighi, E.; Akylbekova, A.; Kløve, B. Groundwater resources. In The Aral Sea Basin, Water for Sustainable Development in Central Asi; Xenarios, S., Schmidt-Vogt, D., Qadir, M., Janusz-Pawletta, B., Abdullaev, I., Eds.; Routledge: London, UK, 2019; pp. 39–51. [Google Scholar]
- Gyawali, B.; Murgulet, D.; Ahmed, M. Quantifying changes in groundwater storage and response to hydroclimatic extremes in a coastal aquifer using remote sensing and ground-based measurements: The Texas gulf coast aquifer. Remote Sens. 2022, 14, 612. [Google Scholar] [CrossRef]
- Ahmed, M.; Aqnouy, M.; El Messari, J.S. Sustainability of Morocco’s groundwater resources in response to natural and anthropogenic forces. J. Hydrol. 2021, 603, 126866. [Google Scholar] [CrossRef]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the Global Mass Change Data Record: GRACE Follow-On Instrument and Science Data Performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Gould, P.G.; Koehler, A.B.; Ord, J.K.; Snyder, R.; Hyndman, R.; Vahid-Araghi, F. Forecasting time series with multiple seasonal patterns. Eur. J. Oper. Res. 2008, 191, 207–222. [Google Scholar] [CrossRef]
- Mwale, F.D.; Adeloye, A.; Rustum, R. Infilling of missing rainfall and streamflow data in the shire river basin, Malawi–A self organizing map approach. Phys. Chem. Earth Parts A/B/C 2012, 50, 34–43. [Google Scholar] [CrossRef]
- Ahmed, M.; Sultan, M.; Elbayoumi, T.; Tissot, P. Forecasting GRACE Data over the African Watersheds Using Artificial Neural Networks. Remote Sens. 2019, 11, 1769. [Google Scholar] [CrossRef] [Green Version]
- Ng, W.; Rasmussen, P.; Panu, U. Infilling missing daily precipitation data at multiple sites using a multivariate truncated normal distribution model. Water 2009, 2009, H31D-0813. [Google Scholar]
- Tum, M.; Günther, K.P.; Böttcher, M.; Baret, F.; Bittner, M.; Brockmann, C.; Weiss, M. Global Gap-Free MERIS LAI Time Series (2002–2012). Remote Sens. 2016, 8, 69. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Jiang, J.; Li, H. Drought and Flood Monitoring of the Liao River Basin in Northeast China Using Extended GRACE Data. Remote Sens. 2018, 10, 1168. [Google Scholar] [CrossRef] [Green Version]
- Forootan, E.; Kusche, J.; Loth, I.; Schuh, W.-D.; Eicker, A.; Awange, J.; Longuevergne, L.; Diekkrüger, B.; Schmidt, M.; Shum, C.K. Multivariate Prediction of Total Water Storage Changes Over West Africa from Multi-Satellite Data. Surv. Geophys. 2014, 35, 913–940. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. A global reconstruction of climate-driven subdecadal water storage variability. Geophys. Res. Lett. 2017, 44, 2300–2309. [Google Scholar] [CrossRef]
- Kenea, T.T.; Kusche, J.; Kebede, S.; Güntner, A. Forecasting terrestrial water storage for drought management in Ethiopia. Hydrol. Sci. J. 2020, 65, 2210–2223. [Google Scholar] [CrossRef]
- Li, F.; Kusche, J.; Rietbroek, R.; Wang, Z.; Forootan, E.; Schulze, K.; Lück, C. Comparison of Data-Driven Techniques to Reconstruct (1992–2002) and Predict (2017–2018) GRACE-Like Gridded Total Water Storage Changes Using Climate Inputs. Water Resour. Res. 2020, 56, e2019WR026551. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Yin, W.; Hu, L.; Han, S.-C.; Zhang, M.; Teng, Y. Reconstructing Terrestrial Water Storage Variations from 1980 to 2015 in the Beishan Area of China. Geofluids 2019, 2019, 3874742. [Google Scholar] [CrossRef]
- De Linage, C.; Famiglietti, J.; Randerson, J. Forecasting terrestrial water storage changes in the amazon basin using atlantic and pacific sea surface temperatures. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 12453–12483. [Google Scholar]
- Pan, M.; Sahoo, A.K.; Troy, T.J.; Vinukollu, R.K.; Sheffield, J.; Wood, A.E.F. Multisource Estimation of Long-Term Terrestrial Water Budget for Major Global River Basins. J. Clim. 2012, 25, 3191–3206. [Google Scholar] [CrossRef]
- Li, F.; Kusche, J.; Chao, N.; Wang, Z.; Löcher, A. Long-Term (1979-Present) Total Water Storage Anomalies Over the Global Land Derived by Reconstructing GRACE Data. Geophys. Res. Lett. 2021, 48, e2021GL093492. [Google Scholar] [CrossRef]
- Becker, M.; Meyssignac, B.; Xavier, L.; Cazenave, A.; Alkama, R.; Decharme, B. Past terrestrial water storage (1980–2008) in the Amazon Basin reconstructed from GRACE and in situ river gauging data. Hydrol. Earth Syst. Sci. 2011, 15, 533–546. [Google Scholar] [CrossRef] [Green Version]
- Hasan, E.; Tarhule, A.; Zume, J.T.; Kirstetter, P.-E. + 50 years of terrestrial hydroclimatic variability in Africa’s transboundary waters. Sci. Rep. 2019, 9, 12327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jing, W.; Zhang, P.; Zhao, X.; Yang, Y.; Jiang, H.; Xu, J.; Yang, J.; Li, Y. Extending GRACE terrestrial water storage anomalies by combining the random forest regression and a spatially moving window structure. J. Hydrol. 2020, 590, 125239. [Google Scholar] [CrossRef]
- Yang, P.; Xia, J.; Zhan, C.; Wang, T. Reconstruction of terrestrial water storage anomalies in Northwest China during 1948–2002 using GRACE and GLDAS products. Water Policy 2018, 49, 1594–1607. [Google Scholar] [CrossRef] [Green Version]
- Sun, A.Y.; Scanlon, B.R.; Save, H.; Rateb, A. Reconstruction of GRACE Total Water Storage Through Automated Machine Learning. Water Resour. Res. 2021, 57, e2020WR028666. [Google Scholar] [CrossRef]
- Talpe, M.J.; Nerem, R.S.; Forootan, E.; Lemoine, F.G.; Enderlin, E.M.; Landerer, F.W.; Schmidt, M. Ice mass change in Greenland and Antarctica between 1993 and 2013 from satellite gravity measurements. J. Geod. 2017, 91, 1283–1298. [Google Scholar] [CrossRef] [Green Version]
- Löcher, A.; Kusche, J. A hybrid approach for recovering high-resolution temporal gravity fields from satellite laser ranging. J. Geod. 2021, 95, 6. [Google Scholar] [CrossRef]
- Loomis, B.D.; Rachlin, K.E.; Luthcke, S.B. Improved Earth Oblateness Rate Reveals Increased Ice Sheet Losses and Mass-Driven Sea Level Rise. Geophys. Res. Lett. 2019, 46, 6910–6917. [Google Scholar] [CrossRef]
- Sośnica, K.; Jäggi, A.; Meyer, U.; Thaller, D.; Beutler, G.; Arnold, D.; Dach, R. Time variable Earth’s gravity field from SLR satellites. J. Geod. 2015, 89, 945–960. [Google Scholar] [CrossRef] [Green Version]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A constellation to study the Earth’s magnetic field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef] [Green Version]
- Forootan, E.; Schumacher, M.; Mehrnegar, N.; Bezděk, A.; Talpe, M.J.; Farzaneh, S.; Zhang, C.; Zhang, Y.; Shum, C.K. An Iterative ICA-Based Reconstruction Method to Produce Consistent Time-Variable Total Water Storage Fields Using GRACE and Swarm Satellite Data. Remote Sens. 2020, 12, 1639. [Google Scholar] [CrossRef]
- Meyer, U.; Sosnica, K.; Arnold, D.; Dahle, C.; Thaller, D.; Dach, R.; Jäggi, A. SLR, GRACE and Swarm Gravity Field Determination and Combination. Remote Sens. 2019, 11, 956. [Google Scholar] [CrossRef] [Green Version]
- Yi, S.; Sneeuw, N. Filling the Data Gaps Within GRACE Missions Using Singular Spectrum Analysis. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021227. [Google Scholar] [CrossRef]
- Velicogna, I.; Wahr, J. Time-variable gravity observations of ice sheet mass balance: Precision and limitations of the GRACE satellite data. Geophys. Res. Lett. 2013, 40, 3055–3063. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y. Smoothing Splines: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Li, W.; Wang, W.; Zhang, C.; Wen, H.; Zhong, Y.; Zhu, Y.; Li, Z. Bridging Terrestrial Water Storage Anomaly During GRACE/GRACE-FO Gap Using SSA Method: A Case Study in China. Sensors 2019, 19, 4144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, F.; Shen, Y.; Chen, T.; Chen, Q.; Li, W. Improved multichannel singular spectrum analysis for post-processing GRACE monthly gravity field models. Geophys. J. Int. 2020, 223, 825–839. [Google Scholar] [CrossRef]
- Wang, F.; Shen, Y.; Chen, Q.; Wang, W. Bridging the gap between GRACE and GRACE follow-on monthly gravity field solutions using improved multichannel singular spectrum analysis. J. Hydrol. 2021, 594, 125972. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Phys. D Nonlinear Phenom. 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Long, D.; Scanlon, B.R.; Longuevergne, L.; Sun, A.Y.; Fernando, D.N.; Save, H. GRACE satellite monitoring of large depletion in water storage in response to the 2011 drought in Texas. Geophys. Res. Lett. 2013, 40, 3395–3401. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Schmied, H.M.; van Beek, L.P.H.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C.; et al. Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proc. Natl. Acad. Sci. 2018, 115, E1080–E1089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scanlon, B.R.; Zhang, Z.; Rateb, A.; Sun, A.; Wiese, D.; Save, H.; Beaudoing, H.; Lo, M.H.; Müller-Schmied, H.; Döll, P.; et al. Tracking Seasonal Fluctuations in Land Water Storage Using Global Models and GRACE Satellites. Geophys. Res. Lett. 2019, 46, 5254–5264. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Oleson, K.W.; Niu, G.-Y.; Yang, Z.-L.; Lawrence, D.; Thornton, P.; Lawrence, P.J.; Stöckli, R.; Dickinson, R.E.; Bonan, G.B.; Levis, S.; et al. Improvements to the Community Land Model and their impact on the hydrological cycle. J. Geophys. Res. 2008, 113, G01021. [Google Scholar] [CrossRef]
- Fan, Y.; Van Den Dool, H. Climate Prediction Center global monthly soil moisture data set at 0.5 resolution for 1948 to present. J. Geophys. Res. Earth Surf. 2004, 109, D10102. [Google Scholar] [CrossRef] [Green Version]
- Döll, P.; Kaspar, F.; Lehner, B. A global hydrological model for deriving water availability indicators: Model tuning and validation. J. Hydrol. 2003, 270, 105–134. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Q.; Werner, A.; Liu, X. GRACE-Based Hydrological Drought Evaluation of the Yangtze River Basin, China. J. Hydrometeorol. 2016, 17, 811–828. [Google Scholar] [CrossRef]
- Nie, N.; Zhang, W.; Zhang, Z.; Guo, H.; Ishwaran, N. Reconstructed Terrestrial Water Storage Change (ΔTWS) from 1948 to 2012 over the Amazon Basin with the Latest GRACE and GLDAS Products. Water Resour. Manag. 2016, 30, 279–294. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L. Grace-rec: A reconstruction of climate-driven water storage changes over the last century, earth syst. Sci. Data 2019, 11, 1153–1170. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, V.G.; Andam-Akorful, S.A.; Dannouf, R.; Adu-Afari, E. A Multi-Sourced Data Retrodiction of Remotely Sensed Terrestrial Water Storage Changes for West Africa. Water 2019, 11, 401. [Google Scholar] [CrossRef] [Green Version]
- Sun, A.Y.; Scanlon, B.R.; Zhang, Z.; Walling, D.; Bhanja, S.N.; Mukherjee, A.; Zhong, Z. Combining Physically Based Modeling and Deep Learning for Fusing GRACE Satellite Data: Can We Learn From Mismatch? Water Resour. Res. 2019, 55, 1179–1195. [Google Scholar] [CrossRef] [Green Version]
- Jing, W.; Di, L.; Zhao, X.; Yao, L.; Xia, X.; Liu, Y.; Yang, J.; Li, Y.; Zhou, C. A data-driven approach to generate past GRACE-like terrestrial water storage solution by calibrating the land surface model simulations. Adv. Water Resour. 2020, 143, 103683. [Google Scholar] [CrossRef]
- Zhu, C.; Zhan, W.; Liu, J.; Chen, M. Application of singular spectrum analysis in reconstruction of the annual signal from GRACE. J. Appl. Geod. 2020, 14, 295–302. [Google Scholar] [CrossRef]
- Sun, Z.; Long, D.; Yang, W.; Li, X.; Pan, Y. Reconstruction of GRACE Data on Changes in Total Water Storage Over the Global Land Surface and 60 Basins. Water Resour. Res. 2020, 56, e2019WR026250. [Google Scholar] [CrossRef]
- Sohoulande, C.D.; Martin, J.; Szogi, A.; Stone, K. Climate-driven prediction of land water storage anomalies: An outlook for water resources monitoring across the conterminous United States. J. Hydrol. 2020, 588, 125053. [Google Scholar] [CrossRef]
- Jing, W.; Zhao, X.; Yao, L.; Di, L.; Yang, J.; Li, Y.; Guo, L.; Zhou, C. Can Terrestrial Water Storage Dynamics be Estimated From Climate Anomalies? Earth Space Sci. 2020, 7, e2019EA000959. [Google Scholar] [CrossRef] [Green Version]
- Jeon, W.; Kim, J.-S.; Seo, K.-W. Reconstruction of Terrestrial Water Storage of GRACE/GFO Using Convolutional Neural Network and Climate Data. J. Korean Earth Sci. Soc. 2021, 42, 445–458. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, S.; He, H.; Yang, K.; Ma, L.; Li, J. Reconstructing GRACE-like TWS anomalies for the Canadian landmass using deep learning and land surface model. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102404. [Google Scholar] [CrossRef]
- Tang, S.; Wang, H.; Feng, Y.; Liu, Q.; Wang, T.; Liu, W.; Sun, F. Random Forest-Based Reconstruction and Application of the GRACE Terrestrial Water Storage Estimates for the Lancang-Mekong River Basin. Remote Sens. 2021, 13, 4831. [Google Scholar] [CrossRef]
- Yang, X.; Tian, S.; You, W.; Jiang, Z. Reconstruction of continuous GRACE/GRACE-FO terrestrial water storage anomalies based on time series decomposition. J. Hydrol. 2021, 603, 127018. [Google Scholar] [CrossRef]
- Mo, S.; Zhong, Y.; Forootan, E.; Mehrnegar, N.; Yin, X.; Wu, J.; Feng, W.; Shi, X. Bayesian convolutional neural networks for predicting the terrestrial water storage anomalies during GRACE and GRACE-FO gap. J. Hydrol. 2021, 604, 127244. [Google Scholar] [CrossRef]
- Mueller, B.; Hirschi, M.; Seneviratne, S.I. New diagnostic estimates of variations in terrestrial water storage based on ERA-Interim data. Hydrol. Process. 2011, 25, 996–1008. [Google Scholar] [CrossRef]
- Eicker, A.; Schumacher, M.; Kusche, J.; Döll, P.; Schmied, H.M. Calibration/Data Assimilation Approach for Integrating GRACE Data into the WaterGAP Global Hydrology Model (WGHM) Using an Ensemble Kalman Filter: First Results. Surv. Geophys. 2014, 35, 1285–1309. [Google Scholar] [CrossRef]
- Kumar, S.V.; Zaitchik, B.F.; Peters-Lidard, C.D.; Rodell, M.; Reichle, R.; Li, B.; Jasinski, M.; Mocko, D.; Getirana, A.; De Lannoy, G.; et al. Assimilation of Gridded GRACE Terrestrial Water Storage Estimates in the North American Land Data Assimilation System. J. Hydrometeorol. 2016, 17, 1951–1972. [Google Scholar] [CrossRef]
- Girotto, M.; De Lannoy, G.J.M.; Reichle, R.H.; Rodell, M. Assimilation of gridded terrestrial water storage observations from GRACE into a land surface model. Water Resour. Res. 2016, 52, 4164–4183. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Rodell, M.; Kumar, S.; Beaudoing, H.K.; Getirana, A.; Zaitchik, B.F.; De Goncalves, L.G.; Cossetin, C.; Bhanja, S.; Mukherjee, A.; et al. Global GRACE Data Assimilation for Groundwater and Drought Monitoring: Advances and Challenges. Water Resour. Res. 2019, 55, 7564–7586. [Google Scholar] [CrossRef] [Green Version]
- Tian, S.; Tregoning, P.; Renzullo, L.J.; Dijk, A.V.; Walker, J.P.; Pauwels, V.; Allgeyer, S. Improved water balance component estimates through joint assimilation of GRACE water storage and SMOS soil moisture retrievals. Water Resour. Res. 2017, 53, 1820–1840. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Han, S.-C.; Tian, S.; Schmied, H.M.; Sutanudjaja, E.H.; Ran, J.; Feng, W. Evaluation of Groundwater Storage Variations Estimated from GRACE Data Assimilation and State-of-the-Art Land Surface Models in Australia and the North China Plain. Remote Sens. 2018, 10, 483. [Google Scholar] [CrossRef] [Green Version]
- Tangdamrongsub, N.; Han, S.-C.; Yeo, I.-Y.; Dong, J.; Steele-Dunne, S.C.; Willgoose, G.; Walker, J.P. Multivariate data assimilation of GRACE, SMOS, SMAP measurements for improved regional soil moisture and groundwater storage estimates. Adv. Water Resour. 2020, 135, 103477. [Google Scholar] [CrossRef]
- Khaki, M.; Forootan, E.; Kuhn, M.; Awange, J.; van Dijk, A.I.J.M.; Schumacher, M.; Sharifi, M.A. Determining water storage depletion within Iran by assimilating GRACE data into the W3RA hydrological model. Adv. Water Resour. 2018, 114, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Soltani, S.S.; Ataie-Ashtiani, B.; Simmons, C.T. Review of assimilating GRACE terrestrial water storage data into hydrological models: Advances, challenges and opportunities. Earth-Sci. Rev. 2021, 213, 103487. [Google Scholar] [CrossRef]
- Nie, W.; Zaitchik, B.F.; Rodell, M.; Kumar, S.V.; Arsenault, K.R.; Li, B.; Getirana, A. Assimilating GRACE Into a Land Surface Model in the Presence of an Irrigation-Induced Groundwater Trend. Water Resour. Res. 2019, 55, 11274–11294. [Google Scholar] [CrossRef]
- Hussein, E.A.; Thron, C.; Ghaziasgar, M.; Bagula, A.; Vaccari, M. Groundwater Prediction Using Machine-Learning Tools. Algorithms 2020, 13, 300. [Google Scholar] [CrossRef]
- Reager, J.T.; Famiglietti, J.S. Characteristic mega-basin water storage behavior using GRACE. Water Resour. Res. 2013, 49, 3314–3329. [Google Scholar] [CrossRef] [Green Version]
- De Linage, C.; Famiglietti, J.S.; Randerson, J.T. Statistical prediction of terrestrial water storage changes in the Amazon Basin using tropical Pacific and North Atlantic sea surface temperature anomalies. Hydrol. Earth Syst. Sci. 2014, 18, 2089–2102. [Google Scholar] [CrossRef] [Green Version]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Dobson, A.J.; Barnett, A. An Introduction to Generalized Linear Models; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kuhn, M. Building predictive models in r using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Coxe, S.; West, S.G.; Aiken, L.S. Generalized linear models. Oxf. Handb. Quant. Methods 2013, 2, 26–51. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Zhou, J.; Li, E.; Yang, S.; Wang, M.; Shi, X.; Yao, S.; Mitri, H.S. Slope stability prediction for circular mode failure using gradient boosting machine approach based on an updated database of case histories. Saf. Sci. 2019, 118, 505–518. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Tao, Y.; Gao, X.; Hsu, K.; Sorooshian, S.; Ihler, A. A Deep Neural Network Modeling Framework to Reduce Bias in Satellite Precipitation Products. J. Hydrometeorol. 2016, 17, 931–945. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT press Cambridge: Cambridge, MA, USA, 2016. [Google Scholar]
- Sun, A.Y. Predicting groundwater level changes using GRACE data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef]
- Bengio, Y. Learning Deep Architectures for AI; Now Publishers Inc: Delft, The Netherlands, 2009. [Google Scholar]
- Guan, K.; Wood, E.F.; Medvigy, D.; Kimball, J.; Pan, M.; Caylor, K.K.; Sheffield, J.; Xu, X.; Jones, M.O. Terrestrial hydrological controls on land surface phenology of African savannas and woodlands. J. Geophys. Res. Biogeosciences 2014, 119, 1652–1669. [Google Scholar] [CrossRef]
- Hilker, T.; Lyapustin, A.I.; Tucker, C.J.; Hall, F.G.; Myneni, R.B.; Wang, Y.; Bi, J.; de Moura, Y.M.; Sellers, P.J. Vegetation dynamics and rainfall sensitivity of the Amazon. Proc. Natl. Acad. Sci. USA 2014, 111, 16041–16046. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Rateb, A.; Anyamba, A.; Kebede, S.; MacDonald, A.M.; Shamsudduha, M.; Small, I.J.; Sun, A.Y.; Taylor, R.G.; Xie, H. Linkages between GRACE water storage, hydrologic extremes, and climate teleconnections in major African aquifers. Environ. Res. Lett. 2021, 17, 014046. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G.; Ronchail, J. Changes in terrestrial water storage versus rainfall and discharges in the Amazon basin. Int. J. Climatol. 2013, 33, 3029–3046. [Google Scholar] [CrossRef] [Green Version]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing earth’s time variable mass distribution with grace using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Peters-Lidard, C.; Kato, H.; Kumar, S.; Gottschalck, J.; Mitchell, K.; Meng, J. Nasa/Noaa’s global land data assimilation system (GLDAS): Recent results and future plans. In Proceedings of the ECMWF/ELDAS Workshop on Land Surface Assimilation, Shinfield, UK, 8–11 November 2004; pp. 61–68. [Google Scholar]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. Earth Surf. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Yang, T.; Wang, C.; Yu, Z.; Xu, F. Characterization of spatio-temporal patterns for various GRACE- and GLDAS-born estimates for changes of global terrestrial water storage. Glob. Planet. Chang. 2013, 109, 30–37. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. Gpm Imerg Final Precipitation l3 1 Month 0.1 Degree × 0.1 Degree V06; Goddard Earth Sciences Data and Information Services Center: Greenbelt, MD, USA, 2019. Available online: https://disc.gsfc.nasa.gov/datasets/GPM_3IMERGM_06/summary?keywords=%22IMERG%20final%22.V06 (accessed on 10 December 2021).
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) Mission for Science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Hennermann, K.; Berrisford, P. Era5 data documentation. In Copernicus Knowledge Base; ECMWF: Reading, UK, 2020; Available online: https://confluence.ecmwf.int/display/CKB/ERA5%3A+data+documentation (accessed on 10 December 2021).
- Mu, Q.; Zhao, M.; Running, W.S. Brief introduction to modis evapotranspiration data set (mod16). Water Resour. Res. 2005, 45, 1–4. [Google Scholar]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Fang, B.; Kansara, P.; Dandridge, C.; Lakshmi, V. Drought monitoring using high spatial resolution soil moisture data over Australia in 2015–2019. J. Hydrol. 2021, 594, 125960. [Google Scholar] [CrossRef]
- Halverson, J.B. The Costliest Hurricane Season in U.S. History. Weather. 2018, 71, 20–27. [Google Scholar] [CrossRef]
- Garrido, A.; Martínez-Santos, P.; Llamas, M.R. Groundwater irrigation and its implications for water policy in semiarid countries: The spanish experience. Hydrogeol. J. 2006, 14, 340. [Google Scholar] [CrossRef]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Pan, Y.; Zhou, J.; Chen, Y.; Hou, X.; Hong, Y.; Scanlon, B.R.; Longuevergne, L. Global analysis of spatiotemporal variability in merged total water storage changes using multiple GRACE products and global hydrological models. Remote Sens. Environ. 2017, 192, 198–216. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Reedy, R.C.; Pool, D.R.; Save, H.; Long, D.; Chen, J.; Wolock, D.M.; Conway, B.D.; Winester, D. Hydrologic implications of GRACE satellite data in the Colorado River Basin. Water Resour. Res. 2015, 51, 9891–9903. [Google Scholar] [CrossRef]
- Song, C.; Ke, L.; Huang, B.; Richards, K.S. Can mountain glacier melting explains the GRACE-observed mass loss in the southeast Tibetan Plateau: From a climate perspective? Glob. Planet. Chang. 2015, 124, 1–9. [Google Scholar] [CrossRef]
- Proulx, R.A.; Knudson, M.D.; Kirilenko, A.; VanLooy, J.A.; Zhang, X. Significance of surface water in the terrestrial water budget: A case study in the Prairie Coteau using GRACE, GLDAS, Landsat, and groundwater well data. Water Resour. Res. 2013, 49, 5756–5764. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, 1–11. [Google Scholar] [CrossRef]
- Charo, A.; Abdalati, W. The 2017–2027 national academies decadal survey for earth science and applications from space: An overview of the report. 42nd COSPAR Sci. Assem. 2018, 42, A3-1. [Google Scholar]
- FAO. Irrigated Crop Calendars; FAO: Rome, Italy, 2021. [Google Scholar]
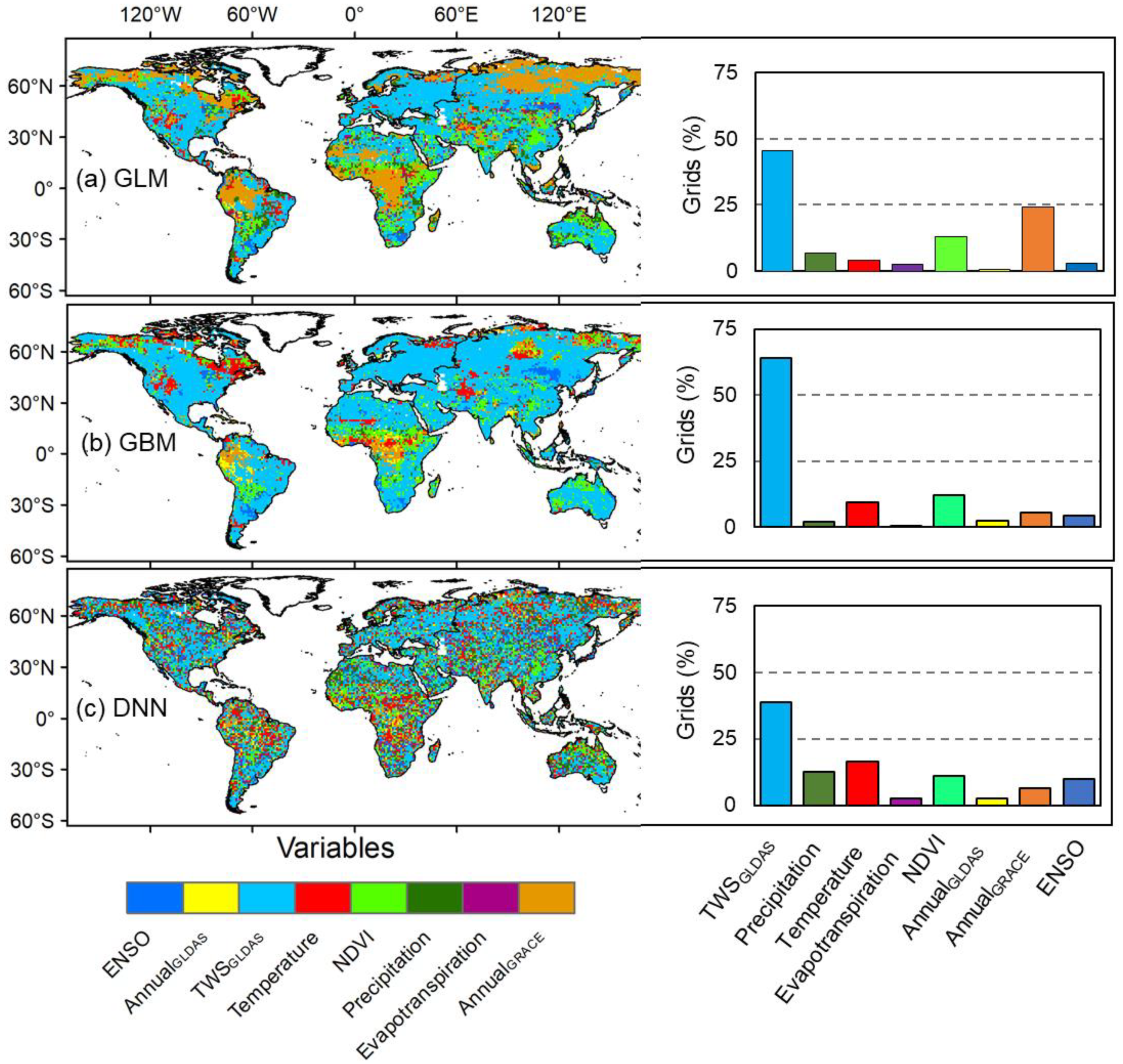
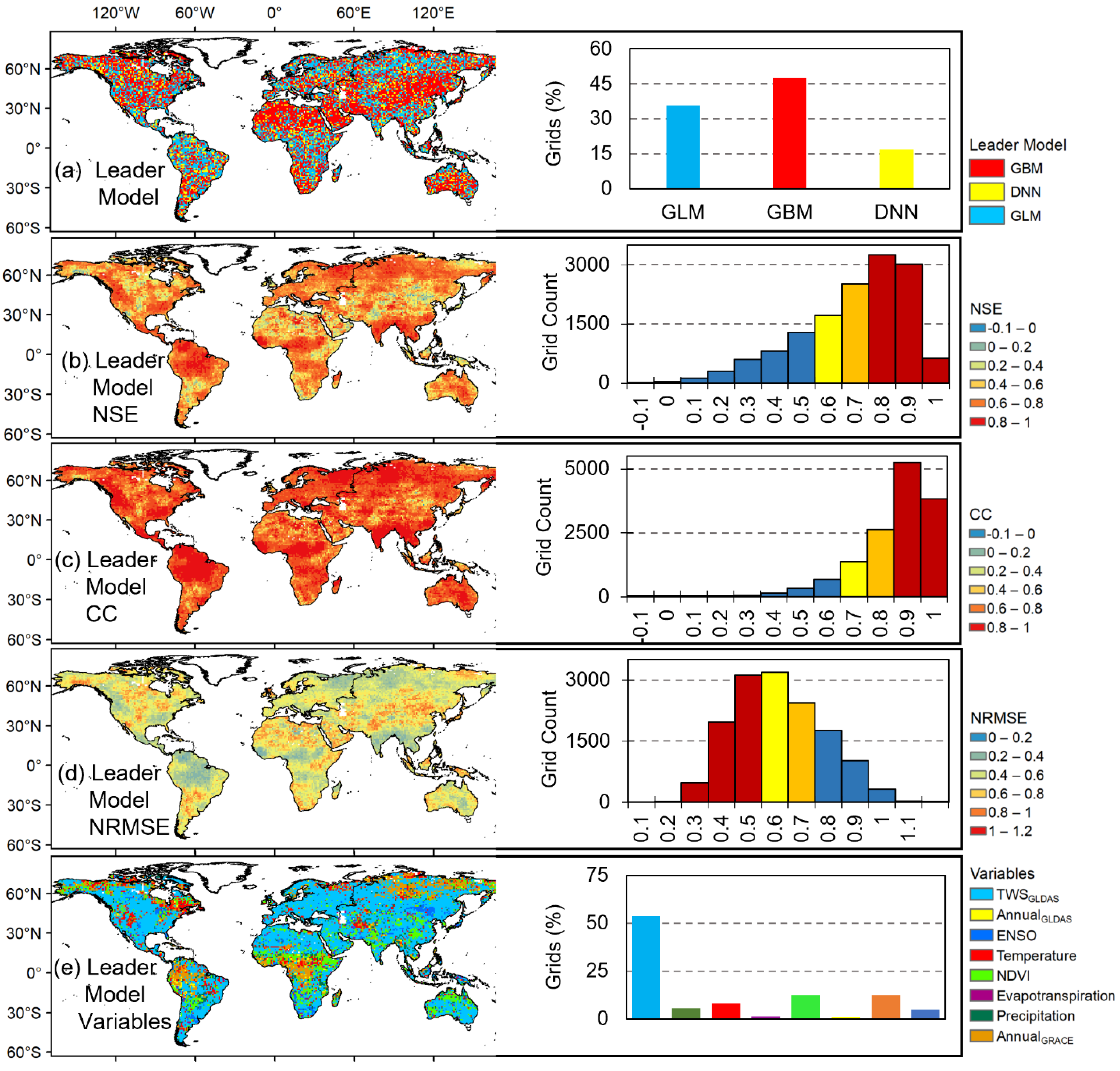
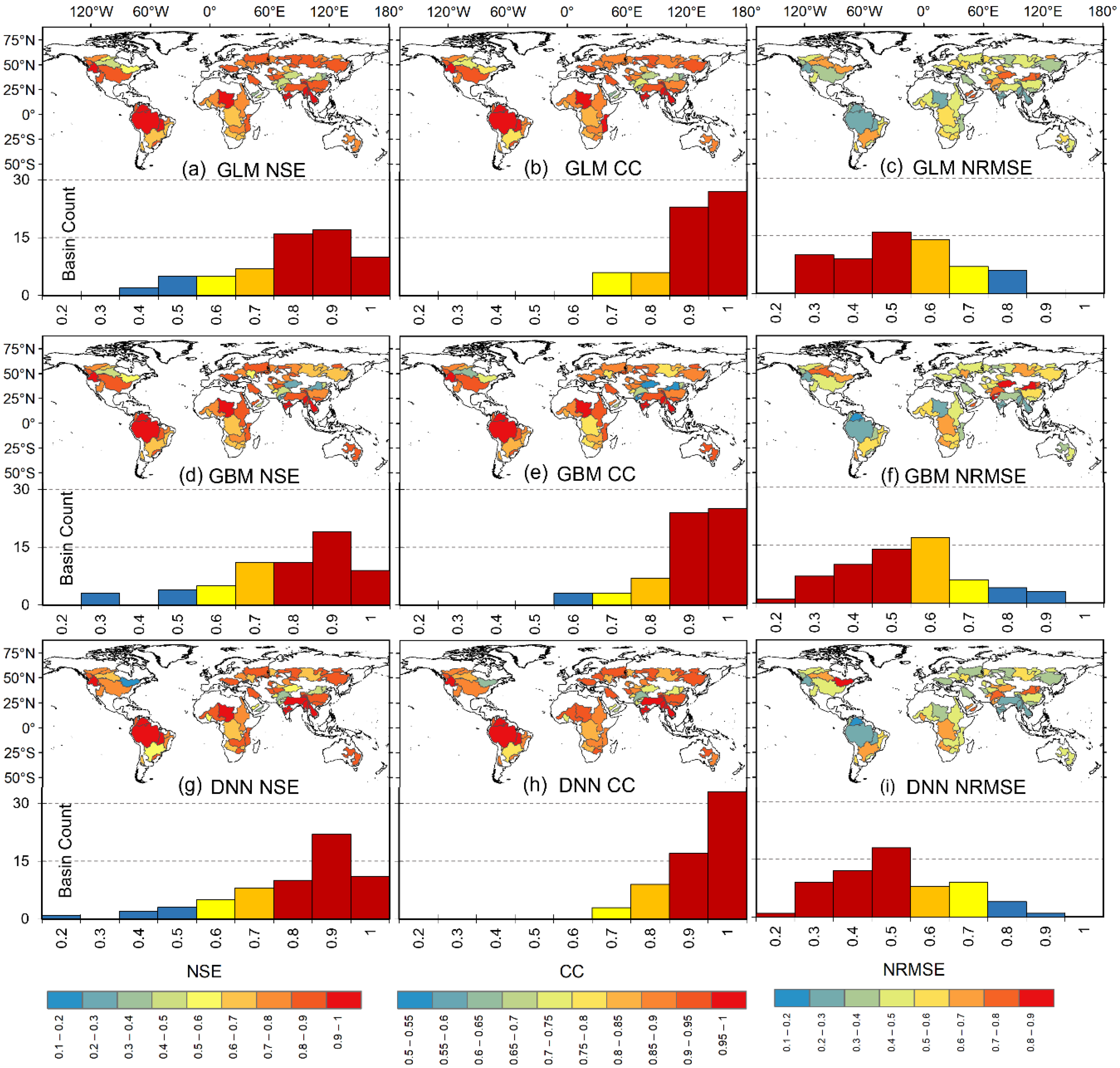
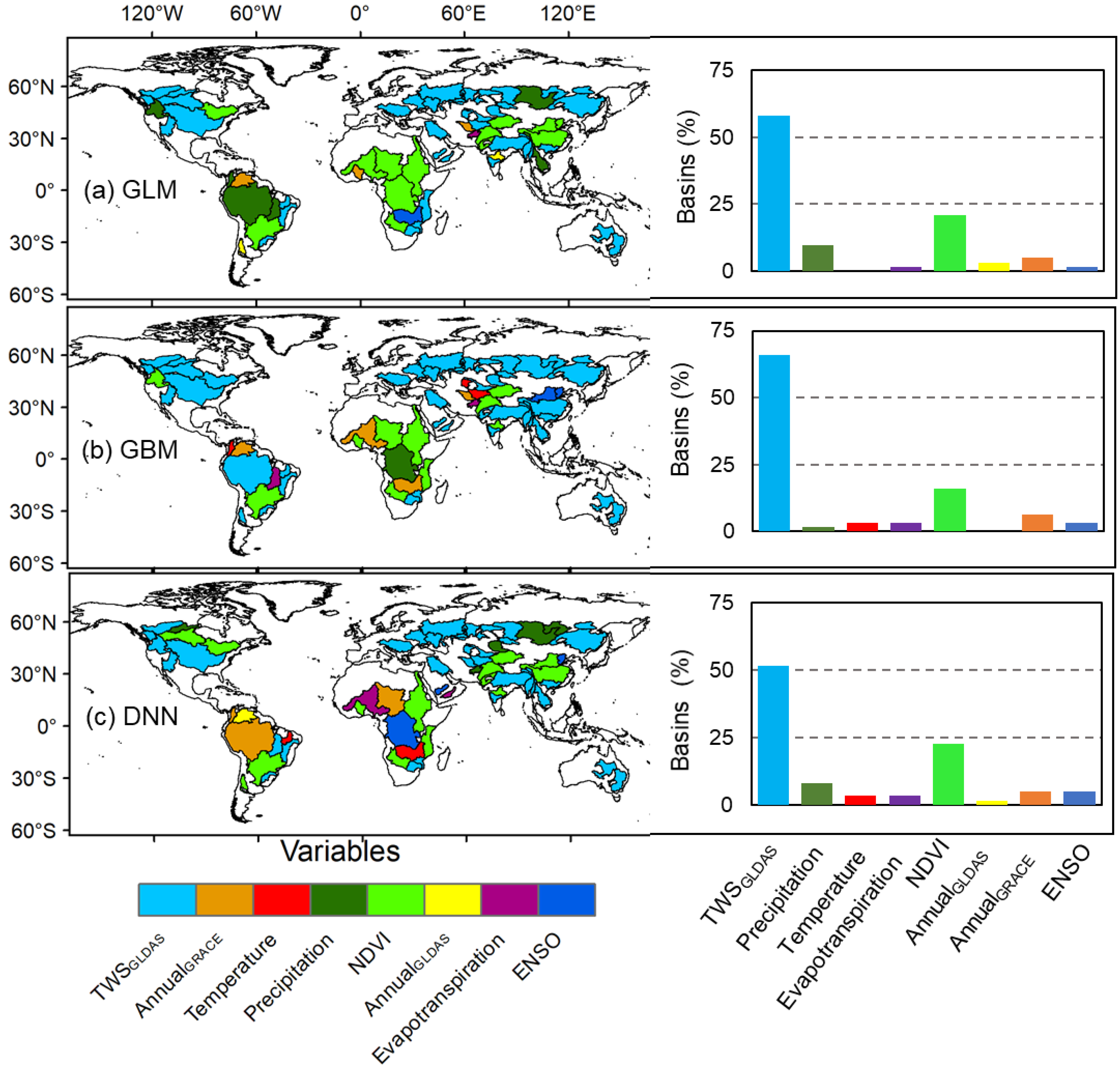
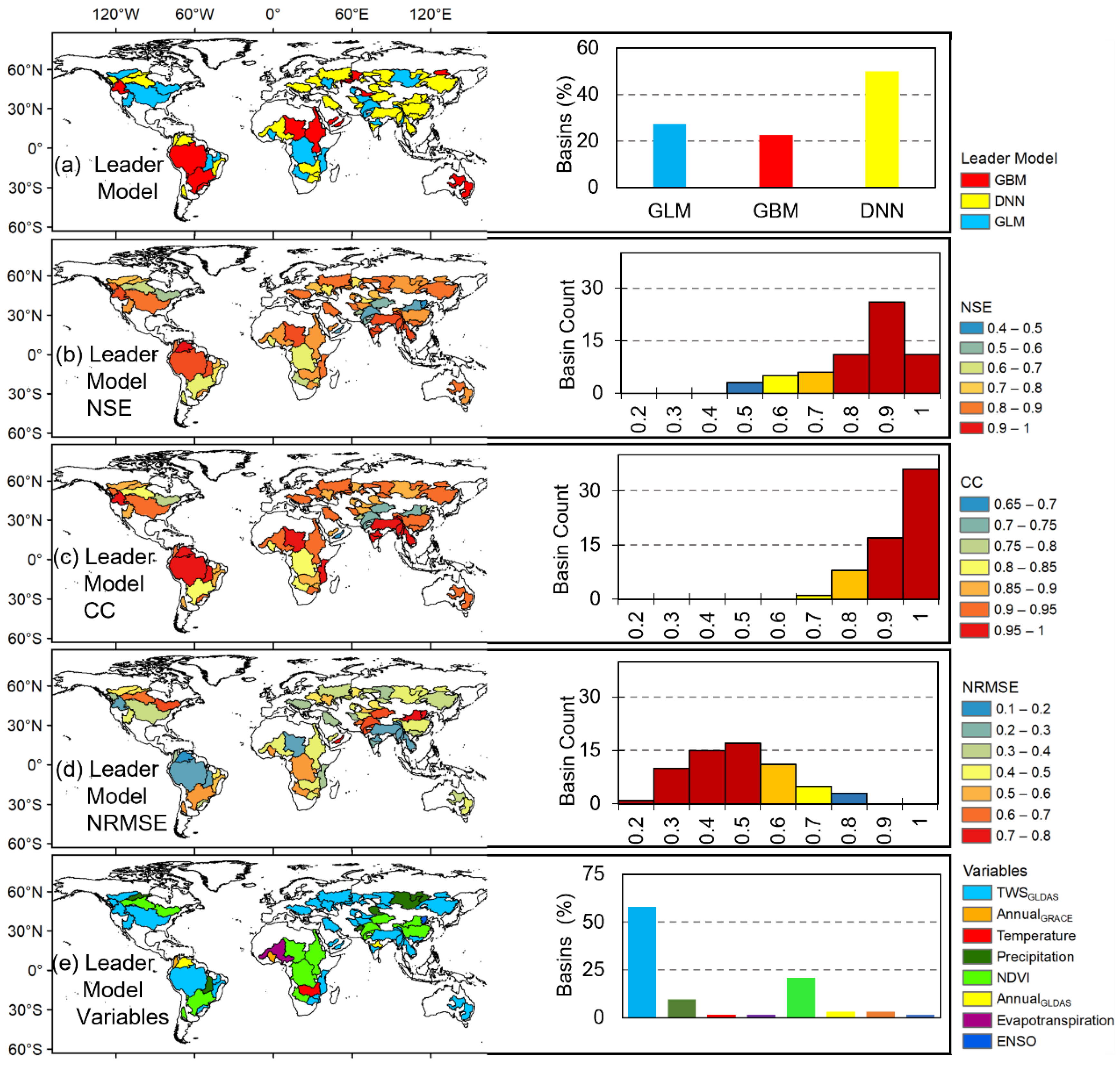
| Grid Scale | ||||
|---|---|---|---|---|
| GLM | GBM | DNN | Leader Model | |
| NSE | 0.55 ± 0.26 | 0.59 ± 0.23 | 0.49 ± 0.28 | 0.65 ± 0.20 |
| CC | 0.74 ± 0.19 | 0.77 ± 0.15 | 0.73 ± 0.19 | 0.81 ± 0.13 |
| NRMSE | 0.63 ± 0.19 | 0.61 ± 0.17 | 0.68 ± 0.19 | 0.56 ± 0.16 |
| Basin Scale | ||||
| GLM | GBM | DNN | Leader Model | |
| NSE | 0.74 ± 0.15 | 0.73 ± 0.17 | 0.75 ± 0.17 | 0.78 ± 0.14 |
| CC | 0.87 ± 0.09 | 0.85 ± 0.11 | 0.88 ± 0.09 | 0.89 ± 0.07 |
| NRMSE | 0.48 ± 0.15 | 0.49 ± 0.16 | 0.46 ± 0.16 | 0.43 ± 0.14 |
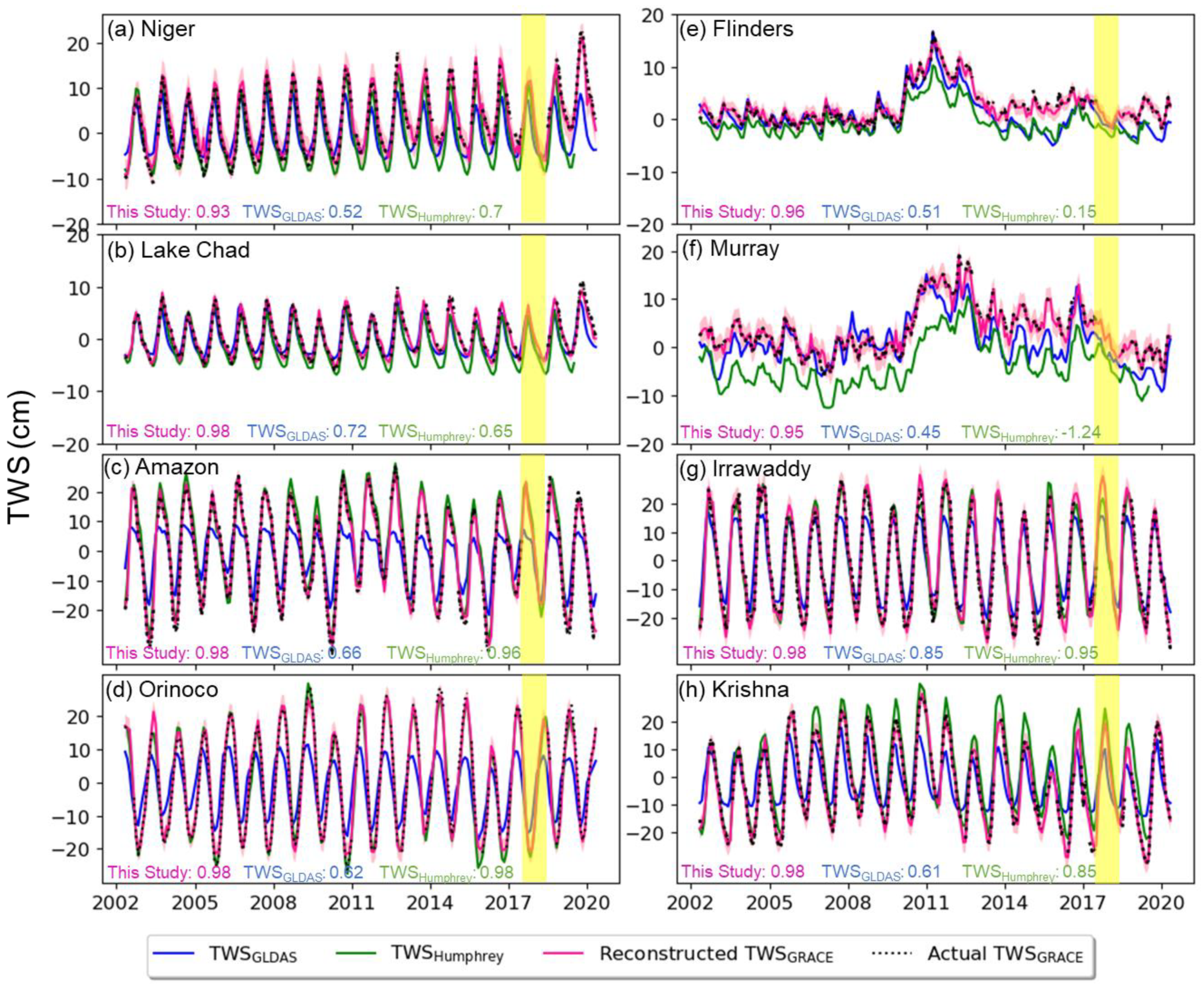
| Reference | Region/Basin | Their Performance * | This Study |
|---|---|---|---|
| Becker et al. [38] | Amazon Basin | CC = 0.9 | CC = 0.98 |
| De Linage et al. [35] | Amazon Basin | R2 = 0.43 | NSE = 0.95 |
| Long et al. [33] | Southwest China | R2 = 0.57–0.91 | NSE = 0.84–0.95 |
| Sośnica et al. [46] | Global | Mean CC = 0.5 | Mean CC = 0.81 |
| Zhang et al. [64] | Yangtze Basin | NSE = 0.83 | NSE = 0.84 |
| Humphrey et al. [30] | Global | CC: Amazon = 0.96; Mississippi = 0.89; Volga = 0.90; Niger = 0.98 | CC: Amazon = 0.98; Mississippi = 0.9, Volga = 0.93 Niger = 0.91 |
| Yang et al. [41] | Northwest China | NSE = 0.2 | NSE = 0.52 |
| Chen et al. [28] | Northeast China | CC = 0.9 | CC = 0.66 |
| Ahmed et al. [25] | Africa | NSE = 0.54–0.94; CC = 0.79–0.97 | NSE = 0.65–0.93; CC 0.82–0.97 |
| Hasan et al. [39] | Africa | NSE = 0.72–0.94 | NSE = 0.65–0.93 |
| Humphrey and Gudmundsson [66] | Global | Median NSE < 0.5; CC < 0.75 | Median NSE = 0.69; CC = 0.85 |
| Ferreira et al. [67] | West Africa | CC = 0.88 | CC = 0.91 |
| Sun et al. [68] | India | CC = 0.94; NSE = 0.87 | CC = 0.84; NSE = 0.71 |
| Li et al. [53] | China | CC = 0.34–0.98; NSE = −0.21–0.95 | CC = 0.44–0.95; NSE = 0.76–0.98 |
| Jing et al. [69] | Nile River Basin | CC = ~0.9 | CC = 0.91 |
| Kenea et al. [31] | Ethiopia | R2 = 0.33–0.73; CC = 0.27–0.77 | NSE = 0.1–0.93; CC = 0.38–0.97 |
| Li et al. [32] | Global | Grid CC = 0.63; Basin CC = 0.6 | Grid CC = 0.8; Basin CC = 0.89 |
| Forootan et al. [48] | Global | CC = 0.89 (p = 0.00105) | CC = 0.8; p < 0.00001 |
| Sun et al. [71] | Global | Basin NSE = 0.7; CC = 0.9; 58% of grids @ NSE > 0.4 | Basin NSE = 0.78; CC = 0.89; 87% of grids @ NSE > 0.4 |
| Sun et al. [42] | United States | CC = 0.95; NSE = 0.85 | CC = 0.82; NSE = 0.67 |
| Jing et al. [73] | Pearl River Basin | R2 = 0.56–0.71 | NSE = 0.81 |
| Sohoulande et al. [72] | United States | 41.2% of area @ R2 > 0.5 | 82.1% of area @ NSE > 0.5 |
| Jeon et al. [74] | Global | NSE = 0.14–0.9 | NSE = 0.35–0.9 |
| Yu et al. [75] | Canada | CC = 0.96 | CC = 0.8 |
| Tang et al. [76] | Lancang-Mekong River basin | Basin CC = 0.97; Grid CC = 0.9 | Basin CC = 0.98; Grid CC = 0.89 |
| Yang et al. [77] | Australia | NSE = 0.96, CC = 0.98 | NSE = 0.66; CC = 0.81 |
| Gyawali et al. [20] | Texas Gulf Coast | CC = 0.85, NSE = 0.73 | CC = 0.83; NSE = 0.67 |
| Mo et al. [78] | Global | 40 basins NSE = 0.44–0.96 | 62 basins NSE = 0.44–0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gyawali, B.; Ahmed, M.; Murgulet, D.; Wiese, D.N. Filling Temporal Gaps within and between GRACE and GRACE-FO Terrestrial Water Storage Records: An Innovative Approach. Remote Sens. 2022, 14, 1565. https://doi.org/10.3390/rs14071565
Gyawali B, Ahmed M, Murgulet D, Wiese DN. Filling Temporal Gaps within and between GRACE and GRACE-FO Terrestrial Water Storage Records: An Innovative Approach. Remote Sensing. 2022; 14(7):1565. https://doi.org/10.3390/rs14071565
Chicago/Turabian StyleGyawali, Bimal, Mohamed Ahmed, Dorina Murgulet, and David N. Wiese. 2022. "Filling Temporal Gaps within and between GRACE and GRACE-FO Terrestrial Water Storage Records: An Innovative Approach" Remote Sensing 14, no. 7: 1565. https://doi.org/10.3390/rs14071565
APA StyleGyawali, B., Ahmed, M., Murgulet, D., & Wiese, D. N. (2022). Filling Temporal Gaps within and between GRACE and GRACE-FO Terrestrial Water Storage Records: An Innovative Approach. Remote Sensing, 14(7), 1565. https://doi.org/10.3390/rs14071565








