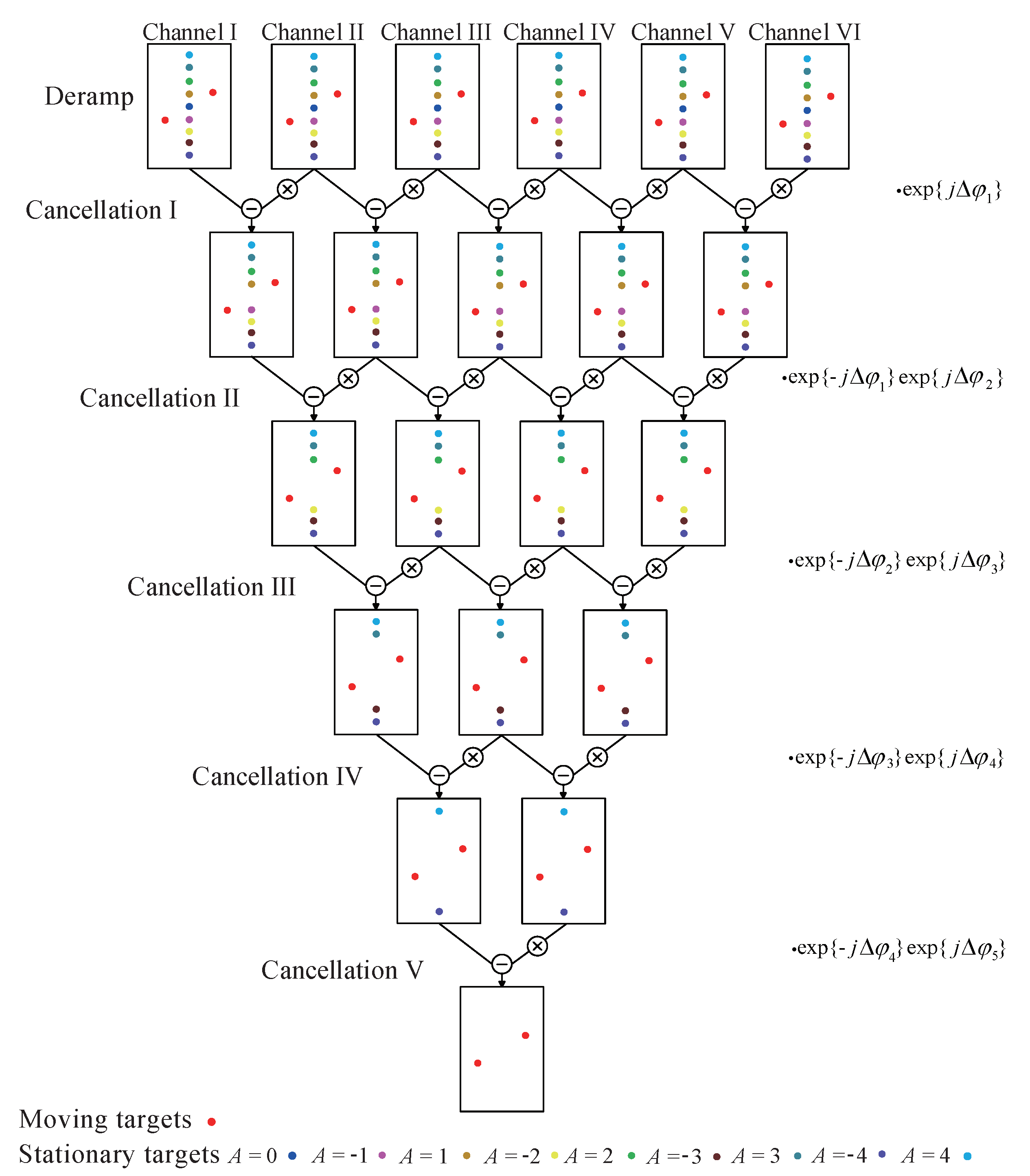
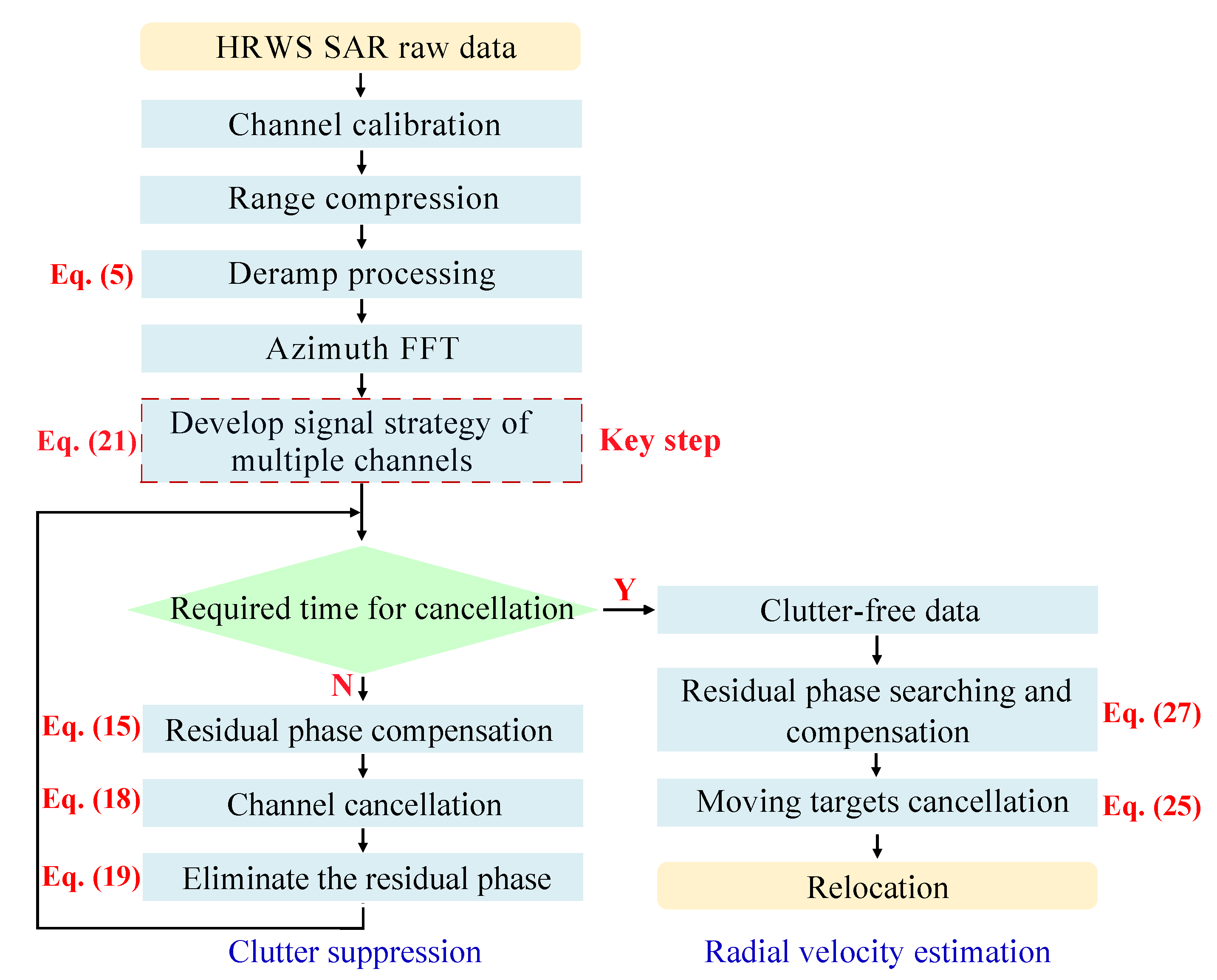
3.2. Multilayer Channel-Cancellation
It is well known that the DPCA algorithm applied into dual-channel SAR-GMTI is very efficient, using the cancellation operation of two spatially co-registered channels to achieve the clutter suppression [
27,
28]. However, the application of channel cancellation in multichannel deramped signals faces several essential issues, which are conducted in this section by thorough analyses and derivations.
In order to achieve clutter cancellation after the deramp processing, the spatial channel co-registration requires further compensation. The signal of a stationary target in the
nth channel is utilized to analyze the phase compensation after the deramp processing, which is expressed as
where
From
, the azimuth envelope of a stationary target between channels is aligned. The last exponential term in Equation (
7) is the difference between channels, which should be correctly compensated to achieve the spatial channel co-registration, and the term is defined as the residual phase in this paper. The actual antenna spacing
can be easily obtained from the SAR system. In addition, we can see that the zero Doppler time
of the specific target is related to the deramped frequency where the monochromatic signal is focused, which is shown in
Figure 2c. The deramped frequency of a stationary target is defined as
. Therefore, the
can be acquired by
where
represents the azimuth frequency rate of stationary targets. Then, the residual phase of the specific target in the
nth channel can be expressed as
The signal after the residual phase compensation is expressed as
From Equation (
10), it is clear that the residual phase between the
nth channel and
mth channel is compensated, and the spatial co-registration is achieved. Therefore, the clutter can be suppressed by the channel cancellation in the deramped frequency domain. However, the deramped frequency of a moving target is affected by its zero Doppler time and radial velocity from Equation (
6), which can be expressed as
where
represents the azimuth frequency rate of the moving target. Then, the zero Doppler time of the moving target is obtained as
, and the signal after the residual phase compensation can be expressed as
From Equation (
12), the last exponential term related to the channel spacing cannot be removed, so the moving target will be retained in the final result after the cancellation. Based on the above analyses, the basic conclusion we can draw is that clutter suppression can be achieved by the channel cancellation in the deramped frequency domain for HRWS SAR-GMTI. Nevertheless, the channel cancellation with deramp processing is not ideal, as discussed in the aforementioned content, and it cannot be directly applied into multichannel HRWS SAR-GMTI. The crucial issue is aliasing effects caused by the deramp processing and the low PRF, and it will be more serious in HRWS SAR than that in usual stripmap SAR. In this part, we analyse the aliasing effects in detail and give an innovative solution to address this serious issue.
From Equations (
6) and (
7), one can conclude that the absolute deramped frequency of a target is determined by its zero Doppler time, which is proportional to the distance from the azimuth center. Therefore, the deramped frequency of some targets in a whole synthetic aperture time will be beyond the PRF limits, which is illustrated by
Figure 3.
Figure 3a describes the frequency and time characteristics of multiple stationary targets in a synthetic aperture time in multichannel HRWS SAR. The deramp function is shown in
Figure 3b, and the compression result after the deramping is shown in
Figure 3c. The deramp function multiplication moves the deramped frequency of some targets beyond the PRF limits (the dashed lines), resulting in serious aliasing, and the solid lines are the monochromatic signals with aliased deramped frequency. The subaperture technique [
40,
41,
42] cannot address this issue.
Consequently, the deramped frequency that we can observe and obtain is the
fractional PRF part of the deramped frequency. We use a prime to distinguish it from the absolute deramped frequency, namely
, and the aliasing number is unknown, which is shown in
Figure 3. Then, the residual phase compensation which is dependent on
cannot be implemented correctly, resulting in failure of the spatial co-registration and channel cancellation.
Moreover, the PRF of a multichannel HRWS SAR system is much lower than the Doppler bandwidth, so the aliasing effects are much more serious than that in the stripmap SAR. After the deramping, targets that in the edges of the observed scene will be aliased for multiple times in the azimuth-frequency domain, which is illustrated in
Figure 3c, i.e.,
where
is defined as the aliasing coefficient, which can be positive or negative, and
is the floor function.
is baseband zero Doppler time of the target, which is obtained by
.
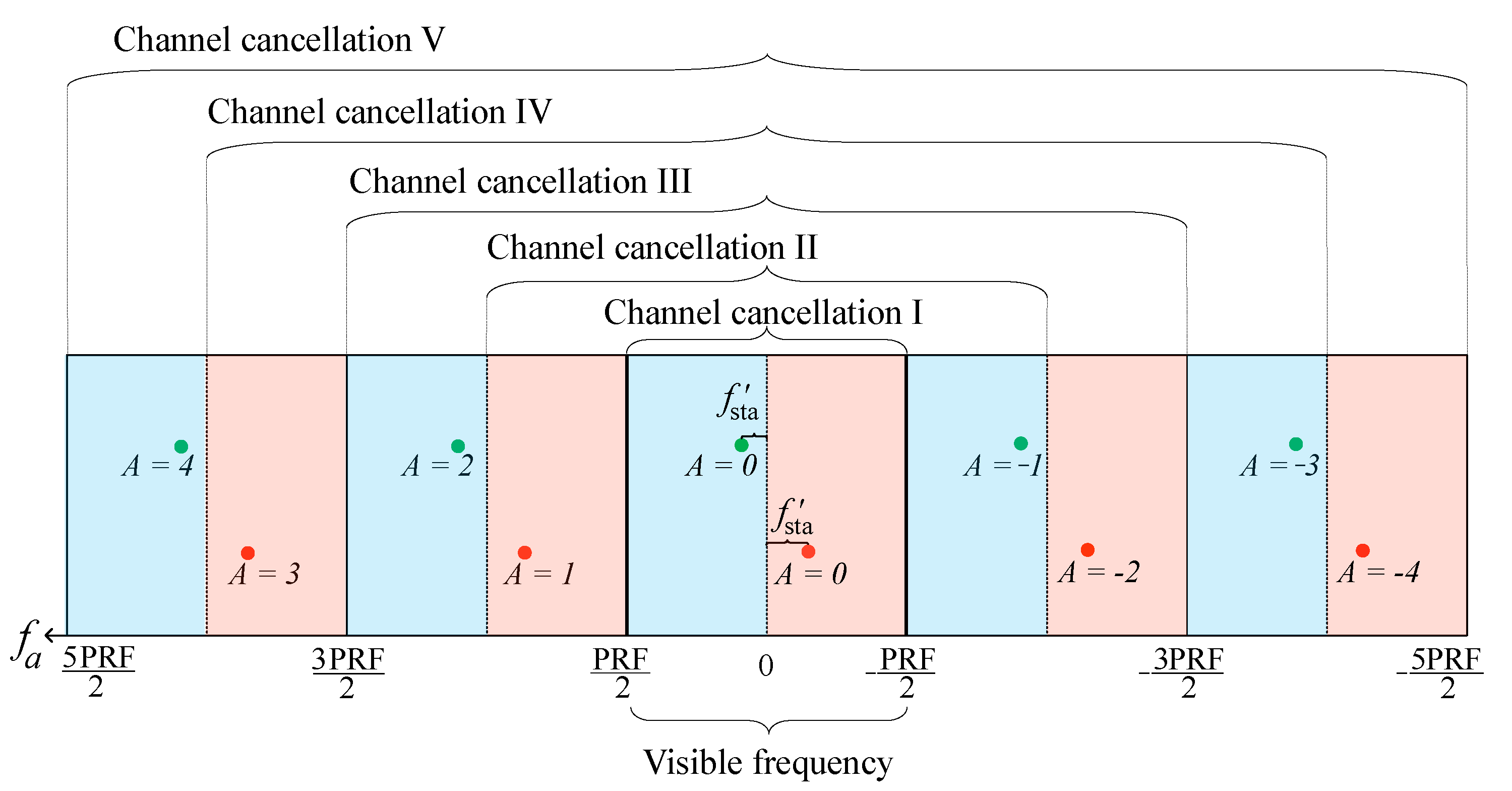
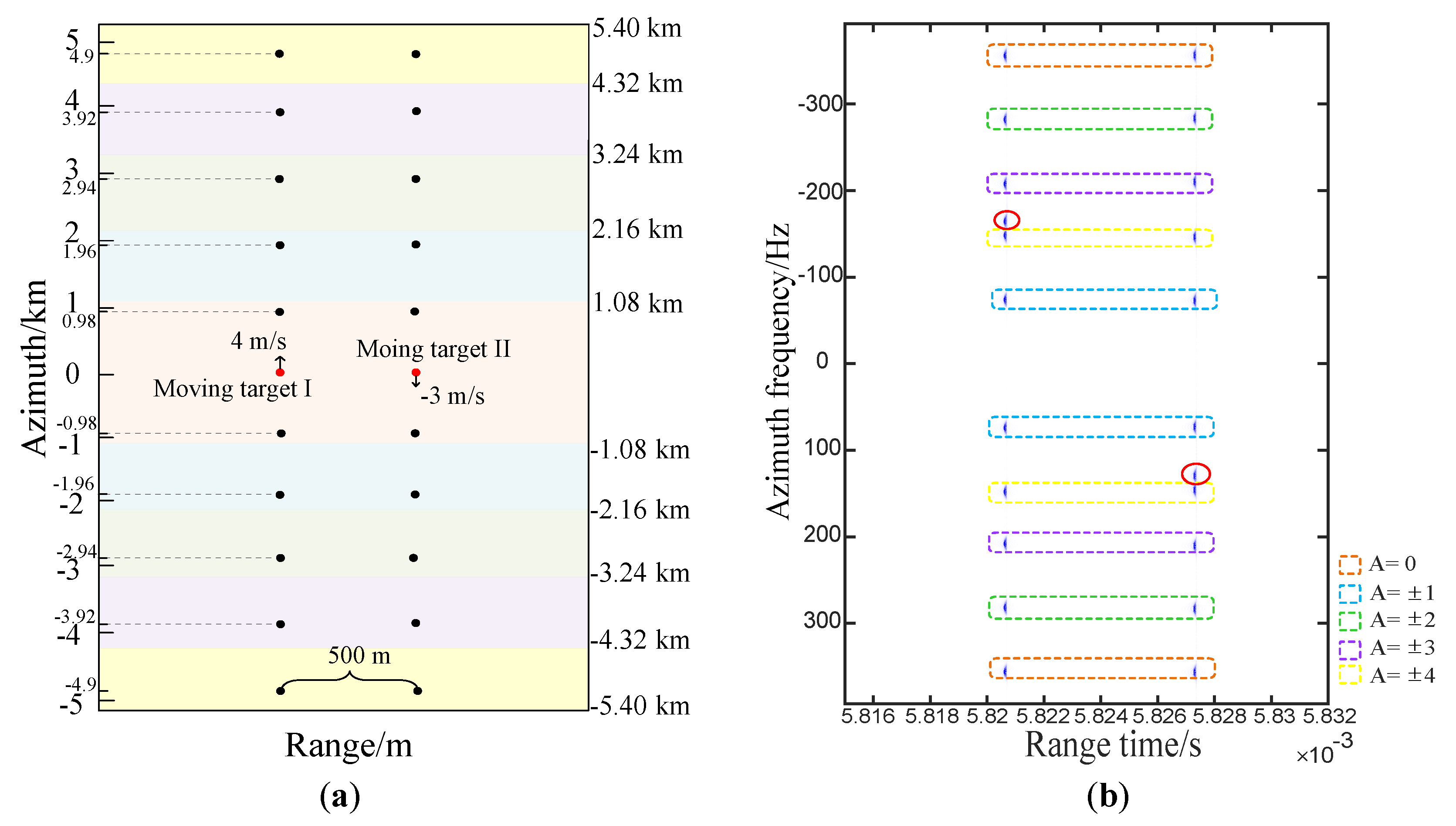
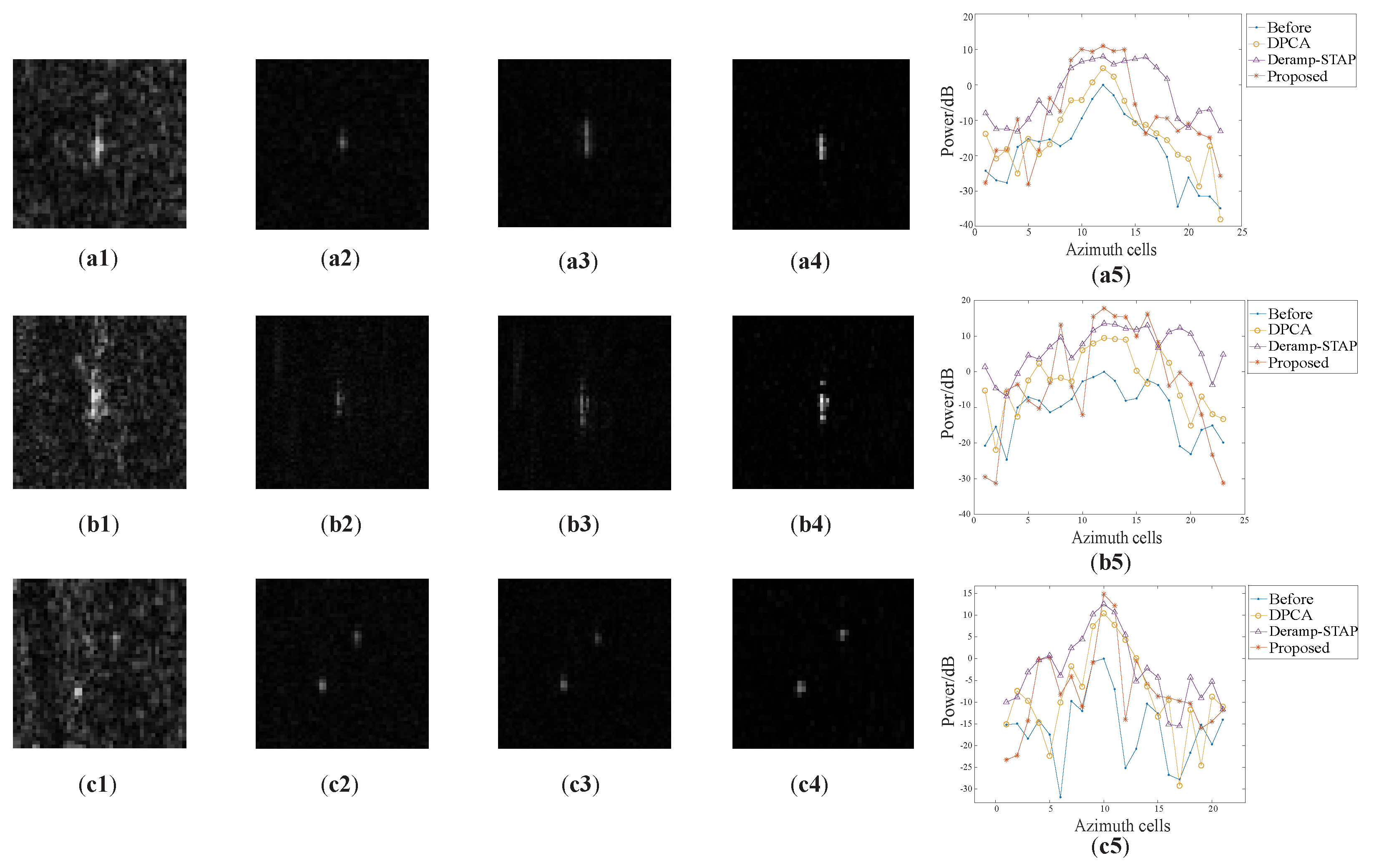
Figure 4 shows the aliasing effects after the deramp processing with 10 stationary targets in an
N-channel HRWS SAR system (
), and the PRF is about one-fifth of the Doppler bandwidth. We can see that the largest aliasing coefficient is 4. all the targets (green points) are focused in the same azimuth cell in the visible frequency domain, and so are the red targets. The targets with the aliasing coefficient
are aliased for four times, and the fifth layer of the channel cancellation is needed to suppress them. With the non-aliased targets, the required layer of the channel cancellation is equal to the Doppler ambiguity.
However, the deramped frequency of a target that we can obtain directly after the deramping is always
, which is shown in
Figure 3c, and the baseband zero Doppler time can be obtained by
The residual phase compensation for the first layer of channel cancellation is defined as
The residual phase of the targets, which is not aliased (
clutter) can be correctly compensated, and it can be suppressed by the first layer of channel cancellation.
is free by the
clutter, but the other aliased targets are still retained. Then, the data without
clutter of multiple channels is performed the second layer of channel cancellation to suppress the stationary targets with the aliasing of
in
(the blue area) and with the aliasing of
in
(the red area), which is shown in
Figure 4. Two key points need to be considered carefully for the implementation of the second layer of channel cancellation, which is elaborated as follows:
First, clutter with aliasing coefficients (different signs and same modulus) must be processed separately. The absolute deramped frequency for the second layer residual phase compensation can be obtained by
, which can be found in
Figure 3c.
The absolute zero Doppler time of the aliased clutter with
in
Figure 4 (the red area in the range of channel cancellation II) can be obtained as
where
is the illumination time. The absolute zero Doppler time of aliased clutter with
in
Figure 4 (the blue area in the range of channel cancellation II) is
. Then, the absolute zero Doppler time of the second layer of channel cancellation is
. Then, the residual phase for the second layer of channel cancellation is
Second, the previous residual phase compensation will affect the subsequent cancellation, so the elimination of must be carried out on the data, which is processed by the first channel cancellation, before the second layer of channel cancellation. Consequently, the second layer of residual phase is .
The signal of the first layer of cancellation between the
nth channel and
mth channel is assumed to be
, which is derived as
The clutter with
cannot be suppressed by channel cancellation due to the obtained zero Doppler time. The second phase term is
, and the signal after the second residual phase compensation can be obtained as
Assume that the other signals after the first layer of channel cancellation are obtained by the
mth and
kth channel. The signal after the second layer of residual phase compensation with
is obtained as
We can see that the difference between the signals with the second layer of residual phase compensation in Equations (
19) and (
20) is the last exponential term. To achieve the second layer of channel cancellation between
and
, the condition can be described as
Equation (
21) is the
signal usage strategy of multiple channels that must be satisfied before the implementation of multilayer channel-cancellation. The time interval between multilayer cancellation is a constant to obtain
The stationary targets with
in
and
in
can be suppressed by the second layer of channel cancellation. Now,
is free by the
,
clutter. The third layer of residual phase compensation is described as
. Keeping to the signal usage strategy of multiple channels according to Equation (
21), the clutter with
can be effectively suppressed. Five layers of channel cancellation are required to suppress all the aliased and non-aliased clutter in the HRWS SAR system, and the clutter-free frequency range is [−5PRF/2, 5PRF/2].