Modelling Within-Season Variation in Light Use Efficiency Enhances Productivity Estimates for Cropland
Abstract
:1. Introduction
2. Materials and Methods
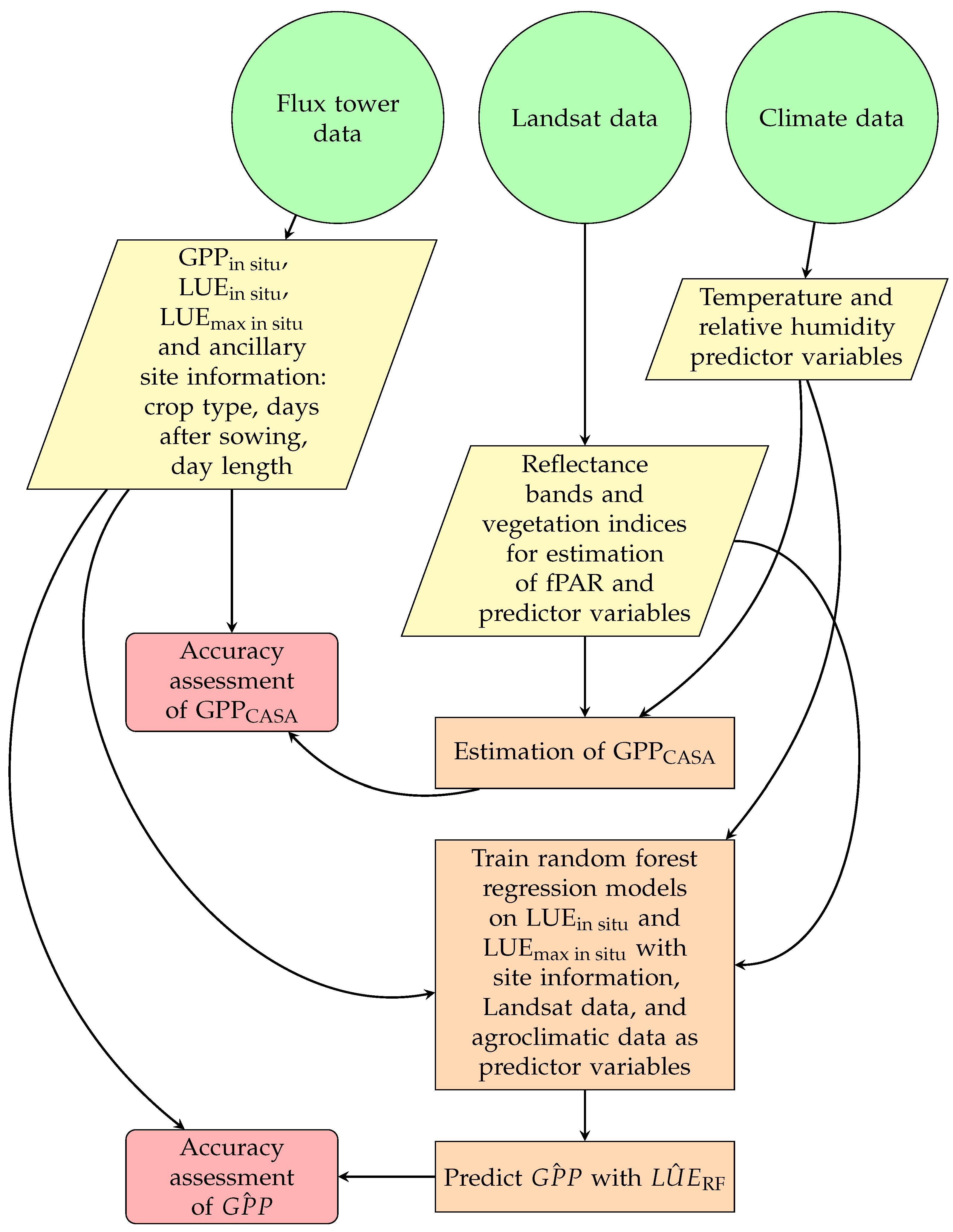
2.1. Overview of Methodology
2.2. Flux Tower Data
2.3. Satellite and Climate Data
2.4. Remote Sensing Estimation of Gross Primary Productivity and Light Use Effiency
2.4.1. Analysis Boundary
2.4.2. Remotely Sensed Gross Primary Productivity
2.4.3. Calculation of Light Use Efficiency and Stress Scalars
2.5. Modelling Light Use Efficiency
2.5.1. Predictor Variables
2.5.2. Random Forest for Light Use Efficiency
3. Results
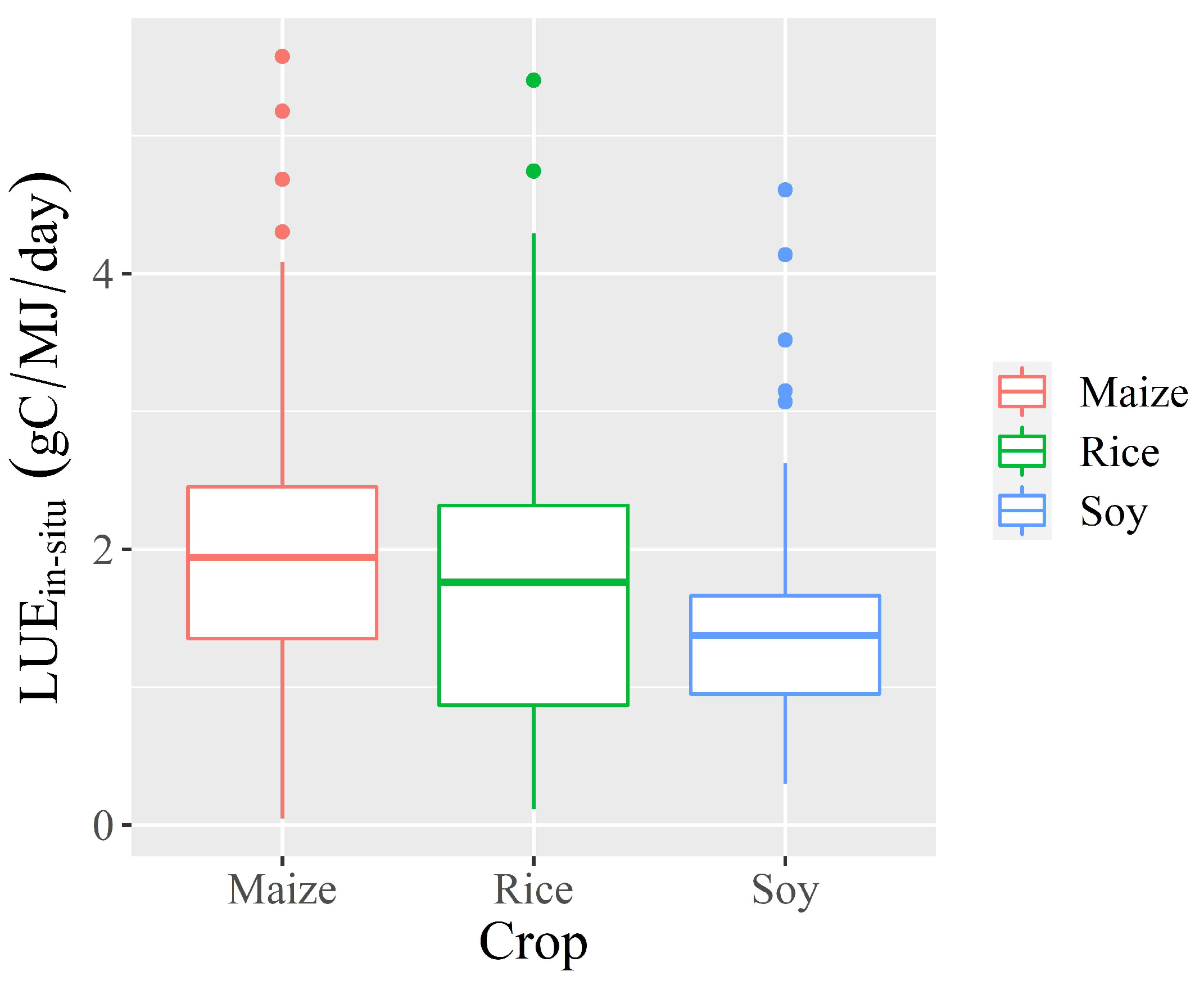
3.1. In Situ Light Use Efficiency
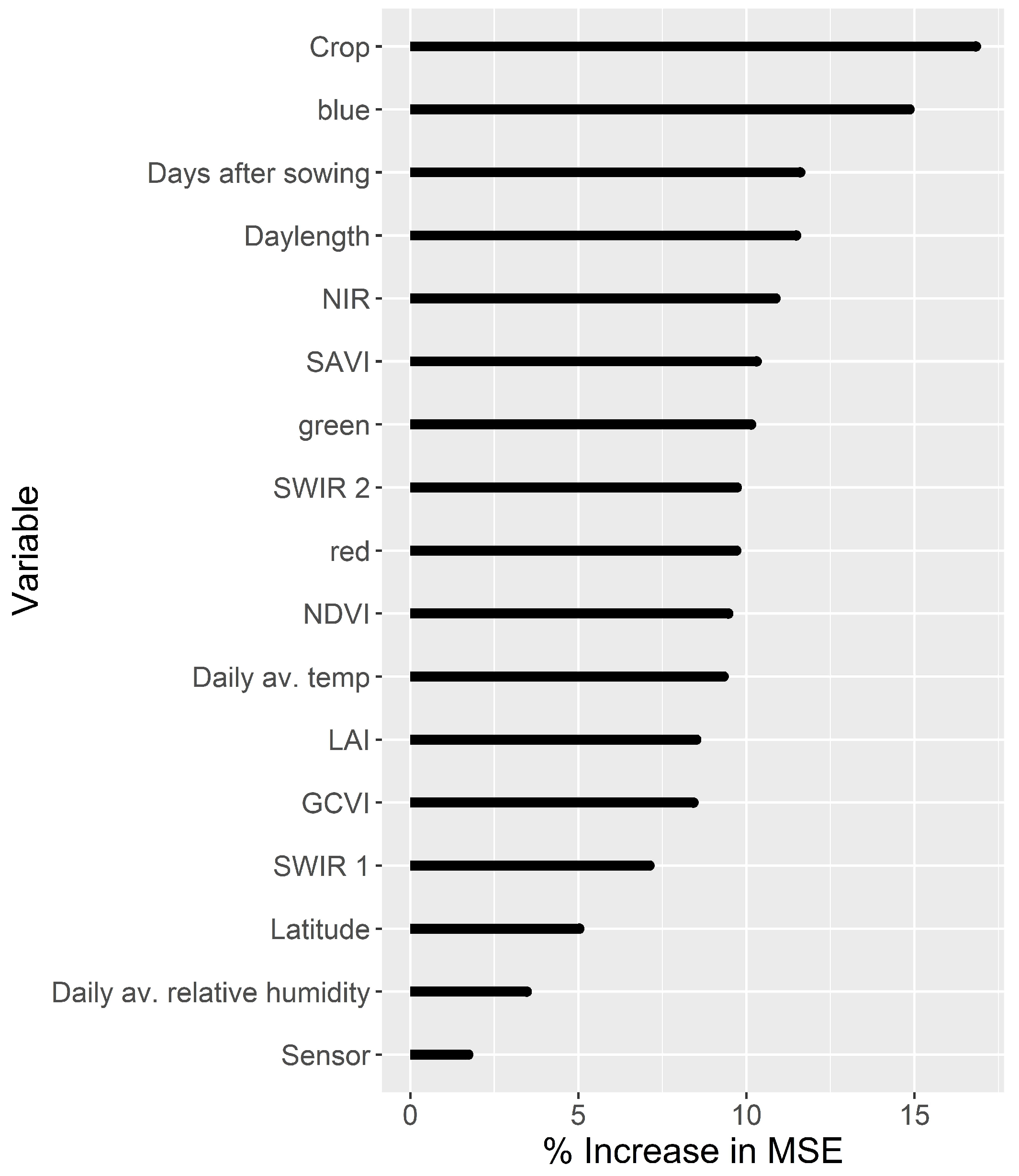
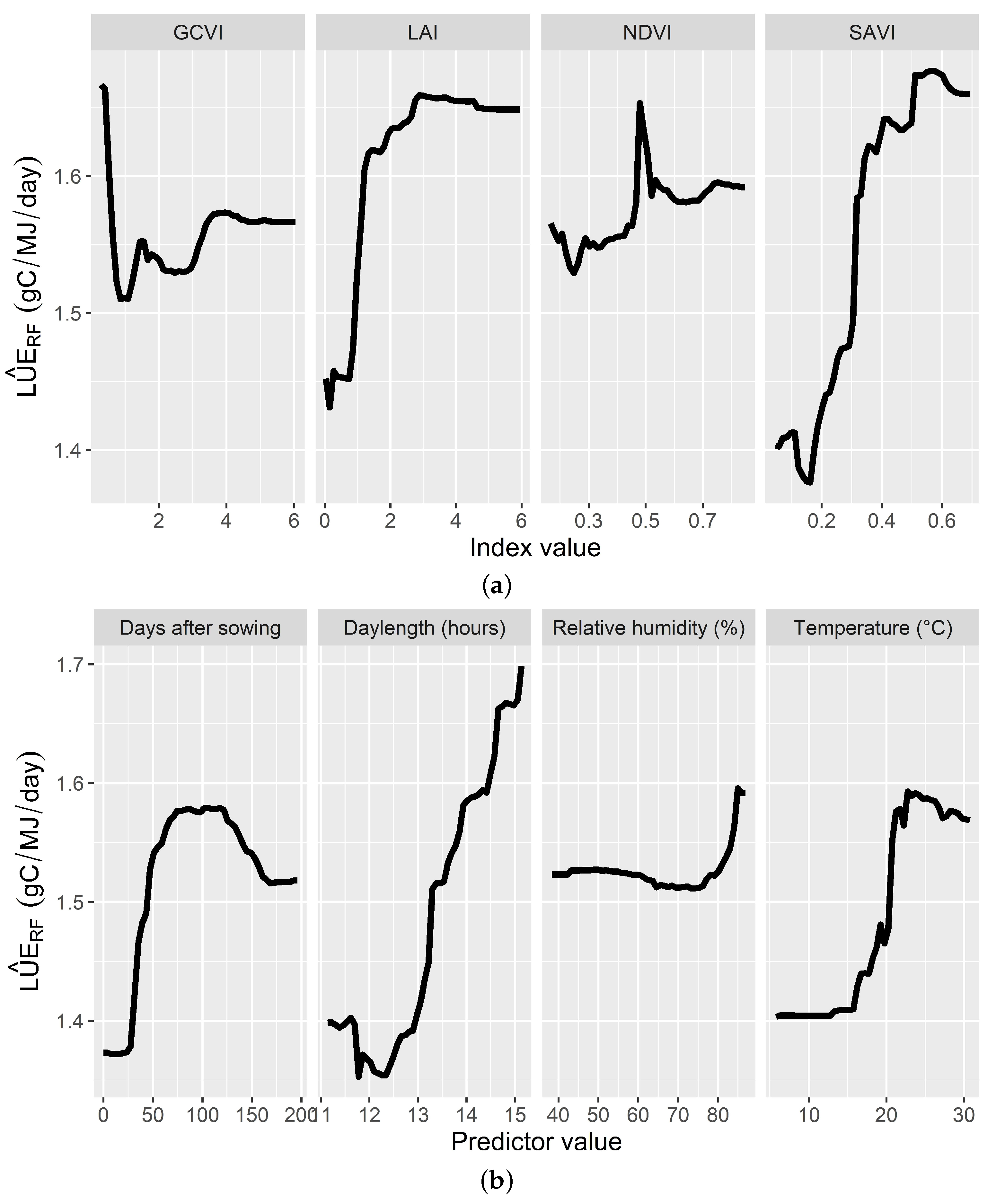
3.2. Prediction of Light Use Efficiency
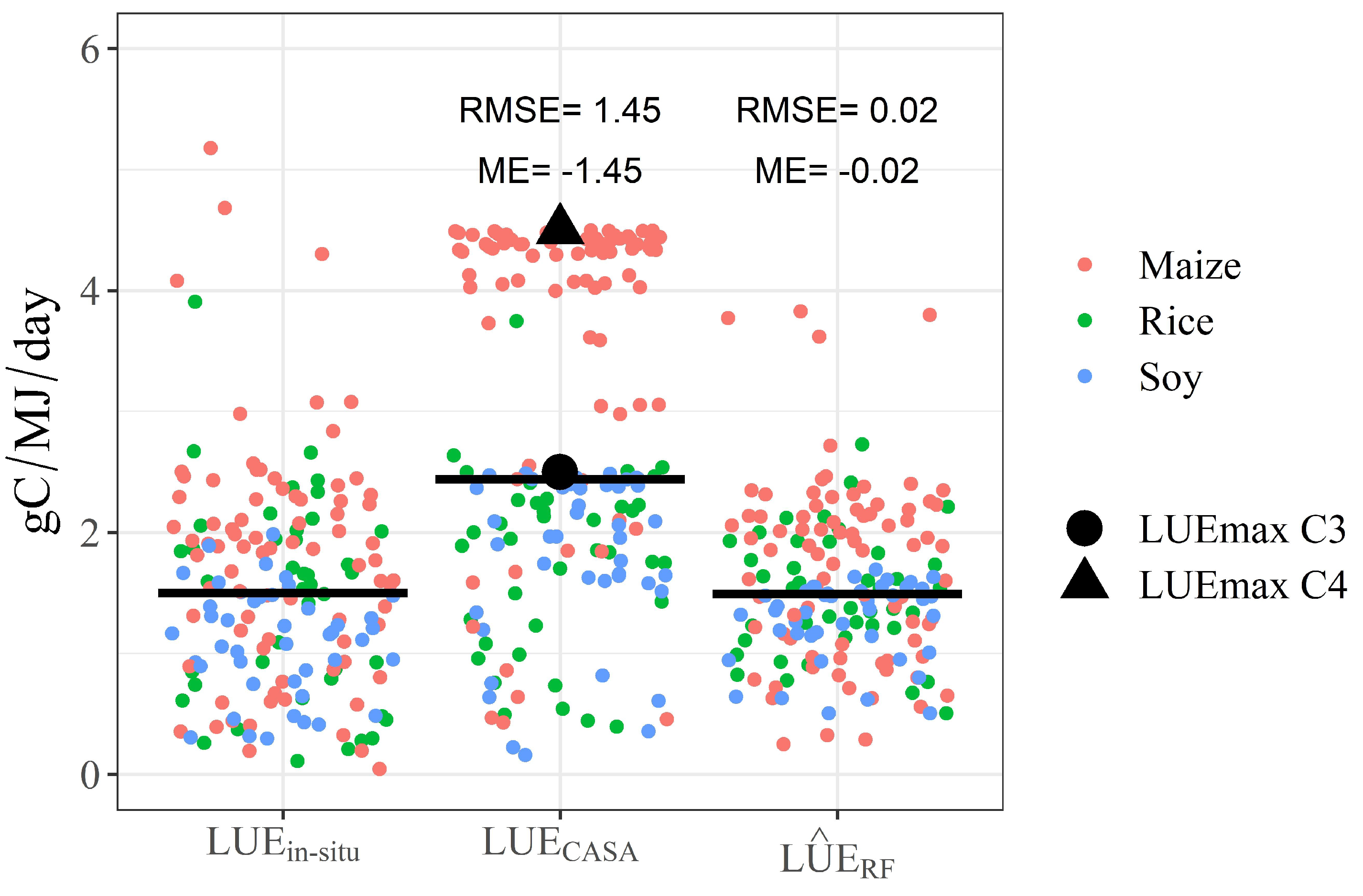
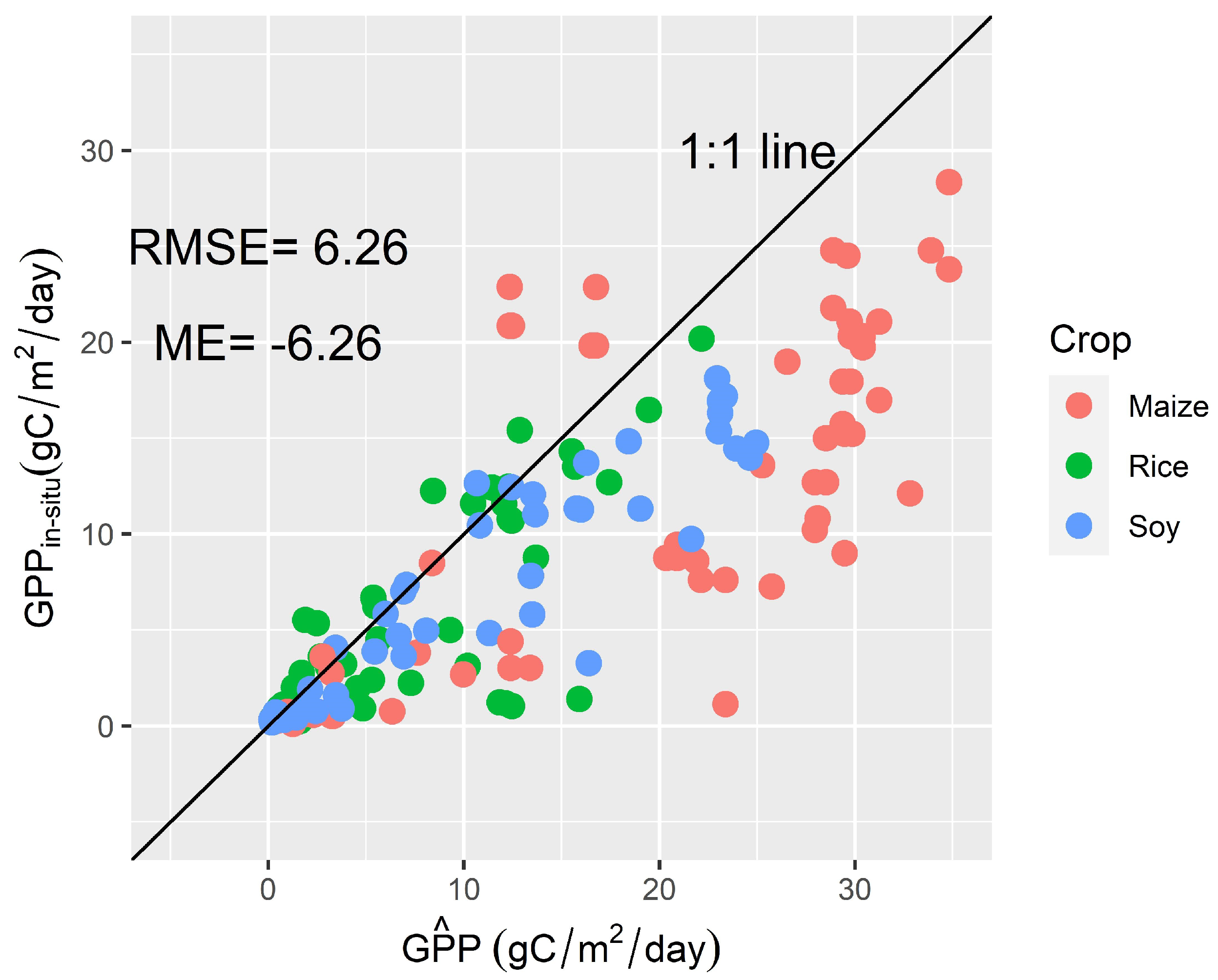
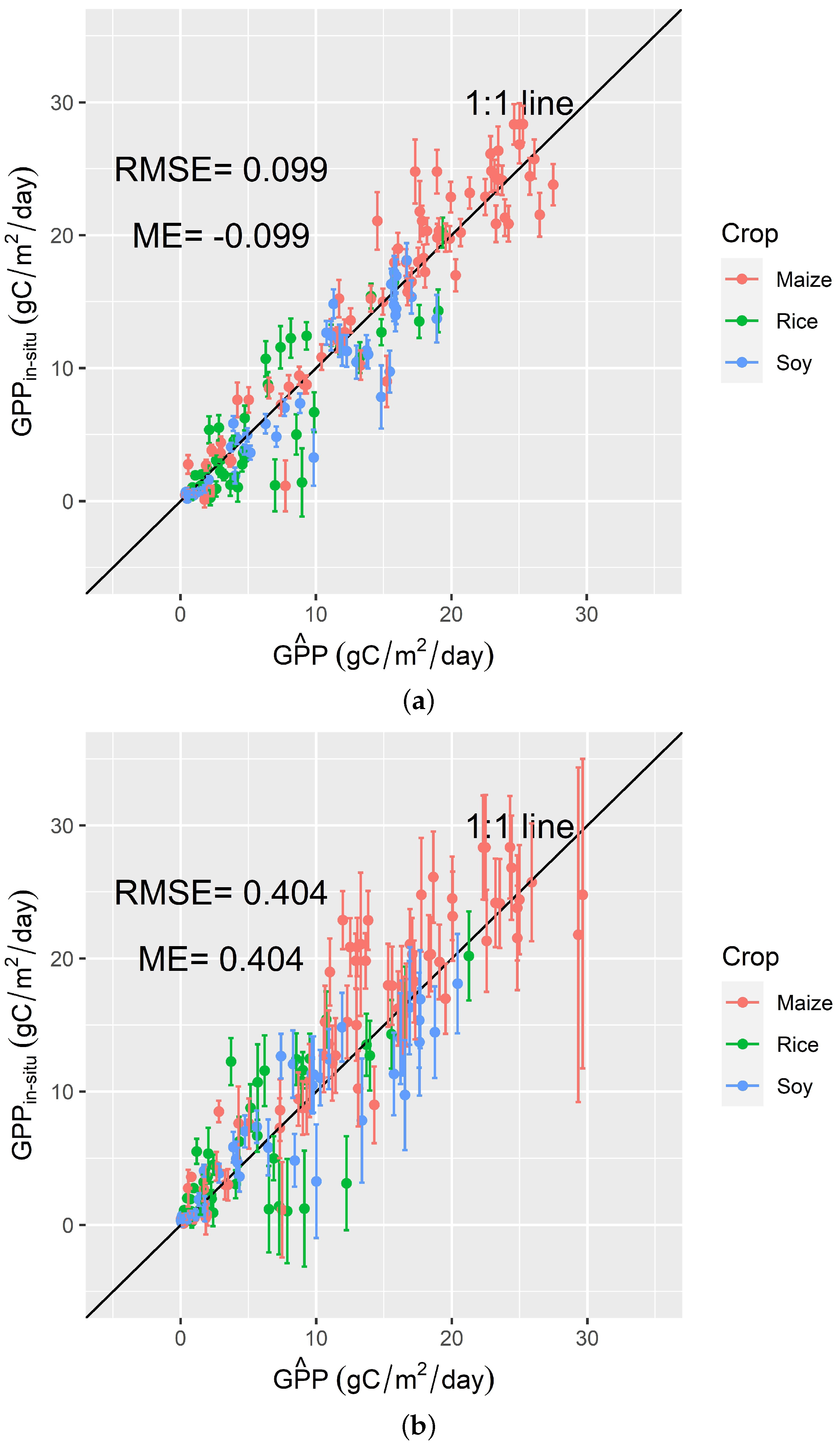
3.3. Estimation of Gross Primary Productivity
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GPP | Gross Primary Productivity |
| GPPin situ | In Situ Gross Primary Productivity |
| Predicted Gross Primary Productivity | |
| NPP | Net Primary Productivity |
| CASA | Carnegie–Ames–Stanford Approach |
| LUE | Light Use Efficiency |
| LUEin situ | In Situ Light Use Efficiency |
| LUECASA | Light Use Efficiency reduced from LUEmax Using CASA Stress Scalars |
| LUEmax | Maximum Light Use Efficiency |
| LUEmax in situ | In Situ Maximum Light Use Efficiency |
| Predicted Light Use Efficiency from Random Forest | |
| fPAR | Fraction of Absorbed Photosynthetically Active Radiation |
| PAR | Photosynthetically Active Radiation |
| DAS | Days after Sowing |
| SMS | Soil Moisture Stress |
| VS | Vapor Stress |
| TS | Temperature Stress |
| NDVI | Normalized Difference Vegetation Index |
| SAVI | Soil-Adjusted Vegetation Index |
| LAI | Leaf Area Index |
| GCVI | Green Chlorophyll Vegetation Index |
References
- Jaafar, H.; Mourad, R. GYMEE: A Global Field-Scale Crop Yield and ET Mapper in Google Earth Engine Based on Landsat, Weather, and Soil Data. Remote Sens. 2021, 13, 773. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Chen, T.; van der Werf, G.R.; Gobron, N.; Moors, E.J.; Dolman, A.J. Global cropland monthly gross primary production in the year 2000. Biogeosciences 2014, 11, 3871–3880. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Ma, Y.; Zhang, D.; Li, Z.; Zhang, W.; Wu, Z.; Wang, H.; Wen, L. High-Resolution Monitoring and Assessment of Evapotranspiration and Gross Primary Production Using Remote Sensing in a Typical Arid Region. Land 2021, 10, 396. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar Radiation and Productivity in Tropical Ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J.L.; Moss, C.J.; Cooke, G.W.; Pirie, N.W.; Bell, G.D.H. Climate and the efficiency of crop production in Britain. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Chen, T.; van der Werf, G.R.; Dolman, A.J.; Groenendijk, M. Evaluation of cropland maximum light use efficiency using eddy flux measurements in North America and Europe. Geophys. Res. Lett. 2011, 38, L14707. [Google Scholar] [CrossRef] [Green Version]
- Lobell, D.B.; Hicke, J.A.; Asner, G.P.; Field, C.B.; Tucker, C.J.; Los, S.O. Satellite estimates of productivity and light use efficiency in United States agriculture, 1982–1998. Glob. Chang. Biol. 2002, 8, 722–735. [Google Scholar] [CrossRef]
- Wang, H.; Jia, G.; Fu, C.; Feng, J.; Zhao, T.; Ma, Z. Deriving maximal light use efficiency from coordinated flux measurements and satellite data for regional gross primary production modeling. Remote Sens. Environ. 2010, 114, 2248–2258. [Google Scholar] [CrossRef]
- Wang, M.; Sun, R.; Zhu, A.; Xiao, Z. Evaluation and Comparison of Light Use Efficiency and Gross Primary Productivity Using Three Different Approaches. Remote Sens. 2020, 12, 1003. [Google Scholar] [CrossRef] [Green Version]
- Mul, M.; Karimi, P.; Coerver, H.; Pareeth, S.; Rebelo, L. Water Productivity and Water Accounting Methodology Manual; Report; IHE Delft Institute for Water Education, International Water Management Institute: Delft, The Netherlands, 2020. [Google Scholar]
- Pareeth, S. PySEBAL Documentation; IHE Delft Institute for Water Education: Delft, The Netherlands, 2020; Available online: https://pysebal-doc.readthedocs.io/en/version3.7.3/ (accessed on 20 January 2022).
- Teixeira, A.H.d.C.; Bastiaanssen, W.G.M.; Ahmad, M.D.; Bos, M.G. Reviewing SEBAL input parameters for assessing evapotranspiration and water productivity for the Low-Middle São Francisco River Basin, Brazil: Part B: Application to the regional scale. Agric. For. Meteorol. 2009, 149, 477–490. [Google Scholar] [CrossRef] [Green Version]
- Donohue, R.J.; Hume, I.H.; Roderick, M.L.; McVicar, T.R.; Beringer, J.; Hutley, L.B.; Gallant, J.C.; Austin, J.M.; van Gorsel, E.; Cleverly, J.R.; et al. Evaluation of the remote-sensing-based DIFFUSE model for estimating photosynthesis of vegetation. Remote Sens. Environ. 2014, 155, 349–365. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gamon, J.A. The need for a common basis for defining light-use efficiency: Implications for productivity estimation. Remote Sens. Environ. 2015, 156, 196–201. [Google Scholar] [CrossRef] [Green Version]
- Gitelson, A.A.; Peng, Y.; Arkebauer, T.J.; Suyker, A.E. Productivity, absorbed photosynthetically active radiation, and light use efficiency in crops: Implications for remote sensing of crop primary production. J. Plant Physiol. 2015, 177, 100–109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef] [Green Version]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Gamon, J.A.; Serrano, L.; Surfus, J.S. The photochemical reflectance index: An optical indicator of photosynthetic radiation use efficiency across species, functional types, and nutrient levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef] [PubMed]
- Penuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar] [CrossRef]
- Burke, M.; Lobell, D.B. Satellite-based assessment of yield variation and its determinants in smallholder African systems. Proc. Natl. Acad. Sci. USA 2017, 114, 2189–2194. [Google Scholar] [CrossRef] [Green Version]
- Dong, T.; Liu, J.; Qian, B.; Jing, Q.; Croft, H.; Chen, J.; Wang, J.; Huffman, T.; Shang, J.; Chen, P. Deriving Maximum Light Use Efficiency From Crop Growth Model and Satellite Data to Improve Crop Biomass Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 104–117. [Google Scholar] [CrossRef]
- Pareeth, S. PySEBAL Script; IHE Delft Institute for Water Education: Delft, The Netherlands, 2020; Available online: https://github.com/spareeth/PySEBAL_dev (accessed on 20 January 2022).
- Xin, Q.; Broich, M.; Suyker, A.E.; Yu, L.; Gong, P. Multi-scale evaluation of light use efficiency in MODIS gross primary productivity for croplands in the Midwestern United States. Agric. For. Meteorol. 2015, 201, 111–119. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.B.; Zhang, Q.; Lyapustin, A.I.; Wang, Y.; Middleton, E.M. Impacts of light use efficiency and fPAR parameterization on gross primary production modeling. Agric. For. Meteorol. 2014, 189-190, 187–197. [Google Scholar] [CrossRef]
- Lecoeur, J.; Ney, B. Change with time in potential radiation-use efficiency in field pea. Eur. J. Agron. 2003, 19, 91–105. [Google Scholar] [CrossRef]
- Peng, Y.; Gitelson, A.A.; Keydan, G.; Rundquist, D.C.; Moses, W. Remote estimation of gross primary production in maize and support for a new paradigm based on total crop chlorophyll content. Remote Sens. Environ. 2011, 115, 978–989. [Google Scholar] [CrossRef]
- Peng, Y.; Gitelson, A.A. Application of chlorophyll-related vegetation indices for remote estimation of maize productivity. Agric. For. Meteorol. 2011, 151, 1267–1276. [Google Scholar] [CrossRef]
- Wei, S.; Yi, C.; Fang, W.; Hendrey, G. A global study of GPP focusing on light-use efficiency in a random forest regression model. Ecosphere 2017, 8, e01724. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Ryu, Y.; Kang, M.; Kim, J. FLUXNET-CH4 KR-CRK Cheorwon Rice Paddy 2015–2018; Seoul National University: Seoul, Korea, 2018. [Google Scholar] [CrossRef]
- Alberto, M.; Wassmann, R. FLUXNET-CH4 PH-RiF Philippines Rice Institute Flooded; International Rice Research Institute: Manila, Philippines, 2014. [Google Scholar] [CrossRef]
- Reba, M.; Runkle, B.; Suvocarev, K. FLUXNET-CH4 US-HRC Humnoke Farm Rice Field—Field A; Delta Water Management Research: Jonesboro, AR, USA, 2017. [Google Scholar] [CrossRef]
- Reba, M.; Runkle, B.; Suvocarev, K. FLUXNET-CH4 US-HRC Humnoke Farm Rice Field—Field C; Delta Water Management Research: Jonesboro, AR, USA, 2017. [Google Scholar] [CrossRef]
- FLUXNET. FLUXNET2015 US-Ne1 Mead—Irrigated Continuous Maize Site; University of Nebraska: Lincoln, NE, USA, 2013. [Google Scholar] [CrossRef]
- FLUXNET. FLUXNET 2015 US-Ne2 Mead—Irrigated Maize-Soybean Rotation Site; University of Nebraska: Lincoln, NE, USA, 2013. [Google Scholar] [CrossRef]
- FLUXNET. FLUXNET 2015 US-Ne3 Mead—Rainfed Maize-Soybean Rotation Site; University of Nebraska: Lincoln, NE, USA, 2013. [Google Scholar] [CrossRef]
- Jaafar, H.H.; Ahmad, F.A. Time series trends of Landsat-based ET using automated calibration in METRIC and SEBAL: The Bekaa Valley, Lebanon. Remote Sens. Environ. 2020, 238, 111034. [Google Scholar] [CrossRef]
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling; Version 3.4-13; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- R Foundation for Statistical Computing. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Fang, H.; Beaudoing, H.K.; Rodell, M.; Teng, W.L.; Vollmer, B.E. Global Land data assimilation system (GLDAS) products, services and application from NASA hydrology data and information services center (HDISC). In Proceedings of the ASPRS 2009 Annual Conference, Baltimore, MD, USA, 9–13 March 2009; pp. 8–13. [Google Scholar]
- Farr, T.; Kobrick, M. Shuttle Radar Topography Mission produces a wealth of data. Eos Trans. Am. Geophys. Union 2000, 81, 583–585. [Google Scholar] [CrossRef]
- De Boer, F. HiHydroSoil: A High Resolution Soil Map of Hydraulic Properties; FutureWater: Wageningen, The Netherlands, 2016; Volume 20. [Google Scholar]
- Levitan, N.; Kang, Y.; Özdoğan, M.; Magliulo, V.; Castillo, P.; Moshary, F.; Gross, B. Evaluation of the Uncertainty in Satellite-Based Crop State Variable Retrievals Due to Site and Growth Stage Specific Factors and Their Potential in Coupling with Crop Growth Models. Remote Sens. 2019, 11, 1928. [Google Scholar] [CrossRef] [Green Version]
- Gitelson, A.A.; Peng, Y.; Arkebauer, T.J.; Schepers, J. Relationships between gross primary production, green LAI, and canopy chlorophyll content in maize: Implications for remote sensing of primary production. Remote Sens. Environ. 2014, 144, 65–72. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.J.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef] [Green Version]
- Chu, H.; Luo, X.; Ouyang, Z.; Chan, W.S.; Dengel, S.; Biraud, S.C.; Torn, M.S.; Metzger, S.; Kumar, J.; Arain, M.A.; et al. Representativeness of Eddy-Covariance flux footprints for areas surrounding AmeriFlux sites. Agric. For. Meteorol. 2021, 301–302, 108350. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Ali, S. A new crop yield forecasting model based on satellite measurements applied across the Indus Basin, Pakistan. Agric. Ecosyst. Environ. 2003, 94, 321–340. [Google Scholar] [CrossRef]
- Daughtry, C.; Gallo, K.; Goward, S.; Prince, S.; Kustas, W. Spectral estimates of absorbed radiation and phytomass production in corn and soybean canopies. Remote Sens. Environ. 1992, 39, 141–152. [Google Scholar] [CrossRef]
- Stewart, J. On the use of the Penrnan-Monteith equation for determining areal evapotranspiration. In Proceedings of the Estimation of Areal Evapotranspiration, Vancouver, BC, Canada, 9–22 August 1987; pp. 3–80. [Google Scholar]
- Stewart, J.B. Modelling surface conductance of pine forest. Agric. For. Meteorol. 1988, 43, 19–35. [Google Scholar] [CrossRef]
- Jarvis, P. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1976, 273, 593–610. [Google Scholar]
- Ritchie, J.T.; Nesmith, D.S. Temperature and crop development. Model. Plant Soil Syst. 1991, 31, 5–29. [Google Scholar]
- Maidment, D.R. Handbook of Hydrology; Number 631.587; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Oren, R.; Sperry, J.; Katul, G.; Pataki, D.; Ewers, B.; Phillips, N.; Schäfer, K. Survey and synthesis of intra-and interspecific variation in stomatal sensitivity to vapour pressure deficit. Plant Cell Environ. 1999, 22, 1515–1526. [Google Scholar] [CrossRef] [Green Version]
- Fuchs, M.; Stanghellini, C. The functional dependence of canopy conductance on water vapor pressure deficit revisited. Int. J. Biometeorol. 2018, 62, 1211–1220. [Google Scholar] [CrossRef]
- Boulet, G.; Delogu, E.; Saadi, S.; Chebbi, W.; Olioso, A.; Mougenot, B.; Fanise, P.; Lili-Chabaane, Z.; Lagouarde, J.P. Evapotranspiration and evaporation/transpiration partitioning with dual source energy balance models in agricultural lands. Proc. Int. Assoc. Hydrol. Sci. 2018, 380, 17–22. [Google Scholar] [CrossRef] [Green Version]
- USGS. What Are the Band Designations for the Landsat Satellites? Available online: https://www.usgs.gov/faqs/what-are-band-designations-landsat-satellites (accessed on 20 January 2022).
- Rouse, J.; Haas, R.; Deering, D.; Schell, J.A.; Harlan, J. Monitoring vegetation systems in the Great Plains with ERTS. ERTS 1973, 1, 309–317. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Hijmans, R.J. Geosphere: Spherical Trigonometry; Version 1.5-14; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Lee, C.; Herbek, J.; Murdock, L.; Schwab, G.; Green, J.; Martin, J.; Bessin, R.; Johnson, D.; Hershman, D.; Vincelli, P.; et al. Corn and Soybean Production Calendar; University of Kentucky Cooperative Extension Service: Lexington, KY, USA, 2007. [Google Scholar]
- FAO. GIEWS—Global Information and Early Warning System—Philippines. 2021. Available online: https://www.fao.org/giews/countrybrief/country.jsp?code=PHL&lang=en (accessed on 29 November 2021).
- FAO. GIEWS—Global Information and Early Warning System—Korea. 2021. Available online: https://www.fao.org/giews/countrybrief/country.jsp?code=KOR&lang=en (accessed on 29 November 2021).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Wager, S. randomForestCI: Confidence Intervals for Random Forests; Version 1.0.0; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Peng, Y.; Gitelson, A.A. Remote estimation of gross primary productivity in soybean and maize based on total crop chlorophyll content. Remote Sens. Environ. 2012, 117, 440–448. [Google Scholar] [CrossRef]
- Sinclair, T.; Muchow, R. Occam’s Razor, radiation-use efficiency, and vapor pressure deficit. Field Crops Res. 1999, 62, 239–243. [Google Scholar] [CrossRef]
- Sinclair, T.; Horie, T. Leaf nitrogen, photosynthesis, and crop radiation use efficiency: A review. Crop Sci. 1989, 29, 90–98. [Google Scholar] [CrossRef]
- Sinclair, T.; Pinter, P., Jr.; Kimball, B.; Adamsen, F.; LaMorte, R.; Wall, G.; Hunsaker, D.; Adam, N.; Brooks, T.; Garcia, R.; et al. Leaf nitrogen concentration of wheat subjected to elevated [CO2] and either water or N deficits. Agric. Ecosyst. Environ. 2000, 79, 53–60. [Google Scholar] [CrossRef]
- Fischer, R.; Howe, G.; Ibrahim, Z. Irrigated spring wheat and timing and amount of nitrogen fertilizer. I. Grain yield and protein content. Field Crops Res. 1993, 33, 37–56. [Google Scholar] [CrossRef]
- Evans, J.R. Nitrogen and photosynthesis in the flag leaf of wheat (Triticumaestivum L.). Plant Physiol. 1983, 72, 297–302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lindquist, J.L.; Arkebauer, T.J.; Walters, D.T.; Cassman, K.G.; Dobermann, A. Maize radiation use efficiency under optimal growth conditions. Agron. J. 2005, 97, 72–78. [Google Scholar] [CrossRef] [Green Version]
- Muchow, R.; Sinclair, T. Nitrogen response of leaf photosynthesis and canopy radiation use efficiency in field-grown maize and sorghum. Crop Sci. 1994, 34, 721–727. [Google Scholar] [CrossRef]
- Isaac, P.; Cleverly, J.; McHugh, I.; Gorsel, E.v.; Ewenz, C.; Beringer, J. OzFlux Data: Network integration from collection to curation. Biogeosciences 2017, 14, 2903–2928. [Google Scholar] [CrossRef] [Green Version]
- Beringer, J.; McHugh, I.; Hutley, L.B.; Isaac, P.; Kljun, N. Dynamic INtegrated Gap-filling and partitioning for OzFlux (DINGO). Biogeosciences 2017, 14, 1457–1460. [Google Scholar] [CrossRef] [Green Version]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies: A review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Barton, C.V.M.; North, P. Remote sensing of canopy light use efficiency using the photochemical reflectance index: Model and sensitivity analysis. Remote Sens. Environ. 2001, 78, 264–273. [Google Scholar] [CrossRef]

| Site Name | Site Code | Years Active | Crop Species | Observations |
|---|---|---|---|---|
| Cheorwon Rice paddy | KR-CRK [31] | 2015–2018 | Rice | 15 |
| Philippines Rice Institute flooded | PH-RiF [32] | 2012–2014 | Rice | 19 |
| Humnoke Farm Rice Field A | US-HRA [33] | 2017 | Rice | 4 |
| Humnoke Farm Rice Field C | US-HRC [34] | 2017 | Rice | 4 |
| Mead-irrigated continuous maize site | US-Ne1 [35] | 2001–2013 | Maize | 47 |
| Mead-irrigated maize–soybean rotation site | US-Ne2 [36] | 2001–2013 | Maize (odd years), soybean (even years) | 33 |
| Mead-rainfed maize–soybean rotation site | US-Ne3 [37] | 2001–2013 | Maize (odd years), soybean (even years) | 46 |
| Constant | Definition | Source |
|---|---|---|
| 0 C | [53,54] | |
| 23 C | [53,54] | |
| 35 C | [53,54] |
| Group | Variable | Definition | Source |
|---|---|---|---|
| Satellite bands | Blue | Landsat-7: 0.45–0.52 m Landsat-8 0.45–0.51 m | [58] |
| Green | Landsat-7: 0.52–0.60 m Landsat-8 0.53–0.59 m | [58] | |
| Red | Landsat-7: 0.63–0.69 m Landsat-8 0.64–0.67 m | [58] | |
| Near Infrared (NIR) | Landsat-7: 0.77–0.90m Landsat-8 0.85–0.88 m | [58] | |
| Shortwave Infrared 1 (SWIR 1) | Landsat-7: 1.55–1.75 m Landsat-8 1.57–1.65 m | [58] | |
| Shortwave Infrared 2 (SWIR 2) | Landsat-7: 2.09–2.35 m Landsat-8 2.11–2.29 m | [58] | |
| Vegetation indices | Normalised Difference Vegetation Index (NDVI) | [59] | |
| Green Chlorophyll Vegetation Index (GCVI) | [60] | ||
| Leaf Area Index (LAI) | From PySEBAL | [12,23] | |
| Soil-Adjusted Vegetation Index (SAVI) | [61] | ||
| Site and image information | Crop Type | Table 1 | |
| Sensor | Landsat-7 or Landsat-8 | ||
| Latitude | Table 1 [30] | ||
| Day length | Calculated on latitude and DOY using geosphere R package | [62] | |
| Agroclimatic variables | Daily Average Temperature | Section 2.3 | |
| Daily Average Relative Humidity | Section 2.3 | ||
| Days after Sowing (DAS) | Approximate sowing dates taken from regional crop calendars | [63,64,65] |
| Measure | Model 1: All Predictors in Table 3 | Model 2: No Crop Type Predictor | Model 3: All Predictors in Table 3, LUEmax as Response |
|---|---|---|---|
| R | 62.94% | 58.30% | 14.19% |
| Mean of squared residuals | 0.28 | 0.32 | 0.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wellington, M.J.; Kuhnert, P.; Renzullo, L.J.; Lawes, R. Modelling Within-Season Variation in Light Use Efficiency Enhances Productivity Estimates for Cropland. Remote Sens. 2022, 14, 1495. https://doi.org/10.3390/rs14061495
Wellington MJ, Kuhnert P, Renzullo LJ, Lawes R. Modelling Within-Season Variation in Light Use Efficiency Enhances Productivity Estimates for Cropland. Remote Sensing. 2022; 14(6):1495. https://doi.org/10.3390/rs14061495
Chicago/Turabian StyleWellington, Michael J., Petra Kuhnert, Luigi J. Renzullo, and Roger Lawes. 2022. "Modelling Within-Season Variation in Light Use Efficiency Enhances Productivity Estimates for Cropland" Remote Sensing 14, no. 6: 1495. https://doi.org/10.3390/rs14061495
APA StyleWellington, M. J., Kuhnert, P., Renzullo, L. J., & Lawes, R. (2022). Modelling Within-Season Variation in Light Use Efficiency Enhances Productivity Estimates for Cropland. Remote Sensing, 14(6), 1495. https://doi.org/10.3390/rs14061495






